HAPS-PPO: A Multi-Agent Reinforcement Learning Architecture for Coordinated Regional Control of Traffic Signals in Heterogeneous Road Networks
Abstract
1. Introduction
- Observation Space Heterogeneity: The physical topology of urban intersections varies greatly, including standard four-way crossroads, three-way T-junctions, and irregular intersections with asymmetric lane counts. Different intersections, or agents, may have access to different traffic information. In MARL, this is often linked to the “partial observability” problem [20], where agents possess distinct observation spaces due to their physical location, sensor configuration, or role. For instance, some may receive detailed vehicle position and speed data, while others only obtain macroscopic information like queue length or vehicle counts [21]. This structural variance results in local state information (e.g., lane occupancy, queue length) that is naturally inconsistent in dimension, leading to variable-length observation vectors.
- Action Space Heterogeneity: Corresponding to the observation space, the set of legal signal phases (actions) for different intersections also varies in size and composition due to their unique geometric and traffic regulations. Agents may execute various types or ranges of actions, resulting in heterogeneous action spaces. This discrepancy is fatal for parameter-sharing MARL algorithms that pursue high efficiency and scalability. A unified policy network designed for a complex intersection (e.g., four phases) will likely generate invalid actions beyond the legal range for a simpler intersection (e.g., three phases), severely hindering effective policy learning and leading to training collapse.
- Identified and formally defined the heterogeneity problem—the heterogeneity of observation and action spaces—that obstructs the application of MARL in real-world TSC, and clarified its fundamental constraints on existing mainstream algorithms, especially parameter-sharing ones.
- Proposed the HAPS-PPO framework to address the heterogeneity challenge systematically. The framework normalizes heterogeneous observations via an OPW and trains dedicated policies for agent groups with different action spaces through a DMSGL mechanism, achieving compatibility with heterogeneous agents within a unified training process.
- Conducted comprehensive empirical evaluations in a high-fidelity heterogeneous simulation environment based on a real-world road network. The results demonstrate that HAPS-PPO significantly outperforms Fixed-time control and various mainstream MARL baselines in improving traffic efficiency.
- Provided a systematic, scalable, plug-and-play solution paradigm for seamlessly migrating parameter-sharing MARL algorithms from idealized homogeneous environments to complex, real-world heterogeneous networks.
2. Related Work
2.1. Reinforcement Learning in Traffic Signal Control
2.1.1. Early Exploration Limitations of Single Agent to Independent Learner Approaches
2.1.2. Mainstream Paradigm CTDE
- Value Function Decomposition Methods: Algorithms like VDN [28] and QMIX [29] achieve coordination by decomposing a centralized global value function into the sum of individual agents’ local value functions. However, their strict constraints on value decomposition (e.g., monotonicity) may limit their expressive power in complex TSC scenarios with high conflict and nonlinear coordination.
- Actor-Critic Methods: Paradigms such as MADDPG [30] and MAPPO [31] maintain an independent policy network (Actor) for each agent while utilizing one or more centralized value networks (Critics) that have access to global information to guide the training of all Actors. The presence of the Critic allows each Actor to receive stable and information-rich gradient signals. Due to its excellent stability and performance, the multi-agent version of PPO, MAPPO, has become a robust baseline for cooperative MARL tasks.
2.1.3. Current Bottleneck: The Neglected Problem of Heterogeneity
3. Methodology: An Adaptive Traffic Signal Control Method for Heterogeneous Urban Road Networks
3.1. Problem Formulation: TSC as a Dec-POMDP
- 1.
- Set of Agents ():
- 2.
- Set of Agents ():
- 3.
- Set of Action Spaces ():
- 4.
- State Transition Function ():
- 5.
- Set of Reward Functions ():
- 6.
- Set of Observation Spaces ():
- 7.
- Joint Observation Function ():
- 8.
- Discount Factor ():
- 9.
- Initial State Distribution ():
3.2. HAPS-PPO Framework Design
3.2.1. Unified Observation Space Representation: Observation Padding Wrapper
- Max-Dimension Identification: During environment initialization, the system iterates through all potential agents and identifies the maximum observation vector dimension, denoted as , across the entire network.
- Real-time Padding: At each simulation time step, when the environment returns the raw observation vectors for each agent, the wrapper dynamically applies post-padding with zeros to each vector, extending its dimension from its original to the unified . The mathematical expression for this mechanism is:
| Algorithm 1: Observation Padding Wrapper |
1://Step 1: Identify the maximum observation dimension 6: end for 7://Step 2: Perform post-padding with zeros on each observation vector {} , padding_width, value = 0) 14: end for |
3.2.2. Policy Network Architecture: Dynamic Multi-Strategy Grouping Learning Based on Action Space Dimension
| Algorithm 2: Dynamic Multi-Strategy Grouping Learning |
| Input: Agent ID agent_id, pre-computed agent groups Output: Policy network policy corresponding to the agent 1://Agent clustering is completed before training starts 2://Example of Groups structure: {3:[agent_1,agent_5],4[agent_2,agent_3,agent_4,agent_6]} 3:// Where the key is the action space cardinality Get Action Space Size(agent_id)// Obtain the action space size of the agent 6://policy Policy Head Registry[group_id]// Find the corresponding policy head from the policy head registry 7://return policy// Return the exclusive policy network (shared backbone + specific head) |
3.3. Algorithm Implementation and Distributed Training
- Saturated Data Collection: Ray’s parallel workers (‘num_workers’) are close to the total number of physical CPU cores to maximize data collection throughput, eliminate CPU bottlenecks, and ensure GPU resources are consistently highly utilized.
- Large-Scale Batch Training: The ‘train_batch_size’ is dynamically set as the product of ‘num_workers’ and ‘rollout_fragment_length’ to ensure each gradient update is based on a large and diverse set of experiences. Concurrently, we significantly increase the ‘sgd_minibatch_size’ (e.g., to 4096) to leverage the parallel computing power of the GPU and improve the efficiency of a single training operation.
- Asymmetric Resource Allocation: A fractional GPU allocation strategy is adopted, assigning almost all GPU computing resources to the primary training process and a nominal, tiny GPU share (e.g., 0.001) to each CPU-intensive data collection worker. This asymmetric allocation model resolves scheduling challenges in RLlib, ensuring the GPU is dedicated to the computationally intensive task of model parameter updates.
4. Experiments
4.1. Experimental Setup
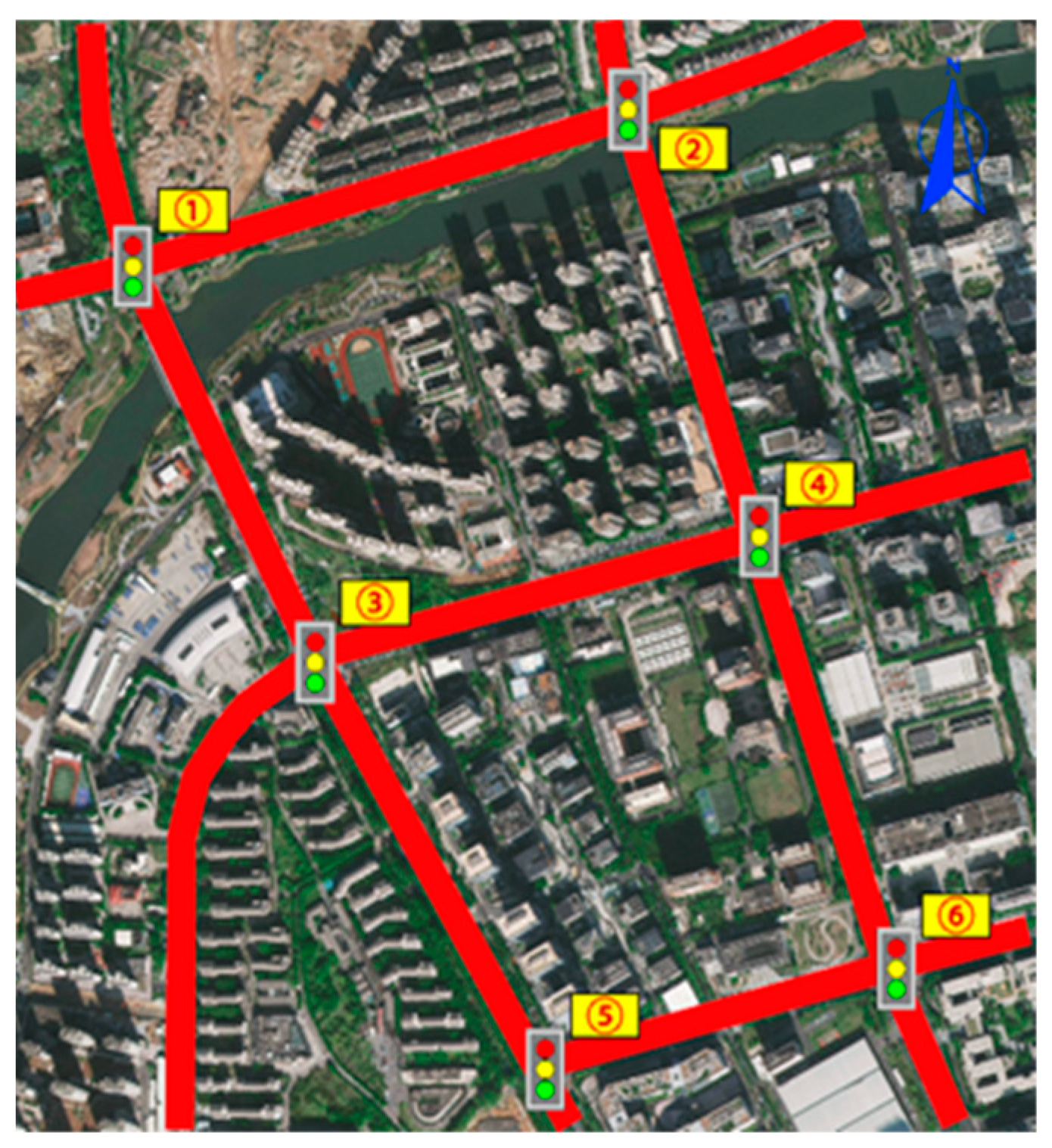
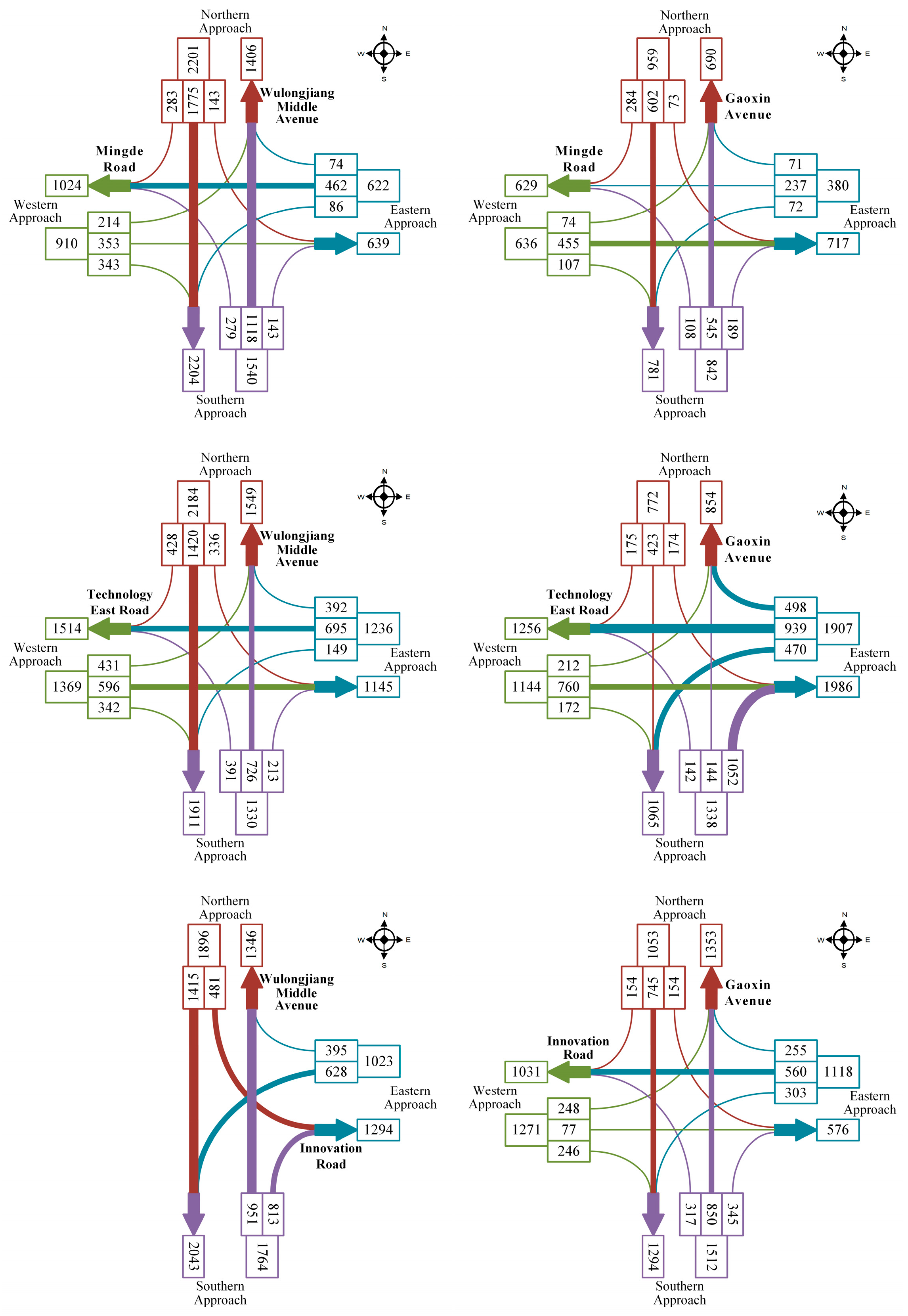
4.1.1. Simulation Environment and Scenario
4.1.2. Algorithm Configuration and Baselines
4.1.3. Model Evaluation
4.2. Experimental Results and Analysis
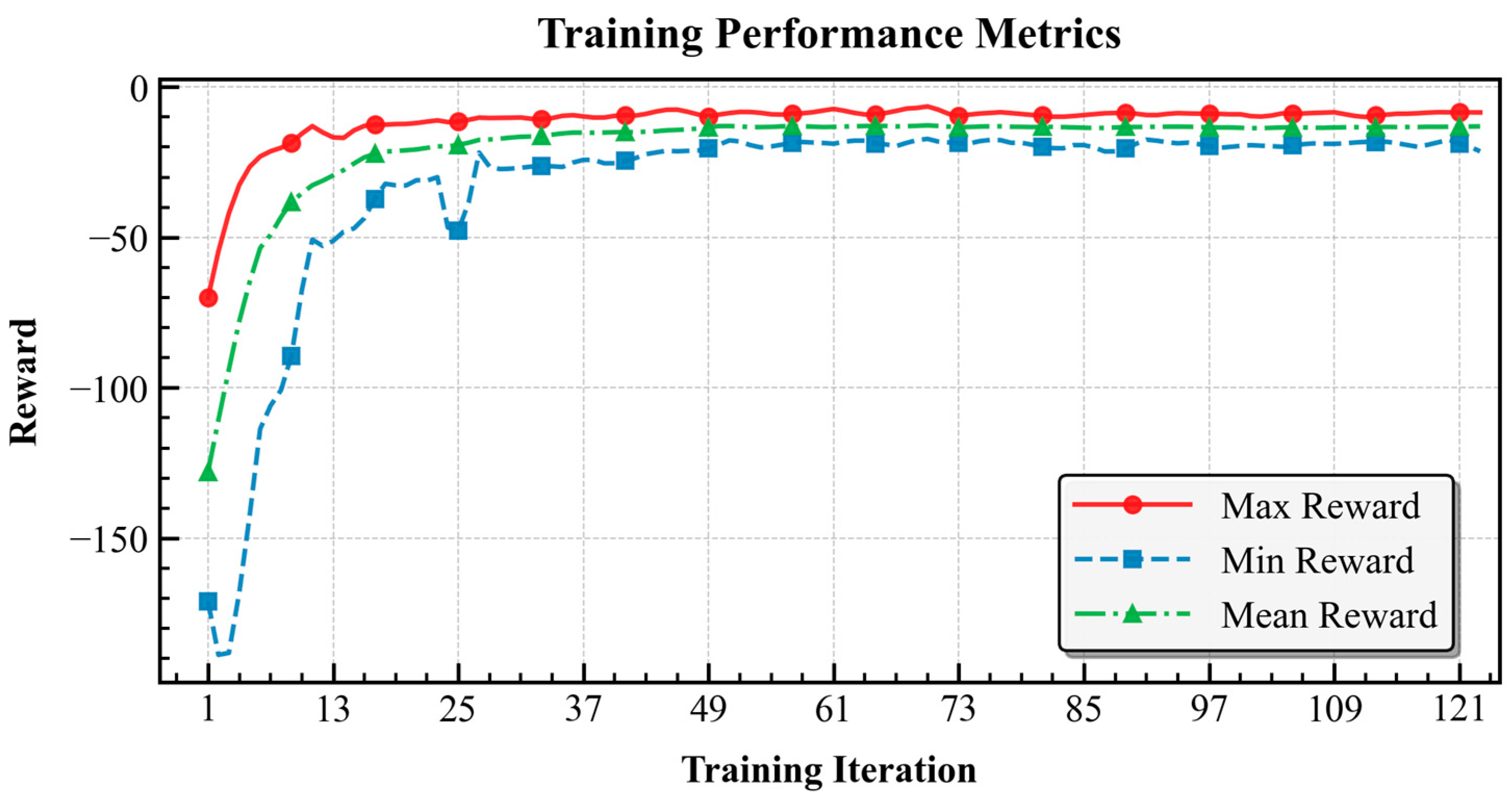
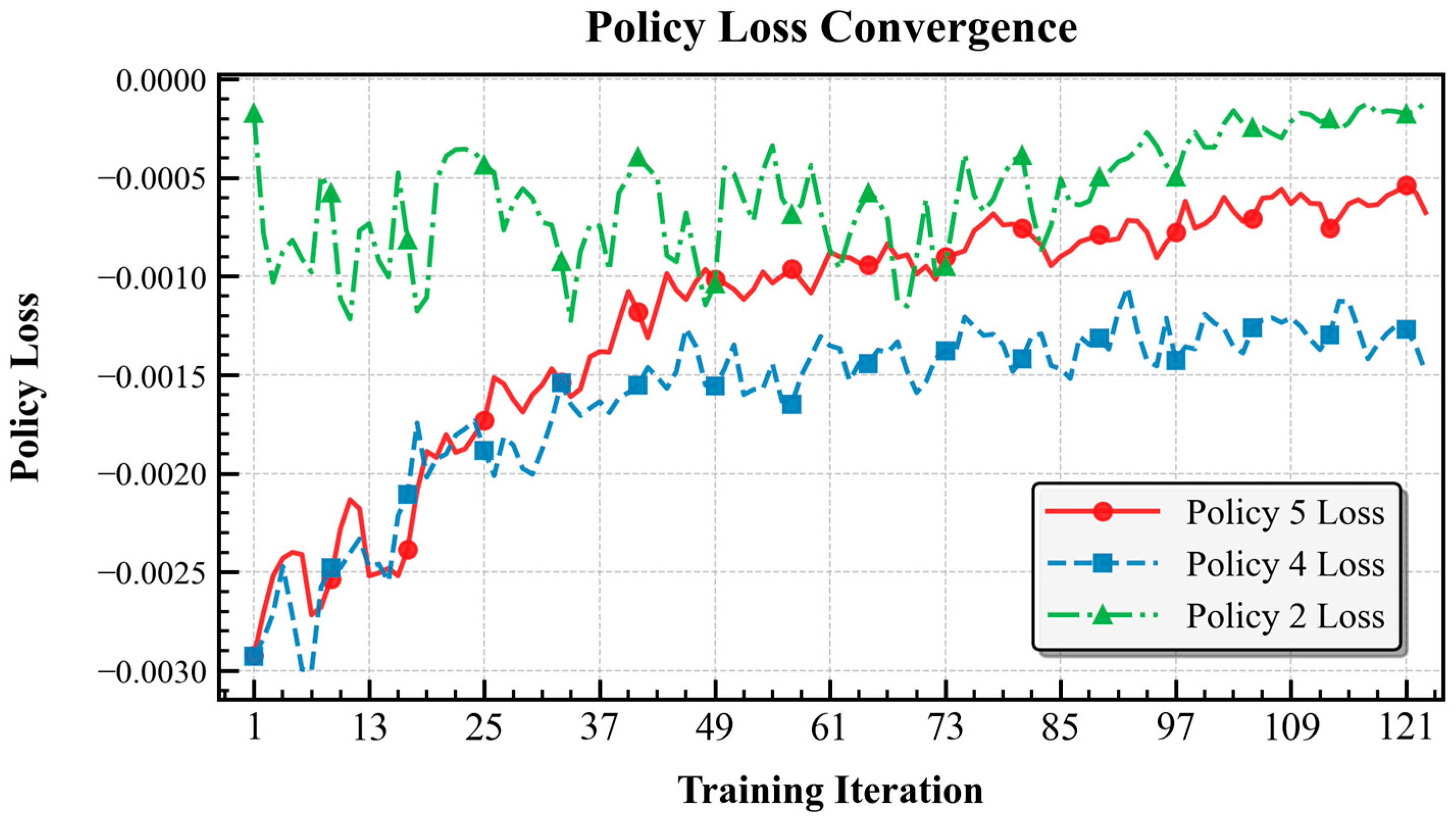
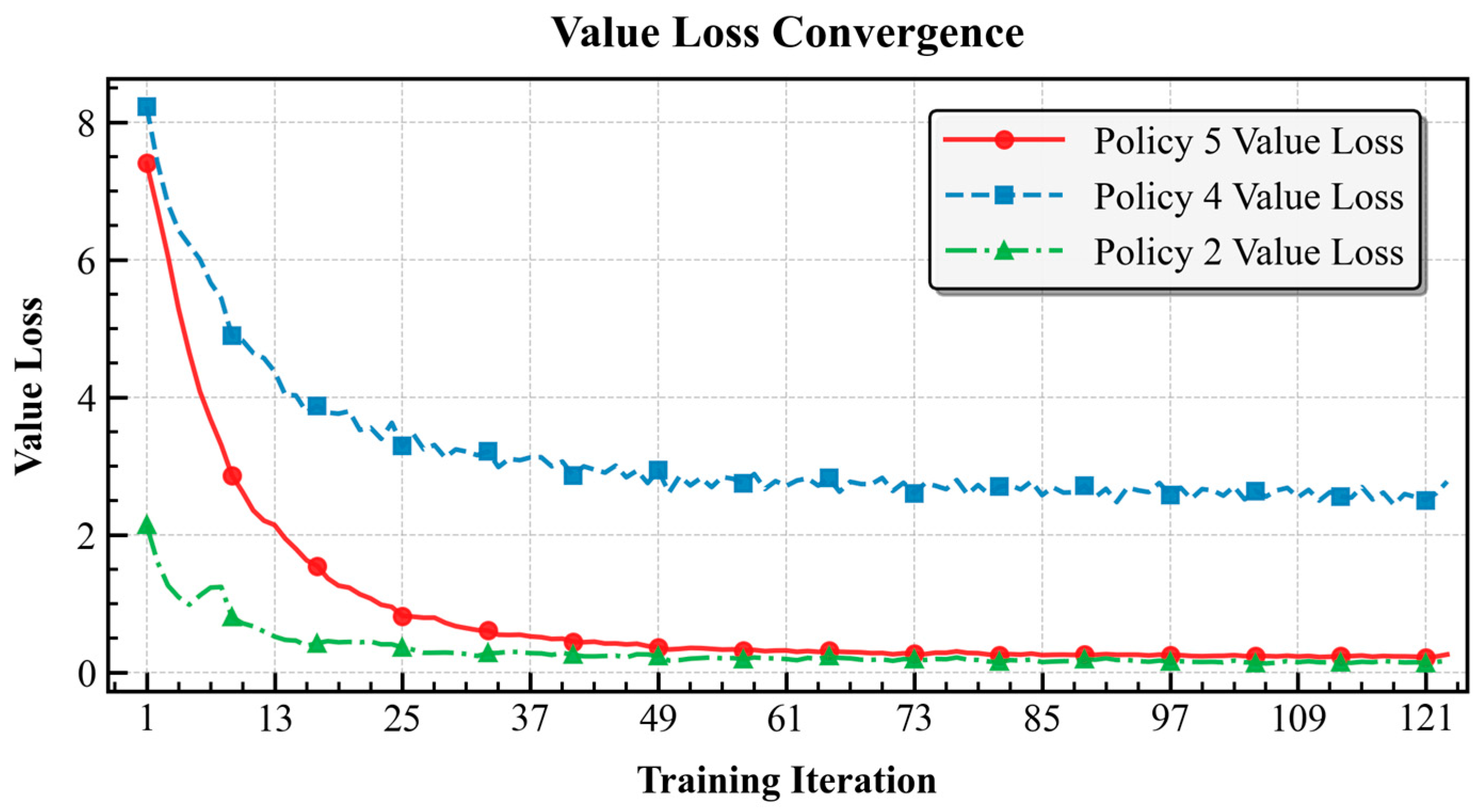
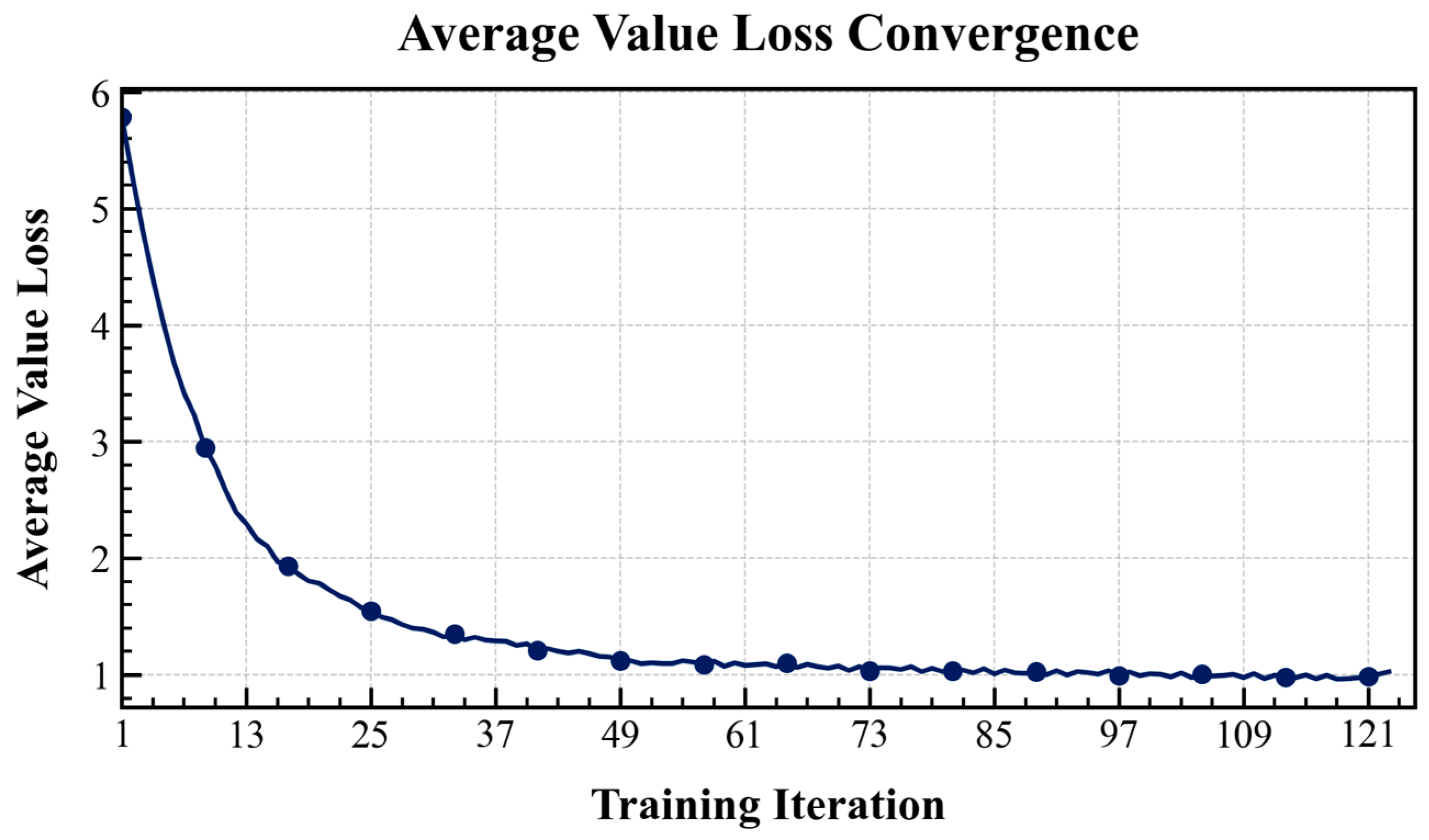
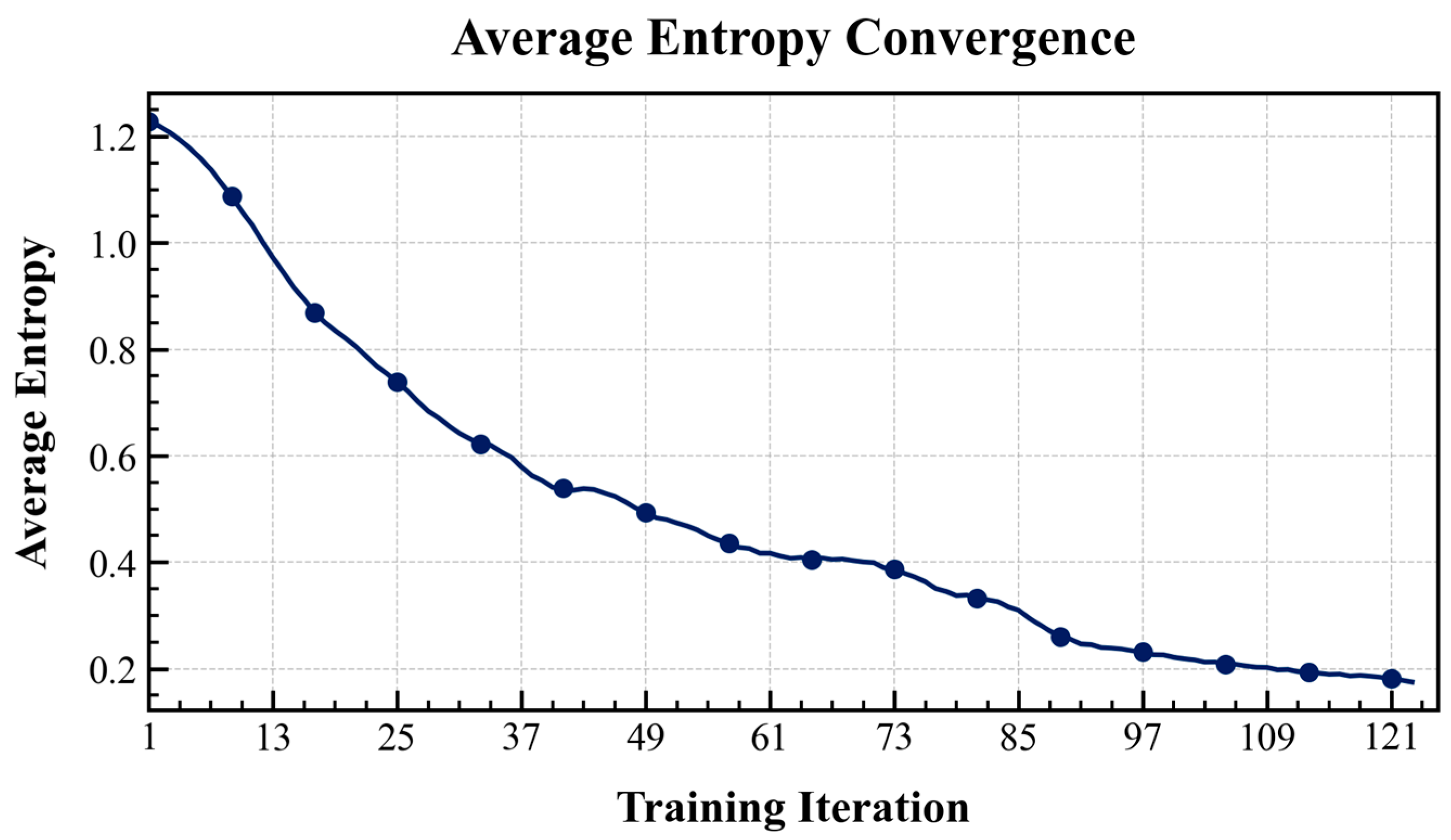
4.2.1. Training Convergence Analysis
4.2.2. Evaluation Metrics
- (1)
- Average Speed:
- (2)
- Avera ge CO2 emissions:
- (3)
- Average Delay Time (ADT):
- (4)
- Average Travel Time (ATT):
- (5)
- Average Waiting Time (AWT):
- (6)
- Completed Trips:
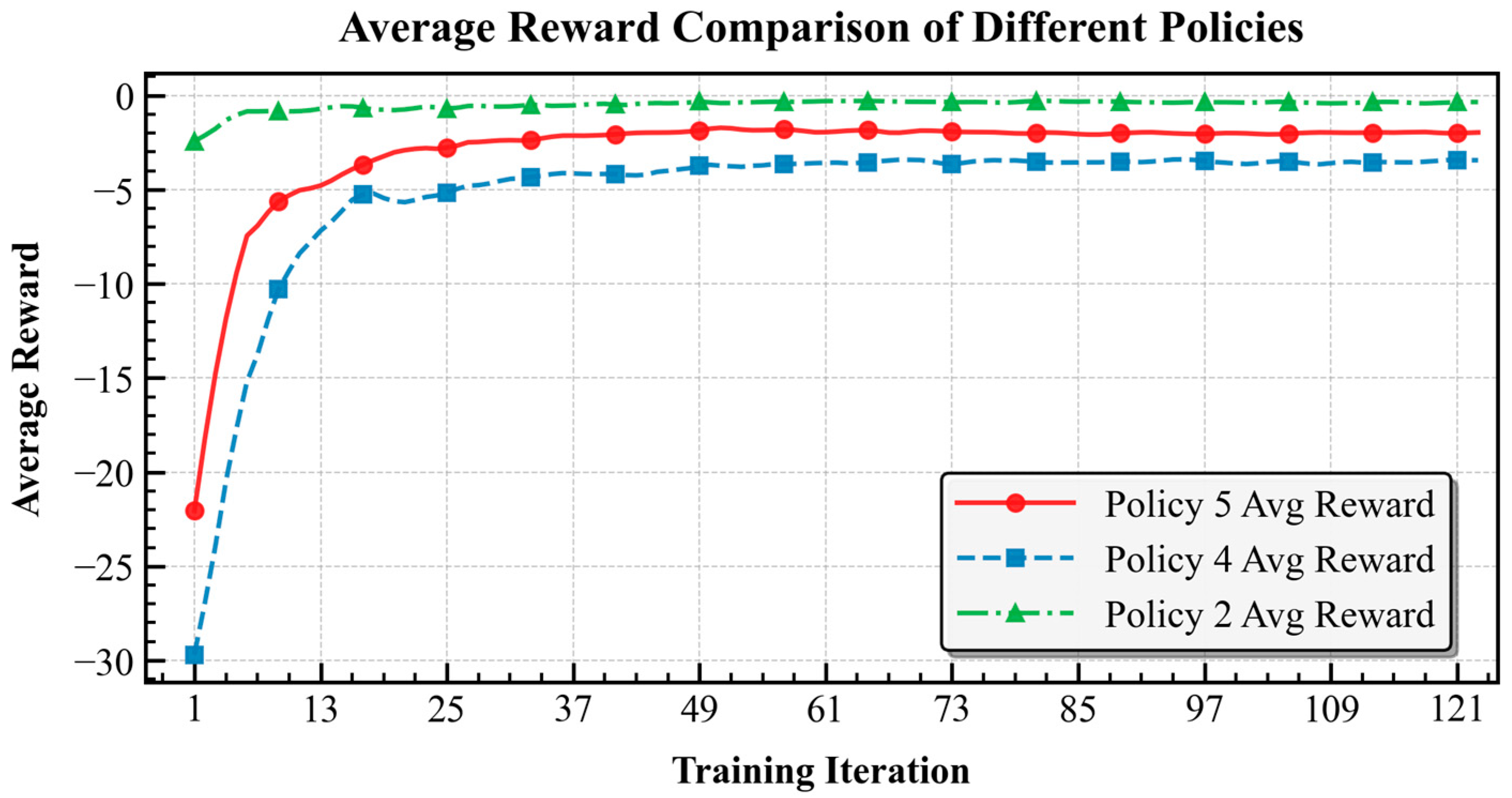
4.2.3. Comparative Analysis
5. Conclusions and Future Work
5.1. Conclusions
5.2. Future Work
- Advanced Policy Architecture for Scalability: While DMSGL effectively handles a moderate number of intersection types, employing separate policy heads may face scalability challenges in metropolitan-scale networks with dozens of unique intersection topologies. Future work will explore more parameter-efficient fine-tuning (PEFT) techniques, such as integrating Adapter modules into the DMSGL mechanism. This would allow for fine-tuning a small set of parameters for each action group while keeping the vast majority of the shared backbone fixed, thus managing a wider variety of action spaces without a linear increase in trainable parameters.
- Multi-Objective Optimization and Heterogeneous Rewards: This study primarily optimized for traffic efficiency (e.g., minimizing waiting time). Future research will extend the HAPS framework to multi-objective optimization, incorporating heterogeneous reward functions that balance global efficiency with local constraints or conflicting goals (e.g., prioritizing public transport, ensuring pedestrian safety, minimizing emissions for specific sensitive areas). Investigating reward-shaping techniques and multi-objective MARL algorithms within the HAPS architecture will be crucial for developing more comprehensive and equitable traffic control policies.
- Enhanced Generalization and Robustness via Meta-Learning: The current model is trained and evaluated on specific traffic patterns. To improve generalization to unseen network topologies, fluctuating demand patterns, and unexpected events (e.g., incidents), we plan to incorporate Meta-Reinforcement Learning (Meta-RL) and Domain Randomization strategies. The goal is to train a meta-policy that can quickly adapt to new heterogeneous intersections or regional control scenarios with minimal fine-tuning, significantly accelerating deployment in novel environments.
- Integrated Perception and Control in V2X Environments: With Vehicle-to-Everything (V2X) communication advancement, future traffic systems will access rich, real-time vehicle-level data. A key direction is expanding the OPW mechanism to fuse this new data modality (e.g., vehicle trajectories, intentions) with infrastructure-based observations. This will enable a shift from reactive control to predictive and cooperative decision-making, where signal controllers can anticipate traffic flow and optimize phases proactively based on a more complete picture of the network state.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schrank, D.; Eisele, B.; Lomax, T. 2021 Urban Mobility Report; Texas A&M Transportation Institute: Bryan, TX, USA, 2021. [Google Scholar]
- Wang, Z.; Xu, L.; Ma, J. Carbon Dioxide Emission Reduction-Oriented Optimal Control of Traffic Signals in Mixed Traffic Flow Based on Deep Reinforcement Learning. Sustainability 2023, 15, 16564. [Google Scholar] [CrossRef]
- Ouyang, Y.; Jain, R.; Varaiya, P. On the Existence of Near-Optimal Fixed Time Control of Traffic Intersection Signals. In Proceedings of the Fifty-Fourth Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016. [Google Scholar]
- Furth, P.G.; Cesme, B. Lost Time and Cycle Length for Actuated Traffic Signal. Transp. Res. Rec. J. Transp. Res. Board 2009, 2128, 152–160. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, K.; Wang, Y.; Liang, X. Enhancing traffic signal control with composite deep intelligence. Expert Syst. Appl. 2024, 244, 123020. [Google Scholar] [CrossRef]
- Sims, A.G.; Dobinson, K.W. The Sydney coordinated adaptive traffic (SCAT) system philosophy and benefits. IEEE Trans. Veh. Technol. 1980, 29, 130–137. [Google Scholar] [CrossRef]
- Hunt, P.B.; Robertson, D.I.; Bretherton, R.D.; Winton, R.I. SCOOT—A Traffic Responsive Method of Coordinating Signals; Urban Networks Division, Traffic Engineering Department, Transport and Road Research Laboratory: London, UK, 1981. [Google Scholar]
- Manandhar, B.; Joshi, B. Adaptive traffic light control with statistical multiplexing technique and particle swarm optimization in smart cities. In Proceedings of the 2018 IEEE 3rd International Conference on Computing, Communication and Security (ICCCS), Kathmandu, Nepal, 25–27 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 210–217. [Google Scholar]
- Haddad, T.A.; Hedjazi, D.; Aouag, S. An IoT-based adaptive traffic light control algorithm for isolated intersection. In Advances in Computing Systems and Applications, Proceedings of the 4th Conference on Computing Systems and Applications, Algiers, Algeria, 20–21 April 2020; Springer International Publishing: Cham, Switzerland, 2021; pp. 107–117. [Google Scholar]
- Yau, K.-L.A.; Qadir, J.; Khoo, H.L.; Ling, M.H.; Komisarczuk, P. A Survey on Reinforcement Learning Models and Algorithms for Traffic Signal Control. ACM Comput. Surv. 2017, 50, 1–38. [Google Scholar] [CrossRef]
- Yılmaz, A.H.Y. Deep Reinforcement Learning for Intelligent Transportation Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11–32. [Google Scholar]
- Prabuchandran, K.J.; Hemanth Kumar, A.N.; Bhatnagar, S. Multi-agent reinforcement learning for traffic signal control. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 2529–2534. [Google Scholar]
- Zhang, Z.; Yang, J.; Zha, H. Integrating independent and centralized multi-agent reinforcement learning for traffic signal network optimization. arXiv 2019, arXiv:1909.10651. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhan, Z.; Lv, F. A Comparative Study of Traffic Signal Control Based on Reinforcement Learning Algorithms. World Electr. Veh. J. 2024, 15, 246. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, J.-M.; Gao, M.-Y.; Zhang, Z. Multi-Agent Deep Reinforcement Learning for Decentralized Cooperative Traffic Signal Control. CICTP 2020, 2020, 458–470. [Google Scholar]
- Chen, Y.; Li, C.; Yue, W.; Zhang, H.; Mao, G. Engineering A Large-Scale Traffic Signal Control: A Multi-Agent Reinforcement Learning Approach. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Virtual, 9–12 May 2021; pp. 1–6. [Google Scholar]
- Zhang, Y.; Su, R.; Zhang, Y.; Sun, C. Modelling and Traffic Signal Control of Heterogeneous Traffic Systems. arXiv 2017, arXiv:1705.03713. [Google Scholar] [CrossRef]
- Chen, B.; Tan, K.; Li, J. HiLight: Heterogeneous Traffic Signal Control for Automatic Drive Guidance Based on Multi-Agent Reinforcement Learning. In Proceedings of the 2024 8th CAA International Conference on Vehicular Control and Intelligence (CVCI), Chongqing, China, 25–27 October 2024; pp. 1–6. [Google Scholar]
- Zhao, H.; Dong, C.; Cao, J.; Chen, Q. A survey on deep reinforcement learning approaches for traffic signal control. Eng. Appl. Artif. Intell. 2024, 133, 108100. [Google Scholar] [CrossRef]
- Do, H.K.; Quynh Dinh, T.; Nguyen, M.D.; Hoa Nguyen, T. Semantic Communication for Partial Observation Multi-Agent Reinforcement Learning. In Proceedings of the 2023 IEEE Statistical Signal Processing Workshop (SSP), Hanoi, Vietnam, 2–5 July 2023; pp. 319–323. [Google Scholar]
- Li, D.; Zhu, F.; Wu, J.; Wong, Y.D.; Chen, T. Managing mixed traffic at signalized intersections: An adaptive signal control and CAV coordination system based on deep reinforcement learning. Expert Syst. Appl. 2024, 238, 121959. [Google Scholar] [CrossRef]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep Learning on Traffic Prediction: Methods, Analysis, and Future Directions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4927–4943. [Google Scholar] [CrossRef]
- Wei, H.; Zheng, G.; Gayah, V.; Li, Z. A Survey on Traffic Signal Control Methods. arXiv 2019, arXiv:1904.08117. [Google Scholar]
- Jamil, Q.U.; Kallu, K.D.; Khan, M.J.; Safdar, M.; Zafar, A.; Ali, M.U. Urban traffic signal control optimization through Deep Q Learning and double Deep Q Learning: A novel approach for efficient traffic management. Multimed. Tools Appl. 2024, 84, 24933–24956. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, M.; Schwarz, C.W.; Li, J.; Xiao, S. Intelligent Traffic Light via Policy-based Deep Reinforcement Learning. Int. J. Intell. Transp. Syst. Res. 2022, 20, 734–744. [Google Scholar] [CrossRef]
- Amato, C. An Introduction to Centralized Training for Decentralized Execution in Cooperative Multi-Agent Reinforcement Learning. arXiv 2024, arXiv:2409.03052. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, S.; Qing, Y.; Chen, K.; Zheng, T.; Song, J.; Song, M. Is Centralized Training with Decentralized Execution Framework Centralized Enough for MARL? arXiv 2023, arXiv:2305.17352. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Marian, W.; Vinicius, C.; Max, Z.; Marc, J.; Nicolas, L.; Joel, S.; Leibo, Z.; et al. Value-Decomposition Networks for Cooperative Multi-Agent Learning Based on Team Reward. In Proceedings of the 17th International Conference on Autonomous Agents and Multi Agent Systems (AAMAS’18), Stockholm, Sweden, 10–15 July 2018; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2018; pp. 2085–2087. [Google Scholar]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. J. Mach. Learn. Res. 2018, 21, 1–51. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of PPO in cooperative multi-agent games. In Proceedings of the 36th International Conference on Neural Information Processing Systems (NIPS’22), Orleans, LA, USA, 28 November–9 December 2022; Curran Associates Inc.: Red Hook, NY, USA, 2022; pp. 24611–24624. [Google Scholar]
- Yang, S.; Yang, B. An inductive heterogeneous graph attention-based multi-agent deep graph infomax algorithm for adaptive traffic signal control. Inf. Fusion 2022, 88, 249–262. [Google Scholar] [CrossRef]
- Wei, H.; Zheng, G.; Yao, H.; Li, Z. IntelliLight: A Reinforcement Learning Approach for Intelligent Traffic Light Control. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD’18), London, UK, 19–23 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 2496–2505. [Google Scholar]
- Bie, Y.; Ji, Y.; Ma, D. Multi-agent Deep Reinforcement Learning collaborative Traffic Signal Control method considering intersection heterogeneity. Transp. Res. Part C Emerg. Technol. 2024, 164, 104663. [Google Scholar] [CrossRef]
- Yang, S.; Yang, B.; Kang, Z.; Deng, L. IHG-MA: Inductive heterogeneous graph multi-agent reinforcement learning for multi-intersection traffic signal control. Neural Netw. 2021, 139, 265–277. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Fan, M.; Sartoretti, G. HeteroLight: A General and Efficient Learning Approach for Heterogeneous Traffic Signal Control. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 1010–1017. [Google Scholar]
- Gu, H.; Wang, S.; Ma, X.; Jia, D.; Mao, G.; Lim, E.G.; Wong, C.P.R. Large-Scale Traffic Signal Control Using Constrained Network Partition and Adaptive Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7619–7632. [Google Scholar] [CrossRef]
- Pritz, P.J.; Leung, K.K. Belief States for Cooperative Multi-Agent Reinforcement Learning Under Partial Observability. arXiv 2025, arXiv:2504.08417. [Google Scholar] [CrossRef]
- Ge, H.; Gao, D.; Sun, L.; Hou, Y.; Yu, C.; Wang, Y.; Tan, G. Multi-Agent Transfer Reinforcement Learning with Multi-View Encoder for Adaptive Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12572–12587. [Google Scholar] [CrossRef]
- He, L.N.; Fu, S.; Zhang, X.; Hu, Q.; Du, W.; Li, H.; Chen, T.; Chen, C.; Jiang, Y.; Zhou, Y.; et al. Baseline and early changes in circulating Serum Amyloid A (SAA) predict survival outcomes in advanced non-small cell lung cancer patients treated with Anti-PD-1/PD-L1 monotherapy. Lung Cancer 2021, 158, 1–8. [Google Scholar] [CrossRef]
- Wang, M.; Wu, L.; Li, M.; Wu, D.; Shi, X.; Ma, C. Meta-learning based spatial-temporal graph attention network for traffic signal control. Knowl.-Based Syst. 2022, 250, 109166. [Google Scholar] [CrossRef]
- Kong, A.Y.; Lu, B.X.; Yang, C.Z.; Zhang, D.M. A Deep Reinforcement Learning Framework with Memory Network to Coordinate Traffic Signal Control. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 3825–3830. [Google Scholar]
- Bokade, R.; Jin, X.; Amato, C. Multi-Agent Reinforcement Learning Based on Representational Communication for Large-Scale Traffic Signal Control. IEEE Access 2023, 11, 47646–47658. [Google Scholar] [CrossRef]
- Liu, J.; Qin, S.; Su, M.; Luo, Y.; Wang, Y.; Yang, S. Multiple intersections traffic signal control based on cooperative multi-agent reinforcement learning. Inf. Sci. 2023, 647, 119484. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Zhang, G.; Dong, S.; Xu, C.-Z. Network-wide traffic signal control optimization using a multi-agent deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103059. [Google Scholar] [CrossRef]
- Yoon, J.; Ahn, K.; Park, J.; Yeo, H. Transferable traffic signal control: Reinforcement learning with graph-centric state representation. Transp. Res. Part C Emerg. Technol. 2021, 130, 103321. [Google Scholar] [CrossRef]
- Luo, H.; Bie, Y.; Jin, S. Reinforcement Learning for Traffic Signal Control in Hybrid Action Space. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5225–5241. [Google Scholar] [CrossRef]
- Ault, J.; Sharon, G. Reinforcement Learning Benchmarks for Traffic Signal Control. In Proceedings of the Thirty-Fifth Conference on Neural Information Processing Systems (NeurIPS 2021) Datasets and Benchmarks Track, Virtual, 7–10 December 2021. [Google Scholar]





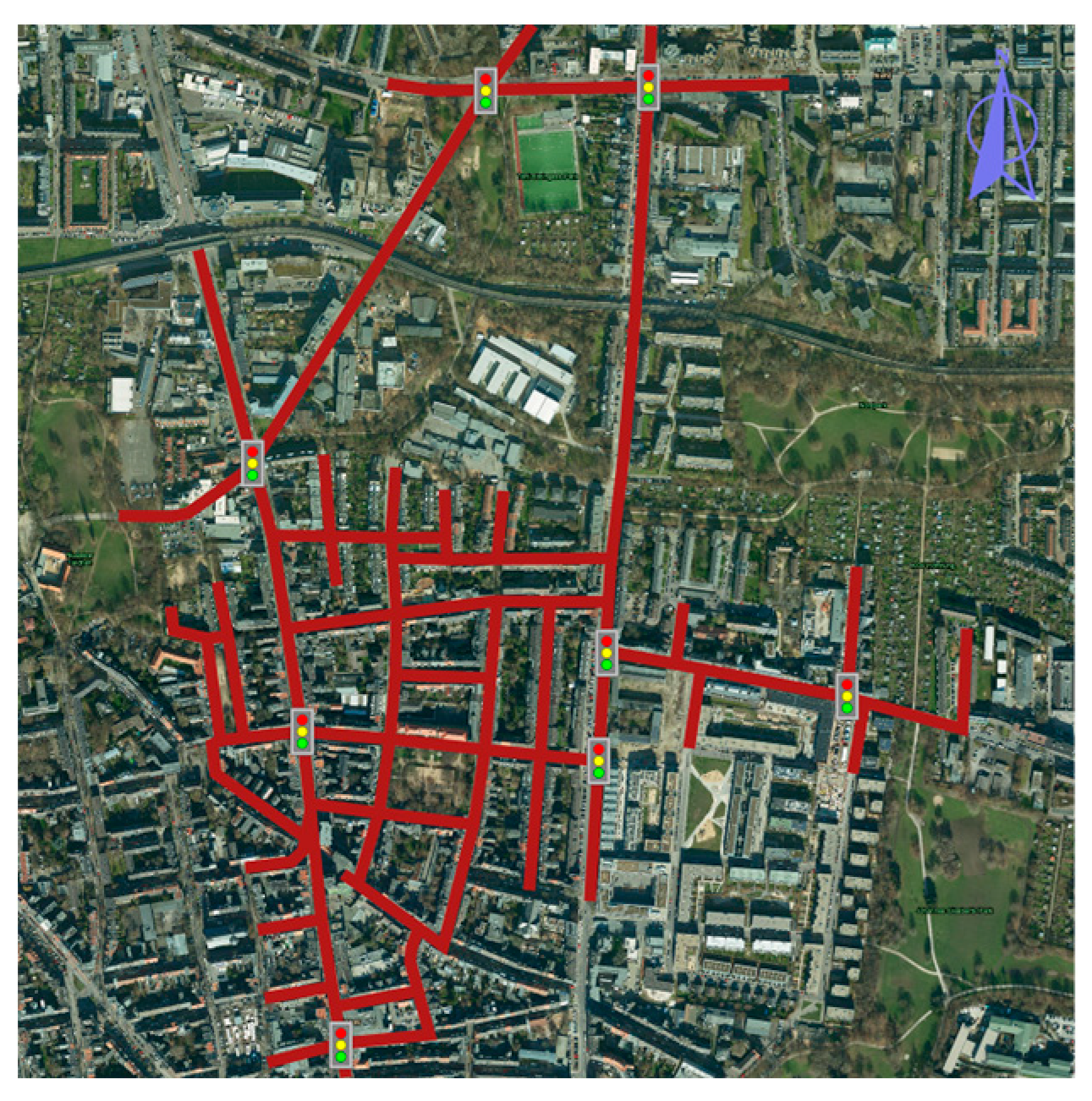
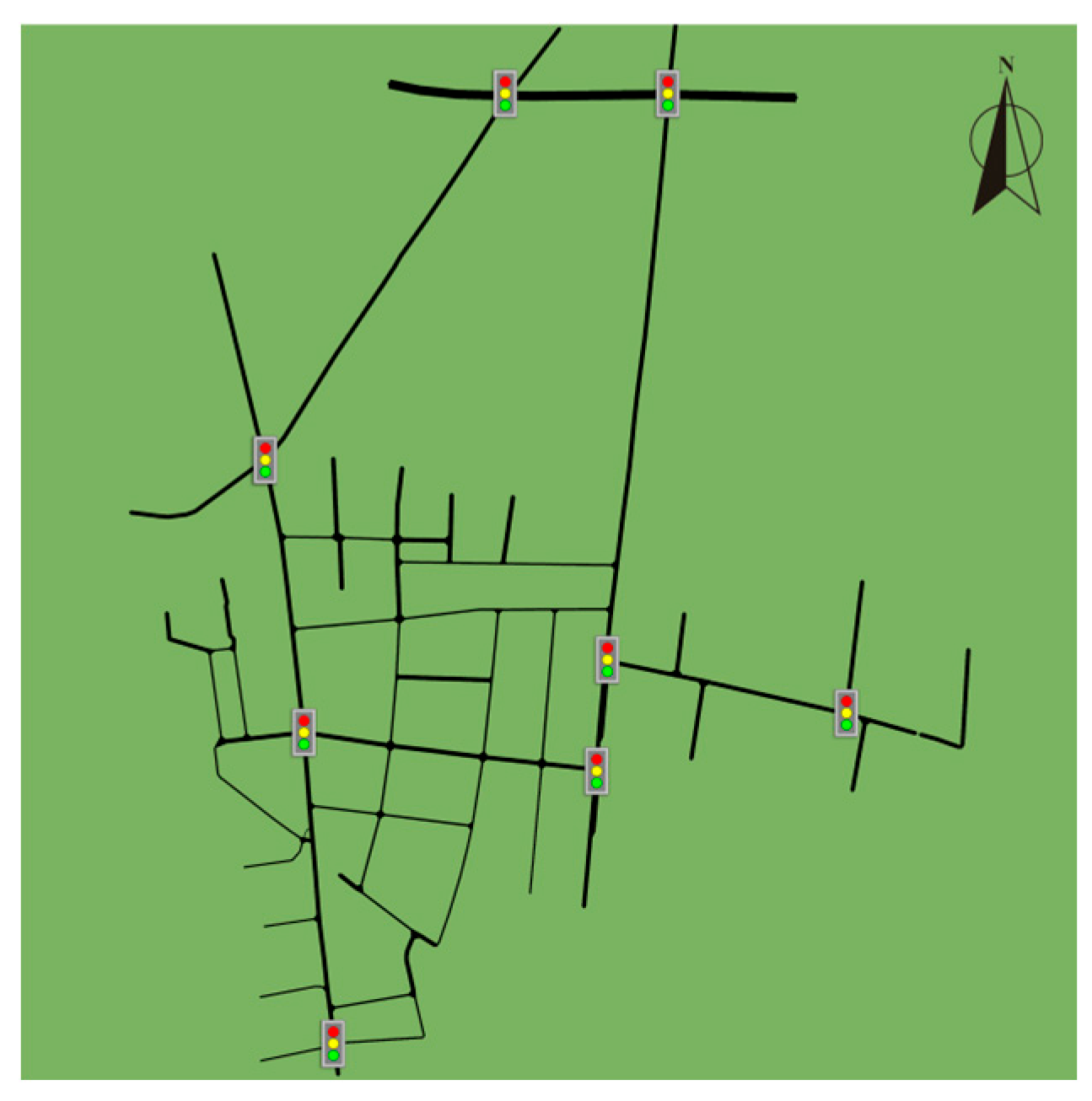
| Fixed-Time Control | Actuated Control | Adaptive Control | |
|---|---|---|---|
| Core Principle | It operates in a fixed pattern based on historical traffic data, preset signal cycle, timing, and green splits. | Dynamically adjusts green light duration based on real-time vehicle detection and predefined logic. | Models and analyzes traffic flow in real-time using sensors and algorithms to predict future states and automatically adjust control parameters. |
| Applicable Scenarios | Scenarios with stable and predictable traffic flow patterns. | Intersections with significant flow disparities between major and minor roads require local responsiveness. | Complex and variable traffic flow scenarios require global optimization. |
| Advantages | 1. Simple equipment, stable and reliable operation. 2. Low operational and maintenance costs. 3. Easy to deploy and scale. | 1. Efficiently utilizes green time, reducing vehicle stops. 2. Responds to local traffic fluctuations, ensuring smooth flow on main arteries. | 1. High flexibility and adaptability, superior control performance. 2. Can integrate intelligent algorithms for complex problems. |
| Limitations | 1. Cannot respond to real-time traffic flow changes. 2. Fixed timing plans. | 1. “Reactive” decision-making, lacking predictive capability. 2. Optimizes individual intersections, potentially shifting congestion elsewhere. | 1. Relies on complex traffic models and expensive infrastructure. 2. Centralized architecture may suffer from computational bottlenecks and latency. |
| TypicalSystems Optimization Goal | Webster’s method, Wattleworth’s ramp metering. Minimize average vehicle delay, multi-objective optimization. | ALINEA algorithm, Furth’s dual-ring actuated control. Reduce vehicle stops and increase the capacity of a single intersection. | SCATS system, SCOOT system, AD-ALINEA, PI-ALINEA. Global traffic efficiency optimization. |
| Notation | Meaning |
|---|---|
| TSC | Traffic Signal Control |
| RL | Reinforcement Learning |
| DRL | Deep Reinforcement Learning |
| MARL | Multi-Agent Reinforcement Learning |
| HAPS-PPO | Heterogeneity-Aware Policy Sharing PPO |
| MDP | Markov Decision Process |
| Dec-POMDP | Decentralized Partially Observable Markov Decision Process |
| OPW | Observation Padding Wrapper |
| DMSGL | Dynamic Multi-Strategy Grouping Learning |
| AC | Actor-Critic |
| PPO | Proximal Policy Optimization |
| CTDE | Centralized Training with Decentralized Execution |
| IL | Independent Learner |
| SUMO | Simulation of Urban Mobility |
| MADQN | Multi-Agent Deep Q Network |
| Placement Name | Parameters | |
|---|---|---|
| Hardware environment | CPU | Intel Core Ultra7 155H |
| RAM | 32GB | |
| GPU | NVIDIA GeForce 4060 | |
| Software environment | Operating system | Windows 11 |
| CUDA | 11.8 | |
| Python | 3.8.10 | |
| Py-Torch | 2.4.1 | |
| Ray RLlib | 2.8.0 | |
| SUMO | 1.21.0 | |
| SUMO-RL | 1.4.5 | |
| Traci | 1.23.1 | |
| gum | 0.26.2 |
| Hyperparameter | Symbol | Value | Description |
|---|---|---|---|
| Learning rate | Learning rate of Actor and Critic networks. | ||
| Discount factor | 0.999 | Discount rate for calculating future rewards, close to 1 indicates more focus on long-term returns. | |
| GAE parameter | 0.95 | Smoothing parameter in Generalized Advantage Estimation. | |
| PPO clipping coefficient | 0.1 | Clipping range in the PPO objective function is used to limit the magnitude of policy updates. | |
| Rollout fragment length | 2048 | Number of experience steps collected by each Worker before synchronizing back to the Driver. | |
| Training batch size | 40,960 | Total sample size used for a single gradient update (20 × 2048). | |
| SGD minibatch size | 4096 | The sample size is fed into the GPU for calculation in a single SGD round. | |
| SGD iteration count | 10 | Number of iterative rounds for policy updates on the same batch of data. | |
| Value function coefficient | 1.0 | Weight of the value function loss in the total loss function. | |
| Entropy coefficient | 0.01 | The weight of entropy reward in the total loss function encourages policy exploration. |
| Hyperparameter | Symbol | Value | Description |
|---|---|---|---|
| Learning rate | Adam optimizer learning rate. | ||
| GAMMA | 0.99 | Discount rate for calculating future rewards, close to 1 indicates more focus on long-term returns. | |
| BUFFER_CAPACITY | 100,000 | Experience Replay Pool Capacity: Stores samples of agent states, actions, rewards, following states, and terminations. | |
| BATCH_SIZE | 1024 | Total number of samples used per gradient update | |
| TAU | 0.001 | Target Net Soft Update Coefficient | |
| EPSILON_START | 1.0 | Initial exploration rate: 100% random action selection during early training | |
| EPSILON_MIN | 0.05 | Minimum exploration rate, the lowest exploration proportion in the late training phase (to avoid falling into local optima due to pure greed) | |
| EPSILON_DECAY | 0.999995 | This proportion reduces the erosion rate decay coefficient after each training step. | |
| Gradient Trimming Maximum Norm | 1.0 | Gradient clipping threshold to prevent gradient explosion. |
| Evaluation Indicator | Average Speed (m/s) | Average CO2 Emissions (g/car) | Average Delay Time(s) | Average Travel Time(s) | Average Waiting Time(s) | Completed Trips | |
|---|---|---|---|---|---|---|---|
| Fixed-time | NO. 1 | 0.9 | 5.7 | 78.99 | 153.76 | 53.32 | 27,189 |
| NO. 2 | 1.1 | 4.2 | |||||
| NO. 3 | 0.9 | 9.3 | |||||
| NO. 4 | 1.5 | 0.3 | |||||
| NO. 5 | 13.3 | 7 | |||||
| NO. 6 | 1.5 | 5.9 | |||||
| MADQN | NO. 1 | 1.2 | 5.4 | 56.43 (−28.56%) | 130.58 (−15.08%) | 31.89 (−40.19%) | 27,458 |
| NO. 2 | 1.2 | 4.3 | |||||
| NO. 3 | 1 | 9.1 | |||||
| NO. 4 | 1.8 | 0.3 | |||||
| NO. 5 | 13.8 | 6.9 | |||||
| NO. 6 | 1.5 | 5.7 | |||||
| HAPS-PPO | NO. 1 | 1.2 | 5.3 | 43.65 (−44.74%) | 117.68 (−23.47%) | 21.54 (−59.60%) | 27,575 |
| NO. 2 | 1.1 | 4.2 | |||||
| NO. 3 | 1 | 8 | |||||
| NO. 4 | 1.9 | 0.2 | |||||
| NO. 5 | 14 | 6.9 | |||||
| NO. 6 | 1.5 | 5.5 |
| Evaluation Indicator | Average Delay Time (s) | Average Travel Time (s) | Average Waiting Time (s) |
|---|---|---|---|
| MPLight | 60.42 (+22.38%) | 123.93 (+8.22%) | 30.34 (+3.30%) |
| Fixed-time | 49.37 | 114.51 | 29.37 |
| FMA2C | 33.28 (−32.59%) | 97.53 (−14.83%) | 14.19 (−51.69%) |
| HAPS-PPO | 30(−39.23%) | 95.63(−16.49%) | 13.97(−52.43%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Fang, H.; Yin, Z.; Zhu, G. HAPS-PPO: A Multi-Agent Reinforcement Learning Architecture for Coordinated Regional Control of Traffic Signals in Heterogeneous Road Networks. Appl. Sci. 2025, 15, 10945. https://doi.org/10.3390/app152010945
Lu Q, Fang H, Yin Z, Zhu G. HAPS-PPO: A Multi-Agent Reinforcement Learning Architecture for Coordinated Regional Control of Traffic Signals in Heterogeneous Road Networks. Applied Sciences. 2025; 15(20):10945. https://doi.org/10.3390/app152010945
Chicago/Turabian StyleLu, Qiong, Haoda Fang, Zhangcheng Yin, and Guliang Zhu. 2025. "HAPS-PPO: A Multi-Agent Reinforcement Learning Architecture for Coordinated Regional Control of Traffic Signals in Heterogeneous Road Networks" Applied Sciences 15, no. 20: 10945. https://doi.org/10.3390/app152010945
APA StyleLu, Q., Fang, H., Yin, Z., & Zhu, G. (2025). HAPS-PPO: A Multi-Agent Reinforcement Learning Architecture for Coordinated Regional Control of Traffic Signals in Heterogeneous Road Networks. Applied Sciences, 15(20), 10945. https://doi.org/10.3390/app152010945





