Research on Space Object Origin Tracing Approach Using Density Peak Clustering and Distance Feature Optimization

Abstract

The exponential growth of space objects in near-Earth and geostationary orbits has posed severe threats to space environment safety, with debris clouds from spacecraft breakup events being a critical concern. Debris cloud tracing, as a key technology for locating breakup points, faces dual challenges of insufficient precision in analytical methods and excessive computational load in numerical methods. To balance traceability accuracy with computational efficiency, this paper proposes a breakup time determination method integrating a clustering algorithm and the minimization of average relative distance. The method first calculates the average relative distance between fragment pairs and preliminarily estimates the breakup epoch using a golden section step-size optimization strategy. Subsequently, the density peak clustering (DPC) algorithm is introduced to eliminate abnormal fragments. The breakup epoch is then refined based on the cleansed fragment dataset, achieving high-precision localization. Validation through simulations of real breakup events demonstrates that this method significantly improves localization accuracy. It establishes a highly reliable temporal benchmark for space collision tracing, debris diffusion prediction, and orbital safety management.

1. Introduction

With the increasing frequency and commercialization of global space activities, the number of space objects in Low Earth Orbit (LEO) and Geostationary Earth Orbit (GEO) has experienced exponential growth. According to a report by the European Space Agency [1], as of 2025, the number of space debris objects larger than 1 cm in size has exceeded 1.2 million, and such debris is capable of causing catastrophic damage. Furthermore, the number of objects larger than 10 cm in size exceeds 50,000. These orbital fragments—resulting from satellite malfunction breakups, rocket stage explosions, and similar events—are exacerbating space environment safety risks on an unprecedented scale.

However, limited by the coverage of ground-based sensors, radar cross-section (RCS) of debris, and orbital altitude differences, fragments from space object breakups often cannot be observed in real time. Small fragments, due to weak reflected signals, are typically captured by radars or optical telescopes 30 min to several hours after breakup. Furthermore, during the initial breakup phase, the debris cloud remains in early orbital convergence with an undispersed spatial distribution, exhibiting high-density clustering characteristics. Its position and velocity vectors overlap extensively with background debris populations, making distinction through traditional correlation algorithms difficult. Additionally, data acquired by globally distributed sensors (e.g., radar stations, optical telescope networks) requires orbit determination and correlation processing, creating a critical temporal blind spot between the breakup moment and the acquisition of initial observational data. Therefore, debris tracing becomes essential when observational capabilities cannot meet real-time breakup identification requirements.

A debris cloud refers to the aggregate formed by numerous fragments from an in-space breakup event, typically lasting less than one orbital period [2]. Debris cloud tracing determines the source of breakup events—including the location and time—by analyzing the proximity of space objects based on orbital mechanics. Current mainstream methods fall into two categories: numerical and analytical. Analytical methods offer faster computational speeds due to simpler operational mechanisms, but may risk missing actual breakup events. Notable examples include the A-N [3,4] method and the Hoots method [5,6]: the former searches for minimum-distance points by interpolating relative distances between fragments and their rate-of-change functions; the latter achieves rapid localization through altitude filtering, geometric constraints, and phase matching. Numerical methods traverse time windows with minimal steps, employing high-precision orbit propagation models to calculate candidate fragments’ positions at each time step while searching for minimum-distance points [7,8]. By precisely simulating orbital evolution, this approach better approximates the actual spatial distribution of debris clouds at breakup. Compared to analytical methods, numerical methods exhibit stronger robustness against complex orbital perturbations and potentially achieve higher localization accuracy—especially under significant initial breakup parameter uncertainty or geometrically complex fragment configurations. Their drawback, however, is enormous computational overhead, requiring repeated state integration and distance calculations for numerous fragments over extended time windows, posing substantial challenges for real-time or large-scale debris cloud tracing applications [9].

In recent years, with the rapid development of machine learning and data-driven methods, their application in the field of space situational awareness has provided new ideas to address the aforementioned challenges. These methods show significant advantages, particularly in anomaly detection and cluster analysis. For example, in satellite platform health monitoring, data-driven anomaly detection frameworks have been proven effective in automating fault diagnosis processes [10]; for satellite telemetry data, advanced clustering algorithms such as deep clustering [11] and hyperparameter adaptive optimization clustering [12] can more accurately identify on-orbit anomaly states, overcoming the limitations of traditional threshold methods or grid search. These studies provide strong evidence for using intelligent algorithms to improve the accuracy and efficiency of space object state analysis.

Specifically regarding the problem of space debris traceability and orbital analysis, the application of clustering algorithms has also made positive progress. For instance, density clustering algorithms like DBSCAN have been successfully used to group space debris for optimizing target selection in active removal missions [13]; mean shift clustering has been applied in navigation satellite data processing [14]; furthermore, studies have improved the classic PAM clustering algorithm for satellite science payload data to detect anomalies [15]. These works validate the effectiveness of clustering techniques in handling space object orbital and observational data. However, most existing research focuses on the static classification or anomaly discrimination of space objects. Research on using clustering technology to dynamically trace back the occurrence time of key space events (such as breakups) remains insufficient. Particularly when dealing with debris clouds generated from breakups, how to effectively integrate clustering denoising with high-precision orbital backtracking models to achieve robust and efficient estimation of the breakup time is still a direction requiring further exploration.

In addition to the aforementioned data-driven state monitoring and anomaly detection methods, research on the evolution modeling of the debris cloud itself, risk analysis, and its long-term environmental effects are also core topics in the space debris field, forming the macro background for traceability analysis. In this direction, scholars have developed various models and methods. For example, the continuum method models the debris cloud as a fluid and aims to integrate uncertainty analysis to improve prediction accuracy [16]; models based on probability density functions characterize the short-term evolution and collision risk of debris clouds in key regions (such as geostationary orbit) by solving boundary value problems [2]; to efficiently handle centimeter-level debris in long-term evolution models, a probabilistic environment propagator has been proposed, which propagates the density distribution of the debris cloud through continuity equations and comprehensively considers scenarios like post-mission disposal [17]. Furthermore, statistical analysis of historical breakup events is fundamental for building realistic debris environment models, and the development of risk assessment tools for debris re-entry into the ground signifies increasingly refined research on the end-of-life behavior of debris clouds [18].

The aforementioned studies, ranging from evolution modeling and risk assessment to end-of-life re-entry analysis, have significantly deepened the understanding of the overall behavior and impact of debris clouds. However, the effectiveness of these macro-models often relies on the precise knowledge of the debris source event, that is, the time and location of the breakup. Currently, research on how to dynamically determine the occurrence time of breakup events with high precision and efficiency, which is a cutting-edge problem, remains insufficient. Particularly when dealing with high-density debris clouds in the initial phase of a breakup, how to effectively integrate clustering denoising technology to eliminate fragments with large observational anomalies or orbital errors, and combine it with high-precision orbital dynamics models to achieve robust estimation of the breakup time, remains a direction requiring in-depth exploration.

This paper proposes a space object breakup time determination method integrating a clustering algorithm and the minimization of average relative distance. It aims to resolve the precision–efficiency trade-off inherent in traditional analytical and numerical methods for space debris breakup events. The method determines the breakup time by calculating the average relative distance between all fragment pairs and statistically identifying the time point with the minimal average distance. Step-size optimization enhances search efficiency. After initial breakup time determination, the density peak clustering (DPC) removes large-error fragments. The refined fragment set undergoes renewed distance calculation and breakup time correction to achieve robust temporal localization, providing a highly reliable time benchmark for space collision tracing, debris diffusion prediction, and orbital safety management.

The remainder of this paper is organized as follows. Section 2 establishes a high-precision dynamic model incorporating multiple perturbative forces and specifies underlying assumptions. Section 3 presents the breakup tracing methodology. Section 4 provides simulation case studies and analyses. Section 5 presents conclusions.

2. Problem Formulation

To achieve precise determination of the breakup epoch of space objects, this paper formulates the breakup time determination problem as an optimization problem based on fragment distance characteristics. To simulate the real space environment and enhance scientific reliability, consideration is given to high-altitude orbital propagation equations, introducing perturbation forces including Earth’s non-spherical gravitational perturbation, atmospheric drag, and others, to construct a more accurate orbit dynamics model.

Based on this model, the relative distance characteristics between fragments are calculated to establish an objective function aimed at determining the most probable breakup epoch by minimizing the average relative distance.

2.1. Scenario Description

Since fragments experience no instantaneous displacement after space object breakup, fragments generated by the same event can be propagated back to a single point under ideal conditions, as illustrated in Figure 1.

In view of this problem, the following assumptions are adopted:

Assumption 1. 

All fragments share identical positions at the breakup instant. Their subsequent orbital propagation is governed solely by the same dynamical model and perturbation forces.

Assumption 2. 

Complete orbital information of fragments is obtainable within one orbital period.

2.2. Model Establishment

2.2.1. Space Stress Model

To accurately characterize the state of space debris in orbit, a high-precision model is employed for orbit extrapolation via numerical integration [19]. The equation of motion for space debris under multiple perturbations is expressed as the following:

$$\left\{\begin{array}{c} \mathit{ṙ}=\mathit{v}\\ \stackrel{.}{\mathit{v}} =-{\displaystyle \frac{\mu }{r^3}}\mathit{r}+{\mathit{a}}_{drag}+{\mathit{a}}_{thirdB}+{\mathit{a}}_{Radiation}+{\mathit{a}}_{Newtonian}\end{array}\right.$$

(1)

In the equation, μ is the Earth’s gravitational constant; ${\mathit{a}}_{drag}$ represents the atmospheric drag acceleration, primarily determined by atmospheric density, the spacecraft’s area-to-mass ratio, and the velocity direction; ${\mathit{a}}_{thirdB}$ is the third-body gravitational perturbation acceleration, usually considering the gravitational effects of the Sun and Moon on the spacecraft’s orbit; ${\mathit{a}}_{Radiation}$ is the solar radiation pressure acceleration, whose magnitude depends on the surface material properties of the spacecraft and the direction of solar incidence; ${\mathit{a}}_{Newtonian}$ is the acceleration caused by post-Newtonian effects, mainly originating from the correction of spacetime curvature, in general, relativity, which is particularly critical for orbit prediction of spacecraft (such as navigation satellites and scientific experimental satellites).

In the process of high-precision orbit prediction, numerical integration methods are typically used to progressively extrapolate the orbital state. Generally speaking, when the initial state vector of the spacecraft is known, combined with the perturbation force model, the total acceleration acting on it at the current moment can be calculated. Subsequently, an appropriate numerical integrator is selected to integrate the equations of motion forward with a fixed time step, thereby predicting the state vector at the next moment. It is important to note that in each integration step, the values of various perturbation accelerations must be updated in real time. It can be said that the construction of an accurate force model and an efficient numerical integration strategy jointly determine the reliability of orbit prediction, making the selection and implementation of the model crucial.

2.2.2. Numerical Integration Method Model

In high-precision orbit prediction, commonly used numerical integration methods can be divided into several categories. From the perspective of differential equation order, they are classified into single-step methods and multi-step methods. Single-step methods require only current state information to compute the next step, whereas multi-step methods rely on multiple previous states. Regarding explicit and implicit formulations: explicit methods feature simple computation but poorer stability, while implicit methods offer better stability at the cost of higher computational complexity. Currently prevalent methods include:

• Runge–Kutta (RK) series: Variable-step single-step methods for first-order ODEs.
• Adams–Bashforth–Moulton (ABM) series: Multi-step predictor-corrector algorithms.
• Runge–Kutta-Nyström (RKN) series: Specialized solvers for second-order ODEs.
• Others: Symplectic integrators, Newton-Cotes formulas, Gear’s methods.

This paper employs the Adams–Bashforth–Moulton predictor-corrector method for orbital propagation. As a multi-step numerical integration algorithm, it offers superior computational efficiency for long-term orbit extrapolation by leveraging historical state information. The method’s variable-order capability allows adaptive balancing of accuracy and computational cost, making it particularly suitable for the intensive trajectory calculations required in debris cloud traceability analysis.

3. Traceability of Breakup Event Occurrence Point

As described in Section 2, a dynamic framework for space debris based on a high-precision orbital perturbation model was established, employing the ABM numerical integration method for orbital extrapolation. This model lays a solid physical and computational foundation for precisely backtracking the historical trajectories of fragments and locating their common spatial origin point. To address the breakup tracing problem under this high-precision model framework—specifically, how to efficiently and robustly search for the most probable breakup time of a space object—this section proposes a breakup time determination method integrating a clustering algorithm and minimization of average relative distance. The details of this method are introduced below.

3.1. Preliminary Breakup Epoch Determination

For debris clouds, a high-precision orbital prediction model is used for propagation. This model balances computational efficiency with comprehensive perturbation modeling—including Earth’s non-spherical gravity, atmospheric drag, third-body gravitation, radiation pressure, and post-Newtonian effects—ensuring extrapolation accuracy and physical realism. Based on initial orbital elements (e.g., TLE data), debris trajectories are propagated in the Earth-Centered Inertial (ECI) frame to obtain position/velocity states at discrete times.

Subsequently, pairwise Euclidean distances between all debris fragments at time t are computed. For debris i and j, their relative distance r_ij is expressed as the following:

$$r_{ij}(t)=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2+{\left(z_i-z_j\right)}^2}$$

(2)

where $\left(x_i,y_i,z_i\right)$ and $\left(x_j,y_j,z_j\right)$ denote the position vectors of fragment i and fragment j in the Earth-Centered Inertial (ECI) frame, respectively. Based on the above calculations, a relative distance matrix D(t) is generated to store the relative distance information of all fragment pairs at time t. Specifically, D(t) is defined as a set:

$$\mathit{D}\left(t\right)=\left[\begin{array}{cc}\begin{array}{l}{r}_{11}\\ r_{12}\\ ...\\ r_{1n}\end{array}& \begin{array}{cc}\begin{array}{l}{r}_{21}\\ r_{22}\\ ...\\ r_{2n}\end{array}& \begin{array}{cc}\begin{array}{c}...\\ ...\\ ...\\ ...\end{array}& \begin{array}{l}{r}_{n1}\\ r_{n2}\\ ...\\ r_{nn}\end{array}\end{array}\end{array}\end{array}\right]$$

(3)

For orbital data in D(t), traverse the time window $[t_{start},t_{end}]$ with step-size $\Delta t$. Compute the average relative distance of the debris cloud at each time point t:

$$\overline{r}(t)={\displaystyle \frac{{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i+1}^N{r}_{ij}}}(t)}{N\times (N-1)/2}}$$

(4)

where N is the total number of fragments. Within this time window, the time point with the minimum average relative distance is defined as the preliminary breakup epoch $t^{\prime }$:

$$\overline{r}(t^{\prime })=\min [\overline{r}(t)]$$

(5)

The preliminary breakup epoch $t^{\prime }$ aids in narrowing the search scope and reducing computational load. Centered on $t^{\prime }$, define a time window $[t^{\prime }-\Delta t,t^{\prime }+\Delta t]$, Within this window, select two evaluation points, t₁ and t₂, respectively:

$$\begin{array}{l}{t}_1=b-\lambda \left(b-a\right)\\ t_2=a+\lambda \left(b-a\right)\end{array}$$

(6)

with $a=t^{\prime }-\Delta t,b=t^{\prime }+\Delta t$, denoting the window’s start and end times, where $\lambda$ is the golden ratio coefficient. During that time window, compute the average relative distances $\overline{r}(t_1)$ and $\overline{r}(t_2)$ using Equation (4), if

$$\stackrel{\sim }{r}\left(t_1\right)<\stackrel{\sim }{r}\left(t_2\right)$$

(7)

retain the left interval and discard the right interval. If

$$\stackrel{\sim }{r}\left(t_1\right)>\stackrel{\sim }{r}\left(t_2\right)$$

(8)

retain the right interval and discard the left interval. As iterations continue, the search interval continuously shrinks. When the interval length falls below the preset precision threshold $\sigma$, the required precision is considered achieved, and the iteration process terminates. At this point, take the midpoint of the smallest interval as the optimal solution, updating $t^{\prime }$ to the following:

$$t^{\prime }={\displaystyle \frac{a+b}{2}}$$

(9)

3.2. Clustering and Noise Removal

Through the above iterative process, a preliminary and relatively precise estimate of the breakup epoch can be obtained. However, due to the presence of various perturbative forces and noise interference in actual breakup events, the preliminary estimated breakup epoch may still contain errors. Furthermore, the debris cloud may contain a large number of outlier data points or noisy debris fragments, all of which can affect the accuracy of breakup epoch determination.

Therefore, to further improve the accuracy of breakup epoch determination, it is necessary to perform cluster analysis and noise removal on the debris data, further optimizing the breakup epoch estimate to achieve more precise localization of the breakup moment.

The DPC algorithm is a density-based spatial clustering algorithm [20]. Its key strength lies in its ability to automatically identify and remove noise points based on the spatial distribution density of debris fragments while preserving the primary debris clusters, enabling fast and efficient breakup epoch determination. The algorithm requires only a single input parameter, r_c (the cutoff distance) [21]. By calculating the local density ${\rho }_i$ and the separation ${\delta }_i$ for each data point, it plots a decision graph to identify density peaks as cluster centers. Subsequently, non-center points are assigned to the cluster of their nearest neighbor with higher density, and low-density outliers are effectively eliminated [22]. The detailed process is as follows:

Step 1: Calculate the local density ${\delta }_i$

For each fragment point, its local density is defined as follows:

$$\begin{array}{c}{\rho }_i={\displaystyle \sum _j}\chi \left(r_{ij}-r_c\right)\\ \chi (x)=\left\{\begin{array}{c}1,x<0\\ 0,x⩾0\end{array}\right.\end{array}$$

(10)

where r_ij represents the distance between fragments i and j, and r_c is the cutoff distance (the sole input parameter). For different datasets, the value of r_c varies and is typically set to the second percentile of the distance distribution. ${\rho }_i$ denotes the number of fragment points within a neighborhood of radius r_c.

Step 2: Calculate the separation ${\delta }_i$

To represent the closest distance from fragment i to a higher-density fragment, it is defined as follows:

$${\delta }_i=\left\{\begin{array}{c}\underset{j:{\rho }_j>{\rho }_i}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(r_{ij}\right), \mathit{i}\mathit{f} \exists j\mathit{s}.\mathit{t}. {\rho }_j>{\rho }_i\hfill \\ \underset{j}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(r_{ij}\right), \mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{w}\mathit{i}\mathit{s}\mathit{e} \end{array}\right.$$

(11)

The separation ${\delta }_i$ characterizes the minimum spanning distance between fragment i and its “density-superior” fragment. When ${\delta }_i$ is large, it indicates that the fragment is spatially distant from all higher-density neighbors and possesses the potential to become a cluster center; when ${\delta }_i$ is small, it implies that the fragment is adjacent to a high-density core and is more likely to be assigned to the cluster containing that core.

Step 3: Clustering process

After defining the local density and separation attributes for all objects, a two-dimensional decision graph is plotted with ${\rho }_i$ and ${\delta }_i$ as the horizontal and vertical axes, respectively, mapping all data objects. Based on the scatter plot, fragment objects with high ${\rho }_i$ and ${\delta }_i$ are identified as cluster centers, as shown in Figure 2.

Figure 2a displays the distribution of a dataset containing 30 data points, and Figure 2b shows the decision graph plotted from these data points. In the figures, blue circles represent ordinary data points that have been successfully assigned to clusters; red circles represent cluster centers automatically identified by the algorithm; and gray circles represent noise points or boundary points that cannot be assigned to any cluster. From the decision graph, it can be observed that Points 7 and 27 are selected as cluster centers due to their high local density and separation.

After determining the cluster centers, the remaining non-center data points are assigned to the cluster of their nearest neighbor with higher density. Furthermore, as seen from the distribution in Figure 2a, Points 10, 12, 13, 15, and 29 are far away from other points and belong to anomalous data. To effectively separate outliers, the set of points belonging to the current cluster and located at a distance not exceeding the cutoff distance d_c from other clusters is defined as the border region. Within this region, the point with the highest density is labeled ${\rho }_b$. Objects in the cluster whose density does not exceed ${\rho }_b$ are then identified as outliers.

Through the above process, the DPC algorithm can effectively perform cluster analysis on the debris data, identifying the main debris clusters and removing noise points. To further improve the accuracy of breakup epoch determination, it is necessary to reapply the steps from Section 3.1 to the cleaned debris set for orbit propagation and distance feature calculation. Specifically, first perform high-precision orbit extrapolation on the cleaned debris set within the candidate time window to obtain the position coordinates of each debris fragment at different times. Subsequently, calculate the Euclidean distance between debris fragments to generate a new relative distance matrix, and compute the average relative distance at each time point. Based on this, employ the golden section method to conduct a rapid search within the candidate time window. By continuously narrowing the search range, efficiently determine the time point t_final corresponding to the minimum average relative distance, and take this as the precisely corrected breakup epoch. This process fully utilizes the high-quality data after cluster analysis, effectively enhancing the accuracy and reliability of breakup epoch localization.

4. Simulation and Analysis

To validate the effectiveness of the proposed method, the breakup event of the US Centaur upper stage (ID: 2018-022B) on 6 September 2024, is selected as a real-world case for simulation experiments [23]. This event was detected and monitored by the US commercial space company Slingshot Aerospace, resulting in hundreds of space debris fragments. This upper stage remained in orbit after launching the GOES-17 meteorological satellite in 2018, operating in a highly elliptical orbit with a perigee geocentric distance of approximately 7634 km, an apogee geocentric distance of approximately 34,953 km, an orbital inclination of 9.4°, and an eccentricity of 0.64. The company first observed the debris cloud at 05:32 UTC on September 6. Therefore, the reliable time interval for the space object breakup is 6 September 2024, from 05:16 UTC to 05:32 UTC. The reference time is around 05:21 UTC [24].

In the simulation experiment, a high-precision orbit propagation model is first used to extrapolate the orbits of the fragments within the set time window (6 September, 04:00:00 UTC to 06:00:00 UTC). A step-size of 10 s, a relative error tolerance of 1 × 10⁻³, and an absolute error tolerance of 1 × 10⁻⁶ are adopted. The trajectories of 132 fragments in the Earth-Centered Inertial (ECI) coordinate system are generated, constructing a three-dimensional position matrix (1440 time points × 3 axes × 132 fragments). Subsequently, the relative distances between all global fragment pairs are calculated, generating a distance matrix containing 8646 fragment pairs. Through iterative calculation, the time point corresponding to the minimum average relative distance is preliminarily determined as 05:17:00 UTC on 6 September 2024. Specific results are shown in Figure 3:

After preliminarily determining the breakup epoch, cluster analysis is further performed on the fragment data to eliminate anomalous fragments and improve the determination accuracy of the breakup epoch. The Density Peak Clustering (DPC) algorithm is adopted to calculate the local density and relative distance for each fragment, thereby clustering the fragments. The cutoff distance r_c is set to the 2nd percentile of the distance distribution. Through cluster analysis, 120 cluster-assigned fragments and 12 noise fragments are identified. After removing the noise fragments, the cluster-assigned fragment set S_clean is retained. Orbit propagation and distance characteristics are recalculated. The clustering results are shown in

Table 1. Debris Clustering Analysis Results Summary Table.

Cluster Result	Quantity	Analysis of Cluster Characteristics
Cluster-Assigned Fragments	120	Concentrated semimajor axis distribution (standard deviation σ = 8.2 km)
		High spatial distribution density (>0.1 fragments/km3)
Noise Fragments	12	Abnormal orbital evolution (semimajor axis deviation > 72 km)
		Spatial isolation (nearest neighbor distance > 35 km)

:

For the cleaned fragment set S_clean, high-precision orbit extrapolation is reperformed within the candidate time window to calculate the position coordinates of each fragment at different times, generating a new relative distance matrix D_clean(t). According to Equation (4), the average relative distance of the cleaned fragment set at each time point is computed. Setting the preliminary breakup epoch of 05:17:00 UTC as the center, a local time window (±30 min) is defined, and the golden section method is used for iterative optimization. Within the local window, test points t₁ and t₂ are inserted according to the golden ratio, and their corresponding average relative distances d₁ and d₂ are calculated. Based on the comparison results, the search interval is progressively narrowed until its length is less than the preset precision threshold σ = 1 s. The results are shown in

Table 2. Breakup Time Determination Results Comparison Table.

	Calculated Breakup Time (UTC)	Reference Breakup Time (UTC)
Original Data	05:17:00	05:21:00
Noise-Reduced Data	05:19:29	05:21:00

:

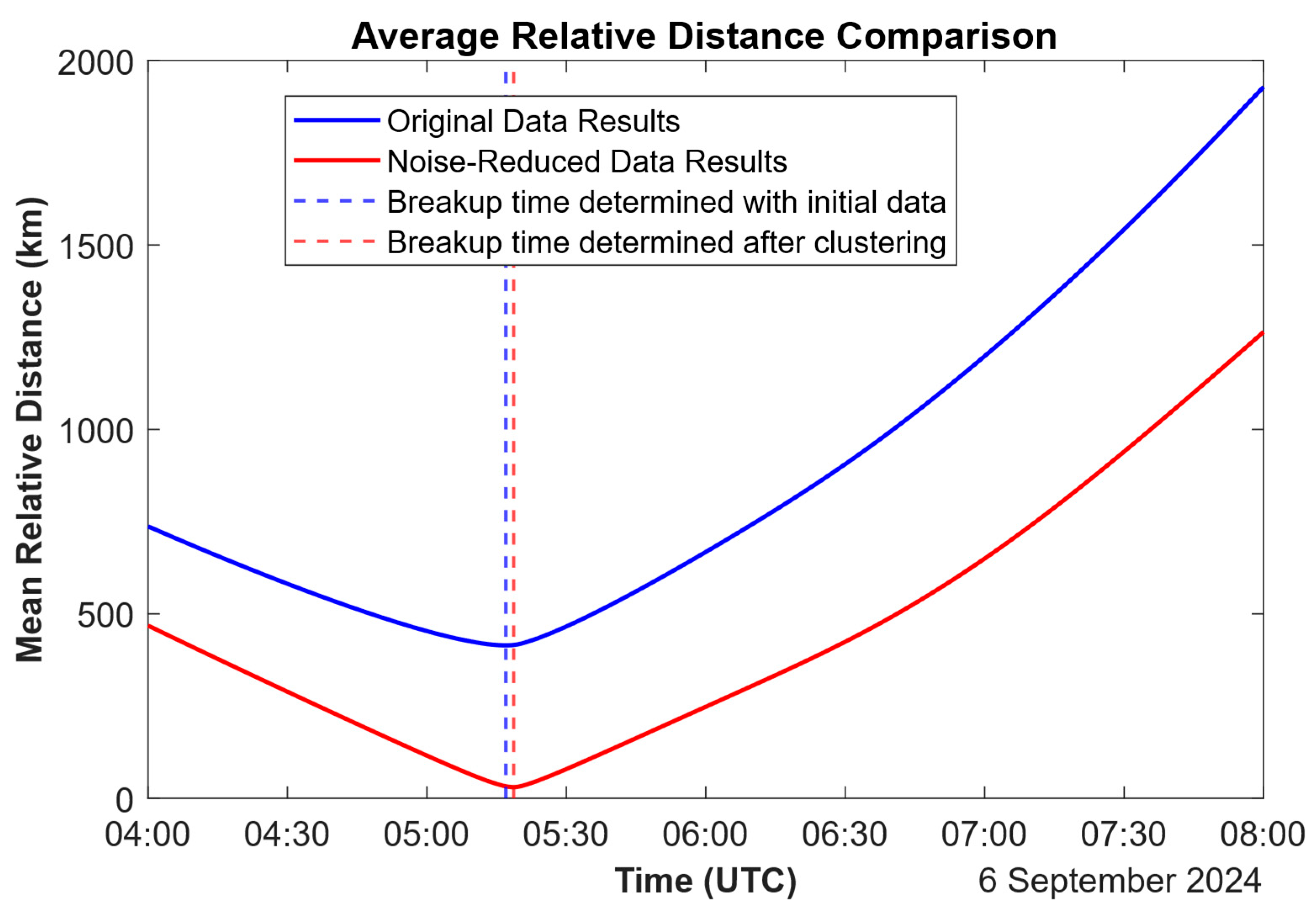
As shown in Figure 4, the horizontal axis is Time, and the vertical axis is the Average Relative Distance (unit: km). The blue curve (representing the original 132 fragments) exhibits a broad minimum region of average distance around 05:17:00 UTC. In contrast, the red curve (representing the 120 valid fragments after cluster filtering) converges to a distinct minimum at 05:19:29 UTC.

Through the above steps, the proposed method successfully refines the determined breakup epoch from the initial estimate of 05:17:00 UTC to 05:19:29 UTC, bringing it closer to the actual breakup time of 05:21:00 UTC. This result validates the effectiveness and accuracy of the proposed method in practical applications, providing reliable technical support for rapid traceability analysis of space object breakup events.

5. Conclusions

This study addresses the challenge of balancing accuracy and efficiency in tracing space object breakup events by proposing a breakup epoch determination method that integrates a clustering algorithm and average relative distance minimization. The method preliminarily identifies the breakup epoch by calculating the average relative distance between fragment pairs combined with a golden section step-size optimization strategy, effectively balancing search precision and computational efficiency. Simultaneously, the DPC density clustering algorithm is introduced to eliminate anomalous fragments, and the breakup epoch is refined based on the cleaned fragment set, enhancing robustness against data noise. Simulation experiments using the breakup event of the US Centaur upper stage (2018-022B) on 6 September 2024, as a case study, demonstrate that this method significantly improves traceability accuracy, achieving a time error of approximately 1 min and 31 s. The results confirm that the proposed method can provide a high-reliability temporal benchmark for space collision traceability, debris diffusion prediction, and orbital safety management. It holds significant engineering application value for enhancing orbital safety management capabilities. Future work could extend this approach to multi-source observational data fusion scenarios to improve traceability stability in complex orbital environments.