Behavior of the Vault in Column-Free Large-Span Metro Stations Under Asymmetric Loading
Abstract
1. Introduction
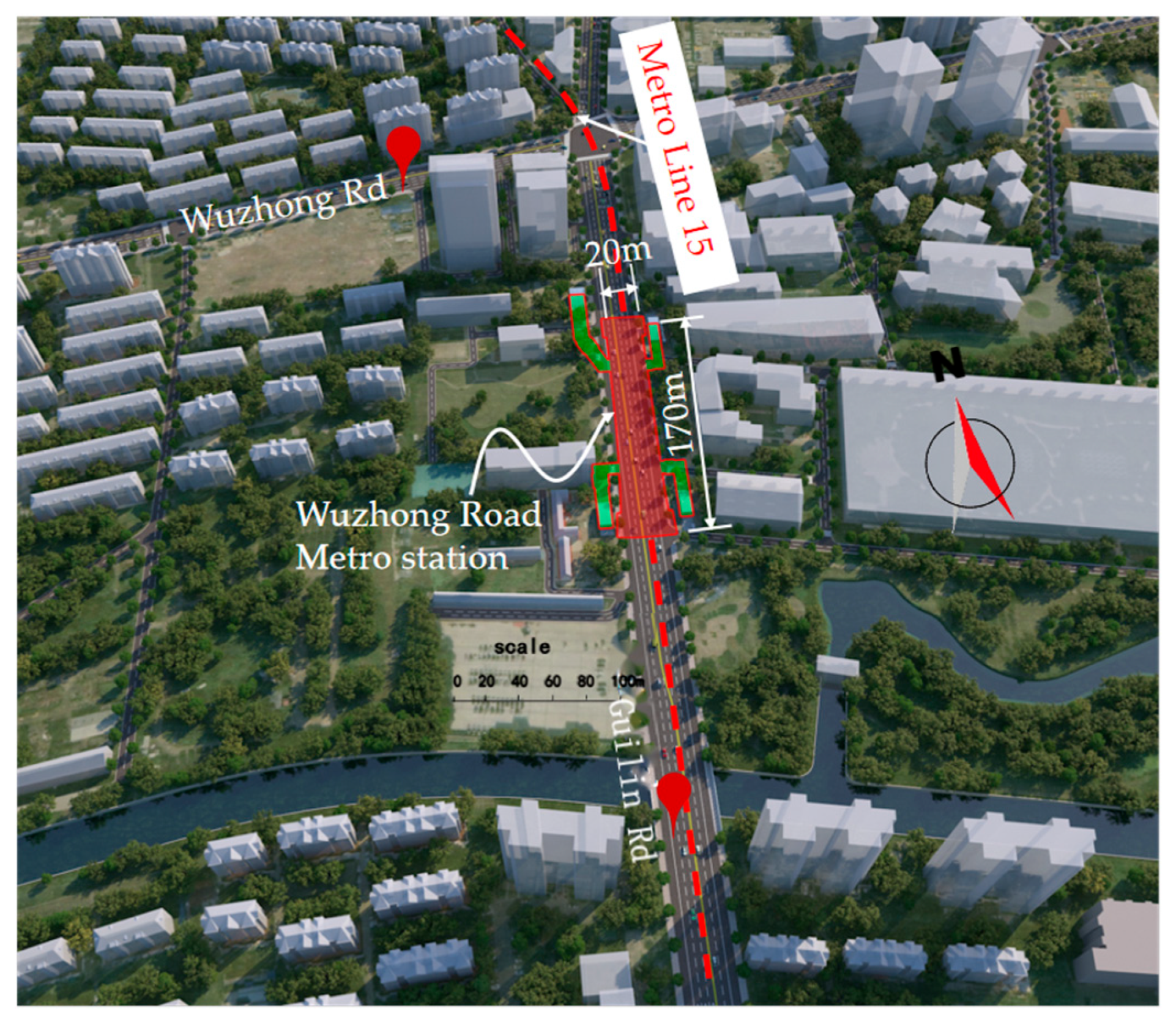
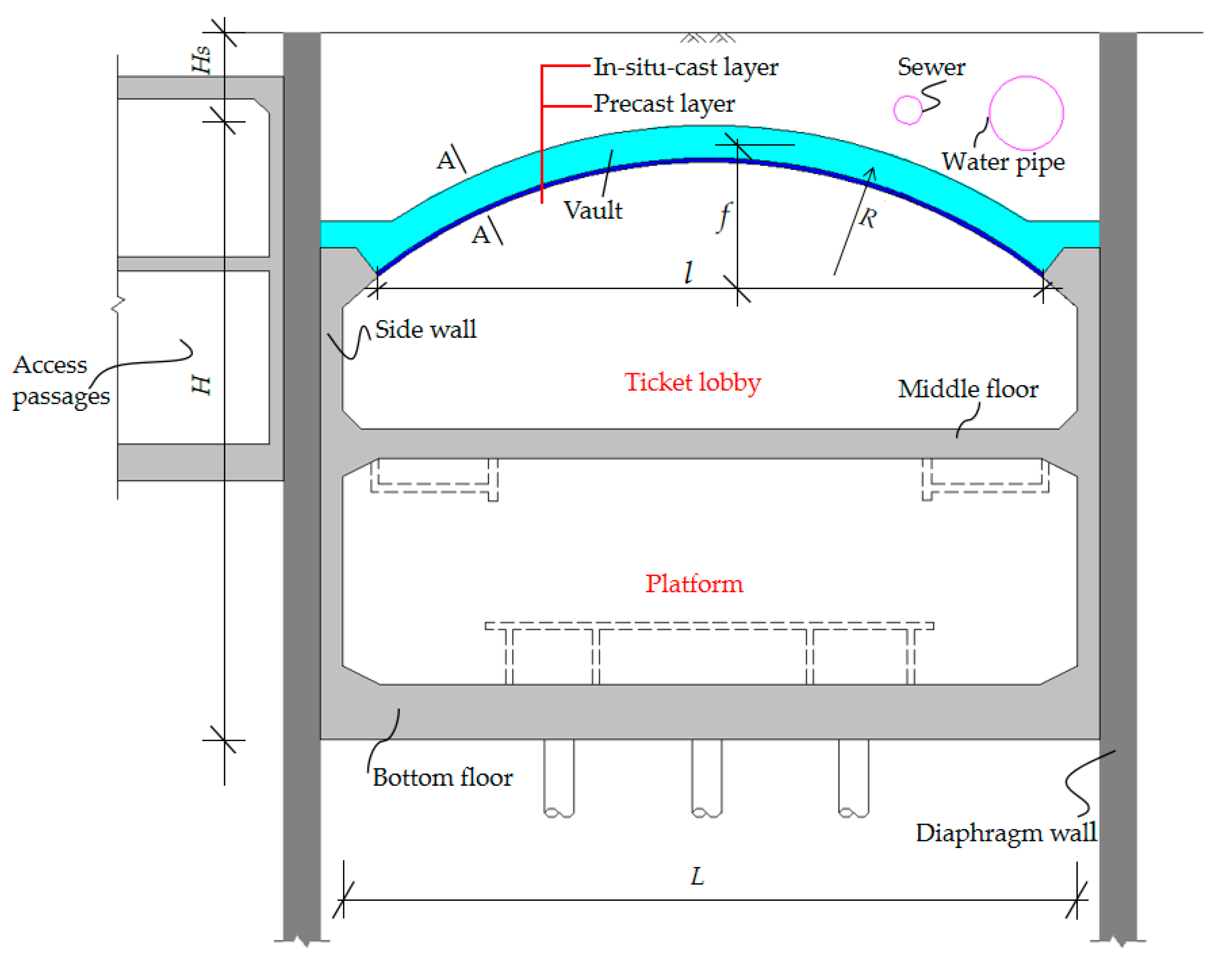
2. Engineering Background
3. Experimental Method and Results
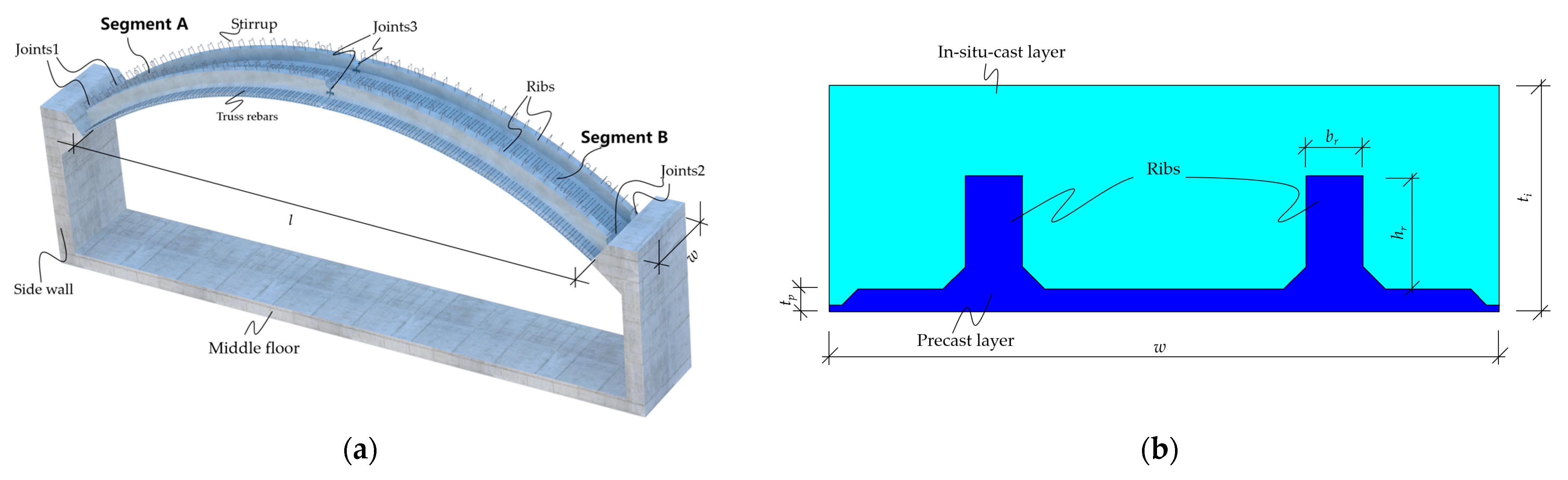
- Arch segments A and B were precast in a factory. After reaching the required concrete strength, they were transported to the construction site.
- The precast segments were assembled on site to form a three-hinged arch, as shown in Figure 3a. Cast in situ concrete was then placed on top of the precast layer to form an integral arch.
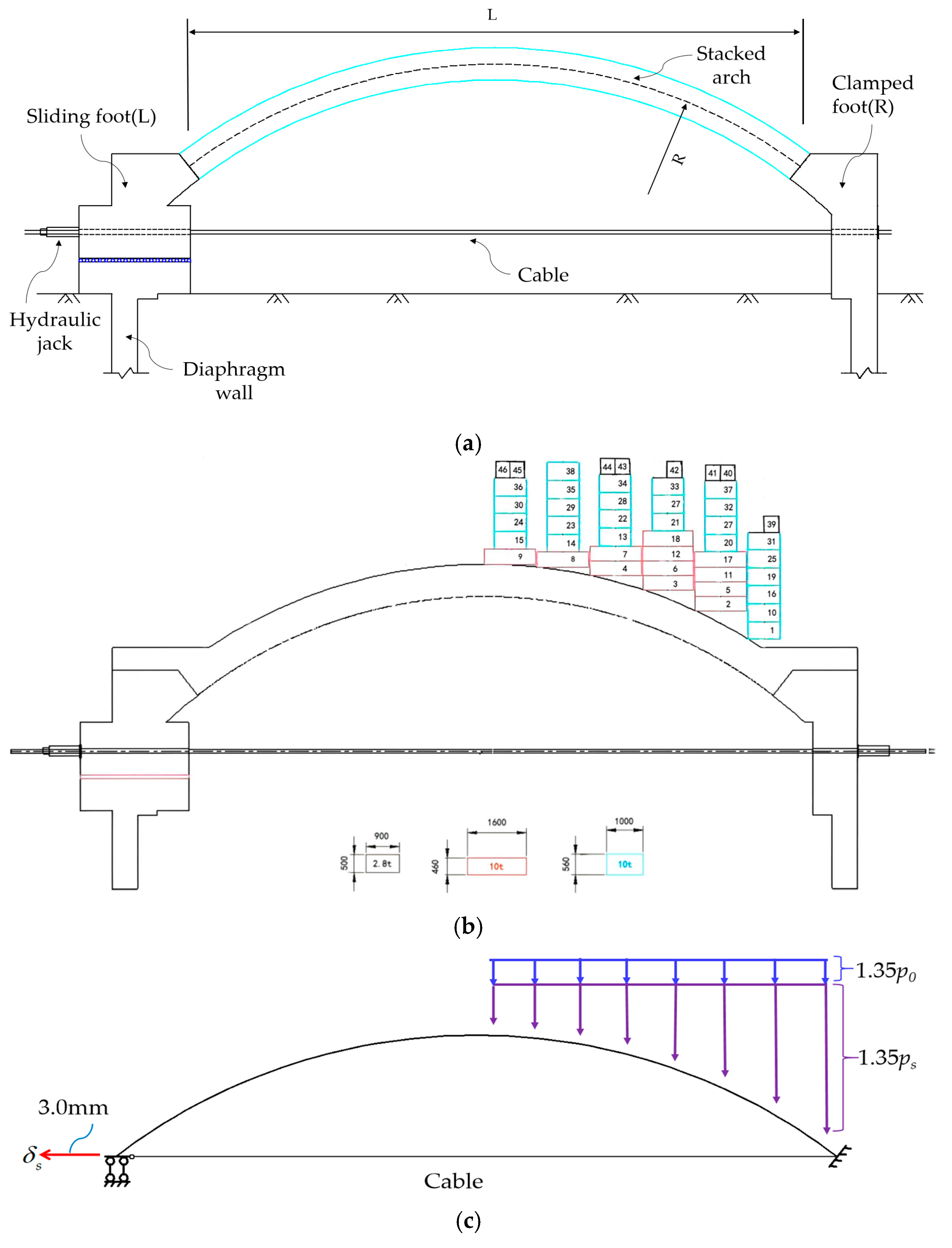
- The test was carried out using a force–displacement hybrid control method [27]. In this test, the horizontal ground pressure was set to zero, while the vertical ground pressure was increased by a safety factor of 1.35. A total of 46 iron blocks were placed on the upper surface of the arch to simulate vertical ground pressure, as illustrated in Figure 4c. By adjusting both the applied load and the prescribed displacement, the internal forces and deformations of the stacked arch were analyzed.
3.1. Test Scheme
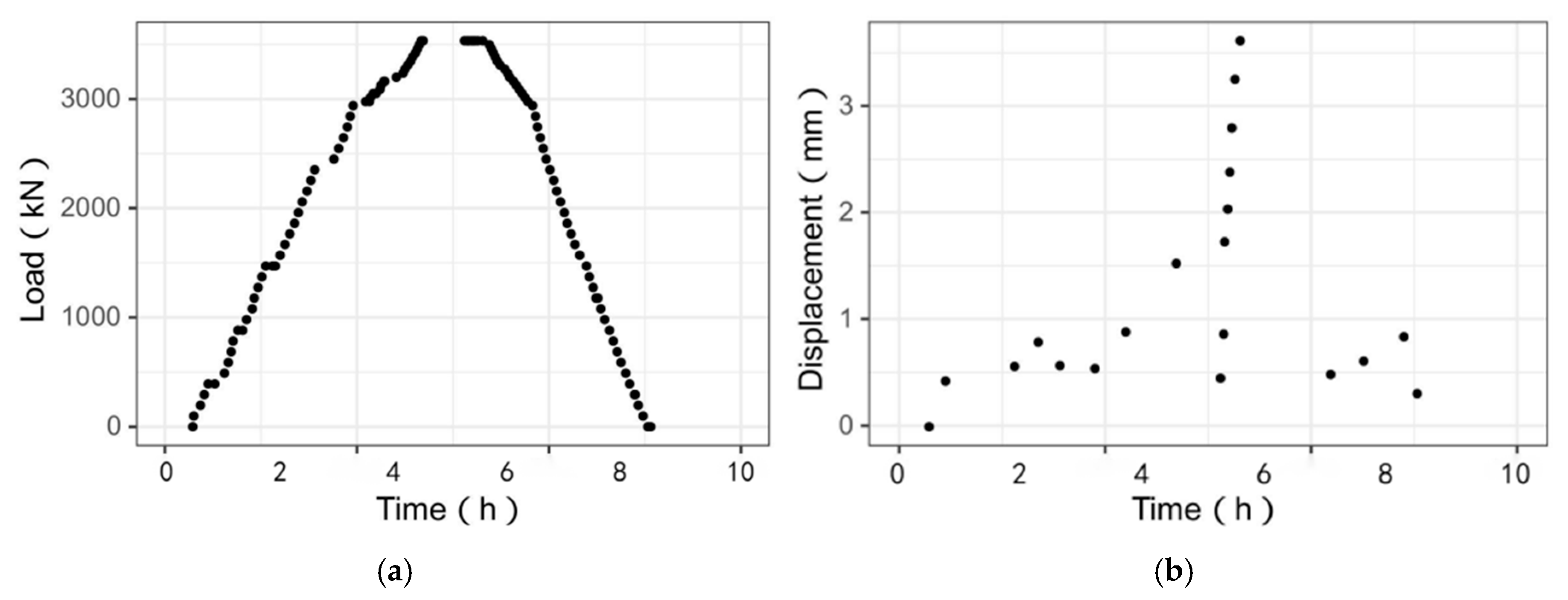
- A crane was used to stack 46 iron blocks in sequence from the fixed arch foot to the arch crown according to the numbering (see Figure 4b for the stacking order). By adjusting the jack load, the displacement of the sliding support was controlled to remain within the range of 1 mm from the initial position during the reloading process until the half-span stacking load was completed.
- After the completion of the half-span stacking load, the horizontal sliding of the left arch foot was achieved by controlling the jack, with an average speed of 0.3 mm per loading level, and the total displacement could reach 3 mm (see Figure 4b). The right arch foot was clamped. The sliding displacement was applied by adjusting the cable tension. Finally, the sliding arch foot was fixed with a restraint, marking the completion of the experiment.
- The counterweight blocks were unloaded in the reverse order of the stacking order, and the support displacement was adjusted back to the initial position.
3.2. Test Equipment
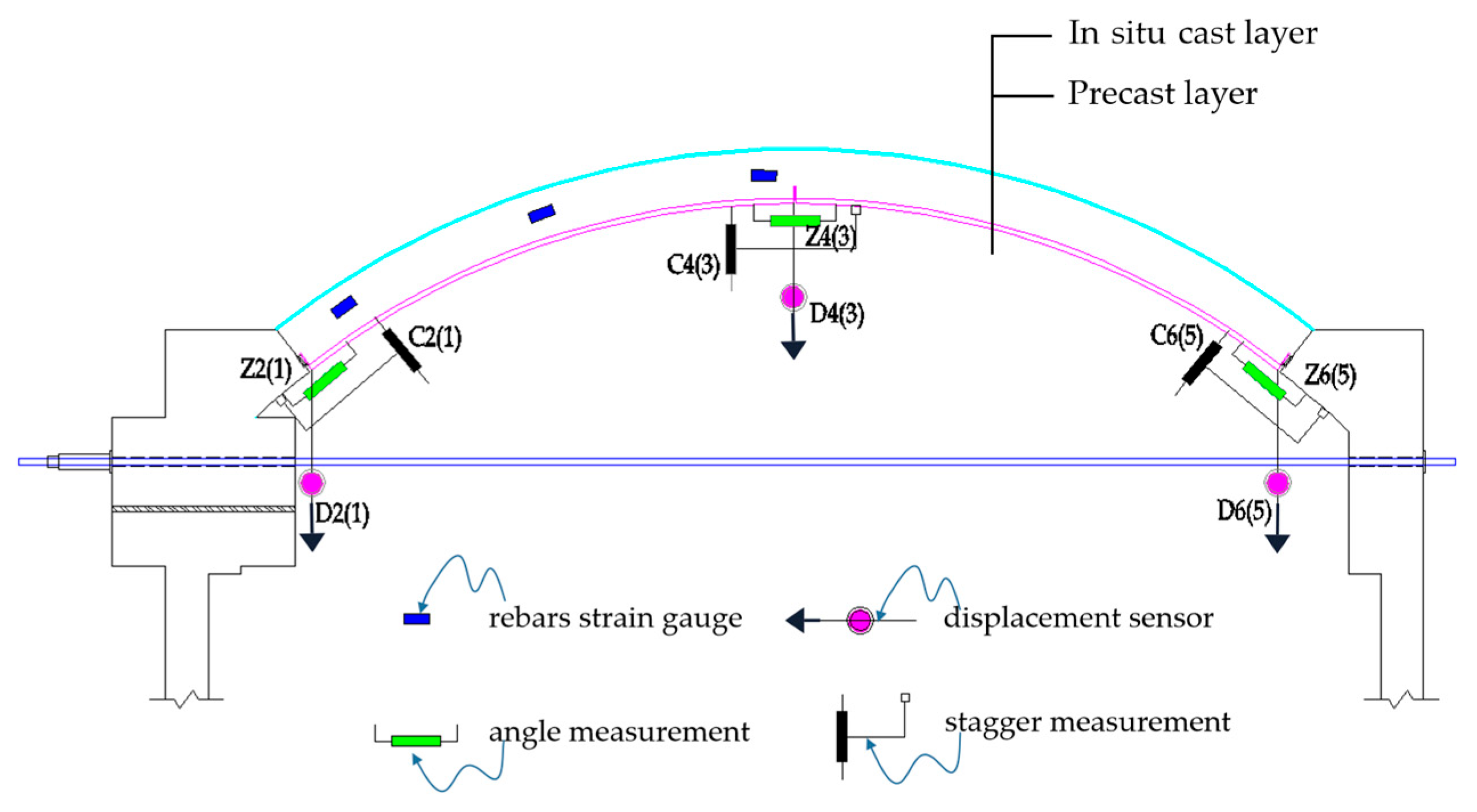
3.3. Monitoring Items
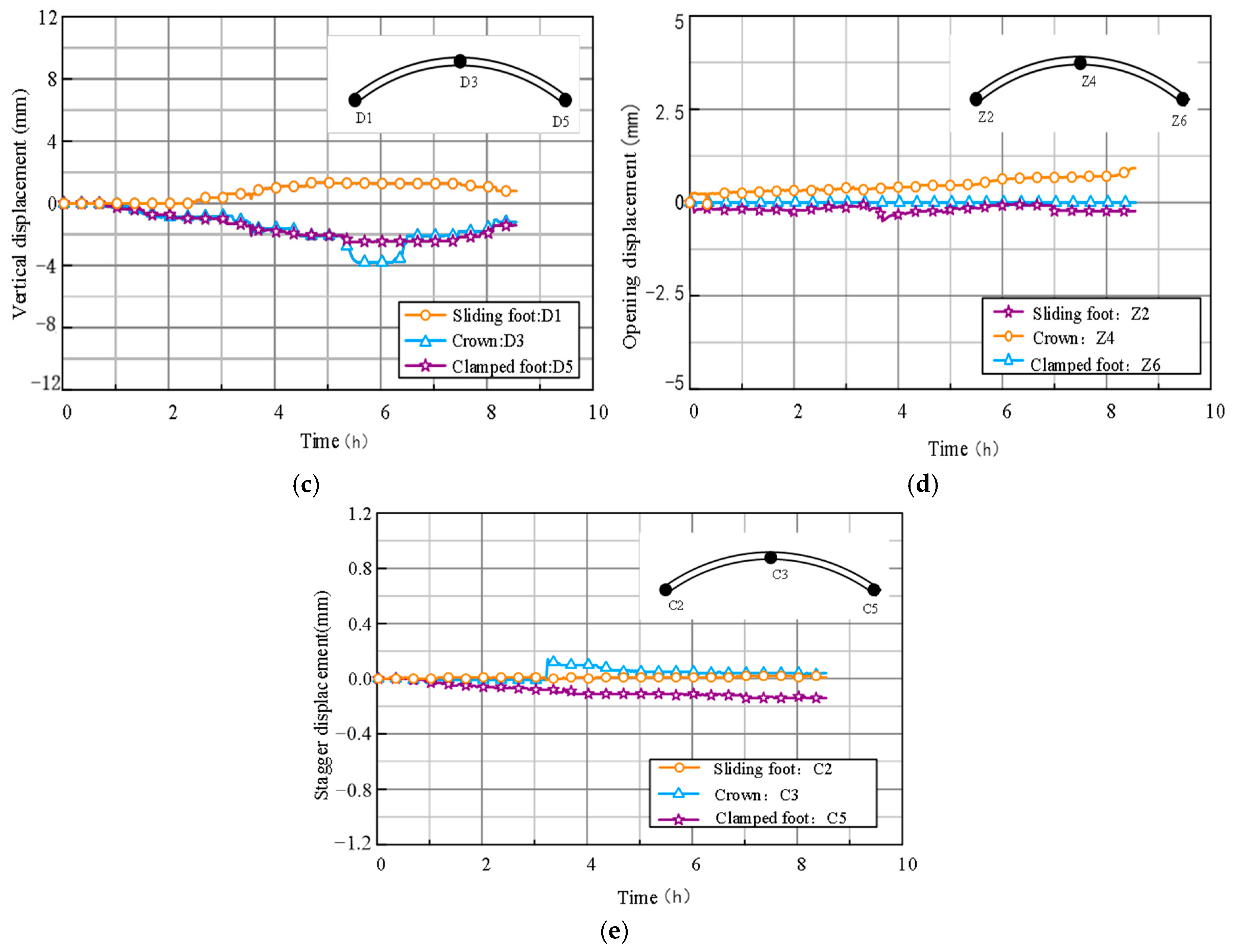
3.4. Structural Deformation
3.5. Structural Stresses
3.5.1. Precast Layer
3.5.2. Cast In Situ Layer
4. Structural Analysis
4.1. Deflection Analysis of the Arch Element
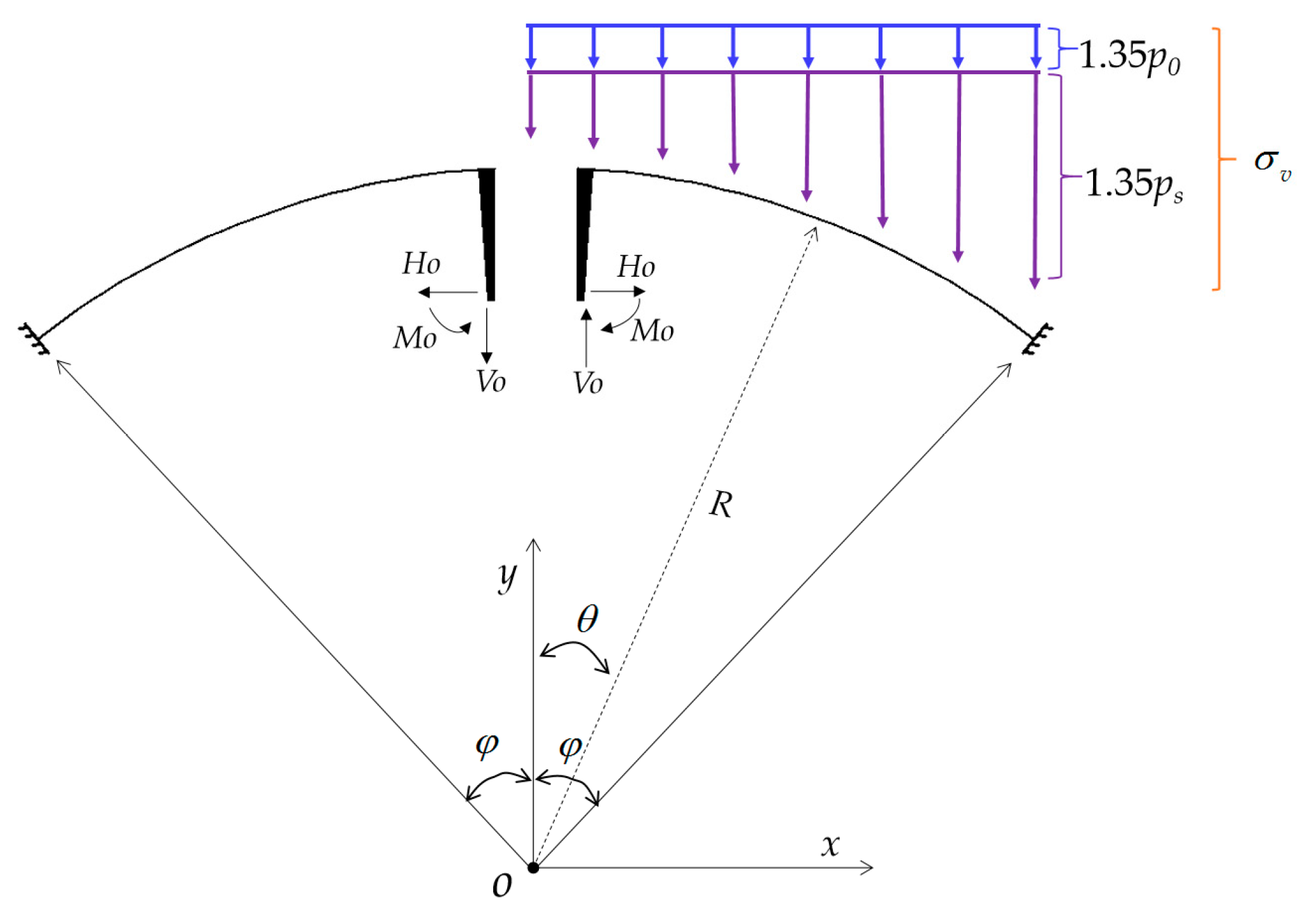
4.2. Analytical Solution of the Clamped Circular Arch Under Asymmetric Loads
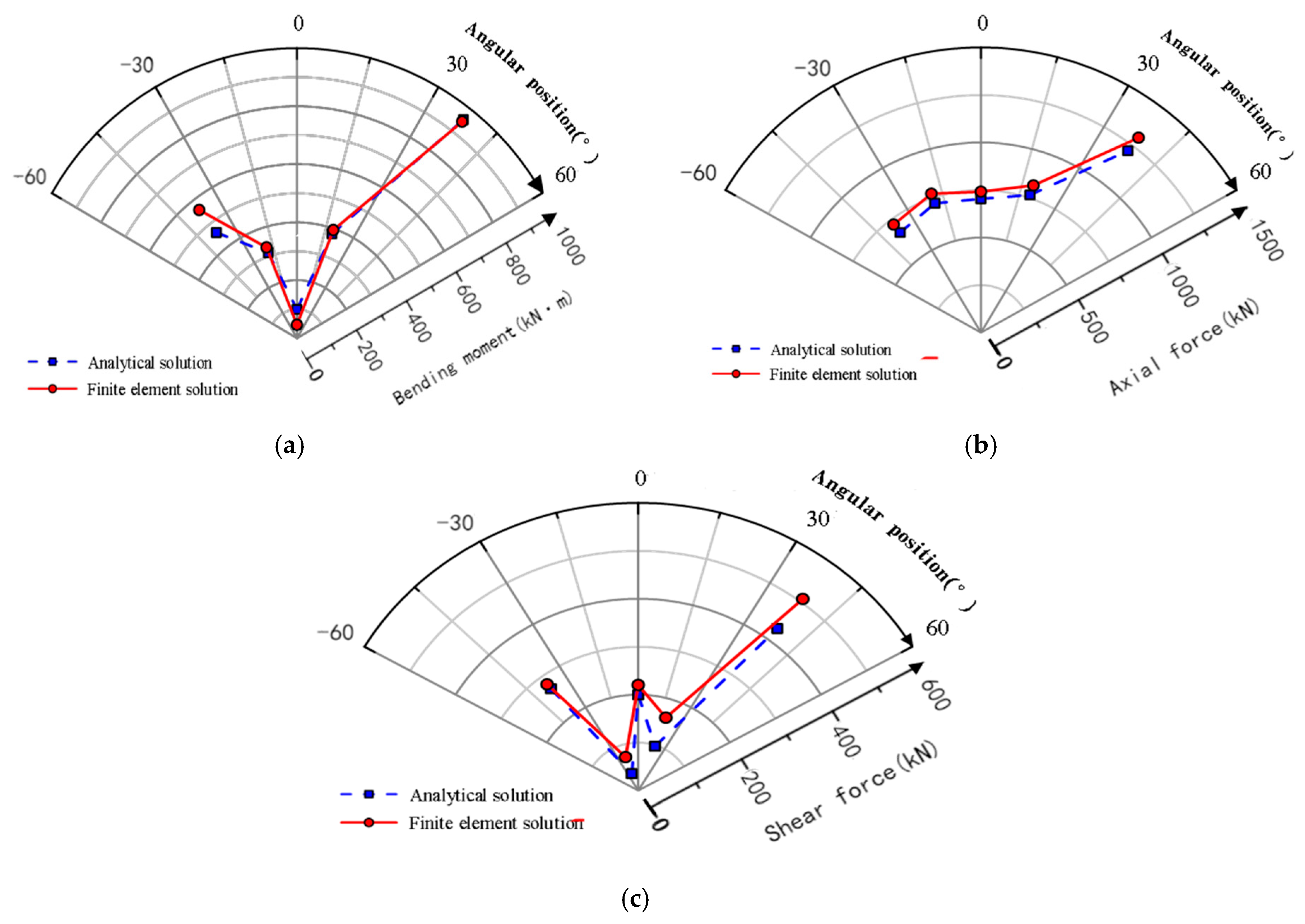
4.3. Internal Force Analysis of the Arch Element
5. Discussion
6. Conclusions
- When the weight of the steel blocks reaches 1.35 times of the vertical ground pressure, the vertical displacement of the arch crown and arch foot, as well as the staggered value and opening value of the joint change slightly. It indicates that the precast layer and cast in situ layer can work together as a whole. When the prescribed displacement of the arch foot is increased to 3 mm, this deflection of the vault crown of 3.79 mm is only 0.02% of the span of the vault. Cross sectional stiffness of the vault combined with precast and cast in situ method is acceptable.
- In the half span loading stage, the full section is compressed, and the arching effect is obvious. When the prescribed displacement of sliding foot is increased further, the arch effect gradually weakened. The maximum tensile stress and compressive stress of the rebars occur at one half of the left and right arches. The change in-internal force of the rebars is basically within the range of −30 MPa and 20 MPa. The results are less than the yield stress of the rebars. It is proven that the stacked arch has a large safety reserve, and there is room for optimal design of the structure.
- The computed value results in an increase in the maximum deflection of the arch by 13.67%, compared to the experimental results, which indicates that the reliability of the numerical simulation method is verified under the same boundary conditions.
- In order to check the validity of the derived analytical solutions of the clamped arch for ground pressure resulting from the vertical ground pressure. Compared to the numerical simulation, the maximum error range is 7.32% to 30.14%. The results are in good agreement with each other. It is verified the reliability of the analytical solution of the clamped circular arch under the asymmetric loads derived from the tested arch. The consistency demonstrated by the mutual verification of full-scale test results, numerical simulation results, and analytical solutions also provides strong support for the reliability of the numerical model and the general applicability of the conclusions.
- During this test, the response of the stacked arch structure to the arch feet displacement is obvious. Therefore, the lateral displacement of arch feet is an important index to control the safety of underground arch structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lu, L.; Qiu, J.; Yuan, Y.; Tao, J.; Yu, H.; Wang, H.; Mang, H. Large-scale test as the basis of investigating the fire-resistance of underground RC substructures. Eng. Struct. 2019, 178, 12–23. [Google Scholar] [CrossRef]
- He, X.; Zhang, Z.; Yuan, Y.; Yu, H.; Bilotta, E. Improving seismic performance of an atrium-style metro station using CFRP composites. Soil Dyn. Earthq. Eng. 2025, 197, 109535. [Google Scholar] [CrossRef]
- Tao, L.; Shi, C.; Ding, P.; Yang, X.; Bao, Y.; Wang, Z. Shaking table test of the effect of an enclosure structure on the seismic performance of a prefabricated subway station. Tunn. Undergr. Space Technol. 2022, 125, 104533. [Google Scholar] [CrossRef]
- Cao, L.; Fang, Q.; Zhang, D.; Chen, T. Subway station construction using combined shield and shallow tunnelling method: Case study of Gaojiayuan station in Beijing. Tunn. Undergr. Space Technol. 2018, 82, 627–635. [Google Scholar] [CrossRef]
- Sadaghiani, M.H.; Dadizadeh, S. Study on the effect of a new construction method for a large span metro underground station in Tabriz-Iran. Tunn. Undergr. Space Technol. 2010, 25, 63–69. [Google Scholar] [CrossRef]
- Pichler, C.; Lackner, R.; Spira, Y.; Mang, H.A. Thermochemomechanical assessment of ground improvement by jet grouting in tunneling. J. Eng. Mech. 2003, 129, 951–962. [Google Scholar] [CrossRef]
- Ayaydin, N.; Ekici, Z.; Walter, H. Metro Istanbul–Kadıköy, an underground station close to the sea and below a historical building. Geomech. Tunnelbau 2008, 1, 189–196. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y. Research of surface settlement for a single arch long-span subway station using the Pipe-roof Pre-construction Method. Tunn. Undergr. Space Technol. 2018, 72, 210–217. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, A. Study on the stability of a large-span subway station constructed by combining with the shaft and arch cover method. Tunn. Undergr. Space Technol. 2022, 127, 104582. [Google Scholar] [CrossRef]
- Zhang, J.L.; Liu, X.; Zhao, J.B. Application of a combined precast and cast-in-situ construction method for large-span underground archs. Tunn. Undergr. Space Technol. 2021, 111, 103795. [Google Scholar] [CrossRef]
- Zhang, J.L.; Liu, X.; Yuan, Y. Transfer relations: Useful basis for computer-aided engineering of circular arch structures. Eng. Comput. 2021, 38, 1287–1302. [Google Scholar] [CrossRef]
- Kim, S.; Chang, S.; Castro-Lacouture, D. Dynamic modeling for analyzing impacts of skilled labor shortage on construction project management. J. Manag. Eng. 2020, 36, 04019035. [Google Scholar] [CrossRef]
- Huang, B.T.; Li, Q.H.; Xu, S.L. Development of reinforced ultra-high toughness cementitious composite permanent formwork: Experimental study and digital image correlation analysis. Compos. Struct. 2017, 180, 892–903. [Google Scholar] [CrossRef]
- Ding, P.; Tao, L.; Yang, X. Three-dimensional dynamic response analysis of a single-ring structure in a precast subway station. Sustain. Cities Soc. 2019, 45, 271–286. [Google Scholar] [CrossRef]
- Tao, L.; Ding, P.; Shi, C. Shaking table test on seismic response characteristics of precast subway station structure. Tunn. Undergr. Space Technol. 2019, 91, 102994. [Google Scholar] [CrossRef]
- Qiu, T.; Chen, X.; Rao, W.; Su, D.; Bao, X.; Hong, C. Intelligent monitoring-based resilience assessment system for prefabricated underground structures based on restorability. Tunn. Undergr. Space Technol. 2025, 158, 106411. [Google Scholar] [CrossRef]
- Qiu, T.; Chen, X.; Chen, K.; Su, D.; Shen, J.; Wang, L.; Zheng, Z. An adaptation resilience assessment framework for key components of prefabricated underground stations. Tunn. Undergr. Space Technol. 2023, 136, 105037. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; McGraw Hill Book Company, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Zhang, J.L.; Vida, C.; Yuan, Y. A hybrid analysis method for displacement-monitored segmented circular tunnel rings. Eng. Struct. 2017, 148, 839–856. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A.; Liu, A. Nonlinear equilibrium and buckling of fixed shallow arches subjected to an arbitrary radial concentrated load. Int. J. Struct. Stab. Dyn. 2017, 17, 1750082. [Google Scholar] [CrossRef]
- Lu, H.; Liu, A.; Pi, Y.L.; Bradford, M.A.; Fu, J.; Huang, Y. Localized loading and nonlinear instability and post-instability of fixed arches. Thin Wall. Struct. 2018, 131, 165–178. [Google Scholar] [CrossRef]
- Stevens, L.K. Carrying capacity of mild-steel arches. ICE Proc. 1957, 6, 493–514. [Google Scholar] [CrossRef]
- Lu, Y.; Cheng, Y.; Han, Q. Experimental investigation into the in-plane buckling and ultimate resistance of circular steel arches with elastic horizontal and rotational end restraints. Thin Wall. Struct. 2017, 118, 164–180. [Google Scholar] [CrossRef]
- Liu, J.P.; Hu, H.F.; Li, J.; Chen, Y.F.; Zhang, L. Flexural behavior of prestressed concrete composite slab with precast inverted T-shaped ribbed panels. Eng. Struct. 2020, 215, 110687. [Google Scholar] [CrossRef]
- Zhang, J.S.; Yao, Y.; Wang, Y.Z. Failure Mode and Ultimate Bearing Capacity of Precast Ribbed Panels Used for Concrete Composite Slabs. Adv. Struct. Eng. 2013, 16, 2005–2017. [Google Scholar] [CrossRef]
- Zheng, W.; Lu, X.; Wang, Y. Flexural behaviour of concrete composite slabs with precast ribbed reactive powder concrete bottom panels. J. Comput. Theor. Nanos 2016, 13, 1831–1839. [Google Scholar] [CrossRef]
- Pan, P.; Nakashima, M.; Tomofuji, H. Online test using displacement-force mixed control. Earthq. Eng. Struct. Dyn. 2005, 34, 869–888. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zhao, J.B.; Liu, X.; Jiang, S.C.; Yang, Z.H.; Jiang, H.C. Experimental investigation on structural behavior of a stacked reinforced-concrete arch. In Proceedings of the Fib Symposium 2019: Concrete—Innovations in Materials, Design and Structures, International Federation for Structural Concrete, Krakow, Poland, 27–29 May 2019; pp. 2270–2277. [Google Scholar]
- Ryu, J.S.; Otsuki, N. Crack closure of reinforced concrete by electrodeposition technique. Cem. Concr. Res. 2002, 32, 159–164. [Google Scholar] [CrossRef]
- Lee, H.X.D.; Wong, H.S.; Buenfeld, N.R. Self-sealing of cracks in concrete using superabsorbent polymers. Cem. Concr. Res. 2016, 79, 194–208. [Google Scholar] [CrossRef]
- Win, P.P.; Watanabe, M.; Machida, A. Penetration profile of chloride ion in cracked reinforced concrete. Cem. Concr. Res. 2004, 34, 1073–1079. [Google Scholar] [CrossRef]
- Shan, B.; Zheng, S.; Ou, J. A stereovision-based crack width detection approach for concrete surface assessment. KSCE J. Civ. Eng. 2016, 20, 803–812. [Google Scholar] [CrossRef]
- GB 50010-2010; State Standard of the People’s Republic of China: Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- Nicoletti, F.; Carbonari, S.; Gara, F. Design tools for pre-design of reinforced concrete beam-column joints based on Eurocode 8. Structures 2022, 39, 958–973. [Google Scholar] [CrossRef]
- Hu, Z.; Wen, W.; Zhai, C.; Pei, S. Seismic resilience of urban metro systems: A review of earthquake effects and performance-based strategies. Tunneling Undergr. Space Technol. 2024, 152, 105920. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; Yao, J.I. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]

| Load Form | Control Variable | Deflection at the Crown | ||
|---|---|---|---|---|
| Prescribed Displacement of the Sliding Foot (mm) | Load (kN) | Experimental Measurement (mm) | Numerical Simulation (mm) | |
| Half span load | 3.0 | Vertical ground pressure × 1.35 | 3.79 | 4.39 |
| Material | Cross-Section (m2) | Constraint Condition | Uniformly Distributed Line Load (kN/m) | Circular Distributed Line Load (kN/m) |
|---|---|---|---|---|
| Concrete (C40) | 1.0 | fixed constraints | 99.78 | 120.48 |
| Safety Threshold | Internal Force | Crack Width (mm) | ||
|---|---|---|---|---|
| Displacement Calculation Value (mm) | Bending Moment (kN·m) | Axial Force (kN) | ||
| 2.29 | 244.38 | 224.92 | 0.02 | Cracks visible |
| 6.76 | 723.00 | 665.40 | 0.20 | Maximum limit [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.-L.; Qiao, G.-H.; Zhou, Z.; Li, C. Behavior of the Vault in Column-Free Large-Span Metro Stations Under Asymmetric Loading. Appl. Sci. 2025, 15, 10944. https://doi.org/10.3390/app152010944
Zhang J-L, Qiao G-H, Zhou Z, Li C. Behavior of the Vault in Column-Free Large-Span Metro Stations Under Asymmetric Loading. Applied Sciences. 2025; 15(20):10944. https://doi.org/10.3390/app152010944
Chicago/Turabian StyleZhang, Jiao-Long, Guan-Hua Qiao, Zheng Zhou, and Cao Li. 2025. "Behavior of the Vault in Column-Free Large-Span Metro Stations Under Asymmetric Loading" Applied Sciences 15, no. 20: 10944. https://doi.org/10.3390/app152010944
APA StyleZhang, J.-L., Qiao, G.-H., Zhou, Z., & Li, C. (2025). Behavior of the Vault in Column-Free Large-Span Metro Stations Under Asymmetric Loading. Applied Sciences, 15(20), 10944. https://doi.org/10.3390/app152010944





