Investigation into Anchorage Performance and Bearing Capacity Calculation Models of Underreamed Anchor Bolts
Abstract
1. Introduction
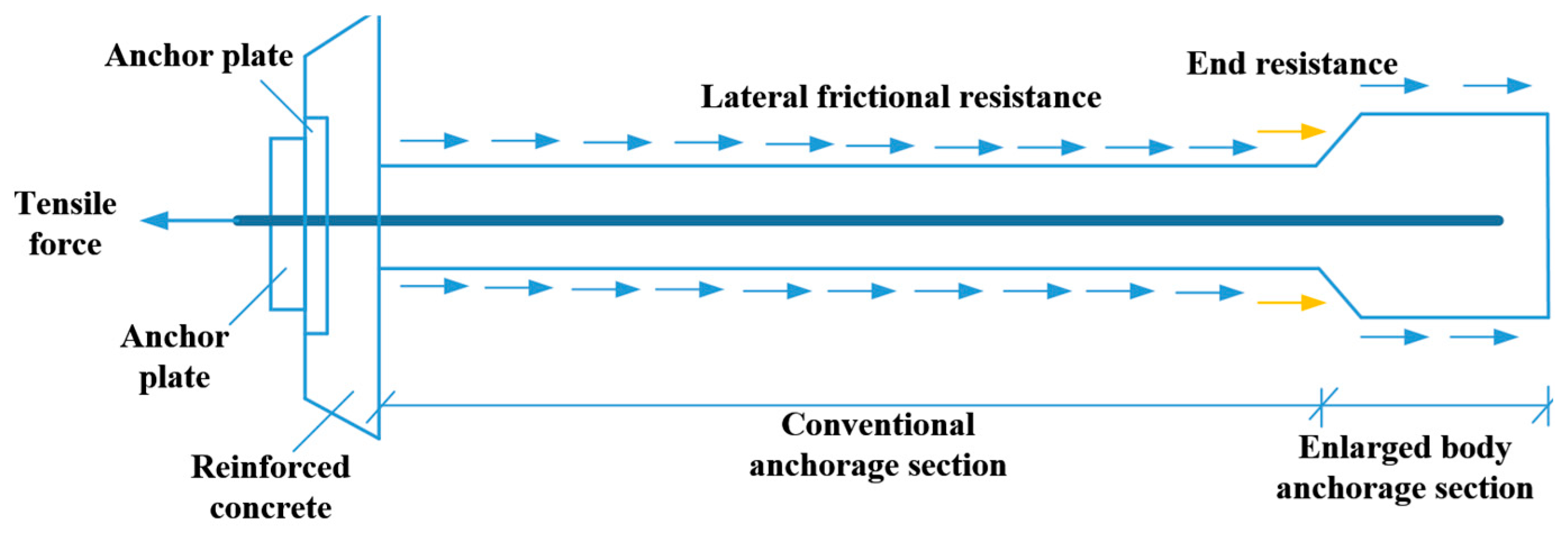
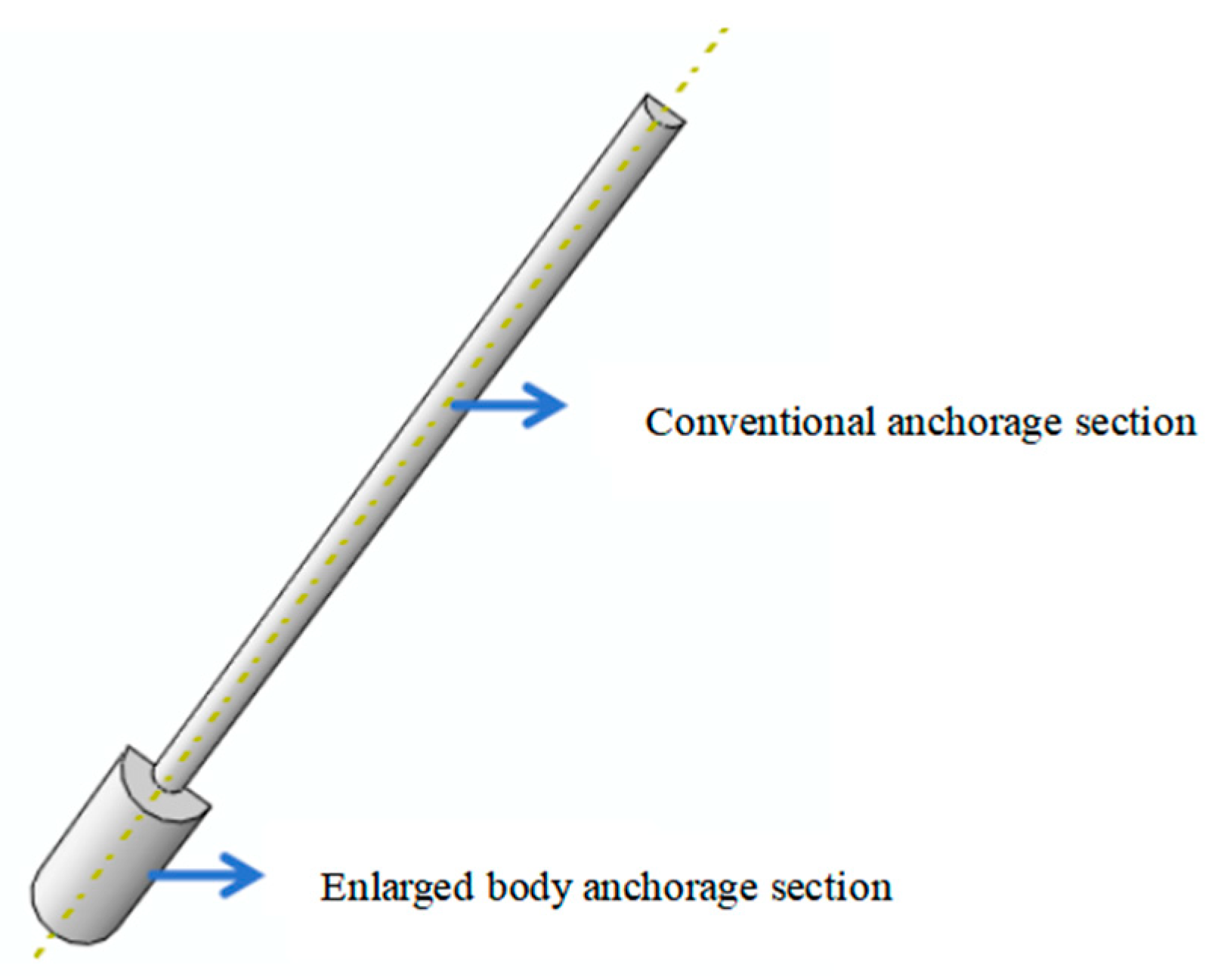
2. Characteristics of Load Transfer for Underreamed Anchor
3. Characteristics of Anchoring by Underreamed Anchors
4. Failure Modes of Soil Surrounding Enlarged Body Anchor Rod
4.1. The Geometric Dimensions and Material Properties of the Model
4.2. The Determination of Contact Stiffness
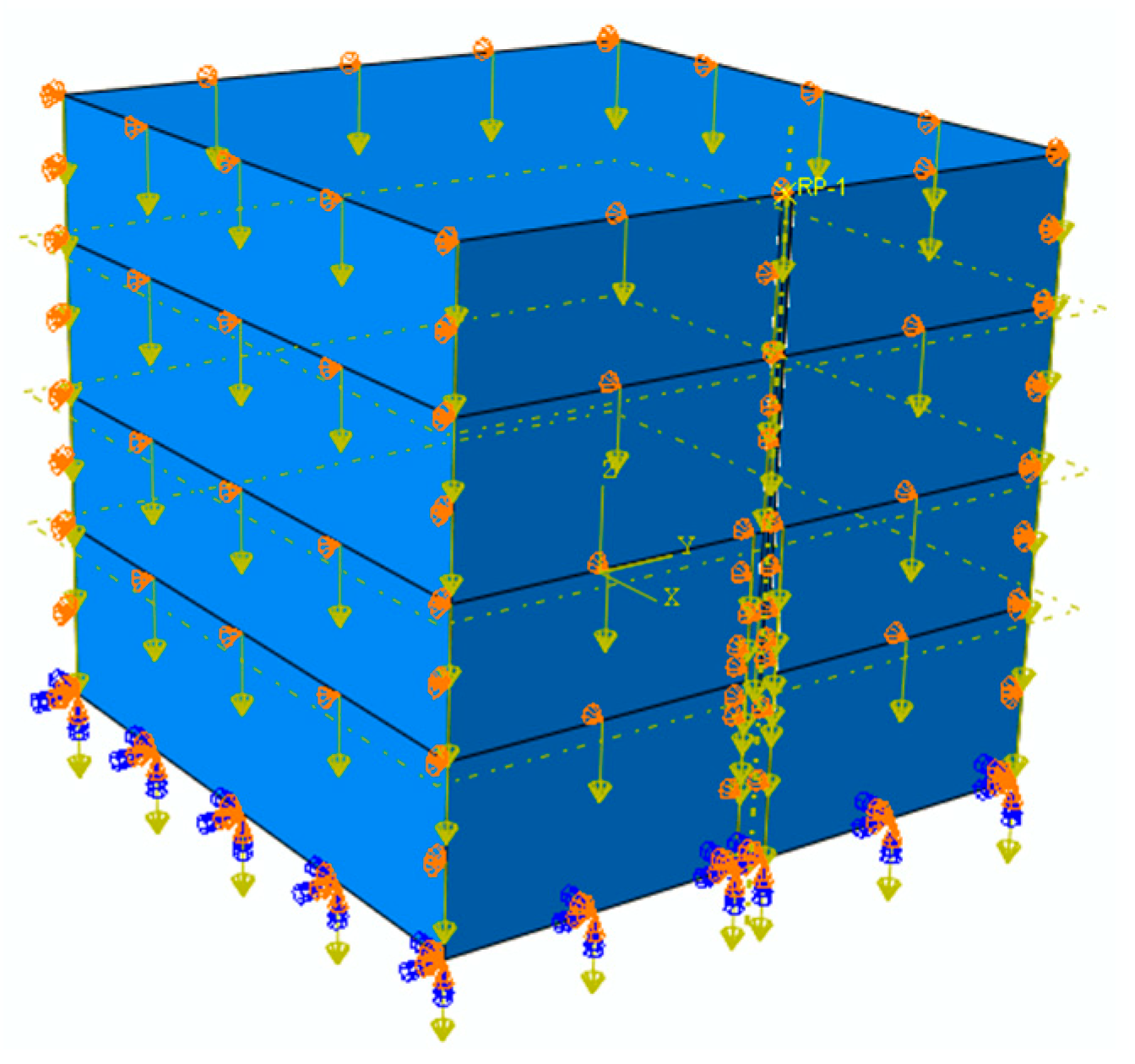
4.3. Boundary Loading and Mesh Generation
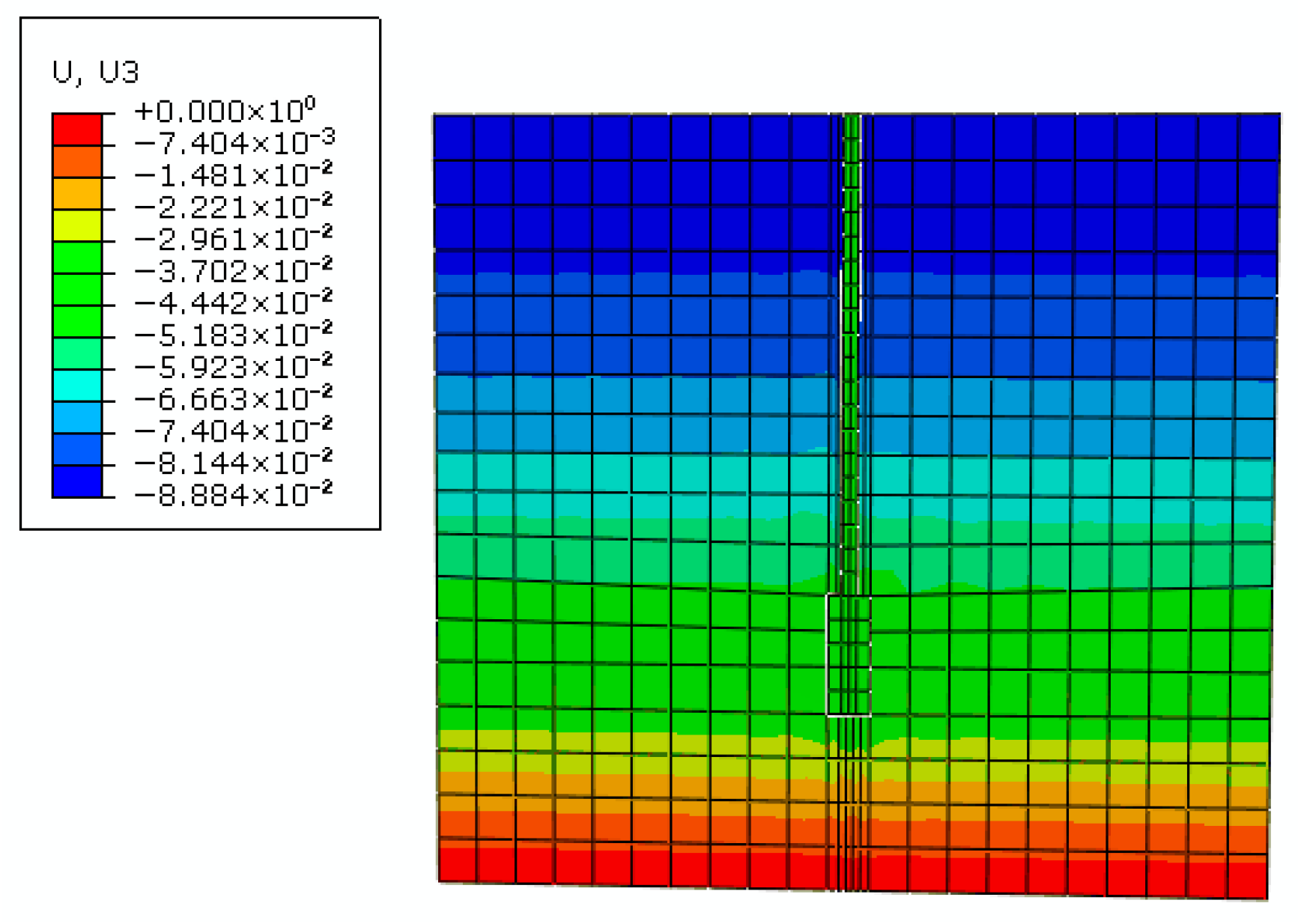
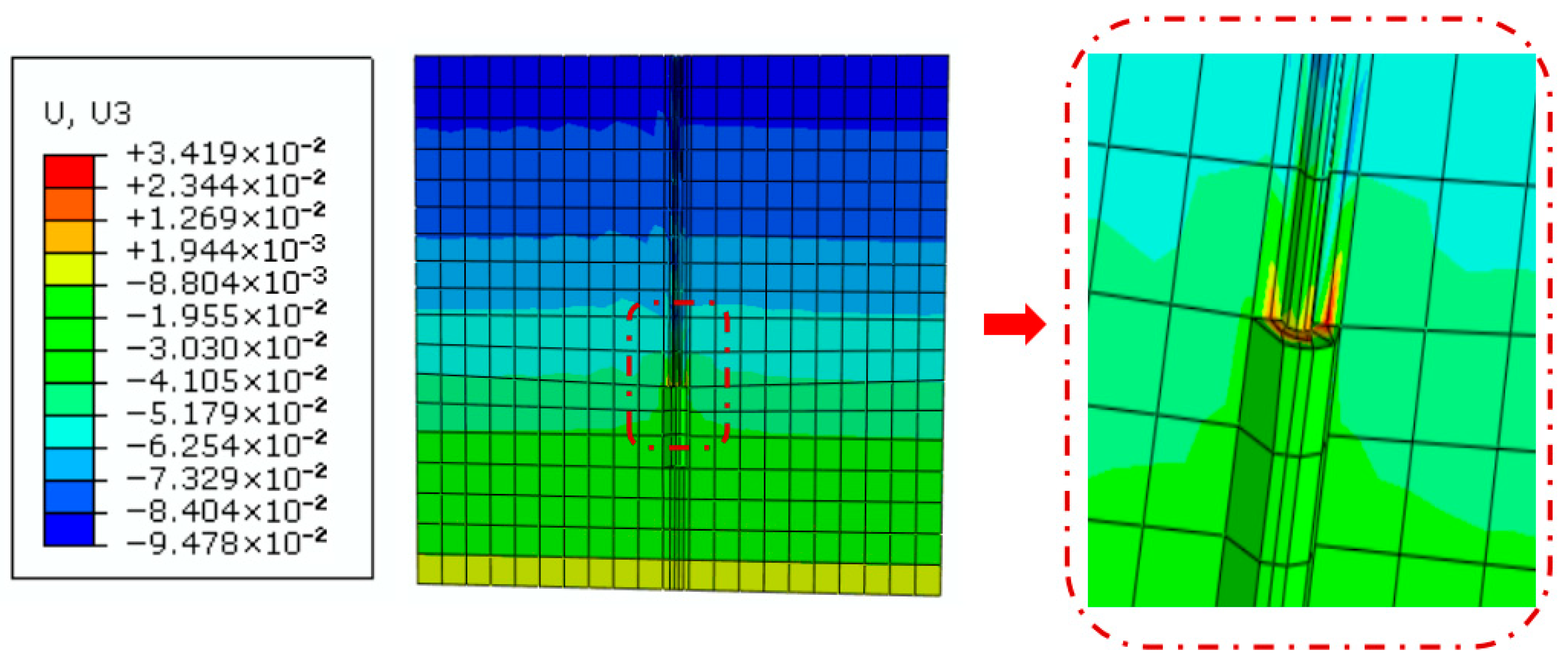
4.4. Analysis of Soil Failure Patterns Around Anchors
5. Analysis of Side Frictional Stress and End-Bearing Capacity
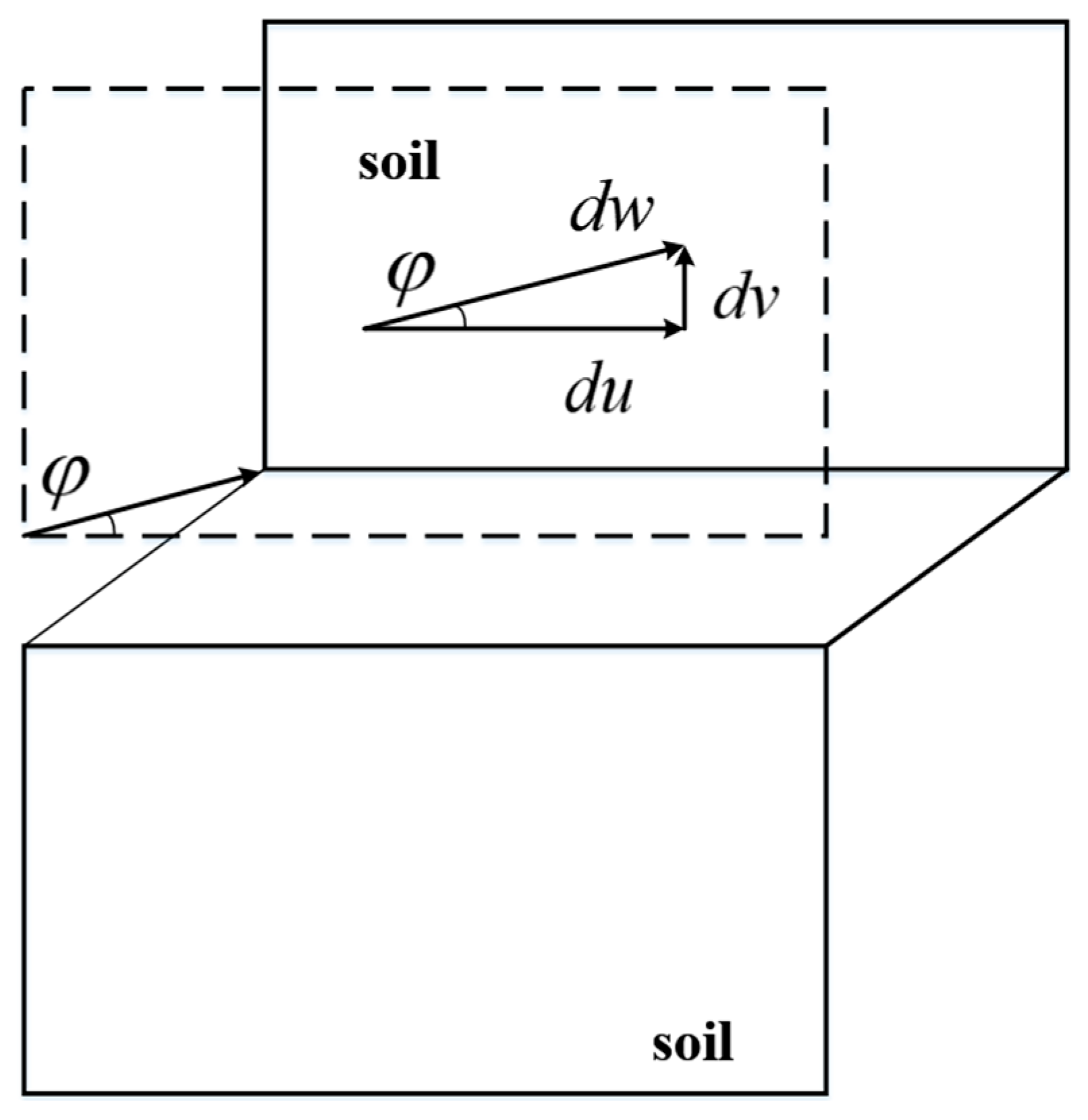
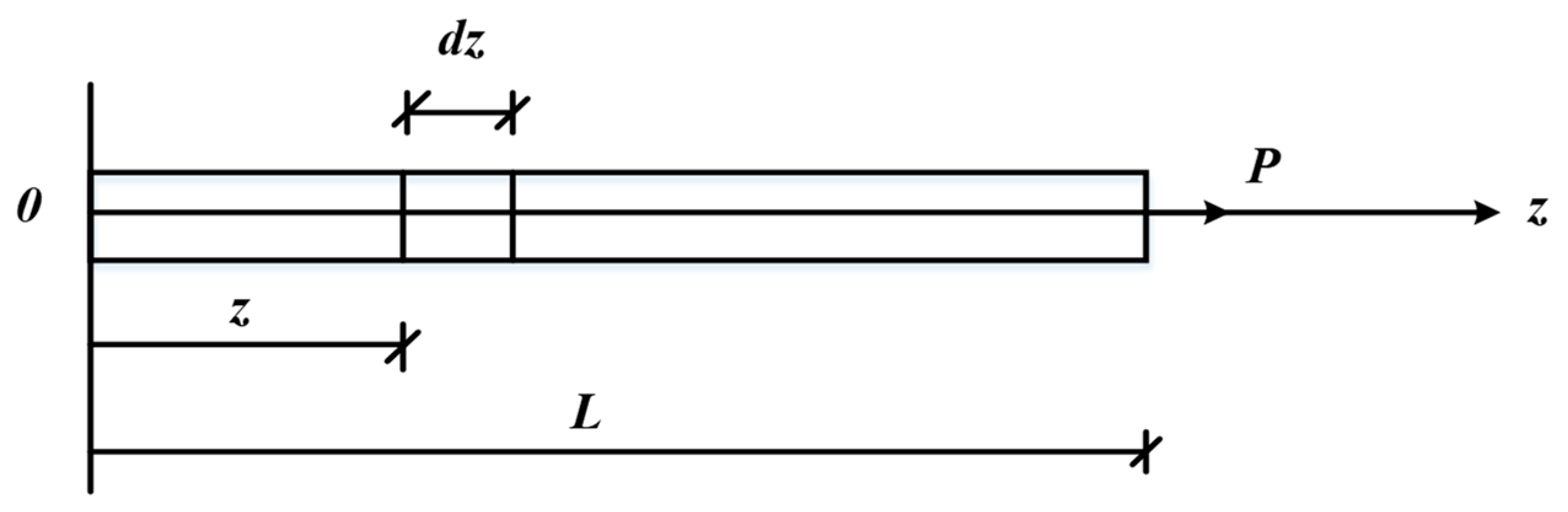
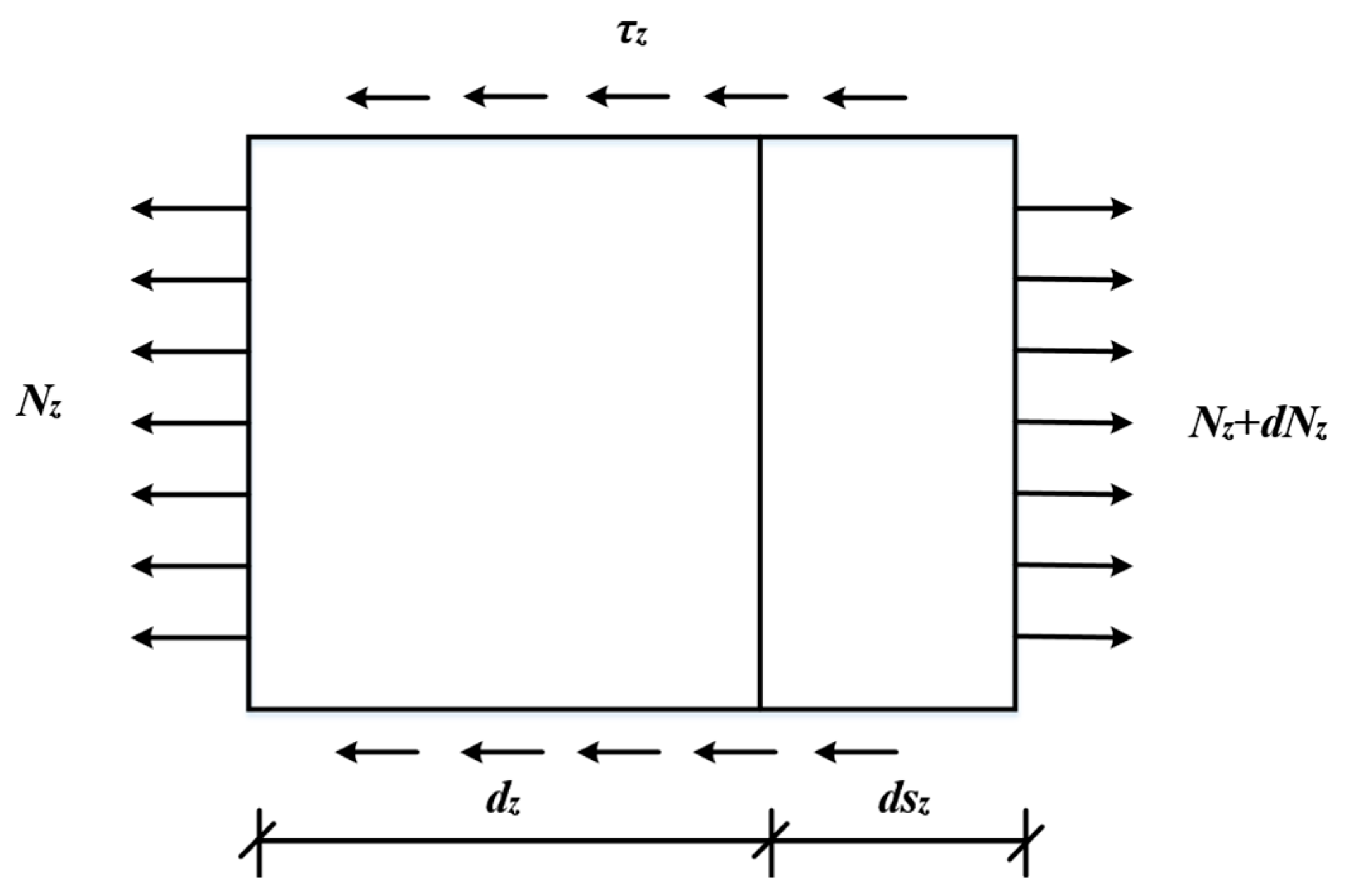
5.1. Analytical Model for Shaft Frictional Stress
- When z = L, the axial force satisfies Nz = P. Substituting this condition into the expression for the axial force, Equation (26), yields
- 2.
- When z = L, τ(L) = 0, substituting this condition into the expression for the interfacial shear stress, Equation (24), yields
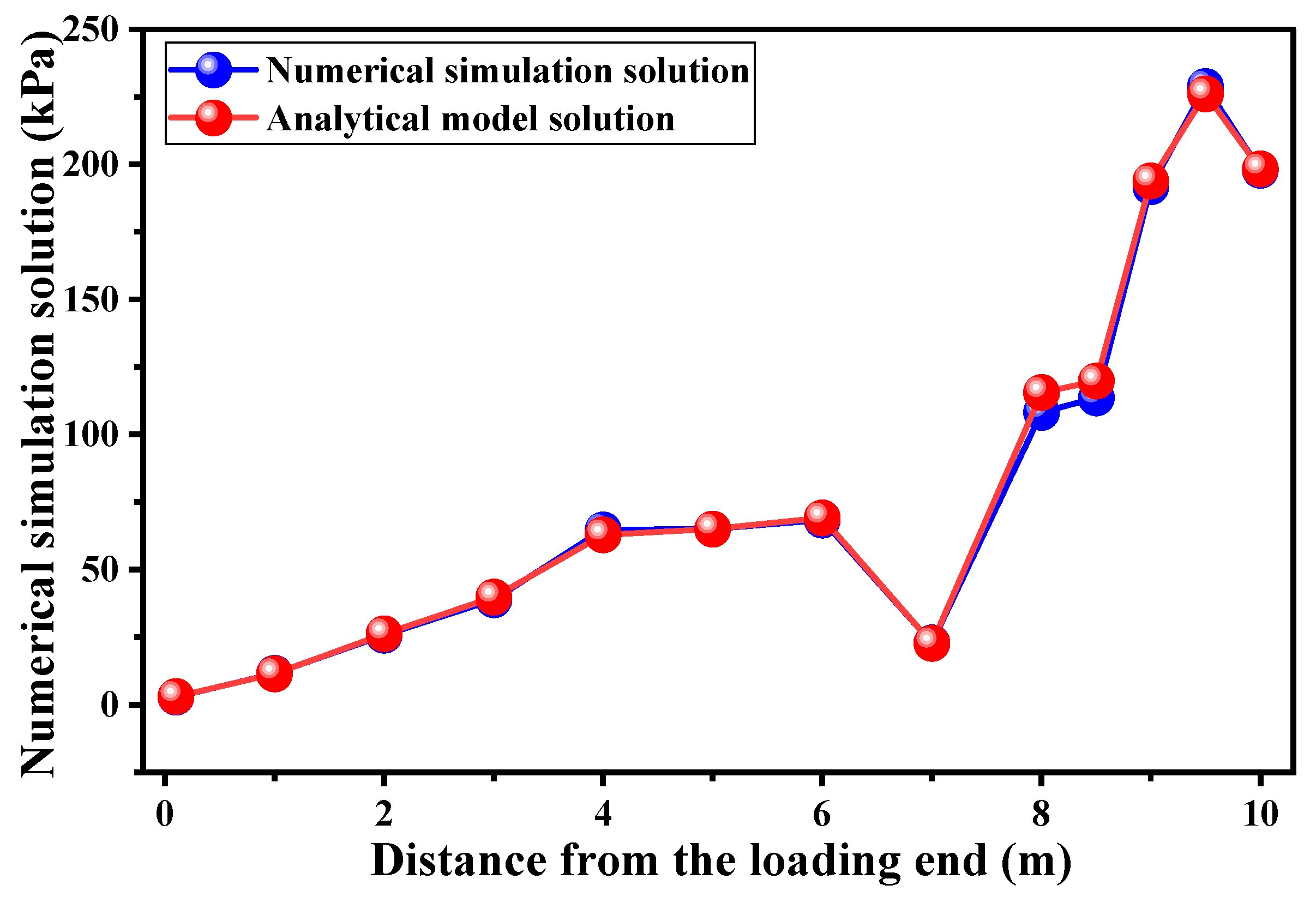
5.2. Numerical Verification of the Analytical Model for Interfacial Shear Stress
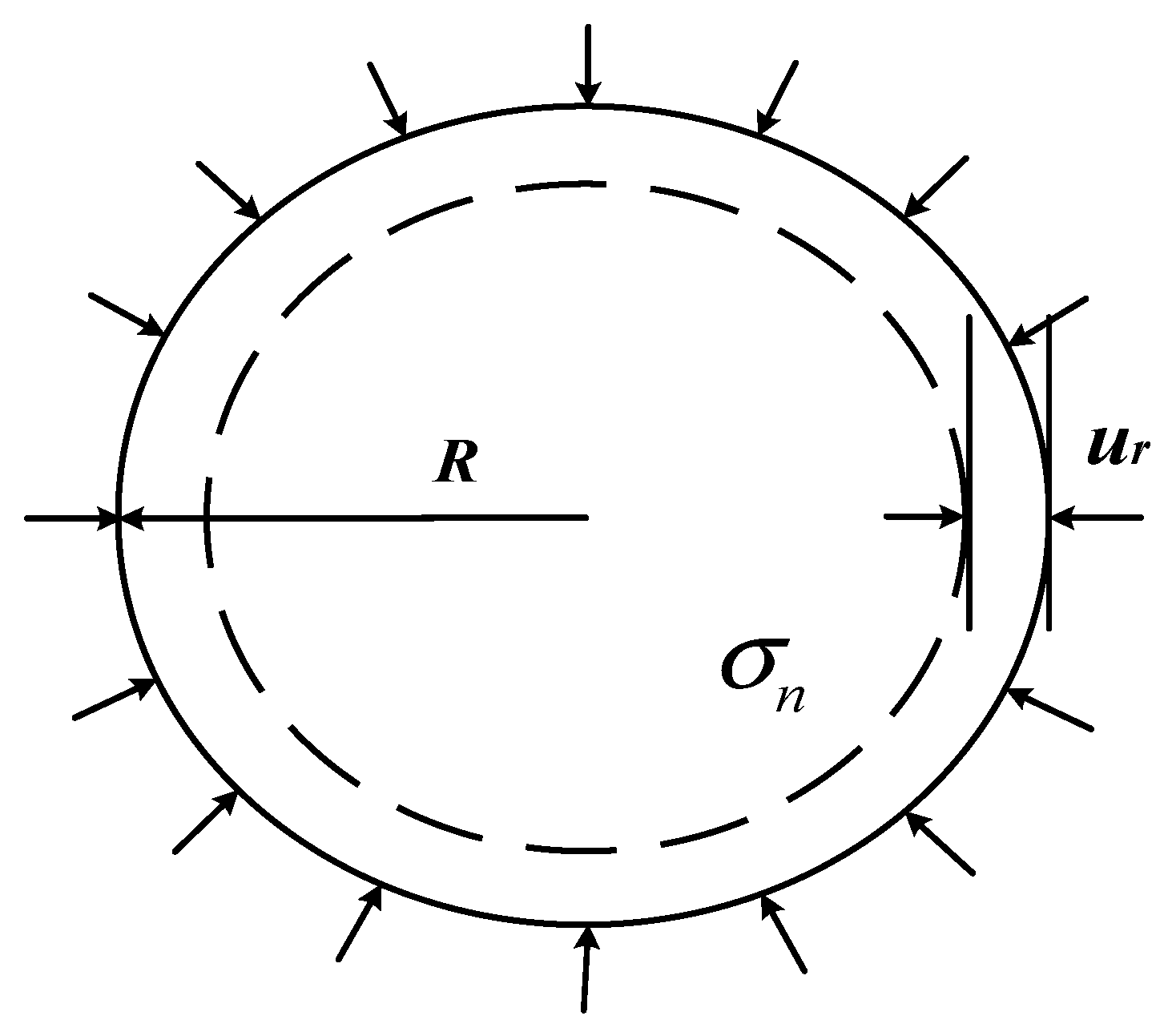
5.3. Analytical Model for End-Bearing Capacity
- The tangent at the outer crown of the ellipsoidal deformation zone to the enlarged anchor head subtends an angle θ with the horizontal plane.
- The ratio of semi-major axis b to semi-minor axis a of the ellipsoidal deformation zone is t.
- The soil mass within the ellipsoidal deformation zone is an axisymmetric model with the longitudinal axis of the underreamed anchor serving as the axis of symmetry.
- R—the radius of the enlarged anchor bulb;
- t—the ratio of the ellipse’s semi-major to semi-minor axis;
- θ—the inclination of the tangent to the ellipse at the crown of the enlarged head with respect to the horizontal;
- a—the semi-major axis of the ellipse;
- b—the semi-minor axis of the ellipse.
- τ—the shear stress acting on the micro-element;
- φ—the internal friction angle of the foundation soil;
- c—the cohesion of the soil surrounding the anchor.
- D0—the maximum width of the elliptical deformation zone of the surrounding soil around the anchor.
- H—the embedment depth of the underreamed anchor.
- —the unit weight of the overlying soil;
- —the internal friction angle of the soil surrounding the anchor;
- —the diameter of the underreamed anchorage segment;
- —the embedment depth of the underreamed anchor;
- —the coefficient of lateral earth pressure of the soil surrounding the anchor.
5.4. Numerical Validation of the End-Bearing Capacity Analytical Model
6. Ultimate Bearing Capacity Evaluation of Underreamed Anchors
7. Conclusions
- The existing side fictional stress distribution model primarily characterizes the distribution of elastic deformation. This paper was based on Mohr–Coulomb strength theory and an associated flow rule, while the model furnishes a closed-form expression describing how the side shear stress evolves along the anchorage segment once plastic deformation is mobilized at the anchor rock–soil interface. Comparisons with high-resolution finite element simulations reveal relative deviations ranging from 0.02% to 6.29%, corroborating that the proposed analytical solution faithfully captures the spatial distribution of plastic side shear stress along the underreamed anchor.
- Based on the clarification of the load transfer mechanism during the local shear failure of the surrounding soil under the vertical pull-out of the underreamed anchor, an end-bearing capacity model is proposed that incorporates factors such as embedment depth, underreamed diameter, soil cohesion, and internal friction angle. The relative error between theoretical predictions and numerical simulations is 0.058%. The analytical model is demonstrated to compute the end-bearing capacity of underreamed anchors with marked accuracy.
- By employing the existing fitting model to calculate the ultimate bearing capacity of the underreamed anchor, this study reveals that the prediction error of the ultimate bearing capacity of underreamed anchors using the adjusted hyperbolic model is 5.7%, while the prediction error using the improved exponential model is 10.6%. The prediction errors using the GM(1,1) model and improved exponential power model are 11.2% and 17.3%, respectively. This indicates that the adjusted hyperbolic model is the optimal model for fitting the load–displacement curve and calculating the ultimate bearing capacity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, H.; Lee, S.R.; Kim, N.K.; Kim, T.H. A numerical study of the pullout behavior of grout anchors underreamed by pulse discharge technology. Comput. Geotech. 2013, 47, 78–90. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, S.; Cai, Q. A model test and the ultimate capacity analysis of multi-underreamed anchors in silty clay. Soil Mech. Found. Eng. 2024, 60, 564–573. [Google Scholar] [CrossRef]
- Guo, G.; Tang, A.; Zhong, G.; Liu, Z.; Hu, X. Underreamed anchor with geotextile bag and its hyperbolic load versus displacement model for capacity prediction. IOP Conf. Ser Earth Environ. 2019, 340, 052077. [Google Scholar] [CrossRef]
- Xia, Y.Y.; Chen, C.; Ni, Q. Comparative modelling of pull-out process of four different anchorages by using transparent soil. Chin. J. Geotech. 2017, 39, 399–407. [Google Scholar] [CrossRef]
- Wang, D.; Hu, R.; Randolph, R.F. Three-dimensional large deformation finite-element analysis of plate anchors in uniform clay. Geotech. Geoenvironmental Eng. 2010, 136, 355–365. [Google Scholar] [CrossRef]
- Hsu, S.T.; Liao, H.J. Uplift behavior of cylindrical anchors in sand. Can. Geotech. J. 1998, 35, 70–80. [Google Scholar] [CrossRef]
- Hyett, A.J.; Bawden, W.F.; Reichert, R.D. The effect of rock mass confinement on the bond strength of fully grouted cable bolts. Int. J. Rock. Mech. Min. Sci. Geomech Abstr. 1992, 29, 503–524. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Li, Y.; Yang, Y.; Sun, T.; Xie, X.; Tang, H. Effect of surrounding rock confinement on the performance of self-expanding bolt. China J. Highw. Transp. 2022, 35, 245–257. [Google Scholar] [CrossRef]
- Zheng, B.; Bayat, M.; Shi, Y.; Cao, M.; Jiang, Y.; Qian, X.; Sumarac, D. A prognostic model of side friction of rock bolt anchoring section based on associated flow law. Kuwait J. Sci. 2025, 52, 100374. [Google Scholar] [CrossRef]
- Zhou, Y.; Liang, J.; Shi, S.; Cai, Q. Ultimate uplift capacity of multi-underreamed anchors in soft soil. Soil Mech. Found. Eng. 2024, 61, 426–435. [Google Scholar] [CrossRef]
- Chen, C.; Xia, Y.; Ni, Q. Investigation on the working mechanism and structural parameters optimization of multiple ball shaped nodular anchors. Soil Mech. Found. Eng. 2020, 57, 49–56. [Google Scholar] [CrossRef]
- Ouyang, P.; Xiao, H.; Shen, Z. Analysis on the Bearing Characteristics of Anchor Bolt Anchoring Interface. Chin. J. Undergr. Sp. Eng. 2024, 20, 575–581. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Zhang, X.; Elmaimouni, L. Study on propagation characteristics of ultrasonic guided wave and detection of the defect in resin bolts. Appl. Acoust. 2022, 195, 108843. [Google Scholar] [CrossRef]
- Zhang, R.; Zheng, J.; Li, P.; Zhang, J.; Yu, S. A method for predicting mechanical behaviour of HPJG-Anchors-Part I: Mechanical characteristics and load transfer models. Comput. Geotech. 2012, 45, 62–73. [Google Scholar] [CrossRef]
- Ensani, A.; Razeghi, H.R.; Mamaghanian, J. A hyperbolic model for mechanical behaviour of marginal soil-geosynthetic interface. Geosynth. Int. 2022, 29, 457–475. [Google Scholar] [CrossRef]
- Yue, Z.; Li, A.; Wang, P. An analytical analysis for the mechanical performance of fully-grouted rockbolts based on the exponential softening model. Int. J. Min. Sci. Technol. 2022, 32, 981–995. [Google Scholar] [CrossRef]
- Luan, Y.; Zhang, Y.; Zhuang, K.; Ding, L.; Sun, J. Research on power characteristics of fully-power variable speed pumped storage units based on hydraulic-mechanical-electrial modeling. Trans. China Electrotech. Soc. 2025, 40, 730–743. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Nie, Y.; Lin, X.; Sun, X. The shear resistance mechanism of prestressed anchor cables in slope reinforcement. Int. J. Rock. Mech. Min. Sci. 2023, 170, 105520. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Y.; Ma, T.; Tang, C. Observed performance of a deep excavation of Qingdao Metro Line 4 in China. Tunn. Undergr. Space Technol. 2022, 123, 104445. [Google Scholar] [CrossRef]
- Chen, C.; Li, W.; Zhu, S.; Chen, Y. Method for calculating soil-grout interface bond strength of pressure-grouted anchors based on viscoelastic-plastic cavity expansion theory. China J. Highw. Transp. 2023, 36, 41–51. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, Y. Effective contact stiffness model for bolted flange joint with spigot. Int. J. Mech. Sci. 2025, 293, 110213. [Google Scholar] [CrossRef]
- Song, Y. Analysis of the stability of tunnels based on the Hoek-Brown and associated flow rule. Xi’an Univ. Archit. Technol. Nat. Sci. Ed. 2020, 52, 248–256. [Google Scholar] [CrossRef]
- Liu, H. Unified sand modeling using associated or non-associated flow rule. Mech. Res. Commun. 2013, 50, 63–70. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Uniform elastic field inside an elliptical inhomogeneity with Neuber’s nonlinear stress-strain law under generalized plane strain deformations. Mech. Adv. Mater. Struct. 2025, 32, 1993–1998. [Google Scholar] [CrossRef]
- Mortezaee, M.; Ghovatmand, M.; Nazemi, A. An application of generalized fuzzy hyperbolic model for solving fractional optimal control problems with caputo-fabrizio derivative. Neural Process Lett. 2020, 52, 1997–2020. [Google Scholar] [CrossRef]
- Song, T.; Pan, B.; Niu, G.; Fu, Y. A novel closed-form solutions method based on the product of exponential model for the minimally invasive surgical robot. Ind. Robot. 2022, 49, 934–946. [Google Scholar] [CrossRef]
- Ge, C.; Xu, Z.; Du, K.; Zhou, C.; Tan, C.; Liu, W.; Xu, S.; Wang, B. An improved inverse power law model for accelerated fatigue life prediction of 6061-T6 and AZ31B-F. Eng. Fail. Anal. 2022, 138, 106381. [Google Scholar] [CrossRef]
- Liu, X.; Peng, H.; Bai, Y.; Zhu, Y.; Liao, L. Tourism flows prediction based on an improved grey GM(1,1) model. Proc. Soc. Behav. Sci. 2014, 138, 767–775. [Google Scholar] [CrossRef]
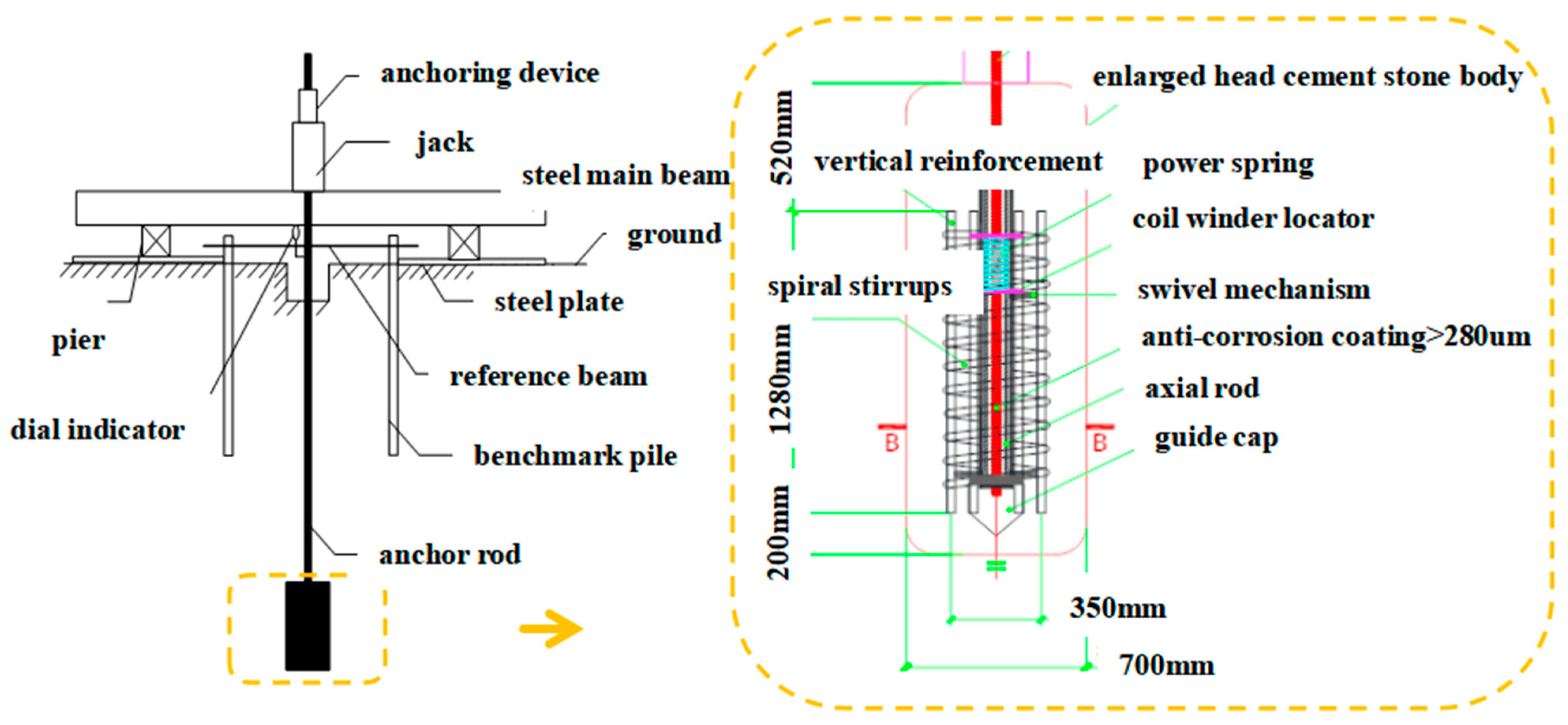
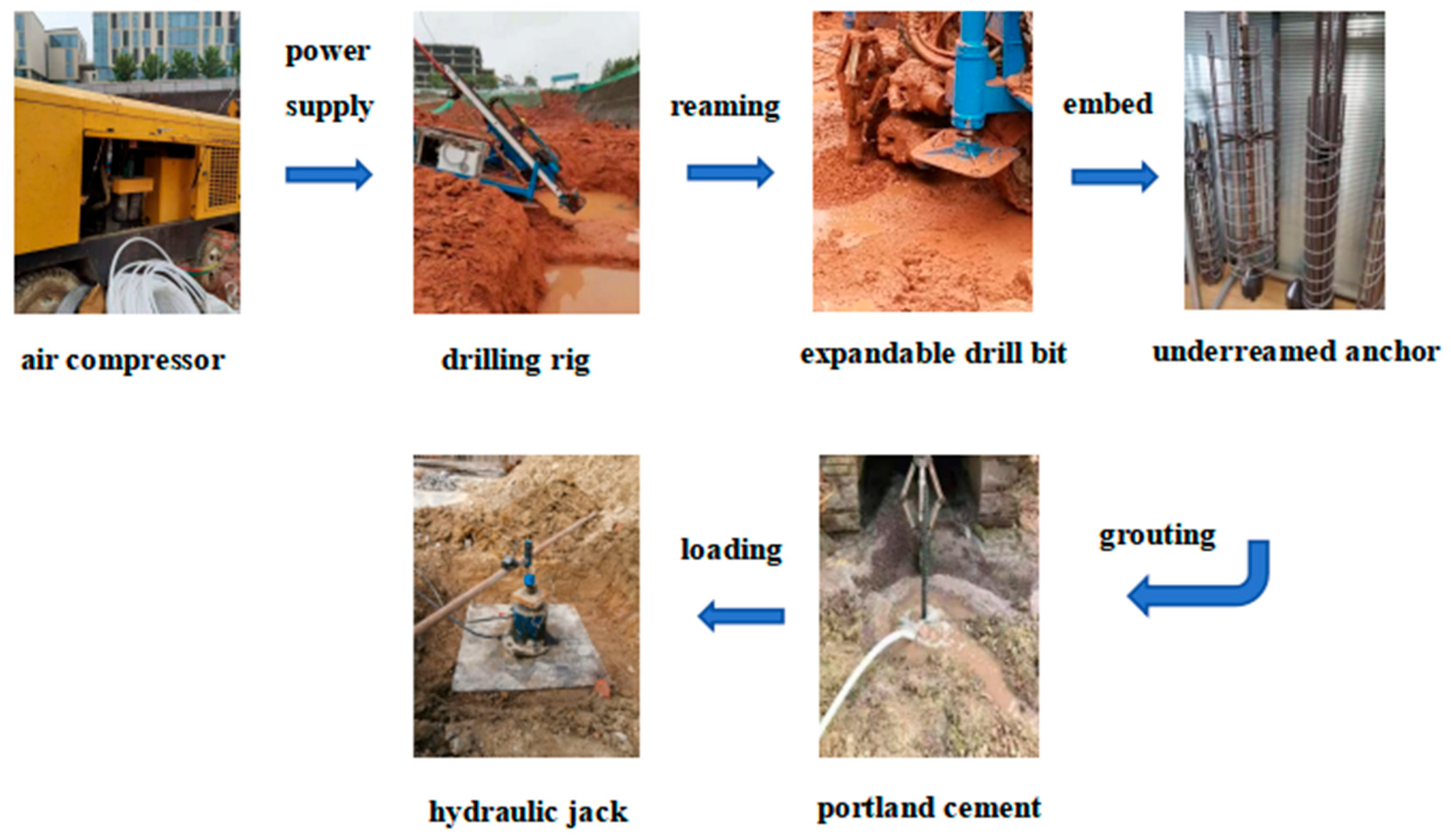
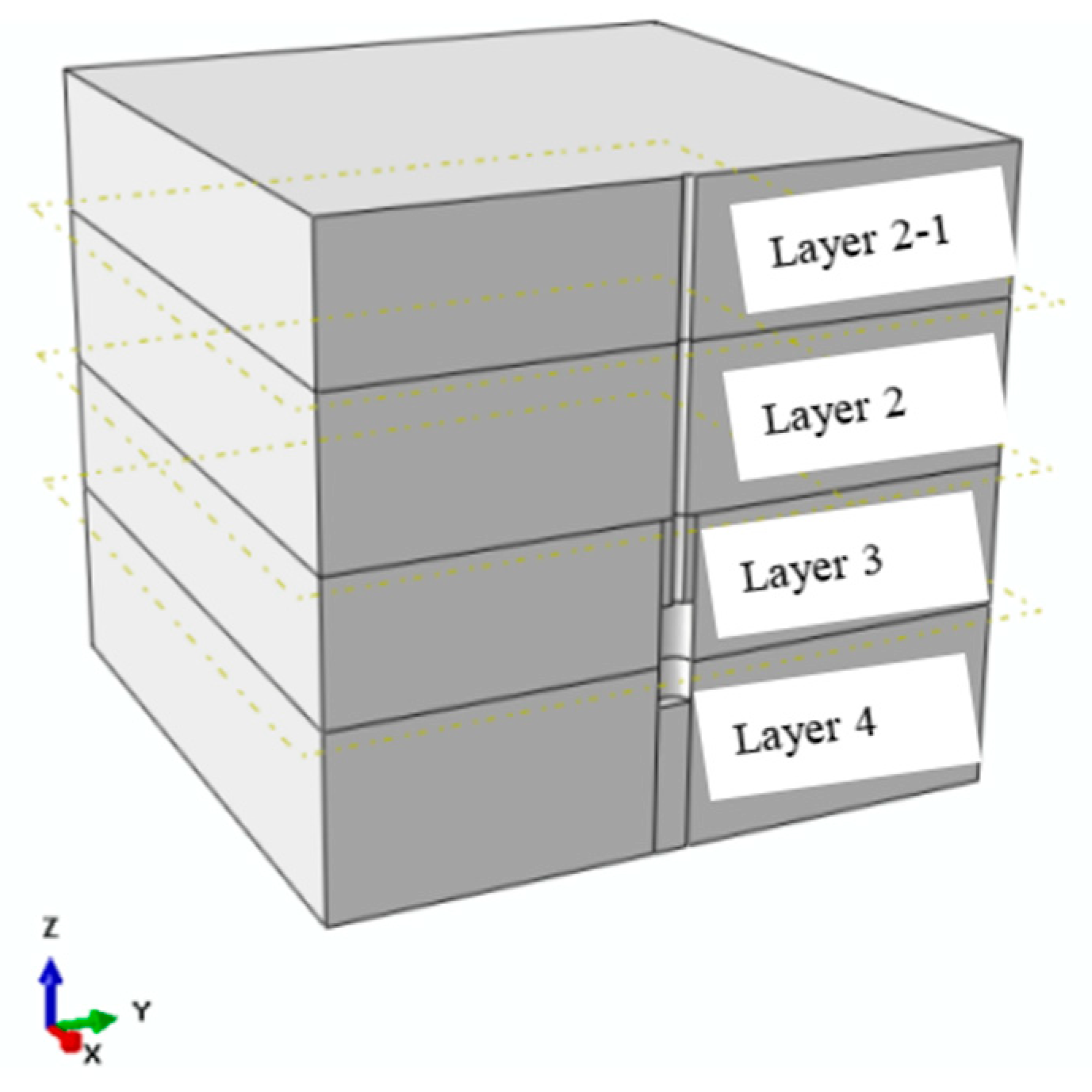


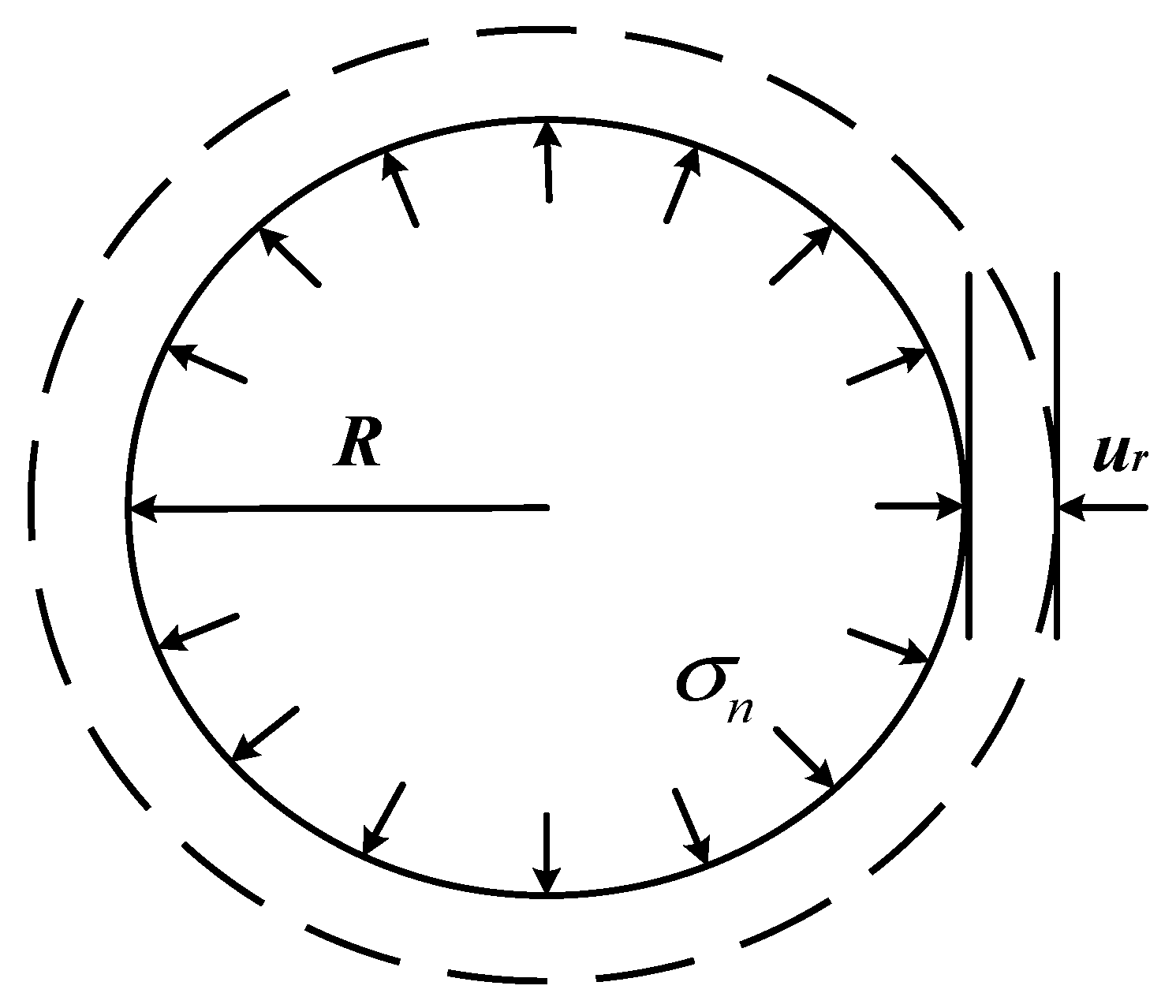


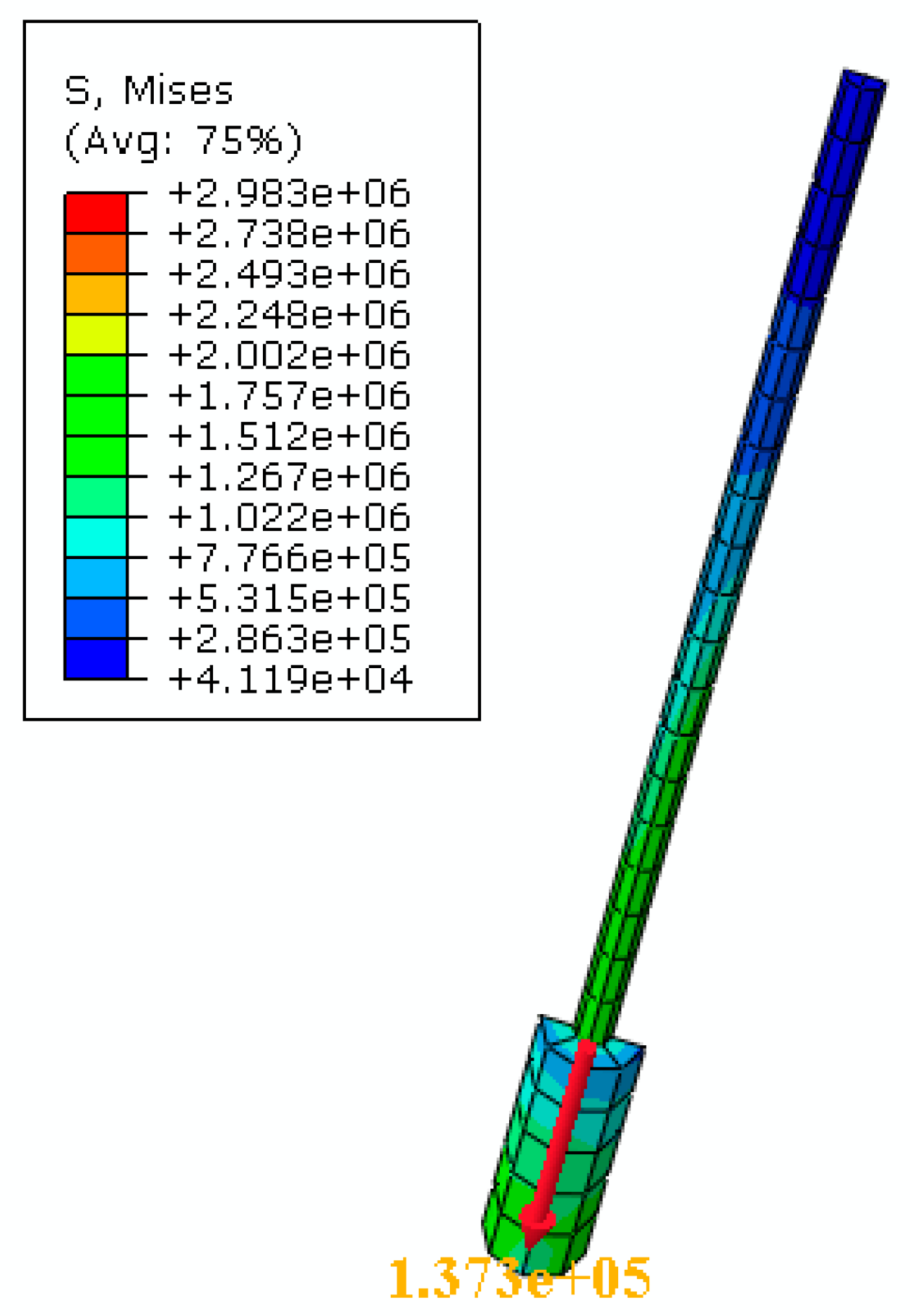
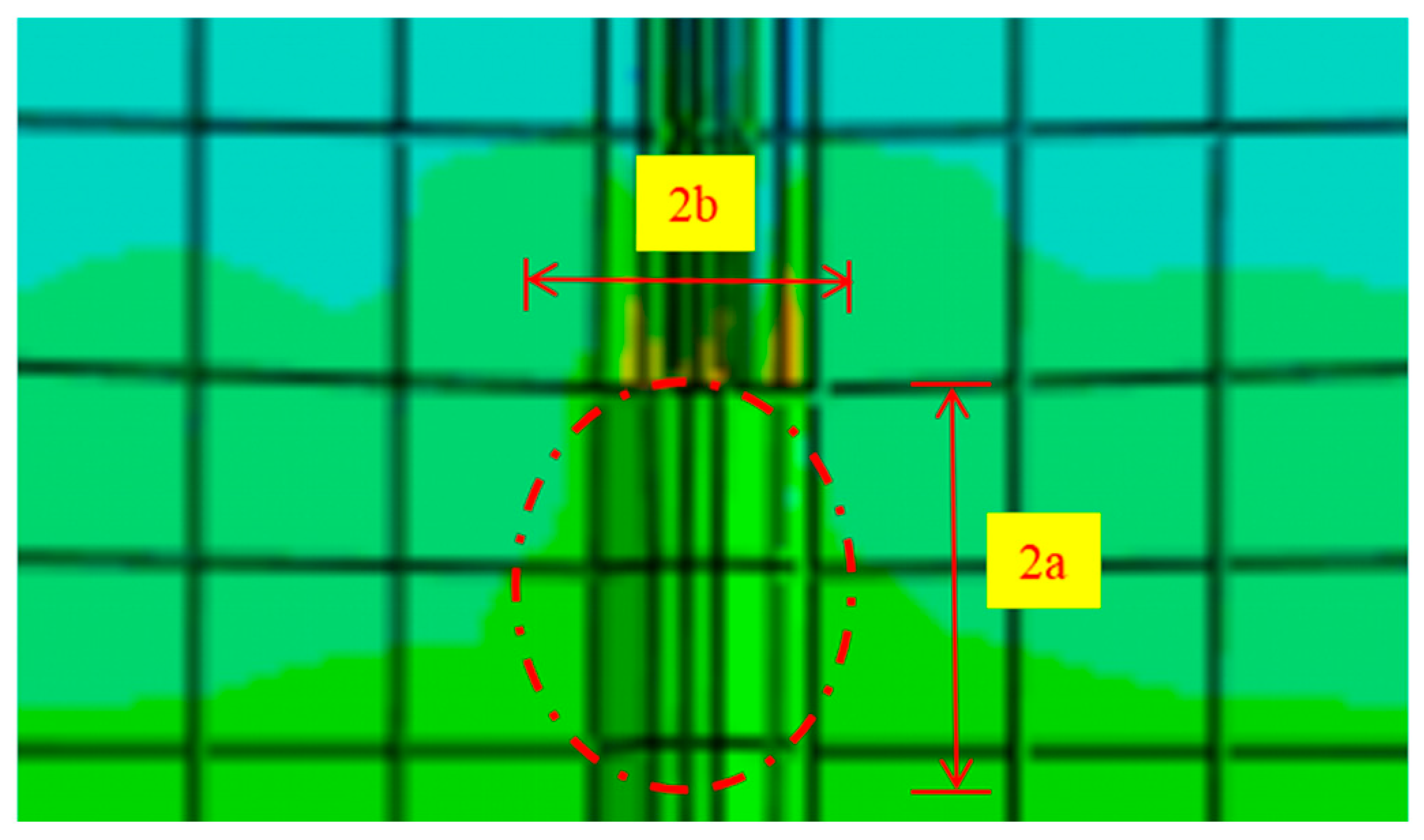
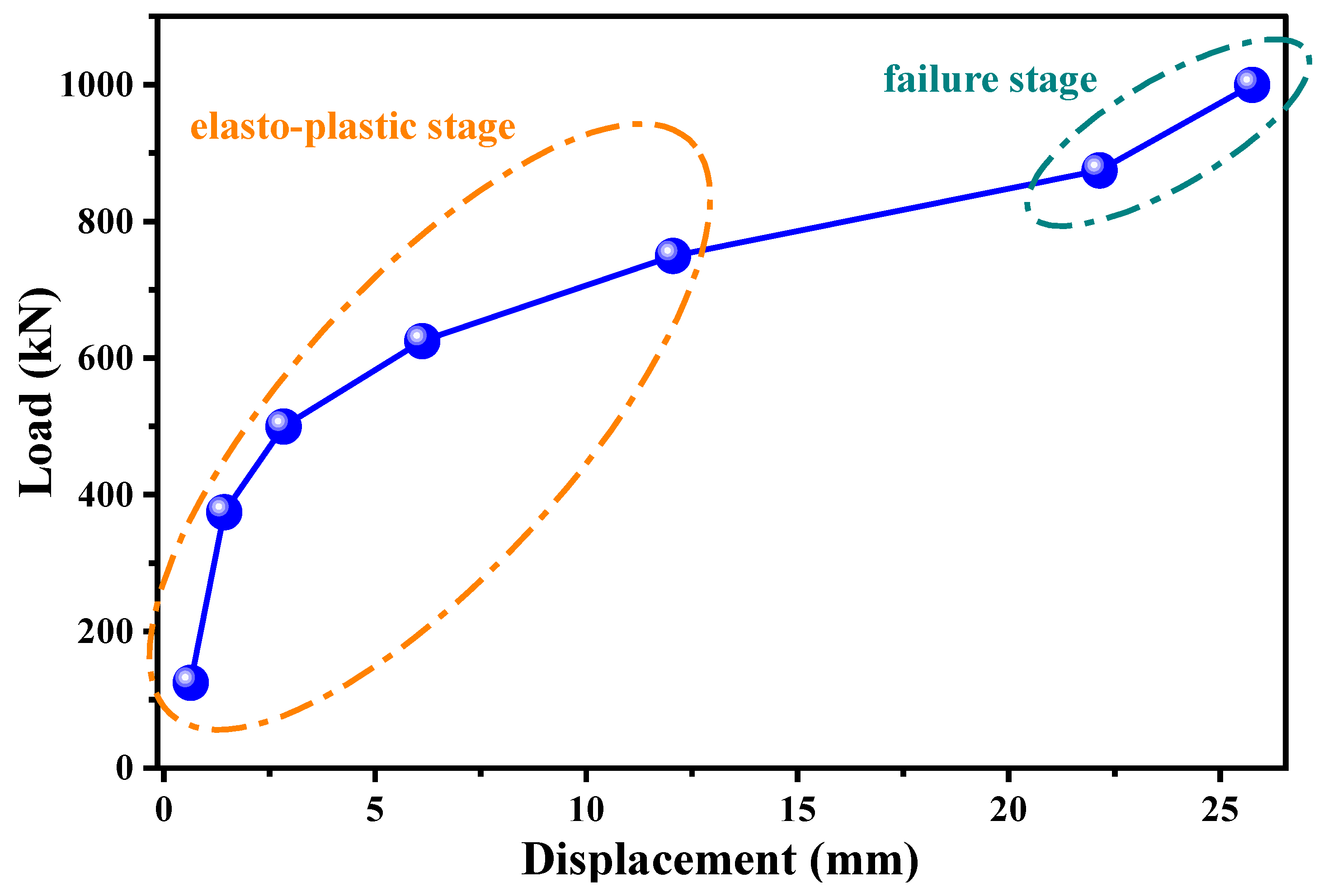
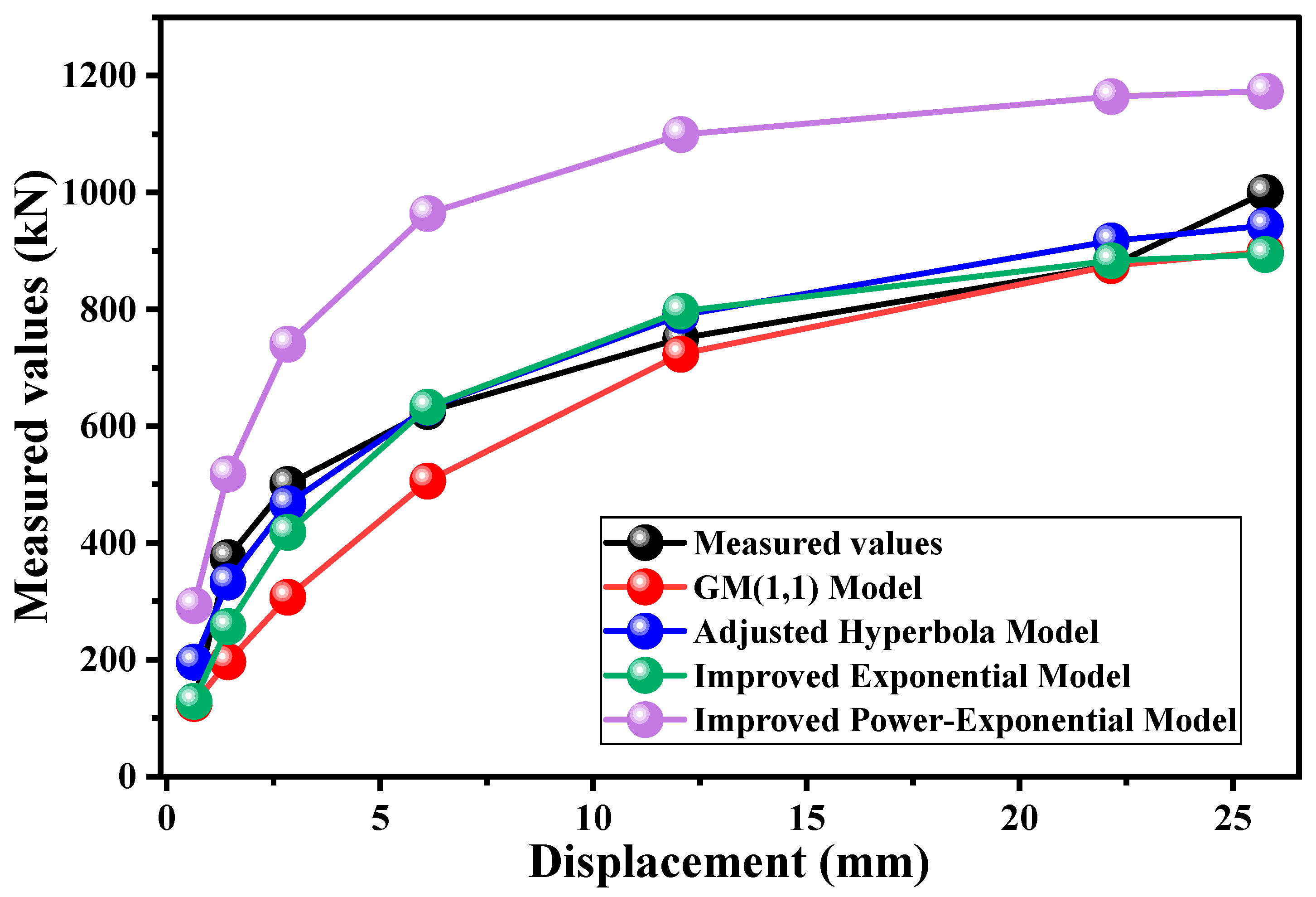
| Layer | Soil | Color | Soil Texture | Layer Thickness |
|---|---|---|---|---|
| 2-1 | Silt clay | Gray | Soft to fluid plastic | 3 m |
| 2 | Gray-brown | Plastic | 3.3 m | |
| 3 | Gray-yellow | Hard plastic | 2.9 m | |
| 4 | Gray-brown | Plastic | 3.8 m | |
| 5 | Gray-yellow | Hard plastic | 1.5 m | |
| 6 | Gray-yellow | Plastic | 6 m | |
| 7 | Brown-yellow | Hard plastic | 6 m |
| Layer | Soil | Density (kg/m3) | Poisson’s Ration | Cohesion (kPa) | Internal Friction Angle (°) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|
| 2-1 | Silt clay | 1870 | 0.3 | 18.0 | 10.3 | 8.56 |
| 2 | 1950 | 34.0 | 16.0 | 11.76 | ||
| 3 | 1990 | 53.9 | 20.6 | 14.84 | ||
| 4 | 2030 | 45.5 | 17.4 | 14.73 | ||
| 5 | 1990 | 55.7 | 21.3 | 17.27 | ||
| 6 | 2020 | 26.9 | 23.4 | 13 | ||
| 7 | 2000 | 55.5 | 17.2 | 16.23 |
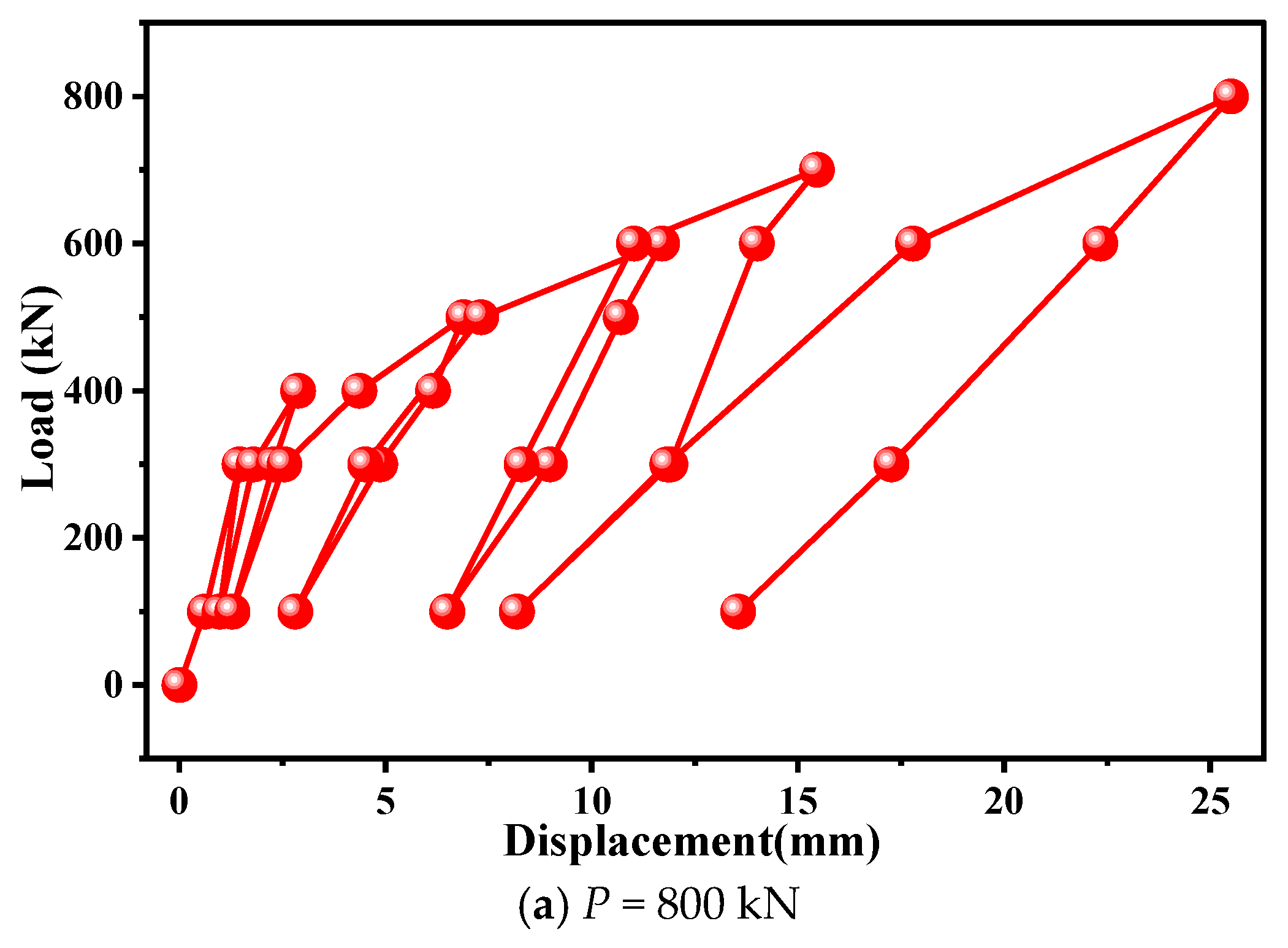
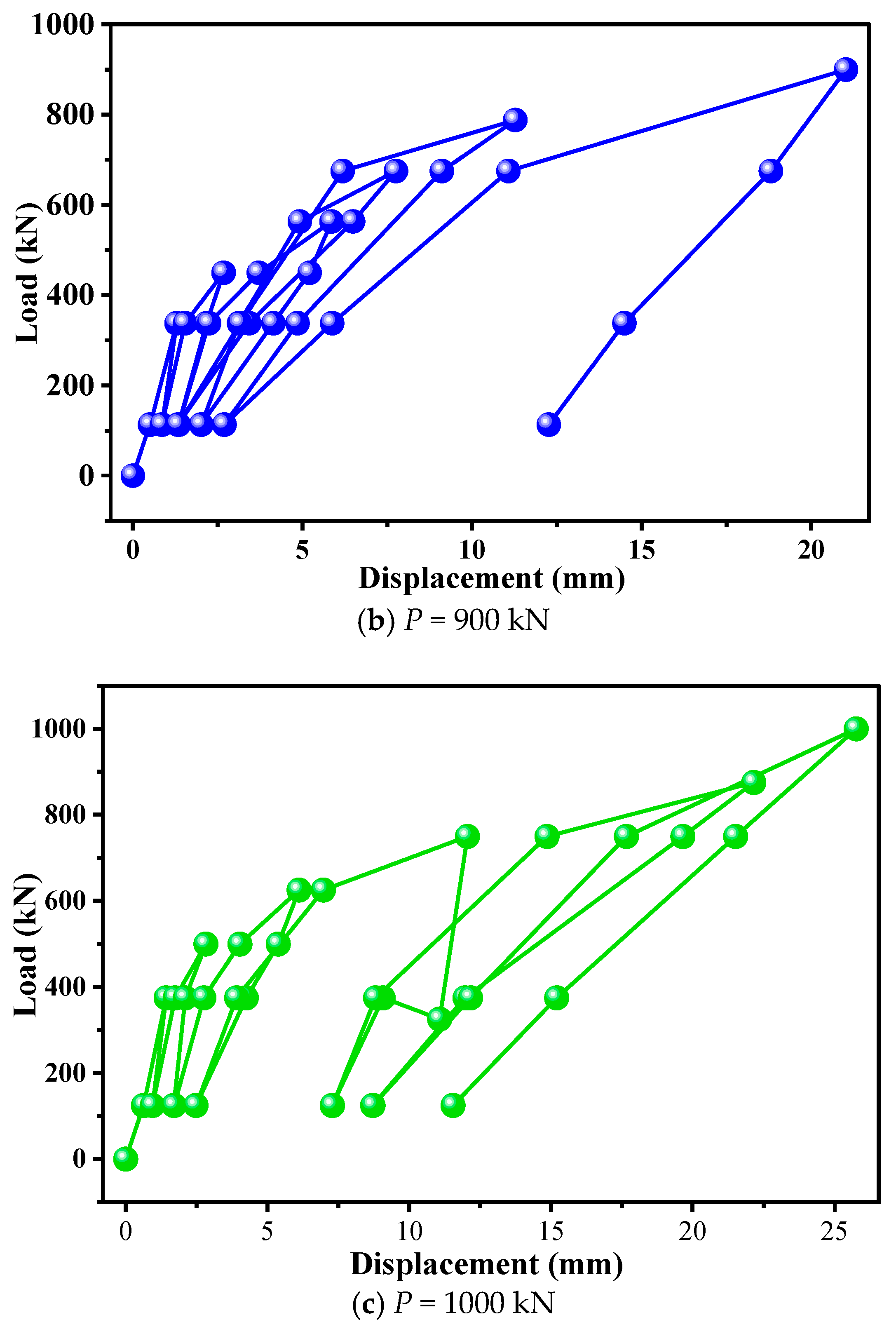
| Loading Increment (%) | Initial Loading | - | - | - | 10 | - | - | - |
| First Cycle | 10 | - | - | 30 | - | - | 10 | |
| Second Cycle | 10 | 30 | - | 40 | - | 30 | 10 | |
| Third Cycle | 10 | 30 | 40 | 50 | 40 | 30 | 10 | |
| Fourth Cycle | 10 | 30 | 50 | 60 | 50 | 30 | 10 | |
| Fifth Cycle | 10 | 30 | 60 | 70 | 60 | 30 | 10 | |
| Sixth Cycle | 10 | 30 | 60 | 80 | 60 | 30 | 10 | |
| Observation time (min) | 5 | 5 | 5 | 10 | 5 | 5 | 5 | |
| Layer | Soil | Thick (m) | Density (kg/m3) | Cohesion (kPa) | Internal Friction Angle (°) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|---|
| 2-1 | Silt clay | 3 | 1870 | 18 | 10.3 | 8.56 |
| 2 | 3.3 | 1950 | 34 | 16 | 11.76 | |
| 3 | 2.9 | 1990 | 53.9 | 20.6 | 14.84 | |
| 4 | 3.8 | 2030 | 45.5 | 17.4 | 14.73 |
| Prediction Model | Function Expression |
|---|---|
| Adjusted Hyperbolic Model | |
| Improved Exponential Model | |
| Improved Exponential power Function Model | |
| GM(1,1) Model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, B.; Feng, T.; Zhang, J.; Wang, H. Investigation into Anchorage Performance and Bearing Capacity Calculation Models of Underreamed Anchor Bolts. Appl. Sci. 2025, 15, 10929. https://doi.org/10.3390/app152010929
Zheng B, Feng T, Zhang J, Wang H. Investigation into Anchorage Performance and Bearing Capacity Calculation Models of Underreamed Anchor Bolts. Applied Sciences. 2025; 15(20):10929. https://doi.org/10.3390/app152010929
Chicago/Turabian StyleZheng, Bin, Tugen Feng, Jian Zhang, and Haibo Wang. 2025. "Investigation into Anchorage Performance and Bearing Capacity Calculation Models of Underreamed Anchor Bolts" Applied Sciences 15, no. 20: 10929. https://doi.org/10.3390/app152010929
APA StyleZheng, B., Feng, T., Zhang, J., & Wang, H. (2025). Investigation into Anchorage Performance and Bearing Capacity Calculation Models of Underreamed Anchor Bolts. Applied Sciences, 15(20), 10929. https://doi.org/10.3390/app152010929






