Numerical Simulation Study on Shear Mechanical Properties of Unfilled Three-Dimensional Rough Joint Surfaces Under Constant Normal Stiffness Boundary Conditions
Abstract
1. Introduction
2. Simulation Scheme
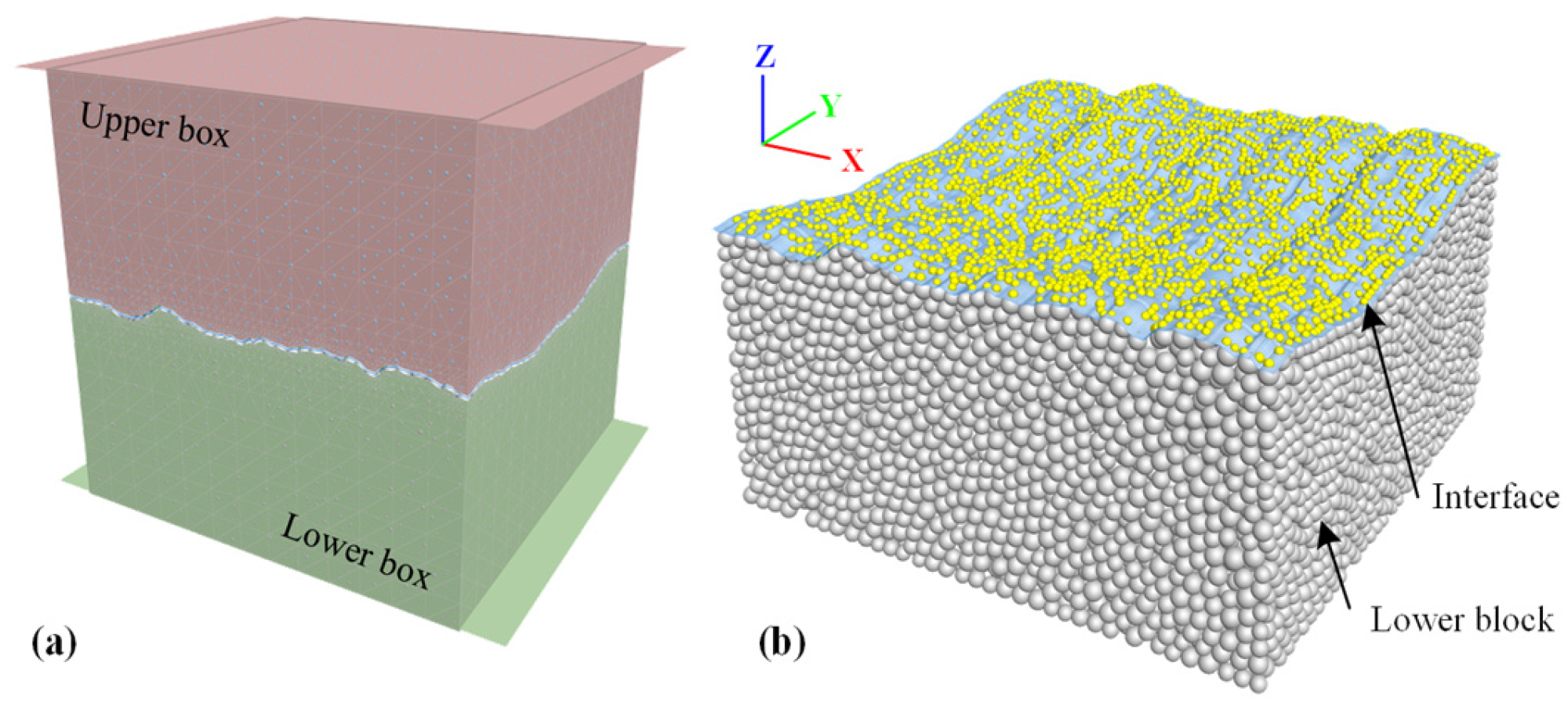
2.1. Establishment of Numerical Model
2.2. Parameter Calibration
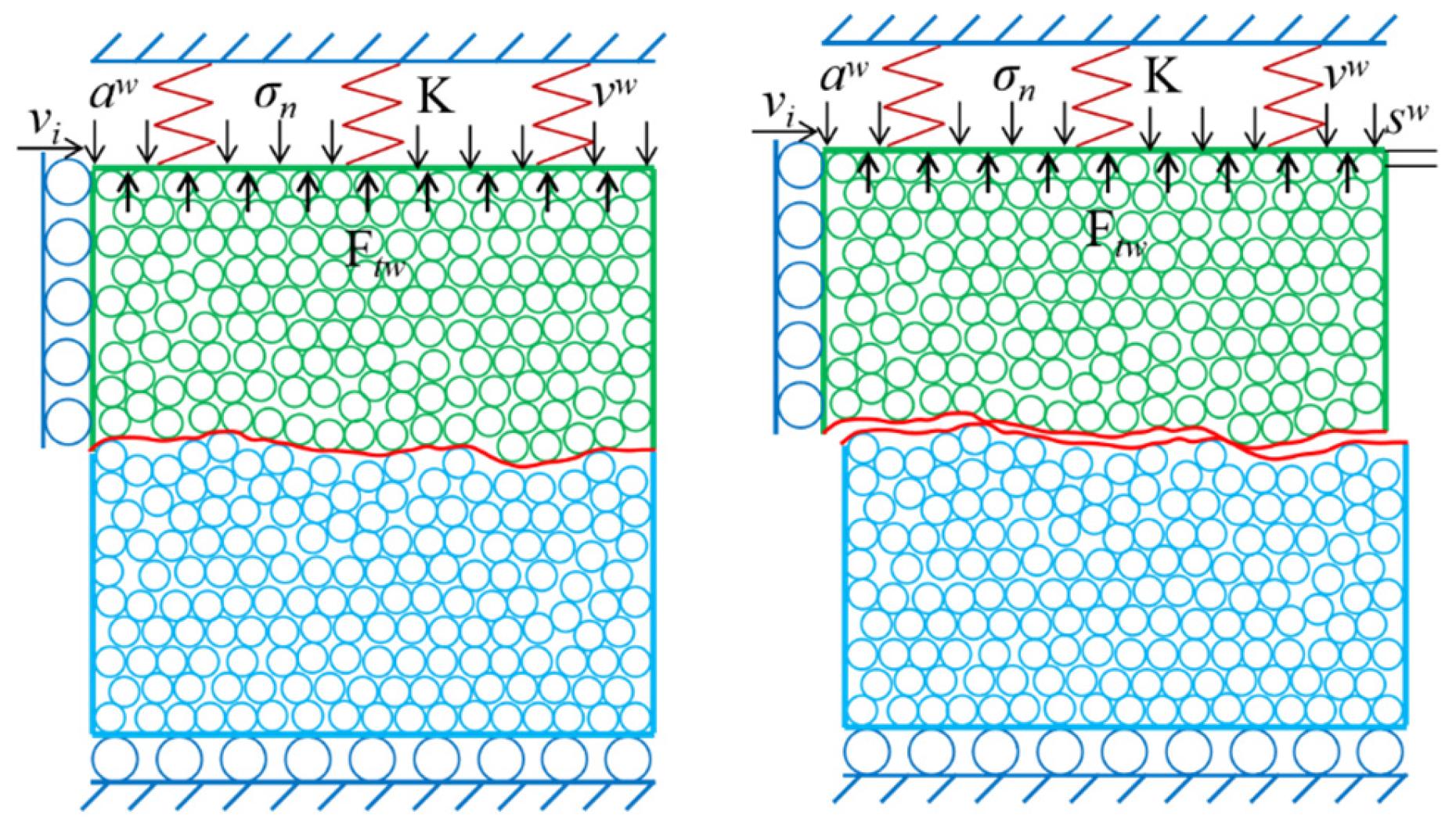
2.3. CNS Boundary Condition Settings
2.4. Numerical Model Loading
3. Simulation Results and Analysis
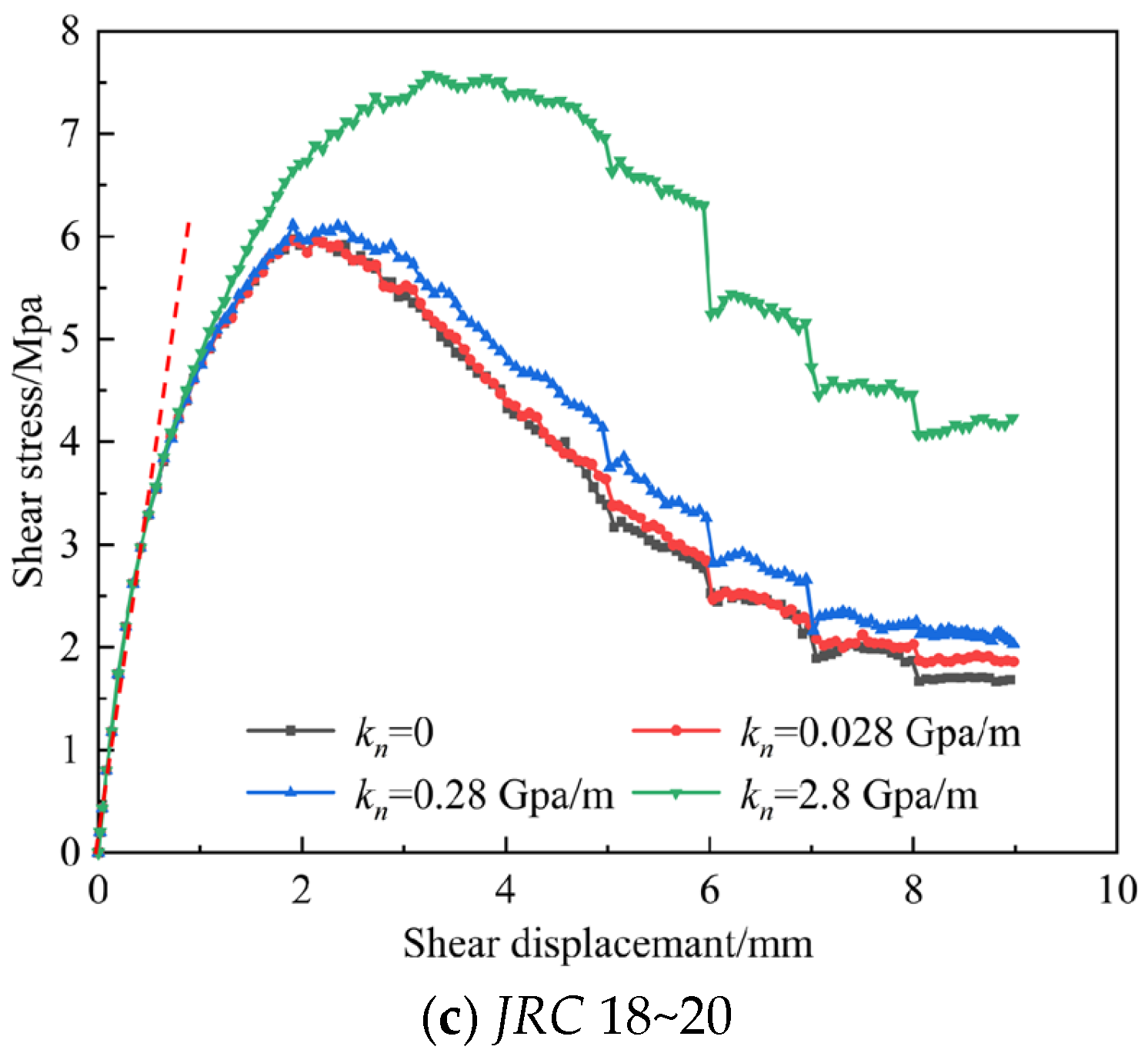
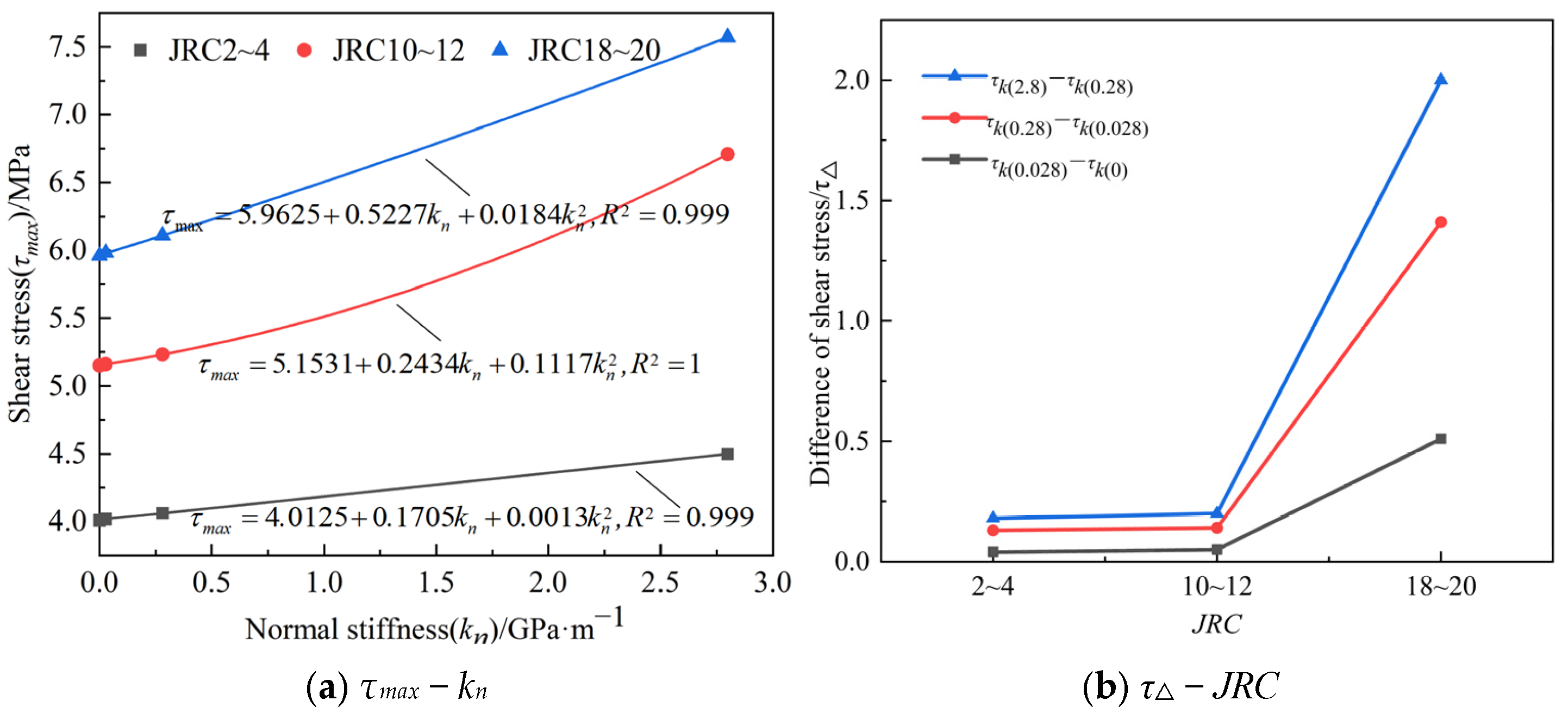
3.1. Shear Stress Evolution
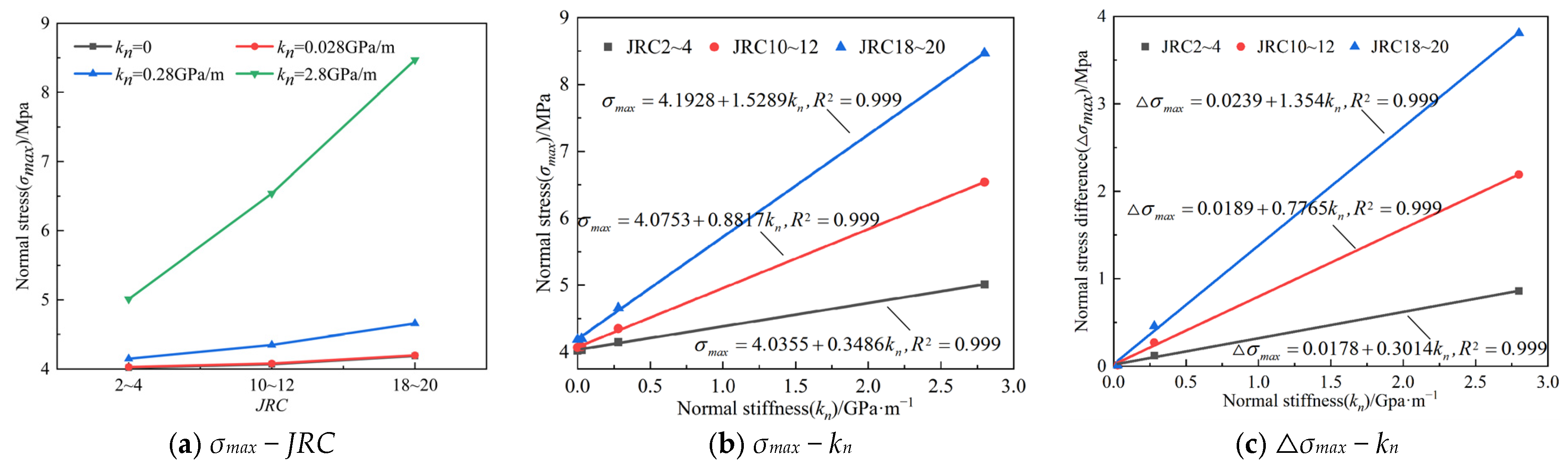
3.2. Evolution of Normal Stress
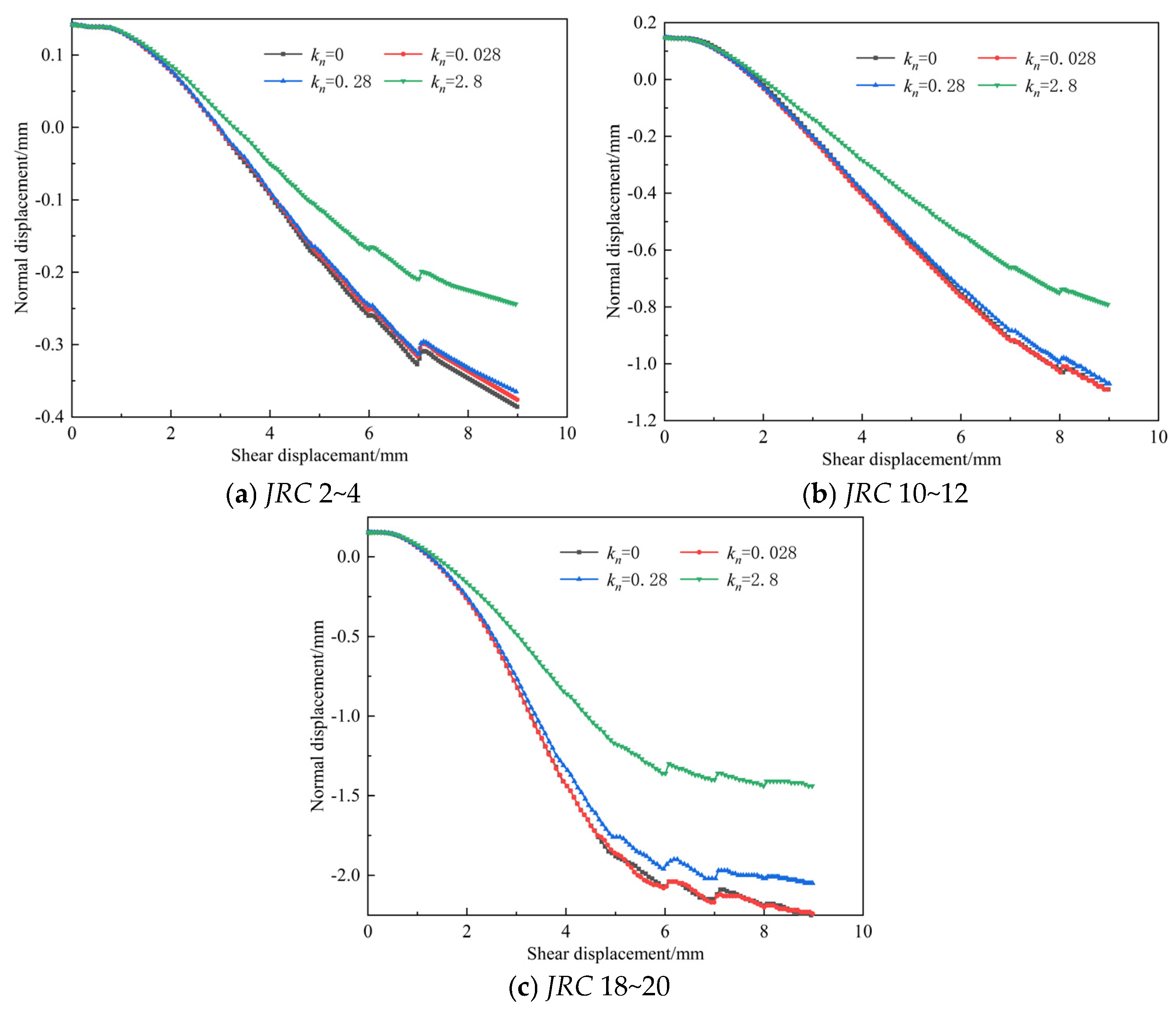
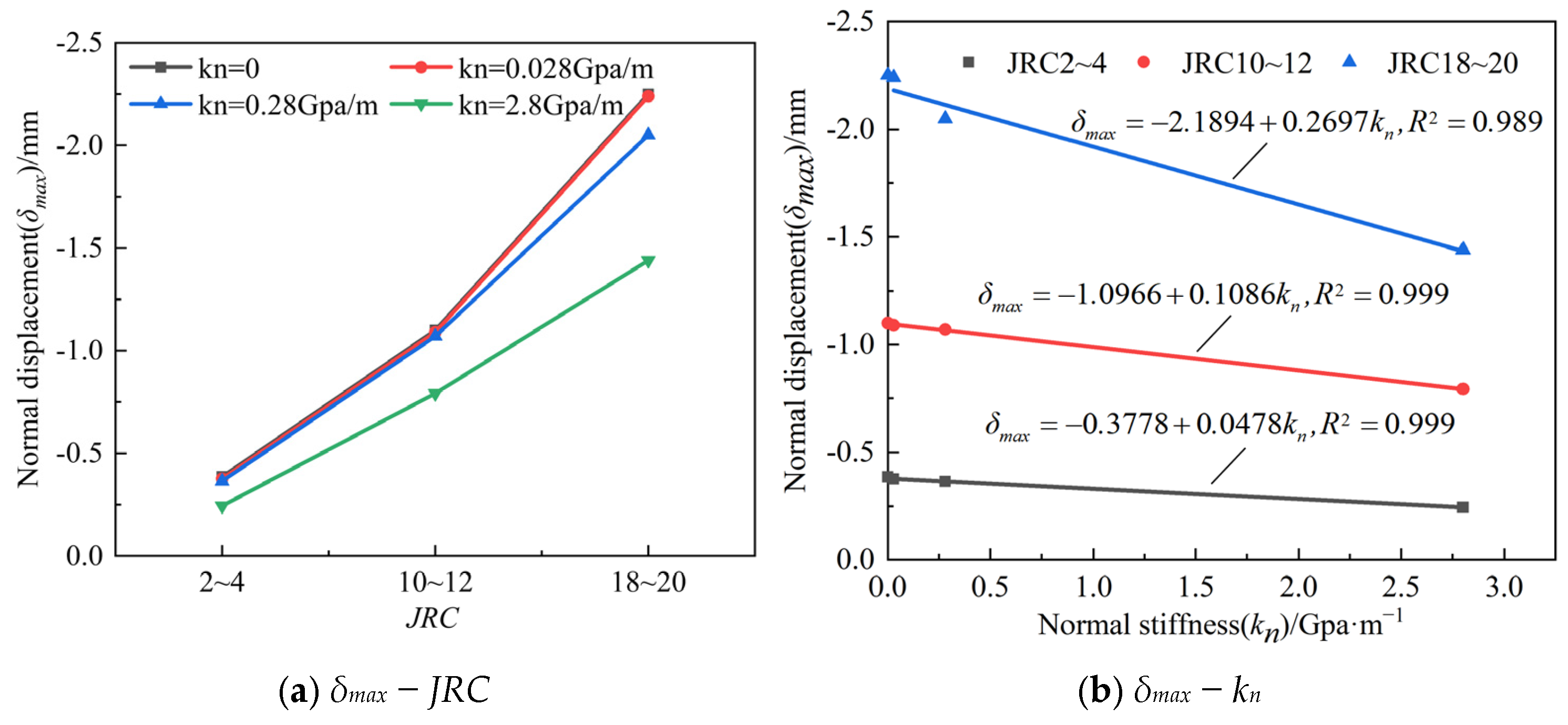
3.3. Normal Displacement Evolution
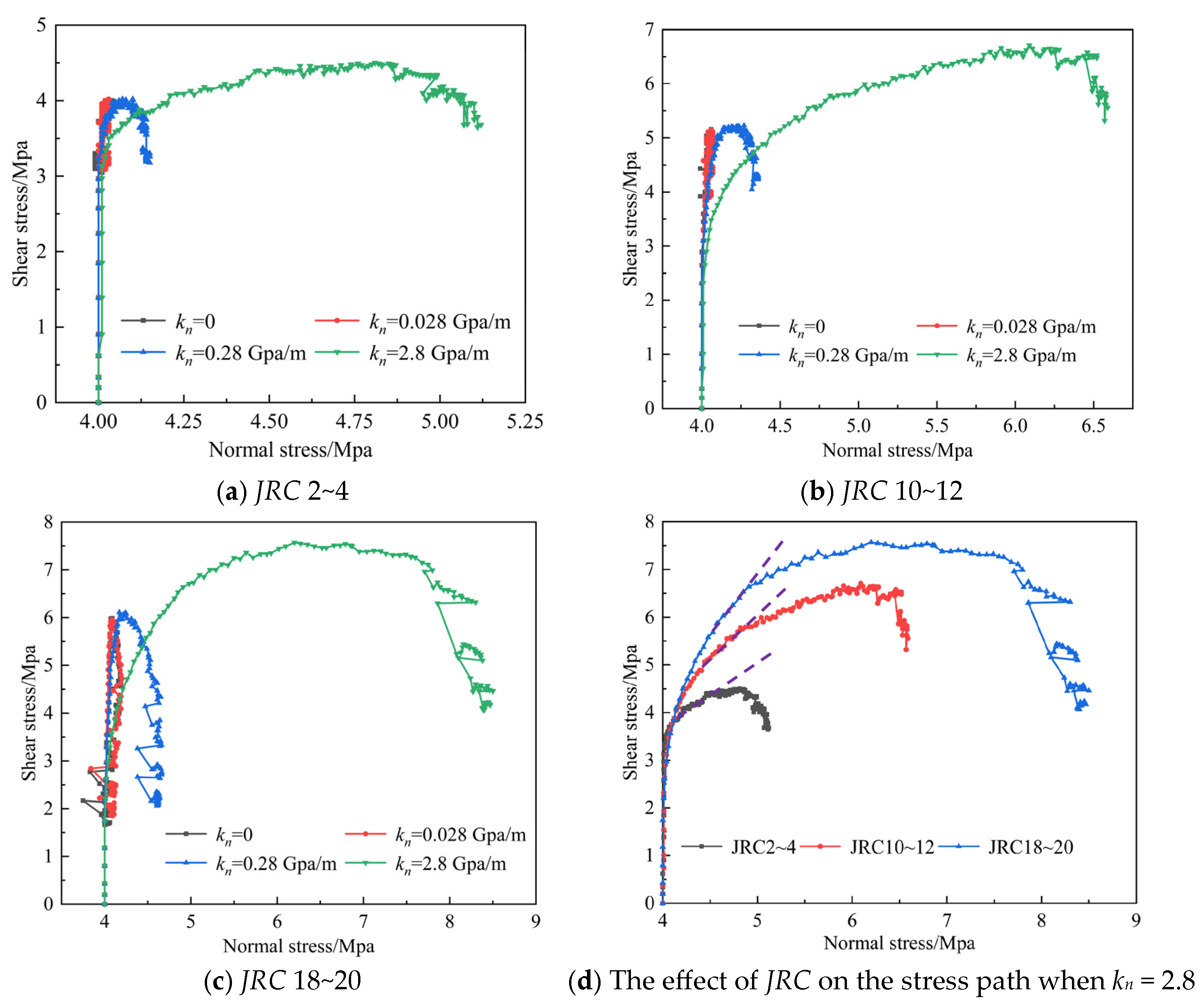
3.4. Shear Stress-Normal Stress Path Evolution
4. Discussion
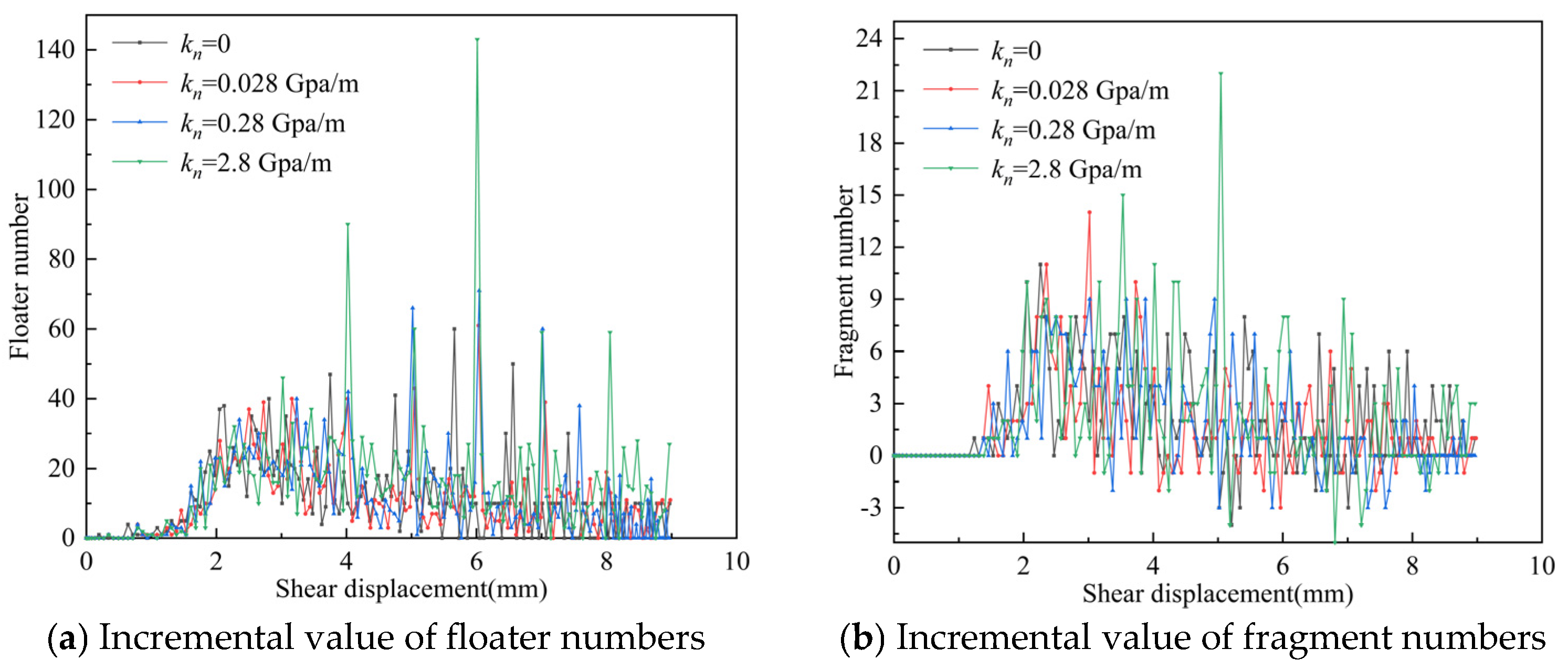
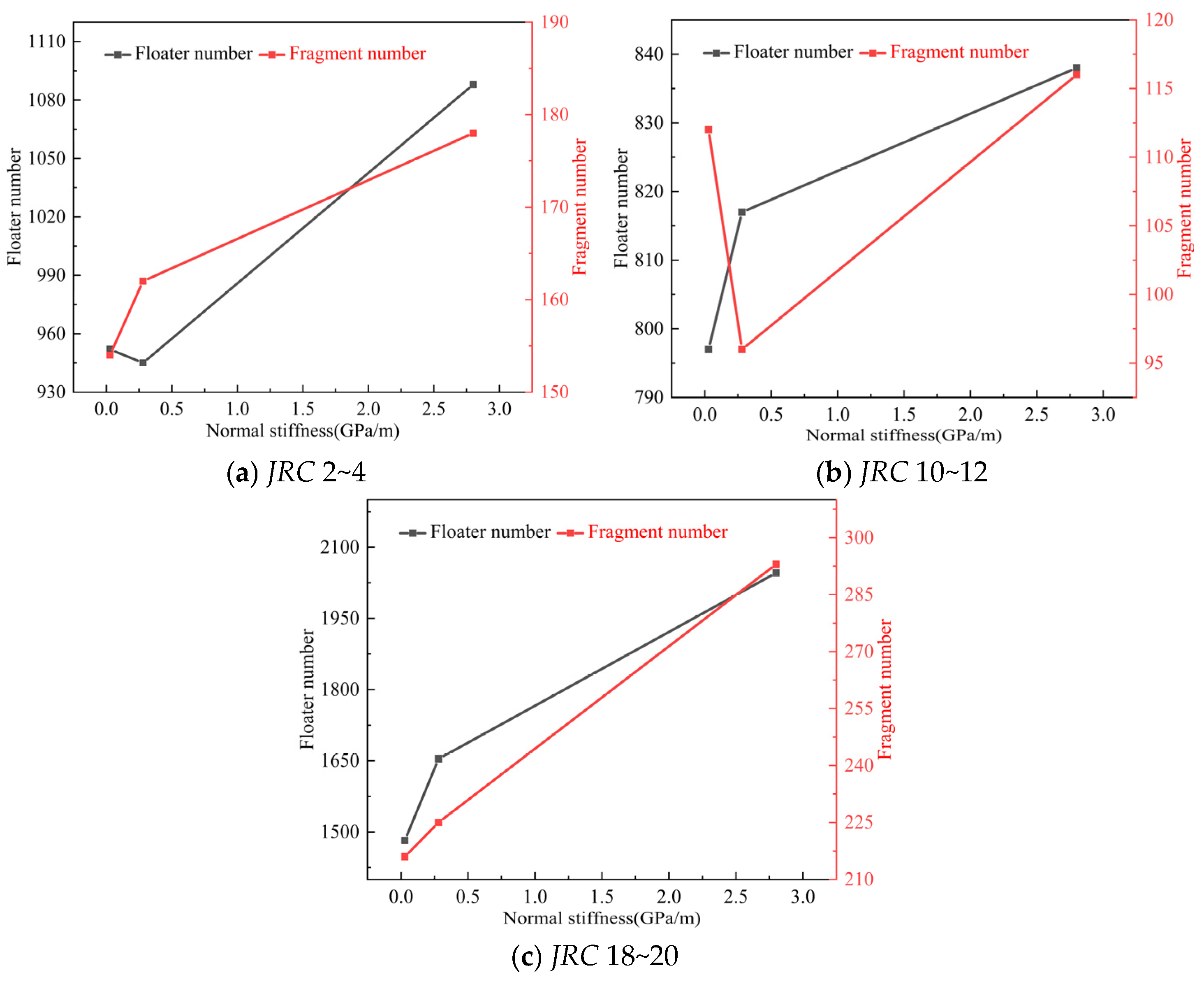
4.1. Floater and Fragment Quantity Analysis
4.2. Block Crack Propagation Analysis
4.3. Progressive Rock Block Fracturing Analysis
5. Conclusions
- The main deformation of the shear simulation process for different normal stiffness-JRC combinations is divided into three stages: the linear stage, the yield stage, and the post-peak stage. The shear stress increases first and then decreases as the shear displacement increases. When the normal stiffness exceeds 0.28 GPa/m, both normal stress and JRC increase gradually with increasing normal stiffness; when the normal stiffness is less than 0.028 GPa/m, normal stress shows no significant change.
- The normal displacement changes from “shear contraction” to “shear expansion” as the shear displacement varies, and it changes from a positive value to a negative value, showing a trend of gradually increasing displacement. When the normal stiffness increases from 0 to 2.8 GPa/m, the maximum normal displacement decreases by 36.79% (JRC 2~4), 28% (JRC 10~12), and 36% (JRC 18~20), respectively. As JRC increases, the maximum normal displacement shows a gradually increasing trend, with an increase of 461.64% to 495.74%. The apparent cohesion cj and internal friction angle φj of the joint surface both show a gradually increasing trend as JRC increases; the peak SRI value increases with increasing JRC and decreases with increasing normal stiffness.
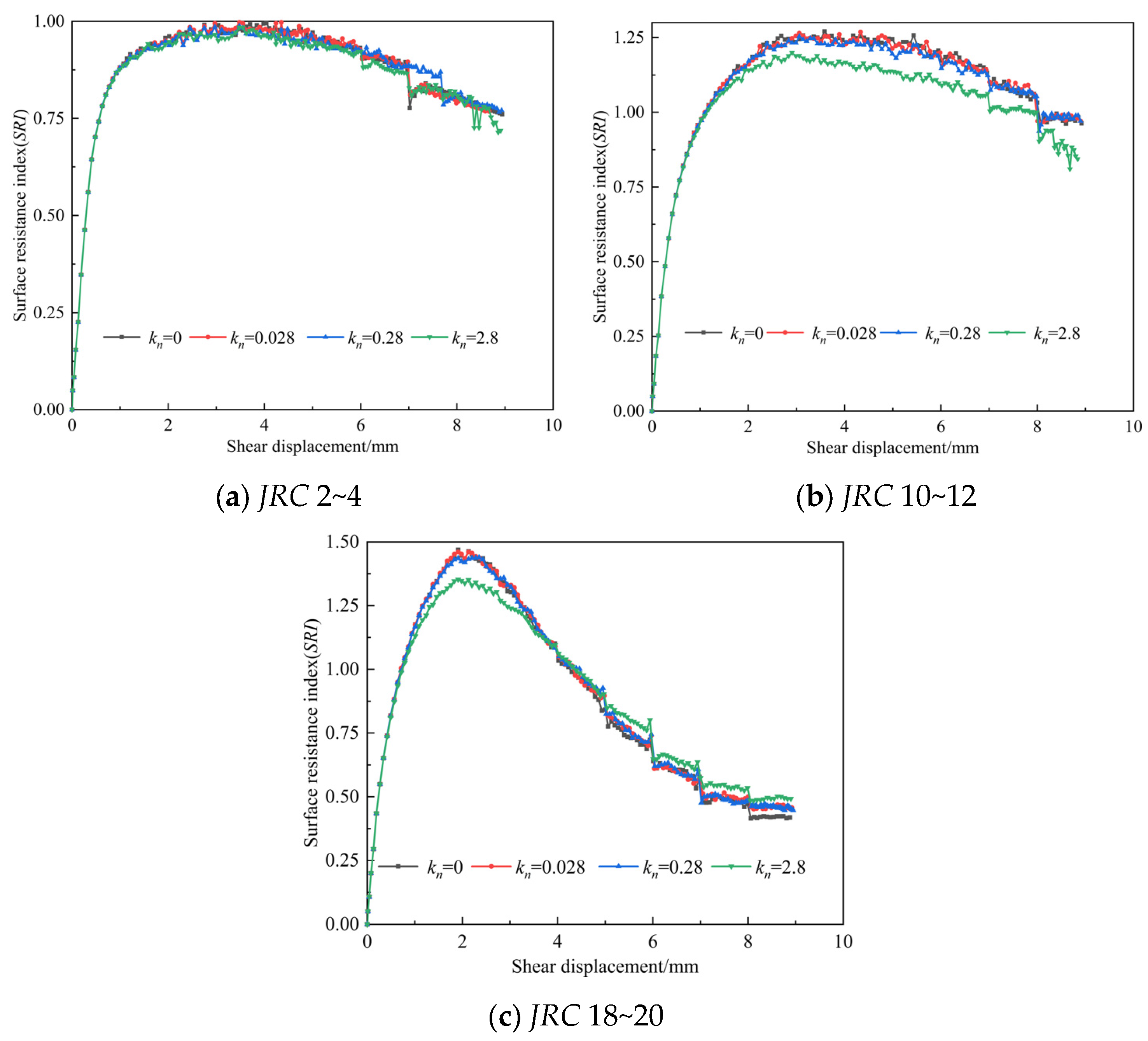
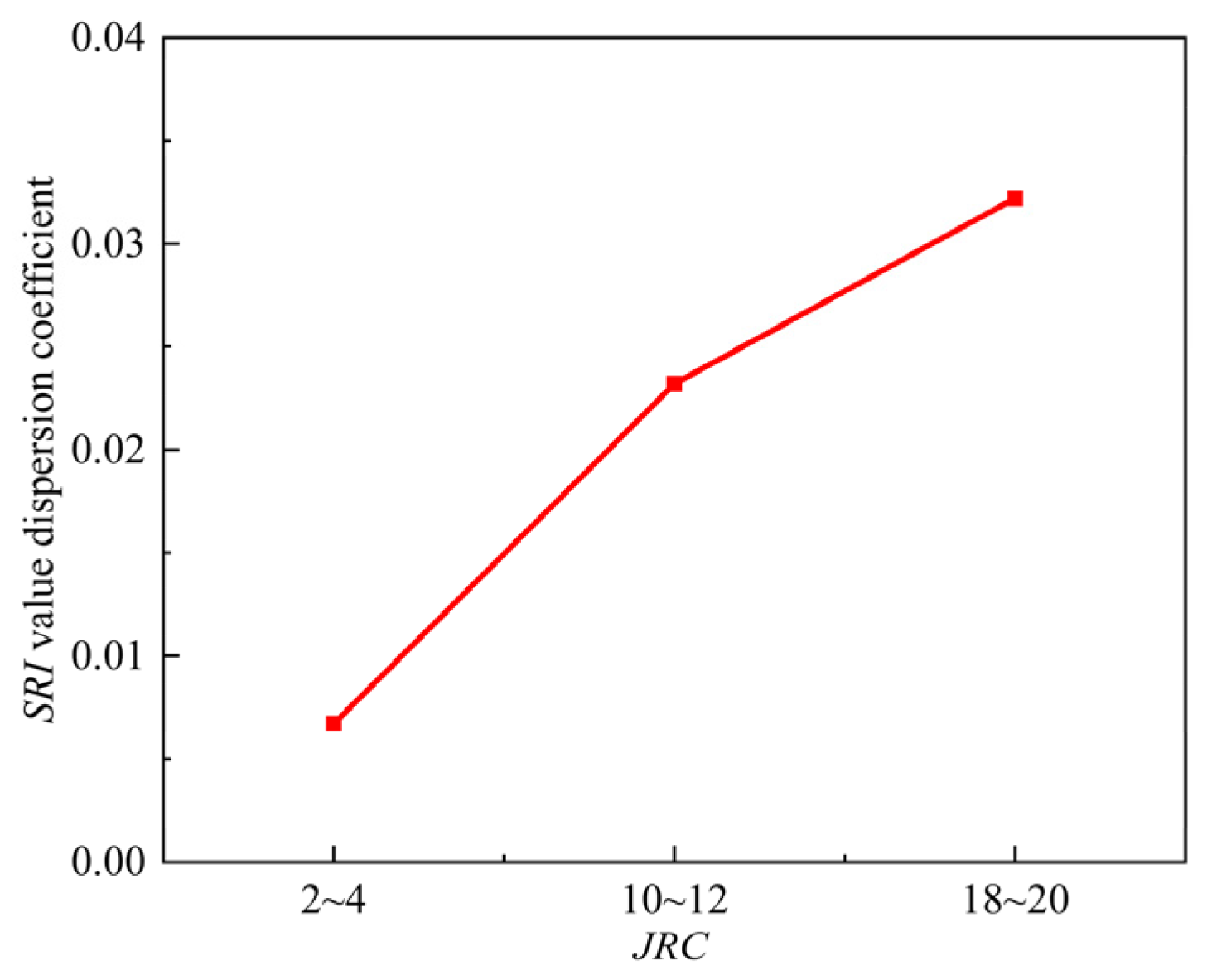
- Under the same JRC, the shapes of the exponential curves for different normal stiffness values are basically the same. Under the same normal stiffness conditions, the shapes of the exponential curves for different JRC values are similar to the shapes of the shear stress-shear displacement curves. The peak SRI value increases with increasing JRC and decreases with increasing kn. As JRC increases, the influence of normal stiffness on the joint surface resistance index becomes greater.
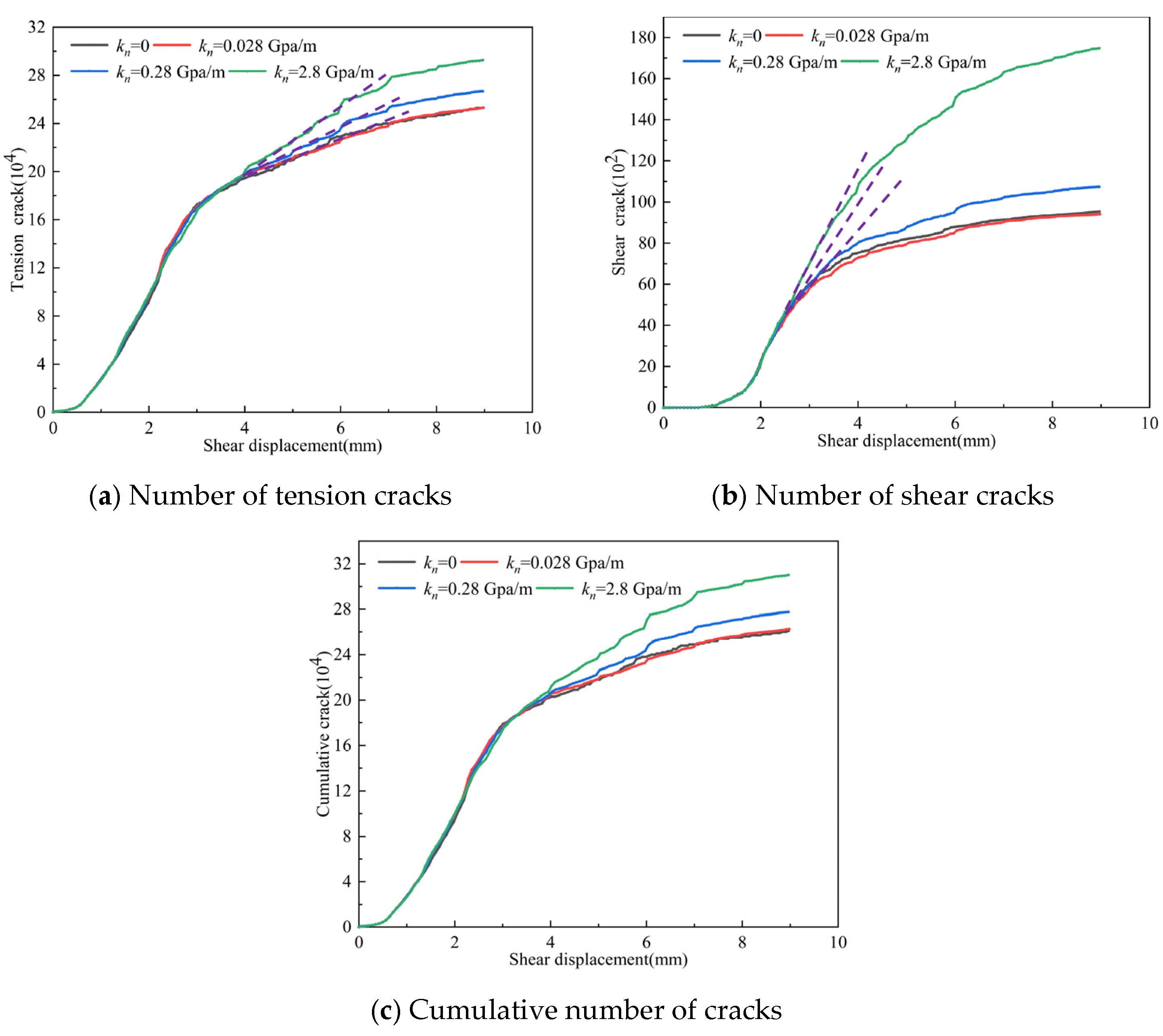
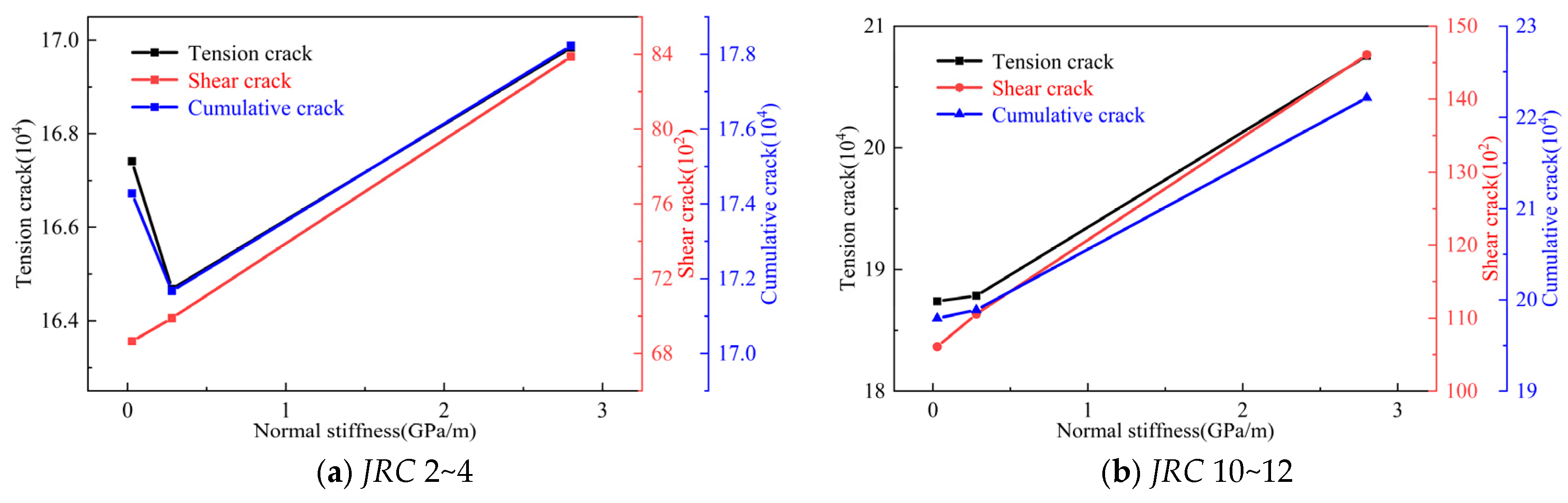
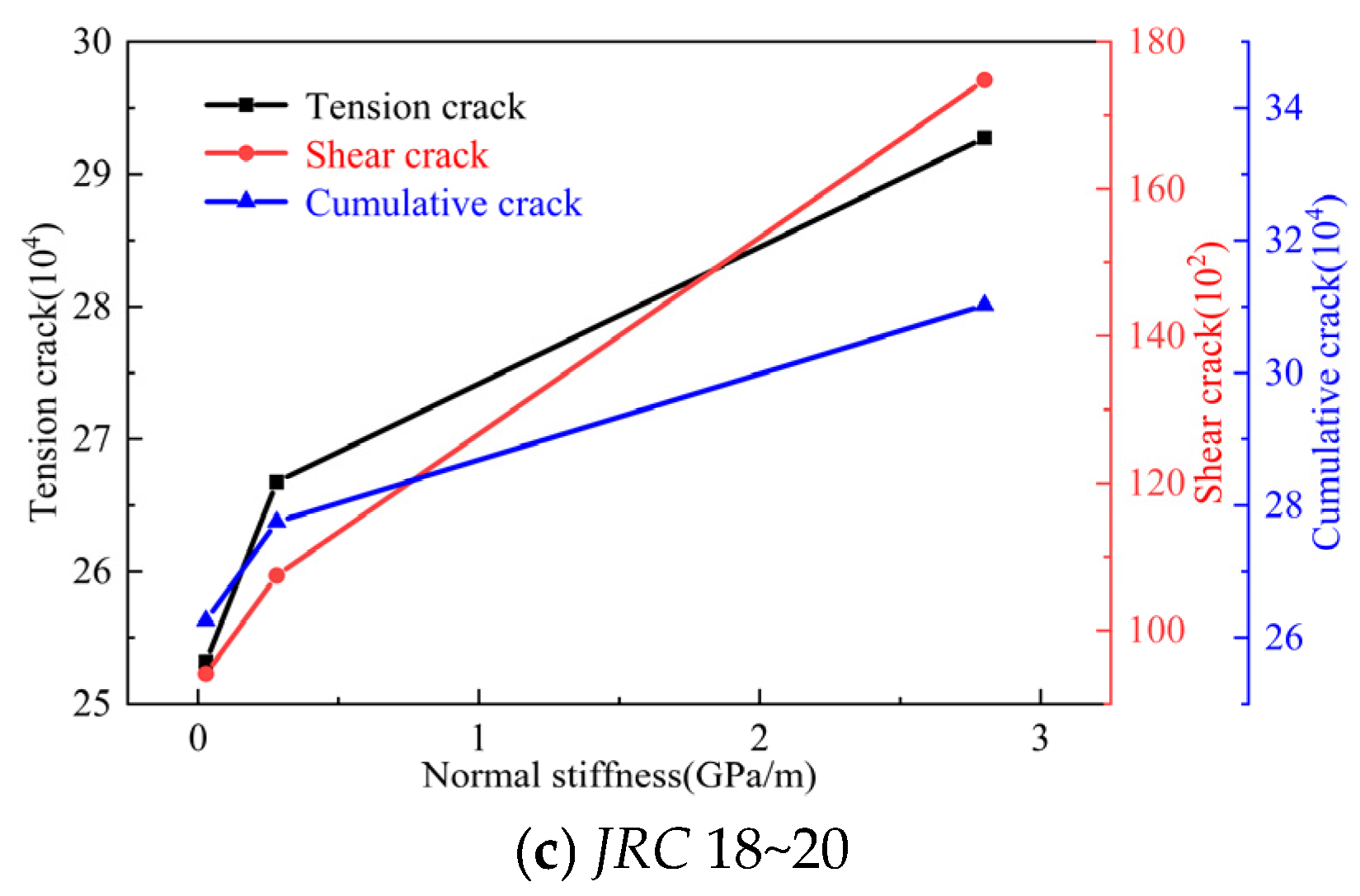
- In JRC 2~4, an increase in normal stiffness promotes the formation of floaters, while the number of fragments first decreases and then increases; in JRC 10~12, an increase in normal stiffness promotes the formation of fragments, while the number of floaters first decreases and then increases; and in JRC 18~20, an increase in normal stiffness promotes the formation of both floaters and fragments. As normal stiffness increases, the number of tensile cracks in JRC 2~4 first decreases and then increases, while the number of shear cracks increases with increasing normal stiffness; in JRC 10~12 and 18~20, both the number of shear cracks and tensile cracks increase with increasing normal stiffness.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Z.Y.; Li, D.Y.; Zhou, T.; Zhu, Q.Q.; Ranjith, P.G. Experimental study of stress wave propagation and energy characteristics across rock specimens containing cemented mortar joint with various thicknesses. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2020, 131, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A damage constitutive model for intermittent jointed rocks under cyclic uniaxial compression. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2018, 103, 289–301. [Google Scholar] [CrossRef]
- Xie, S.; Lin, H.; Wang, Y.; Cao, R.; Yong, R.; Du, S.; Li, J. Nonlinear shear constitutive model for peak shear-type joints based on improved Harris damage function. Arch. Civ. Mech. Eng. 2020, 20, 95. [Google Scholar] [CrossRef]
- Zhang, K.E.; Li, N.A.; Liu, W.; Xie, J. Experimental study of the mechanical, energy conversion and frictional heating characteristics of locking sections. Eng. Fract. Mech. 2020, 228, 106905. [Google Scholar] [CrossRef]
- Cui, G.J.; Zhang, C.Q.; Han, H.C. Experiment study on shear behavior of artificial joint under CNL and CNS boundary conditions. Chin. J. Rock Mech. Eng. 2019, 38 (Suppl. 2), 3384–3392. [Google Scholar]
- Bahaaddini, M. Effect of boundary condition on the shear behaviour of rock joints in the direct shear test. Rock Mech. Rock Eng. 2017, 50, 1141–1155. [Google Scholar] [CrossRef]
- Shang, J.; Zhao, Z.; Ma, S. On the shear failure of incipient rock discontinuities under CNL and CNS boundary conditions: Insights from DEM modelling. Eng. Geol. 2018, 234, 153–166. [Google Scholar] [CrossRef]
- Guti’errez-Ch, J.G.; Senent, S.; Melentijevic, S.; Jimenez, R. Distinct element method simulations of rock-concrete interfaces under different boundary conditions. Eng. Geol. 2018, 240, 123–139. [Google Scholar] [CrossRef]
- Haeri, H.; Sarfarazi, V.; Zhu, Z.M.; Marji, M.F.; Masoumi, A. Investigation of shear behavior of soil-concrete interface. Smart Struct. Syst. 2019, 23, 81–90. [Google Scholar]
- Saadat, M.; Taheri, A. A cohesive grain based model to simulate shear behaviour of rock joints with asperity damage in polycrystalline rock. Comput. Geotech. 2020, 117, 103254. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, B.W.; Hong, C.J. Shear properties of two-order morphology of rock joints. Chin. J. Geotech. Eng. 2022, 44, 1434–1442. [Google Scholar]
- Lu, H.F.; Zhu, C.D.; Liu, Q.S. Study on shear mechanical properties of structural planes grouted with different materials. Chin. J. Rock Mech. Eng. 2021, 40, 1803–1811. [Google Scholar]
- Wang, S.; Pu, H.; Wang, L.G. Shear performance and damage mechanism of the grout-rock interface under high temperature in coal gasification grouting reinforcement of rock mass. J. Min. Saf. Eng. 2025, 1–16. [Google Scholar] [CrossRef]
- Zhang, X.B.; Yi, L.; Yao, C. Comparative Study on Shear Mechanical Properties and Failure Mechanism of Rough Structural Surfaces under CNL and DNL Boundary Conditions. Chin. J. Rock Mech. Eng. 2025, 44, 865–880. [Google Scholar] [CrossRef]
- Zhu, T.T.; Zhu, H.H.; Li, A. Morphological Characteristics and Anisotropy of Roughness of Shear Fracture Surfaces in Sandstone. J. Hunan Univ. (Nat. Sci). 2025, 52, 239–248. [Google Scholar]
- Heuze, F.E. Dilatant effects of rock joints. In Proceedings of the 4th International Congress on Rock Mechanics, Montreux, Switzerland, 2–8 September 1979; A. A. Balkema: Rotterdam, The Netherlands, 1979; pp. 169–175. [Google Scholar]
- Belem, T.; Souley, M.; Homand, F. Method for quantification of wear of sheared joint walls based on surfacemorphology. Rock Mech. Rock Eng. 2009, 42, 883–910. [Google Scholar] [CrossRef]
- Li, B.; Bao, R.; Wang, Y. Permeability evolution of two-dimensional fracture networks during shear under constant normal stiffness boundary conditions. Rock Mech. Rock Eng. 2020, 54, 409–428. [Google Scholar] [CrossRef]
- Han, G.S.; Xiong, F.; Zhou, Y. Research progress on shear characteristics of rock joints under constant normal stiffness boundary conditions. Shock. Vib. 2021, 2021, 9670151. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Zhang, S.H.; Luan, H.J. Experimental study on shear characteristics of bolted rock joints under constant normal stiffness boundary conditions. Chin. J. Rock Mech. Eng. 2021, 40, 663–675. [Google Scholar]
- Indraratna, B.; Haque, A.; Aziz, N. Laboratory modelling of shear behaviour of soft joints under constant normal stiffness conditions. Comput Geotech. 1998, 16, 17–44. [Google Scholar] [CrossRef]
- Liu, R.C.; Yin, Q.; Yang, H.Q. Cyclic shear mechanical properties of 3D rough joint surfaces under constant normal stiffness (CNS) boundary conditions. Chin. J. Rock Mech. Eng. 2021, 40, 1092–1109. [Google Scholar]
- Jiao, F.; Xu, J.; Peng, S.J. Experimental Study on Shear Mechanical Properties and Damage Evolution Laws of Artificial Structural Surfaces under Normal Tangential Stiffness Conditions. J. China Coal Soc. 2023, 48, 4065–4077. [Google Scholar]
- Park, J.; Song, J. Numerical simulation of a direct shear test on a rock joint using a bonded-particle model. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B.K. Numerical direct shear tests to model the shear behaviour of rock joints. Comput. Geotech. 2013, 51, 101–115. [Google Scholar] [CrossRef]
- Asadi, M.S.; Rasouli, V.; Barla, G. A bonded particle model simulation of shear strength and asperity degradation for rough rock fractures. Rock Mech. Rock Eng. 2012, 45, 649–675. [Google Scholar] [CrossRef]
- Ge, Y.; Tang, H.; Eldin, M.A.M.E.; Wang, L.; Wu, Q.; Xiong, C. Evolution process of natural rock joint roughness during direct shear tests. Int. J. Geomech. 2017, 17, E4016013. [Google Scholar] [CrossRef]
- Yang, K.; Hu, Q.; Zhao, H.; Zhao, M.; Zhou, S. Numerical study on the shear behavior of concrete-rock joints with similar triangular asperities. Comput. Geotech. 2023, 159, 105468. [Google Scholar] [CrossRef]
- Oh, J.; Li, Y.; Mitra, R. A numerical study on dilation of a saw-toothed rock joint under direct shear. Rock Mech. Rock Eng. 2017, 50, 913–925. [Google Scholar] [CrossRef]
- Meng, F.; Song, J.; Yue, Z.; Zhou, H.; Wang, X.; Wang, Z. Failure mechanisms and damage evolution of hard rock joints under high stress: Insights from PFC2D modeling. Eng. Anal. Bound. Elem. 2022, 135, 394–411. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Teh, C.I. Influence of grain size on strength of polymineralic crystalline rock: New insights from DEM grain-based modeling. J. Rock Mech. Geotech. Eng. 2021, 13, 755–766. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, Q.; Nie, X.; Yao, Z.; Li, C.; Wang, J.; Ren, L. 3D anisotropic microcracking mechanisms of shale subjected to direct shear loading: A numerical insight. Eng. Fract. Mech. 2024, 298, 109950. [Google Scholar] [CrossRef]
- Ríos-Bayona, F.; Johansson, F.; Mas-Ivars, D.; Sánchez-Juncal, A.; Bolin, A. Using PFC2D to simulate the shear behaviour of joints in hard crystalline rock. B Eng. Geol. Environ. 2022, 81, 381. [Google Scholar] [CrossRef]
- Barton, N.R.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R. Parametric study of smooth joint parameters on the shear behaviour of rock joints. Rock Mech. Rock Eng. 2015, 48, 923–940. [Google Scholar] [CrossRef]
- Yang, K.X.; Liu, Y.N.; Zhao, H. Experimental Study and Discrete Element Simulation on Shear Characteristics of Sandstone-Concrete Structural Interfaces. J. Hunan Univ. (Nat. Sci.) 2024, 51, 165–176. [Google Scholar]
- Lee, Y.; Park, J.; Song, J. Model for the shear behavior of rock joints under CNL and CNS conditions. Int. J. Rock Mech. Min. Sci. 2014, 70, 252–263. [Google Scholar] [CrossRef]
- Xiong, L.; Wu, S. Numerical simulation of micro-cracking and energy budget in porous rocks under contractional regimes across the brittle-ductile transition. J. Struct. Geol. 2021, 148, 104376. [Google Scholar] [CrossRef]




| Parameter Type | Value |
|---|---|
| Elastic modulus, GPa | 4.2 |
| Poisson’s ratio | 0.2 |
| Uniaxial compressive strength, MPa | 27.4 |
| Friction angle, ° | 37.62 |
| Shear stiffness, GPa/m | 6.42 |
| Normal stiffness, GPa/m | 28.771 |
| JRC | JRC 2–4 | JRC 10–12 | JRC 18–20 | |
|---|---|---|---|---|
| kn | ||||
| 0 | 0.998 | 1.271 | 1.468 | |
| 0.028 | 0.997 | 1.268 | 1.461 | |
| 0.28 | 0.989 | 1.254 | 1.438 | |
| 2.8 | 0.984 | 1.199 | 1.352 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhao, K.; Xiong, L.; Zeng, P.; Gong, C.; Chen, Y. Numerical Simulation Study on Shear Mechanical Properties of Unfilled Three-Dimensional Rough Joint Surfaces Under Constant Normal Stiffness Boundary Conditions. Appl. Sci. 2025, 15, 10827. https://doi.org/10.3390/app151910827
Xu X, Zhao K, Xiong L, Zeng P, Gong C, Chen Y. Numerical Simulation Study on Shear Mechanical Properties of Unfilled Three-Dimensional Rough Joint Surfaces Under Constant Normal Stiffness Boundary Conditions. Applied Sciences. 2025; 15(19):10827. https://doi.org/10.3390/app151910827
Chicago/Turabian StyleXu, Xinmu, Kui Zhao, Liangfeng Xiong, Peng Zeng, Cong Gong, and Yifan Chen. 2025. "Numerical Simulation Study on Shear Mechanical Properties of Unfilled Three-Dimensional Rough Joint Surfaces Under Constant Normal Stiffness Boundary Conditions" Applied Sciences 15, no. 19: 10827. https://doi.org/10.3390/app151910827
APA StyleXu, X., Zhao, K., Xiong, L., Zeng, P., Gong, C., & Chen, Y. (2025). Numerical Simulation Study on Shear Mechanical Properties of Unfilled Three-Dimensional Rough Joint Surfaces Under Constant Normal Stiffness Boundary Conditions. Applied Sciences, 15(19), 10827. https://doi.org/10.3390/app151910827






