Multiscale Time Series Modeling in Energy Demand Prediction: A CWT-Aided Hybrid Model
Abstract
1. Introduction
- Offering a different hybrid model to simulate real-world electrical energy supply and demand developments;
- MSSW mechanism utilizing the Continuous Wavelet Transform technique for optimal extraction of time series patterns;
- Enhancing forecast accuracy in noisy or irregular time series;
- Incorporating the Random Forest algorithm into the model to circumvent potential overfitting issues when employing LSTM and GRU models in conjunction;
- The model’s capacity to generate precise forecasts, even during periods of peak and valley demand.
2. Related Works and Research Questions
- How does the consideration of multi-scale temporal dependencies affect the accuracy of electricity demand forecasting?
- To what extent does the integration of LSTM’s long-term memory capacity with GRU’s computational efficiency surpass the performance of classical ML and DL baselines?
- Can the proposed model sustain its forecasting performance and demonstrate generalization ability when validated on an independent dataset?
3. Methodology
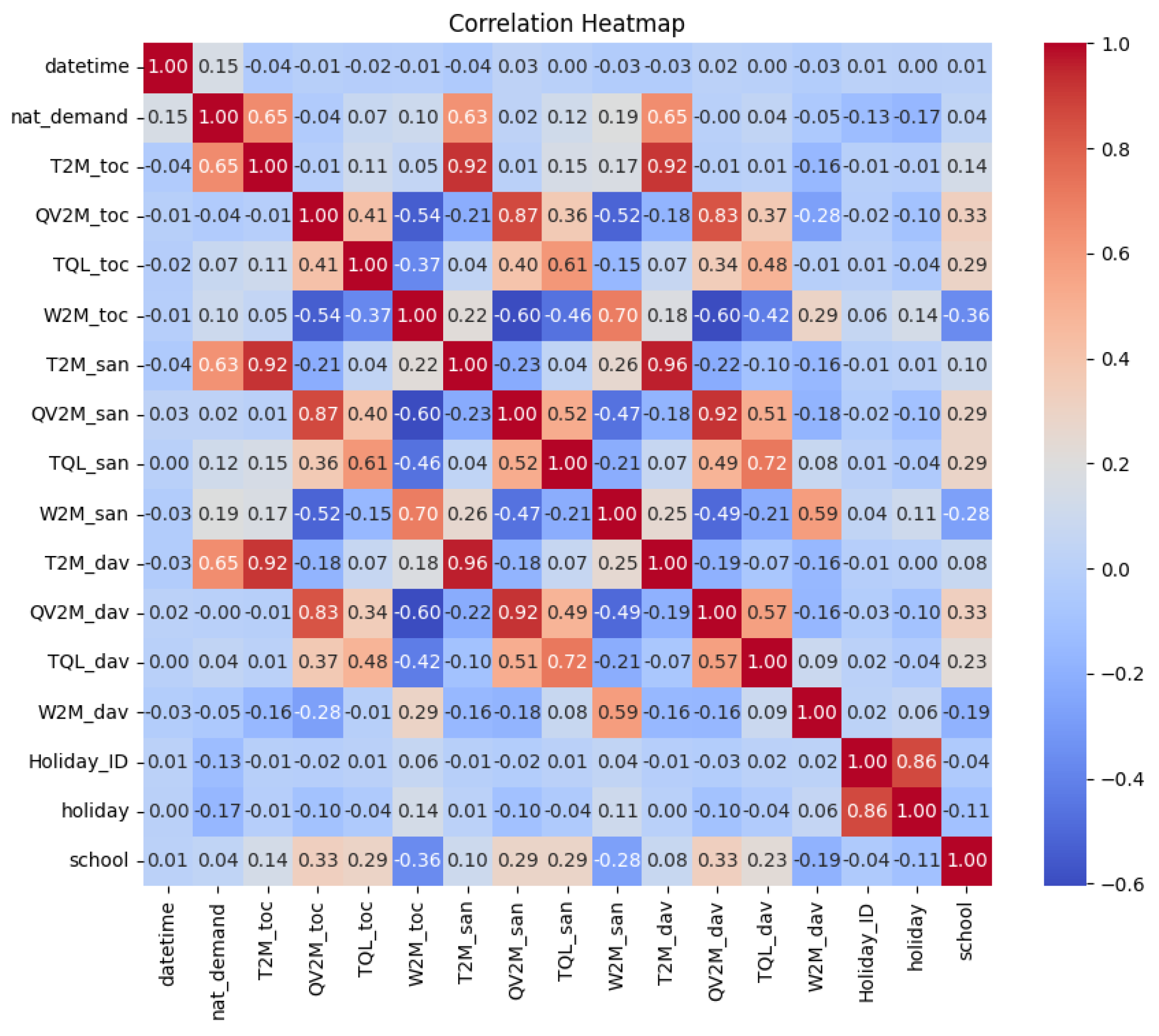
3.1. Dataset Used and Feature Selection
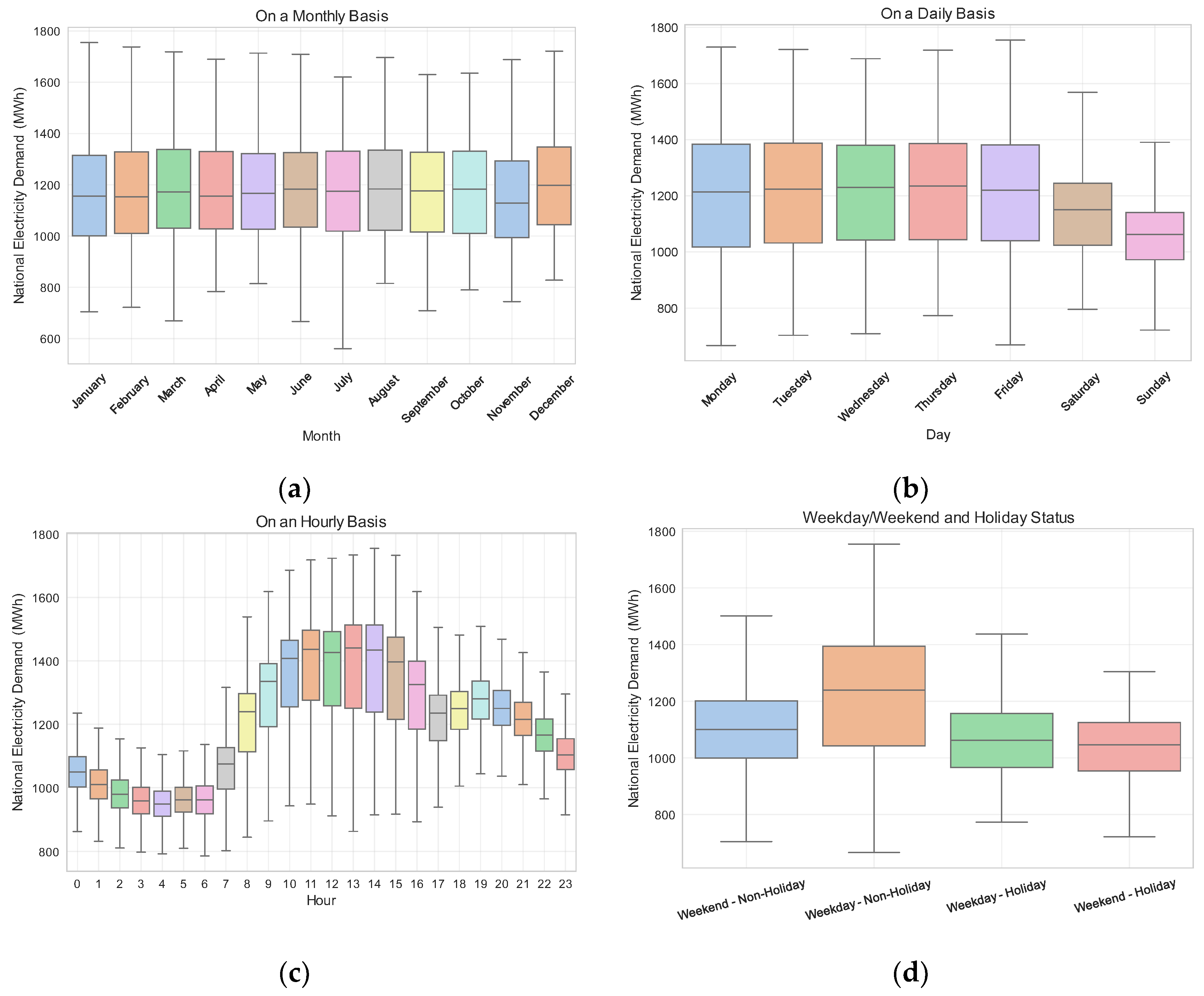
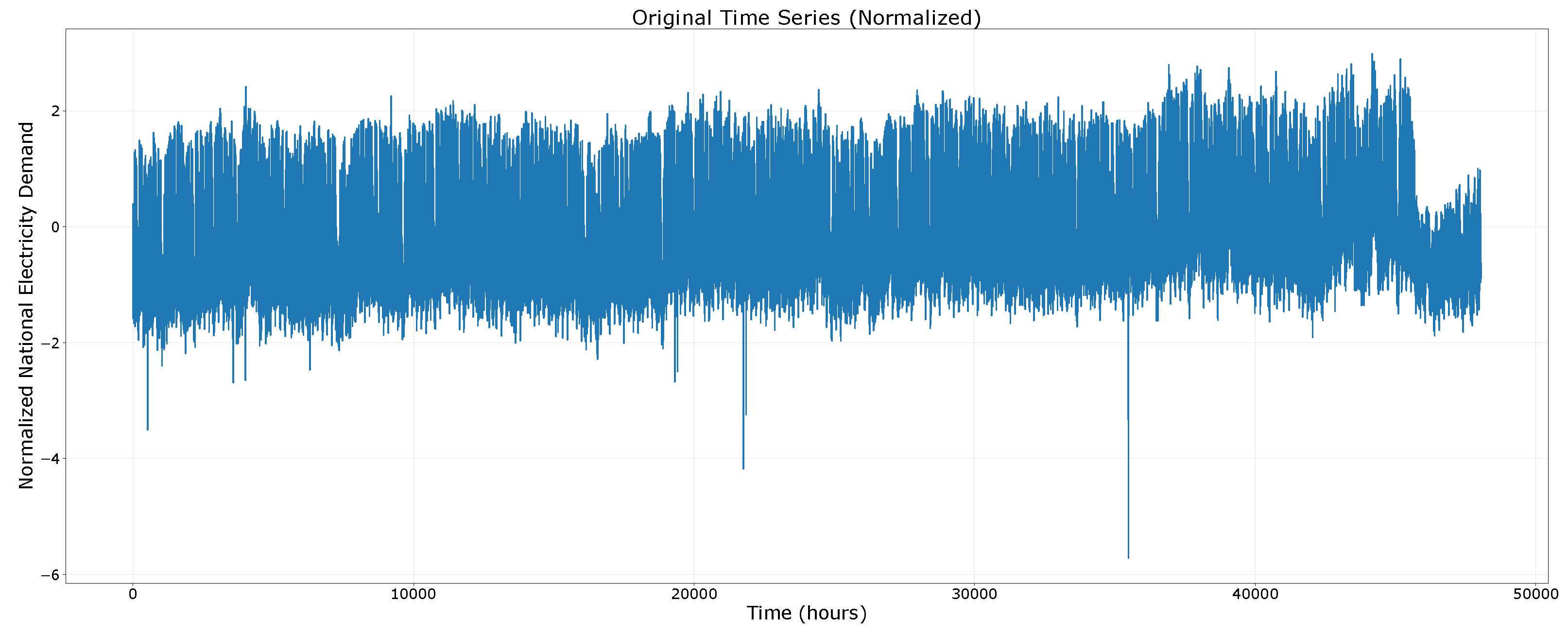
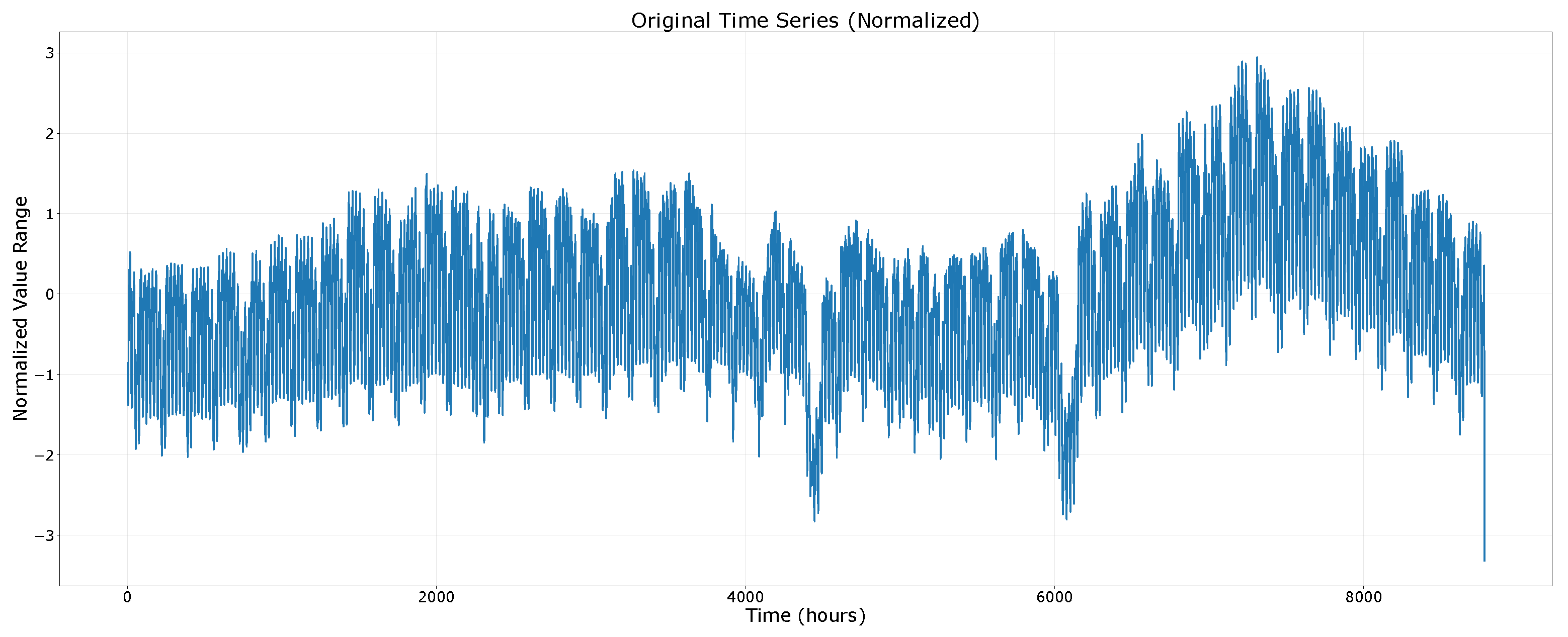
3.2. Electricity Demand Behavior Analysis
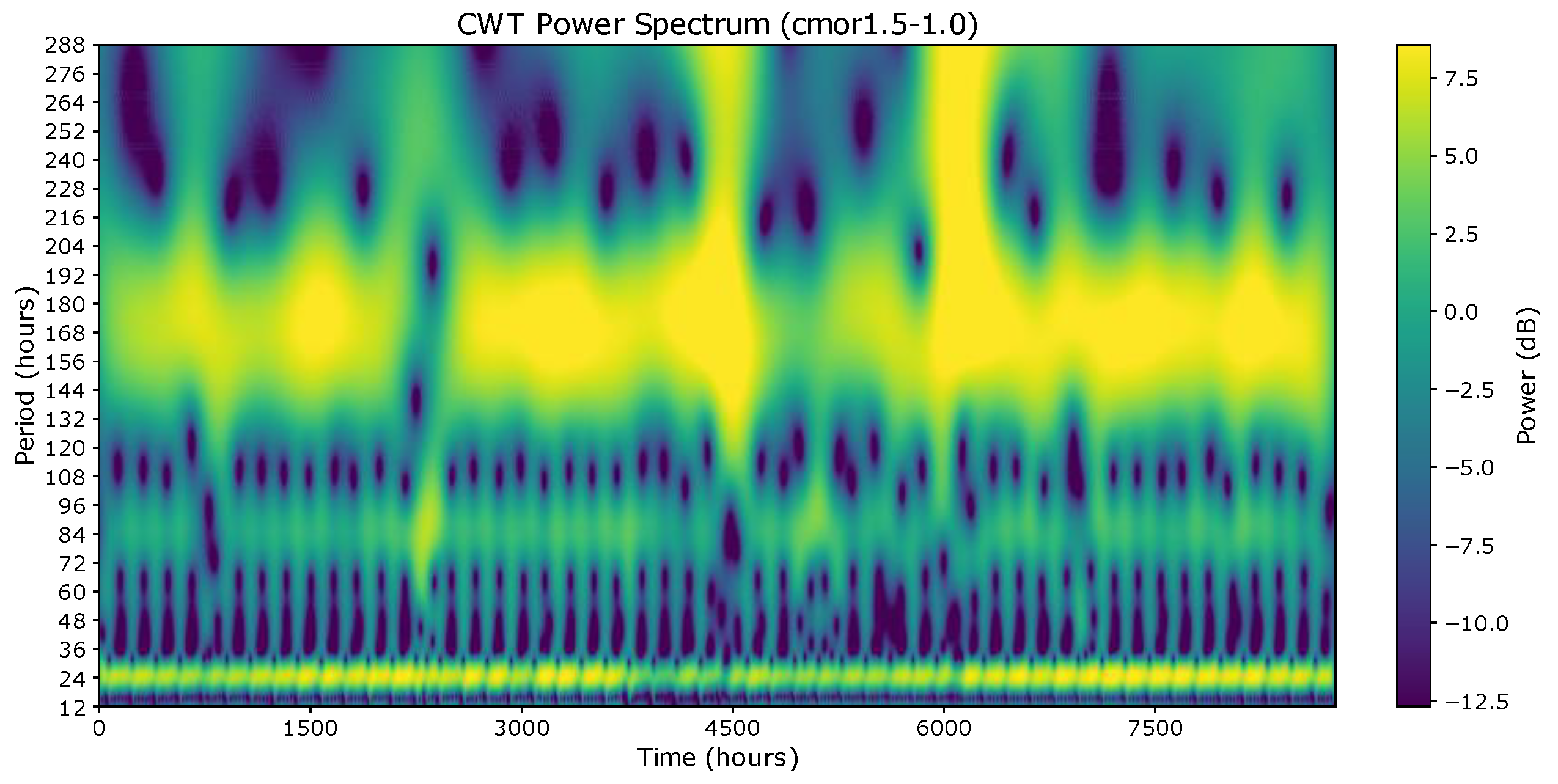
3.3. Continuous Wavelet Transform
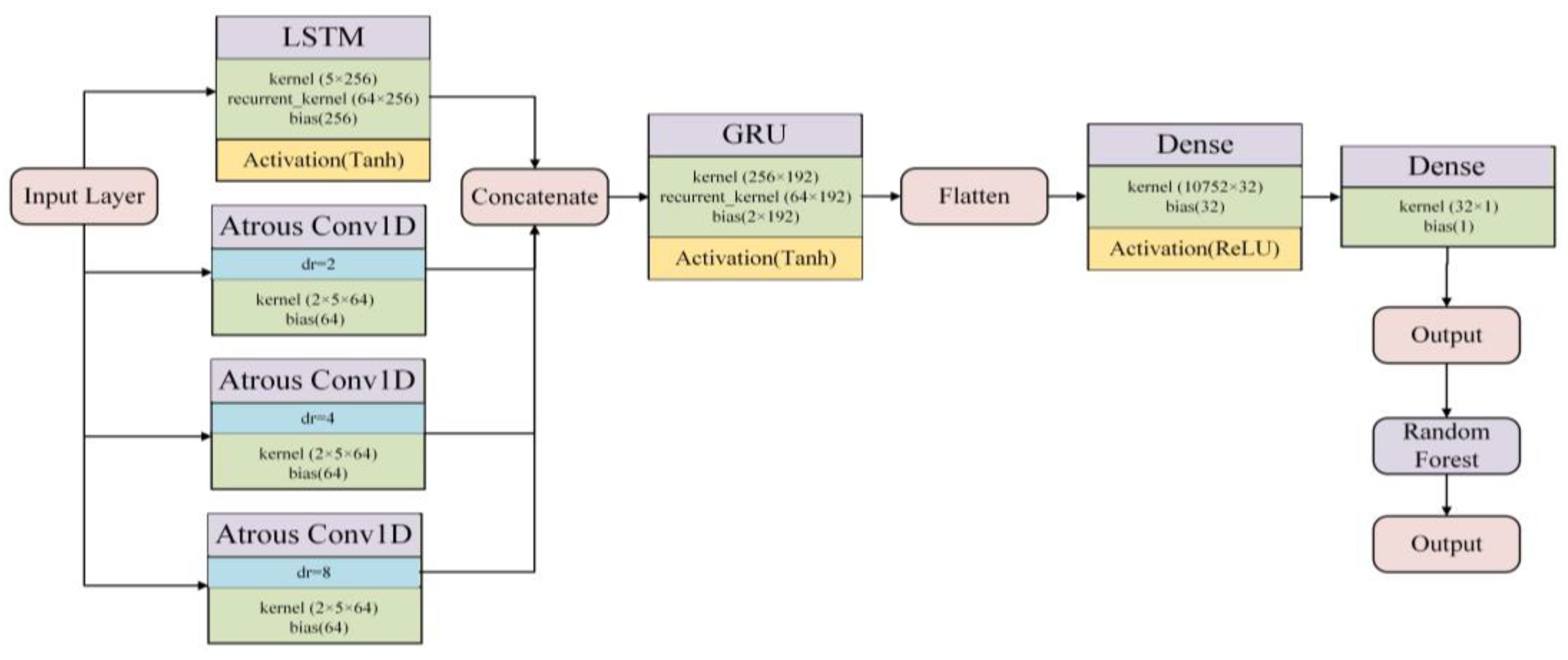
3.4. Proposed Deep Learning-Based Prediction Model
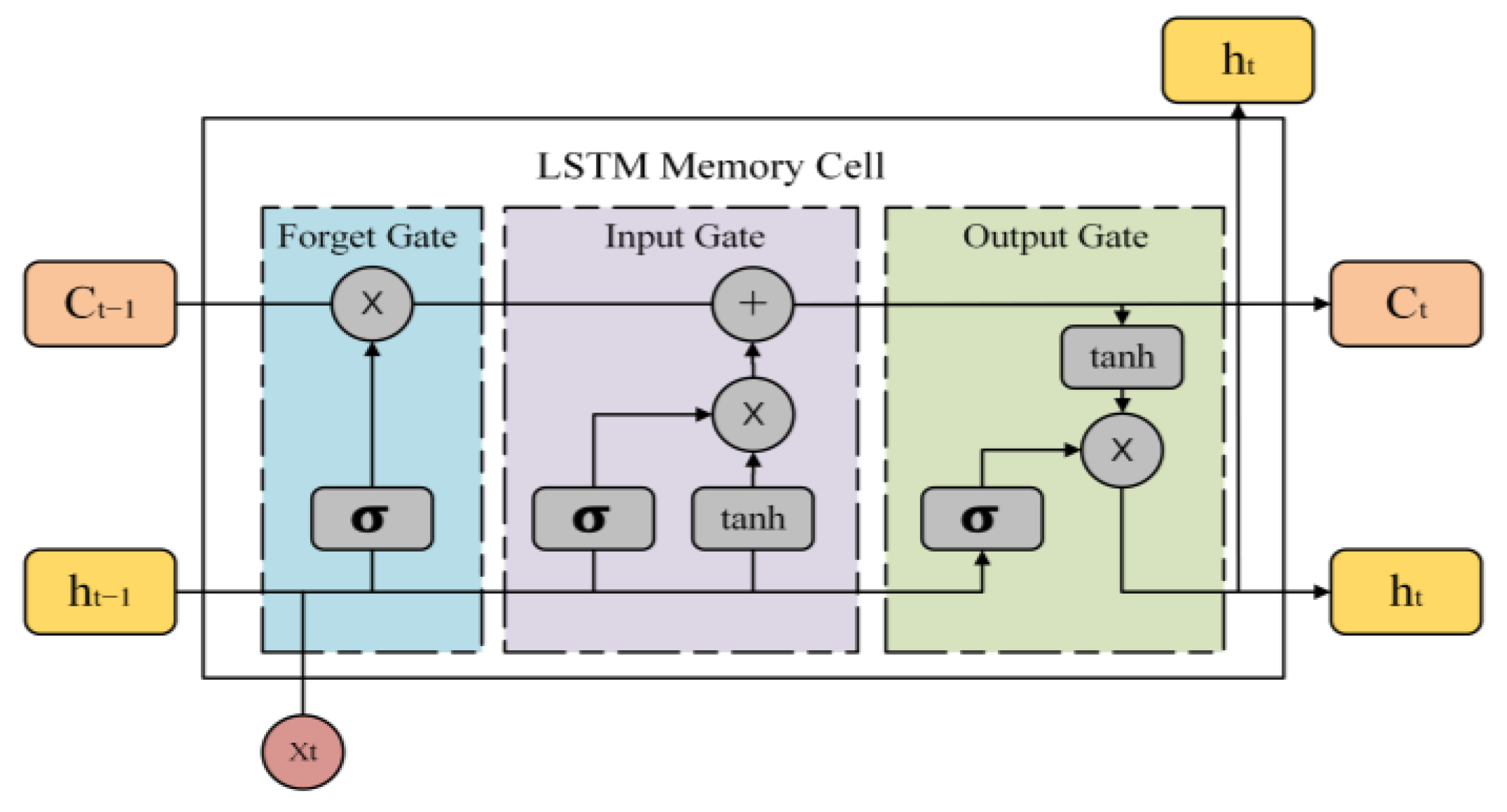
3.4.1. Long Short-Term Memory Unit
3.4.2. Gated Recurrent Unit
3.4.3. Random Forest Model
4. Experimental Results
4.1. Dataset Preparation and CWT Experiments
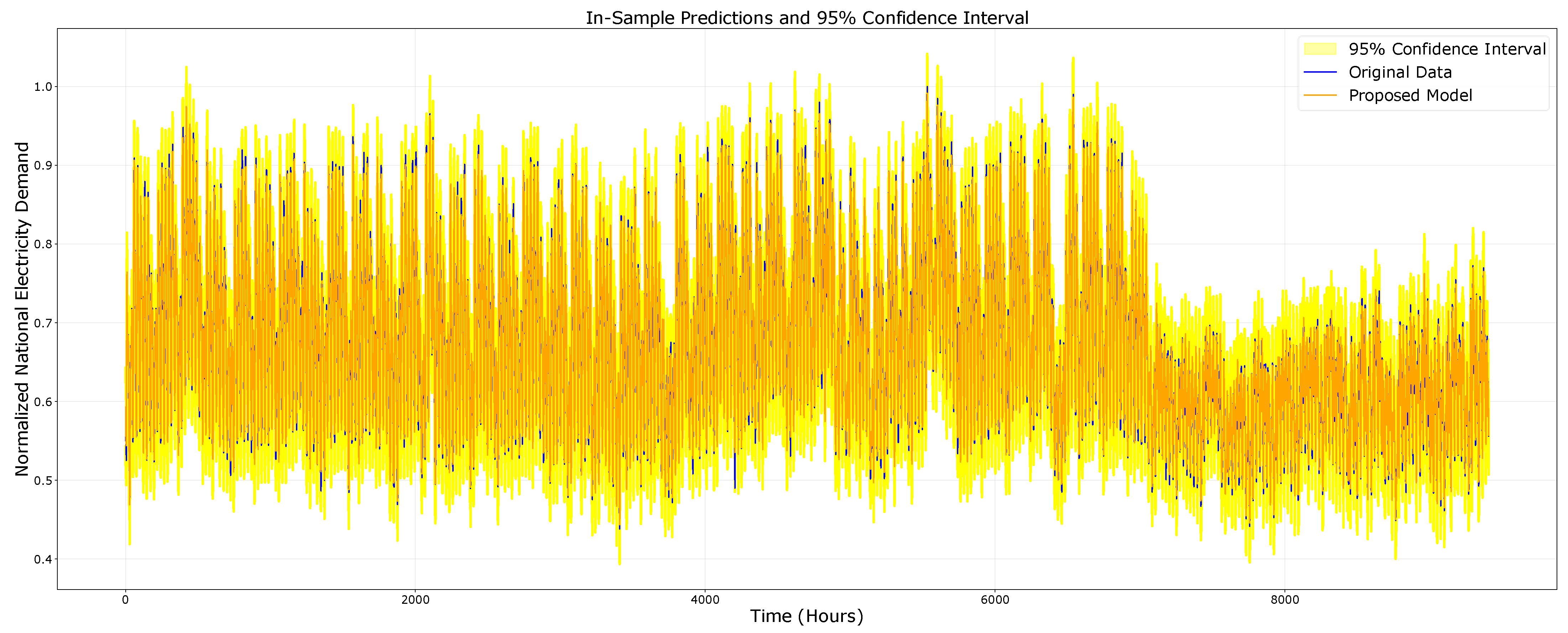
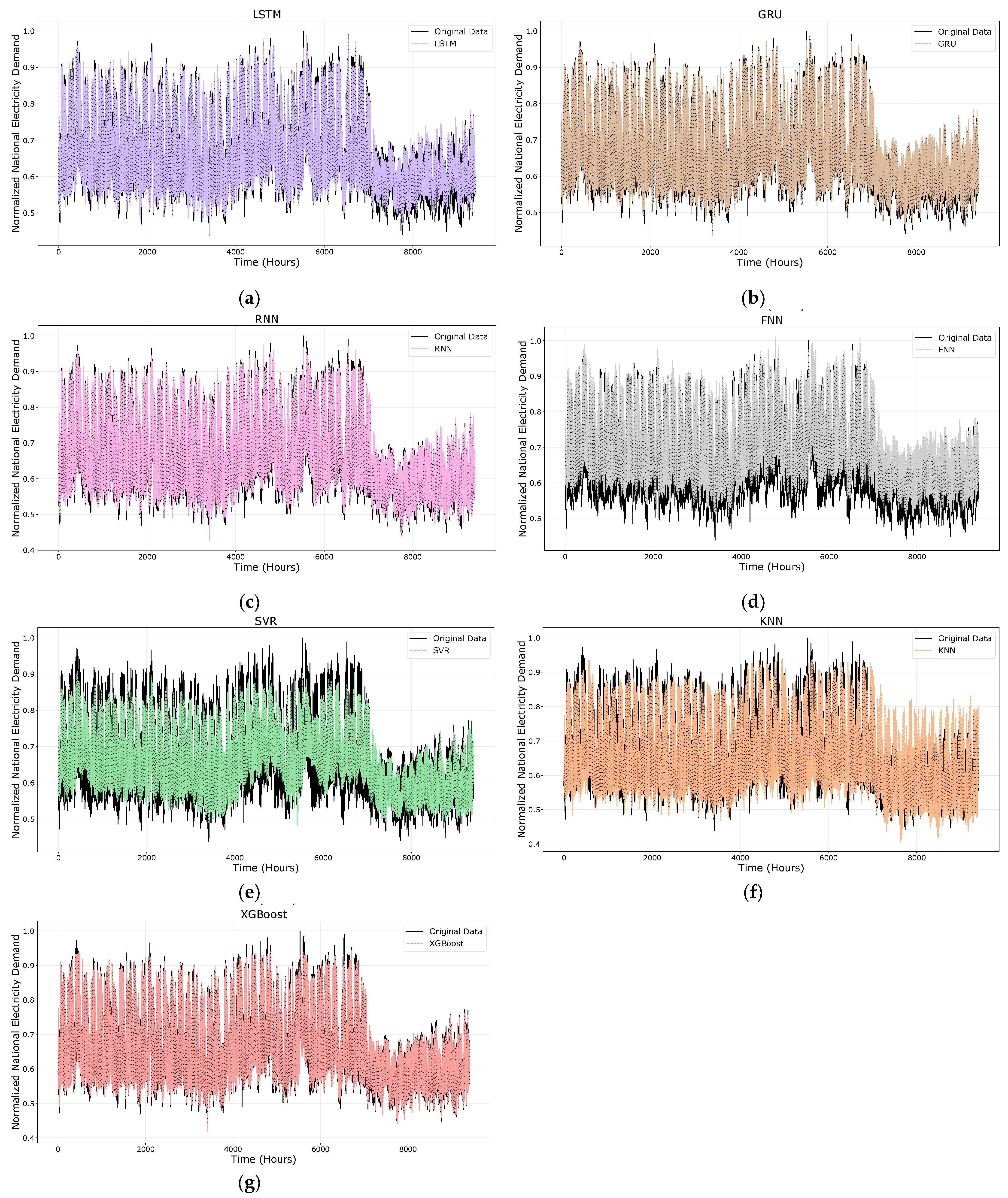
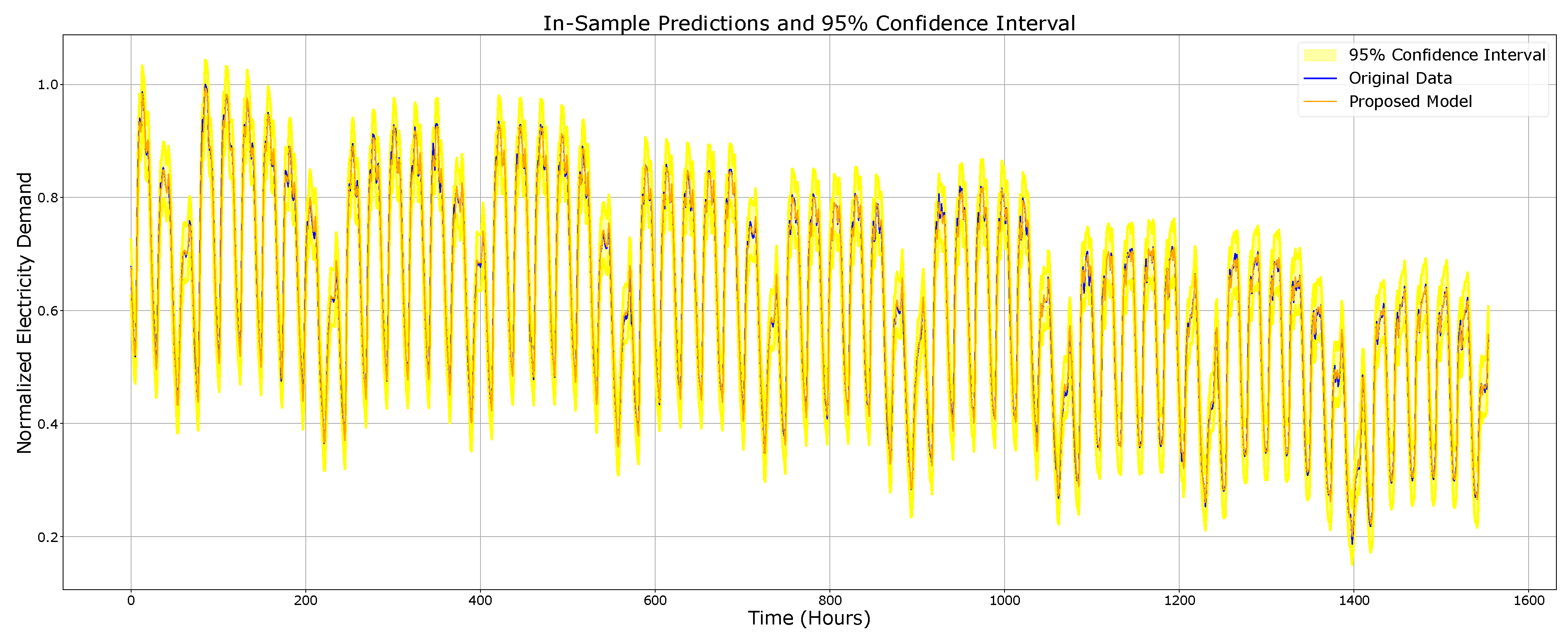
4.2. Model Evaluation
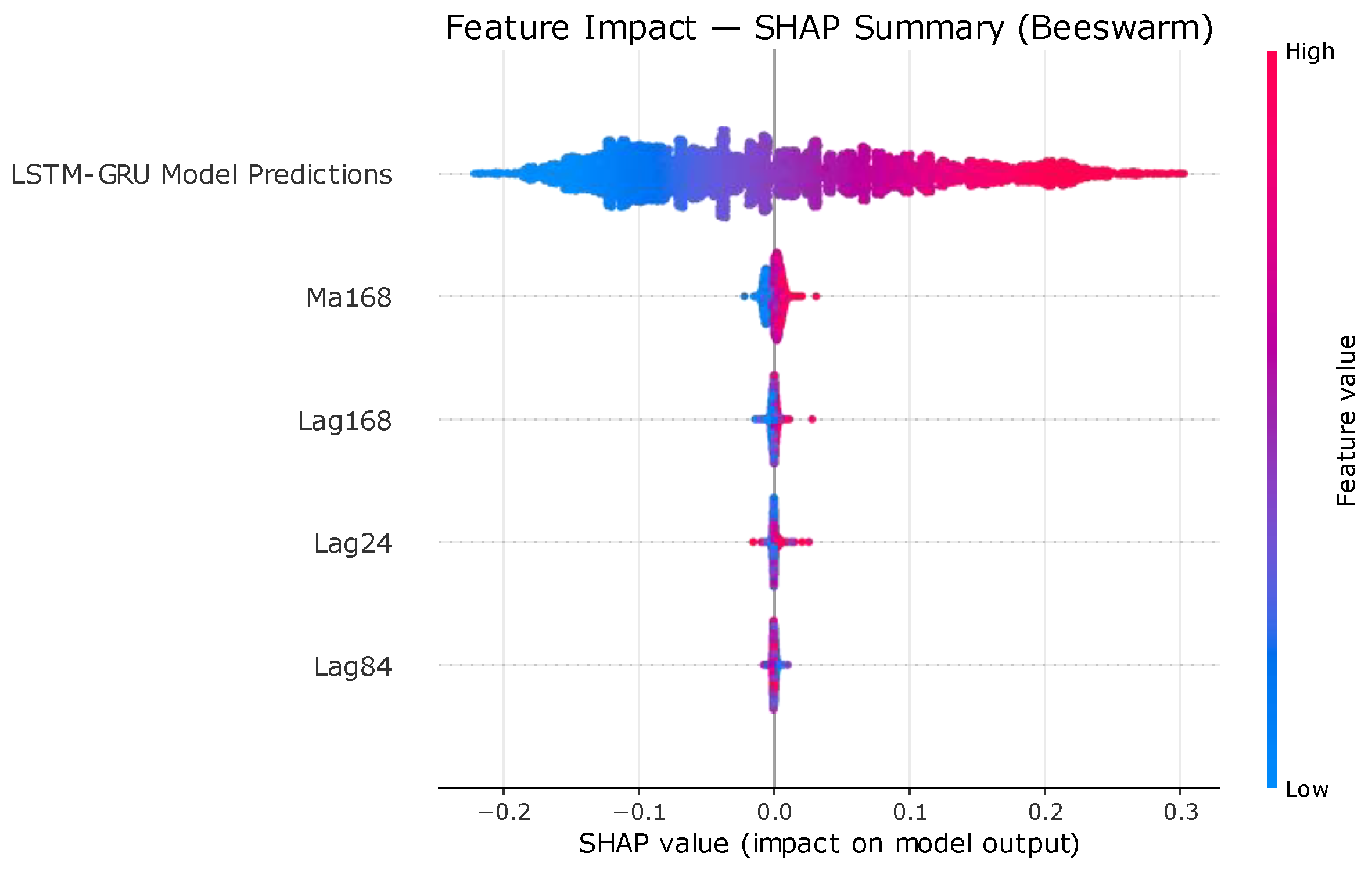
4.3. Ablation Studies
4.4. Evaluation of Generalization Performance on a Secondary Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CWT | Continuous Wavelet Transform |
| DL | Deep Learning |
| FNN | Feedforward Neural Network |
| GRU | Gated Recurrent Unit |
| KNN | K-Nearest Neighbors |
| LSTM | Long Short-Term Memory |
| ML | Machine Learning |
| RNN | Recurrent Neural Network |
| SVR | Support Vector Regression |
| XGBoost | Extreme Gradient Boosting |
References
- Atputharajah, A.; Saha, T.K. Power System Blackouts—Literature Review. In Proceedings of the 2009 International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 28–31 December 2009; pp. 460–465. [Google Scholar]
- Wang, Y.; Gu, A.; Zhang, A. Recent Development of Energy Supply and Demand in China, and Energy Sector Prospects through 2030. Energy Policy 2011, 39, 6745–6759. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Hug, G. Cost-Oriented Load Forecasting. Electric Power Systems Research 2022, 205, 107723. [Google Scholar] [CrossRef]
- Wang, S.; Li, C.; Lim, A. Why Are the ARIMA and SARIMA Not Sufficient. arXiv 2021, arXiv:1904.07632. [Google Scholar] [CrossRef]
- Aderibigbe, A.O.; Ani, E.C.; Ohenhen, P.E.; Ohalete, N.C.; Daraojimba, D.O. Enhancing Energy Efficiency With Ai: A Review Of Machine Learning Models In Electricity Demand Forecasting. Eng. Sci. Technol. J. 2023, 4, 341–356. [Google Scholar] [CrossRef]
- Benti, N.E.; Chaka, M.D.; Semie, A.G. Forecasting Renewable Energy Generation with Machine Learning and Deep Learning: Current Advances and Future Prospects. Sustainability 2023, 15, 7087. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Y.; Guo, B.; Luo, X.; Peng, Q.; Jin, Z. A Hybrid Sparrow Search Algorithm of the Hyperparameter Optimization in Deep Learning. Mathematics 2022, 10, 3019. [Google Scholar] [CrossRef]
- Aguilar Madrid, E.; Antonio, N. Short-Term Electricity Load Forecasting with Machine Learning. Information 2021, 12, 50. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-Term Load Forecasting Based on LSTM Networks Considering Attention Mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Aouad, M.; Hajj, H.; Shaban, K.; Jabr, R.A.; El-Hajj, W. A CNN-Sequence-to-Sequence Network with Attention for Residential Short-Term Load Forecasting. Electr. Power Syst. Res. 2022, 211, 108152. [Google Scholar] [CrossRef]
- Ibrahim, B.; Rabelo, L.; Gutierrez-Franco, E.; Clavijo-Buritica, N. Machine Learning for Short-Term Load Forecasting in Smart Grids. Energies 2022, 15, 8079. [Google Scholar] [CrossRef]
- Joy, C.P.; Pillai, G.; Chen, Y.; Mistry, K. Micro-Genetic Algorithm Embedded Multi-Population Differential Evolution Based Neural Network for Short-Term Load Forecasting. In Proceedings of the 2021 56th International Universities Power Engineering Conference: Powering Net Zero Emissions, UPEC 2021—Proceedings, online, 31 August 2021. [Google Scholar]
- Sun, L.; Qin, H.; Przystupa, K.; Majka, M.; Kochan, O. Individualized Short-Term Electric Load Forecasting Using Data-Driven Meta-Heuristic Method Based on LSTM Network. Sensors 2022, 22, 7900. [Google Scholar] [CrossRef]
- Shohan, M.J.A.; Faruque, M.O.; Foo, S.Y. Forecasting of Electric Load Using a Hybrid LSTM-Neural Prophet Model. Energies 2022, 15, 2158. [Google Scholar] [CrossRef]
- Valencia, V.A.N.; Sanchez-Galan, J.E. Use of Attention-Based Neural Networks to Short-Term Load Forecasting in the Republic of Panama. In Proceedings of the Proceedings of the 2022 IEEE 40th Central America and Panama Convention, CONCAPAN 2022, Panama City, Panama, 9–12 November 2022. [Google Scholar]
- Abumohsen, M.; Owda, A.Y.; Owda, M. Electrical Load Forecasting Using LSTM, GRU, and RNN Algorithms. Energies 2023, 16, 2283. [Google Scholar] [CrossRef]
- Mounir, N.; Ouadi, H.; Jrhilifa, I. Short-Term Electric Load Forecasting Using an EMD-BI-LSTM Approach for Smart Grid Energy Management System. Energy Build. 2023, 288, 113022. [Google Scholar] [CrossRef]
- Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On Short-Term Load Forecasting Using Machine Learning Techniques and a Novel Parallel Deep LSTM-CNN Approach. IEEE Access 2021, 9, 31191–31212. [Google Scholar] [CrossRef]
- Ullah, K.; Ahsan, M.; Hasanat, S.M.; Haris, M.; Yousaf, H.; Raza, S.F.; Tandon, R.; Abid, S.; Ullah, Z. Short-Term Load Forecasting: A Comprehensive Review and Simulation Study with CNN-LSTM Hybrids Approach. IEEE Access 2024, 12, 111858–111881. [Google Scholar] [CrossRef]
- Ijaz, K.; Hussain, Z.; Ahmad, J.; Ali, S.F.; Adnan, M.; Khosa, I. A Novel Temporal Feature Selection Based LSTM Model for Electrical Short-Term Load Forecasting. IEEE Access 2022, 10, 82596–82613. [Google Scholar] [CrossRef]
- Rafi, S.H.; Al-Masood, N.; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, T.; Zheng, X.; Liu, Y.; Zhuang, Z.; Mohamed, M.A. An Innovative Method-Based CEEMDAN–IGWO–GRU Hybrid Algorithm for Short-Term Load Forecasting. Electr. Eng. 2022, 104, 3137–3156. [Google Scholar] [CrossRef]
- Su, Z.; Zheng, G.; Wang, G.; Hu, M.; Kong, L. An IDBO-Optimized CNN-BiLSTM Model for Load Forecasting in Regional Integrated Energy Systems. Comput. Electr. Eng. 2025, 123, 110013. [Google Scholar] [CrossRef]
- Shah, S.A.H.; Ahmed, U.; Bilal, M.; Khan, A.R.; Razzaq, S.; Aziz, I.; Mahmood, A. Improved Electric Load Forecasting Using Quantile Long Short-Term Memory Network with Dual Attention Mechanism. Energy Rep. 2025, 13, 2343–2353. [Google Scholar] [CrossRef]
- Asghar Majeed, M.; Phichaisawat, S.; Asghar, F.; Hussan, U. Data-Driven Optimized Load Forecasting: An LSTM-Based RNN Approach for Smart Grids. IEEE Access 2025, 13, 99018–99031. [Google Scholar] [CrossRef]
- Zheng, D.; Qin, J.; Liu, Z.; Zhang, Q.; Duan, J.; Zhou, Y. BWO–ICEEMDAN–ITransformer: A Short-Term Load Forecasting Model for Power Systems with Parameter Optimization. Algorithms 2025, 18, 243. [Google Scholar] [CrossRef]
- Ahranjani, Y.K.; Beiraghi, M.; Ghanizadeh, R. Short Time Load Forecasting for Urmia City Using the Novel CNN-LTSM Deep Learning Structure. Electr. Eng. 2025, 107, 1253–1264. [Google Scholar] [CrossRef]
- Fan, C.; Li, G.; Xiao, L.; Yi, L.; Nie, S. Short-Term Power Load Forecasting in City Based on ISSA-BiTCN-LSTM. Cogn. Comput. 2025, 17, 39. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, J.; Qiu, P.; Zhang, X.; Shuai, C. Short-Term Power Load Forecasting Based on TCN-BiLSTM-Attention and Multi-Feature Fusion. Arab. J. Sci. Eng. 2025, 50, 5475–5486. [Google Scholar] [CrossRef]
- Martirosyan, A.; Ilyushin, Y.; Afanaseva, O.; Kukharova, T.; Asadulagi, M.; Khloponina, V. Development of an Oil Field’s Conceptual Model. Int. J. Eng. 2025, 38, 381–388. [Google Scholar] [CrossRef]
- Sadowsky, J. Investigation of Signal Characteristics Using the Continuous Wavelet Transform. Johns Hopkins Apl Tech. Dig. 1996, 17, 258–269. [Google Scholar]
- Küçük, M.; Ağiralioğlu, N. Dalgacık Dönüşüm Tekniği Kullanılarak Hidrolojik Akım Serilerinin Modellenmesi. İtüdergisi/D 2011, 5, 69–80. [Google Scholar]
- Arı, N.; Özen, Ş.; Çolak, Ö.H. Dalgacık Teorisi; Palme Yayıncılık: Ankara, Turkey, 2008; pp. 23–27. [Google Scholar]
- Wang, J.; Jiang, W.; Li, Z.; Lu, Y. A New Multi-Scale Sliding Window LSTM Framework (MSSW-LSTM): A Case Study for GNSS Time-Series Prediction. Remote Sens. 2021, 13, 3328. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Optimal Deep Learning LSTM Model for Electric Load Forecasting Using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric Load Forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Son, N.; Shin, Y. Short- and Medium-Term Electricity Consumption Forecasting Using Prophet and GRU. Sustainability 2023, 15, 15860. [Google Scholar] [CrossRef]
- Li, W.; Logenthiran, T.; Woo, W.L. Multi-GRU Prediction System for Electricity Generation’s Planning and Operation. IET Gener. Transm. Distrib. 2019, 13, 1630–1637. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.Y.; Baik, S.W. A Novel CNN-GRU-Based Hybrid Approach for Short-Term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-Term Electricity Load Forecasting Model Based on EMD-GRU with Feature Selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Ke, K.; Hongbin, S.; Chengkang, Z.; Brown, C. Short-Term Electrical Load Forecasting Method Based on Stacked Auto-Encoding and GRU Neural Network. Evol. Intell. 2019, 12, 385–394. [Google Scholar] [CrossRef]
- Dudek, G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies 2022, 15, 7547. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Piedad, E.; Kuo, C.-C. Energy Consumption Load Forecasting Using a Level-Based Random Forest Classifier. Symmetry 2019, 11, 956. [Google Scholar] [CrossRef]
- Li, C.; Tao, Y.; Ao, W.; Yang, S.; Bai, Y. Improving Forecasting Accuracy of Daily Enterprise Electricity Consumption Using a Random Forest Based on Ensemble Empirical Mode Decomposition. Energy 2018, 165, 1220–1227. [Google Scholar] [CrossRef]
- Mallala, B.; Ahmed, A.I.U.; Pamidi, S.V.; Faruque, M.O.; Reddy M, R. Forecasting Global Sustainable Energy from Renewable Sources Using Random Forest Algorithm. Results Eng. 2025, 25, 103789. [Google Scholar] [CrossRef]
- Sui, Q.; He, H.; Liang, J.; Li, Z.; Su, C. Short-Term Scheduling of Integrated Electric-Hydrogen-Thermal Systems Considering Hydroelectric Power Plant Peaking for Hydrogen Vessel Navigation. IEEE Trans. Sustain. Energy 2025, 16, 3082–3094. [Google Scholar] [CrossRef]


| Work/Source | Dataset | Input Features | Method/Model | Key Results of the Error Metrics |
|---|---|---|---|---|
| IDBO-optimized CNN-BiLSTM [23] | Arizona State University (RIES) load operation data (Electrical (EL), Cooling (CL), Heat (HL)). One full year (8760 data points). | Multi-energy loads (EL, CL, HL). Min-Max scaling applied. | CNN-BiLSTM model optimized using the Improved Dung-Beetle Optimization (IDBO) algorithm to tune hyperparameters. CNN extracts features; BiLSTM learns time series dependencies. | EL: MAPE: 3.46%, RMSE: 956.45, R2: 0.98. CL: MAPE: 3.02%, RMSE: 178.21, R2: 0.98. HL: MAPE: 1.97%, RMSE: 17.25, R2: 0.98. |
| DA-QLSTM [24] | IESCO (Islamabad Electric Supply Company, 13,128 points, 2 years) and Panama City (48,048 points, 6 years) load data. | IESCO: Temperature, dew point, humidity. Panama: Temperature, relative humidity, wind speed. MinMax scaled. | DA-QLSTM (Quantile LSTM with Dual Attention Mechanism). Integrates temporal and feature-wise attention. Uses a custom quantile loss function for probabilistic forecasts (predicting 0.5, 0.6, 0.9 quantiles). | IESCO: MAPE: 4.06%, RMSE: 64.62, MAE: 41.61. Panama: MAPE: 1.66%, RMSE: 27.83, MAE: 19.17. |
| RNN-LSTM [25] | Historical load, renewable energy generation, and weather data (Smart Grids/Power Systems). | Historical load values and external features (weather, time). | RNN-LSTM (Recurrent Neural Network with LSTM units). Optimizes MSE loss using Adam optimizer. | RMSE: 2.2889, MAE: 1.104, MAPE: 1.538% |
| BWO–ICEEMDAN–iTransformer [26] | Singapore electricity load, price, and weather data (2019–2020), 30 min intervals. | Decomposed load subsequences. Highly correlated factors selected via SCC: Electricity Price, Relative Humidity, and Temperature. Input sequence length 96, output 48. | BWO–ICEEMDAN–iTransformer. ICEEMDAN decomposes data. BWO (Beluga Whale Optimization) optimizes ICEEMDAN parameters (Nstd, NR). iTransformer predicts decomposed components. | R2: 0.9873, MAE: 48.0014, RMSE: 66.2221. |
| CNN-LSTM [27] | Urmia City (Iran) load and weather data, 3 consecutive years (2009–2011). | Historical load consumption trends and upcoming weather conditions. | Hybrid CNN-LSTM Deep Learning Structure. CNN extracts features; 3-layer LSTM performs time series prediction. Includes a Dropout layer to mitigate overfitting. | MAPE: 0.956%, RMSE: 1.476. |
| ISSA-BiTCN-LSTM [28] | Electric load and weather data from Los Angeles, Tetouan, and Johor. | Power load and weather features (Temperature, Humidity, Wind speed, etc.), varying by city. | ISSA-BiTCN-LSTM. Parallel hybrid model combining BiTCN (local features) and LSTM (long-term dependencies). ISSA (Improved Salp Swarm Algorithm) optimizes 5 hyperparameters (kernel size, filters, batch size, epochs, neurons). | RMSE: 925.11 kW, MAE: 732.63 kW, NRMSE: 0.019, MAPE: 1.034%. |
| TCN-BiLSTM-Attention [29] | Australia regional load, electricity price, and meteorological data (2006–2010), 30 min intervals. | Multivariate Time Series: Power Load, Electricity Price, Dry Bulb Temperature, Dew Point Temperature, Wet Bulb Temperature, Humidity. | TCN-BiLSTM-Attention. Hybrid architecture: TCN (temporal feature extraction) + BiLSTM (long/short-term dependencies) + Attention Mechanism (multivariate correlation and weighting). Optimized using Grid Search. | MAE: 225.531, RMSE: 276.792, MAPE: 2.8%, R2: 0.959 |
| Column Name | Description | Unit |
|---|---|---|
| datetime | Date-time index corresponding to Panama time-zone UTC-05:00 (index) | |
| nat_demand | National electricity load (Target or Dependent variable) | MWh |
| T2M_toc | Temperature at 2 m in Tocumen, Panama City | °C |
| QV2M_toc | Relative humidity at 2 m in Tocumen, Panama City | % |
| TQL_toc | Liquid precipitation in Tocumen, Panama City | |
| W2M_toc | Wind Speed at 2 m in Tocumen, Panama City | m/s |
| T2M_san | Temperature at 2 m in Santiago city | °C |
| QV2M_san | Relative humidity at 2 m in Santiago city | % |
| TQL_san | Liquid precipitation in Santiago city | |
| W2M_san | Wind Speed at 2 m in Santiago city | m/s |
| T2M_dav | Temperature at 2 m in David city | °C |
| QV2M_dav | Relative humidity at 2 m in David city | % |
| TQL_dav | Liquid precipitation in David city | |
| W2M_dav | Wind Speed at 2 m in David city | m/s |
| Holiday_ID | Unique identification number | integer |
| Holiday | Holiday binary indicator | 1 = holiday, 0 = regular day |
| school | School period binary indicator | 1 = school, 0 = vacations |
| Parameter | Explanation |
|---|---|
| s | Scale parameter (s > 1: the function expands over time axis and the amplitude decreases) (s < 1: the function shrinks over time axis and the amplitude grows) (s < 0: the symmetry is defined in relation to the point t = 0) |
| Shift parameter (τ > 0: a shift to the right in the time axis) (τ < 0: a shift to the left in the time axis) | |
| Normalization factor with different scales | |
| Function to be transformed | |
| Complex conjugate of the wavelet function |
| Layer | Layer Name | Other Layer Parameters | Output Shape | Params | |
|---|---|---|---|---|---|
| 1 | Input Layer | - | (168, 5) | 0 | |
| 2 | LSTM | activation = tanh, return_sequences = True | (168, 64) | 17,920 | |
| 3 | Conv1D | activation = linear, padding = causal, strides = (1,) | (168, 64) | 704 | |
| 4 | Conv1D | activation = linear, padding = causal, strides = (1,) | (168, 64) | 704 | |
| 5 | Conv1D | activation = linear, padding = causal, strides = (1,) | (168, 64) | 704 | |
| 6 | Concatenate | - | (168, 256) | 0 | |
| 7 | GRU | activation = tanh, return_sequences = True | (168, 64) | 61,824 | |
| 8 | Flatten | - | (10,752, 1) | 0 | |
| 9 | Dense | activation = relu | (32, 1) | 344,096 | |
| 10 | Dense | activation = linear | (1, 1) | 33 | |
| Total params: 1,277,957 Trainable params: 425,985 Non-trainable params: 0 Optimizer params: 851,972 | Optimizer: Adam Loss function: MSE Learning rate: 0.001 Batch size: 32 Epoch: 50 | ||||
| Parameter | Explanation |
|---|---|
| Forget gate output, input gate output, output gate output | |
| Sigmoid activation function | |
| Forget gate weight matrix, input gate weight matrix, output gate weight matrix, cell weight matrix | |
| Previous hidden state | |
| Input at time t | |
| Bias vectors | |
| Candidate cell state | |
| Current cell state, previous cell state | |
| Current hidden state (Its output is transferred to the next time step and the model.) |
| Parameter | Explanation |
|---|---|
| Update gate vector, reset gate vector | |
| Sigmoid activation function | |
| Update gate weight matrix, reset gate weight matrix, weight matrix for input data | |
| Previous hidden state | |
| Input at time t | |
| Bias vectors | |
| Candidate hidden state | |
| Weight matrices for recurrent connections | |
| Current hidden state |
| Parameter | Explanation |
|---|---|
| - | |
| Number of samples in that leaf node | |
| The sum of the target values of all training samples in the corresponding leaf node | |
| Total number of decision trees in the forest |
| Method | MAE | RMSE | MAPE (%) | Peak Error (%) | Valley Error (%) | Energy Error (%) |
|---|---|---|---|---|---|---|
| LSTM | 0.017 | 0.022 | 2.549 | 1.069 | 0.314 | 0.0306 |
| GRU | 0.016 | 0.021 | 2.468 | 1.735 | 0.615 | 0.7425 |
| RNN | 0.014 | 0.019 | 2.152 | 2.509 | 2.493 | 0.4935 |
| FNN | 0.041 | 0.048 | 6.447 | 1.016 | 11.250 | 5.8283 |
| SVR | 0.035 | 0.044 | 5.156 | 9.097 | 10.108 | 0.7697 |
| KNN | 0.040 | 0.057 | 6.125 | 5.905 | 6.932 | 0.2542 |
| XGBoost | 0.013 | 0.018 | 1.985 | 5.523 | 5.401 | 0.0622 |
| Proposed Model | 0.007 | 0.009 | 1.051 | 0.846 | 1.233 | 0.0015 |
| Lag Values | MAE | RMSE | MAPE (%) | Peak Error (%) | Valley Error (%) | Energy Error (%) |
|---|---|---|---|---|---|---|
| 24, 84, 168, ma168 | 0.007 | 0.009 | 1.051 | 0.846 | 1.233 | 0.0015 |
| 24, 48, ma168 | 0.015 | 0.020 | 2.281 | 0.904 | 2.939 | 0.0098 |
| 24, 72, ma168 | 0.008 | 0.010 | 1.075 | 0.436 | 1.457 | 0.0005 |
| 24, 96, ma168 | 0.028 | 0.038 | 4.287 | 4.563 | 7.160 | 0.0173 |
| 24, 168, ma168 | 0.007 | 0.009 | 1.120 | 0.563 | 1.547 | 0.0033 |
| 24, 48, 72, ma168 | 0.027 | 0.036 | 4.111 | 3.239 | 7.974 | 0.0024 |
| 24, 48, 96, ma168 | 0.007 | 0.010 | 1.176 | 0.417 | 1.795 | 0.0004 |
| 24, 48, 168, ma168 | 0.022 | 0.029 | 3.401 | 2.841 | 3.263 | 0.0017 |
| 24, 72, 168, ma168 | 0.007 | 0.010 | 1.129 | 0.556 | 1.202 | 0.0038 |
| 24, 96, 168, ma168 | 0.015 | 0.020 | 2.265 | 1.598 | 1.880 | 0.0067 |
| 24, 48, 72, 96, ma168 | 0.011 | 0.014 | 1.631 | 0.748 | 2.325 | 0.0011 |
| 24, 48, 72, 168, ma168 | 0.008 | 0.010 | 1.188 | 0.689 | 1.323 | 0.0001 |
| Condition | MAE | RMSE | MAPE (%) | Peak Error (%) | Valley Error (%) | Energy Error (%) |
|---|---|---|---|---|---|---|
| -Random Forest | 0.010 | 0.013 | 1.478 | 1.422 | 3.937 | 0.2169 |
| -LSTM | 0.025 | 0.033 | 3.670 | 3.172 | 2.737 | 0.0133 |
| -GRU | 0.014 | 0.018 | 2.108 | 1.021 | 1.605 | 0.0060 |
| -CNN | 0.008 | 0.010 | 1.130 | 0.869 | 1.487 | 0.0017 |
| FULL Model | 0.007 | 0.009 | 1.051 | 0.846 | 1.233 | 0.0015 |
| Method | MAE | RMSE | MAPE (%) | Peak Error (%) | Valley Error (%) | Energy Error (%) |
|---|---|---|---|---|---|---|
| LSTM | 0.044 | 0.053 | 8.445 | 0.018 | 26.326 | 6.3093 |
| GRU | 0.026 | 0.036 | 4.405 | 0.809 | 24.422 | 2.1734 |
| RNN | 0.038 | 0.049 | 7.005 | 2.418 | 1.658 | 2.7249 |
| FNN | 0.045 | 0.051 | 7.566 | 6.959 | 15.771 | 6.9249 |
| SVR | 0.092 | 0.124 | 14.537 | 21.071 | 26.379 | 6.6130 |
| KNN | 0.053 | 0.069 | 9.061 | 11.818 | 35.266 | 1.1835 |
| XGBoost | 0.027 | 0.036 | 4.404 | 14.222 | 5.519 | 0.7836 |
| Proposed Model | 0.005 | 0.006 | 0.925 | 0.399 | 8.227 | 0.0032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sezer, E.; Yıldırım, G.; Özdemir, M.T. Multiscale Time Series Modeling in Energy Demand Prediction: A CWT-Aided Hybrid Model. Appl. Sci. 2025, 15, 10801. https://doi.org/10.3390/app151910801
Sezer E, Yıldırım G, Özdemir MT. Multiscale Time Series Modeling in Energy Demand Prediction: A CWT-Aided Hybrid Model. Applied Sciences. 2025; 15(19):10801. https://doi.org/10.3390/app151910801
Chicago/Turabian StyleSezer, Elif, Güngör Yıldırım, and Mahmut Temel Özdemir. 2025. "Multiscale Time Series Modeling in Energy Demand Prediction: A CWT-Aided Hybrid Model" Applied Sciences 15, no. 19: 10801. https://doi.org/10.3390/app151910801
APA StyleSezer, E., Yıldırım, G., & Özdemir, M. T. (2025). Multiscale Time Series Modeling in Energy Demand Prediction: A CWT-Aided Hybrid Model. Applied Sciences, 15(19), 10801. https://doi.org/10.3390/app151910801







