Seismic Performance Assessment of 170 kV Line Trap Systems Through Shake Table Testing and Finite Element Analysis
Abstract
1. Introduction
- It presents, to the authors’ knowledge, the first full-scale shake table tests performed on a line trap,
- It provides a comparative evaluation of near-fault and far-fault ground motion effects on such equipment.
2. Description of 170 kV Line Trap
3. Experimental Studies
3.1. Test Instrumentation
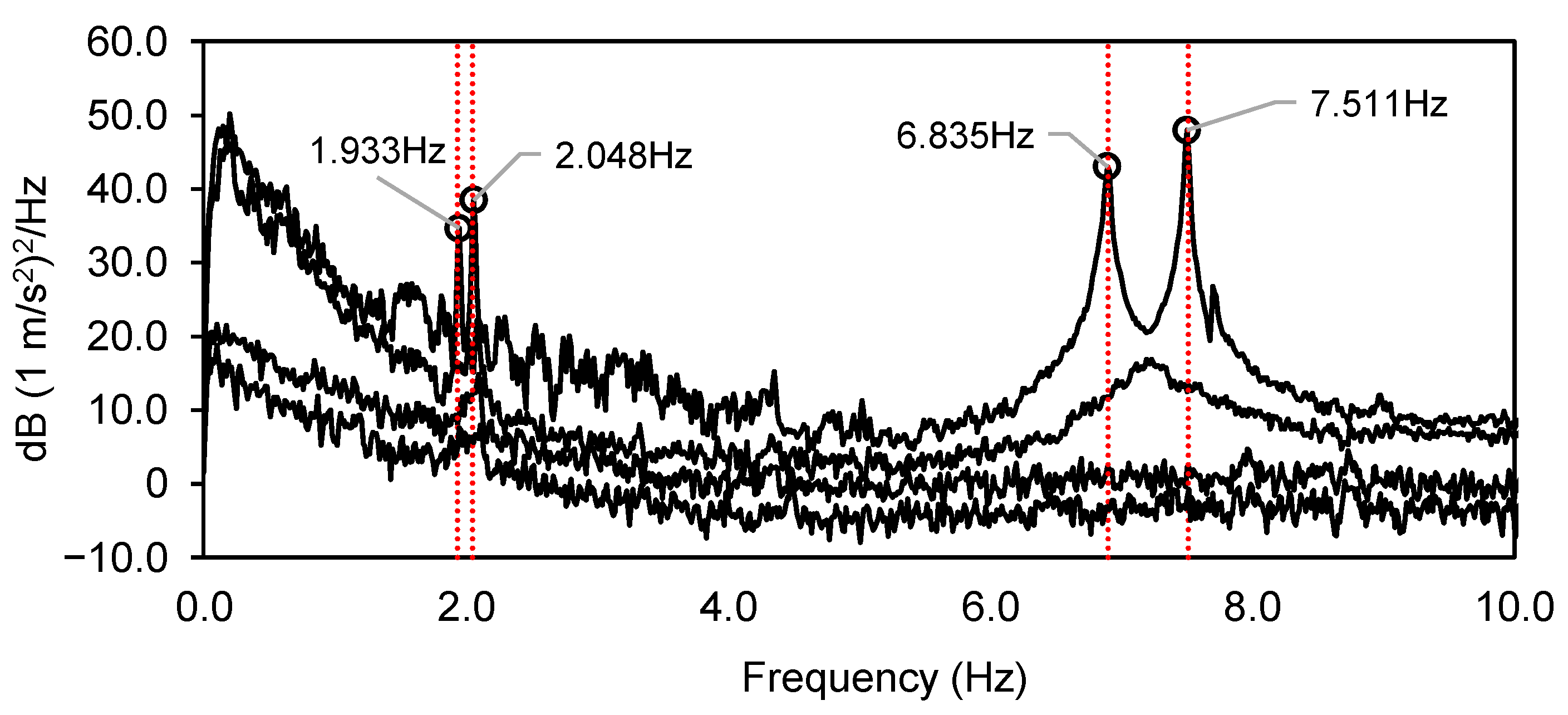
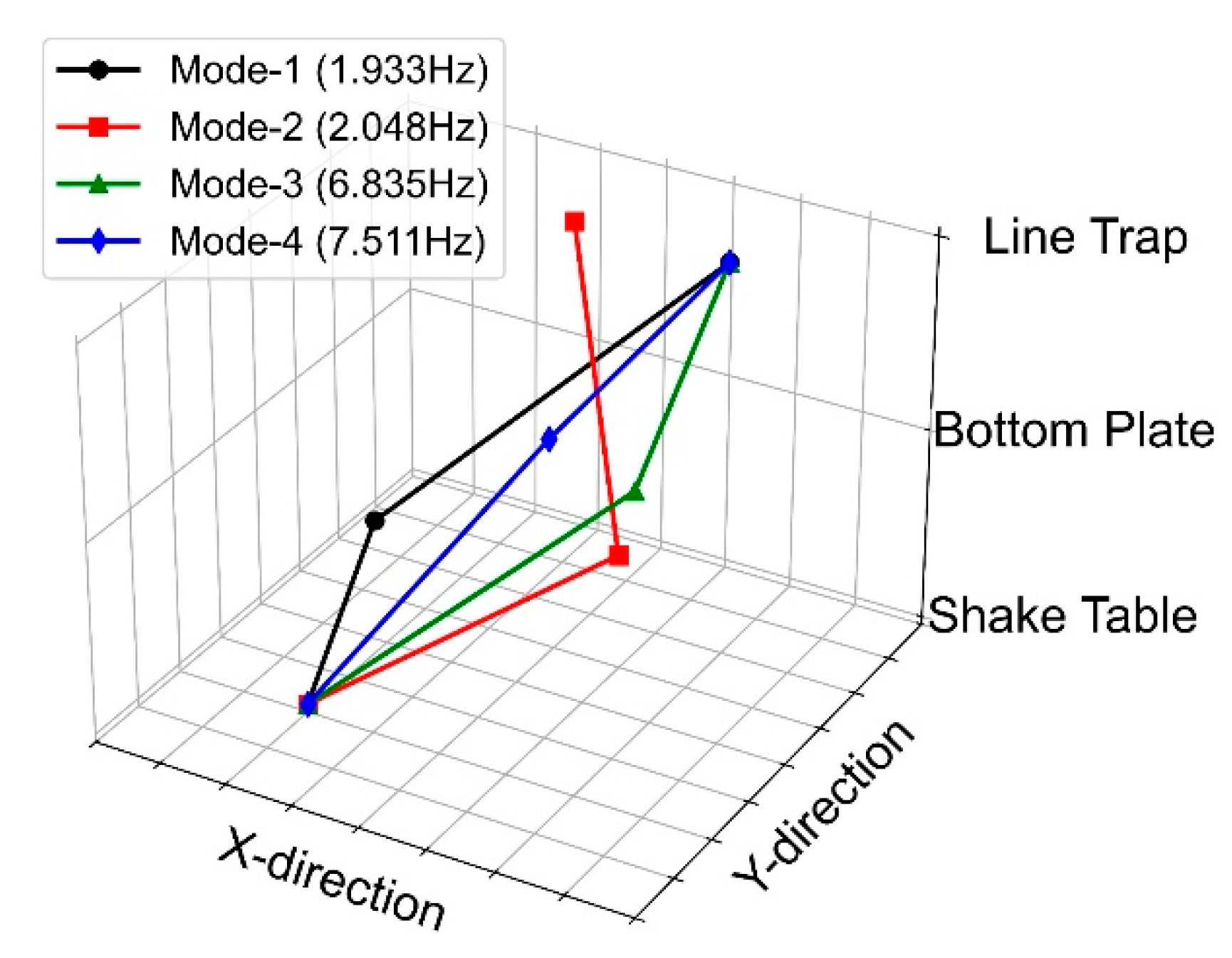
3.2. Ambient Vibration Tests
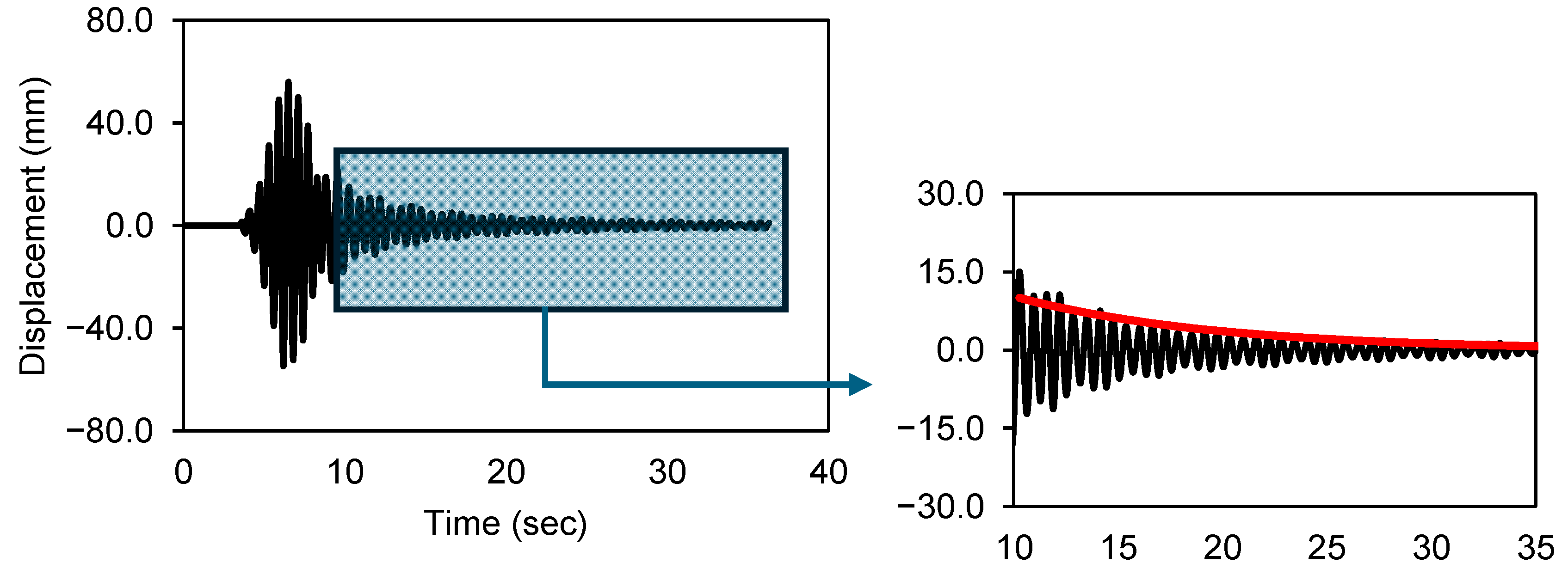
3.3. Shake Table Tests
4. Numerical Studies
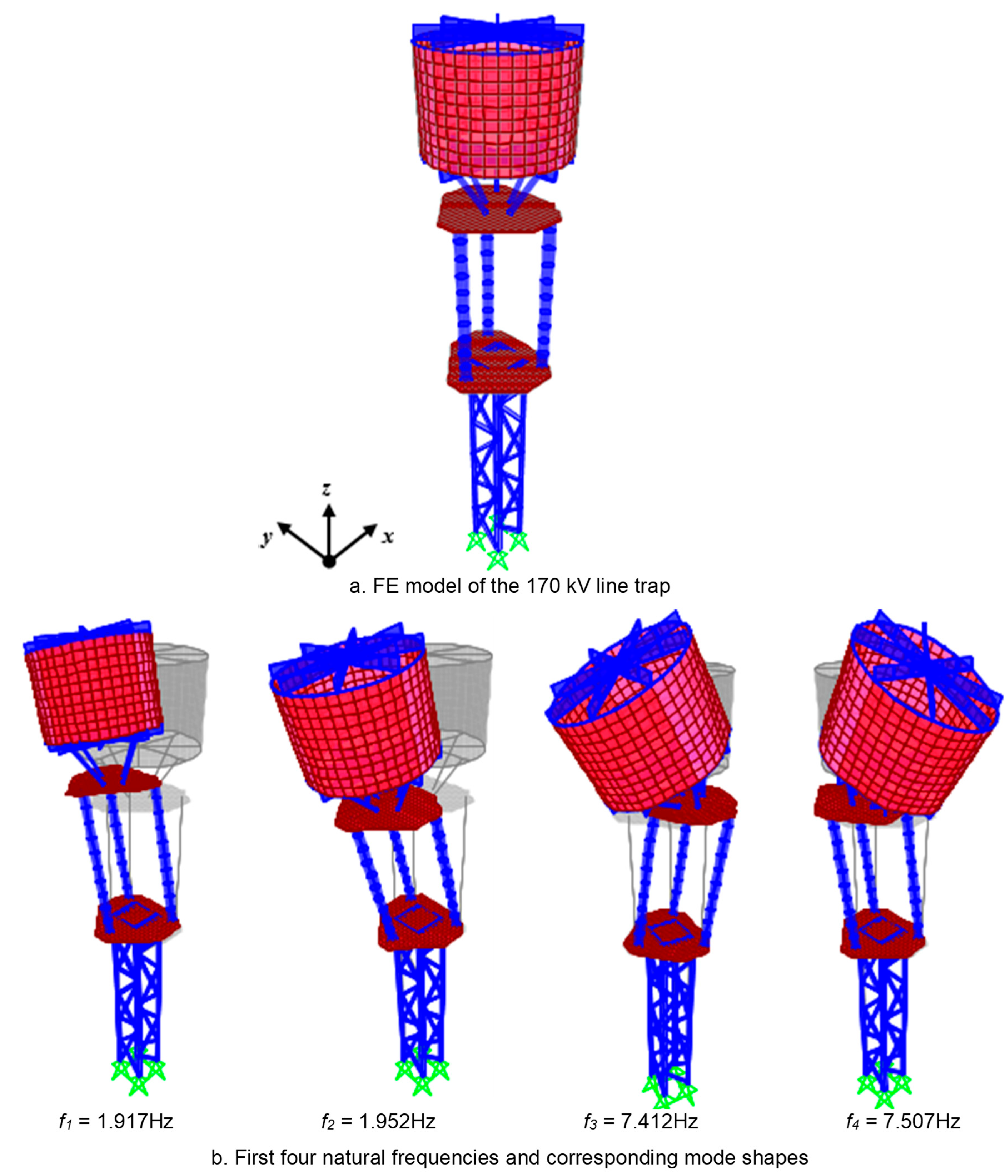
4.1. FE Model of the 170 kV Line Trap
4.2. Selection of Ground Motions
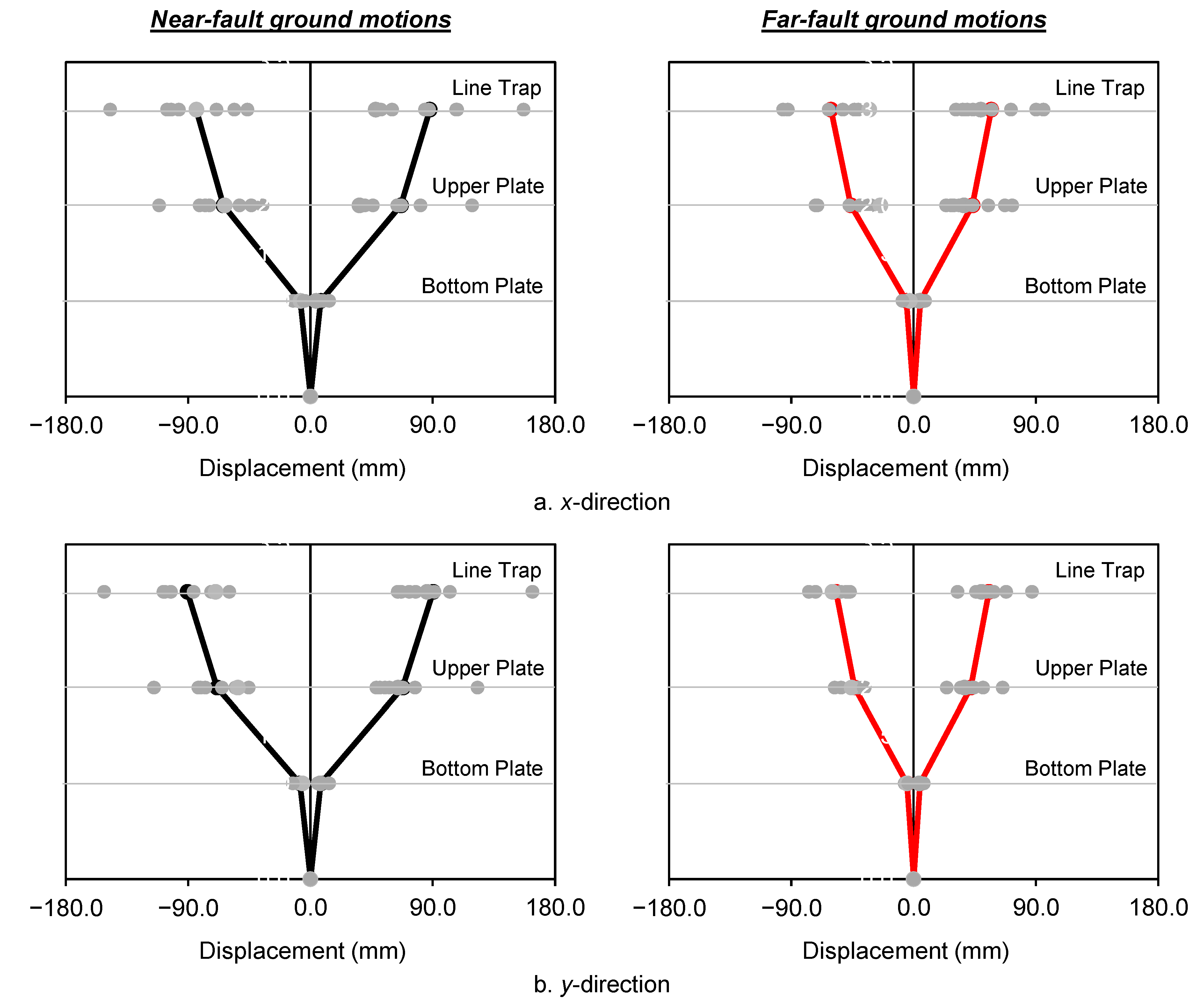
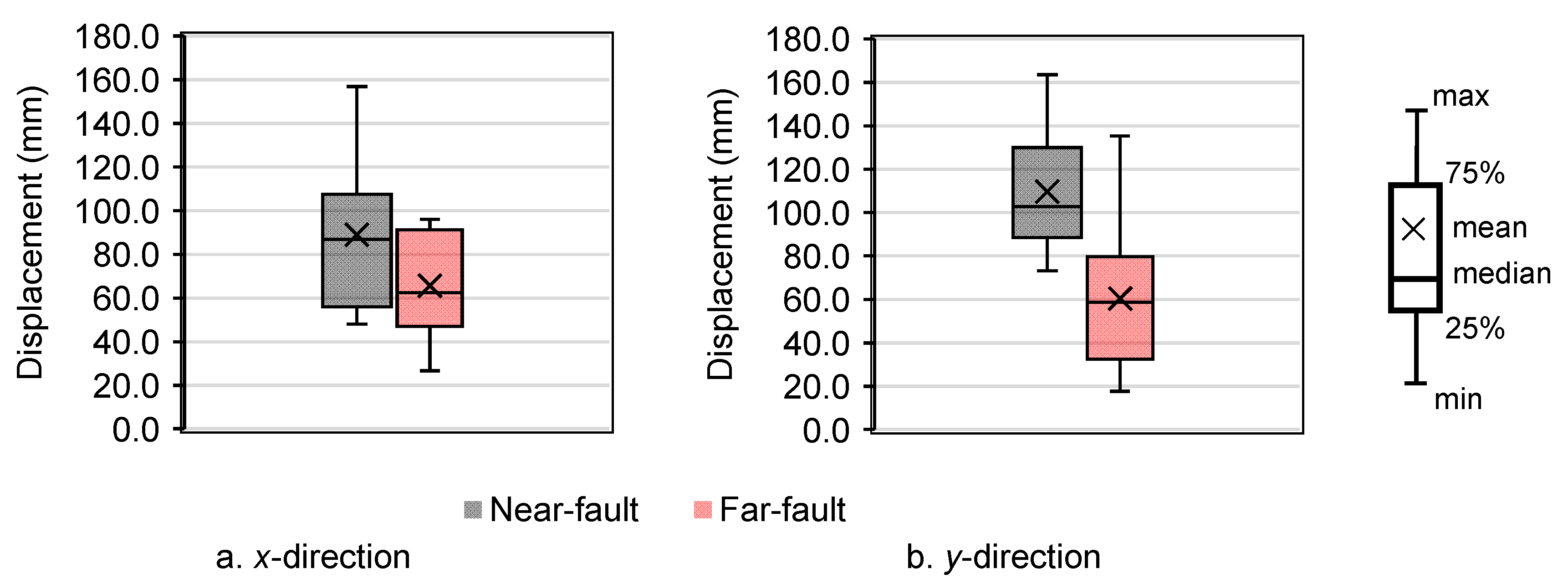
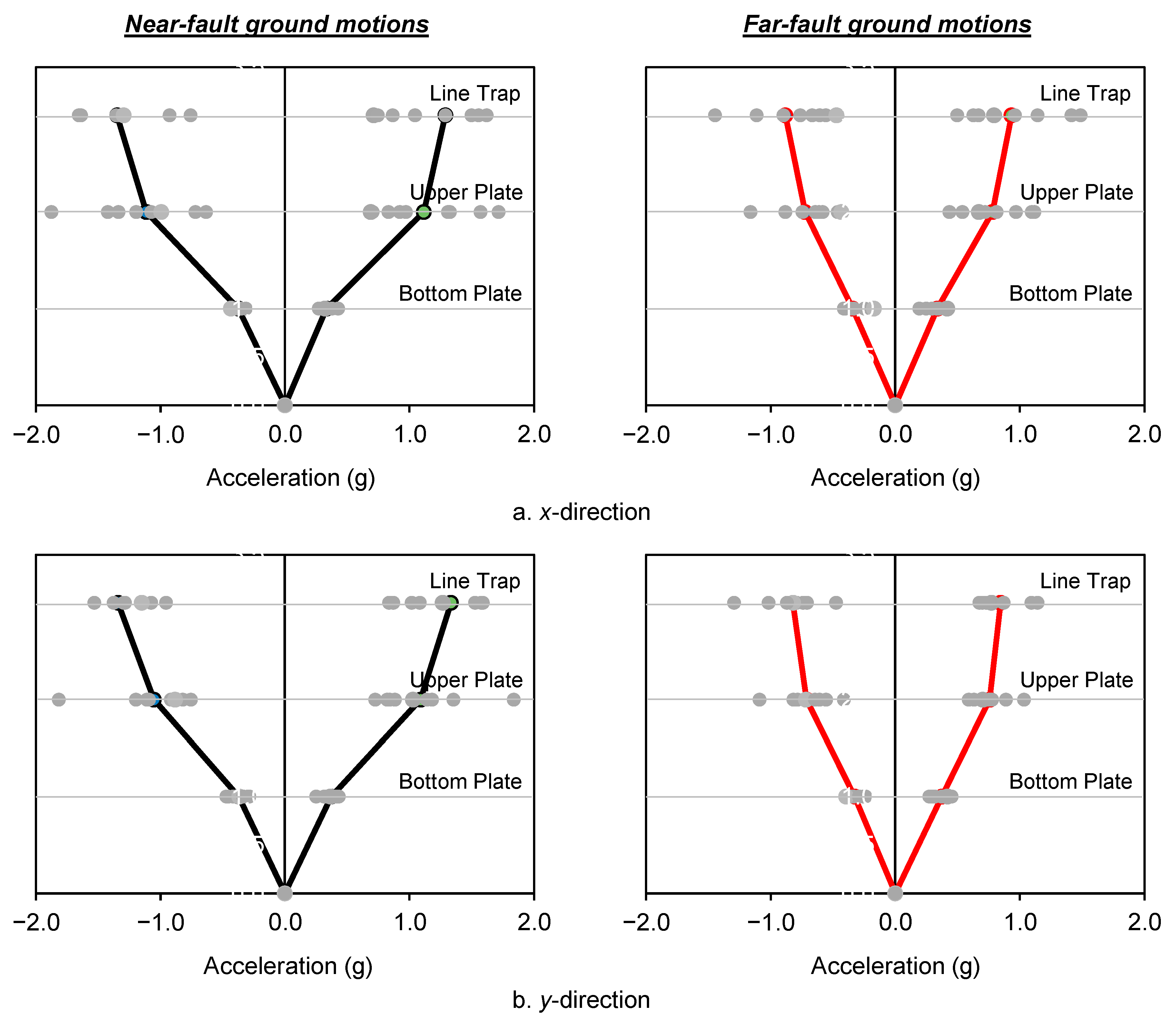
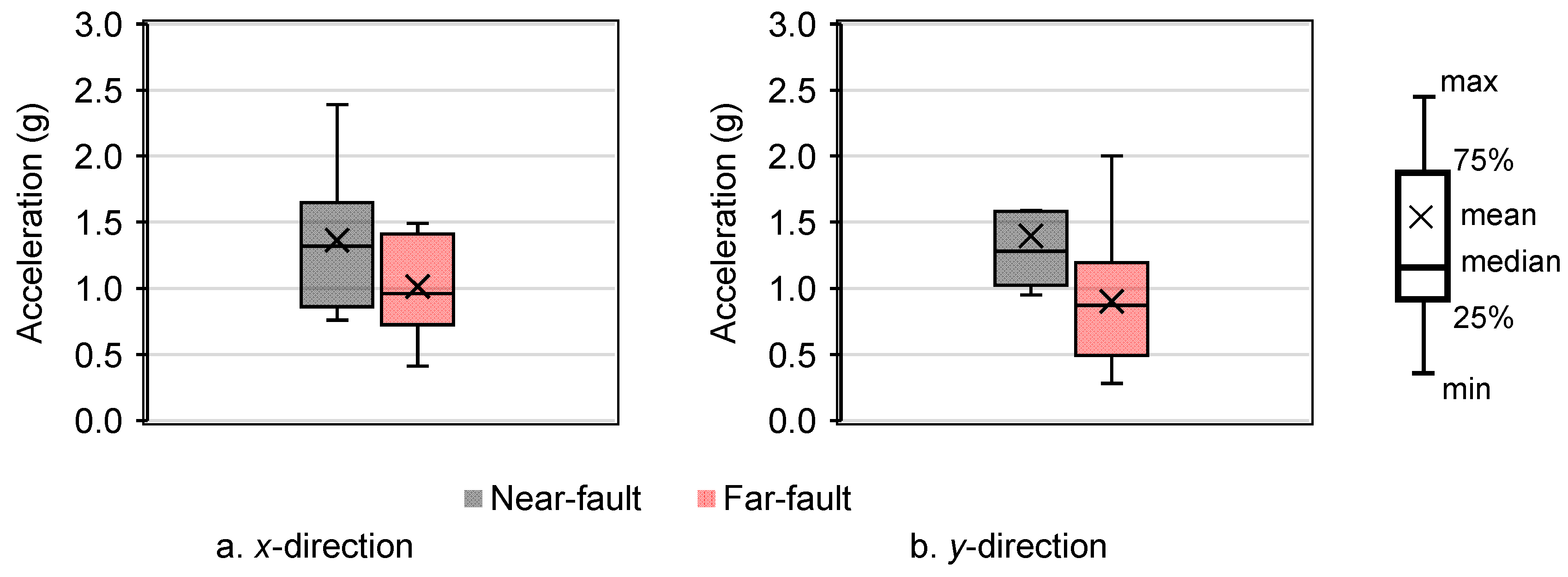
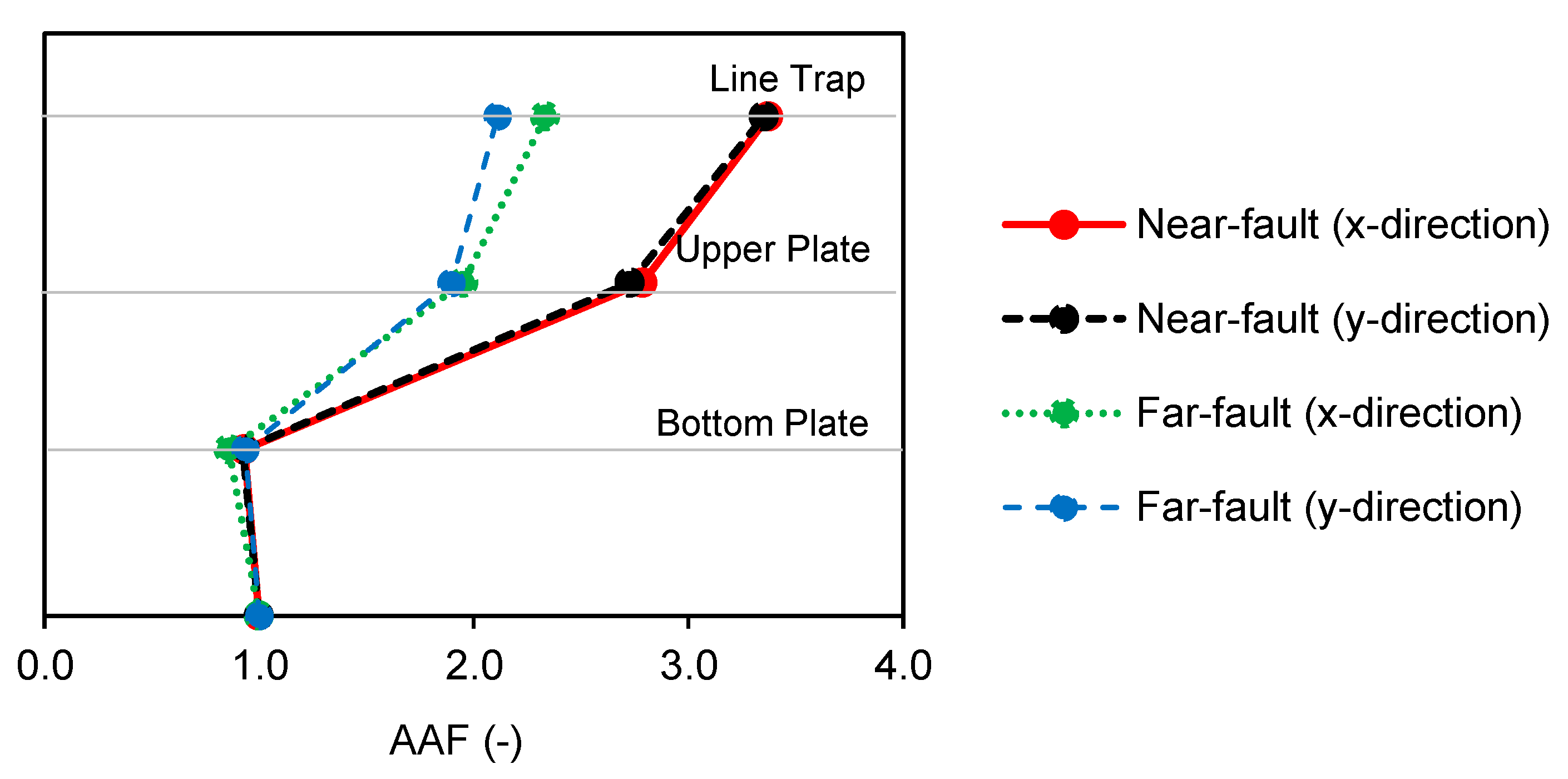
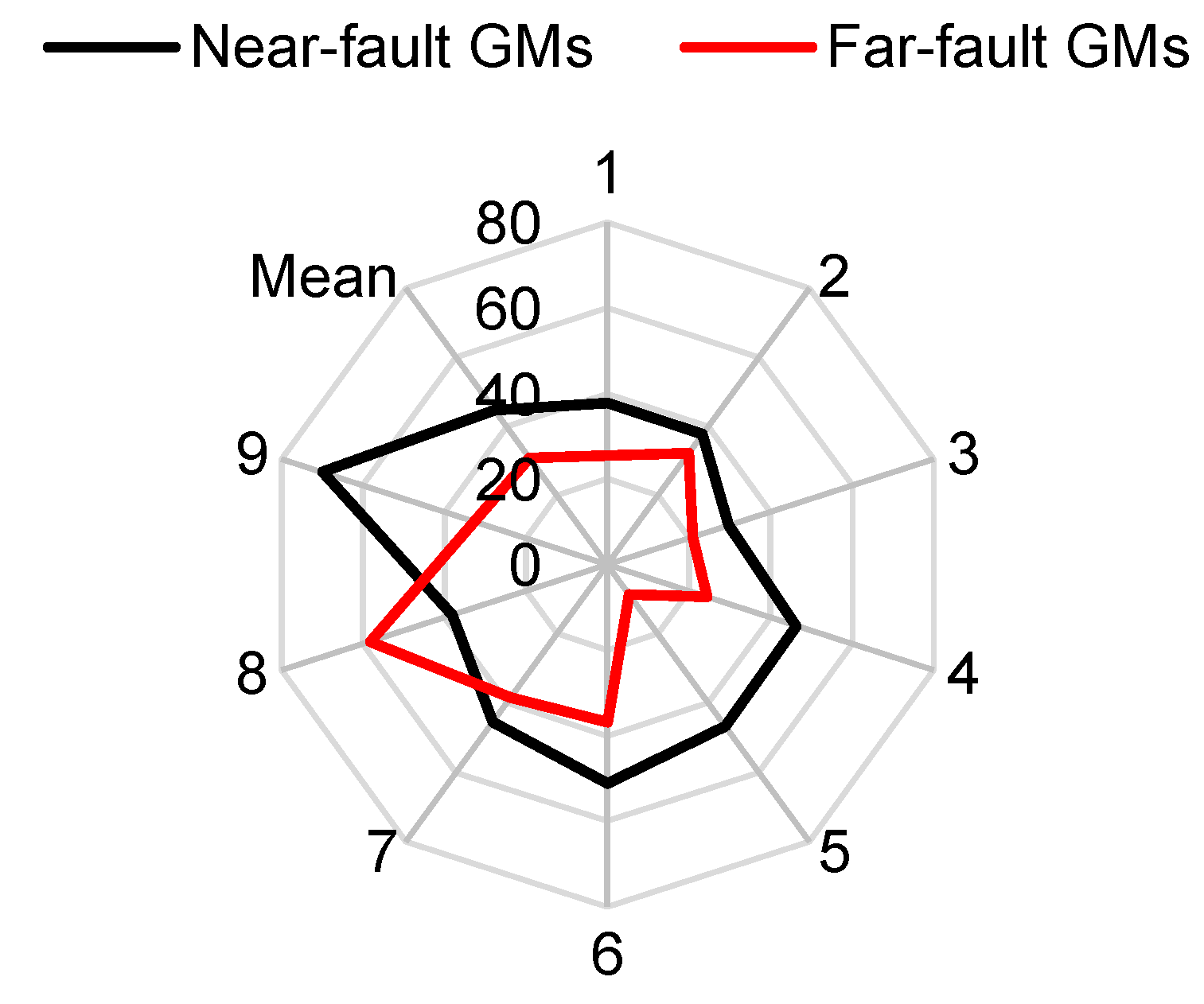
4.3. Dynamic Responses Under to Near-Fault and Far-Fault Ground Motions
5. Limitations and Sources of Uncertainty
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stearns, C.C.; Filiatrault, A. Electrical Substation Equipment Interaction: Experimental Rigid Conductor Studies; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2005. [Google Scholar]
- Sezen, H.; Whittaker, A.S. Seismic performance of industrial facilities affected by the 1999 Turkey earthquake. J. Perform. Constr. Facil. 2006, 20, 28–36. [Google Scholar] [CrossRef]
- Ma, G.L.; Xie, Q. Seismic analysis of a 500-kV power transformer of the type damaged in the 2008 Wenchuan earthquake. J. Perform. Constr. Facil. 2018, 32, 04018007. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, M.; Wu, Y. Vulnerability study of electric power grid in different intensity area in Wenchuan earthquake. In Proceedings of the 15th World Conference of Earthquake Engineering (WCEE), Lisboa, Portugal, 24–28 September 2012. [Google Scholar]
- Schiff, A.J. Guide to Improved Earthquake Performance of Electric Power Systems; National Institute of Standards and Technology, Building and Fire Research Laboratory: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Ashrafi, S.A.H.N. Issues of Seismic Response and Retrofit for Critical Substation Equipment. Doctoral Dissertation, New Jersey Institute of Technology, Newark, NJ, USA, 2003. [Google Scholar]
- Wang, M.; He, J. Shake table test and finite element model for evaluating seismic performance of 220 kV transformer-bushing systems. Earthq. Spectra 2023, 39, 1755–1778. [Google Scholar] [CrossRef]
- Wilcoski, J.; Smith, S.J. Fragility Testing of a Power Transformer Bushing; USA-CERL Technical Report 97/57; US Army Corps of Engineers, Construction Engineering Research Laboratories: Champaign, IL, USA, 1997. [Google Scholar]
- Ersoy, S.; Saadeghvaziri, M.A. Seismic response of transformer-bushing systems. IEEE Trans. Power Deliv. 2004, 19, 131–137. [Google Scholar] [CrossRef]
- Whittaker, A.S.; Fenves, G.L.; Gilani, A.S. Earthquake performance of porcelain transformer bushings. Earthq. Spectra 2004, 20, 205–223. [Google Scholar] [CrossRef]
- Filiatrault, A.; Matt, H. Experimental seismic response of high-voltage transformer-bushing systems. Earthq. Spectra 2005, 21, 1009–1025. [Google Scholar] [CrossRef]
- Filiatrault, A.; Matt, H. Seismic response of high voltage electrical transformer–bushing systems. J. Struct. Eng. 2006, 132, 287–295. [Google Scholar] [CrossRef]
- Koliou, M.; Filiatrault, A.; Reinhorn, A.M. Seismic response of high-voltage transformer-bushing systems incorporating flexural stiffeners II: Experimental study. Earthq. Spectra 2013, 29, 1353–1367. [Google Scholar] [CrossRef]
- Mosalam, K.M.; Günay, S.; Takhirov, S. Response evaluation of interconnected electrical substation equipment using real-time hybrid simulation on multiple shaking tables. Earthq. Eng. Struct. Dyn. 2016, 45, 2389–2404. [Google Scholar] [CrossRef]
- Zareei, S.A.; Hosseini, M.; Ghafory-Ashtiany, M. Evaluation of power substation equipment seismic vulnerability by multivariate fragility analysis: A case study on a 420 kV circuit breaker. Soil Dyn. Earthq. Eng. 2017, 92, 79–94. [Google Scholar] [CrossRef]
- Wen, J.; Xie, Q. Seismic evaluation of ±800 kV UHVDC disconnect switch by shake table test. J. Eng. 2019, 2019, 2772–2776. [Google Scholar] [CrossRef]
- Cavalieri, F.; Donelli, G.; Pinho, R.; Dacarro, F.; Bernardo, N.; de Nigris, M. Shake table testing of voltage and current transformers and numerical derivation of corresponding fragility curves. Infrastructures 2022, 7, 171. [Google Scholar] [CrossRef]
- Tian, L.; Gai, X.; Qu, B. Shake table tests of steel towers supporting extremely long-span electricity transmission lines under spatially correlated ground motions. Eng. Struct. 2017, 132, 791–807. [Google Scholar] [CrossRef]
- Tian, L.; Yang, M.; Liu, J.; Ma, Z.; Gong, J.; Chen, H.; Luo, X. Shake table test and seismic fragility analysis of transmission tower-line system considering duration effect. Thin-Walled Struct. 2024, 197, 111584. [Google Scholar] [CrossRef]
- Günay, S.; Mosalam, K.; Takhirov, S. Real-time hybrid simulation in a shaking table configuration for parametric studies of high-voltage equipment and IEEE693 development. Nucl. Eng. Des. 2015, 295, 901–909. [Google Scholar] [CrossRef]
- Moustafa, M.A.; Mosalam, K.M. Structural performance of porcelain and polymer post insulators in high voltage electrical switches. J. Perform. Constr. Facil. 2016, 30, 04016002. [Google Scholar] [CrossRef]
- Ullah, N.; Ali, S.M.; Shahzad, R.; Khan, F. Seismic qualification and time history shake-table testing of high voltage surge arrester under seismic qualification level moderate. Cogent Eng. 2018, 5, 1431375. [Google Scholar] [CrossRef]
- Li, S.; Tsang, H.H.; Cheng, Y.; Lu, Z. Seismic testing and modeling of cylindrical electrical equipment with GFRP composite insulators. Compos. Struct. 2018, 194, 454–467. [Google Scholar] [CrossRef]
- Dinh, N.H.; Lee, S.J.; Kim, J.Y.; Choi, K.K. Study on seismic performance of a mold transformer through shaking table tests. Appl. Sci. 2020, 10, 361. [Google Scholar] [CrossRef]
- Li, H. Shaking Table Test on Seismic Performance of Combined High Voltage Circuit Breaker. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 446, p. 042027. [Google Scholar]
- Wen, B.; Moustafa, M.A.; Junwu, D. Seismic fragilities of high-voltage substation disconnect switches. Earthq. Spectra 2019, 35, 1559–1582. [Google Scholar] [CrossRef]
- Cui, J.; Che, A.; Li, S.; Cheng, Y. A maximum-entropy-based multivariate seismic vulnerability analysis method for power facilities: A case study on a ±1100-kV dry type smoothing reactor. Eng. Fail. Anal. 2022, 142, 106740. [Google Scholar] [CrossRef]
- Cheng, Y.; Xue, Y.; Du, W.; Lu, Z. Experimental study on influence of soil–structure interaction on seismic performance of UHV transformer. J. Earthq. Eng. 2023, 27, 3024–3059. [Google Scholar] [CrossRef]
- Zhu, W.; Xie, Q.; Liu, X. Seismic failure risk analysis of ±800 kV coupling filter circuit considering material strength deviation. Structures 2023, 47, 1566–1578. [Google Scholar] [CrossRef]
- Alessandri, S.; Giannini, R.; Paolacci, F.; Malena, M. Seismic retrofitting of an HV circuit breaker using base isolation with wire ropes. Part 1: Preliminary tests and analyses. Eng. Struct. 2015, 98, 251–262. [Google Scholar] [CrossRef]
- Alessandri, S.; Giannini, R.; Paolacci, F.; Amoretti, M.; Freddo, A. Seismic retrofitting of an HV circuit breaker using base isolation with wire ropes. Part 2: Shaking-table test validation. Eng. Struct. 2015, 98, 263–274. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, S.; Lu, Z.; Liu, Z.; Zhu, Z. Seismic risk mitigation of cylindrical electrical equipment with a novel isolation device. Soil Dyn. Earthq. Eng. 2018, 111, 41–52. [Google Scholar] [CrossRef]
- Lee, D.; Constantinou, M.C. Combined horizontal–vertical seismic isolation system for high-voltage–power transformers: Development, testing and validation. Bull. Earthq. Eng. 2018, 16, 4273–4296. [Google Scholar] [CrossRef]
- Karami-Mohammadi, R.; Mirtaheri, M.; Salkhordeh, M.; Mosaffa, E.; Mahdavi, G.; Hariri-Ardebili, M.A. Seismic mitigation of substation cable connected equipment using friction pendulum systems. Struct. Eng. Mech. 2019, 72, 785–796. [Google Scholar]
- Takhirov, S.; Kempner, L.; Riley, M.; Fujisaki, E.; Low, B. Seismic protection of high-voltage equipment by friction dampers: Numerical modelling correlated with full-scale component tests. In Proceedings of the COMPDYN-2019, 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019; pp. 24–26. [Google Scholar]
- Yang, Z.; Xie, Q.; He, C.; Xue, S. Numerical investigation of the seismic response of a UHV composite bypass switch retrofitted with wire rope isolators. Earthq. Eng. Eng. Vib. 2021, 20, 275–290. [Google Scholar] [CrossRef]
- Naeem, A.; Kim, J. Seismic retrofit of 3000 kVA power transformer using friction dampers and prestressed tendons. Structures 2021, 32, 641–650. [Google Scholar] [CrossRef]
- Zhang, R.; Cao, M.; Huang, J. Study on seismic response and parameter influence in a transformer–bushing with inerter isolation system. Buildings 2022, 12, 530. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L.; Cheng, Y.; Lu, Z.; Zhu, Z. Seismic performance improvement using bolt-on isolators on interconnected slender electrical equipment. Eng. Struct. 2023, 289, 116238. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Hu, Y.; Chen, Q.; Peng, J.; Xie, Y.; Wang, J. Study on three-dimensional dynamic stability of open-pit high slope under blasting vibration. Lithosphere 2022, 2021, 6426550. [Google Scholar] [CrossRef]
- Kaya, A.; Adanur, S.; Bello, R.A.; Genç, A.F.; Okur, F.Y.; Sunca, F.; Günaydın, M.; Altunışık, A.C.; Sevim, B. Post-earthquake damage assessments of unreinforced masonry (URM) buildings by shake table test and numerical visualization. Eng. Fail. Anal. 2023, 143, 106858. [Google Scholar] [CrossRef]
- Türkay, A. Determination of Dynamic Characteristics of Composite Cantilever Beams Using Experimental and Analytical Methods. Buildings 2025, 15, 1608. [Google Scholar] [CrossRef]
- Hüsem, M.; Nasery, M.M.; Okur, F.Y.; Altunişik, A.C. Experimental evaluation of damage effect on dynamic characteristics of concrete encased composite column-beam connections. Eng. Fail. Anal. 2018, 91, 129–150. [Google Scholar] [CrossRef]
- Jacobsen, N.J.; Andersen, P.; Brincker, R. Using enhanced frequency domain decomposition as a robust technique to harmonic excitation in operational modal analysis. In Proceedings of the ISMA2006: International Conference on Noise & Vibration Engineering, Leuven, Belgium, 18–20 September 2006. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification from ambient responses using frequency domain decomposition. In Proceedings of the 18th International Modal Analysis Conference (IMAC), San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- PULSE, version 7.1; PULSE Operational Modal Analysis Software; Structural Vibration Solution: Aalborg, Denmark, 2021.
- Wang, M.; Liu, K.; Guragain, R.; Shrestha, H.; Ma, X. Shake table tests on the two-storey dry-joint stone masonry structures reinforced with timber laces and steel wires. Bull. Earthq. Eng. 2019, 17, 2199–2218. [Google Scholar] [CrossRef]
- Tomassetti, U.; Correia, A.A.; Candeias, P.X.; Graziotti, F.; Campos Costa, A. Two-way bending out-of-plane collapse of a full-scale URM building tested on a shake table. Bull. Earthq. Eng. 2019, 17, 2165–2198. [Google Scholar] [CrossRef]
- Sunca, F.; Altunişik, A.C.; Kaya, A.; Genç, A.F.; Şahin, M.C.; Karahasan, A.K. Shake table tests on story-to-story pounding between adjacent RC buildings. Structures 2024, 69, 107544. [Google Scholar] [CrossRef]
- Mayorca, P.; Sathiparan, N.; Guragain, R.; Meguro, K. Comparison of the seismic performance of different strength masonry structures retrofitted with PP-band meshes. In Proceeding of the 5th International Symposium on New Technologies for Urban Safety of Mega Cities in Asia, Phuket, Thailand, 16–17 November 2006. [Google Scholar]
- Jeon, B.G.; Chang, S.J.; Kim, S.W.; Park, D.U.; Chun, N. Experimental study on the acceleration amplification ratio of cable terminations for electric power facilities. Energies 2024, 17, 5641. [Google Scholar] [CrossRef]
- Adanur, S.; Altunişik, A.C.; Bayraktar, A.; Akköse, M. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges. Nat. Hazards 2012, 64, 593–614. [Google Scholar] [CrossRef]
- Akköse, M.; Şimşek, E. Non-linear seismic response of concrete gravity dams to near-fault ground motions including dam-water-sediment-foundation interaction. Appl. Math. Model. 2010, 34, 3685–3700. [Google Scholar] [CrossRef]
- Davoodi, M.; Jafari, M.K.; Hadiani, N. Seismic response of embankment dams under near-fault and far-field ground motion excitation. Eng. Geol. 2013, 158, 66–76. [Google Scholar] [CrossRef]
- Güllü, H.; Karabekmez, M. Effect of near-fault and far-fault earthquakes on a historical masonry mosque through 3D dynamic soil-structure interaction. Eng. Struct. 2017, 152, 465–492. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G. Effects of near-fault and far-fault ground motions on nonlinear dynamic response and seismic damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 2013, 53, 217–229. [Google Scholar] [CrossRef]
- Gong, J.; Yang, T.; Shao, Y.; Du, Y.; Chen, C.; Deng, L. Response and fragility of long-span truss structures in ultra-high voltage substation subjected to near-fault pulse-like and far-field ground motions. Structures 2024, 63, 106363. [Google Scholar] [CrossRef]
- FEMA P695. Quantification of Building Seismic Performance Factors; Federal Emergency Management Agency: Washington, DC, USA, 2009. [Google Scholar]
- PEER. Peer Strong Ground Motion Database. Available online: https://ngawest2.berkeley.edu/ (accessed on 4 June 2025).
- Bayraktar, A.; Altunişik, A.C.; Sevim, B.; Kartal, M.E.; Türker, T.; Bilici, Y. Comparison of near-and far-fault ground motion effect on the nonlinear response of dam–reservoir–foundation systems. Nonlinear Dyn. 2009, 58, 655–673. [Google Scholar] [CrossRef]
- Güllü, H.; Özel, F. Microtremor measurements and 3D dynamic soil–structure interaction analysis for a historical masonry arch bridge under the effects of near-and far-fault earthquakes. Environ. Earth Sci. 2020, 79, 338. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Sunca, F.; Genç, A.F.; Tavşan, C. Post-earthquake damage assessments of historic mosques and effects of near-fault and far-fault ground motions on seismic responses. Int. J. Archit. Herit. 2023, 17, 1043–1078. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Sunca, F.; Sevim, B. Modal parameter identification and seismic assessment of historical timber structures under near-fault and far-fault ground motions. Structures 2023, 47, 1624–1651. [Google Scholar] [CrossRef]
- Li, X.; Peng, J.; Xie, Y.; Li, Q.; Zhou, T.; Wang, J.; Zheng, W. Influence of high-temperature treatment on strength and failure behaviors of a quartz-rich sandstone under true triaxial condition. Lithosphere 2022, 2022, 3086647. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Öztürk, M.M.; Genç, A.F.; Günaydin, M.; Kaya, A.; Akbulut, Y.E.; Sunca, F. Dynamic characteristics changes of masonry arches exposed to elevated temperature. Constr. Build. Mater. 2024, 418, 135423. [Google Scholar] [CrossRef]
- Gong, J.; Zhi, X.; Shang, W.; Fan, F. Shaking table test and numerical analysis of dynamic coupling effect between suspended system and OLF1000. Eng. Struct. 2020, 207, 110224. [Google Scholar] [CrossRef]
- Moustafa, M.A.; Mosalam, K.M. Finite element modeling and assessment of seismic response of electrical substations porcelain post insulators. Soil Dyn. Earthq. Eng. 2021, 150, 106895. [Google Scholar] [CrossRef]
- Li, Z.J.; Gong, J.; Shao, Y.B.; Huang, W.F.; Zhang, X. Axial compressive behaviors of multi-cavity concrete-filled double-skin tubular stub columns. J. Constr. Steel Res. 2024, 216, 108619. [Google Scholar] [CrossRef]

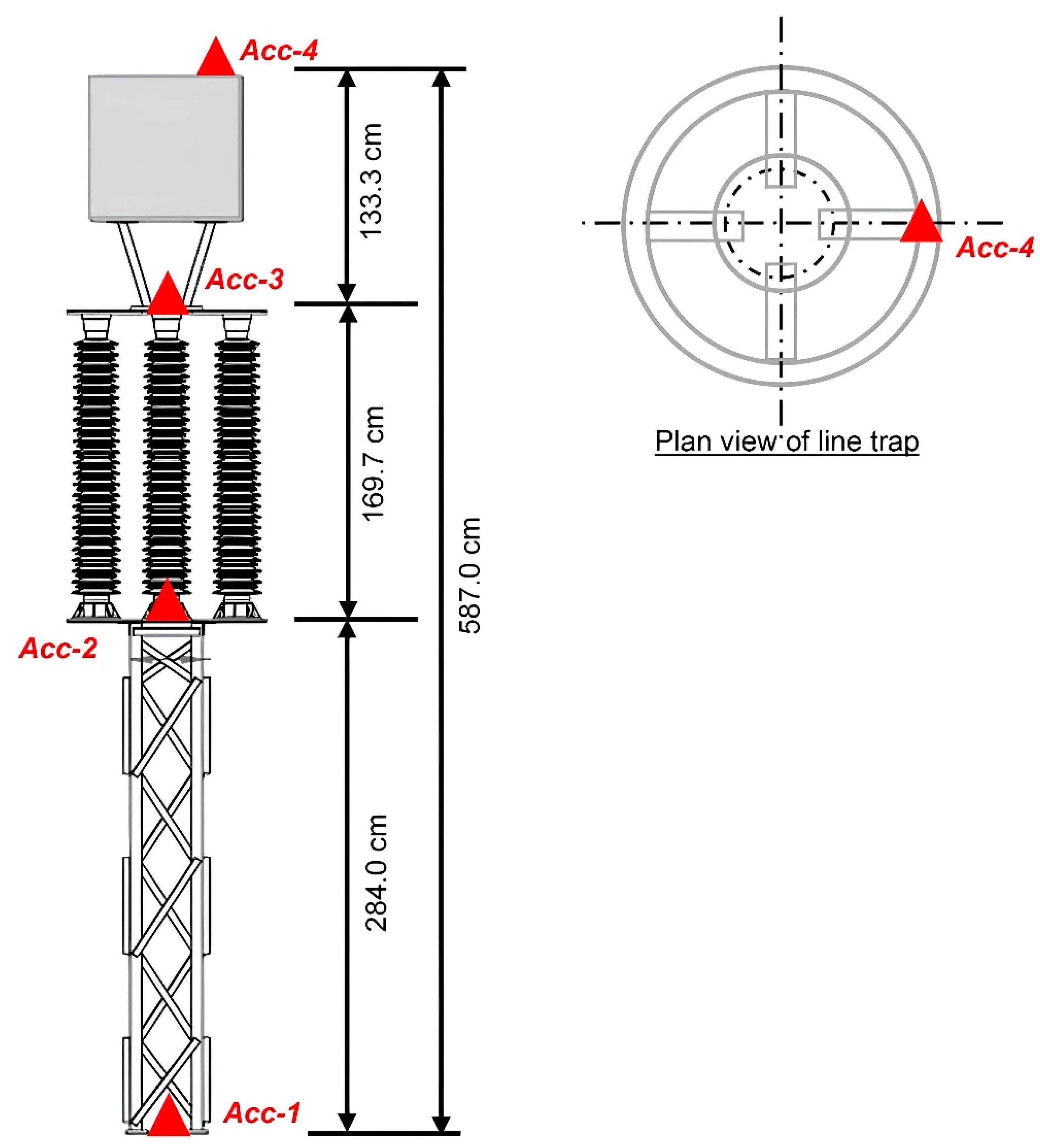



| Accelerometer | Acceleration (g) | Relative Displacement (mm) |
| Acc-1 | 0.236 | -- |
| Acc-2 | 0.195 | 24.093 |
| Acc-3 | 0.861 | 68.570 |
| Acc-4 | 0.956 | 77.745 |
| Mode | Numerical Frequencies (Hz) | Experimental Frequencies (Hz) | Differences (%) |
|---|---|---|---|
| 1 | 1.917 | 1.933 | 0.83 |
| 2 | 1.952 | 2.048 | 4.69 |
| 3 | 7.412 | 6.835 | 8.44 |
| 4 | 7.507 | 7.511 | 0.05 |
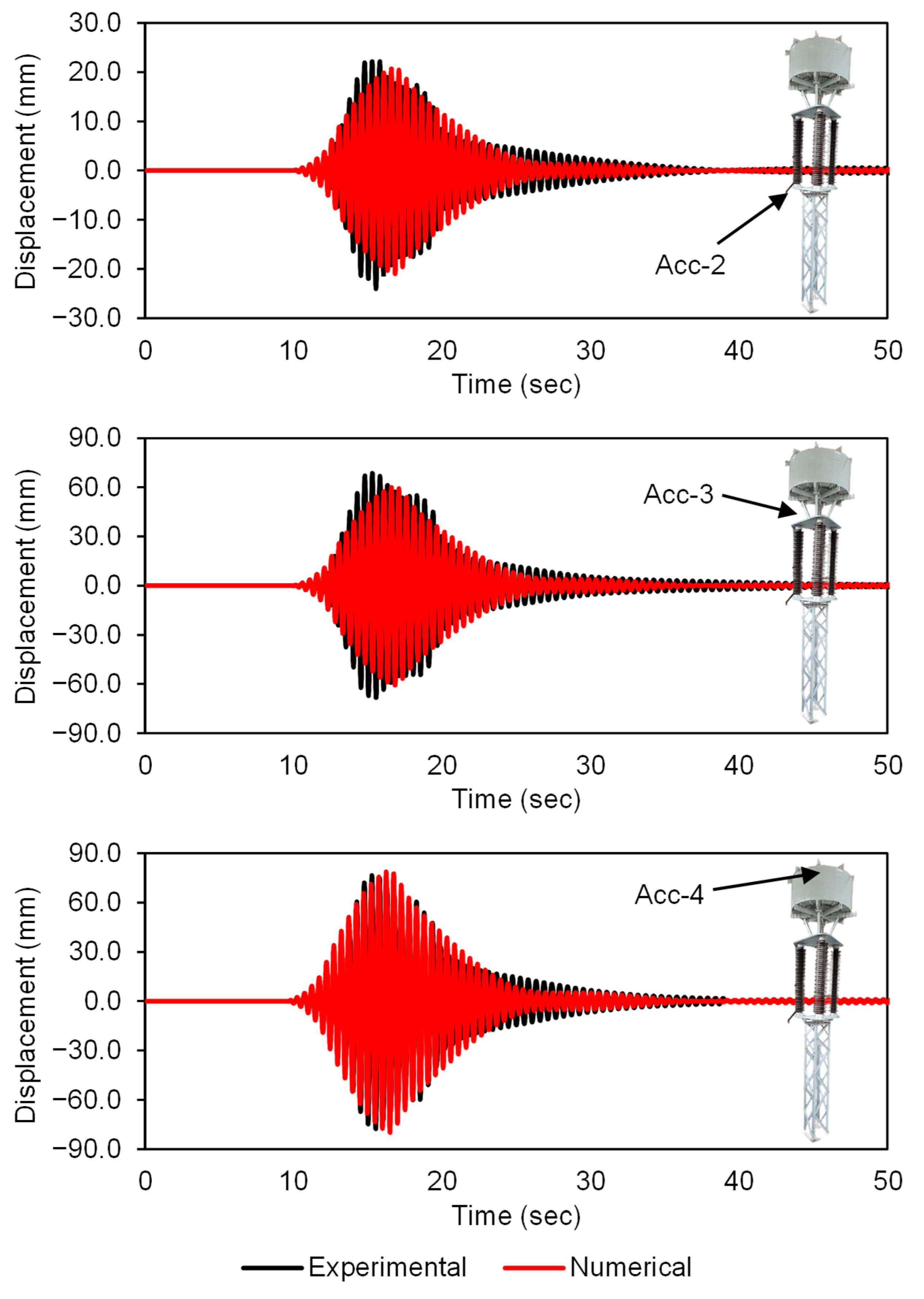
| Acc. | Experimental Results (mm) | Numerical Results (mm) | Differences (%) |
|---|---|---|---|
| Acc-2 | 24.093 | 20.995 | 12.85 |
| Acc-3 | 68.570 | 60.794 | 11.34 |
| Acc-4 | 77.745 | 79.944 | 2.82 |
| Far-Fault Ground Motions | |||||
|---|---|---|---|---|---|
| No | Earthquake Name | Year | Station Name | Mw | Rrup(km) |
| 1 | Imperial Valley-06 | 1979 | Delta | 6.53 | 22.03 |
| 2 | Imperial Valley-06 | 1979 | El Centro Array #11 | 6.53 | 12.56 |
| 3 | Loma Prieta | 1989 | Capitola | 6.93 | 15.23 |
| 4 | Landers | 1992 | Coolwater | 7.28 | 19.74 |
| 5 | Landers | 1992 | Yermo Fire Station | 7.28 | 23.62 |
| 6 | Kobe_Japan | 1995 | Nishi-Akashi | 6.9 | 7.08 |
| 7 | Kobe_Japan | 1995 | Shin-Osaka | 6.9 | 19.15 |
| 8 | Kocaeli_Turkey | 1999 | Duzce | 7.51 | 15.37 |
| 9 | Hector Mine | 1999 | Hector | 7.13 | 11.66 |
| Near-fault ground motions | |||||
| 1 | Imperial Valley-06 | 1979 | El Centro Array #6 | 6.53 | 1.35 |
| 2 | Irpinia_Italy-01 | 1980 | Sturno (STN) | 6.90 | 10.84 |
| 3 | Erzincan_Turkey | 1992 | Erzincan | 6.69 | 4.38 |
| 4 | Cape Mendocino | 1992 | Petrolia | 7.01 | 8.18 |
| 5 | Landers | 1992 | Lucerne | 7.28 | 2.19 |
| 6 | Northridge-01 | 1994 | Rinaldi Receiving Sta | 6.69 | 6.50 |
| 7 | Northridge-01 | 1994 | Sylmar–Olive View. | 6.69 | 5.30 |
| 8 | Kocaeli_Turkey | 1999 | Izmit | 7.51 | 7.21 |
| 9 | Duzce_Turkey | 1999 | Duzce | 7.14 | 6.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunca, F. Seismic Performance Assessment of 170 kV Line Trap Systems Through Shake Table Testing and Finite Element Analysis. Appl. Sci. 2025, 15, 10734. https://doi.org/10.3390/app151910734
Sunca F. Seismic Performance Assessment of 170 kV Line Trap Systems Through Shake Table Testing and Finite Element Analysis. Applied Sciences. 2025; 15(19):10734. https://doi.org/10.3390/app151910734
Chicago/Turabian StyleSunca, Fezayil. 2025. "Seismic Performance Assessment of 170 kV Line Trap Systems Through Shake Table Testing and Finite Element Analysis" Applied Sciences 15, no. 19: 10734. https://doi.org/10.3390/app151910734
APA StyleSunca, F. (2025). Seismic Performance Assessment of 170 kV Line Trap Systems Through Shake Table Testing and Finite Element Analysis. Applied Sciences, 15(19), 10734. https://doi.org/10.3390/app151910734






