New Methodology for Evaluating Uncertainty in Mineral Resource Estimation
Abstract
1. Introduction
2. Theoretical Framework
2.1. Simple Normal Equation Simulation (SNESIM)
2.2. Geological Setting
3. Materials and Methods
3.1. Materials
3.2. Methods
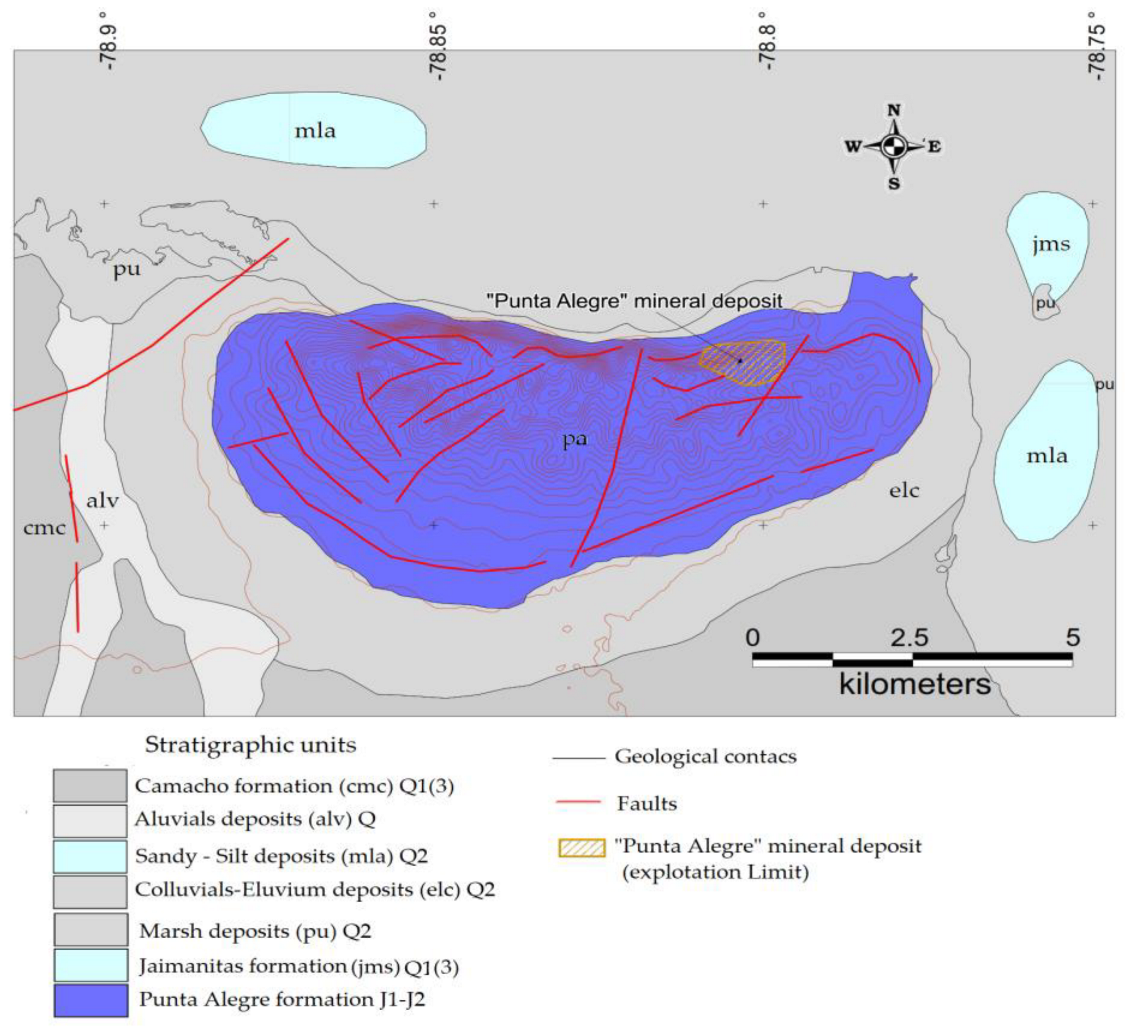
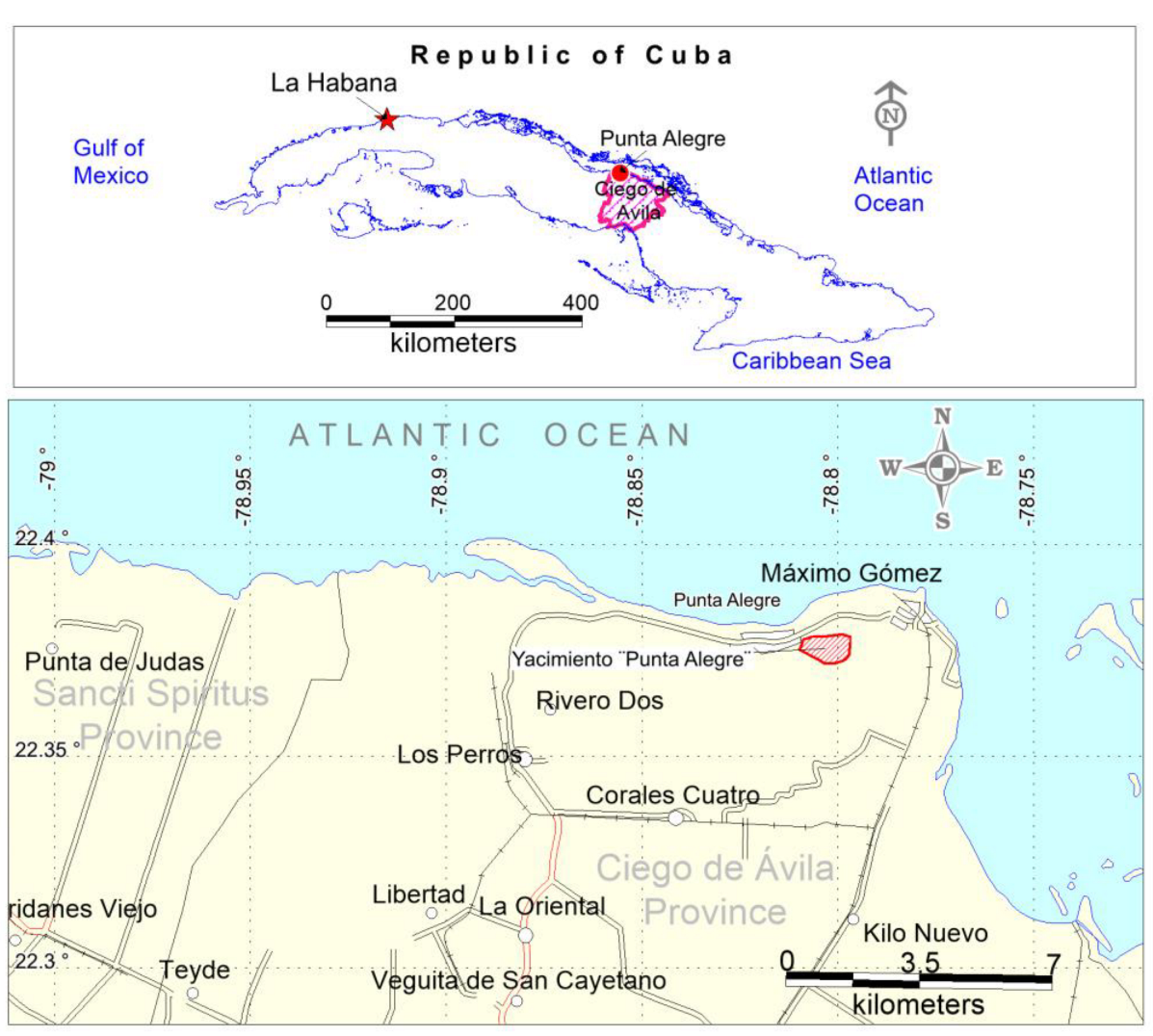
3.2.1. Study Area
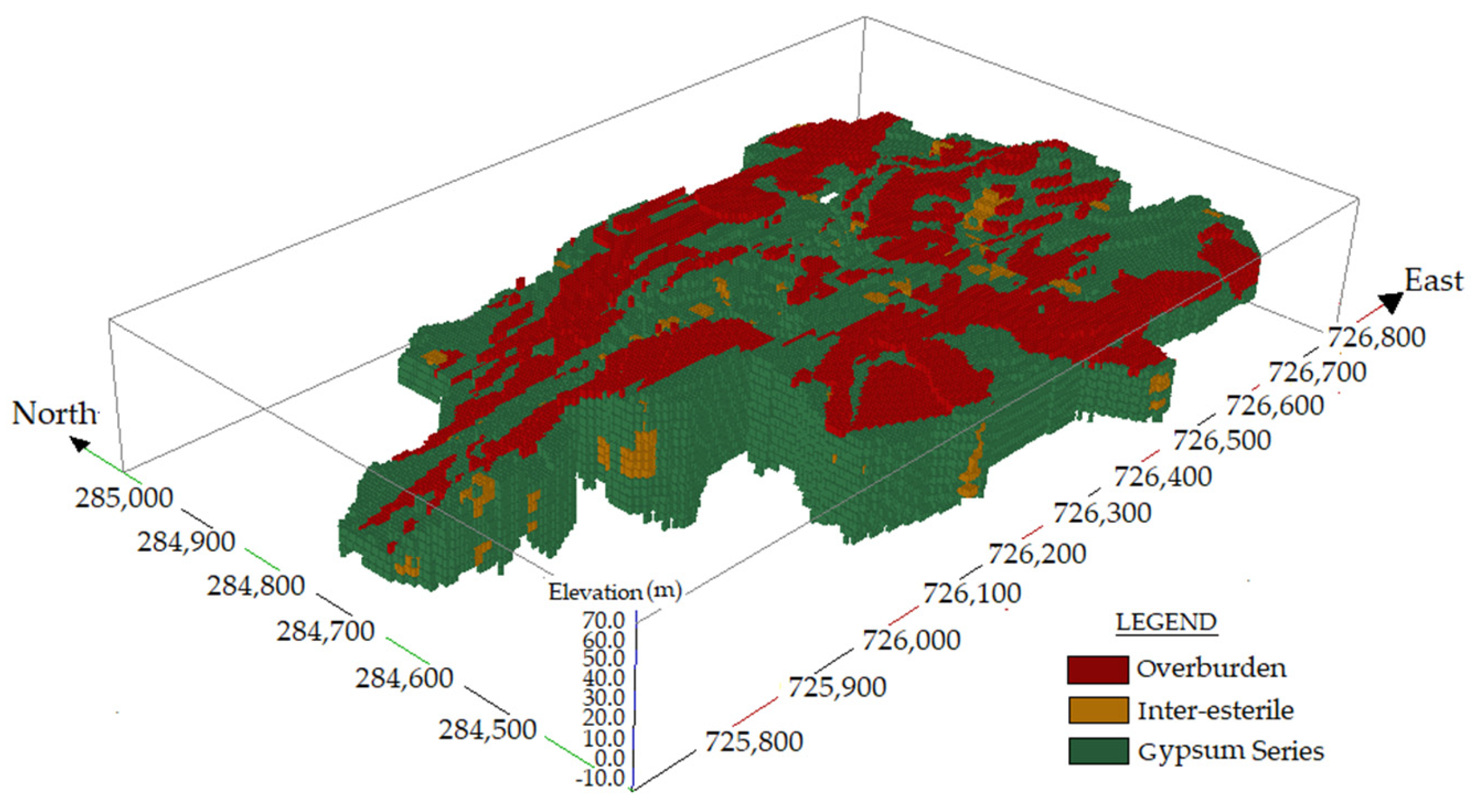
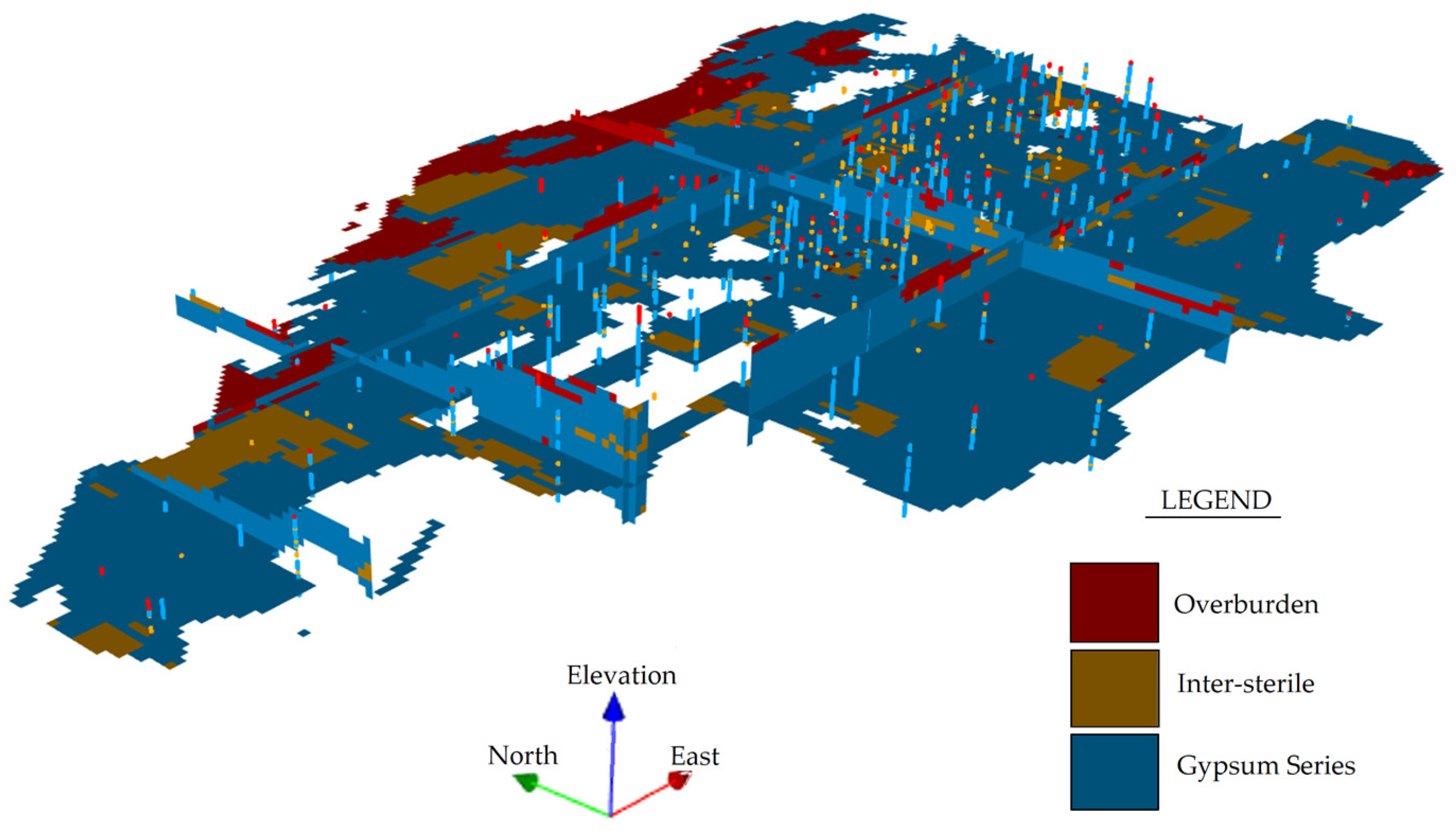
3.2.2. Geological Modeling of the Punta Alegre Deposit
3.2.3. Identification of Non-Mineral Envelopes
3.2.4. Building the Training Image (TI)
3.2.5. Composites
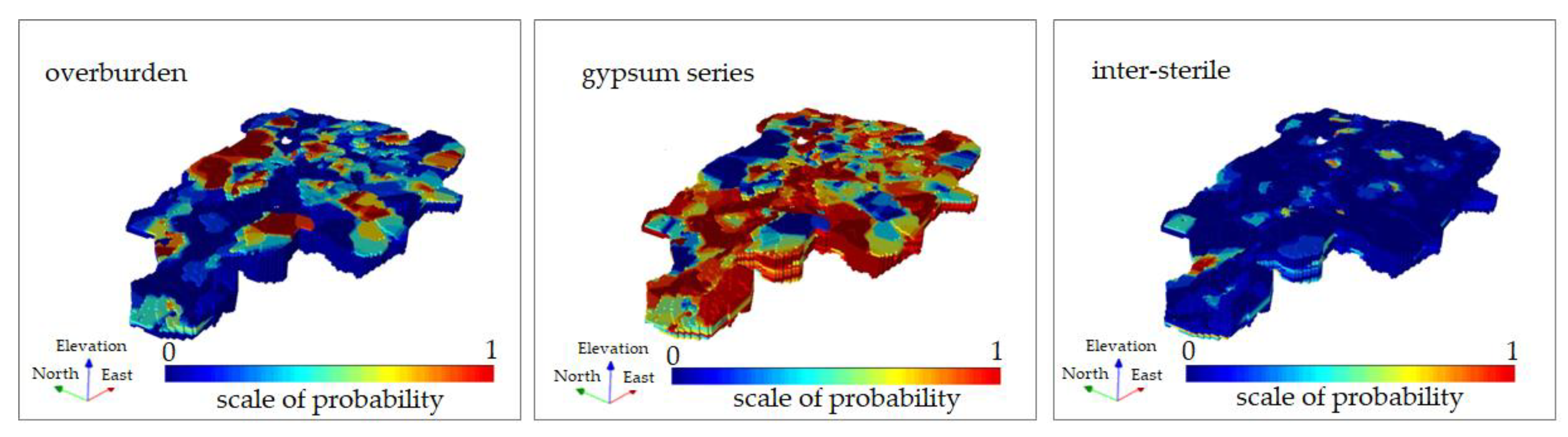
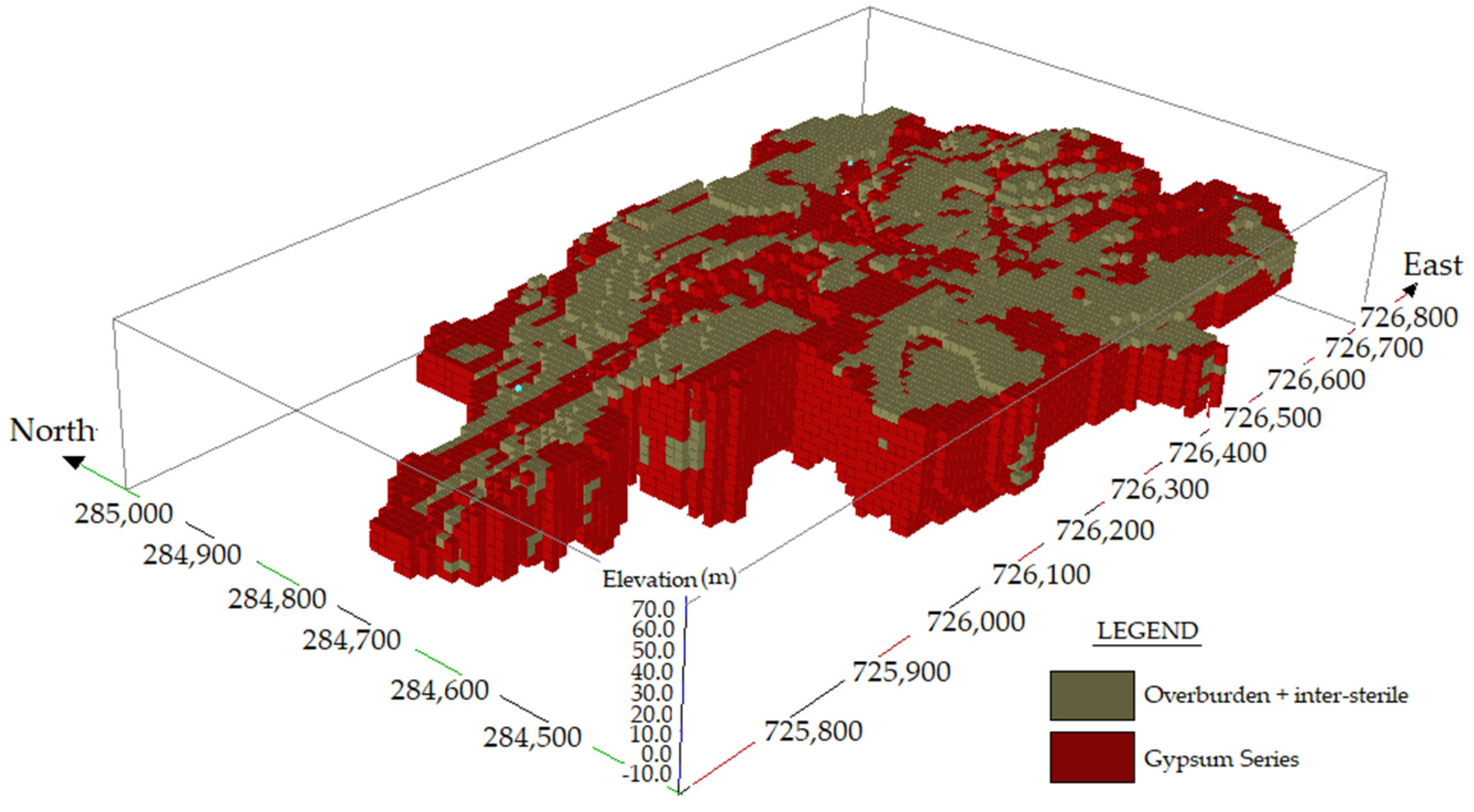
3.2.6. Prior Probability Maps of the Overburden, the Valuable Mineral (Gypsum) and the Intercalated Sterile (‘Inter-Sterile’)
4. Results and Discussion
4.1. Results
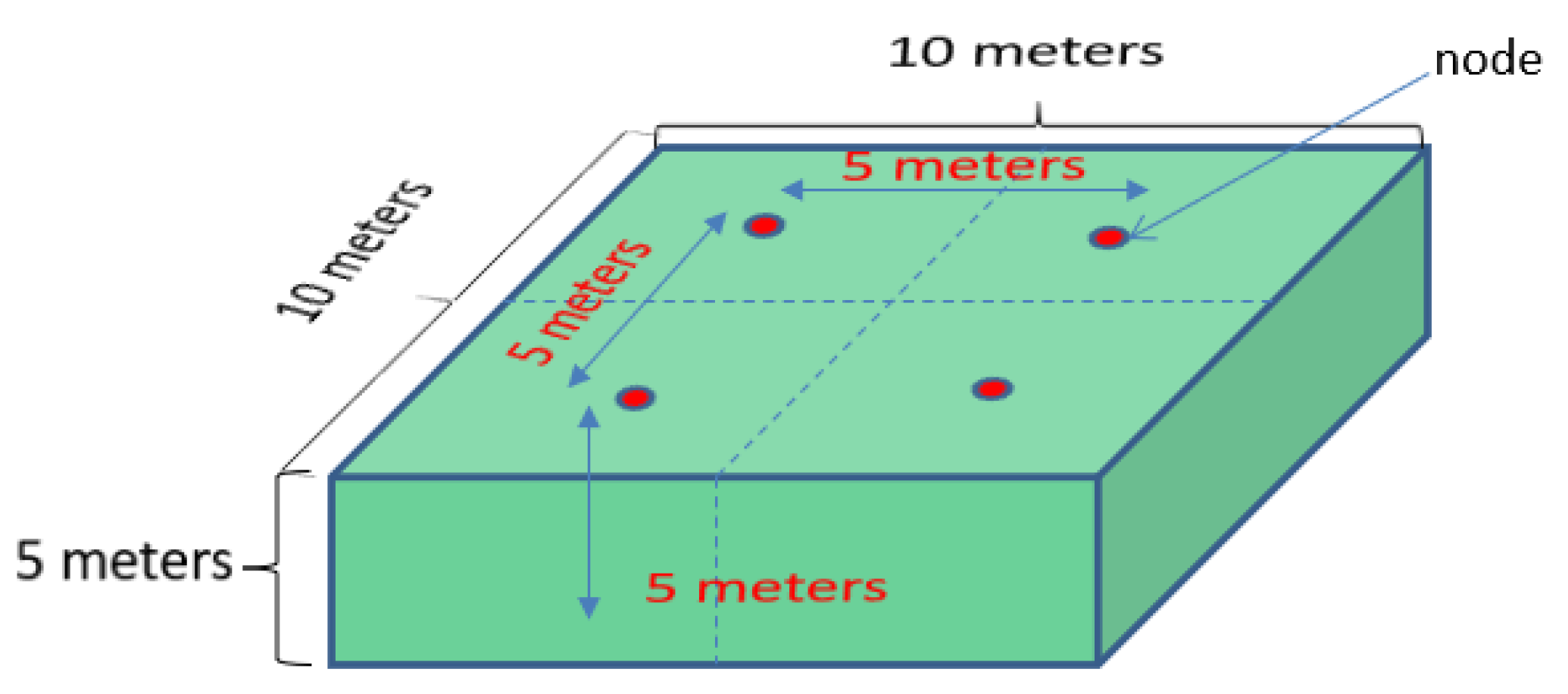
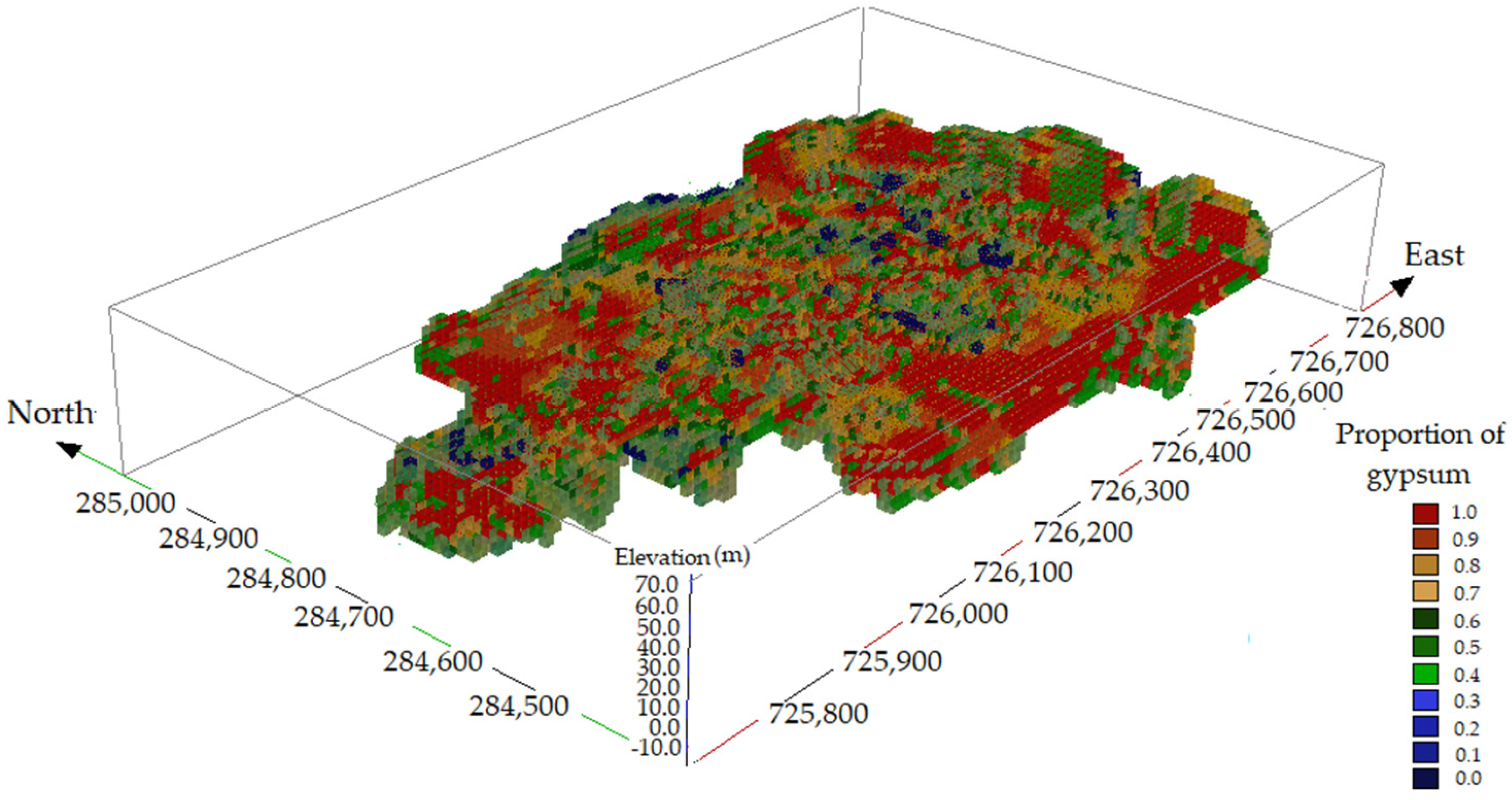
4.1.1. Deterministic Model for Gypsum in 10 × 10 × 5 m Panels
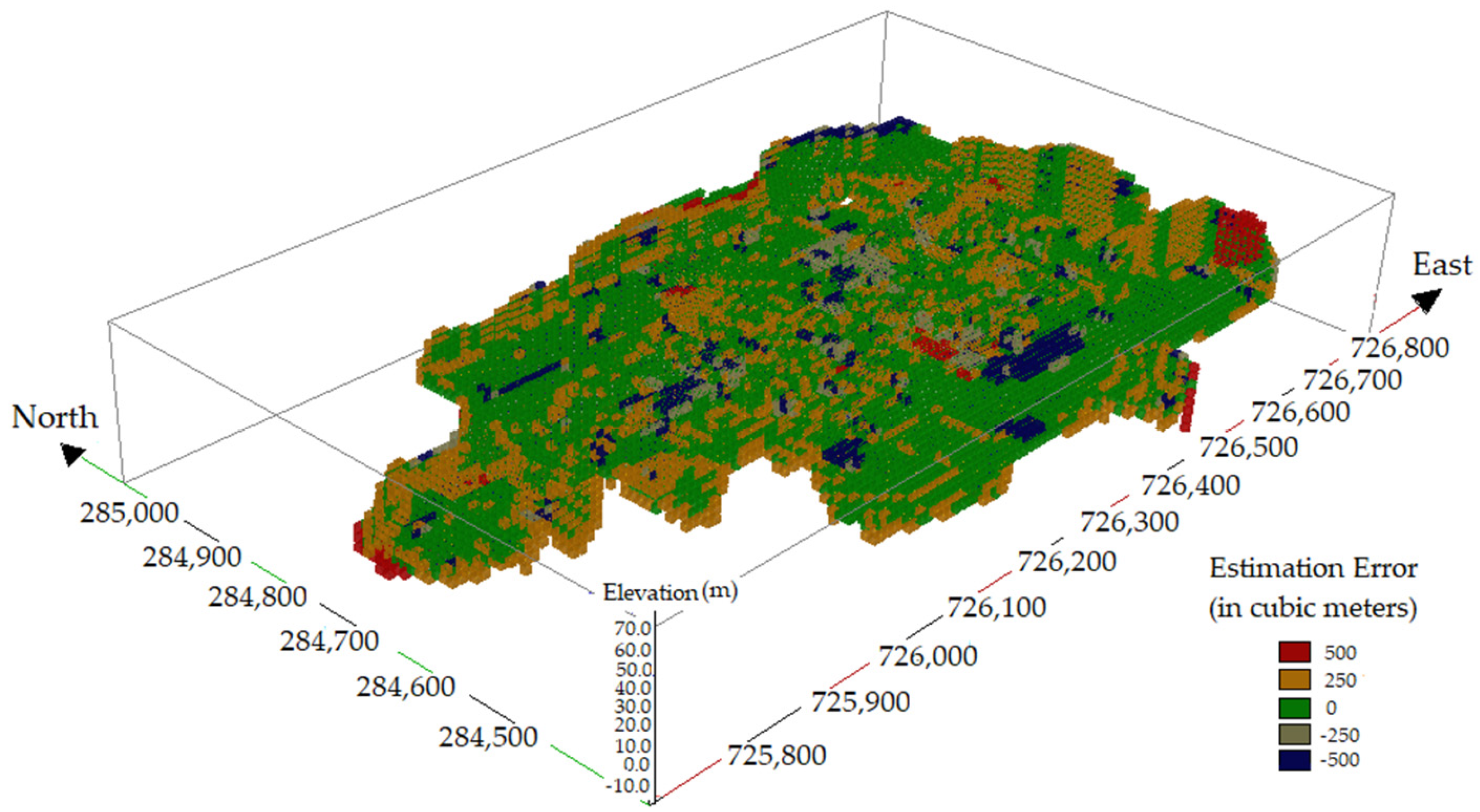
4.1.2. Model of the Average Proportions of Gypsum in the 10 × 10 × 5 m Panels
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA; London, UK, 2014; p. 337. ISBN 978-1-4020-5716-8. [Google Scholar] [CrossRef]
- Van Der Grijp, Y.M. Application of Simulation Techniques for Modelling Uncertainty Associated with Gold Mineralization. Master’s Thesis, Faculty of Engineering and the Built Environment, University of the Witwatersrand, Johannesburg, South Africa, 2014; p. 70. Available online: https://core.ac.uk/download/pdf/39676262.pdf (accessed on 11 April 2025).
- Deutsch, C.V. The Place of Geostatistical Simulation through the Life Cycle of a Mineral Deposit. Minerals 2023, 13, 1400. [Google Scholar] [CrossRef]
- Caers, J. Modeling Spatial Uncertainty. In Modeling Uncertainty in the Earth Sciences; John Wiley & Sons, Ltd.: Oxford, UK, 2011; pp. 93–106. ISBN 9781119992639. [Google Scholar] [CrossRef]
- Dowd, P. Quantifying the Impacts of Uncertainty. In Handbook of Mathematical Geosciences: Fifty Years of IAMG; Springer Open: Cham, Switzerland, 2018; Chapter 18; pp. 349–373. ISBN 978-3-319-78998-9. [Google Scholar] [CrossRef]
- Júnior, S.; da Silva, A.A. Simulação de Litotipos de Depósito de Minério de Ferro com Geoestatística de Múltiplos Pontos. Master’s Thesis, Universidade Federal Do Rio Grande Do Sul. Programa de Pós-Graduação em Engenharia de Minas, Farroupilha, Brasil, 2013; p. 102. Available online: https://lume.ufrgs.br/handle/10183/79828 (accessed on 16 February 2024).
- Gómez-Hernández, J.J.; Srivastava, R.M. One Step at a Time: The Origins of Sequential Simulation and Beyond. Math. Geosci. 2021, 53, 193–209. [Google Scholar] [CrossRef]
- Abulkhair, S.; Madani, N. Stochastic modeling of iron in coal seams using two-point and multiple-point geostatistics: A case study. Min. Metall. Explor. 2022, 39, 1313–1331. [Google Scholar] [CrossRef]
- Guardiano, F.B.; Srivastava, R.M. Multivariate Geostatistics: Beyond Bivariate Moments. In Geostatistics Tróia ’92; Soares, A., Ed.; Quantitative Geology and Geostatistics; Springer: Dordrecht, The Netherlands, 1993; Volume 5. [Google Scholar] [CrossRef]
- Strebelle, S. Conditional Simulation of Complex Geological Structures Using Multiple-Point Statistics. Math. Geol. 2002, 34, 1–21. [Google Scholar] [CrossRef]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Mathematical Geosciences; Cambridge University Press: Cambridge, UK, 2009; Volume 41, pp. 353–356. ISBN 978-0-521-51414-9. [Google Scholar]
- Tahmasebi, P. Multiple point statistics: A review. In Handbook of Mathematical Geosciences: Fifty years of IAMG; Springer Open: Cham, Switzerland, 2018; Chapter 30; pp. 613–643. ISBN 978-3-319-78998-9. [Google Scholar] [CrossRef]
- Talesh Hosseini, S.; Asghari, O.; Torabi, S.A.; Abedi, M. An Optimum Selection of Simulated Geological Models by Multi-Point Geostatistics and Multi-Criteria Decision-Making Approaches; a Case Study in Sungun Porphyry-Cu deposit, Iran. J. Min. Environ. 2020, 11, 481–503. [Google Scholar] [CrossRef]
- Avalos, S.; Ortiz, J.M. Multiple-Point Statistics: Tools and Methods. Predictive Geometallurgy and Geostatistics Lab, Queen’s University, Annual Report, 2020, Paper 2020-03. pp. 33–60. Available online: https://qspace.library.queensu.ca/handle/1974/28556 (accessed on 11 February 2014).
- Strebelle, S. Multiple-Point Statistics Simulation Models: Pretty Pictures or Decision-Making Tools? Math. Geosci. 2021, 53, 267–278. [Google Scholar] [CrossRef]
- Osterholt, V.; Dimitrakopoulos, R. Simulation of Orebody Geology with Multiple-Point Geostatistics—Application at Yandi Channel Iron Ore Deposit, WA, and Implications for Resource Uncertainty. In Advances in Applied Strategic Mine Planning; Dimitrakopoulos, R., Ed.; Springer: Cham, Switzerland, 2018; pp. 335–352. [Google Scholar] [CrossRef]
- Paithankar, A.; Chatterjee, S. Grade and Tonnage Uncertainty Analysis of an African Copper Deposit Using Multiple-Point Geostatistics and Sequential Gaussian Simulation. Nat. Resour. Res. 2018, 27, 419–436. [Google Scholar] [CrossRef]
- Strebelle, S. Sequential Simulation Drawing Structures from Training Images. Ph.D. Thesis, Stanford Center for Reservoir Forecasting, Stanford University, Stanford, CA, USA, 2000; p. 24, UMI Number: 3000105. Available online: https://github.com/SCRFpublic/snesim-standalone/blob/master/snesimtheory.ppt (accessed on 10 April 2024).
- Amarante, F.A.N.; Rolo, R.M.; Costa, J.F.C.L. Assessing geologic model uncertainty—A case study comparing methods. REM—Int. Eng. J. 2019, 72, 643–653. [Google Scholar] [CrossRef]
- Iturralde-Vinent, M.; Marrero, F. Nuevos datos sobre las estructuras diapíricas de Punta Alegre y Turiguanó, en la Provincia Ciego de Avila. Rev. Cienc. Tierra Espac. 1982, 9, 47–55. [Google Scholar]
- Meyerhoff, A.A.; Hatten, C.W. Diapiric Structures in Central Cuba1. In Diapirism and Diapirs: A symposium; Braunstein, J., O’Brien, G.D., Eds.; American Association of Petroleum Geologists: Tulsa, OK, USA, 1968; pp. 315–357. [Google Scholar] [CrossRef]
- Sánchez Arango, J.R. Las Evaporitas en Cuba y su Relación con Escenarios Exploratorios de Hidrocarburos. Memorias, Trabajos y Resúmenes V Convención Cubana de Ciencias de la Tierra (Geociencias’ 2013) Sociedad Cubana de Geología, 2013. p. 12. PETRO1-O2. SSN-2307-499X. Available online: http://www.redciencia.cu/geobiblio/paper/2013_Sanchez_Arango_PETRO1-O2.pdf (accessed on 16 February 2024).
- Rojas-Consuegra, R.; Tamayo Castellanos, Y.; Torres Díaz, M.; Pérez Peña, M.V. Reevalución Estratigráfica Integral de Bloques para la Exploración de Hidrocarburos; Internal Archive; Unpublished Report; National Office of Mineral Resources of the Republic of Cuba: La Habana, Cuba, 2020; Available online: https://www.minem.gob.cu/es/actividades/geologia/informes-concluidos (accessed on 16 February 2024).
- Lukač, M. Estratigrafía y génesis de la sal gema en Punta Alegre y en Loma Cunagua, Provincia de Camagüey. Rev. Tecnológica 1969, 1, 20–42. Available online: http://www.redciencia.cu/geobiblio/geobiblio.html#L (accessed on 16 February 2024).
- Kazak, Y.; Setién, C.; Hurtado, J. Informe General Sobre los Trabajos Detallados de Exploración Geológica en yeso, en los años 1964–1965,1967–1970 y 1976–1977, Yacimiento Punta Alegre; Internal Archive; Oficina Nacional de Recursos Minerales: La Habana, Cuba, 1981; p. 255. [Google Scholar]
- Instituto de Geología y Paleontología of Cuba. Léxico Estratigráfico de Cuba; Instituto de Geología y Paleontología of Cuba: Havana, Cuba, 2014; ISBN 978-959-7117-57-5. Available online: https://isbn.cloud/9789597117575/lexico-estratigrafico-de-cuba-2013/ (accessed on 12 February 2024).
- Cala, E.L.; Delgado, D.E.G. Stratigraphy of Cuba. In Geology of Cuba; Pardo Echarte, M.E., Ed.; Regional Geology Reviews; Springer Nature: Cham, Switzerland, 2021; pp. 143–188. [Google Scholar] [CrossRef]
- Ducloz, C. Apuntes sobre el yeso del Valle de Yumurí Matanzas. Apuntes sobre el yeso del valle de Yumuri Matanzas. Mem. Soc. Cuba. Hist. Nat. Felipe Poey 1960, 25, 1–9. Available online: https://archive-ouverte.unige.ch/unige:156815 (accessed on 16 February 2024).
- Instituto de Geología y Paleontología of Cuba. Mapa Geológico Hoja Punta Alegre a Escala 1:100000; 2011.a ed.; Internal Report; Instituto de Geología y Paleontología (Cuba): La Habana, Cuba, 2011; Available online: https://www.igp.minem.cu/ (accessed on 16 February 2024).
- Ortíz, E. Re-Estimación de Recursos para la Concesión del Yacimiento «Yeso Punta Alegre»; Internal Report No.: 3281; CEPRONIQUEL: La Habana, Cuba, 2018; p. 79. [Google Scholar]
- Palmer, L.W. Compositing and regularization of drillhole data for geostatistical resource estimation. J. S. Afr. Inst. Min. Metall. 2024, 124, 331–338. [Google Scholar] [CrossRef]
- Marwanza, I.; Nas, C.; Azizi, M.A.; Simamora, J.H. Comparison between moving windows statistical method and kriging method in coal resource estimation. J. Phys. Conf. Ser. 2019, 1402, 033016. [Google Scholar] [CrossRef]
- Anggara, B.; Marwanza, I.; Ahmad Azizi, M.; Dahani, W. Subandrio. Fitting the variogram model of nickel laterite using root means square error in Morowali, Central Sulawesi. IOP Conf. Ser. Earth Environ. Sci. 2021, 882, 012042. [Google Scholar] [CrossRef]
- Garnier-Villarreal, M. Introducción al análisis geoestadístico de datos en geociencias: Teoría y aplicación. Rev. Geol. Am. Cent. 2022, 67, 26–48. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Nimmo, M.J. ML and AI for resource estimation—What could possibly go wrong? Nothing! Everything! In Proceedings of the Mineral Resource Estimation Conference 2023, Perth, Australia, 24–25 May 2023.
- Lindi, O.T.; Aladejare, A.E.; Ozoji, T.M.; Ranta, J.P. Uncertainty Quantification in Mineral Resource Estimation. Nat. Resour. Res. 2024, 33, 2503–2526. [Google Scholar] [CrossRef]




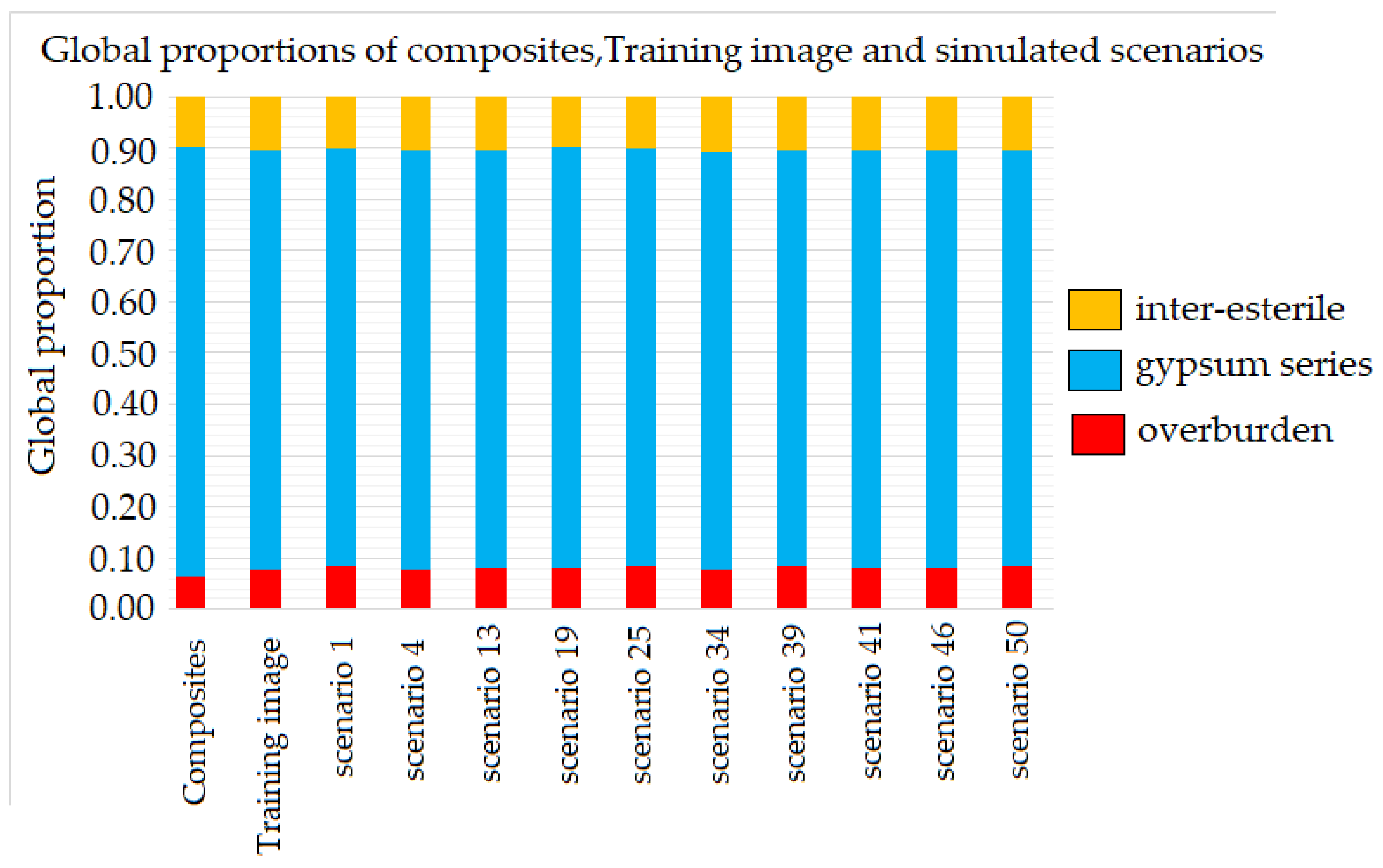


| Lithologies | Composites | Training Image (TI) | Simulated Scenarios | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 13 | 19 | 25 | 34 | 39 | 41 | 46 | 50 | |||
| Overburden | 0.07 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 |
| Gypsum series | 0.84 | 0.82 | 0.81 | 0.82 | 0.82 | 0.82 | 0.82 | 0.81 | 0.81 | 0.81 | 0.82 | 0.81 |
| Inter-sterile | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.11 | 0.10 | 0.10 | 0.10 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias, J.A.; Carballo, A.; Estévez, E.; Rojas, R.; Martín, D.A.; Costafreda, J.L. New Methodology for Evaluating Uncertainty in Mineral Resource Estimation. Appl. Sci. 2025, 15, 10616. https://doi.org/10.3390/app151910616
Arias JA, Carballo A, Estévez E, Rojas R, Martín DA, Costafreda JL. New Methodology for Evaluating Uncertainty in Mineral Resource Estimation. Applied Sciences. 2025; 15(19):10616. https://doi.org/10.3390/app151910616
Chicago/Turabian StyleArias, José Alberto, Alain Carballo, Elmidio Estévez, Reinaldo Rojas, Domingo A. Martín, and Jorge L. Costafreda. 2025. "New Methodology for Evaluating Uncertainty in Mineral Resource Estimation" Applied Sciences 15, no. 19: 10616. https://doi.org/10.3390/app151910616
APA StyleArias, J. A., Carballo, A., Estévez, E., Rojas, R., Martín, D. A., & Costafreda, J. L. (2025). New Methodology for Evaluating Uncertainty in Mineral Resource Estimation. Applied Sciences, 15(19), 10616. https://doi.org/10.3390/app151910616