A Modular Perspective on the Evolution of Deep Learning: Paradigm Shifts and Contributions to AI
Abstract
1. Introduction
2. Literature Review
2.1. Foundational Reviews
2.2. Technical Challenges
2.3. Model-Specific Advances
2.4. Domain Applications
2.5. Gaps in Existing Work
2.6. Deep Neural Networks and Its Variants
2.6.1. Autoencoders
2.6.2. Convolutional Neural Networks
2.6.3. Recurrent Neural Networks
2.6.4. Long Short-Term Memory Networks
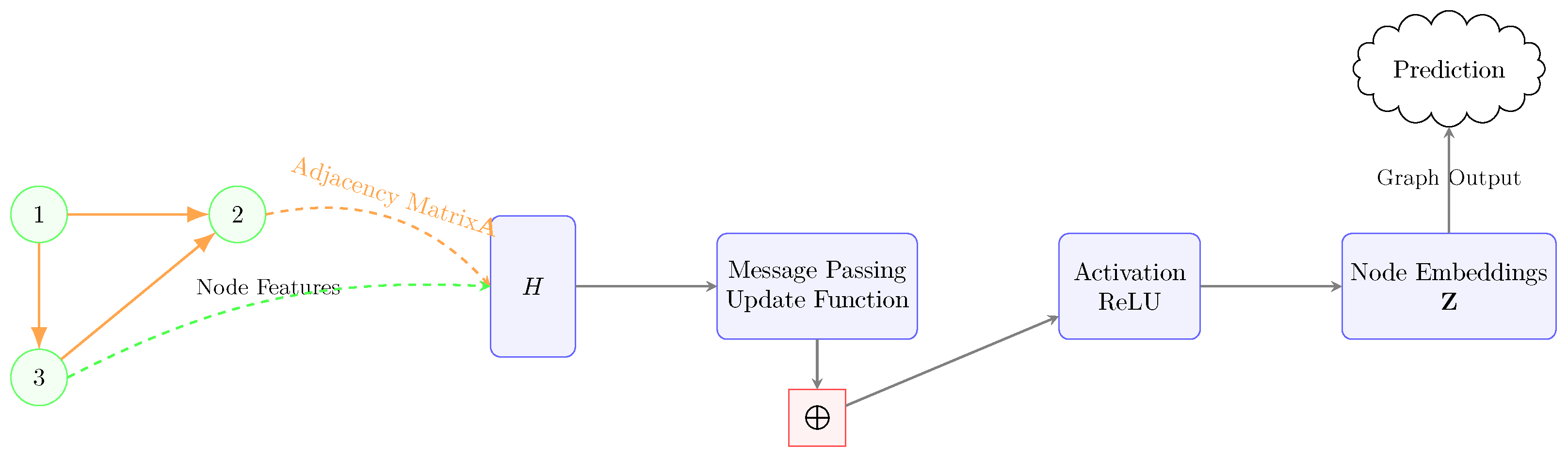
2.6.5. Graph Neural Networks
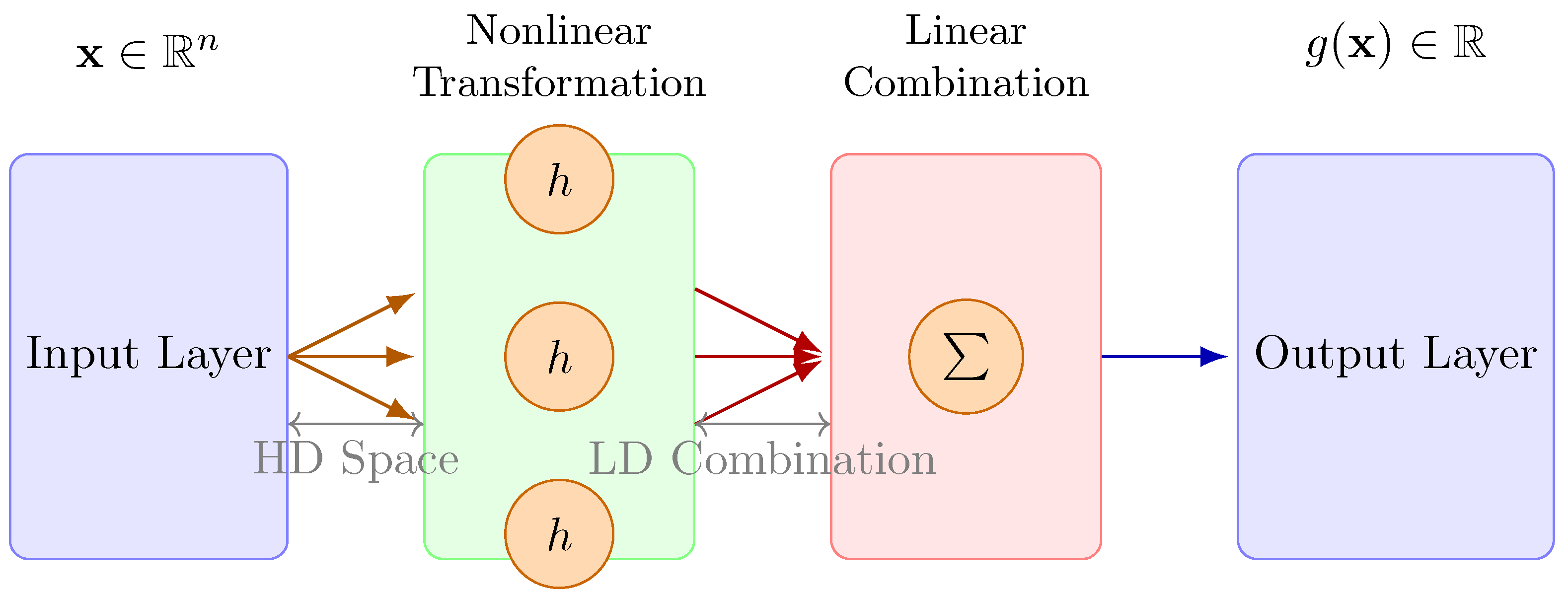
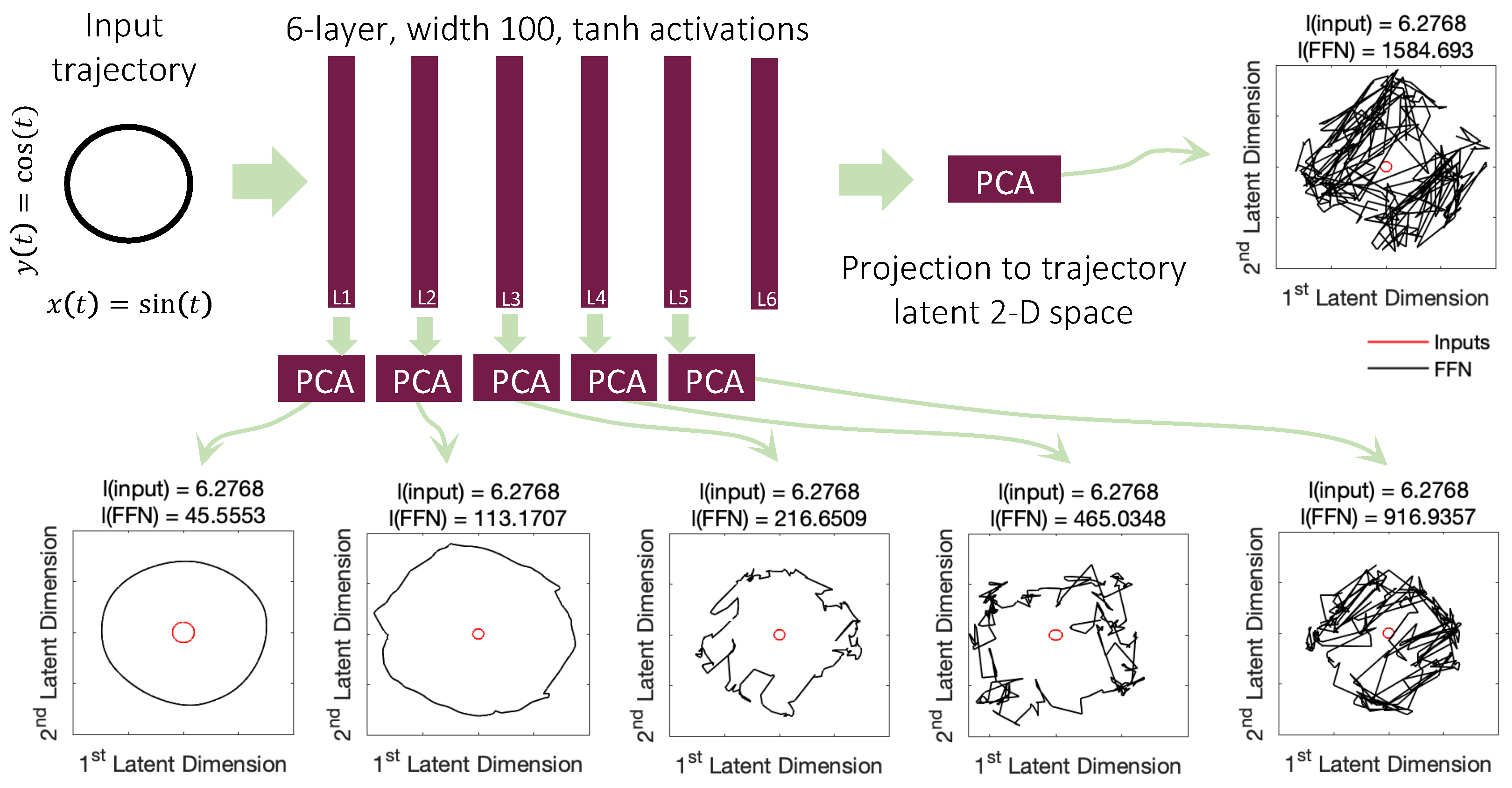
2.6.6. Kolmogorov–Arnold Networks
2.6.7. Bayesian Neural Networks
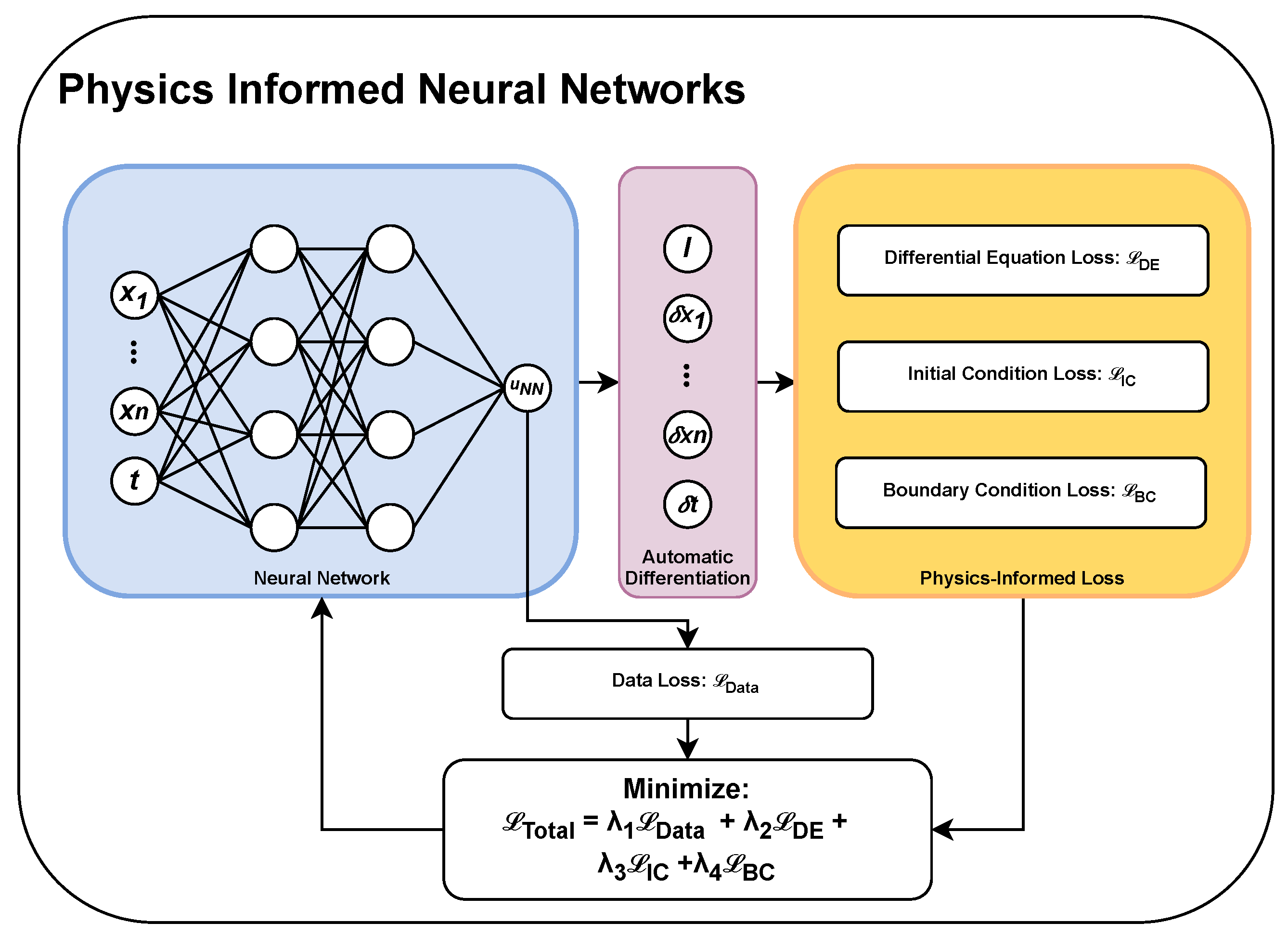
2.6.8. Physics-Informed Neural Networks
2.6.9. Liquid Neural Networks
2.7. Deep Generative Models and Variants
2.7.1. Generative Adversarial Networks
2.7.2. Boltzmann Machine
2.7.3. Variational Autoencoder
2.7.4. Diffusion Models
2.8. Transformer and Its Variants
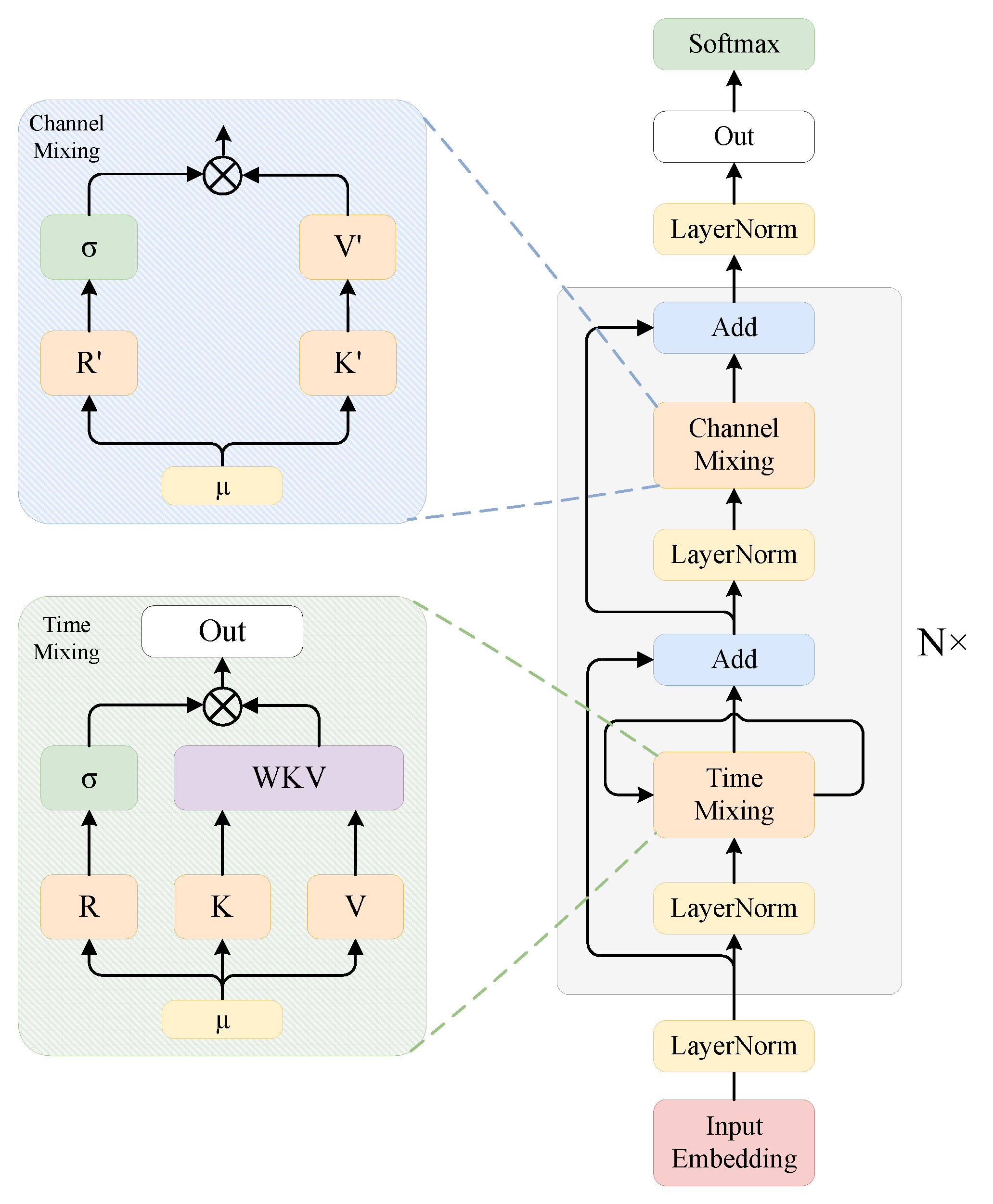
2.9. RWKV and Its Variants
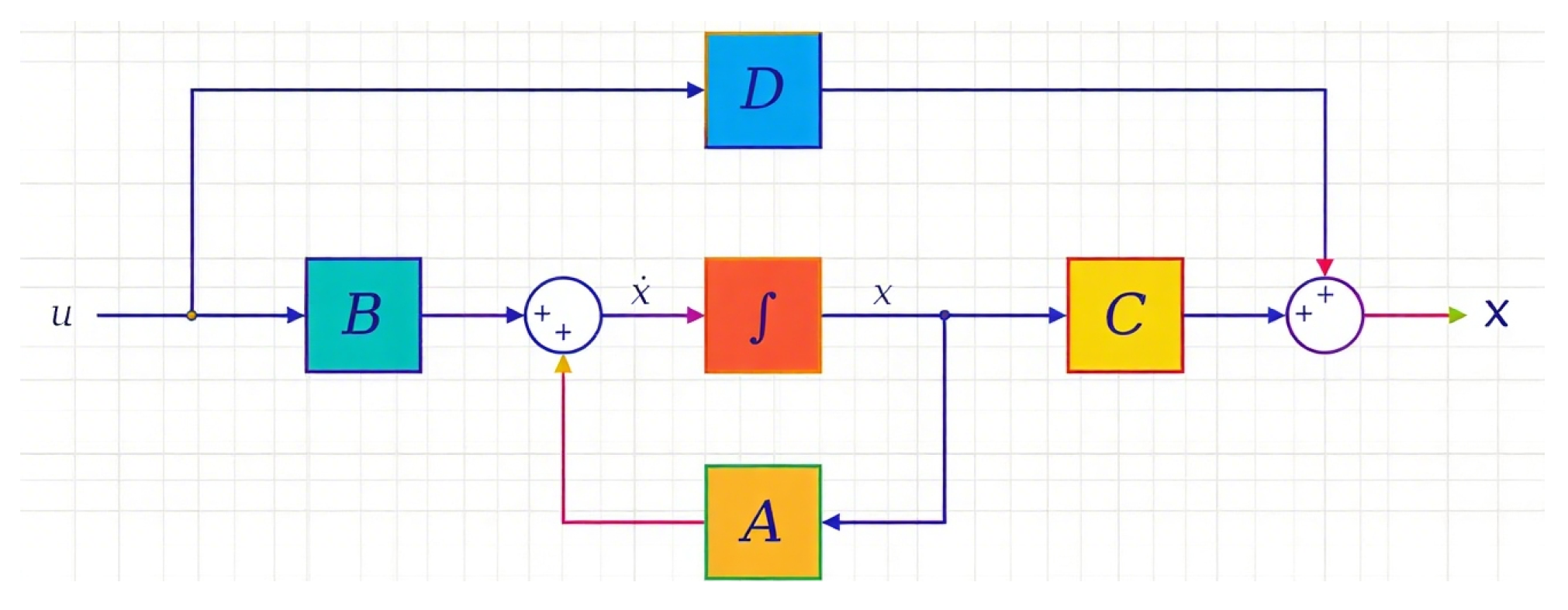
2.10. State Machine and Its Variants
2.11. Reinforcement Learning Algorithms
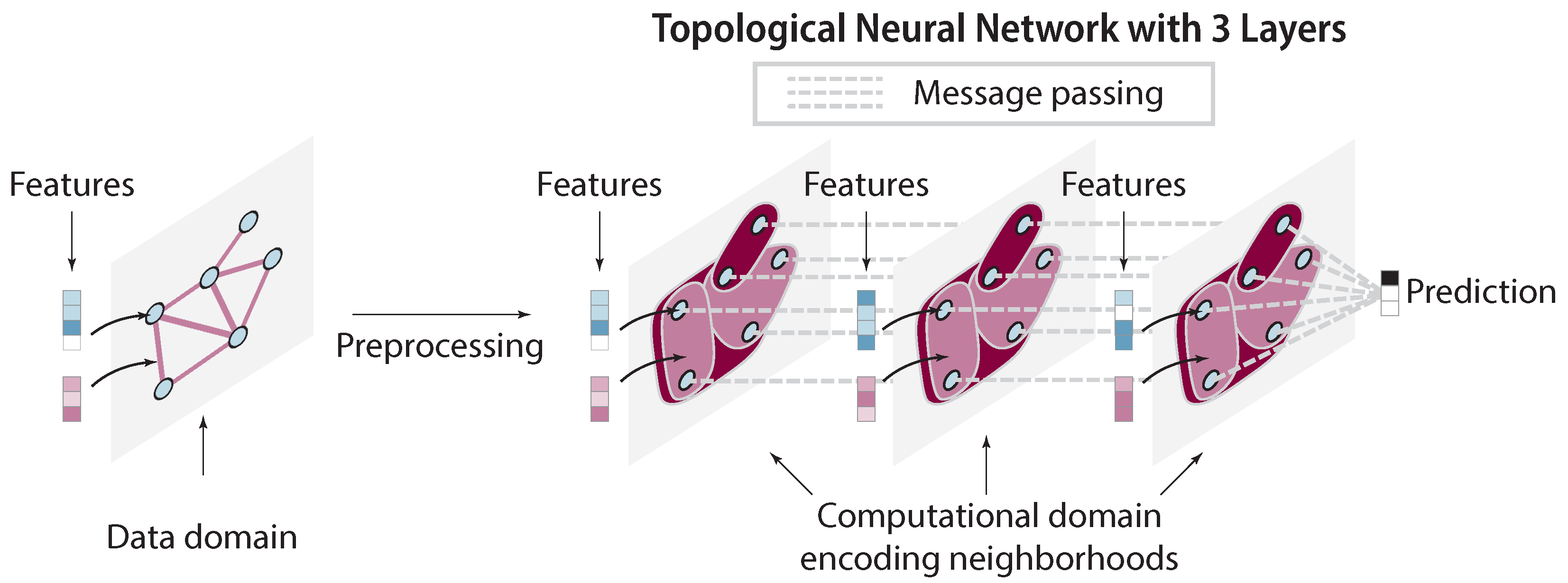
2.12. Topological Deep Learning and Its Variants
2.13. Spiking Neural Networks
2.14. Benchmarks and Performances of the Deep Learning Models
3. Innovation Trends of Deep Learning on AI’s Modular Viewpoint
3.1. Innovations in Feature Extraction Methods
3.2. Innovations in Normalization Methods
3.3. Innovations in Algorithm Module Enhancement and Hybridization
3.3.1. Architecture Modification
3.3.2. Automated and Lightweighting Design
3.3.3. Module Integration and Stitching
3.4. Innovations in Optimization Methods
3.4.1. Parameter Optimization
3.4.2. Activation Function Design
3.4.3. Techniques to Prevent Overfitting
3.4.4. Efficient Adaptation and Modularization
3.5. Innovations in Transfer Learning Applications
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Newell, A.; Simon, H.A. Computer science as empirical inquiry: Symbols and search. Commun. ACM 1976, 19, 113–126. [Google Scholar] [CrossRef]
- Lindsay, R.K.; Buchanan, B.G.; Feigenbaum, E.A.; Lederberg, J. DENDRAL: A case study of the first expert system for scientific hypothesis formation. Artif. Intell. 1993, 61, 209–261. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; Computational and Biological Learning Society: Cambridge, UK, 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I.; Sutskever, H. Improving Language Understanding by Generative Pre-Training; Technical Report; OpenAI: San Francisco, CA, USA, 2018. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, PmLR, Vienna, Austria, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollar, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleands, LA, USA, 18–24 June 2022; IEEE Computer Society: Washington, DC, USA, 2022; pp. 15979–15988. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Bossert, L.N.; Loh, W. Why the carbon footprint of generative large language models alone will not help us assess their sustainability. Nat. Mach. Intell. 2025, 7, 164–165. [Google Scholar] [CrossRef]
- Xua, B.; Yang, G. Interpretability research of deep learning: A literature survey. Inf. Fusion 2024, 115, 102721. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Chattha, M.A.; Malik, M.I.; Dengel, A.; Ahmed, S. Addressing data dependency in neural networks: Introducing the Knowledge Enhanced Neural Network (KENN) for time series forecasting+. Mach. Learn. 2025, 114, 30. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Minar, M.R.; Naher, J. Recent advances in deep learning: An overview. arXiv 2018, arXiv:1807.08169. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y. A comprehensive survey on regularization strategies in machine learning. Inf. Fusion 2022, 80, 146–166. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. Int. Conf. Mach. Learn. 2013, 28, 1139–1147. [Google Scholar]
- Brauwers, G.; Frasincar, F. A general survey on attention mechanisms in deep learning. IEEE Trans. Knowl. Data Eng. 2021, 35, 3279–3298. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft Comput. 2023, 138, 110176. [Google Scholar] [CrossRef]
- Li, Z.; Xia, T.; Chang, Y.; Wu, Y. A Survey of Rwkv. arXiv 2024, arXiv:2412.14847. [Google Scholar] [CrossRef]
- Chen, M.; Mei, S.; Fan, J.; Wang, M. An overview of diffusion models: Applications, guided generation, statistical rates and optimization. arXiv 2024, arXiv:2404.07771. [Google Scholar] [CrossRef]
- Ji, T.; Hou, Y.; Zhang, D. A comprehensive survey on kolmogorov arnold networks (kan). arXiv 2024, arXiv:2407.11075. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PmLR, Virutal, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Chen, X.; Wang, L.; Zhang, H. Deep Learning in Medical Image Analysis: Current Trends and Future Directions. Information 2023, 15, 755. [Google Scholar] [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A comparison review of transfer learning and self-supervised learning: Definitions, applications, advantages and limitations. Expert Syst. Appl. 2024, 242, 122807. [Google Scholar] [CrossRef]
- Botvinick, M.; Ritter, S.; Wang, J.X.; Kurth-Nelson, Z.; Blundell, C.; Hassabis, D. Reinforcement learning, fast and slow. Trends Cogn. Sci. 2019, 23, 408–422. [Google Scholar] [CrossRef]
- Hassabis, D.; Kumaran, D.; Summerfield, C.; Botvinick, M. Neuroscience-Inspired Artificial Intelligence. Neuron 2017, 95, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Bau, D.; Zhou, B.; Khosla, A.; Oliva, A.; Torralba, A. Network dissection: Quantifying interpretability of deep visual representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3319–3327. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. arXiv 2017, arXiv:1710.09829. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
- Graves, A.; Wayne, G.; Danihelka, I. Neural Turing Machines. arXiv 2014, arXiv:1410.5401. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Hensenki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Ng, A.Y. Sparse Autoencoder; CS294A Lecture Notes; Stanford University: Stanford, CA, USA, 2011; Volume 72, pp. 1–19. [Google Scholar]
- Zhang, X.; Li, X.; Wang, X.; Wang, X.; Wang, A.; Deng, J. Contrastive Learning of Visual Representations: A Survey. arXiv 2021, arXiv:2106.02697. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Liu, S.; Li, H.; Shi, L.; Ji, C.; Cao, J.; Lu, X.; Cao, Y. Independently recurrent neural network (IndRNN): Building a longer and deeper RNN. arXiv 2018, arXiv:1803.04831. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Yu, Y.; Salakhutdinov, R.; Caruana, R. Dilated recurrent neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2018; pp. 2728–2738. [Google Scholar]
- Jaeger, H. Echo State Networks; GMD-Forschungszentrum Informationstechnik: Sankt Augustin, Germany, 2001. [Google Scholar]
- Bradbury, J.; Merity, S.; Xiong, C.; Li, R.; Socher, R. Quasi-recurrent neural networks. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Zhang, S.X.; Zhao, R.; Liu, C.; Li, J.; Gong, Y. Recurrent support vector machines for speech recognition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; IEEE: New York, NY, USA, 2016; pp. 5885–5889. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.k.; Woo, W.c. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Beck, M.; Pöppel, K.; Spanring, M.; Auer, A.; Prudnikova, O.; Kopp, M.; Klambauer, G.; Brandstetter, J.; Hochreiter, S. xlstm: Extended long short-term memory. Adv. Neural Inf. Process. Syst. 2024, 37, 107547–107603. [Google Scholar]
- Alkin, B.; Beck, M.; Pöppel, K.; Hochreiter, S.; Brandstetter, J. Vision-lstm: xlstm as generic vision backbone. arXiv 2024, arXiv:2406.04303. [Google Scholar]
- Neil, D.; Pfeiffer, M.; Liu, S.C. Phased LSTM: Accelerating Recurrent Network Training for Long or Event-Sparse Time Series. Adv. Neural Inf. Process. Syst. 2016, 29, 3882–3890. [Google Scholar]
- Kalchbrenner, N.; Danihelka, I.; Graves, A. Grid Long Short-Term Memory. arXiv 2015, arXiv:1507.01526. [Google Scholar]
- Fukao, T.; Iizuka, H.; Kurita, T. Multidimensional Long Short-Term Memory. arXiv 2016, arXiv:1602.06289. [Google Scholar]
- Tai, K.S.; Socher, R.; Manning, C.D. Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Beijing, China, 27–34 July 2015; pp. 1556–1566. [Google Scholar]
- Zhou, P.; Shi, W.; Tian, J.; Qi, Z.; Li, B.; Hao, H.; Xu, B. Attention-based bidirectional long short-term memory networks for relation classification. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 2: SHORT Papers), Dublin, Ireland, 22–27 May 2016; pp. 207–212. [Google Scholar]
- Lei, T.; Neubig, G.; Jaakkola, T. Training RNNs as Fast as CNNs. arXiv 2017, arXiv:1709.02755. [Google Scholar]
- Tang, S.; Li, B.; Yu, H. ChebNet: Efficient and stable constructions of deep neural networks with rectified power units via Chebyshev approximation. Commun. Math. Stat. 2024, 1–27. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Xu, K.; Chen, L.; Wang, S. Kolmogorov-arnold networks for time series: Bridging predictive power and interpretability. arXiv 2024, arXiv:2406.02496. [Google Scholar] [CrossRef]
- Tang, T.; Chen, Y.; Shu, H. 3D U-KAN implementation for multi-modal MRI brain tumor segmentation. arXiv 2024, arXiv:2408.00273. [Google Scholar]
- Shuai, H.; Li, F. Physics-informed kolmogorov-arnold networks for power system dynamics. IEEE Open Access J. Power Energy 2025, 12, 46–58. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 1050–1059. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. arXiv 2015, arXiv:1505.05424. [Google Scholar] [CrossRef]
- Fortunato, M.; Blundell, C.; Vinyals, O. Bayesian recurrent neural networks. arXiv 2017, arXiv:1704.02798. [Google Scholar]
- Wu, Y.; Sicard, B.; Gadsden, S.A. Physics-informed machine learning: A comprehensive review on applications in anomaly detection and condition monitoring. Expert Syst. Appl. 2024, 255, 124678. [Google Scholar] [CrossRef]
- Lütjens, B.; Crawford, C.H.; Veillette, M.; Newman, D. Spectral pinns: Fast uncertainty propagation with physics-informed neural networks. In Proceedings of the Symbiosis of Deep Learning and Differential Equations, Virutal, 14 December 2021. [Google Scholar]
- Fang, Z. A high-efficient hybrid physics-informed neural networks based on convolutional neural network. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5514–5526. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, D.; Zhang, D.; Zeng, J.; Wang, N.; Zhang, H.; Yan, J. Theory-guided hard constraint projection (HCP): A knowledge-based data-driven scientific machine learning method. J. Comput. Phys. 2021, 445, 110624. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Khalid, S.; Yazdani, M.H.; Azad, M.M.; Elahi, M.U.; Raouf, I.; Kim, H.S. Advancements in Physics-Informed Neural Networks for Laminated Composites: A Comprehensive Review. Mathematics 2024, 13, 17. [Google Scholar] [CrossRef]
- Hasani, R.; Lechner, M.; Amini, A.; Rus, D.; Grosu, R. Liquid Time-constant Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Virutal, 2–9 February 2021; Volume 35, pp. 7657–7666. [Google Scholar]
- Hasani, R.; Lechner, M.; Amini, A.; Liebenwein, L.; Ray, A.; Tschaikowski, M.; Teschl, G.; Rus, D. Closed-form continuous-time neural networks. Nat. Mach. Intell. 2022, 4, 992–1003. [Google Scholar] [CrossRef]
- Kumar, K.; Verma, A.; Gupta, N.; Yadav, A. Liquid Neural Networks: A Novel Approach to Dynamic Information Processing. In Proceedings of the 2023 International Conference on Advances in Computation, Communication and Information Technology (ICAICCIT), Faridabad, India, 23–24 November 2023; IEEE: New York, NY, USA, 2023; pp. 725–730. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Karras, T.; Aittala, M.; Laine, S.; Lehtinen, J.; Aila, T. Alias-free generative adversarial networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10509–10518. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, W.; Zhu, Z.; Yu, H. CLIP-GAN: Stacking CLIPs and GAN for Efficient and Controllable Text-to-Image Synthesis. IEEE Trans. Multimedia 2025, 27, 3702–3715. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, W.T.; Tenenbaum, J.B. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 82–90. [Google Scholar]
- Sauer, A.; Chitta, K.; Müller, J.; Geiger, A. Projected gans converge faster. Adv. Neural Inf. Process. Syst. 2021, 34, 17480–17492. [Google Scholar]
- Hinton, G.E.; Sejnowski, T.J.; Ackley, D.H. Boltzmann Machines: Constraint Satisfaction Networks that Learn; Carnegie-Mellon University, Department of Computer Science: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Salakhutdinov, R.; Mnih, A.; Hinton, G. Restricted Boltzmann machines for collaborative filtering. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 791–798. [Google Scholar] [CrossRef]
- Tang, Y.; Salakhutdinov, R.; Hinton, G. Deep Lambertian Networks. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, Scotland, 26 June–1 July 2012. [Google Scholar]
- Salakhutdinov, R.; Hinton, G.E. Deep Boltzmann machines. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics, Paris, France, 27–29 October 2009; pp. 448–455. [Google Scholar]
- Feng, Z.; Winston, E.; Kolter, J.Z. Monotone deep Boltzmann machines. arXiv 2023, arXiv:2307.04990. [Google Scholar] [CrossRef]
- Liu, J.G.; Wang, L. Differentiable learning of quantum circuit Born machines. Phys. Rev. A 2018, 98, 062324. [Google Scholar] [CrossRef]
- Amin, M.H.; Andriyash, E.; Rolfe, J.; Kulchytskyy, B.; Melko, R. Quantum boltzmann machine. Phys. Rev. X 2018, 8, 021050. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Mescheder, L.; Nowozin, S.; Geiger, A. Adversarial variational bayes: Unifying variational autoencoders and generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2391–2400. [Google Scholar]
- Gulrajani, I.; Kumar, K.; Ahmed, F.; Taiga, A.A.; Visin, F.; Vazquez, D.; Courville, A. PixelVAE: A Latent Variable Model for Natural Images. In Proceedings of the International Conference on Learning Representations, Toulan, France, 24–26 April 2017. [Google Scholar]
- Vahdat, A.; Kautz, J. NVAE: A Deep Hierarchical Variational Autoencoder. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; pp. 19667–19679. [Google Scholar]
- Knop, S.; Spurek, P.; Tabor, J.; Podolak, I.; Mazur, S.; Jastrzebski, S. Cramer-Wold Auto-Encoder. J. Mach. Learn. Res. 2020, 21, 6594–6621. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based Generative Modeling through Stochastic Differential Equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion Models Beat GANs on Image Synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Krishnamoorthy, S.; Mashkaria, S.M.; Grover, A. Diffusion models for black-box optimization. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 17842–17857. [Google Scholar]
- Chen, M.; Huang, K.; Zhao, T.; Wang, M. Score approximation, estimation and distribution recovery of diffusion models on low-dimensional data. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 4672–4712. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Wang, J.; Li, H. Informer: Beyond efficient transformer for long sequence time-series forecasting. arXiv 2020, arXiv:2012.07436. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, H.; Zhang, S.; Wang, J.; Li, H. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. arXiv 2021, arXiv:2105.13100. [Google Scholar]
- Liu, Y.; Li, G.; Payne, T.R.; Yue, Y.; Man, K.L. Non-stationary transformer for time series forecasting. Electronics 2024, 13, 2075. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Payne, T.R.; Yue, Y.; Man, K.L. iTransformer: Inverse sequence modeling for time series forecasting. arXiv 2023, arXiv:2301.01234. [Google Scholar]
- Woo, S.; Park, J.; Lee, S.; Kim, I.S. ETSformer: Exponential smoothing transformers for time series forecasting. arXiv 2022, arXiv:2202.01381. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, S.; Zhou, H.; Wang, J.; Li, H. ShapeFormer: Morphological attention for time series forecasting. arXiv 2023, arXiv:2301.01234. [Google Scholar]
- Zhu, X.; Wang, W.; Chen, Z.; Chen, Y.; Duan, J.; Dai, J. Deformable DETR: Deformable transformers for end-to-end object detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 515–531. [Google Scholar]
- Fedus, W.; Bapna, D.; Chu, C.; Clark, D.; Dauphin, Y.; Elsen, E.; Hall, A.; Huang, Y.; Jia, Y.; Jozefowicz, R.; et al. Switch transformers: Scaling to trillion parameter models with mixture-of-experts. arXiv 2021, arXiv:2101.00391. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, H.; Wu, H.; Wang, J.; Li, H. Crossformer: A cross-scale transformer for long-term time series forecasting. arXiv 2022, arXiv:2201.00809. [Google Scholar]
- Peng, B.; Alcaide, E.; Anthony, Q.; Albalak, A.; Arcadinho, S.; Biderman, S.; Cao, H.; Cheng, X.; Chung, M.; Grella, M.; et al. Rwkv: Reinventing rnns for the transformer era. arXiv 2023, arXiv:2305.13048. [Google Scholar] [CrossRef]
- Peng, B.; Goldstein, D.; Anthony, Q.; Albalak, A.; Alcaide, E.; Biderman, S.; Cheah, E.; Ferdinan, T.; Hou, H.; Kazienko, P.; et al. Eagle and finch: Rwkv with matrix-valued states and dynamic recurrence. arXiv 2024, arXiv:2404.05892. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, R.; Goldstein, D.; Alcaide, E.; Hou, H.; Lu, J.; Merrill, W.; Song, G.; Tan, K.; Utpala, S.; et al. Rwkv-7 “goose” with expressive dynamic state evolution. arXiv 2025, arXiv:2503.14456. [Google Scholar]
- Yang, Z.; Li, J.; Zhang, H.; Zhao, D.; Wei, B.; Xu, Y. Restore-rwkv: Efficient and effective medical image restoration with rwkv. arXiv 2024, arXiv:2407.11087. [Google Scholar] [CrossRef]
- Yuan, H.; Li, X.; Qi, L.; Zhang, T.; Yang, M.H.; Yan, S.; Loy, C.C. Mamba or rwkv: Exploring high-quality and high-efficiency segment anything model. arXiv 2024, arXiv:2406.19369. [Google Scholar]
- Hou, H.; Zeng, P.; Ma, F.; Yu, F.R. Visualrwkv: Exploring recurrent neural networks for visual language models. arXiv 2024, arXiv:2406.13362. [Google Scholar] [CrossRef]
- Gu, T.; Yang, K.; An, X.; Feng, Z.; Liu, D.; Cai, W.; Deng, J. RWKV-CLIP: A robust vision-language representation learner. arXiv 2024, arXiv:2406.06973. [Google Scholar]
- He, Q.; Zhang, J.; Peng, J.; He, H.; Li, X.; Wang, Y.; Wang, C. Pointrwkv: Efficient rwkv-like model for hierarchical point cloud learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 3410–3418. [Google Scholar]
- Somvanshi, S.; Islam, M.M.; Mimi, M.S.; Polock, S.B.B.; Chhetri, G.; Das, S. From S4 to Mamba: A Comprehensive Survey on Structured State Space Models. arXiv 2025, arXiv:2503.18970. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Gu, A.; Kim, K.; Lee, A. S4: Structured State Space Sequence Modeling. In Proceedings of the International Conference on Learning Representations, Virutal, 25–29 April 2022. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.; Mirza, A.G.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Hajij, M.; Zamzmi, G.; Papamarkou, T.; Miolane, N.; Guzmán-Sáenz, A.; Ramamurthy, K.N.; Birdal, T.; Dey, T.K.; Mukherjee, S.; Samaga, S.N.; et al. Topological deep learning: Going beyond graph data. arXiv 2022, arXiv:2206.00606. [Google Scholar]
- Guo, W. Feature Extraction Using Topological Data Analysis for Machine Learning and Network Science Applications. Ph.D. Thesis, University of Washington, Washington, DC, USA, 2020. [Google Scholar]
- Love, E.R.; Filippenko, B.; Maroulas, V.; Carlsson, G. Topological convolutional layers for deep learning. J. Mach. Learn. Res. 2023, 24, 1–35. [Google Scholar]
- Pham, P. A Topology-Enhanced Multi-Viewed Contrastive Approach for Molecular Graph Representation Learning and Classification. Mol. Inform. 2025, 44, e202400252. [Google Scholar] [CrossRef]
- Papillon, M.; Sanborn, S.; Hajij, M.; Miolane, N. Architectures of Topological Deep Learning: A Survey on Topological Neural Networks. arXiv 2023, arXiv:2304.10031. [Google Scholar]
- Kundu, S.; Zhu, R.J.; Jaiswal, A.; Beerel, P.A. Recent advances in scalable energy-efficient and trustworthy spiking neural networks: From algorithms to technology. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: New York, NY, USA, 2024; pp. 13256–13260. [Google Scholar]
- Nunes, J.D.; Carvalho, M.; Carneiro, D.; Cardoso, J.S. Spiking neural networks: A survey. IEEE Access 2022, 10, 60738–60764. [Google Scholar] [CrossRef]
- Lee, J.; Kwak, J.Y.; Keum, K.; Sik Kim, K.; Kim, I.; Lee, M.J.; Kim, Y.H.; Park, S.K. Recent Advances in Smart Tactile Sensory Systems with Brain-Inspired Neural Networks. Adv. Intell. Syst. 2024, 6, 2300631. [Google Scholar] [CrossRef]
- Dold, D.; Petersen, P.C. Causal pieces: Analysing and improving spiking neural networks piece by piece. arXiv 2025, arXiv:2504.14015. [Google Scholar] [CrossRef]
- Kheradpisheh, S.R.; Mirsadeghi, M.; Masquelier, T. BS4NN: Binarized spiking neural networks with temporal coding and learning. Neural Process. Lett. 2022, 54, 1255–1273. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Yu, C.; Gu, Z.; Li, D.; Wang, G.; Wang, A.; Li, E. Stsc-snn: Spatio-temporal synaptic connection with temporal convolution and attention for spiking neural networks. Front. Neurosci. 2022, 16, 1079357. [Google Scholar] [CrossRef]
- Ding, J.; Pan, Z.; Liu, Y.; Yu, Z.; Huang, T. Robust stable spiking neural networks. arXiv 2024, arXiv:2405.20694. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Dong, J.; Liu, Y.; Long, M.; Wang, J. Deep time series models: A comprehensive survey and benchmark. arXiv 2024, arXiv:2407.13278. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent neural networks: A comprehensive review of architectures, variants, and applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Alam, F.; Islam, M.; Deb, A.; Hossain, S.S. Comparison of deep learning models for weather forecasting in different climatic zones. J. Comput. Sci. Eng. (JCSE) 2024, 5, 12–19. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Sun, H. Tlnets: Transformation learning networks for long-range time-series prediction. arXiv 2023, arXiv:2305.15770. [Google Scholar]
- Jiang, M.; Wang, K.; Sun, Y.; Chen, W.; Xia, B.; Li, R. MLGN: Multi-scale local-global feature learning network for long-term series forecasting. Mach. Learn. Sci. Technol. 2023, 4, 045059. [Google Scholar] [CrossRef]
- Sun, G.; Qi, X.; Zhao, Q.; Wang, W.; Li, Y. SVSeq2Seq: An Efficient Computational Method for State Vectors in Sequence-to-Sequence Architecture Forecasting. Mathematics 2024, 12, 265. [Google Scholar] [CrossRef]
- Bayat, S.; Isik, G. Assessing the Efficacy of LSTM, Transformer, and RNN Architectures in Text Summarization. In Proceedings of the International Conference on Applied Engineering and Natural Sciences, Konya, Turkey, 10–12 July 2023; Volume 1, pp. 813–820. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Xie, S.; Girshick, R.; Dollar, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Los Alamitos, CA, USA, 2017; pp. 5987–5995. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Li, B.; Wang, S.; Chen, G. Wavelet Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 7, 74973–74985. [Google Scholar]
- Chen, Y.; Dai, X.; Liu, M.; Chen, D.; Lu, Y.; Liu, Z. Dynamic ReLU. In ECCV 2020: 16th European Conference; Springer: Cham, Switzerland, 2020; Volume 17, pp. 351–367. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, R.; Zhang, Y.; Li, P.; Zhang, H. Multi-scale convolutional transformer network for motor imagery classification. Sci. Rep. 2023, 15, 12935. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y.; Wang, J. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar] [CrossRef]
- Bai, Y.; Xu, Y.; Xu, K.; Li, W.; Liu, J.M. TOPS-speed complex-valued convolutional accelerator for feature extraction and inference. Nat. Commun. 2025, 16, 292. [Google Scholar] [CrossRef] [PubMed]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Mnih, V.; Heess, N.; Graves, A.; Kavukcuoglu, K. Recurrent models of visual attention. Adv. Neural Inf. Process. Syst. 2014, 27, 2204–2212. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Jiang, M.; Zeng, P.; Wang, K.; Liu, H.; Chen, W.; Liu, H. FECAM: Frequency enhanced channel attention mechanism for time series forecasting. Adv. Eng. Inform. 2023, 58, 102158. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar] [CrossRef]
- Su, J.; Ahmed, M.; Lu, Y.; Pan, S.; Bo, W.; Liu, Y. Roformer: Enhanced transformer with rotary position embedding. Neurocomputing 2024, 568, 127063. [Google Scholar] [CrossRef]
- Alayrac, J.B.; Donahue, J.; Luc, P.; Miech, A.; Barr, I.; Hasson, Y.; Lenc, K.; Mensch, A.; Millican, K.; Reynolds, M.; et al. Flamingo: A visual language model for few-shot learning. Adv. Neural Inf. Process. Syst. (NeurIPS) 2022, 35, 23716–23736. [Google Scholar]
- Liu, H.; Zaharia, M.; Abbeel, P. Ring attention with blockwise transformers for near-infinite context. arXiv 2023, arXiv:2310.01889. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Si, C.; Yu, W.; Zhou, P.; Zhou, Y.; Wang, X.; Yan, S. Inception transformer. Adv. Neural Inf. Process. Syst. 2022, 35, 23495–23509. [Google Scholar]
- Wan, C.; Yu, H.; Li, Z.; Chen, Y.; Zou, Y.; Liu, Y.; Yin, X.; Zuo, K. Swift parameter-free attention network for efficient super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 6246–6256. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance Normalization: The Missing Ingredient for Fast Stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Wu, Y.; He, K. Group normalization. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Salimans, T.; Kingma, D.P. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 901–909. [Google Scholar]
- Yao, Z.; Cao, Y.; Zheng, S.; Huang, G.; Lin, S. Cross-Iteration Batch Normalization. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: New York, NY, USA, 2021; pp. 12326–12335. [Google Scholar]
- Zhang, B.; Sennrich, R. Root mean square layer normalization. Adv. Neural Inf. Process. Syst. 2019, 32, 12381–12392. [Google Scholar]
- Wang, H.; Ma, S.; Dong, L.; Huang, S.; Zhang, D.; Wei, F. Deepnet: Scaling transformers to 1000 layers. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 6761–6774. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, X.; He, K.; LeCun, Y.; Liu, Z. Transformers without normalization. arXiv 2025, arXiv:2503.10622. [Google Scholar] [CrossRef]
- Singh, S.; Krishnan, S. Filter Response Normalization Layer: Eliminating Batch Dependence in the Training of Deep Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 11234–11243. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. Adv. Neural Inf. Process. Syst. 2016, 29, 2234–2242. [Google Scholar]
- Perez, E.; Strub, F.; De Vries, H.; Dumoulin, V.; Courville, A. Film: Visual reasoning with a general conditioning layer. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleands, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Jing, Y.; Liu, X.; Ding, Y.; Wang, X.; Ding, E.; Song, M.; Wen, S. Dynamic Instance Normalization for Arbitrary Style Transfer. In Proceedings of the AAAI Conference on Artificial Intelligence. Association for the Advancement of Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020; Volume 34, pp. 4369–4376. [Google Scholar]
- Luo, P.; Ren, J.; Peng, Z.; Zhang, R.; Li, J. Differentiable learning-to-normalize via switchable normalization. arXiv 2018, arXiv:1806.10779. [Google Scholar]
- Karras, T.; Laine, S.; Aittala, M.; Hellst, J.; Lehtinen, J.; Aila, T. Analyzing and Improving the Image Quality of StyleGAN. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 8107–8116. [Google Scholar]
- Park, T.; Liu, M.Y.; Wang, T.C.; Zhu, J.Y. Semantic Image Synthesis With Spatially-Adaptive Normalization. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: New York, NY, USA, 2019; pp. 2332–2341. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. arXiv 2018, arXiv:1802.05957. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Huang, G.; Sun, Y.; Liu, Z.; Sedra, D.; Weinberger, K.Q. Deep Networks with Stochastic Depth. In Proceedings of the Computer Vision–ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 646–661. [Google Scholar]
- Rahman, M.M.; Marculescu, R. UltraLightUNet: Rethinking U-Shaped Network with Multi-Kernel Lightweight Convolutions for Medical Image Segmentation. OpenReview 2025. Available online: https://openreview.net/forum?id=BefqqrgdZ1 (accessed on 12 August 2025).
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar] [CrossRef]
- Yu, F.; Wang, D.; Shelhamer, E.; Darrell, T. Deep layer aggregation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2403–2412. [Google Scholar]
- Gomez, A.N.; Ren, M.; Urtasun, R.; Grosse, R.B. The reversible residual network: Backpropagation without storing activations. Adv. Neural Inf. Process. Syst. 2017, 30, 2211–2221. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. SMASH: One-Shot Model Architecture Search through HyperNetworks. arXiv 2017, arXiv:1708.05344. [Google Scholar] [CrossRef]
- Cai, S.; Shu, Y.; Wang, W. Dynamic routing networks. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 3588–3597. [Google Scholar]
- Tan, M.; Le, Q.V. Mixconv: Mixed depthwise convolutional kernels. arXiv 2019, arXiv:1907.09595. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. RepVGG: Making VGG-style ConvNets Great Again. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13733–13742. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.P. Binaryconnect: Training deep neural networks with binary weights during propagations. In Proceedings of the NIPS 2015, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Denton, E.; Zaremba, W.; Bruna, J.; LeCun, Y.; Fergus, R. Exploiting linear structure within convolutional networks for efficient evaluation. In Proceedings of the NIPS 2014, Montreal, QC, Canada, 8–13 December 2014; pp. 1269–1277. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both weights and connections for efficient neural network. In Proceedings of the NIPS 2015, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Zhao, B.; Cui, Q.; Song, R.; Qiu, Y.; Liang, J. Decoupled Knowledge Distillation. arXiv 2022, arXiv:2203.08679. [Google Scholar] [CrossRef]
- Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. FitNets: Hints for thin deep nets. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ba, J.; Kiros, J.R.; Hinton, G.E. Attention Transfer. In Proceedings of the NIPS 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Lee, D.H. Overhaul Distillation: A Method for Knowledge Transfer in Neural Networks. arXiv 2015, arXiv:1506.02581. [Google Scholar]
- Cho, Y.; Min, K.h.; Lee, J.; Shin, M.; Lee, D.H.; Yang, H.J. Relational Knowledge Distillation. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019; pp. 7624–7632. [Google Scholar]
- Tian, Y.; Krishnan, D.; Isola, P. Contrastive Representation Distillation. In Proceedings of the ICLR, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Zhu, Y.; Hua, G.; Wang, L. Knowledge Transfer via Distillation of Activation Boundaries Formed by Deep Neural Classifiers. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yang, Y.; Shen, C.c.l.; Wang, Z.; Dick, A.; Hengel, A.v.d. Deep Mutual Learning. arXiv 2017, arXiv:1706.00384. [Google Scholar] [CrossRef]
- Zhang, J.W.; Li, G.; Li, Y.; Li, B.; Li, G.; Wang, X. Dynamic Knowledge Distillation. arXiv 2020, arXiv:2007.12355. [Google Scholar] [CrossRef]
- Zhang, J.W.; Li, G.; Wang, X.; Li, G. Online Knowledge Distillation from the Wisest. In Proceedings of the CVPR, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Qiao, S.; Chen, L.C.; Yuille, A. DetectoRS: Detecting Objects with Recursive Feature Pyramid and Switchable Atrous Convolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10213–10224. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8759–8768. [Google Scholar]
- Ghiasi, G.; Lin, T.Y.; Le, Q.V. NAS-FPN: Learning Scalable Feature Pyramid Architecture for Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7036–7045. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Guu, K.; Lee, K.; Tung, Z.; Pasupat, P.; Chang, M. Retrieval augmented language model pre-training. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 3929–3938. [Google Scholar]
- Borgeaud, S.; Mensch, A.; Hoffmann, J.; Cai, T.; Rutherford, E.; Millican, K.; Van Den Driessche, G.B.; Lespiau, J.B.; Damoc, B.; Clark, A.; et al. Improving language models by retrieving from trillions of tokens. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 2206–2240. [Google Scholar]
- Shi, Z. Incorporating Transformer and LSTM to Kalman Filter with EM algorithm for state estimation. arXiv 2021, arXiv:2105.00250. [Google Scholar] [CrossRef]
- Shen, S.; Chen, J.; Yu, G.; Zhai, Z.; Han, P. KalmanFormer: Using transformer to model the Kalman Gain in Kalman Filters. Front. Neurorobotics 2025, 18, 1460255. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; He, Y.; Wu, D.; Chen, H.Y.; Fan, J.; Liu, H. Transformers Simulate MLE for Sequence Generation in Bayesian Networks. arXiv 2025, arXiv:2501.02547. [Google Scholar] [CrossRef]
- Han, Y.; Guangjun, Q.; Ziyuan, L.; Yongqing, H.; Guangnan, L.; Qinglong, D. Research on fusing topological data analysis with convolutional neural network. arXiv 2024, arXiv:2407.09518. [Google Scholar]
- Nesterov, Y. A method for unconstrained convex minimization problem with the rate of convergence O(1/k2). Dokl. Ussr 1983, 269, 543–547. [Google Scholar]
- Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5-Rmsprop, Coursera: Neural Networks for Machine Learning; Technical Report; University of Toronto: Toronto, ON, Canada, 2012; Volume 6. [Google Scholar]
- Martens, J.; Grosse, R. Optimizing Neural Networks with Kronecker-Factored Approximate Curvature. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. In Proceedings of the International Conference on Machine Learning, PMLR, Addis Ababa, Ethiopia, 17–23 July 2022; pp. 2206–2240. [Google Scholar]
- Chen, C.; Wang, Y.; Zhou, X.; Zhang, G.; Zhang, J.; Tang, X.; Luo, W. A Symbolic Method for Training Neural Networks. arXiv 2023, arXiv:2310.00068. [Google Scholar]
- Liu, Z.; Wang, X.; Li, Y.; Song, X.; Xu, W. Sophia: A Scalable Stochastic Second-Order Optimizer for Language Model Pre-training. arXiv 2023, arXiv:2309.17467. [Google Scholar]
- Salimans, T.; Ho, J.; Chen, X.; Sidor, S.; Sutskever, I. Evolution Strategies as a Scalable Alternative to Reinforcement Learning. arXiv 2017, arXiv:1703.03864. [Google Scholar] [CrossRef]
- Huang, C.L.; Wang, C.J. A GA-based feature selection and parameters optimizationfor support vector machines. Expert Syst. Appl. 2006, 31, 231–240. [Google Scholar] [CrossRef]
- Pan, J.S.; Zhang, L.G.; Wang, R.B.; Snášel, V.; Chu, S.C. Gannet optimization algorithm: A new metaheuristic algorithm for solving engineering optimization problems. Math. Comput. Simul. 2022, 202, 343–373. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. arXiv 2015, arXiv:1506.01186. [Google Scholar]
- Smith, L.N.; Thomson, N.J. Super-Convergence: Very Fast Training of Neural Networks Using Standard Learning Rate Schedules. arXiv 2017, arXiv:1708.07120. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30, p. 3. [Google Scholar]
- Farid, A.; Hussain, F.; Khan, K.; Shahzad, M.; Khan, U.; Mahmood, Z. A fast and accurate real-time vehicle detection method using deep learning for unconstrained environments. Appl. Sci. 2023, 13, 3059. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A self-gated activation function. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Shazeer, N. GLU Variants Improve Transformer. arXiv 2020, arXiv:2002.05202. [Google Scholar] [CrossRef]
- Misra, D. Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Shakarami, A.; Yeganeh, Y.; Farshad, A.; Nicolè, L.; Ghidoni, S.; Navab, N. VeLU: Variance-enhanced Learning Unit for Deep Neural Networks. arXiv 2025, arXiv:2504.15051. [Google Scholar]
- Qiu, S.; Xu, X.; Cai, B. FReLU: Flexible Rectified Linear Units for Improving Convolutional Neural Networks. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1223–1228. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.D.N.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved Training of Wasserstein GANs. arXiv 2017, arXiv:1704.00028. [Google Scholar] [CrossRef]
- Bottou, L.; LeCun, Y. Early Stopping—But When? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Larochelle, H.; Bengio, Y. Snapshot Ensembles: Train 1, Get M for Free. arXiv 2007, arXiv:1704.00109. [Google Scholar]
- Izmailov, P.; Podoprikhin, D.; Garipov, T.; Vetrov, D.; Wilson, A.G. Averaging Weights Leads to Wider Optima and Better Generalization. arXiv 2018, arXiv:1803.05407. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Monographs on Statistics & Applied Probability; Chapman & Hall/CRC: Boca Raton, FL, USA, 1994. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar] [CrossRef]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient Object Localization Using Convolutional Networks. In Proceedings of the CVPR, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wan, L.; Zeiler, M.D.; Zhang, S.; LeCun, Y.; Fergus, R. Regularization of Neural Networks using DropConnect. In Proceedings of the ICML, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Krueger, D.; Zoneout, T.C. Zoneout: Regularizing RNNs by Randomly Preserving Hidden Units. In Proceedings of the ICLR, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. In Proceedings of the NeurIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Welling, M. Variational Dropout and the Local Reparameterization Trick. In Proceedings of the NeurIPS, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gal, Y.; Hron, J.; Kendall, A. Concrete Dropout. In Proceedings of the NeurIPS 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Goodfellow, I.; Warde-Farley, D.; Mirza, M.; Courville, A.; Bengio, Y. Maxout networks. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 1319–1327. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. AutoAugment: Learning Augmentation Strategies from Data. arXiv 2018, arXiv:1805.09501. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.; Chun, S.; Choe, J.; Yoo, Y. Cutmix: Regularization strategy to train strong classifiers with localizable features. arXiv 2019, arXiv:1905.04899. [Google Scholar] [CrossRef]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive mixtures of local experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Shazeer, N.; Mirhoseini, A.; Maziarz, K.; Davis, A.; Le, Q.; Hinton, G.; Dean, J. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv 2017, arXiv:1701.06538. [Google Scholar]
- Lepikhin, D.; Lee, H.; Xu, Y.; Chen, D.; Firat, O.; Huang, Y.; Krikun, M.; Shazeer, N.; Chen, Z. Gshard: Scaling giant models with conditional computation and automatic sharding. arXiv 2020, arXiv:2006.16668. [Google Scholar] [CrossRef]
- Lewis, M.; Bhosale, S.; Dettmers, T.; Goyal, N.; Zettlemoyer, L. Base layers: Simplifying training of large, sparse models. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 6265–6274. [Google Scholar]
- Ma, J.; Zhao, Z.; Yi, X.; Chen, J.; Hong, L.; Chi, E.H. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Munich, Germany, 8–14 September 2018; pp. 1930–1939. [Google Scholar] [CrossRef]
- Mustafa, B.; Riquelme, C.; Puigcerver, J.; Jenatton, R.; Houlsby, N. Multimodal contrastive learning with limoe: The language-image mixture of experts. Adv. Neural Inf. Process. Syst. 2022, 35, 9564–9576. [Google Scholar]
- Zhang, X.; Shen, Y.; Huang, Z.; Zhou, J.; Rong, W.; Xiong, Z. Mixture of attention heads: Selecting attention heads per token. arXiv 2022, arXiv:2210.05144. [Google Scholar] [CrossRef]
- Reisser, M.; Louizos, C.; Gavves, E.; Welling, M. Federated mixture of experts. arXiv 2021, arXiv:2107.06724. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022; Volume 1, p. 3. [Google Scholar]
- Houlsby, N.; Giurgiu, A.; Jastrzebski, S.; Morrone, B.; De Laroussilhe, Q.; Gesmundo, A.; Attariyan, M.; Gelly, S. Parameter-efficient transfer learning for NLP. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2790–2799. [Google Scholar]
- Dao, T.; Fu, D.; Ermon, S.; Rudra, A.; Ré, C. Flashattention: Fast and memory-efficient exact attention with io-awareness. Adv. Neural Inf. Process. Syst. 2022, 35, 16344–16359. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Gretton, A.; Borgwardt, K.; Rasch, M.; Schölkopf, B.; Smola, A. A kernel method for the two-sample-problem. Adv. Neural Inf. Process. Syst. 2006, 19, 513–520. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
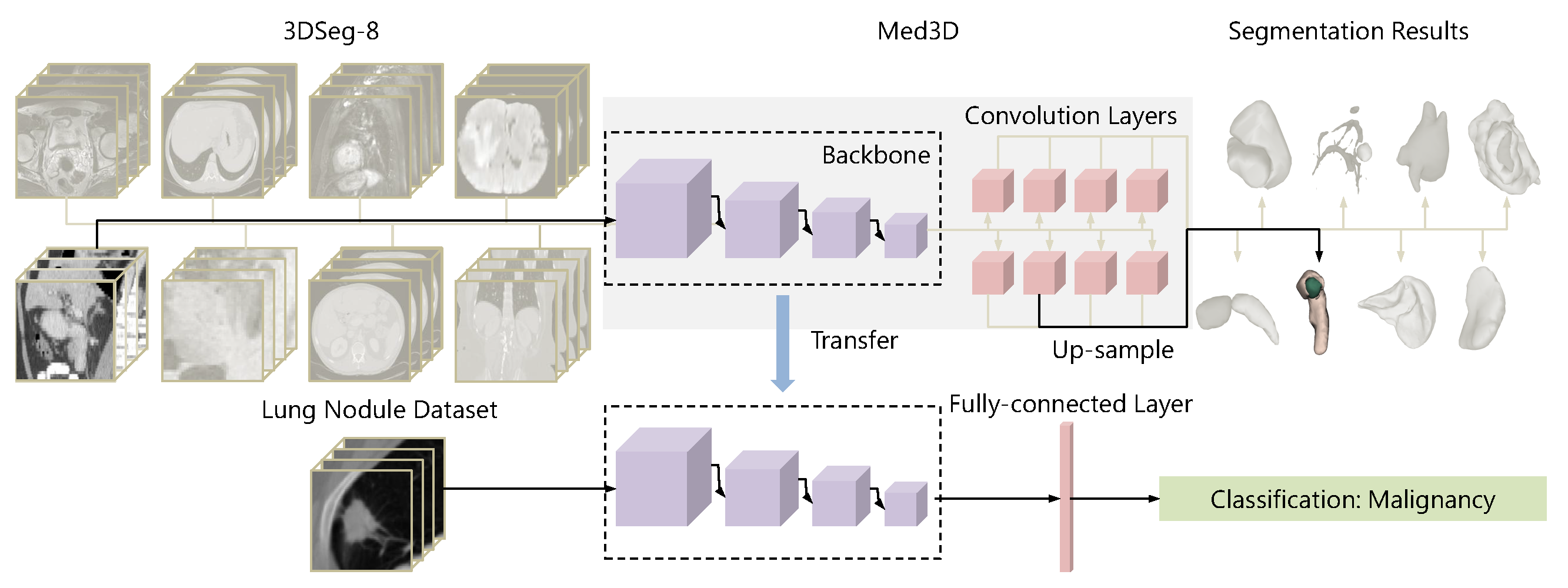
- Chen, S.; Ma, K.; Zheng, Y. Med3d: Transfer learning for 3d medical image analysis. arXiv 2019, arXiv:1904.00625. [Google Scholar] [CrossRef]
- Bargshady, G. Inception-CycleGAN: Cross-modal transfer learning for COVID-19 diagnosis. Expert Syst. Appl. 2022, 201, 117092. [Google Scholar]
- Kathamuthu, N.D.; Subramaniam, S.; Le, Q.H.; Muthusamy, S.; Panchal, H.; Sundararajan, S.C.M.; Alrubaie, A.J.; Zahra, M.M.A. A deep transfer learning-based convolution neural network model for COVID-19 detection using computed tomography scan images for medical applications. Adv. Eng. Softw. 2023, 175, 103317. [Google Scholar] [CrossRef]
- Michau, G.; Fink, O. Adversarial transfer learning for zero-shot anomaly detection in industrial systems. IEEE Trans. Ind. Inform. 2021, 18, 5388–5397. [Google Scholar]
- Zhang, L.; Wang, H.; Li, Y. Blockchain-based federated learning for secure multi-plant fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 231, 108965. [Google Scholar]
- Chen, J.; Sun, W.; Li, X.; Hou, B. Domain adaptive R-CNN for cross-domain aircraft detection in satellite imagery. ISPRS J. Photogramm. Remote. Sens. 2022, 183, 90–101. [Google Scholar]
- Cao, J.; Yan, M.; Jia, Y.; Tian, X.; Zhang, Z. Application of a modified Inception-v3 model in the dynasty-based classification of ancient murals. EURASIP J. Adv. Signal Process. 2021, 2021, 1–25. [Google Scholar] [CrossRef]
- Cao, H.; Gu, H.; Guo, X.; Rosenbaum, M. Risk of Transfer Learning and its Applications in Finance. arXiv 2023, arXiv:2311.03283. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, Z.; Póczos, B.; Carbonell, J. Characterizing and avoiding negative transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11293–11302. [Google Scholar]


| Model | Improvement | Application Scenarios |
|---|---|---|
| Transformer | Self-attention mechanism enabling parallel sequence processing, replacing traditional RNNs | Natural Language Processing (NLP), machine translation, image segmentation |
| BERT | Bidirectional Transformer with masked language modeling (MLM) | Text classification, question answering |
| GPT Series | Autoregressive generation with unidirectional Transformer | Text generation, dialogue systems |
| T5 | Unified text-to-text Transformer framework | Multi-task learning, text generation |
| Longformer | Sparse attention (local sliding window + global attention), reduces complexity to O(n) | Long-text summarization, document understanding |
| Reformer | Locality-Sensitive Hashing (LSH) for key grouping, reversible residuals for memory efficiency | Genome sequence analysis, music generation |
| Transformer-XL | Recurrence mechanism (caching previous segments) with relative positional encoding | Language modeling, dialogue systems |
| Linformer | Low-rank projection to compress key value matrices (O(n) complexity) | Real-time translation, large-scale text processing |
| Performer | FAVOR+ (Fast Attention Via Orthogonal Random features) for linear time attention | Protein sequence modeling, image generation |
| BioBERT | Domain-specific pretraining on biomedical/scientific corpora | Medical literature mining, chemical entity recognition |
| Vision Transformer (ViT) | Image-patching strategy for standard Transformer adaptation | Image classification, object detection |
| Switch Transformer | Mixture-of-Experts (MoE) with dynamic token routing (trillion-scale parameters) | Large-scale pretraining |
| Deformable DETR | Deformable attention with dynamic receptive fields for faster convergence | Computer vision (e.g., COCO dataset detection) |
| Informer | ProbSparse self-attention and distillation for O(L log L) complexity | Long-sequence forecasting (energy consumption, weather) |
| AutoFormer | Autocorrelation mechanism capturing periodic dependencies | Energy demand forecasting |
| Non-stationary Transformer | Hybrid attention (stationary/ non-stationary components) | Non-stationary time series prediction |
| Crossformer | Hierarchical cross-scale attention for multivariate interactions | Traffic flow prediction |
| iTransformer | Inverted dimension modeling with variable-specific encoding | Multivariate forecasting |
| ETSformer | Integration of Exponential Smoothing (ETS) decomposition with frequency attention | Medical time series analysis |
| ShapeFormer | Morphological attention for local waveform patterns | Biosignal classification |
| Section | Variable in Appearance Order | Explanation |
|---|---|---|
| Section 2.6 | The input vector. | |
| The weighted vector/ matrix. | ||
| b | The bias. | |
| The activation function(such as Sigmoid, ReLU). | ||
| y | The output. | |
| The value function. | ||
| z | The feature representation. | |
| The decoder and encoder. | ||
| O | The output feature map/ layer. | |
| F | The residual function in ResNet. | |
| The constant mapping. | ||
| S | The output value of the hidden layer in RNN. | |
| U | The weight matrix from the input layer to the hidden layer. | |
| V | The weight matrix from the hidden layer to the output layer. | |
| The cell state. | ||
| , | The input gate, output gate, and forget gate. | |
| The computation of activations in LSTM. | ||
| The node feature matrix in GNN. | ||
| The normalized adjacency matrix. | ||
| D | The degree matrix. | |
| The dataset. | ||
| The Kullback–Leibler (KL) divergence. | ||
| , , , and | The total loss, partial differential equation loss, iniitial condition loss, and boundary condition loss in PINNs. | |
| The weights for the adjustment in PINNs. | ||
| The hidden state in LNN. | ||
| The input in LNN. | ||
| Section 2.7 | D and G | The discriminator and generator. |
| The logarithmic loss function. | ||
| The set of visible units in the Boltzmann Machine. | ||
| The set of hidden units in the Boltzmann Machine. | ||
| The energy of the state in the Boltzmann Machine. | ||
| The model parameters. | ||
| The partition function. | ||
| The logistic function. | ||
| A standard Wiener process. | ||
| The weighting function. | ||
| The score function. | ||
| Section 2.8 | Query, Key, and Value. | |
| The dimension of the key vectors. | ||
| Section 2.9 | and | The components in RWKV. |
| The word at t. | ||
| Section 2.11 | The state transition density function. | |
| s and | The current state and the new state. | |
| a | The action. | |
| U | The cumulated future reward. | |
| The reward at time t. |
| Function | Equation (Forward) | Range | VD | Cost | Best Practice/Pairing |
|---|---|---|---|---|---|
| Classic (‘80-’00) | |||||
| Sigmoid | (0,1) | H | low | Prob. output, shallow nets | |
| Tanh | (−1,1) | H | low | RNN pre-2010 | |
| Softmax | (0,1) | – | med | Final layer, multi-class | |
| Non-saturating/adaptive (2010s) | |||||
| ReLU | [0,∞) | L | very low | Default CNN/FC | |
| L-ReLU | (−∞,∞) | L | very low | Sparse/audio nets | |
| ELU | (−,∞) | L | low | Smooth zero-centre | |
| Swish | or learn | (−∞,∞) | L | low | Deep CNN, NAS-found |
| GELU | (−∞,∞) | L | med | Transformers, BERT, GPT | |
| Dynamic/conditional (2020s) | |||||
| SwiGLU | (−∞,∞) | L | med–high | FFN inside Transformers | |
| D-ReLU | , k = input cond. | [0,∞) | L | med | Mobile CNN, few-shot |
| VeLU | (−,) | L | med | Variance-sensitive tasks | |
| FReLU | , = spatial context | [0,∞) | L | low | Object detection, Seg |
| Mish | (−∞,∞) | L | low | General-purpose CNN | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Wang, Y.; Watada, J. A Modular Perspective on the Evolution of Deep Learning: Paradigm Shifts and Contributions to AI. Appl. Sci. 2025, 15, 10539. https://doi.org/10.3390/app151910539
Wei Y, Wang Y, Watada J. A Modular Perspective on the Evolution of Deep Learning: Paradigm Shifts and Contributions to AI. Applied Sciences. 2025; 15(19):10539. https://doi.org/10.3390/app151910539
Chicago/Turabian StyleWei, Yicheng, Yifu Wang, and Junzo Watada. 2025. "A Modular Perspective on the Evolution of Deep Learning: Paradigm Shifts and Contributions to AI" Applied Sciences 15, no. 19: 10539. https://doi.org/10.3390/app151910539
APA StyleWei, Y., Wang, Y., & Watada, J. (2025). A Modular Perspective on the Evolution of Deep Learning: Paradigm Shifts and Contributions to AI. Applied Sciences, 15(19), 10539. https://doi.org/10.3390/app151910539









