Abstract
Understanding and interpreting human emotions through neurophysiological signals has become a central goal in affective computing. This paper presents a focused survey of recent advances in emotion recognition using tensor factorization techniques specifically applied to functional Near-Infrared Spectroscopy (fNIRS) data. We examine how tensor-based frameworks have been leveraged to capture the temporal, spatial, and spectral characteristics of fNIRS brain signals, enabling effective dimensionality reduction and latent pattern extraction. Focusing on third-order tensor constructions (trials × channels × time), we compare the use of Canonical Polyadic (CP) and Tucker decompositions in isolating components representative of emotional states. The review further evaluates the performance of extracted features when classified by conventional machine learning models such as Random Forests and Support Vector Machines. Emphasis is placed on comparative accuracy, interpretability, and the advantages of tensor methods over traditional approaches for distinguishing arousal and valence levels. We conclude by discussing the relevance of these methods for the development of real-time, explainable, emotion-aware systems in wearable neurotechnology, with a particular focus on medical applications such as mental health monitoring, early diagnosis of affective disorders, and personalized neurorehabilitation.
1. Introduction
Affective computing is an interdisciplinary field, which seeks to enable machines to recognize, interpret, and respond to human emotions and increasingly relies on neurophysiological data to gain insights into internal affective states [1,2,3]. Among the non-invasive neuroimaging modalities, functional Near-Infrared Spectroscopy (fNIRS) has garnered attention due to its portability, low cost, and capacity to monitor cortical hemodynamic responses with reasonable spatial and temporal resolution [4,5,6]. These advantages make fNIRS a suitable tool for emotion recognition tasks in both laboratory and real-world settings [4,5].
Emotions are often modeled along continuous dimensions such as valence (pleasantness) and arousal (intensity), rather than discrete categories [7,8]. Accurately decoding these dimensions from brain signals remains a complex task, particularly given the high-dimensional and multi-way nature of fNIRS data, which typically spans temporal, spatial (channel), and experimental (trial or subject) dimensions [9,10]. Traditional machine learning approaches often flatten such data, potentially discarding valuable structural information and leading to suboptimal performance.
The novelty and contribution of our article lies in the use of tensor-based approaches, which offer a powerful framework for processing high-dimensional data, which is common in affective computing and medical applications (e.g., electroencephalogram (EEG), functional Magnetic Resonance Imaging (fMRI), video, and multimodal signals). These methods preserve the inherent structure of data across domains (such as time, high-dimensional space, and frequency), enabling more accurate and interpretable feature extraction. In affective computing, tensor decompositions help capture complex emotional patterns from simultaneous multimodal inputs such as facial expressions, speech, and physiological signals. In medical applications, they enable more efficient analysis of high-dimensional datasets in disease diagnosis, brain imaging, and patient monitoring. As a result, tensor-based models contribute to improved efficiency, reliability, and insight in emotion recognition and medical analytics, providing opportunities to develop new, more effective approaches in early diagnosis and monitoring of behaviors and their disorders, both related to disease processes and natural aging processes [11].
The gaps and challenges observed so far demonstrate that, despite their advantages, tensor-based approaches face challenges related to computational complexity, especially when dealing with large-scale or real-time data. Many methods are not robust to noise and missing data, which are common in medical and affective datasets. There is also a gap in standardization, as different studies use different tensor models and preprocessing steps, making comparison and reproducibility of results difficult. Integration with deep learning remains limited, and few frameworks effectively combine tensor structures and neural networks. Furthermore, most existing models struggle to generalize between subjects or contexts, highlighting the need for more adaptive and personalized tensor-based solutions [12].
In order to address these limitations, this study adopts a tensor factorization framework to preserve and exploit the intrinsic multi-dimensional structure of fNIRS signals [13]. Tensor decomposition techniques such as Tucker and CANDECOMP/PARAFAC (CP) allow for unsupervised extraction of low-dimensional components that capture latent spatial–temporal–emotional dynamics [14]. These compressed representations can subsequently be used as input features for supervised learning models aimed at classifying affective states.
The structure of this paper is as follows. In Section 2, we explain in detail the materials and methods selection. Then, in Section 3, we describe the fNIRS technology in the context of affective computing. Section 4 follows, outlining traditional approaches for fNIRS signal analysis. The specifics of tensor-based approaches in this regard are presented in Section 5. Section 6 constitutes a comprehensive analysis of related work, providing a review of state-of-the-art approaches for tensor-based fNIRS data analysis. Finally, Section 7 contains a thorough discussion of the findings, as well as the most relevant conclusions.
As far as tensor-based decomposition is concerned, we decided to use this approach due to the fact that this typically allows reducing dimensionality/compressing models or revealing latent factors in multi-way data. As such, tensor-based decomposition is applicable with other machine learning (ML)/deep learning (DL) models affecting their performance due to compressing layers or speeding up inference, e.g., for convolutional neural network (CNN) models, or reducing recurrent weights for RNN models. Since the main goal is to apply tensor-based decomposition to emotion recognition, we focused in this paper rather on presenting the whole decomposition process rather than performing an in-depth comparison of how various models, like CNN or RNN, work in themselves.
2. Materials and Methods of the Review
A search of leading bibliometric databases using the specified keywords “tensor” and “affective computing” (more specific searches did not yield results) using the partial PRISMA 2020 paradigm yielded the following results: Scopus: 10 articles from 2016–2025, WoS: 21 articles from 2016–2025, PubMed: 0, DBLP: 0. Inclusion criteria included original articles, conference papers, and reviews published in English since 2016. Exclusion criteria included publication languages other than English, publications older than 2016, and publication types such as letters to the editor or editorials. The resulting set of publications was further refined by manually re-screening the articles and removing irrelevant publications and duplicates to establish the final sample. A total of 21 publications from 2016 to 2025 were included in the review. Ten selected PRISMA 2020 (PRISMA 2020 checklist, Supplementary Materials) items were used in the search: Item 3 (rationale), Item 4 (objectives), Item 5 (eligibility criteria), Item 6 (information sources), Item 7 (search strategy), Item 8 (selection process), Item 9 (data collection process), Item 13a (synthesis methods), Item 20b (synthesis results), and Item 23a (discussion). Only one Sustainable Development Goal was identified: Good Health and Well-Being. No lead authors or affiliations were observed. The National Natural Science Foundation of China funded the largest number of studies (3). A summary of the review findings is presented in Figure 1, Figure 2, Figure 3 and Figure 4 below.
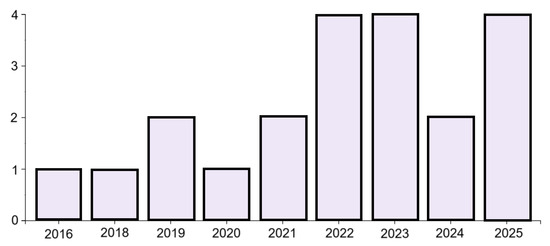
Figure 1.
Publications by year.
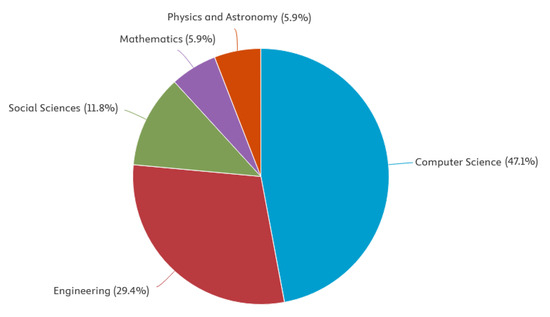
Figure 2.
Publications by area.
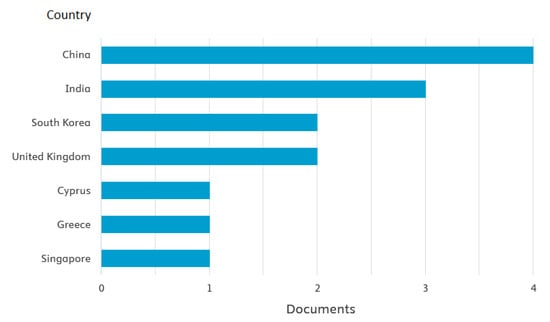
Figure 3.
Publications by country.
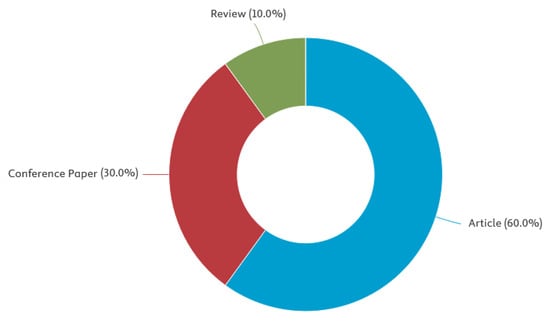
Figure 4.
Publications by type.
3. Functional Near-Infrared Spectroscopy (fNIRS)
Functional Near-Infrared Spectroscopy (fNIRS) is a non-invasive neuroimaging technique that measures hemodynamic (blood flow) responses associated with neural activity [10,15]. By detecting changes in oxygenated and deoxygenated hemoglobin concentrations using near-infrared light, fNIRS is able to capture cortical brain function [16,17], particularly in the prefrontal cortex [18]. Its relative portability, cost-effectiveness, and better tolerance to motion artifacts make it suitable for wearable applications [19], as opposed to other techniques, e.g., fMRI [20].
In the context of affective computing, fNIRS has become recognized for its ability to capture slow-varying hemodynamic signals [21,22], often linked to emotional processing. Studies have demonstrated correlations between fNIRS signals and affective states [23], particularly within the dimensions of arousal and valence [24]. The spatial resolution of the fNIRS enables the location of brain regions involved in emotion regulation, complementing electrophysiological methods [25].
fNIRS operates with a shallow penetration depth [26], restricting the measurements to cortical surfaces. Moreover, it has relatively low temporal resolution [27]. These constraints reduce its applicability to tasks that require rapid detection of transient emotional states. As a result, fNIRS is often combined with EEG [22,27] due to their complementary spatial and temporal resolution characteristics.
fNIRS in Affective Computing
fNIRS is becoming increasingly prevalent in the field of affective computing [22,28,29], enabling the monitoring and interpretation of human emotions by measuring brain activity, particularly within the prefrontal cortex (PFC).
The key fields of interest in Affective Computing using fNIRS are (see: Figure 5):
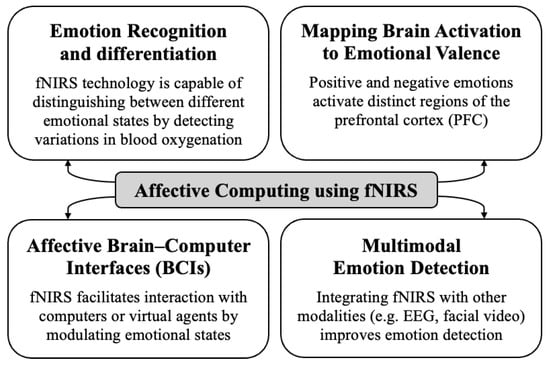
Figure 5.
Key domains of affective computing with the implementation of fNIRS brain signals.
- Emotion Recognition and Differentiation [30]:fNIRS technology is capable of distinguishing between different emotional states by detecting variations in blood oxygenation within the brain. Research has shown that fNIRS can differentiate not only between positive and negative emotions but also between various forms of positive emotions, such as joy, gratitude, and serenity. These emotions exhibit different patterns of hemodynamic response in the frontal cortex. By applying machine learning to these signals, researchers can effectively classify clusters of emotions with significant accuracy, thereby advancing the development of sophisticated emotion recognition systems.
- Mapping Brain Activation to Emotional Valence [24]:Research using fNIRS indicates that positive and negative emotions activate distinct regions of the prefrontal cortex (PFC). Positive emotions are associated with greater activation in the bilateral dorsolateral prefrontal cortex (DLPFC) and the orbitofrontal cortex (OFC), while negative emotions are associated with increased activation in the medial prefrontal cortex (mPFC). These findings support the concept of lateralized emotional processing in the brain and confirm fNIRS as a valuable tool to objectively capture neural activity related to emotions.
- Affective Brain–Computer Interfaces (BCIs) [31]:fNIRS facilitates the development of affective BCIs, allowing users to interact with computers or virtual agents by modulating their emotional states. For example, asymmetric activity in DLPFC, measured by fNIRS, has been used to control the facial expressions of virtual agents, allowing users to engage in affective communication through neurofeedback. This approach allows for the volitional activation of specific brain regions associated with emotion, which are typically not within conscious control.
- Multimodal Emotion Detection [22]:Integrating fNIRS with other modalities, such as EEG and facial video analysis, improves the accuracy and robustness of emotion detection systems. fNIRS offers an “internal” perspective on emotion generation, complementing external observations, like facial expressions, and electrophysiological signals from EEG.
4. Traditional Approach in Affective Computing
Traditional methods for analyzing fNIRS data face several fundamental limitations that hinder their ability to capture the full complexity of brain activity signals [32]. The vectorization method is used prior to the flattening of the data, which increases the dimensionality of the feature space, potentially leading to a situation where the number of features greatly exceeds the number of observations, resulting in overfitting and poor generalization. Furthermore, vectorized approaches struggle to account for the natural correlation structures that exist between channels, time points, and wavelengths in the fNIRS data, severely limiting their ability to extract meaningful patterns from the neural signal [33].
The widely used grand averaging method in fNIRS analysis aggregates oxygenated hemoglobin data over specified time windows and multiple channels within a given region of interest [34]. While this approach simplifies the data, it risks a significant loss of crucial temporal and spatial information, effectively reducing the data dimensionality and discarding potentially valuable patterns. Such simplification may obscure subtle but significant brain activity patterns associated with emotional states [35].
While deep learning techniques have shown advancements over traditional machine learning methods, they still grapple with effectively managing the multidimensional nature of fNIRS data. For example, in grip force tasks in the following study [36], LSTM-based deep learning methods achieved an accuracy of 82.86%, compared to 71.70% for classic machine learning approaches using extracted features. However, these deep learning methods often require vectorizing the input data, which disrupts the natural structure of the fNIRS signals and compromises the integrity of spatial–temporal relationships within the data set [37].
Machine learning and deep learning excel in processing large volumes of fNIRS data and uncovering intricate patterns that traditional techniques often miss. However, their effectiveness depends on having extensive training datasets, and they may be susceptible to overfitting [38].
4.1. Dimensionality Reduction Techniques in Neuroimaging
Neuroimaging data, obtained by methods such as fNIRS, EEG, and positron emission tomography (PET), are characterized by their extreme high dimensionality and relatively limited sample sizes. This imbalance presents significant challenges for data analysis, including the risk of overfitting, increased computational demands, and challenges in interpretation. Dimensionality reduction (DR) techniques are crucial in the field of neuroimaging. These methods facilitate the extraction of informative, low-dimensional representations from complex brain data, while preserving essential information pertinent to neuroscientific and clinical inquiries. According to [13], dimensionality reduction methods for brain imaging data can be broadly categorized into two main classes:
- feature selection;
- feature extraction.
Feature selection methods are designed to identify a subset of the most relevant features from the original dataset, while discarding redundant or irrelevant variables. In contrast, feature extraction methods transform the original data into a new, lower-dimensional feature space, often through mathematical mappings (e.g., PCA, ICA), where the new features retain the most informative characteristics of the original data.
4.2. Motivation for Tensor Factorization Techniques
Tensor factorization provides a framework for analyzing multidimensional data while preserving its structure. Methods like Tucker and CP decompose tensors into low-rank components that maintain interdependencies across modes (e.g., time, channel, subject). This approach facilitates the extraction of compact and interpretable latent features, which can enhance the sensitivity of models to emotion-related neural dynamics.
Furthermore, tensor methods enable dimensionality reduction in a way that aligns with the natural organization of the data, reducing the risk of overfitting while preserving relevant variance [39]. This is especially valuable in fNIRS research, where datasets often have high dimensionality but limited sample sizes [35]. By uncovering the underlying structure and removing redundancy, tensor factorization can reveal the core components of emotional responses, which are essential for building robust and generalizable classifiers.
The use of tensor factorization is motivated not only by its mathematical elegance and efficiency, but also by its ability to bridge the gap between complex neurophysiological signals and meaningful psychological states. This positions it as a powerful tool in the advancement of affective computing systems based on neuroimaging data.
Recent literature supports tensor decomposition, especially Tucker and CP models, as a powerful alternative to traditional preprocessing of brain signals, such as EEG and fNIRS, among others. These methods preserve spatio-temporal structure and enable interpretable, multimodal affective analysis. When combined with EEG or integrated into BCI systems, tensor methods significantly improve emotion classification accuracy, interpretability, and generalizability, even under small-sample constraints. Some research indicates that this approach can be successfully applied in affective computing [40,41].
4.3. Tensor Decomposition
Tensor decomposition serves as a fundamental framework in the analysis of multidimensional data, facilitating the extraction of latent factors and the reduction in dimensionality in high-order datasets [42]. Among the various decomposition methods, the Parallel Factor Analysis (CANDECOMP/PARAFAC or CP) and the Tucker decomposition stand out due to their mathematical rigor and broad applicability across diverse fields, including machine learning, signal processing, and psychometrics [43].
Tensor decomposition has emerged as a robust analytical technique for fNIRS data, effectively addressing several limitations associated with traditional signal processing methods. This is because fNIRS signals are inherently multidimensional, involving temporal, spatial, and often subject- or condition-related dimensions [44]. Conventional analysis techniques, such as grand averaging, tend to collapse these dimensions, which can obscure meaningful patterns and interactions present in the data. In contrast, tensor decomposition preserves the multidimensional structure, facilitating a more nuanced and comprehensive analysis [35].
4.3.1. Canonical-Polyadic Decomposition
The CP decomposition approximates a given tensor as a sum of a finite number of rank one tensors. Data sparsity or structural patterns can substantially lower the complexity of the computational cost of this method [39,43]. The CP decomposition is valued for its uniqueness properties under some conditions and its interpretability, as each component corresponds to a rank-one structure in the original data. In our study, a 3D tensor composed of (trials × channels × time) is used.
The CP decomposition approximates a 3D tensor (1):
where , , , , and the operators: ‘∘’—the outer (tensor) product of vectors; ‘·’—scalar multiplication.
The minimal R is the tensor rank.
4.3.2. Tucker Decomposition
The Tucker decomposition generalizes the concept of tensor factorization by introducing a core tensor that encapsulates interactions among components in different modes [45]. For the same third-order tensor , the Tucker model is expressed as (2):
where (core tensor) and , , (factor matrices). By the 1-mode, 2-mode and 3-mode products are denoted.
The core tensor captures multi-way interactions, which enables dimensionality reduction and hierarchical feature extraction.
5. Tensor-Based Approaches in Medical Applications
In medicine, tensor-based approaches have emerged as powerful tools for analyzing complex and multidimensional biomedical data, particularly in the processing of brain and various physiological signals [46,47]. Traditional matrix-based methods struggle to capture the intricate spatial, temporal, and spectral relationships present in these data, which are critical for accurate diagnosis and treatment planning; however, tensor decomposition methods have demonstrated robust performance in feature extraction, denoising, and pattern recognition, enabling more precise identification of neurological conditions, such as Alzheimer’s disease, Parkinson’s disease, stroke, and ADHD [47,48,49]. Moreover, by integrating datasets from multiple modalities, including EEG, imaging, and electronic health records, tensor-based techniques offer deeper insights into disease mechanisms and patient states [50]. Coupled with advances in affective computing, these methods also facilitate emotion recognition and mental health monitoring, supporting personalized care and enhancing the clinician’s ability to interpret complex neurophysiological phenomena [47,51].
Tensor-Based Approaches Using fNIRS Signals
fNIRS, as also mentioned above, provides a non-invasive means of monitoring brain activity by measuring hemodynamic responses linked to neural function [52,53,54]. The multidimensional nature of fNIRS data—encompassing spatial (channels), temporal (time points), and spectral (wavelengths) components—poses significant challenges for conventional analytical techniques, which often rely on matrix-based representations and thus may overlook crucial higher-order relationships [55]. Tensor-based approaches, on the other hand, have emerged as powerful tools for capturing and analyzing such complex, multi-way dependencies within fNIRS data [35,50].
By leveraging multi-dimensional tensor representations of fNIRS signals, researchers can extract latent patterns associated with cognitive and emotional states [51]. These insights inform the development of explainable, real-time systems for both clinical and human–computer interaction contexts.
Through tensor decomposition and related methods, researchers can effectively disentangle overlapping sources of physiological and non-physiological signals, enhance noise reduction, and extract informative features relevant to diverse clinical tasks [46,51]. For instance, tensor factorization enables the separation of hemodynamic patterns across different brain regions, time scales, and stimulus conditions, improving sensitivity in detecting neural correlates of disorders such as autism spectrum disorder, depression, stroke, and traumatic brain injury [35,56,57]. This facilitates the identification of subtle biomarkers and supports the tracking of disease progression or recovery over time.
The integration of tensor-based analysis with multimodal datasets, such as combining fNIRS with EEG or behavioral metrics, further amplifies the richness of information that can be gleaned from patient studies. By fusing data across multiple measurement types, tensor methods reveal latent structures and shared dynamics that might otherwise go unnoticed, offering deeper insights into complex brain–behavior interactions and enabling more accurate patient stratification and personalized intervention strategies.
In the aforementioned domain of affective computing, tensor-based techniques have proven particularly effective for decoding emotional and cognitive states from fNIRS signals [46,50,51]. By extracting multidimensional patterns associated with affective processes, these approaches support robust emotion recognition, cognitive load assessment, and continuous mental health monitoring, with promising implications for both clinical diagnostics and adaptive human–computer interfaces [51,58].
In summary, the application of tensor-based approaches to fNIRS data is ushering in a new era of multidimensional biomedical signal analysis [46]. These methods enhance our ability to interpret, diagnose, and intervene in neurophysiological and affective processes, ultimately contributing to more precise, personalized, and effective medical care.
6. Related Work
As the main scope of this paper is, on one hand, to present fNIRS data and specifically discuss its complexity and multidimensionality, and on the other hand, to focus on using tensor-based decomposition to widen applicability of various ML/DL based approaches to their analysis, our related work analysis will include mostly these papers which fall into either or both of these areas.
The fNIRS technology’s suitability for measuring brain regions involved in emotion functions makes it particularly valuable for investigating the neural correlates of emotional states [29]. The typical workflow of fNIRS-based emotion recognition begins with signal acquisition, followed by preprocessing to remove noise and artifacts [59]. The paper in [30] has shown that oxygenated hemoglobin (HbO) data generally provides better emotion classification results compared to deoxygenated hemoglobin (HbR) data.
Feature engineering remains pivotal for capturing emotion-related hemodynamic patterns. Temporal features like signal mean and slope are widely used, while frequency-domain analysis via Fast Fourier Transform (FFT) reveals oscillatory signatures tied to valence and arousal indicators [60]. Feature extraction is a critical step in fNIRS-based emotion recognition. Commonly used statistical features include the mean, variance, kurtosis, peak, and slope of the fNIRS signal. The signal mean has been widely used and has been shown to be particularly effective for emotion classification [30]. These features are often inputted into machine learning models or, more recently, deep learning architectures for further processing [59].
fNIRS generates rich spatio-temporal data that naturally form a high-order tensor, encompassing dimensions such as time, channels, and trials or subjects (Figure 6) [50]. Traditional machine learning pipelines often preprocess this data by collapsing it into two-dimensional matrices through vectorization or averaging. Although this simplifies the analysis, it disregards the inherent multi-way structure of the signal and may obscure subtle yet informative patterns distributed across multiple dimensions.
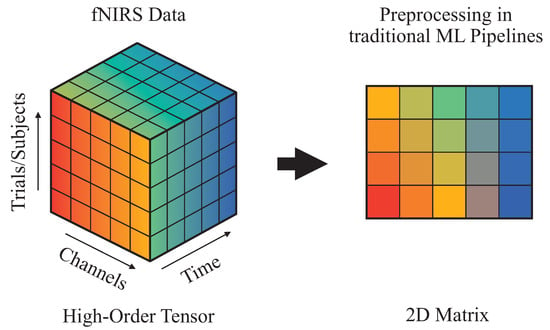
Figure 6.
Dimensionality deduction of fNIRS signals in traditional pipelines.
Brain signals data, such as EEG and fNIRS, are inherently multidimensional, capturing variation across time, space (channels), and conditions (trials/subjects). As mentioned above, traditional analysis methods flatten this data, often losing the inter-modal correlations that are crucial for decoding affective states. Tensor decomposition, by contrast, allows the preservation and modeling of this high-order structure. Techniques like CP and Tucker decomposition have been increasingly adopted to capture latent, interpretable components in brain signals.
Despite the growing use of fNIRS in neuroscience, analytical approaches—particularly the widely used grand averaging method—remain limited, often collapsing spatial and temporal dimensions and risking loss of critical signal information. In contrast, tensor decomposition methods, such as CP and Tucker, preserve multi-dimensional structure and extract latent patterns without prior assumptions about the hemodynamic response. Applying these methods to infant fNIRS datasets, researchers found that tensor decomposition not only replicated traditional findings but also revealed additional, previously undetected patterns. These results underscore its value as a robust and interpretable alternative for fNIRS signal analysis. Code is openly available on GitHub, and Bayesian inference was used to explore interaction effects. Chan et al. (2023) [35] directly compared tensor decomposition vs. grand averaging in fNIRS data and showed that tensor methods better preserved spatiotemporal signatures of emotional processing.
In another work, Barnhardt et al. (2025) [61] extended this to consumer neuroscience, using tensor decomposition to differentiate prefrontal activation during conceptual emotion processing (e.g., brand perception). They show that recent models of semantic memory distinguish between semantic control (LIFG) and semantic representation (LATL). This study combined selection and competition demands in a novel task using brand-name product images, with fNIRS capturing brain activity. Both tensor decomposition and grand averaging analyses revealed increased LIFG activation under competition, replicating prior findings. In particular, bilateral ATL activation also emerged, possibly due to the unique design of the task or its reinterpretation as an ad hoc categorization task. The consistent results across methods further support tensor decomposition as a reliable tool for fNIRS analysis.
In their paper, Karahan et al. [50] analyzed various brain signals, where modern neuroimaging generates vast multimodal data sets with various spatial and temporal resolutions, presenting challenges for data fusion. These data naturally form multi-way (tensor) structures that can be reduced to a small set of latent components. Their study introduces Markov–Penrose diagrams, combining Bayesian DAGs with tensor network notation, to clarify complex analysis tasks such as multimodal fusion and inverse problems. It also frames the Granger causal analysis as a tensor regression problem, allowing atomic decomposition of brain networks. Applications to EEG and fMRI highlight the method’s potential across neuroscience and beyond.
Neuroimaging techniques generate increasingly complex and multidimensional brain data across medicine, psychology, and neuroscience. Tensor-based methods are well suited to capture this multi-way structure, enabling effective analysis of large-scale, high-resolution signals. The review by Erol and Hunyadi [62] offers a comprehensive overview of tensor applications in neuroimaging, addressing current successes, practical challenges, and future directions in medical technology.
In the era of increasingly multidimensional brain imaging data, tensor-based methods have emerged as powerful tools for modeling the complex spatial, temporal, and inter-subject structures inherent in neuroimaging. The review by Tang et al. [13] provides a systematic exploration of tensor decomposition techniques across modalities such as fNIRS, EEG, and fMRI, highlighting their effectiveness in capturing latent patterns, improving interpretability, and enabling data fusion. With a focus on scalability and integration into medical technology, the paper also addresses key practical challenges and outlines future directions for advancing tensor-based neuroinformatics.
Lin et al. in their work [56] applied task-specific tensor modeling for subject-level neurovascular coupling. They showed that it can be effective in decoding emotion and motor responses with minimal loss of information.
Ghintoni et al. [63] presented a systematic review of advanced neuroimaging techniques and deep learning algorithms for emotion detection, with a focus on integrating modalities like fNIRS, EEG, and fMRI. The review emphasizes the role of tensor decomposition and other dimensionality reduction methods in enhancing multimodal data fusion, classification performance, and the interpretability of cognitive-affective states. A comparative radar analysis underscores how tensor-based approaches address the challenges of scalability, spatiotemporal resolution, and cross-modal complexity in neuroimaging.
Chan et al. in their work [35] demonstrated that tensor decomposition methods, such as CP and Tucker models, can uncover significant and novel hemodynamic patterns in fNIRS data that are often lost in traditional grand averaging approaches, offering a more comprehensive and assumption-free analysis framework. One of their key findings was that tensor decomposition revealed brain activation patterns that remained undetected using grand averaging, offering deeper insights into brain function.
In another interesting work, Hssayeni et al. [57] proposed a combined approach using tensor decomposition and ANOVA to analyze fNIRS data in infants, demonstrating that Canonical Polyadic Decomposition (CPD) can reveal distinct temporal and spatial brain activation patterns that are often missed by traditional grand averaging and ANOVA methods. This approach provides deeper insights into developmental cognitive processes and enhances the interpretability of infant neuroimaging data.
Tensor decomposition techniques are highly effective for analyzing fNIRS data, as they preserve the intrinsic multi-dimensional structure of the signals—capturing spatial (channels), temporal (time), and experimental (trials/subjects) dimensions simultaneously. Unlike traditional averaging or vectorization methods, tensors enable the extraction of latent components that reflect meaningful hemodynamic patterns linked to cognitive or emotional states. This leads to improved classification, interpretability, and integration with other modalities in affective computing and neuroimaging research.
Tensor decomposition methods have emerged as powerful tools for analyzing the complex, multi-dimensional nature of fNIRS data. Their ability to preserve temporal, spatial, and spectral information makes them particularly well-suited for medical applications, such as monitoring neurocognitive function, assessing mental health, and supporting diagnostic decision making.
Background to the Study
The integration of neurophysiological signals, particularly those derived from fNIRS, into affective computing has seen rapid advancements in the past decade. Emotion recognition is essential to improve human–computer interaction, mental health diagnostics, and personalized neurorehabilitation. fNIRS, being a noninvasive and portable brain imaging technique, provides valuable insights into the functional state of the brain by measuring hemodynamic responses associated with neural activity. This study investigates the emerging use of tensor factorization techniques to enhance the understanding of these signals in the context of emotion recognition.
Recent literature reveals a growing interest in the application of tensor factorization techniques such as CP and Tucker decomposition in emotion recognition. These methods decompose the high-dimensional data into factors that represent distinct features of brain activity, potentially uncovering hidden emotional patterns related to arousal and valence levels. The comparative performance of these tensor-based methods, when classified using traditional machine learning algorithms like Random Forests and Support Vector Machines (SVM), is also of significant interest in this field.
A bibliometric analysis of prominent databases, including Scopus, Web of Science (WoS), PubMed, and DBLP, was conducted using the keywords “tensor” AND “affective computing”. This search yielded the following results:
- Scopus: 10 articles published between 2016 and 2025.
- WoS: 21 articles within the same time period.
- PubMed: No results.
- dblp: No results.
The limited number of studies reflects a relatively new research trajectory in this domain, with tensor-based approaches still in the early stages of exploration. Notably, there are no clear leading authors or institutions within this field, though the National Natural Science Foundation of China has funded three studies, highlighting the increasing interest in tensor-based emotion recognition in China.
As this area of research evolves, there is a growing emphasis on the potential applications of emotion-aware systems in wearable neurotechnology. These systems, designed to be real-time and explainable, have significant promise for improving mental health monitoring, facilitating early diagnosis of affective disorders, and enhancing personalized neurorehabilitation therapies. The findings of this study contribute to the broader goal of Sustainable Development Goal 3: Good Health and Well-Being, which aims to ensure healthy lives and promote well-being for all at all ages.
By exploring the effectiveness of tensor factorization in fNIRS-based emotion recognition, this research provides valuable insights into the development of advanced emotion-aware systems that could revolutionize the field of medical diagnostics and human–computer interaction.
7. Discussion and Conclusions
Recent studies underscore the growing utility of tensor factorization techniques, such as the Tucker decomposition and CANDECOMP/PARAFAC (CP), for decoding affective states from fNIRS data. fNIRS neuroimaging inherently produces highly structured, multiway data, encompassing dimensions such as time, spatial channels, stimulus conditions, and even spectral information when multiple wavelengths are recorded. Tensor-based methodologies preserve this multi-dimensional architecture, providing a natural framework for extracting latent features that reflect complex and subtle interactions across all relevant domains. Unlike traditional vectorized or matrix-based approaches—which often require data flattening and may thus discard meaningful interactions—tensors capture the intricate, underlying patterns linked to emotional processing in the brain.
A growing body of comparative analyses demonstrates that features derived from tensor decompositions may, in most cases, significantly boost emotion classification performance. For example, studies focusing on distinguishing high-valence from low-valence or high-arousal versus low-arousal states report increased accuracy and robustness when employing tensor-based feature sets versus conventional signal processing or shallow learning strategies. The capacity of tensor methods to retain structural information is especially valuable in cross-session or inter-subject classification tasks, where individual variability and limited sample sizes often present challenges. By compactly representing essential patterns while discarding redundant or noisy dimensions, tensor factorization mitigates overfitting—a persistent concern in neuroimaging given typically scarce training datasets—and fosters improved generalization to new subjects or experimental contexts. There is also one substantial advantage of tensor factorization; it may lead to substantial data simplification (e.g., allows data flattening) and as a result, it allows using less complex and less resource-hungry models, thus potentially improving model training times and their final performance.
Crucially, the potential advantages of tensor decomposition are not limited to classification accuracy. The interpretable nature of the decomposed components provides a window into the underlying neurophysiological mechanisms of affective processing. For instance, spatial components may map onto functionally relevant brain regions, while temporal modes can reveal event-related or oscillatory dynamics of emotional responses. This interpretability facilitates hypothesis-driven analysis and hypothesis generation, advancing not only technical performance but also neuroscientific understanding of emotion. Furthermore, tensor analysis is well-suited for seamless data integration in multimodal affective computing scenarios. The modular structure of tensor models allows researchers to combine fNIRS data with other sources, such as EEG, peripheral physiological signals, or behavioral metrics (e.g., facial expressions or voice), within a unified factorization framework. Such integration has been shown to increase the robustness and breadth of affective state decoding, capturing multi-faceted emotional phenomena that are otherwise difficult to discern with single-modality approaches.
In summary, the literature increasingly positions tensor factorization not merely as an advanced dimensionality reduction tool, but as a foundational analytical paradigm in next-generation affective computing with fNIRS. Its complementary strengths—enhanced classification accuracy, statistical robustness, interpretability, and modularity for multimodal integration—have made it a methodological cornerstone for advancing emotion recognition, facilitating translational progress in neuroadaptive technologies, mental health monitoring, and affective brain–computer interfaces.
7.1. Limitations of Current Studies
Current research on tensor-based approaches in affective computing and medical applications frequently overlooks the distinctive characteristics and unresolved challenges of fNIRS data analysis. A significant limitation arises from the prevalent use of synthetic datasets or small, narrowly focused experimental cohorts, which often fail to capture the substantial inter- and intra-subject variability and the ecological complexity encountered in real-world medical settings. This restricts the generalizability and practical relevance of research outcomes. Moreover, while a substantial body of literature and comparative reviews center on EEG or fMRI modalities, comprehensive evaluations that focus specifically on fNIRS remain scarce. As a result, there is a lack of systematic benchmarks assessing tensor models under the unique constraints of fNIRS signal properties, such as lower spatial resolution and pronounced vulnerability to motion artifacts and physiological noise.
Many existing tensor decomposition models—originally developed for higher-resolution or less motion-sensitive neuroimaging data—are not well-adapted to these challenges. They typically fail to address the distinct spatial sparsity and signal-to-noise issues associated with fNIRS, potentially leading to suboptimal feature extraction and reduced robustness in emotion recognition or clinical diagnostic tasks. Additionally, the computational demands of popular tensor factorization algorithms are rarely calibrated to the relatively low sampling rates but high channel and condition dimensionality inherent to fNIRS datasets. This can result in inefficient use of computational resources and may limit the feasibility of deploying tensor-based models in real-time or resource-constrained clinical environments.
Integration of fNIRS within multimodal fusion frameworks—such as combining with EEG, physiological, or behavioral data—remains an underexplored area within the tensor-based affective computing literature. Few studies propose tensor architectures or fusion strategies explicitly tailored for the idiosyncrasies of fNIRS data, missing opportunities to leverage the complementary strengths of joint modalities in affective state decoding and medical applications. Furthermore, most reviews stop short of critically appraising the clinical or real-time deployability of tensor-based approaches, focusing instead on theoretical or offline performance metrics. This leaves a substantial gap between algorithmic innovation and practical implementation, with limited translation into user-facing neuroadaptive systems or decision-support tools suitable for deployment in diverse clinical and everyday contexts [64].
7.2. Further Research Plans
This research should aim to find a balance between computational efficiency and physiological validity for real-world applications in healthcare and emotion monitoring. Future research should focus on developing tensor-based models specifically tailored to fNIRS data, which are inherently high-dimensional (channels × time × trials × subjects). This requires improved tensor decomposition techniques that cope with the low signal-to-noise ratio and motion artifacts in fNIRS signals. Combining spatial and temporal domains within tensor models can improve the physiological interpretability of affective and medical responses. Another research direction is the development of adaptive tensor structures that can dynamically adapt to individual differences, improving personalization in emotion recognition and monitoring central nervous system health. Integrating tensor-based approaches with Deep Learning (DL), such as combining tensor decomposition with convolutional or graph neural networks, could provide improved feature learning from fNIRS data. Cross-modality tensor fusion methods could help combine fNIRS with EEG, facial expressions, or heart rate to improve the robustness of computational systems for affective computing. Real-time tensor processing for fNIRS would enable the application of tensor-based neurofeedback and brain–computer interfaces in clinical settings. There is also a need to build large-scale, annotated fNIRS datasets for benchmarking tensor-based algorithms. Tensor-based transfer learning studies could address the issue of subject and session variability, a common limitation in fNIRS applications.
Tensor decomposition can be efficiently integrated into existing ML/DL frameworks as a feature extraction step that reduces high-dimensional fNIRS signals into compact, interpretable representations. Instead of flattening multi-channel spatiotemporal data, tensor factorization preserves multi-way structure, enabling downstream models (such as SVMs or random forests) to exploit richer patterns. In DL, tensor decomposition can act as a preprocessing layer that introduces low-rank approximations of the original data into CNNs, recurrent neural networks (RNNs), or transformer neural networks, increasing computational efficiency while preserving discriminative features. Tensorized representations can be embedded directly into neural architectures via tensor regression layers or tensorized weight matrices, reducing the number of parameters and mitigating overfitting in small-sample affective computing studies. In multimodal applications, tensor fusion techniques allow for the integration of fNIRS with other physiological signals (EEG, heart rate, etc.), enabling models to learn collaboratively across modalities. Tensor decomposition supports unsupervised feature discovery, complementing supervised deep models by identifying hidden emotional states without heavy reliance on labeled datasets. Positioning tensor methods as both standalone feature extractors and structural amplifiers in neural networks, it is worth emphasizing their dual role in increasing interpretability and efficiency in affective computing and clinical emotion recognition.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app151910525/s1. PRISMA 2020 checklist (partial only) [65].
Author Contributions
Conceptualization, A.K.-S. and M.P. (Mariusz Pelc); methodology, A.K.-S., M.P. (Michal Podpora), D.M. and M.P. (Mariusz Pelc); software, A.K.-S., M.P. (Michal Podpora), D.M. and M.P. (Mariusz Pelc); validation, A.K.-S., M.P. (Michal Podpora), M.P. (Maciej Piasecki), E.R., D.M. and M.P. (Mariusz Pelc); formal analysis, A.K.-S., M.P. (Michal Podpora), D.M. and M.P. (Mariusz Pelc); investigation, A.K.-S., M.P. (Michal Podpora), M.P. (Maciej Piasecki), E.R., D.M. and M.P. (Mariusz Pelc); resources, A.K.-S., M.P. (Michal Podpora) and M.P. (Mariusz Pelc); data curation, A.K.-S., M.P. (Michal Podpora), A.L. and M.P. (Mariusz Pelc); writing—original draft preparation, A.K.-S., M.P. (Michal Podpora), D.M., M.P. (Maciej Piasecki), E.R., A.L., A.S. and M.P. (Mariusz Pelc); writing—review and editing, A.K.-S., M.P. (Michal Podpora), D.M., M.P. (Maciej Piasecki), E.R., A.L., A.S. and M.P. (Mariusz Pelc); visualization, A.L., D.M. and A.S.; supervision, A.K.-S., M.P. (Maciej Piasecki), M.P. (Michal Podpora), D.M. and M.P. (Mariusz Pelc); funding acquisition, A.K.-S. and M.P. (Maciej Piasecki). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADHD | attention-deficit/hyperactivity disorder |
| ANOVA | analysis of variance |
| BCI | Brain-Computer Interface |
| CNN | convolutional neural network |
| CP | Canonical Polyadic |
| CPD | Canonical Polyadic Decomposition |
| DL | deep learning |
| DLPFC | dorsolateral prefrontal cortex |
| EEG | electroencephalography |
| FFT | Fast Fourier Transform |
| fMRI | functional Magnetic Resonance Imaging |
| fNIRS | functional near-infrared spectroscopy |
| HbO | oxygenated hemoglobin |
| HbR | deoxygenated hemoglobin |
| LSTM | Long short-term memory |
| ML | machine learning |
| mPFC | medial prefrontal cortex |
| OFC | orbitofrontal cortex |
| PET | Positron Emission Tomography |
| PFC | prefrontal cortex |
| RNN | recurrent neural network |
| SVM | Support Vector Machine |
| WoS | Web of Science |
References
- Wang, Y.; Song, W.; Tao, W.; Liotta, A.; Yang, D.; Li, X.; Gao, S.; Sun, Y.; Ge, W.; Zhang, W.; et al. A systematic review on affective computing: Emotion models, databases, and recent advances. Inf. Fusion 2022, 83, 19–52. [Google Scholar] [CrossRef]
- Pei, G.; Li, H.; Lu, Y.; Wang, Y.; Hua, S.; Li, T. Affective computing: Recent advances, challenges, and future trends. Intell. Comput. 2024, 3, 0076. [Google Scholar] [CrossRef]
- Afzal, S.; Khan, H.A.; Piran, M.J.; Lee, J.W. A comprehensive survey on affective computing; challenges, trends, applications, and future directions. IEEE Access 2024, 12, 96150–96168. [Google Scholar] [CrossRef]
- Klein, F.; Kohl, S.H.; Lührs, M.; Mehler, D.M.; Sorger, B. From lab to life: Challenges and perspectives of fNIRS for haemodynamic-based neurofeedback in real-world environments. Philos. Trans. B 2024, 379, 20230087. [Google Scholar] [CrossRef]
- Ruotsalo, T.; Traver, V.J.; Kawala-Sterniuk, A.; Leiva, L.A. Affective relevance. IEEE Intell. Syst. 2024, 39, 12–22. [Google Scholar] [CrossRef]
- Dehais, F.; Ayaz, H.; Kawala-Sterniuk, A.; Ladouce, S.; Barreto, C.; Karwowski, W. Non-Invasive Brain-Computer Interfaces. In Interaction Techniques and Technologies in Human-Computer Interaction; CRC Press: Boca Raton, FL, USA, 2024; pp. 406–440. [Google Scholar]
- Friedman, B.H.; Thayer, J.F. Is emotion physiology more compatible with discrete, dimensional, or appraisal accounts? In Emotion Theory: The Routledge Comprehensive Guide; Routledge: Oxfordshire, UK, 2024; pp. 488–510. [Google Scholar]
- Kragel, P.A.; Sander, D.; LaBar, K.S. Can Brain Data Be Used to Arbitrate Among Emotion Theories? In Emotion Theory: The Routledge Comprehensive Guide; Routledge: Oxfordshire, UK, 2024; pp. 511–542. [Google Scholar]
- Pinti, P.; Tachtsidis, I.; Hamilton, A.; Hirsch, J.; Aichelburg, C.; Gilbert, S.; Burgess, P.W. The present and future use of functional near-infrared spectroscopy (fNIRS) for cognitive neuroscience. Ann. N. Y. Acad. Sci. 2020, 1464, 5–29. [Google Scholar] [CrossRef]
- Ferrari, M.; Quaresima, V. A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 2012, 63, 921–935. [Google Scholar] [CrossRef] [PubMed]
- Cortinas-Lorenzo, K.; Lacey, G. Big team science reveals promises and limitations of machine learning efforts to model physiological markers of affective experience. R. Soc. Open Sci. 2025, 12, 241778. [Google Scholar] [CrossRef] [PubMed]
- Cortinas-Lorenzo, K.; Lacey, G. Toward Explainable Affective Computing: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13101–13121. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, D.; Li, X. Dimensionality reduction methods for brain imaging data analysis. ACM Comput. Surv. (CSUR) 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Taguchi, Y. Tensor decomposition-based unsupervised feature extraction applied to matrix products for multi-view data processing. PLoS ONE 2017, 12, e0183933. [Google Scholar] [CrossRef]
- Boas, D.A.; Elwell, C.E.; Ferrari, M.; Taga, G. Twenty years of functional near-infrared spectroscopy: Introduction for the special issue. Neuroimage 2014, 85, 1–5. [Google Scholar] [CrossRef]
- Naseer, N.; Hong, K.S. fNIRS-based brain-computer interfaces: A review. Front. Hum. Neurosci. 2015, 9, 3. [Google Scholar] [CrossRef] [PubMed]
- Leff, D.R.; Orihuela-Espina, F.; Elwell, C.E.; Athanasiou, T.; Delpy, D.T.; Darzi, A.W.; Yang, G.Z. Assessment of the cerebral cortex during motor task behaviours in adults: A systematic review of functional near infrared spectroscopy (fNIRS) studies. Neuroimage 2011, 54, 2922–2936. [Google Scholar] [CrossRef]
- Causse, M.; Chua, Z.; Peysakhovich, V.; Del Campo, N.; Matton, N. Mental workload and neural efficiency quantified in the prefrontal cortex using fNIRS. Sci. Rep. 2017, 7, 5222. [Google Scholar] [CrossRef]
- Paulmurugan, K.; Vijayaragavan, V.; Ghosh, S.; Padmanabhan, P.; Gulyás, B. Brain–computer interfacing using functional near-infrared spectroscopy (fNIRS). Biosensors 2021, 11, 389. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Zhao, W.; Lu, C.; Du, H.; Chi, P. Interpersonal neural synchronization during social interactions in close relationships: A systematic review and meta-analysis of fNIRS hyperscanning studies. Neurosci. Biobehav. Rev. 2024, 158, 105565. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhao, C.; Wang, F.; Zhang, D. Inter-brain amplitude correlation differentiates cooperation from competition in a motion-sensing sports game. Soc. Cogn. Affect. Neurosci. 2021, 16, 552–564. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Zhang, X. EEG–fNIRS-Based emotion recognition using graph convolution and capsule attention network. Brain Sci. 2024, 14, 820. [Google Scholar] [CrossRef]
- Tang, T.B.; Chong, J.S.; Kiguchi, M.; Funane, T.; Lu, C.K. Detection of emotional sensitivity using fNIRS based dynamic functional connectivity. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 894–904. [Google Scholar] [CrossRef]
- Ruotsalo, T.; Mäkelä, K.; Spapé, M.M.; Leiva, L.A. Affective relevance: Inferring emotional responses via fNIRS neuroimaging. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, Taipei, Taiwan, 23–27 July 2023; pp. 1796–1800. [Google Scholar]
- Wu, D.; Lu, B.L.; Hu, B.; Zeng, Z. Affective brain–computer interfaces (abcis): A tutorial. Proc. IEEE 2023, 111, 1314–1332. [Google Scholar] [CrossRef]
- Gunadi, S.; Leung, T.S.; Elwell, C.E.; Tachtsidis, I. Spatial sensitivity and penetration depth of three cerebral oxygenation monitors. Biomed. Opt. Express 2014, 5, 2896–2912. [Google Scholar] [CrossRef]
- Li, R.; Yang, D.; Fang, F.; Hong, K.S.; Reiss, A.L.; Zhang, Y. Concurrent fNIRS and EEG for brain function investigation: A systematic, methodology-focused review. Sensors 2022, 22, 5865. [Google Scholar] [CrossRef]
- Spapé, M.; Mäkelä, K.; Ruotsalo, T. NEMO: A Database for Emotion Analysis Using Functional Near-infrared Spectroscopy. IEEE Trans. Affect. Comput. 2023, 15, 1166–1177. [Google Scholar] [CrossRef]
- Yükselen, G.; Öztürk, O.C.; Canlı, G.D.; Erdoğan, S.B. Investigating the Neural Correlates of Processing Basic Emotions: A Functional Near-Infrared Spectroscopy (fNIRS) Study. bioRxiv 2023. [Google Scholar] [CrossRef]
- Si, X.; He, H.; Yu, J.; Ming, D. Cross-subject emotion recognition brain–computer interface based on fNIRS and DBJNet. Cyborg Bionic Syst. 2023, 4, 0045. [Google Scholar] [CrossRef] [PubMed]
- Trambaiolli, L.R.; Tiwari, A.; Falk, T.H. Affective neurofeedback under naturalistic conditions: A mini-review of current achievements and open challenges. Front. Neuroergonomics 2021, 2, 678981. [Google Scholar] [CrossRef] [PubMed]
- Doherty, E.J.; Spencer, C.A.; Burnison, J.; Čeko, M.; Chin, J.; Eloy, L.; Haring, K.; Kim, P.; Pittman, D.; Powers, S.; et al. Interdisciplinary views of fNIRS: Current advancements, equity challenges, and an agenda for future needs of a diverse fNIRS research community. Front. Integr. Neurosci. 2023, 17, 1059679. [Google Scholar] [CrossRef]
- Hüsser, A.; Caron-Desrochers, L.; Tremblay, J.; Vannasing, P.; Martínez-Montes, E.; Gallagher, A. Parallel factor analysis for multidimensional decomposition of functional near-infrared spectroscopy data. Neurophotonics 2022, 9, 045004. [Google Scholar] [CrossRef]
- Chan, J.; Wilcox, T.; Hssayeni, M.; Ghoraani, B. Multidimensional Analysis of Functional Near-Infrared Spectroscopy (fNIRS) Signal using Tucker Decomposition. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 1317–1321. [Google Scholar] [CrossRef]
- Chan, J.Y.; Hssayeni, M.D.; Wilcox, T.; Ghoraani, B. Exploring the feasibility of tensor decomposition for analysis of fNIRS signals: A comparative study with grand averaging method. Front. Neurosci. 2023, 17, 1180293. [Google Scholar] [CrossRef]
- Liu, J.; Song, T.; Shu, Z.; Han, J.; Yu, N. fNIRS Feature Extraction and Classification in Grip-Force Tasks. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 1087–1091. [Google Scholar]
- Cao, Z. Simple but effective: Rethinking the ability of deep learning in fnirs to exclude abnormal input. In Proceedings of the 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Bari, Italy, 28 August–1 September 2024; IEEE: New York, NY, USA, 2024; pp. 1971–1976. [Google Scholar]
- Hu, H.; Lin, X.; Ye, Z.; Fang, L.; Gao, H.; Zhang, Q. Application of functional near-infrared spectroscopy (fNIRS) in tinnitus research: Contemporary insights and perspectives. Front. Psychol. 2024, 15, 1334660. [Google Scholar] [CrossRef]
- Liu, X.; Parhi, K.K. Tensor decomposition for model reduction in neural networks: A review [feature]. IEEE Circuits Syst. Mag. 2023, 23, 8–28. [Google Scholar] [CrossRef]
- Wang, C.; Sahebi, S.; Torkamaan, H. STRETCH: Stress and Behavior Modeling with Tensor Decomposition of Heterogeneous Data. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, Melbourne, VIC, Australia, 14–17 December 2021; IEEE: New York, NY, USA, 2022. WI-IAT’21. pp. 453–462. [Google Scholar] [CrossRef]
- Liao, C.Y.; Li, C.Y.; Fang, W.C. AI-Based Emotion Recognition System with Tensor Decomposition Optimized Pre-processing. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Penghu, Taiwan, 15–17 September 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Papastergiou, T.; Zacharaki, E.I.; Megalooikonomou, V. Tensor Decomposition for Multiple-Instance Classification of High-Order Medical Data. Complexity 2018, 2018, 8651930. [Google Scholar] [CrossRef]
- Yu, H.; Larsen, K.G.; Christiansen, O. Optimization methods for tensor decomposition: A comparison of new algorithms for fitting the CP (CANDECOMP/PARAFAC) model. Chemom. Intell. Lab. Syst. 2025, 257, 105290. [Google Scholar] [CrossRef]
- Sztuka, I.M.; Kühn, S. Neurocognitive dynamics and behavioral differences of symmetry and asymmetry processing in working memory: Insights from fNIRS. Sci. Rep. 2025, 15, 4740. [Google Scholar] [CrossRef]
- Auddy, A.; Xia, D.; Yuan, M. Tensor methods in high dimensional data analysis: Opportunities and challenges. arXiv 2024, arXiv:2405.18412. [Google Scholar] [CrossRef]
- Sedighin, F. Tensor methods in biomedical image analysis. J. Med. Signals Sens. 2024, 14, 16. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Yamada, K. Machine learning studies on major brain diseases: 5-year trends of 2014–2018. Jpn. J. Radiol. 2019, 37, 34–72. [Google Scholar] [CrossRef]
- Lima, A.A.; Mridha, M.F.; Das, S.C.; Kabir, M.M.; Islam, M.R.; Watanobe, Y. A comprehensive survey on the detection, classification, and challenges of neurological disorders. Biology 2022, 11, 469. [Google Scholar] [CrossRef]
- Hamdi, S.M.; Wu, Y.; Boubrahimi, S.F.; Angryk, R.; Krishnamurthy, L.C.; Morris, R. Tensor decomposition for neurodevelopmental disorder prediction. In Proceedings of the Brain Informatics: International Conference, BI 2018, Arlington, TX, USA, 7–9 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 339–348. [Google Scholar]
- Karahan, E.; Rojas-Lopez, P.A.; Bringas-Vega, M.L.; Valdés-Hernández, P.A.; Valdes-Sosa, P.A. Tensor analysis and fusion of multimodal brain images. Proc. IEEE 2015, 103, 1531–1559. [Google Scholar] [CrossRef]
- Joshi, R.; Jadeja, M. The Synergy of Clinical Psychology and Affective Computing: Advancements in Emotion Recognition and Therapy. In Affective Computing for Social Good: Enhancing Well-Being, Empathy, and Equity; Springer: Berlin/Heidelberg, Germany, 2024; pp. 21–45. [Google Scholar]
- León-Carrión, J.; León-Domínguez, U. Functional near-infrared spectroscopy (fNIRS): Principles and neuroscientific applications. Neuroimaging Methods 2012, 97, 48–74. [Google Scholar]
- Quaresima, V.; Ferrari, M. A mini-review on functional near-infrared spectroscopy (fNIRS): Where do we stand, and where should we go? Photonics 2019, 6, 87. [Google Scholar] [CrossRef]
- Udina, C.; Avtzi, S.; Durduran, T.; Holtzer, R.; Rosso, A.L.; Castellano-Tejedor, C.; Perez, L.M.; Soto-Bagaria, L.; Inzitari, M. Functional near-infrared spectroscopy to study cerebral hemodynamics in older adults during cognitive and motor tasks: A review. Front. Aging Neurosci. 2020, 11, 367. [Google Scholar] [CrossRef]
- Ahmed, I.; Raihan, A.S. Spatiotemporal data analysis: A review of techniques, applications, and emerging challenges. In Multimodal and Tensor Data Analytics for Industrial Systems Improvement; Springer: Berlin/Heidelberg, Germany, 2024; pp. 125–166. [Google Scholar]
- Lin, J.; Lu, J.; Shu, Z.; Han, J.; Yu, N. Subject-Specific Modeling of EEG-fNIRS Neurovascular Coupling by Task-Related Tensor Decomposition. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 452–461. [Google Scholar] [CrossRef] [PubMed]
- Hssayeni, M.D.; Wilcox, T.; Ghoraani, B. Tensor decomposition of functional near-infrared spectroscopy (fNIRS) signals for pattern discovery of cognitive response in infants. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; IEEE: New York, NY, USA, 2020; pp. 394–397. [Google Scholar]
- Sinha, N. Affective computing and emotion-sensing technology for emotion recognition in mood disorders. In Enhanced Telemedicine and e-Health: Advanced IoT Enabled Soft Computing Framework; Springer: Berlin/Heidelberg, Germany, 2021; pp. 337–360. [Google Scholar]
- Hou, M.; Zhang, X.; Chen, G.; Huang, L.; Sun, Y. Emotion Recognition Based on a EEG–fNIRS Hybrid Brain Network in the Source Space. Brain Sci. 2024, 14, 1166. [Google Scholar] [CrossRef] [PubMed]
- Akhter, J.; Nazeer, H.; Naseer, N.; Naeem, R.; Kallu, K.D.; Lee, J.; Ko, S.Y. Improved performance of fNIRS-BCI by stacking of deep learning-derived frequency domain features. PloS ONE 2025, 20, e0314447. [Google Scholar] [CrossRef]
- Barnhardt, T.M.; Chan, J.Y.; Ghoraani, B.; Wilcox, T. Effects of Competition on Left Prefrontal and Temporal Cortex During Conceptual Comparison of Brand-Name Product Pictures: Analysis of fNIRS Using Tensor Decomposition. Brain Sci. 2025, 15, 127. [Google Scholar] [CrossRef]
- Erol, A.; Hunyadi, B. Tensors for neuroimaging: A review on applications of tensors to unravel the mysteries of the brain. In Tensors for Data Processing; Academic Press: Cambridge, MA, USA, 2022; pp. 427–482. [Google Scholar]
- Halkiopoulos, C.; Gkintoni, E.; Aroutzidis, A.; Antonopoulou, H. Advances in Neuroimaging and Deep Learning for Emotion Detection: A Systematic Review of Cognitive Neuroscience and Algorithmic Innovations. Diagnostics 2025, 15, 456. [Google Scholar] [CrossRef] [PubMed]
- Aranyi, G.; Pecune, F.; Charles, F.; Pelachaud, C.; Cavazza, M. Affective Interaction with a Virtual Character Through an fNIRS Brain-Computer Interface. Front. Comput. Neurosci. 2015, 10, 70. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).