Risk Analysis and Resilience of Humanitarian Aviation Supply Chains: A Bayesian Network Approach

Abstract

The humanitarian aviation supply chain (HASC) serves as a critical conduit for delivering essential aid to populations affected by disasters and conflicts, especially when ground routes are inaccessible. However, HASCs operate in high-risk environments marked by instability, infrastructure damage, and operational challenges. Existing risk assessment approaches often struggle to account for the complex interdependencies among the many factors influencing mission success and supply chain resilience. This study introduces a comprehensive risk analysis framework for HASCs using Bayesian networks (BNs). The BN model integrates data on factors such as political instability, infrastructure damage, adverse weather, crew fatigue, and aircraft maintenance. Through quantitative analysis, the framework identifies critical vulnerabilities and assesses the likelihood of mission failure.

1. Introduction

In the face of escalating global crises, from natural disasters to protracted conflicts, the humanitarian aviation supply chain (HASC) serves as an indispensable lifeline, delivering life-saving aid to the world’s most vulnerable and inaccessible regions. When terrestrial routes are compromised or non-existent, aviation provides the critical link to transport personnel, medical supplies, and food. Organizations like the United Nations Humanitarian Air Service (UNHAS) exemplify this, operating a vast fleet of aircraft that constitute a backbone for the entire humanitarian community. In 2023 alone, UNHAS airlifted 4800 metric tonnes of cargo and transported over 388,000 humanitarian and development workers across 21 countries, delivering life-saving supplies and personnel to some of the world’s most inaccessible areas [1]. This capability is often the sole means of access, making aviation not just a logistical choice but a fundamental enabler of emergency responses and recovery. Partnerships within the aviation industry, such as those fostered by Airbus and Airlink, further amplify this impact by mobilizing resources and strengthening logistics [2], underscoring the sector’s vital role in global humanitarian efforts.

The inherent complexity of HASC operations presents unique scientific challenges that demand a multidisciplinary analytical approach. Unlike conventional commercial aviation supply chains that operate within established regulatory frameworks and stable environments, the HASC functions at the intersection of multiple complex adaptive systems. This operational domain encompasses supply chain management theory, risk assessment methodologies, network analysis, decision science under uncertainty, and crisis management protocols. The scientific complexity arises from the emergent properties of these interconnected systems, where traditional linear risk assessment models prove inadequate for capturing the dynamic, non-linear relationships between risk factors. The stochastic nature of humanitarian crises, combined with the temporal urgency of response operations, creates a research environment where conventional supply chain optimization theories must be adapted to accommodate extreme uncertainty and resource constraints.

From a systems science perspective, the HASC represents a prime example of a complex adaptive system operating under extreme conditions. The network exhibits characteristics of self-organization, emergence, and non-linear dynamics, where small perturbations in one component can cascade through the entire system, leading to disproportionate impacts on operational effectiveness. This phenomenon, known as the “butterfly effect” in chaos theory, is particularly pronounced in humanitarian contexts where the interdependencies between political stability, infrastructure integrity, weather patterns, and human factors create a web of complex interactions that challenge traditional analytical frameworks. The scientific interest lies not merely in understanding individual risk factors but in comprehending how these factors interact synergistically to produce emergent behaviors that cannot be predicted from studying components in isolation.

Despite its critical importance, the HASC operates in inherently high-risk environments characterized by volatility, uncertainty, and infrastructural collapse. The effectiveness of these operations is not merely a matter of logistical efficiency but of life and death, necessitating a rigorous and proactive approach to risk analysis. The operational environment itself presents profound challenges, from navigating conflict zones to contending with extreme weather conditions. For civil aviation accident severity prediction, while pilot factors are relevant, the operational context, including the phase of flight and adverse weather, is more significantly correlated with the severity of incidents [3,4]. The multidisciplinary nature of HASC risk assessment is scientifically compelling because it requires the integration of theories from operations research, probability theory, behavioral psychology, meteorology, geopolitics, and organizational behavior. Each discipline contributes essential insights, yet none alone is sufficient to capture the full complexity of the operational environment. This necessitates the development of novel analytical frameworks that can synthesize knowledge across domains while maintaining mathematical rigor and empirical validity.

To address this critical need for a structured and comprehensive risk assessment that can handle such scientific complexity, this study employs a Bayesian network (BN) methodology. The complex and interdependent nature of risks within the HASC requires a model that can capture and quantify the probabilistic relationships between various contributing factors while accommodating the inherent uncertainty and non-linearity of the system. As demonstrated in recent research on humanitarian supply chain performance evaluation, BNs provide a robust framework for modeling such complex systems [5]. This approach represents a significant methodological advancement by enabling the formal integration of diverse epistemological sources within a unified probabilistic framework. By constructing a BN model, it is possible to analyze how different variables, such as political instability, infrastructure damage, crew fatigue, and aircraft maintenance, collectively influence the probability of mission success and the overall performance of the supply chain. The scientific contribution of this work lies in demonstrating how advanced probabilistic modeling techniques can be adapted to handle the extreme operational conditions characteristic of humanitarian environments, thereby advancing both theoretical understanding and practical capability in crisis management systems.

This analytical rigor will enable the identification of critical vulnerabilities and the development of targeted, evidence-based mitigation strategies, ultimately enhancing the resilience and effectiveness of the humanitarian aviation supply chain. Moreover, the methodological framework developed in this study contributes to the broader scientific discourse on modeling complex adaptive systems under extreme uncertainty, offering insights that extend beyond humanitarian logistics to inform risk assessments in other high-stakes, dynamic operational environments.

The remainder of this paper is structured as follows: Section 2 provides a comprehensive review of the relevant literature. Section 3 outlines the identification of key risk factors and their interrelationships, culminating in the construction of the Bayesian network model. Section 4 presents a quantitative analysis of the BN model, accompanied by a discussion of the results. Finally, the conclusions are summarized in Section 5.

2. Literature Review

To provide a comprehensive foundation for this study on risk analysis in the HASC, this literature review synthesizes recent research from two key perspectives: humanitarian supply chain (HSC) management and risk analysis in civil aviation.

HSC research has increasingly emphasized resilience, performance measurement, and risk management in disaster response and ongoing crises. Ref. [6] provides a systematic review of performance measurements in the HSC, categorizing metrics into efficiency, effectiveness, and equity. This foundational work emphasizes the role of data-driven approaches in evaluating HSC outcomes, setting the stage for probabilistic models like BNs. Ref. [7] explores agility in the HSC from an organizational capability perspective, using empirical data from humanitarian organizations. The authors argue that developing specific capabilities, such as effective information processing and flexible decision-making structures, enhances responsiveness, which is crucial for aviation-dependent supply chains in remote areas. Ref. [8] reviews HSC strategies for mitigating risks, focusing on prepositioning, partnerships, and modular logistics. The study highlights how actors in humanitarian operations address supply chain disruptions through collaborative networks, drawing from case studies in conflict zones. A thematic literature review by [9] analyzes over 200 articles, identifying key themes such as coordination, performance metrics, and sustainability in HSCs. The authors underscore the need for agile frameworks to handle uncertainty, which aligns with the HASC’s volatile environments. Ref. [10] investigates factors influencing HSC effectiveness during droughts in Zimbabwe, using a quantitative exploratory design with survey data from 130 government and NGO officials.

Ref. [11] presents a deep Q-network-based approach for optimizing emergency supply distributions in humanitarian logistics, considering varying disaster impacts and supply demands across affected areas. The problem is modeled as a Markov decision process, balancing efficiency, effectiveness, and equity. Ref. [12] addresses the pressing challenge of managing risks within HSCs, with a specific focus on natural disaster contexts in India. The authors underscore the escalating importance of HSCs given the increasing frequency and severity of natural disasters, which exacerbate risks of resource scarcity, transportation disruptions, and logistical failures. The primary objective of the study is to systematically identify these risks and propose a novel mitigation framework by leveraging Industry 5.0 technologies, which emphasize human-centric, advanced technological solutions. This dual focus on risk analysis and technological innovation positions the paper as a timely contribution to the field of humanitarian logistics. Ref. [13] explores the critical issue of enhancing the resilience of humanitarian supply chains during natural disasters and pandemics. The primary objective of the study is to identify and rank sustainability enablers that can strengthen RHSCs, using the fuzzy Analytic Hierarchy Process (AHP) to provide a structured evaluation framework. This focus on sustainability and resilience aims to offer actionable insights for improving supply chain performance in crisis contexts, making the study both timely and relevant to humanitarian logistics.

For the risk analysis in civil aviation, Ref. [14] addresses the pressing need to enhance airport security through structured risk assessment methodologies, with a particular emphasis on the post-9/11 era. The authors underscore the heightened global focus on aviation security, which is driven by the vulnerabilities exposed by terrorist attacks, and aim to develop comprehensive risk management frameworks. The primary objective is to identify, quantify, and optimize security measures by integrating threat, vulnerability, and criticality analyses, thereby safeguarding airport infrastructure and ensuring the safety of civil aviation. This focus on systematic risk assessments positions the study as a critical contribution to the field of aviation security. Ref. [15] applies fuzzy sets to analyze air traffic incidents, proposing a model for incident severity assessments. The authors’ approach handles uncertainty in aviation data, making it relevant to humanitarian flights in degraded conditions. Ref. [16] introduces an optimization model for aircraft rerouting under uncertainty, using stochastic programming to minimize risks from weather and airspace constraints. This has direct applications to HASC route planning in volatile regions. Ref. [17] offers a detailed examination of the causes and risk factors associated with civil aviation accidents, focusing on three critical categories: (in-flight) loss of control, controlled flight into terrain, and runway excursion. These accident types are noted for their high fatality rates and the intricate interplay of human, mechanical, and environmental factors contributing to their occurrence. The primary objective of the study is to review the evolution of risk analysis methodologies over the past three decades, with a particular emphasis on the transformative role of big data and artificial intelligence in enhancing aviation safety. By synthesizing existing research and accident data, the authors aim to highlight the potential of advanced technologies in predicting and preventing aviation incidents while identifying ongoing challenges in their implementation. Ref. [4] presents a sophisticated investigation into the role of pilot-related factors in civil aviation accidents. Its primary objective is to elucidate the causal relationships between various risk factors and accident outcomes, with a specific focus on pilot contributions. Utilizing data from 163 pilot-related accidents recorded in the National Transportation Safety Board database spanning 2008 to 2020, the study employs a BN framework to model these interdependencies probabilistically. This data-driven approach aims to enhance the understanding of accident causation, thereby informing aviation safety improvements.

The reviewed literature collectively highlights a growing emphasis on resilience, data-driven decision-making, and technological innovation in both HSC management and civil aviation risk analysis. HSC studies stress the importance of agility, coordination, and sustainability to navigate volatile environments, while aviation research demonstrates the efficacy of probabilistic and analytical tools, such as BNs, in modeling complex risk interdependencies. However, a notable gap persists: the tailored application of advanced probabilistic frameworks to HASCs, where unique operational challenges, such as navigating conflict zones and extreme weather, demand specialized risk assessment tools. This study addresses this gap by introducing a BN-based framework specifically designed for HASCs to model intricate relationships among geopolitical, environmental, and human factors.

3. Risk Factor Identification and the BN Framework

The development of an effective risk analysis model for the HASC demands a rigorous and systematic methodology that integrates insights from diverse empirical sources, including aviation safety studies and humanitarian logistics research. This section articulates the process, beginning with the identification and analysis of critical risk factors, followed by the construction of a BN as the analytical framework. The BN’s architecture, node definitions, dependency structure, and probabilistic specifications are thoroughly explored to illustrate how the model captures the intricate risk landscape of HASC operations and facilitates resilience-enhancing strategies.

3.1. Rationale for BNs in HASC Risk Analysis

BNs are probabilistic graphical models that represent a set of variables and their conditional dependencies within a directed acyclic graph. They are particularly advantageous for HASC risk analysis due to their ability to model complex uncertainties prevalent in humanitarian aviation contexts, such as conflict zones, disaster-affected regions, or areas with limited infrastructure. These environments often yield incomplete or heterogeneous data, posing challenges for traditional risk assessment methods. BNs excel in such scenarios by synthesizing quantitative data (e.g., historical incident rates) with qualitative inputs (e.g., expert judgments) into a cohesive probabilistic framework.

Moreover, BNs support dual inference capabilities: predictive reasoning, which estimates the likelihood of mission failure given specific risk conditions, and diagnostic reasoning, which identifies probable causes of observed failures. This flexibility is grounded in Bayes’ theorem, which ensures that probability updates remain consistent and evidence-based as new information emerges. For instance, if a mission encounters delays, the BN can trace the contributing factors—whether geopolitical tensions, weather disruptions, or crew fatigue—offering actionable insights for mitigation. This adaptability and mathematical rigor position BNs as a robust tool for enhancing operational resilience in the volatile settings typical of humanitarian aviation.

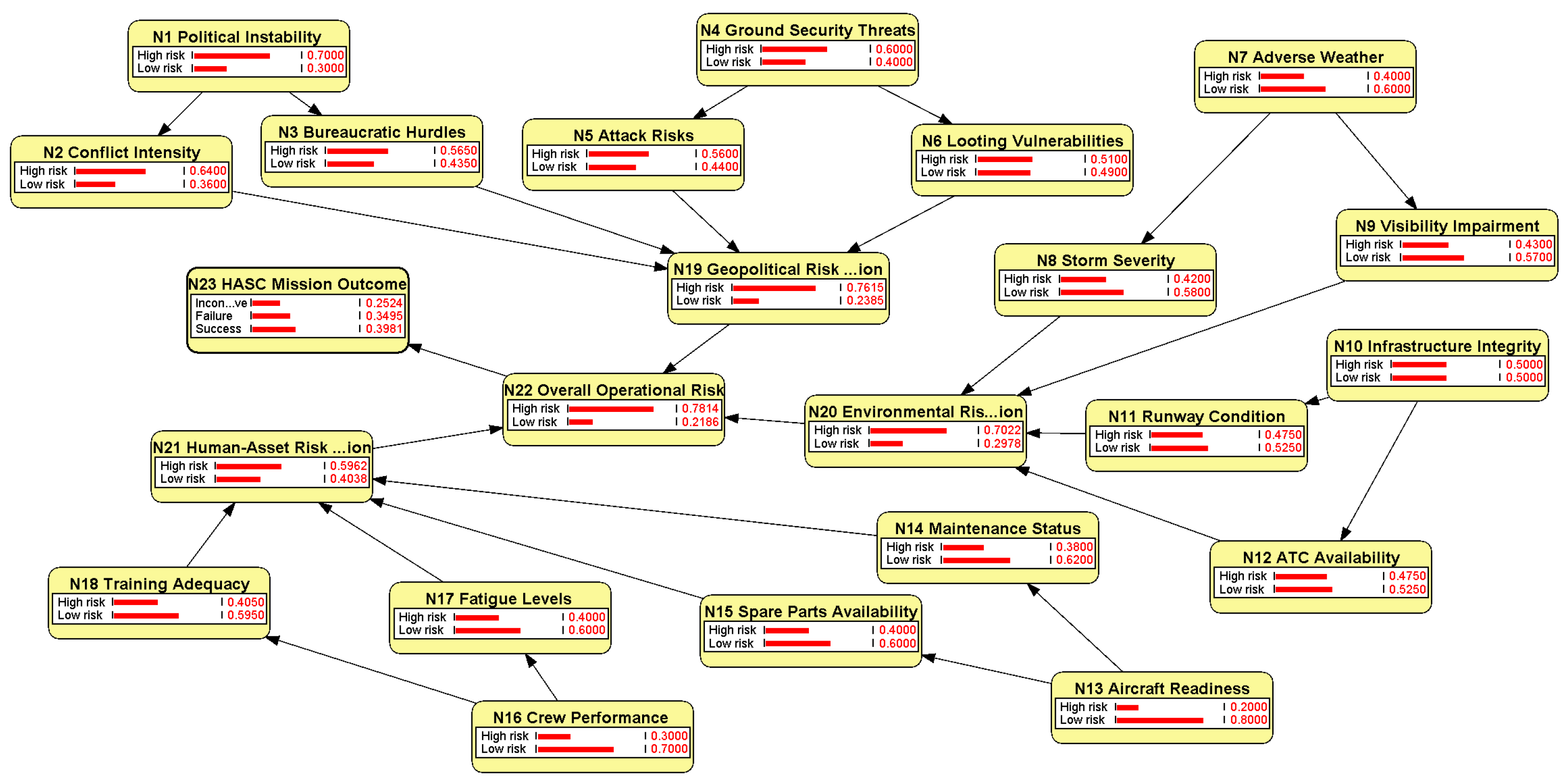
3.2. Proposed Network Structure and Node Definitions

The BN designed for HASC risk analysis adopts a multi-layered architecture comprising 23 nodes, organized into a hierarchical structure that mirrors the causal flow of risks from individual factors to aggregated outcomes. This design reflects the real-world dynamics of humanitarian aviation, where specific risks in geopolitical, environmental, or human domains propagate through the supply chain, influencing overall mission success. The network is divided into three primary layers:

1

Foundational Layer (Nodes N1–N18): This layer encompasses individual risk factors derived from aviation safety research (e.g., [4]) and humanitarian logistics studies (e.g., [5]). These nodes are grouped into three domains:

• Geopolitical and Security: This domain encompasses risks such as political instability, conflict intensity, and ground security threats, reflecting the challenges of operating in unstable regions.
• Operational and Environmental: This domain includes weather-related risks, infrastructure conditions, and air traffic control availability, variables critical to aviation safety and logistics efficiency.
• Asset and Human Factors: This domain covers aircraft readiness, maintenance logistics, and crew performance, addressing the technical and human elements of mission execution.

Within each domain, nodes are interconnected to capture hierarchical dependencies. For example, ‘Political Instability’ (N1) influences ‘Conflict Intensity’ (N2), as unstable governance often escalates into armed conflicts that disrupt operations.

2

Intermediate Aggregation Layer (Nodes N19–N21): These nodes synthesize risks within their respective domains:

• N19: Geopolitical risk aggregation integrates conflict intensity, bureaucratic hurdles, attack risks, and looting vulnerabilities, providing a consolidated view of security-related threats.
• N20: Environmental risk aggregation combines storm severity, visibility impairment, runway conditions, and ATC (air traffic control) availability, assessing operational feasibility under environmental constraints.
• N21: Human-asset risk aggregation aggregates maintenance status, spare part availability, fatigue levels, and training adequacy to evaluate the readiness of personnel and equipment.

This aggregation reduces complexity while preserving the model’s ability to pinpoint domain-specific risk contributions.

3

Outcome Layer (Nodes N22–N23):

• N22: Overall operational risk serves as the central node, synthesizing inputs from N19, N20, and N21 to provide a holistic risk assessment.
• N23: The HASC mission outcome depends solely on N22, representing the probability of mission success or failure, such as the timely delivery of aid.

This layered structure facilitates a logical progression of risk analysis, enabling stakeholders to trace how individual factors contribute to broader outcomes. For instance, severe storms (N8) may impair visibility (N9) and degrade runway conditions (N11), increasing environmental risk (N20), which in turn elevates overall operational risk (N22) and jeopardizes mission success (N23).

To enhance clarity, the information in

Table 1. BN node definitions and dependencies.

Node ID	Attribute	Parent ID(s)
N1	Political Instability	None
N2	Conflict Intensity	N1
N3	Bureaucratic Hurdles	N1
N4	Ground Security Threats	None
N5	Attack Risks	N4
N6	Looting Vulnerabilities	N4
N7	Adverse Weather	None
N8	Storm Severity	N7
N9	Visibility Impairment	N7
N10	Infrastructure Integrity	None
N11	Runway Condition	N10
N12	ATC Availability	N10
N13	Aircraft Readiness	None
N14	Maintenance Status	N13
N15	Spare Part Availability	N13
N16	Crew Performance	None
N17	Fatigue Levels	N16
N18	Training Adequacy	N16
N19	Geopolitical Risk Aggregation	N2, N3, N5, N6
N20	Environmental Risk Aggregation	N8, N9, N11, N12
N21	Human-Asset Risk Aggregation	N14, N15, N17, N18
N22	Overall Operational Risk	N19, N20, N21
N23	HASC Mission Outcome	N22

below is refined with detailed node descriptions and their dependencies, ensuring each node’s role in the HASC context is explicit.

3.3. Dependencies and Risk Propagation

The dependencies within the BN are established based on causal relationships informed by existing studies. For example,

• Political instability (N1) increases the likelihood of conflict intensity (N2) and bureaucratic hurdles (N3), as unstable regions often experience heightened conflict and regulatory delays that impede aviation operations.
• Adverse weather (N7) directly influences storm severity (N8) and visibility impairment (N9), reflecting how meteorological conditions exacerbate operational risks.
• Crew performance (N16) affects fatigue levels (N17) and training adequacy (N18), as human factors are pivotal in managing mission demands under stress.

These dependencies enable the model to capture risk propagation. For instance, an increase in conflict intensity (N2) heightens attack risks (N5), which elevates geopolitical risk aggregation (N19). This, in turn, contributes to higher overall operational risk (N22), potentially compromising the mission outcome (N23). Such a structure allows stakeholders to identify critical pathways and prioritize interventions, such as enhancing security measures in conflict zones or improving crew rest protocols.

3.4. Conditional Probability Specification: The Noisy-OR Model

Specifying conditional probability tables (CPTs) in a BN with multiple parent nodes poses a significant challenge due to the exponential increase in required parameters. For example, a node with four parents, each with two states (e.g., high risk and low risk), would require $2^4=16$ probability entries per child state, a number that grows unwieldy with additional parents or states. In the HASC BN, intermediate nodes (N19–N21) and the central node (N22) each have multiple parents, necessitating a scalable approach.

The Noisy-OR model is adopted to address this complexity. This canonical model assumes that each parent can independently cause the effect (e.g., high risk), with a “leak” probability ($p_{\mathrm{leak}}$) accounting for unmodeled factors. The probability that the effect does not occur, given a set of active parents, is calculated as follows:

$$P(Y=\mathrm{false}\mid X)=(1-p_{\mathrm{leak}})\prod _{i\in I}(1-p_i)$$

where

• Y is the child node state (e.g., low risk);
• X represents the states of parent nodes;
• I is the set of active parents (e.g., those in a high-risk state);
• $p_i$ is the causal probability of parent i triggering the effect;
• $p_{\mathrm{leak}}$ is the probability of the effect occurring due to unaccounted influences.

Practical Example: Consider geopolitical risk aggregation (N19) with parents N2 (conflict intensity), N3 (bureaucratic hurdles), N5 (attack risks), and N6 (looting vulnerabilities). Suppose each parent has causal probabilities of $p_i=0.4$ and $p_{\mathrm{leak}}=0.05$. If N2 and N5 are active (high risk), the probability of low geopolitical risk is

$$P(N19=\mathrm{low}\mid N2=\mathrm{high},N5=\mathrm{high})=(1-0.05)\times (1-0.4)\times (1-0.4)=0.342$$

Thus, the probability of high geopolitical risk is $1-0.342=0.658$. This streamlined approach reduces the need to specify probabilities for all parent combinations, requiring only one $p_i$ per parent and a single $p_{\mathrm{leak}}$, significantly easing elicitation from experts in data-scarce humanitarian contexts.

The Noisy-OR model’s application to N19, N20, N21, and N22 ensures that the BN remains expressive yet computationally manageable, aligning with the practical constraints of HASC operations where full datasets are rarely available.

The proposed BN framework demonstrates inherent adaptability across diverse mission contexts. Geographic-specific risk factors can be incorporated through parameter recalibration, while mission-specific requirements can be addressed through structural modifications. This flexibility ensures the model’s applicability across different humanitarian aviation scenarios, from conflict zones to natural disaster responses.

4. Results and Analysis

4.1. Input Data

The HASC relies on a BN to model and analyze the multifaceted risks inherent in delivering aid under challenging conditions, such as conflict zones, disaster-affected regions, or areas with limited infrastructure. This subsection delineates the probabilistic input data required to parameterize the BN, encompassing prior probabilities for root nodes, CPTs for nodes with single parents, Noisy-OR parameters for aggregation nodes with multiple parents, and the CPT for the final node representing the mission outcome. Each node in the network is assumed to have binary states—high risk and low risk—except for the final node, N23, which adopts success and failure states to reflect the mission’s ultimate objective. These probabilities are carefully assigned to mirror the operational realities of humanitarian aviation, ensuring the model’s utility for risk assessments and decision-making.

The specification process begins with the root nodes, which lack parent nodes and thus require prior probabilities to establish their baseline risk levels. These nodes, N1 (political instability), N4 (ground security threats), N7 (adverse weather), N10 (infrastructure integrity), N13 (aircraft readiness), and N16 (crew performance), represent foundational risk factors influencing the HASC. For N1, political instability, the prior probability of a high-risk state is set to $P(\mathrm{N}1=\mathrm{High} \mathrm{Risk})=0.7$. This reflects the frequent occurrence of state fragility or civil unrest in regions necessitating humanitarian intervention. Similarly, N4, ground security threats, is assigned $P(\mathrm{N}4=\mathrm{High} \mathrm{Risk})=0.6$, acknowledging the substantial security challenges in operational areas like conflict zones, though it is not as pervasive as political instability. N7, adverse weather, receives $P(\mathrm{N}7=\mathrm{High} \mathrm{Risk})=0.4$, indicating a moderate likelihood of meteorological disruptions, such as storms or heavy precipitation, which vary across operational environments. For N10, infrastructure integrity, a balanced prior of $P(\mathrm{N}10=\mathrm{High} \mathrm{Risk})=0.5$ is chosen, recognizing that infrastructure in disaster-affected areas is equally likely to be compromised or adequate, depending on prior damage and repair efforts. N13, aircraft readiness, is given $P(\mathrm{N}13=\mathrm{High} \mathrm{Risk})=0.2$, reflecting the effectiveness of maintenance protocols, tempered by logistical challenges in remote settings. Lastly, N16, crew performance, is assigned $P(\mathrm{N}16=\mathrm{High} \mathrm{Risk})=0.3$, capturing the robustness of trained crews while accounting for stress and fatigue in demanding missions. These prior probabilities establish the initial risk profile, setting the stage for subsequent dependencies within the network.

Next, the nodes with single parents require CPTs to define how the parent’s state influences the child’s risk level. These nodes include N2 (conflict intensity), N3 (bureaucratic hurdles), N5 (attack risks), N6 (looting vulnerabilities), N8 (storm severity), N9 (visibility impairment), N11 (runway condition), N12 (ATC availability), N14 (maintenance status), N15 (spare part availability), N17 (fatigue levels), and N18 (training adequacy). Each CPT specifies the probability of the child node being in a high-risk state given the parent’s state, with the complementary low-risk probability derived as $1-P(\mathrm{High} \mathrm{Risk})$. The assignments are tailored to the specific relationships, ensuring realism and variability.

For N2, conflict intensity, with parent N1 (political instability), the CPT is defined as $P(\mathrm{N}2=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}1=\mathrm{High} \mathrm{Risk})=0.85$ and $P(\mathrm{N}2=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}1=\mathrm{Low} \mathrm{Risk})=0.15$. Political instability strongly drives conflict escalation, as fragile governance often leads to armed insurgencies disrupting operations, justifying the high conditional probability under instability, while a small residual risk persists even in stable regions. N3, bureaucratic hurdles, which are also dependent on N1, is assigned $P(\mathrm{N}3=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}1=\mathrm{High} \mathrm{Risk})=0.70$ and $P(\mathrm{N}3=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}1=\mathrm{Low} \mathrm{Risk})=0.25$. Unstable regions frequently impose regulatory delays, though international coordination may occasionally mitigate this, supporting a slightly lower probability than that for conflict intensity. Moving to N5, attack risks, with parent N4 (ground security threats), the probabilities are $P(\mathrm{N}5=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}4=\mathrm{High} \mathrm{Risk})=0.80$ and $P(\mathrm{N}5=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}4=\mathrm{Low} \mathrm{Risk})=0.20$. Security threats directly heighten the likelihood of attacks on aircraft or personnel, a critical concern in volatile areas, with a modest risk persisting even in safer contexts. For N6, looting vulnerabilities, which are also dependent on N4, the CPT is $P(\mathrm{N}6=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}4=\mathrm{High} \mathrm{Risk})=0.65$ and $P(\mathrm{N}6=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}4=\mathrm{Low} \mathrm{Risk})=0.30$. Security risks increase looting potential, but protective measures like escorts moderate this effect, while baseline vulnerabilities remain in low-risk scenarios.

In the environmental domain, N8, storm severity, depends on N7 (adverse weather) with $P(\mathrm{N}8=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}7=\mathrm{High} \mathrm{Risk})=0.90$ and $P(\mathrm{N}8=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}7=\mathrm{Low} \mathrm{Risk})=0.10$. Adverse weather almost certainly intensifies storms, severely impacting flight safety, with minimal storm risk in benign conditions. Similarly, N9, visibility impairment, which is also tied to N7, has $P(\mathrm{N}9=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}7=\mathrm{High} \mathrm{Risk})=0.85$ and $P(\mathrm{N}9=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}7=\mathrm{Low} \mathrm{Risk})=0.15$. Poor weather frequently reduces visibility, though navigation aids slightly lessen this effect in adverse conditions, and rare impairments occur otherwise. For N11, runway condition, with parent N10 (infrastructure integrity), the probabilities are $P(\mathrm{N}11=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}10=\mathrm{High} \mathrm{Risk})=0.75$ and $P(\mathrm{N}11=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}10=\mathrm{Low} \mathrm{Risk})=0.20$. Compromised infrastructure typically degrades runways, though temporary repairs mitigate this, with occasional wear in maintained facilities. N12, ATC availability, which is also dependent on N10, is assigned $P(\mathrm{N}12=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}10=\mathrm{High} \mathrm{Risk})=0.70$ and $P(\mathrm{N}12=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}10=\mathrm{Low} \mathrm{Risk})=0.25$. Poor infrastructure reduces air traffic control reliability, but backup systems sustain services, with intermittent disruptions possible even in good conditions.

In the human-asset domain, N14, maintenance status, depends on N13 (aircraft readiness), with $P(\mathrm{N}14=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}13=\mathrm{High} \mathrm{Risk})=0.70$ and $P(\mathrm{N}14=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}13=\mathrm{Low} \mathrm{Risk})=0.30$. Unreadiness often stems from maintenance issues, though other factors like crew errors also contribute, with minor lapses possible in ready aircraft. N15, spare part availability, which is also tied to N13, has $P(\mathrm{N}15=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}13=\mathrm{High} \mathrm{Risk})=0.60$ and $P(\mathrm{N}15=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}13=\mathrm{Low} \mathrm{Risk})=0.35$. Readiness issues may indicate part shortages, but alternative logistics moderate this, with logistical challenges persisting even in prepared scenarios. For N17, fatigue levels, with parent N16 (crew performance), the CPT is $P(\mathrm{N}17=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}16=\mathrm{High} \mathrm{Risk})=0.75$ and $P(\mathrm{N}17=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}16=\mathrm{Low} \mathrm{Risk})=0.25$. Suboptimal performance increases fatigue under demanding conditions, though rest protocols mitigate this, with fatigue possible even in high-performing crews. Lastly, N18, training adequacy, which is also dependent on N16, is assigned $P(\mathrm{N}18=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}16=\mathrm{High} \mathrm{Risk})=0.65$ and $P(\mathrm{N}18=\mathrm{High} \mathrm{Risk}\mid \mathrm{N}16=\mathrm{Low} \mathrm{Risk})=0.30$. Performance risks may reflect training gaps, but experienced crews reduce this effect, with residual needs in well-performing teams.

The aggregation nodes N19 (geopolitical risk aggregation), N20 (environmental risk aggregation), N21 (human-asset risk aggregation), and N22 (overall operational risk) each have multiple parents, necessitating the Noisy-OR model to manage the complexity of specifying full CPTs. The Noisy-OR model assumes each parent independently contributes to the child’s high-risk state, with a leak probability accounting for unmodeled factors. The probability of a low-risk state is calculated as $P(\mathrm{Child}=\mathrm{Low} \mathrm{Risk}\mid \mathrm{Parents})=(1-p_{\mathrm{leak}}){\prod }_{i\in I}(1-p_i)$, where I is the set of parents in high-risk states, $p_i$ is the causal probability per parent, and $p_{\mathrm{leak}}$ is the leak probability. The causal probabilities $p_i$ are assigned distinct values ranging from 0.3 to 0.7 to reflect the varying degrees of influence of each parent node, ensuring a realistic representation of their contributions to risk. The leak probability is uniformly set at $p_{\mathrm{leak}}=0.05$ across all aggregation nodes, representing a small but non-negligible chance of high risk due to unmodeled factors when all parents are in a low-risk state. The parameters are presented in

Table 2. Noisy-OR parameters for aggregation nodes.

Node	Parents	Causal Probabilities (${\mathit{p}}_{\mathit{i}}$)	Leak Probability (${\mathit{p}}_{\mathbf{leak}}$)
N19: Geopolitical Risk Aggregation	N2, N3, N5, N6	$p_2=0.6$, $p_3=0.4$, $p_5=0.6$, $p_6=0.4$	0.05
N20: Environmental Risk Aggregation	N8, N9, N11, N12	$p_8=0.7$, $p_9=0.6$, $p_{11}=0.5$, $p_{12}=0.3$	0.05
N21: Human-Asset Risk Aggregation	N14, N15, N17, N18	$p_{14}=0.6$, $p_{15}=0.4$, $p_{17}=0.5$, $p_{18}=0.5$	0.05
N22: Overall Operational Risk	N19, N20, N21	$p_{19}=0.6$, $p_{20}=0.5$, $p_{21}=0.4$	0.05

, followed by a detailed rationale for the chosen values.

The causal probabilities $p_i$ are carefully selected to mirror the operational significance and relative impact of each parent node within the HASC context, avoiding a uniform value (e.g., 0.4) to capture the diversity of risk contributions. Below, the reasoning for each node’s parameters is elaborated:

• N19: Geopolitical Risk Aggregation.
  Parents: N2 (Conflict Intensity), N3 (Bureaucratic Hurdles), N5 (Attack Risks), and N6 (Looting Vulnerabilities).

  -

  $p_2=0.6$: Conflict intensity is assigned a high causal probability due to its direct and severe impact on operational safety in conflict zones, where active hostilities can disrupt flights or ground operations.

  -

  $p_3=0.4$: Bureaucratic hurdles have a moderate influence, as regulatory delays or permit issues in unstable regions can impede logistics, though their effect is less immediate than physical threats.

  -

  $p_5=0.6$: Attack risks, like conflict intensity, warrant a high probability given their potential to directly endanger personnel and assets, a critical concern in volatile areas.

  -

  $p_6=0.4$: Looting vulnerabilities are moderately impactful, as they threaten supply chain integrity but can often be mitigated by security measures, reducing their severity relative to direct attacks.

• N20: Environmental Risk Aggregation.
  Parents: N8 (Storm Severity), N9 (Visibility Impairment), N11 (Runway Condition), and N12 (ATC Availability).

  -

  $p_8=0.7$: Storm severity receives the highest probability due to its critical and immediate effect on flight safety, as severe weather can ground aircraft or cause delays, posing a paramount risk in humanitarian missions.

  -

  $p_9=0.6$: Visibility impairment is highly influential, impairing navigation and landing, though it is slightly less disruptive than storms due to potential mitigation via instruments, justifying a slightly lower value.

  -

  $p_{11}=0.5$: The runway condition has a significant but moderate impact, as degraded runways affect takeoff and landing safety, yet repairs or alternative sites can temper this risk.

  -

  $p_{12}=0.3$: ATC availability is assigned the lowest probability, as while air traffic control is essential for coordination, backup systems or procedural adjustments can mitigate its absence, reducing its relative influence.

• N21: Human-Asset Risk Aggregation.
  Parents: N14 (Maintenance Status), N15 (Spare Parts Availability), N17 (Fatigue Levels), and N18 (Training Adequacy).

  -

  $p_{14}=0.6$: Maintenance status is critical, as poor maintenance directly compromises aircraft reliability, necessitating a high probability to reflect its pivotal role in operational readiness.

  -

  $p_{15}=0.4$: Spare part availability has a moderate effect, as shortages can delay repairs but are secondary to maintenance execution, and they are often manageable through logistics planning.

  -

  $p_{17}=0.5$: Fatigue levels significantly influence crew performance, particularly under demanding conditions, warranting a substantial yet balanced probability due to mitigation via rest protocols.

  -

  $p_{18}=0.5$: Training adequacy is equally important, as inadequate training impairs emergency handling, with its moderate-to-high value reflecting the need for skilled crews in high-stakes missions.

• N22: Overall Operational Risk.
  Parents: N19 (Geopolitical Risk Aggregation), N20 (Environmental Risk Aggregation), and N21 (Human-Asset Risk Aggregation).

  -

  $p_{19}=0.6$: Geopolitical risk aggregation is assigned a high probability due to its broad and severe implications for operational feasibility, as security threats often dictate mission viability.

  -

  $p_{20}=0.5$: Environmental risk aggregation has a significant impact, though slightly less than geopolitical factors, as weather-related risks can sometimes be mitigated through planning or rerouting.

  -

  $p_{21}=0.4$: Human-asset risk aggregation is moderately influential, as while critical, human and asset issues are often manageable through preparation, making it less dominant than external risks.

The leak probability $p_{\mathrm{leak}}=0.05$ is uniformly applied across all nodes to account for minor, unmodeled risks, such as rare events or external disruptions, ensuring the model remains robust and adaptable. These varied $p_i$ values, ranging from 0.3 to 0.7, provide a nuanced representation of risk dynamics, enabling the BN to effectively synthesize complex dependencies into actionable insights for HASC stakeholders.

The CPT for node N23 (HASC mission outcome) depends solely on N22 (overall operational risk) and categorizes the mission outcome into three possible states: success, failure, and inconclusive. The probabilities for each state are derived from the risk associated with operational conditions, as determined by the level of risk in N22. To incorporate uncertainty into the analysis, the CPT for node N23 uses a Beta distribution. The Beta distribution is chosen because it effectively models probabilities bounded between 0 and 1, and it allows for flexibility in capturing the inherent uncertainty in predicting the outcome of humanitarian missions under varying levels of operational risk. For high operational risk, the Beta distribution is parameterized with ${\alpha }_{\mathrm{High}}=2$ and ${\beta }_{\mathrm{High}}=5$, reflecting a strong belief in the possibility of failure. For low operational risk, the parameters ${\alpha }_{\mathrm{Low}}=8$ and ${\beta }_{\mathrm{Low}}=2$ are used, indicating a higher likelihood of success.

These input data-prior probabilities, tailored CPTs for single-parent nodes, Noisy-OR parameters, and the final CPT collectively enable the BN to capture the complex risk dynamics of HASC operations, supporting both predictive and diagnostic analyses to enhance mission resilience in challenging humanitarian contexts.

4.2. Analysis of the Results

The results of the HASC BN are illustrated in Figure 1. These probabilities provide critical insights into the risk landscape of humanitarian aviation missions, highlighting the interplay between various risk factors and their aggregated impact on mission outcomes.

The analysis shows that political instability (N1) is a key factor in determining the overall risk landscape. With a probability of 0.7000 for high-risk conditions, political instability significantly impacts mission success. Furthermore, conflict intensity (N2), which is highly correlated with political instability, also contributes to the operational risk, with a high risk probability of 0.6400. These findings underscore the importance of political stability in determining the feasibility of humanitarian missions.

Attack risks (N5) exhibit a significant probability of 0.5600 in high-risk scenarios, indicating that the threat of attacks poses a considerable danger to aviation operations in conflict zones. Similarly, geopolitical risk aggregation (N19), which integrates various geopolitical factors, shows a high probability of 0.7615 under high-risk conditions, reflecting the substantial influence of the geopolitical environment on the overall mission risk.

The overall operational risk (N22), which is influenced by factors such as geopolitical and environmental risks, is shown to have a high probability of 0.7814 under high-risk conditions. This reinforces the idea that missions are most vulnerable when the operational environment is unstable. As a result, the HASC mission outcome (N23) reflects the high-risk scenario with a failure probability of 0.3495 and a success probability of 0.3981, indicating that high operational risk significantly diminishes the likelihood of success, with a notable portion of outcomes classified as inconclusive (0.2524).

5. Conclusions

This study advances the risk assessment of the HASC by introducing a BN-based framework designed to evaluate the complex interplay of factors influencing mission success in high-risk humanitarian aviation operations. Drawing on the critical role of HASC as a lifeline for delivering aid to disaster- and conflict-affected regions, the research constructs a 23-node BN model that captures probabilistic relationships among geopolitical, environmental, and human-asset risk factors. These findings offer actionable insights for decision-makers to optimize logistics in volatile, resource-constrained environments.

Beyond aviation support, the BN framework can be adapted for other humanitarian operations through risk factor parameterization adjustments. The probabilistic modeling approach is particularly suitable for operations characterized by uncertainty and interdependent risk factors, enabling rapid model transfer and application across diverse humanitarian contexts.

Despite its contributions, the proposed framework exhibits several limitations that warrant consideration. The reliance on literature-derived estimates for parameterizing conditional probabilities within the Noisy-OR model introduces potential subjectivity, as these estimates may vary or reflect biases, particularly in data-scarce humanitarian contexts. Furthermore, the model’s scope, while comprehensive, may not fully encapsulate all emergent risk factors, such as sudden diplomatic shifts or rare environmental anomalies, due to the inherent complexity and unpredictability of real-world operations. Data availability poses an additional constraint, with incomplete or inconsistent records limiting the precision of prior probabilities for certain nodes. In addition, the current study primarily constructs the BN model based on theoretical underpinnings and assumed data due to the challenges of accessing historical HASC mission data. These limitations highlight the need for continuous validation and refinement to ensure the model’s applicability across diverse operational settings.

Future research can enhance this framework by addressing these shortcomings and expanding its scope. Incorporating real-time data streams, such as satellite-based weather monitoring or live conflict zone updates, could improve the model’s responsiveness to dynamic conditions. Exploring advanced probabilistic models, such as dynamic Bayesian networks, may better capture temporal dependencies and evolving risks, offering a more adaptive risk assessment tool. Applying the BN framework to specific case studies, such as urban disaster relief or pandemic response missions, would test its generalizability and uncover context-specific vulnerabilities. Future validation efforts should focus on establishing partnerships with humanitarian aviation organizations to access historical mission data. This would enable retrospective analysis of the model’s predictive accuracy and facilitate iterative refinement of the probabilistic parameters through expert feedback loops and empirical validation. Additionally, integrating machine learning techniques to refine parameter estimation or conduct predictive analytics could enhance the model’s precision and foresight. These directions promise to build on the current study, further solidifying the BN approach as a cornerstone for proactive risk management and fostering more resilient humanitarian aviation operations capable of meeting the demands of global crises. Additionally, beyond aviation support, the BN framework can be adapted for other humanitarian operations through risk factor parameterization adjustments. The probabilistic modeling approach is particularly suitable for operations characterized by uncertainty and interdependent risk factors, enabling rapid model transfer and application across diverse humanitarian contexts.