Influence of Bedding Angle on Mechanical Behavior and Grouting Reinforcement in Argillaceous Slate: Insights from Laboratory Tests and Field Experiments
Abstract
1. Introduction
2. Experimental Materials and Methods
2.1. Rock Specimens and Laboratory Testing Methods
2.2. Field Grouting Trial: Materials and Experimental Protocol
3. Results and Discussion
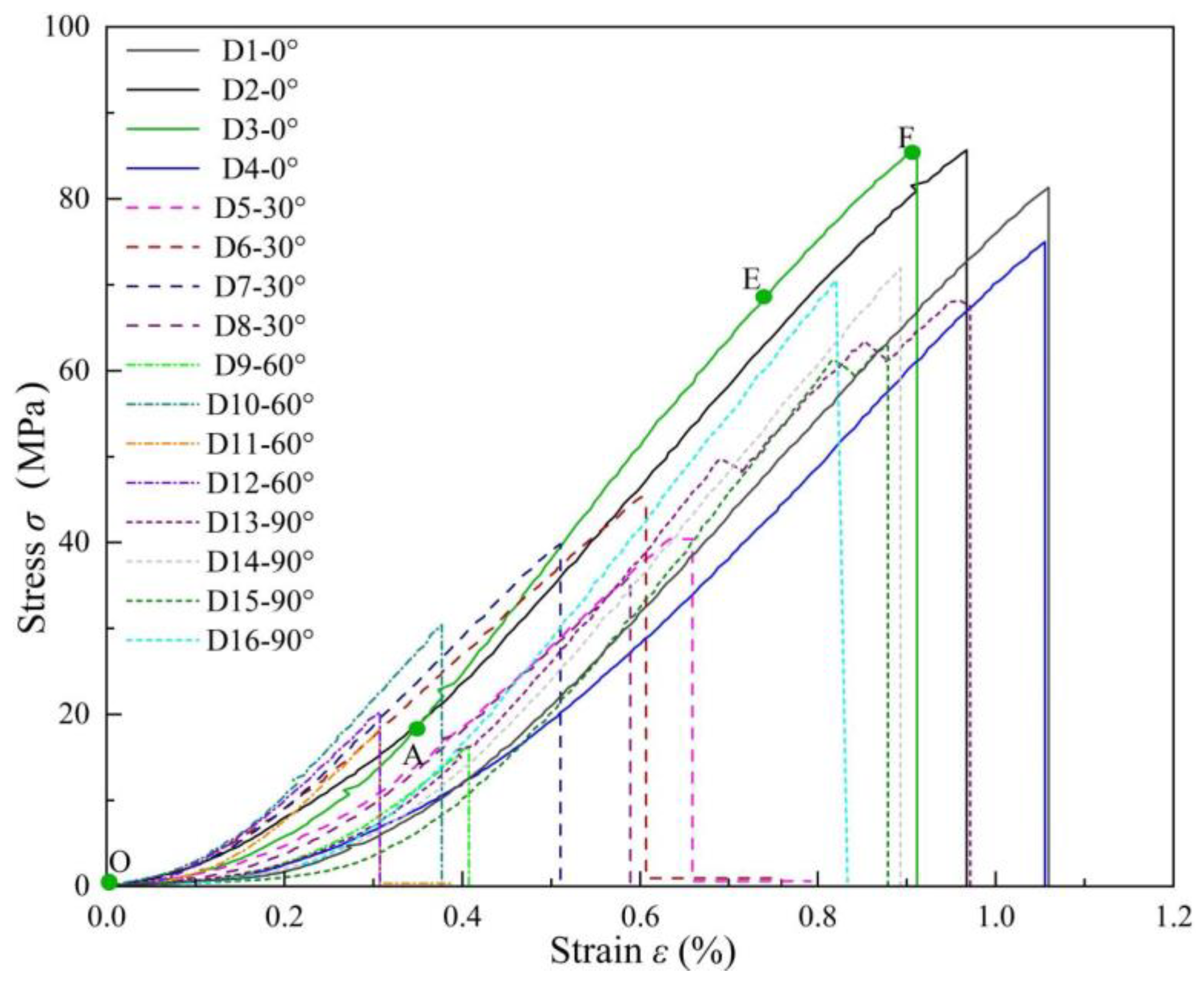
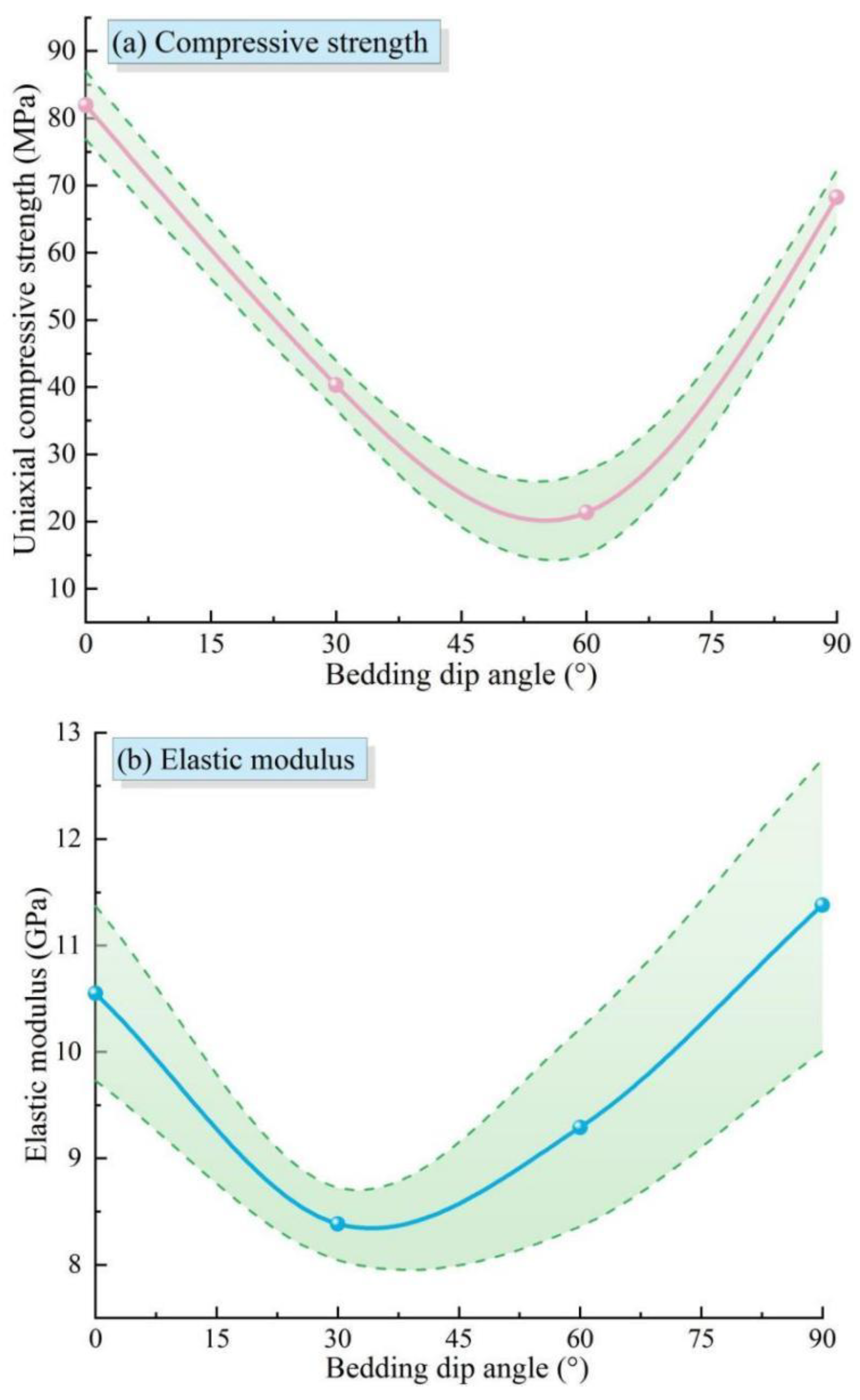
3.1. Uniaxial Compression Test Results and Analysis
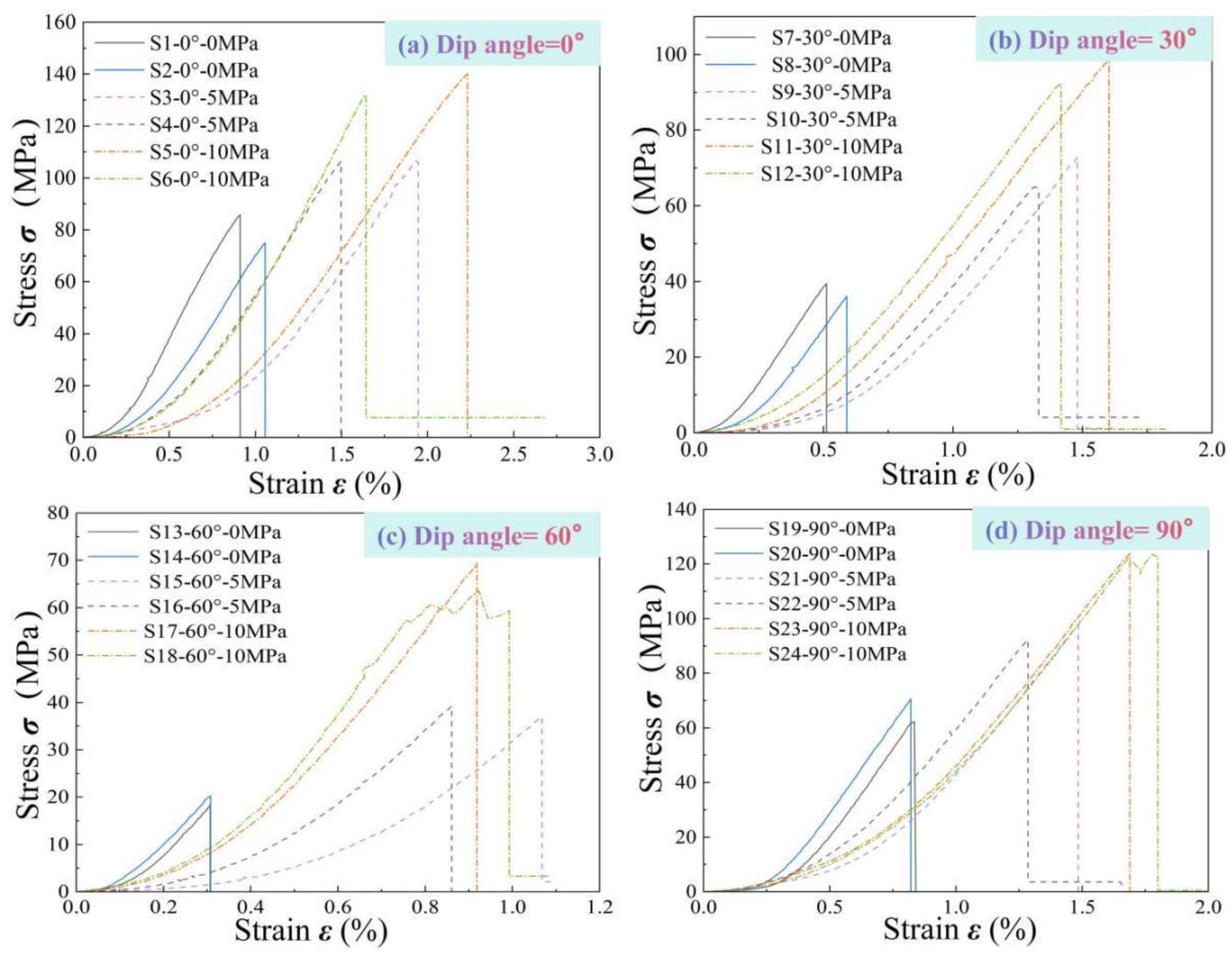
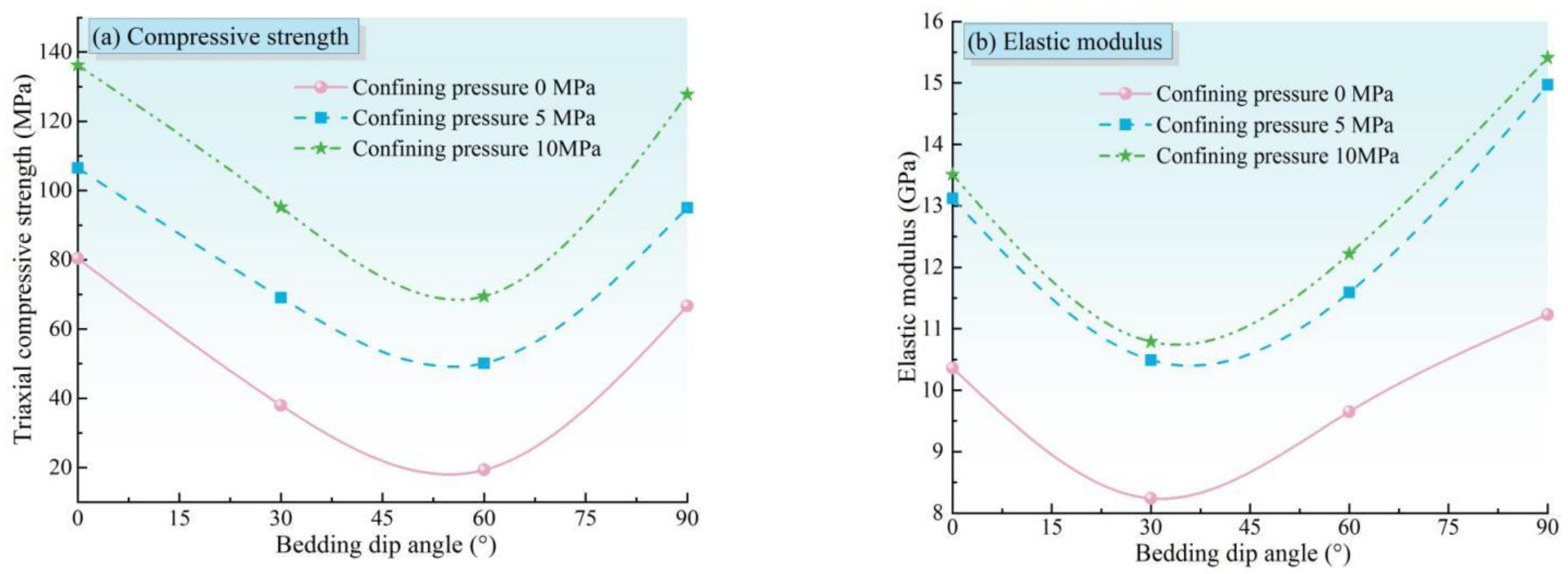
3.2. Triaxial Compression Test Results and Analysis
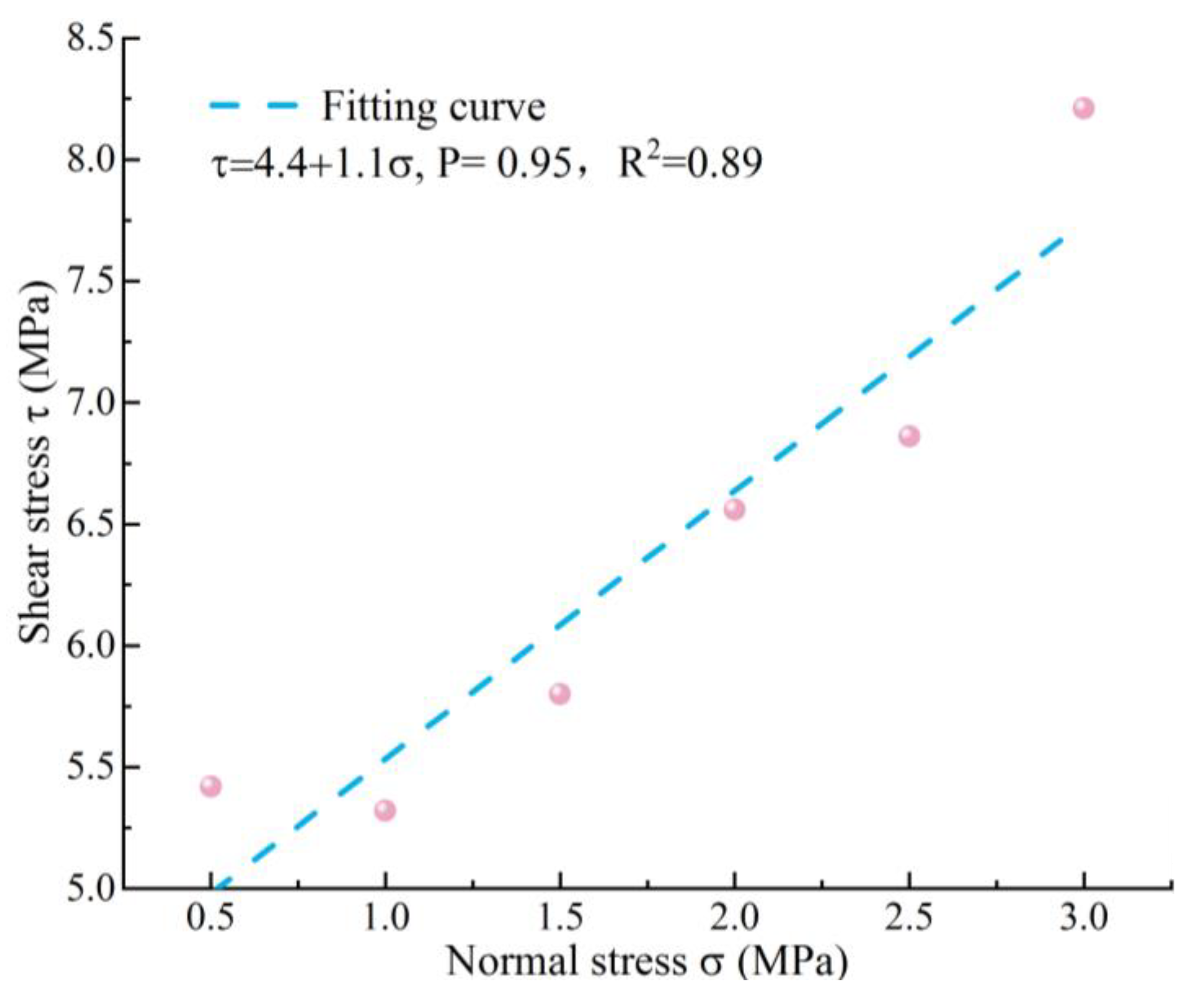
3.3. Direct Shear Test Results and Analysis
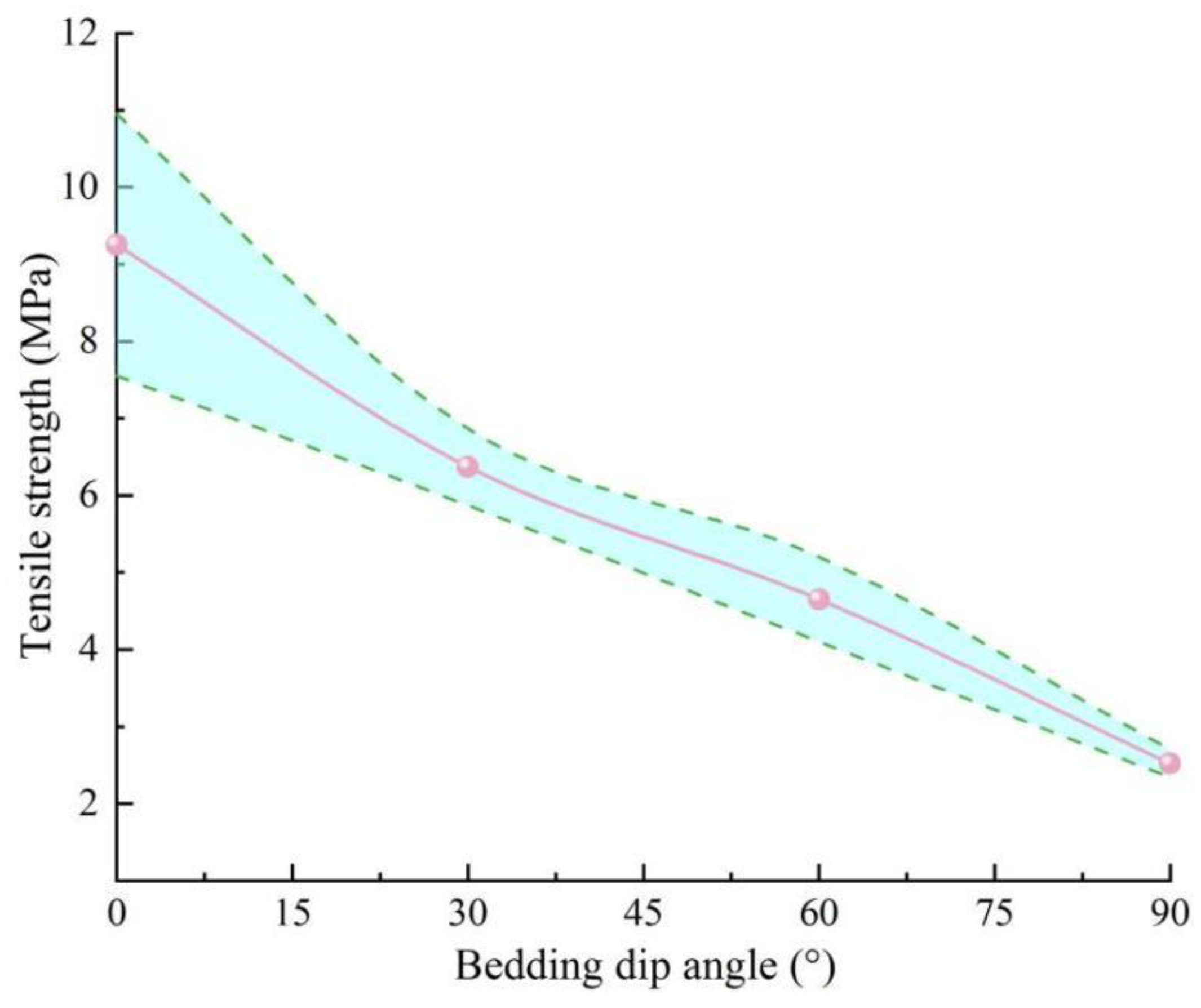
3.4. Tensile Strength Analysis via Brazilian Splitting Test
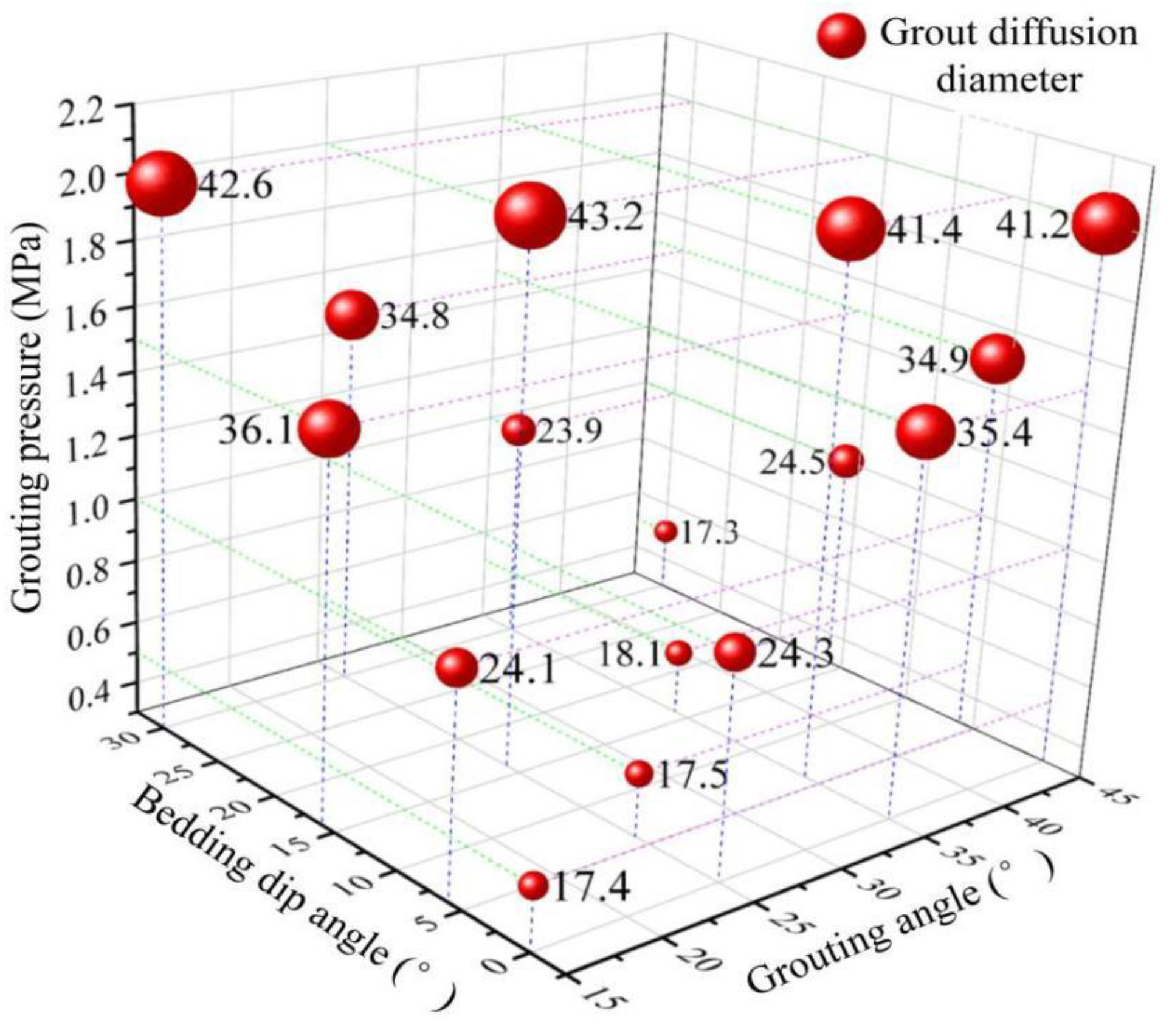
3.5. Field Grouting Test Results and Analysis
4. Conclusions
- (1)
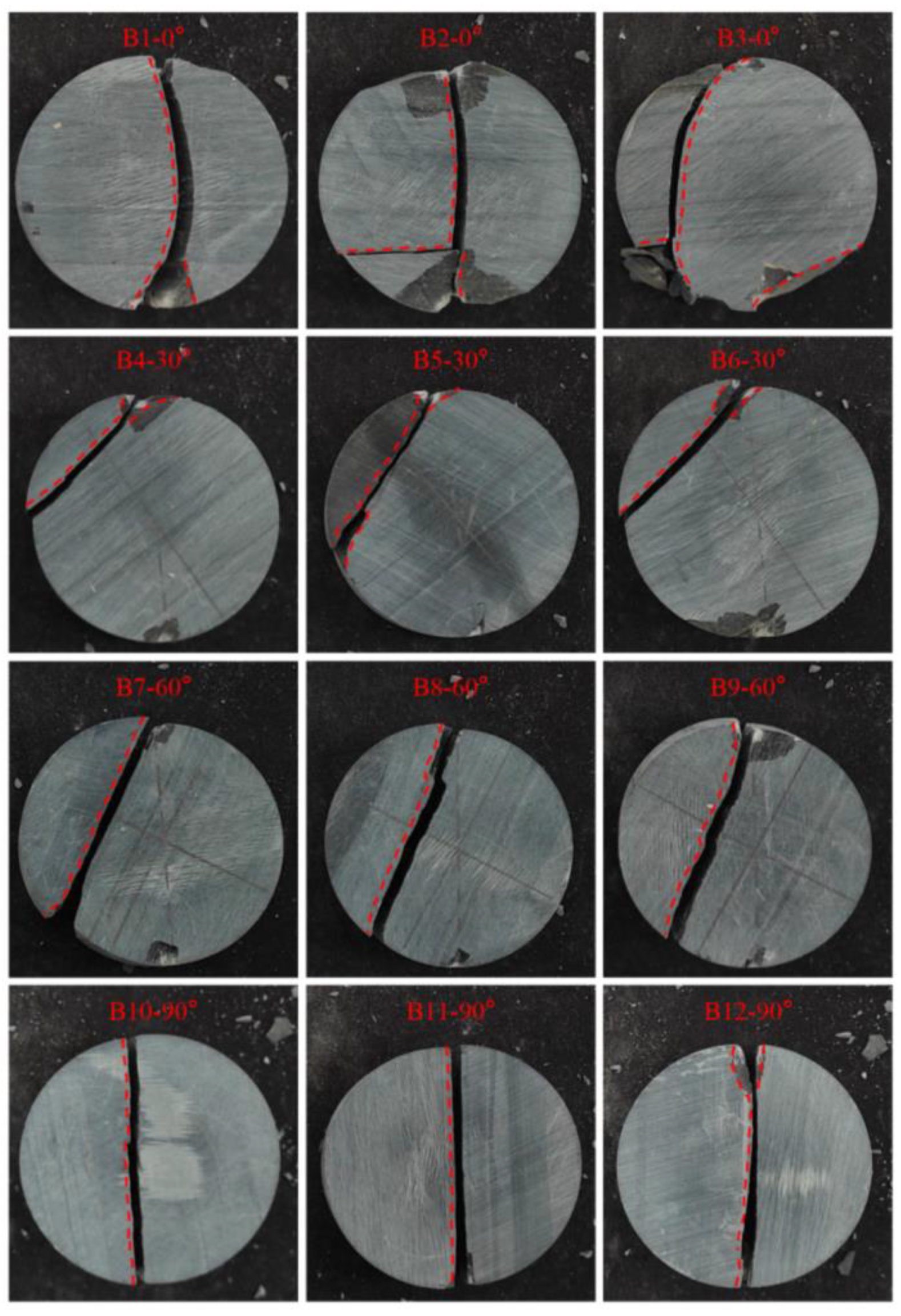
- The bedding dip angle significantly influences the failure mode of AS. Rock specimens with bedding dip angles of 0° and 30° primarily experience splitting tensile failure across bedding planes and partial shear failure; those with a 60° dip angle mainly undergo shear-slip failure, while specimens with a 90° dip angle predominantly exhibit splitting tensile failure. An increase in confining pressure causes the failure mode of rock specimens to transition from splitting tension to more complex shear-slip or compound failure, and a greater bedding dip angle leads to a change in the failure mode of rock specimens in splitting tests from arc-shaped and central cracks to cracks along bedding planes.
- (2)
- In the compression tests on AS, the stress–strain curves, along with the stress-displacement curves in splitting tests, mainly undergo four stages: crack closure, elastic deformation, crack propagation, and post-peak failure. As the bedding dip angle increases, the ultimate strain and peak stress in compression tests exhibit a trend of initially decreasing and then increasing, whereas they continuously decline in splitting tests.
- (3)
- The bedding dip angle significantly affects mechanical parameters of AS, such as compressive strength and elastic modulus. As the bedding dip angle varies from 0° to 90°, both the compressive strength and shear strength initially decrease and then increase, reaching their maximum at 0° and minimum at 60°. The shear strength of the rock bedding planes is notably lower than that of the matrix. Additionally, the tensile strength of the rock exhibits a declining trend with an increase in the bedding dip angle.
- (4)
- The high consistency of bedding in AS facilitates the regular diffusion of grout, which predominantly forms a near-circular diffusion zone centered around the borehole on the bedding plane.
- (5)
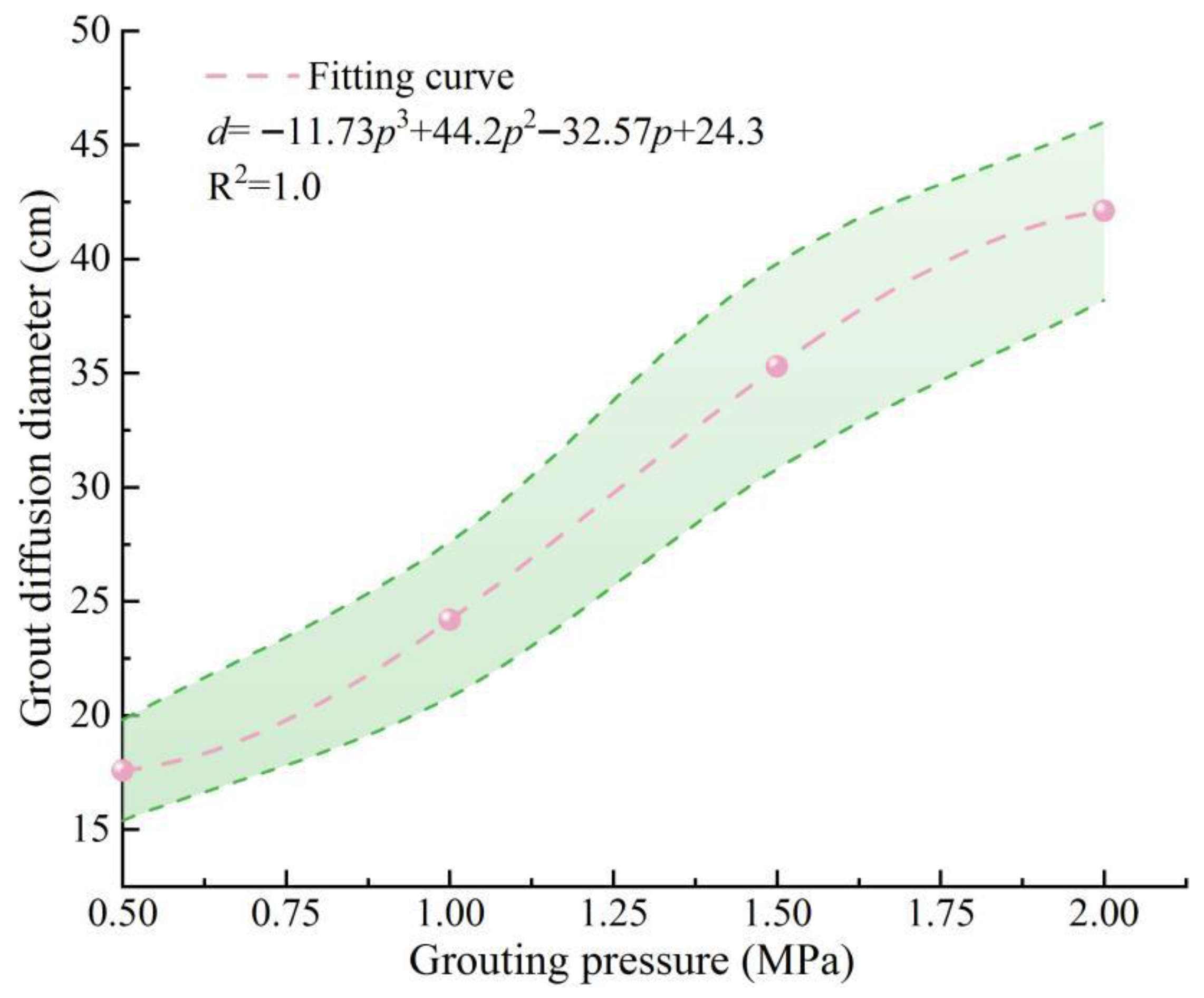
- Among the factors influencing the diffusion range of the grout, the bedding dip angle and grouting angle have relatively minor impacts, while the grouting pressure exerts a significant influence. A higher grouting pressure leads to a larger diffusion range; when the pressure exceeds 1.5 MPa, the increase in the diffusion range diminishes, and the diffusion is mainly concentrated within a region with a diameter ranging from 17.3 to 43.2 cm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zuo, Q.J.; Li, Z.M.; Zhang, Z.J.; Tang, L.S.; Li, P.; Han, B.X.; Li, X.Y. Anisotropy of argillaceous slate swelling evolution in water-rich environment. Chin. J. Rock Mech. Eng. 2022, 44, 2210–2224. [Google Scholar] [CrossRef]
- Wenk, H.R.; Yu, R.; Cardenes, V.; Lopez-Sanchez, M.A.; Sintubin, M. Fabric and anisotropy of slates: From classical studies to new results. J. Struct. Geol. 2020, 138, 104066. [Google Scholar] [CrossRef]
- Squitieri, A.; Amicone, S.; Dinckal, A.; Altaweel, M.; Gur-Arieh, S.; Rohde, J.; Herr, J.J.; Pietsch, S.; Miller, C. A multi-method study of a chalcolithic kiln in the bora plain (Iraqi Kurdistan): The evidence from excavation, micromorphological and pyrotechnological analyses. Open Archaeol. 2022, 8, 853–872. [Google Scholar] [CrossRef]
- Han, K.Y.; Zhang, H.; Ding, X.Z.; Ren, L.D.; Shi, C.L.; Pang, J.F. Zircon U-Pb ages and Lu-Hf isotope of the Dongchuan Group in central Yunnan, China, and their geological significance. Acta Geol. Sin. 2020, 94, 1093–1116. [Google Scholar] [CrossRef]
- Li, E.; Wei, Y.; Chen, Z.; Zhang, L. Experimental and numerical investigations of fracture behavior for transversely isotropic slate using semi-circular bend method. Appl. Sci. 2023, 13, 2418. [Google Scholar] [CrossRef]
- Li, H.; Zhu, K.; Chen, Y.; Chen, B.G.; Zeng, B.W.; Zhang, Z.Q. Formulation and implementation of elastoplastic constitutive model for carbonaceous slate. Bull. Eng. Geol. Environ. 2023, 82, 93. [Google Scholar] [CrossRef]
- Ho, N.C.; van der Pluijm, B.A.; Peacor, D.R. Static recrystallization and preferred orientation of phyllosilicates: Michigamme Formation, northern Michigan, USA. J. Struct. Geol. 2001, 23, 887–893. [Google Scholar] [CrossRef]
- Price, W.R.; Ronck, C.L. Quarrying for world heritage designation: Slate tourism in North Wales. Geoheritage 2019, 11, 1839–1854. [Google Scholar] [CrossRef]
- Cardenes, V.; de León, M.P.; Rodríguez, X.A.; Rubio-Ordonez, X.A.; Rubio-Ordoñez, A. Roofing slate industry in Spain: History, geology, and geoheritage. Geoheritage 2019, 11, 19–34. [Google Scholar] [CrossRef]
- Hu, P.; Guo, W.; Wei, L. Applicability study on modified argillaceous slate as subgrade filling for high-speed railway. Appl. Sci. 2022, 12, 2227. [Google Scholar] [CrossRef]
- Abenojar, J.; López de Armentia, S.; Martínez, M.A. Slate–cork laminate enhanced with silicone for habitat industry application. Fire 2024, 7, 166. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Feng, X.T.; Xu, D.P.; Fan, Q.X. Experimental investigation of the mechanical behavior of bedded rocks and its implication for high sidewall caverns. Rock Mech. Rock Eng. 2016, 49, 3643–3669. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Wang, L.; Tang, H.; Liang, Y. Evaluation of rock slope stability for Yujian River dam site by kinematic and block theory analyses. Comput. Geotech. 2011, 38, 846–860. [Google Scholar] [CrossRef]
- Zeng, W.; Chen, Z.; Xie, Y.; Chen, Q. Investigation of damage and creep for bedding’s carbonaceous slate with chemical erosion effect. Materials 2023, 16, 5163. [Google Scholar] [CrossRef]
- Zuo, Q.; He, X.F.; Wu, Y.Y.; Yi, Q.L.; Zhu, S.; Liu, Y.L.; Jiang, J. Swelling evolution mechanism for argillaceous slate in a hydrochemical environment. Q. J. Eng. Geol. Hydrogeol. 2024, 57, qjegh2023114. [Google Scholar] [CrossRef]
- Zuo, Q.J.; Li, P.; Li, X.Y.; Chen, F.B. Swelling damage evolution of argillaceous slate in a water-rich environment. Q. J. Eng. Geol. Hydrogeol. 2023, 56, qjegh2022128. [Google Scholar] [CrossRef]
- Tang, S.B.; Li, J.M.; Ding, S.; Zhang, L.T. The influence of water-stress loading sequences on the creep behavior of granite. Bull. Eng. Geol. Environ. 2022, 81, 482. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Liu, H.; Gao, X.J.; Feng, Y.H. Meso–macro damage deterioration of weakly cemented red sandstone under the coupling effect of high-humidity and uniaxial loading. Eng. Fail. Anal. 2023, 143, 106911. [Google Scholar] [CrossRef]
- Liu, M.; Luo, X.; Bi, R.; Zhou, J.; Du, K. Impacts of bedding angle and cementation type of bedding planes on mechanical behavior of thin-layer structured bedded rocks under uniaxial compression. Geomech. Energy Environ. 2023, 35, 100473. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.; Zhang, Y.; Lei, J.; Li, X.; Huang, X.; Xu, C. Experimental study on mechanical properties of anisotropic slate under different water contents. Appl. Sci. 2024, 14, 1473. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Liu, X.; Zhou, Y. An experimental investigation on the foliation strike-angle effect of layered hard rock under engineering triaxial stress path. Materials 2023, 16, 5987. [Google Scholar] [CrossRef]
- Deng, X.; Shi, J.; Li, X.; Wang, R.; Zhang, J.; Yang, X. The secondary development and application of the improved nishihara creep model in soft rock tunnels. Buildings 2023, 13, 2082. [Google Scholar] [CrossRef]
- Li, L.; Yu, W.; Zhang, X.; Ming, R.; Wang, Q.; Lv, X. Comparative analysis of fracture characteristics and mechanical properties of shale and slate based on triaxial compression test. Chem. Technol. Fuels Oils 2021, 57, 813–817. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Jia, H.; Du, X.; Wang, Z.; Pan, G.; Zhang, M. Fitting of anisotropic strength parameters of laminated shale and its influence on wellbore instability. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 43. [Google Scholar] [CrossRef]
- Steiakakis, E.; Xiroudakis, G.; Lazos, I.; Vavadakis, D.; Bazdanis, G. Stability Analysis of a Multi-Layered Slope in an Open Pit Mine. Geosciences 2023, 13, 359. [Google Scholar] [CrossRef]
- Ren, S.; Tao, Z.; He, M.; Pang, S.; Li, M.; Xu, H. Stability analysis of open-pit gold mine slopes and optimization of mining scheme in Inner Mongolia, China. J. Mt. Sci. 2020, 17, 2997–3011. [Google Scholar] [CrossRef]
- He, M.C. Latest progress of soft rock mechanics and engineering in China. J. Rock Mech. Geotech. Eng. 2014, 6, 165–179. [Google Scholar] [CrossRef]
- Peng, Y.X.; Wu, L.; Peng, H.H.; Hao, Y.; An, Y.L. Theoretical and experimental study on rock resistance coefficient of soft rock tunnel considering creep effect. Arab. J. Sci. Eng. 2020, 45, 4333–4342. [Google Scholar] [CrossRef]
- Kien, D.V.; Anh, D.N.; Thai, D.N. Numerical simulation of the stability of rock mass around large underground cavern. Civ. Eng. J. 2022, 8, 81–91. [Google Scholar] [CrossRef]
- Song, J.; Lu, Z.; Pan, Y.; Ji, J.; Gao, Y. Investigation of seismic displacements in bedding rock slopes by an extended Newmark sliding block model. Landslides 2023, 21, 461–477. [Google Scholar] [CrossRef]
- Chen, G.; Jin, J.; Meng, X.; Qi, T.; Shi, W.; Chong, Y.; Yang, Y.; Bian, S. Influence of tectonic effects on the formation and characteristics of landslide dams on the NE Tibetan Plateau: A case study in the Bailong River Basin, China. Landslides 2024, 21, 2135–2153. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, W.Z.; Lu, K.P.; Yang, G.L. Study on failure mechanism and numerical simulation of argillaceous slate in southeastern Guizhou. ACS Omega 2023, 8, 33444–33451. [Google Scholar] [CrossRef]
- Kharichkin, A.I.; Babich, D.D.; Galimov, I.M.; Chernyatin, D.V. Influence of load parameters during landslide slope reinforcement with soil nails based on self-drilling hollow steel bars on their bearing capacity and strength properties. Bull. Sci. Res. Cent. Constr. 2024, 40, 70–79. [Google Scholar] [CrossRef]
- Deng, C.; Li, L.; Hu, H.; Xu, Z.; Zhou, Y.; Yin, Q.; Chen, J. Effect of magnetized water on the fundamental grouting properties of cement grout under varying magnetization conditions. Sci. Rep. 2025, 15, 700. [Google Scholar] [CrossRef]
- Liu, L.P.; Wang, X.G.; Pi, J.; Cao, R.L.; Duan, Q.W.; Zhang, Q. Rock mass behavior during high pressure grouting: An in-situ experimental investigation. Rock Mech. Rock Eng. 2025, 28, 2531–2547. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Li, G. Research on the Self-Drilling Anchor Pull-Out Test Model and the Stability of an Anchored Slope. Appl. Sci. 2025, 15, 5132. [Google Scholar] [CrossRef]
- Zhang, S.; Shang, D.; Jiang, Y.; Zhang, J.; Chen, H.; Jiang, T. Shear behavior of bolt–grout interfaces under constant normal stiffness: Influence of grout strength and thickness. Deep. Undergr. Sci. Eng. 2025, 1–14. [Google Scholar] [CrossRef]
- Li, L.; Deng, C.; Chen, Y.; Xu, Z.; Yan, W.; Zhou, Y. Experimental analysis of the slurry diffusion behavior characteristics of point source grouting and perforated pipe grouting in sandy soil. Buildings 2025, 15, 1133. [Google Scholar] [CrossRef]
- Yan, W.Q.; Deng, C.; Cai, Y.H.; Chu, A.K.; Shen, S.F.; Wu, X.Y. The optimization study of karst-filling clay-cement grout based on orthogonal experiment and regression analysis. Materials 2025, 18, 1943. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Deng, C.; Zhou, Y.; Tan, Q.; Yan, W.; Zhou, D.; Zhou, Y. Stability and rheological properties of grouts with waste glass powder as cement replacement: Influences of content and alkali activator. Materials 2025, 18, 353. [Google Scholar] [CrossRef] [PubMed]
- Sang, H.; Liu, B.; Liu, Q.; Kang, Y.; Lu, C. Study of Grouting Reinforcement Mechanism in Fractured Rock Mass and Its Engineering Application. Int. J. Geomech. 2024, 24, 04024057. [Google Scholar] [CrossRef]
- Zhang, G.S.; Xiao, M.L.; Zhang, Y.D.; Liu, H.Z.; Zhuo, L.; Xie, H.Q.; He, J.D. Experimental and numerical study on the mechanical properties of compressively precracked sandstone repaired by grouting. Constr. Build. Mater. 2022, 350, 128816. [Google Scholar] [CrossRef]
- SL/T 264—2020; Test Regulations for Rock in Water Resources and Hydropower Engineering. China Water & Power Press: Beijing, China, 2020.
- ASTM D7012-14; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens Under Varying States of Stress and Temperatures. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D3967-16; Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens. ASTM International: West Conshohocken, PA, USA, 2016.
- GB 50330-2013; Technical Code for Building Slope Engineering. Standards Press of China: Beijing, China, 2013.
- Mu, W.; Li, L.; Liu, H.; Ren, B.; Chen, J.; Wang, X. An experimental study on fracturing response and slurry flow of high-pressure grouting in fractured rock. Rock Mech. Rock Eng. 2024, 57, 4533–4558. [Google Scholar] [CrossRef]
- Bolina, F.L.; München, R.M.; Lago, B.D.; Kodur, V. A comparative study between ultra-high-performance concrete structures and normal strength concrete structures exposed to fire. Structures 2024, 68, 107197. [Google Scholar] [CrossRef]







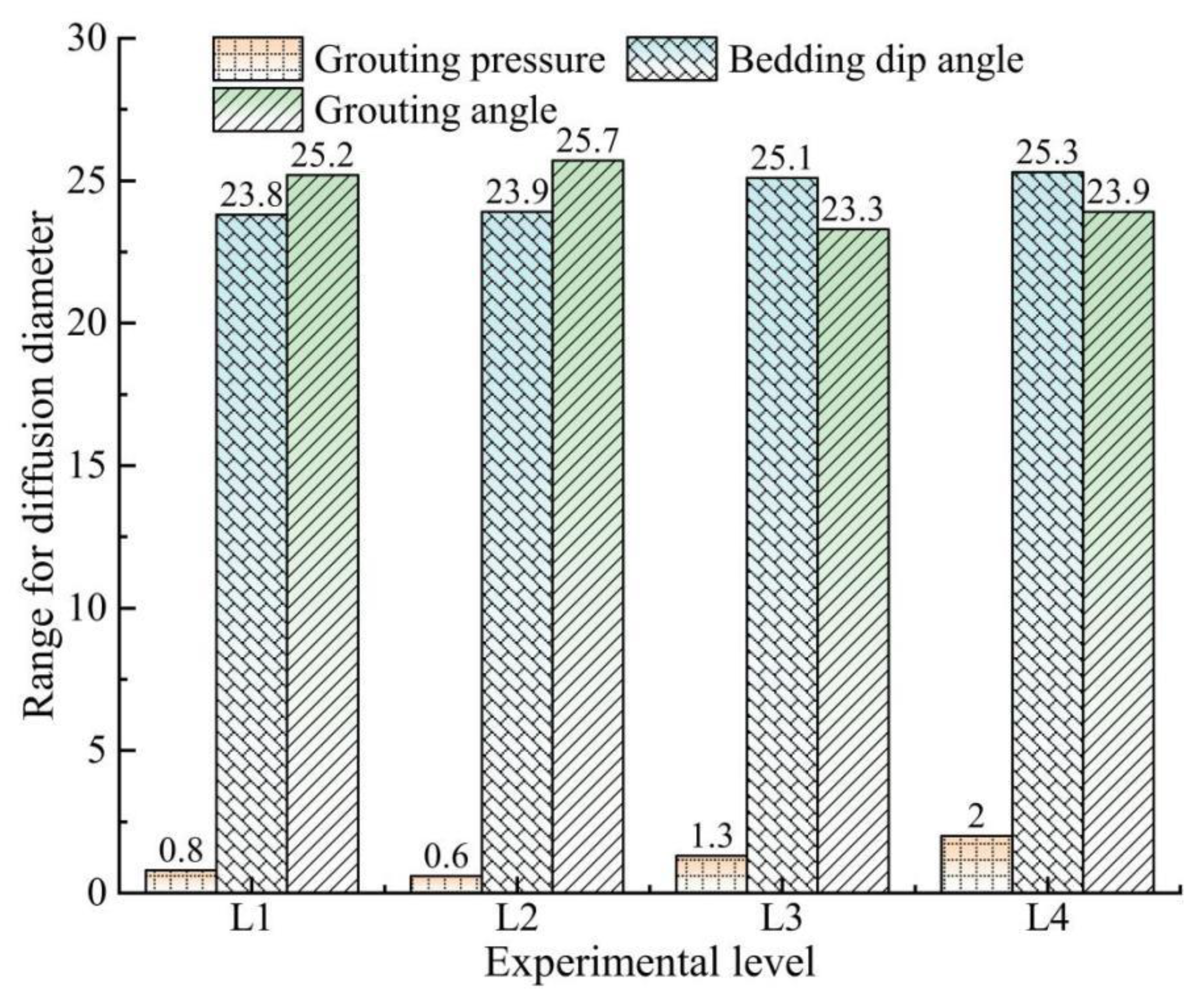
| Test Level | Influencing Factor | ||
|---|---|---|---|
| Bedding Dip Angle (°) | Grouting Pressure (MPa) | Injection Angle (°) | |
| L1 | 0 | 0.5 | 15 |
| L2 | 6 | 1.0 | 25 |
| L3 | 16 | 1.5 | 35 |
| L4 | 30 | 2.0 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Deng, C.; Yin, Q.; Chen, Y.; Rao, J.; Zhou, Y.; Yan, W. Influence of Bedding Angle on Mechanical Behavior and Grouting Reinforcement in Argillaceous Slate: Insights from Laboratory Tests and Field Experiments. Appl. Sci. 2025, 15, 10415. https://doi.org/10.3390/app151910415
Zeng X, Deng C, Yin Q, Chen Y, Rao J, Zhou Y, Yan W. Influence of Bedding Angle on Mechanical Behavior and Grouting Reinforcement in Argillaceous Slate: Insights from Laboratory Tests and Field Experiments. Applied Sciences. 2025; 15(19):10415. https://doi.org/10.3390/app151910415
Chicago/Turabian StyleZeng, Xinfa, Chao Deng, Quan Yin, Yi Chen, Junying Rao, Yi Zhou, and Wenqin Yan. 2025. "Influence of Bedding Angle on Mechanical Behavior and Grouting Reinforcement in Argillaceous Slate: Insights from Laboratory Tests and Field Experiments" Applied Sciences 15, no. 19: 10415. https://doi.org/10.3390/app151910415
APA StyleZeng, X., Deng, C., Yin, Q., Chen, Y., Rao, J., Zhou, Y., & Yan, W. (2025). Influence of Bedding Angle on Mechanical Behavior and Grouting Reinforcement in Argillaceous Slate: Insights from Laboratory Tests and Field Experiments. Applied Sciences, 15(19), 10415. https://doi.org/10.3390/app151910415






