Evaluation of Dental Trauma Splints in Early Permanent Dentition Through Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
3. Results
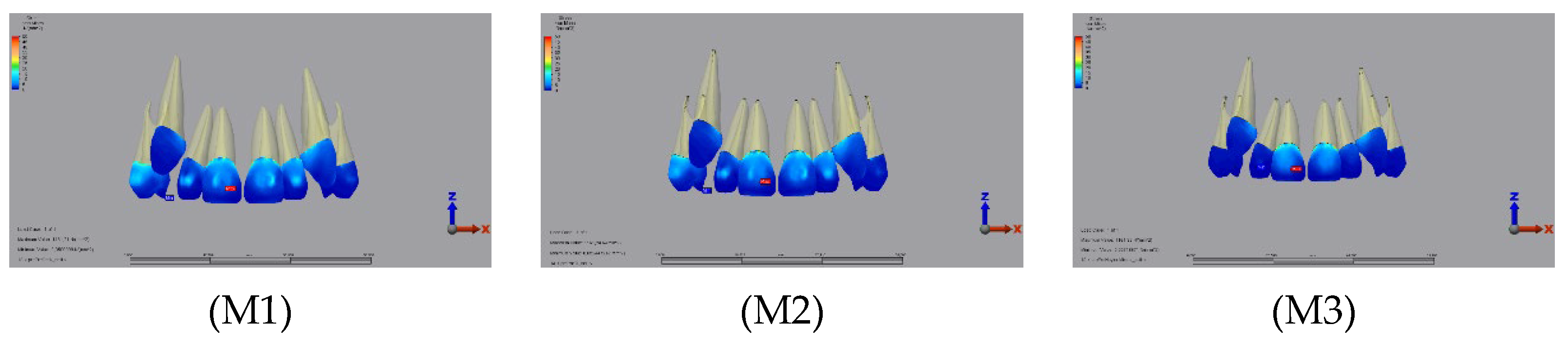
3.1. Von Mises Stress Values Formed in Models with Vertical Force Application
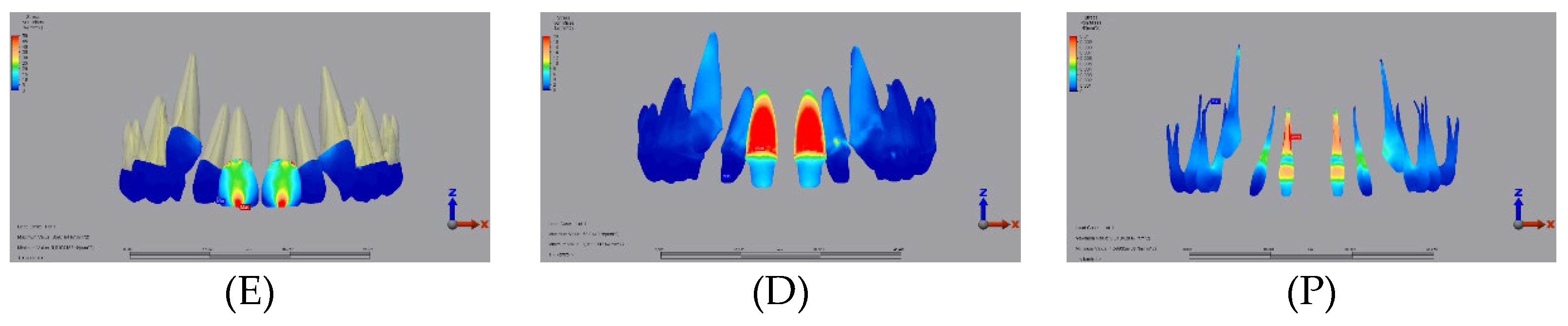
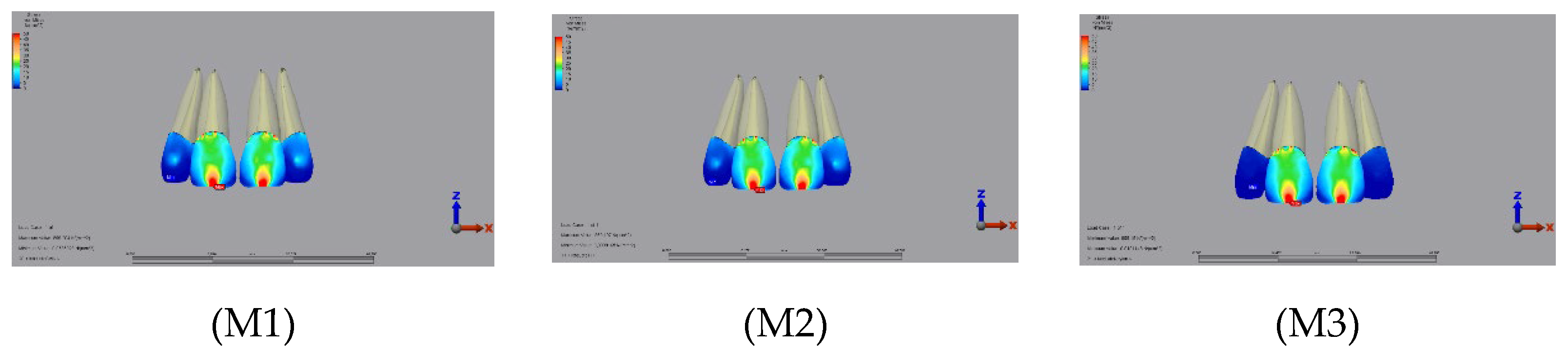
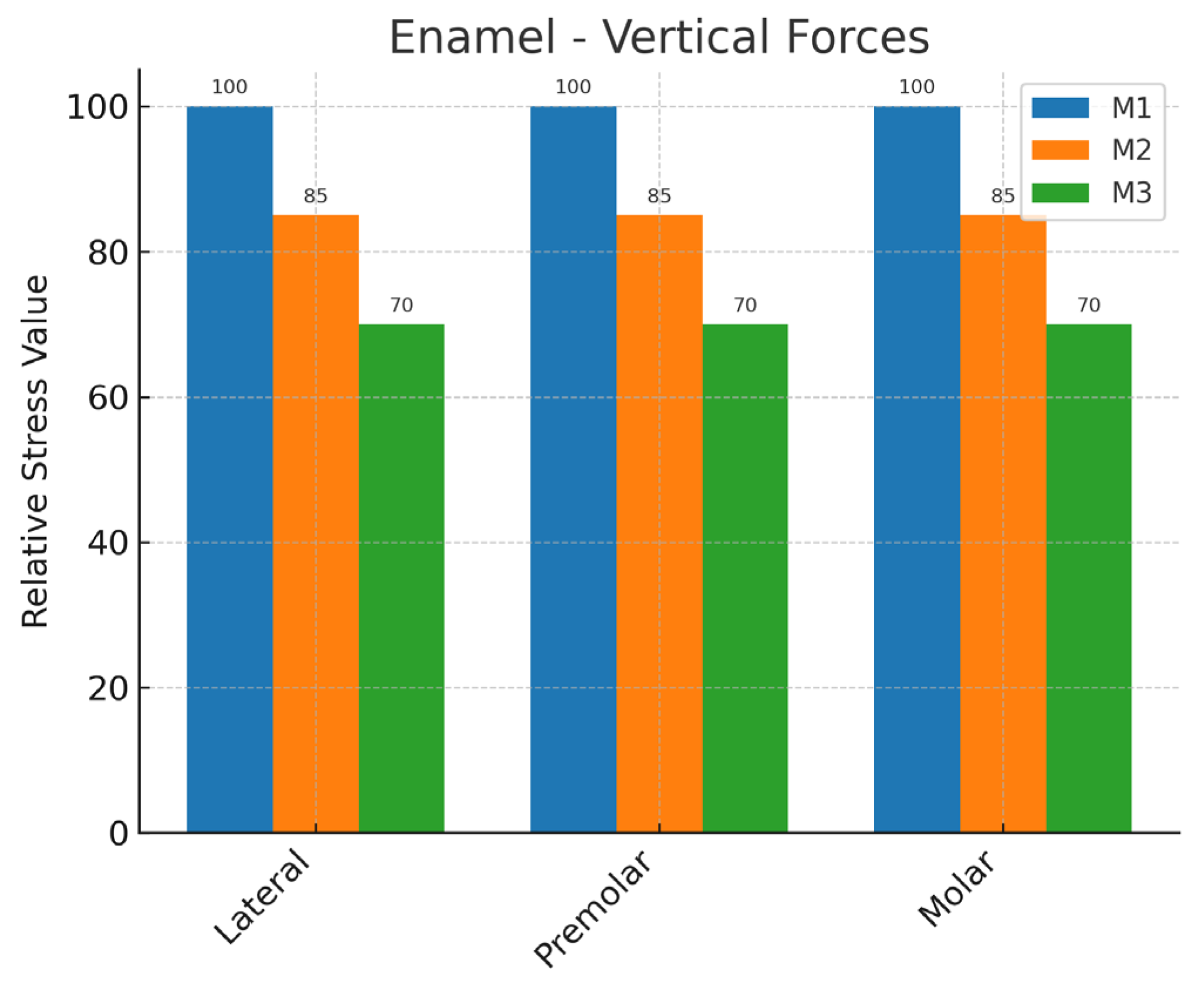
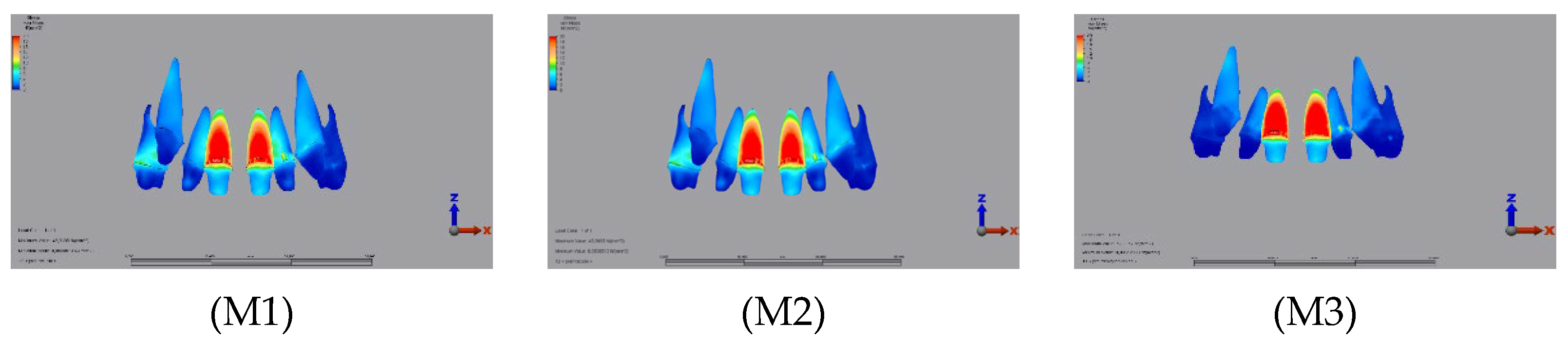
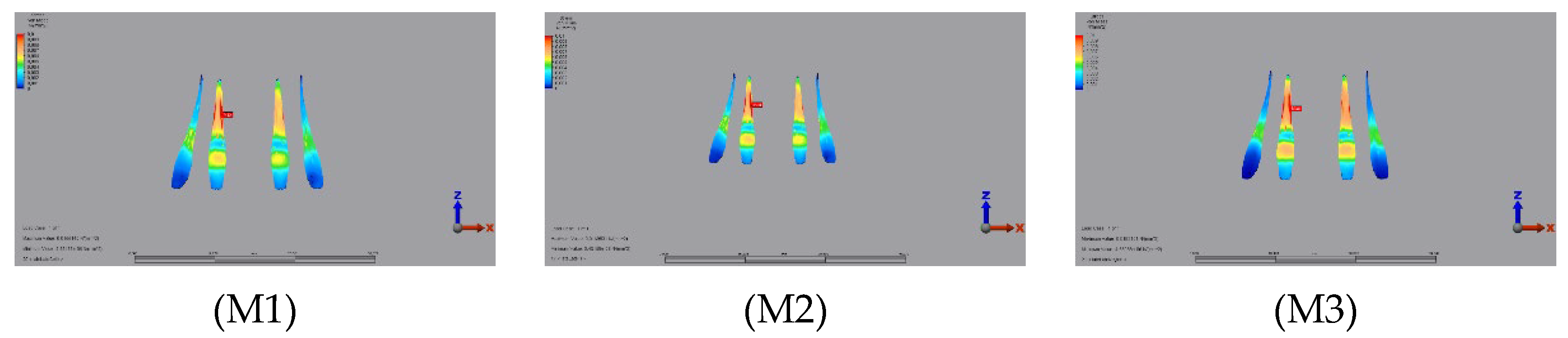
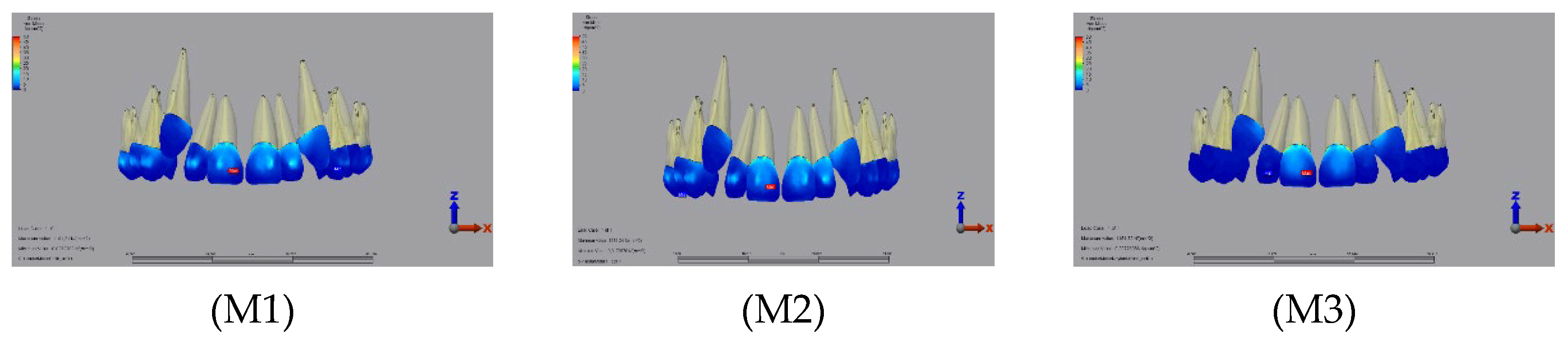
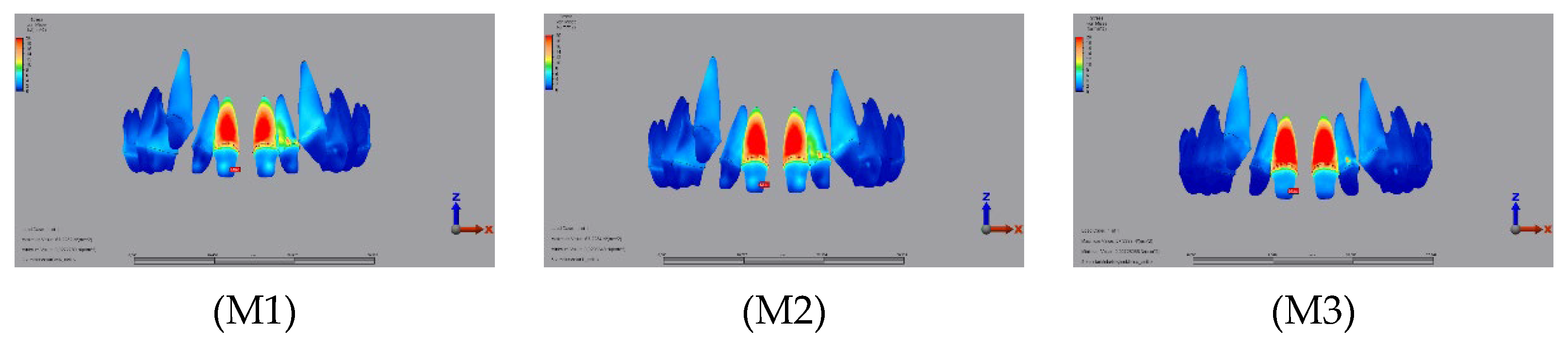
3.1.1. Enamel
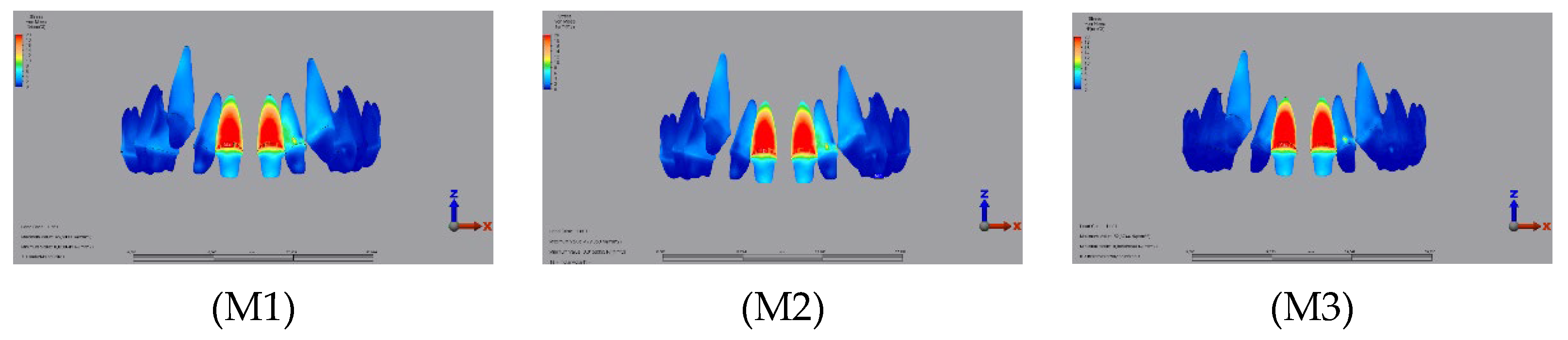
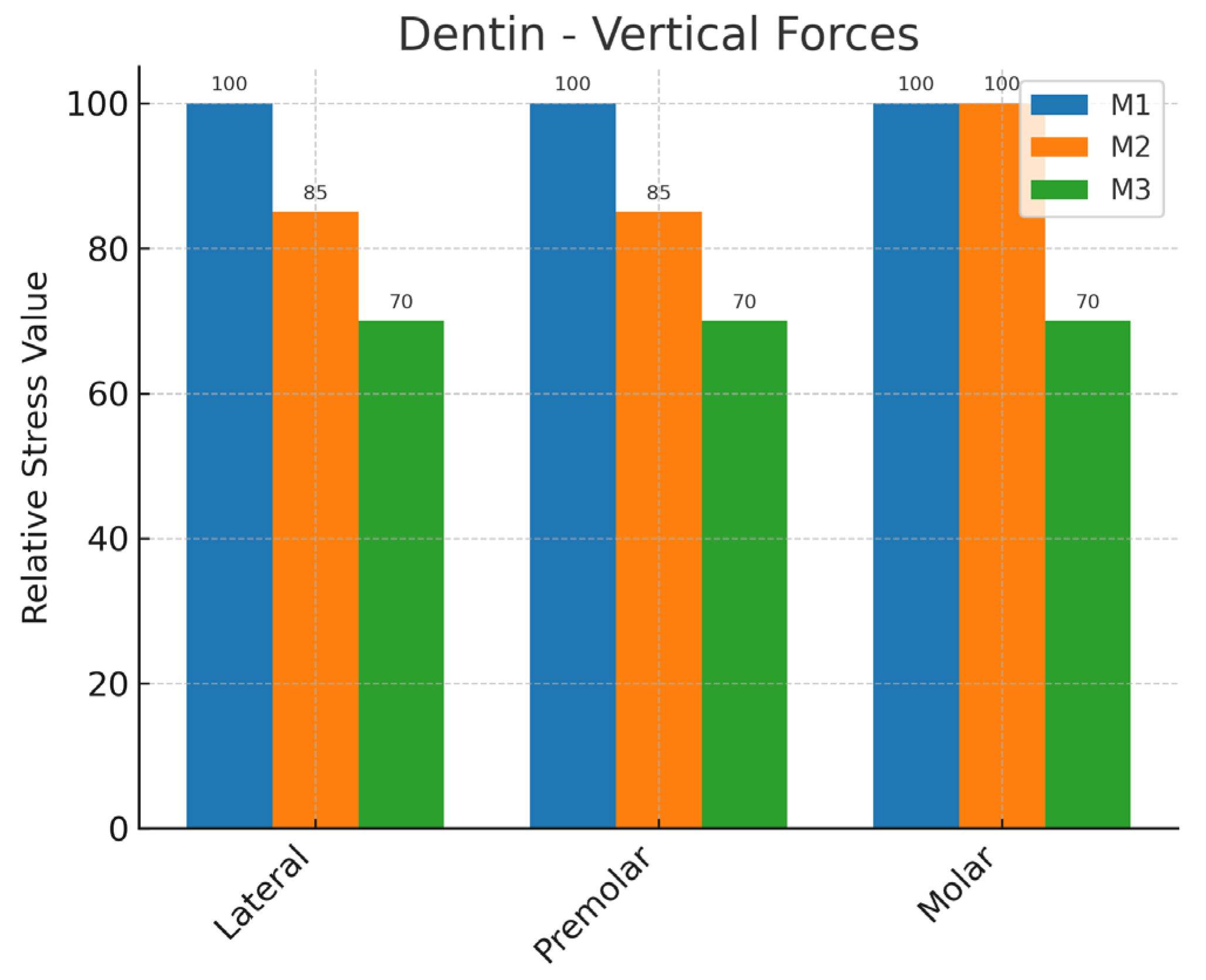
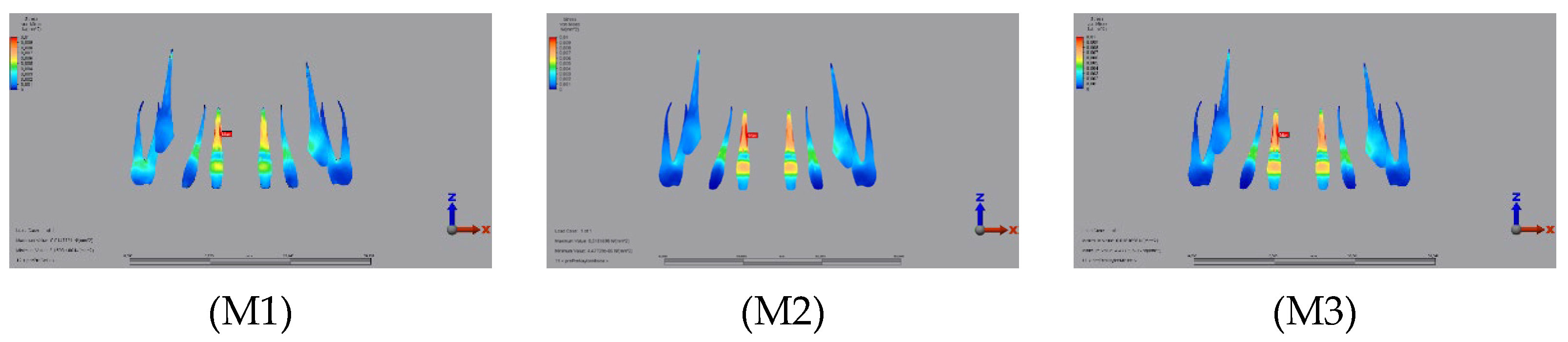
3.1.2. Dentin
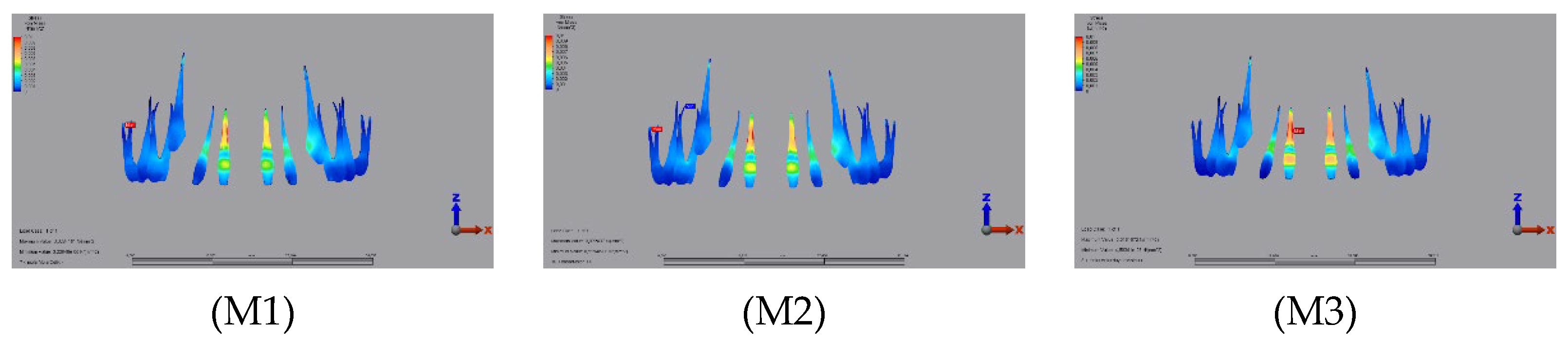
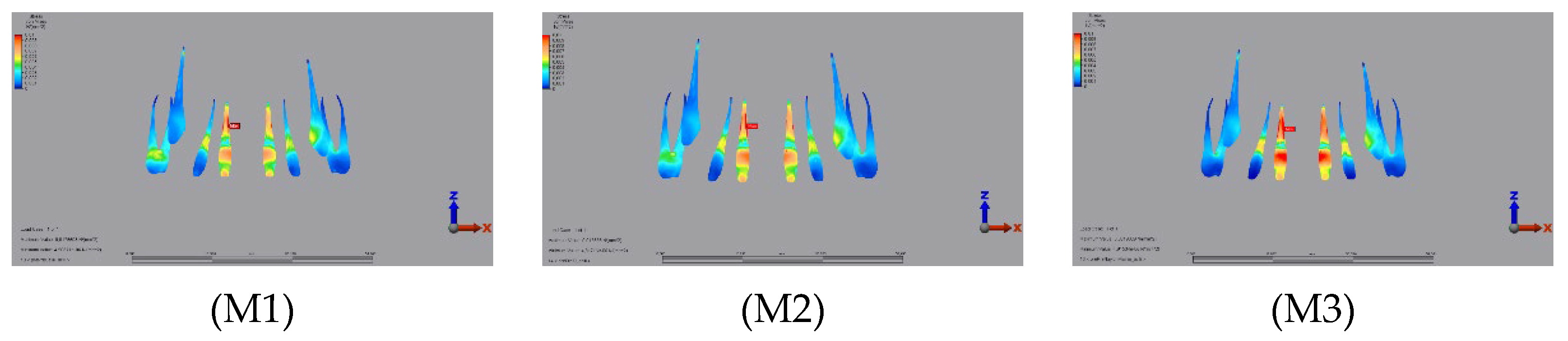
3.1.3. Pulp
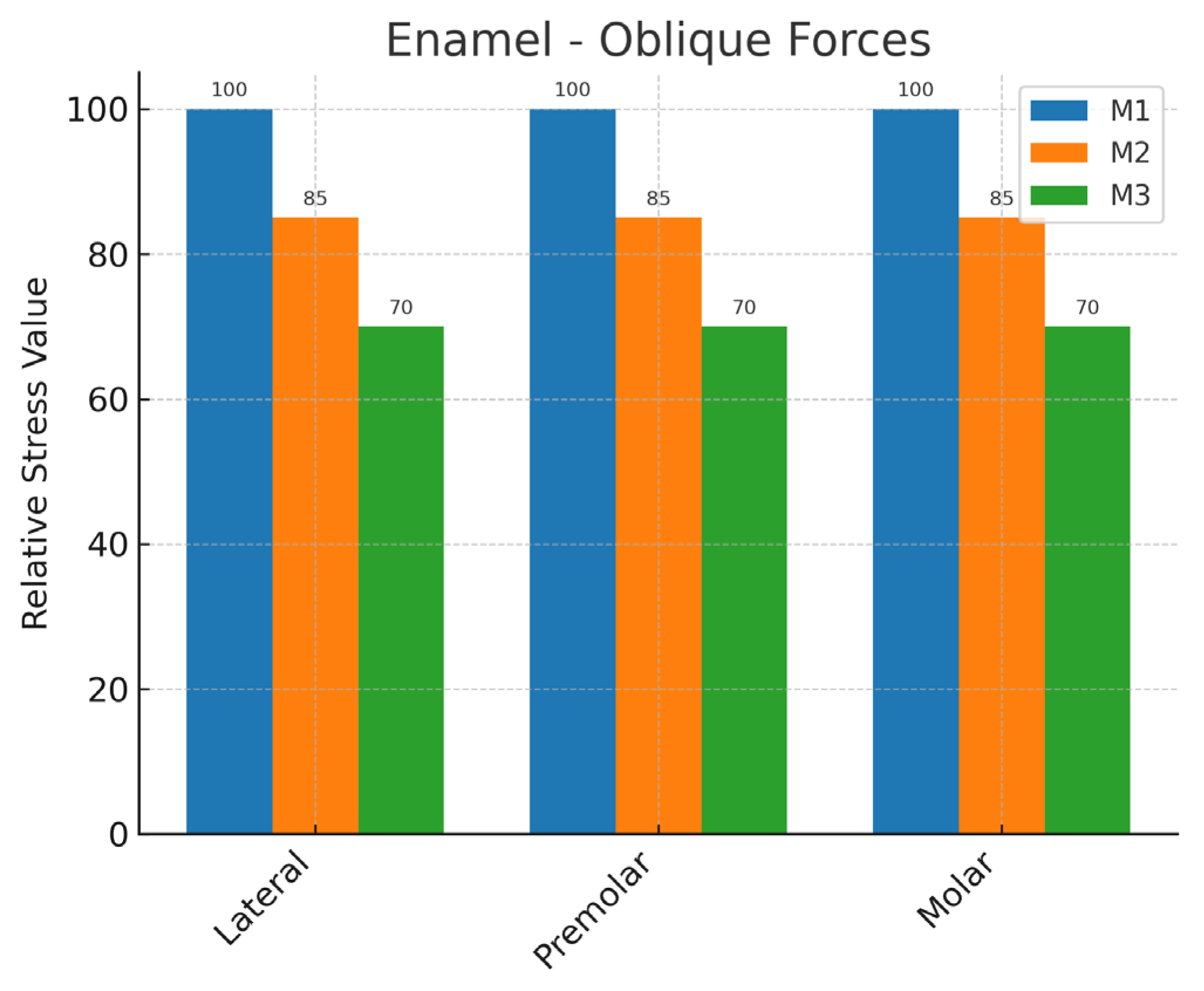
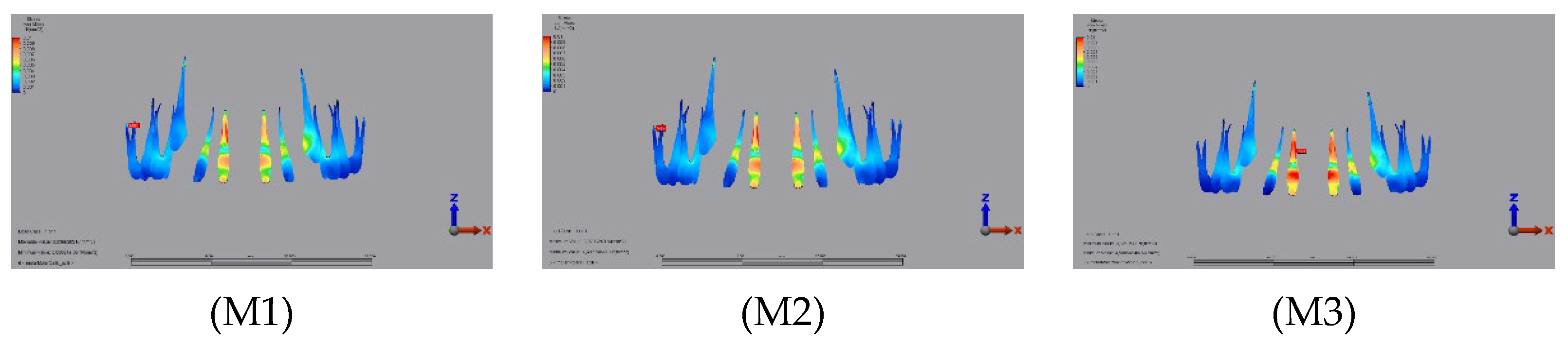
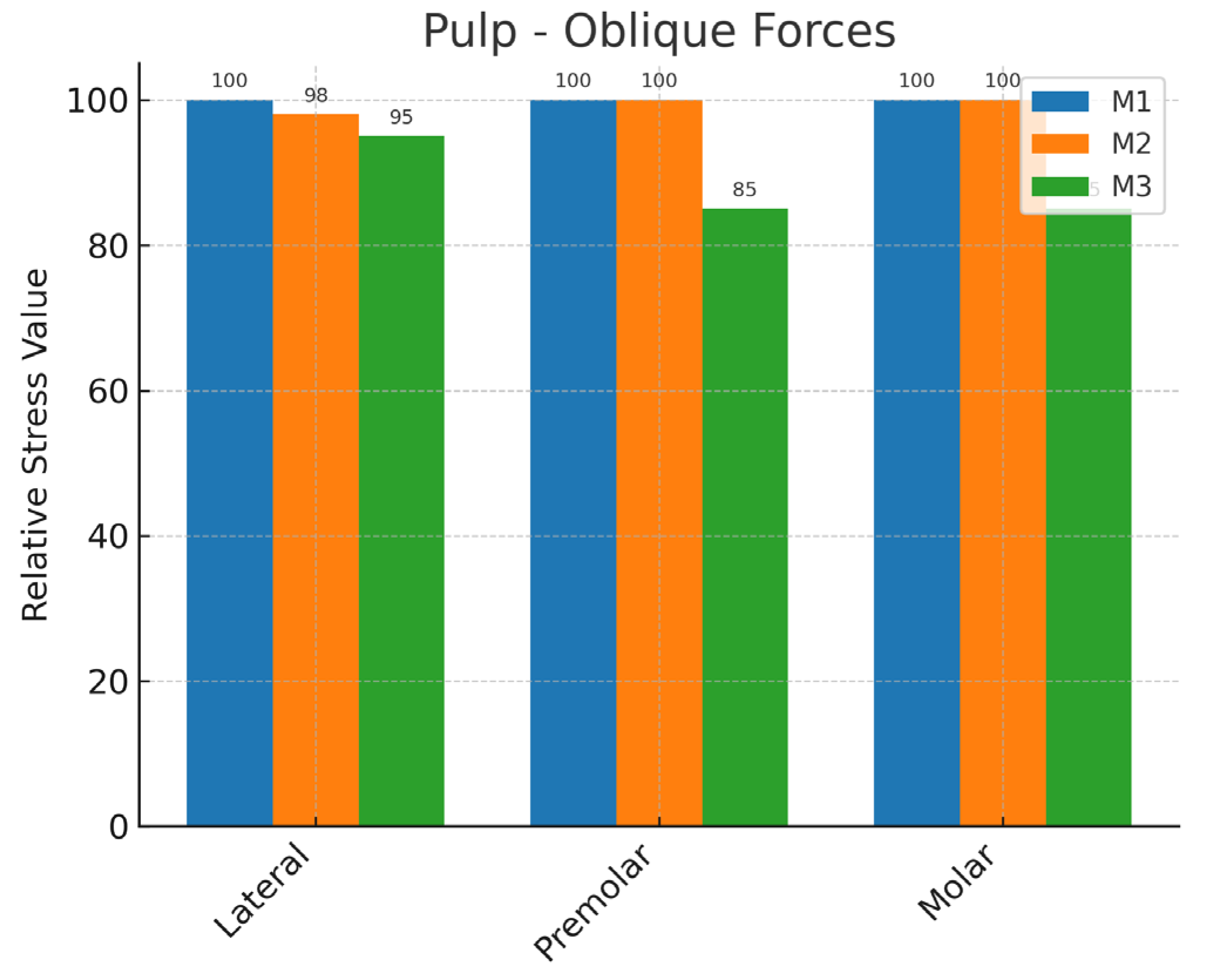
3.2. Von Mises Stress Values Formed in Models with Oblique Force Application
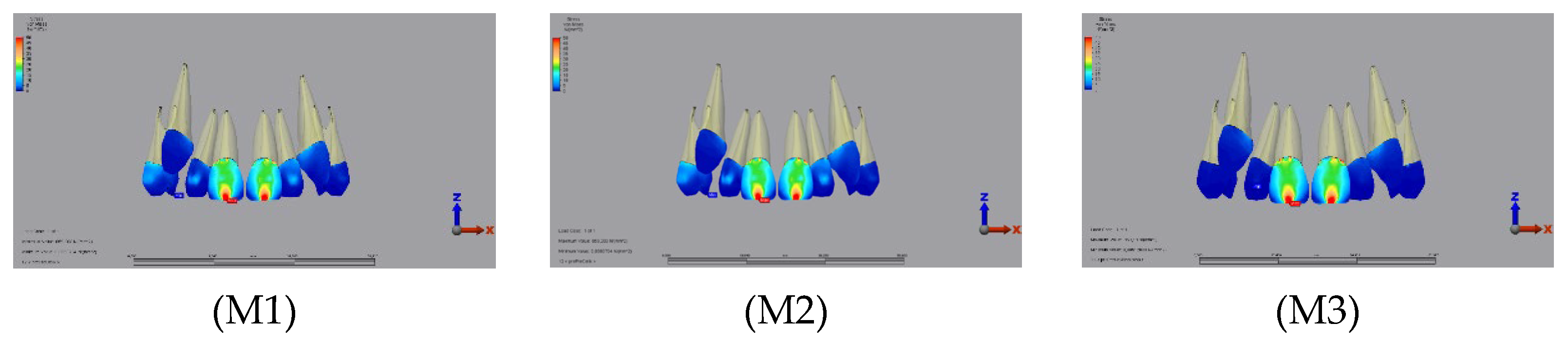
3.2.1. Enamel
3.2.2. Dentin
3.2.3. Pulp
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEA | Finite Element Analysis |
| DICOM | Digital Imaging and Communications in Medicine |
| E | Enamel |
| D | Dentin |
| P | Pulp |
| CG | Control Group |
| M1 | Model 1 |
| M2 | Model 2 |
| M3 | Model 3 |
| M1 | Composite Orthodontic Wire Splinted Tooth Model |
| M2 | Titanium Trauma Splinted Tooth Model |
| M3 | Nylon Wire Splinted Tooth Model |
References
- Glendor, U.L.F. Epidemiology of traumatic dental injuries—A 12-year review of the literature. Dent. Traumatol. 2008, 24, 603–611. [Google Scholar] [CrossRef]
- Kahler, B.; Hu, J.Y.; Marriot-Smith, C.S.; Heithersay, G.S. Splinting of teeth following trauma: A review and a new splinting recommendation. Aust. Dent. J. 2016, 61, 59–73. [Google Scholar] [CrossRef]
- Trope, M. Avulsion of permanent teeth: Theory to practice. Dent. Traumatol. 2011, 27, 281–294. [Google Scholar] [CrossRef]
- Andersson, L. Traumatic dental injuries. In Oral and Maxillofacial Surgery; John Wiley & Sons: New York, NY, USA, 2025; pp. 751–771. [Google Scholar]
- Burcak Cengiz, S.; Stephan Atac, A.; Cehreli, Z.C. Biomechanical effects of splint types on traumatized tooth: A photoelastic stress analysis. Dent. Traumatol. 2006, 22, 133–138. [Google Scholar] [CrossRef]
- Poiate, I.A.V.P.; De Vasconcellos, A.B.; De Santana, R.B.; Poiate, E., Jr. Three-dimensional stress distribution in the human periodontal ligament in masticatory, parafunctional, and trauma loads: Finite element analysis. J. Periodontol. 2009, 80, 1859–1867. [Google Scholar] [CrossRef]
- Belevcikli, M.; Altan, H.; Altan, A. Surgical extrusion of anterior teeth with intrusion traumatic injury: A report of two cases. Eur. Endod. J. 2020, 5, 295. [Google Scholar] [CrossRef]
- Kwan, S.C.; Johnson, J.D.; Cohenca, N. The effect of splint material and thickness on tooth mobility after extraction and replantation using a human cadaveric model. Dent. Traumatol. 2012, 28, 277–281. [Google Scholar] [CrossRef]
- Güngör, M.A.; Artunc, C.; Sonugelen, M.; Toparli, M. The evaluation of the removal forces on the conus crowned telescopic prostheses with the finite element analysis (FEA). J. Oral Rehabil. 2002, 29, 1069–1075. [Google Scholar] [CrossRef] [PubMed]
- Vilela, A.B.; Soares, P.B.; Almeida, G.A.; Veríssimo, C.; Rodrigues, M.P.; Versluis, A.; Soares, C.J. Three-dimensional finite element stress analysis of teeth adjacent to a traumatized incisor. Dent. Traumatol. 2019, 35, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.M.; Ou, K.L.; Wang, W.N.; Chiu, W.T.; Lin, C.T.; Lee, S.Y. Dynamic finite element analysis of the human maxillary incisor under impact loading in various directions. J. Endod. 2005, 31, 723–727. [Google Scholar] [CrossRef] [PubMed]
- Giesen, E.B.; Ding, M.; Dalstra, M.; van Eijden, T.M. Mechanical properties of cancellous bone in human mandibular condyle are anisotropic. J. Biomech. 2001, 34, 799–803. [Google Scholar] [CrossRef]
- Lettry, S.; Seedhom, B.B.; Berry, E.; Cuppone, M. Quality assessment of the cortical bone of the human mandible. Bone 2003, 32, 35–44. [Google Scholar] [CrossRef]
- Gurbuz, T.; Sengul, F.; Altun, C. Finite element stress analysis of short-post core and over restorations prepared with different restorative materials. Dent. Mater. J. 2008, 27, 499–507. [Google Scholar] [CrossRef]
- Sumanariu, C.A.; Amza, C.G.; Baciu, F.; Vasile, M.I.; Nicoara, A.I. Comparative Analysis of Mechanical Properties: Conventional vs. Additive Manufacturing for Stainless Steel 316L. Materials 2024, 17, 4808. [Google Scholar] [CrossRef]
- Elias, C.N.; Lima, J.H.C.; Valiev, R.; Meyers, M.A. Biomedical applications of titanium and its alloys. JOM 2008, 60, 46–49. [Google Scholar] [CrossRef]
- Da Silva, L.A.B.; Nelson-Filho, P.; da Silva, R.A.B.; Flores, D.S.H.; Heilborn, C.; Johnson, J.D.; Cohenca, N. Revascularization and periapical repair after endodontic treatment using apical negative pressure irrigation versus conventional irrigation plus triantibiotic intracanal dressing in dogs’ teeth with apical periodontitis. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endodontology 2010, 109, 779–787. [Google Scholar] [CrossRef]
- Gupta, M.; Madhok, K.; Kulshrestha, R.; Chain, S.; Kaur, H.; Yadav, A. Determination of stress distribution on periodontal ligament and alveolar bone by various tooth movements—A 3D FEM study. J. Oral Biol. Craniofacial Res. 2020, 10, 758–763. [Google Scholar] [CrossRef] [PubMed]
- Aykaç, V.; Ulusoy, Ç.; Türköz, Ç. Effects of a newly designed orthodontic miniplate platform for elevating the miniplate over the gingiva: A 3-dimensional finite element analysis. Am. J. Orthod. Dentofac. Orthop. 2015, 148, 110–122. [Google Scholar] [CrossRef]
- Pari, A.; Ilango, P.; Subbareddy, V.; Katamreddy, V.; Parthasarthy, H. Gingival diseases in childhood—A review. J. Clin. Diagn. Res. JCDR 2014, 8, ZE01. [Google Scholar] [CrossRef]
- Hellsing, G. On the Regulation of Interincisor Bite Force in Man. J. Oral Rehabil. 1980, 7, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Saikiran, K.V.; Gurunathan, D.; Nuvvula, S.; Jadadoddi, R.K.; Kumar, R.H.; Birapu, U.C. Prevalence of Dental Trauma and Their Relationship to Risk Factors among 8–15-Year-Old School Children. Int. J. Dent. 2022, 2022, 3343827. [Google Scholar] [CrossRef]
- Skaare, A.B.; Jacobsen, I. Dental injuries in Norwegians aged 7–18 years. Dent. Traumatol. 2003, 19, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Altun, C.; Cehreli, Z.C.; Güven, G.; Acikel, C. Traumatic intrusion of primary teeth and its effects on the permanent successors: A clinical follow-up study. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endodontology 2009, 107, 493–498. [Google Scholar] [CrossRef] [PubMed]
- de Andrade Veras, S.R.; Bem, J.S.P.; de Almeida, E.C.B.; Lins, A. Dental splints: Types and time of immobilization post tooth avulsion. J. Istanb. Univ. Fac. Dent. 2017, 51 (Suppl. 1), S69–S75. [Google Scholar] [CrossRef]
- Boldt, J.; Knapp, W.; Proff, P.; Rottner, K.; Richter, E.J. Measurement of tooth and implant mobility under physiological loading conditions. Ann. Anat.-Anat. Anz. 2012, 194, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Kehoe, J.C. Splinting and replantation after traumatic avulsion. J. Am. Dent. Assoc. 1986, 112, 224–230. [Google Scholar] [CrossRef]
- Berthold, C.; Thaler, A.; Petschelt, A. Rigidity of commonly used dental trauma splints. Dent. Traumatol. 2009, 25, 248–255. [Google Scholar] [CrossRef]
- Sobczak-Zagalska, H.; Emerich, K. Assessment of a power chain as a new dental trauma splint and its comparison with two commonly used splinting materials. Appl. Sci. 2020, 10, 8398. [Google Scholar] [CrossRef]
- Rieger, M.R.; Mayberry, M.; Brose, M.O. Finite element analysis of six endosseous implants. J. Prosthet. Dent. 1990, 63, 671–676. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, M.; Zhao, R.; Liu, H.; Tian, M.; Zhong, S.; Bai, S. Effects of periodontal splints on biomechanical behaviors in compromised periodontal tissues and cement layer: 3D finite element analysis. Polymers 2022, 14, 2835. [Google Scholar] [CrossRef]
- Fidancıoğlu, Y.D. Evaluation of Stress Distributions Created by Different Splint Types Applied to Traumatized Teeth Using Finite Element Analysis. Ph.D. Thesis, Necmettin Erbakan University, Konya, Turkey, 2020. [Google Scholar]
- Vilela, A.B.F.; Soares, P.B.F.; Versluis, A.; Soares, C.J. Dental trauma splints for the mixed dentition–a finite element analysis of splint material, splint extension, missing teeth, and PDL representation. Dent. Traumatol. 2022, 38, 495–504. [Google Scholar] [CrossRef] [PubMed]
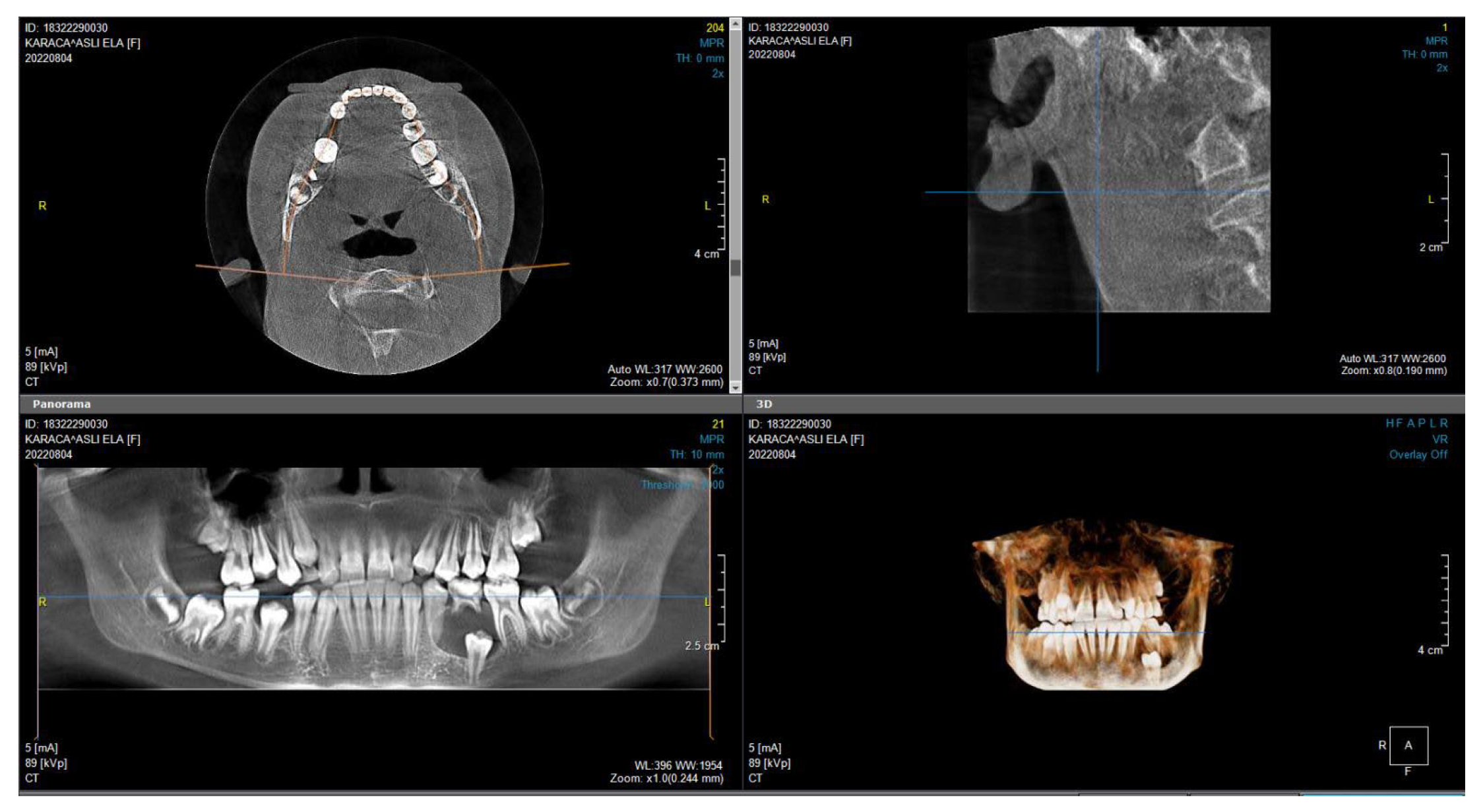
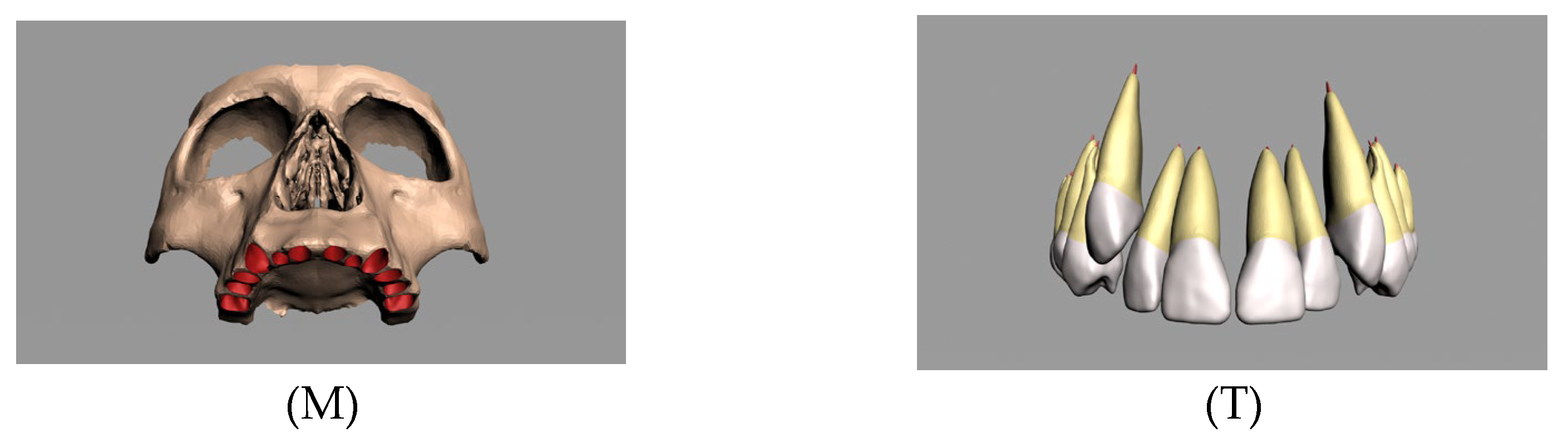
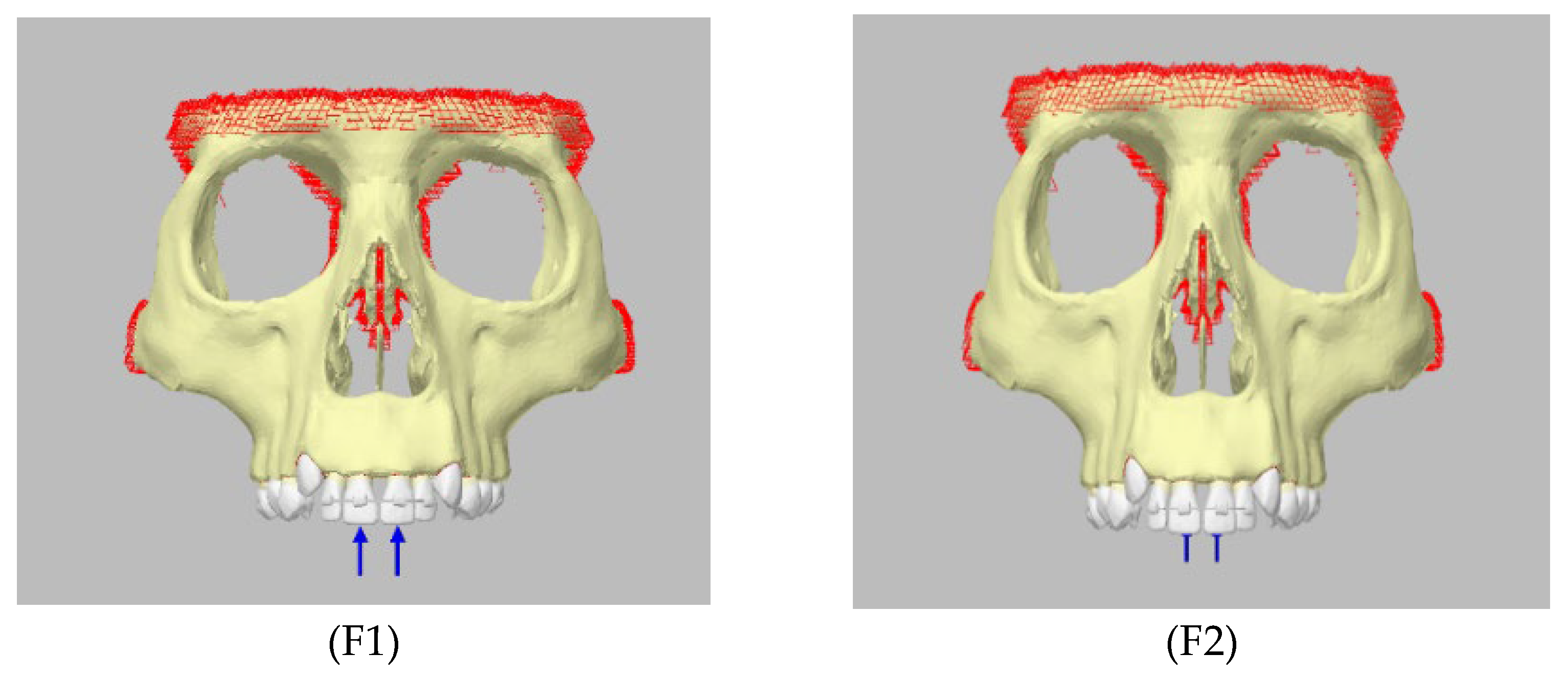
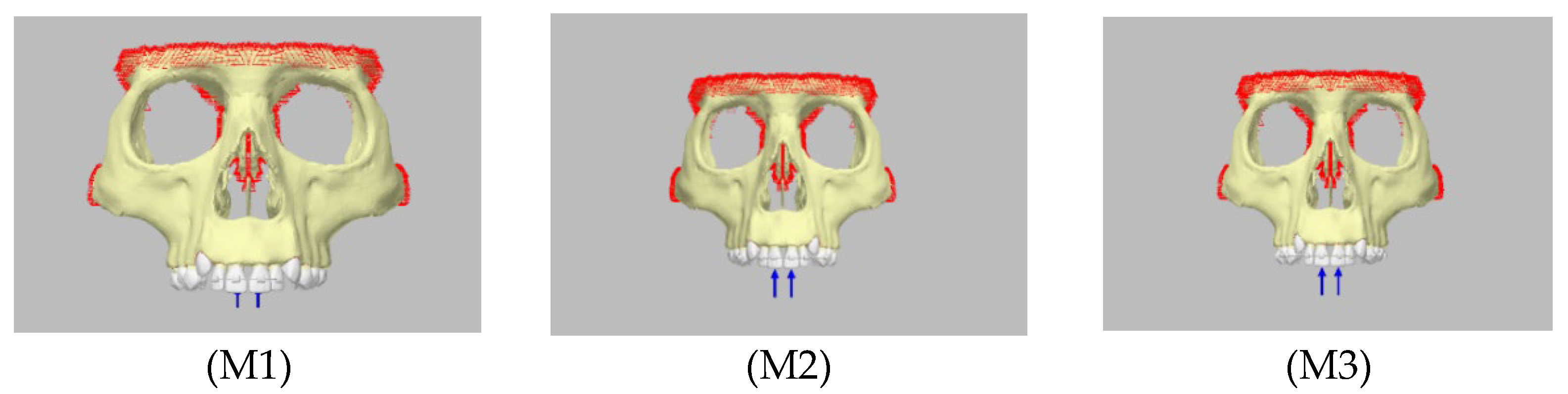










| Elements | Nodes | |
|---|---|---|
| Control Group | 2,677,417 | 494,570 |
| Lateral | 2,685,356 | 496,873 |
| First Premolar | 2,688,950 | 498,172 |
| First Molar | 499,799 | 500,799 |
| Materials | Elastic Modulus (MPa) | Poisson’s Ratio (µ) | Reference |
|---|---|---|---|
| Enamel | 77,900 | 0.33 | [11] |
| Dentin | 16,600 | 0.41 | [11] |
| Pulp | 6.99 | 0.45 | [11] |
| PDL | 50 | 0.45 | [11] |
| Trabecular Bone | 431 | 0.30 | [12] |
| Cortical Bone | 11,500 | 0.30 | [13] |
| Composite | 10,000 | 0.24 | [14] |
| Stainless Steel Wire | 200,000 | 0.30 | [15] |
| Titanium | 110,000 | 0.34 | [16] |
| Nylon Fishing Line | 2700 | 0.3 | [14] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaim, S.B.; Kahvecioğlu, F. Evaluation of Dental Trauma Splints in Early Permanent Dentition Through Finite Element Analysis. Appl. Sci. 2025, 15, 10307. https://doi.org/10.3390/app151910307
Zaim SB, Kahvecioğlu F. Evaluation of Dental Trauma Splints in Early Permanent Dentition Through Finite Element Analysis. Applied Sciences. 2025; 15(19):10307. https://doi.org/10.3390/app151910307
Chicago/Turabian StyleZaim, Sevde Berfu, and Firdevs Kahvecioğlu. 2025. "Evaluation of Dental Trauma Splints in Early Permanent Dentition Through Finite Element Analysis" Applied Sciences 15, no. 19: 10307. https://doi.org/10.3390/app151910307
APA StyleZaim, S. B., & Kahvecioğlu, F. (2025). Evaluation of Dental Trauma Splints in Early Permanent Dentition Through Finite Element Analysis. Applied Sciences, 15(19), 10307. https://doi.org/10.3390/app151910307







