Prioritizing Early-Stage Start-Up Investment Alternatives Under Uncertainty: A Venture Capital Perspective

Abstract

Early-stage start-up selection is a critical yet challenging task for venture capital (VC) investors due to high uncertainty, limited historical data, and rapidly evolving business environments. Traditional evaluation processes often fall short in systematically handling multiple qualitative and uncertain factors that influence start-up success. As a result, there is a growing demand for robust decision models that can support VC firms in identifying promising early-stage ventures more accurately and consistently. This study presents a hybrid fuzzy multi-criteria decision-making approach tailored to the needs of venture capital investment under uncertainty. The model integrates expert judgment using the proportional spherical fuzzy AHP method to evaluate the relative importance of key dimensions. Then, spherical fuzzy TOPSIS is applied to rank investment alternatives based on their overall performance rankings. The proposed framework enables VC decision-makers to incorporate both subjective insights and data ambiguity in a structured and transparent way. It offers a practical tool to enhance the reliability of early-stage investment evaluations and improve the effectiveness of venture capital portfolio strategies.

1. Introduction

The start-up arena has generally been identified as a very dynamic and competitive field, where constant innovation and rapid technological advancement are dominant dynamics [1]. In such an area, early-growth investment decisions have been identified as fundamentally strategic for venture capital (VC) firms due to the significant potential to profoundly influence portfolio performance and ultimate economic outcomes [2,3]. Significant potential for returns comes hand-in-hand with vast levels of riskiness; hence, making a choice under such a context becomes a complex and consequential task [4].

The unpredictability of early-stage investments has been attributed to various sources, including sparse data availability, changing market configurations, and the unpredictability of technology adoption [5]. For most instances, start-ups are engaged in new or disruptive industries lacking solid benchmarks, and projecting future success is exceptionally difficult [6]. Consequently, evaluations are often made based on qualitative assessments of attributes such as the founding team’s knowledge, effort, and network quality [7]. Whilst such intangible attributes are deemed important, they are subject to subjectivity and rational biases and may lower the accuracy of decisions [8,9].

It has been observed that traditional evaluation approaches are insufficient to systematically address the multi-criteria, subjective, and imprecise characteristics of early-stage venture assessments [8]. Classical decision models typically rely on precise numerical inputs and assume independence among evaluation criteria, conditions that rarely reflect real-world investment environments [10]. Furthermore, the conversion of expert opinions into crisp numerical scores has been shown to lead to information loss and to oversimplify the uncertainty inherent in the decision process [11].

On the other hand, to address these limitations, multi-criteria decision-making (MCDM) methods have been increasingly employed in the venture capital domain, as they enable structured evaluations across multiple and often conflicting criteria [12]. In particular, fuzzy-logic-based MCDM models have been proposed to accommodate the vagueness and subjectivity present in expert assessments [13]. Fuzzy AHP and fuzzy TOPSIS are among the most frequently applied approaches, as they combine subjective judgments with quantitative performance data to produce more consistent rankings [14]. However, conventional fuzzy set theory cannot fully capture hesitation in decision making, which is critical when experts face uncertainty in their evaluations [15].

Spherical fuzzy sets have been introduced to overcome this shortcoming by allowing membership, non-membership, and hesitancy degrees to be simultaneously modeled under a unit-sphere constraint [16]. This expanded representation of uncertainty has been demonstrated to enhance decision quality in situations of complexity and ambiguity, such as technology choice and supplier evaluation [17]. From this base, proportional spherical fuzzy sets have been introduced as a means of keeping the proportional relations among these degrees, offering an even richer structure for the representation of uncertainty [18].

Early-stage start-up selection is difficult. Data are scarce, markets move fast, and expert opinions are uncertain and hesitant. Classic scoring methods lose information when they require experts to provide precise numbers. Fuzzy MCDM models keep this uncertainty and make rankings more reliable. Figure 1 depicts an end-to-end pipeline for venture capital investment decisions. Step 1 prepares the portfolio and creates meta-rules from success criteria to identify early-stage start-ups. Step 2 classifies start-up companies as mature or early-stage. Step 3 ranks early-stage start-ups under uncertainty, which is the focus of this paper. Step 4 presents personalized investment decisions that use the Step 3 ranking together with investor preferences to create tailored recommendations.

This study designs and evaluates Step 3. Steps 1–2 provide inputs to Step 3 (criteria, data, and expert judgments). Step 3 outputs an investment priority list and sensitivity insights. These outputs are used in Step 4 to create investor-specific advice. Steps 1, 2, and 4 are out of scope here but are shown to clarify the overall logic.

In this work, a hybrid model combining the proportional spherical fuzzy analytic hierarchy process (PSF-AHP) and spherical fuzzy TOPSIS (PSF-TOPSIS) is introduced to facilitate VC investment decisions under ambiguity. The PSF-AHP was utilized to determine the weights of evaluation criteria by proportionally adapting to residual hesitation in pairwise comparisons [19]. The spherical fuzzy TOPSIS was then utilized to determine the rankings of start-up alternatives according to their performance on the weighted criteria [16]. By preserving the spherical fuzzy representations until the final ranking level, the model ensures that the inherent ambiguity of expert judgment persists, resulting in more robust and realistic outcomes compared to conventional crisp or traditional fuzzy approaches.

In this study, proportional spherical fuzzy AHP and TOPSIS were preferred over alternative approaches such as west–worst method, DEMATEL, VIKOR, or PROMETHEE. The maturity and clarity of the chosen pair have been widely demonstrated: spherical fuzzy TOPSIS provides a transparent distance-based ranking, and spherical fuzzy AHP offers a well-structured hierarchy for expert judgments [20,21]. Although other methods have shown success in various decision-making problems, the early-stage venture context was judged to require explicit retention of hesitation and uncertainty until the final ranking, which is directly enabled by spherical or proportional spherical fuzzy extensions [17,20,22]. Some alternatives impose strict preference structures (e.g., the best–worst) or require additional modeling to capture interdependencies, which can increase complexity in multi-expert settings [22]. By contrast, AHP could be readily adopted by experts, and TOPSIS could provide traceable rankings via distances to ideal and negative ideal solutions. In addition, fuzzy AHP/TOPSIS variants have been actively used in investment and start-up evaluation studies, which supports comparability of our results with the existing literature [23,24].

The contributions of this study are threefold: (i) the extension of proportional spherical fuzzy set theory to the VC investment context; (ii) the development of a hybrid PSF-AHP and spherical fuzzy TOPSIS framework that maintains uncertainty throughout the evaluation process; and (iii) the empirical validation of the proposed model in a real-world case study, demonstrating its advantages over classical approaches in generating balanced, transparent rankings and sensitivity results. The remainder of the paper is organized as follows: Section 2 reviews the relevant literature, Section 3 explains preliminaries of proportional spherical fuzzy sets, Section 4 outlines the proposed methodology. Section 5 presents the case study results, while Section 6 compares the applied method with the traditional AHP&TOPSIS. Section 7 displays the sensitivity analysis results for decision-makers’ weights. Section 8 concludes with the main findings and implications for future research.

2. Literature Review

This section presents a review of the existing literature relevant to the study. The discussion is structured into three main subsections. Section 2.1 examines research on venture capital, including definitions, investment cycles, and the decision-making priorities of venture capitalists in early-stage start-up investments, as well as recent shifts toward data-driven and algorithm-assisted approaches. Section 2.2 reviews studies that apply multi-criteria decision-making methods to start-up evaluation, with a focus on techniques.

For each area, methodological trends, theoretical frameworks, and key gaps in the literature are identified in Section 2.3 to position the contribution of the proposed PSF AHP&TOPSIS model.

2.1. Studies on Venture Capital

Venture capital (VC) is a cornerstone of financing for high-growth start-ups, following an investment cycle that includes deal sourcing, screening, due diligence, investment, and exit [25,26]. During this process, VC investors prioritize a mix of qualitative and quantitative criteria. Empirical evidence shows that the management team is often the most critical factor in investment selection, with other factors such as market size, product uniqueness, and industry growth playing supporting roles [25]. At the early stage, with high uncertainty and minimal historical data, investors rely on proxies such as founders’ experience, passion, and networks, alongside market attractiveness and technology merit [27]. However, overreliance on intuition can introduce bias, a challenge increasingly acknowledged in recent research [28,29]. Across investor types, achieving a successful exit (initial public offering—IPO or acquisition) is widely recognized as the primary measure of venture success [26].

From a methodological perspective, traditional VC decision-making has been analyzed through information asymmetry, principal–agent theory, and cognitive perspectives [30]. Recently, there has been a notable shift toward data-driven VC models that integrate machine learning and big data analytics [31,32]. Examples include proprietary analytics platforms that track millions of start-ups and predictive models that estimate the likelihood of successful exits. While promising, such algorithmic approaches are mostly used as decision-support tools rather than replacements for expert judgment [33].

The existing literature lacks systematic decision models that simultaneously handle multiple and subjective criteria. There are also inconsistencies in the reported importance of certain factors across studies, suggesting a need for structured frameworks that can integrate qualitative judgments with quantitative data. Additionally, few studies have rigorously evaluated the performance of algorithmic tools compared to traditional methods [31,34,35].

This research addresses the above gaps by introducing a hybrid fuzzy multi-criteria decision-making model for early-stage VC investment. The proposed approach integrates proportional spherical fuzzy sets into the VC domain for the first time, allowing for richer modeling of uncertainty and hesitation in expert evaluations.

2.2. Studies on MCDM-Based Start-Up Selection

Start-up investment decisions inherently involve multiple, often conflicting criteria. MCDM methods such as AHP, TOPSIS, and data envelopment analysis (DEA) have been increasingly used to structure and improve these decisions [36,37,38]. Fuzzy variants of these methods are particularly suited for handling subjective judgments and uncertainty [23,39]. For example, fuzzy AHP has been used to determine criteria weights [36,40], while fuzzy TOPSIS ranks alternatives based on their closeness to an ideal solution [39]. DEA models have been adapted with fuzzy inputs to evaluate relative efficiency among start-ups [38].

Common evaluation criteria in the literature include entrepreneur/team quality, technological uniqueness, market opportunity, scalability, financial viability, and risk factors [37]. Hybrid models combining multiple MCDM methods are also emerging. For instance, Nguyen and Chu [37] employed a DEMATEL-ANP-based fuzzy PROMETHEE II approach to address interdependencies among criteria.

Non-fuzzy MCDM methods often require precise numerical inputs, which are unrealistic for early-stage start-ups. Converting qualitative judgments into crisp scores leads to information loss and false precision [23]. Many models also assume independence among criteria, ignoring possible interrelationships [22,41,42,43].

The proposed PSF AHP&TOPSIS model advances existing approaches by capturing membership, non-membership, and hesitation degrees, thus preserving more information from expert judgments. By combining PSF-AHP for weighting and spherical fuzzy TOPSIS for ranking, the model maintains uncertainty throughout the process until the final defuzzification step. This results in a ranking that better reflects the inherent ambiguity of early-stage start-up evaluation, filling a critical gap in the literature.

2.3. Main Contribution

To the authors’ best knowledge, no prior study has directly implemented the PSF AHP combined with PSF TOPSIS for start-up evaluation. However, several recent studies have applied spherical fuzzy extensions in MCDM contexts. For instance, Kieu et al. [44] integrated SF-AHP with CoCoSo for distribution center selection; Sharaf [20] employed spherical fuzzy TOPSIS and VIKOR for hydrogen storage system evaluation; Radovanović et al. [45] combined SF-AHP with Grey MARCOS for professor performance assessment; and Kutlu-Gundogdu et al. utilized SFS-based AHP [21] in environmental decision-making and SFS–based TOPSIS [46] in 3D printer selection. These studies underline the growing interest in handling uncertainty through spherical fuzzy logic, while highlighting that PSF AHP & PSF TOPSIS in venture capital contexts remain unexplored and novel.

This study contributes to the literature on venture capital (VC) decision-making and start-up evaluation by introducing a novel hybrid MCDM framework that integrates PSF-AHP with PSF-TOPSIS. While recent research has increasingly applied fuzzy MCDM techniques to address uncertainty and subjectivity in start-up selection, no prior work has combined the proportional spherical fuzzy variant of AHP with TOPSIS in the context of venture capital. The proposed approach enables the simultaneous modeling of membership, non-membership, and hesitancy degrees, thus preserving more information from expert judgments than traditional fuzzy or crisp methods.

The main methodological contribution lies in enhancing the robustness and realism of early-stage investment evaluation. Existing studies on VC selection have primarily relied on qualitative assessments, data-driven algorithms, or classical MCDM approaches, each of which has limitations: qualitative assessments are prone to bias, purely algorithmic methods require large datasets and often lack transparency, and classical MCDM methods assume precise inputs and independence among criteria. By integrating PSF-AHP for criteria weighting and spherical fuzzy TOPSIS for alternative ranking, the proposed framework addresses these issues by explicitly capturing uncertainty, rigorously handling subjective evaluations, and maintaining transparency throughout the decision-making process.

From an application perspective, this study operationalizes the proposed framework in evaluating five early-stage start-up alternatives across thirteen criteria that encompass innovation capacity, human capital quality, market presence, strategic partnerships, and financial resources. The case study demonstrates that the PSF-based model yields materially different rankings from a classical AHP–TOPSIS approach, indicating its sensitivity to hesitation and partial agreement in expert evaluations. This evidence highlights the model’s practical value in producing more balanced and realistic rankings, especially in environments characterized by high uncertainty and limited historical data.

Shortly, the contributions of this research are threefold: (i) it extends the use of proportional spherical fuzzy set theory into the VC investment decision domain; (ii) it develops a hybrid PSF AHP&TOPSIS model capable of preserving expert uncertainty until the final decision stage; and (iii) it empirically demonstrates the superiority of the proposed model over classical approaches in generating consistent, transparent, and context-sensitive investment rankings.

3. Preliminaries of Proportional Spherical Fuzzy Sets

A spherical fuzzy set (SFS) can be characterized as a mathematical construct defined over a universe of discourse X, where its formal definition is established through the mathematical relationship presented in Equation (1). This type of fuzzy set represents an extension of conventional fuzzy set theory, incorporating spherical geometric properties in its membership function formulation to capture uncertainty and imprecision more comprehensively than traditional approaches.

$${\tilde{\Phi }}_S=\left\{〈x,({\mu }_{{\Phi }_S}\left(x\right),{\nu }_{{\Phi }_S}\left(x\right),{\pi }_{{\Phi }_S}\left(x\right))|x\in X〉\right\}$$

(1)

where ${\mu }_{{\tilde{\Phi }}_S}:X\to \left[0,1\right],v_{{\tilde{\Phi }}_S}:X\to \left[0,1\right],{\pi }_{{\tilde{\Phi }}_S}:X\to \left[0,1\right]$ and $0\le {\left({\mu }_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2+{\left(v_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2+{\left({\pi }_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2\le 1,\forall x\in X$.

For any element x, the values ${\mu }_{{\tilde{\Phi }}_S}\left(x\right)$, $v_{{\tilde{\Phi }}_S}\left(x\right)$, and ${\pi }_{{\tilde{\Phi }}_S}\left(x\right)$ denote the membership, non-membership, and hesitancy degrees of x in ${\tilde{\Phi }}_S$, respectively.

The proportional relationships among ${\mu }_{{\tilde{\Phi }}_S}\left(x\right)$, $v_{{\tilde{\Phi }}_S}\left(x\right)$, and ${\pi }_{{\tilde{\Phi }}_S}\left(x\right)$ are evaluated by the expert as specified in Equations (2)–(4), satisfying Equation (5).

$${\mu }_{{\tilde{\Phi }}_S}\left(x\right)=k_1{r}_{{\tilde{\Phi }}_S}\left(x\right)$$

(2)

$$v_{{\tilde{\Phi }}_S}\left(x\right)=k_3{r}_{{\tilde{\Phi }}_S}\left(x\right)$$

(3)

$${\pi }_{{\tilde{\Phi }}_S}\left(x\right)=k_2{r}_{{\tilde{\Phi }}_S}\left(x\right)$$

(4)

$${\left(r_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2+{\left(k_1{r}_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2+{\left(k_2{r}_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2+{\left(k_3{r}_{{\tilde{\Phi }}_S}\left(x\right)\right)}^2=1$$

(5)

In proportional spherical fuzzy sets (PSFSs, ${\tilde{\Phi }}_P$), the refusal degree represents the remaining degree of uncertainty after accounting for the proportionally adjusted membership, non-membership, and hesitancy values, thereby capturing the unutilized portion of the unit sphere constraint. The refusal degree is determined by Equation (6).

$$r_{{\tilde{\Phi }}_S}\left(x\right)=\sqrt{{\displaystyle \frac{1}{1+{\left(k_1\right)}^2+{\left(k_2\right)}^2+{\left(k_3\right)}^2}}}$$

(6)

Subsequently, each element within the set is defined by Equation (7).

$${\tilde{\Phi }}_P=\left\{〈x;(k_1\sqrt{D},k_2\sqrt{D},k_3\sqrt{D})|x\in X〉\right\}$$

(7)

where $D=1/\left(1+k_1^2+k_2^2+k_3^2\right)$.

Given two PSFSs ${\tilde{\Phi }}_{PA}$ and ${\tilde{\Phi }}_{PB}$, the addition and multiplication operations are described in Equations (8) and (9), respectively [46].

$${\tilde{\Phi }}_{PA}\oplus {\tilde{\Phi }}_{PB}=\left\{〈x;\left(\begin{array}{c}{k}_{A1}\sqrt{D_A}+k_{B1}\sqrt{D_B}-k_{A1}\sqrt{D_A}\times k_{B1}\sqrt{D_B},\\ k_{A2}\sqrt{D_A}\times k_{B2}\sqrt{D_B},\\ k_{A3}\sqrt{D_A}\times k_{B3}\sqrt{D_B}\end{array}\right)|x\in X〉\right\}$$

(8)

$${\tilde{\Phi }}_{PA}\otimes {\tilde{\Phi }}_{PB}=\left\{〈x;\left(\begin{array}{c}{k}_{A1}\sqrt{D_A}\times k_{B1}\sqrt{D_B},\\ k_{A2}\sqrt{D_A}+k_{B2}\sqrt{D_B}-k_{A2}\sqrt{D_A}\times k_{B2}\sqrt{D_B},\\ k_{A3}\sqrt{D_A}+k_{B3}\sqrt{D_B}-k_{A3}\sqrt{D_A}\times k_{B3}\sqrt{D_B}\end{array}\right)|x\in X〉\right\}$$

(9)

where $D_A=1/(1+k_{A1}^2+k_{A2}^2+k_{A3}^2)$ and $D_B=1/(1+k_{B1}^2+k_{B2}^2+k_{B3}^2)$.

Equations (10) and (11) define the power operations and scalar multiplication, respectively [21].

$${\tilde{\Phi }}_{SA}^{\lambda }=\left\{〈x;\left(1-{\left(1-k_{A1}\sqrt{D_A}\right)}^{\lambda },{\left(k_{A2}\sqrt{D_A}\right)}^{\lambda },{\left(k_{A3}\sqrt{D_A}\right)}^{\lambda }\right)|x\in X〉\right\}$$

(10)

$$\lambda ·{\tilde{\Phi }}_{SA}=\left\{〈x;\left(1-{\left(1-k_{A1}\sqrt{D_A}\right)}^{\lambda },{\left(k_{A2}\sqrt{D_A}\right)}^{\lambda },{\left(k_{A3}\sqrt{D_A}\right)}^{\lambda }\right)|x\in X〉\right\}$$

(11)

Definition 1.

Consider a set of proportional spherical fuzzy numbers (PSFNs) ${\alpha }_j$ where j = 1,2,$\dots ,n$. The proportional spherical fuzzy weighted averaging (PSFWA) operator represents a mapping from $P{S}^n$ to $PS$ defined in Equation (12) [46].

$$PSFW{A}_w\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)={\oplus }_{j=1}^n\left(w_j{\alpha }_j\right)$$

(12)

where $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ represents the weight vector of ${\alpha }_j$$(j=1,2,\dots ,n)$ with $w_j>0$ and ${\sum }_{j=1}^n{w}_j=1$. Subsequently,

$$\begin{array}{c}PSFW{A}_w\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\hfill \\ \left\{〈x;\left(1-\prod _{j=1}^n{\left(1-k_{1j}\sqrt{D_j}\right)}^{w_j},\prod _{j=1}^n{\left(k_{2j}\sqrt{D_j}\right)}^{w_j},\prod _{j=1}^n{\left(k_{3j}\sqrt{D_j}\right)}^{w_j}\right)|x\in X〉\right\}\hfill \end{array}$$

(13)

where $D_j=1/(1+k_{1j}^2+k_{2j}^2+k_{3j}^2)$.

Definition 2.

Given a complete PSFN ${\tilde{\Phi }}_{PA}=\left(k_{A1},k_{A2},k_{A3}\right)$, the score function $S_{{\tilde{\Phi }}_{PA}}$ is defined by Equation (14) [21].

$$S_{{\tilde{\Phi }}_{PA}}=k_{A1}\sqrt{D_A}+{\displaystyle \frac{1}{2}}{k}_{A2}\sqrt{D_A}-k_{A3}\sqrt{D_A}$$

(14)

Definition 3.

Consider $x\in X$ as a universal set and two PSFNs. The Euclidean distance is then specified by Equation (15) [21].

$$\begin{array}{c}{d}_E\left({\tilde{\Phi }}_{SA},{\tilde{\Phi }}_{SB}\right)=\hfill \\ {\displaystyle \frac{1}{n}}\sum _{i=1}^n\sqrt{{\left(k_{A1i}\sqrt{D_{Ai}}-k_{B1i}\sqrt{D_{Bi}}\right)}^2+{\left(k_{A2i}\sqrt{D_{Ai}}-k_{B2i}\sqrt{D_{Bi}}\right)}^2+{\left(\sqrt{D_{Ai}}-\sqrt{D_{Bi}}\right)}^2}\hfill \end{array}$$

(15)

4. Proportional Spherical Fuzzy AHP-TOPSIS Methodology

This section introduces two main part of the applied methodology, proportional spherical fuzzy AHP in Section 4.1 and proportional spherical fuzzy TOPSIS in Section 4.2.

4.1. Proportional Spherical Fuzzy AHP

The analytic hierarchy process decomposes complex problems into smaller subproblems using pairwise comparison matrices. The solutions obtained from these subproblems are subsequently integrated to derive the comprehensive solution for the original complex problem. A pairwise comparison matrix for m criteria can be formulated using proportional pairs as presented in Equation (16) [47].

$$\begin{array}{c}{\tilde{\Phi }}_S\left(k_{1ij},k_{2ij},k_{3ij}\right)=\hfill \\ \left[\begin{array}{ccc}(VLN,0,0)& \dots & (k_{11m},k_{21m},k_{31m})\\ ⋮& \ddots & ⋮\\ (k_{3m1},k_{2m1},k_{1m1})& \dots & (VLN,0,0)\end{array}\right],i=1,\dots ,m;j=1,\dots ,m\hfill \end{array}$$

(16)

where reciprocal relationships exist such that $k_{1ji}=k_{3ij}$, $k_{2ji}=k_{2ij}$, and $k_{3ji}=k_{1ij}$. VLN represents a very large number, such as ${10}^{10}$.

Table 1. Linguistic PSF terms and values for criteria.

Linguistic Term	Abbreviation	k1	k2	k3	${\mathit{\mu }}_{{\tilde{\mathbf{\Phi }}}_{\mathit{S}}}\left(\mathit{x}\right)$	${\mathit{v}}_{{\tilde{\mathbf{\Phi }}}_{\mathit{S}}}\left(\mathit{x}\right)$	${\mathit{\pi }}_{{\tilde{\mathbf{\Phi }}}_{\mathit{S}}}\left(\mathit{x}\right)$	${\mathit{r}}_{{\tilde{\mathbf{\Phi }}}_{\mathit{S}}}\left(\mathit{x}\right)$
Absolutely Strong	AS	9	1	0	0.99	0.00	0.11	0.11
Very Strong	VS	8	2	1	0.96	0.12	0.24	0.12
Fairly Strong	FS	7	3	2	0.88	0.25	0.38	0.13
Slightly Strong	SS	6	4	3	0.76	0.38	0.51	0.13
Exactly Equal	E	5	5	5	0.57	0.57	0.57	0.11
Slightly Weak	SW	4	6	3	0.51	0.38	0.76	0.13
Fairly Weak	FW	3	7	2	0.38	0.25	0.88	0.13
Very Weak	VW	2	8	1	0.24	0.12	0.96	0.12
Absolutely Weak	AW	1	9	0	0.11	0.00	0.99	0.11

establishes the linguistic expressions along with their associated PSF proportions and corresponding SFS, encompassing membership, non-membership, hesitancy, and refusal degrees.

Table 2. Linguistic PSF terms and values for alternatives (sorted from highest to lowest).

Linguistic term	Abbreviation	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{k}}_3$
Certainly High	CH	1	0	9
Very High	VH	2	1	8
High	H	3	2	7
Above Average	AA	4	3	6
Average	A	5	5	5
Below Average	BA	6	3	4
Low	L	7	2	3
Very Low	VL	8	1	2
Certainly Low	CL	9	0	1

displays the linguistic PSF scale utilized for alternative assessment. Intermediate values between consecutive terms may be allocated when an expert exhibits uncertainty in choosing among these terms [18].

The crisp pairwise comparison matrix is derived using the score function and is presented in Equation (17).

$$P=\left[\begin{array}{ccc}1& \dots & S_{{\tilde{\Phi }}_{S_{1m}}}\left(k_{11m},k_{21m},k_{31m}\right)\\ ⋮& \ddots & ⋮\\ S_{{\tilde{\Phi }}_{S_{m1}}}\left(k_{3m1},k_{2m1},k_{1m1}\right)& \dots & 1\end{array}\right]$$

(17)

Subsequently, by applying the score function from Equation (14), the crisp pairwise comparison matrix in Equation (17) is obtained. The pairwise comparison matrix calculations given in Equation (18) are applied to all matrices within the hierarchy of the considered problem. If the second row yields a positive value, proceed with the second row; however, if it generates a negative value, continue with the third row.

$$S_{{\tilde{\Phi }}_{SA}}\left(k_{1ij},k_{2ij},k_{3ij}\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}i=j\hfill \\ 10\times \left(k_{1ij}\sqrt{D_{ij}}+{\displaystyle \frac{k_{2ij}\sqrt{D_{ij}}}{2}}-k_{3ij}\sqrt{D_{ij}}\right),\hfill & \mathrm{if}{k}_{1ij}\ge k_{3ij}\hfill \\ {\displaystyle \frac{1}{10\times \left(k_{3ji}\sqrt{D_{ji}}+\frac{k_{2ji}\sqrt{D_{ji}}}{2}-k_{1ji}\sqrt{D_{ji}}\right)}},\hfill & \mathrm{if}{k}_{3ij}>k_{1ij}\hfill \end{array}\right.$$

(18)

4.2. Proportional Spherical Fuzzy TOPSIS

The procedural steps of the PSF TOPSIS methodology are delineated below.

Step 1. Identify the evaluation criteria and alternatives, then obtain the PSF decision matrices from decision-makers as shown in Equation (19).

$$\tilde{D}(k_{1ij},k_{2ij},k_{3ij})=\begin{array}{c}\begin{array}{cccc}\hfill & \hfill C_1& \hfill \dots & C_n\end{array}\\ \begin{array}{cc}\hfill \begin{array}{c}{A}_1\\ ⋮\\ A_m\end{array}& \hfill \left[\begin{array}{ccc}(k_{111},k_{211},k_{311})& \dots & (k_{11n},k_{21n},k_{31n})\\ ⋮& (k_{1ij},k_{2ij},k_{3ij})& ⋮\\ (k_{1m1},k_{2m1},k_{3m1})& \dots & (k_{1mn},k_{2mn},k_{3mn})\end{array}\right]\end{array}\end{array}$$

(19)

Step 2. Aggregate the d decision matrices using Equation (13) to obtain ${\tilde{D}}_{Agg}({\mu }_{ij},{\nu }_{ij},{\pi }_{ij})$.

Step 3. Derive the weighted aggregated decision matrix as specified in Equation (20).

$${\tilde{D}}_{Agg}^{\tilde{w}}\left({\mu }_{ij},v_{ij},{\pi }_{ij}\right)={\tilde{w}}_j\otimes {\tilde{D}}_{Agg}\left({\mu }_{ij},v_{ij},{\pi }_{ij}\right)$$

(20)

Step 4. Exchange the membership and non-membership degrees in an SFN to transform a cost criterion into a benefit criterion.

An SFN representing a cost criterion $\left({\mu }_{ij},v_{ij},{\pi }_{ij}\right)$ is transformed into a benefit criterion as $\left(v_{ij},{\mu }_{ij},{\pi }_{ij}\right)$.

Step 5. Identify the positive ideal solution (PIS) and negative ideal solution (NIS) within the weighted aggregated decision matrix according to Equations (21) and (22), respectively. The SF PIS and SF NIS are utilized in subsequent steps after being established through the score function [20].

$$\widetilde{PIS}\iff \underset{\forall i}{max}\left\{{\left({\mu }_{ij}-{\displaystyle \frac{{\pi }_{ij}}{2}}\right)}^2-{\left(v_{ij}-{\displaystyle \frac{{\pi }_{ij}}{2}}\right)}^2\right\},j=1,2,\dots ,m$$

(21)

$$\widetilde{NIS}\iff \underset{\forall i}{min}\left\{{\left({\mu }_{ij}-{\displaystyle \frac{{\pi }_{ij}}{2}}\right)}^2-{\left(v_{ij}-{\displaystyle \frac{{\pi }_{ij}}{2}}\right)}^2\right\},j=1,2,\dots ,m$$

(22)

Step 6. Calculate the distances from each alternative to the SF-PIS and the SF-NIS according to Equations (23) and (24) [46].

$$D_i^{*}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{j=1}^n\left({\left({\mu }_{ij}-{\mu }_j^{*}\right)}^2+{\left(v_{ij}-v_j^{*}\right)}^2+{\left({\pi }_{ij}-{\pi }_j^{*}\right)}^2\right)}$$

(23)

$$D_i^{-}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{j=1}^n\left({\left({\mu }_{ij}-{\mu }_j^{-}\right)}^2+{\left(v_{ij}-v_j^{-}\right)}^2+{\left({\pi }_{ij}-{\pi }_j^{-}\right)}^2\right)}$$

(24)

Step 7. Calculate the closeness coefficient to ideal solutions for each alternative using Equation (25) [46].

$$C{C}_i={\displaystyle \frac{D_i^{-}}{D_i^{-}+D_i^{*}}}$$

(25)

Step 8. Rank the alternatives from the largest $C{C}_i$ to the smallest $C{C}_i$. The largest $C{C}_i$ indicates the best alternative.

5. Case Study

In this case study, the evaluation of early-stage start-up investment opportunities is conducted using the proposed PSF AHP & TOPSIS methodology. All computational analyses were performed on a PC equipped with an Intel Core i7 processor Intel Corporation, Santa Clara, CA, USA; 3.2 GHz) and 16 GB RAM. Python (Version 3.8; Python Software Foundation, Wilmington, DE, USA) and Microsoft Excel (Microsoft Corporation, Redmond, WA, USA; 2019 version) were utilized for the implementation of the PSF-AHP and PSF-TOPSIS models.

5.1. Criteria and Alternatives

This research is based on 13 fundamental criteria that assess early-stage start-up investment opportunities across various dimensions of venture viability and strategic potential. Each criterion has been carefully selected to capture the essential considerations in evaluating the feasibility and attractiveness of venture capital investments. These criteria span multiple domains, including founder capabilities, team composition, innovation capacity, market presence, strategic partnerships, institutional support, financial backing, and product differentiation. All criteria represent benefit criteria where higher values indicate more favorable investment characteristics. In addition, five other potential start-up projects are discussed and evaluated in terms of their investment appropriateness based on these thorough assessment dimensions.

Evaluation criteria used in venture capital decisions can be broadly categorized into two approaches, depending on their assessment methodology: data-driven and expert-opinion-driven criteria. The difference serves to explain how investment decisions are arrived at and justified in practice. Data-driven criteria are based on quantifiable, objective, and verifiable data, measured by concrete metrics and factual data sources. These criteria have reduced subjectivity and offer standardized yardsticks consistently applicable across multiple investment opportunities. They generally encompass numeric values, recorded accounts, or quantifiable results independently verified by external databases, official listings, or records.

Expert-opinion-based criteria, on the other hand, are subject to human judgment, qualitative determination, and subjective understanding via professional practice and knowledge domain expertise. They are difficult to quantify and cannot be standardized because they encapsulate intricate qualitative elements necessitating subtle knowledge of market forces, human behavior, and strategic implications. Expert judgment intervenes when we need to measure intangible assets, relationship quality, or strategic fit qualitatively rather than solely by numeric metrics.

Their union provides an integrated model of evaluation that balances objective measurability and awareness of context. As data-driven parameters ensure uniformity and reduce bias, expert-opinion-driven parameters highlight the subtle, qualitative issues that routinely govern venture success but are hard to quantify; these hybrid parameters better enable venture capitalists to make more informed decisions through the marriage of hard facts and experiential knowledge.

Among the 13 criteria identified for start-up evaluation, five criteria (C3, C6, C9, C11, C13) are primarily data-driven, while eight criteria (C1, C2, C4, C5, C7, C8, C10, C12) require expert opinion for practical assessment.

Data-driven criteria can be evaluated using quantifiable, verifiable data sources:

• Innovation and Patent Ownership (C3): This can be measured through patent databases, intellectual property registrations, and official records. Quantifiable indicators include the number of patents, patent citations, and the strength of the IP portfolio [48,49].
• Accelerator or Incubator Involvement (C6): Verified through program materials, graduation rosters, and public databases. Quality and performance can be evaluated based on past success rates and graduate records [50,51].
• Initial Amount of Funding (C9): Definite monetary figures can be confirmed via investment records, the United States Securities and Exchange Commission (SEC) documents, and funding databases such as Crunchbase, enabling explicit quantitative comparisons [52].
• University/Top School Affiliation (C11): Verified through university rankings and academic records. Institution rankings provide standardized, objective metrics [49].
• Professional Investors or Angels Support (C13): Verifiable from funding rounds, investor databases, and official records. The track record and reputational score of investors are further objective indicators [53].

Expert-opinion-driven criteria require human judgment and qualitative evaluation.

• Founders’ Track Record (C1): While previous projects may be objectively identified, evaluating their “success” requires multi-angle analysis of market conditions, role responsibilities, and transferable skills [25].
• Team Diversity and Complementarity (C2): Determining how team members’ skills complement each other involves assessing team dynamics, skill complementarity, and organizational performance, which are complex to measure [48].
• Online Channel Start-up Visibility (C4): While follower counts are measurable, the quality and impact of visibility require judgment on content quality, engagement value, and brand perception [54].
• Strategic Alliances (C5): Assessing alliance value needs expert evaluation of alliance strength, mutual benefit, and sustainability, not just the count of partnerships [55].
• Founders’ Industry Experience (C7): Requires judgment to determine relevance and depth of prior experience and its applicability to current market needs [25].
• Advisory Board Involvement (C8): Extends beyond listing board members; it requires evaluating advisor engagement, expertise relevance, and actual contributions.
• Team Size and Commitment (C10): Size can be measured, but dedication assessment depends on behavioral indicators, work habits, and loyalty evidence [25].
• Product Differentiation (C12): Determining uniqueness and competitive advantage requires expert market analysis, technology evaluation, and competitive positioning [48].

5.2. PSF AHP Application

Three experts were chosen for complementary perspectives: DM1 (VC partner; >10 years; >30 seed/Series-A deals), DM2 (industry domain expert; >12 years; prior accelerator mentor), DM3 (academic/entrepreneurship scholar; >10 years; methodological expertise). Experts were selected based on their domain depth, deal exposure, and methodological familiarity. Weighting: Consistent with expertise and role, $w_{DM1}=0.25,w_{DM2}=0.30,w_{DM3}=0.45$ were used in aggregation, ensuring that more experienced or influential evaluators had a proportionally greater impact on the aggregated results. Robustness to these weights is examined in Section 7.

Table 3. Linguistic PSF evaluation of decision-makers for pairwise criteria comparison.

DM1

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C1

E

SW

FW

VS

VS

SS

E

SS

E

FW

FS

FS

E

C2

SS

E

E

AW

FS

VS

SS

FS

FS

VS

VS

FS

FS

C3

FS

E

E

E

FS

FS

FS

FS

FS

FS

VS

FS

FS

C4

VW

AS

E

E

FW

E

VW

FW

VW

VW

E

VS

VW

C5

VW

FW

FW

FS

E

SW

VW

E

FW

VW

FS

SW

FW

C6

SW

VW

FW

E

SS

E

VW

E

E

FW

FS

E

SW

C7

E

SW

FW

VS

VS

VS

E

VS

VS

FW

SS

FS

SS

C8

SW

FW

FW

FS

E

E

VW

E

SW

FW

SS

SW

FW

C9

E

FW

FW

VS

FS

E

VW

SS

E

FW

VS

FS

SW

C10

FS

VW

FW

VS

VS

FS

FS

FS

FS

E

SW

SS

FS

C11

FW

VW

VW

E

FW

FW

SW

SW

VW

SS

E

E

SW

C12

FW

FW

FW

VW

SS

E

FW

SS

FW

SW

E

E

E

C13

E

FW

FW

VS

FS

SS

SW

FS

SS

FW

SS

E

E

DM2

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C1

E

FW

VW

VS

FS

FS

SW

FS

SS

FW

VS

SS

SS

C2

FS

E

E

E

FW

FS

FS

FS

FS

SS

VS

FS

AW

C3

VS

E

E

FS

FW

VS

FS

VS

FS

FW

AS

FS

AW

C4

VW

E

FW

E

SW

FW

VW

SW

VW

VW

E

VW

E

C5

FW

FS

FS

SS

E

SW

VS

E

VW

VW

FS

E

FW

C6

FW

FW

VW

FS

SS

E

FW

SS

E

SW

VS

E

SW

C7

SS

FW

FW

VS

VW

FS

E

FS

FS

VW

FS

VS

SS

C8

FW

FW

VW

SS

E

SW

FW

E

SW

FW

SS

SW

FW

C9

SW

FW

FW

VS

VS

E

FW

SS

E

FW

VS

SS

E

C10

FS

SW

FS

VS

VS

SS

VS

FS

FS

E

FS

FS

VS

C11

VW

VW

AW

E

FW

VW

FW

SW

VW

FW

E

AS

AS

C12

SW

FW

FW

VS

E

E

VW

SS

SW

FW

AW

E

VS

C13

SW

AS

AS

E

FS

SS

SW

FS

E

VW

AW

VW

E

DM3

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C1

E

E

FW

AS

AS

SS

SW

VS

SS

SW

VS

VS

E

C2

E

E

SW

VS

VS

FS

E

FS

FS

E

VS

FS

SS

C3

FS

SS

E

AS

VS

VS

FS

VS

FS

SS

VS

FS

FS

C4

AW

VW

VW

E

VW

SW

AW

VW

VW

FS

E

AW

FS

C5

AW

VW

FW

VS

E

SS

FW

E

FW

E

SS

E

FS

C6

SW

FW

E

SS

SW

E

SW

SS

SS

SW

FS

E

VW

C7

SS

E

FW

AS

FS

SS

E

FS

SS

SW

VS

VS

FW

C8

VW

FW

FW

VS

E

SW

FW

E

SW

VW

SS

E

SW

C9

SW

FW

E

VS

FS

SW

SW

SS

E

FW

FS

FS

E

C10

SS

E

VW

FW

E

SS

SS

VS

FS

E

FS

VS

FS

C11

VW

VW

FW

E

SW

FW

VW

SW

FW

FW

E

AS

AS

C12

VW

FW

SW

AS

E

E

VW

E

FW

VW

AW

E

VS

C13

E

SW

SS

FW

FW

VS

FS

SS

E

FW

AW

VW

E

presents the pairwise comparisons of the evaluation criteria conducted by three decision-makers. These comparisons were expressed using linguistic terms from the PSF scale shown in Table 1. Each linguistic term was mapped to its corresponding PSFS parameters, enabling the qualitative judgments to be converted into a consistent numerical representation. The resulting values reflect the relative importance, or priority, assigned to each criterion in relation to the others.

The pairwise comparison matrix used in this process is square, with each diagonal element being “Exactly Equal (E)”, representing that a criterion is equally important as itself. The elements above and below the diagonal are reciprocal to each other, meaning that if the entry in row i, column j expresses the importance of criterion i over criterion j, then the entry in row j, column i expresses the inverse relationship (the relative importance of criterion j over criterion i). This reciprocal property maintains logical consistency within the matrix and is a fundamental requirement of the AHP.

The evaluations from the three DMs are consolidated using Equation (13) to obtain an aggregated pairwise comparison matrix. This process applies the PSFWA operator, which combines the individual linguistic assessments of each DM according to their assigned weights. The resulting aggregated values are presented in

Table 4. Aggregated PFS pairwise comparison matrix.

	C1			C2			C3			C4			C5
	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$
C1	0.11	0.00	0.00	0.51	0.40	0.70	0.34	0.20	0.90	0.98	0.00	0.17	0.97	0.00	0.19
C2	0.70	0.40	0.51	0.11	0.00	0.00	0.55	0.48	0.65	0.82	0.00	0.44	0.88	0.18	0.40
C3	0.90	0.20	0.34	0.65	0.48	0.55	0.11	0.00	0.00	0.94	0.00	0.24	0.88	0.18	0.40
C4	0.17	0.00	0.98	0.44	0.00	0.82	0.24	0.00	0.94	0.11	0.00	0.00	0.37	0.20	0.88
C5	0.19	0.00	0.97	0.40	0.18	0.88	0.40	0.18	0.88	0.88	0.20	0.37	0.11	0.00	0.00
C6	0.46	0.34	0.81	0.34	0.21	0.91	0.27	0.14	0.94	0.74	0.37	0.49	0.63	0.38	0.65
C7	0.72	0.44	0.53	0.51	0.45	0.75	0.38	0.25	0.88	0.98	0.07	0.18	0.84	0.18	0.70
C8	0.36	0.23	0.91	0.38	0.25	0.88	0.28	0.15	0.94	0.91	0.24	0.37	0.57	0.57	0.57
C9	0.53	0.44	0.72	0.38	0.25	0.88	0.38	0.25	0.88	0.96	0.12	0.24	0.91	0.21	0.34
C10	0.84	0.31	0.44	0.49	0.43	0.80	0.66	0.31	0.73	0.86	0.18	0.67	0.88	0.36	0.41
C11	0.28	0.15	0.94	0.24	0.12	0.96	0.20	0.09	0.97	0.57	0.57	0.57	0.44	0.31	0.84
C12	0.37	0.24	0.91	0.38	0.25	0.88	0.38	0.25	0.88	0.95	0.07	0.60	0.63	0.53	0.56
C13	0.55	0.52	0.64	0.55	0.52	0.70	0.81	0.18	0.78	0.71	0.34	0.72	0.75	0.25	0.71
	C6			C7			C8			C9			C10
	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$
C1	0.81	0.34	0.46	0.53	0.44	0.72	0.91	0.23	0.36	0.72	0.44	0.53	0.44	0.31	0.84
C2	0.91	0.21	0.34	0.75	0.45	0.51	0.88	0.25	0.38	0.88	0.25	0.38	0.80	0.43	0.49
C3	0.94	0.14	0.27	0.88	0.25	0.38	0.94	0.15	0.28	0.88	0.25	0.38	0.73	0.31	0.66
C4	0.49	0.37	0.74	0.18	0.07	0.98	0.37	0.24	0.91	0.24	0.12	0.96	0.67	0.18	0.86
C5	0.65	0.38	0.63	0.70	0.18	0.84	0.57	0.57	0.57	0.34	0.21	0.91	0.41	0.36	0.88
C6	0.11	0.00	0.00	0.41	0.28	0.87	0.72	0.44	0.53	0.67	0.50	0.55	0.48	0.35	0.80
C7	0.87	0.28	0.41	0.53	0.44	0.72	0.91	0.22	0.35	0.87	0.28	0.41	0.41	0.28	0.88
C8	0.53	0.44	0.72	0.35	0.22	0.91	0.62	0.62	0.62	0.51	0.38	0.76	0.32	0.20	0.92
C9	0.55	0.50	0.67	0.41	0.28	0.87	0.76	0.38	0.51	0.92	0.20	0.32	0.38	0.25	0.88
C10	0.80	0.35	0.48	0.88	0.28	0.41	0.92	0.20	0.32	0.88	0.25	0.38	0.63	0.63	0.63
C11	0.34	0.21	0.91	0.36	0.23	0.91	0.51	0.38	0.76	0.31	0.18	0.93	0.51	0.29	0.83
C12	0.57	0.57	0.57	0.28	0.15	0.94	0.69	0.48	0.54	0.42	0.29	0.85	0.36	0.23	0.91
C13	0.89	0.27	0.40	0.74	0.33	0.63	0.84	0.31	0.44	0.63	0.53	0.56	0.34	0.21	0.91
	C11			C12			C13
	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$
C1	0.94	0.15	0.28	0.91	0.24	0.37	0.64	0.52	0.55
C2	0.96	0.12	0.24	0.88	0.25	0.38	0.70	0.25	0.83
C3	0.97	0.09	0.20	0.88	0.25	0.38	0.78	0.18	0.81
C4	0.57	0.57	0.57	0.60	0.07	0.95	0.72	0.34	0.71
C5	0.84	0.31	0.44	0.56	0.53	0.63	0.71	0.25	0.75
C6	0.91	0.21	0.34	0.57	0.57	0.57	0.40	0.27	0.89
C7	0.91	0.23	0.36	0.94	0.15	0.28	0.63	0.33	0.74
C8	0.76	0.38	0.51	0.54	0.48	0.69	0.44	0.31	0.84
C9	0.93	0.18	0.31	0.85	0.29	0.42	0.56	0.53	0.63
C10	0.83	0.29	0.51	0.91	0.23	0.36	0.91	0.21	0.34
C11	0.36	0.23	0.91	0.97	0.19	0.26	0.97	0.11	0.36
C12	0.26	0.19	0.26	0.57	0.57	0.57	0.92	0.27	0.34
C13	0.36	0.27	0.36	0.34	0.27	0.92	0.62	0.62	0.62

, representing a unified set of evaluations that proportionally reflect both the judgments and expertise levels of the decision-makers.

The score function, as defined in Equation (14), is applied to convert the proportional spherical fuzzy evaluations into a crisp pairwise comparison matrix, as shown in

Table 5. Crisp aggregated pairwise comparison matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
C1	0.05	0.01	0.03	0.13	0.17	0.11	0.01	0.11	0.09	0.01	0.12	0.12	0.10
C2	0.16	0.16	0.23	0.06	0.12	0.15	0.22	0.11	0.14	0.42	0.12	0.11	0.00
C3	0.27	0.47	0.20	0.11	0.12	0.17	0.29	0.13	0.14	0.18	0.13	0.11	0.02
C4	0.01	0.04	0.02	0.02	0.00	0.01	0.01	0.00	0.00	0.03	0.04	0.00	0.05
C5	0.01	0.02	0.03	0.10	0.02	0.05	0.02	0.05	0.00	0.01	0.09	0.03	0.02
C6	0.01	0.02	0.02	0.07	0.04	0.03	0.01	0.07	0.08	0.02	0.11	0.05	0.00
C7	0.17	0.03	0.03	0.13	0.05	0.14	0.01	0.11	0.14	0.01	0.10	0.13	0.02
C8	0.01	0.02	0.02	0.10	0.06	0.00	0.01	0.05	0.01	0.01	0.07	0.02	0.01
C9	0.01	0.02	0.03	0.12	0.15	0.03	0.01	0.08	0.16	0.01	0.11	0.10	0.06
C10	0.23	0.03	0.14	0.04	0.14	0.11	0.29	0.12	0.14	0.25	0.07	0.12	0.20
C11	0.01	0.02	0.02	0.04	0.00	0.00	0.01	0.00	0.00	0.02	0.00	0.14	0.20
C12	0.01	0.02	0.03	0.06	0.07	0.06	0.01	0.07	0.00	0.01	0.02	0.05	0.21
C13	0.07	0.15	0.20	0.03	0.04	0.14	0.13	0.09	0.08	0.01	0.02	0.00	0.09

. This process produces the numerical weights of the criteria using the PSF AHP method, where each weight is computed as the arithmetic mean of the aggregated crisp scores in the corresponding row of the pairwise comparison matrix. These weights, illustrated in Figure 2, are then used as inputs for the subsequent PSF TOPSIS analysis.

The importance ranking shows a clear emphasis on innovation, human capital quality, and team structure. Innovation and Patent Ownership (C3) is given the highest weight (0.180), indicating that technological novelty and intellectual property are regarded as the strongest indicators of investment potential. Team Diversity and Complementarity (C2) (0.154) and Team Size and Commitment (C10) (0.145) also rank highly, underscoring the perceived importance of a balanced and dedicated team in early-stage venture success.

Criteria such as Founders’ Industry Experience (C7), Founders’ Track Record (C1), and Professional Investors or Angels Support (C13), each with weights of around 0.081–0.082, occupy a middle tier, suggesting that experience and investor backing are considered valuable but secondary to innovation and team structure. Lower-weighted factors, including Product Differentiation (C12) (0.048), Accelerator or Incubator Participation (C6) (0.040), and University/Top School Affiliation (C11) (0.036), indicate that while ecosystem connections and product uniqueness are relevant, they play a more supportive role. The least-weighted factors—Strategic Alliances (C5), Advisory Board Presence (C8), and Start-up Visibility in Online Channels (C4)—suggest that external partnerships and visibility are seen as less decisive at this stage, possibly due to their indirect impact on core venture viability.

5.3. PSF TOPSIS Application

The decision-makers (DMs) evaluate 5 alternatives based on 13 criteria. In this study, the structure of these evaluations is presented in

Table 6. PSF decision matrices for alternatives.

		C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
DM1	A1	CH	CL	H	CL	VL	L	CL	A	L	L	CL	VL	BA
	A2	CH	CH	VH	CL	A	CL	VL	VL	VL	BA	VL	VL	AA
	A3	CL	VL	VL	L	L	L	CH	VL	A	BA	VL	CL	L
	A4	A	H	CL	H	L	A	BA	H	H	L	AA	BA	H
	A5	H	VH	CH	L	CL	AA	H	L	A	H	BA	BA	BA
DM2	A1	AA	L	A	VL	BA	A	L	BA	BA	L	L	L	L
	A2	A	L	VL	VL	L	AA	L	H	L	BA	AA	H	AA
	A3	A	L	H	AA	H	A	L	H	L	H	BA	H	A
	A4	A	VL	H	VH	CL	VH	VH	H	BA	BA	H	VL	L
	A5	A	AA	A	AA	CH	A	AA	A	AA	BA	H	BA	BA
DM3	A1	AA	L	A	VL	BA	A	L	L	BA	L	L	L	H
	A2	A	L	VL	VL	L	AA	L	H	L	BA	AA	H	AA
	A3	A	L	H	AA	H	A	L	AA	L	H	BA	H	A
	A4	A	VL	H	VH	CL	VH	VH	H	BA	L	H	VL	L
	A5	A	AA	A	AA	CH	A	AA	H	AA	BA	BA	BA	BA

. The assessments are initially expressed in linguistic terms, which are then systematically converted into PSFNs using the predefined linguistic-to-PSF scale given in Table 2. This transformation ensures that qualitative judgments can be represented in a quantitative form suitable for further analysis. As an example,

Table 7. DM1’s PFS decision matrices for alternatives.

	C1			C2			C3			C4			C5			C6			C7
	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$
A1	0.43	0.00	0.81	0.93	0.00	0.28	0.53	0.47	0.64	0.97	0.00	0.20	0.84	0.29	0.42	0.69	0.47	0.52	0.93	0.20	0.32
A2	0.28	0.00	0.93	0.80	0.00	0.48	0.91	0.12	0.34	0.97	0.00	0.20	0.84	0.31	0.42	0.81	0.00	0.47	0.91	0.22	0.35
A3	0.64	0.47	0.53	0.34	0.12	0.91	0.68	0.21	0.64	0.66	0.34	0.64	0.59	0.25	0.71	0.69	0.47	0.52	0.80	0.20	0.77
A4	0.20	0.00	0.97	0.20	0.00	0.97	0.64	0.34	0.66	0.28	0.14	0.94	0.98	0.00	0.15	0.34	0.18	0.84	0.43	0.19	0.92
A5	0.42	0.29	0.84	0.42	0.31	0.84	0.71	0.25	0.59	0.15	0.00	0.98	0.70	0.00	0.57	0.56	0.52	0.62	0.48	0.35	0.80
	C8			C9			C10			C11			C12			C13
	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$	$\mu$	$\pi$	$\nu$
A1	0.80	0.38	0.46	0.76	0.34	0.47	0.86	0.24	0.37	0.93	0.20	0.32	0.88	0.22	0.34	0.67	0.27	0.71
A2	0.68	0.22	0.81	0.91	0.22	0.35	0.75	0.37	0.50	0.73	0.32	0.68	0.68	0.22	0.81	0.50	0.37	0.75
A3	0.63	0.28	0.74	0.83	0.34	0.43	0.46	0.27	0.83	0.79	0.32	0.44	0.77	0.20	0.80	0.67	0.55	0.57
A4	0.36	0.24	0.85	0.66	0.33	0.65	0.83	0.28	0.40	0.40	0.28	0.82	0.93	0.19	0.32	0.77	0.24	0.59
A5	0.65	0.40	0.76	0.54	0.46	0.73	0.70	0.35	0.66	0.68	0.34	0.68	0.76	0.38	0.51	0.76	0.38	0.51

demonstrates the conversion of DM1’s linguistic decision matrix into its corresponding PSF numerical format (the evaluations of the other two experts are not presented here due to space limitations), illustrating the intermediate step between expert judgments and the computational phase of the PSF TOPSIS method.

PIS and NIS values within the weighted aggregated decision matrix are determined using Equations (21) and (22), respectively, as presented in

Table 8. PIS and NIS values.

	PIS	NIS	${\mathit{D}}^{*}$	${\mathit{D}}^{-}$
A1	−0.40	−0.95	C2	C1
A2	−0.37	−0.98	C3	C1
A3	−0.67	−0.92	C3	C4
A4	−0.53	−0.99	C10	C1
A5	−0.62	−1.00	C3	C4

. The symbols $D^{*}$ and $D^{-}$ represent the calculated distances from each alternative to the PIS and NIS, respectively, and are obtained by applying Equations (23) and (24). A detailed breakdown of these distances for each criterion and alternative is provided in

Table 9. Distances to PIS ($D^{*}$) and NIS ($D^{-}$).

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	${\mathit{D}}^{*}$
A1	0.2	0	0.15	0.11	0.13	0.2	0.05	0.159	0.12	0.04	0.09	0.093	0.12	0.33
A2	0.2	0	0	0.12	0.12	0.1	0.04	0.182	0.05	0.05	0.15	0.153	0.16	0.333
A3	0	0	0	0.06	0.05	0	0.01	0.049	0.01	0.02	0.02	0.022	0.03	0.166
A4	0.2	0.1	0.01	0.17	0.04	0.1	0.1	0.14	0.05	0	0.13	0.016	0.03	0.294
A5	0.1	0	0	0.14	0.07	0.1	0.05	0.058	0.04	0	0.05	0.025	0.01	0.212
	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	$D^{-}$
A1	0	0.2	0.08	0.01	0.02	0	0.1	0.016	0.03	0.13	0.03	0.03	0.02	0.226
A2	0	0.1	0.24	0.02	0.03	0	0.11	0.006	0.09	0.12	0.02	0.013	0.02	0.244
A3	0	0	0.06	0	0	0	0.04	4E-04	0.05	0.01	0.01	0.011	0.05	0.141
A4	0	0	0.1	0	0.08	0	0.01	0.002	0.03	0.16	0	0.079	0.06	0.201
A5	0	0	0.14	0	0.02	0	0.03	0.021	0.04	0.12	0.03	0.053	0.09	0.22

to show the criterion-level computations underlying the aggregated $D^{*}$ and $D^{-}$ values. These distance values are subsequently used in the computation of the closeness coefficients ($CC$), which form the basis for the final ranking of alternatives in the PSF TOPSIS method.

Subsequently, the closeness to ideal solutions ($C{C}_i$) for each alternative is computed using Equation (25). Figure 3 presents the closeness scores and ranking of alternatives. The analysis of the closeness coefficients indicates that Alternative A5 achieved the highest performance score, suggesting that it is the most favorable option under the evaluated criteria. Alternatives A2 and A3 followed closely, occupying the second and third ranks, respectively, while A1 and A4 were positioned lower in the ranking, with minimal difference between their scores. This distribution implies that the decision-making model effectively differentiated among the alternatives, with A5 demonstrating a comparatively stronger alignment to the ideal solution, whereas A1 and A4 exhibited relatively weaker conformity to the established evaluation parameters.

6. Comparative Analysis

For the comparative analysis, this study also applies the crisp AHP-TOPSIS, VIKOR, and PROMETHEE II using the same decision-makers’ inputs. The pairwise comparisons presented in Table 3 were converted for the crisp decision-making procedure, using the linguistic evaluations given in

Table 10. Crisp linguistic scale for criteria.

PSF Term	Classical AHP Equivalent	Numeric Value
AS (Absolutely Strong)	Extremely More Important	9
VS (Very Strong)	Very Strongly More Important	7
FS (Fairly Strong)	Strongly More Important	5
SS (Slightly Strong)	Moderately More Important	3
E (Exactly Equal)	Equally Important	1
SW (Slightly Weak)	Moderately Less Important	1/3
FW (Fairly Weak)	Strongly Less Important	1/5
VW (Very Weak)	Very Strongly Less Important	1/7
AW (Absolutely Weak)	Extremely Less Important	1/9

in the appropriate form.

Table 11. Aggregated pairwise comparison matrix and weights.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	Weight
C1	1.00	0.47	0.18	7.84	7.09	3.50	0.44	5.12	2.28	0.25	6.44	4.99	1.39	0.119
C2	2.13	1.00	0.61	1.39	2.21	5.44	2.13	5.00	5.00	2.26	7.00	5.00	1.27	0.118
C3	5.53	1.64	1.00	4.36	2.21	6.44	5.00	6.44	5.00	1.51	7.55	5.00	1.60	0.155
C4	0.13	0.72	0.26	1.00	0.20	0.38	0.13	0.20	0.14	0.71	1.00	0.34	1.27	0.019
C5	0.14	0.45	0.53	4.99	1.00	0.90	0.53	1.00	0.18	0.34	3.97	0.76	0.85	0.046
C6	0.29	0.18	0.37	2.66	1.12	1.00	0.23	2.28	1.64	0.29	5.53	1.00	0.23	0.049
C7	2.28	0.47	0.20	7.84	1.87	4.32	1.00	5.44	4.32	0.23	5.12	6.44	0.89	0.118
C8	0.20	0.20	0.18	4.99	1.00	0.44	0.18	1.00	0.33	0.17	3.00	0.55	0.25	0.036
C9	0.44	0.20	0.41	7.00	5.53	0.61	0.23	3.00	1.00	0.20	6.02	4.29	0.76	0.086
C10	3.97	0.44	0.45	1.41	2.92	3.41	4.40	5.82	5.00	1.00	2.54	5.12	5.53	0.122
C11	0.16	0.14	0.15	1.00	0.25	0.18	0.20	0.33	0.17	0.39	1.00	5.20	3.95	0.038
C12	0.20	0.20	0.25	2.96	1.32	1.00	0.16	1.83	0.23	0.20	0.19	1.00	4.30	0.040
C13	0.72	0.79	2.12	0.79	1.17	4.39	1.13	3.97	1.32	0.18	0.25	0.23	1.00	0.053

presents the aggregated decision matrix in this context. The criteria weights are used for alternative ranking in the classical TOPSIS method. The linguistic evaluations in Table 6 were converted into crisp numbers with the same linguistic expressions with numerical values starting from 9 for Certainly High to 1 for Certainly Low.

6.1. Crisp AHP-TOPSIS Results

Table 12. Distances to ideal solutions and alternative ranking.

	${\mathit{D}}^{*}$	${\mathit{D}}^{-}$	${\mathit{CC}}_{\mathit{i}}$	Rank
A1	0.70	0.43	0.38	4
A2	0.75	0.16	0.18	5
A3	0.21	0.71	0.77	1
A4	0.29	0.67	0.70	2
A5	0.38	0.61	0.62	3

indicates the final alternative rankings. The highest closeness coefficient ($C{C}_i$) was obtained by Alternative A3 (0.77), indicating that it is positioned closest to the ideal solution and, therefore, ranked first. This is followed by A4 (0.70) and A5 (0.62), which also exhibit relatively strong proximity to the ideal point. In contrast, A1 (0.38), and particularly A2 (0.18), demonstrate lower closeness coefficients, reflecting a greater distance from the ideal solution and resulting in lower rankings.

6.2. VIKOR Results

The aggregated decision matrix was normalized by linear normalization, and the weighted normalized matrix was obtained by multiplying it by the AHP weights. For each alternative, the group utility measure (S) and the individual regret measure (R) were calculated by summing and maximizing the weighted gaps from the best performance values, respectively. The compromise index (Q) was then computed using the standard formula with $v=0.5$ (equal emphasis on group utility and individual regret). Finally, alternatives were ranked in ascending order according to their Q values. The smallest Q indicated the best compromise solution.

The VIKOR analysis identified A5 as the best compromise solution, with the lowest Q value, as shown in

Table 13. VIKOR ranking results.

Alt.	S	R	Q (v = 0.5)	Rank
A5	0.283	0.056	0.000	1
A4	0.481	0.111	0.526	2
A3	0.531	0.119	0.631	3
A1	0.680	0.122	0.833	4
A2	0.651	0.155	0.964	5

. Both the group utility measure and the individual regret measure for A5 were found to be the smallest among all alternatives, which confirmed its robustness. Alternatives A4 and A3 occupied the middle ranks, whereas A1 and A2 showed significantly larger Q values, indicating weaker performance. The ranking remained stable when the parameter v was varied between 0.4 and 0.6, suggesting that the result is not sensitive to the compromise weighting.

6.3. PROMETHEE II Results

Pairwise preference indices were calculated for each pair of alternatives across all criteria. These indices were weighted by the AHP weights and aggregated to compute the overall preference flows. For each alternative, the positive flow (${\varphi }^{+}$) measured how strongly it outranked others, and the negative flow (${\varphi }^{+}$) measured how strongly it was outranked by others. The net flow ($\varphi ={\varphi }^{+}-{\varphi }^{-}$) determines the overall performance score. Alternatives were then ranked in descending order of net flows.

The PROMETHEE II analysis also ranked A5 as the best alternative, as it achieved the highest positive flow and the highest net flow, as shown in

Table 14. PROMETHEE ranking results.

Alt.	${\mathit{\varphi }}^{+}$	${\mathit{\varphi }}^{-}$	Net $\mathit{\varphi }$	Rank
A5	0.748	0.233	0.515	1
A4	0.483	0.465	0.018	2
A3	0.467	0.515	−0.047	3
A2	0.453	0.530	−0.077	4
A1	0.262	0.670	−0.408	5

. It indicates that A5 outperformed most other alternatives in pairwise comparisons. A4 was placed second with a small positive net flow, while A3 and A2 had slightly negative net flows. A1 recorded the lowest net flow, suggesting that it was dominated by other alternatives in most criteria. The overall consistency between the PROMETHEE II ranking and the VIKOR results supports the conclusion that A5 is the most favorable choice under the crisp benchmarks.

6.4. Discussion on Comparison Results

The ranking differences between the PSF AHP & TOPSIS results ($A5>A3>A2>A1>A4$) and the classical AHP & TOPSIS results ($A3>A4>A5>A1>A2$) can be attributed primarily to the way uncertainty, vagueness, and subjective judgments are handled in the two methods.

In classical AHP & TOPSIS, linguistic assessments are first converted into fixed numerical values based on a predefined crisp scale. This process forces expert opinions into exact numbers without preserving the hesitation or degree of uncertainty behind them. As a result, some nuanced differences in decision-maker perceptions can be lost, and extreme values may disproportionately influence the overall ranking.

When the proposed fuzzy model is compared with additional crisp benchmarks, namely, VIKOR and PROMETHEE II, a high level of consistency is observed regarding the best alternative. Both methods also ranked A5 as the most favorable option, although the middle-order positions showed some variation. In VIKOR, the compromise index emphasized both group utility and individual regret, resulting in the order $A5>A4>A3>A1>A2$. PROMETHEE II, which relies on pairwise preference flows, produced the order $A5>A4>A3>A2>A1$. These differences are expected because VIKOR focuses on minimizing maximum regret, while PROMETHEE aggregates outranking flows across all alternatives.

In contrast, PSF AHP & TOPSIS retains and mathematically represents membership, non-membership, and hesitancy degrees simultaneously through proportional spherical fuzzy sets. This means that uncertainty and partial agreement between decision-makers are explicitly modeled, leading to a more faithful aggregation of expert judgments. Consequently, the weighting of criteria and the scoring of alternatives in PSF TOPSIS reflect a richer and more realistic representation of the decision environment, especially in early-stage venture evaluation, where qualitative and imprecise information dominates.

Despite the variations in intermediate positions, the agreement on A5 as the top-ranked option across PSF AHP & TOPSIS, VIKOR, and PROMETHEE II strengthens the robustness of the study’s findings. The observed differences also underline that crisp benchmarks may either amplify or dampen certain decision-maker preferences depending on the structure of the method. By contrast, the fuzzy approach ensures that hesitation and partial consensus are preserved throughout, leading to rankings that better reflect the inherent uncertainty of early-stage investment decisions.

The superiority of PSF AHP & TOPSIS lies in its ability to:

• Capture hesitation in expert evaluations, preventing overconfidence in uncertain assessments;
• Balance influence among decision-makers with varying degrees of certainty;
• Preserve more information from linguistic inputs, thus avoiding information loss in the fuzzification-to-crisp conversion.

In contexts like venture capital investment firm selection, where data is incomplete, subjective judgments are inevitable, and uncertainty is high, PSF AHP & TOPSIS provides a more robust and realistic decision-making framework than its classical counterpart.

7. Sensitivity Analysis

Sensitivity analysis allows the assessment of the robustness of the decision outcomes by identifying alternatives whose rankings remain stable versus those that fluctuate significantly. Such analysis ensures that the final choice is not overly dependent on a specific weighting scenario, thereby increasing the reliability and validity of the decision-making process. In this study, a one-at-a-time approach was conducted for the sensitivity analysis. In this method, the weight of a single parameter (e.g., DM1’s weight) is varied across a predefined range while keeping all other parameters constant. This isolates the effect of that parameter on the rankings, enabling a clear understanding of how changes in the selected parameter alone influence the decision outcomes. The analysis was repeated for DM2 and DM3, and similar results were obtained, confirming the robustness of the findings.

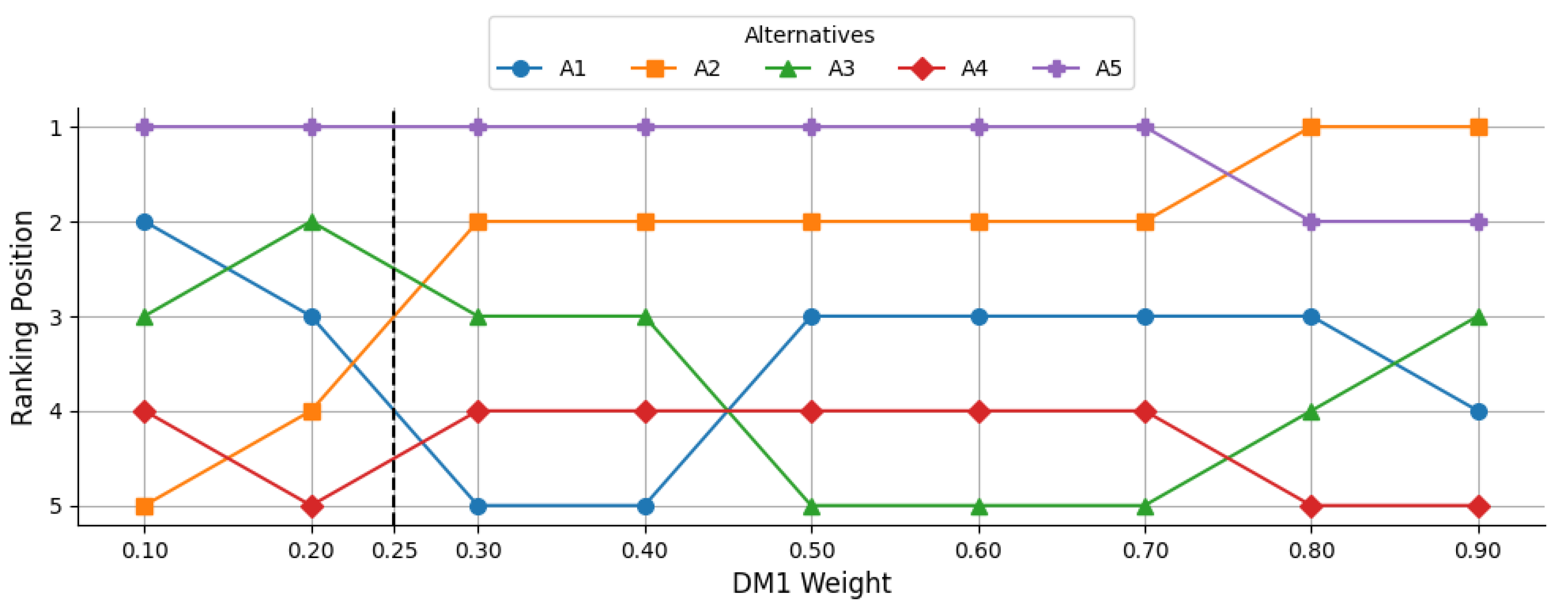
7.1. Effect of Changes in DM1 Weights on Alternative Ranking

Figure 4 illustrates how the ranking positions of the five alternatives (A1–A5) vary as the weight of DM1 increases from 0.1 to 0.9. The vertical axis is inverted so that rank 1 appears at the top, representing the most preferred position.

It can be observed that A5 consistently remains in the lowest rank throughout the weight variation, with only a minor improvement at the highest weight levels. A4 maintains a stable, high-ranking position, suggesting that its preference is less sensitive to DM1’s weight changes. Conversely, A1, A2, and A3 exhibit notable fluctuations, with A1 and A3 alternating between mid- and top-ranking positions, and A2 experiencing a gradual decline in preference as DM1’s weight increases.

These patterns indicate that the influence of DM1’s weight is most pronounced for A1, A2, and A3, whereas A4 and A5 are comparatively stable in their rankings. This stability in A4’s case suggests robustness to preference weight changes, while A5’s persistently low ranking implies consistently poor performance relative to other alternatives.

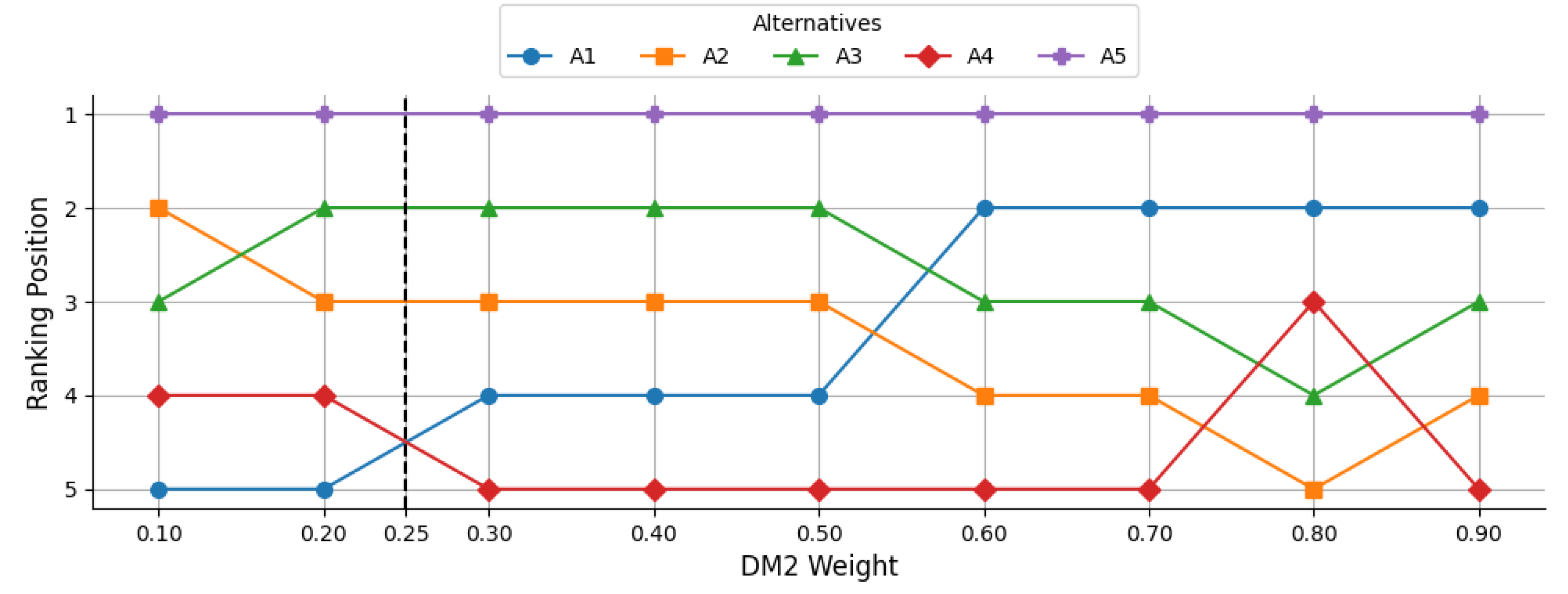
7.2. Effect of Changes in DM2 Weights on Alternative Ranking

Figure 5 depicts the sensitivity analysis of DM2. It can be observed that A5 remains consistently in the lowest position (rank 1) across all weight levels, suggesting a stable but unfavorable performance. A1 starts in the top rank position but experiences a sharp drop to mid-level rankings as DM2’s weight increases beyond 0.50, indicating a strong sensitivity to DM2’s preferences. In contrast, A2 and A3 maintain relatively stable middle positions, with minor shifts between ranks 2 and 4. A4 displays notable fluctuation, particularly achieving the highest rank around mid-weight values (0.30–0.50) before decreasing slightly at higher weights.

The sensitivity analysis suggests that the rankings for A2 and A3 are relatively robust to changes in DM2’s weight, while A1 and A4 are more sensitive, experiencing substantial positional changes. A5’s consistently poor ranking indicates that its evaluation is largely unaffected by DM2’s weight, but also that it is unlikely to be a competitive option under any weighting scenario.

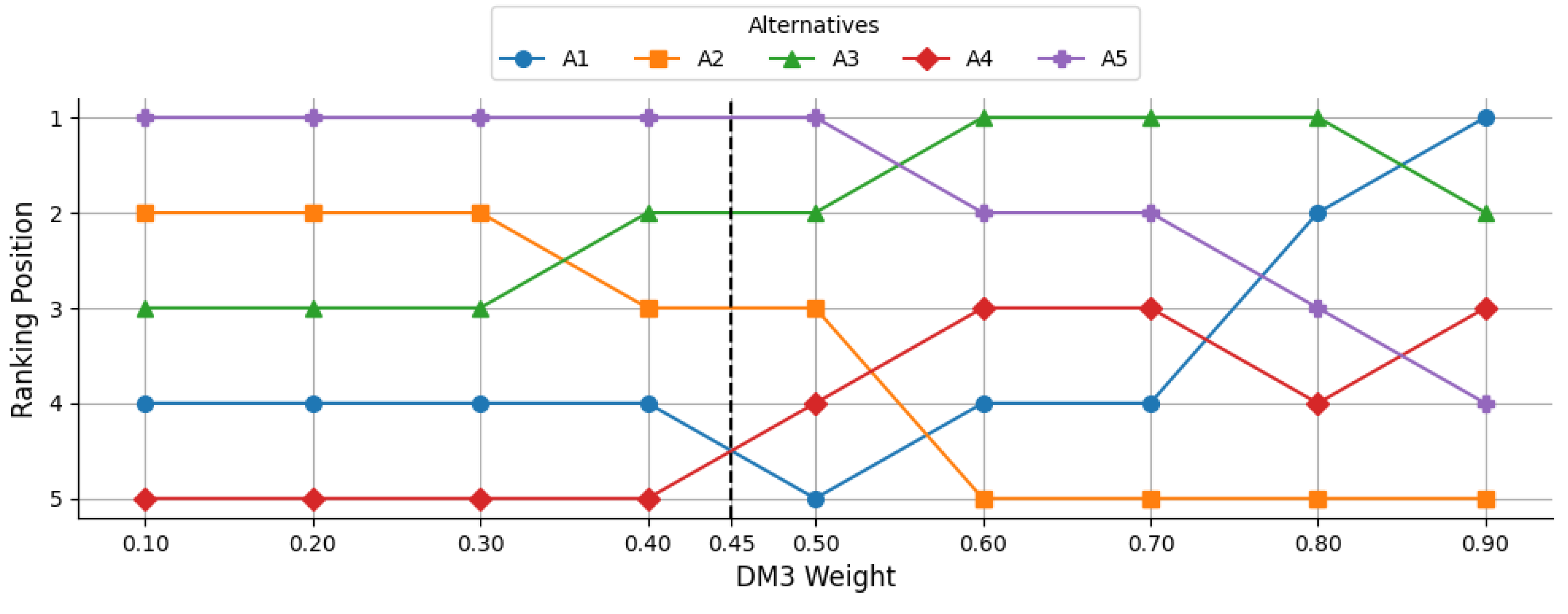
7.3. Effect of Changes in DM3 Weights on Alternative Ranking

For DM3, the results in Figure 6 reveal that A5 initially holds the highest preference at lower weight levels but steadily declines, ending in a much lower position when DM3’s weight reaches 0.90. In contrast, A3 shows a consistent improvement as DM3’s weight increases, particularly after 0.60, where it remains within the top two positions. A2 appears stable in mid-to-high rankings at the outset but gradually moves toward lower positions with higher DM3 weights. A1 experiences a notable upward shift in preference at higher weights, ultimately securing the top rank at 0.90. A4 begins in the lowest positions and fluctuates within the mid-ranks at higher weights, without a clear upward trend. Overall, these patterns indicate that A1 and A3 benefit most from increased DM3 weighting, while A5’s performance deteriorates, and A2 and A4 exhibit mixed sensitivity, demonstrating that the decision outcome is highly contingent on DM3’s weight allocation.

8. Conclusions and Discussion

Early-stage start-up selection remains a highly complex and uncertain decision-making process in the venture capital domain, requiring careful consideration of both quantitative and qualitative factors. In this study, the proportional spherical fuzzy (PSF) AHP&TOPSIS approach was implemented to evaluate five start-up alternatives against thirteen strategic criteria, encompassing innovation capability, team quality, market presence, and financial resources. The PSF-based method produced a ranking of A5 (0.5088) > A3 (0.4604) > A2 (0.4230) > A1 (0.4064) > A4 (0.4058), with Alternative A5 demonstrating the strongest proximity to the ideal solution. In comparison, classical AHP&TOPSIS ranked the alternatives as A3 (0.77) > A4 (0.70) > A5 (0.62) > A1 (0.38) > A2 (0.18), showing notable differences in order and magnitude. These findings confirm that PSF AHP&TOPSIS more effectively captures hesitation and preserves the richness of expert evaluations, resulting in rankings that reflect a more nuanced decision environment.

The comparative results between PSF AHP&TOPSIS and classical AHP&TOPSIS illustrate the impact of uncertainty modeling on decision-making outcomes. In the classical approach, linguistic judgments are converted into fixed numerical values, leading to potential loss of information and oversimplification of expert opinions. This process may inadvertently emphasize extreme assessments and diminish the influence of moderate but strategically important factors. For example, in the classical TOPSIS results, Alternative A3 achieved the highest score of 0.77, driven by strong performance in key criteria, while Alternative A2 scored only 0.18, placing last.

In contrast, PSF AHP&TOPSIS incorporates membership, non-membership, and hesitancy degrees, allowing for partial agreement and varied confidence levels to be directly represented. This method produced more balanced closeness coefficients, with the top-ranked alternative (A5) scoring 0.5088 and the lowest (A4) still achieving 0.4058, indicating a narrower spread. Such a distribution suggests that PSF modeling mitigates the risk of disproportionately low or high scores resulting from rigid crisp assignments.

Furthermore, the PSF approach led to a more even distribution of criteria weights, with Innovation & Patent Ownership (C3) receiving the highest weight (0.180) and the least important criteria, such as start-up Visibility in Online Channels (C4), still maintaining measurable influence (0.018). This balance ensures that decision outcomes are shaped by a broad spectrum of factors, aligning with the multi-faceted nature of venture capital investment decisions.

The application results demonstrate that PSF AHP&TOPSIS is more resilient to the biases introduced by extreme or uncertain evaluations, making it better suited for complex, information-scarce environments like early-stage investment selection. Its ability to integrate both quantitative and qualitative inputs while preserving uncertainty provides decision-makers with a more realistic and defensible basis for resource allocation.

In the context of this study, the sensitivity analysis serves as a critical step to evaluate the robustness and reliability of the final rankings generated by the proposed PSF AHP&TOPSIS model. By varying, in a one-at-a-time way, the weight attributed to each of the decision-makers, the analysis removes the influence of single evaluators on the final outcome of the decision. The analysis thereby determines the alternatives that are resistant to such changes and those that are more susceptible to such changes. Robustness of rankings means independence of preference for such alternatives from an undue influence of a single, particular decision-maker. Overt changes, on the other hand, are symptomatic of weaknesses of the final outcome of the decision, where an investment recommendation may be overturned by an infinitesimal shift of an evaluator’s weight. The results are, thus, helpful in interpreting resilience of model results, constructing greater confidence in recommendations, and directing the decision-makers toward less susceptible-to-bias or undue-influence approach strategies.

These results are derived from a single case with five alternatives and thirteen attributes and, thus, may restrict generalizability. Expert judgment necessitates inherent subjectivity, and the PSF parameterization further relies on the linguistic scale chosen. Higher dataset sizes may further enhance computational complexity, necessitating optimization to accommodate real-time decision situations.

Future studies may further widen the analysis scope to more start-up options and criteria, and thereby permit more extensive model validation. Applications across industries may provide an examination of the model’s applicability across industries. Combining proportional spherical fuzzy approaches with predictive analysis or machine learning may further improve model scalability and forecasting capability. Long-term, prospective studies of the actual performance of investments selected using the method may further establish the method’s usefulness.