Logistics Companies’ Efficiency Analysis and Ranking by the DEA-Fuzzy AHP Approach

Abstract

The logistics industry saw substantial growth in the second half of the 20th century, and logistics companies play a vital role in today’s modern market. Constant shifts in the market present challenges for logistics firms, which must find the optimal balance between achieved goals and utilized resources. The primary indicator that reflects this relationship is efficiency. Measuring and monitoring efficiency in logistics companies is extremely demanding because the final product is not a tangible item; instead, it often consists of transportation, storage, transloading, and forwarding services that require extensive resources. This paper focuses on measuring and improving efficiency. Numerous approaches and methods for evaluating the efficiency of logistics companies are examined. To measure and enhance efficiency, as well as rank companies based on operational efficiency, a three-phase DEA-fuzzy AHP model has been developed. This model was tested using a real-world example by analyzing the efficiency of ten logistics companies in the Republic of Serbia. The results of the analysis indicate the applicability of this model for measuring and improving the efficiency of logistics companies, as well as for their ranking.

1. Introduction

Contemporary business operations are marked by constant market competition, regardless of the specific industry [1,2]. This heightened rivalry necessitates that organizational structures become critical factors in business success, requiring all operational activities to be strategically aligned and economically sustainable for both service providers and end users [3,4]. As consumer purchasing decisions are increasingly shaped by organizational performance, the significance of systematic performance measurement and monitoring continues to rise. Accordingly, academic literature emphasizes that a company’s success is more closely linked to the maturity and sophistication of its performance measurement systems [5].

One of the fundamental indicators of operational effectiveness is the ratio between invested resources and the outcomes achieved [6]. This ratio is often considered as efficiency, though the term itself is complex and lacks a universally accepted definition. In the context of logistics, efficient systems and processes provide a variety of benefits, including cost savings through optimal resource use, improvements in service speed and quality, and the enhancement in customer-perceived value, which ultimately leads to greater customer satisfaction and loyalty [7]. Additionally, logistics efficiency positively impacts other stakeholders within the supply chain by enabling faster information flow and improved coordination [8].

To address the complexities of performance evaluation under conditions of uncertainty and multidimensionality, this study explores the integration of Data Envelopment Analysis (DEA) and fuzzy Multi-Criteria Decision-Making (fuzzy MCDM) methods. The DEA method is a non-parametric technique rooted in mathematical programming that measures the relative efficiency of decision-making units (DMUs) using quantitative input and output data, without requiring predefined weights for criteria [9,10,11]. In contrast, fuzzy MCDM approaches—such as the fuzzy Analytical Hierarchy Process (AHP) and fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)—allow for the inclusion of subjective expert judgments and the modeling of ambiguity and imprecision through fuzzy numbers and linguistic variables [12,13,14]. While traditional MCDM assumes precise and well-defined input data [15,16,17,18], fuzzy MCDM employs fuzzy logic to handle ambiguity and vagueness in the evaluation of criteria and alternatives [19,20,21]. By combining DEA and fuzzy MCDM, an analytical framework is formed that facilitates objective efficiency assessment while accommodating the uncertainties and vagueness inherent in real-world decision-making contexts [22,23,24]. In this combination, DEA identifies efficient alternatives, which are subsequently ranked using a fuzzy MCDM technique based on expert preferences. This integrated approach enables a more comprehensive performance evaluation by simultaneously considering quantitative indicators and qualitative assessments [25,26].

Furthermore, the methodology for performance evaluation differs significantly between manufacturing enterprises and service-oriented organizations, such as logistics firms [27]. In manufacturing, final products are tangible and result from standardized production processes, making inputs and outputs easier to quantify and assess. Conversely, logistics services involve intangible and time-sensitive outputs, where performance depends heavily on the efficient use of resources such as space, time, labor, and technology. Core logistics services encompass transportation, warehousing, transshipment, and freight forwarding. Notably, research by [28] presents an original decision-making framework for optimal forklift selection in warehousing systems by integrating the Full Consistency method (FUCOM) and Multi-objective Optimization On the basis of Ratio Analysis (MOORA) methods within a neutrosophic environment, utilizing Single-Valued Triangular Neutrosophic Numbers (SVTNNs) and a novel linear programming model to determine criterion weights and rank alternatives [29].

Following the introductory discussion and theoretical framing of efficiency in logistics, the second chapter provides a critical review of current literature, identifying contemporary approaches to measuring logistics performance. The third chapter presents fundamental models for measuring the efficiency of logistics companies and a method for ranking them based on a modified hierarchical method designed to support decision-making through artificial intelligence, which facilitates overcoming ambiguities and uncertainties among decision-makers. In the fourth chapter, the three-phase model developed in this paper is tested with a real example. The first phase of the DEA-Fuzzy AHP model involves the collection and analysis of data regarding logistics companies in the Republic of Serbia. The second phase of the model measures and analyzes the efficiency of logistics companies and proposes ways to improve efficiency. After applying the third phase of the model developed for ranking logistics companies, their ranking and selection of the most efficient company are performed. Finally, the paper concludes with final considerations and directions for future research in this area.

2. Literature Review

2.1. The Development of the Logistics Service Industry

Successfully operating in a saturated market requires more than simply meeting customer demands—it demands maximizing efficiency to exceed expectations, retain existing clients, and attract new ones. While many companies acknowledge the importance of efficiency, few manage to achieve sustained market success, making efficiency a critical strategic objective [30].

Efficiency has long been a topic of academic and professional interest, yet no universally accepted definition exists, due to the diversity of perspectives and contexts in which the term is applied [31,32,33,34,35]. Generally, efficiency refers to the effective utilization of resources—such as time, effort, and cost—to achieve a desired output. It is commonly expressed as the input–output ratio, often measured against an ideal benchmark as a percentage [36].

This input–output relationship is foundational to the core logistics principle of reproduction: achieving maximum results with minimum investment [37]. In one of the earliest works on the subject, Farrell emphasized labor productivity as a central efficiency metric [38]. Later, Gleason and Barnum made an important distinction between effectiveness—doing the right things—and efficiency—doing the right things the right way [39]. Building on these foundations, Min and Joo introduced the concept of operational or operating efficiency, described as the input–output ratio, as a practical tool for assessing company performance, especially in logistics systems [40].

2.2. DEA and Its Application in the Logistics Service Industry

The Data Envelopment Analysis (DEA) method has been widely applied to measure operational efficiency in logistics-related contexts [41]. For instance, a study [42] evaluated the operational performance of intermodal terminals involved in grain exports in Southeastern Brazil. Results showed that only 25% of terminals achieved full technical efficiency, while most suffered from scale inefficiencies, indicating underutilization of infrastructure.

Research in Malaysia [43] further extended DEA applications by introducing an efficiency optimization framework for publicly traded logistics firms that incorporates operational risk. By integrating the Basic Indicator Approach (BIA) to quantify operational risk capital as an output factor, the study identified inefficiencies and proposed targeted improvements.

Financial efficiency has also been assessed through DEA models. A study [44] analyzed ten Turkish logistics firms across seven years using both CCR and BCC models. While results varied, the analysis identified 2015 as the most efficient year under CCR, with the BCC model reporting the highest average efficiency (99.1%).

Lastly, efficiency in related service industries has been examined. In Saudi Arabia, DEA, window DEA, and AHP were used to measure efficiency in telecommunications providers [45]. STC consistently outperformed competitors, and the window DEA approach proved useful for tracking efficiency over time.

2.3. FAHP and Its Application in the Logistics Service Industry

Recent studies highlight the relevance of the fuzzy analytic hierarchy process (FAHP) and other hybrid MCDM approaches in efficiency evaluation. For instance, a study [46] applied AHP within healthcare supply chains to identify 16 strategic indicators covering environmental, social, economic, and logistical dimensions. This Circular SCOR model provided actionable insights into integrating circular economy goals into logistics systems.

The integration of FAHP and related methods supports the identification of key performance indicators and allows organizations to prioritize efficiency alongside sustainability, quality of service, and risk considerations [47,48]. By aligning logistics performance metrics with organizational objectives and external sustainability targets, FAHP complements DEA by addressing qualitative and multi-criteria decision-making challenges [49,50,51].

2.4. Summary

The literature highlights efficiency as both a theoretical concept and a practical performance measure. DEA has emerged as the dominant tool for evaluating logistics efficiency, while FAHP provides a complementary approach for capturing qualitative and multi-dimensional aspects of performance. Despite these advances, research focusing directly on the efficiency of logistics service companies remains limited. This study aims to address this gap by proposing a structured and flexible framework that can guide both strategic planning and operational improvements in logistics enterprises.

3. Materials and Methods

Most models for measuring efficiency in logistics are based on the Data Envelopment Analysis (DEA) method, which—together with its various extensions—allows the integration of a large number of heterogeneous indicators (criteria) into a single composite efficiency measure [52,53,54]. These indicators, which exist at different levels of logistics systems, can be incorporated into the model with appropriate adjustments, making DEA a flexible and widely used tool.

However, despite its strengths, existing efficiency measurement models in logistics exhibit significant limitations. These shortcomings highlight the need for both the refinement of existing models and the development of new, more systematic approaches tailored to the complexities of logistics operations.

Efficiency measurement becomes particularly challenging when multiple, and often conflicting, goals must be addressed across different subsystems, processes, and activities. The need to consolidate diverse indicators—financial, technical, technological, environmental, and social—further adds to this complexity. In such contexts, measuring and improving efficiency require a structured decomposition of logistics subsystems and processes, followed by a clear definition and quantification of individual activities.

Establishing a logical and clearly defined sequence of activities and processes enables managers to gain a realistic picture of system performance, identify potential inefficiencies, and better allocate resources. Each activity consumes specific inputs to generate defined outputs. Relying solely on partial, single-ratio efficiency indicators (e.g., assessing the productivity of a single resource) is insufficient for concluding overall system efficiency. Therefore, it is necessary to define a comprehensive efficiency indicator—one that encompasses multiple relevant outcomes and the total resources required to achieve them [55].

Performance measurement, as a concept, involves quantifying both the efficiency and effectiveness of actions. In both academic literature and practical applications, logistics performance is often assessed using key performance indicators (KPIs) [56]. These include partial productivity indicators (e.g., number of deliveries per vehicle), financial indicators (e.g., marginal revenue), cost-related metrics (e.g., capital turnover, return on investment), and quality-based indicators.

To overcome some of the limitations of single-method approaches, this paper proposes a three-phase DEA-Fuzzy AHP model for evaluating efficiency and conducting a multi-criteria analysis. The DEA method is used to identify efficient decision-making units and assess their performance, making it particularly suitable for benchmarking. However, one of DEA’s known limitations is its inability to rank efficient units beyond assigning them a score of 1. To address this, the fuzzy AHP method is introduced as a complementary approach for ranking these units based on subjective expert evaluations under uncertainty (Figure 1).

The following section presents the theoretical background of both the DEA and fuzzy AHP methods, along with an explanation of their integration and practical application in the context of logistics performance evaluation.

3.1. DEA Method

The DEA method derives its name from the way it “envelops” observed data to identify an efficiency “frontier,” which is then used to estimate the performance of all entities being assessed. The method is a frontier-based method that involves a series of optimizations—one for each Decision Making Unit (DMU) included in the analysis. For each DMU, a maximum performance score is calculated relative to all other units in the observed population, under the condition that each unit lies on or below the efficiency frontier. The efficiency score provided by DEA is relative, as it depends on which and how many units are included in the analysis, as well as the number and structure of the inputs and outputs considered [57].

The method characterizes each DMU as relatively efficient or relatively inefficient. According to the authors of the DEA method, a DMU can be classified as efficient only if the following two conditions are not met [52]:

• It is possible to increase any of its outputs without increasing any of its inputs and without decreasing any of its other outputs.
• It is possible to decrease any of its inputs without decreasing any of its outputs and without increasing any of its inputs.

For each inefficient DMU, DEA identifies the content and level of inefficiency for each input and output. The level of inefficiency is determined by comparing it with a singular reference DMU or with a convex combination of other reference DMUs that exist on the efficiency frontier and that use proportionally the same level of inputs and produce proportionally the same or higher levels of outputs [57].

There are two basic types of models: CCR and BCC [1]. The CCR model is also known as the DEA model with constant returns to scale, and the BCC model is the DEA model with variable returns to scale.

CCR models measure the overall technical efficiency of a unit, which includes pure technical efficiency and scale efficiency. It is assumed that units operate at constant returns to scale, that is, an increase in inputs must result in a proportional increase in output. The efficiency frontier given by CCR models is also in the shape of a convex cone [58].

The BCC model measures pure technical efficiency, that is, it provides a measure of efficiency that ignores the effect of scale by comparing a given DMU only with other units of similar scale [59]. The efficiency of scale, which indicates whether the observed unit is operating at the optimal scale of operations, can be obtained by dividing the efficiency measure given by the CCR model (total technical efficiency) by the efficiency measure given by the BCC model (pure technical efficiency) [56].

DEA models can generally take two forms: either input-oriented or output-oriented. Input-oriented (also known as input minimization or contraction) aims to minimize the inputs required to produce the required amount of output. On the other hand, output-oriented (also known as output maximization or expansion) attempts to maximize outputs at a given level of inputs. In applications involving inflexible inputs (not fully under control), output-oriented models would be more appropriate.

CCR Model

Many studies describe the mathematical basis of the CCR model in more detail [60,61]. The input-oriented CCR model is obtained by converting a nonlinear problem into a linear problem, which is then easily solved by the linear programming (LP) method. This results in an optimal solution, where the optimization criterion is the minimization of the value of the objective function under given constraints (a system of linear inequalities). The CCR input-oriented model is shown in (1):

$$\begin{array}{c}DE{A}_{input}=\min {\displaystyle \sum _{i=1}^m}{w}_i{x}_{i-input}\\ st:\\ {\displaystyle \sum _{i=1}^m}{w}_i{x}_{ij}-{\displaystyle \sum _{i=m+1}^{m+s}}{w}_i{y}_{ij}\ge 0,\hspace{1em}j=1,\dots ,n\\ {\displaystyle \sum _{i=m+1}^{m+s}}{w}_i{y}_{i-output}=1\\ w_i\ge 0,i=1,\dots ,m+s\end{array}$$

(1)

A DMU consists of m input parameters for each alternative x_ij, while s represents the output parameters for each alternative y_ij, taking into account the weights of the parameters denoted by w_i. In the formulas, n represents the total number of DMUs. The output-oriented CCR model, where the optimization criterion is the maximization of the value of the objective function, is efficiency in this model [60]. This maximizes the outputs for the same inputs. The CCR output-oriented model is shown in (2):

$$\begin{array}{c}DE{A}_{output}=\max {\displaystyle \sum _{i=m+1}^{m+s}}{w}_i{y}_{i-output}\\ st:\\ -\left({\displaystyle \sum _{i=1}^m}{w}_i{x}_{ij}\right)+{\displaystyle \sum _{i=m+1}^{m+s}}{w}_i{y}_{ij}\le 0,\hspace{1em}j=1,\dots ,n\\ {\displaystyle \sum _{i=1}^m}{w}_i{x}_{i-input}=1\\ w_i\ge 0,\hspace{1em}i=1,\dots ,m+s\end{array}$$

(2)

To obtain the efficiency index for each DMU, it is necessary to apply Equation (3):

$$Efficiency = {\displaystyle \frac{\max \mathrm{O}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t} (\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t} \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s})}{\min \mathrm{I}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t} (\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t} \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s})}}$$

(3)

Contextually, the mathematically set task can be described as follows: Determine the values of the weights of (independent variable) inputs and outputs such that the decision-making unit (DMU) has the highest relative efficiency (dependent variable) in the output orientation or inefficiency in the input orientation, and that the weighted sum of the inputs of the respective DMU is equal to one and the other DMUs is greater than or equal to zero.

3.2. AHP Method in Fuzzy Environment

The Analytic Hierarchy Process (AHP) is a decision-making method based on the human ability to assess the relative importance of elements through pairwise comparisons [62,63,64]. It enables the determination of priorities among elements of a hierarchy, such as alternatives, criteria, subcriteria, etc., based on expert judgments expressed using an absolute fundamental scale, most commonly the Saaty scale. This approach allows both qualitative and quantitative factors to be evaluated on a common ratio scale, even when the original data differ in type or unit of measurement.

The AHP reduces multidimensional problems to a single-dimensional scale of priorities by structuring the decision problem into a hierarchy: the goal at the top level, followed by criteria, potential subcriteria, and finally the alternatives at the bottom level. The method assumes that any complex decision problem can be decomposed hierarchically to capture all relevant components and their interrelationships.

The process involves pairwise comparisons of elements at each hierarchical level to their contribution to the element above. The Saaty scale—a quasi-standard in AHP—translates verbal judgments into numerical values on a 1–9 scale, facilitating consistent and structured evaluation. These comparisons yield relative weights, represented as a priority vector on a ratio scale, where the sum of weights equals one. The method is built upon four key postulates: (1) reciprocal judgments, (2) homogeneity of elements, (3) hierarchical structuring, and (4) the ability to derive rankings. It can also be extended to group decision-making by aggregating judgments from multiple decision-makers. One of the main challenges in applying AHP is constructing a valid and comprehensive hierarchical structure and accurately determining relative weights at each level [65].

Fuzzy Logic is based on the theory of fuzzy sets, introduced to mathematically model linguistic uncertainty [66]. Unlike classical sets, where an element either belongs or does not belong to a set, fuzzy sets allow partial membership, represented by any real number in the interval [0, 1]. While classical sets have a single membership function, fuzzy sets can be described by infinitely many membership functions. This flexibility allows fuzzy logic to better model imprecision inherent in human reasoning and language [67,68].

The most commonly used forms of membership functions are triangular functions, trapezoidal functions, Gaussian curves, and bell curves.

The algorithmic form of the AHP method is:

Step 1. Structuring the decision problem in a hierarchy;

Step 2. Comparing the elements of the hierarchy in pairs;

Step 3. Determining the relative importance of the compared elements and checking for consistency.

After structuring the decision problem in a hierarchy and performing the pairwise comparison procedure at all levels of the hierarchy, a synthesis of all evaluations should be performed to obtain the final, total vector of relative weights of alternatives and thus their rank. The hierarchy is considered at 3 levels: goal, criteria, and alternatives.

Determining the consistency index is important because it allows for measuring the error in judgment. Given that, in (4), ${\mathsf{\lambda }}_{\mathbf{m}\mathbf{a}\mathbf{x}}=\mathbf{n}$ when complete consistency holds, and ${\mathsf{\lambda }}_{\mathbf{m}\mathbf{a}\mathbf{x}}>\mathbf{n}$ when there is even the slightest inconsistency, it is intuitively clear that the value ${\mathsf{\lambda }}_{\mathbf{m}\mathbf{a}\mathbf{x}}<\mathbf{n}$ represents a convenient measure of the degree of consistency. Saaty defined the degree of consistency CR as follows:

$$CR={\displaystyle \frac{{\mathsf{\lambda }}_{max}-n}{2\mathrm{n}-1}}$$

(4)

To determine the consistency index of a matrix, it is necessary to compare its consistency degree CR with the mean value of CR of a large number of randomly generated matrices of the same dimensions. The mean value of the CR of a large number of generated matrices is called the random consistency index (RI).

Table 1. Random consistency index RI.

n	1	2	3	4	5	6	7	8	9	10	…
RI	0.00	0.00	0.52	0.89	1.11	1.25	1.35	1.40	1.45	1.49	…

gives the values of RI for different dimensions of the comparison matrix.

Based on the above, it can be said finally that the matrix consistency index is equal to

$$CI={\displaystyle \frac{\mathrm{C}\mathrm{R}}{\mathrm{R}\mathrm{I}}}$$

(5)

Therefore, CI parameter shows how the observed matrix and randomly generated matrices relate in terms of their consistency index. The value CI = 0.1 is the upper limit of inconsistency that is acceptable.

The approach to fuzzification also requires a modified initial decision matrix, i.e., the pairwise comparison matrix (including cases where the weighting coefficients of the criteria and the ranking of alternatives are defined). The modified matrix includes a new element—the degree of confidence—which is defined alongside the performed comparison where is ${\gamma }_{ji}= {\gamma }_{ij}$ [22,23].

$$\begin{array}{l}\hspace{1em}\hspace{1em}\begin{array}{cccc}\hspace{1em}\hspace{0.33em}\hspace{0.33em}{K}_1& \hspace{1em}\hspace{1em}{K}_2& \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.17em}\dots & \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{K}_n\end{array}\\ A=\begin{array}{c}{K}_1\\ K_2\\ ⋮\\ K_n\end{array}\left[\begin{array}{cccc}{a}_{11};{\gamma }_{11}& a_{12};{\gamma }_{12}& \dots & a_{1n};{\gamma }_{1n}\\ a_{21};{\gamma }_{21}& a_{22};{\gamma }_{22}& \dots & a_{2n};{\gamma }_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n1};{\gamma }_{n1}& a_{n2};{\gamma }_{n2}& \dots & a_{nn};{\gamma }_{nn}\end{array}\right]\end{array}$$

(6)

The left and right distributions differ from one comparison to another when various levels of confidence are introduced. Adjustments occur according to the following expression:

$$T=\left(t_1,t_2,t_3\right)=\left\{\begin{array}{ccc}{t}_1=\gamma t_2,& t_1\le t_2,& t_1,t_2\in \left[1/\mathrm{9,9}\right]\\ t_2=t_2,& ,& t_2\in \left[1/\mathrm{9,9}\right]\\ t_3={\left(2-\gamma \right)t}_2,& t_3\le t_2,& t_2,t_3\in \left[1/\mathrm{9,9}\right]\end{array}\right\}$$

(7)

where the value t₂ represents the linguistic expression from the classical Saaty scale, which, in the fuzzy number, has the maximum membership degree t₂ = 1.

Let the relative weight of each alternative ${\mathrm{A}}_{\mathrm{i}}$ from the set of alternatives $\mathrm{A}\left({\mathrm{A}}_{\mathrm{i}}\in \mathrm{A}\right)$ with respect to the r-th subcriterion corresponding to criterion ${\mathrm{K}}_{\mathrm{j}}$ be denoted as ${\mathrm{w}}_{{\mathrm{A}}_{\mathrm{i}}}^{{\mathrm{K}}_{\mathrm{j}\mathrm{r}}}$. Let the relative weight of the r-th subcriterion with respect to its parent criterion ${\mathrm{K}}_{\mathrm{j}}$ be denoted as ${\mathrm{w}}_{{\mathrm{K}}_{\mathrm{j}\mathrm{r}}}^{{\mathrm{K}}_{\mathrm{j}}}$, and the relative weight of each criterion ${\mathrm{K}}_{\mathrm{j}}$ with respect to the overall goal be denoted as ${\mathrm{w}}_{\mathrm{K}\mathrm{j}}$. Then, the total relative weight of the alternative ${\mathrm{A}}_{\mathrm{i}}\in \mathrm{A}$ is expressed as follows [13,22,23]:

$$w_{A_i}=\sum _j{w}_{K_j}\sum _r{w}_{K_{jr}}^{K_j}{w}_{A_i}^{K_{jr}} \forall A_i\in A$$

(8)

Based on the values of ${\mathrm{w}}_{\mathrm{A}\mathrm{i}}$, the final ranking of the alternatives is determined by a descending order of values. At the end of process, the fuzzy number is converted into a real number [69].

$$A={\displaystyle \frac{\left(\left(t_3-t_1\right)+\left(t_2-t_1\right)\right)}{3}}+t_1$$

(9)

Any change in the hierarchy structure requires a recalculation of priorities in the new hierarchy at a higher level than where the change occurred. In other words, the priorities at a lower level depend on the priorities of the elements at the higher level.

4. Model Application

4.1. Overview of Used Criteria and Data

Given the large number of logistics companies operating in the Republic of Serbia and the lack of prescribed data that each company must maintain, it is challenging to identify criteria that meet the business needs and records of each company whose data was utilized. After several months of conducting surveys and consultations with logistics experts, a decision was made to consider ten logistics companies (LCs) for model testing. The names of the companies are not disclosed, due to the nature of their business. After reviewing the data received from the companies and having those involved in transport and logistics complete the questionnaire, six criteria were selected and used the year level (

Table 2. The selected and used criteria.

No.	Criteria	Explanation of Criteria	Unit	Character
C1	Number of vehicles	Vehicles used in the company	[number]	Min
C2	Fuel costs	Cost of fuel consumed during transportation during one year	[euro]	Min
C3	Vehicle engagement time	The time the vehicle was hired outside the company’s fleet	[h]	Min
C4	Distance traveled	Distance traveled by all vehicles in one year	[km]	Max
C5	Transported quantity	Transported cargo quantities by vehicles during one year	[t]	Max
C6	Vehicle utilization	Vehicle load capacity utilization during transport	[%]	Max

). Criteria (C₁–C₃) represent input criteria, while criteria (C₄–C₆) represent output criteria. The choice of criteria (C₁–C₆) was guided by both practical relevance and expert validation. The selected criteria represent a balance between input-oriented aspects (resources and costs) and output-oriented measures (performance and service quality), ensuring that the model reflects real business priorities. Thus, their inclusion was the result of expert consensus and the availability of reliable companies’ data.

The data obtained from the logistics companies were processed, selected according to criteria, and are presented in

Table 3. Data obtained from logistics companies.

DMU Decision Making Unit	LC Logistics Companies	C1 Number of Vehicles	C2 Fuel Costs	C3 Vehicle Engagement Time	C4 Distance Traveled	C5 Transported Quantity	C6 Vehicle Utilization
DMU1	LC1	29	2370.5	6500	114,122	5,994,686	86
DMU2	LC2	15	590.2	2647	32,795	917,034	87
DMU3	LC3	37	5149.9	10,771	226,242	19,279,019	81
DMU4	LC4	21	3837.3	7142	159,893	7,474,618	98
DMU5	LC5	18	1098.2	3776	53,641	1,326,588	98
DMU6	LC6	24	3308.4	6079	153,413	3,988,841	99
DMU7	LC7	12	1057.7	3133	61,369	1,192,797	90
DMU8	LC8	22	3492.5	2462	54,769	3423	98
DMU9	LC9	16	2320.6	1525	38,813	1721	86
DMU10	LC10	13	1904.9	939	33,334	1334	76

.

4.2. DEA Method Application

The data collected for testing the model met all the conditions defined in the previous part. The input and output-oriented DEA CCR model was used for the calculations. The input criteria included the number of vehicles, fuel costs, and vehicle engagement time, while the output criteria comprised the distance traveled, quantity transported, and vehicle utilization. Based on Equations (1) and (2), systems of linear equations were formulated, for which the MS EXCEL program package was utilized to find the solution.

Utilizing the solutions from all ten logistics companies and obtaining values for DEA-output and DEA-input, Formula (3) was applied to obtain the DEA-Final values (

Table 4. DEA model solution values.

DMU	DEA-Input	DEA-Output	DEA-Final
DMU1	1.037	0.963	0.928
DMU2	1.000	1.000	1.000
DMU3	1.000	1.000	1.000
DMU4	1.000	1.000	1.000
DMU5	1.155	0.865	0.748
DMU6	1.000	1.000	1.000
DMU7	1.000	1.000	1.000
DMU8	1.307	0.764	0.584
DMU9	1.125	0.888	0.789
DMU10	1.000	1.000	1.000

).

Table 4 shows that DMU2, DMU3, DMU4, DMU6, DMU7, and DMU10 received a score of one, indicating efficiency. These six companies were included in the subsequent fuzzy-AHP model analysis.

In contrast, DMU1, DMU5, DMU8, and DMU9 were excluded from further consideration due to inefficiency, as indicated by scores below one. In addition to assessing efficiency, the DEA method also serves to improve efficiency, i.e., to indicate how inefficient DMUs can become efficient (

Table 5. Results obtained by the DEA method.

DMU Decision Making Unit	LC Logistics Companies	C1 Number of Vehicles	C2 Fuel Costs	C3 Vehicle Engagement Time	C4 Distance Traveled	C5 Transported Quantity	C6 Vehicle Utilization
DMU1	LC1	7.467004	0	635.1409	0	0	17.71902
DMU2	LC2	0	0	0	0	0	0
DMU3	LC3	0	0	0	0	0	0
DMU4	LC4	0	0	0	0	0	0
DMU5	LC5	0.402932	0	0	0	0	0
DMU6	LC6	0	0	0	0	0	0
DMU7	LC7	0	0	0	0	0	0
DMU8	LC8	0	323.0135	0	0	482,844.0	0
DMU9	LC9	0	80.23866	0	2077.830	172,291.4	0
DMU10	LC10	0	0	0	0	0	0

). DMU9 is assessed as inefficient with scores of 0.789 and 0.888, respectively (Table 4). This means that Logistics Company 9 will become efficient if it reduces fuel costs C₂ and distance traveled C₄ and increases quantities transported C₅ (Table 5).

The DEA and fuzzy-AHP results complement each other but do not necessarily align directly. The DEA method identifies which companies are efficient (score = 1) and provides improvement guidelines for inefficient ones, while fuzzy-AHP ranks the efficient companies based on multiple qualitative and strategic criteria. Thus, a company with a DEA score of 1 may not rank highest in fuzzy-AHP if it performs weaker on sustainability, risk, or service quality dimensions. This integration shows that DEA ensures efficiency, while fuzzy-AHP differentiates among efficient firms for strategic decision-making.

4.3. Fuzzy-AHP Method Application

Using the fuzzy-AHP method, a ranking of 6 logistics companies that are assessed as efficient will be performed. The nature of the DEA method makes it impossible to select the most efficient company, but rather shows the best possible results and only indicates whether the companies are efficient or not. For this reason, as well as due to the subjectivity in the importance of the criteria, the fuzzy-AHP method was used. Further calculations take into account the remaining 6 logistics companies that were rated 1, i.e., which are efficient. An overview of the data for the remaining companies is shown in

Table 6. Data on efficient logistics companies.

LC Logistics Companies	C1 Number of Vehicles	C2 Fuel Costs	C3 Vehicle Engagement Time	C4 Distance Traveled	C5 Transported Quantity	C6 Vehicle Utilization
LC2	15	590.2	2647	32,795	917,034	87
LC3	37	5149.9	10,771	226,242	19,279,019	81
LC4	21	3837.3	7142	159,893	7,474,618	98
LC6	24	3308.4	6079	153,413	3,988,841	99
LC7	12	1057.7	3133	61,369	1,192,797	90
LC10	13	1904.9	939	33,334	1334	76

.

To rank logistics companies, it is essential to first determine the weights of the criteria. To enhance transparency and traceability, a summary of the logistics experts’ input data is included in Appendix A, presenting the initial evaluations from experts at various companies that serve as the basis for the computational analysis and the rankings. When the logistics experts’ input data are combined using the geometric mean [47,70,71], a pairwise comparison of the criteria is obtained, and their values are presented in

Table 7. Matrix of comparison of criteria by pairs.

	b1	b2	b3	b4	b5	b6
b1	1.00	0.33	0.20	0.25	0.50	0.17
b2	3.00	1.00	0.33	0.33	3.00	0.17
b3	5.00	3.00	1.00	2.00	6.00	2.00
b4	4.00	3.00	0.50	1.00	5.00	0.33
b5	2.00	0.33	0.17	0.20	1.00	0.33
b6	6.00	6.00	0.50	3.00	3.00	1.00

. A detailed view of the calculation is provided in Appendix B.

To determine whether there is no error in reasoning, it is necessary to check the consistency index. The consistency index (CI) is calculated based on Equations (4) and (5), and in this case, it is 0.075, which is less than 0.1, where CR = 0.093, and λ_max = 6.465. This indicates that there is no error in reasoning, allowing for the continuation of further calculations.

In this case, fuzzification is achieved by introducing a confidence level (triangular fuzzy numbers) (

Table 8. Confidence level.

	L	M	R	Fuzzification
very small VM	0	0	0.20	0.066667
small M	0.10	0.25	0.40	0.25
medium S	0.30	0.50	0.70	0.50
large L	0.55	0.75	0.95	0.75
very large VL	0.80	1	1	0.933333

).

Table 9. Confidence level matrix by criteria.

	C1	C2	C3	C4	C5	C6
C1	1.000	0.933	0.750	0.750	0.750	0.933
C2	0.933	1.000	0.750	0.933	0.933	0.250
C3	0.750	0.750	1.000	0.067	0.933	0.500
C4	0.750	0.933	0.067	1.000	0.500	0.933
C5	0.750	0.933	0.933	0.500	1.000	0.933
C6	0.933	0.250	0.500	0.933	0.933	1.000

presents the confidence level matrix used for the fuzzification, derived from Equation (6).

After the fuzzification is performed, the left and right distributions are calculated. The left and right distributions are calculated based on Equation (7).

Table 10. Distribution values by criteria.

	Left	Median	Right
C1	0.028	0.042	0.065
C2	0.069	0.099	0.170
C3	0.179	0.325	0.575
C4	0.103	0.183	0.323
C5	0.039	0.058	0.089
C6	0.168	0.294	0.542

shows the values of the left, middle, and right distributions by criteria.

Then, the results are summed up by criteria for the left, right, and middle values of the distribution, and the weights of the criteria are determined, followed by their normalization. The values of the weights of the criteria are shown in

Table 11. Weights of the criteria.

Criteria	C1 Number of Vehicles	C2 Fuel Costs	C3 Vehicle Engagement Time	C4 Distance Traveled	C5 Transported Quantity	C6 Vehicle Utilization
Weights of the criteria	0.0403	0.1007	0.3220	0.1817	0.0554	0.2999
Rank	6	4	1	3	5	2

.

After determining the weights of the criteria, the normalization of the values of the companies by criteria and the calculation of the total relative weight are carried out based on Equations (8) and (9). Figure 2 shows the hierarchical structure with the normalized values of the companies by criteria.

The overall relative weights obtained by calculation, as well as the ranking of the companies, are shown in Figure 3, from which it can be seen that the best-ranked logistics company is LC3, with a total relative weight of 0.298, indicating its dominant position in terms of overall efficiency. Directly behind are companies LC4 and LC6, with values of 0.218 and 0.197, respectively. These three companies represent reference examples of best practices in the logistics sector.

Companies LC7 and LC2 occupy central positions in the ranking, with relative weights of 0.113 and 0.096. Despite certain positive characteristics, the obtained results point to the need for improvement in several areas of logistics performance. The lowest-ranked entity is LC10, with a total relative weight of 0.078, reflecting the lowest level of efficiency among the analyzed companies. This result may stem from underdeveloped logistics capacities or inefficient resource utilization.

The findings can serve as a foundation for strategic planning and enhancing logistics processes in each company. Additionally, analyses of this type facilitate transparent performance comparisons and data-driven decision-making.

5. Sensitivity Analysis Approach

Decision-makers (DMs) base their choices on accumulated knowledge and practical experience, which are systematically organized and rationalized. The MCDM techniques provide essential support by selecting the most appropriate option among several feasible alternatives. Since the relative importance of criteria varies, assigning accurate weights directly influences the quality of the decision outcome. Weighting approaches can be divided into objective, derived from the intrinsic structure of the data and technological parameters, and subjective, based on expert judgment that is either elicited directly or modeled through formal procedures [72].

Among subjective weighting techniques, the fuzzy AHP has gained prominence due to its theoretical soundness and its capacity to detect inconsistencies in expert assessments [73]. However, decision problems often involve uncertain or variable data, necessitating sensitivity analysis to examine the robustness of results. Sensitivity analysis enables decision-makers to understand how strongly changes in criterion weights or performance evaluations may alter the ranking of alternatives, thereby revealing the most influential criteria.

This chapter investigates the stability of rankings concerning incremental variations in criterion weights, identifying the minimal perturbation necessary to change the current preference order. The perspective provides deeper insights into the robustness and reliability of fuzzy AHP-based decision processes.

At the beginning of the sensitivity analysis, note that the data were normalized as required by the fuzzy AHP shown in Figure 2. Then, the final preferences Pi (i = 1, 2, 3, …, m) are calculated, followed by ranking the alternatives (

Table 12. Current final preferences.

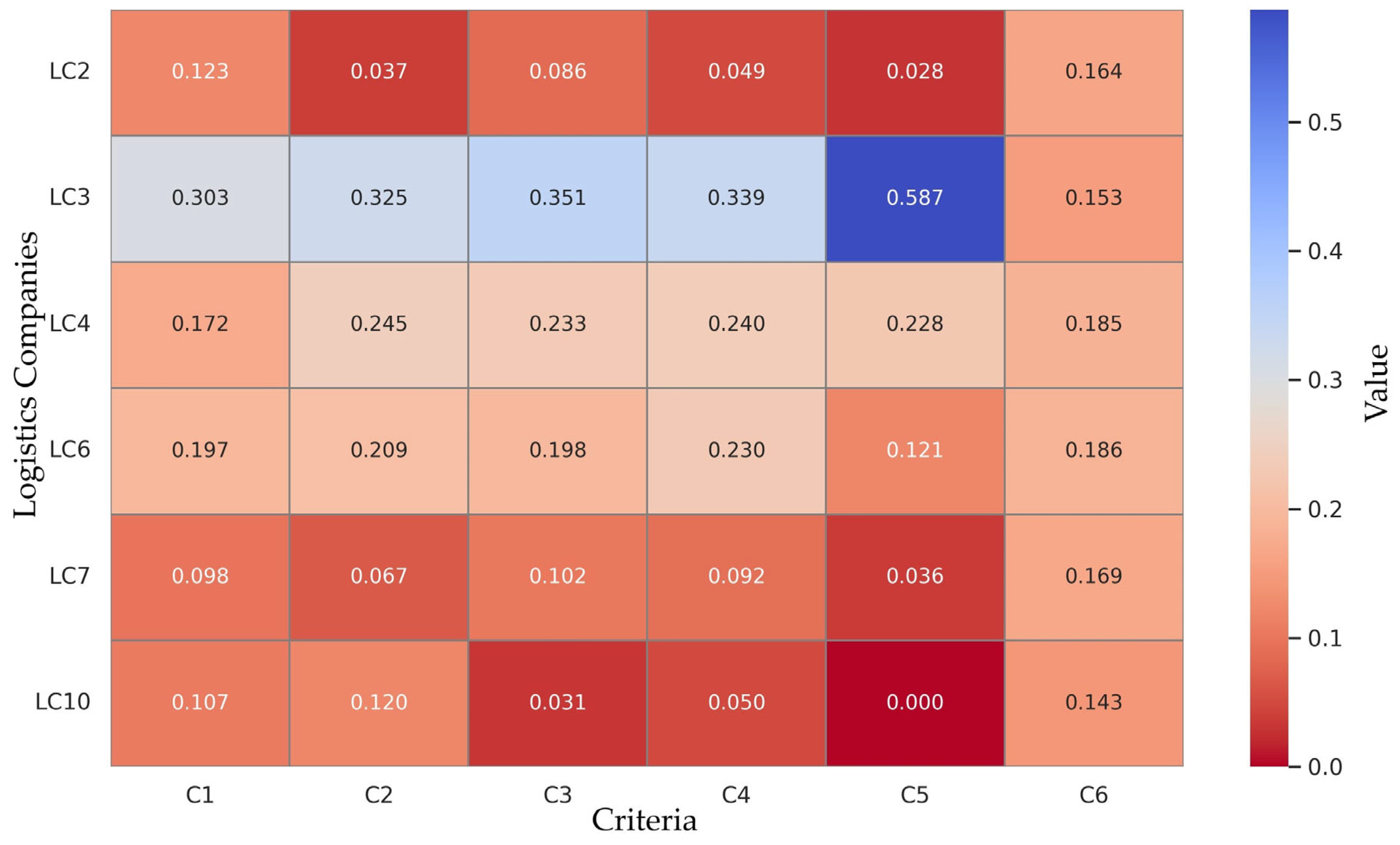
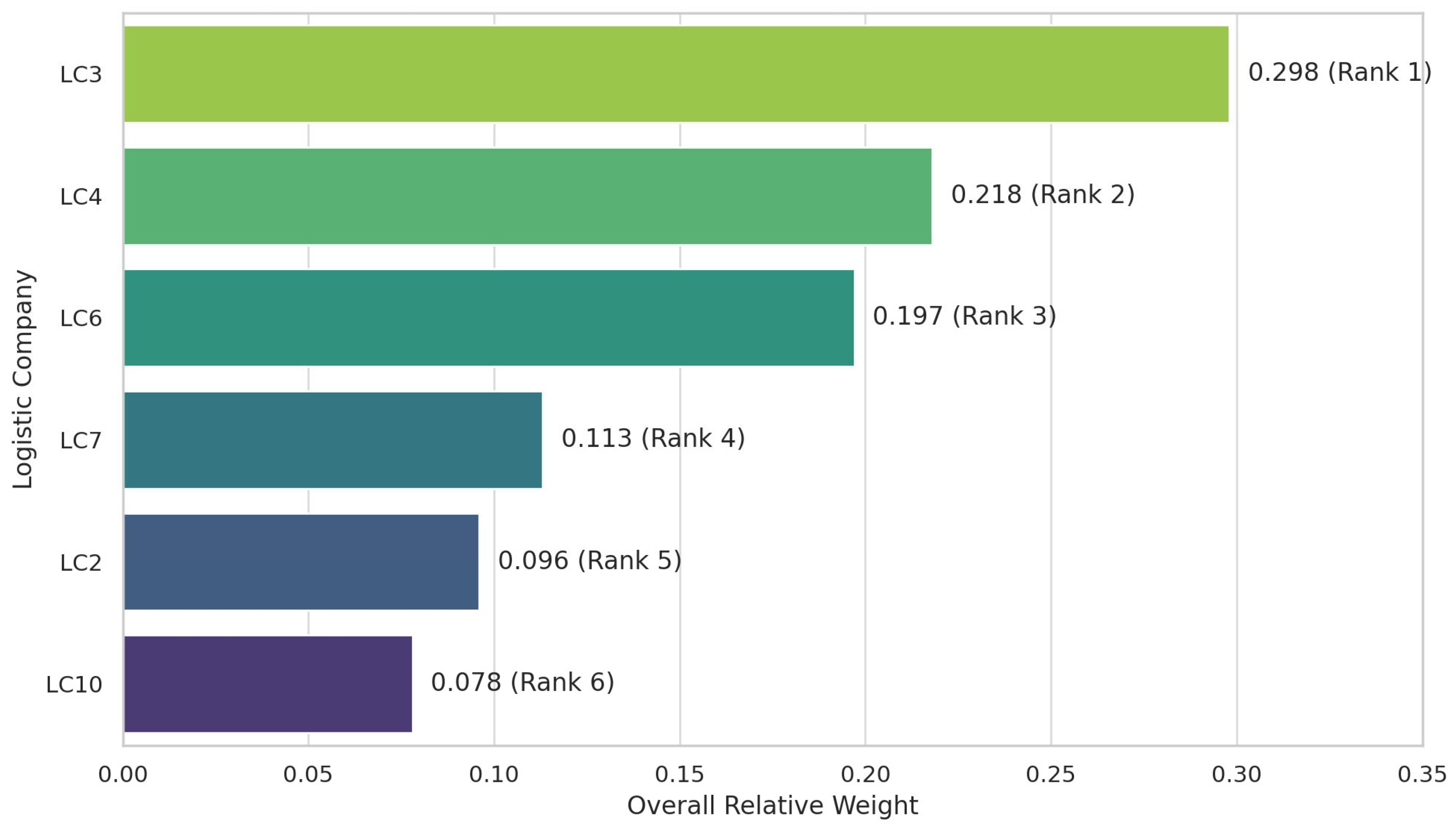
Logistic Companies	Criteria	C1	C2	C3	C4	C5	C6	Preference Pi	Rank
	wi	0.0403	0.1007	0.3220	0.1817	0.0554	0.2999
LC2		0.0049	0.0038	0.0278	0.0089	0.0015	0.0491	0.0961	5
LC3		0.0122	0.0327	0.1129	0.0616	0.0325	0.0457	0.2978	1
LC4		0.0069	0.0247	0.0749	0.0435	0.0126	0.0553	0.2180	2
LC6		0.0079	0.0210	0.0637	0.0418	0.0067	0.0559	0.1971	3
LC7		0.0040	0.0067	0.0328	0.0167	0.0020	0.0508	0.1131	4
LC10		0.0043	0.0121	0.0098	0.0091	0.0000	0.0429	0.0782	6

), where LC3 is the most preferred (best) alternative, P₂ ≥ P₃ ≥ P₄ ≥ P₅ ≥ P₂ ≥ P₁.

After creating the pairs of alternatives, based on [74], the absolute change in criteria weights (

Table 13. All possible values (absolute change in criteria weights).

Pair of Alternatives	C1	C2	C3	C4	C5	C6
	0.0403	0.1007	0.3220	0.1817	0.0554	0.2999
LC2–LC3	N/F	0.0231	0.0496	0.0292	0.0096	0.2166
LC2–LC4	N/F	0.0185	0.0452	0.0250	0.0150	0.1082
LC2–LC6	N/F	0.0180	0.0440	0.0216	0.0232	0.0888
LC2–LC7	0.0213	0.0095	0.0144	0.0091	0.0131	0.0165
LC2–LC10	−0.0206	−0.0055	−0.0502	−0.0175	−12.2504	−0.0204
LC3–LC4	−0.1405	−0.1058	−0.1203	−0.1129	−0.2057	−0.0659
LC3–LC6	−0.1552	−0.1567	−0.1784	−0.1484	−0.4865	−0.0824
LC3–LC7	−0.5694	−0.8992	−0.6349	−0.6809	−2.9850	−0.1662
LC3–LC10	−0.6248	−0.5935	−2.5181	−1.4899	−3172.5720	−0.2340
LC4–LC6	−0.0183	−0.0245	−0.0245	−0.0218	−0.0391	−0.0207
LC4–LC7	−0.1836	−0.3851	−0.2392	−0.2733	−0.6574	−0.1142
LC4–LC10	−0.2258	−0.2849	−1.0630	−0.6704	−783.0627	−0.1802
LC6–LC7	−0.1680	−0.2628	−0.1630	−0.2100	−0.2810	−0.0924
LC6–LC10	−0.2194	−0.2064	−0.7695	−0.5471	−355.4211	−0.1548
LC7–LC10	−0.0322	−0.0193	−0.1162	−0.0641	−31.1525	−0.0413

) and the percent change in criteria weights (

Table 14. All possible values (percent change in criteria weights).

Pair of Alternatives	C1	C2	C3	C4	C5	C6
	0.0403	0.1007	0.3220	0.1817	0.0554	0.2999
LC2–LC3	N/F	22.9446	15.3950	16.0931	17.3057	72.2393
LC2–LC4	N/F	18.3966	14.0354	13.7655	26.9831	36.0944
LC2–LC6	N/F	17.8920	13.6647	11.8891	41.9009	29.6087
LC2–LC7	52.8554	9.4266	4.4659	5.0061	23.6018	5.4860
LC2–LC10	−51.0853	−5.4804	−15.6019	−9.6501	−22,096.5767	−6.8022
LC3–LC4	−349.1817	−105.0162	−37.3634	−62.1266	−371.1183	−21.9850
LC3–LC6	−385.5430	−155.5260	−55.3920	−81.7068	−877.5421	−27.4619
LC3–LC7	−1414.7395	−892.5494	−197.1935	−374.7528	−5384.2077	−55.4239
LC3–LC10	−1552.2715	−589.0822	−782.0610	−820.0868	−5,722,500.2422	−78.0152
LC4–LC6	−45.4105	−24.3345	−7.6221	−11.9834	−70.6054	−6.8951
LC4–LC7	−456.1379	−382.2848	−74.2777	−150.4538	−1185.8451	−38.0925
LC4–LC10	−560.8752	−282.7546	−330.1303	−368.9751	−1,412,442.8587	−60.0899
LC6–LC7	−417.5050	−260.8718	−50.6342	−115.6138	−506.8265	−30.8193
LC6–LC10	−545.1891	−204.9109	−238.9938	−301.1055	−641,087.8686	−51.6297
LC7–LC10	−79.8999	−19.2017	−36.1031	−35.3049	−56,190.9771	−13.7574
Criticality degrees Dk	45.4105	5.4804	4.4659	5.0061	17.3057	5.4860
Sensitivity coefficient sens (Ck)	0.0220	0.1825	0.2239	0.1998	0.0578	0.1823

The Percent-Any (PA) critical criterion is identified by locating the lowest relative value across all entries in Table 14. Such smallest value is 4.4659% and it corresponds to criterion C₃ between LC2 (5th place)–LC7 (4th place). Also, the Criticality degrees of six criteria are: D₁ = |−45.4105| = 45.4105, D₂ = |−5.4804| = 5.4804, D₃ = 4.4659, D₄ = 5.0061, D₅ = 17.3057 and D₆ = 5.4860. The reciprocal of criticality degree representing the Sensitivity coefficients of the six criteria are: sens(C₁) = 0.0220, sens(C₂) = 0.1825, sens(C₃) = 0.2239, sens(C₄) = 0.1998, sens(C₅) = 0.0578, and sens(C₆) = 0.1823. That is, the most sensitive decision criterion is C₃. It can be concluded that variations in the weighting coefficients do not compromise the position of the highest-ranked alternative.

) are calculated. In these tables, negative values denote increases, while positive values reflect decreases. It is also important to emphasize that these changes—whether given as percentages or absolute figures—are presented before the normalization process.

At this point, it should be stated that a decision maker can define the most critical criterion in absolute changes: Absolute-Top (AT) and Absolute-Any (AA). From Table 13, it can be easily verified that the AT criterion is C4 (0.0091) between LC2 (5th place)–LC7 (4th place) and the AA criterion is C2 (−0.0055) between LC2 (5th place)–LC10 (6th place) (the corresponding minimum changes are boldfaced).

6. Conclusions

Logistics companies are complex systems, and their intricacy and integration can often pose challenges when monitoring and measuring performance. The goal of measuring efficiency is to assess a company’s level of efficiency and identify actions to improve it.

Measuring and improving efficiency, regardless of the type or size of the company, is essential for successful business operations. Based on existing literature and practice, the main problems and objectives of the research were defined. The necessity for models to measure and enhance the efficiency of processes in logistics companies was established.

A three-phase DEA-fuzzy AHP model was developed and presented: the first phase involves data collection and analysis of logistics companies, the second phase is dedicated to measuring and improving efficiency, and the third phase focuses on multi-criteria decision-making to select the most efficient company.

Based on the collected data on logistics companies in the Republic of Serbia and the questionnaire conducted with logistics experts, six criteria were selected for testing the model. Data for each of the ten logistics companies included in the analysis were selected in accordance with these criteria. Input- and output-oriented DEA CCR models were applied to measure efficiency. It overcomes the subjectively imposed preferences of the decision maker because it allows for the determination of weighting coefficients to maximize efficiency. Based on input and output data, the DEA method evaluates whether a unit under consideration is efficient compared to the other units included in the analysis. Upon completion of the calculations, a score of 1 was assigned to six logistics companies, indicating an assessment of full efficiency.

Combining the DEA method with fuzzy logic systems and the AHP method is essential due to the inherent nature of the DEA method. DEA is designed for the comparative analysis of the efficiency of decision-making units based on multiple criteria, which necessitates integration with other methods to validate results and to identify relevant criteria for assessing efficiency. Fuzzification of the AHP method is implemented to address the uncertainty of decision-makers when comparing criteria and ranking alternatives. This approach allows the values of the criteria to adjust based on the decision-maker’s degree of confidence. As confidence increases, the weight of the corresponding criterion also increases; conversely, it decreases with lower levels of confidence.

Applying the developed model to rank logistics companies shows that this approach allows for the optimal selection among available alternatives, indicating that the fuzzy AHP method can effectively assist in formulating decision-making strategies. The proposed model significantly reduces the uncertainty faced by decision-makers and enables less experienced individuals to make optimal decisions. The developed model, as conceptualized, could also be applied to other decision-making scenarios, especially when decision-makers have varying degrees of confidence.

To rank the remaining six logistics companies assessed as efficient using the DEA method, the initial step involved determining the weights of the criteria. To ensure the reliability of these weights, a questionnaire was conducted to gather expert opinions from professionals in the field of logistics. The criteria were compared in pairs, degrees of confidence were defined, and the initial matrix was subsequently fuzzified. Final values were then defuzzified to derive the criterion weights. Furthermore, the values of the alternatives were normalized according to the defined criteria, enabling the evaluation and ranking of the companies by efficiency. The stability of rankings under incremental variations in criterion weights is analyzed, identifying the minimal perturbation required to alter the established preference order and thereby offering deeper insights into the robustness of the fuzzy AHP decision-making process. The findings demonstrate that fluctuations in weighting coefficients do not affect the position of the top-ranked alternative.

Market changes arising from the development of technology and information systems, as well as shifts in user requirements, will directly impact the efficiency of logistics companies. Developing a model to assess the impact of these changes on efficiency, including the integration of new indicators, represents a key direction for future research.