Effect of Neighboring Hole Impacts on Inter-Hole Dynamic Presplitting Process with Consideration of Crack Width Variations
Abstract
1. Introduction
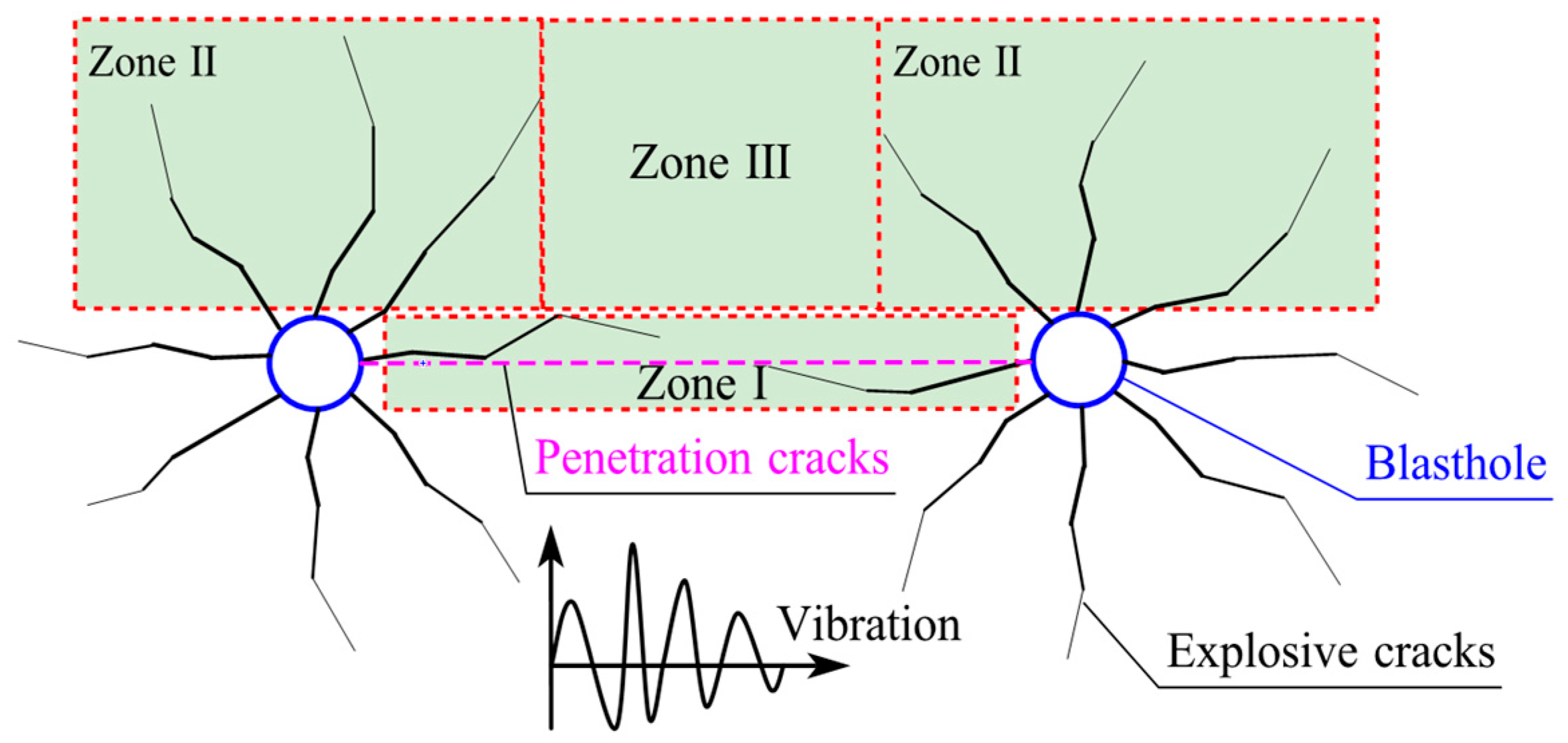
2. Mechanism Analysis of Inter-Hole Dynamic Cracking Formation
2.1. Dynamic Cracking Tendency Under Different Loads
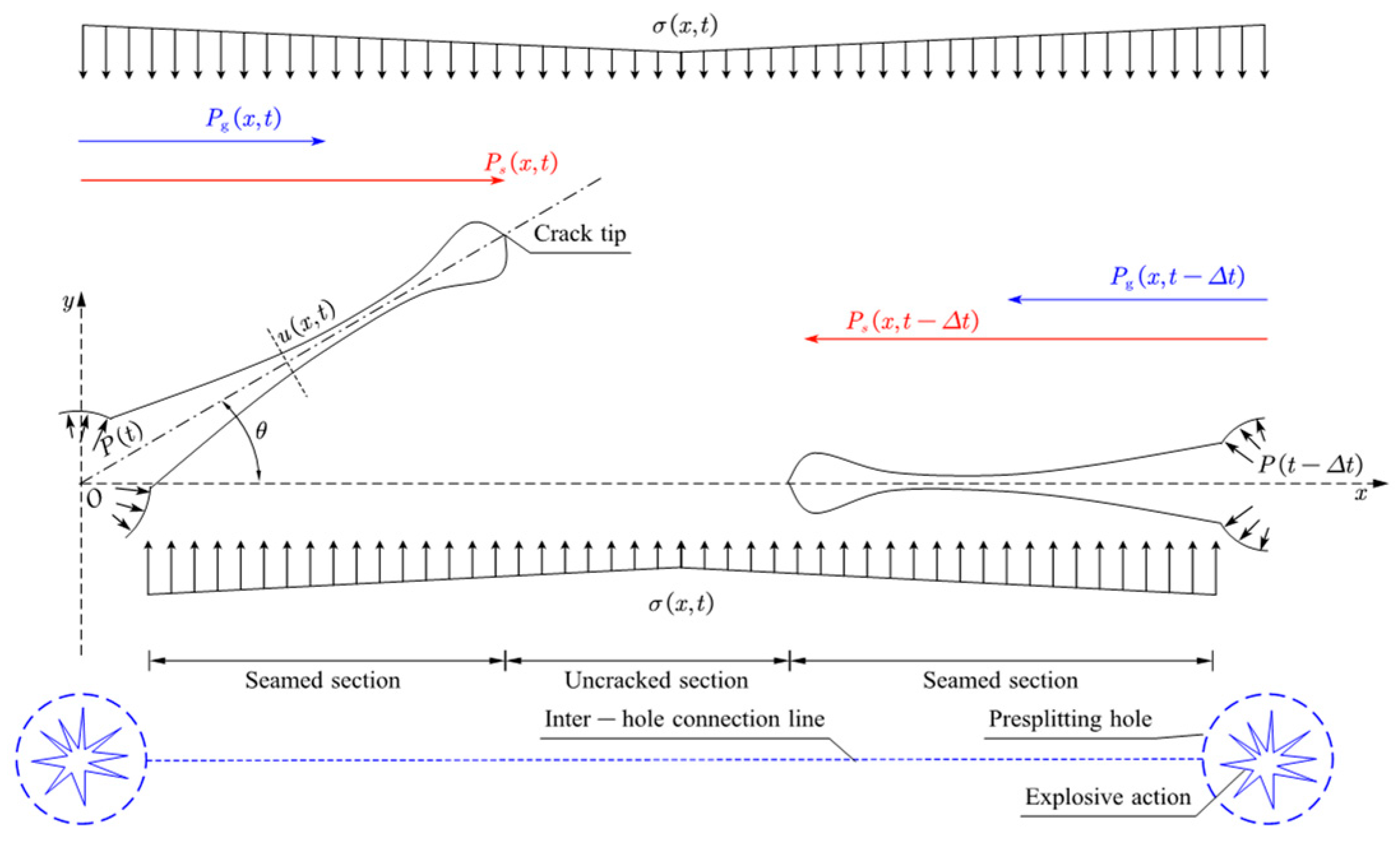
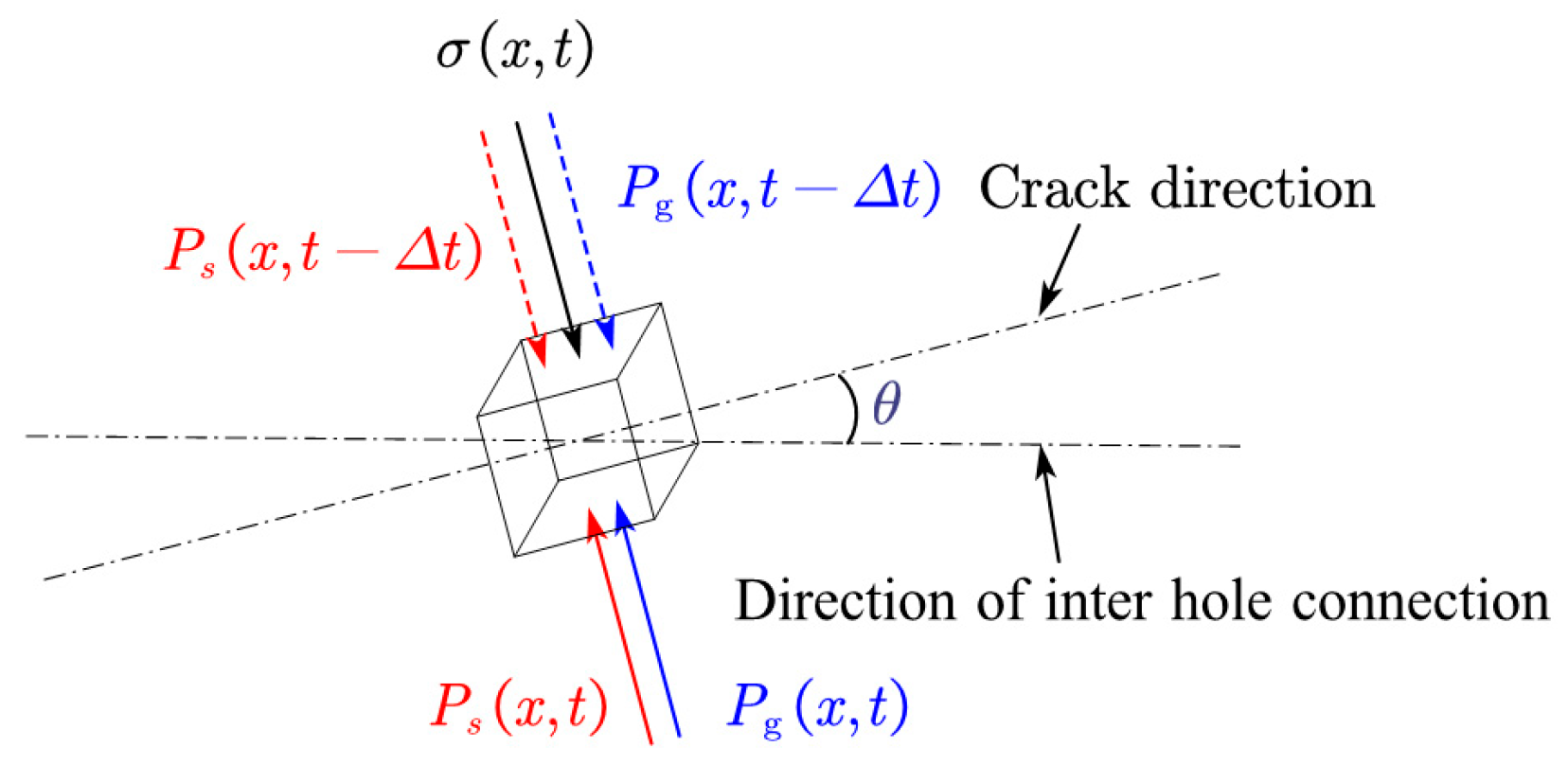
2.2. Inter-Hole Crack Dynamic Driving Model Based on Explosion Load and Ground Stress Transient Unloading
3. Numerical Simulation
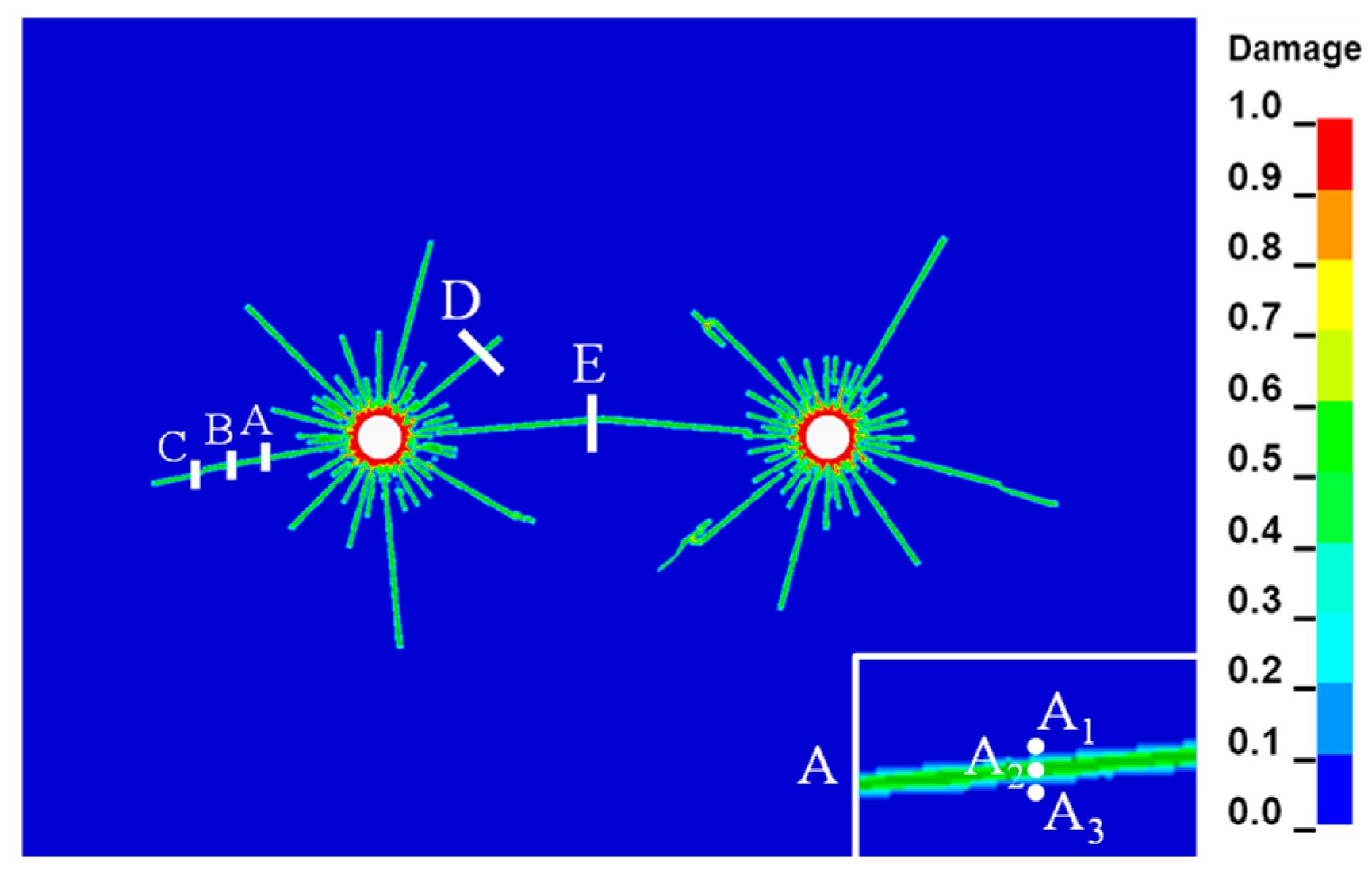
3.1. Numerical Model
3.2. Parameter Selection and Verification
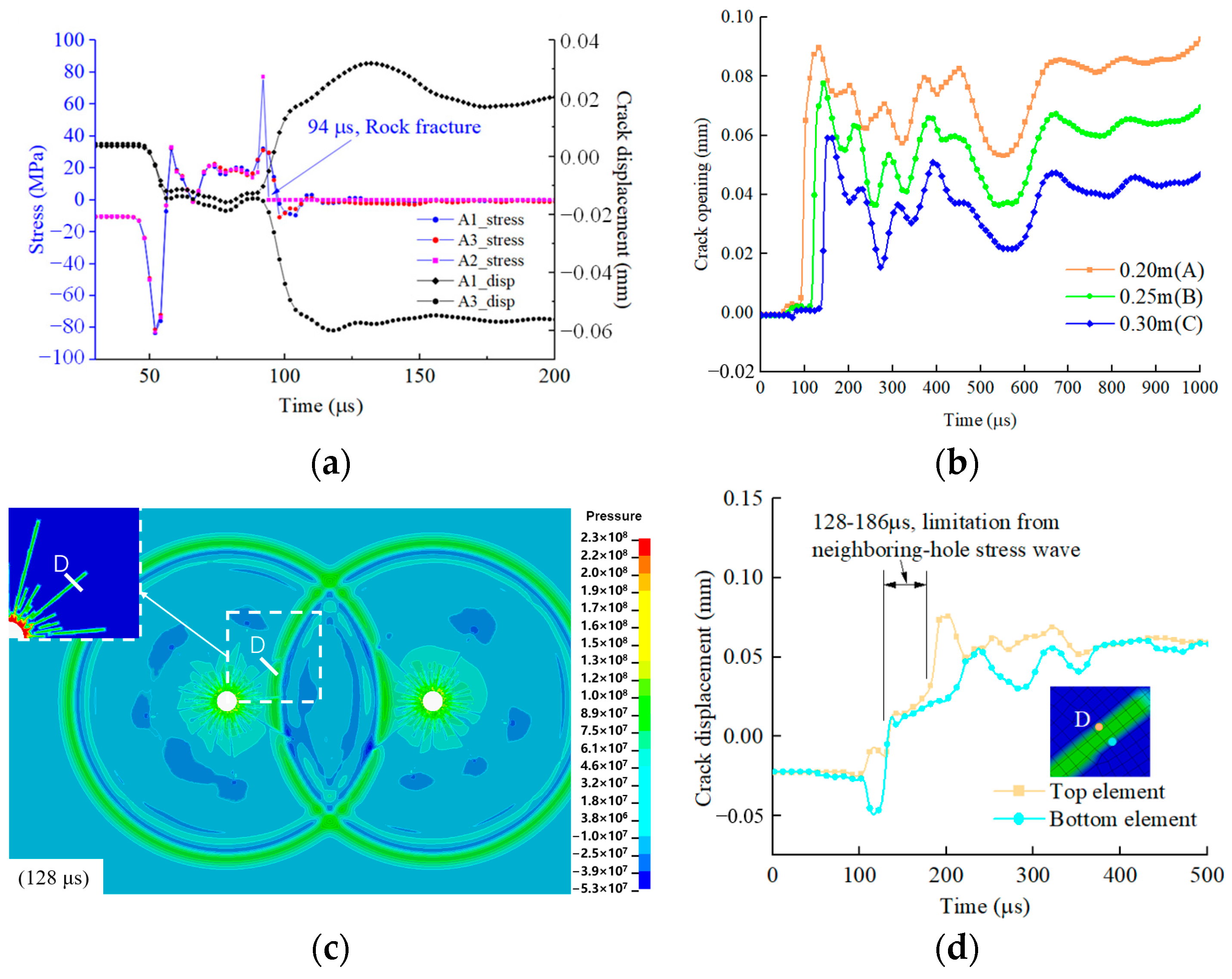
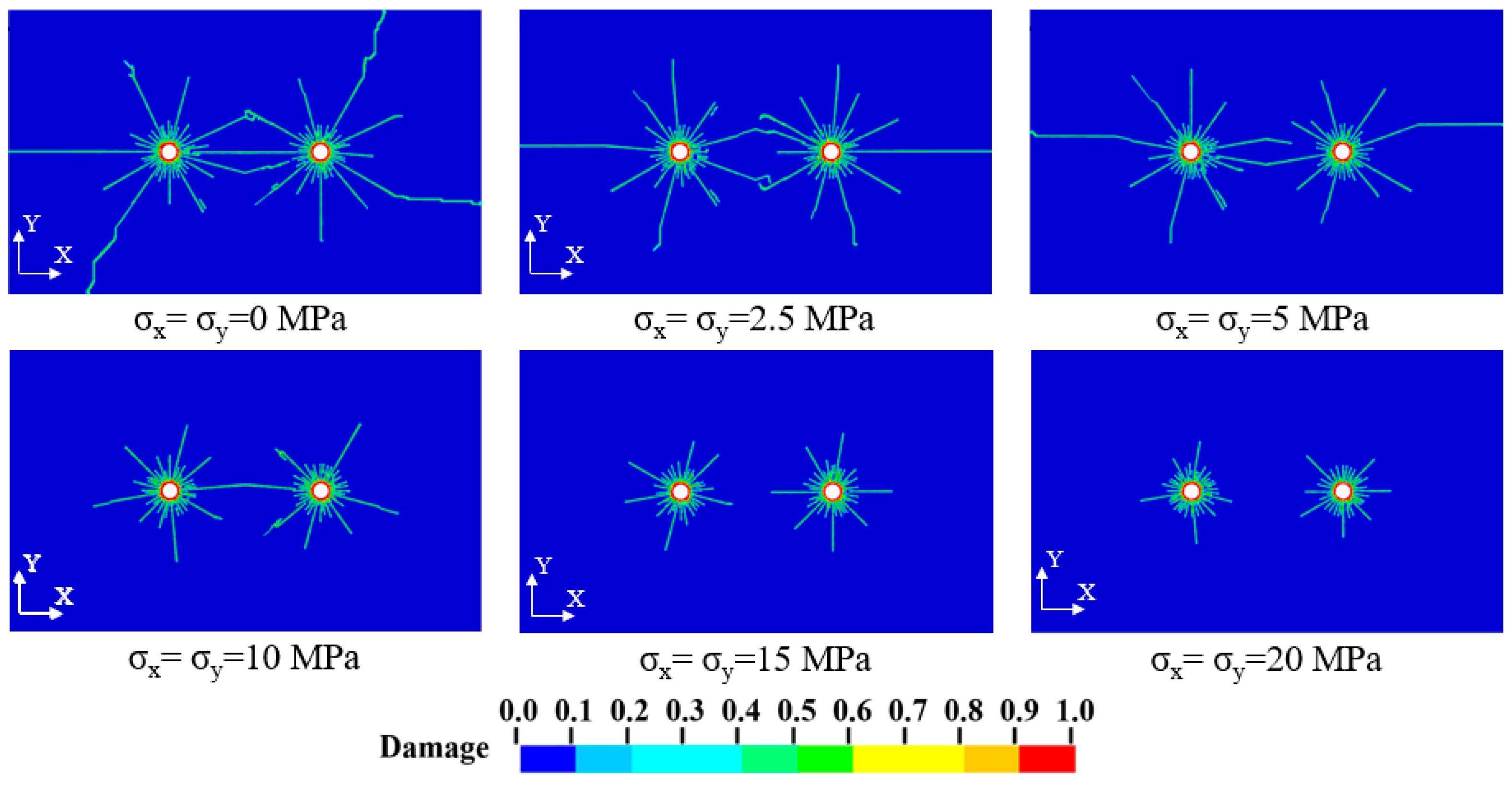
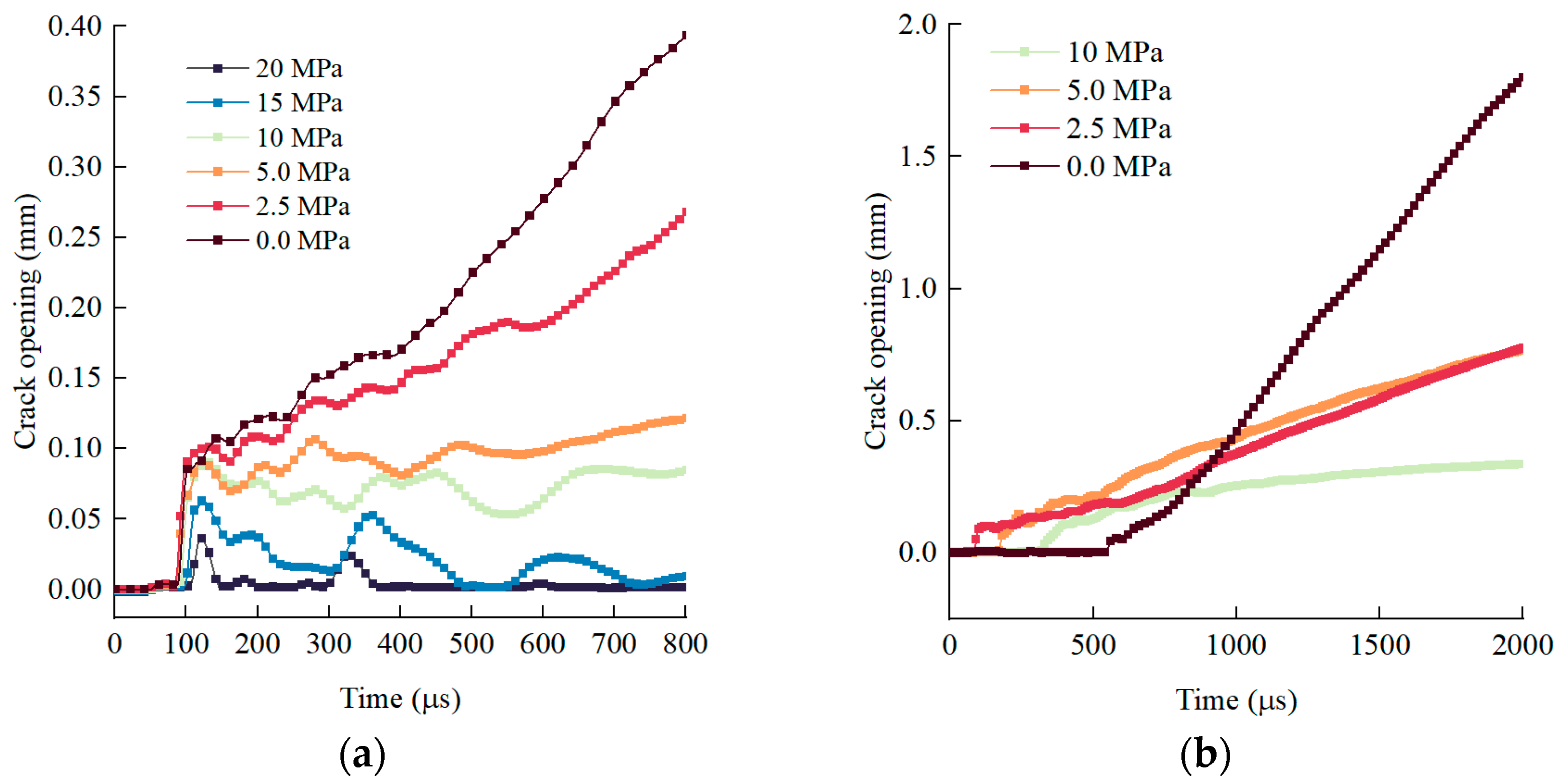
3.3. Result Analysis
3.3.1. Dynamic Cracking Process of Inter-Hole Presplitting
3.3.2. Influence of Stress Conditions on Inter-Hole Cracking Process
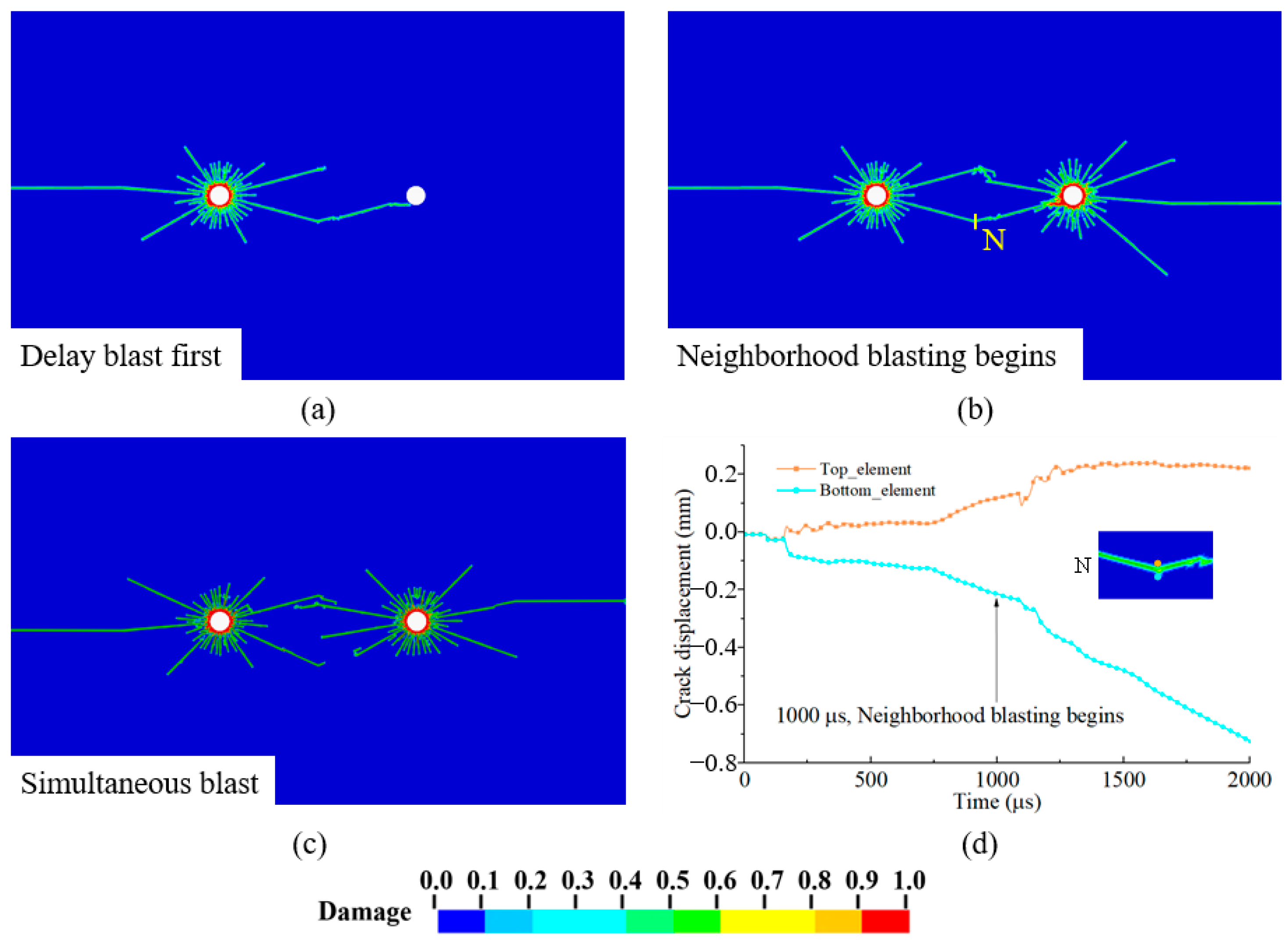
3.3.3. Influence of Blasting Delay Time on Inter-Hole Cracking Process
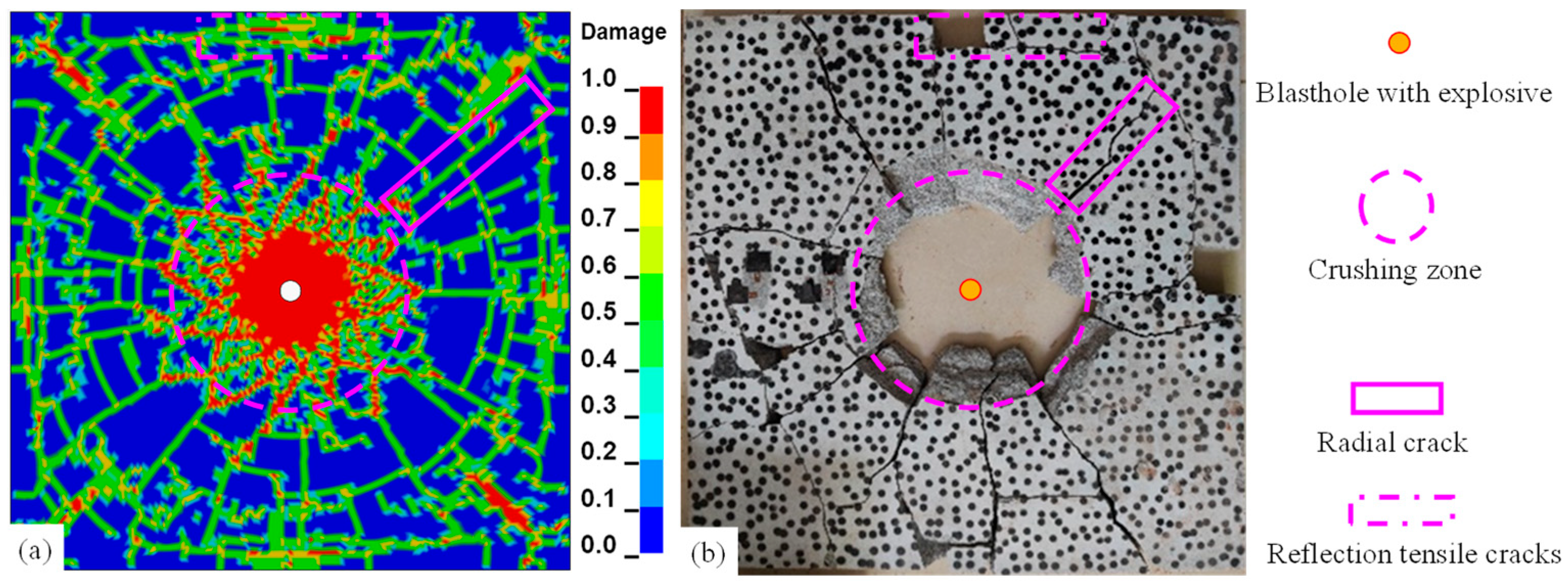
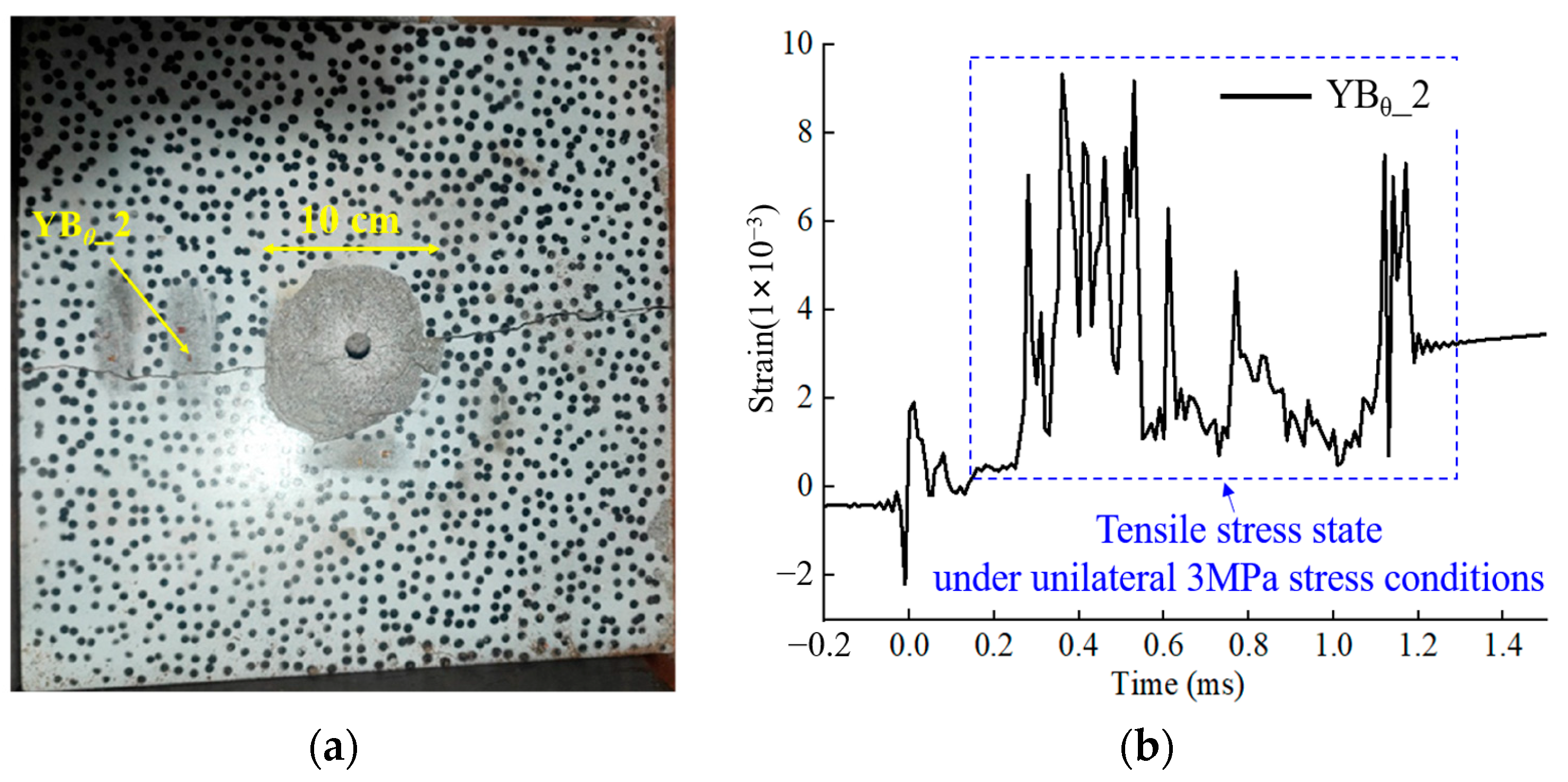
4. Inter-Hole Explosion Verification Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Huang, J.; Luo, Y.; Dong, Q.; Li, Y.; Wan, Y.; Liu, T. Numerical simulation of blast vibration and crack forming effect of rock-anchored beam excavation in deep underground caverns. Shock Vib. 2017, 2017, 1812080. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, J.; Li, X.; Liu, T.; Bian, X.; Luo, Y. Characteristics of the elevation amplification effect of vibration velocity in rock surrounding underground cavities under different stress conditions. Soil Dyn. Earthq. Eng. 2023, 165, 107704. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, G.D.; Cui, X.Z.; Zhao, X.H.; Wu, J.G.; Wang, L.H. Low-Frequency Characteristics of Vibrations Induced by Transient Unloading of In Situ Stress and Its Influence on Safety of a Deeply Buried Tunnel. Int. J. Geomech. 2024, 24, 04023288. [Google Scholar] [CrossRef]
- Banadaki, M.D.; Mohanty, B. Numerical simulation of stress wave induced fractures in rock. Int. J. Impact Eng. 2012, 40, 16–25. [Google Scholar] [CrossRef]
- Saadatmand Hashemi, A.; Katsabanis, P. The effect of stress wave interaction and delay timing on blast-induced rock damage and fragmentation. Rock Mech. Rock Eng. 2020, 53, 2327–2346. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, J.; Leng, Z.; Yang, G.; Liu, X.; Tian, B. Punching Mechanism of Air-Deck Stemming for Drilling Blasting and Its Influence on Rock Fragmentation. Rock Mech. Rock Eng. 2024, 57, 3917–3935. [Google Scholar] [CrossRef]
- Córdova, E.; Gottreux, I.; Anani, A.; Ferrada, A.; Contreras, J. Blasting and preconditioning modelling in underground cave mines under high stress conditions. J. S. Afr. Inst. Min. Metall. 2021, 121, 71–80. [Google Scholar] [CrossRef]
- Sanchidrián, J.A.; Segarra, P.; López, L.M. Energy components in rock blasting. Int. J. Rock Mech. Min. 2007, 44, 130–147. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, M.; Yi, C.; Lu, W.; Yan, P. Quantitative Study of the Action on Rock Mass Failure under the Shock Wave and Gas Pressure in Bench Blasting. Int. J. Geomech. 2023, 23, 04023135. [Google Scholar] [CrossRef]
- Trivino, L.F.; Mohanty, B. Assessment of crack initiation and propagation in rock from explosion-induced stress waves and gas expansion by cross-hole seismometry and FEM–DEM method. Int. J. Rock Mech. Min. Sci. 2015, 77, 287–299. [Google Scholar] [CrossRef]
- Hino, K. Fragmentation of rock through blasting and shock wave theory of blasting. In Proceedings of the 1st US Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 23–25 April 1956. [Google Scholar]
- Sazid, M.; Singh, T.N. Two-dimensional dynamic finite element simulation of rock blasting. Arab. J. Geo-Sci. 2013, 6, 3703–3708. [Google Scholar] [CrossRef]
- Langefors, U.; Kihlström, B. The Modern Technique of Rock Blasting; Wiley: New York, NY, USA, 1963; Volume 405. [Google Scholar]
- Langefors, U. Fragmentation in rock blasting. In Proceedings of the 7th Symp. on Rock Mechanics, Pennsylvania State University, University Park, PA, USA, 14–16 June 1965; pp. 1–21. [Google Scholar]
- Kutter, H.K.; Fairhurst, C. On the fracture process in blasting. Int. J. Rock Mech. Min. Sci. 1971, 8, 181–202. [Google Scholar] [CrossRef]
- Hagan, T.N. Rock breakage by explosives. Acta Astronaut. 1979, 6, 329–340. [Google Scholar] [CrossRef]
- Dally, J.W.; Fourney, W.L.; Holloway, D.C. Influence of containment of the bore hole pressures on explosive induced fracture. Int. J. Rock Mech. Min. Sci. 1975, 12, 5–12. [Google Scholar] [CrossRef]
- Larocque, G.; Favreau, R. Blasting research at the Mines Branch. In Proceedings of the 12th US Symposium on Rock Mechanics (USRMS), Rolla, MO, USA, 16–18 November 1970. [Google Scholar]
- Rossmanith, H.; Daehnke, A.; Nasmillner, R.; Kouzniak, N.; Ohtsu, M.; Uenishi, K. Fracture mechanics applications to drilling and blasting. Fatigue Fract. Eng. Mater. Struct. 1997, 20, 1617–1636. [Google Scholar] [CrossRef]
- Daehnke, A.; Rossmanith, H.; Knasmillner, R. Blast-induced dynamic fracture propagation. In Rock Fragmentation by Blasting; CRC Press: Boca Raton, FL, USA, 2020; pp. 13–18. [Google Scholar]
- Duvall, W.I.; Petkof, B. Spherical Propagation of Explosion-Generated Strain Pulses in Rock; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1959.
- Yi, C.; Johansson, D.; Nyberg, U.; Beyglou, A. Stress Wave Interaction Between Two Adjacent Blast Holes. Rock Mech. Rock Eng. 2016, 49, 1803–1812. [Google Scholar] [CrossRef]
- Ding, C.; Yang, R.; Feng, C. Stress wave superposition effect and crack initiation mechanism between two adjacent boreholes. Int. J. Rock Mech. Min. Sci. 2021, 138, 104622. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, P.; He, H.; Lu, W.; Liu, B.; Zhu, J.; Cheng, Y. Experimental investigations of the effect of millisecond-delay time on the blast vibration reduction with electronic detonators. J. Vib. Control. 2023, 29, 4204–4215. [Google Scholar] [CrossRef]
- Yi, C.; Sjöberg, J.; Johansson, D.; Petropoulos, N. A numerical study of the impact of short delays on rock fragmentation. Int. J. Rock Mech. Min. 2017, 100, 250–254. [Google Scholar] [CrossRef]
- He, C.; Chen, D.; Xiao, J.; Lu, L.; Guo, Z. Experimental study of crack propagation and failure around a horseshoe tunnel during nearby blasting. Int. J. Rock Mech. Min. Sci. 2021, 139, 104628. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.; Xu, L.; Yang, R.; Chao, Y.J. Fracture path of cracks emigrating from two circular holes under blasting load. Theor. Appl. Fract. Mech. 2020, 108, 102559. [Google Scholar] [CrossRef]
- Pu, C.; Yang, X.; Zhao, H.; Chen, Z.; Xiao, D. Numerical investigation on crack propagation and coalescence induced by dual-borehole blasting. Int. J. Impact Eng. 2021, 157, 103983. [Google Scholar] [CrossRef]
- Xu, P.; Yang, R.; Guo, Y.; Chen, C.; Yang, Y.; Zuo, J. Investigation of the interaction mechanism of two dynamic propagating cracks under blast loading. Eng. Fract. Mech. 2022, 259, 108112. [Google Scholar] [CrossRef]
- Li, X.; Liu, K.; Qiu, T.; Sha, Y.; Yang, J. Study of presplit blasting under high in-situ stress. Eng. Fract. Mech. 2023, 288, 109360. [Google Scholar] [CrossRef]
- Li, X.; Liu, K.; Yang, J.; Qiu, T.; Sha, Y. Effects of in-situ stress on rock cracking in presplit blasting. Comput. Geotech. 2024, 168, 106124. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Huang, L.; Sha, Y.; Yang, J.; Zhao, X.; Ma, S.; Hong, Z. Investigation on Rock Fracturing in Presplit Blasting Under Various Initial Stresses. Rock Mech. Rock Eng. 2024, 57, 6927–6950. [Google Scholar] [CrossRef]
- Yang, L.; Yang, A.; Chen, S.; Fang, S.; Huang, C.; Xie, H. Model experimental study on the effects of in situ stresses on pre-splitting blasting damage and strain development. Int. J. Rock Mech. Min. 2021, 138, 104587. [Google Scholar] [CrossRef]
- Yang, L.; Chen, S.; Yang, A.; Huang, C.; Xie, H. Numerical and experimental study of the presplit blasting failure characteristics under compressive stress. Soil Dyn. Earthq. Eng. 2021, 149, 106873. [Google Scholar] [CrossRef]
- Liu, X.; Yan, P.; Lu, W.; Lu, A.; Zhang, X.; Chen, M.; Wang, G. Numerical investigation of an improved deep-hole presplitting method based on notched blasting for deep-buried high sidewall structures. J. Build. Eng. 2023, 70, 106310. [Google Scholar] [CrossRef]
- Liu, K.; Li, Q.; Wu, C.; Li, X.; Li, J. Optimization of spherical cartridge blasting mode in one-step raise excavation using pre-split blasting. Int. J. Rock Mech. Min. 2020, 126, 104182. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Hao, H.; Li, X.; Sha, Y.; Wang, W.; Liu, X. Study on the raising technique using one blast based on the combination of long-hole presplitting and vertical crater retreat multiple-deck shots. Int. J. Rock Mech. Min. 2019, 113, 41–58. [Google Scholar] [CrossRef]
- Dubner, H.; Abate, J. Numerical Inversion of Laplace Transforms by Relating Them to the Finite Fourier Cosine Transform. J. ACM 1968, 15, 115–123. [Google Scholar] [CrossRef]
- Hallquist, J. LS-DYNA Theory Manual 19. Livermore Software Technology Corporation (LSTC); ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Kucewicz, M.; Baranowski, P.; Małachowski, J.; Trzciński, W.; Szymańczyk, L. Numerical Modelling of Cylindrical Test for Determining Jones—Wilkins—Lee Equation Parameters. In Proceedings of the 14th International Scientific Conference: Computer Aided Engineering, CAE 2018; Rusiński, E., Pietrusiak, D., Eds.; Lecture Notes in Mechanical Engineering. Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Baranowski, P.; Kucewicz, M.; Gieleta, R.; Stankiewicz, M.; Konarzewski, M.; Bogusz, P.; Pytlik, M.; Małachowski, J. Fracture and fragmentation of dolomite rock using the JH-2 constitutive model: Parameter determination, experiments and simulations. Int. J. Impact Eng. 2020, 140, 103543. [Google Scholar] [CrossRef]
- Kang, P.; Zhaopeng, L.; Quanle, Z.; Zhenyu, Z.; Jiaqi, Z. Static and dynamic mechanical properties of granite from various burial depths. Rock Mech. Rock Eng. 2019, 52, 3545–3566. [Google Scholar] [CrossRef]
- Kucewicz, M.; Baranowski, P.; Małachowski, J. Determination and validation of Karagozian-Case Concrete constitutive model parameters for numerical modeling of dolomite rock. Int. J. Rock Mech. Min. Sci. 2020, 129, 104302. [Google Scholar] [CrossRef]
- Liu, X.; Yan, P.; Lu, W.; Zhu, J.; Zhang, X.; Lu, A.; Chen, M.; Wang, G. Investigation of dynamic crack formation mechanism based on a new crack dynamic driving model. Comput. Geotech. 2023, 159, 105471. [Google Scholar] [CrossRef]
- Sazid, M.; Singh, T.N. Numerical assessment of spacing–burden ratio to effective utilization of explosive energy. Int. J. Min. Sci. Technol. 2015, 25, 291–297. [Google Scholar] [CrossRef]
- Tao, J.; Yang, X.-G.; Li, H.-T.; Zhou, J.-W.; Fan, G.; Lu, G.-D. Effects of in-situ stresses on dynamic rock responses under blast loading. Mech. Mater. 2020, 145, 103374. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Wang, W.; Su, X.; Li, Z.; Li, J.; Wen, L.; Chang, J.; Sun, X. Numerical study on the fracturing mechanism of shock wave interactions between two adjacent blast holes in deep rock blasting. Earthq. Eng. Eng. Vib. 2019, 18, 735–746. [Google Scholar] [CrossRef]
- Fukuda, D.; Moriya, K.; Kaneko, K.; Sasaki, K.; Sakamoto, R.; Hidani, K. Numerical simulation of the fracture process in concrete resulting from deflagration phenomena. Int. J. Fract. 2013, 180, 163–175. [Google Scholar] [CrossRef]










| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Density | 3471 kg/m3 | Shear modulus | 32.09 GPa |
| Strain rate parameters | 1.0 | Parameter for strain rate dependence | 0.005 |
| Pressure component, K1 | 46.6 GPa | Pressure component, K2 | −18 GPa |
| Pressure component, K3 | 3980 GPa | ||
| Intact normalized strength parameter, A | 0.70 | Fractured normalized strength parameter, B | 0.23 |
| Intact strength parameter, N | 0.61 | Fractured strength parameter, M | 0.61 |
| Maximum tensile pressure strength, T | 54 MPa | Maximum normalized fractured strength | 0.25 |
| Hugoniot elastic limit | 4.5 GPa | Pressure component of Hugoniot elastic limit | 2.578 |
| Bulk factor, β | 0.5 | ||
| Damage coefficient, D1 | 0.005 | Damage coefficient, D2 | 0.7 |
| Density (kg/m3) | Detonation Velocity (m/s) | P (GPa) | A (GPa) |
|---|---|---|---|
| 1130 | 4805 | 7.4 | 252 |
| B (GPa) | R1 | R2 | ω |
| 15.6 | 6.08 | 2.05 | 0.25 |
| ρ (kg/m3) | PC | MU | C0 | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|---|---|
| 1.18 | −1 | 1.7456 × 10−5 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 |
| Test Conditions | Presplit Hole 1 | Presplit Hole 2 | Side Blasting Hole 3 |
|---|---|---|---|
| Simultaneous presplitting | MS1 | MS1 | MS3 |
| Millisecond presplitting | MS1 | MS3 | MS5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yan, P.; Zhu, J.; Yang, X.; Zhang, X.; Zhou, C.; Lu, W.; Chen, M.; Wang, G.; Wang, Y. Effect of Neighboring Hole Impacts on Inter-Hole Dynamic Presplitting Process with Consideration of Crack Width Variations. Appl. Sci. 2025, 15, 10036. https://doi.org/10.3390/app151810036
Liu X, Yan P, Zhu J, Yang X, Zhang X, Zhou C, Lu W, Chen M, Wang G, Wang Y. Effect of Neighboring Hole Impacts on Inter-Hole Dynamic Presplitting Process with Consideration of Crack Width Variations. Applied Sciences. 2025; 15(18):10036. https://doi.org/10.3390/app151810036
Chicago/Turabian StyleLiu, Xiao, Peng Yan, Jin Zhu, Xiasen Yang, Xiangyu Zhang, Chao Zhou, Wenbo Lu, Ming Chen, Gaohui Wang, and Yang Wang. 2025. "Effect of Neighboring Hole Impacts on Inter-Hole Dynamic Presplitting Process with Consideration of Crack Width Variations" Applied Sciences 15, no. 18: 10036. https://doi.org/10.3390/app151810036
APA StyleLiu, X., Yan, P., Zhu, J., Yang, X., Zhang, X., Zhou, C., Lu, W., Chen, M., Wang, G., & Wang, Y. (2025). Effect of Neighboring Hole Impacts on Inter-Hole Dynamic Presplitting Process with Consideration of Crack Width Variations. Applied Sciences, 15(18), 10036. https://doi.org/10.3390/app151810036







