Unsupervised Learning of Fine-Grained and Explainable Driving Style Representations from Car-Following Trajectories

Abstract

Fine-grained modeling of driving styles is critical for decision making in autonomous driving. However, existing methods are constrained by the high cost of manual labeling and a lack of interpretability. This study proposes an unsupervised disentanglement framework based on a variational autoencoder (VAE), which, for the first time, enables the automatic extraction of interpretable driving style representations from car-following trajectories. The key innovations of this work are threefold: (1) a dual-decoder VAE architecture is designed, leveraging driver identity as a proxy label to guide the learning of the latent space; (2) self-dynamics and interaction dynamics features are decoupled, with an attention mechanism employed to quantify the influence of the lead vehicle; (3) a bidirectional interpretability verification framework is established between latent variables and trajectory behaviors. Evaluated on a car-following dataset comprising 25 drivers, the model achieves a Driver Identification accuracy of 98.88%. Mutual information analysis reveals the physical semantics encoded in major latent dimensions. For instance, latent dimension z₂₂ is strongly correlated with the minimum following distance and car-following efficiency. One-dimensional latent traversal further confirms that individual dimensions modulate specific behavioral traits: increasing z₂₂ improves safety margins by 18% but reduces efficiency by 23%, demonstrating that it encodes a trade-off between safety and efficiency. This work provides a controllable representation framework for driving style transfer in autonomous systems and offers a more granular approach for analyzing driver behavior in car-following scenarios, with potential for extension to broader driving contexts.

1. Introduction

With the rapid development of intelligent transportation systems, understanding driving behavior has become increasingly critical [1,2,3]. Autonomous driving systems must recognize and model diverse driving styles to enable precise control and decision making [4,5,6]. However, existing approaches still struggle to capture driver-specific styles with sufficient accuracy. In mixed traffic environments, identifying the behavior of surrounding human drivers is essential for scene prediction, where driving style constitutes an important element of scene semantics [7]. Incorporating driving style into the decision-making process is, thus, vital for improving safety, comfort, and efficiency in real-world autonomous driving.

Car-following behavior is a core element of vehicle motion on highways and urban expressways [8,9]. Driver style directly influences headway adjustment, acceleration, and deceleration strategies, thereby shaping traffic flow dynamics. For example, aggressive driving often leads to abrupt accelerations and decelerations, which increase traffic oscillations and congestion [10]. Accurate modeling of car-following styles supports traffic management, enhances behavior prediction, and provides reliable decision support for autonomous vehicles, contributing to improved safety and efficiency.

Driving style modeling can generally be categorized into short-term and long-term perspectives. The short-term perspective focuses on immediate and localized driving decisions, which are typically influenced by the current state of the ego vehicle, surrounding vehicles, and environmental semantics [11]. Long-term modeling captures stable driving habits observed over extended periods. In microscopic traffic flow analysis, short-term modeling is especially important [12]. In car-following scenarios, vehicle motion reflects dynamic responses to the leading vehicle, forming a temporal interaction process [13]. Fine-grained short-term style modeling is, therefore, crucial for real-time traffic flow evaluation and safety assessment in autonomous driving.

Existing methods for style identification mainly adopt supervised or unsupervised learning [8]. Supervised approaches rely on expert-labeled data and handcrafted features to classify styles such as conservative, neutral, or aggressive [14,15]. While intuitive, these methods are costly and limited to discrete categories. Unsupervised approaches, by contrast, extract latent style representations directly from trajectories or physiological signals, enabling scalable analysis without annotations [16]. However, their black-box nature weakens interpretability and makes it difficult to link latent features with physical driving behavior.

In summary, current methods face two main challenges: high annotation costs and weak interpretability. Supervised methods require extensive labeled data and lack adaptability to new environments, while unsupervised methods often generate high-dimensional features without clear semantic meaning. Moreover, the disentanglement of driving style representations remains unresolved, leading to oversimplified interpretations and underuse of latent space richness. This problem is especially pronounced in car-following scenarios, where longitudinal control dominates and scene diversity is limited, further complicating the identification of fine-grained styles.

To address these challenges, this study proposes an unsupervised method for extracting driving style representations using a variational autoencoder (VAE) with a disentangled latent space to improve interpretability. A two-stage pipeline is designed: in the first stage, a VAE learns latent style variables from car-following trajectories with driver identity as a proxy label; in the second stage, disentanglement is achieved through mutual information estimation and latent traversal, linking latent dimensions with interpretable semantics. This approach avoids predefined labels and enables the automatic extraction of meaningful and controllable style features directly from raw trajectory data.

The main contributions of this study are as follows: (1) We propose an unsupervised VAE-based method for extracting driving style representations, guided by driver identity rather than manual labels. This significantly reduces annotation costs while improving model adaptability. (2) We develop an interpretable latent space framework capable of assigning fine-grained and continuous semantics to each dimension of the driving style representation. This framework is applicable to real-time behavior analysis, driving style transfer in autonomous systems, and safety evaluation tasks.

The remainder of this paper is organized as follows: Section 2 presents a literature review of existing methods and recent advances in Driving Style Recognition. Section 3 introduces the proposed methodology, including the model architecture, the VAE design, and the disentanglement strategy for the latent space. Section 4 details the experiment and data preprocessing. Section 5 reports results and performance evaluations. Finally, Section 6 summarizes the contributions.

2. Literature Review

Modeling driving styles plays an increasingly central role in autonomous driving systems, especially for precise control and personalized driving strategies. Current research on driving-style modeling follows two main threads: Driving Style Recognition (DSR) and Driver Identification (DI). The former focuses on mapping behavioral features into a semantic space of driving styles, while the latter distinguishes drivers by exploiting the uniqueness of individual behavior. Although both lines of work have made substantial progress, they still exhibit limitations in interpretability, style disentanglement, and scenario adaptability. The following review summarizes the state of the art and the challenges that motivate the present study.

2.1. Driving Style Recognition (DSR)

Traditional approaches to Driving Style Recognition have largely relied on statistical features and manual labels, typically reducing driving style to discrete categories (e.g., “aggressive” vs. “conservative”). Vaitkus et al. [17], for example, constructed a binary “aggressive–conservative” classifier from vehicle accelerometer data and reported 100% classification accuracy in a fixed-route scenario. However, dependence on manual labels makes preprocessing time-consuming and poorly adaptable to varied real-world conditions. To reduce labeling costs, semi-supervised methods have emerged: Wang et al. (2017) [18] proposed an S3VM framework that generates pseudo-labels via k-means clustering and, with only a few labeled samples, improved classification accuracy by about 10%, significantly lowering annotation requirements. Nevertheless, such discrete categorization, while easy to interpret and implement, fails to capture fine-grained variation in driving style [19,20,21].

More recently, deep learning models have substantially improved style representation capacity. CNNs, RNNs, and Transformers have been widely applied to model trajectory behavior sequences. For instance, Ye et al. [22] proposed D-CRNN, which combines convolutional neural networks (CNNs) and recurrent neural networks (RNNs) to capture temporal features from trajectory data and thereby improve style recognition accuracy. Cai et al. [23] presented a CNN–LSTM hybrid that achieves over 93% classification accuracy on driving operation time series. At the same time, generative modeling approaches have begun to appear: Choi et al. [24] proposed the DSA-GAN architecture, which couples a style recognition module with a conditional generator to produce trajectories conditioned on driving style, improving prediction accuracy and behavioral consistency. Despite these advances, deep-learning-based methods are still constrained by discretized labels, and the latent variables they produce are often difficult to interpret physically. Consequently, many existing DSR methods compress style representations into discrete categories and thereby ignore the continuity and complexity of driving styles, limitations that hinder precise style control and personalization.

2.2. Driver Identification (DI)

DI is founded on the hypothesis that driving behavior contains individual-specific signatures. Its development has provided important lessons for DSR. Traditional DI approaches relied heavily on feature engineering. For example, Kwak et al. [25] extracted driving pattern features via wavelet transforms and, combined with XGBoost, achieved 96.18% binary classification accuracy in highway scenarios. With the rise of representation learning, deep networks have markedly improved DI performance. Azadani et al. [26] introduced an RCN residual network that learns driving “fingerprints” directly from CAN-bus data, validating behavioral uniqueness with 99.3% accuracy. Abdennour et al. [27] used triplet-loss-based unsupervised embedding learning to substantially reduce dependence on labeled data.

Notably, DI has achieved breakthroughs in car-following scenarios. Lu et al.’s [28] Hetero Model jointly models within-driver state fluctuations (e.g., adjustments of following gap) and between-driver behavioral variability (e.g., acceleration distributions) and achieved an 82.3% online identification rate on 15 s car-following sequences, demonstrating that short-term longitudinal control behavior contains discriminative individual features. Advances in temporal modeling further strengthened discrimination: Govers et al. [29] (2024) designed a time-shift Transformer (MTST) and, combined with ensemble methods, raised identification rates to 97%. Li et al.’s [30] ATTraj2vec employs multi-level attention to fuse motion and spatiotemporal features, offering a new paradigm for behavioral representation. Ding et al. [31] extracted features according to driver behavioral heterogeneity and used a mixture-of-Gaussians approach to distinguish drivers, producing interpretable findings. Hu et al. [32] explored generative approaches in DI by using a convolutional conditional variational autoencoder (CCVAE) to expand the sample space; they achieved up to a 20% performance gain on several metrics, even when training on only 2% of the original data.

Although DI excels at differentiating drivers, its core objective is identity recognition rather than style modeling. Therefore, DI-derived representations typically lack explicit semantic mappings to concrete behavioral metrics. This limits their practical use in autonomous driving systems, since they offer insufficient interpretability and controllability. In the long run, high discriminability in DI does not automatically translate into generative capabilities for driving style, which remains a major open challenge.

2.3. Research Gap

A comparison of the two research strands reveals three pressing problems that remain unresolved. First, most existing methods employ discretized style labels and cannot effectively capture fine-grained style differences. They also overly depend on manual annotation. Second, current models generally lack a mechanism to map learned representations to physical behavioral indicators, leaving style interpretability weak. Third, existing approaches struggle to handle dynamic style changes that occur in specific car-following scenarios.

3. Methodology

This study proposes a VAE-based framework to extract driving style representations from trajectory data. A dual-decoder architecture is used: one decoder reconstructs trajectories, and the other classifies drivers, linking latent variables to driving styles. Using trajectory data and driver identities as proxy labels reduces manual annotation and captures both individual and general driving patterns. The disentangled latent space provides interpretable dimensions for detailed, controllable driving style representation in autonomous systems.

3.1. Driving Style-Aware Dual-Decoder VAE Architecture

In car-following scenarios, driving style extraction is challenging due to limited dynamics, as vehicle motion is largely influenced by the lead vehicle. A dual-decoder variational autoencoder (VAE) is proposed (Figure 1), separating trajectory features into vehicle dynamics and interactions with the lead vehicle, improving the accuracy and interpretability of driving style modeling.

The input data consist of multivariate time-series data $x\in {\mathbb{R}}^{\left(N+M\right)\times T}$ derived from car-following trajectories. At each time step, $N$ and $M$ represent the self-dynamics and interaction dynamics feature dimensions, reflecting the driver’s style stability over short time intervals. By selecting appropriate dimensions of the multivariate time series, both the vehicle’s own kinematic features $x^{style}\in {\mathbb{R}}^{N\times T}$ and the interaction feature sequence with the lead vehicle $x^{style}\in {\mathbb{R}}^{M\times T}$, which further enhances the understanding of driving style. To capture the complex relationships more effectively, the input data are mapped to a higher-dimensional space through an embedding layer:

$$H_1^{self}=\tanh \left({\mathrm{W}}_{1,self}^{\mathrm{T}}{x}^{self}+b_{1,self}\right);H_1^{mutual}=\tanh \left({\mathrm{W}}_{1.mutual}^{\mathrm{T}}{x}^{mutual}+b_{1.mutual}\right)$$

(1)

where $W$ and $b$ are learnable weights and biases, and $H_1^{self}$, $H_1^{mutual}$ represent time-series data with $H$ dimensions. For the self-dynamics feature embedding $H_1^{self}$, the parameters of the $j,j\in 1,\dots ,C$ filter in the 1D convolutional network are ${\mathrm{W}}_{j,cnn}^{self}\in {\mathbb{R}}^{L\times H}$, with $L$ being the kernel size. Using $L/2$ as the convolutional filter, the result of the $j^{th}$ filter at the $i^{th}$ step is shown in Equation (2):

$$H_{i,j,cnn}^{self}=\mathrm{ReLu}\left(W_{j,cnn}^{self}{H}_{1,\left[{\displaystyle \frac{L}{2}}\left(i-1\right)+1:{\displaystyle \frac{L}{2}}\left(i-1\right)+L\right]}^{self}+b_{j,cnn}^{self}\right)$$

(2)

where $H^{self}$ term in the ReLu function represents the subsequence of length $L$ at time step t, $b_{j,cnn}^{self}$ is the learnable bias, and $H_{i,j,cnn}^{self}$ can be considered as the local embedding of the self-dynamics feature. By concatenating the features from all $C$ filters, we obtain the final embedding $H_{cnn}^{self}\in {\mathbb{R}}^{3\times C}$, with the sequence length adjusted using a convolution sequence length formula.

Similarly, the interaction dynamics feature $H_1^{mutual}$ can be obtained using the same 1D convolutional process. The proposed model employs an interaction attention mechanism to capture the relationship between the vehicle’s dynamics and the lead vehicle’s motion, reflecting the influence of the lead vehicle on the driver’s behavior through attention weights:

$$Q_i=H_{cnn,i}^{self}\cdot W_{q,i}\in {\mathbb{R}}^{3\times C}$$

(3)

$$K_i=H_{cnn,i}^{self}\cdot W_{k,i}\in {\mathbb{R}}^{3\times C}$$

(4)

$$V_i=H_{cnn,i}^{self}\cdot W_{v,i}\in {\mathbb{R}}^{3\times C}$$

(5)

where Q, K, and V represent query, key, and value, respectively, and correspond to the output of each attention head. The query and key undergo a dot product to measure their correlation, and the results are normalized using the Softmax function to generate attention weights, which adjust the model’s focus on the most relevant features for accurate driving style modeling:

$$Att\left(Q_{h,l},K_{h,l},V_{h,l}\right)=\mathrm{softmax}\left({\displaystyle \frac{Q_{h,l}{K}_{h,l}^{\mathrm{T}}}{\sqrt{C}}}\right)V_{h,l}$$

(6)

The results from all attention heads are concatenated and passed through linear mapping to obtain the fused self-dynamics features with interaction dynamics information:

$$MHAtt=\left[Att\left(Q_{1,l},K_{1,l},V_{1,l}\right),\dots ,Att\left(Q_{\left|h\right|,l},K_{\left|h\right|,l},V_{\left|h\right|,l}\right)\right]W_l^{MHATT}$$

(7)

This study employs a self-attention mechanism to improve global perception by adapting attention weights based on intrinsic relationships, with the encoder in the variational autoencoder mapping the attention mechanism output to the mean and standard deviation of the latent variables. The flattened output $H^{Attn}$ is mapped into a one-dimensional tensor $H^{F\_Attn}\in {\mathbb{R}}^{3C}$ and passed through a linear layer to reshape it. Then, two distinct linear layers are used to obtain the mean and variance of the latent variable space corresponding to the trajectory, as described in Equations (8) and (9):

$$mu=W^{mu}\left(\mathrm{ReLu}\left(W_2^{\mathrm{T}}{H}^{F\_Attn}+b_2\right)\right)+b_{mu}\in {\mathbb{R}}^Z$$

(8)

$$std=\mathrm{SoftPlus}\left(W^{std}\left(\mathrm{ReLu}\left(W_2^{\mathrm{T}}{H}^{F\_Attn}+b_2\right)\right)+b^{std}\right)\in {\mathbb{R}}^Z$$

(9)

The reparameterization trick is used to sample latent variables from a standard normal distribution, and these latent variables are used to model the driving style, as shown in Equation (10):

$$z=mu+\epsilon \cdot std\in {\mathbb{R}}^Z,\epsilon \sim \mathcal{N}\left(0,1\right)$$

(10)

Latent variables are used in the decoder to reconstruct trajectories and guide driver classification. The multilayer perceptron (MLP) decoder reduces expressiveness to enhance style feature learning and generate both trajectory reconstructions and driver predictions:

$$\widehat{x}={\mathrm{MLP}}^{\mathrm{Recon}}\left(z\right)\in {\mathbb{R}}^{(N+M)\times T}$$

(11)

$$\widehat{y}=\underset{y}{\arg \max }\left(\mathrm{softmax}\left({\mathrm{MLP}}^{class}\left(z\right)\right)\right)\in \mathbb{R}$$

(12)

The classification VAE outputs a tensor where each dimension represents the likelihood of the trajectory originating from a specific driver, with the highest index indicating the classified driver.

3.2. Loss Function and Multi-Task Learning Algorithm Design

The loss function consists of regularizing the latent variable distribution using Kullback–Leibler divergence to ensure it aligns with the prior distribution and minimizing the reconstruction error to prevent overfitting and maintain a well-structured latent space:

$${\mathrm{Loss}}^{\mathrm{KLD}}={\displaystyle \frac{1}{2}}{\displaystyle \sum _{z=1}^{\left|Z\right|}\left[{\left(m{u}_z\right)}^2+{\left(st{d}_z\right)}^2-1-\log {\left(st{d}_z\right)}^2\right]}$$

(13)

where the subscript $z$ represents the index of the dimension in the latent variable space.

The second part of the VAE loss function measures reconstruction error by calculating the difference between the reconstructed and original trajectories, typically using Mean Squared Error (MSE), to ensure accurate data generation by the decoder:

$${\mathrm{Loss}}^{\mathrm{Recon}}={\displaystyle \frac{1}{2}}{‖x-\widehat{x}‖}_2^{1/2}$$

(14)

In traditional VAE, these two loss terms are usually weighted and combined in a linear fashion to obtain the final loss function, typically expressed as the weighted sum of reconstruction error and KL divergence, as shown in Equation (15):

$${\mathrm{Loss}}^{\mathrm{VAE}}={\mathrm{Loss}}^{\mathrm{Recon}}+\beta \cdot {\mathrm{Loss}}^{\mathrm{KLD}}$$

(15)

The loss function ensures that the VAE retains data features while preventing excessive latent variable coupling, and in this study, an additional classification decoder is introduced to enhance the differentiation of driver styles by comparing the predicted and actual driver IDs:

$${\mathrm{Loss}}^{\mathrm{Class}}=-1_{\left\{y=\widehat{y}\right\}}\cdot \log \left({\mathrm{MLP}}^{\mathrm{class}}{\left(z\right)}_y\right)$$

(16)

This loss term ensures that latent variables both reconstruct trajectory data and identify the driver, with the VAE’s training objective defined by the weighted sum of reconstruction error, KL divergence, and driver classification loss:

$$\mathrm{Loss}={\omega }_1\cdot {\mathrm{Loss}}^{\mathrm{Class}}+{\omega }_2\cdot {\mathrm{Loss}}^{\mathrm{VAE}}$$

(17)

where ${\omega }_1$, ${\omega }_2$ are the weights. The weighted combination allows the model to balance accurate trajectory reconstruction and driving style differentiation, with the weight coefficients controlling the model’s focus on style and trajectory information.

The total loss consists of reconstruction, KL divergence, and driver classification losses, each with distinct objectives. Traditional methods use fixed-weight coefficients, leading to imbalances and high computational costs. This study introduces an optimization strategy, prioritizing style representation while stabilizing trajectory generation. A gradient projection method based on Lagrangian relaxation is used to update the encoder parameters, ensuring that the gradient of the primary task does not negatively impact the secondary task, as in Algorithm 1.

Algorithm 1 Gradient update method based on Lagrangian relaxation

1. INPUT: ${\mathrm{Loss}}^{\mathrm{Class}}$ and ${\mathrm{Loss}}^{\mathrm{VAE}}$ 2. OUTPUT: Gradient of Encoder $g_E$, Gradient of Classification Decoder $g_C$, Gradient of Reconstruction Decoder $g_R$ 3. Initialize: optimizer with zero_grad 4.   1. Calculate use ${\mathrm{Loss}}^{\mathrm{Class}}$ (16), Calculate VAE Loss use ${\mathrm{Loss}}^{\mathrm{VAE}}$, 5.   2. ${\mathrm{Loss}}^{\mathrm{Class}}.\mathrm{backward}\left(\right)$, save gradient $\left\{g_E^1,g_C\right\}$ for Encoder and Decoder 6.    ${\mathrm{Loss}}^{\mathrm{VAE}}.\mathrm{backward}\left(\right)$, save gradient $\left\{g_E^2,g_R\right\}$ for Encoder and Decoder, 7.   3. Update the gradient of Encoder use: $g_E=g_E^1+g_E^2·{\displaystyle \frac{\mathrm{relu}\left(-〈g_E^1,g_E^2〉\right)}{{‖g_E^1‖}^2}}$ 8.    Save the gradient of Classification Decoder and Reconstruction Decoder use: $g_C=g_C$, $g_R=g_R$ 9.   4. Optimizer. Step ()

3.3. Representation Variable Disentanglement Framework

Although VAE-derived latent variables lack clear physical meanings, this study introduces a two-stage analysis process, Trajectory-to-Latent and Latent-to-Trajectory, to map latent dimensions to driving behaviors, enhancing interpretability, discriminability, and controllability for style generation and prediction. The first stage analyzes the correlation between latent variables and driving behavior metrics from a statistical perspective. Specifically, for the $i$th trajectory sample $x_i$, we extract the values of each latent variable dimension and the corresponding $j$th physical behavior indicators, denoted as $y_{i,j}$. By inputting this sample into a pre-trained encoder, we obtain the corresponding representation vector $z_i$, with the $k$th dimension of this vector denoted as $z_{i,k}$.

The mutual information (MI) $\mathrm{I}\left(z_k,y_j\right)$ and Pearson correlation coefficient (Corr) ${\rho }_{z_k,y_j}$ between each latent variable $z_k=\underset{i}{\cup }{z}_{i,k}$ are calculated, and the physical indicators use Formulas (18) and (19):

$$\mathrm{I}\left(z_k,y_j\right)={\displaystyle \sum _i^{N}P\left(z_{i,k},y_{i,j}\right)\cdot \log \frac{P\left(z_{i,k},y_{i,j}\right)}{P\left(z_{i,k}\right)P\left(y_{i,j}\right)}}$$

(18)

$${\rho }_{z_k,y_j}={\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{i=1}^N\left(\frac{y_{i,j}-{\overline{y}}_j}{\sigma \left({\overline{y}}_j\right)}\right)\left(\frac{z_{i,k}-{\overline{z}}_k}{\sigma \left({\overline{z}}_k\right)}\right)}$$

(19)

This design combines statistical analysis and generative modeling to interpret latent variable dimensions. It identifies key dimensions through feature correlations and examines how changes in these dimensions affect driving behavior, providing a clear mapping of latent variables’ control over style features and supporting style generation tasks.

4. Experiment

4.1. Data Description and Preprocessing

The data used in this study are derived from a car-following experiment conducted on 3 January 2013, along Innovation Avenue in Hefei, China. The experimental route spans a total of 3.2 km [33]. The location of the experiment is situated on a suburban road, and there were no other traffic disturbances during the experiment. All vehicles involved in the experiment were equipped with high-precision GPS devices, collecting position and speed data at a frequency of 10 Hz. The GPS positioning error is approximately ±1 m, and the speed error is approximately ±1 km/h. The experiment was conducted with a fleet of 25 vehicles arranged longitudinally, with driver identifiers ranging from 0 to 24. During each experimental run, the lead vehicle maintained a constant preset speed, with different speed settings for each experiment, including 7, 15, 20, 25, 30, 35, 40, 45, 50, 55, and 60 km per hour. The speed of the lead vehicle could fluctuate within these bounds. The other vehicles were required to follow the lead vehicle according to their respective driving habits, with overtaking and lane changing prohibited during the experiment. More experimental details can be found in the reference.

All GPS sensors used in the experiment were subject to standardized calibration procedures. Factory specifications guaranteed a positional accuracy of ±1 m and a velocity accuracy of ±1 km/h, which were verified through static field tests before the experimental runs. To ensure temporal consistency across vehicles, each data logger was synchronized to Coordinated Universal Time (UTC) at the start of every trial using satellite-based signals. Additional cross-checks were carried out at fixed intervals during the driving cycles to confirm that clock drift remained within the sub-second range. These measures collectively reinforced the reliability of the trajectory data employed in the subsequent analysis.

The HF dataset was selected for its two major advantages: First, the dataset records long-duration trajectory data of multiple drivers under the same controlled environment, with each experiment lasting approximately 6 min. This duration allows for sufficient extraction of short-term driving behavior without resulting in overly homogeneous behavior. Second, the same driver participated in multiple rounds of experiments, creating rich internal behavioral variations within the data.

For preprocessing the raw trajectory data of the HF dataset, a series of operations was performed: A sliding window was applied to smooth the speed sequence to eliminate high-frequency noise. Differential calculations were then performed to obtain acceleration and jerk information, extracting more dynamic and continuous control features. In terms of trajectory segmentation, the original trajectories were divided into fixed-length segments, each containing 200 time steps, ensuring that each segment both contains sufficient temporal information to capture driving behavior and is not too long to avoid coarse style expression.

To effectively control the overlap between samples and ensure sufficient coverage of the style space, a fixed-interval sampling strategy was used during segmentation, where a trajectory segment was extracted every 25 frames. Unlike traditional sliding-window-based dense sampling, this method significantly reduces the temporal redundancy between samples, avoiding overfitting caused by high overlap. This approach aids in balancing the sampling distribution from a global perspective without sacrificing sample representativeness, improving the model’s ability to express the continuous style spectrum. It also helps to capture the dynamic evolution of a driver’s internal style over different time periods, providing a richer data foundation for style transfer and trajectory synthesis.

Finally, to include as many driving behaviors as possible, all experimental data with different lead vehicle speeds were used. For sample balance, only one group of data was selected for each speed setting. All trajectory segments were standardized according to the dataset size, and the data were split into training, validation, and testing sets in a 0.75:0.125:0.125 ratio.

4.2. Model Architecture and Training Hyperparameter Specification

The Style-Aware Dual-Decoder variational autoencoder (VAE) was designed to extract fine-grained and interpretable representations of driving style from car-following trajectories. The architecture comprises an encoder, two decoders, and attention modules, balancing two objectives: trajectory reconstruction and style identification. This design enables an unsupervised mapping from sequential trajectory data into a latent semantic space of driving styles. To strengthen modeling capacity, the framework integrates one-dimensional convolutional networks, interaction attention, and self-attention mechanisms, each of which contributes to improved temporal feature representation and cross-vehicle dynamic coupling.

The input trajectories were first embedded into a 128-dimensional vector space through a linear projection layer, allowing richer representation of interactions among different feature dimensions. Convolutional operations were then applied separately to self-dynamics and interaction dynamics, each convolutional layer containing 64 filters with a kernel size of 64, in order to capture local variations in vehicle motion sequences. On top of these features, a dual-layer interaction attention network with eight heads per layer and an output dimension of 64 was introduced to model the semantic relationships between the following vehicle and its leader. A self-attention module with two layers of eight heads and an output dimension of 64 was also included to capture temporal dependencies across driving events.

The latent variables generated by the encoder were passed into two decoders: one dedicated to trajectory reconstruction and the other to label classification. The reconstruction decoder employed a three-layer multilayer perceptron with hidden layers of size 256 to restore the high-dimensional input trajectories. The classification decoder also adopted a three-layer structure with hidden layers of size 128 to approximate the distribution of driver identity, used as a proxy variable to guide the latent space toward meaningful style semantics.

The entire model adopted the ReLu activation function in all hidden layers to improve nonlinear representation, and a dropout rate of 0.4 was consistently applied to mitigate overfitting risks. Optimization was performed using the Adam optimizer with an initial learning rate of 0.001 and a batch size of 128, and training was conducted for a maximum of 1000 epochs with early stopping based on validation loss. These hyperparameter settings were determined through preliminary experiments and align with established practices in sequential modeling, providing a balance between convergence stability and generalization performance. All structural parameters are summarized in

Table 1. Model architecture parameters.

Parameter Name	Description	Value
Linear Embedding Dimension	Dimension of linear embedding layer	128
Embedding Dimension of 1dCNN	Output dimension of a 1D convolutional network	64
Number of 1dCNN filters	Number of filters in a 1D convolutional network	64
Kernel Size of 1dCNN	Width of the convolution kernel	64
Number of Mutual Attn Heads	Number of heads in mutual attention layers	8
Mutual Attn Output Dimension per Head	Output dimension per head in mutual attention	64
Number of Mutual Attn layers	Number of mutual attention layers	2
Number of Self-Attention Heads	Number of heads in self-attention layers	8
Self Attn Output Dimension per Head	Output dimension per head in self-attention	64
Number of Self-Attention layers	Number of self-attention layers	2
Number of Classification Decoder layers	Number of layers in the classification decoder	3
Hidden Dimension of Classification Decoder	Hidden layer size in the classification decoder	128
Number of Reconstruction Decoder layers	Number of layers in the reconstruction decoder	3
Hidden Dimension of Reconstruction Decoder	Hidden layer size in the reconstruction decoder	256
Activation Function	Activation function used in all layers of all Decoder layers	ReLu
Dropout	Dropout rate to prevent overfitting	0.4

.

The Adam optimizer is used during training, along with a CosineAnnealingLR learning rate scheduler, and the initial learning rate is set to 5 × 10⁻⁵. Given the large model capacity and the need for training stability, the batch size is set to 128, and an early stopping mechanism (patience of 30) is employed to prevent overfitting. A fixed random seed (126) is used to ensure the reproducibility of the results. The experiments were executed on a workstation with an NVIDIA RTX 3090 GPU (24 GB memory) (Manufacturer: NVIDIA Corporation; Santa Clara, CA, USA), an AMD Ryzen 9 5950X CPU, and 128 GB RAM (Manufacturer: Advanced Micro Devices, Inc.; Santa Clara, CA, USA). Under this computational environment, a complete training cycle with a maximum of 1000 epochs required approximately 6.5 h.

Table 2. Training hyperparameters.

Parameter Name	Description	Value
Epoch Num	Total number of training epochs	1000
Learning Rate	Initial learning rate value	5 × 10−5
Learning Rate Scheduler	Strategy for adjusting the learning rate	CosineAnnealingLR
Optimizer Type	Gradient optimization algorithm	Adam
Batch Size	Sample Size per training iteration	128
Early Stopping Patience	Epochs to wait before stopping training	30
Random Seed	Seed for reproducible initialization	126

provides all the training hyperparameter configurations for model reproducibility and comparison.

To statistically validate that driver labels correspond to distinct behavioral patterns, a one-way analysis of variance (ANOVA) was performed separately on each car-following indicator, with driver identity serving as the grouping factor. For each indicator, the null hypothesis H₀ stated that there was no significant difference in the mean values across drivers, while the alternative hypothesis H₁ stated that at least one driver exhibited a significantly different mean value. The tested indicators included minimum time gap, acceleration variance, and following efficiency, among others. In every case, the ANOVA results rejected the null hypothesis at the 1% significance level (p < 0.01), confirming that the distribution of each behavioral metric differed systematically across drivers. These consistent findings indicate that the driver labels reflect statistically distinguishable driving modes rather than random fluctuations, thereby validating their suitability as proxy variables for extracting latent driving style representations.

It should be noted that to assess the stability of the proposed framework under different random initializations, the training procedure was repeated five times with independent random seeds. The performance metrics, including accuracy, precision, recall, and F1-score, exhibited standard deviations below 0.452% across runs. This low variance confirms that the reported improvements are consistent and do not rely on a particular initialization, thereby reinforcing the robustness of the empirical findings.

4.3. Evaluation Metrics, Baseline Model, and Trajectory Features

To comprehensively assess the model’s ability to distinguish and explain driving style representations, this section will unfold in three parts: First, we consider the evaluation metrics used to measure Driver Identification ability. Second, the baseline model design logic employed in this study includes variants of our model with different KL divergence coefficients and several representative comparative models. The trajectory behavior metrics system was extracted for the driving style interpretability analysis, which will assist in the subsequent interpretation of latent variable dimensions in terms of behavior semantics. Considering that driving styles exhibit strong individual differences between drivers, the recognition performance is quantified through four commonly used metrics: accuracy, precision, recall, and F1-score. Calculation methods are presented in Equations (20)–(23).

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$

(20)

$$\mathrm{MacPrecision}={\displaystyle \frac{1}{C}}\cdot {\displaystyle \sum _{i=1}^C\frac{{\mathrm{TP}}_i}{{\mathrm{TP}}_i{+\mathrm{FP}}_i}}$$

(21)

$$\mathrm{MacRecall}={\displaystyle \frac{1}{C}}\cdot {\displaystyle \sum _{i=1}^C\frac{{\mathrm{TP}}_i}{{\mathrm{TP}}_i{+\mathrm{FN}}_i}}$$

(22)

$$\mathrm{MacF}1={\displaystyle \frac{1}{C}}\cdot {\displaystyle \sum _{i=1}^C\frac{2\cdot {\mathrm{MacPercision}}_i\cdot {\mathrm{MacRecall}}_i}{{\mathrm{MacPercision}}_i{+\mathrm{MacRecall}}_i}}$$

(23)

Accuracy measures the proportion of correctly classified samples, which is the most straightforward performance reflection. Precision describes the proportion of samples identified as belonging to a specific driver that are correctly classified, reflecting the model’s reliability. Recall quantifies the proportion of the total samples of a given driver that are correctly identified, emphasizing the model’s sensitivity. The F1-score and the harmonic mean of precision and recall provide a balanced reflection of classification performance. These metrics serve as a solid quantitative foundation for subsequent style clustering and individual behavior modeling.

For the evaluation of the model’s representation interpretability and generalization performance, this study further sets up multiple baseline models to conduct comparative experiments. First, within our model structure, to examine the impact of the latent variable distribution regularization term on the interpretability of the representation dimensions, we employed the β-VAE architecture as the base framework and constructed several control experiments with different KL divergence weight coefficients (β). The β parameter, as a tuning term, controls the level of consistency between the latent space and the standard normal distribution. Smaller values of β focus more on trajectory reconstruction quality but may cause latent variable coupling and a loss of interpretability. Larger values of β emphasize latent space regularization, improving the disentanglement and separation of dimensions but may sacrifice some generation and validation accuracy. Therefore, through experiments with different β values, we aim to explore the optimal balance between identification performance, style interpretability, and trajectory reconstruction ability.

Additionally, we introduce several typical models to evaluate the performance advantages of our proposed model in the driving style extraction task. These comparison models include traditional machine learning methods and various deep neural network architectures, all using Driver Identification tasks as the evaluation criterion, allowing us to measure the discriminative ability of style representations from a classification accuracy standpoint. The following is a brief introduction to the baseline models:

• SVM: Constructs an optimal separating hyperplane to perform classification.
• XGBoost: Uses ensemble learning strategies to enhance modeling of nonlinear relationships.
• NN (MLP): A basic fully connected neural network that flattens trajectory data along the time dimension and inputs them directly into a multilayer perceptron for driver classification via nonlinear mappings.
• Transformer: Does not distinguish between self-dynamics and interaction dynamics features, inputting all trajectory data into a self-attention mechanism to learn style representations by capturing global dependencies across time steps.
• LSTM-Transformer: Uses a Long Short-Term Memory (LSTM) network to extract sequential features of the trajectory, which are then fed into a Transformer module for further modeling of temporal context dependencies. The LSTM model consisted of a single recurrent layer, which was used to capture temporal dependencies in driving behavior sequences.
• CNN-Transformer: First applies 1D convolution (1D-CNN) to extract local temporal features, which are then input into a Transformer network to enhance global relationship modeling.

It is worth noting that the above neural network structures do not distinguish between self-dynamics and interaction dynamics features, nor do they explicitly model the influence of the lead vehicle on driving behavior. All attention mechanisms are implemented as purely self-attention mechanisms. For all Transformer-based models, a two-stage training scheme was applied. During the pre-training stage, the models were trained on a large-scale, unlabeled naturalistic driving trajectory dataset using tasks of next-step vehicle state prediction, enabling the acquisition of general representations of driving dynamics. In the fine-tuning stage, the pre-trained parameters were adapted to the experimental dataset to address the specific objective of driving style characterization. By comparing with our proposed model, which introduces interaction attention mechanisms, we can effectively analyze the impact of different feature organization methods and modeling granularities on driving style representation performance.

In terms of driving style interpretability, we base the evaluation on a behavior metrics system with clear physical and engineering meanings, extracting 15 behavior feature indicators from trajectory segments, as shown in

Table 3. Driving behavior indicators.

Category	Feature Name	Formula	Physical Meaning
Driving Aggressiveness 1	Acceleration Intensity Index	${\displaystyle \frac{1}{T}}{\displaystyle \sum _t\left|a_t\right|}$	Measures the overall intensity of acceleration and deceleration
	Hard Acceleration Frequency	${\displaystyle \frac{1}{T}}{\displaystyle \sum _t{1}_{\left[a_t>2.5\right]}}$	Proportion of time spent on hard acceleration
	Peak Acceleration Rate of Change	${\max }_t\left({\displaystyle \frac{\Delta a_t}{\Delta t}}\right)$	Maximum rate of change in acceleration (jerk)
Driving Smoothness	Coefficient of Variation of Acc.	${\displaystyle \frac{{\sigma }_a}{{\mu }_a}}$	Ratio of acceleration fluctuations to its mean value
	Root Mean Square of Jerk	$\sqrt{{\displaystyle \frac{1}{T}}{{\displaystyle \underset{0}{\overset{T}{\int }}\left(\frac{da\left(t\right)}{dt}\right)}}^{2}dt}$	Overall fluctuation in the acceleration rate of change
	Acceleration Stability Duration	${\displaystyle \frac{1}{T}}{\displaystyle \sum _t{1}_{\left[{\mathrm{a}}_t<0.5\right]}}$	A measure of how long the vehicle maintains steady velocity
Car-Following Safety	Minimum Time Gap	${\min }_t\left({\displaystyle \frac{\Delta x_t}{\Delta v_t}}\right)$	Smallest distance-time ratio throughout the trip
	Min Safety Margin	${\displaystyle \frac{1}{T}}{\displaystyle \sum _t{1}_{\left[\mathrm{TTC}\left(t\right)<3\right]}}$	Time proportion with Time-to-Collision (TTC) < 3 s
	Covariance of velocity difference and Distance	$\mathrm{Cov}\left(\Delta v_t,\Delta x_t\right)$	Coordination between relative speed and headway
Traffic Efficiency	Average Following Efficiency	${\displaystyle \frac{1}{T}}{\displaystyle \underset{0}{\overset{T}{\int }}\frac{v_t}{\Delta x_t}}dt$	Output speed per unit of distance
	Speed Recovery Time	$t_{\mathrm{recover}}-t_{\mathrm{decel}}$	Time required to reach target speed after deceleration
	Acceleration–Speed Phase Lag	$\underset{\tau }{\arg \max }\mathrm{Corr}\left(a_t,v_{t+\tau }\right)$	Temporal coordination between acceleration decisions and speed states
Higher-Order Indicators	Driving Style Entropy	$-{\displaystyle \sum _{t}p\left(a_t\right)\log }p\left(a_t\right)$	Entropy level of the acceleration distribution
	Safety-Efficiency-Stability Index	The weighted sum of all the above indicators.	Trade-off between speed efficiency and safety risk
	Trajectory Smoothness	$\sqrt{{\displaystyle \frac{1}{T}}{{\displaystyle \underset{0}{\overset{T}{\int }}\left(\frac{d^{2}a\left(t\right)}{d{t}^2}\right)}}^{2}dt}$	Second-order difference of jerk

¹ It should be noted that the categories of aggressive, normal, and conservative driving were not assigned in advance but were introduced as an interpretive framework. The classification was grounded in measurable indicators: aggressive driving corresponds to shorter time headways and higher following efficiency, conservative driving to larger margins and lower efficiency, and normal driving to intermediate values. This framework facilitates a clearer interpretation of the latent dimensions in terms of recognizable driving tendencies.

. These indicators are categorized into five major groups: driving aggressiveness, driving smoothness, car-following safety, traffic efficiency, and higher-order composite indicators. The indicators not only have clear physical explanations at the behavioral level but are also widely used in practical engineering tasks such as driving behavior interpretation, collision prediction, and intelligent driving control, thereby forming the basic basis for semantic interpretation of style representations.

5. Results

5.1. Model Performance

To verify whether the proposed representation can distinguish between different driving styles, the Driver Identification task is introduced as an indirect evaluation metric. Although this study does not directly rely on style labels, the assumption is that each driver demonstrates both consistency and individuality in behavioral tendencies. If the learned representation can effectively differentiate among drivers, it implies that the latent space captures salient and discriminative aspects of driving style rather than noise or incidental features. In this sense, classification accuracy serves not only as a straightforward test of prediction performance but also as an indicator of how well the representation preserves stylistic variations embedded in trajectory data. A higher recognition rate reflects that the extracted features encode stable behavioral signatures, thereby supporting the validity of the proposed framework for style-oriented modeling. Conversely, misclassifications may signal overlaps in driving tendencies across individuals, showing the challenge of modeling subtle intra-class similarities and inter-class differences in naturalistic driving data.

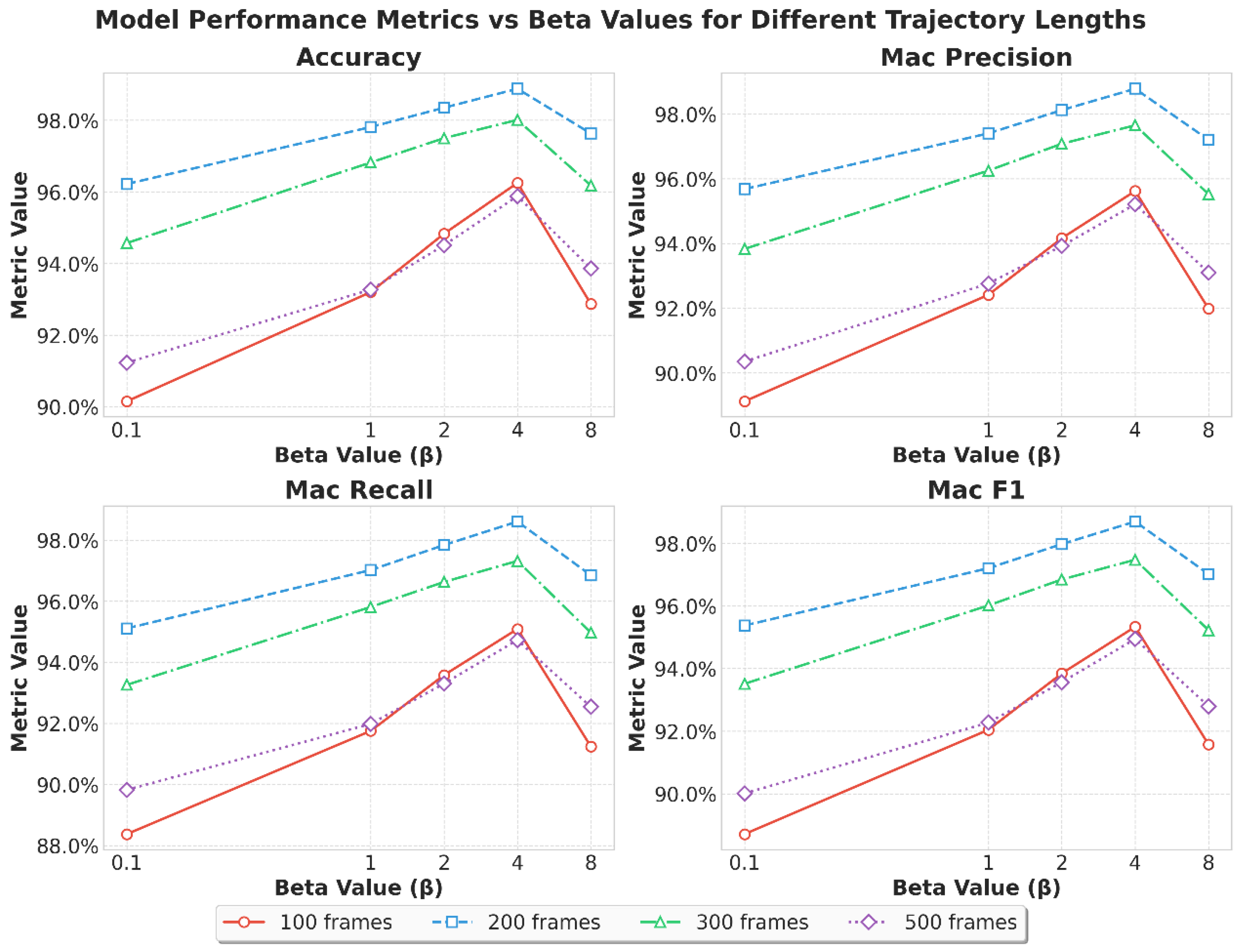
To assess the model’s performance in the classification task using the extracted driving style representations, hyperparameter selection is analyzed across two core variables: the input trajectory length, with candidate intervals of 100, 200, 300, and 500 time steps, and the KL divergence regularization coefficient (Beta) in the variational autoencoder, with values of 0.1, 1, 2, 4, and 8. The trajectory length determines how much temporal context is retained: shorter sequences may capture only local maneuvers, whereas longer sequences provide richer dynamics but risk reducing short-term behavioral signals. Similarly, the Beta coefficient regulates the trade-off between disentangling meaningful latent dimensions and maintaining reconstruction fidelity. A low Beta may lead to overfitting by prioritizing reconstruction, while a high Beta may enforce excessive regularization and suppress expressive capacity. By systematically evaluating different combinations, the results reveal how the representation balances temporal richness with latent space structure. Identifying the optimal configuration ensures that subsequent analyses rest on a stable foundation and also demonstrates the sensitivity of representation quality to these key hyperparameters, which is an important consideration for deploying the framework across diverse traffic scenarios.

Figure 2 presents the identification performance of the proposed model under different combinations of trajectory length and Beta values, evaluated using accuracy, precision, recall, and F1-score. Each subplot uses the horizontal axis to denote the Beta value and the vertical axis to denote the metric value, with the four curves representing different trajectory lengths. The results reveal that a trajectory length of 200 achieves the most stable and highest overall performance, with accuracy reaching 0.988 at Beta = 4. This indicates that a 200-length input window balances temporal context and variability, capturing sufficient behavioral fluctuations without excessive averaging. In contrast, a trajectory length of 100 consistently produces the weakest results, suggesting that too short an observation window fails to cover critical driving dynamics, thereby reducing the model’s ability to separate styles. A trajectory length of 500, while providing more data, performs worse than 200 or 300, as the longer horizon dilutes instantaneous behavioral differences, making style-specific signals less distinguishable. The 300-length model performs close to the 200-length case but shows slight degradation at higher Beta values, implying that while mid-term sequences reflect driver behavior, they are more sensitive to strong disentanglement constraints. These findings emphasize that input length directly governs the richness and clarity of the behavioral cues available to the model.

The trend of Beta values shows a consistent turning-point phenomenon across all metrics. When Beta is below 4, performance is uniformly poor, as weak KL divergence constraints lead to entangled latent variables with limited separability, making style distinction unreliable. As Beta increases, performance improves steadily, reaching an optimal point at Beta = 4, where the model preserves sufficient behavioral information while enhancing disentanglement. This configuration provides both clear latent semantics and strong classification results, demonstrating the critical balance between information retention and the independence of latent dimensions. However, beyond Beta = 8, the metrics decline, demonstrating that excessive regularization reduces latent variable capacity and suppresses subtle style details, ultimately lowering separability. This pattern confirms that appropriate disentanglement strength is essential for uncovering meaningful structure in driving styles.

The experimental results in

Table 4. Performance comparison across models ¹.

Model	Accuracy	Mac Precision	Mac Recall	Mac F1
SVM(RBF-Kernel)	0.7836	0.7721	0.7689	0.7702
XGBoost	0.8619	0.8523	0.8476	0.8494
NN(MLP)	0.8024	0.8037	0.7962	0.7993
Transformer	0.9027	0.8964	0.8921	0.8938
LSTM-Transformer	0.9265	0.9218	0.9193	0.9202
CNN-Transformer	0.9412	0.9376	0.9348	0.9359
Proposed Model	0.9888	0.9878	0.9861	0.9869

¹ To confirm the robustness of the reported performance, the training and evaluation were repeated across five independent runs with different random seeds. Performance metrics were averaged across these runs, yielding mean accuracies of 98.88% ± 0.463%, mean precisions of 98.78% ± 0.489%, mean recalls of 98.61% ± 0.471%, and mean F1-scores of 98.69% ± 0.468%. These small variances across runs confirm that the proposed framework produced consistent and reproducible outcomes, independent of initialization.

identify the optimal configuration as a trajectory length of 200 and a Beta value of 4. This setting enables the model to capture essential driving fluctuations while maintaining a robust and interpretable latent structure, leading to excellent classification stability and style distinction. Beyond its immediate numerical performance, this configuration establishes a reliable foundation for subsequent analyses, including the examination of driver heterogeneity and the interpretability of the learned representations. It demonstrates that careful calibration of temporal window size and disentanglement strength is crucial for extracting meaningful and actionable driving style features in intelligent transportation research.

The optimal trajectory length, model hyperparameters, and external baseline models were compared, with the results shown in Table 4. Our model performs the best, particularly compared to various neural networks. As described in Section 4.3, these networks lack the distinction between self-dynamics and interaction dynamics, leading to a decrease in model accuracy.

5.2. Driving Behavior Heterogeneity

In Section 5.1, it was verified that the extracted representations effectively distinguish between different drivers. However, whether these representations truly reflect the actual driving behaviors of drivers still requires further investigation. To thoroughly validate the effectiveness of these representations, it is necessary to examine whether they can reflect the heterogeneity of driving behaviors, i.e., the behavioral differences both between different drivers and within the same driver under varying environments.

5.2.1. Driver External Heterogeneity

Driver external heterogeneity refers to the behavioral differences exhibited by different drivers. The validity of the clustering results was further examined using two internal evaluation metrics. The silhouette coefficient, defined on the interval [−1, 1], measures how similar each sample is to its own cluster compared with other clusters, where values closer to 1 indicate higher intra-cluster cohesion and clearer inter-cluster separation. The Davies–Bouldin index is a non-negative score that evaluates the average ratio of within-cluster dispersion to between-cluster separation, where lower values correspond to more distinct clusters. The clustering analysis yielded a silhouette coefficient of 0.624 and a Davies–Bouldin index of 0.317. Relative to K-means clustering, these results correspond to improvements of 13.862% and 16.437%, respectively, demonstrating that the proposed framework produced more reliable and well-differentiated clusters in the latent driving style space.

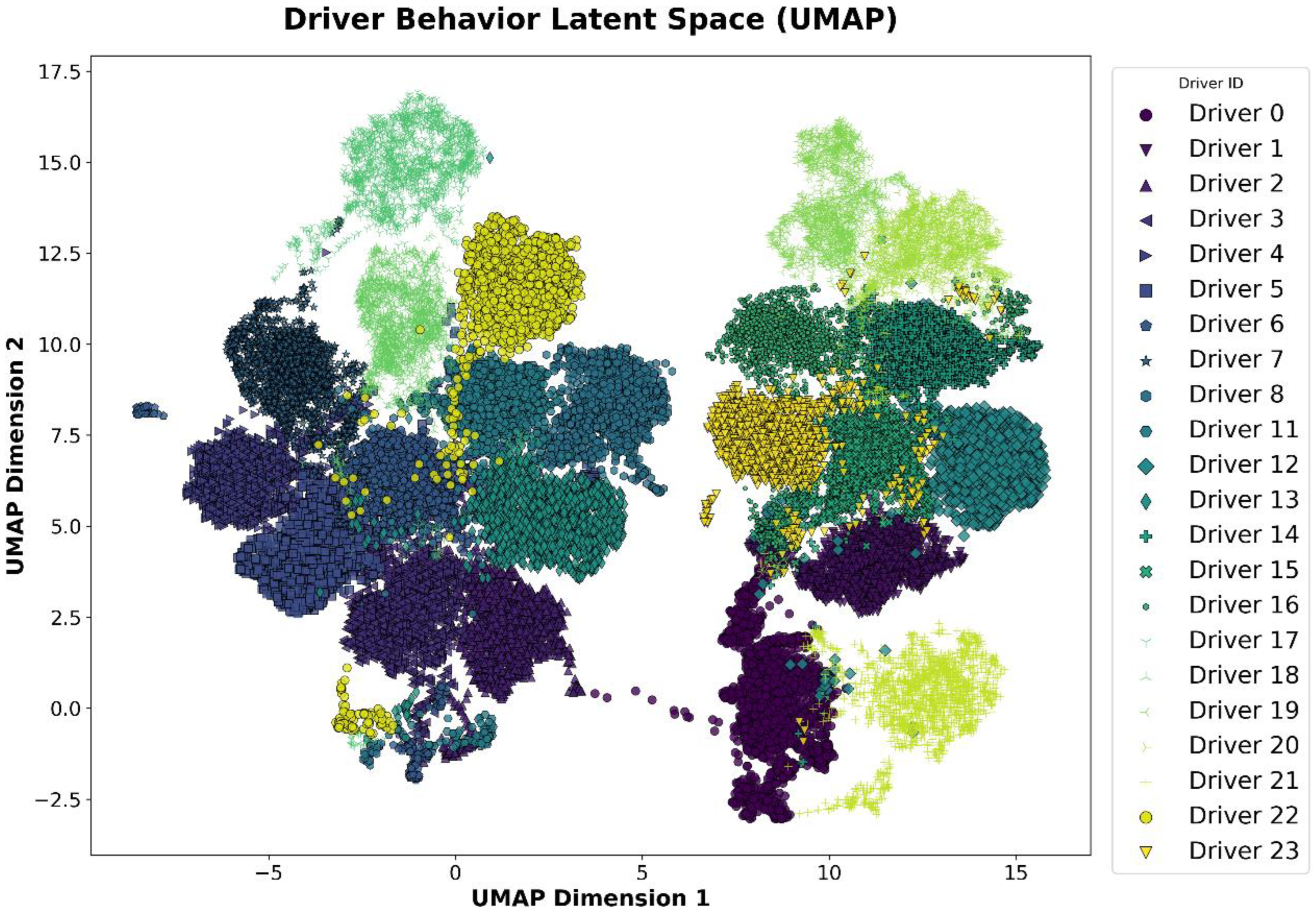
To verify whether the learned representations can effectively distinguish between the behaviors of different drivers, dimensionality reduction was applied to the driver style representations, and the reduced representations were used for driver differentiation. Specifically, this study employed the UMAP (Uniform Manifold Approximation and Projection) algorithm to reduce the dimensionality of the style representations. The aim was to map the high-dimensional driver style representations into a low-dimensional space to visually showcase the differences between driver styles. To assess the stability of the UMAP projection, the algorithm was executed 10 times with independent random seeds. Across these runs, the driver clusters exhibited consistent separation in the latent space, while the relative geometric layout varied slightly due to the stochastic nature of the embedding process. This repetition confirmed that the clustering patterns were robust and reflected inherent differences in driving style representations rather than random initialization effects.

Figure 3 presents the results after dimensionality reduction using UMAP. It is clear that the reduced representations are significantly separated in the two-dimensional space, indicating that the learned representations can effectively distinguish between different drivers’ styles. During the UMAP reduction, different colors represent different drivers, and the distribution of each point reflects the position of that driver in the style space. From these results, the extracted style representations not only distinguish between drivers but also reveal the behavioral pattern differences among various drivers to some extent.

5.2.2. Driver Internal Heterogeneity

In addition to external heterogeneity, driver internal heterogeneity should not be overlooked. Internal heterogeneity refers to the behavioral differences exhibited by the same driver under different environmental conditions. To verify whether the representations can adapt to and reflect the behavioral variations in the same driver in different scenarios, we analyzed the behavior of the same driver from multiple perspectives.

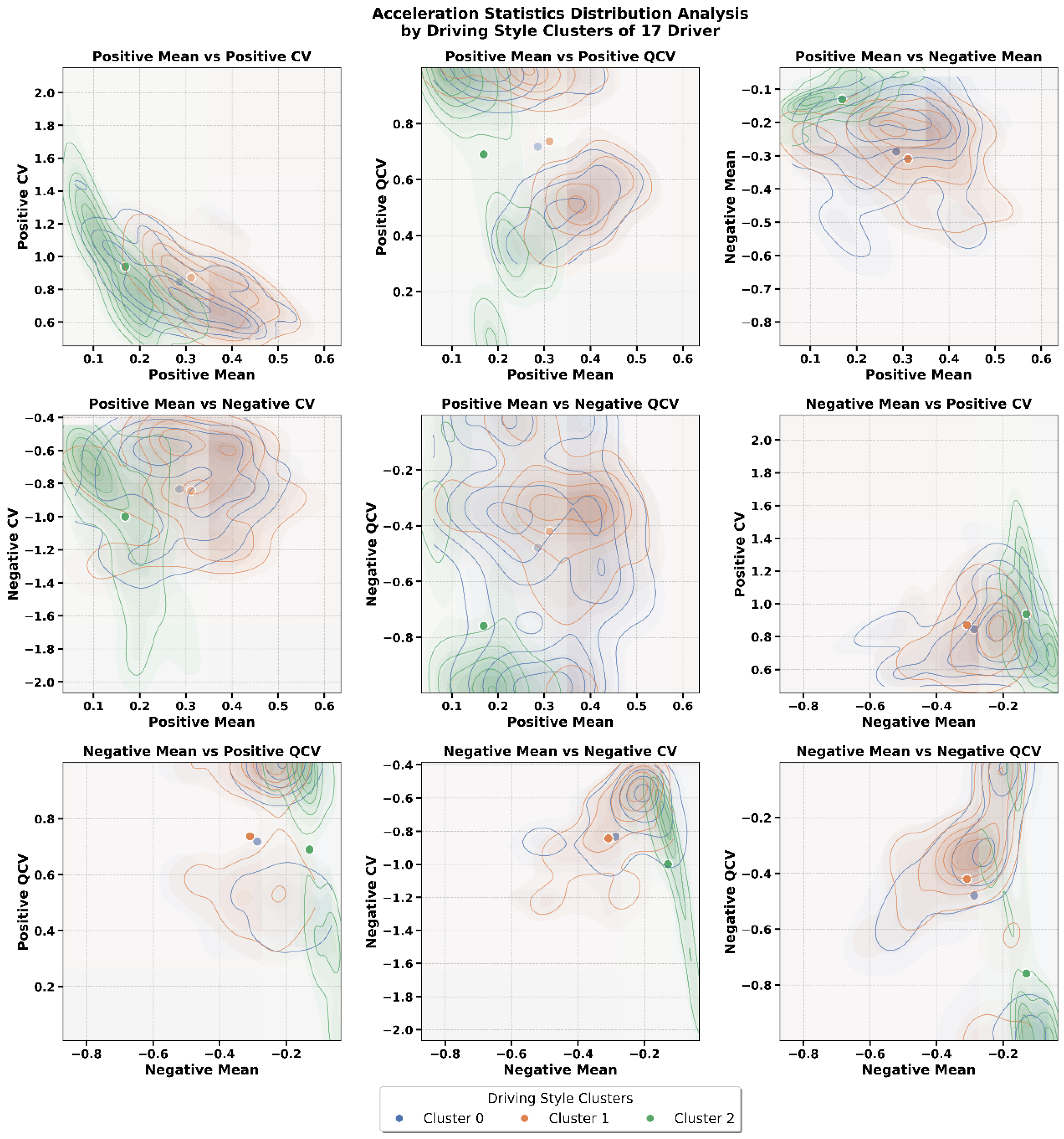
First, we extracted the driving behavior representations of the same driver under different experimental conditions and performed Gaussian Mixture Clustering on the data within these subspaces. The optimal number of clusters for each set was determined using silhouette coefficients, which enabled the classification of a single driver’s behavior under different scenarios. For each cluster, the mean acceleration, acceleration coefficient of variation, and interquartile coefficient of variation were statistically analyzed. These statistics help in analyzing the behavioral differences between clusters and comparing the variations across these distributions.

Figure 4 shows the visualization of acceleration distributions for Driver 17. The acceleration feature distribution for this driver was divided into three categories, indicating that Driver 17’s behaviors were classified into three groups. Despite all the trajectories originating from the same driver, significant behavioral differences exist between categories, particularly between the second and first groups. A closer examination reveals that the first group is characterized by mild acceleration and deceleration, corresponding to conservative and smooth driving. The second group exhibits frequent changes in acceleration, suggesting a more aggressive response style in dynamic traffic contexts. The zero class shows irregular fluctuations with higher peaks, which may reflect abrupt maneuvers under unexpected conditions.

Each category of trajectories, thus, captures a distinct aspect of the driver’s behavior, demonstrating that even a single driver displays multiple operational modes depending on situational demands. This internal variability demonstrates the heterogeneity of driving behavior and underscores the importance of capturing intra-driver differences in addition to inter-driver distinctions. Through these analyses, it is confirmed that the extracted representations not only separate different drivers’ styles but also reveal meaningful substructures within the same driver’s behavior, thereby providing a more fine-grained and realistic characterization of driving style.

5.3. Driving Style Representation Disentanglement

5.3.1. Correlation Between Driving Style Representation Dimensions and Raw Trajectory

The physical behavioral semantics of the learned driving style representations are further explored. From a statistical perspective, we analyze the coupling relationship between each representation dimension and the raw trajectory behavioral indicators. Specifically, we treat each latent variable in the driving style representations learned by the VAE model as the object of study. We calculate the mutual information and Pearson correlation coefficient between each latent variable and several trajectory features with physical meanings, in order to assess the potential of these latent variables for physical explanation in style modeling. In the calculation process, mutual information measures the nonlinear dependency between variables, while Pearson correlation quantifies their linear relationship strength.

Table 5. Correlation between driving style representation dimensions and raw trajectory features.

Feature Name	Mutual Information	Pearson Correlation	Top Representation Dimension
Acceleration Intensity Index	0.0519	0.1464	31, 22, 24
Hard Acceleration Frequency	0.0142	0.0760	28,17,31
Peak Acceleration of Change	0.1182	0.1904	4, 24, 20
Coefficient of Variation of Acc.	0.0583	0.1449	31, 22, 17
Root Mean Square of Jerk	0.0568	0.2037	4, 24, 20
Acceleration Stability Duration	0.0480	0.1351	28, 21, 31
Minimum Time Gap	0.0922,	0.0742	28, 22, 21
Min Safety Margin	0.1029	0.1136	22, 21, 28
Covariance of velocity difference and Distance	0.0264	0.0255	21, 0, 28
Average Following Efficiency	0.0453	0.0637	22, 21, 9
Speed Recovery Time	0.0123	0.0849	22, 14, 31
Acceleration–Speed Phase Lag	0.0123	0.0849	22, 14, 31
Driving Style Entropy	0.0383	0.1478	24, 4, 20
Safety–Efficiency–Stability Index	0.0216	0.0236	22, 23, 8
Trajectory Smoothness	0.0510	0.2021	24, 4, 20

presents the core results of this statistical analysis. We selected 15 physical behavior indicators that cover five categories: driving aggressiveness, smoothness, safety, efficiency, and higher-order behavior features. For each indicator, the three most strongly correlated style dimensions are listed.

The results show that most behavioral indicators have significant coupling relationships with specific latent dimensions, and these associations exhibit consistent numerical patterns. For instance, the “maximum acceleration rate of change” demonstrates a mutual information value of 0.1182 and a Pearson coefficient of 0.1904 with dimensions 4, 24, and 20, suggesting that instantaneous variations in acceleration are strongly influenced by these style dimensions. Similarly, “jerk root mean square” relies on the same set of dimensions, showing that short-term oscillations in acceleration are governed by a consistent subset of latent variables. These findings imply that the model does not distribute behavioral semantics randomly across the latent space; instead, it systematically aligns certain behavioral tendencies with specific style dimensions. Such alignment increases the interpretability of the representation and provides a structured foundation for style manipulation tasks.

Further analysis of frequency distributions reveals that dimensions 22, 24, and 31 frequently recur across multiple behavioral indicators, making them dominant style factors with broad influence. Dimension 22 is consistently associated with indicators, such as “minimum time gap,” “minimum safety margin,” “following efficiency,” and “acceleration variance coefficient,” thereby defining a stable “safety–efficiency” axis. Dimension 24 strongly regulates “trajectory smoothness,” “jerk RMS,” and “style entropy,” suggesting its role in moderating comfort and behavioral complexity. Dimension 31, on the other hand, is linked with “acceleration intensity” and “recovery time,” characterizing aggressiveness and responsiveness in car-following behavior. These high-frequency dimensions demonstrate clear semantic projections onto specific behavioral categories, serving as key variables for controlling and transferring driving styles. The emergence of such dominant dimensions reflects the model’s ability to disentangle the latent space into meaningful behavioral substructures rather than arbitrary encodings.

From the perspective of indicators, behavioral attributes can also be mapped onto clusters of style dimensions, reinforcing the semantic interpretability of the representation. For example, “driving aggressiveness” is primarily reflected by acceleration intensity and hard acceleration frequency, which correlate with dimensions 31, 28, and 17. This indicates that aggressiveness is tied to the driver’s control intensity and psychological thresholds in decision making. By contrast, “driving smoothness” indicators such as jerk and trajectory continuity are predominantly associated with dimensions 4, 24, and 20, suggesting that these dimensions encode the temporal regularity and comfort level of operations. Safety-related metrics, including minimum time gap and risk time gap ratio, concentrate around dimensions 22, 21, and 28, confirming the model’s sensitivity to car-following safety margins. Meanwhile, efficiency-related measures such as “speed recovery time” and “following efficiency” are largely regulated by dimensions 22, 14, and 31, reflecting the adaptive delay and compensation mechanisms in longitudinal driving.

The influence of latent dimensions on behavioral indicators shows clear clustering and specialization, indicating that the learned style representation possesses strong semantic separation properties. This clustering pattern suggests that the framework is not only capable of distinguishing drivers at the classification level but also of constructing latent behavioral mappings in the absence of explicit style labels. Such properties are critical for subsequent applications in personalized driving modeling, style transfer, and the development of adaptive strategies in intelligent transportation systems.

5.3.2. Dimensional Scanning of Driving Style Representations

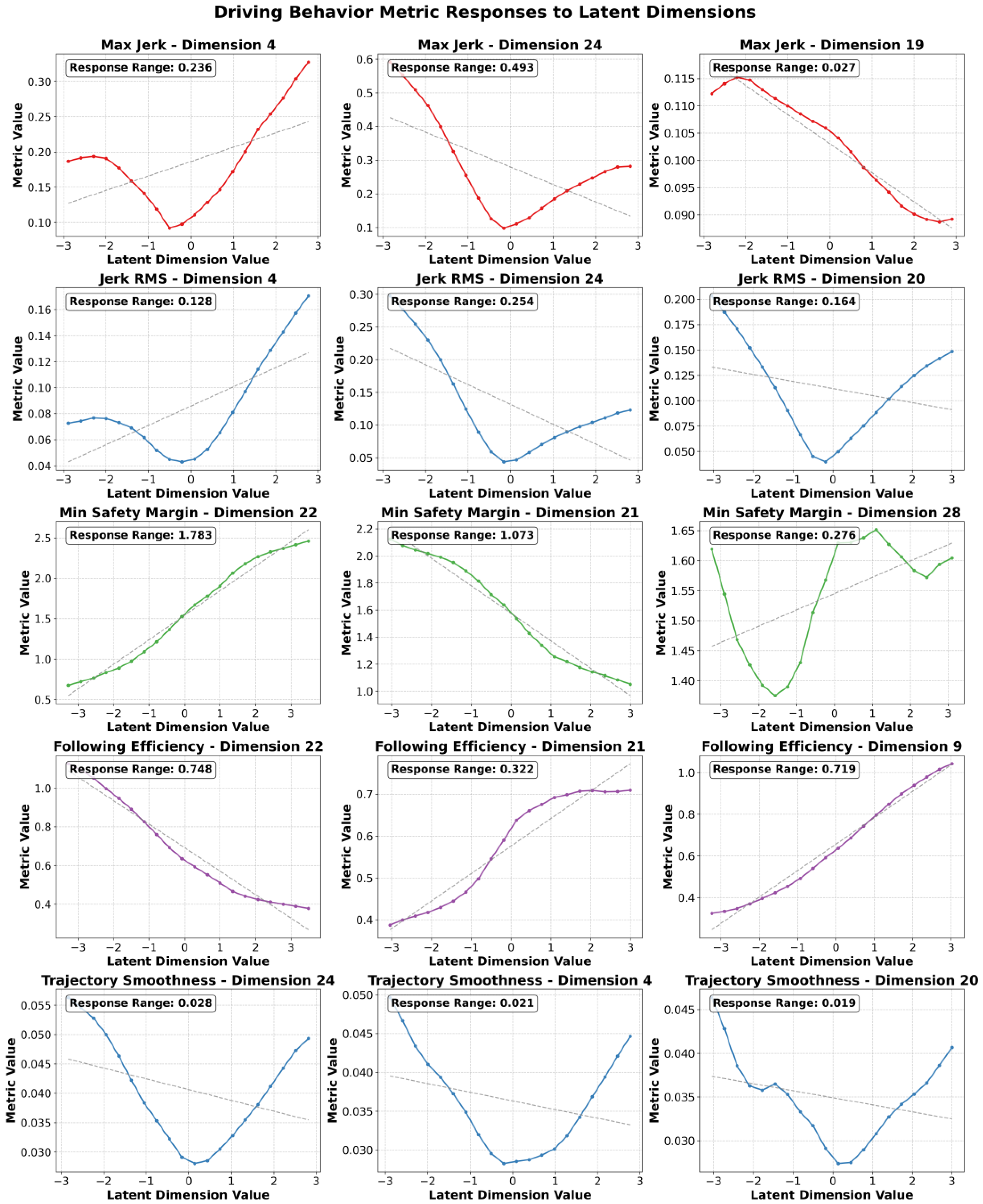
To further explore the physical behavioral semantics of the learned driving style representation, this section investigates the quantitative regulation patterns of each dimension in the latent space on driving behavior from a statistical perspective. The experiment uses a unidimensional scanning strategy: the non-target dimensions are fixed at their mean values, and 20 values are uniformly sampled within ±3 standard deviations of the target dimension. These values are then passed through the decoder to generate corresponding trajectories, from which 15 behavioral indicators are calculated. This design eliminates the interference from dimensional coupling through a controlled variable approach, enabling a direct observation of the independent impact of the target dimension on driving behavior. For the five categories of features, the ones with the highest average mutual information (MI) are selected, and their corresponding three most related latent variable dimensions are scanned, resulting in the feature variation scan plots for the generated trajectories, as shown in Figure 5.

To quantitatively assess the robustness of the dimensional scanning results, the coefficient of variation (CV) was calculated for the distributions of curves across drivers under different latent dimensions. Among the jerk-related curves, such as “Max Jerk—Dimension 24” and “Jerk RMS—Dimension 20”, the variability was moderate, with CV values ranging from 7.412% to 8.305%, indicating that short-term acceleration fluctuations were represented consistently but not identically across drivers. The safety efficiency trade-off curves, including “Min Safety Margin—Dimension 22” and “Following Efficiency—Dimension 22”, exhibited the highest variability, with CV values of 11.274% and 10.863%, respectively, reflecting substantial heterogeneity in spacing strategies and following efficiency preferences among drivers. By contrast, the smoothness-related curves, for example, “Trajectory Smoothness—Dimension 24”, displayed the lowest variability, with CV values around 5.328%, suggesting that comfort-oriented responses were relatively stable across drivers. The CV values of the curves ranged from 5.013% to 11.274%, all within a controlled range. These findings confirm that although certain latent dimensions revealed stronger inter-driver differences than others, the dimensional scanning analysis yielded robust and interpretable curve patterns across multiple drivers.

The experimental results also reveal four key regulation patterns between latent variables and driving behavior:

(1)

Linear Curve Control: For example, the maximum acceleration decreases as z19 increases, while z22 simultaneously controls the minimum time gap and following efficiency. This phenomenon also suggests that z22 is a trade-off dimension. When z22 increases, the minimum safety distance decreases by 18%, indicating improved safety, while the speed recovery time decreases by 23%, indicating a reduction in efficiency. This demonstrates that the essence of this dimension is a safety–efficiency trade-off decision factor.

(2)

Linear Non-Saturation Control: For example, z21 controls the following efficiency, which saturates in the intervals [−3, 1] and [2, 3], but in the interval [−1, 2], the following efficiency rapidly increases as z21 increases. This suggests that the adjustable range needs to be adjusted based on the degree of change in the dimension.

(3)

U-shaped Curve Control: It is observed that the feature values of many trajectories decrease and then increase with the change in certain dimensions. This means that when adjusting these features, the monotonicity of the dimension needs to be defined.

(4)

Irregular Curve Control: For some features, their changes do not show a clear monotonic relationship with the dimension, such as the minimum safety distance feature with z28. If this feature needs to be adjusted, its monotonicity must be distinguished. However, as shown in Figure 5, the trajectory feature change range controlled by z28 (0.276) is much smaller than that of z22 (1.783) and z21 (1.073). This phenomenon suggests that when adjusting dimensions to generate more detailed trajectory curves, there are key dimensions that should be prioritized.

6. Discussion

This study proposed an unsupervised learning framework based on a dual-decoder variational autoencoder to extract fine-grained and interpretable driving style representations from car-following trajectories. The framework effectively captured latent behavioral factors without relying on predefined style categories, enabling the identification of both inter-driver heterogeneity and intra-driver variability. The learned representations provided a meaningful view into the underlying dynamics of driver behavior, showing their potential utility in intelligent transportation systems. The results demonstrated the feasibility of deriving driving style representations under suburban expressway conditions. The framework successfully associated micro-level trajectory dynamics with broader driving style tendencies. The robustness of the representations was confirmed by repeated experiments across multiple random initializations, as well as clustering validity analyses that showed stable and meaningful group structures. These findings support the capacity of the framework to produce consistent and reproducible results.

The analysis revealed important limitations. The experimental setting was restricted to suburban expressways, where traffic flow conditions are relatively controlled and homogeneous. While this design reduces external variability and allows clearer observation of car-following behaviors, it inevitably raises questions regarding the generalizability of the findings to more complex urban environments. Urban traffic is characterized by frequent interactions at intersections, diverse vehicle types with different performance characteristics, mixed traffic involving non-motorized modes, and higher traffic densities that create rapid fluctuations in speed and headway. These conditions introduce substantial variability and behavioral heterogeneity that may not be adequately captured under the current experimental constraints. Consequently, the applicability of the learned representations to dense city networks, multimodal traffic flows, and highly dynamic driving contexts remains uncertain. Addressing this limitation will be crucial for extending the framework to real-world applications, particularly in areas such as adaptive traffic management, safety assessment, and human-centered autonomous driving, where robustness across varied environments is essential. Future research should, therefore, aim to validate and refine the framework using naturalistic driving datasets collected from diverse road types, including urban arterials, intersections, and congested corridors, to ensure broader external validity.

Another limitation lies in the manual interpretation of latent dimensions, which inevitably introduces subjectivity and constrains scalability. Although the semantic assignment of latent factors was grounded in measurable behavioral indicators, the interpretation process relied on post hoc analysis rather than an integrated and automated procedure. This reliance reduces both the efficiency and the objectivity of latent space exploration, and it hampers the framework’s capacity to adapt rapidly to new data environments or unseen driving contexts. Moreover, manual interpretation makes it difficult to ensure consistency across different datasets or research teams, potentially limiting the reproducibility and comparability of results. Future research should, therefore, consider integrating causal inference techniques and information-theoretic approaches to achieve automated disentanglement and interpretation of latent variables. By systematically identifying causal relationships between latent dimensions and observable driving behaviors, such methods could reduce dependence on human judgment and enhance scientific rigor. In addition, automation would enable the framework to scale more effectively to larger and more heterogeneous datasets, such as those involving multimodal signals or diverse traffic scenarios while preserving interpretability.

The current framework also focuses solely on vehicle trajectory data and does not account for physiological or cognitive signals that reflect the internal state of drivers. While trajectory information provides direct evidence of observable car-following behaviors, it cannot fully capture the latent psychological and physiological mechanisms underlying decision making. Incorporating multimodal information such as heart rate variability, electrodermal activity, and eye-tracking data could provide richer and more comprehensive representations of driving style. These additional modalities can serve as proxies for driver stress, workload, and attention allocation, thereby complementing external kinematic data with internal state indicators. Integrating such heterogeneous data sources would not only strengthen the interpretability of latent dimensions but also facilitate the modeling of how internal states modulate observable behaviors. In the broader context of intelligent transportation systems, this integration could improve personalized safety assessments, adaptive driver assistance, and the robustness of autonomous vehicle decision making in mixed traffic environments. A multimodal approach has the potential to bridge the gap between external behavior analysis and internal cognitive mechanisms, enabling a deeper and more holistic understanding of driver heterogeneity.

The interpretable driving style representations developed in this framework could serve as a foundation for adaptive driver modeling in autonomous vehicles, enabling decision-making processes that explicitly account for the heterogeneous behaviors of surrounding drivers. Such human-centered modeling has the potential to improve safety in mixed-traffic environments by allowing autonomous systems to anticipate and respond to diverse driving styles rather than relying on uniform behavioral assumptions. In the domain of traffic management, the framework could facilitate real-time monitoring of driver heterogeneity at the system level, thereby supporting more accurate prediction of traffic flow instabilities, shockwave propagation, and bottleneck formation. This capability would further enable the design of proactive congestion mitigation strategies, ranging from adaptive signal control to dynamic traffic assignment. Beyond system-level control, the disentangled and interpretable representations also provide a robust basis for individualized safety assessments and personalized feedback systems. By linking latent behavioral traits with measurable risk indicators, the framework can be used to identify at-risk drivers, deliver targeted behavioral interventions, and enhance training programs for novice or professional drivers.

7. Conclusions

This study addressed a central challenge in intelligent transportation systems: how to extract fine-grained and interpretable driving style representations from car-following trajectories in the absence of manual annotations. To this end, an unsupervised decoupled learning framework based on a dual-decoder variational autoencoder was proposed and validated.

The first contribution lies in the model design. By leveraging driver identity labels as proxy variables, the framework eliminated the dependence on manual annotations and achieved a Driver Identification accuracy of 98.88% on the HF dataset, outperforming strong baselines. The explicit separation of self-dynamics and interaction dynamics, supported by an interaction attention mechanism, enabled micro-level encoding of car-following behavior using only longitudinal motion variables. This feature decoupling provided the structural basis for subsequent semantic interpretation of driving styles.

The second contribution focused on interpretability validation. Statistical correlation analyses revealed clear mappings between latent variables and behavioral indicators, such as the safety–efficiency trade-off captured by dimension z₂₂ and smoothness reflected by dimension z₂₄. Latent-to-trajectory generation further confirmed the causal control of these dimensions, with systematic changes in safety margins and efficiency. This dual validation established both statistical and generative interpretability, offering actionable semantics for latent driving-style dimensions.

The third contribution demonstrated the ability to capture behavioral heterogeneity. Visualization through UMAP confirmed the discriminative separation of drivers in latent space, while clustering of multi-scenario trajectories from individual drivers revealed consistent intra-individual variability. Together, these findings underscore the framework’s potential to model both inter-individual differences and intra-individual dynamics, providing valuable tools for managing behavioral uncertainties in mixed traffic flow.

Several limitations should be noted. Short-term modeling emphasizes localized decisions shaped by dynamic vehicle–environment interactions, whereas long-term modeling reflects enduring behavioral tendencies across contexts. While the present framework primarily targeted short-term trajectory-based style extraction, its architecture can be extended to integrate long-term behavioral patterns, thereby bridging micro-level decision dynamics with macro-level consistency. In addition, the analysis was based on controlled car-following experiments on suburban arterials with constant-lead-vehicle settings. This design minimized external disturbances but restricted applicability to uninterrupted longitudinal following. The identified latent dimensions should, therefore, be validated in urban, intersection, and congested scenarios before broader deployment.

Future research can proceed along three main directions. First, validation across diverse road types and traffic environments is essential to assess generalization and scalability. Second, the automation of latent space decoupling through causal discovery or disentanglement algorithms may further reduce reliance on manual scanning. Third, the fusion of heterogeneous data sources, including physiological signals, environmental perception, and trajectory information, offers a promising pathway toward multimodal driving style modeling. Such advancements would extend the present framework into a comprehensive tool for intelligent transportation systems, enabling safer, more adaptive, and human-centered autonomous driving.