Dynamic Response of Methane Explosion and Roadway Surrounding Rock in Restricted Space: A Simulation Analysis of Fluid-Solid Coupling
Abstract
1. Introduction
2. Numerical Simulation Methods and Control Equations
2.1. Governing Equations for Methane-Air Mixture Explosion Simulations
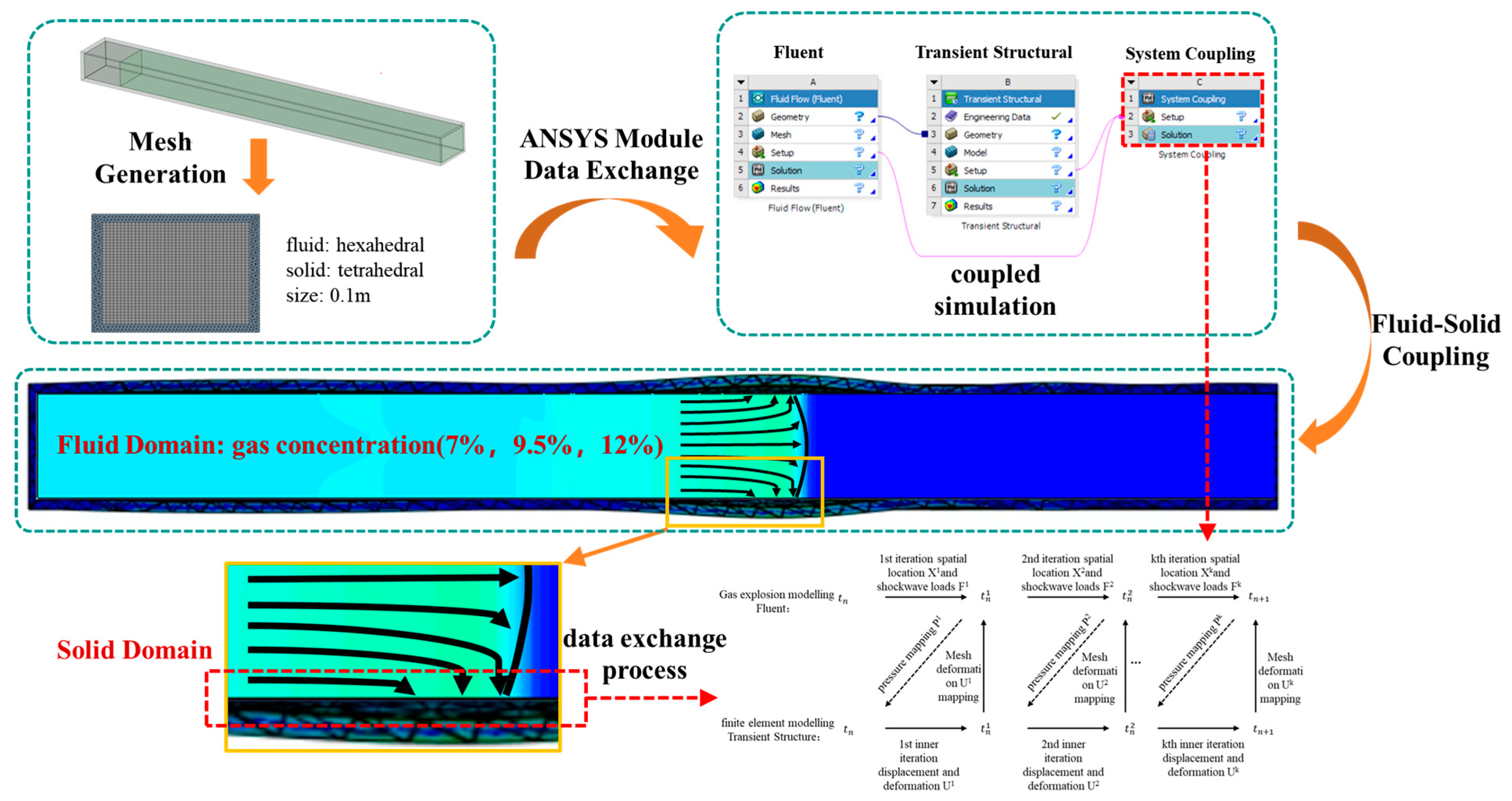
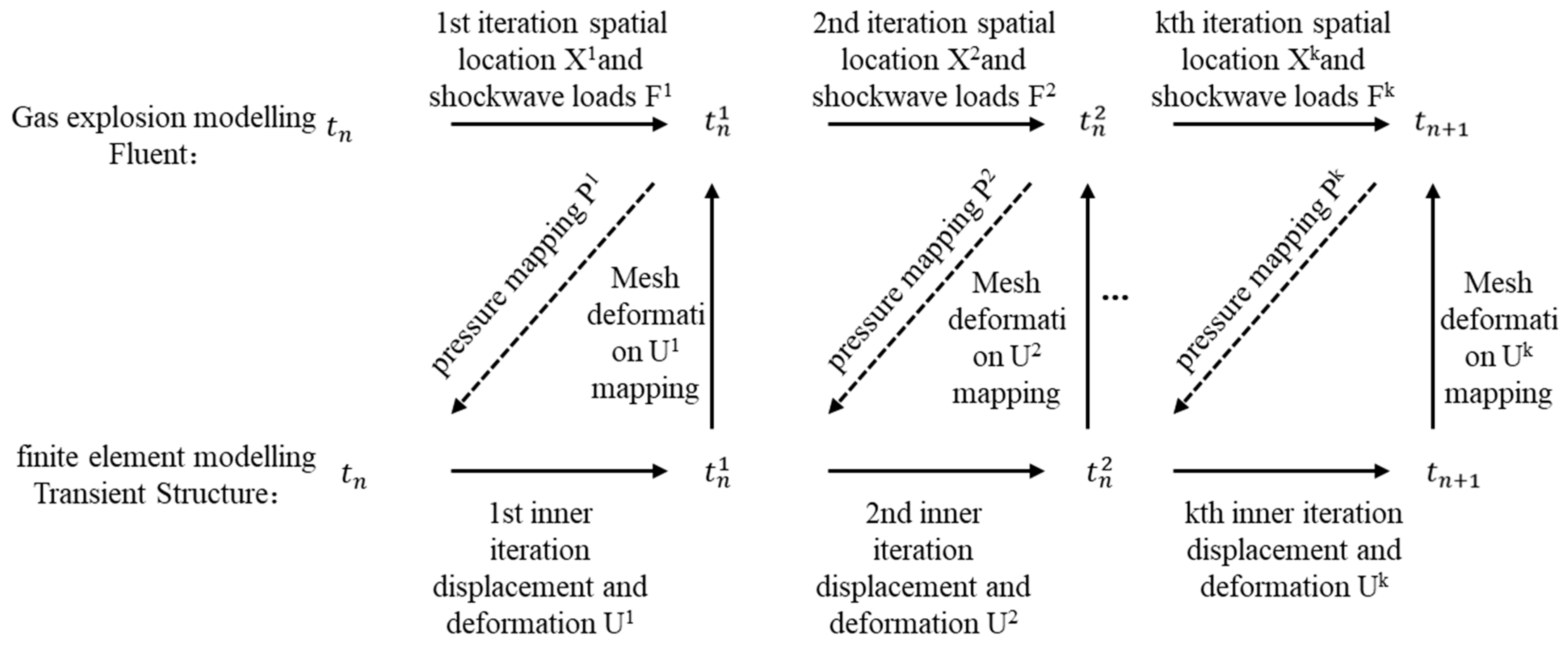
2.2. Bi-Directional Fluid-Structure Interaction Method for Gas Explosion Simulations
2.3. Numerical Modeling of Fluid-Solid Coupling
3. Analysis of the Evolutionary Pattern of Wall Loads in a Gas Explosion
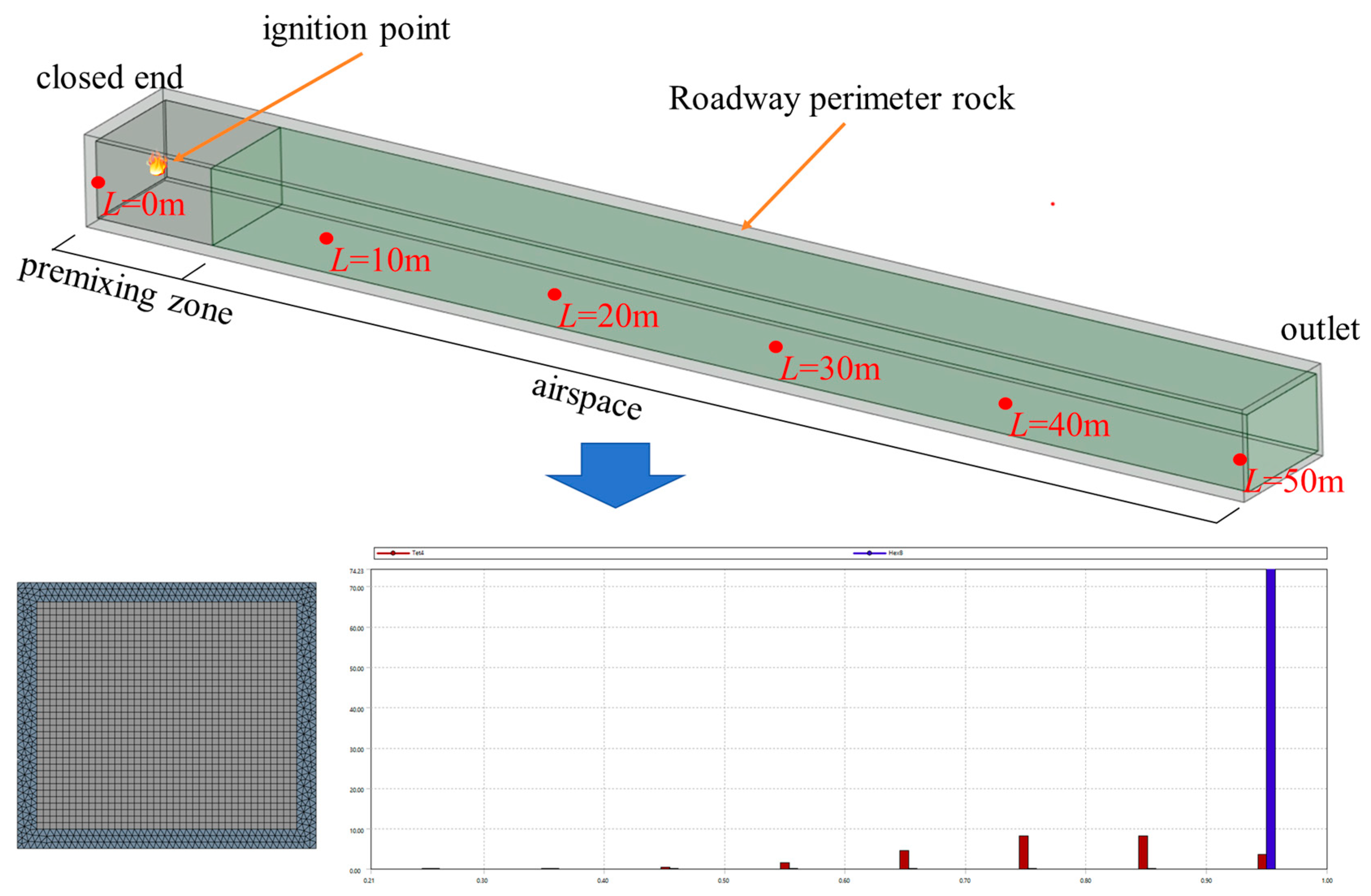
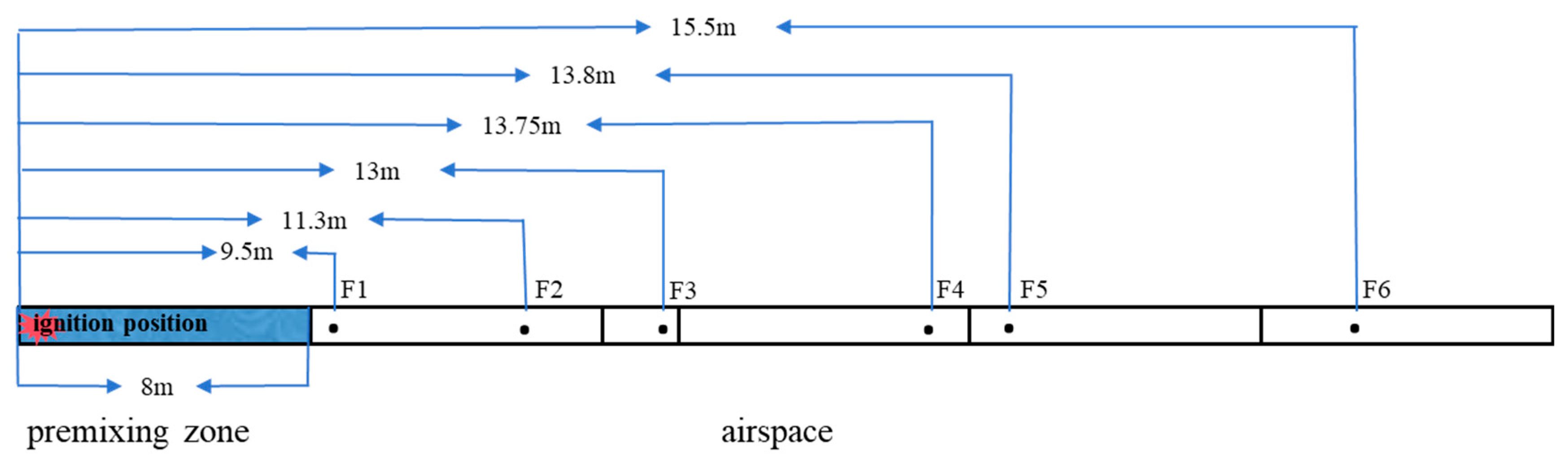
3.1. Numerical Model Validation
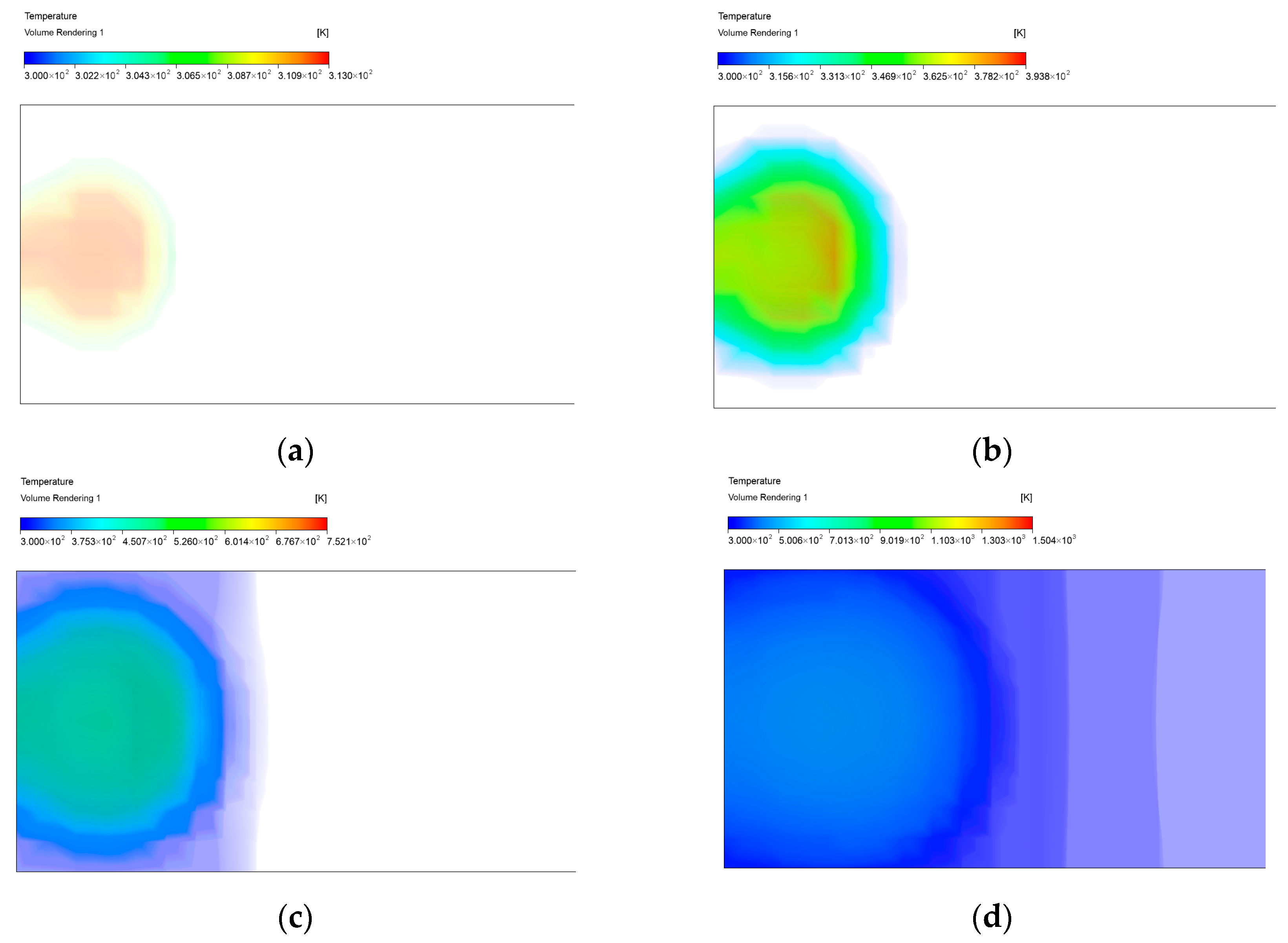
3.2. Conversion of Combustion and Explosion Shock Waves
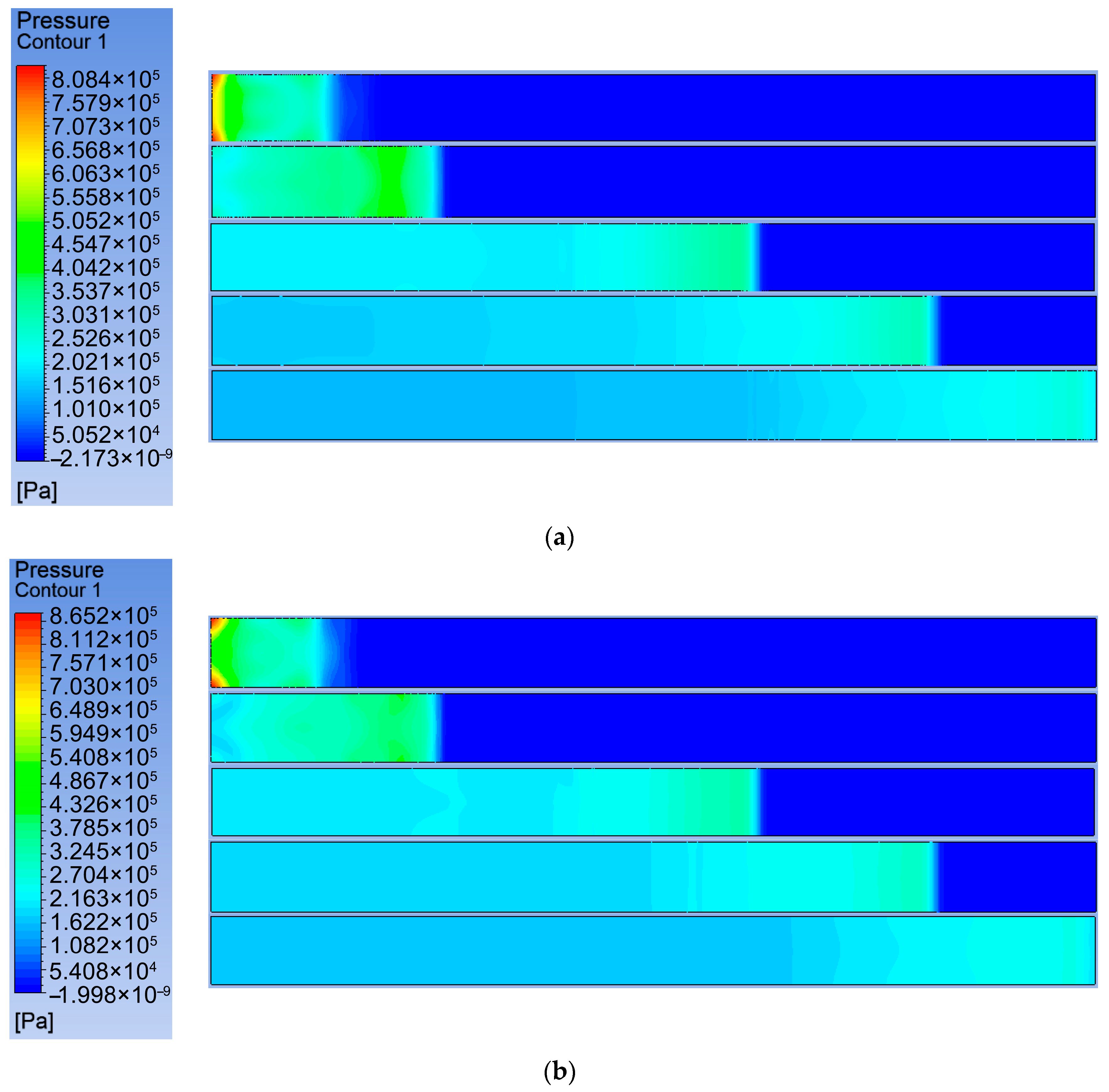
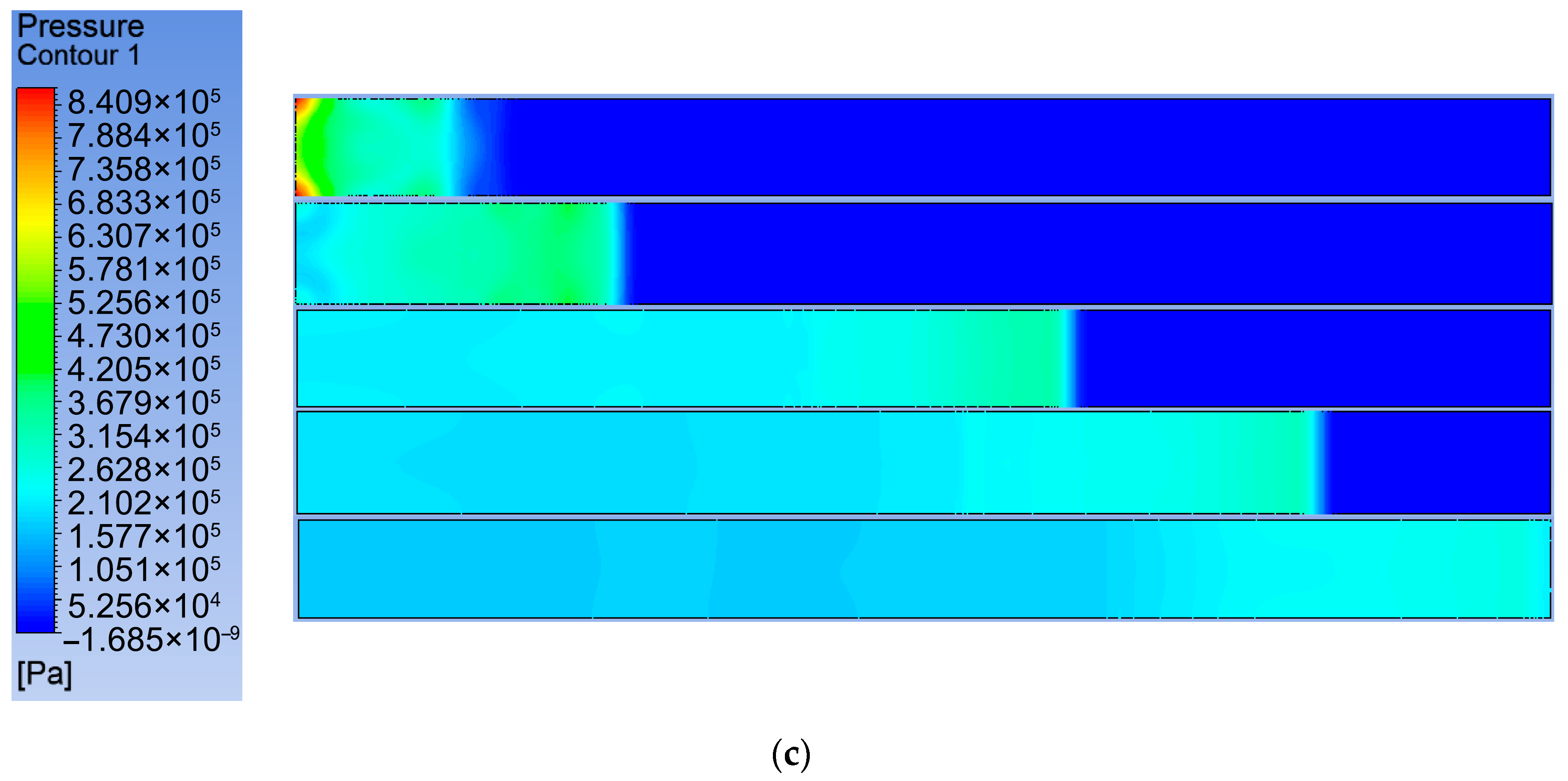
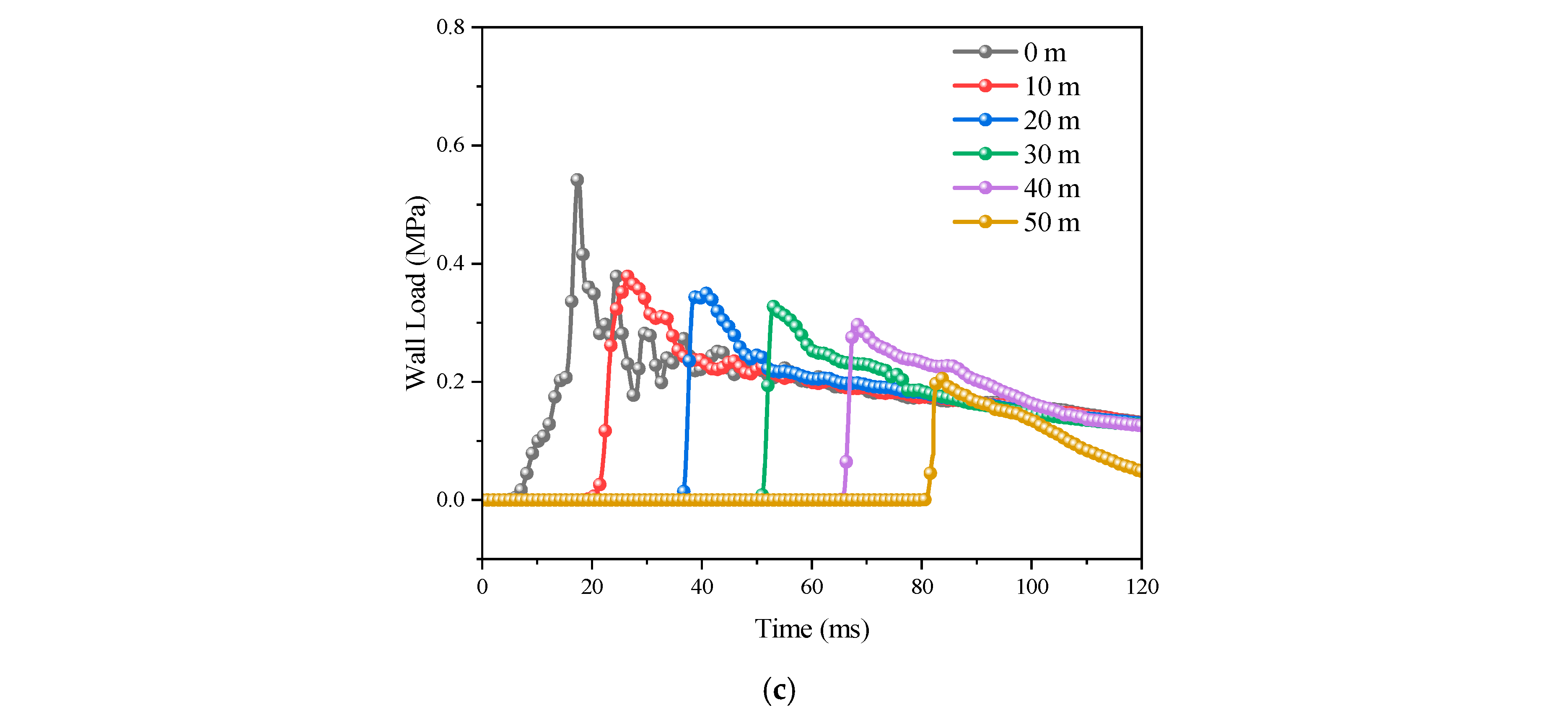
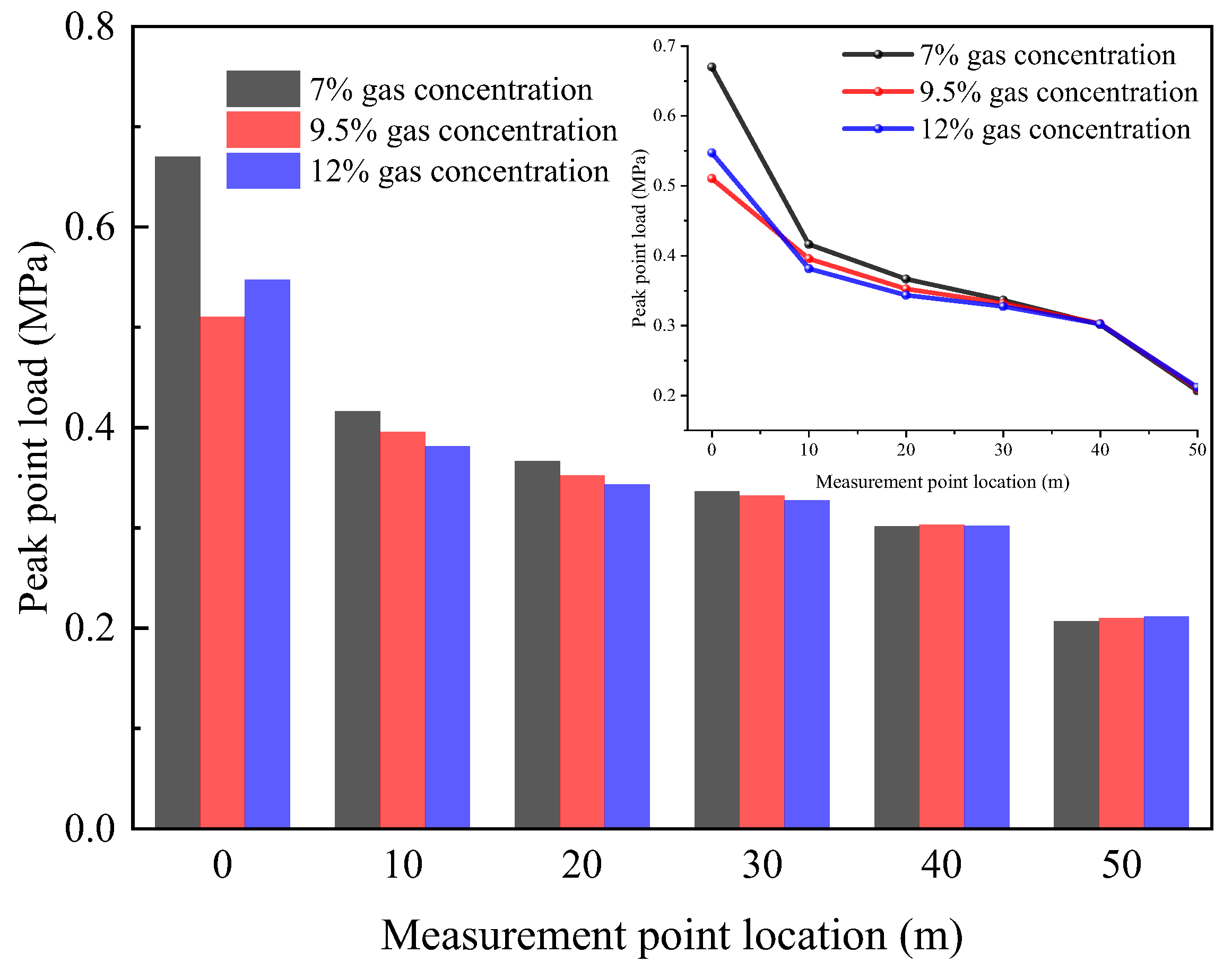
3.3. Laws of Shock Wave Propagation in Gas Explosions
4. Stress and Strain Analysis of Tunnel Wall Under Flow-Solid Coupling
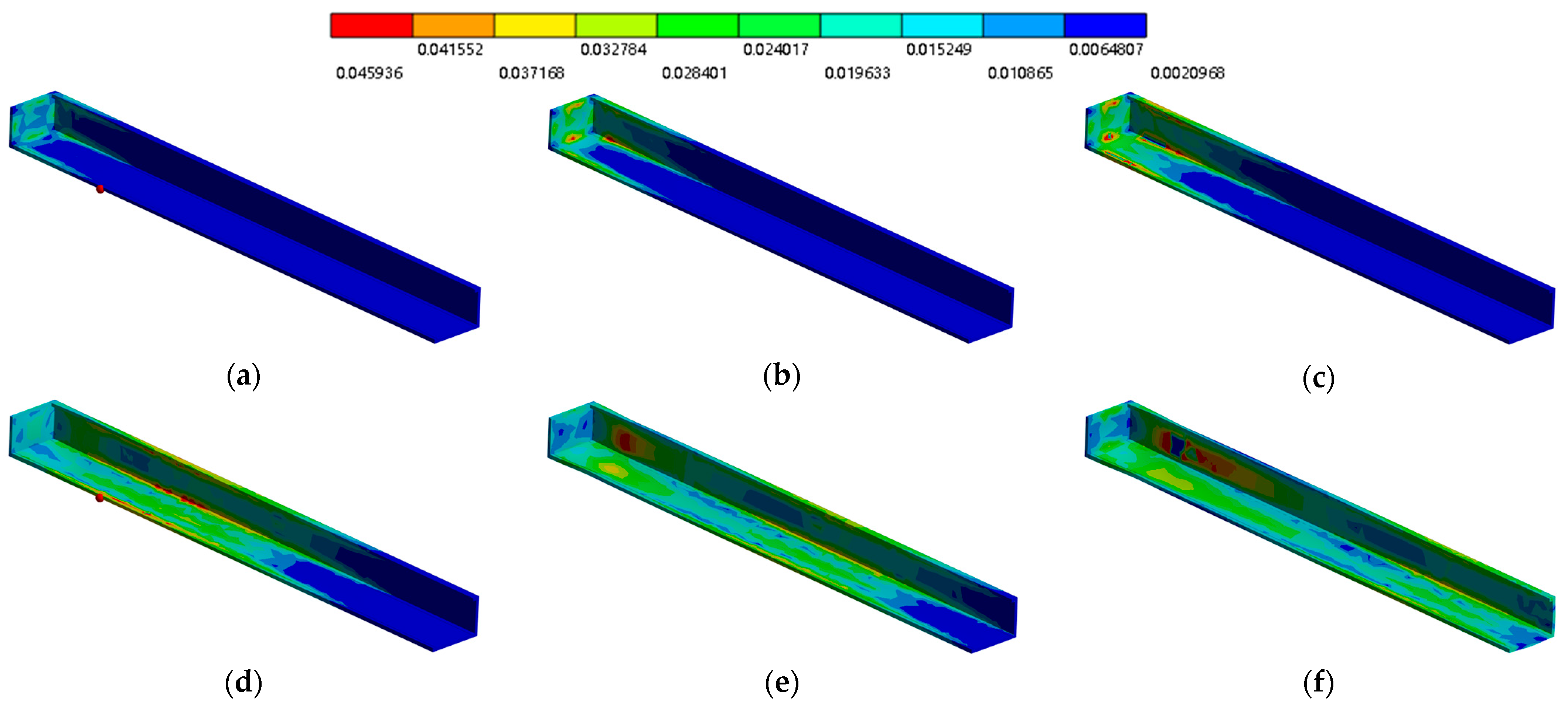
4.1. Stress Analysis of Tunnel Wall Under Fluid-Solid Coupling
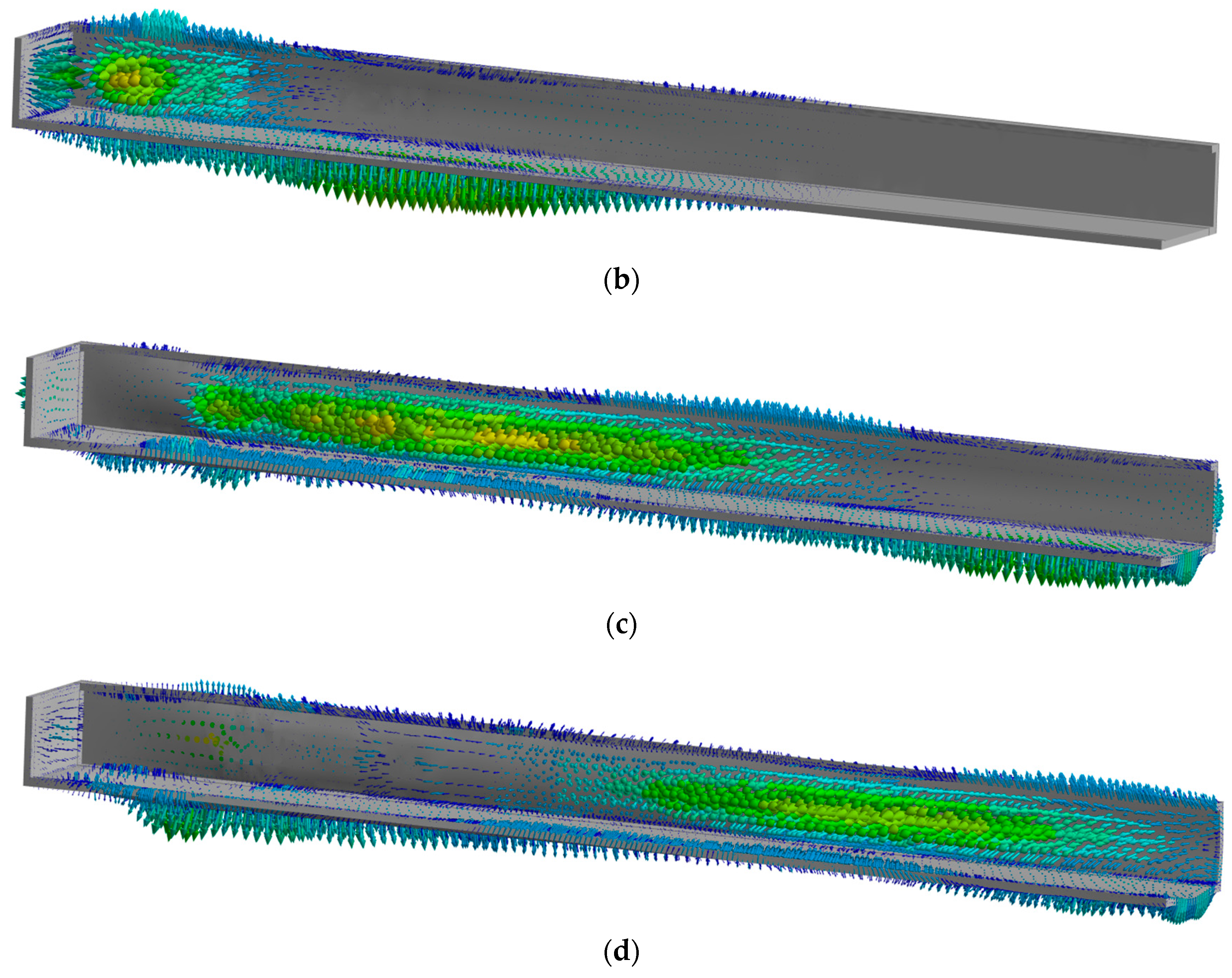
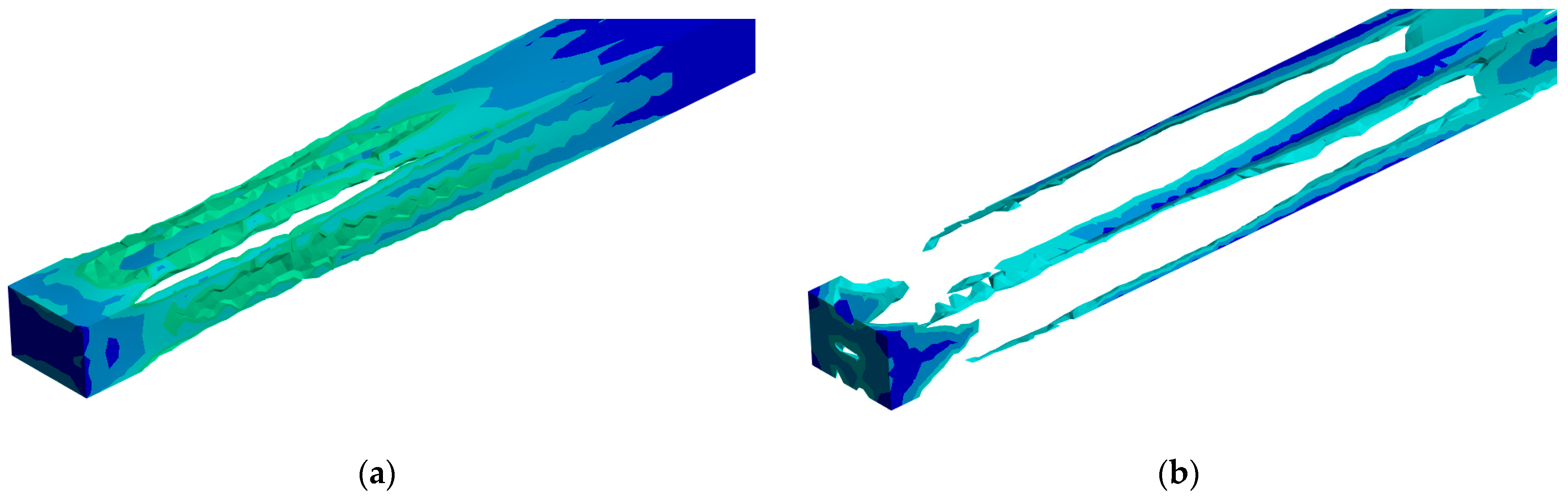
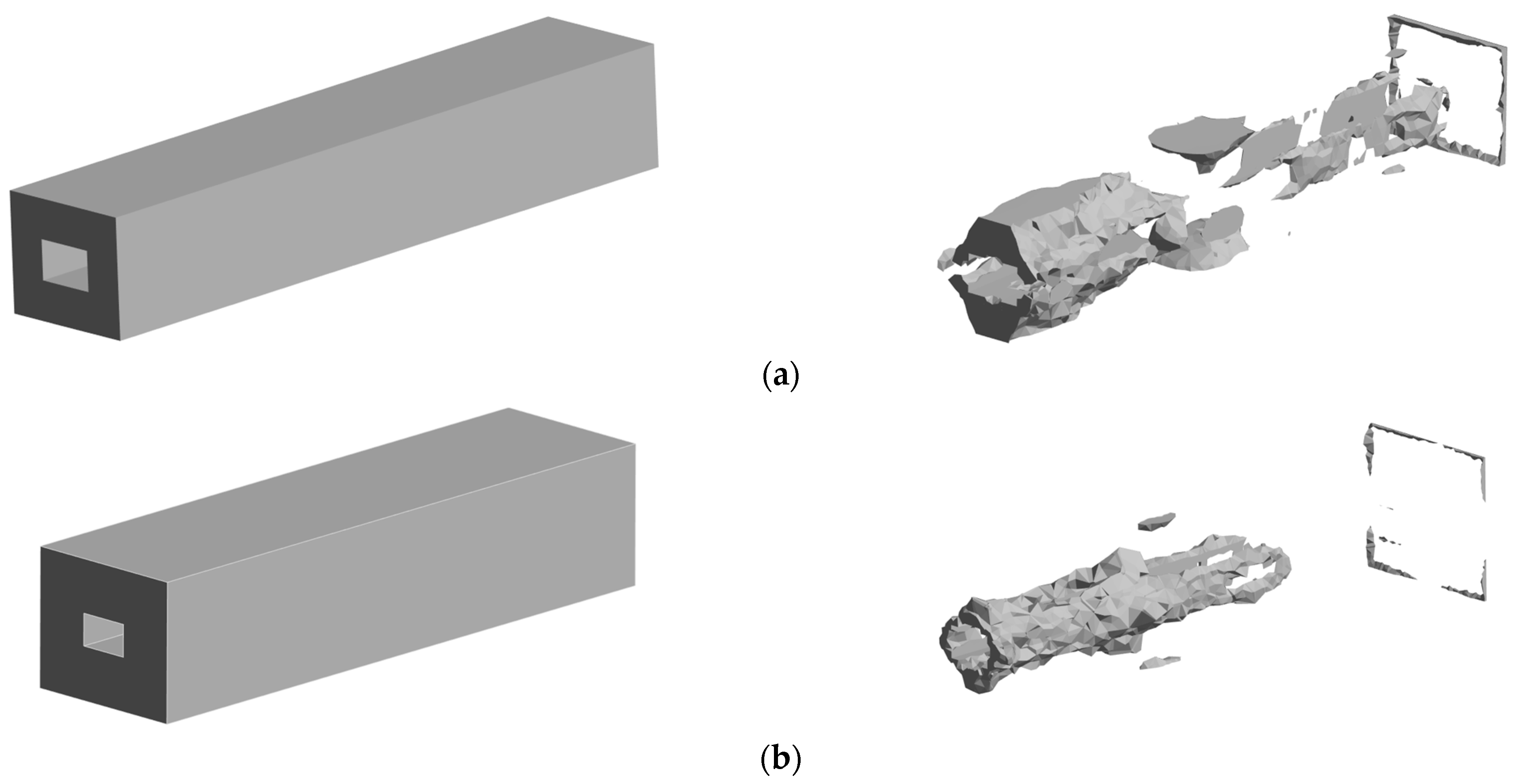
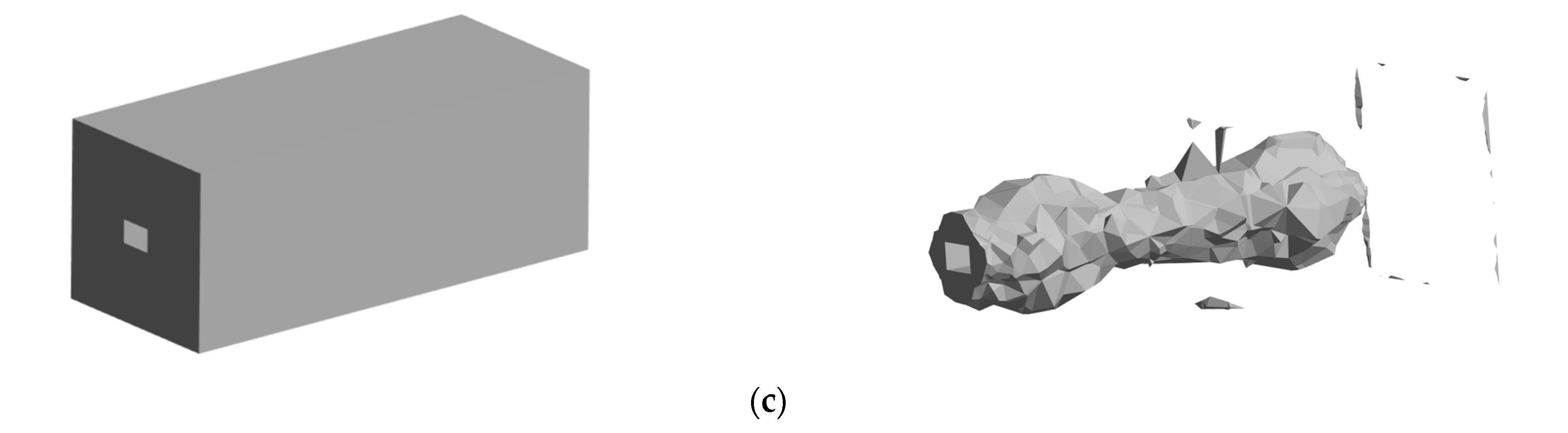
4.2. Characterization of Damage Analysis of Roadway Perimeter Rock Under Fluid-Solid Coupling
4.3. Strain Thresholding Results for Thicker Perimeter Rock Models
5. Conclusions
- (1)
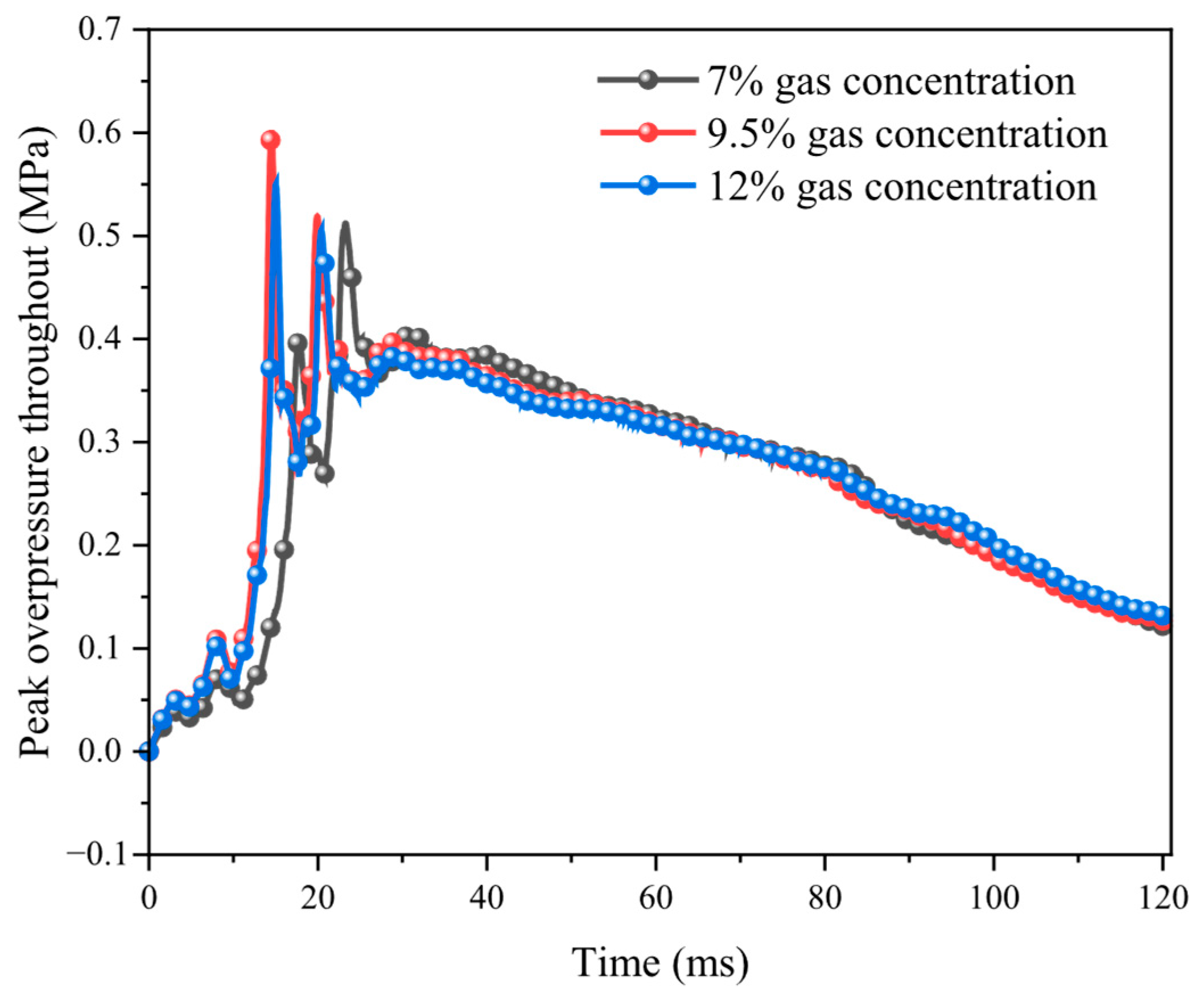
- The methane volume fraction and shock wave overpressure show a significant quadratic relationship, and the equivalent condition () produces the maximum overpressure peaks of and compared with those of the lean combustion/rich combustion condition, and its pressure decay rate constant is reduced by and compared with that of the other conditions. This phenomenon is highly consistent with the laminar flow combustion velocity extreme value characteristics and the CJ burst theory.
- (2)
- The dynamic evolution of the surrounding rock stress field is revealed through the numerical simulation of fluid-solid coupling. The initial shock stage at the closed end is interfered with by multiple reflected waves to produce stress aggregation, and the maximum von Mises stress is 2.09 MPa, which is in accordance with the Saint-Venant principle; the steady-state propagation stage shows hyperbolic decay characteristics of the stress wave, and the phase difference between the neighboring monitoring points is converged; and the open end of the boundary dissipation stage is aggravated by the stress fluctuation due to the turbulence-coupled resonance.
- (3)
- The initial elastic deformation forms a high-strain kernel; the plastic accumulation stage is caused by the redirected migration of the strain field, which triggers the central bulge; and the residual stage is caused by the permanent deformation of the open end by the reverse attenuation. There is a significant difference in the displacement between the bottom plate of the wall and the two gangs. The initial displacement is more concentrated. With the propagation of the shock wave, the displacement area increases but the displacement velocity decreases. By increasing the thickness of the perimeter rock, the movement of the base plate perimeter rock is oriented towards the outside, resulting in less strain near the roadway than on the side away from the roadway, leading to more internal damage to the perimeter rock. Tension-shear stress in the center of the roof plate formed band damage, and the anchor support and buffer layer effectively suppressed the damage expansion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Fu, G.; Lyu, Q.; Li, X.; Chen, Y.; Wu, Y.; Xie, X. Modelling and analysis of unsafe acts in coal mine gas explosion accidents based on network theory. Process Saf. Environ. 2023, 170, 28–44. [Google Scholar]
- Wang, B.; Lv, Y.; Liu, C. Research on fire early warning index system of coal mine goaf based on multi-parameter fusion. Sci. Rep. 2024, 14, 485. [Google Scholar] [CrossRef]
- Kang, Y.; Wu, Z.; Ma, S.; Zhao, M.; Li, W. CFD-based assessment and visualization of the failure consequences of LPG tankers. J. Loss Prev. Process Ind. 2023, 82, 105008. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, Y.; Ma, G. CFD-based AHP-TOPSIS decision-making model for gas explosion overpressure mitigation measures in underground utility tunnels. J. Loss Prev. Process Ind. 2024, 89, 105299. [Google Scholar] [CrossRef]
- Mandal, J.; Goel, M.; Agarwal, A. Underground structures subjected to various blast loading scenarios: A scoping review. Arch. Comput. Methods Eng. 2022, 29, 2491–2512. [Google Scholar] [CrossRef]
- Jia, Q.; Xue, S.; Si, X.; Si, R.; Wang, L.; Liu, X.; Li, Z. Dynamics of gas composition and thermal behavior post explosions: An experimental investigation across varied initial concentrations. Case Stud. Therm. Eng. 2024, 59, 104564. [Google Scholar] [CrossRef]
- Gao, K.; Liu, Z.; Wu, C.; Li, J.; Liu, K.; Liu, Y.; Li, S. Effect of low gas concentration in underground return tunnels on characteristics of gas explosions. Process Saf. Environ. 2021, 152, 679–691. [Google Scholar] [CrossRef]
- Li, R.; Si, R.; Wang, L. Propagation of gas explosions of different volumes in a large test tunnel. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 3222–3234. [Google Scholar] [CrossRef]
- Yang, K.; Si, R.; Huang, Z.; Wang, L.; Zhao, J.; Li, Z. Experimental study on the deflagration to detonation transition process of gas explosions in engineering-scale pipelines. Fuel 2025, 384, 133995. [Google Scholar] [CrossRef]
- Tan, B.; Liu, Y.; Liu, H.; Wang, H.; Li, T. Research on size effect of gas explosion in the roadway. Tunn. Undergr. Space Technol. 2021, 112, 103921. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, J.; Zhou, R.; Cai, J.; Bai, Y.; Pang, L. Effects of the length and pressure relief conditions on propagation characteristics of natural gas explosion in utility tunnels. J. Loss Prev. Process Ind. 2022, 75, 104679. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Fang, Q.; Yan, H.; Chen, L. Performance of utility tunnels under gas explosion loads. Tunn. Undergr. Space Technol. 2021, 109, 103762. [Google Scholar] [CrossRef]
- Liu, W.; Mu, C.; Li, Z. Influence of cavity structure on gas explosion characteristics in coal mine. Powder Technol. 2022, 398, 117084. [Google Scholar] [CrossRef]
- Yuan, M.; Hu, Q.; Huang, Z.; Shen, X.; Qian, X.; Yang, H.; Qi, S.; Jiang, J.; Xia, D. Gas explosion impact behavior and disaster analysis based on structural failure: Numerical modeling. J. Loss Prev. Process Ind. 2024, 87, 105234. [Google Scholar] [CrossRef]
- Cheng, J.; Fu, Q.; Wang, Z.; Qin, Y.; Jiang, H.; Gao, K.; Zhang, L. Dynamic response characteristics and structural optimization of isolation seal under the impact of gas explosion. J. Loss Prev. Process Ind. 2023, 84, 105095. [Google Scholar] [CrossRef]
- Cheng, C.; Si, R.; Wang, L.; Jia, Q.; Xin, C.; Chen, X. Experimental study on the effect of initial accumulation pattern on gas explosion and explosion suppression in a real roadway. Case Stud. Therm. Eng. 2023, 51, 103544. [Google Scholar] [CrossRef]
- Cheng, C.; Si, R.; Wang, L.; Jia, Q.; Xin, C. Explosion and explosion suppression of gas/deposited coal dust in a realistic environment. Fuel 2024, 357, 129710. [Google Scholar] [CrossRef]
- Gui, M.; Zhang, L.; Cui, H.; Zhang, H. Turbulent combustion related with detoantion. Acta Aerodyn. Sin. 2019, 38, 515–531. [Google Scholar]
- Maremonti, M.; Russo, G.; Salzano, E.; Tufano, V. Numerical simulation of gas explosions in linked vessels. J. Loss Prev. Process Ind. 1999, 12, 189–194. [Google Scholar] [CrossRef]
- Du, J.; Chen, J.; Zhu, L.; Guo, L.; Wang, F.; Hu, X. Numerical study on the dynamic response of gas explosion in uneven coal mine tunnels using CESE reaction dynamics model. Appl. Sci. 2024, 14, 2372. [Google Scholar] [CrossRef]
- Mo, L.; Wang, R.; Yang, H.; Yang, Y.; Wu, X.; Jia, W.; Li, C.; Chen, C. Dynamic response of spherical tanks subjected to the explosion of hydrogen-blended natural gas. Fuel 2024, 377, 132834. [Google Scholar] [CrossRef]
- Zheng, G.; Shi, J.; Li, L.; Li, Q.; Gu, Z.; Xu, W.; Lu, B.; Wang, C. Fluid-solid coupling-based vibration generation mechanism of the multiphase vortex. Processes 2023, 11, 568. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, C.; Shi, Z.; Li, Y.; Zhao, Y.; Wu, X. A fluid–solid coupling model for hydraulic fracture of deep coal seam based on finite element method. Phys. Fluids 2024, 36, 066609. [Google Scholar] [CrossRef]
- Tan, W.; Chen, Z.; Li, Z.; Yan, H. Thermal-fluid-solid coupling simulation and oil groove structure optimization of wet friction clutch for high-speed helicopter. Machines 2023, 11, 296. [Google Scholar] [CrossRef]
- Shamsuddin, D.S.N.A.; Fekeri, A.F.M.; Muchtar, A.; Khan, F.; Khor, B.C.; Lim, B.H.; Rosli, M.I.; Takriff, M.S. Computational fluid dynamics modelling approaches of gas explosion in the chemical process industry: A review. Process Saf. Environ. 2023, 170, 112–138. [Google Scholar] [CrossRef]
- Qiu, J. Study on Propagation Characteristics of Shock Wave in Pipe Network and Simulation of Catastrophic Process for Gas Explosion. Ph.D. Thesis, Anhui University of Science and Technology, Huainan, China, 2018. [Google Scholar]
- Oran, E.S.; Gamezo, V.N. Origins of the deflagration-to-detonation transition in gas-phase combustion. Combust. Flame 2007, 148, 4–47. [Google Scholar] [CrossRef]
- Saif, M.; Wang, W.; Pekalski, A.; Levin, M.; Radulescu, M.I. Chapman–Jouguet deflagrations and their transition to detonation. Proc. Combust. Inst. 2017, 36, 2771–2779. [Google Scholar] [CrossRef]
- Kumar, K.; Bandyopadhyay, P.; Singh, S.; Dharodi, V.S.; Sen, A. Kelvin-Helmholtz instability in a compressible dust fluid flow. Sci. Rep. 2023, 13, 3979. [Google Scholar] [CrossRef] [PubMed]
- Nagy, T.; Valkó, É.; Sedyó, I.; Zsély, I.G.; Pilling, M.J.; Turányi, T. Uncertainty of the rate parameters of several important elementary reactions of the H2 and syngas combustion systems. Combust. Flame 2015, 162, 2059–2076. [Google Scholar] [CrossRef]
- Li, S. Stress or strain? Proc. R. Soc. A 2024, 480, 20240269. [Google Scholar] [CrossRef]
- Gong, B.; Wan, X.; Huo, X.; Liu, Y.; Deng, C.; Wang, D.; Dai, L. Development of a strain-based fracture assessment approach for X80 steel pipe welded girth by modified Mohr-Coulomb model. Int. J. Press. Vessel. Pip. 2023, 206, 105056. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Zhou, X.-P. Integrated acoustic-optic-mechanics (AOM) multi-physics field characterization methods for a crack: Tension vs. shear. Eng. Fract. Mech. 2023, 287, 109339. [Google Scholar] [CrossRef]
- Yu, Z.; Haoran, S.; Xiaohui, L.; Wenju, Z. Failure characteristics and constitutive model of coal rock at different strain rates. Explos. Shock Waves 2021, 41, 053103. [Google Scholar]



| Parameter Type | a | |||||
|---|---|---|---|---|---|---|
| parameter value | 2350 | 2500 | 0.25 | 1.5 | 24 | 920 |
| Measurement Point Location | F1 | F2 | F3 | F4 | F5 | F6 |
|---|---|---|---|---|---|---|
| Experiment 1 | 0.4188 | 0.7954 | 0.7500 | 0.4075 | 0.4009 | 0.3311 |
| Experiment 2 | 0.4115 | 0.8983 | 0.7232 | 0.5796 | 0.5090 | 0.3167 |
| Experiment 3 | 0.4232 | 0.7479 | 0.6361 | 0.5123 | 0.4788 | 0.3288 |
| Experimental mean | 0.4178 | 0.8139 | 0.7031 | 0.4998 | 0.4629 | 0.3255 |
| Numerical simulation results | 0.4418 | 0.7731 | 0.6892 | 0.5004 | 0.4782 | 0.3525 |
| Relative error | +5.74% | −5.01% | −1.98% | +0.12% | +3.46% | +8.29 |
| /MPa | ||
|---|---|---|
| 24.8 | 12.8 | 2.95 |
| 33.8 | 14.7 | 1.63 |
| 42.3 | 23.2 | 1.41 |
| 46.2 | 23.4 | 1.74 |
| 53.8 | 32.3 | 1.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Q.; Ding, P.; Yan, Z.; Zhu, Y.; Zhang, J. Dynamic Response of Methane Explosion and Roadway Surrounding Rock in Restricted Space: A Simulation Analysis of Fluid-Solid Coupling. Appl. Sci. 2025, 15, 9454. https://doi.org/10.3390/app15179454
Zheng Q, Ding P, Yan Z, Zhu Y, Zhang J. Dynamic Response of Methane Explosion and Roadway Surrounding Rock in Restricted Space: A Simulation Analysis of Fluid-Solid Coupling. Applied Sciences. 2025; 15(17):9454. https://doi.org/10.3390/app15179454
Chicago/Turabian StyleZheng, Qiangyu, Peijiang Ding, Zhenguo Yan, Yaping Zhu, and Jinlong Zhang. 2025. "Dynamic Response of Methane Explosion and Roadway Surrounding Rock in Restricted Space: A Simulation Analysis of Fluid-Solid Coupling" Applied Sciences 15, no. 17: 9454. https://doi.org/10.3390/app15179454
APA StyleZheng, Q., Ding, P., Yan, Z., Zhu, Y., & Zhang, J. (2025). Dynamic Response of Methane Explosion and Roadway Surrounding Rock in Restricted Space: A Simulation Analysis of Fluid-Solid Coupling. Applied Sciences, 15(17), 9454. https://doi.org/10.3390/app15179454








