Sensitivity of the Threshold Current for Switching of a Magnetic Tunnel Junction to Fabrication Defects and Its Application in Physical Unclonable Functions
Abstract
1. Introduction
2. PUFs Based on Magnetic Tunnel Junctions
Threshold Current-Based PUF
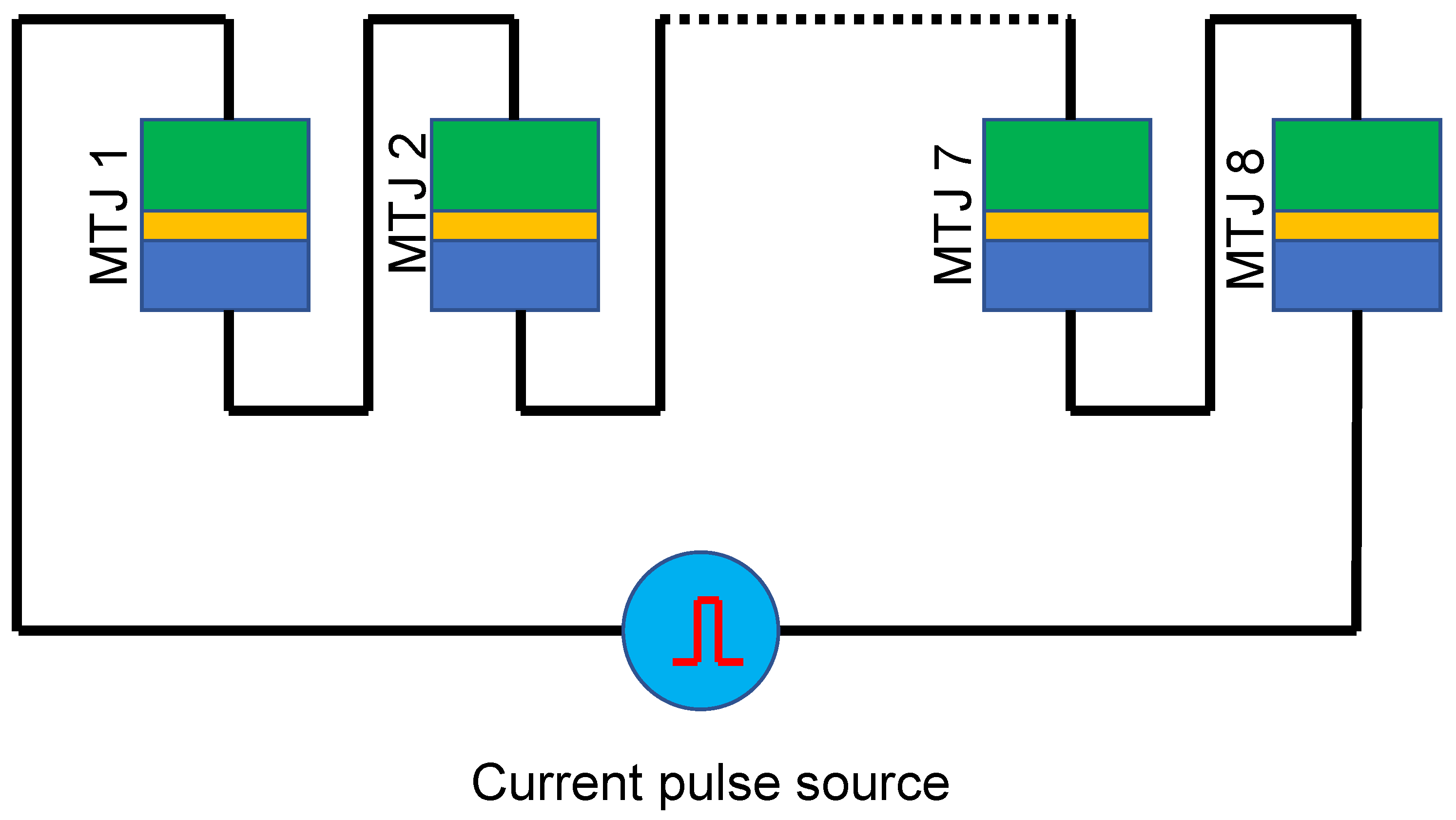
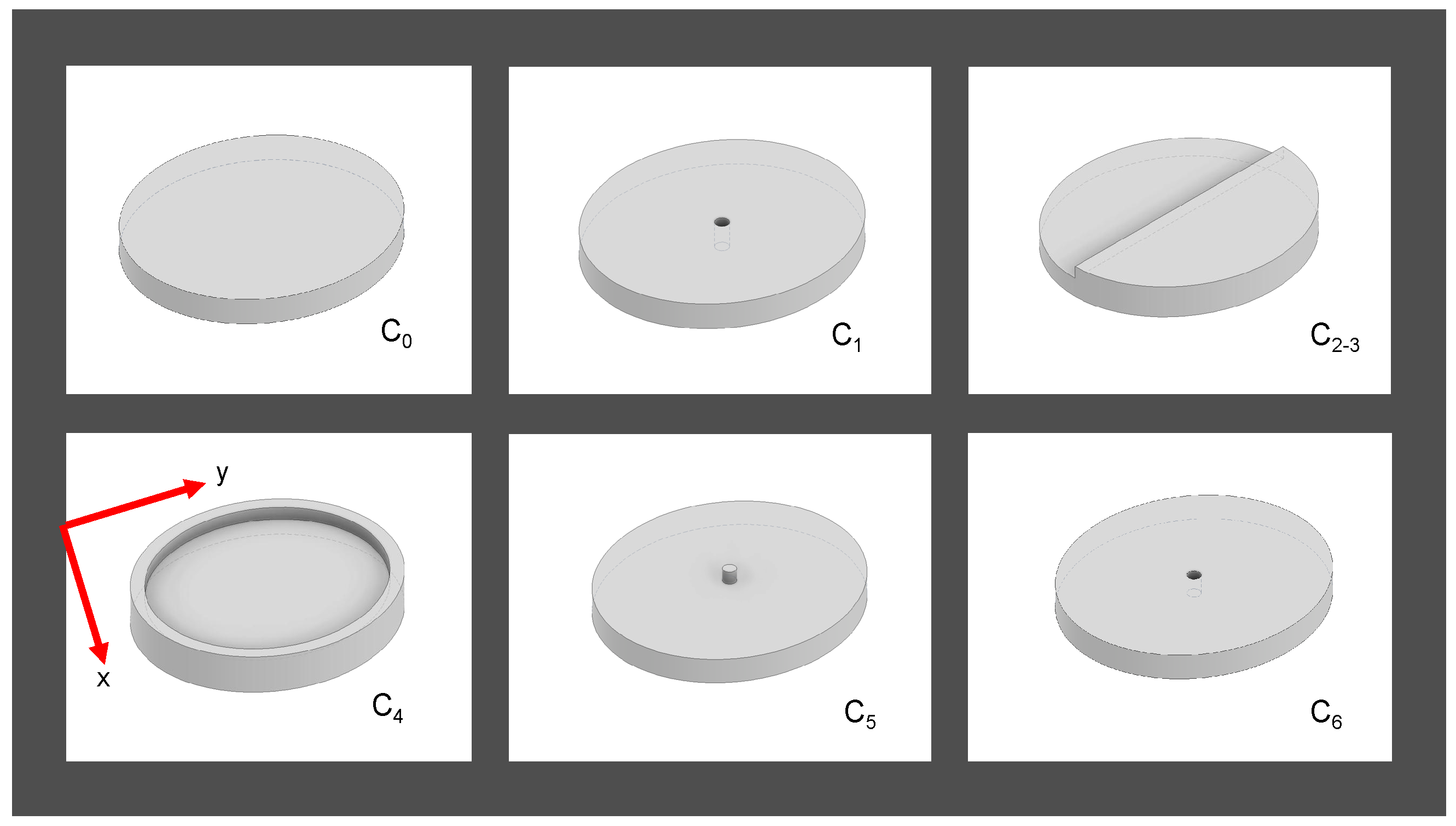
3. Materials and Methods
4. Results and Discussion
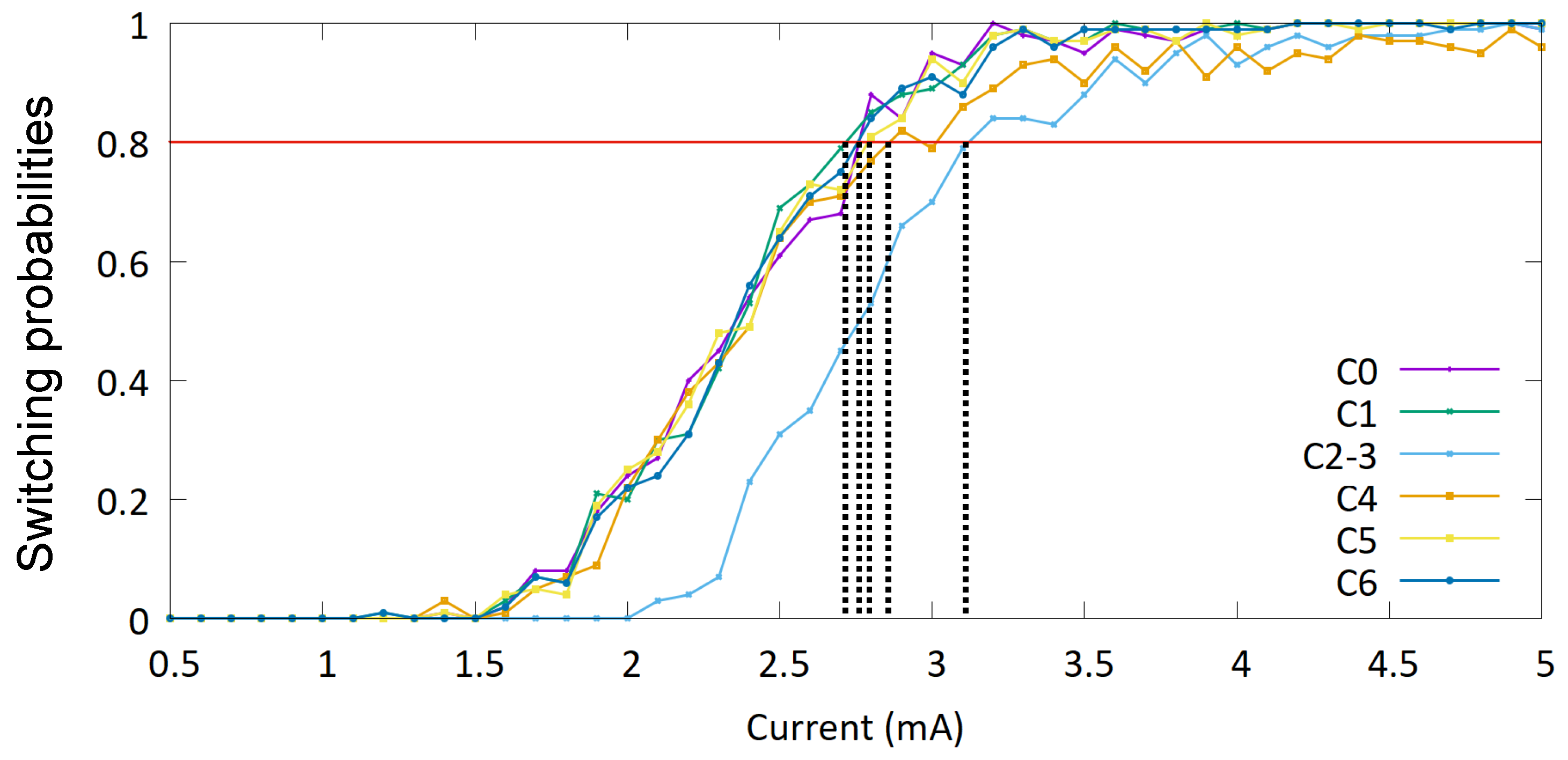
4.1. PUF Behavior
4.2. Inter-Hamming Distance
4.3. Sensitivity to Temperature and Intra-Hamming Distance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Herder, C.; Yu, M.-D.; Farinaz, K.; Devadas, S. Physical Unclonable Functions and Applications: A Tutorial. Proc. IEEE 2014, 102, 1126. [Google Scholar] [CrossRef]
- Chen, H.; Song, M.; Guo, Z.; Li, R.; Zou, Q.; Luo, S.; Zhang, S.; Luo, Q.; Hong, J.; You, L. Highly Secure Physically Unclonable Cryptographic Primitives Based on Interfacial Magnetic Anisotropy. Nano Lett. 2018, 18, 7211. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Zhang, S.; Zhang, J.; Xu, N.; Li, R.; Guo, Z.; Yun, J.; Song, M.; Zou, Q.; Xi, L.; et al. Reconfigurable Physical Unclonable Function Based on Spin-Orbit Torque Induced Chiral Domain Wall Motion. IEEE Elec. Dev. Lett. 2021, 42, 597. [Google Scholar] [CrossRef]
- Kumar, A.; Sahay, S.; Suri, M. Switching-Time Dependent PUF Using STT-MRAM. In Proceedings of the 2018 31th International Conference on VLSI Design and 2018 17th International Conference on Embedded Systems (IEEE), Pune, India, 6–10 January 2018. [Google Scholar]
- Das, J.; Kevin, S.; Srinath, R.; Drew, B.; Bhanja, S. MRAM PUF: A novel geometry based magnetic PUF with integrated CMOS. IEEE Trans. Nanotechnol. 2015, 14, 436–443. [Google Scholar] [CrossRef]
- Zhang, L.; Fong, X.; Chang, C.H.; Kong, Z.H.; Roy, K. Feasibility study of emerging non-volatile memory based physical unclonable functions. In Proceedings of the IEEE 6th International Memory Workshop, Taipei, Taiwan, 18–21 May 2014; pp. 1–4. [Google Scholar]
- Marukame, M.; Tanamoto, T.; Mitani, Y. Extracting physically unclonable function from spin transfer switching characteristics in magnetic tunnel junctions. IEEE Trans. Magn. 2014, 50, 3402004. [Google Scholar] [CrossRef]
- Vatajelu, E.I.; Natale, G.D.; Barbareschi, M.; Torres, L.; Indaco, M.; Prinetto, P. STT-MRAM-based PUF architecture exploiting magnetic tunnel junction fabrication-induced variability. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2016, 13, 5. [Google Scholar] [CrossRef]
- Rose, G.S.; McDonald, N.; Yan, L.-K.; Wysocki, B. A write-time based memristive puf for hardware security applications. In Proceedings of the 2013 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 18–21 November 2013; pp. 830–833. [Google Scholar]
- Available online: https://www.ugent.be/we/solidstatesciences/dynamat/en/mumax (accessed on 10 August 2025).
- Winters, D.; Abeed, M.A.; Sahoo, S.; Barman, A.; Bandyopadhyay, S. Reliability of magnetoelastic switching of nonideal nanomagnets with defects: A case study for the viability of straintronic logic and memory. Phys. Rev. Appl. 2019, 12, 034010. [Google Scholar] [CrossRef]
- Brown, W.F., Jr. Thermal Fluctuations of a Single-Domain Particle. Phys. Rev. 1963, 130, 1677. [Google Scholar] [CrossRef]
- Sun, J.Z. Spin current interaction with a monodomain magnetic body: A model study. Phys. Rev. B 2000, 62, 570. [Google Scholar] [CrossRef]
- Sun, J.Z. Current-driven magnetic switching in manganite trilayer junctions. J. Magn. Magn. Mater. 1999, 202, 157. [Google Scholar] [CrossRef]
- Bandyopadhyay, S. Magnetic Straintronics: An Energy-Efficient Hardware Paradigm for Digital and Analog Information Processing; Synthesis Lectures on Engineering, Science and Technology; Springer Nature: New York, NY, USA, 2022. [Google Scholar]

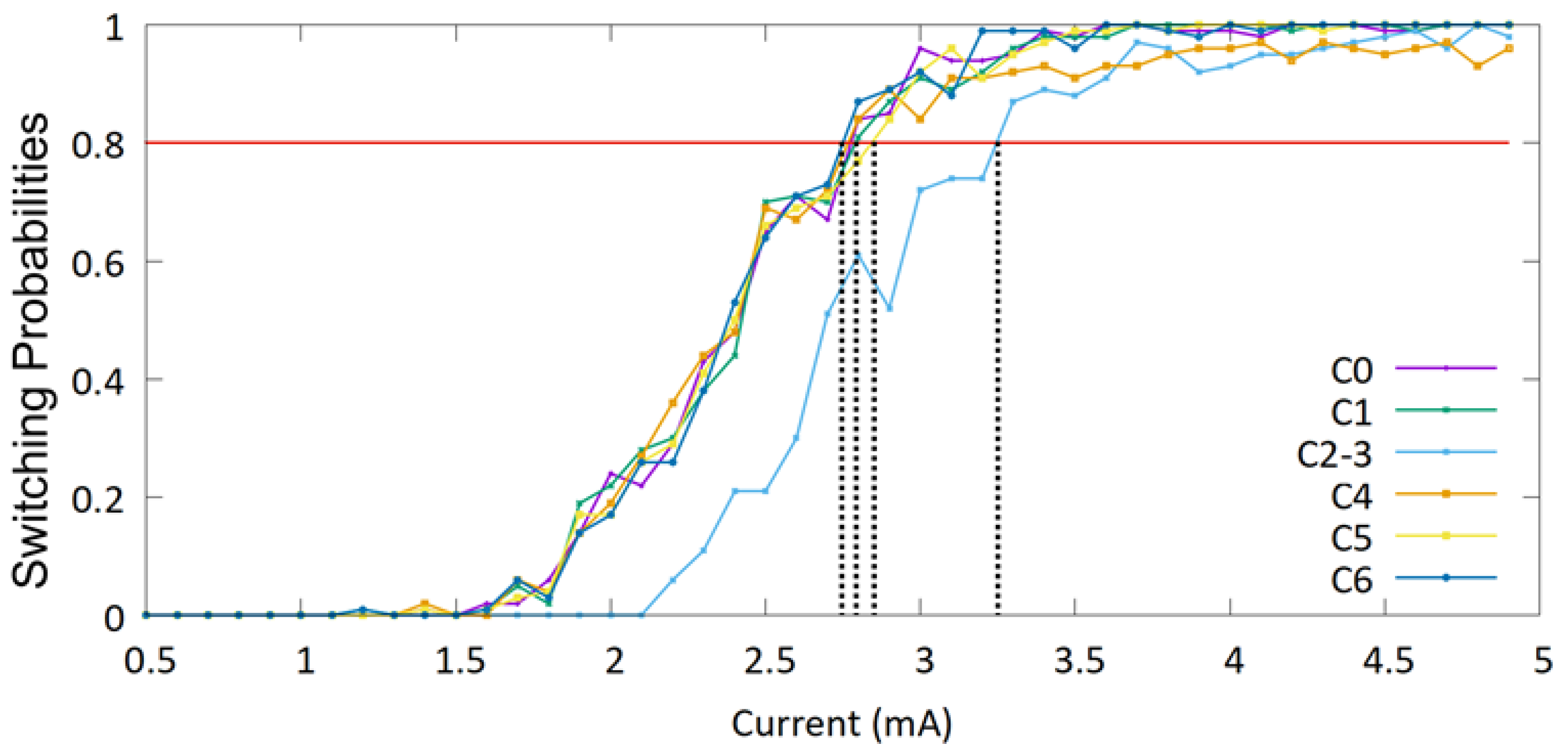

| Defect | Threshold Current (mA) | Threshold Current Density (A/m2) |
|---|---|---|
| 2.77 | 3.91 | |
| 2.79 | 3.94 | |
| 3.26 | 4.61 | |
| 2.77 | 3.91 | |
| 2.84 | 4.00 | |
| 2.74 | 3.87 |
| Defect Distribution | Response Bit Stream |
|---|---|
| Unit 1: | 110 |
| Unit 2: | 101 |
| Unit 3: | 110 |
| Unit 4: | 101 |
| Unit 5: | 011 |
| Unit 6: | 011 |
| Defect | Threshold Current (mA) | Threshold Current Density (A/m2) |
|---|---|---|
| 2.75 | 3.89 | |
| 2.72 | 3.84 | |
| 3.12 | 4.41 | |
| 2.82 | 3.99 | |
| 2.80 | 3.95 | |
| 2.75 | 3.88 |
| Defect | Threshold Current (mA) | Threshold Current Density (A/m2) |
|---|---|---|
| 0.65 | 8.98 | |
| 0.66 | 9.12 | |
| 0.78 | 1.07 | |
| 0.68 | 9.40 | |
| 0.66 | 9.12 | |
| 0.65 | 8.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, J.; Rahman, R.; Bandyopadhyay, S. Sensitivity of the Threshold Current for Switching of a Magnetic Tunnel Junction to Fabrication Defects and Its Application in Physical Unclonable Functions. Appl. Sci. 2025, 15, 9548. https://doi.org/10.3390/app15179548
Huber J, Rahman R, Bandyopadhyay S. Sensitivity of the Threshold Current for Switching of a Magnetic Tunnel Junction to Fabrication Defects and Its Application in Physical Unclonable Functions. Applied Sciences. 2025; 15(17):9548. https://doi.org/10.3390/app15179548
Chicago/Turabian StyleHuber, Jacob, Rahnuma Rahman, and Supriyo Bandyopadhyay. 2025. "Sensitivity of the Threshold Current for Switching of a Magnetic Tunnel Junction to Fabrication Defects and Its Application in Physical Unclonable Functions" Applied Sciences 15, no. 17: 9548. https://doi.org/10.3390/app15179548
APA StyleHuber, J., Rahman, R., & Bandyopadhyay, S. (2025). Sensitivity of the Threshold Current for Switching of a Magnetic Tunnel Junction to Fabrication Defects and Its Application in Physical Unclonable Functions. Applied Sciences, 15(17), 9548. https://doi.org/10.3390/app15179548









