Deep Learning-Based Optimization of Central Angle and Viewpoint Configuration for 360-Degree Holographic Content
Abstract
1. Introduction
2. Related Work
2.1. Depth Map Estimation from Monocular-Image Information
2.2. Depth Map Estimation from Stereo-Image Information
2.3. Depth Map Estimation from Multi-View Image Information
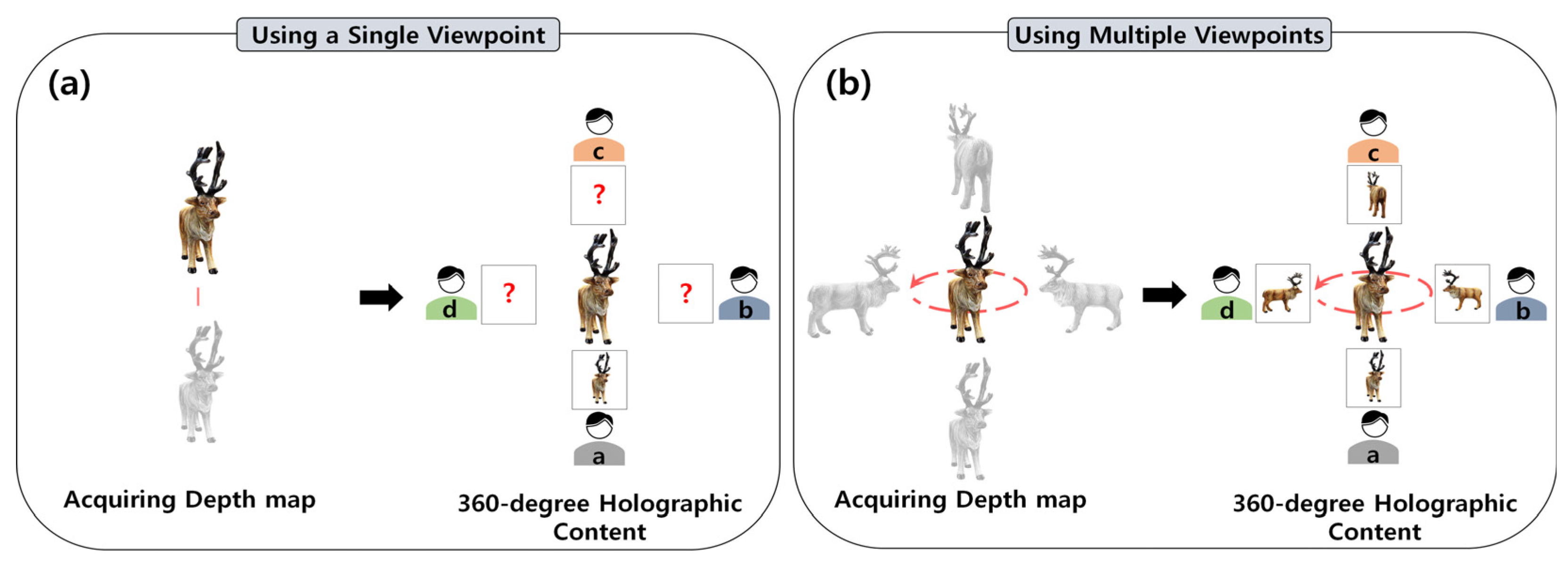
2.4. Object-Centered Depth Map Acquisition for 360-Degree Digital Holography
3. Proposed Method
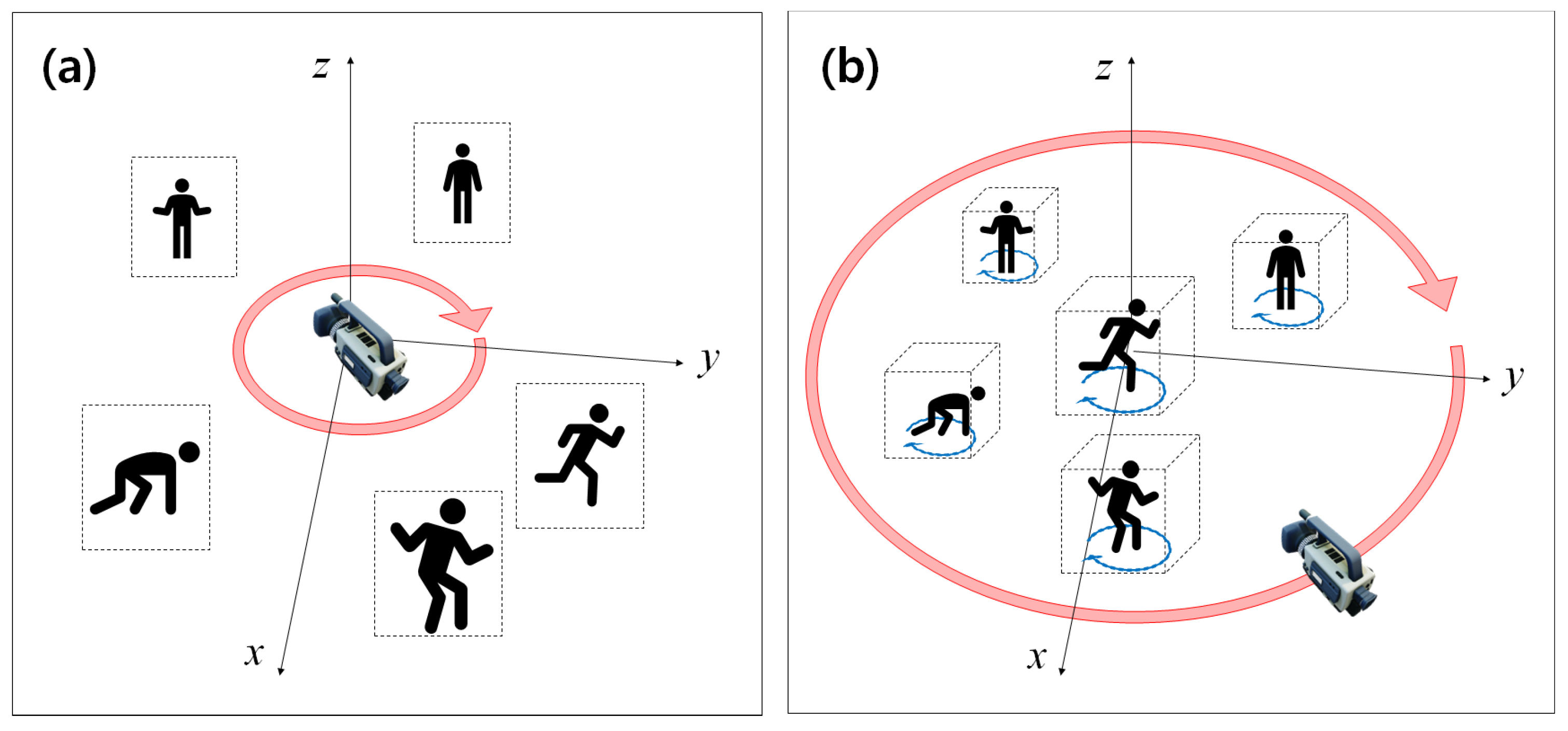
3.1. Data Generation
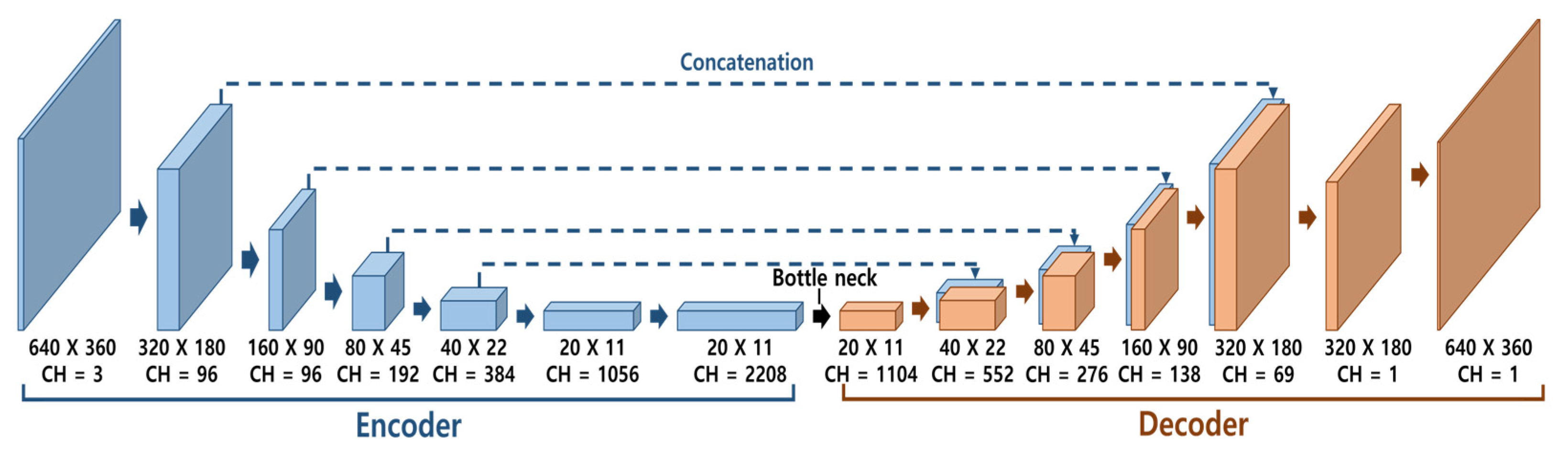
3.2. Model Architecture
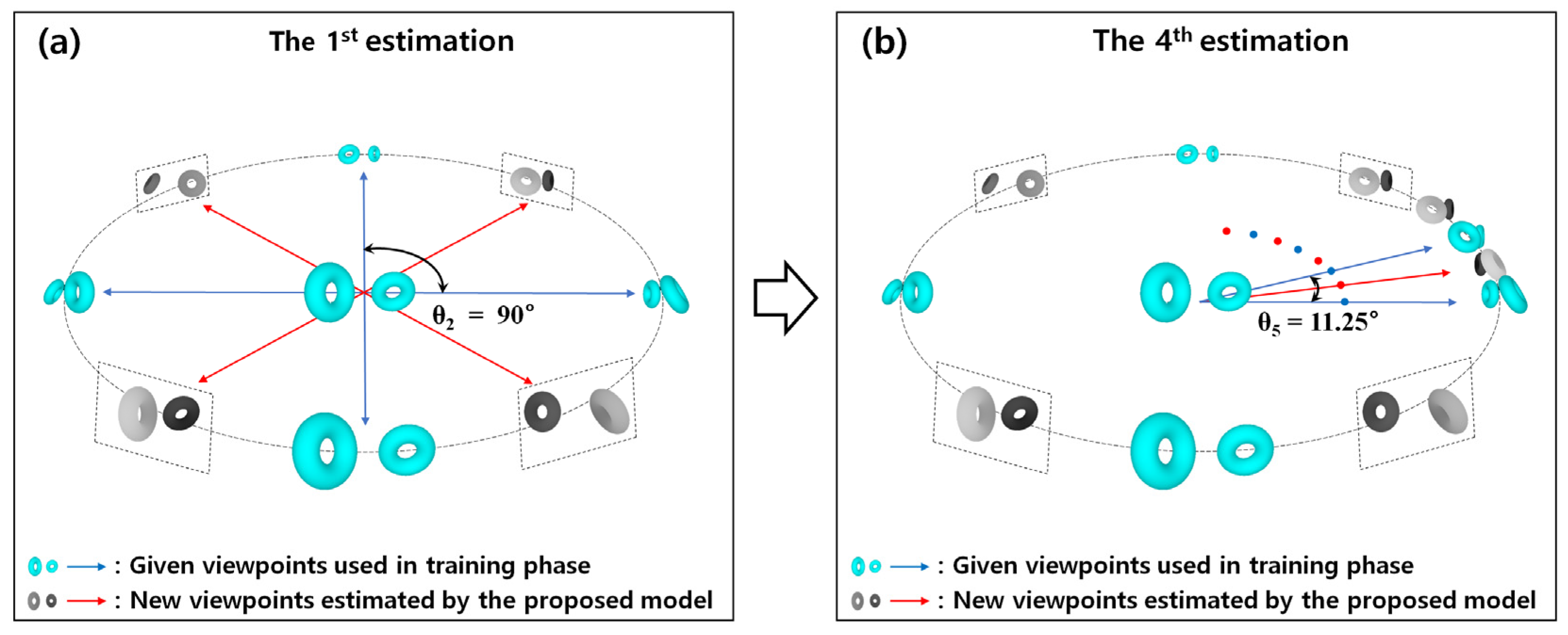
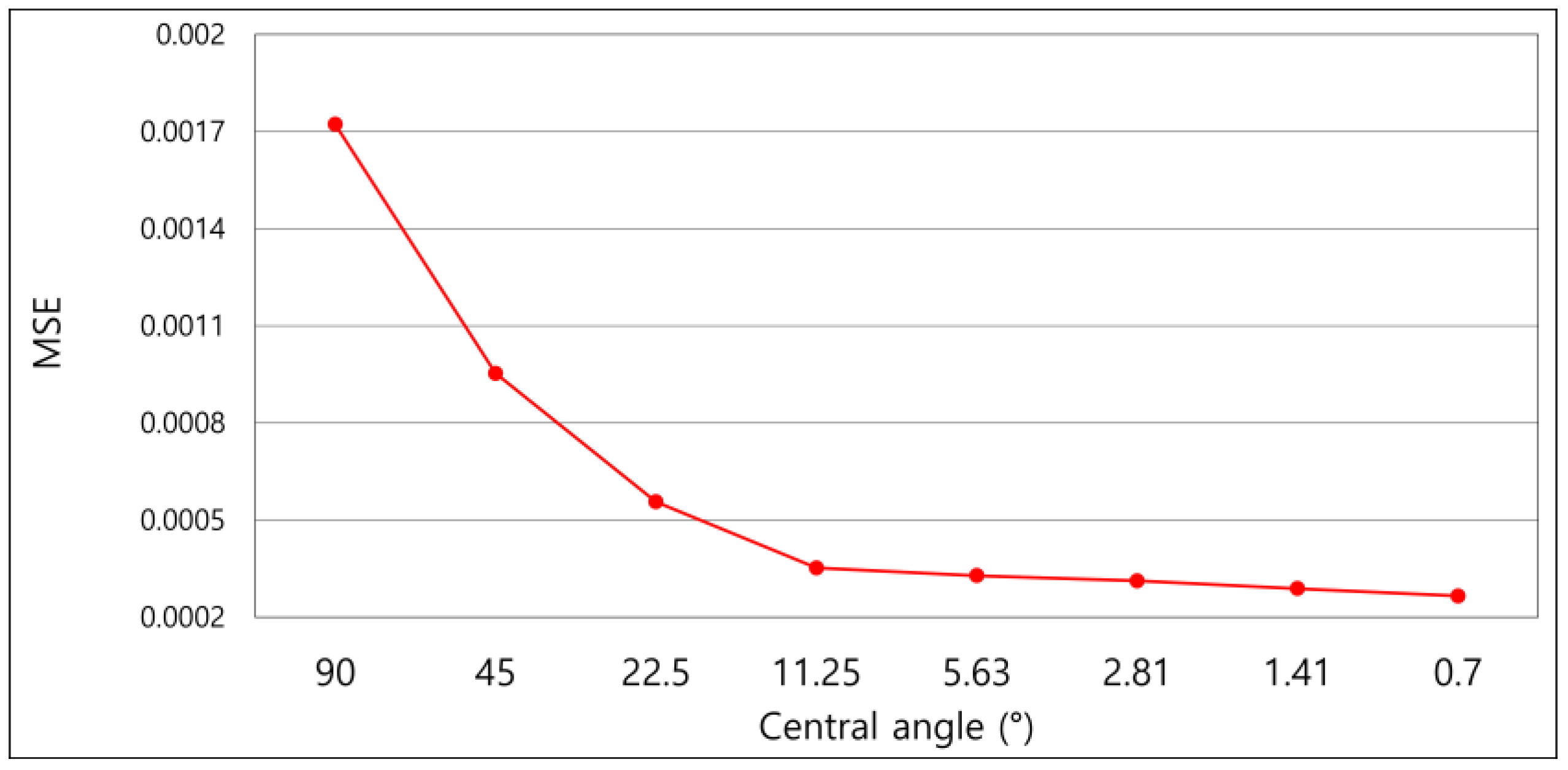
3.3. Process to Optimize Central Angles
4. Experiment Results and Discussion
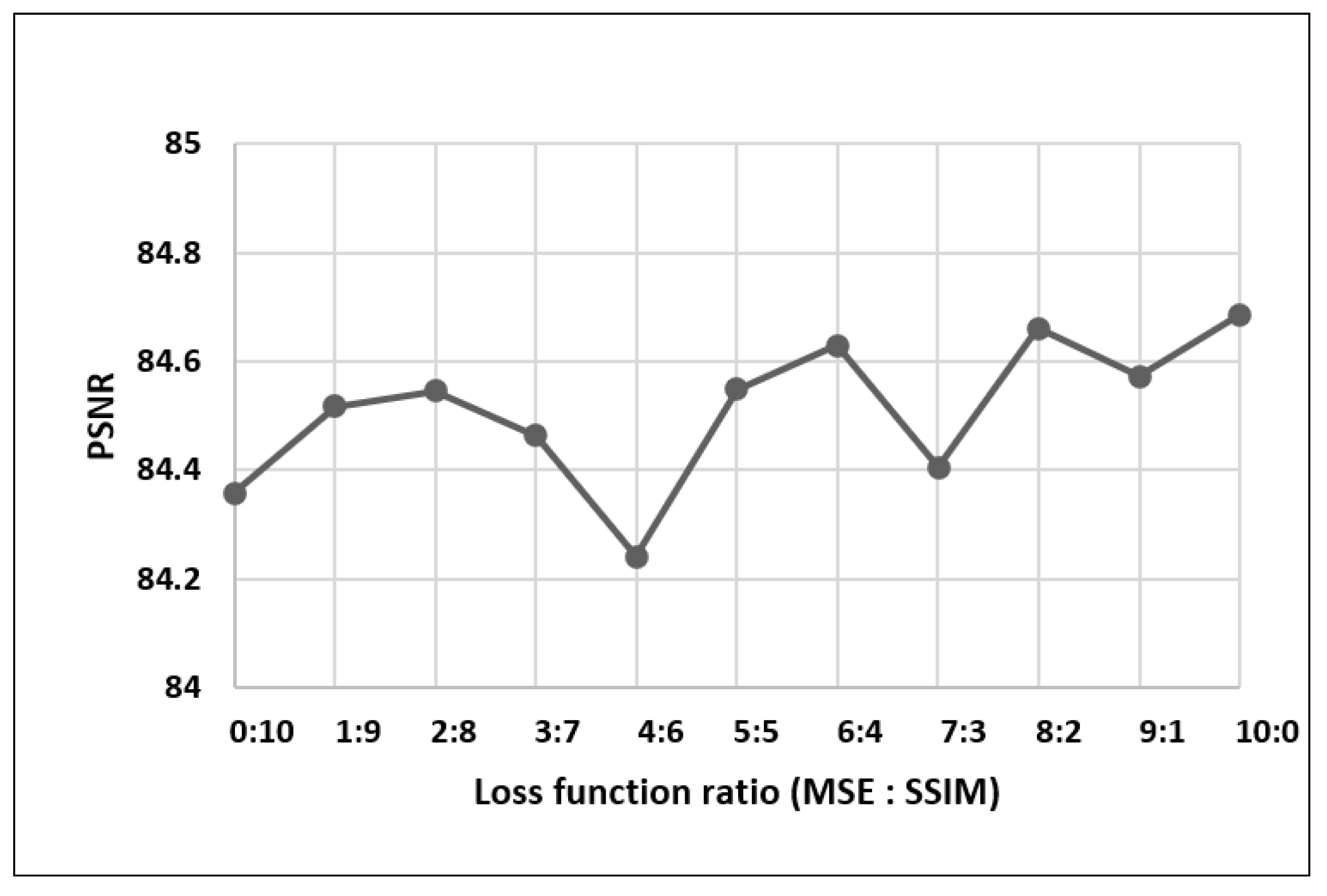
4.1. Depth Map Estimation Results Comparison
4.2. CGH Synthesis and Reconstruction Results Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CGH | Computer-Generated Hologram |
| 3D | Three-Dimensional |
| H3D | Holographic Three-Dimensional |
| CNN | Convolutional Neural Network |
| HDD | Holographic Dense Depth |
| MSE | Mean Squared Error |
| GPU | Graphics Processing Unit |
| ACC | Accuracy |
| XR | Extended Reality |
| AR | Augmented Reality |
References
- Shi, L.; Li, B.; Kim, C.; Kellnhofer, P.; Matusik, W. Towards real-time photorealistic 3D holography with deep neural networks. Nature 2021, 591, 234–239. [Google Scholar] [CrossRef] [PubMed]
- Park, S.M.; Kim, Y.G. A metaverse: Taxonomy, components, applications, and open challenges. IEEE Access 2022, 10, 4209–4251. [Google Scholar] [CrossRef]
- Mozumder, M.; Theodore, A.; Athar, A.; Kim, H. The metaverse applications for the finance industry, its challenges, and an approach for the metaverse finance industry. In Proceedings of the 2023 25th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 19–22 February 2023; pp. 407–410. [Google Scholar]
- Lee, H.; Kim, H.; Jun, T.; Son, W.; Kim, C.; Yoon, M. Hybrid Approach of Holography and Augmented-Reality Reconstruction Optimizations for Hyper-Reality Metaverse Video Applications. IEEE Trans. Broadcast. 2023, 69, 916–926. [Google Scholar] [CrossRef]
- Shin, S.; Eun, J.; Lee, S.; Lee, C.; Hugonnet, H.; Yoon, D.; Park, Y. Tomographic measurement of dielectric tensors at optical frequency. Nat. Mater. 2022, 21, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Jun, T.; Lee, H.; Chae, B.G.; Yoon, M.; Kim, C. Deep-learning based 3D birefringence image generation using 2D multi-view holographic images. Sci. Rep. 2024, 14, 9879. [Google Scholar] [CrossRef] [PubMed]
- Haleem, A.; Javaid, M.; Singh, R.; Suman, R.; Rab, S. Holography and its applications for industry 4.0: An overview. Internet Things Cyber-Phys. Syst. 2022, 2, 42–48. [Google Scholar] [CrossRef]
- Zhong, C.; Sang, X.; Yan, B.; Li, H.; Chen, D.; Qin, X. Real-time realistic computer-generated hologram with accurate depth precision and a large depth range. Opt. Express 2022, 30, 40087–40100. [Google Scholar] [CrossRef] [PubMed]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process. Syst. 2014, 27, 2366–2374. [Google Scholar]
- Li, B.; Shen, C.; Dai, Y.; Van Den Hengel, A.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical CRFs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1119–1127. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G.; Reid, I. Learning depth from single monocular images using deep convolutional neural fields. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2024–2039. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Shen, X.; Lin, Z.; Cohen, S.; Price, B.; Yuille, A. Towards unified depth and semantic prediction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2800–2809. [Google Scholar]
- Lore, K.; Reddy, K.; Giering, M.; Bernal, E. Generative adversarial networks for depth map estimation from RGB video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1177–1185. [Google Scholar]
- Aleotti, F.; Tosi, F.; Poggi, M.; Mattoccia, S. Generative adversarial networks for unsupervised monocular depth prediction. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland; pp. 234–241. [Google Scholar]
- Alhashim, I.; Wonka, P. High quality monocular depth estimation via transfer learning. arXiv 2018, arXiv:1812.11941. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Yang, Z.; Wang, P.; Xu, W.; Zhao, L.; Nevatia, R. Unsupervised learning of geometry with edge-aware depth-normal consistency. arXiv 2017, arXiv:1711.03665. [Google Scholar] [CrossRef]
- Alagoz, B. Obtaining depth maps from color images by region based stereo matching algorithms. arXiv 2008, arXiv:0812.1340. [Google Scholar]
- Joung, S.; Kim, S.; Ham, B.; Sohn, K. Unsupervised stereo matching using correspondence consistency. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 2518–2522. [Google Scholar]
- Garg, R.; Bg, V.; Carneiro, G.; Reid, I. Unsupervised CNN for single view depth estimation: Geometry to the rescue. In Proceedings of the European Conference on Computer Vision–ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 740–756. [Google Scholar]
- Luo, Y.; Ren, J.; Lin, M.; Pang, J.; Sun, W.; Li, H.; Lin, L. Single view stereo matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 155–163. [Google Scholar]
- Wu, Z.; Wu, X.; Zhang, X.; Wang, S.; Ju, L. Spatial correspondence with generative adversarial network: Learning depth from monocular videos. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7494–7504. [Google Scholar]
- Shekhar, S.; Xiong, H. Encyclopedia of GIS; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Pei, Z.; Wen, D.; Zhang, Y.; Ma, M.; Guo, M.; Zhang, X.; Yang, Y. MDEAN: Multi-view disparity estimation with an asymmetric network. Electronics 2020, 9, 924. [Google Scholar] [CrossRef]
- Zioulis, N.; Karakottas, A.; Zarpalas, D.; Alvarez, F.; Daras, P. Spherical view synthesis for self-supervised 360 depth estimation. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; pp. 690–699. [Google Scholar]
- Feng, Q.; Shum, H.; Shimamura, R.; Morishima, S. Foreground-aware dense depth estimation for 360 images. J. WSCG 2020, 28, 79–88. [Google Scholar] [CrossRef]
- Autodesk Maya. 2025. Available online: https://www.autodesk.com/products/maya/overview (accessed on 11 July 2025).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Hossein Eybposh, M.; Caira, N.; Atisa, M.; Chakravarthula, P.; Pégard, N. DeepCGH: 3D computer-generated holography using deep learning. Opt. Express 2020, 28, 26636–26650. [Google Scholar] [CrossRef] [PubMed]
- Lee, W. Sampled Fourier transform hologram generated by computer. Appl. Opt. 1970, 9, 639–643. [Google Scholar] [CrossRef] [PubMed]
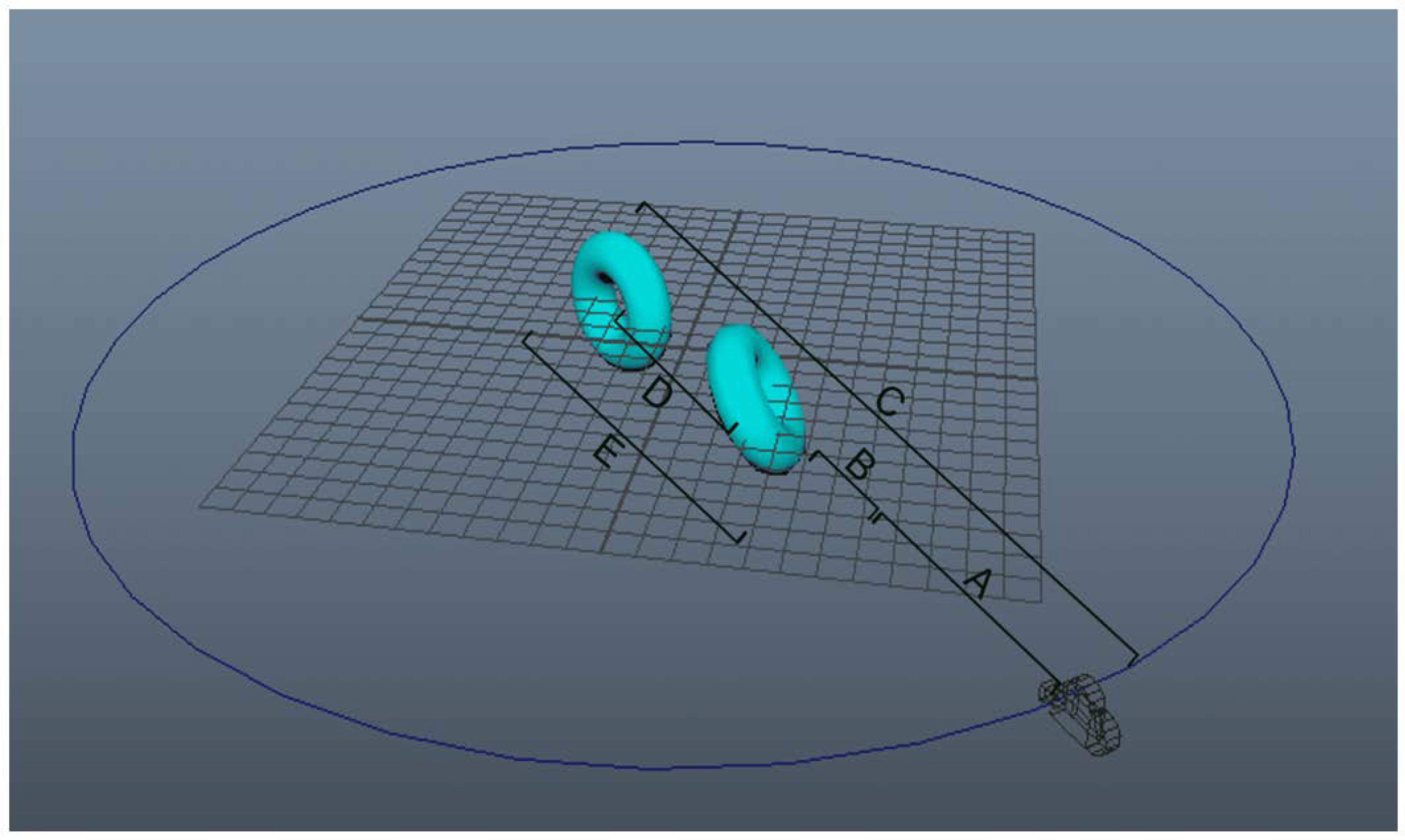





| A: Distance from virtual camera to 255 depth | 11 cm |
| B: Margin from depth boundary to object | 2.0 cm |
| C: Distance from virtual camera to 0 depth | 28.7 cm |
| D: Distance between two objects (center to center) | 8.3 cm |
| E: Distance from 0 depth to 255 depth | 14.2 cm |
| Radius of camera’s rotation path (R) | 20 cm |
| Central Angle (°) | 11.25 | 5.63 | 0.7 |
| Depth Map Learning Time (min:s) | 3:32 | 7:04 | 113:04 |
| CGH’s Synthesis Time (min:s) | 12:10 | 97:17 | 1556:29 |
| CGH’s Reconstruction Time (min:s) | 4:06 | 32:48 | 524:48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Lee, Y.; Yoon, M.; Kim, C. Deep Learning-Based Optimization of Central Angle and Viewpoint Configuration for 360-Degree Holographic Content. Appl. Sci. 2025, 15, 9465. https://doi.org/10.3390/app15179465
Kim H, Lee Y, Yoon M, Kim C. Deep Learning-Based Optimization of Central Angle and Viewpoint Configuration for 360-Degree Holographic Content. Applied Sciences. 2025; 15(17):9465. https://doi.org/10.3390/app15179465
Chicago/Turabian StyleKim, Hakdong, Yurim Lee, MinSung Yoon, and Cheongwon Kim. 2025. "Deep Learning-Based Optimization of Central Angle and Viewpoint Configuration for 360-Degree Holographic Content" Applied Sciences 15, no. 17: 9465. https://doi.org/10.3390/app15179465
APA StyleKim, H., Lee, Y., Yoon, M., & Kim, C. (2025). Deep Learning-Based Optimization of Central Angle and Viewpoint Configuration for 360-Degree Holographic Content. Applied Sciences, 15(17), 9465. https://doi.org/10.3390/app15179465







