Transient Stability Analysis and Enhancement Strategies for AC Side of Hydro-Wind-PV VSC-HVDC Transmission System
Abstract
1. Introduction
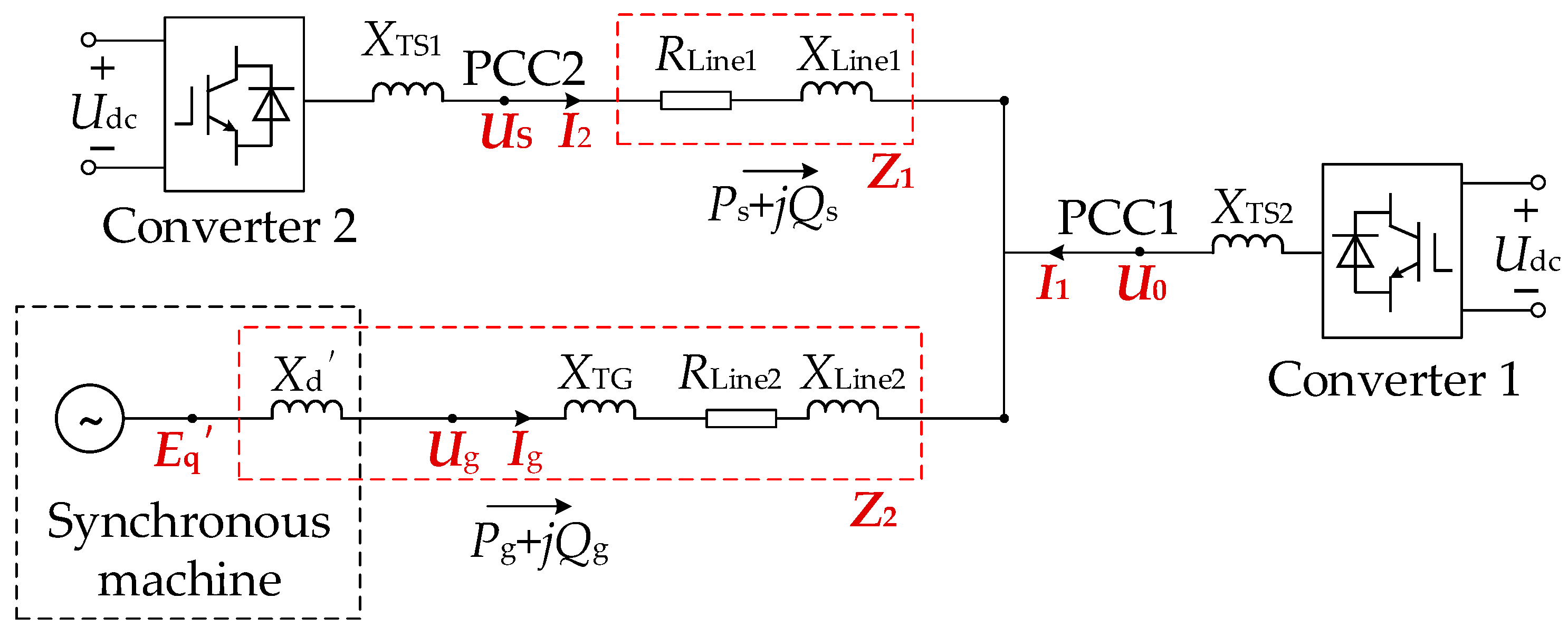
2. The Sending-End AC System of a Hydro-Wind-PV VSC-HVDC Transmission System
- The DC voltage of the sending-end converter station is kept constant by energy storage or other converter stations, with its dynamic variations neglected in the study;
- The inner-loop current controllers of converters, including both VSC-HVDC converters and renewable energy converters, respond significantly faster than outer-loop controllers [27], allowing the current inner-loop dynamics to be disregarded in transient stability analysis;
- The SGs in this study employ the classical second-order model, maintaining constant q-axis transient EMF E′q during transient processes;
- The resistive components in the equivalent impedances of transformers and SGs are relatively small, thus their influence is neglected;
- Limited by overcurrent capability, converters will switch to current-limiting mode upon detecting a voltage drop below the threshold during severe AC-side short-circuit faults.
- The AC bus node of Converter 2 is denoted as PCC2;
- RLine1 and XLine1 represent the resistance and reactance of Line 1, respectively;
- RLine2 and XLine2 represent the resistance and reactance of Line 2, respectively;
- XTs1 and XTs2 represent the connection reactance of Converter 1 and Converter 2, respectively;
- XTG represents the leakage reactance of the SG’s step-up transformer;
- X′d represents the transient reactance of the SG;
- Z1 and Z2 represent the equivalent impedances between PCC2 and PCC1, and between the E′q node and PCC1, respectively;
- U0 and I1 represent the voltage and injected current at PCC1, respectively;
- Us, I2, Ps and Qs represent the voltage, injected current, active power output and reactive power output at PCC2, respectively;
- Ug, Ig, Pg and Qg represent the terminal voltage, injected current, active power output and reactive power output of the SG, respectively.
3. Generic Model for Transient Stability Analysis of Sending-End AC Systems
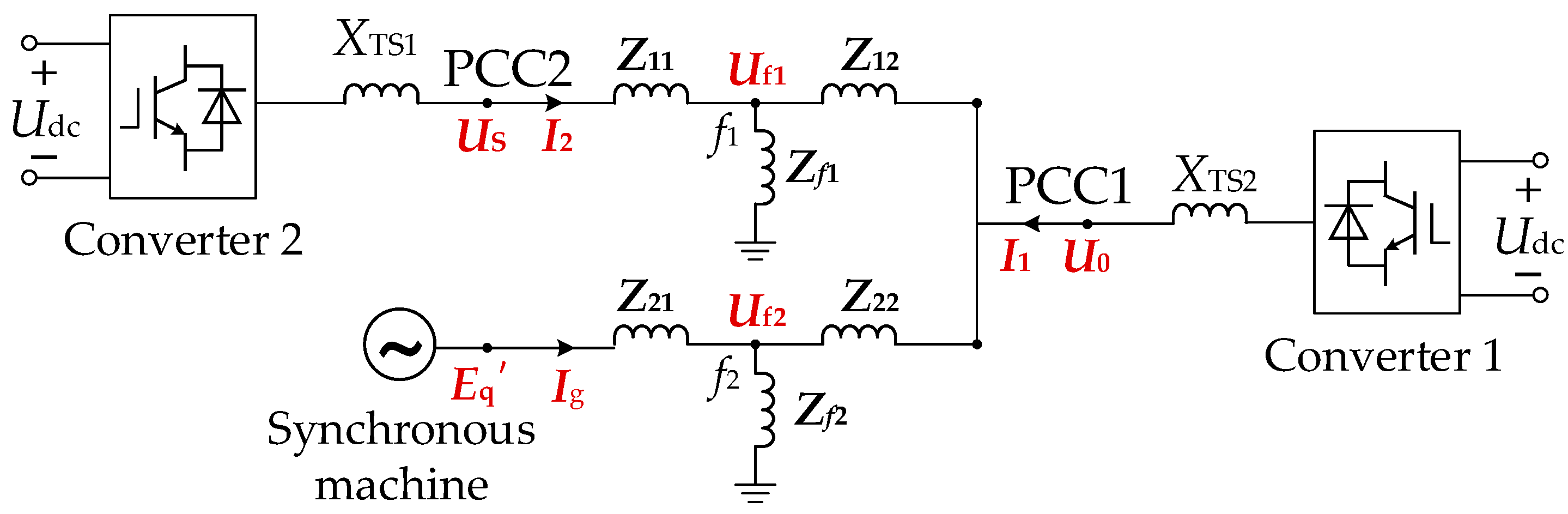
3.1. Generic Equivalent Circuit Model
- Uf1 and Uf2 represent the voltage phasors at fault points f1 and f2, respectively;
- Zf1 and Zf2 denote the equivalent impedances of faults occurring on Line 1 and Line 2, respectively, which are determined by the fault type;
- Z11 and Z12 represent the impedances between fault point f1 and the PCC2, and between f1 and the PCC of Converter 1, respectively;
- Z21 and Z22 represent the impedances between fault point f2 and the transient EMF equivalent point of the SG, and between f2 and the PCC1, respectively;
- The ratio of Zi2 to Zi is defined as Ki (i = 1 or 2), which characterizes the relative distance between fault point fi and Converter 1.
3.2. Transient Stability Analysis Model for GFM Converters
3.3. Transient Stability Analysis Model for GFL Converters
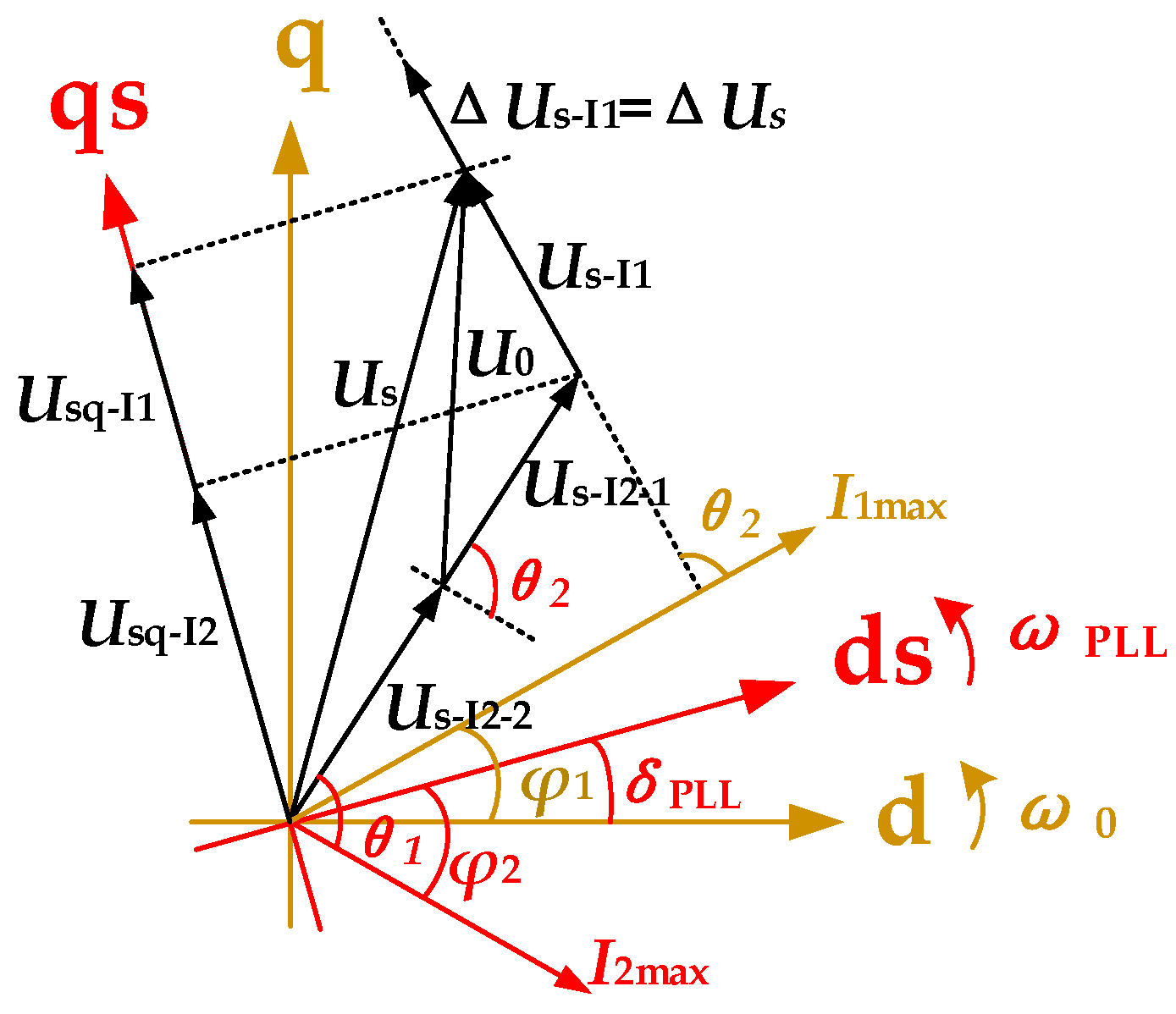
- δPLL represents the angle between the ds-axis and d-axis;
- Jsi, Pmsi, Pesi, and Dsi denote Converter 2’s equivalent inertia coefficient, equivalent mechanical power, equivalent electromagnetic power, and equivalent damping coefficient, respectively;
- i indicates the system operating state, where i = 0 corresponds to normal operation and i = 1 or 2 indicates a fault on Line 1 or Line 2, respectively. The same meaning applies hereafter.
- L1 and R1 represent the inductance and resistance values of impedance Z1, respectively;
- L2 and R2 denote the inductance and resistance values of impedance Z2, respectively;
- Isd and Isq are the ds-axis and qs-axis components of the current phasor Is.
3.4. Transient Stability Analysis Model for SGs
4. Transient Stability Analysis of the Sending-End AC System
4.1. Transient Stability Assessment
4.2. Factors Affecting Transient Stability
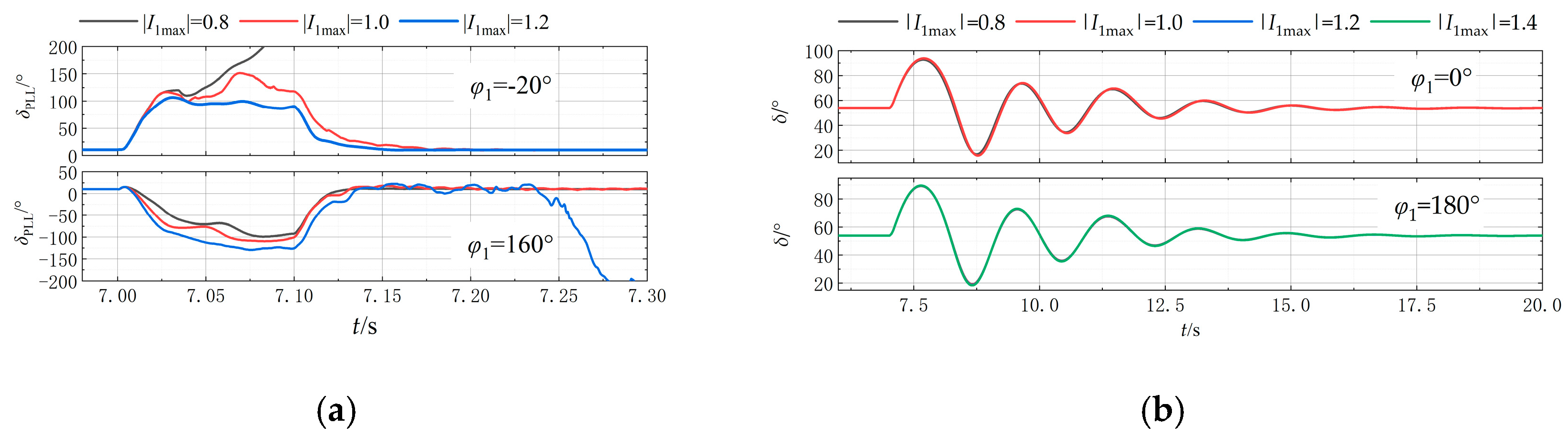
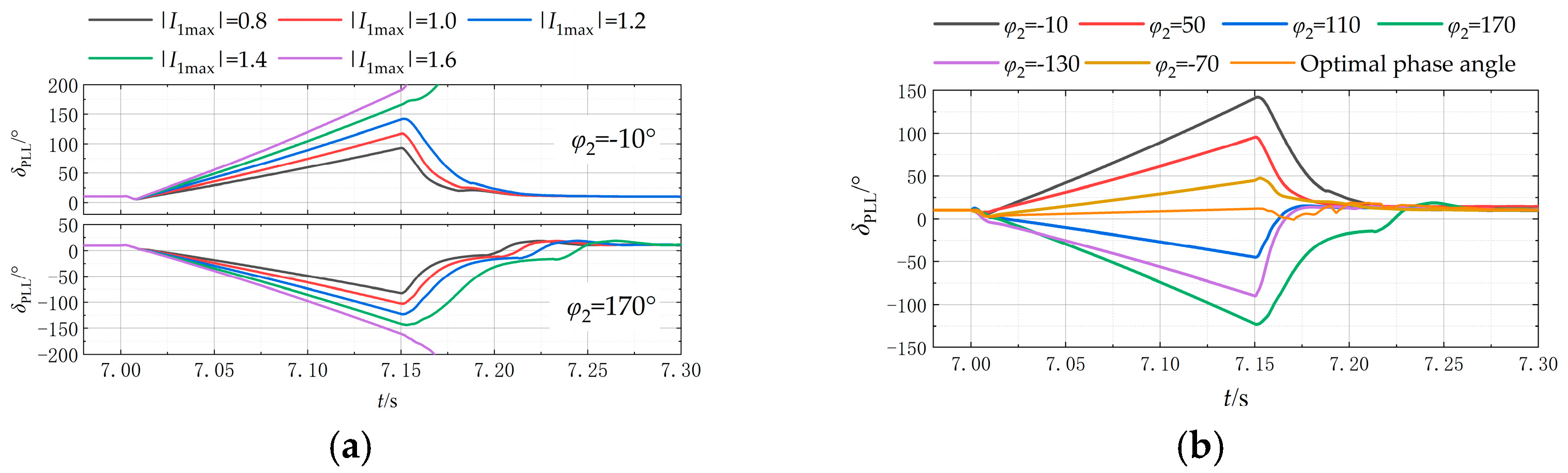
4.2.1. Limiting Current in Converter Current-Limiting Mode
- If the initial value of Usq (Usq0) is nonzero and |I1max| results in |Usq-I1| < |Usq-I2|, δPLL will monotonically increase (if Usq0 > 0) or decrease (if Usq0 < 0).
- As |I1max| increases, δPLL may either stabilize due to damping or exhibit oscillatory growth/decay, depending on the phase of I1max.
- If the phase of I1max remains unchanged, further increasing |I1max| will cause δPLL that was stabilizing due to damping to continue stabilizing, while δPLL that was oscillating will either oscillate more prominently or transition to a stable state.
4.2.2. Fault Location
5. Parameter Tuning Methodology for Transient Stability Enhancement
5.1. Parameter Tuning Methodology for GFL Converter Outgoing Line Faults
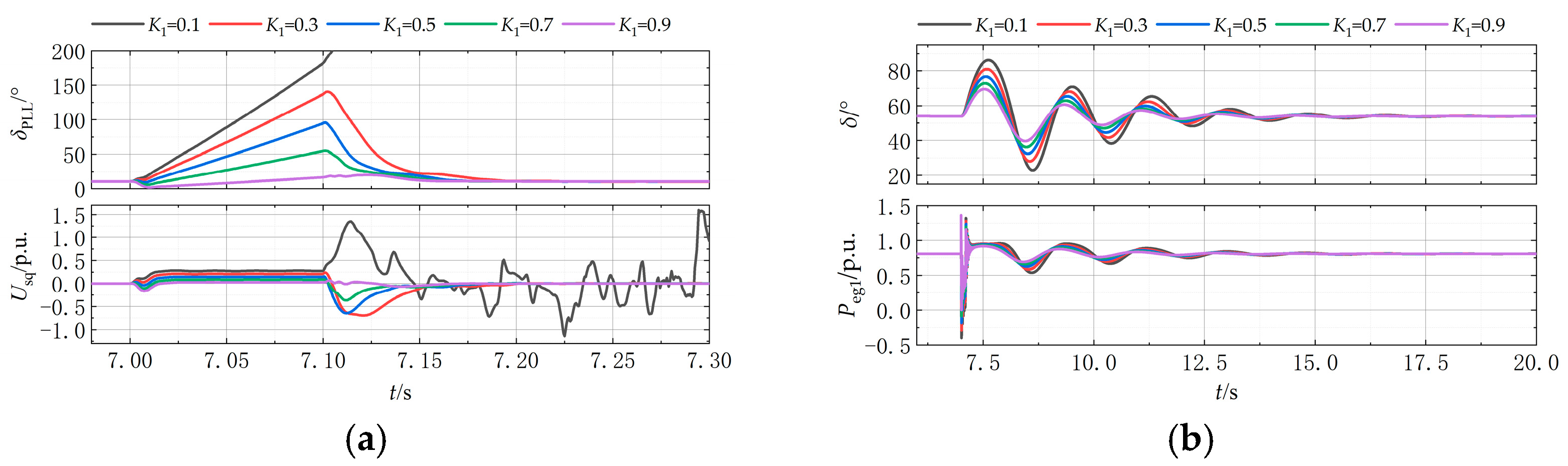
5.1.1. Parameter Tuning Methodology for SG
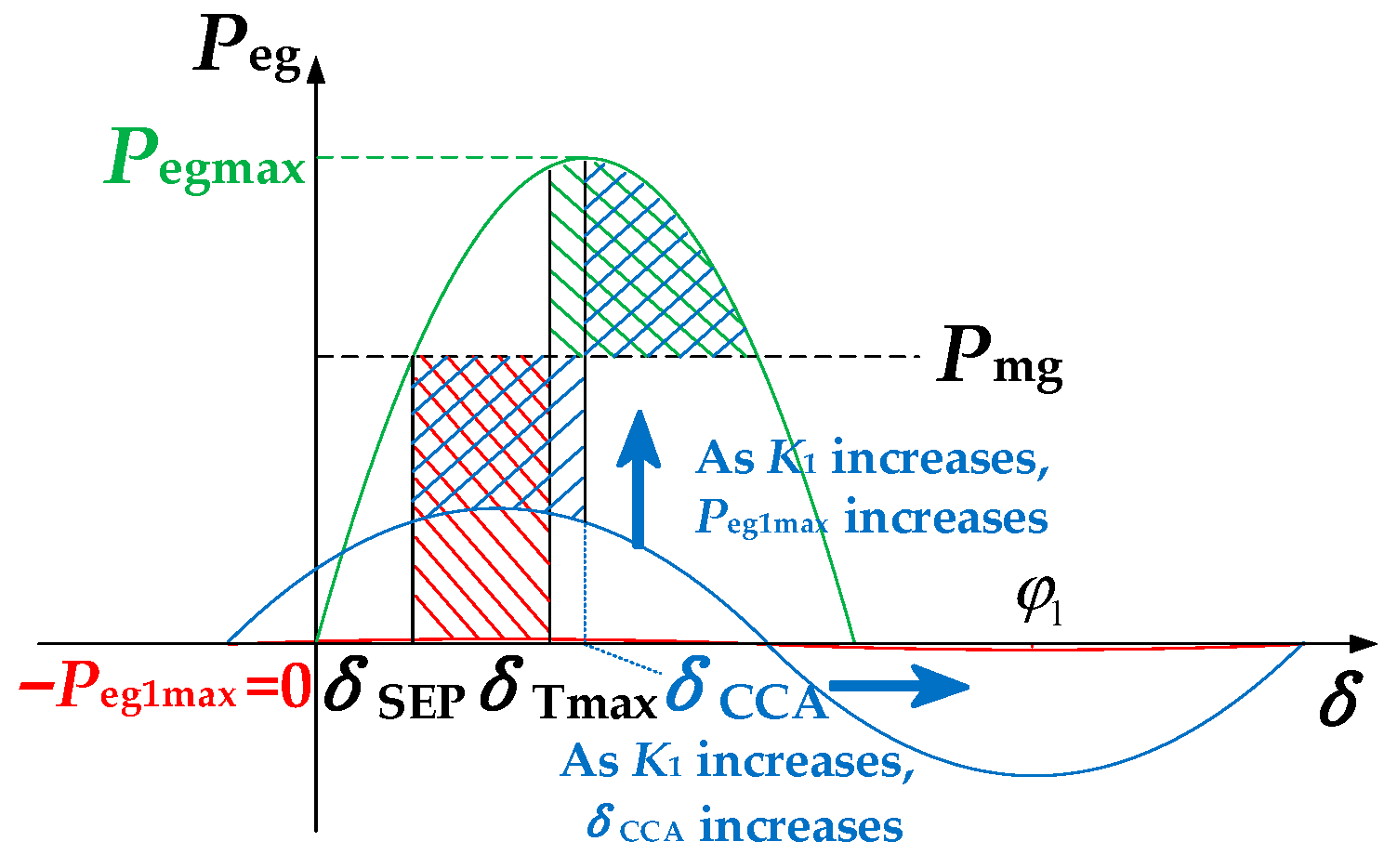
- For a given δT, S+ reaches the minimum value among all possible φ1 settings;
- δT corresponds to the δCCA under this specific φ1.
- For any fault location along Line 1, δCCA remains greater than δCCA-min;
- This φ1 value maximally increases δCCA in the vicinity of δCCA-min.
5.1.2. Parameter Tuning Methodology for GFL Converter
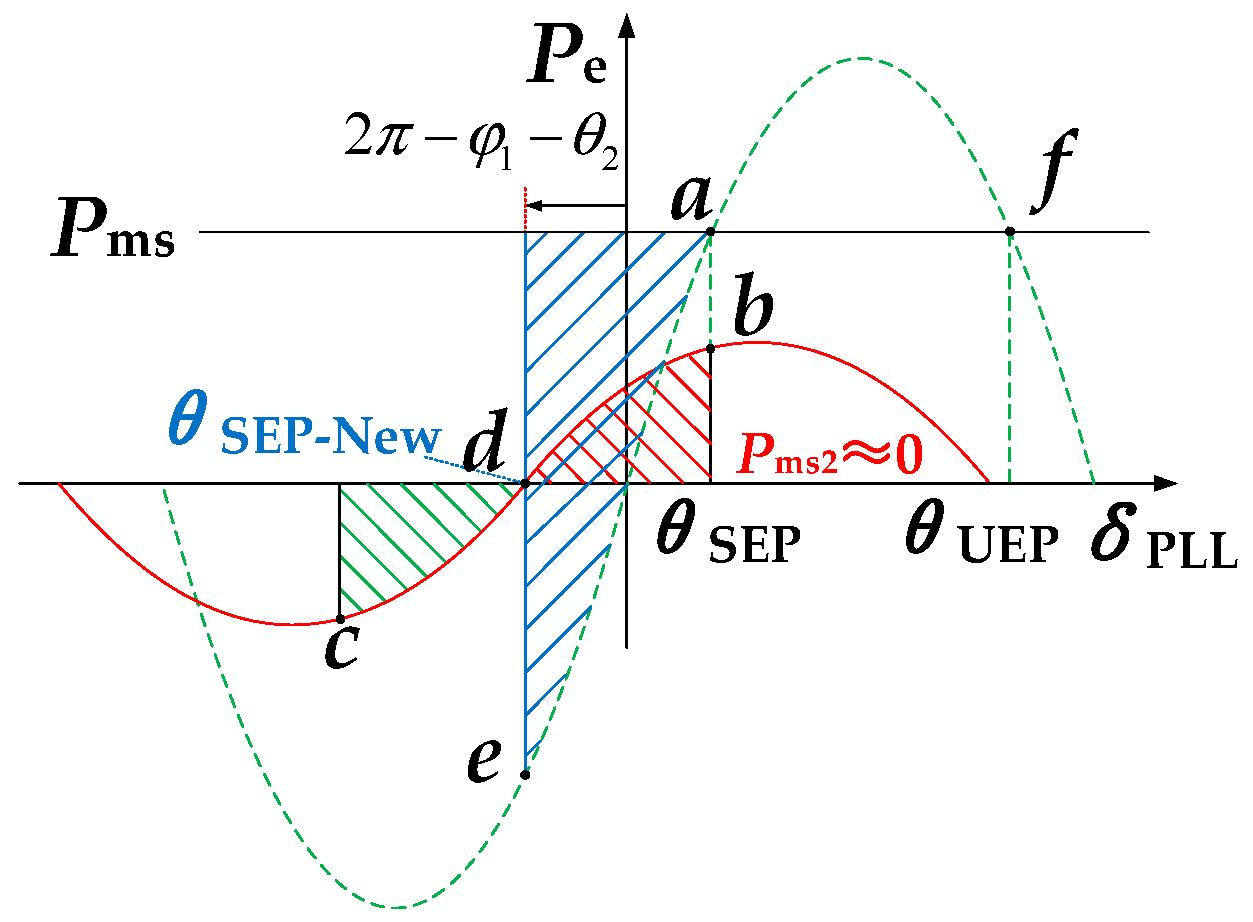
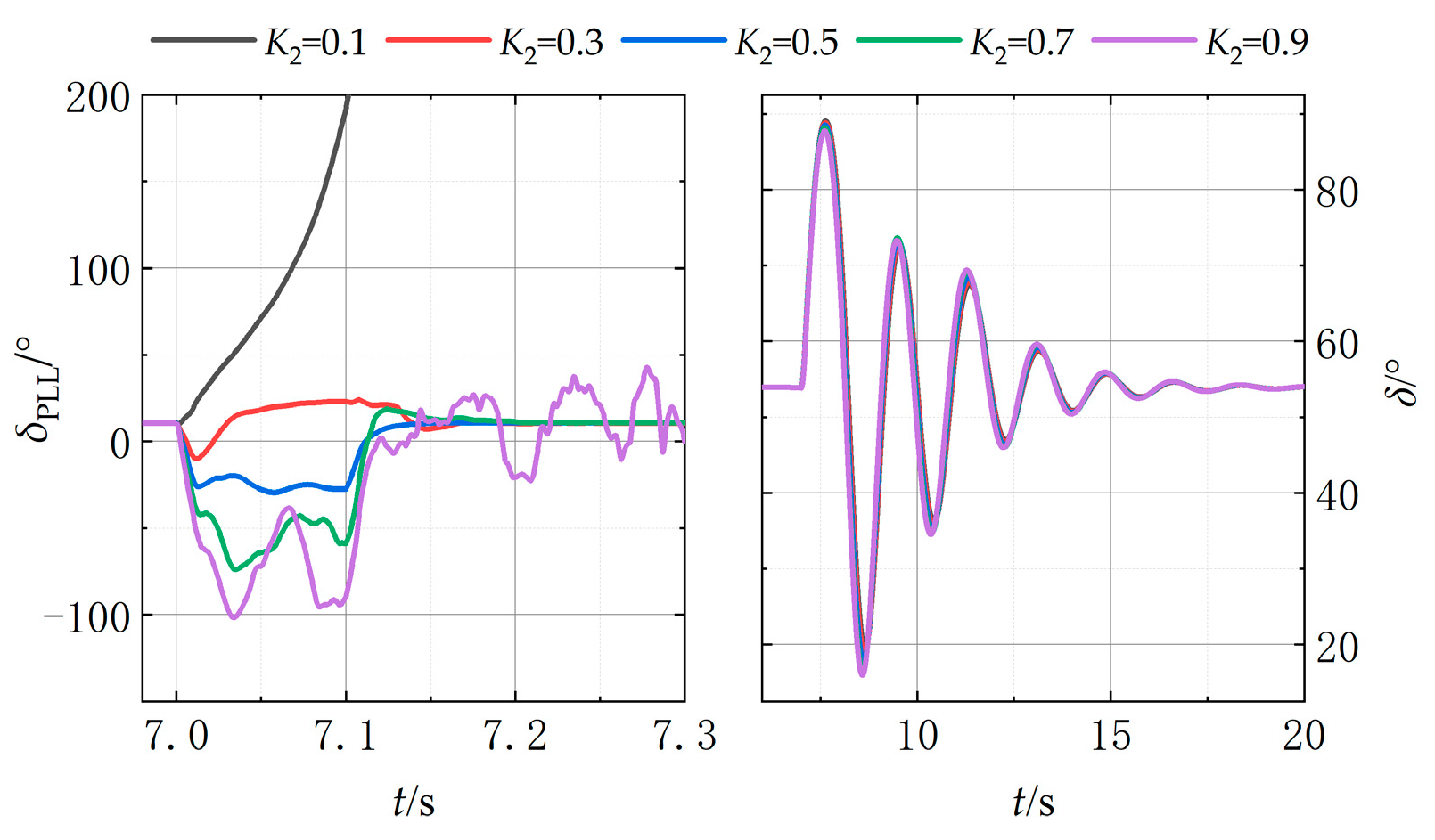
5.2. Parameter Tuning Methodology for SG Outgoing Line Faults
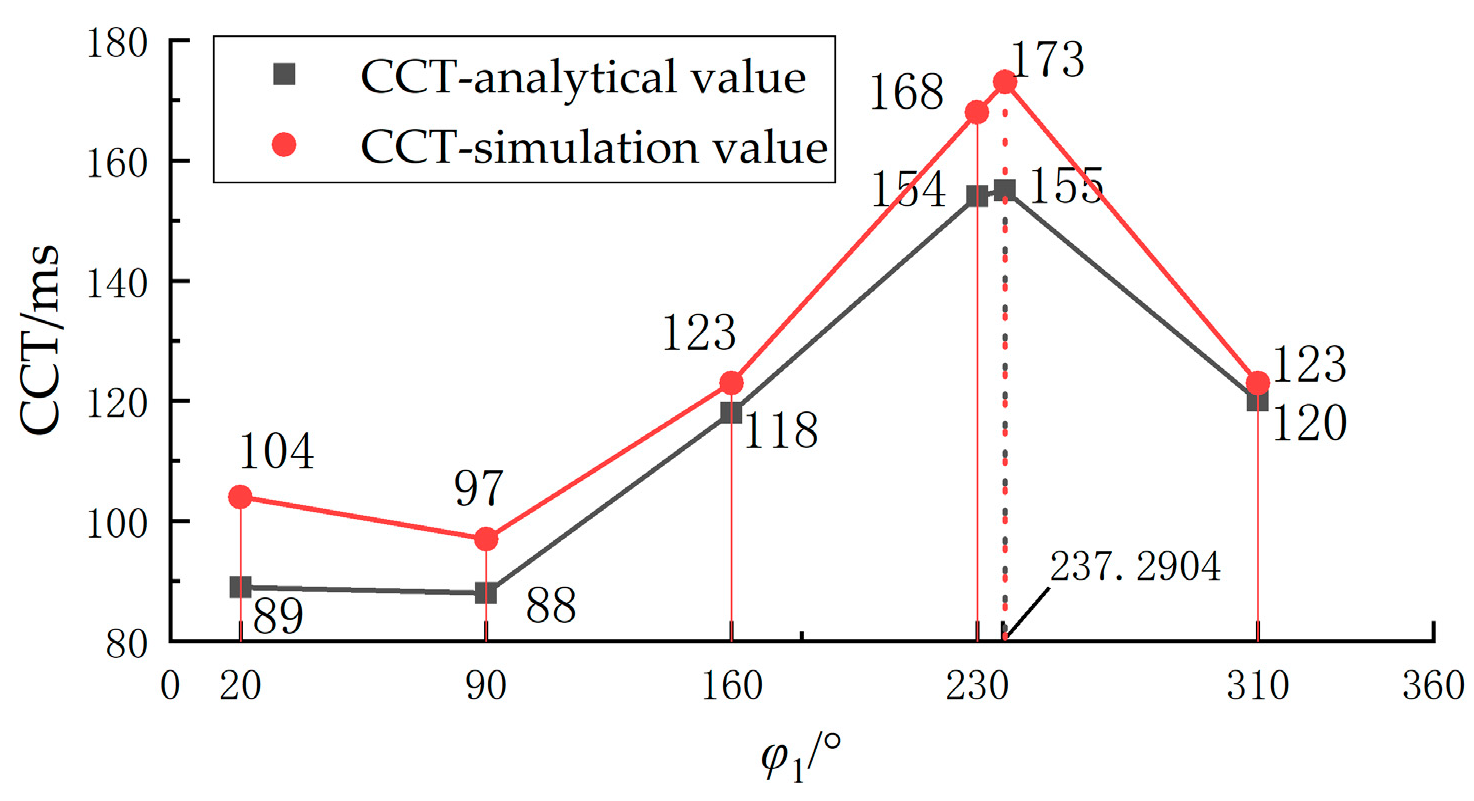
6. Results
6.1. Case Overview
6.2. Simulation of Transient Stability Influencing Factors
7. Conclusions
- In the context of hydro-wind-PV VSC-HVDC transmission, multiple types of equipment are mutually coupled. Various factors influence its transient stability by affecting the phase and magnitude of the PLL input phasor Usq and the electromagnetic power of synchronous machines.
- The energy transfer paths and control interactions during transient processes are related to the fault location, parameter settings of the current-limiting mode in converter stations, and the operational states of the equipment.
- This paper derives an optimal phase angle calculation formula for the current-limiting mode of converters and proposes a tuning method for extending the current-limiting mode duration during the recovery stage. These measures aim to enhance system transient stability when transmission line faults occur. The correctness of the analysis and the effectiveness of the proposed method are verified by PSCAD.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| PV | Photovoltaic |
| VSC | Voltage Source Converter |
| HVDC | High-Voltage Direct Current |
| MMC | Modular Multilevel Converter |
| GFM | Grid-Forming |
| GFL | Grid-Following |
| SG | Synchronous Generator |
| PLL | Phase-locked Loops |
| EMF | Electromotive Force |
| EAC | Equal Area Criterion |
| CCT | Critical Clearing Time |
| SEP | Stable Equilibrium Point |
| UEP | Unstable Equilibrium Point |
| CCA | Critical Clearing Angle |
Appendix A
Appendix A.1
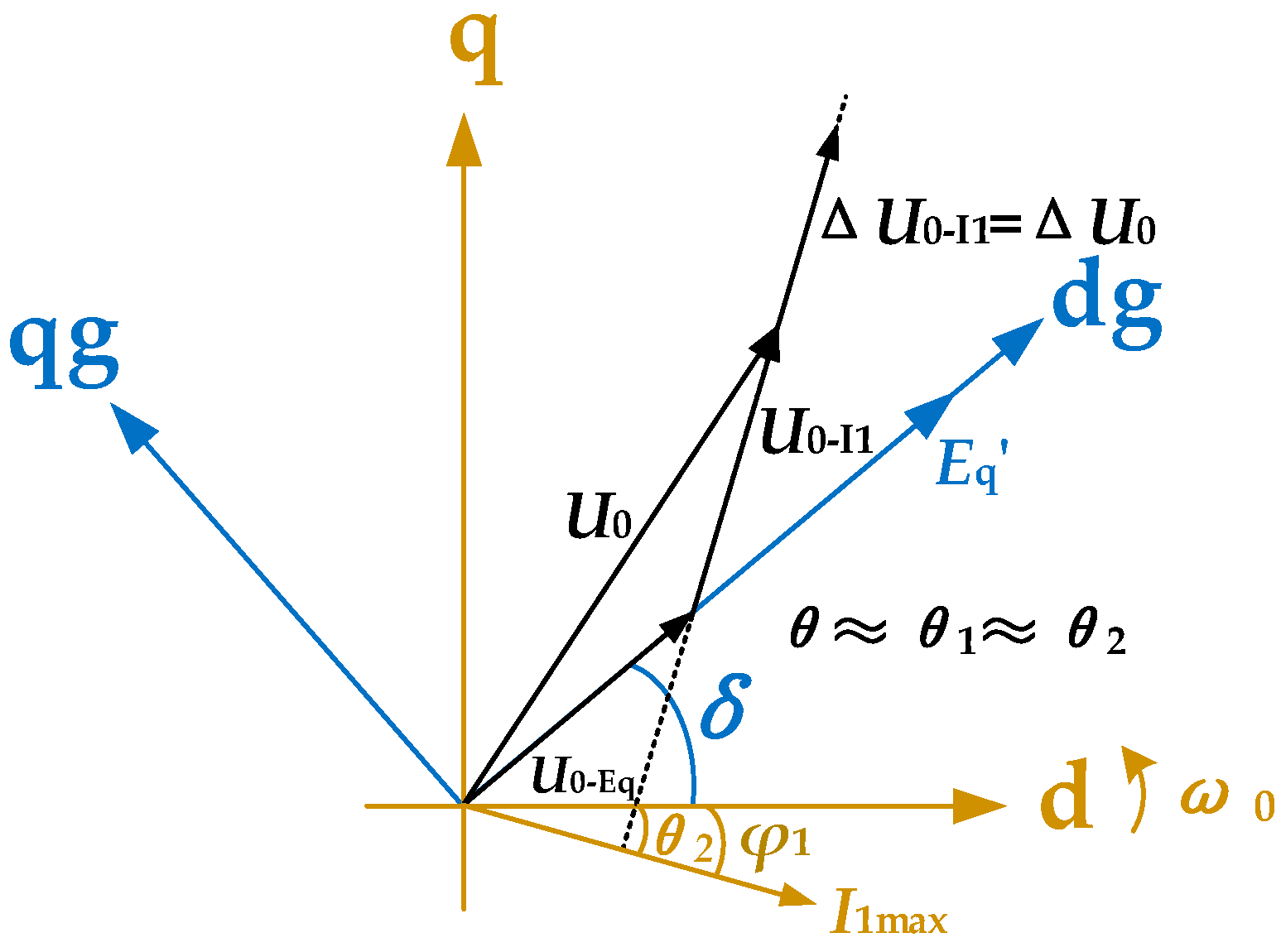
- δ denotes the angle between E′q and the dg-axis of the dgqg rotating frame;
- ω represents the angular velocity corresponding to δ;
- δPLL indicates the angular displacement between the dq frame and dgqg frame.
Appendix A.2
References
- Xu, J.; Zhang, W.; Liu, W.; Li, Y.; Tian, X.; Liu, C.; Wei, L. Study on the driving force and challenges of developing power grid with high penetration of renewable energy. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, Y.; Lei, Z.; Lu, Z.; Liu, S.; Xie, Y.; Liu, M. An Optimization Method for Distributed Energy Resource Aggregators to Participate in Electricity Market Bidding Considering PV Uncertainty and Distribution Network Security Check. Guangdong Electr. Power 2024, 37, 138–146. [Google Scholar]
- Tang, W.; Nie, X.; Qian, T.; Guo, C.; Chen, W. Review and Prospect on Application Technologies of Energy Storage for Safety and Stability of New Power System. Guangdong Electr. Power 2024, 37, 3–15. [Google Scholar]
- International Renewable Energy Agency. Renewable Capacity Statistics 2025; IRENA Publications: Abu Dhabi, United Arab Emirates, 2025; pp. 58–61.
- National Energy Administration Releases National Power Industry Statistics for January–August 2024. Available online: https://www.nea.gov.cn/2024-09/23/c_1212399359.htm (accessed on 23 September 2024).
- Gantumur, S.; Bekhbat, G. Challenges of hybrid DGs for islanded micro-grid operation in west region energy system of Mongolia. In Proceedings of the 2016 11th International Forum on Strategic Technology (IFOST), Novosibirsk, Russia, 1–3 June 2016. [Google Scholar] [CrossRef]
- Dusenge, P.; Niyonsaba, J.D.A.; Samvura, J.D.D.; Bikorimana, J.; Rwahama, T.; Mudaheranwa, E. Feasibility study of hybrid Hydro-PV power plant possible deployment in remote rural area. In Proceedings of the 2022 IEEE PES/IAS Power Africa, Kigali, Rwanda, 22–26 August 2022. [Google Scholar] [CrossRef]
- Tian, Z. Further Promoting the Development of New Energy in Western China. China Ind. 2010, 3, 16. [Google Scholar]
- Ci, Z. Overview of New Energy Development and Utilization in Tibet, China. Energy Eng. 1996, 16, 6. [Google Scholar]
- Yang, J.; Dai, Q.; Zhou, Y. Research on Wind Resource Utilization of Plateau Mountain Wind Farms. In Proceedings of the Internet of Things and New Power Technologies—Yunnan Power Technology Forum 2014, Kunming, China, 8 December 2014; p. 254. [Google Scholar]
- Sun, Q.; Li, D.; Wang, R.; Sui, Z.; Yao, J.; Shen, Q.; Yu, X. Power System with High Shares of Renewables and Power Electronics: A New Stability Criterion and Classification. Proc. CSEE 2024, 44, 3016–3036. [Google Scholar]
- Sultan, H.M.; Kuznetsov, O.N.; Menesy, A.S.; Kamel, S. Optimal Configuration of a Grid-Connected Hybrid PV/Wind/Hydro-Pumped Storage Power System Based on a Novel Optimization Algorithm. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 12–14 March 2020. [Google Scholar] [CrossRef]
- Yang, L. Distribution Pattern and Spatiotemporal Changes of Bulk Energy Development and Utilization in China. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2012. [Google Scholar]
- Zhao, J. HVDC Transmission Technologies at the Frontier. Electr. Power 2005, 38, 1–6. [Google Scholar]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-Based HVDC Power Transmission Systems: An Overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Luo, B.; Chen, Y.; Liu, Z.; Miao, S.M.; Wang, H.R.; Zhang, H. Short-Term Optimal Dispatch Model for Maximizing Expectation of Accommodation Power of Cascade Hydro-Photovoltaic Complementary System. Autom. Electr. Power Syst. 2023, 47, 66–75. [Google Scholar]
- Rao, H.; Huang, W.; Guo, Z.; Zhou, Y. Practical Experience of VSC-HVDC Transmission in Large Grid. High Volt. Eng. 2022, 48, 3347–3355. [Google Scholar]
- Tan, J.; He, C.; Chen, B.; Liu, T.; Nan, L.; Yin, Y. Distributionally Robust Optimal Scheduling Method of Power System Considering Hydropower-Photovoltaic-Pumped Storage Complementarity and DC Transmission. Proc. CSEE 2024, 44, 5947–5960. [Google Scholar]
- Zhan, C.; Wu, H.; Wang, X.; Wang, J.; Tian, X.; Lu, Y. An Overview of Stability Studies of GFM Voltage Source Converters. Proc. CSEE 2023, 43, 2339–2359. [Google Scholar]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources—An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, X.; Wu, G.; Li, S.; Xue, Y.; Xu, Z. Analysis of Transient Synchronization Stability of Power System with GFM/GFL Nonsynchronous-Machine Sources. Acta Energiae Solaris Sin. 2024, 45, 218–228. [Google Scholar]
- Wang, X.; Du, W.; Wang, H. Stability Analysis of Grid-Tied VSC Systems Under Weak Connection Conditions. Proc. CSEE 2018, 38, 1593–1604. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef]
- Ruan, L.; Wang, Y.; Xiao, X.; Wang, H.; Xu, Q.; Jia, C. Dynamic Interaction Control Characteristic Analysis of GFL and GFM Inverters. Smart Power 2024, 52, 103–110. [Google Scholar]
- Huang, S.; Yao, J.; Zhong, Q.; Gong, S.; Xu, H. Transient Synchronization Stability Analysis of Hybrid Power System with GFL and GFM Renewable Energy Generation Units. Proc. CSEE 2024, 44, 8378–8392. [Google Scholar]
- Research on the Power Transmission Capability of PV-Hydro Complementary MMC-HVDC Transmission System. Available online: http://kns.cnki.net/kcms/detail/11.2107.tm.20240829.1325.014.html (accessed on 10 September 2024).
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current Limiting Control with Enhanced Dynamics of GFM Converters During Fault Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1062–1073. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters with GFM Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Ju, P.; Hu, J. Synchronization Stability Analysis and Unified Synchronization Control Structure of Grid-Connected Power Electronic Devices. Electr. Power Autom. Equip. 2020, 40, 10–25. [Google Scholar]
- Xiang, Z.; Ni, Q.; Li, Z.; Xu, J.; Xue, Y.; Zhang, Z.; Xu, Z. Transient Stability Mechanism Analysis of GFL MMC-HVDC. J. Electr. Eng. 2023, 18, 250–259. [Google Scholar]
- Wang, X.F. Modern Power System Analysis; Science Press: Beijing, China, 2003. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; pp. 279, 831, 835. [Google Scholar]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F. Large Signal Synchronizing Instability of PLL-Based VSC Connected to Weak AC Grid. IEEE Trans. Power Syst. 2019, 34, 3220–3229. [Google Scholar] [CrossRef]
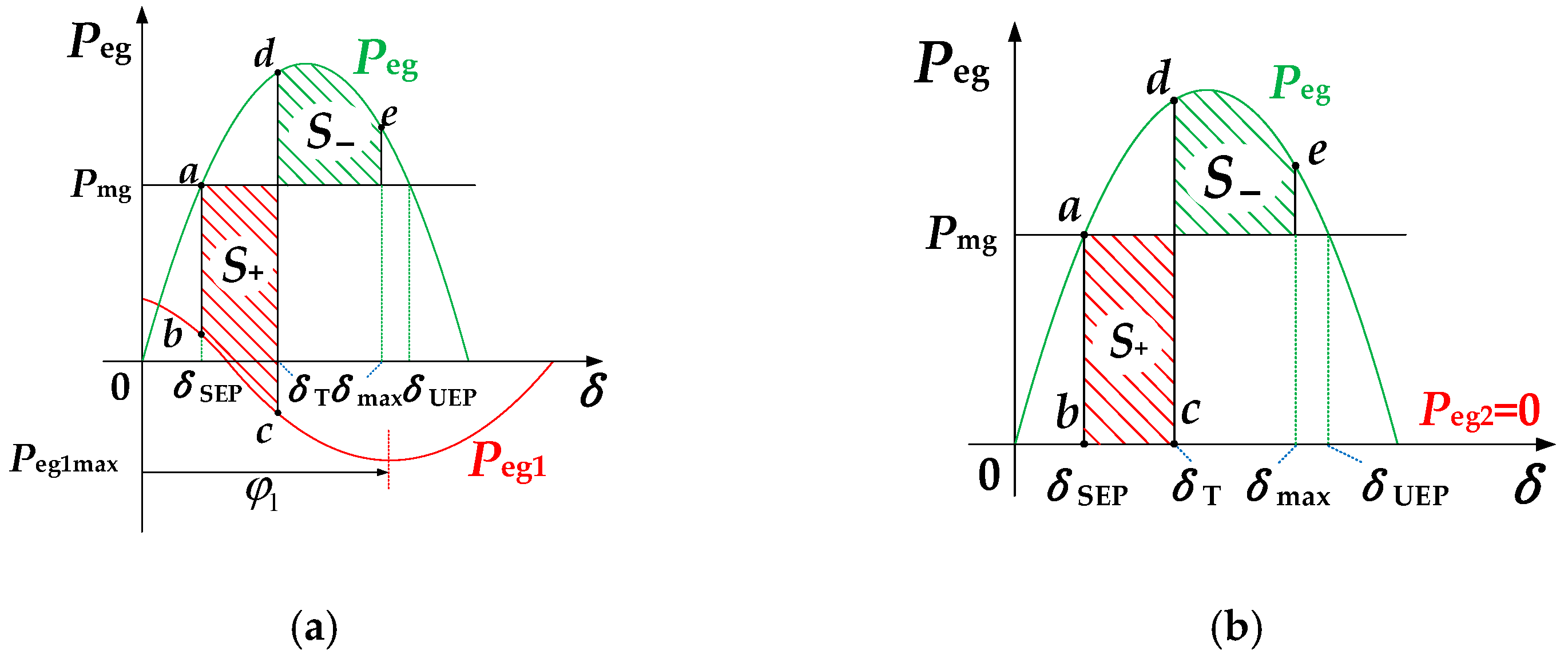
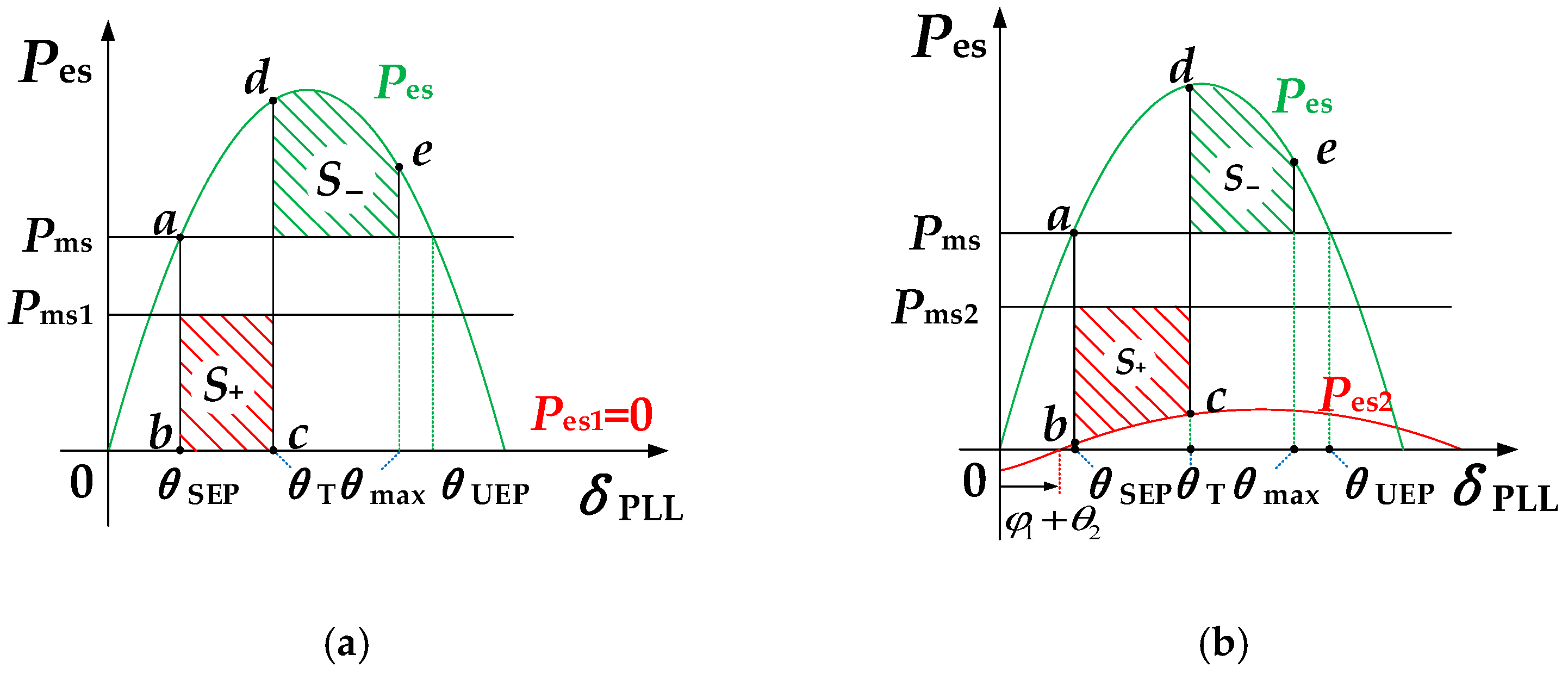

| Equipment | Parameter | Value |
|---|---|---|
| Converter 1 | Rated Capacity/MVA | 1000 |
| Rated DC Voltage/kV | 400 | |
| AC-side Voltage/kV | 230 | |
| Converter 2 | Rated Capacity/MVA | 500 |
| Rated DC Voltage/kV | 400 | |
| AC-side Voltage/kV | 230 | |
| SG | Rated Capacity/MVA | 500 |
| Rated Voltage/kV | 10 | |
| Line 1 | Line Impedance/p.u. | 0.046 |
| Impedance Angle/° | 84.2904 | |
| Line 2 | Line Impedance/p.u. | 0.185 |
| Impedance Angle/° | 84.2904 |
| Delay Time/s | CCT/ms | Dominant Unstable Equipment |
|---|---|---|
| 0.000 | 30 | Converter 2 |
| 0.005 | 102 | Converter 2 |
| 0.010 | 124 | SG |
| 0.015 | 124 | SG |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ma, Y.; Fang, J.; Ma, K.; Jiang, H.; Zhang, Z.; Xu, Z. Transient Stability Analysis and Enhancement Strategies for AC Side of Hydro-Wind-PV VSC-HVDC Transmission System. Appl. Sci. 2025, 15, 9456. https://doi.org/10.3390/app15179456
Li X, Ma Y, Fang J, Ma K, Jiang H, Zhang Z, Xu Z. Transient Stability Analysis and Enhancement Strategies for AC Side of Hydro-Wind-PV VSC-HVDC Transmission System. Applied Sciences. 2025; 15(17):9456. https://doi.org/10.3390/app15179456
Chicago/Turabian StyleLi, Xinwei, Yanjun Ma, Jie Fang, Kai Ma, Han Jiang, Zheren Zhang, and Zheng Xu. 2025. "Transient Stability Analysis and Enhancement Strategies for AC Side of Hydro-Wind-PV VSC-HVDC Transmission System" Applied Sciences 15, no. 17: 9456. https://doi.org/10.3390/app15179456
APA StyleLi, X., Ma, Y., Fang, J., Ma, K., Jiang, H., Zhang, Z., & Xu, Z. (2025). Transient Stability Analysis and Enhancement Strategies for AC Side of Hydro-Wind-PV VSC-HVDC Transmission System. Applied Sciences, 15(17), 9456. https://doi.org/10.3390/app15179456








