Quantum-Enhanced Battery Anomaly Detection in Smart Transportation Systems

Abstract

Ensuring the safety, reliability, and longevity of Lithium-ion (Li-ion) batteries is crucial for sustainable integration of Electric Vehicles (EVs) within Intelligent Transportation Systems (ITSs). However, thermal stress and degradation-induced anomalies can cause sudden performance failures, posing critical operational and safety risks. Capturing complex, non-linear, and high-dimensional patterns remains challenging for traditional Machine Learning (ML) models. We propose a hybrid anomaly detection method that incorporates a Variational Quantum Neural Network (VQNN), which uses the principles of quantum mechanics, such as superposition, entanglement, and parallelism, to learn complex non-linear patterns. The VQNN is integrated with Isolation Forest (IF) and a Median Absolute Deviation (MAD)-based spike characterisation method to form a Quantum Anomaly Detector (QAD). This method distinguishes between normal and anomalous spikes in battery behaviour. Using an Arrhenius-based model, we simulate how the State of Health (SoH) and voltage of a Li-ion battery reduce as temperatures increase. We perform experiments on NASA battery datasets and detect abnormal spikes in 14 out of 168 cycles, corresponding to $8.3$% of the cycles. The QAD achieves the highest Receiver Operating Characteristic Area Under the Curve (ROC-AUC) of $0.9820$, outperforming the baseline IF model by $7.78\%$. We use ML to predict the SoH and voltage changes when the temperature varies. Gradient Boosting (GB) achieves a voltage Mean Squared Error (MSE) of $0.001425$, while Support Vector Regression (SVR) achieves the highest $R^2$ score of $0.9343$. These results demonstrate that Quantum Machine Learning (QML) can be applied for anomaly detection in Battery Management Systems (BMSs) within intelligent transportation ecosystems and could enable EVs to autonomously adapt their routing and schedule preventative maintenance. With these capabilities, safety will be improved, downtime minimised, and public confidence in sustainable transport technologies increased.

1. Introduction

The global shift towards sustainable transportation has increased the demand for reliable Lithium-ion (Li-ion) batteries in Electric Vehicles (EVs), and it has also established battery monitoring as a crucial aspect in urban Intelligent Transportation Systems (ITSs) [1]. EVs are essential for reducing carbon emissions and combating climate change. EV growth projections show that by the year 2030, around 60% of all automobile sales will be electric. This will reshape urban mobility, and as a result, there will be a need for intelligent transportation solutions.

Researchers in [2] discuss that Li-ion batteries are the most common type of energy storage systems due to their high energy density, efficiency, and long cycle life. Their integration into intelligent transportation networks introduces challenges that extend beyond individual EV performance. In Connected and Autonomous Vehicle (CAV) environments, battery health directly impacts fleet coordination, traffic flow optimisation, and urban energy grid stability. CAVs require real-time battery management to optimise routing and coordinate charging schedules. Smart cities that deploy autonomous fleets, ride-sharing networks and delivery services require efficient Battery Management Systems (BMSs) that can predict and coordinate battery degradation events in the transportation network. CAVs can also share their battery health status through Vehicle-to-Vehicle (V2V) and Vehicle-to-Infrastructure (V2I) networks.

Safety concerns remain in Li-ion batteries, e.g., the risk of thermal runaway, which could be triggered by overcharging, External Short Circuiting (ECS), mechanical damage, or thermal stress [3]. Exothermic reactions in Li-ion batteries could cause a sharp increase in internal temperature [3]. This can lead to Solid Electrolyte Interface (SEI) decomposition, releasing oxygen from the cathode and the emission of flammable gases [3,4,5]. These processes increase internal pressure, posing serious risks of fire or explosion. Contributing factors include Joule heating, electrode side reactions, corrosion, and water exposure and are accelerated by the dynamic operating conditions of urban transportation environments [6,7].

Li-ion battery degradation involves complex, interconnected electrochemical and mechanical processes that evolve continuously throughout the battery’s operational lifetime. The mechanisms that cause these changes are the growth of the SEI layer, lithium plating, loss of active material, breakdown of the electrolyte, and changes in the structure of the electrode materials. The rate of degradation is affected by factors such as temperature profiles, charge–discharge cycling patterns, depth of discharge, C-rates, and the battery’s history of use. Abrupt spikes in battery health performance indicators, such as State of Health (SoH), internal resistance, and temperature profiles, are a crucial aspect of battery health. They could serve as early warnings that could prevent disasters if identified promptly. However, measurement problems, e.g., sensor noise, calibration drift, and environmental changes, can cause artificial fluctuations.

EV battery health monitoring is a crucial component in urban ITSs. Battery health status is important as EVs balance route optimisation and service reliability across transportation networks. Range anxiety, often attributed to the limited availability of Charging Points (CPs), can also be increased by battery degradation in ITSs. Memon et al. [8] reviewed the rapid expansion of EV infrastructure and standardisation challenges in Europe. In our previous work, we proposed GEECharge, a data-driven approach for optimal CP distribution in Dublin, using parameters, e.g., population density, Points Of Interest (POIs), and the most used roads, using principles in mobile sensing [9,10,11,12]. Li-ion batteries can be integrated with renewable energy sources from microgrids [13,14].

We aim to enhance BMSs by detecting abnormal spikes in the SoH data. When SEI reforms or internal resistance is reduced, battery capacity could recover temporarily. We define a spike as a point where the absolute deviation between observed SoH, $s_c$, during cycle, c, and the expected value, ${\widehat{s}}_c$, from a smoothed degradation curve exceeds a predefined threshold $\tau$,

$$\left|s_c-{\widehat{s}}_c\right|>\tau .$$

(1)

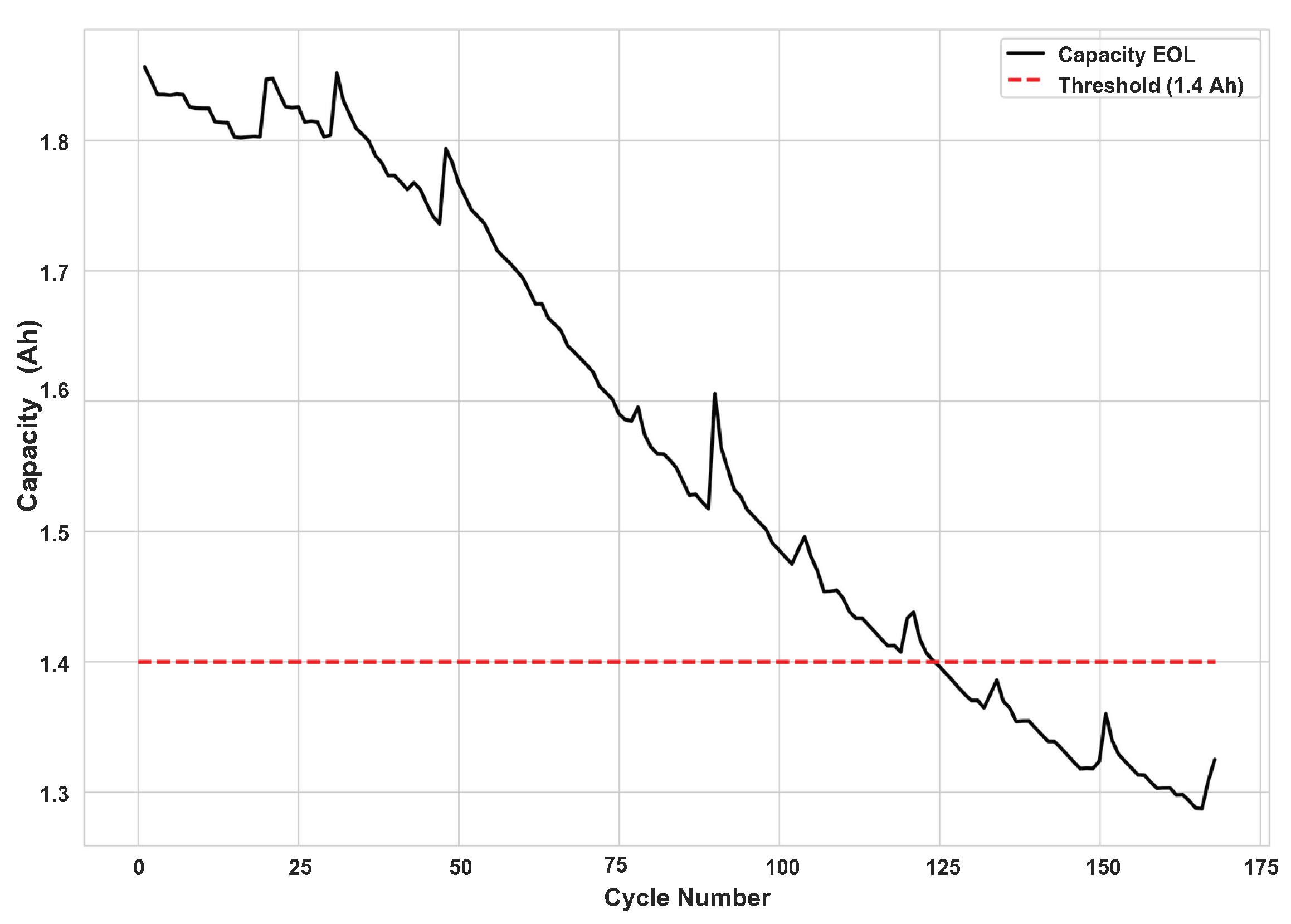
Commonly used datasets, such as NASA battery datasets, exhibit spikes, as illustrated in Figure 1. Existing BMSs use reactive monitoring approaches to detect anomalies only after they appear in battery performance parameters. Traditional Machine Learning (ML) methods for battery health prediction struggle with the high-dimensional and non-linear data. Researchers in [15] used a kinetic-based analysis to model thermal runaway, although the method required detailed chemical parameters, which could be challenging to measure. In contrast, research in [16] developed an inexpensive on-board device for dynamic impedance monitoring during overcharging, making it more practical for real-world deployment. The method provided less insight into chemical reaction kinetics. Although the Arrhenius-type chemical kinetics model has been used to predict thermal behaviour, early identification of SoH anomalies remains a persistent challenge [15].

Advancements in EV battery life prediction focus on improving safety and longevity. Gu et al. [17] proposed a model that can predict thermal runaway up to five hours in advance by integrating strain evolution with multidimensional parameters, e.g., temperature, voltage, and capacity. Although the method offers very early warnings, it requires sophisticated sensors that are not easily integrated into the mass market. In comparison, researchers in [18] developed a hybrid FEA-TimeMixer model that extracts long-term and short-term SoH degradation features to improve prediction accuracy across multiple horizons with moderate data requirements, but the finite element component may be computationally intensive. Sultan et al. [19] combined active cell balancing with ML to both equalise State of Charge (SoC) and predict Remaining Useful Life (RUL), achieving high R² values and reduced error rates. However, the model could be made complex during circuit balancing.

Long Short-Term Memory (LSTM) was proposed for use in battery health prediction [20]. Model-based methods capture patterns in EV Li-ion battery chemical reactions but struggle with generalisation [21,22]. In contrast, data-driven methods learn patterns from historical data and often achieve a higher predictive performance. Classical models include Neural Networks (NNs), LSTMs, and Support Vector Machines (SVMs) [23,24], which are relatively easy to implement. The models fail to exploit long-term dependencies. To overcome this, hybrid and advanced architectures such as Transformer-based NNs [25], autoencoders [26], CNN-LSTM [27], Attention-LSTM [28], Gated Recurrent Units (GRUs)–Recurrent Neural Networks (RNNs) [29], and Bayesian NNs [30] have been proposed for RUL prediction. Qu et al. [31] integrated Particle Swarm Optimisation (PSO) with LSTM and attention mechanisms to reduce Root Mean Squared Error (RMSE) in SoH prediction, although PSO can increase convergence time. The enhanced Particle Filter method is proposed for improved RUL estimation compared to standard filters [32]. Despite their successes, classical data-driven models struggle with processing non-linear and high-dimensional data as well as generalisation across battery chemistries and usage scenarios. LSTM networks have consistently performed better in SoH prediction [24,27,31]. Although the models handle sequence dependencies better, they still require large labelled datasets.

Researchers in [33] proposed a self-attention mechanism for detecting self-discharge anomalies in Li-ion batteries. The proposed method requires high-quality historical production data and may not generalise well to batteries with different chemistries. Researchers in [34] proposed LSTM-based variational autoencoders for unsupervised anomaly detection in power grids. A Spatiotemporal Graph Convolutional Adversarial Network (SGCAN) in [35] demonstrated high efficacy in anomaly detection by exploiting the relational structure of sensor networks, which can be adapted to battery pack monitoring where cells are interconnected. Graph learning, which adds computational complexity, could impact the usage of battery systems. Zhao et al. [36] proposed a hybrid ML model to localise early internal short circuits in battery packs, combining electrochemical knowledge with ML classifiers to improve detection precision and fault localisation accuracy. However, electrochemical parameters vary across battery types. Researchers in [37] used Quantum Autoencoders (QAEs) to detect anomalies in high-energy physics, although the model was evaluated on a low-dimensional simulated dataset.

QML holds promise for ITS applications since it can learn complex, high-dimensional, and non-linear relationships [38]. Superposition enables the simultaneous parallel exploration of multiple degradation pathways [38]. Entanglement can capture complex correlations between features [38]. Quantum Variational Classifiers (QVCs) show a superior performance compared to classical approaches in battery health prediction [39]. Researchers in [40] demonstrated that Quantum Support Vector Machines (QSVMs) could perform well in traffic sign recognition tasks. Hybrid quantum–classical models have been used in various transportation applications [41]. In video quality prediction, quantum models trained on just $0.6$% of the training data required by a GRU, achieved comparable performance [42]. Techniques such as IQGO improve quantum circuit optimisation, increasing the efficiency of models [43]. Ngo et al. [44] proposed a QNN-based regression model for simulating capacity degradation, capturing non-linear relationships between SoH and operational cycles. Researchers in [45] demonstrated how QML can be used to predict molecular energy. Mutua et al. [46] used a Variational Quantum Neural Network (VQNN) to predict the SoH of Li-ion batteries. The researchers highlighted that quantum models require longer training times. A summary of the models is presented in

Table 1. Summary and comparative analysis of data-driven, model-based, and quantum-enhanced battery health prediction and anomaly detection models. This table contrasts key features, strengths, and limitations of the existing models.

Model	Key Features	Strengths	Limitations
LSTM [18,20]	Sequence-to-sequence mapping; long-term dependencies	Used for SoH/RUL time series	Needs large labelled datasets
GRU-RNN [29]	Gated updates for sequence data	Fewer parameters than LSTM; fast	May fail to capture hidden dependencies
CNN-LSTM [27]	Combines spatial–temporal patterns	Learns local voltage/capacity features	Data-intensive; computationally costly
Attention-LSTM [28]	Learns feature importance via attention	Better interpretability	Risk of overfitting on small data
Transformer [25]	Self-attention; global dependencies	State-of-the-art sequence modelling	High memory and compute demand
Autoencoder [26]	Compressed latent features	Good for anomaly detection	Weak extrapolation capacity
SVM [23]	Margin-based classifier	Simple, interpretable	Struggles in high-dimensional data
Bayesian NN [30]	Probabilistic uncertainty	Robust to noisy data	Computationally heavy
Particle Filter [32]	Sequential Monte Carlo tracking	Non-linear dynamic estimation	Sensitive to noise and tuning
LSTM+PSO [31]	Optimised LSTM through swarm methods	Reduced $\mathrm{RMSE}$	Convergence time depends on parameters
Kinetics-Based [15]	Arrhenius-type thermal laws	Physically interpretable	Needs precise chemistry parameters
FEA-TimeMixer [18]	Finite element with temporal layers	Multi-horizon forecasting	Computationally heavy FEA
Active Balancing + ML [19]	Hardware balancing + ML RUL	Equalises $\mathrm{SoC}$; extends life	Added cost and hardware complexity
SAE-GAAE [33]	Self-attention generative adversarial autoencoder	99.05% accuracy; 100% recall in self-discharge anomaly detection	Needs high-quality production data; limited generalisation across chemistries
LSTM-VAE [34]	LSTM-based variational autoencoder	Captures temporal dependencies in multivariate time series	Computationally intensive; not battery-specific without adaptation
SGCAN [35]	Spatiotemporal graph convolutional adversarial network	Models cell interconnections for anomaly detection	Requires accurate graph topology; added computational complexity
Hybrid Model-Based + ML [36]	Electrochemical modelling + ML classifiers	Improves precision and localises early internal short circuits	Relies on precise electrochemical parameters; computationally heavy
QVC/QNN [39,44]	Quantum-enhanced variational circuits	Captures high-dimension correlations	Sensitive to NISQ noise; hardware limits
QSVM [40]	Quantum kernel classifiers	Outperforms SVM on complex data	Quantum kernel choice critical
Hybrid QML [41,45]	Classical pre-processing + quantum layers	Balanced trade-off; data-efficient	Immature deployment; error mitigation needed
QAE [37]	QAE to detect anomalies in high-energy physics	Demonstrates superior anomaly detection performance	Evaluated on a low-dimensional simulated dataset instead of large real-world scenarios.
VQNN [46]	VQNN for SoH prediction	Models non-linear battery degradation, outperforms classical models	Requires longer training time

.

The transition to autonomous vehicle fleets introduces new challenges that individual battery monitoring approaches could struggle to address. We address the need for battery health monitoring in smart transportation systems. This research’s aims are as follows: (1) Integrate QML and classical unsupervised learning models to detect anomalous spikes in battery data more effectively. (2) Benchmark the anomaly detection performance of hybrid QML against classical techniques. (3) Analyse the behaviour of voltage and SoH parameters when the temperature varies.

Our primary research question is as follows: How can a VQNN be used to improve anomaly detection in batteries of connected EVs? We hypothesise the following:

Hypothesis 1. 

A hybrid model consisting of a VQNN and an Isolation Forest (IF) can detect anomalous battery behaviour more accurately than classical models, providing the reliability needed in smart transportation applications.

Hypothesis 2. 

A temperature increase accelerates battery degradation and is strongly correlated with a drop in SoH and voltage, enabling predictive thermal management in transportation networks.

We contribute the following to smart transportation battery management:

• We demonstrate that our proposed Quantum Anomaly Detector (QAD) model improves anomaly detection, achieving a Receiver Operating Characteristic Area Under the Curve (ROC-AUC) of $0.9820$, outperforming the classical IF by $7.78\%$.
• Our results show that the Gradient Boosting (GB) achieves the lowest voltage Mean Squared Error (MSE) of $0.001425$ under varying temperature conditions, indicating its robustness in modelling battery voltage dynamics under thermal stress.
• We demonstrate quantitatively how an increase in temperature accelerates battery degradation, providing a method for proactive battery management.

The integration of QML with IF presents a promising approach for anomaly detection in EV battery monitoring. This could enhance safety, reliability, and operational efficiency. The findings contribute to the development of next-generation smart transportation infrastructure.

We structure the remainder as follows. Section 2 provides an overview of QML and encoding strategies used for modelling battery degradation. Section 3 presents the integration of QML with classical models to detect anomalies in battery data. Section 4 describes the hybrid model results and the implications. Section 5 concludes this paper and highlights future research directions.

2. Fundamentals of Quantum Machine Learning

Quantum computing utilises the principles of quantum mechanics, including superposition and entanglement, to process information [47]. A quantum computer is a device that can process quantum computations [47]. A qubit is the basic unit of information used to encode data in quantum computing [47]. We use the state vector to describe a qubit as

$$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle ,$$

(2)

where $\alpha ,\beta \in \mathbb{C}$ are complex probability amplitudes satisfying the normalisation condition,

$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1.$$

(3)

This enables quantum systems to process information in multiple states simultaneously, a phenomenon known as quantum parallelism. Qubits are manipulated using gates that operate on the principles of unitary transformations. The Hadamard is a matrix gate in quantum computing that transforms a qubit $|0\rangle$ into ${\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0\rangle +|1\rangle )$. VQNNs are constructed using fundamental gates, including the Pauli gates X, Y, and Z, the phase-shift gates S and T, and the controlled gate CNOT.

A quantum circuit consists of a series of quantum gates interconnected by wires [47]. The circuit uses Controlled-X (CX) and Controlled-Z (CZ) gates to introduce entanglement to capture feature interactions. A quantum circuit applies unitary transformations U to the state vector $|\psi \rangle$ of the quantum system. Compared to classical logic gates, which can be irreversible, quantum operations are inherently reversible because of their unitary nature, preserving information throughout the computation.

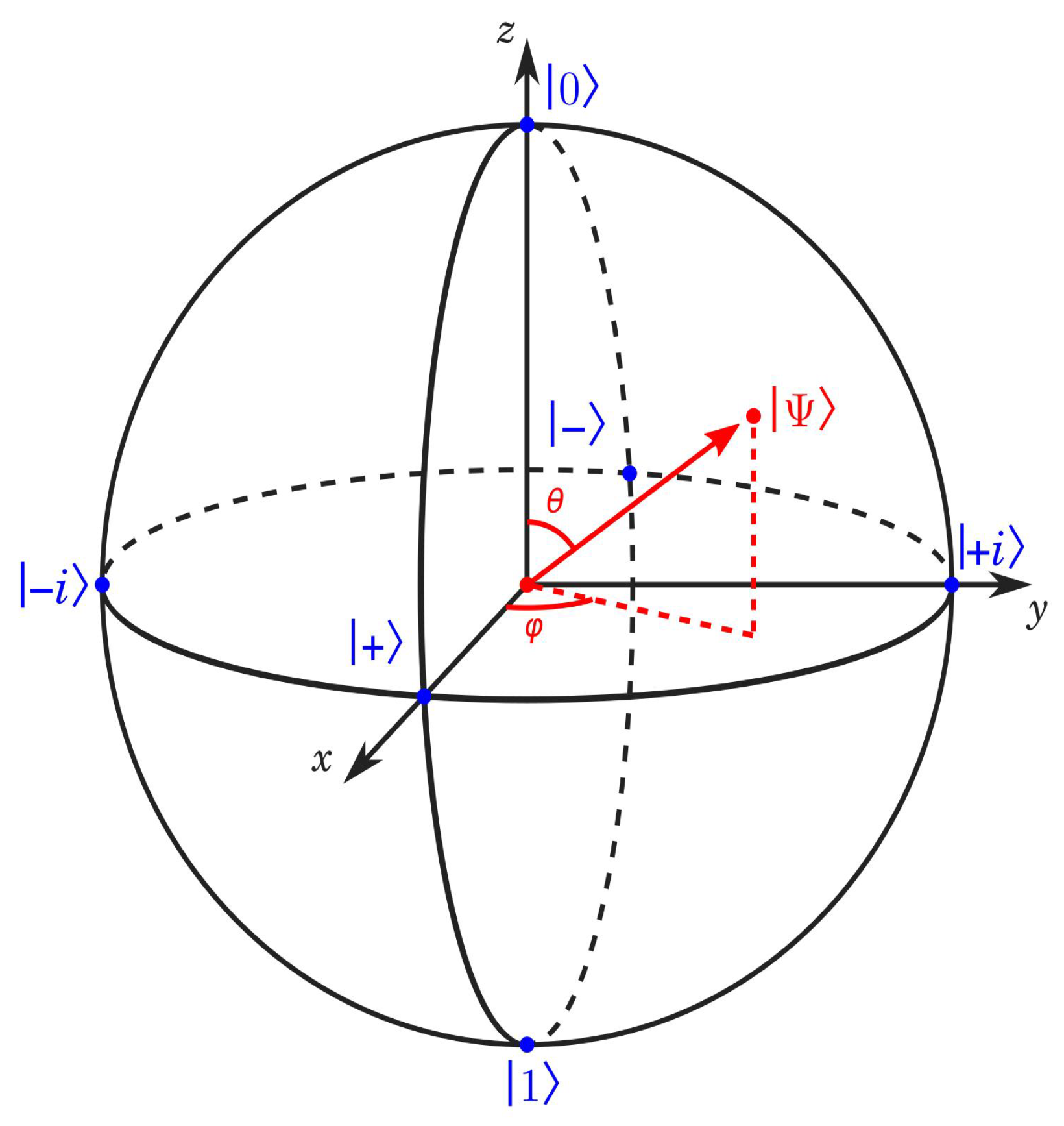
The Bloch sphere provides a geometric representation of a single-qubit quantum state, as shown in Figure 2. It visualises how quantum gates manipulate qubits by rotating their state vectors around specific axes. For example, the Pauli X, Y, and Z gates perform $\pi$-rotations about the corresponding axes on the Bloch sphere. Parameterised rotation gates $R_X\left(\theta \right)$, $R_Y\left(\theta \right)$, and $R_Z\left(\theta \right)$ apply unitary rotations of the qubit state by an angle $\theta$ around the x, y, and z axes, respectively, where $R_X\left(\theta \right)=e^{-i\theta X/2},R_Y\left(\theta \right)=e^{-i\theta Y/2},R_Z\left(\theta \right)=e^{-i\theta Z/2},$ where X, Y, and Z are the corresponding Pauli operators.

These single-qubit gates allow for precise control of qubit states within the two-dimensional complex Hilbert space. Gates, e.g., the Controlled-NOT (CNOT) and the Controlled-Z (CZ), introduce entanglement between qubits. These gates create correlations between them, resulting in entangled quantum states that cannot be separated into individual components. Entanglement is a key quantum property that allows quantum models to capture complex joint patterns. We represent the general quantum state of a system with n qubits as

$$|\psi \rangle =\sum _{i=0}^{2^n-1}{c}_i|i\rangle ,\mathrm{where}{c}_i\in \mathbb{C},\sum _{i=0}^{2^n-1}{\left|c_i\right|}^2=1.$$

(4)

The notation $|i\rangle$ represents the computational basis states. For example, $|0\rangle$, $|1\rangle$, $|10\rangle$, …, and $c_i$ are the complex probability amplitudes that describe the contribution of each basis state to the system’s overall quantum state.

Data can be encoded using various techniques. For example, the classical data,

$$x=[x_0,x_1,\dots ,x_{2^n-1}],$$

(5)

is expressed using amplitude encoding in the quantum state’s amplitudes as

$$|\psi \rangle ={\displaystyle \frac{1}{\left|x\right|}}\sum _{i=0}^{2^n-1}{x}_i|i\rangle .$$

(6)

This encoding is efficient since it represents $2^n$ classical values using n qubits. Basis encoding, expressed as $x\mapsto |i\rangle$, maps classical data directly to computational basis states. The notation i indicates the binary representation of the classical input. Angle encoding encodes classical properties into the angles of a single qubit. For example, in the set $\{x_1,x_2,\dots ,x_n\}$, angle encoding can operate as

$$|x\rangle =\underset{i=1}{\overset{n}{⨂}}{R}_y\left(x_i\right)|0\rangle ,R_y\left(x_i\right)=\left[\begin{array}{cc}cos(x_i/2)& -sin(x_i/2)\\ sin(x_i/2)& cos(x_i/2)\end{array}\right].$$

(7)

For SoH prediction in Li-ion batteries, angle encoding is well-suited because the input features, e.g., voltage, current, and temperature, are continuous and real values. Angle encoding is also hardware-efficient and easier to implement on Noisy Intermediate-Scale Quantum (NISQ) devices compared to more complex methods, such as amplitude encoding.

In the first step in Figure 3, the circuit is initialised with qubits in the state ${|0\rangle }^{\otimes n}$. The second step applies a series of parameterised unitary transformations using quantum gates to encode input data and perform computations. The third step of the circuit performs quantum measurements, collapsing the quantum state into classical outcomes that are used for prediction or classification tasks. This change from the input state to the output state is expressed as

$$|{\psi }_{\mathrm{out}}\rangle =U_k{U}_{k-1}\cdots U_1|{\psi }_{\mathrm{in}}\rangle .$$

(8)

Quantum gates are represented by the unitary operators $U_j$. Quantum unitary matrices and functions represent quantum gates on one or more qubits. The CNOT gate creates an entangled state between two qubits. The CNOT gate operates as

$$\mathrm{CNOT}\left(\right|a\rangle \otimes |b\rangle )=|a\rangle \otimes |a\oplus b\rangle ,$$

(9)

where $a,b\in \{0,1\}$ and ⊕ denotes addition modulo-2. The notation ⊗ denotes the tensor product. We use the tensor product ⊗ to combine the states of two qubits.

The combination of expressive data encoding, tunable quantum circuits, and entangled representations makes VQNNs suitable for predictive tasks such as battery health prediction.

Let $\mathbf{x}\in {\mathbb{R}}^d$ denote a classical input vector of dimension d, representing the features of the sample to be classified. The mapping $U\left(\mathbf{x}\right)$ is a fixed, non-trainable feature map that encodes $\mathbf{x}$ into a quantum state via parameterised quantum gates, while $V\left(\mathit{\omega }\right)$ is a variational ansatz comprising trainable unitary operations with parameters $\mathit{\omega }=\{{\omega }_1,{\omega }_2,\dots ,{\omega }_p\}$. The observable $\widehat{O}$ (typically a tensor product of Pauli operators) is measured to extract a real-valued output corresponding to the model’s prediction. We define the set of trainable parameters optimised during learning as $\mathit{\omega }$. After applying the full variational quantum circuit, defined as

$$U(\mathbf{x},\mathit{\omega })=V\left(\mathit{\omega }\right)·U\left(\mathbf{x}\right),$$

(10)

where $U\left(\mathbf{x}\right)$ encodes the classical input features $\mathbf{x}$, and $V\left(\mathit{\omega }\right)$ is a parameterised unitary representing the trainable variational layers, with parameter vector $\mathit{\omega }$, the output of the VQNN is computed by measuring the expectation value of a Hermitian observable $\widehat{O}$ with respect to the output quantum state,

$$f(\mathbf{x};\mathit{\omega })=\langle 0|U^{†}(\mathbf{x},\mathit{\omega })\widehat{O}U(\mathbf{x},\mathit{\omega })|0\rangle .$$

(11)

For computational efficiency, we apply ansatz compression using PennyLane’s transpilation-based gate optimisation to the variational component of the VQNN feature extractor. This optimisation reduces the gate count by fusing consecutive single-qubit rotations, merging adjacent rotations around the same axis, and cancelling inverse gate pairs. We represent the variational ansatz as a unitary $\mathcal{V}(\mathit{\omega })$ of the form,

$$\mathcal{V}\left(\mathit{\omega }\right)=\prod _{\ell =1}^{N_{\ell }}\prod _{g=1}^{G_{\ell }}{G}_{\ell ,g}({\omega }_{\ell ,g}),$$

(12)

where $N_{\ell }$ is the number of layers in the ansatz, $G_{\ell }$ is the set of gates in layer ℓ, and ${\omega }_{\ell ,g}$ are the trainable parameters (equivalent to $\mathit{\theta }$ in earlier notation). Ansatz compression seeks a transformation $\mathcal{T}:\mathcal{U}\to \mathcal{U}$ such that,

$${\mathcal{V}}^{\prime }\left(\mathit{\omega }\right)=\mathcal{T}(\mathcal{V}(\mathit{\omega })),{\mathcal{V}}^{\prime }\left(\mathit{\omega }\right)\equiv \mathcal{V}\left(\mathit{\omega }\right),\forall \omega ,$$

(13)

while minimising the circuit complexity,

$$C\left(\mathcal{V}\right)=\alpha D\left(\mathcal{V}\right)+\beta N_{2\mathrm{q}}\left(\mathcal{V}\right)+\gamma N_{1\mathrm{q}}\left(\mathcal{V}\right),$$

(14)

where $D\left(\mathcal{V}\right)$ is the circuit depth, $N_{2\mathrm{q}}\left(\mathcal{V}\right)$ and $N_{1\mathrm{q}}\left(\mathcal{V}\right)$ are the two- and single-qubit gate counts, and $\alpha ,\beta ,\gamma$ are cost weights. This produces a compressed ansatz ${\mathcal{V}}^{\prime }\left(\mathit{\omega }\right)$ satisfying $C({\mathcal{V}}^{\prime }\left(\mathit{\omega }\right))<C(\mathcal{V}\left(\mathit{\omega }\right))$, thereby preserving the overall unitary action while reducing redundant parameterised operations and maintaining the same functional mapping from inputs to outputs.

3. QML and Isolation Forest Integration

We present a hybrid quantum–classical model for detecting anomalous spikes in Li-ion batteries. We evaluate the model using the NASA Prognostics Center of Excellence battery datasets, where we detect and predict degradation anomalies based on electrochemical and operational parameters. These datasets were generated at NASA Ames Research Center at Moffett Field, California, USA using a dedicated testbed comprising of Li-ion 18650-sized rechargeable batteries. We use battery B0005 for training and battery B0006 for testing as used in [48,49]. The batteries were cycled at room temperature using a Constant Current (CC) charging phase at $1.5\mathrm{A}$ until reaching $4.2\mathrm{V}$, followed by a Constant Voltage (CV) phase until the current dropped below $20\mathrm{mA}$. Discharge occurred at $2\mathrm{A}$ until the voltage threshold was met. Cycling continued until the capacity dropped from $2.0\mathrm{Ah}$ to $1.4\mathrm{Ah}$, marking the EoL corresponding to 70% of the initial capacity, as shown in Figure 1. Electrochemical Impedance Spectroscopy (EIS) from $0.1\mathrm{Hz}$ to $5\mathrm{kHz}$ assessed internal battery behaviour.

For each discharge cycle, $c\in \{1,2,\dots ,N\}$, we extract the following features: discharge capacity $Q_c$, mean voltage $V_c$, mean and extreme temperatures $T_c$, $T_{\max ,c}$, $T_{\min ,c}$, mean current $I_c$, and temperature variation $\Delta T_c=T_{\max ,c}-T_{\min ,c}$. We define the battery’s $s_c$ as

$$s_c={\displaystyle \frac{Q_c}{Q_0}},$$

(15)

where $Q_0$ is the initial discharge capacity measured in the first cycle $c=1$. Its change per cycle is

$$\Delta s_c=s_c-s_{c-1}.$$

(16)

We investigate how $s_c$ varies using the Median Absolute Deviation (MAD). We define the median operator as $D\left(·\right)$ and define the MAD in cycle c as

$$M_c=D\left(\left\{\left|s_i-D\left(s_i\right)\right||i\in [c-2,c+2]\right\}\right),$$

(17)

where $D\left(·\right)$ denotes the median operator over a five-cycle window centred at c. We use this window to balance local sensitivity to degradation spikes while maintaining robustness to noise. We fit a fifth-degree polynomial,

$$p\left(c\right)=a_5{c}^5+a_4{c}^4+a_3{c}^3+a_2{c}^2+a_{1}c+a_0,$$

(18)

to capture the degradation trends, where c denotes the battery cycle count. Its first and second derivatives,

$$\begin{array}{cc}\hfill p^{\prime }\left(c\right)& =5a_5{c}^4+4a_4{c}^3+3a_3{c}^2+2a_{2}c+a_1,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill p^{″}\left(c\right)& =20a_5{c}^3+12a_4{c}^2+6a_{3}c+2a_2,\hfill \end{array}$$

(20)

capture the slope and curvature of degradation. The polynomial coefficients are denoted as $a_5$, $a_4$, $a_3$, $a_2$, $a_1$, and $a_0$. We select a fifth-degree polynomial because it captures the non-linear behaviour of SoH degradation while avoiding overfitting, which becomes a risk with higher-degree polynomials, especially given the limited cycle data. This design decision is motivated as follows. We compute the MSE of the SoH predictions across polynomial degrees, and we observe that the improvement from degree 4 to degree 5 is minimal. Therefore, degree 5 is selected as a suitable model. Lower-degree models, e.g., linear or quadratic models, struggle to represent the complex curvature and points observed in empirical degradation patterns. We define the feature vector representing each cycle as

$${\mathbf{x}}_c=[\Delta s_c,\Delta T_c,V_c,M_c,p^{\prime }\left(c\right),p^{″}\left(c\right)].$$

(21)

To detect discharge cycles exhibiting anomalous spikes, we apply an unsupervised IF model ${\mathcal{F}}_{\mathrm{IF}}\left(·\right)$, where $·$ denotes the extracted set of features derived from battery B0005’s health indicators [50]. We also apply the Local Outlier Factor (LOF) model ${\mathcal{F}}_{\mathrm{LOF}}\left(·\right)$ to the same feature set to capture local density-based anomalies. We compare the performance of IF and LOF in identifying abnormal discharge behaviour. Compared to traditional models that rely on a distance threshold, $ϵ$, the IF model isolates anomalies using the principle of recursive partitioning. Instead of manually adjusting the parameter $ϵ$, we use a Bayesian Gaussian Mixture Model (BGMM) as proposed by Perini et al. [51]. We use the approach to estimate the contamination rate $\eta$. We train the IF model to generate initial anomaly scores and then fit a BGMM to these scores to estimate the posterior probabilities of belonging to each mixture component. The component with the highest mean anomaly score is considered anomalous, and its mixture weight provides an estimate of the contamination rate $\eta$. This estimate is used to retrain the IF model.

The anomaly scores for each cycle c are defined as

$$z_c^{\left(m\right)}=-{\mathcal{F}}_m\left({\widehat{\mathbf{x}}}_c\right),$$

(22)

where $m\in \{\mathrm{IF},\mathrm{LOF}\}$, and ${\mathcal{F}}_m$ denotes its corresponding scoring function. A higher anomaly score $z_c^{\left(m\right)}$ indicates a higher likelihood of abnormality. We apply a percentile-based thresholding approach to label abnormal cycles. Let ${\theta }_z^{\left(m\right)}$ denote the chosen percentile threshold (85th, 90th, or 95th) corresponding to method $m\in \{\mathrm{IF},\mathrm{LOF}\}$. We also define the SoH deviation threshold as

$${\theta }_{\Delta s}=\lambda ·\overline{M},$$

(23)

where $\lambda \in \{2.0,2.5,3.0\}$ and $\overline{M}$ is the mean MAD over all cycles. Extreme values strongly influence the traditional standard deviation. Since battery data may include rare but significant deviations due to spikes or sensor errors, using the standard deviation can inflate thresholds, making it difficult to reliably detect hidden anomalies.

Leys et al. [52] proposed using the absolute deviation around the median instead of the standard deviation for robust statistical analysis. This makes MAD a better choice for capturing deviations in battery data. The researchers recommended a scaling factor of $2.5$ for the MAD. Based on empirical evaluation, we selected the 85th anomaly score percentile and a MAD scaling factor of $2.0$ as suitable hyperparameters. This choice was guided by experiments that maximised the ROC-AUC performance across a grid of tested thresholds and multipliers. For instance, the proposed QAD model achieved its highest ROC-AUC score of $0.982036$ under these hyperparameters, demonstrating robustness in anomaly detection. A cycle is labelled anomalous if $z_c^{\left(m\right)}>{\theta }_z^{\left(m\right)}$ and $|\Delta s_c|>{\theta }_{\Delta s}$, where $\left(m\right)$ denotes IF or LOF.

We use the Arrhenius model to simulate thermally accelerated degradation because it directly models how reaction rates depend on temperature, which underlies capacity loss in Li-ion batteries [53,54,55]. Compared to complex physics-based or data-driven models, the Arrhenius framework offers a physically interpretable, computationally efficient, and validated method for approximating thermal stress effects on SoH. Other impedance-based models require detailed electrochemical measurements. Therefore, the Arrhenius model provides a suitable balance between physical realism and computational practicality for our anomaly detection pipeline. We implement the Arrhenius model for predicting future SoH under increased temperatures,

$$\begin{array}{cc}\hfill k\left(T\right)& =k_{0}exp\left[\gamma (T-T_0)\right],\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill s\left(n\right)& =s_{0}exp[-k\left(T\right)n],\hfill \end{array}$$

(25)

where $k_0$ is the baseline degradation rate constant, $T_0$ is the reference ambient temperature, $\gamma$ is a temperature sensitivity coefficient, n is the cycle index, and $s_0$ is the initial SoH. This simulation enables the prediction of accelerated degradation due to thermal stress.

To implement our QAD hybrid model, we use a VQNN for feature extraction. Each classical feature vector ${\mathbf{x}}_c\in {\mathbb{R}}^6$ is transformed into a quantum-augmented feature vector via a parameterised quantum embedding function $\mathcal{Q}(·;\mathit{\theta })$ such that

$${\mathit{\varphi }}_c=\mathcal{Q}({\mathbf{x}}_c;\mathit{\theta })\in {\mathbb{R}}^q,$$

(26)

where q is the number of qubits measured, and $\mathit{\theta }$ are the trainable parameters. The quantum-enhanced vector is then

$${\widehat{\mathbf{x}}}_c={[{\mathbf{x}}_c^{\top },{\mathit{\varphi }}_c^{\top }]}^{\top }\in {\mathbb{R}}^{6+q}.$$

(27)

We implement quantum embedding using the PennyLane simulator with 8 qubits representing the quantum state. PennyLane provides native integration with standard ML frameworks (PyTorch, TensorFlow) and supports differentiation of variational circuits, enabling seamless hybrid quantum–classical training. Although Qiskit is a mature alternative, its coupling to classical deep learning frameworks is less direct and requires additional manual handling of gradients. This makes PennyLane well-suited for our QAD model, which relies on joint optimisation of QML and classical anomaly detection models. We empirically choose the number of qubits and circuit layers. The VQNN feature extractor has $N_{\ell }=8$ layers. Classical battery health features are encoded into quantum states through ${\mathrm{R}}_{\mathrm{Y}}$ and ${\mathrm{R}}_{\mathrm{Z}}$ rotations. Each variational layer applies parameterised single-qubit rotations in $\mathrm{U}3$ form to all qubits, followed by an entanglement block using $\mathrm{CNOT}$ gates between neighbouring qubits. To make it more expressive, it adds $\mathrm{CRX}$ gates and a single global $\mathrm{PhaseShift}$ gate. To improve the performance of Noisy Intermediate-Scale Quantum (NISQ) devices and reduce their sensitivity to noise, PennyLane’s transpilation-based optimisation employs ansatz compression. This approach combines consecutive single-qubit rotations and eliminates inverse gate pairs. This lowers the depth of the circuit without changing its unitary action. To obtain the circuit outputs, we measure the expectation values of the Pauli-Z, Pauli-X, and Pauli-Y operators for each qubit. These values are then combined with the original classical characteristics to make quantum–classical hybrid feature vectors that may be used for anomaly detection. These embeddings are concatenated with classical features to build enriched feature sets that are then used to develop two additional models. We integrate the VQNN with IF to construct the QAD and with LOF to develop Q-LOF.

We define the anomaly scores for these models as

$$\begin{array}{cc}\hfill z_c^{\mathrm{QAD}}& =-{\mathcal{F}}_{\mathrm{QAD}}\left({\widehat{\mathbf{x}}}_c\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill z_c^{\mathrm{Q}-\mathrm{LOF}}& =-{\mathcal{F}}_{\mathrm{Q}-\mathrm{LOF}}\left({\widehat{\mathbf{x}}}_c\right),\hfill \end{array}$$

(29)

and the corresponding thresholds ${\theta }_z^{\mathrm{QAD}}$, ${\theta }_z^{\mathrm{Q}-\mathrm{LOF}}$ are selected from percentile ranges as described in Equations (22) and (23). A battery cycle is classified as anomalous if the anomaly score exceeds the threshold and the SoH changes $|\Delta s_c|$ surpasses ${\theta }_{\Delta s}$. To distinguish between thermally induced and normal degradation spikes, we label a cycle as a normal spike if

$${\displaystyle \frac{1}{2}}{\theta }_{\Delta s}<|\Delta s_c|\le {\theta }_{\Delta s},\mathrm{and}\Delta T_c>\overline{\Delta T},$$

(30)

where $\overline{\Delta T}$ is the average temperature variation across all cycles.

We use SHapley Additive exPlanations (SHAP) for model interpretability to quantify the contribution of each feature to the anomaly score [56,57]. We adopted SHAP to explain model predictions due to its solid game-theoretic foundation [56,57]. We evaluate model performance using metrics such as ROC-AUC, Precision–Recall AUC (PR-AUC), and the false-negative rate. We perform the Mann–Whitney $U_{mw}$ test to compare the distributions of voltage and temperature. Let $X_u$ and $X_r$ represent the samples of a feature, e.g., $T_c$ or $V_c$, from abnormal and normal cycles, respectively. The $U_{mw}$ statistic for voltage is computed as

$$U_{mw}=\sum _{i=1}^{n_u}\sum _{j=1}^{n_r}\mathbb{I}(V_{u,i}>V_{r,j}),$$

(31)

where $n_u$ and $n_r$ denote the number of samples from abnormal and normal cycles, respectively, and $\mathbb{I}\left(·\right)$ denotes the indicator function, which equals 1 if the condition inside is true and 0 otherwise. We evaluate statistical significance at the $\alpha =0.05$ level as it helps balance Type I and Type II error rates while maintaining sufficient statistical power for detecting meaningful differences in voltage or temperature distributions [58,59].

We simulate a fleet of $K=100$ EVs, each initialised with random SoH, temperature, and degradation profiles. We use four temperature rise scenarios, $+0\%$, $+10\%$, $+20\%$, and $+30\%$, for simulation, with Arrhenius degradation models applied to emulate temperature-accelerated ageing. EVs exposed to high-temperature environments $T\ge 100 °$C face thermal runaway. We use ML models to predict future SoH and voltage from temperature-related features. We use Random Forest Regression (RFR), Support Vector Regression (SVR), GB, LSTM, and Bi-LSTM models. We choose RFR because of its ability to capture non-linear relationships in the data, while SVR is selected due to its robustness to outliers. The GB is used due to its strong performance on non-linear, structured datasets, e.g., those encountered in battery degradation. We choose LSTM and Bi-LSTM because the battery SoH and voltage data are sequential. LSTM can capture long-term temporal dependencies from past cycles, while Bi-LSTM incorporates both the past and future context during training.

We evaluate the models using MSE and Mean Absolute Error (MAE). MSE penalises large deviations, making it suitable for battery health monitoring, while MAE provides a balanced assessment of prediction quality. The MSE for SoH prediction is defined as

$${\mathcal{L}}_s={\displaystyle \frac{1}{N}}\sum _{c=1}^N{(s_c-{\widehat{s}}_c)}^2$$

(32)

where ${\mathcal{L}}_s$ denotes the MSE loss for s, N is the total number of battery discharge cycles, $s_c$ is the true SoH in cycle c, and ${\widehat{s}}_c$ is the predicted value of s in cycle c. We evaluate the MSE for the prediction of V as

$${\mathcal{L}}_V={\displaystyle \frac{1}{N}}\sum _{c=1}^N{(V_c-{\widehat{V}}_c)}^2$$

(33)

where ${\mathcal{L}}_V$ denotes the MSE loss for V, $V_c$ is the measured V in cycle c, and ${\widehat{V}}_c$ is the predicted V in the same cycle. The loss functions ${\mathcal{L}}_s$ and ${\mathcal{L}}_V$ help to evaluate the models’ performance.

4. QML and Isolation Forest Evaluation

We find the following:

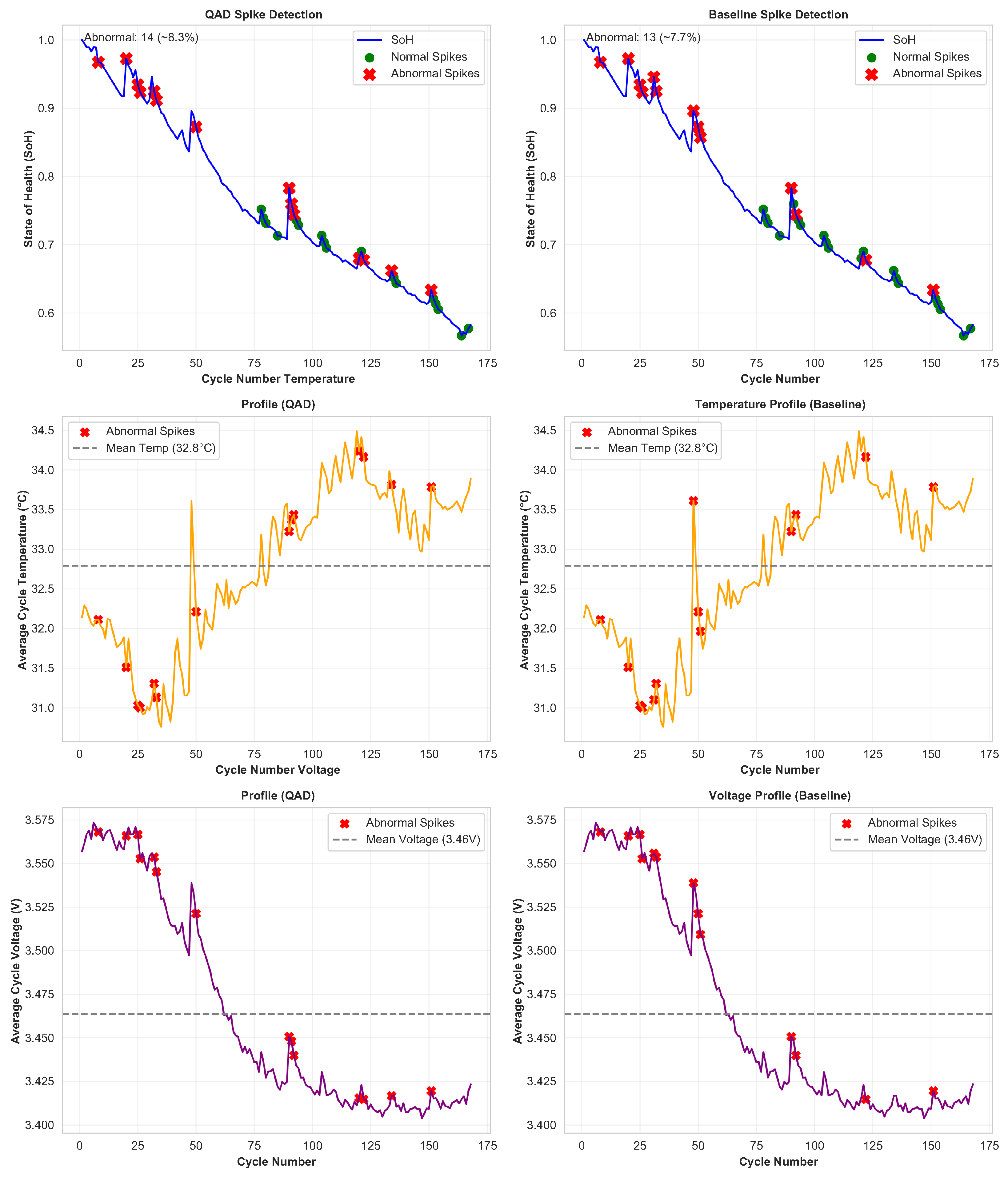
• Out of 168 discharge cycles, 14 are classified as having abnormal spikes.
• The QAD achieves the highest ROC-AUC of $0.9820$, outperforming the baseline IF model by $7.78\%$ and achieving a PR-AUC of $0.1250$.
• The GB achieves the lowest voltage MSE of $0.001425$ compared to the Bi-LSTM, which achieves an MSE of $0.002382$ in voltage prediction when the temperature changes.
• In our simulation, a 30% increase in battery temperature leads to an $18\%$ SoH and $4.8\%$ voltage loss, showing that thermal stress accelerates degradation.
• Non-linear degradation requires higher-order degree modelling.

We perform experiments on NASA battery datasets and detect 14 abnormal spikes out of 168 cycles in the B0006 battery, as shown in Figure 4. This corresponds to $8.3$% of the cycles. Temperature and SoH have a Spearman correlation coefficient of $-0.8011$ and a p-value which is less than $0.05$. This suggests that as the operating temperature of the battery increases, the SoH tends to decrease. The negative sign reflects the inverse association. The significant p-value shows that higher temperatures are strongly and inversely associated with lower SoH.

The first set of subplots in row 1 of Figure 4 shows that the QAD model detects 14 abnormal spikes. We classify abnormal spikes as sudden reductions in SoH that exceed 5% compared to the previous cycles. This threshold is chosen as an early-warning signal, capturing pre-failure conditions well before the cell reaches its EoL. Cadini et al. [63] worked on the state-of-life prognosis of Li-ion batteries to automatically detect deviations from the expected degradation dynamics. The researchers introduced an artificial $5\%$ capacity drop between consecutive charge cycles to simulate sudden degradation events. The researchers were able to represent critical anomalies such as electrode delamination or electrolyte degradation, warranting pre-emptive maintenance. We incorporate the classification of abnormal spikes in both training and testing phases; the model learns to detect these early-stage anomalies from battery B0005 and is evaluated on battery B0006. This ensures that QAD’s anomaly detection capability is transferable across different cells, thereby supporting safer and more reliable EV battery management. The second set of subplots in row 2 of Figure 4 displays temperature trends, where many abnormal spikes occurred above 32 °C. However, some are observed below this threshold, suggesting that temperature alone is not the sole driver of degradation anomalies. We plot voltage against discharge cycles, where abnormal spikes indicate voltage drops. Voltage abnormal events drop below $3.5\mathrm{V}$ compared to a typical nominal average of $3.7\mathrm{V}$ observed during regular discharge operation.

EVs’ predictable performance is crucial in urban ITSs. Detection of anomalous spikes is important in proactive maintenance scheduling. Real-time spike monitoring in urban mobility can support decision-making, e.g., dispatching Mobile Charging Units (MCUs) to charge EVs with low charge that are unable to reach a charging station. This is crucial in connected transport ecosystems. In smart cities, real-time spike detection enables proactive maintenance, where battery checks could be scheduled, and dynamic routing, allowing an EV to be rerouted to the nearest CP or MCU, thereby minimising downtime in urban fleets.

To capture the temporal degradation behaviour of the Li-ion battery, we fit polynomial regression models of varying degrees to the SoH trend across 168 discharge cycles. As shown in

Table 2. Comparison of polynomial degrees for SoH fitting using the MSE as the evaluation metric. Increasing the polynomial degree reduces the MSE, with a degree-5 polynomial achieving the best fit. The results suggest that higher-order polynomials capture the non-linear degradation behaviour of batteries more accurately. We use degree 5 as the most suitable model, as it improves fit over lower degrees while offering only marginal gains beyond degree 4.

Polynomial Degree	MSE (SoH)
1	0.000255
2	0.000254
3	0.000088
4	0.000074
5	0.000073

, increasing the polynomial degree progressively reduces the MSE, with the fifth-degree polynomial achieving the lowest MSE of $0.000073$. These results indicate that high-order polynomials are more effective at modelling the non-linear nature of battery ageing. The improvement from degree 4 to degree 5 is minimal, providing a precise fit without increasing model complexity or overfitting. Accurate SoH curve fitting enables more reliable life-cycle prediction, which is essential for scheduling battery maintenance, managing fleet energy logistics, and avoiding unexpected service interruptions in urban transportation networks. This curve can also inform adaptive charging strategies and dynamic energy routing in the V2X system.

Table 3. Best parameters and evaluation metrics for each anomaly detection model. The QAD model achieves the highest ROC-AUC and PR-AUC scores, showing a superior anomaly detection performance compared to both classical and quantum baselines, including QAE, while maintaining zero false negatives across all configurations.

Model	Percentile	MAD Mult.	ROC-AUC	PR-AUC	False Negatives
Baseline IF	85	2.5	0.9042	0.0294	0
Baseline LOF	85	2.0	0.8855	0.0488	0
Quantum AE	85	2.0	0.8825	0.0463	0
QAD	85	2.0	0.9820	0.1250	0
Q-LOF	85	2.0	0.9701	0.0833	0

shows that the QAD achieved an ROC-AUC of $0.9820$ and a PR-AUC of $0.1250$, outperforming the IF baseline and all other models. The Q-LOF achieved an ROC-AUC of $0.9701$ and a PR-AUC of $0.0833$, also outperforming the LOF baseline. The QAE baseline achieved an ROC-AUC of $0.8825$ and a PR-AUC of $0.0463$, which is lower than both QAD and Q-LOF. This suggests that while QAE can capture some anomaly structure through reconstruction-error-based scoring, the hybrid QAD architecture offers superior separability of anomalous cycles in the high-dimensional battery health feature space. The QAD model delivers better performance across all metrics, supporting our hypothesis that quantum-enhanced models can improve anomaly detection for connected EV battery monitoring.

We perform an ablation study to evaluate the contribution of quantum feature extraction in quantum-enhanced anomaly detection. We compare three configurations: (1) models trained with quantum features extracted via our VQNN, (2) models trained with the same architecture but using random features, and (3) baseline models without feature augmentation. Quantum features achieve a mean ROC-AUC of $0.9760$ and PR-AUC of $0.1042$, while random features achieve a mean ROC-AUC of $0.9311$ and mean PR-AUC of $0.0401$. Baseline features achieve a mean ROC-AUC of $0.8949$ and a mean PR-AUC of $0.0391$. Quantum features provide $4.8$% improvement in ROC-AUC over random features and a $9.1$% improvement in ROC-AUC over baseline features. These results provide empirical evidence that quantum feature extraction is a contributor to the improvement of QAD anomaly detection performance.

We further evaluate our proposed model using the CALCE battery dataset, which contains battery cells of different chemistries and from different manufacturing sources compared to the NASA dataset. We use 50 discharge cycles for training and 28 for testing. The QAD model identifies five anomalies in the test set and achieves a PR-AUC score of $0.362930$, outperforming the baseline IF model, which achieves a score of $0.285171$ under the same conditions. The overall performance on the CALCE dataset is lower than on the NASA dataset, primarily because the CALCE dataset has fewer cycles and a reduced feature set. The results show that QAD can generalise across different datasets, indicating its potential in real-world deployments involving diverse EV battery data.

Our hybrid anomaly detection framework uses a VQNN to encode high-dimensional classical battery features, e.g., SoH, voltage, and temperature, into a quantum Hilbert space via parameterised quantum circuits. This approach overcomes the inherent limitations of classical ML models when dealing with complex, non-linear, and high-dimensional patterns. Using quantum kernels, QAD maps input battery data into a feature space whose dimensionality grows exponentially with the number of qubits. This enables the extraction of complex non-linear relationships and entanglement-based feature correlations that may remain undetected in classical spaces. This research novelty lies in combining quantum feature extraction with classical anomaly detection. A pipeline is created, achieving both expressive representational power and mature decision boundaries. Integrating such a hybrid quantum–classical anomaly detection system into BMSs allows EVs to identify pre-failure conditions with greater certainty, thereby enhancing operational safety in dense urban mobility networks. This is critical in preventing catastrophic events such as thermal runaway, which may arise from temperature-driven anomalies, and in reducing the risk of route-critical battery failures. Minimising undetected anomalies directly contributes to improved reliability, availability, and trust in EV deployments within urban transportation systems.

We compare the performance of the RFR, GB, SVR, LSTM, and Bi-LSTM prediction models in

Table 4. Performance metrics for predictive models estimating SoH and terminal voltage in EV batteries. The GB achieves the best performance. The SVR and Bi-LSTM achieve the best $R^2$ scores.

Model	SoH ${\mathit{R}}^2$	SoH MSE	SoH MAE	Voltage ${\mathit{R}}^2$	Voltage MSE	Voltage MAE
RF	0.778609	0.003373	0.046337	0.500967	0.001765	0.035259
SVR	0.934284	0.001002	0.029238	0.339625	0.002335	0.043286
GB	0.810595	0.002888	0.044287	0.597334	0.001425	0.029947
LSTM	0.789509	0.002704	0.046747	−0.117558	0.003411	0.053457
Bi-LSTM	0.917923	0.001055	0.028368	0.219305	0.002382	0.043603

. The models predict SoH and voltage when temperature varies. In SoH prediction, SVR achieves the highest $R^2$ score of $0.9343$ and the lowest MSE $0.001002$, while Bi-LSTM follows with an $R^2$ score of $0.9179$ and achieves the lowest MAE of $0.02837$. In voltage prediction, GB achieves the highest $R^2$ of $0.5973$, the lowest MSE of $0.001425$, and the lowest MAE of $0.02995$. SoH is more predictable because it is a degradation metric, while voltage is more sensitive to instantaneous conditions.

As shown in

Table 5. Summary of computational cost for different predictive models. SVR has the lowest computational training cost, while Bi-LSTM has the highest training and inference time.

Model	Training Time (s)	Inference Time (s)	Relative Cost (Train)	Relative Cost (Inference)
SVR	0.44	0.0020	Lowest	Lowest
RF	57.40	0.1010	Low	Low
GB	146.08	0.0075	Medium	Very Low
LSTM	156.53	0.2360	High	High
Bi-LSTM	407.84	0.5690	Highest	Highest

, SVR has the lowest computational training cost of around $0.5$ s and with an inference time of $0.002$ s. The Bi-LSTM has the highest training time of $407.84$ s and inference time of $0.569$ s. The RF, GB, and LSTM have moderate training cost and fast inference. Bi-LSTM is more computationally expensive due to bidirectional passes. The prediction of SoH and voltage could allow EV users to plan maintenance strategies and reduce operational costs. This could also support intelligent charging coordination, allowing EVs with less charge to be given priority while scheduling maintenance during periods of low demand.

We simulate temperature to evaluate the relationship between thermal stress and battery degradation. The results in

Table 6. Predicted effects of increasing operating temperature on battery degradation. This table shows a rise in the percentage loss of SoH and voltage as ambient temperature increases. This demonstrates the impact of thermal conditions on battery health.

Temperature Increase	SoH Loss (%)	Voltage Loss (%)
+0%	9.3	2.4
+10%	11.7	3.1
+20%	14.5	3.8
+30%	18.0	4.8

show that thermal stress accelerates degradation. The findings demonstrate that even modest temperature increases can accelerate capacity loss and voltage degradation. These findings show the importance of thermal monitoring in EVs. In modern transportation systems, which frequently operate under variable and extreme climatic conditions, predictive modelling plays a crucial role in safeguarding the safety, reliability, and longevity of Li-ion batteries. For urban EVs, the results imply that high-risk batteries can be flagged for replacement before thermal runaway risks escalate. The results can help in thermal-aware routing, where cooler routes could be prioritised during heatwaves.

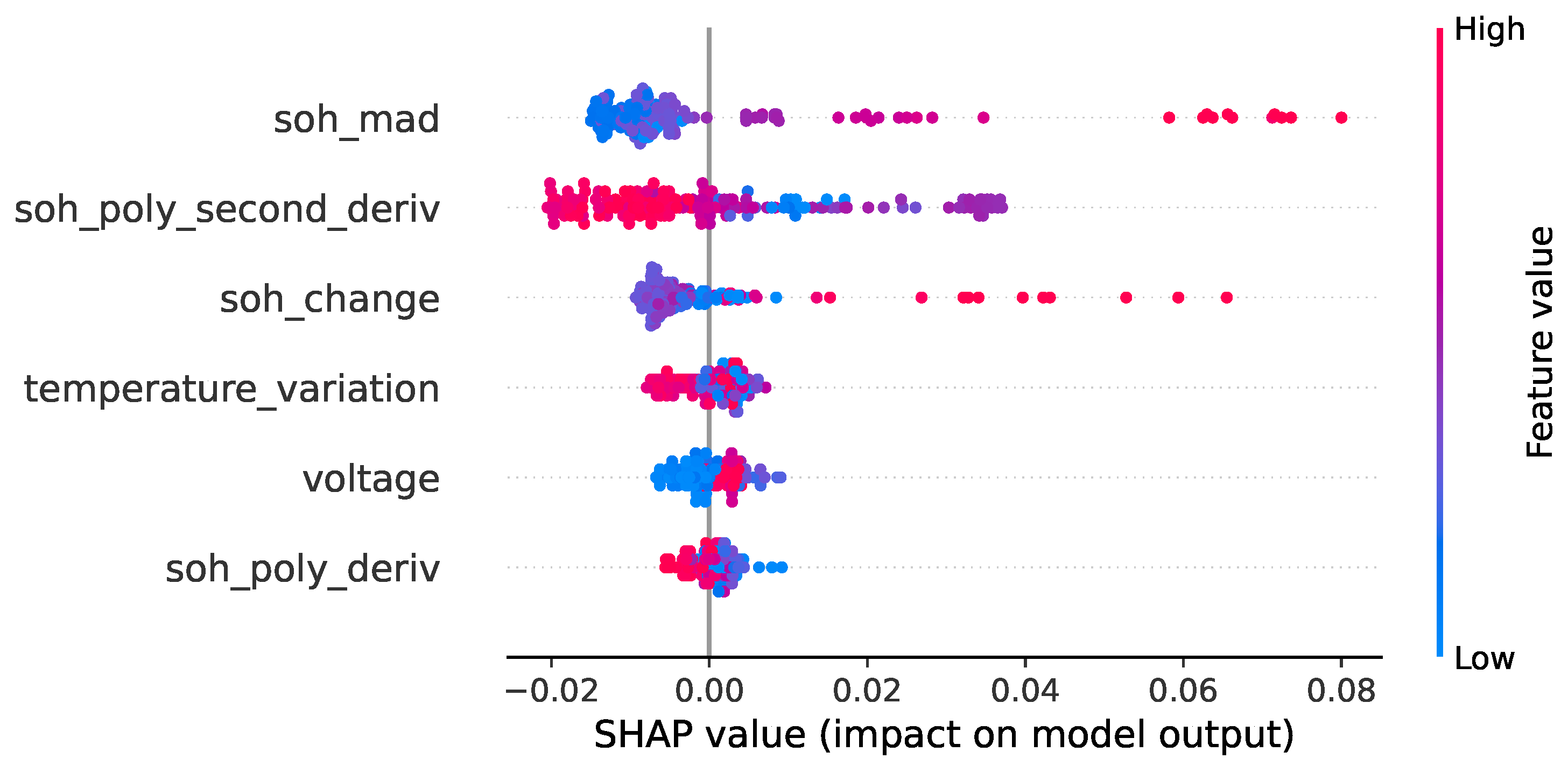
Figure 5 shows that SoH derivative, voltage, and temperature are the most influential features. This suggests that the values have a significant impact on the model’s output. These models can be embedded into EV control units to forecast range, prioritise charging schedules, and alert to early replacement needs. This could ensure operational efficiency for electric taxis, delivery fleets, and public buses in smart transportation systems.

Our results provide empirical evidence that QML, when integrated with classical models, can be helpful in battery monitoring. Although unsupervised classical models such as IF and LOF are applicable in anomaly detection, quantum enhancement brings value in capturing hidden anomalies that could escalate into catastrophic failures. Zero false positives ensure reliable operation in transportation systems without disruptions. The findings could help transport operators transition from reactive to proactive maintenance strategies, hence extending fleet lifespan while still maintaining service reliability in urban mobility.

We attribute the superior performance of QAD to the principles of quantum computing. Superposition enables the QAD to encode classical features into a compact Hilbert space. This increases the model’s expressive power. The entanglement property introduces dependencies between features that appear independent, thus uncovering latent patterns between them, for example, temperature and SoH. Quantum parallelism enables data to be processed in parallel streams, which enhances the isolation of events such as abnormal battery spikes compared to classical models that process data sequentially. Classical feature mappings function within a Euclidean space ${\mathbb{R}}^d$, where the dimensionality and linearity of transformations constrain separability. Quantum feature mappings use parameterised unitaries to put classical inputs $\mathbf{x}\in {\mathbb{R}}^d$ into a quantum state $\left|\varphi \right(\mathbf{x})\rangle$ in a $2^n$-dimensional complex Hilbert space ${\mathcal{H}}^{2^n}$. This exponential scaling in representational dimension enables the QAD to formulate non-linear decision boundaries that would necessitate huge kernels. Quantum states allow amplitude interference, enabling a constructive or destructive combination of computational paths, enriching the expressivity of quantum feature maps. This improves margin maximisation between normal and anomalous battery states.

In connected EV monitoring, anomalies could occupy sparse and irregular regions of the feature space. The quantum feature map enhances small geometric distinctions between normal and abnormal states in the Hilbert space. This makes them more linearly separable in the next stage of anomaly detection. This makes QAD perform better than the classical baseline and QAE. The limitation of QAD is that quantum models run on NISQ devices, which are prone to decoherence and gate noise that can affect the accuracy of measurements. Although our research uses simulations, future deployment on real devices would require error mitigation techniques, e.g., zero-noise extrapolation, probabilistic error cancellation, or measurement error mitigation to address the challenges posed by NISQ devices. This would strengthen the practical relevance of the proposed framework.

The training of the quantum feature extractor took approximately 1935 s, with an inference time of 118 s. Once the features were generated, training the QAD required $4.2$ s, compared to $2.4$ s for the baseline IF. These results indicate that the feature extraction stage dominates the computational cost of applying QML in anomaly detection. To reduce the computational time of the quantum feature extractor, we applied ansatz compression. The quantum feature extractor took around $1367.03$ s, with an inference time of $87.61$ s. The QAD model training took $1.37$ s compared to $4.2$ s before ansatz compression. These results provide empirical evidence that the compressed ansatz could be more suitable for deployment on NISQ hardware, where shorter circuits are inherently more noise-resilient. In future work, we will explore additional strategies to reduce computational cost further and support real-time BMS applications. These include qubit pruning to minimise the active circuit width, parameter-initialisation heuristics to accelerate convergence, gate merging and cancellation to simplify the circuit, and parameter sharing across layers to reduce the number of independent trainable parameters. We will also investigate measurement grouping to minimise the number of distinct quantum measurements required, as well as the use of gradient-free optimisers to decrease training overhead further.

As research in quantum hardware advances, Quantum Processing Units (QPUs) could accelerate feature extraction and reduce reliance on costly classical simulations. Future work could integrate real-time traffic data for dynamic charging coordination. We train the models with temperature-dependent features; however, additional factors, such as cycling rates, ageing mechanisms, and environmental variations, could also influence battery behaviour. Integrating multimodal sensor data, such as impedance and acoustic signals, could help develop models that adapt to varying operational profiles. Our results demonstrate the potential of ML-based spike detection for proactively monitoring battery health and forecasting degradation risks, thereby contributing to a safer and more resilient BMS. This could reduce battery failures, e.g., thermal runaway, and the risk of EV battery fires. Our approach can be integrated into BMSs to adapt operating parameters under thermal stress, enhance battery safety, extend lifespan, improve consumer confidence, and support the transition to green energy.

5. Conclusions

We present a method for detecting abnormal degradation spikes in Li-ion batteries and predicting battery health under thermal stress conditions in this paper. The method identifies high-risk spikes by targeting sudden SoH reductions instead of transient voltage fluctuations. Abnormal spikes are detected in 14 out of 168 discharge cycles. As global EV adoption accelerates, ensuring battery safety and reliability is crucial to maintaining consumer confidence, optimising operational performance, and promoting environmental sustainability. Thermal-induced degradation is a precursor to battery fires and shows the need for proactive monitoring. In urban EV ecosystems, battery failures can cause service disruptions, traffic congestion, safety risks, and financial loss. Proactive detection of Li-ion battery degradation patterns could allow EVs to autonomously adapt their routing, schedule preventative maintenance, and avoid routes with high thermal exposure. This paper lays the foundation for a BMS that aligns with the operational, environmental, and safety demands of future smart cities.