Unveiling State-of-Charge Effects on Elastic Properties of LiCoO₂ via Deep Learning and Empirical Models

Abstract

This study investigates the mechanical properties of LiCoO₂ (LCO) cathode materials under varying states of charge (SOCs) using both an empirical Buckingham potential model and a machine learning-based Deep Potential (DP) model. The results reveal a substantial decrease in Young’s modulus with decreasing SOC. Analysis of stress factors identified pairwise interactions, particularly those involving Co³⁺ and Co⁴⁺, as key drivers of this mechanical evolution. The DP model demonstrated superior performance by providing consistent and reliable predictions reflected in a smooth and monotonic stiffness decrease with SOC, in contrast to the large fluctuations observed in the classical Buckingham potential results. The study further identifies the increasing dominance of Co⁴⁺ interactions at low SOCs as a contributor to localized stress concentrations, which may accelerate crack initiation and mechanical degradation. These findings underscore the DP model’s capability to capture SOC-dependent mechanical behavior accurately, establishing it as a robust tool for modeling battery materials. Moreover, the calculated SOC-dependent mechanical properties can serve as critical input for continuum-scale models, improving their predictive capability for chemo-mechanical behavior and degradation processes. This integrated multiscale modeling approach can offer valuable insights for developing strategies to enhance the durability and performance of lithium-ion battery materials.

1. Introduction

Lithium-ion batteries (LIBs) are indispensable in modern technology, powering applications from portable electronics to electric vehicles due to their high energy density, long lifespan, and efficiency [1,2]. A critical component influencing LIB performance and durability is the cathode material. Among the various candidates, lithium cobalt oxide (LiCoO₂, LCO) was the first widely commercialized cathode and continues to be used in high-energy-density applications, especially in thin-film [3] and solid-state battery research [4]. Its layered structure, well-defined electrochemical profile, and stable cycling performance make it a model system for fundamental studies.

Despite LCO’s well-characterized electrochemical behavior, its mechanical integrity across varying states of charge (SOCs) remains underexplored. Mechanical degradation, such as particle cracking and interfacial delamination, is a major contributor to capacity fade and safety risks in LIBs [5,6,7]. While prior studies have investigated mechanical properties at either fully lithiated or delithiated states, a systematic understanding of how elastic properties evolve with lithium content is lacking. Given that Young’s modulus and stress evolution are key inputs for continuum models that predict electrode-level degradation, understanding these SOC-dependent mechanical behaviors is both timely and essential.

Experimental characterization of SOC-dependent elasticity is inherently difficult due to lithium’s low atomic number, complex charge compensation mechanisms, and structural heterogeneity. As a result, atomistic simulations have become essential tools to investigate mechanical properties of battery materials. Molecular dynamics (MD) simulations using empirical force fields have been extensively employed to assess elastic constants, fracture mechanisms, and diffusion-induced stresses in oxide cathodes [8,9,10]. For instance, studies on LiNi_1/3Mn_1/3Co_1/3O₂ and LiMn₂O₄ have successfully captured trends in SOC-dependent stiffness and anisotropic deformation using classical potentials with core–shell models [11].

Several MD simulation studies have investigated LiCoO₂ to better understand its structural, transport, and mechanical behavior. Fallahzadeh and Farhadian performed MD simulations using a Lennard-Jones-based force field to analyze lithium-ion diffusion in LCO under varying voltage and lithium content [12]. They reported diffusion coefficients and anisotropic transport trends consistent with experimental data. Kong et al. developed a charge-transfer modified embedded-atom method (CT-MEAM) to model the Li–Co–O system, demonstrating its ability to capture dynamic charge transfer, phase stability, and cathode voltages across Li-rich and Li-deficient compounds [13]. More recently, Lee et al., proposed a second nearest-neighbor modified embedded-atom method (2NNMEAM) combined with a charge equilibration scheme (Qeq) and applied it to simulate lithium diffusion and mechanical properties in Li_1−xCoO₂ [14]. Their model reproduced key properties such as elastic constants, migration barriers, and redox potentials in good agreement with DFT and experimental results.

However, empirical force fields often rely on parameters fitting to specific chemistries, limiting their transferability across phases or charge states. This is particularly problematic for complex charge compensation phenomena in LCO, where the Co³⁺/Co⁴⁺ ratio evolves with lithiation. First-principles methods like density functional theory (DFT) offer quantum-level accuracy but are computationally prohibitive for the system sizes required to model microstructural effects.

To address this trade-off, machine learning-based potentials such as the Deep Potential (DP) model have recently gained traction [15,16]. By training on DFT data, DP models preserve quantum mechanical fidelity while enabling simulations of large and realistic supercells. Recent applications of DP and related machine learning interatomic potentials such as Gaussian Approximation Potentials (GAP), the Spectral Neighbor Analysis Potential (SNAP), and SchNet have demonstrated remarkable accuracy in predicting formation energies, phase stability, and thermal transport properties in materials [17,18,19].

In this study, we investigate the elastic behavior of LCO across a wide range of SOCs using both an empirical Buckingham potential and a DP model trained on ab initio data. The Buckingham potential has been one of the few available and widely adopted interatomic potentials for LCO in classical molecular simulations. Its popularity stems from analytical simplicity and low computational cost, which make it suitable for large-scale simulations. However, it is limited in its ability to accurately capture complex bonding environments, electronic effects, and structural evolution under diverse operating conditions. In contrast, machine learning-based potentials such as the DP model offer higher fidelity by learning interatomic interactions directly from quantum-mechanical data, making them more transferable across different chemistries and states of charge. The two models are systematically compared in terms of their ability to predict mechanical responses and capture stress evolution mechanisms. Our findings reveal that the DP model provides more consistent and accurate predictions, particularly at low SOCs where structural instabilities emerge. The study further identifies the increasing dominance of Co⁴⁺–O interactions as a key driver of localized stress concentrations, which may promote crack initiation. These results not only validate the robustness of machine learning-based potentials but also provide critical input parameters for multiscale models of electrode degradation, ultimately informing the design of more durable battery systems.

2. Method

2.1. System Preparation

The hexagonal O₃-LiCoO₂ structure, characterized by the R3̅m space group, represents the most thermodynamically stable phase and is typically obtained through conventional synthesis processes [20,21]. The unit cell used in our study is illustrated in Figure 1, with lattice constants of a = 5.685 Å, b = 4.264 Å, and c = 14.145 Å [22]. The unit cell comprises 12 lithium, 12 cobalt, and 24 oxygen atoms, corresponding to a fully lithiated cathode.

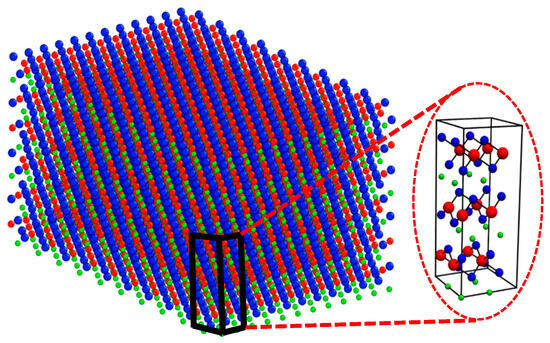
Figure 1. Schematic of the LCO unit cell and a 4 × 6 × 2 supercell model, illustrating lithium (green), cobalt (red), and oxygen (blue) atoms.

To generate various SOC states, lithium ions were systematically removed to achieve SOC values of 0.91, 0.83, 0.75, 0.66, 0.58, 0.50, 0.41, 0.33, 0.25, and 0.16. Following lithium removal at each SOC level, the remaining lithium could adopt multiple configurations. To maintain system neutrality, one cobalt atom changes valence from Co³⁺ to Co⁴⁺, introducing additional configurational variability.

Table 1 lists the number of possible atomic configurations for each SOC state. Each configuration exhibits a distinct initial energy, which was calculated using a single time step. Figure 2 presents the initial potential energy of all possible configurations for a representative case of 0.5 SOC, arranged in ascending order. We selected configurations within the low-energy range, based on the assumption that atomic structures tend to stabilize in energetically favorable states. The calculated elastic modulus values represent the average of these selected structures to ensure reliable and consistent results.

Table 1. Number of possible configurations for each SOC.

SOC	Configurations
1.00	1
0.91	144
0.83	4356
0.75	48,400
0.66	245,025
0.58	627,264
0.50	853,776
0.41	627,264
0.33	245,025
0.25	48,400
0.16	4356

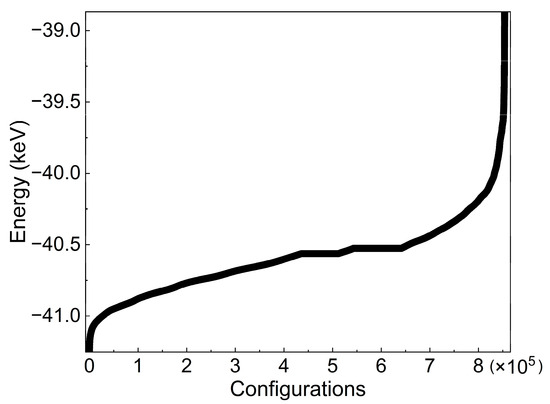
Figure 2. Representative initial energy curve of all possible configurations at 0.5 SOC, arranged in ascending order.

To accurately characterize the material’s properties and dynamic response, a larger simulation structure is required. The final structure was constructed by replicating the unit cell 4 × 4 × 2 times along the x, y, and z axes, respectively.

2.2. Analytical Model

The interactions between LCO ions involve both long-range Coulombic forces and short-range pairwise interactions. The Buckingham potential is employed to describe the short-range interactions, defined as follows:

$$E=A{e}^{-r/\rho }-{\displaystyle \frac{C}{{r_{ij}}^6}}$$

(1)

where r_ij represents the distance between atoms i and j [8,9,23]. The parameter C governs the attractive forces, while ρ defines the repulsive interactions. The parameter A represents the magnitude of short-range Pauli repulsion due to overlapping electron clouds. A higher value of A leads to a stronger repulsive force at short interatomic distances. The parameter ρ governs the decay length of this repulsion; a smaller ρ implies a more rapidly decaying repulsive interaction. Together, A and ρ define the steepness and position of the repulsive wall of the potential. The parameter C accounts for van der Waals attraction. In cases where C = 0, as seen in the Li–O interaction, long-range attraction is dominated by Coulombic interactions, rather than van der Waals forces. The parameters A, ρ, and C are empirical constants, with their values provided in Table 2.

Table 2. Parameters of Buckingham potential.

Interaction Pair	A (eV)	ρ (Å)	C (eVÅ6)	Reference
Li+–O2−	632.1018	0.2906	0.00	[8]
Co3+–O2−	1329.82	0.3087	0.00	[8]
Co4+–O2−	1102.03	0.2984	0.00	[24]
O2−–O2−	22,764.3	0.149	65.0	[8]

To account for electronic polarization effects, the adiabatic core–shell model is implemented, which is an effective approach for simulating the dielectric properties of ceramic oxides [8,25]. The core–shell model has been widely utilized in previous studies to investigate layered cathode materials [8,26]. In this model, the core, representing the heavier component, governs pairwise interactions, while the shell, carrying the highest charge, contributes to the system’s polarizability. The total charge of a core–shell pair is the sum of the core charge (q) and the shell charge (Y). The shell is connected to the core via a spring force F_s, defined by the following:

$${\mathrm{F}}_{\mathrm{s}}={\displaystyle \frac{\mathrm{k}}{2}}{r}^2$$

(2)

where k is a parameterized spring constant, and r is the distance between the core and the shell. The parameters for the core–shell model, including charges and spring constants for each ion, are summarized in Table 3 [8]. Since the core–shell model parameters for Co⁴⁺ are not available in existing references, we estimated the shell charge (Y) by maintaining the same core charge (0.96) as used for Co³⁺, resulting in a shell charge of 3.04 to preserve the total formal charge of +4. Additionally, the spring constant (k) was assumed to be the same as that of Co³⁺ to ensure consistency within the core–shell model.

Table 3. Core–shell model parameters.

Ion	Y (e)	k (eVÅ−2)
Li+	1.0	9999.0
Co3+	2.04	196.3
Co4+	3.04	196.3
O2−	–2.96	65.0

The selected structure from all possible configurations was equilibrated for 50 picoseconds (ps) at 300 K using the NPT ensemble. The initial stress values of all equilibrated structures were averaged, and only those structures with initial stress values close to the average were selected for stretching. A timestep of 1 femtosecond (fs) and periodic boundary conditions were applied throughout the simulation. For the stress–strain response, 0.5% stretching was applied to the selected structures using the NVT ensemble and equilibrated over 50 ps. The final stress value and its contributing factors were determined by calculating the difference between the final virial stress and the initial virial stress. In this study, the stress components are categorized as follows: ‘pairwise’ represents the short-range interatomic forces modeled by the Buckingham potential, ‘bond’ refers to the core–shell spring interaction, and ‘long-range’ corresponds to Coulombic electrostatic interactions.

2.3. Deep Potential Model

In this study, the elastic behavior of LCO cathode material was investigated using the Deep Potential Molecular Dynamics (DeePMD) approach implemented in DeePMD-kit integrated with LAMMPS. The training of the Deep Potential (DP) model employed structural and density functional theory (DFT) data derived from Hu et al. [27]. The workflow of DeePMD-kit is illustrated in Figure 3.

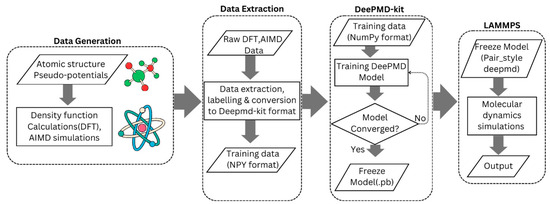
Figure 3. Workflow of DeePMD-kit.

To develop the DP model, the potential energy surface (PES) was fitted using a deep neural network trained on atomic-level energies, forces, and stresses obtained via DFT + U calculations [16,28]. The DP framework maps atomic environments into local descriptors that are invariant to translation, rotation, and permutation. Atomic interactions within a specified cutoff radius were described using local atomic descriptors, ensuring both scalability and computational extensivity [29].

The neural network architecture included fully connected layers with rectified linear unit (ReLU) activation functions, incorporating residual connections to enhance training stability [30]. Training inputs consisted of local descriptors derived from atomic coordinates, avoiding direct use of raw Cartesian coordinates. To refine the model accuracy iteratively, active learning strategies were employed, including the incorporation of high-error configurations and by using on-the-fly training during molecular dynamics simulations [31,32].

The training dataset, consisting of DFT-derived energies, forces, and stresses, was prepared using DeePMD-kit’s data extraction workflow [33,34]. This involved converting raw simulation data into computationally efficient binary Numpy format compatible with DeePMD-kit [35]. Model training continued iteratively, with regular validation checks until convergence criteria were satisfied, ensuring optimal predictive performance. The finalized trained model was exported in TensorFlow’s Protocol Buffers (.pb) format, enabling efficient integration with LAMMPS.

The DP model was trained using 45 DFT + U datasets of LCO structures representing O3, O1, and spinel phases, sourced from the work of Hu et al. [27]. Training was conducted on 35 datasets (1400 configurations), with 10 datasets (400 configurations) reserved for testing. The model architecture included a 6.0 Å cutoff, descriptor network (25–50-100), and fitting network with three 240-neuron ResNet layers. Root-mean-square errors (RMSEs) on the test set were 10.55 meV/atom for energy and 63.53 meV/Å for force. This model was applied to simulate the mechanical behavior of Li_xCoO₂ in regions of phase space well represented in the training data.

The trained DP model was validated by comparing its predictions against DFT + U reference data, including formation energies, atomic forces, and voltage plateaus for the Li_xCoO₂ system. Figure 4 presents a confusion matrix demonstrating the accuracy of the energy predictions, confirming model reliability at an accuracy of 92.01%.

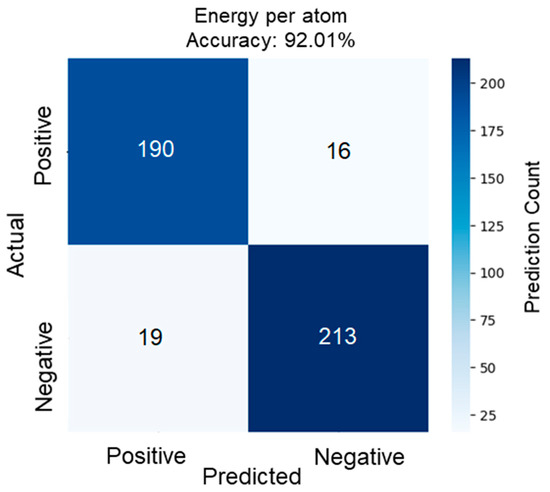
Figure 4. Confusion matrix of predicted versus actual energy per atom values for the trained DeePMD-kit model.

Atomistic simulations for elastic behavior were performed in LAMMPS using the frozen DeePMD-kit model [33]. The system configuration adopted the hexagonal O₃-LiCoO₂ structure with the R3̅m space group and periodic boundary conditions. Initial structures at different states of charge (SOCs) were equilibrated at 300 K for 50 ps with a timestep of 1 fs under an NPT ensemble to achieve system stabilization. Subsequently, an engineering strain rate of 0.005 per timestep was applied, stretching the system at a constant temperature (300 K) using an NVT ensemble.

3. Results

3.1. Validation

The models were validated by comparing their calculated lattice constants with established reference data [14,36,37,38]. The lattice constants for both the analytical Buckingham potential model and the machine learning-based DP models were determined by measuring the dimensions of the equilibrated systems. The calculated lattice constants are presented in Figure 5, with a detailed comparison summarized in Table 4.

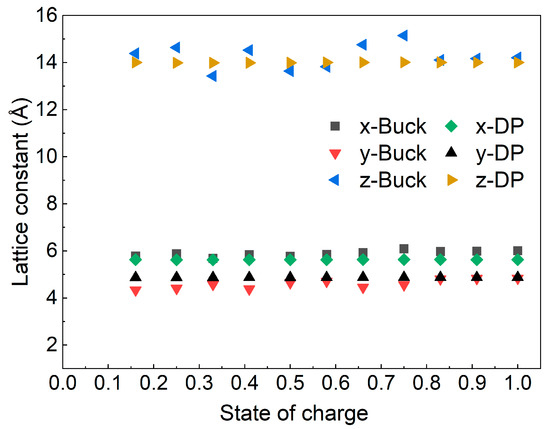
Figure 5. Variation of lattice constants along the x, y, and z directions as a function of SOC. Results are shown for both Buckingham potential (Buck) and Deep Potential (DP) models.

Our results demonstrate good agreement with previously reported values, confirming the reliability of the interatomic potentials employed in this study. Notably, in the Buckingham potential model, the lattice constants exhibit a slight decrease as lithium content is reduced, consistent with trends observed in earlier studies with other cathode materials [39,40,41]. This behavior aligns with the expected structural response to lithium deintercalation, where the reduced lithium content leads to contraction of the crystal structure due to diminished Coulombic repulsion and bonding rearrangements.

Table 4. Lattice parameters of LCO with varying SOC.

SOC	Buckingham Potential		Deep Potential		Previous Studies
	a (Å)	c (Å)	a (Å)	c (Å)	a (Å)	c (Å)	Reference
1.00	6.01	14.21	5.62	14.00	5.631	14.054	[36]	DFT
					5.629	14.052	[37]	DFT
					5.652	14.207	[38]	DFT
					5.680	14.160	[42]	DFT
					5.583	13.593	[14]	MD
					2.859 *	14.02	[43]	DFT
					2.816 *	14.04	[44]	NI **
					2.840 *	14.16	[42]	DFT
0.91	5.99	14.17	5.62	14.00
0.83	5.97	14.11	5.63	14.01
0.75	6.09	15.15	5.63	14.00	2.811 *	14.226	[45]	NPD ***
0.66	5.93	14.76	5.63	14.00	2.811 *	14.286	[45]	NPD ***
0.58	5.85	13.83	5.62	14.00
0.50	5.77	13.64	5.62	13.99	4.865	14.420	[46]	XRD
0.41	5.84	14.53	5.62	13.99
0.33	5.68	13.43	5.62	13.98
0.25	5.88	14.64	5.62	13.99
0.16	5.78	14.39	5.63	14.01

* Half of the unit cell length in the a-direction. ** NI: Nanoindentation. *** NPD: Neutron powder diffraction.

Table 4. Lattice parameters of LCO with varying SOC.

SOC	Buckingham Potential		Deep Potential		Previous Studies
	a (Å)	c (Å)	a (Å)	c (Å)	a (Å)	c (Å)	Reference
1.00	6.01	14.21	5.62	14.00	5.631	14.054	[36]	DFT
					5.629	14.052	[37]	DFT
					5.652	14.207	[38]	DFT
					5.680	14.160	[42]	DFT
					5.583	13.593	[14]	MD
					2.859 *	14.02	[43]	DFT
					2.816 *	14.04	[44]	NI **
					2.840 *	14.16	[42]	DFT
0.91	5.99	14.17	5.62	14.00
0.83	5.97	14.11	5.63	14.01
0.75	6.09	15.15	5.63	14.00	2.811 *	14.226	[45]	NPD ***
0.66	5.93	14.76	5.63	14.00	2.811 *	14.286	[45]	NPD ***
0.58	5.85	13.83	5.62	14.00
0.50	5.77	13.64	5.62	13.99	4.865	14.420	[46]	XRD
0.41	5.84	14.53	5.62	13.99
0.33	5.68	13.43	5.62	13.98
0.25	5.88	14.64	5.62	13.99
0.16	5.78	14.39	5.63	14.01

* Half of the unit cell length in the a-direction. ** NI: Nanoindentation. *** NPD: Neutron powder diffraction.

3.2. Elastic Modulus

The stiffness for 11 SOCs was calculated using the analytical empirical Buckingham potential model for the selected optimized and equilibrated structures. The results, presented in Figure 6, show a substantial decrease in stiffness from 452 GPa for a fully lithiated state to 130 GPa at 16% lithiation. This significant variation highlights the material’s sensitivity to changes in the state of charge, as reflected in its mechanical properties.

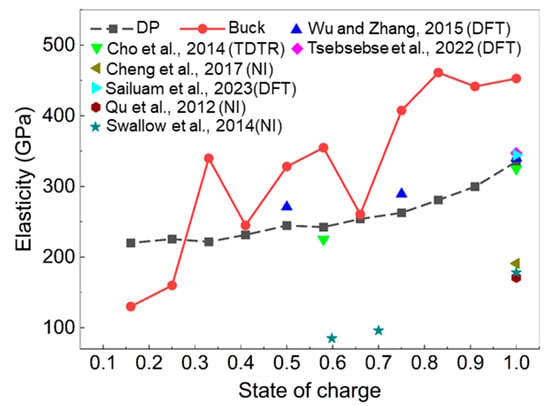
Figure 6. Evolution of the elastic constant as a function of SOC for the Buckingham potential (Buck) and Deep Potential (DP) models. Experimental references include Ref. [47] (TDTR, time-domain thermoreflectance) and Refs. [44,48,49], (NI, nanoindentation). DFT values from Refs. [42,43,50] are also included for comparison.

Notably, comparisons with similar oxides have shown differences of up to 50% in elastic modulus values [10]. The substantial variation in elastic moduli observed in our results is consistent with the pronounced SOC-dependent changes reported for LiCoO₂ in previous studies [42]. Such large differences have been attributed to lithium concentration-driven changes in Co–O bond strength, evolving cation valence states, and associated structural distortions. This agreement further supports the robustness of our calculated results and highlights the expected mechanical behavior of LCO under varying SOC conditions.

The improved reliability of the DP model compared to the analytical Buckingham model arises from both its data-driven foundation and its ability to generalize across different states of charge. The DP model is trained on a diverse set of DFT-calculated structures that span a wide range of lithium contents and atomic configurations, allowing it to capture subtle changes in bonding environments, local stress fields, and Co³⁺/Co⁴⁺ interactions across the SOC spectrum. In contrast, the Buckingham model relies on fixed formal charges and predefined pairwise parameters, which do not adapt to the evolving electronic structure during delithiation. As shown in Figure 6, the DP model predictions exhibit closer agreement with experimental reference values at multiple SOCs, further supporting its validity. This consistency highlights the DP model’s strength not only in reproducing known data but also in reliably interpolating mechanical behavior in regimes where experimental measurements are scarce.

To investigate the source of variance in the calculated Young’s modulus, the contributing factors were decomposed into virial stress components, including pairwise energy, bond energy, long-range Coulombic interactions, and kinetic energy contributions (Figure 7a). Notably, the pairwise stress component (green curve) closely overlaps with the total stress (black curve) across all SOCs, confirming that short-range interactions alone account for nearly all of the mechanical response characteristics. The analysis reveals that pairwise interactions play a dominant role in the observed changes in stiffness, while kinetic and long-range contributions remain minimal and stable. This dominance of pairwise interactions emphasizes the importance of short-range bonding changes in determining mechanical properties under varying SOC conditions.

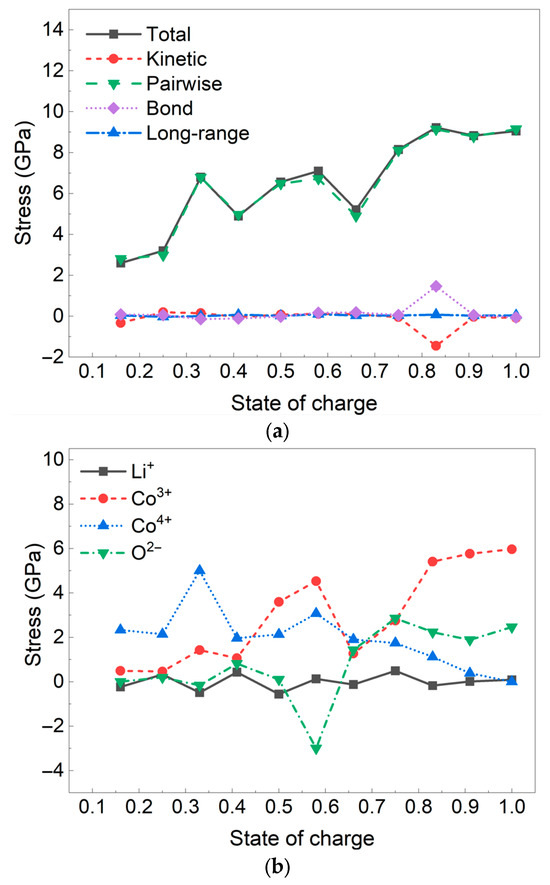
Figure 7. Stress component σ_x as a function of SOC. (a) Decomposition of the total stress into kinetic, pair, bond, and long-range contributions. (b) Element-specific contributions to stress.

The pairwise energy contribution arises from interactions between four types of particles: Li⁺, Co³⁺, Co⁴⁺, and O²⁻. The corresponding pairwise energy components are shown in Figure 7b. As the SOC decreases, the population of Co³⁺ ions diminishes, while that of Co⁴⁺ ions increases. Since Co⁴⁺ has a smaller ionic radius, local contraction of Co–O bonds occurs, which is confirmed by the reduction in lattice constants. The localized lattice contraction introduces internal stress gradients, particularly at low SOCs, which can serve as points of structural instability initiation.

Additionally, Co⁴⁺ carries a higher positive charge than Co³⁺, resulting in stronger electrostatic interactions with neighboring oxygen ions. These intensified interactions further promote localized stress buildup in specific regions, as shown by the sharp increase in Co⁴⁺ stress contribution at SOC < 0.4. Figure 8 presents the spatial distributions of shear strain fields at representative low, medium, and high SOCs, illustrating the structure at low SOC exhibits higher shear strain distribution. Moreover, Co⁴⁺ forms stronger Co–O bonds compared to Co³⁺, enhancing localized stiffening. This combination of lattice contraction, intensified Coulombic interactions, and bond stiffening generates a stress mismatch, which promotes crack initiation and propagation, particularly at low SOCs.

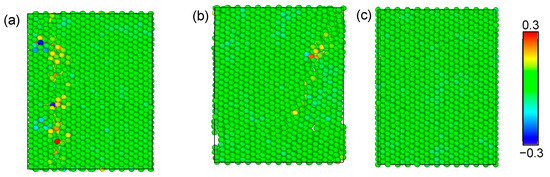
Figure 8. Shear strain distribution at a strain of 0.09 for (a) SOC = 0.25, (b) SOC = 0.5, and (c) SOC = 0.83.

Notably, in Figure 7a, the pairwise contribution dominates the total stress profile, reinforcing its primary role in stress evolution, while bonds and long-range interactions remain minimal. The abrupt increase in total stress near SOC ~0.4 may indicate a critical point for mechanical instability, potentially linked to lattice distortions or defect accumulation.

Conversely, contributions from Li⁺–O²⁻ and Co³⁺–O²⁻ interactions decrease, further contributing to the decline in stiffness as SOC is reduced. These combined effects highlight the potential mechanical instability that emerges as SOC decreases, emphasizing the importance of considering SOC-dependent stress distributions when evaluating material degradation mechanisms.

The stress–strain curves for various SOC conditions, calculated using the machine learning-based DP model, are shown in Figure 9. The slope of these curves was used to calculate the stiffness values, which are presented in Figure 6. The results exhibit a clear monotonic decrease in stiffness with SOC, with a minor increase observed at 0.5 SOC. This slight peak may be attributed to a transient strengthening effect linked to optimal cation distribution or localized bonding rearrangements. Notably, the DP model’s predictions consistently fall within 10% tolerance of reported values, further supporting its reliability and accuracy in capturing SOC-dependent mechanical behavior. The relatively lower experimental moduli in Figure 6 may result from the indirect nature of nanoindentation measurements and the influence of defects and grain boundaries, whereas our simulations are based on a defect-free perfect crystal structure.

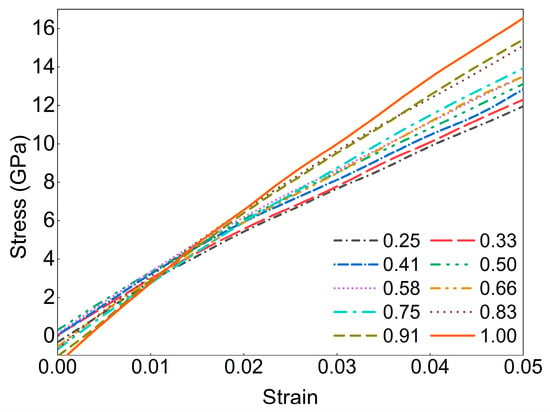
Figure 9. Stress–strain curves in the x direction for various SOC obtained by DP model.

Interestingly, the Buckingham model predicts higher modulus values than both the DP model and reference data. This overestimation is likely due to the Buckingham model’s reliance on full formal charges, which are known to exaggerate Coulombic interactions [11,51]. While the calculated values are elevated, the overall trend remains consistent with both the DP model and experimental references. Adjusting the formal charges to reduced values could improve the Buckingham model’s quantitative accuracy.

When comparing the two models, the DP model demonstrates notable advantages in several aspects. First, it exhibits improved consistency, with minimal fluctuations across SOC states, resulting in smoother and more predictable trends. Second, the DP model shows closer agreement with reference data, as its predictions align well with experimental values and fall within an acceptable tolerance limit. Lastly, the DP model offers enhanced physical realism by effectively capturing the evolving contributions of Co³⁺ and Co⁴⁺ interactions, thereby providing a more accurate representation of the material’s true behavior.

The results also reveal important implications for mechanical stability. As SOC decreases, the increasing dominance of Co⁴⁺ interactions introduces localized stress concentrations, which may promote crack initiation and accelerate electrode degradation. Furthermore, the variation in oxygen’s contribution suggests evolving Co–O bonding environments that may contribute to structural instability at low SOC levels. These findings highlight the need to account for SOC-driven mechanical changes when designing cycling protocols or developing electrode coatings to mitigate fracture risks.

Overall, these findings underscore the superior accuracy and reliability of the machine learning-based DP model. Its improved predictive capabilities make it a promising tool for future studies, particularly for investigating the mechanical behavior of cathode materials under various electrochemical conditions.

Recent work by F. Guo et al. has highlighted the importance of mechanical degradation mechanisms, such as modulus softening, particle cracking, and interface delamination, in dictating the long-term electrochemical performance and safety of lithium-ion batteries [52]. In this context, mechanical properties such as elastic modulus and fracture energy evolve with cycling and can be directly linked to state-of-health (SOH) indicators. As damage accumulates, the material’s ability to maintain structural integrity under electrochemical and thermal stresses degrades, reducing its remaining useful life (RUL). Our findings on strain localization and mechanical response at different states of charge suggest that such mechanical descriptors could be integrated into future battery prognostics models, providing a more comprehensive understanding of degradation and lifetime estimation.

4. Conclusions

This study provides a thorough analysis of the mechanical properties of cathode materials under different SOCs using both an empirical Buckingham potential model and machine learning-based Deep Potential models. The Buckingham potential model showed a significant reduction in Young’s modulus as the SOC decreased, indicating that the mechanical behavior of the material is highly sensitive to changes in structure and ionic state. Analyzing the stress factors revealed that pairwise interactions, particularly involving Co³⁺ and Co⁴⁺, play a dominant role in driving these changes. The transition from Co³⁺ to Co⁴⁺ and the resulting alterations in bonding characteristics were identified as key mechanisms influencing the observed trends.

In contrast, the Deep Potential model, which uses advanced machine learning techniques, demonstrated significant advantages over the analytical model. It provided more consistent and reliable predictions with minimal fluctuations, closely aligning with reference data within an acceptable tolerance range. The model’s ability to capture a clear linear trend, along with its robustness and adaptability, highlights its potential for more accurate simulations of mechanical properties in energy storage materials.

Moreover, the analysis revealed that the Buckingham model’s sharp fluctuations at lower SOCs could be linked to structural instability or phase transition effects. The increased dominance of Co⁴⁺ interactions at lower SOCs introduces localized stress concentrations, which may enhance crack initiation and accelerate electrode degradation. This observation underscores the importance of considering SOC-dependent mechanical changes when designing battery cycling protocols or developing protective coatings to mitigate fracture risks.

Importantly, the calculated mechanical properties provide valuable input for continuum-scale models that are widely used in studying the chemo-mechanical behavior and mechanical degradation of LCO materials due to aging. By incorporating SOC-dependent material properties, continuum models can improve the prediction of stress evolution, crack formation, and degradation processes in LCO-based battery systems, enabling the design of more durable and stable electrodes.

Overall, the findings validate the superiority of the Deep Potential model for studying complex cathode materials. Its predictive accuracy and capacity to unveil intricate material behaviors make it a valuable tool for future research and development. This approach shows promise for optimizing the design of advanced materials with tailored mechanical properties, ultimately facilitating the development of more efficient and reliable energy storage systems.