Abstract
Composite materials are increasingly used in industrial applications, particularly in the aeronautic sector. However, their susceptibility to impact damage remains a critical concern, making damage tolerance a key focus for design and manufacturing. One approach to improving damage tolerance involves interleaving elastomeric films within polymeric composites, though this introduces experimental and numerical complexities. In particular, numerical simulations require reliable modelling techniques to predict the structural effects of hybridisation. This paper tested two different stacking sequences, differing in the number and placement of the elastomeric layers, under quasi-static indentation conditions. A numerical analysis was carried out using two distinct formulations of Hashin’s failure criteria and a continuum damage model, implemented through specifically developed User Material Subroutines. The experimental and numerical results were then compared, and the advantages and drawbacks of each modelling technique were discussed and compared.
1. Introduction
The evolution of advanced composite structures in modern engineering has been driven mainly by the adoption of polymeric composite materials (PCMats), due to their structural versatility, lightweight composition, and tuneable performance characteristics [1,2]. Among the diverse range of PCMats, carbon fibre-reinforced polymers (CFRPs) have emerged due to their outstanding mechanical performance [3]. These materials exhibit exceptional strength-to-weight ratios, high stiffness, and remarkable environmental and chemical degradation resistance [4], making them adequate for aerospace, automotive, and structural engineering applications [5,6]. However, despite their many advantages, CFRPs are not without limitations. Notably, they suffer from low interlaminar shear strength, reduced structural integrity after impact events, and suboptimal vibrational behaviour [7]. Their limited ability to dampen mechanical vibrations poses challenges in dynamic environments, potentially affecting performance and durability, especially in structural applications. To overcome these limitations and to expand the functional capabilities of CFRPs, the integration of elastomers (ELs) has emerged as a promising approach in both the automotive and aerospace industries. These polymers exhibit high elasticity and intrinsic damping properties, enabling the efficient dissipation of vibrational and impact energy. Elastomer-modified resins, produced by blending the elastomeric phase into the matrix in liquid form, can significantly improve delamination resistance, impact toughness, and vibrational damping [8,9]. However, despite the potential benefits for laminate behaviour, this approach requires a resin formulation specifically tailored to ensure compatibility with the elastomer. Moreover, the integration of an elastomeric phase alters the matrix characteristics and may adversely affect the overall performance of the composite, potentially compromising its mechanical strength, thermal stability, and thermomechanical behaviour while also contributing to an undesirable increase in weight.
Interleaving ultrathin elastomeric sheets or mats between the plies of traditional CFRP layups is a new technique that promises to solve these drawbacks. This new group of materials—often referred to as Hybrid Polymeric Composite Materials (HyPCMats)—enables property enhancement, such as damping or toughening, without altering the original resin system used in commercially available prepregs. Consequently, it offers a versatile solution for tailoring composite behaviour whilst preserving the standard mechanical integrity and processing compatibility of CFRP materials.
The integration of elastomeric materials in traditional composite stacking sequences to produce HyPCMats is well-documented in the existing literature. These materials have been studied in many different conditions: quasi-static crashing [10,11], tensile and flexural tests [12], and in combination with metal foils [13] or other fibre prepregs [14,15]. In particular, research has primarily focused on using elastomeric materials to enhance the impact resistance and energy absorption of fibre metal laminates (FMLs). Liu et al. in [16] focused their research on how elastomeric interlayers influence the composite’s ability to resist impact-induced damage, such as delamination, cracking, and plastic deformation. The findings suggest that the rubber layer enhances the composite’s ability to absorb energy and reduces the extent of delamination and matrix cracking. Taherzadeh-Fard et al. [17] explored the resistance of FMLs to perforation. They tested sandwich specimens (natural rubber elastomer mats, glass/epoxy plies, and aluminium 6061-T6 layers) under different impact velocities. The findings revealed that positioning the elastomer layer closer to the impact-facing surface significantly enhanced energy absorption due to improved load distribution. As the impact velocity increased, the elastomer became more efficient in dissipating energy, which was due to the outward shift in the damage initiation point within the elastomer layer. Düring et al. [18] investigated the impact performance of a hybrid glass fibre composite combined with thin steel and elastomer layers. Through experimental drop weight impact tests and compression after impact (CAI) assessments, researchers examined how the position and proportion of additional layers influence damage resistance and residual strength. The results indicate that the placement of elastomeric layers has a significant effect on the damage area, which affects the residual strength of the laminates. Sarlin et al. [19] conducted a comprehensive experimental investigation into the low-velocity impact behaviour of layered steel/rubber/GFRP hybrid structures, focusing on the effects of varying impact energy levels and rubber layer thicknesses. Their study emphasised the function of the rubber interlayer in reducing stress and distributing the impact load more evenly across the composite material. The most significant reduction in damage was observed when comparing structures without rubber to those with the thinnest rubber layer, whilst varying the thickness of the elastomeric layer between 0.5 mm and 1.5 mm did not have any noticeable impact. Mohotti et al. [20] explored the deformation characteristics of structures incorporating elastomeric materials under dynamic loading. Their results demonstrated that elastomers not only improved the energy dissipation capacity of the composite but also effectively minimised residual plastic deformation after impact, thereby enhancing structural recoverability. Khodadadi et al. [21] investigated the impact response of bilayer aluminium–rubber plates through a series of controlled impact tests. They reported that placing the rubber layer on the front face of the plate significantly improved the energy absorption performance, primarily due to the rubber’s ability to deform elastically and mitigate the initial shock. This configuration reduced stress transmission to the underlying aluminium layer and delayed the onset of structural damage.
Other researchers have focused their work on the integration of the elastomeric layers in more traditional carbon/epoxy components. CFRPs, while offering excellent mechanical performance, are typically characterised by low impact resilience and a tendency to delaminate, even under low-energy impact conditions. The introduction of elastomeric interleaves between CFRP plies improves interlaminar strength, thereby reducing delamination and enhancing the overall damage tolerance of the composite structure. Sadowski et al. [22] varied the positioning of elastomeric interleaves within the laminate structure to evaluate the influence on energy absorption and damage tolerance under dynamic loading. The results demonstrated that the integration of elastomer layers significantly enhances impact performance and crack resistance. Li et al. in [23] focused on how variations in the thickness of a protective rubber layer, applied to the CFRP specimens’ upper surface, influenced performance under low-velocity impacts. Their results indicated that the threshold load, energy absorption, and maximum displacement of the CFRP laminate with a protective layer increased with impact energy. In [24], Stellinger et al. investigated the integration of a rubber layer into CFRP tubes to improve their resistance to low-velocity impacts. Using experimental tests, the authors found that the rubber interlayer significantly reduced internal damage by absorbing and dissipating impact energy. Krollmann et al. in [25] tested different CFRP/elastomer stacking sequences in low-velocity impact loadings at different energy levels, followed by compression after impact (CAI) tests. The results revealed that increasing the number of elastomeric layers significantly reduced peak impact forces and damage areas whilst enhancing energy absorption by up to 21% and improving impact tolerance. The improved performance was attributed to shear decoupling provided by the elastomer layers, leading to higher deformation compliance and the mitigation of fibre fracture as a dominant damage mechanism.
Despite extensive research available in the literature, only a few studies incorporate both experimental and numerical analyses, highlighting the ongoing need for the reliable modelling of elastomeric behaviour when integrated in CFRPs. A recent study by Tang et al. [26] combined experimental testing with finite element analysis using the built-in ABAQUS Hashin model to investigate CFRP–elastomer laminates under low-velocity impact. Their approach relied on shell elements and applied a linear stiffness degradation scheme, limiting the ability to capture out-of-plane effects and progressive failure. A thorough understanding and control of the complex behaviours of PCMats, in fact, require the use of advanced modelling techniques supported by rigorous experimental validation [27]. This highlights the importance of not only fabricating multilayer composite structures but also evaluating their performance and simulating their mechanical response to ensure the reliability of the manufacturing process. A wide range of modelling strategies can be employed to analyse composite materials, generally categorised into micro-scale, meso-scale, and macro-scale approaches. These differ in the level of detail at which the material is represented: micro-scale models explicitly describe the constituents, allowing for a detailed analysis of local damage mechanisms; meso-scale models represent individual plies or laminae as homogeneous orthotropic layers, capturing ply-level damage mechanisms; macro-scale models treat the laminate or structure as a homogenised continuum, focusing on the overall structural response and global damage progression while reducing computational cost. Concurrently, computational homogenisation (e.g., Finite Element Square method or FE2) approaches, such as explicit direct FE2 (D-FE2) and hybrid direct FE2, deliver micro-level fidelity by coupling each Gauss point to a representative micro-model, but their computational burden limits them to coupon-scale studies [28,29]. Macroscopic finite element approaches, while less detailed, run orders of magnitude faster and thus remain the practical choice for whole-component optimisation and certification-oriented simulations.
Over time, numerous damage modelling approaches have been proposed to predict the mechanical strength and failure mechanisms of PCMats [30,31,32,33]; among these, progressive damage models have emerged as the most commonly employed due to their ability to capture the evolution of damage under various loading conditions [23,34]. El Idrissi et al. [35] conducted a detailed study on the damage initiation and progression in composite laminates subjected to flexural loading, using an advanced numerical model that incorporated both intralaminar and interlaminar damage mechanisms. Intralaminar damage was predicted using a 2D Puck’s failure criterion, whilst interlaminar delamination was modelled using cohesive zone modelling (CZM) to capture the onset and propagation of delamination along predefined interfaces. This dual approach yielded highly accurate predictions of damage evolution, outperforming the model by Linde et al. [36]. Although Linde’s model successfully predicted the ultimate strength of fibre metal laminates with open-hole geometries, it was limited to simulating only two failure modes and lacked the resolution needed to capture detailed progressive failure.
Continuum models like Linde’s inherently face limitations due to homogenisation, which inadequately represent complex intralaminar and matrix failure behaviours [37]. Furthermore, Kakei et al. [38] emphasised that micromechanical approaches alone are insufficient for evaluating complete damage accumulation in composites, suggesting that significant theoretical modifications are required for existing brittle damage models.
On the other hand, the Puck model, despite incorporating specific failure modes, such as fibre breakage and matrix cracking, may not account for all possible failure mechanisms in complex loading scenarios [39]. In addition, the determination of the fracture angle is particularly challenging, especially when considering nonlinear stress–strain behaviour under combined compressive, tension, and shear loads [40]. To address these limitations, Yang et al. [41] and, more recently, Shen et al. [42] proposed a more refined Hashin-type model, combined with progressive damage, specifically designed to simulate the flexural behaviour of laminated composites under three-point bending. Their model combined Hashin’s failure criterion (for intralaminar damage) with CZM (for interlaminar failure), thereby considering a broader spectrum of failure phenomena. In total, these models could account for distinct failure modes, including fibre tension/compression, matrix tension/compression, and delamination, offering a more comprehensive representation of the complex failure mechanisms typically observed in experimental testing. The simulation results closely matched the experimental load–deflection curves, validating the robustness and accuracy of the model in predicting not only the onset of damage but also its progression through various stages of structural degradation.
The Hashin composite damage model has been a part of Abaqus since v6.6, allowing for a progressive failure analysis of composite structures in its 2D form. This model is based on Hashin–Rotem failure criteria for intralaminar damage initiation [43] and can be applied using both Abaqus/Explicit and Abaqus/Standard solvers. Whilst the Abaqus built-in implementation provides a simple tool for structural analysts, it is limited to applications involving plane stress elements, such as shells or continuum shells, thus hindering the possibility of adopting solid elements. To apply this model to solid elements, it is necessary to implement Velocity-based User-defined MATerial (VUMAT) subroutines or User-defined MATerial (UMAT) subroutines, depending on the analysis type.
Relying solely on 2D elements does not adequately capture the behaviour of a structure. For a comprehensive analysis, 3D solid elements are preferable, especially in scenarios where stress varies in all three dimensions or when the precise tracking of phenomena such as damage or cracks throughout the material’s volume is required [44,45,46,47]. To accurately represent the complete 3D behaviour of materials, modifications to the Hashin damage model are required. This updated version must then be implemented through a subroutine in Finite Element Method software [48,49].
In this study, CFRP laminates were reinforced with elastomeric films placed in varying numbers and configurations, and their response was evaluated under quasi-static indentation (QSI). The goal was to investigate how these films affect material behaviour and delamination onset. Experimental tests were performed alongside finite element simulations in Abaqus. The numerical models used user-defined implementations (UMATs) of both 2D and 3D Hashin damage criteria, while interlaminar failure was captured using standard bilinear cohesive elements. The objective was to assess and compare the models’ damage evaluation performance under a complex loading condition, i.e., quasi-static indentation. Numerical predictions showed good agreement with the experimental results, validating the modelling approach and confirming the predictive capability of both formulations.
2. Materials and Methods
This section provides a detailed overview of the characteristics of the materials and the experimental and numerical procedures that were implemented.
2.1. Constituent Material Characterisation and Manufacturing of HyPCMat Laminates
2.1.1. Polymeric Composite Material
A unidirectional carbon fibre prepreg, manufactured by Delta Tech S.p.A. (Lucca, IT), was selected for this study. The material incorporates Toray T700S (Toray Industries, Inc., Tokyo, Japan) high-strength carbon fibres pre-impregnated with 40% by weight of DT120 (Delta Tech S.p.A., Lucca, Italy) epoxy resin, designed for improved toughness. The prepreg exhibits an areal weight of 300 g/m2, with an average cured ply thickness of 0.322 mm ± 0.4%, based on measurements from three fabricated panels.
2.1.2. Elastomeric Film
The elastomeric interlayer material used in this study is Kraibon AA6CFZ, a rubber-based film made from ethylene–propylene–diene monomer (EPDM) provided by Gummiwerk KRAIBURG GmbH & Co. KG (Waldkraiburg, Germany). It has an average thickness of 360 μm and a density of 1030 kg/m3. The elastomer undergoes vulcanisation during the autoclave curing cycle of the CFRP laminate, enabling co-curing without changing the standard manufacturing process. Its formulation provides strong adhesion to the epoxy matrix.
2.1.3. HyPCMat Manufacturing and Sample Preparation
Hybrid laminates were stacked in a climate-controlled clean room maintained at 21 °C and 26% relative humidity. Throughout lamination, elastomeric films were interleaved by applying pre-cut patches directly onto the uncured prepreg surface. Two distinct stacking sequences were produced, each differing in the number of elastomer-modified interfaces, as illustrated in Figure 1.
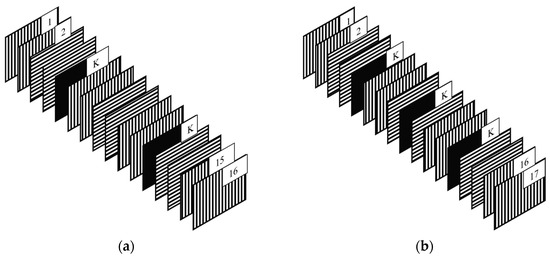
Figure 1.
Laminate stacking sequence: (a) KL2 configuration, (b) KL3 configuration.
The first configuration, referred to as KL2, follows the stacking sequence [02/902/K/02/902/02/K/902/02], whilst the second one, KL3, is arranged as [02/902/K/02/90/K/90/02/K/902/02]. All laminates were cured in an autoclave at 135 °C for 2 h under an external pressure of 6 bar, using a heating and cooling rate of 2 °C/min.
After curing, specimens were cut from the laminate plates using a diamond saw tool and visually inspected for any defects. Rectangular composite specimens were cut with nominal dimensions of 150 × 100 mm. The average thickness was 5.11 mm for the KL2 configuration and 5.41 mm for KL3.
2.2. Indentation Tests
Quasi-static indentation (QSI) tests were carried out with the indentation fixture as per the ASTM D6264-98(04) standard using an Instron 8033 (Instron Ltd., High Wycombe, UK) universal testing machine equipped with a 25 kN load cell.
As illustrated in Figure 2, each specimen was positioned on a fixed aluminium support featuring a central opening window measuring 125 × 75 mm.
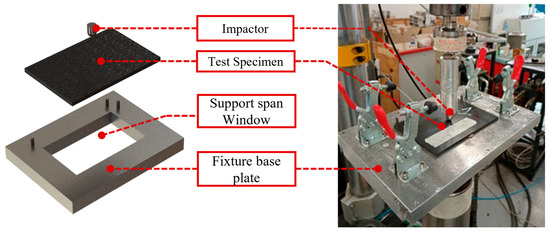
Figure 2.
Test set-up.
Proper alignment was ensured using three guide pins that facilitated the accurate centring of the plate. In this study, the plates were tested in a simply supported configuration. A steel hemispherical impactor, with a diameter of 12.7 mm, was used to apply the load at a constant displacement rate of 1 mm/min. Load and displacement data were recorded continuously throughout the experiment. To ensure the reliability and consistency of the results, tests were conducted on three specimens for each stacking sequence, all under identical experimental conditions.
2.3. Numerical Simulation
2.3.1. FEA Model
The numerical analysis was conducted using Abaqus/Standard 2023 to assess the mechanical response of the two plate configurations. The KL2 plate consisted of 16 individual solid components, while the KL3 plate consisted of 17 solid layers. The PCMat was modelled using 8-node, reduced integration 3D solid elements (C3D8R). In contrast, the rubber material was represented using the hybrid version of the same element type (C3D8RH) to properly simulate its nearly incompressible characteristics. To enhance solution stability, a stiffness control technique was applied as described in [12]. The impactor and the loading supports were defined as discrete rigid bodies using 4-node rigid elements (R3D4).
2.3.2. Material Models for Numerical Analysis
To accurately represent the behaviour of the composite plates under indentation, a nonlinear material model incorporating progressive damage mechanics was utilised through a user-defined material (UMAT) subroutine, in conjunction with a cohesive zone model. Within the UMAT subroutine, linear orthotropic elastic properties were used to characterise the intralaminar response of the PCMAT up to the point of failure. A 2D [50] and a full 3D [42] Hashin-type failure criterion were selected to predict intralaminar damage initiation. To enhance readiness, the failure modes of the two criteria are summarised in Table 1.

Table 1.
Models’ failure modes: fibre failure in tensile (FT), fibre failure in compression (FC), in-plane matrix failure in tensile test (IMT), in-plane matrix crushing (IMC), out-of-plane matrix failure in tensile test (OMT), and out-of-plane matrix crushing (OMC).
In the preceding formulae, denotes the normal strains, whilst denotes the shear stresses. The parameters , , and correspond to the ultimate tensile strengths in the longitudinal, transverse, and through-thickness directions, respectively. Similarly, , , and indicate the ultimate compressive strengths along the same orientations. The shear strengths in the longitudinal–transverse, longitudinal–through-thickness, and transverse–through-thickness planes are given by , , and , respectively. The elastic and strength properties used for the PCMat were obtained from the authors’ earlier research and are reported here in Table 2.

Table 2.
Material properties of PCMat.
To capture the intralaminar failure and its evolution, a Continuum Damage Mechanic (CDM)-based approach was implemented [51,52]. Damage is considered by lowering the values of the respective stiffness components of the element:
where (i, j = 1 6; i = j) corresponds to the element’s initial stiffness components, whilst (i, j = 1 6; i = j) indicates the stiffness components following the onset of damage.
The damage parameters are for the in-plane matrix damage and for the fibre damage for both models; an additional damage, , representing the out-of-plane matrix damage, is introduced in the 3D model. The damage parameters are evaluated as a function of the stiffness components and strain after damage initiation. They progress steadily from 0 (indicating no damage) to 1 (indicating complete damage) based on the following relationship:
where is the fracture energy of the fibre or the matrix, depending on the failure mode, and is the characteristic length of the element. As reported in [41], the use of and contributes to minimising the mesh sensitivity of numerical simulations, which is a typical issue in modelling materials characterised by a strain-softening response.
2.3.3. Cohesive Zone Model
Interlaminar delamination was considered using a CZM approach. At the interface of each PCMat volume, 0.001 mm thick cohesive elements (COH3D8) were employed to represent the epoxy interlayer [42]. The elastic behaviour of the CZM material was modelled through the following relationship:
where is the nominal traction stress vector which describes the stresses caused by three different types of deformation: one in the normal direction and the two shear modes and . For the damage initiation of interface elements, a quadratic stress criterion was applied, and the Benzeggagh–Kenane (BK) law [53] was employed to predict the initiation and propagation of delamination damage:
where , , and are the maxima of the nominal stress of the interface when the separation is entirely governed by the distinct fracture mode. The total critical fracture energy () can be calculated as follows:
where and are the normal and shear critical fracture energies, respectively, and , , and are the energy release rates under Mode I, Mode II, and Mode III, in that order. η is an empirical material parameter in the BK law [27,53]. Validated CZM parameters for the interlaminar model are listed in Table 3.

Table 3.
The material properties of the cohesive interface.
2.3.4. Material Model for Elastomeric Film
Several strain energy potentials in Abaqus/Standard (including Neo-Hookean [54], Yeoh [55], Arruda–Boyce [56], and Marlow [57]) were preliminarily assessed for numerical stability. Based on previous investigations [12,58], the Marlow model was selected for its ability to capture the response of rubber materials with high accuracy. This phenomenological, data-driven formulation derives the deviatoric behaviour directly from the results of tensile tests (Figure 3), interpolated as a function of the first deviatoric strain invariant. The strain energy density is expressed as follows:
where and represent the deviatoric and volumetric contributions, is the first deviatoric strain invariant, and denotes the elastic volume ratio. The volumetric term is defined using a Poisson’s ratio of 0.49 to represent near-incompressible behaviour.
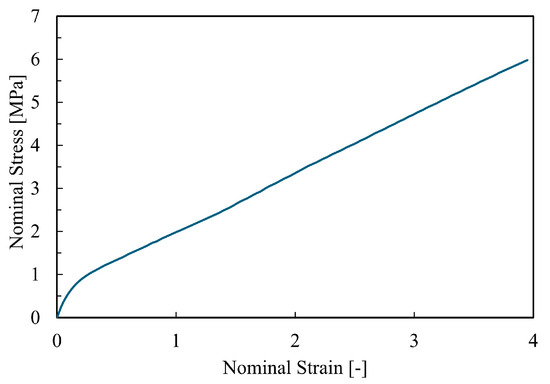
Figure 3.
The stress–strain curve of the elastomer in a uniaxial tension test.
3. Results
The results from both experimental and numerical analyses of the two laminates subjected to quasi-static indentation are shown in Figure 4. All tested laminates demonstrated good repeatability with the coefficient of variation (CV) for the maximum force and displacement consistently below 5%. The laminate KL2 failed at a maximum force of 9731 ± 52 N, whilst the laminate KL3 failed at a maximum load of 5309 ± 54 N.
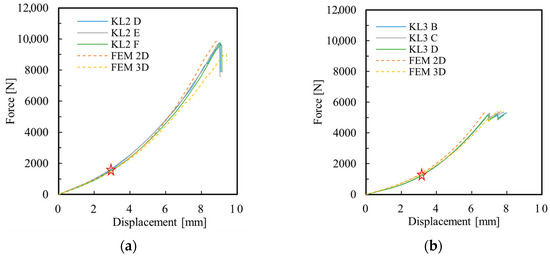
Figure 4.
Experimental and numerical load–displacement curves for (a) laminate KL2 and (b) laminate KL3, with the divergent point from the numerical models highlighted in red.
Specimens from both laminates exhibited a nonlinear trend in stiffness that increased to a different peak, followed by a sharp drop and eventual load recovery. The experimental curves for the KL2 laminate (Figure 4a) began to show noticeable divergence around 6 mm of displacement, with KL2 E exhibiting a slightly lower stiffness and peak force compared to KL2 D and KL2 F. Prior to this point (in the range 0–4 mm), the curves were nearly indistinguishable, indicating that damage initiation, if present, had a negligible effect on the global structural response. In contrast, the KL3 laminate (Figure 4b) exhibited a lower overall stiffness and a more gradual failure behaviour. The experimental curves (KL3 B, KL3 C, and KL3 D) displayed a consistent nonlinear trend with minimal scatter, and no abrupt post-peak drop was observed. Instead, the presence of localised load drops near the peak suggests the activation of specific damage mechanisms, such as matrix cracking, interfacial debonding, and fibre breaking.
These events did not immediately compromise the global response, indicating a more progressive and spatially localised failure mode compared to the behaviour of KL2. Overall, whilst both configurations perform consistently, the KL2 sequence provides greater stiffness, whereas the KL3 sequence may offer enhanced flexibility. However, this increase in flexibility comes at the cost of a slight reduction in load-bearing capacity and greater susceptibility to early-stage microcracking.
The simulations using the 2D and 3D approaches exhibit distinct trends for both the KL2 and KL3 laminates, as depicted in Figure 4. The Hashin 2D failure model consistently demonstrates greater stiffness compared to the average experimental load–displacement curves (see Figure 4a,b), predicting peak forces up to 1% higher for the KL2 laminate (9841 N vs. 9731 N). In contrast, the 3D model exhibits greater compliance, underestimating the peak load by approximately 7% (9032 N). For the KL3 laminate, both 2D and 3D simulations yield nearly identical results (5443 N and 5448 N, respectively), both exceeding the experimental average of 5309 N by about 3%. Although the curves for the 2D and 3D failure models overlap at lower displacements, the curves for the KL2 laminate begin to diverge at a displacement of 3.1 mm (Figure 4a). In contrast, the divergence for the KL3 laminate occurs at approximately 3 mm (Figure 4b). By critically comparing the formulas presented in Table 1, the 3D failure model accounts for out-of-plane deformations , , and , which are essential to trigger damage. Additionally, the damage evolution model in the 3D formulation includes the additional damage parameter to account for matrix degradation in the out-of-plane direction. To investigate the reasons for the discrepancy between the two models, a comprehensive analysis of the damage parameters was conducted. The simulation results for the KL2 sample at the onset of divergence in load–displacement curves are presented in Figure 5.
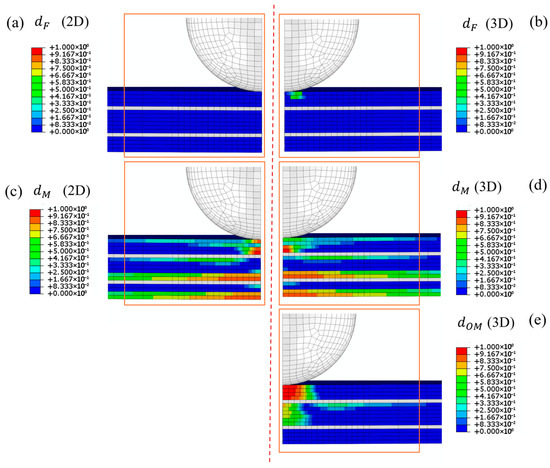
Figure 5.
Numerical results for KL2 sample at divergence point in load–displacement curves. (a) Damage parameter for fibre following 2D Hashin criteria, (b) damage parameter for fibre following 3D Hashin criteria, (c) in-plane damage parameter for matrix calculated using 2D Hashin criteria, (d) in-plane damage parameter of matrix calculated using 3D Hashin criteria, (e) out-of-plane damage parameter of matrix calculated using 3D Hashin criteria.
As shown in Figure 5a, which illustrates the fibre damage parameter for the 2D model, no fibre damage occurred at this stage. In contrast, the 3D model (Figure 5b) shows that some elements beneath the indenter are already exhibiting signs of degradation. The in-plane matrix damage parameter appears to be comparable between the two models, as visible in Figure 5c,d. Additionally, the out-of-plane matrix damage parameter , illustrated in Figure 5e, indicates that the material in volumes 1–4 has already undergone complete degradation. It can be argued that the different evolution of numerical curves in KL2 samples is mainly due to the highest sensitivity of the 3D model in capturing the through-thickness effects.
The numerical results for the KL3 sample at the point where the load–displacement curves begin to diverge are given in Figure 6.
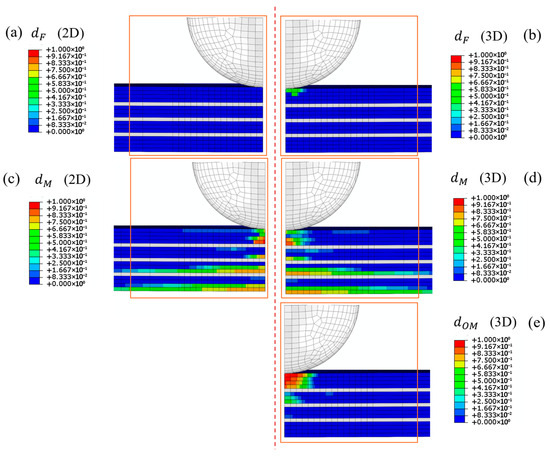
Figure 6.
Numerical results for KL3 sample at onset of divergence in load–displacement curves. (a) Damage parameter for fibre following 2D Hashin criteria, (b) damage parameter for fibre following 3D Hashin criteria, (c) in-plane damage parameter for matrix calculated using 2D Hashin criteria, (d) in-plane damage parameter of matrix calculated using 3D Hashin criteria, (e) out-of-plane damage parameter of matrix calculated using 3D Hashin criteria.
Figure 6a,b show the fibre damage parameter : in this configuration, the 2D model shows no fibre damage, whilst the 3D model contains damaged elements within volumes 1 and 2 due to out-of-plane shear stresses.
In-plane matrix damage, shown in Figure 6c,d, is minimal at this stage and exhibits a similar distribution in both the 2D and 3D damage models. However, as illustrated in Figure 6e, the out-of-plane matrix damage parameter, defined only in the 3D model, reached a value of one in some elements within the first three volumes. These findings confirm that the 3D damage model is more effective at capturing the initiation of out-of-plane failure, although it has reduced stiffness during its progression.
Figure 7 depicts the experimental and numerical results for the KL2 laminate at the end of the indentation process. The optical micrograph in Figure 7a shows a polished cross-section of a representative sample from the KL2 laminate after quasi-static indentation. Damage is primarily localised beneath the indenter, where the highest levels of through-thickness compressive and shear stresses are concentrated. In addition, the lower section of the laminate appears curved due to inherent permanent deformation.
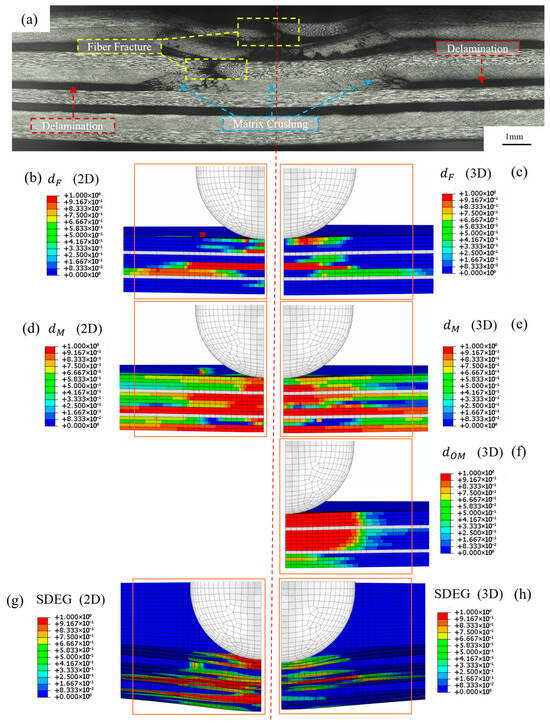
Figure 7.
Cross-section micrographic and numerical results for sample of laminate KL2 at end of indentation. (a) Optical micrography of laminate under loading point, (b) damage parameter for fibre following 2D Hashin criteria, (c) damage parameter for fibre following 3D Hashin criteria, (d) in-plane damage parameter for matrix calculated using 2D Hashin criteria, (e) in-plane damage parameter of matrix calculated using 3D Hashin criteria, (f) out-of-plane damage parameter of matrix calculated using 3D Hashin criteria, (g) interlaminar failure within 2D Hashin model, (h) interlaminar failure within 3D Hashin model.
The image also shows clear signs of fibre kinking and fibre breakage in the upper and mid-thickness plies, particularly within the top plies that are directly under the loading hemisphere. Severed or fragmented fibre bundles are visible, indicating compressive failure and localised rupture. This is accompanied by matrix cracking, with cracks extending laterally along the fibre–matrix interfaces and across the ply boundaries. These cracks remain confined to the upper region of the laminate. Notably, the lower half of the laminate appears undamaged at this magnification, suggesting that the progression of damage was effectively limited in depth. It can be argued that the presence of elastomeric interlayers contributed to crack deflection and energy dissipation, which in turn limited the through-thickness propagation. Significantly, there is no experimental evidence of delamination or debonding at the interfaces between the CFRP and elastomer (Figure 7a). The elastomer layers exhibit strong adhesion with the surrounding plies, which supports the experimental findings and justifies their classification as bonded within the numerical simulations.
Figure 7b illustrates the distribution of the fibre damage parameter calculated using the 2D Hashin failure criterion within the 3D finite element model of the KL2 laminate. This parameter indicates fibre failure resulting from tensile and compressive stresses in the fibre direction, as defined by the 2D Hashin formulation. The results reveal extensive fibre damage throughout the upper half of the laminate, with the damage parameter reaching a value of 1 (complete failure) in volumes 2, 4, and 8–9. This pattern suggests that the 2D criterion predicts widespread fibre breakage, not only directly beneath the indenter but also into mid-thickness regions. However, a comparison with the cross-sectional optical micrograph (Figure 7a) shows that the actual fibre breakage was more localised, primarily concentrated in the top plies. The 2D Hashin criterion, which does not account for out-of-plane stress components, tends to distribute fibre failure more broadly through the thickness than what is experimentally observed. Figure 7c shows the fibre damage distribution predicted using the 3D Hashin failure criterion. In contrast to the broader failure zones depicted in Figure 7b, the fibre damage computed using the 3D Hashin criterion is significantly more localised. Damage is primarily concentrated in the uppermost layers and at mid-thickness, specifically in volumes 1–2 and 8–9, where fibre breakage is expected due to the combined effects of surface indentation and internal bending.
This spatial confinement closely aligns with the damage observed in the cross-sectional micrograph (Figure 7a), where fibre failure was visually confirmed only in these areas. The improved agreement is attributed to the 3D criterion’s inclusion of out-of-plane shear, which enhances the activation of fibre failure modes under complex multiaxial loading. Overall, the 3D Hashin model proves to be an effective tool for capturing the complex failure mechanisms in hybrid composite laminates, offering a more reliable basis for the design and analysis of structures subjected to out-of-plane loads. Utilising this model improves the understanding of damage mechanisms by accounting for the complexities of shear coupling and ply interactions. Figure 7d,e present the in-plane matrix damage predicted using the 2D Hashin and 3D Hashin failure criteria, respectively. Both models identify similar regions of matrix failure, most notably in volumes 2–3, 5–6, and 8–10, corresponding to the area beneath and adjacent to the indenter. This consistency is expected, as the in-plane matrix failure formulation is nearly the same in both criteria. Figure 7f displays the out-of-plane matrix damage parameter, predicted solely by the 3D Hashin failure criterion. This figure shows that this damage is concentrated directly beneath the indenter, affecting the upper and mid-thickness regions, specifically volumes 1 through 10. This pattern results from the through-thickness compressive and shear stresses that occur during quasi-static indentation. These stresses cannot be captured by damage models that only consider in-plane effects. This finding is especially relevant for thicker laminates or hybrid composites, such as the KL2 configuration, where stress redistributions at ply interfaces and stiffness mismatches can lead to the activation of interlaminar stress components. The predicted damage aligns well with the observed microcracking and compression damage in the central cross-section (Figure 7a). This correlation strongly suggests that out-of-plane matrix degradation significantly contributes to the failure process. Figure 7g,h show the predicted interlaminar failure using cohesive elements embedded between the CFRP plies in the KL2 laminate model. Although the cohesive zone model (CZM) formulation is identical in both cases, the input stress fields result from simulations based on the 2D Hashin (Figure 7g) and 3D Hashin (Figure 7h) failure criteria. In Figure 7g, extensive delamination is observed, with cohesive failure predicted across nearly all interfaces beneath and around the indenter. This widespread interlaminar damage reflects the overestimated matrix degradation and fibre failure in the underlying 2D simulation, which promotes large stress redistributions into the interfaces. In contrast, Figure 7h shows more localised delamination, confined to the region near the interface between volumes 9 and 10. This pattern aligns well with the experimental observations shown in Figure 7a, where a single delamination is visible near the mid-thickness of the laminate. The comparison highlights that the accuracy of predictions made by the cohesive element model is significantly affected by the effectiveness of the intralaminar damage model. The 2D stress field tends to overstate interfacial loading, whereas the 3D formulation provides a more precise representation of interlaminar stresses. This improved accuracy allows for a more targeted activation of CZM.
Following the analysis of the KL2 laminate, the KL3 configuration is evaluated using the same methodology to investigate the effects of stacking sequence on the damage evolution mechanisms. The micrographic cross-section and simulation results for laminate KL3 after indentation are presented in Figure 8.
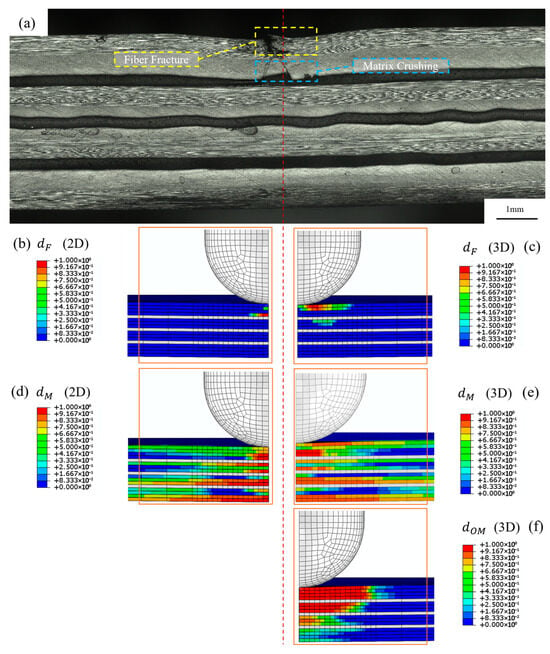
Figure 8.
Cross-section micrographic and numerical results for sample of laminate KL3 at end of indentation. (a) Optical micrography of laminate under loading point, (b) damage parameter for fibre following 2D Hashin criteria, (c) damage parameter for fibre following 3D Hashin criteria, (d) in-plane damage parameter for matrix calculated using 2D Hashin criteria, (e) in-plane damage parameter of matrix calculated using 3D Hashin criteria, (f) out-of-plane damage parameter of matrix calculated using 3D Hashin criteria.
The micrographic inspection illustrated in Figure 8a confirmed that damage was concentrated in the upper layers and beneath the indenter, with no observable permanent deformation. Clear signs of localised fibre breakage and matrix cracking are markedly observable. In contrast to the KL2 sample, this specimen does not exhibit any marked signs of delamination, indicating excellent toughness.
At the final converged step, fibre damage in the 2D model (Figure 8b) approaches the value 1 only in a limited region of volume 4. In contrast, the 3D model (Figure 8c) demonstrates full degradation primarily localised beneath the indenter (volumes 1–2), which aligns with the experimental findings presented in Figure 8a. At the final step, in-plane matrix damage in the 2D model (Figure 8d) is localised to specific regions of the laminate, particularly in volumes 3–4, 6, 8, 11–12, and 16–17. Similarly, the 3D model also shows in-plane matrix damage localised in volumes 3–4, as illustrated in Figure 8e,d. The out-of-plane damage indicates deeper failure, extending to the second elastomer layer. Notably, no clear delamination areas are observed in the case of intralaminar damage, further supporting the reliability of the numerical model.
The computational cost of the simulations was assessed for both the 2D and 3D numerical models, with all runs performed with eight cores to ensure a consistent comparison. The required simulation times were 269 and 439 min for KL2 and 284 and 660 min for KL3 for the 2D and 3D models, respectively.
In conclusion, both 2D and 3D Hashin formulations offer valuable but distinct insights; however, considering the computational times, the choice remains in balancing the faster simulation approach against the greater level of detail. Although the 2D model tends to overestimate damage and the 3D model may slightly underestimate it, these tendencies do not lessen their respective usefulness. Instead, they reflect different levels of accuracy and assumptions that can be aligned effectively with specific phases of a design process. The 2D Hashin model proves advantageous in early-stage or conservative studies where in-plane behaviour and computational efficiency are fundamental. In contrast, the 3D model provides a more comprehensive and reliable assessment for advanced simulations, particularly where complex stress states or out-of-plane effects are critical. Additionally, it is particularly valuable when the configuration of damage is a significant outcome of the analysis.
4. Conclusions
This study investigated the implementation and evaluation of Hashin’s 2D and 3D damage models to simulate the behaviour of a hybrid composite laminate subjected to quasi-static indentation. To more accurately simulate delamination and interlaminar failure, cohesive zone elements were implemented at the ply interfaces. Experimental tests on two distinct laminate configurations were performed and used as a benchmark for validating the numerical models, enabling a direct comparison between simulated and experimental damage mechanisms and load–displacement outcomes.
The 2D Hashin model was limited in its predictive capability. It captured in-plane failure mechanisms reasonably well but overestimated the peak load and failed to reflect through-thickness damage and delamination. On the other hand, the 3D Hashin-type model more accurately reproduced the complex failure behaviour observed in experiments, though it slightly underestimated the maximum load. It provided a more physically realistic representation of damage initiation and progression, particularly under conditions dominated by complex stress states.
The rubber interlayer was shown to play a valuable role in damage suppression, effectively redistributing local stresses and reducing the severity and extent of damage. This behaviour was observed in the experimental results and captured adequately by the 3D numerical model but not by the 2D approach, which lacks the necessary sensitivity to out-of-plane effects.
Following the successful implementation of both the 2D and 3D versions of the Hashin damage model, and the subsequent comparison of the results with experimental data, it can be asserted that the selection of the appropriate modelling strategy can be effectively aligned with the specific phase of the design process or the project requirements. From a design perspective, in fact, the 2D Hashin model may be suitable for early-stage design or conservative sizing studies, where in-plane behaviour predominates and computational speed is a priority. However, for high-fidelity simulations aimed at predicting complex damage mechanisms, particularly where out-of-plane loading or impact is involved, the 3D Hashin model offers a significantly more robust and reliable tool for structural assessment.
Author Contributions
Conceptualisation, L.R. and M.P.F.; methodology, L.R. and L.S.; software, L.S.; validation, L.S., M.P.F. and L.R.; formal analysis, L.R. and M.P.F.; investigation, F.S. and L.S.; resources, L.R.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, L.S., F.S. and M.P.F.; visualisation, F.S.; supervision, L.R. and M.P.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by MOST—Sustainable Mobility National Research Center—and received funding from the European Union NextGenerationEU (Piano Nazionale di Ripresa e Resilienza (PNRR)—Missione 4 Componente 2, Investimento 1.4—D.D. 1033 17 June 2022, CN00000023, CUP: J33C22001120001) and Ecosystem for Sustainable Transition in Emilia-Romagna Project, funded under the National Recovery and Resilience Plan (NRRP), Mission 04 Component 2 Investment 1.5—NextGenerationEU, Call for tender n. 3277 dated 30 December 2021 Award Number: 0001052 dated 23 June 2022 CUP: B33D21019790006. Leonardo Salvi acknowledges the funding of CYPHER “CYberPHysical Components and advanced matERials for monitoring and sensing”, funded under PR FESR EMILIA ROMAGNA 2021–2027, CUP: E37G22000470007. Francesco Semprucci acknowledges the support of the SMALSAT “Solar Panel Design for the SMAL-SAT nanosate lite” project, funded under PR FESR EMILIA ROMAGNA 2021–2027 CUP: J47G22000720003.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HyPCMat | Hybrid Polymer Composite Material |
| CFRP | Carbon Fibre-Reinforced Polymer |
| FML | Fibre Metal Laminate |
| CAI | Compression After Impact |
| D-FE2 | Direct Finite Element Square |
| FE2 | Finite Element Square |
| GFRP | Glass Fibre-Reinforced Polymer |
| EL | Elastomer |
| CZM | Cohesive Zone Modelling |
| CV | Coefficient of Variation |
| BK | Benzeggagh–Kenane |
| UMAT | User-Defined Material |
References
- Falaschetti, M.P.; Rondina, F.; Zavatta, N.; Gragnani, L.; Gironi, M.; Troiani, E.; Donati, L. Material Characterization for Reliable Resin Transfer Molding Process Simulation. Appl. Sci. 2020, 10, 1814. [Google Scholar] [CrossRef]
- Falaschetti, M.P.; Birnie Hernández, J.; Semprucci, F.; Raimondi, L.; Serradimigni, D.; Troiani, E.; Donati, L. Analysis of the Crushing Behavior of Flat Composite Plates Produced by Sheet Molding Compound. In Proceedings of the Dynamic Response and Failure of Composite Materials, DRAF 2024, Ischia, Italy, 17–21 June 2024; Lecture Notes in Mechanical Engineering. Lopresto, V., Papa, I., Eds.; Springer: Cham, Switzerland, 2025; pp. 40–48. [Google Scholar]
- Wanhill, R.J.H. Carbon Fibre Polymer Matrix Structural Composites. In Aerospace Materials and Material Technologies; Springer: Singapore, 2017; pp. 309–341. ISBN 978-981-10-2134-3. [Google Scholar]
- Falaschetti, M.P.; Scafé, M.; Zavatta, N.; Troiani, E. Hygrothermal Ageing Influence on BVI-Damaged Carbon/Epoxy Coupons under Compression Load. Polymer 2021, 13, 2038. [Google Scholar] [CrossRef]
- Falaschetti, M.P.; Semprucci, F.; Birnie Hernández, J.; Troiani, E. Experimental and Numerical Assessment of Crashworthiness Properties of Composite Materials: A Review. Aerospace 2025, 12, 122. [Google Scholar] [CrossRef]
- Falaschetti, M.P.; Semprucci, F.; Raimondi, L.; Serradimigni, D. Experimental and Numerical Assessment of Sheet Molding Compound Composite Crushing Behavior. J. Mater. Eng. Perform. 2025, 34, 15281–15292. [Google Scholar] [CrossRef]
- Falaschetti, M.P.; Rondina, F.; Maccaferri, E.; Mazzocchetti, L.; Donati, L.; Zucchelli, A.; Giorgini, L. Improving the Crashworthiness of CFRP Structures by Rubbery Nanofibrous Interlayers. Compos. Struct. 2023, 311, 116845. [Google Scholar] [CrossRef]
- Maccaferri, E.; Mazzocchetti, L.; Benelli, T.; Brugo, T.M.; Zucchelli, A.; Giorgini, L. A Thermoplastic Elastomeric Nanofibrous Membrane as CFRP Modifier to Boost Both Delamination and Damping Performance. Macromol. Symp. 2022, 405, 2100233. [Google Scholar] [CrossRef]
- Vescovini, A.; Cruz, J.A.; Ma, D.; Colombo, C.; Salerno, A.; Bianchi, O.; Amico, S.C.; Manes, A. Experimental Investigation on Low-Velocity Impact Behavior of Glass, Kevlar, and Hybrid Composites with an Elastomeric Polyurethane Matrix. Compos. Part C Open Access 2024, 13, 100426. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Tan, W. Experimental and Numerical Studies on the Impact Response of Damage-Tolerant Hybrid Unidirectional/Woven Carbon-Fibre Reinforced Composite Laminates. Compos. Part B Eng. 2018, 136, 101–118. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Dear, J.P. An Experimental and Numerical Study on the Crush Behaviour of Hybrid Unidirectional/Woven Carbon-Fibre Reinforced Composite Laminates. Int. J. Mech. Sci. 2019, 164, 105160. [Google Scholar] [CrossRef]
- Raimondi, L.; Bernardi, F. Advanced Hybrid Laminates: Elastomer Integration for Optimized Mechanical Properties. Int. J. Adv. Manuf. Technol. 2025, 136, 3177–3195. [Google Scholar] [CrossRef]
- Dhaliwal, G.S.; Newaz, G.M. Experimental and Numerical Investigation of Flexural Behavior of Hat Sectioned Aluminum/Carbon Fiber Reinforced Mixed Material Composite Beam. Compos. Part B Eng. 2020, 182, 107642. [Google Scholar] [CrossRef]
- Massarwa, E.; Emami Tabrizi, I.; Yildiz, M. Mechanical Behavior and Failure of Glass/Carbon Fiber Hybrid Composites: Multiscale Computational Predictions Validated by Experiments. Compos. Struct. 2021, 260, 113499. [Google Scholar] [CrossRef]
- Acosta, J.D.; Idarraga, G.; Maimí, P.; Jalalvand, M.; Meza, J.M. Numerical Modelling of Multi-Directional Thin-Ply Carbon/Glass Hybrid Composites with Open Holes under Tension. Mech. Mater. 2024, 190, 104921. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, G.; Liu, E.; Li, X.; Shu, X.; Hao, X. Experimental Investigation on the Low-Velocity Impact Responses of Hybrid CFRP–Elastomer–Metal Laminates with Various Rubber Layer Positions and Impact Energies. Mech. Adv. Mater. Struct. 2025. [Google Scholar] [CrossRef]
- Taherzadeh-Fard, A.; Liaghat, G.; Ahmadi, H.; Razmkhah, O.; Chitsaz Charandabi, S.; Zarezadeh-mehrizi, M.A.; Khodadadi, A. Experimental and Numerical Investigation of the Impact Response of Elastomer Layered Fiber Metal Laminates (EFMLs). Compos. Struct. 2020, 245, 112264. [Google Scholar] [CrossRef]
- Düring, D.; Petersen, E.; Stefaniak, D.; Hühne, C. Damage Resistance and Low-Velocity Impact Behaviour of Hybrid Composite Laminates with Multiple Thin Steel and Elastomer Layers. Compos. Struct. 2020, 238, 111851. [Google Scholar] [CrossRef]
- Sarlin, E.; Apostol, M.; Lindroos, M.; Kuokkala, V.T.; Vuorinen, J.; Lepistö, T.; Vippola, M. Impact Properties of Novel Corrosion Resistant Hybrid Structures. Compos. Struct. 2014, 108, 886–893. [Google Scholar] [CrossRef]
- Mohotti, D.; Ngo, T.; Raman, S.N.; Ali, M.; Mendis, P. Plastic Deformation of Polyurea Coated Composite Aluminium Plates Subjected to Low Velocity Impact. Mater. Des. 2014, 56, 696–713. [Google Scholar] [CrossRef]
- Khodadadi, A.; Liaghat, G.; Shahgholian-Ghahfarokhi, D.; Chizari, M.; Wang, B. Numerical and Experimental Investigation of Impact on Bilayer Aluminum-Rubber Composite Plate. Thin-Walled Struct. 2020, 149, 106673. [Google Scholar] [CrossRef]
- Sadowski, T.; Golewski, P.; Craciun, E. Internal Structure Influence on the Impact Strength and Dynamic Fracture Toughness of Hybrid Polymer Matrix Composites with Integrated Elastomer Interlayers. Compos. Struct. 2021, 258, 113375. [Google Scholar] [CrossRef]
- Li, X.; Liu, P.; Cheng, H.; Liu, C.; Zhu, Y.; Zhang, K. Experimental and Numerical Analysis of Low-Velocity Impact Damage of CFRP Laminates with Negative Poisson Ratio (NPR) Rubber Protective Layer. Thin-Walled Struct. 2023, 191, 111066. [Google Scholar] [CrossRef]
- Stelldinger, E.; Kühhorn, A.; Kober, M. Experimental Evaluation of the Low-Velocity Impact Damage Resistance of CFRP Tubes with Integrated Rubber Layer. Compos. Struct. 2016, 139, 30–35. [Google Scholar] [CrossRef]
- Krollmann, J.; Schreyer, T.; Veidt, M.; Drechsler, K. Impact and Post-Impact Properties of Hybrid-Matrix Laminates Based on Carbon Fiber-Reinforced Epoxy and Elastomer Subjected to Low-Velocity Impacts. Compos. Struct. 2019, 208, 535–545. [Google Scholar] [CrossRef]
- Li, Z.; Ma, Z.; Wang, C.; Gu, Y.; Cong, S.; Wang, J.; Wang, B. Impact Resistance and Damage Mechanisms of CFRP with Elastomeric Interlayers under Low-Velocity Impacts. Polym. Compos. 2025, 1–13. [Google Scholar] [CrossRef]
- Falaschetti, M.P.; Rondina, F.; Zavatta, N.; Troiani, E.; Donati, L. Effective Implementation of Numerical Models for the Crashworthiness of Composite Laminates. Eng. Fail. Anal. 2024, 160, 108196. [Google Scholar] [CrossRef]
- Liu, K.; Meng, L.; Zhao, A.; Wang, Z.; Chen, L.; Li, P. A Hybrid Direct FE2 Method for Modeling of Multiscale Materials and Structures with Strain Localization. Comput. Methods Appl. Mech. Eng. 2023, 412, 116080. [Google Scholar] [CrossRef]
- Liu, K.; Tian, L.; Gao, T.; Wang, Z.; Li, P. An Explicit D-FE2 Method for Transient Multiscale Analysis. Int. J. Mech. Sci. 2025, 285, 109808. [Google Scholar] [CrossRef]
- Tsai, S.W.; wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically-Based Failure Models and Criteria for Laminated Fibre-Reinforced Composites with Emphasis on Fibre Kinking: Part I: Development. Compos. Part A Appl. Sci. Manuf. 2006, 37, 63–73. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure Analysis of FRP Laminates by Means of Physically Based Phenomenological Models. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier Science: Amsterdam, The Netherlands, 2004; pp. 832–876. ISBN 9780080531571. [Google Scholar]
- Rondina, F.; Falaschetti, M.P.; Zavatta, N.; Donati, L. Numerical Simulation of the Compression Crushing Energy of Carbon Fiber-Epoxy Woven Composite Structures. Compos. Struct. 2023, 303, 116300. [Google Scholar] [CrossRef]
- El Idrissi, H.; Seddouki, A. A Comprehensive Study of the Flexural Behaviour and Damage Evolution of Composite Laminates Using a Progressive Failure Model. Int. J. Adv. Manuf. Technol. 2023, 127, 3869–3890. [Google Scholar] [CrossRef]
- Linde, P.; de Boer, H. Modelling of Inter-Rivet Buckling of Hybrid Composites. Compos. Struct. 2006, 73, 221–228. [Google Scholar] [CrossRef]
- Van Der Meer, F.P.; Sluys, L.J. Continuum Models for the Analysis of Progressive Failure in Composite Laminates. J. Compos. Mater. 2009, 43, 2131–2156. [Google Scholar] [CrossRef]
- Kakei, A.A.G.; Epaarachchi, J.A.; Islam, M.M.; Leng, J. Development of Fracture and Damage Modeling Concepts for Composite Materials. In Structural Health Monitoring Technologies and Next-Generation Smart Composite Structures; CRC Press: Boca Raton, FL, USA, 2016; pp. 341–368. ISBN 9781315373492. [Google Scholar]
- Meon, M.S.; Husain, H.; Saedon, J.B.; Shawal, S.; Mohamad Nor, N.H.; Rao, M.N.; Schröder, K.U. Capability Analysis of Puck Damage Model in Predicting the Damage Behavior of Unidirectional Composite Laminates under Different Scenarios. IOP Conf. Ser. Mater. Sci. Eng. 2020, 834, 012028. [Google Scholar] [CrossRef]
- Matthias Deuschle, H.; Kröplin, B.H. Finite Element Implementation of Puck’s Failure Theory for Fibre-Reinforced Composites under Three-Dimensional Stress. J. Compos. Mater. 2012, 46, 2485–2513. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wang, Y.Q.; Gao, H.; Li, R.; Bao, Y. A Progressive Damage Model for Predicting Damage Evolution of Laminated Composites Subjected to Three-Point Bending. Compos. Sci. Technol. 2017, 151, 85–93. [Google Scholar] [CrossRef]
- Shen, B.; Liu, H.; Lv, S.; Li, Z.; Cheng, W. Progressive Failure Analysis of Laminated CFRP Composites under Three-Point Bending Load. Adv. Mater. Sci. Eng. 2022, 2022, 3047319. [Google Scholar] [CrossRef]
- Bogert, P.B.; Satyanarayana, A.; Chunchu, P.B. Comparison of Damage Path Predictions for Composite Laminates by Explicit and Standard Finite Element Analysis Tools. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; Volume 3, pp. 1919–1941. [Google Scholar] [CrossRef]
- Brust, A.F.; Xu, L.; Kemp, D. The Impact of FEA Modeling Techniques for Level 3 Dent Engineering Critical Assessment: Shell Vs. Solid Elements. In Proceedings of the ASME 2024 Pressure Vessels & Piping Conference, Bellevue, WA, USA, 28 July–2 August 2024; Volume 2. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, S.W. A Solid Element Formulation for Large Deflection Analysis of Composite Shell Structures. Comput. Struct. 1988, 30, 269–274. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, G.; Wang, X. Displacement and Stress Analysis of Laminated Composite Plates Using an Eight-Node Quasi-Conforming Solid-Shell Element. Curved Layer. Struct. 2017, 4, 8–20. [Google Scholar] [CrossRef]
- Yi, T. The Progressive Failure Analysis of Uni-Directional Fibre Reinforced Composite Laminates. J. Mech. 2020, 36, 159–166. [Google Scholar] [CrossRef]
- Zhang, Y.; Van Paepegem, W.; De Corte, W. An Enhanced Progressive Damage Model for Laminated Fiber-Reinforced Composites Using the 3D Hashin Failure Criterion: A Multi-Level Analysis and Validation. Materials 2024, 17, 5176. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P.; Kermanidis, T. A Three-Dimensional Progressive Damage Model for Bolted Joints in Composite Laminates Subjected to Tensile Loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 663–675. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, B.; Wang, S. Finite Element Analysis on Impact Response and Damage Mechanism of Composite Laminates under Single and Repeated Low-Velocity Impact. Aerosp. Sci. Technol. 2022, 129, 107810. [Google Scholar] [CrossRef]
- Rahul, K.; Yudhanto, A.; Ravindranath, P.K.; Jack, D.A. Progressive Damage Modeling in Open Hole Composite Laminates with Ultrasound-Informed Drilling-Induced Delamination. Compos. Part A Appl. Sci. Manuf. 2024, 184, 108262. [Google Scholar] [CrossRef]
- HU, J.; ZHANG, K.; CHENG, H.; ZOU, P. Modeling on Mechanical Behavior and Damage Evolution of Single-Lap Bolted Composite Interference-Fit Joints under Thermal Effects. Chin. J. Aeronaut. 2021, 34, 230–244. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- van Hoogstraten, P.A.A.; Slaats, P.M.A.; Baaijens, F.P.T. A Eulerian Approach to the Finite Element Modelling of Neo-Hookean Rubber Material. In Integration of Theory and Applications in Applied Mechanics; Springer: Dordrecht, The Netherlands, 1990; pp. 277–294. [Google Scholar]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive Models of Rubber Elasticity: A Review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Marlow, R.S. A General First-Invariant Hyperelastic Constitutive Model. In Constitutive Models for Rubber; Swets & Zeitlinger: Lisse, The Netherlands, 2003; pp. 157–160. [Google Scholar]
- Li, Z.; Ma, Z.; Wang, J.; Wang, B.; Yang, N. Low-Velocity Impact Behavior and Damage Mechanisms of Honeycomb Sandwich Structures with Elastomeric Interlayers in CFRP Skins. Thin-Walled Struct. 2024, 205, 112482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).