Optimization Design Method of Pipe-Insulating Joints Based on Surrogate Model and Genetic Algorithm
Abstract
1. Introduction
2. Methods
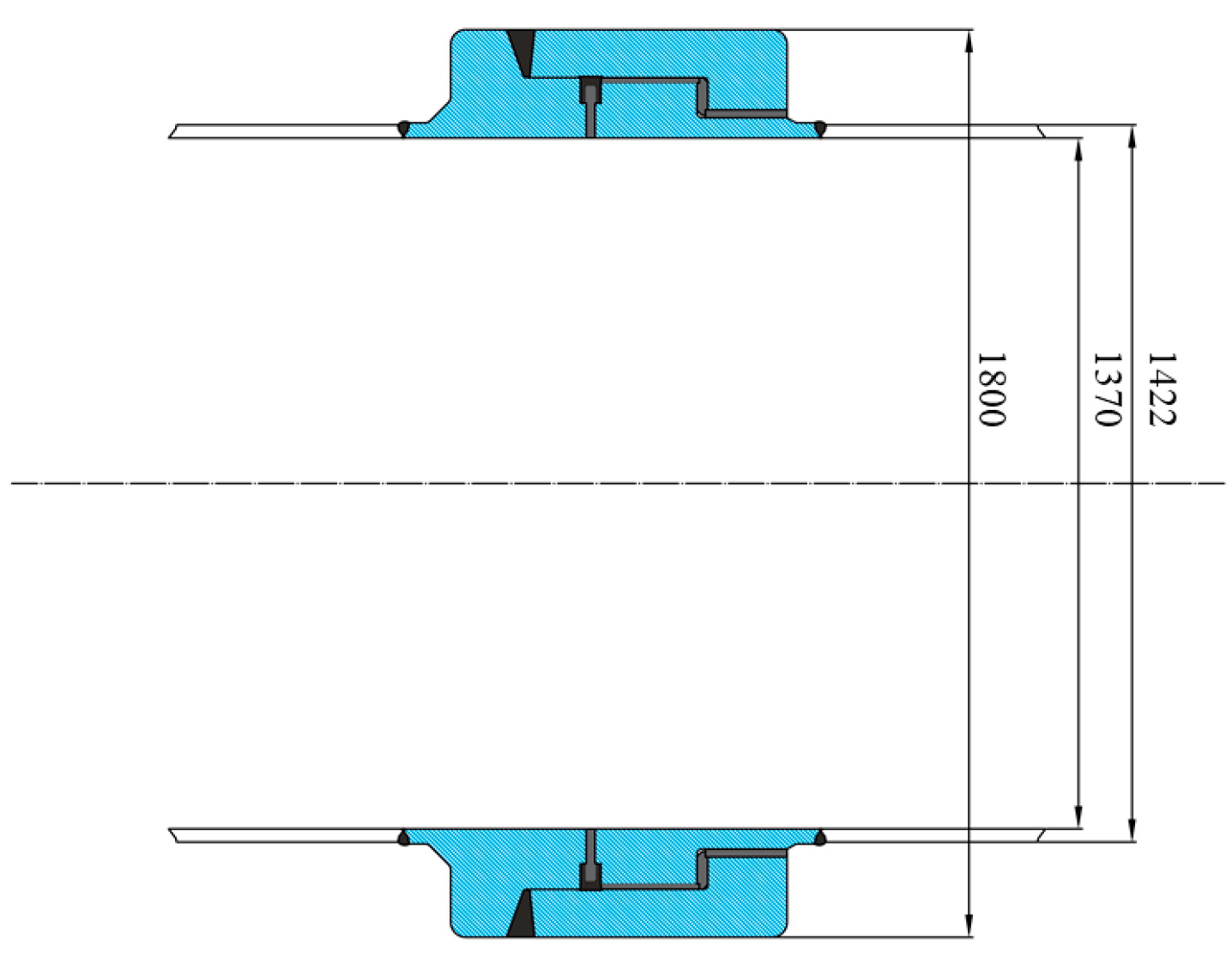
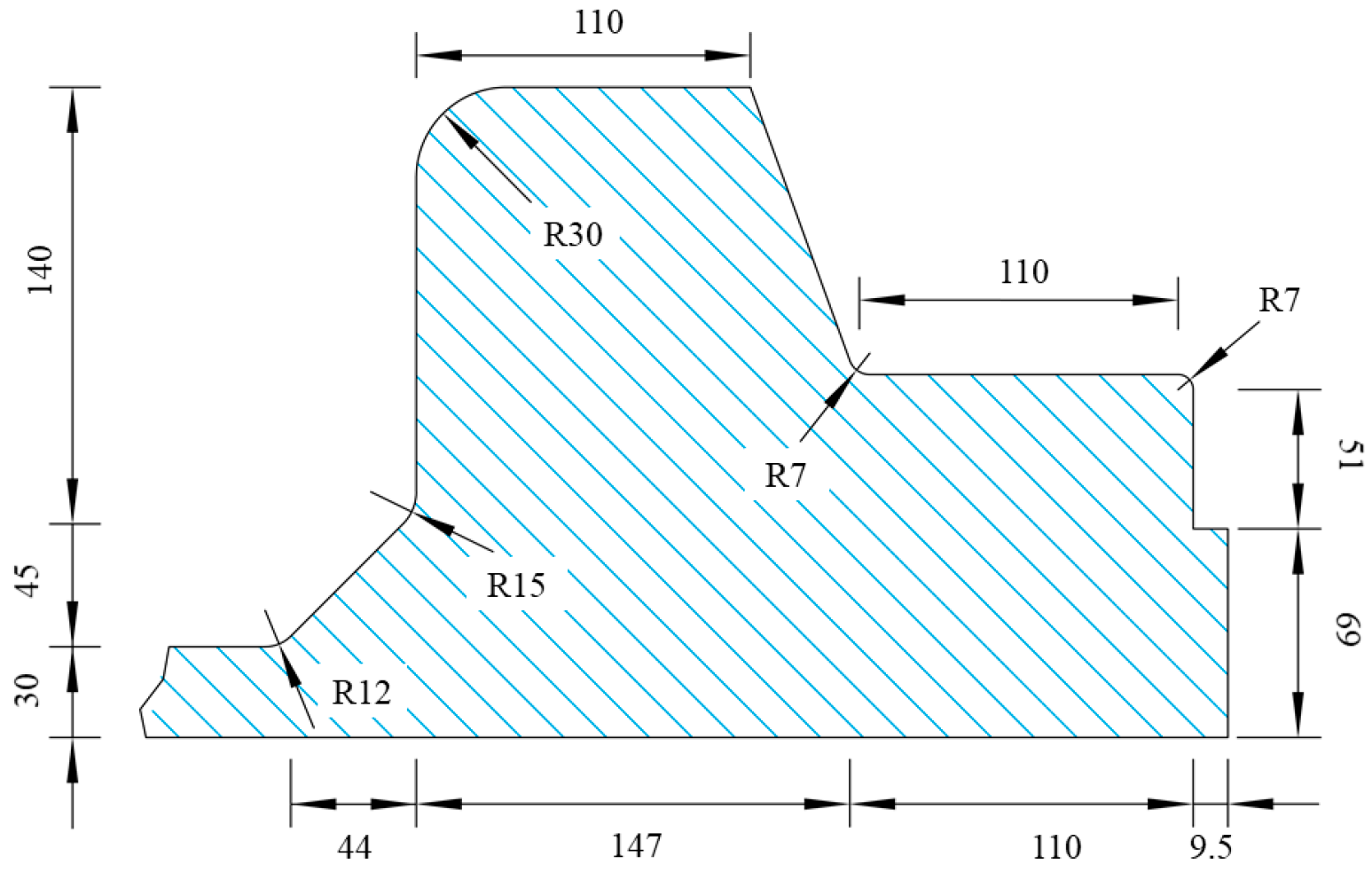
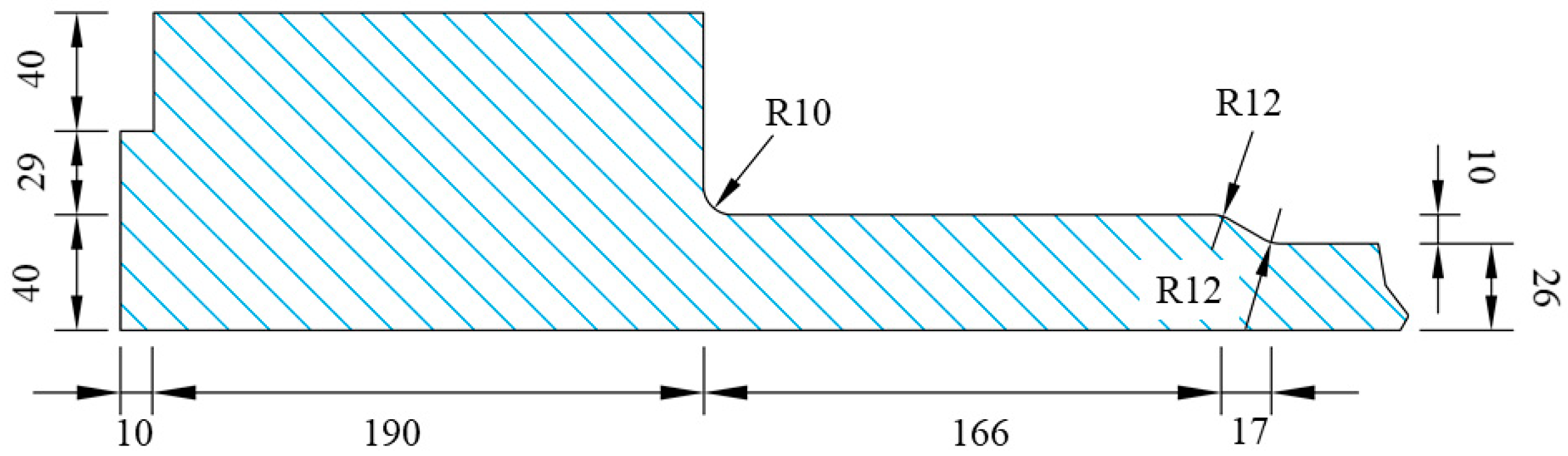
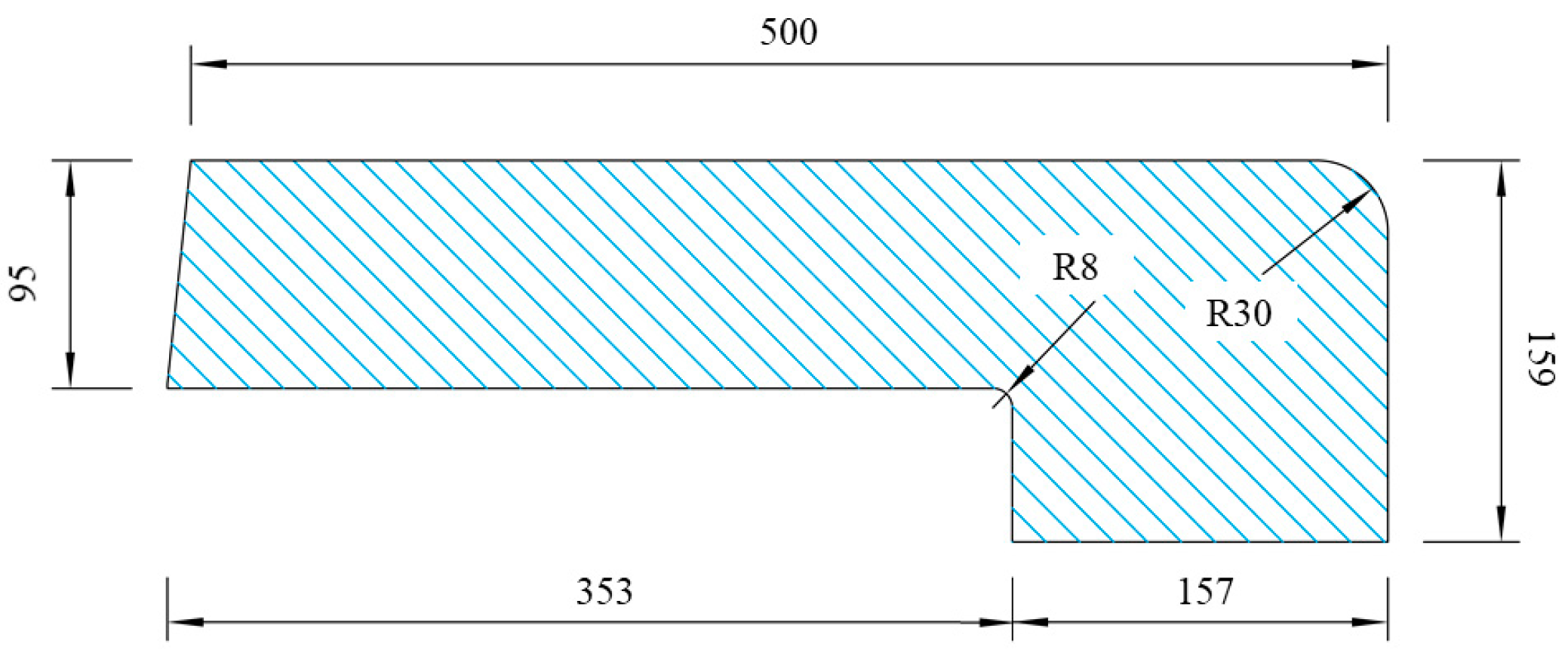
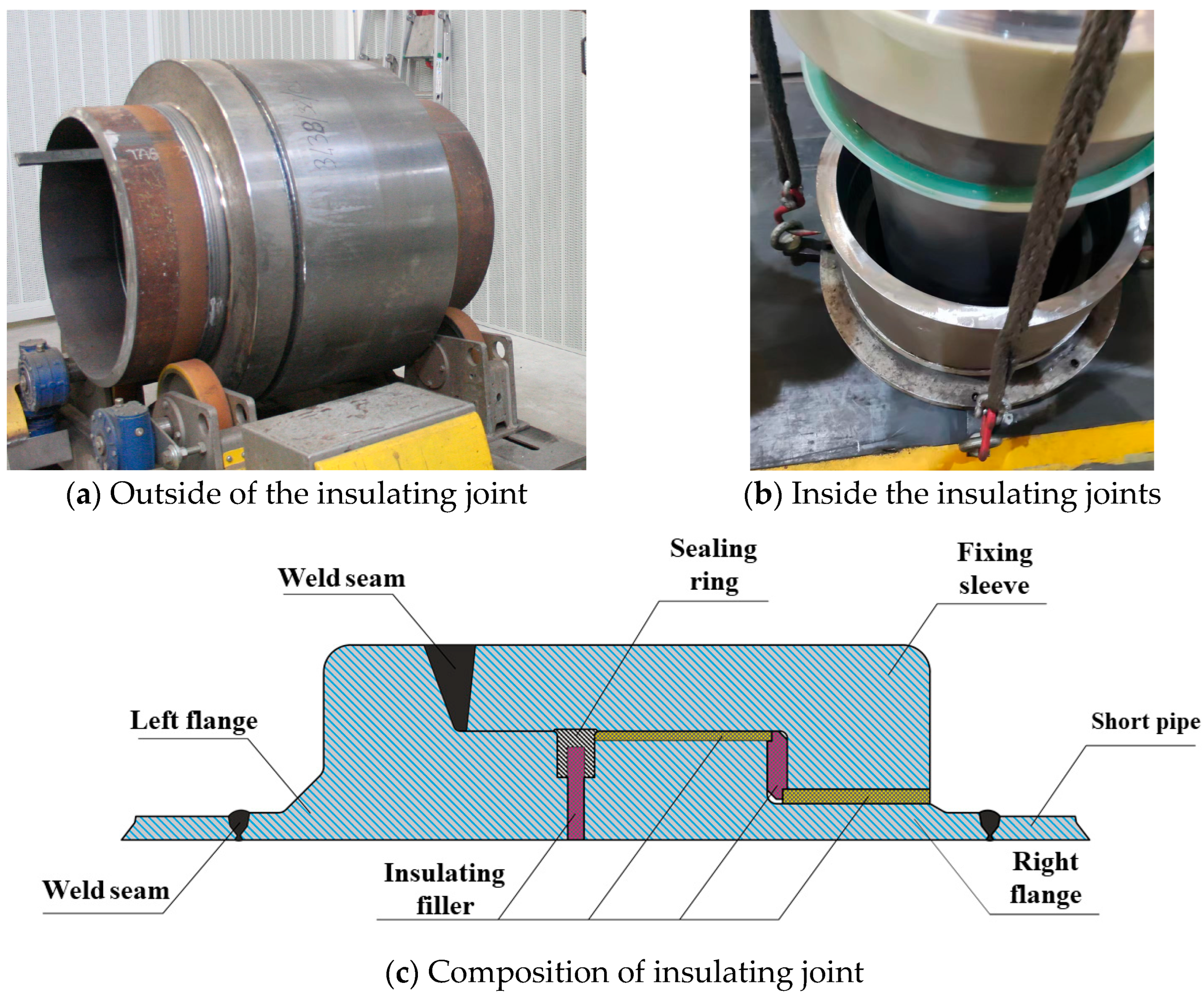
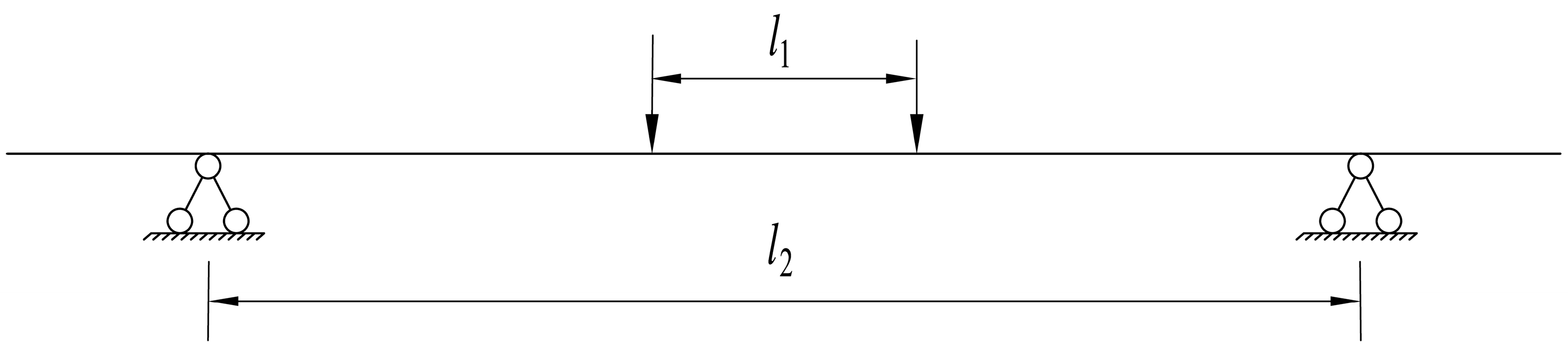
2.1. Finite Element Model for Insulating Joint
2.2. Surrogate Model
2.2.1. Construction of the Training Dataset
2.2.2. Surrogate Model Evaluation Methods
2.3. Mathematical Formulation of Optimization Problems
3. Results
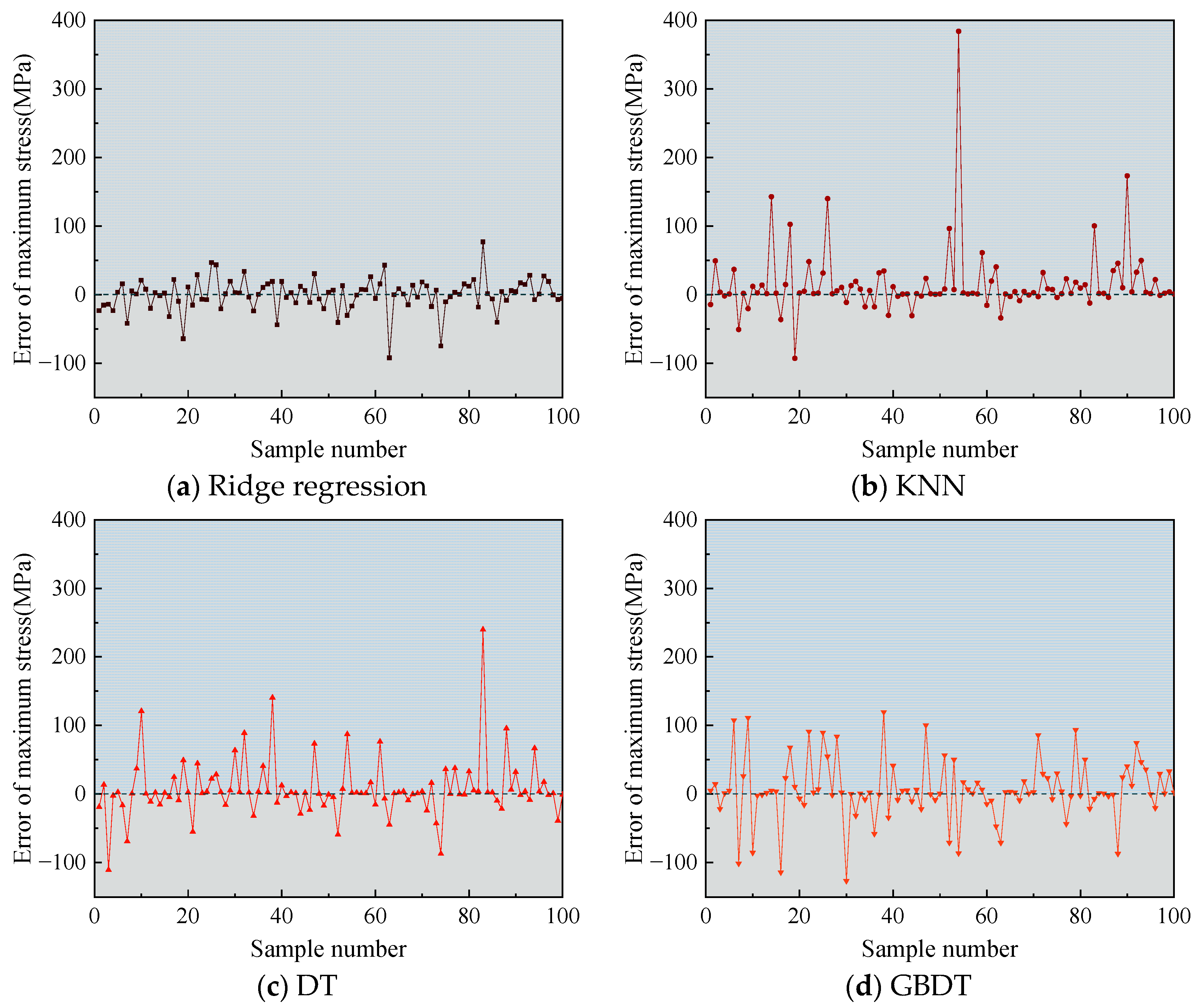
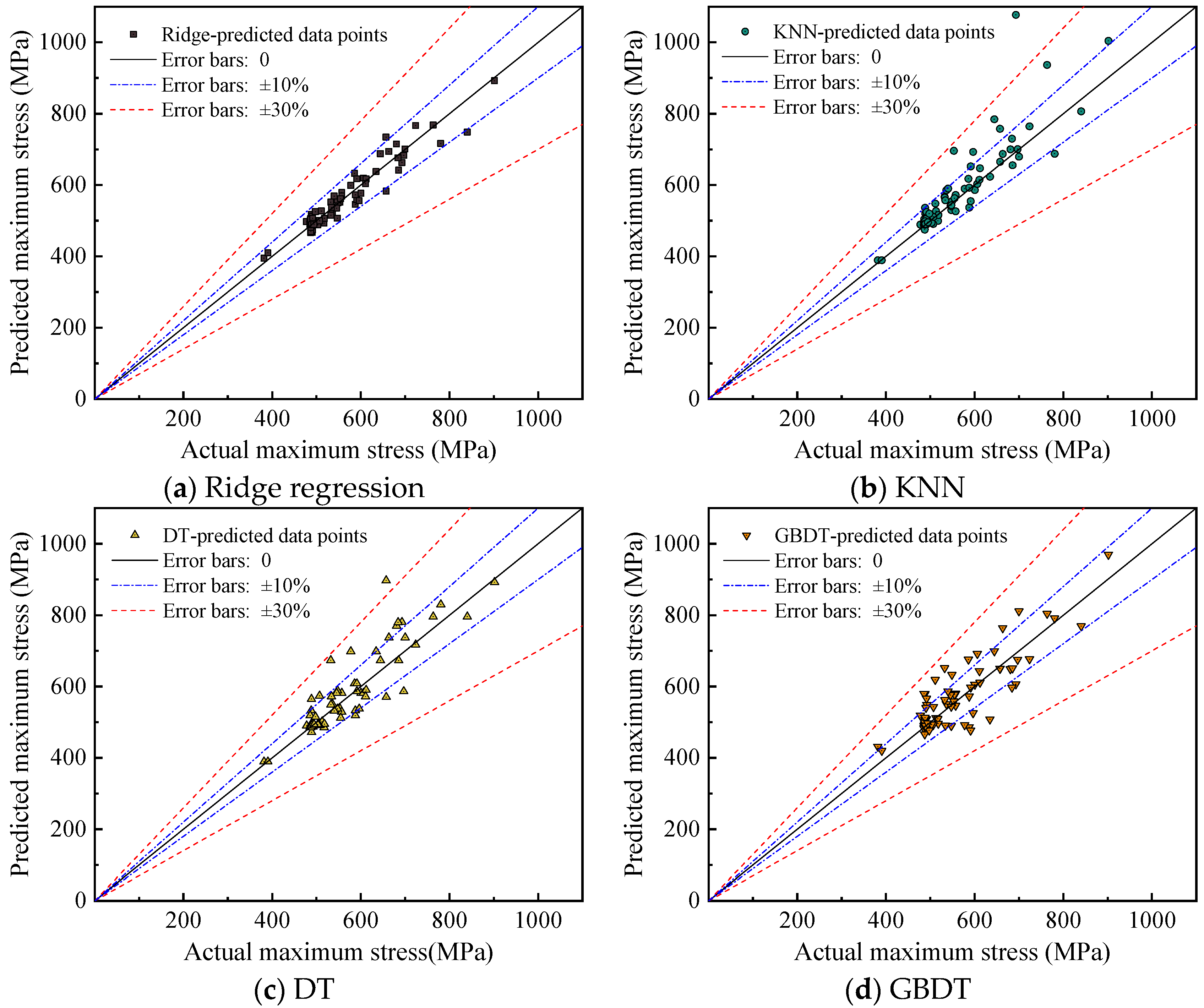
3.1. Surrogate Model Evaluation Results
3.2. Surrogate Model–Genetic Algorithm Optimization Results
4. Conclusions
- (1)
- The overall finite element analysis of the insulated joints before optimization reveals that the maximum stress in the joint, under the most adverse condition of four-point bending, is located at the right flange. The overall average stress of the insulating joint is relatively low, indicating a significant space for optimization.
- (2)
- Based on the parametric computational results of the right flange dimensions, a surrogate model for calculating the maximum stress of the right flange can be constructed. The one established using the ridge regression algorithm demonstrated the best predictive performance, with an R2 value of 0.928 for the random test set and relative errors all below 10%.
- (3)
- The optimization algorithm established by integrating the surrogate model with genetic algorithms can optimize the dimensions of the right flange under various optimization objectives, demonstrating exact optimization performance. Among all the dimensional parameters, rB1 exhibits a strong correlation with the maximum stress, with its optimal value increasing as the stress limit decreases, indicating that the chamfer radius has a greater influence on improving the stress concentration effect in the right flange. The maximum stress obtained from the finite element analysis based on the optimized dimension parameters for the right flange has a maximum relative error of 8.98% and an average relative error of 4.63% compared to the optimization target. Based on the optimized dimensions, the predicted maximum stress of the right flange by the surrogate model has a maximum relative error of 9.65% and an average relative error of 5.33% compared to finite element calculations. Compared to improving material strength, optimizing cross-sectional dimensions is more efficient for stress optimization of the right flange.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
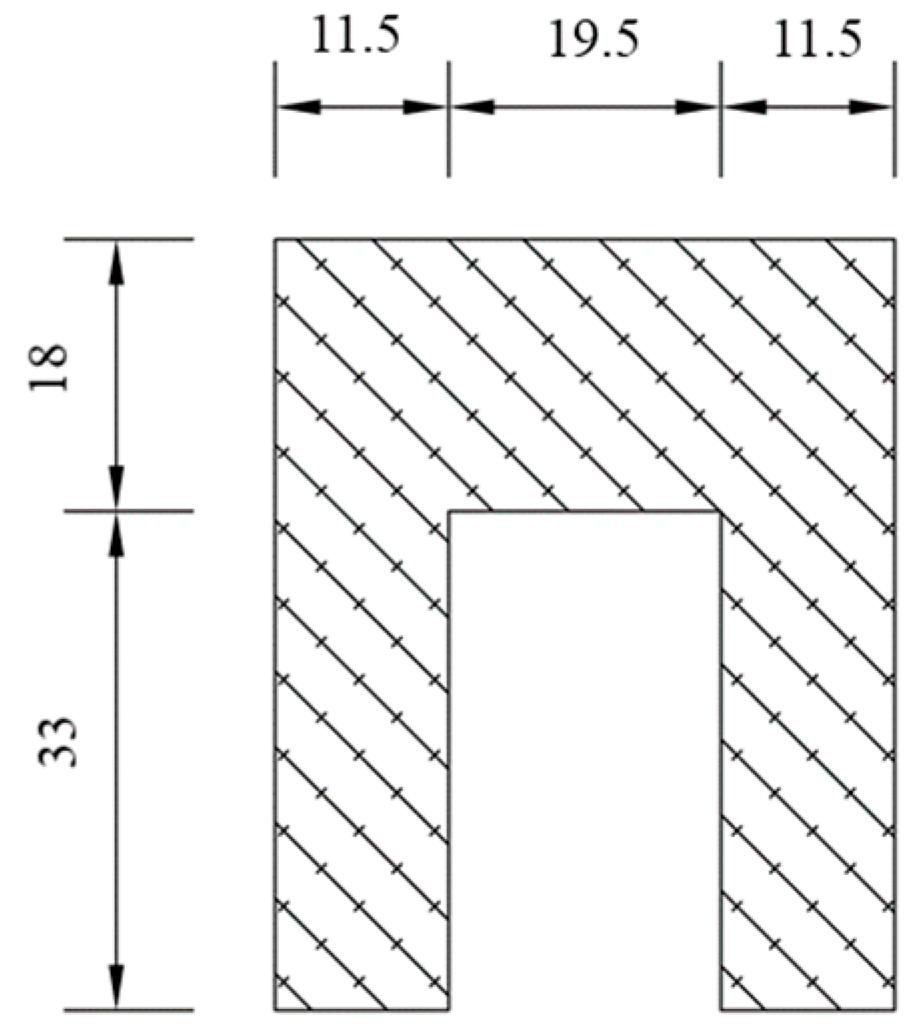
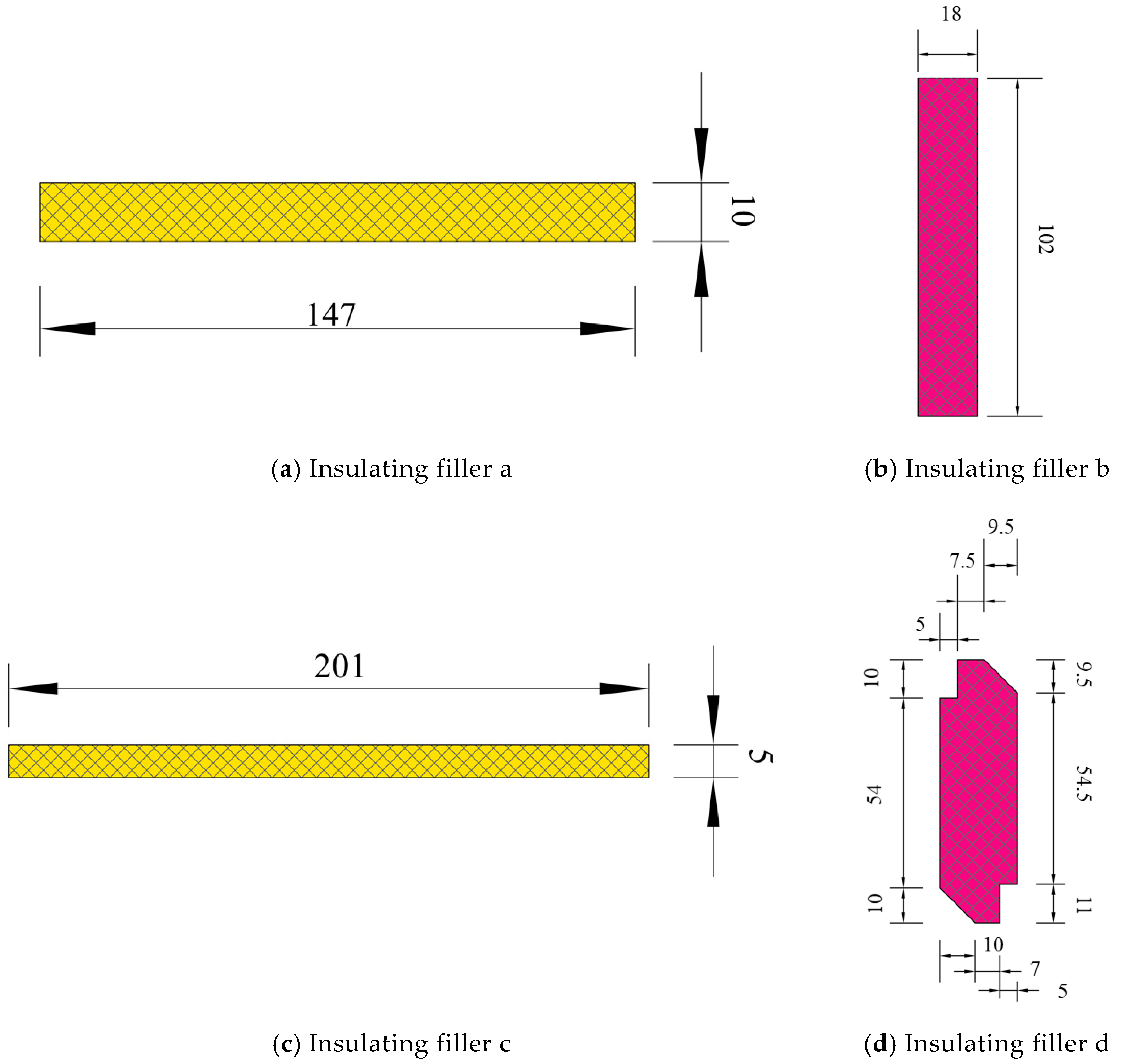
References
- Liao, Q.; Liang, Y.; Tu, R.; Huang, L.; Zheng, J.; Wang, G.; Zhang, H. Innovations of carbon-neutral petroleum pipeline: A review. Energy Rep. 2022, 8, 13114–13128. [Google Scholar] [CrossRef]
- Bariha, N.; Mishra, I.M.; Srivastava, V.C. Hazard analysis of failure of natural gas and petroleum gas pipelines. J. Loss Prev. Process Ind. 2016, 40, 217–226. [Google Scholar] [CrossRef]
- Shalaeva, D.S.; Kukartseva, O.I.; Tynchenko, V.S.; Kukartsev, V.V.; Aponasenko, S.V.; Stepanova, E.V. Analysis of the development of global energy production and consumption by fuel type in various regions of the world. IOP Conf. Ser. Mater. Sci. Eng. 2020, 952, 012025. [Google Scholar] [CrossRef]
- Chen, S.-Y.; Zhang, Q.; Mclellan, B.; Zhang, T.-T. Review on the petroleum market in China: History, challenges and prospects. Pet. Sci. 2020, 17, 1779–1794. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, N.; Zhou, C.; Luo, X.; Sun, J. Evaluate of anti-explosion for high-pressure gas steel pipeline subjected to ground explosion. J. Constr. Steel Res. 2021, 177, 106429. [Google Scholar] [CrossRef]
- Cui, G.; Li, Z.-L.; Yang, C.; Wang, M. The influence of DC stray current on pipeline corrosion. Pet. Sci. 2016, 13, 135–145. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Ben Seghier, M.E.A.; Zayed, T. A comprehensive review of corrosion protection and control techniques for metallic pipelines. Eng. Fail. Anal. 2023, 143, 106885. [Google Scholar] [CrossRef]
- Li, J.; Sun, C.; Roostaei, M.; Mahmoudi, M.; Fattahpour, V.; Zeng, H.; Luo, J.-L. Corrosion Failure and Control of Carbon Steel and Anti-Corrosion Performance Evaluation of Candidate Materials in Thermal Applications. In Proceedings of the SPE Thermal Well Integrity and Design Symposium, Banff, AB, Canada, 19–21 November 2019; p. D011S003R004. [Google Scholar] [CrossRef]
- Jiang, G.; Hu, D.; Ji, C.; Song, Y. The Research of Corrosion Mechanism and Protection Measure of Waterflood Pipes. In Proceedings of the ICPTT 2009: Advances and Experiences with Pipelines and Trenchless Technology for Water, Sewer, Gas, and Oil Applications, Shanghai, China, 18–21 October 2009; pp. 508–520. [Google Scholar] [CrossRef]
- Camitz, G. Water mains and distribution pipes in soil—External corrosion and protection methods. Water Supply 2001, 1, 97–105. [Google Scholar] [CrossRef]
- King, F.; Cheng, Y.; Gray, L.; Drader, B.; Sutherby, R. Field Assessment of FBE-Coated Pipelines and the Implications for Stress Corrosion Cracking. In Proceedings of the 4th International Pipeline Conference, Parts A and B, Calgary, AB, Canada, 29 September–3 October 2002; pp. 1619–1628. [Google Scholar] [CrossRef]
- Yang, Z.; Cui, G.; Li, Z.; Liu, J. Study on the interference between parallel pipelines and optimized operation for the cathodic protection systems. Anti-Corros. Methods Mater. 2019, 66, 195–202. [Google Scholar] [CrossRef]
- Ahmed, S.; Orth, V.; Foley, M.; Kottas, K.; Teodoriu, C. Designing in-house cathodic protection system to assess the long-term integrity of natural gas pipelines. J. Nat. Gas Sci. Eng. 2021, 94, 104116. [Google Scholar] [CrossRef]
- Wang, G.F.; Deng, B.; Zhang, H.B.; Yang, F.P.; Zhang, L.; Ren, G.Q. Failure Analysis of Leakage for Insulating Joint at Natural Gas Pipeline. J. Fail. Anal. Prev. 2022, 22, 292–297. [Google Scholar] [CrossRef]
- Vorster, T.E.; Klar, A.; Soga, K.; Mair, R.J. Estimating the Effects of Tunneling on Existing Pipelines. J. Geotech. Geoenviron. Eng. 2005, 131, 1399–1410. [Google Scholar] [CrossRef]
- Sahu, M.K.; Chattopadhyay, J.; Dutta, B.K. Fracture studies of straight pipes subjected to internal pressure and bending moment. Int. J. Press. Vessels Pip. 2015, 134, 56–71. [Google Scholar] [CrossRef]
- Hobbs, R.E. Pipeline buckling caused by axial loads. J. Constr. Steel Res. 1981, 1, 2–10. [Google Scholar] [CrossRef]
- Ma, B.; Zhu, Y.; Jin, F.; Ding, Q.; Guo, X. A lightweight optimal design model for bolted flange joints without gaskets considering its sealing performance. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 232, 234–255. [Google Scholar] [CrossRef]
- Hosseinzadeh, R.; Cheraghi, N.; Taheri, F. An Engineering Approach for Design and Analysis of Metallic Pipe Joints Under Torsion by the Finite Element Method. J. Strain Anal. Eng. Des. 2006, 41, 443–452. [Google Scholar] [CrossRef]
- Couchaux, M.; Hjiaj, M.; Ryan, I.; Bureau, A. Bolted circular flange connections under static bending moment and axial force. J. Constr. Steel Res. 2019, 157, 314–336. [Google Scholar] [CrossRef]
- Ma, C.; Duan, Y.; Huang, K.; Mo, Q.; Chen, Q.; Fu, T. Research on the Mechanical Properties and Structural Optimization of Pipe String Joint under Deep Well Fracturing Operation. Processes 2024, 12, 835. [Google Scholar] [CrossRef]
- Dai, K.; Du, H.; Luo, Y.; Han, R.; Li, J. Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model. Materials 2023, 16, 6815. [Google Scholar] [CrossRef]
- Collini, L.; Giglio, M.; Garziera, R. Thermomechanical stress analysis of dissimilar welded joints in pipe supports: Structural assessment and design optimization. Eng. Fail. Anal. 2012, 26, 31–49. [Google Scholar] [CrossRef]
- Bahadori, A. Oil and Gas Pipelines and Piping Systems: Design, Construction, Management, and Inspection; Gulf Professional Publishing: Houston, TX, USA, 2016; ISBN 978-0-12-803841-3. [Google Scholar]
- Bai, Q.; Bai, Y. Subsea Pipeline Design, Analysis, and Installation; Gulf Professional Publishing: Houston, TX, USA, 2014; ISBN 978-0-12-386889-3. [Google Scholar]
- SY/T 0516-2008; Technical Code for Insulating Joint and Insulating Flange. Southwest Company, China Petroleum Engineering Co., Ltd.: Chengdu, China, 2008.
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-58111-0. [Google Scholar]
- Rao, S.S. The Finite Element Method in Engineering; Elsevier: Amsterdam, The Netherlands, 2010; ISBN 978-0-08-095204-8. [Google Scholar]
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications; Taylor & Francis: Abingdon, UK, 2005; ISBN 978-0-203-94235-2. [Google Scholar]
- Liu, X.; Qin, J.; Zhao, K.; Featherston, C.A.; Kennedy, D.; Jing, Y.; Yang, G. Design optimization of laminated composite structures using artificial neural network and genetic algorithm. Compos. Struct. 2023, 305, 116500. [Google Scholar] [CrossRef]
- Xia, X.; Wu, D.; Yang, F.; Hu, M.; Ma, L.; Li, M.; Dong, X.; Duan, Z. Early underground pipeline collapse detection and optimization based on water hammer vibration signal. Int. J. Press. Vessels Pip. 2023, 206, 105045. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Peng, J.; Geng, X.; Gao, M.; Miao, X. Prediction of mechanical properties for typical pressure vessel steels by small punch test combined with machine learning. Int. J. Press. Vessels Pip. 2023, 206, 105060. [Google Scholar] [CrossRef]
- Nguyen-Sy, T.; Wakim, J.; To, Q.-D.; Vu, M.-N.; Nguyen, T.-D.; Nguyen, T.-T. Predicting the compressive strength of concrete from its compositions and age using the extreme gradient boosting method. Constr. Build. Mater. 2020, 260, 119757. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Zhou, Q.; Wu, J.; Xue, T.; Jin, P. A two-stage adaptive multi-fidelity surrogate model-assisted multi-objective genetic algorithm for computationally expensive problems. Eng. Comput. 2021, 37, 623–639. [Google Scholar] [CrossRef]
- Miao, Z.; Margetts, L.; Vasileiou, A.N.; Yin, H. Surrogate model development using simulation data to predict weld residual stress: A case study based on the NeT-TG1 benchmark. Int. J. Press. Vessels Pip. 2023, 206, 105014. [Google Scholar] [CrossRef]
- Tu, S.; Ren, X.; He, J.; Zhang, Z. Stress–strain curves of metallic materials and post-necking strain hardening characterization: A review. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 3–19. [Google Scholar] [CrossRef]
- Schön, J. Coefficient of friction for aluminum in contact with a carbon fiber epoxy composite. Tribol. Int. 2004, 37, 395–404. [Google Scholar] [CrossRef]
- GB/T 37358-2019; Friction Pendulum Isolation Bearings for Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Naseri Nasab, M.; Jahangir, H.; Hasani, H.; Majidi, M.-H.; Khorashadizadeh, S. Estimating the punching shear capacities of concrete slabs reinforced by steel and FRP rebars with ANN-Based GUI toolbox. Structures 2023, 50, 1204–1221. [Google Scholar] [CrossRef]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.A.; Hussein, H.M. Prediction of Ecofriendly Concrete Compressive Strength Using Gradient Boosting Regression Tree Combined with GridSearchCV Hyperparameter-Optimization Techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef]



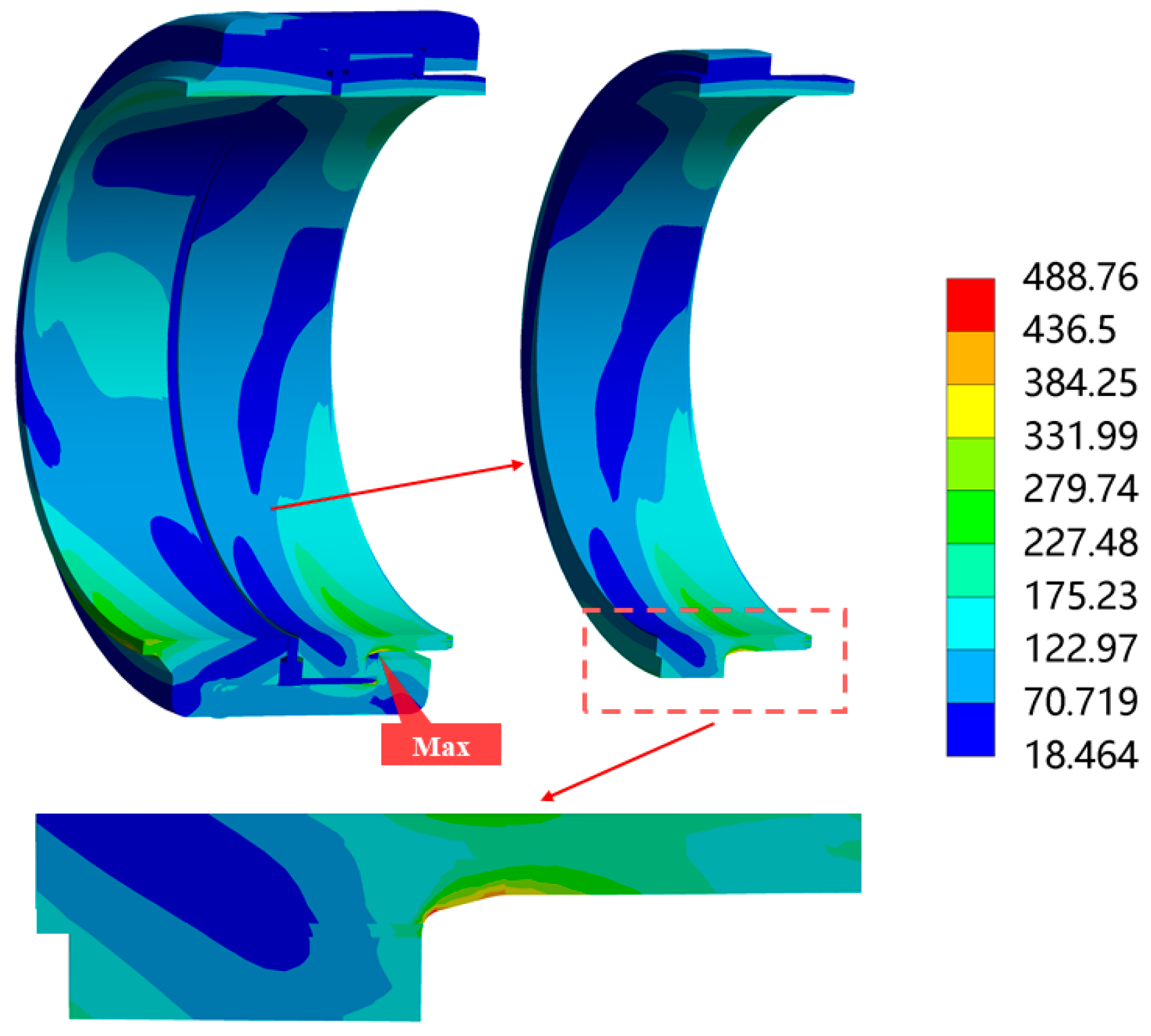
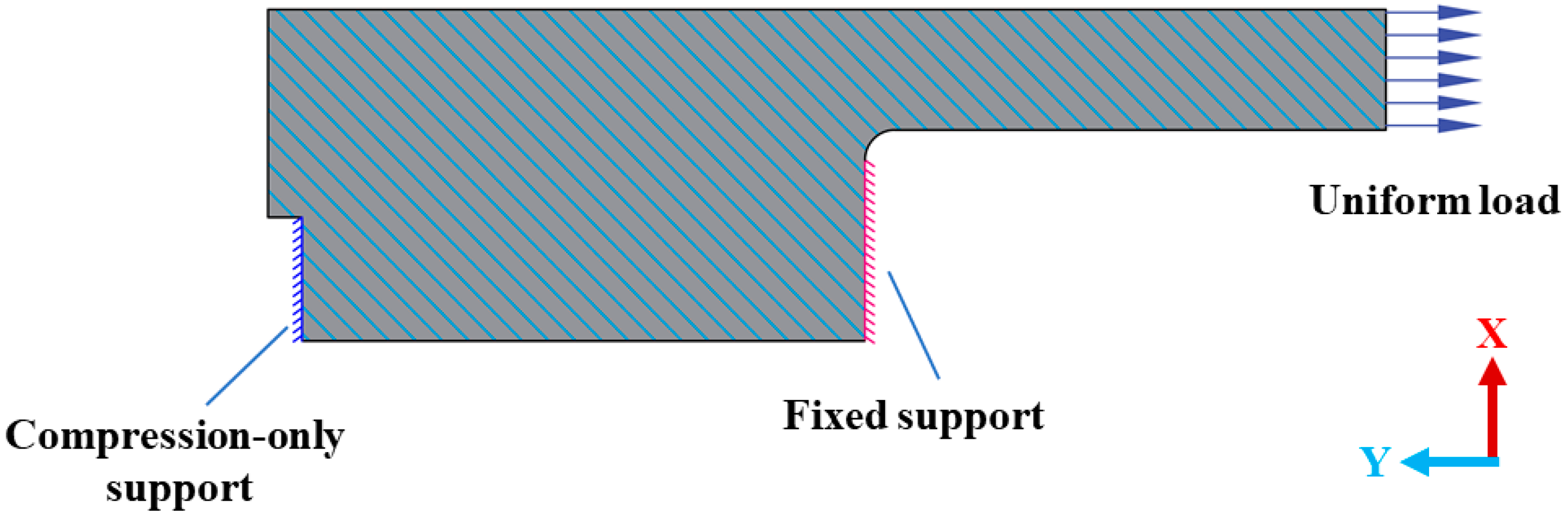

| Materials | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio | |
|---|---|---|---|---|
| Steel | 7850 | 206,000 | 0.3 | |
| Epoxy Glass Laminated Plate | Vertical Direction | 2000 | 45,000 | 0.4 |
| Horizontal Direction | 10,000 | 0.3 | ||
| No. | bB1 (mm) | bB2 (mm) | tB1 (mm) | tB2 (mm) | rB1 (mm) |
|---|---|---|---|---|---|
| 1 | 76 | 66.4 | 28 | 28 | 5 |
| 2 | 114 | 99.6 | 32 | 42 | 10 |
| 3 | 152 | 132.8 | 36 | 56 | 15 |
| 4 (current design values) | 190 | 166 | 40 | 70 | 20 |
| 5 | 228 | 199.2 | 44 | 84 | 25 |
| Dimension Type | bB1 | bB2 | tB1 | tB2 | rB1 |
|---|---|---|---|---|---|
| Range of values (mm) | 60.8~273.6 | 53.1~239 | 28~44 | 22.4~328.3 | 4~30 |
| Algorithm Type | MAE | RMSE | R2 | |||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | Training Set | Test Set | |
| Ridge regression | 19.704 | 22.882 | 38.563 | 60.115 | 0.993 | 0.981 |
| KNN | 57.261 | 77.789 | 175.502 | 286.975 | 0.830 | 0.679 |
| DT | 14.482 | 19.993 | 25.730 | 38.758 | 0.996 | 0.991 |
| GBDT | 2.766 | 23.402 | 5.824 | 55.864 | 0.999 | 0.985 |
| Evaluation Indicators | Ridge Regression | KNN | DT | GBDT |
|---|---|---|---|---|
| MAE | 16.526 | 24.412 | 24.312 | 29.653 |
| RMSE | 23.719 | 54.040 | 44.097 | 45.647 |
| R2 | 0.928 | 0.627 | 0.751 | 0.733 |
| Dimension Type | bB1 | bB2 | tB1 | tB2 | rB1 |
|---|---|---|---|---|---|
| Range of values (mm) | 76~228 | 66.4~199.2 | 28~44 | 28~84 | 5~25 |
| Optimized Targets (MPa) | Optimized Dimensions (mm) | ||||
|---|---|---|---|---|---|
| bB1 | bB2 | tB1 | tB2 | rB1 | |
| σ ≤ 0.7σmax = 339.5 | 228 | 66.4 | 41.8 | 84 | 14.4 |
| σ ≤ 0.8σmax = 388 | 212.3 | 66.4 | 40.9 | 84 | 13.3 |
| σ ≤ 0.9σmax = 436.5 | 183.3 | 66.4 | 36.3 | 84 | 13.7 |
| σ ≤ σmax = 485 | 76 | 66.4 | 28 | 70.4 | 9.2 |
| σ ≤ 1.1σmax = 533.5 | 76 | 66.4 | 28 | 53 | 6.3 |
| σ ≤ 1.2σmax = 582 | 76 | 66.8 | 28 | 47.5 | 5 |
| Optimization Targets (MPa) | Stresses Calculated by Finite Element (MPa) | Relative Error in Genetic Algorithm Optimization (%) | Stresses Calculated by the Surrogate Model (MPa) | Relative Error in Surrogate Model (%) | Cross-Sectional Area (mm2) | Optimization Rate (%) |
|---|---|---|---|---|---|---|
| σ | σf | |σf − σ|/σ | σr | |σr − σf|/σf | S | (S − S0)/S0 |
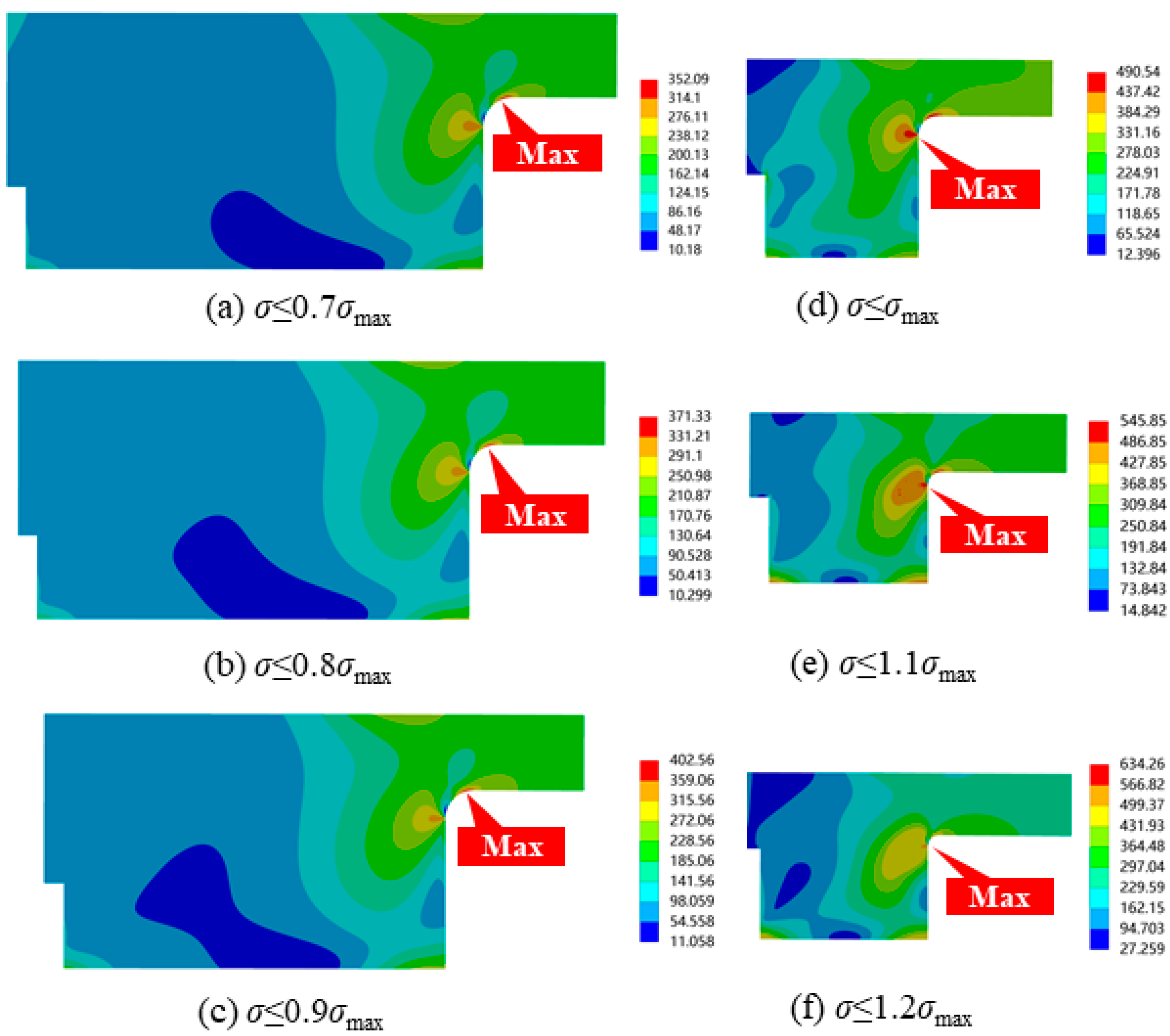
| σ ≤ 0.7σmax = 339.5 | 352.09 | 3.71 | 336.41 | 5.77 | 32,802 | −16.25 |
| σ ≤ 0.8σmax = 388 | 371.33 | 4.30 | 387.22 | 4.28 | 30,538 | −8.23 |
| σ ≤ 0.9σmax = 436.5 | 402.56 | 7.78 | 432.25 | 7.37 | 25,661 | 9.06 |
| σ ≤ σmax = 485 | 490.54 | 1.14 | 482.51 | 1.64 | 9906 | 64.89 |
| σ ≤ 1.1σmax = 533.5 | 545.85 | 1.93 | 527.95 | 3.28 | 8451 | 70.05 |
| σ ≤ 1.2σmax = 582 | 634.26 | 8.98 | 573.07 | 9.65 | 7942 | 71.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Yang, Z.; Dong, J.; Yue, Y.; Tian, L.; Ma, P. Optimization Design Method of Pipe-Insulating Joints Based on Surrogate Model and Genetic Algorithm. Appl. Sci. 2025, 15, 7601. https://doi.org/10.3390/app15137601
Guo C, Yang Z, Dong J, Yue Y, Tian L, Ma P. Optimization Design Method of Pipe-Insulating Joints Based on Surrogate Model and Genetic Algorithm. Applied Sciences. 2025; 15(13):7601. https://doi.org/10.3390/app15137601
Chicago/Turabian StyleGuo, Chen, Zheng Yang, Jianbo Dong, Yanchao Yue, Linjun Tian, and Ping Ma. 2025. "Optimization Design Method of Pipe-Insulating Joints Based on Surrogate Model and Genetic Algorithm" Applied Sciences 15, no. 13: 7601. https://doi.org/10.3390/app15137601
APA StyleGuo, C., Yang, Z., Dong, J., Yue, Y., Tian, L., & Ma, P. (2025). Optimization Design Method of Pipe-Insulating Joints Based on Surrogate Model and Genetic Algorithm. Applied Sciences, 15(13), 7601. https://doi.org/10.3390/app15137601





