Abstract
Temperature dependencies of the density, heat capacity at constant pressure, and isobaric thermal expansion coefficient are investigated for two liquid metal nuclear reactor coolants: pure sodium and sodium–potassium eutectic alloy (31.9 at. %Na). The variational method of the thermodynamic perturbation theory is used for the calculations. The calculations were carried out in temperature ranges of 373–1673 K for Na and 273–1573 K for 0.319Na-0.681K. The accuracy of two local pseudopotentials and three exchange–correlation functions is estimated. It is shown that two combinations between the pseudopotential and exchange–correlation function can be recommended for predicting the properties at high temperatures for which experimental information is absent.
1. Introduction
Liquid sodium is used in nuclear engineering as a coolant for the first circuit of fast neutron reactors. This metal has high corrosion resistance, low toxicity, and low cost. In addition, it ensures simplicity of technological operations necessary to maintain the specified quality of the coolant during repair work. However, the intense interaction of this metal with water leads to the need of using a second circuit in the reactor system, which prevents the products of their interaction from entering the active zone [1,2,3,4].
The sodium–potassium liquid eutectic alloy (31.9 atomic %Na [5]) has found its application in the second circuit of a fast neutron nuclear reactor. Also, this coolant is used in low-power space nuclear stations. The very low melting point of the eutectic Na–K alloy (−12.3 °C) allows for the simplification of the design and makes the operation of the nuclear power system easier [6,7].
In addition, the liquid Na–K is employed in many other branches of the industry such as materials’ synthesis, biomedicine, microelectronics, catalysis, and sustainable chemistry [8,9]; this, additionally, makes it interesting to study this alloy at any composition.
In the current century, the physical properties of Na and Na–K alloy in the liquid state are intensively studied by different theoretical methods [10,11,12,13,14,15,16,17,18,19,20,21,22]. A significant part of the aforementioned works was performed in the frameworks of the thermodynamic perturbation theory (TPT) in conjunction with the pseudopotential method. Such an approach was also successfully applied to investigations of other liquid metals and alloys [23,24,25,26,27,28,29,30,31,32,33,34].
The numerical solving of the Gibbs–Bogoliubov inequality (the variational method) is most widely used among the TPT methods in studies of liquid metals and their alloys (see, for example, Refs. [10,11,12,13,14,15,16,23,24,25,26,27,28,29]). The main advantage of the variational method is the minimization of the Helmholtz free energy with respect to the parameters of the reference system. This makes it possible to not use any experimental information to determine them.
Starting from our early work [25], within this method we used an additional minimization with respect to the mean atomic volume that gives an opportunity to avoid input experimental data on density of the melt under consideration. This makes the approach completely free from inputting any experimental data about the system under study, since the only input information required is the values of the pseudopotential parameters, which are determined for pure substances at zero absolute temperature.
Recently, this approach resulted in very positive results for thermodynamic properties of the equiatomic liquid Na–K, Na–Rb, K–Rb, and Na–Cs binary alloys at [15,16].
In the present work, we estimate its suitability to investigate the thermophysical properties (namely, the isobaric heat capacity, , and isobaric thermal expansion coefficient, ) of Na and Na–K coolants in the wide range of temperatures (from 273 K to 1673 K) and compare an accuracy of different pseudopotential models used for calculations.
2. Theory
In this work, both quantities under consideration are calculated numerically by using the following thermodynamic relations, respectively (hereafter in Section 2, all macroscopic quantities are given per atom):
where is the temperature; is the pressure; is the entropy; is the density; is the mean atomic volume.
The calculations are performed on the basis of the right-hand side of the Gibbs–Bogoliubov inequality [35,36,37] by means of the minimization of the Helmholtz free energy, , in the reciprocal space (see, for example, Refs. [29,38]):
where is the Boltzmann constant; and are the first- and second-order terms of the pseudopotential perturbation theory ( has the physical meaning of the band structure energy); is the Madelung energy arising from the direct pairwise Coulomb repulsions between ions; is the entropy of the hard sphere (HS) reference system (we use the analytical expressions for the one-component HS fluid and for the binary HS mixture obtained in the work [38]); and are the electron-gas contributions to the internal energy and the entropy, respectively (hereafter in Section 2, all characteristics are given in atomic units (a.u.)):
where is the valence (for the binary alloy, , where is the valence of the i-th component; is the concentration of the i-th component in the alloy); is the Fermi wave vector; is the exchange–correlation energy taken here in the Nozieres–Pines approach [39], which was successfully used earlier for liquid Na–K [38] and for other alkali metal liquids [12,14,15].
The contribution is expressed for pure metal and for the binary metal alloy, respectively, as follows:
where and are the form factors of the unscreened-ion pseudopotentials in the pure metal and in the binary alloy for the i-th-kind ion, respectively; is the modulus of the wave vector, .
In the present work, the Krasco–Gurskii (KG) model pseudopotential [40] and the Animalu–Heine (AH) model pseudopotential [41] in the local approximation [42] with the following form factors are used:
where , , , , and , , , are the parameters in the pure metal and in the alloy for the i-th-kind ion (put here the same as the ones for the corresponding pure metals), respectively.
Equations (6) and (7) are transformed easily into closed form for both pseudopotentials under consideration as follows:
Expressions for and are written as a band structure and Madelung contributions, respectively, averaged over the HS reference system:
where is the Hartree dielectric function; is the exchange–correlation function; is the Kronecker symbol; and are the structure factor of the one-component fluid and partial structure factors of the binary mixture in the Ashcroft–Langreth form [43], respectively:
(at )
where is the Fourier transform of the direct correlation function, ; are the Fourier transforms of the partial direct correlation functions, obtained for the HS binary mixture in the exact form in Ref. [43] (see Appendix B in Ref. [43]).
The analytical expressions for and the corresponding were obtained in Ref. [44] and Ref. [45], respectively, as follows:
where ; ; ; ; ; is the hard sphere diameter (the single parameter of the one-component HS model).
The analytical expression for in the same approximation was derived in Ref. [38]:
Here,
where ; ; and are the partial hard sphere diameters.
Three exchange–correlation functions are used in this work, the Geldart–Vosko (GV) [46], Vashishta–Singwi (VS) [47], and Toigo–Woodruff (TW) [48], respectively:
where ,
where and are tabulated in Ref. [47], and which is fully tabulated in Ref. [48].
The values of the pseudopotentials’ parameters are taken from the work [42] (Table 1) where they were fitted at from the condition that the shear modulus of each metal is equal to the experimental one.

Table 1.
Input values of pseudopotential parameters.
The valence of the pure Na as well as and in the alloy are put equal to 1.
The minimization is fulfilled by means of the simplex method simultaneously with respect to and with respect to for the pure metal,
and simultaneously with respect to and with respect to and , for the binary alloy,
where .
All calculations were performed using the “Fortran” language on a single-processor computer.
3. Results and Discussion
The calculations for the pure Na and Na–K eutectic alloy are carried out in the temperature ranges of 373–1673 K and 273–1573 K, respectively. The important feature of the used calculation procedure is that the mean atomic volumes are defined during its fulfillment due to conditions (28) and (30) for the pure metal and binary alloy, respectively. As a result, for both coolants we obtained the theoretical values of densities at each temperature under consideration (Figure 1 and Figure 2).
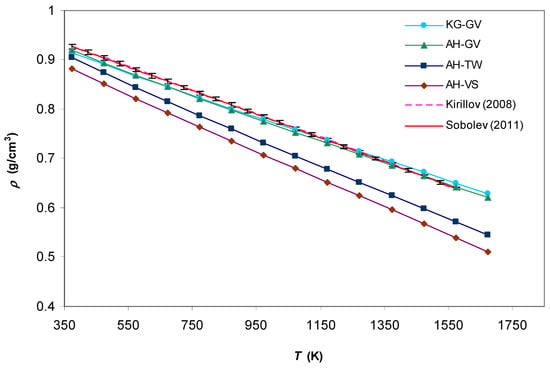
Figure 1.
Density of liquid Na calculated for different pseudopotential models in comparison with experimental data [3,4].
Experimental data for the density of liquid Na are taken from the most recent and complete handbooks [3,4]. The corresponding polynomial series suggested in the former is based on the results listed in Refs. [49,50] and is written as follows:
The polynomial series recommended in Ref. [4] is based on the results listed in Ref. [49] as follows:
As seen in Figure 1, both experimental approximations (32) and (33) provide results very close to each other and to the calculated results for two pseudopotential models, KG–GV and AH–GV. At the same time, two other combinations between the pseudopotential and the exchange–correlation function (AH–TW and AH–VS) lead to some disagreement with experimental results which increases with the increase in the temperature.
For the density of Na–K eutectic alloy (Figure 2) the same two combinations (KG–GV and AH–GV) provide better agreement with the experiment [50], but this agreement is not as excellent as in the case of the pure Na.
The results obtained for the isobaric thermal expansion coefficients are presented in Figure 3 and Figure 4. Experimental data for Na were defined using differentiations of Equations (32) and (33) by means of Equation (2). To define the experimental for the Na–K eutectic alloy we used an analogous procedure. For this aim the following linear approximation (with = 0.9937) of the density was derived as follows on the basis of experimental data [50]:
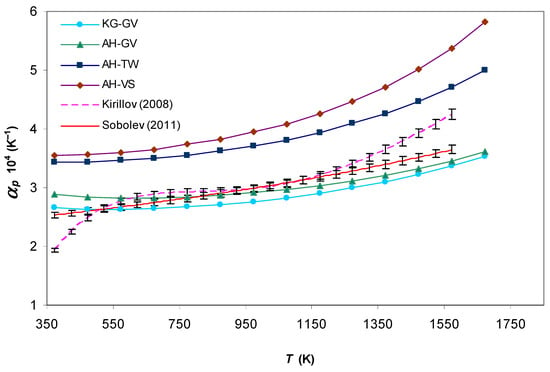
Figure 3.
Isobaric thermal expansion coefficient of liquid Na calculated for different pseudopotential models in comparison with experimental data [3,4].
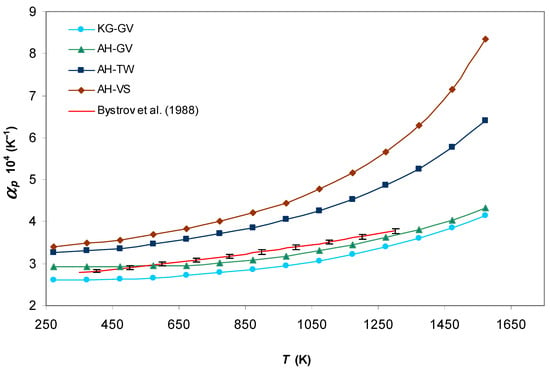
Figure 4.
Isobaric thermal expansion coefficient of liquid Na–K eutectic alloy calculated for different pseudopotential models in comparison with experimental data [50].
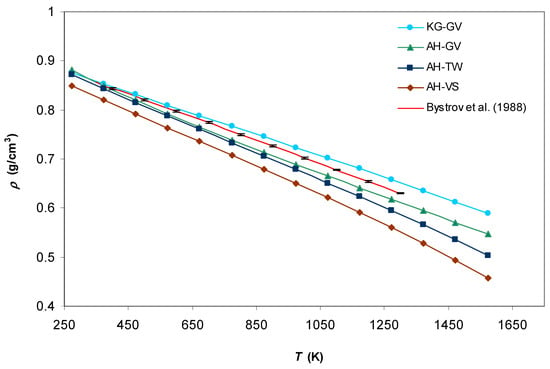
Figure 2.
Density of liquid Na–K eutectic alloy calculated for different pseudopotential models in comparison with experimental data [50].
Figure 3 shows that the maximal deviation of theoretical from experiment [4] for each of the KG–GV and AH–GV combinations is 10%. Therewith, the results of the former combination agree better with experiment [4] approximately up to , while the results of the latter show better agreement beyond this temperature. The behavior of the experimental curve [3] possibly points to the fact that the derivative of Equation (32) is not sufficiently accurate. Otherwise, it can be asserted that the accuracy of the AH–TW combination increases with the increase in temperature. Notably, the deviation of AH–TW results from the experiment [4] lies in the range 20–25%.
A similar picture is observed for of the Na–K eutectic alloy (Figure 4): the best agreement with the experiment is achieved for the AH–GV combination and the close results are obtained for KG–GV.
Experimental data on the heat capacity at constant pressure for liquid Na are approximated by two polynomial series taken in the works [3] and [4], respectively, as follows:
Experimental values of at five temperatures for the Na–K eutectic alloy were reported in [50].
For both coolants under study all theoretical dependencies reproduce the existence of the minima observed in the experimental curves (Figure 5 and Figure 6). At low temperatures, all theoretically obtained are approximately the same for each coolant and deviate from the corresponding experimental dependencies within 10%, while at high temperatures, the better agreement with experiments occurs for the KG–GV and AH-GV combinations. In the case of the Na–K eutectic alloy, these two combinations obviously predict results for temperatures higher than 1200 K (Figure 6).
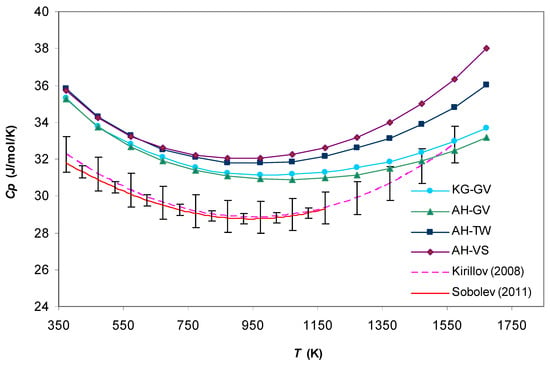
Figure 5.
Heat capacity at constant pressure of liquid Na calculated for different pseudopotential models in comparison with experimental data [3,4].
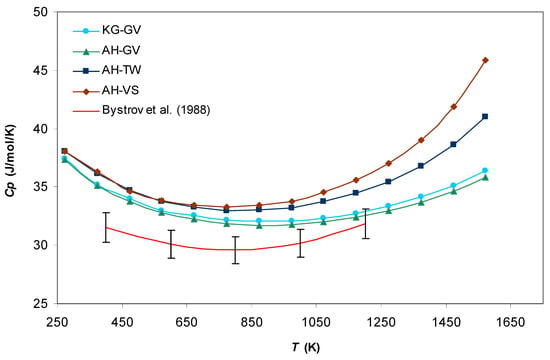
Figure 6.
Heat capacity at constant pressure of liquid Na–K eutectic alloy calculated for different pseudopotential models in comparison with experimental data [50].
Generally, the calculated temperature dependencies of densities, isobaric thermal expansivities, and heat capacities show that the choice of the exchange–correlation function can play a more significant role for the quantitative results than the choice of the pseudopotential form. This stems from the fact that in the present paper in all cases the results obtained with the KG–GV and AH–GV combinations essentially agree better with experimental data than the results obtained using the AH–TW and AH–VS combinations.
4. Conclusions
It is shown that the variational method of the thermodynamic perturbation theory is a workable instrument for the study of liquid metal coolants. The obtained results are in good agreement with the experiment or have predictive ability.
In the framework of the used approach the best pseudopotential model (the combination of the Animalu–Heine local pseudopotential with the Geldart–Vosko exchange–correlation function) was found. This model can be recommended as a tool for calculations of thermophysical properties of alkali metal coolants.
The applicable temperature ranges for the best pseudopotential model and is approximately 1300–1700 K for liquid Na and 1200–1600 K for liquid Na–K eutectic alloy.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Ural Federal University Program of Development within the Priority-2030 Program).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Subbotin, V.I.; Arnol’dov, M.N.; Kozlov, F.A.; Shimkevich, A.L. Liquid-metal coolants for nuclear power. At. Energy 2002, 92, 29–40. [Google Scholar] [CrossRef]
- Olivier, T.J.; Radel, R.F.; Nowlen, S.P.; Blanchat, T.K.; Hewson, J.C. Metal Fire Implications for Advanced Reactors, Part 1: Literature Review; Sandia Report, SAND2007-6332, Unlimited Release; OSTI: Oak Ridge, TN, USA, 2007. [Google Scholar]
- Kirillov, P.L. (Ed.) Thermophysical Properties of Materials for Nuclear Engineering: A Tutorial and Collection of Data; IAEA: Vienna, Austria, 2008. [Google Scholar]
- Sobolev, V. Database of Thermophysical Properties of Liquid Metal Coolants for GEN-IV. Sodium, Lead, Lead-Bismuth Eutectic (and Bismuth), Scientific Report of the Belgian Nuclear Research Centre, SCK-CEN-BLG-1069, November 2010. [rev. Dec. 2011]; Belgian Nuclear Research Centre: Mol, Belgium, 2011. [Google Scholar]
- Bale, C.W. The K-Na (potassium-sodium) system. Bull. Alloy Phase Diagr. 1982, 3, 313–318. [Google Scholar] [CrossRef]
- Loginov, N.I. Sodium-potassium eutectic alloy: Achievements and problems. Quest. At. Sci. Technol. Nucl.-React. Constants 2024, 2, 259–268. (In Russian) [Google Scholar]
- Ulyanov, V.V.; Koshelev, M.M.; Kremleva, V.S.; Bragin, D.S.; Prikazchikova, A.A. Features of purification and control of sodium-potassium eutectic alloy. Izv. Vyss. Uchebnykh Zaved. Yad. Ehnergetika 2024, 127–137. (In Russian) [Google Scholar] [CrossRef]
- Leonchuk, S.S.; Falchevskaya, A.S.; Nikolaev, V.; Vinogradov, V.V. NaK alloy: Underrated liquid metal. J. Mater. Chem. A 2022, 10, 22955–22976. [Google Scholar] [CrossRef]
- Leonchuk, S.S.; Falchevskaya, A.S.; Morozova, P.A.; Gromov, N.V.; Vinogradov, V.V. NaK alloy as a versatile reagent for template-free synthesis of porous metal- and metalloid-based nanostructures. Chem. Commun. 2024, 60, 4814–4817. [Google Scholar] [CrossRef] [PubMed]
- Mon, K.K. Application of hard sphere perturbation theory for thermodynamics of model liquid metals. Phys. Rev. E 2001, 63, 061203. [Google Scholar] [CrossRef]
- Mizuno, A.; Masaki, T.; Itami, T. Theoretical prediction of atomic volume for liquid metals based on the hard sphere model combined with NFE theory. Chem. Phys. Lett. 2002, 363, 337–342. [Google Scholar] [CrossRef]
- Dubinin, N.E. Thermodynamics of alkali metals melts. J. Opt. Adv. Mater. 2003, 5, 1259–1262. [Google Scholar]
- Grosdidier, B.; Al-Busaidi, M.S.; Osman, S.M. Transferable individual local pseudopotential for expanded liquid metals. J. Non-Cryst. Solids 2007, 353, 3484–3487. [Google Scholar] [CrossRef]
- Dubinin, N.; Yuryev, A.; Vatolin, N. Gibbs–Bogoliubov variational procedure with the square-well reference system. J. Non-Equilibr. Thermodyn. 2010, 35, 289–300. [Google Scholar] [CrossRef]
- Dubinin, N.E. The variational calculation of bulk moduli for liquid binary alloys of alkali metals. Acta Phys. Polon. A 2017, 131, 237–239. [Google Scholar]
- Dubinin, N.E. The heat capacity at constant pressure in the nearly-free-electron approximation for binary liquid alloys of alkali metals. High Temp.-High Press. 2018, 47, 205–211. [Google Scholar]
- Uddin, M.S.; Gosh, R.C.; Bhuiyan, G.M. Investigation of surface tension, viscosity and diffusion coefficients for liquid simple metals. J. Non-Cryst. Solids 2018, 499, 426–433. [Google Scholar] [CrossRef]
- Bhuiyan, G.M.; Abbas, F.I. Local minimum in pair potentials of polyvalent metals: A limitation of pseudopotential theory. Int. J. Mod. Phys. B 2019, 33, 1950049. [Google Scholar] [CrossRef]
- Dubinin, N.E. Square-well self-diffusion coefficients in liquid binary alloys of alkali metals within the mean spherical approximation. J. Alloys Compd. 2019, 803, 1100–1104. [Google Scholar]
- Bryk, T.; Demchuk, T.; Wax, J.-F.; Jakse, N. Pressure-induced effects in the spectra of collective excitations in pure liquid metals. J. Phys. Condens. Matter 2020, 32, 184002. [Google Scholar]
- Becker, S.; Meyer, N.; Xu, H.; Wax, J.-F. Viscosity of liquid Na–K alloys from molecular dynamics simulations. J. Phys. Condens. Matter 2020, 32, 194005. [Google Scholar]
- Wax, J.-F.; Mocchetti, E. Simulation study of the collective excitations in liquid sodium under high pressure. J. Phys. Condens. Matter 2023, 35, 304003. [Google Scholar]
- Kovneristyi, Y.K.; Vatolin, N.A.; Gurskaya, E.G.; Landa, A.I.; Romankevitch, M.V.; Yuryev, A.A. Ab initio calculation of the thermodynamic properties of liquid alloys with the application to Ni-Al. A nonlocal resonant pseudopotential approach. J. Non-Cryst. Solids 1990, 117–119, 589–592. [Google Scholar] [CrossRef]
- Landa, A.I.; Yuryev, A.A.; Ruban, A.V.; Gurskaya, E.G.; Kovneristyi, Y.K.; Vatolin, N.A. Pseudopotential calculation of thermodynamic properties and glass transition temperatures of binary Ni-Al alloys. J. Phys. Condens. Matter 1991, 3, 9229–9243. [Google Scholar] [CrossRef]
- Dubinin, N.E.; Yuryev, A.A.; Vatolin, N.A. Thermodynamic properties of ternary liquid metal alloys. High Temp. Mater. Process. 1995, 14, 285–290. [Google Scholar] [CrossRef]
- Kitamura, H. Equation of state for expanded fluid mercury: Variational theory with many body interaction. J. Chem. Phys. 2007, 126, 134509. [Google Scholar] [CrossRef] [PubMed]
- Greeff, C.W. Tests of Monte Carlo perturbation theory for the free energy of liquid copper. J. Chem. Phys. 2008, 128, 184104. [Google Scholar] [CrossRef]
- Tsai, K.H.; Wu, T.-M. Entropy of a model for liquid Ga: Contribution due to Friedel oscillations. Comput. Phys. Commun. 2011, 182, 62–64. [Google Scholar] [CrossRef]
- Dubinin, N.E.; Vatolin, N.A.; Filippov, V.V. Thermodynamic perturbation theory in studies of metal melts. Russ. Chem. Rev. 2014, 83, 987–1002. [Google Scholar] [CrossRef]
- Ueda, S.; Morita, K. Theoretical calculation of the free energy of mixing of liquid transition-metal alloys using a bond-order potential and thermodynamic perturbation theory. J. Non-Cryst. Solids 2020, 528, 119743. [Google Scholar] [CrossRef]
- Bhuiyan, G.M. Microscopic origin of immiscibility and segregation in liquid metallic binary alloys. Bangladesh J. Phys. 2020, 27, 1–25. [Google Scholar] [CrossRef]
- Abbas, F.I.; Bhuiyan, G.M.; Kasem, R. Critical properties of segregation for Al1−xBix liquid binary alloys. J. Phys. Soc. Jpn. 2020, 89, 114004. [Google Scholar]
- Bogdanova, Y.A.; Gubin, S.A.; Maklashova, I.V. Calculation of thermodynamic properties of metals and their binary alloys by the perturbation theory. Metals 2021, 11, 1548. [Google Scholar] [CrossRef]
- Abbas, F.I.; Bhuiyan, G.M. A study of thermodynamics of mixing for Al1−xZnx liquid binary alloy. Phys. B 2022, 647, 414365. [Google Scholar] [CrossRef]
- Lukes, T.L.; Jones, R. Inequalities and variational methods in classical statistical mechanics. J. Phys. A Proc. Phys. Soc. 1968, 1, 29–33. [Google Scholar] [CrossRef]
- Isihara, A. The Gibbs–Bogoliubov inequality. J. Phys. A Proc. Phys. Soc. 1968, 1, 539–548. [Google Scholar]
- Mansoori, G.A.; Canfield, F.B. Variational approach to the equilibrium thermodynamic properties of simple liquids. I. J. Chem. Phys. 1969, 51, 4958–4967. [Google Scholar] [CrossRef]
- Umar, I.H.; Meyer, A.; Watabe, M.; Young, W.H. Thermodynamic calculations for liquid alloys with an application to sodium-potassium. J. Phys. F Met. Phys. 1974, 4, 1691–1706. [Google Scholar] [CrossRef]
- Nozieres, P.; Pines, D. Correlation energy of a free electron gas. Phys. Rev. 1958, 111, 442–454. [Google Scholar] [CrossRef]
- Krasco, G.L.; Gurskii, Z.A. Concerning one model pseudopotential. Lett. ZhETF 1969, 9, 596–601. [Google Scholar]
- Animalu, A.O.E.; Heine, V. The screened model potential for 25 elements. Phil. Mag. 1965, 12, 1249–1270. [Google Scholar] [CrossRef]
- Vaks, V.G.; Trefilov, A.V. On the theory of the atomic properties of liquid metals. Solid State Phys. 1977, 19, 244–258. [Google Scholar]
- Ashcroft, N.W.; Langreth, D.C. Structure of binary liquid mixtures. I. Phys. Rev. 1967, 156, 685–692. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Lekner, J. Structure and resistivity of liquid metals. Phys. Rev. 1966, 145, 83–90. [Google Scholar] [CrossRef]
- Jones, H. Method for finding the equation of state of liquid metals. J. Chem. Phys. 1971, 55, 2640–2642. [Google Scholar] [CrossRef]
- Geldart, D.J.W.; Vosko, S.H. The screening function of an interacting electron gas. Can. J. Phys. 1966, 44, 2137–2171. [Google Scholar] [CrossRef]
- Vashishta, P.; Singwi, K. Electron correlation at metallic densities. Phys. Rev. B 1972, 6, 875–887. [Google Scholar] [CrossRef]
- Toigo, F.; Woodruff, T.O. Calculation of the dielectric function for a degenerate electron gas with interactions. I. Phys. Rev. B 1970, 2, 3958–3966. [Google Scholar] [CrossRef]
- Ohse, R.W. (Ed.) Handbook of Thermodynamic and Transport Properties of Alkali Metals; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- Bystrov, P.M.; Kagan, D.N.; Krechetova, G.A.; Shpilrain, E.E. Liquid Metal Coolants of Heat Pipes and Power Plants; Nauka: Moscow, Russia, 1988. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).