Abstract
Based on the literature data on the structure of liquid Pu, the pair contribution to the EAM potential of liquid Pu is calculated and the embedding potential is determined using the dependence of density on temperature. The properties of liquid Pu are calculated at temperatures up to 5000 K and at ambient pressure, as well as upon cooling to 500 K. Agreement with experiment is obtained for density, bulk modulus, and viscosity. Self-diffusion coefficients are calculated. The Stokes–Einstein relation is well satisfied at all temperatures above the melting point but, below it, the deviations are observed, increasing upon cooling. The heat capacity of the real liquid is significantly higher than that of the models. Excess surface energy is considered.
1. Introduction
Liquid Pu is a very interesting object to investigate. It is the heaviest metal but radioactive and chemically active. There are a vast number of works on its physicochemical properties under different conditions. Because of experimental complications in direct measurements, most of the properties of liquid Pu were determined by computer modeling, including the ab initio calculation method. The interparticle potential plays the leading role in the calculations, which allows for simulation of many properties of the liquid phase. The interparticle potential in the modified embedded atom method (MEAM) form was determined for all the Pu phases at once in pioneering work by M. Baskes [1]. The number of properties was investigated with this potential using computer calculations and applying the theory of liquids.
MEAM potential [1] was constructed to describe all six crystal phases and the liquid one at once. However, it appeared that the properties of the liquid phase were described not adequately well. Obviously, for a liquid Pu, a more correct potential may be obtained, considering only this phase alone. Such potential would be useful also in the study of amorphous Pu. Obtaining such potential is the main goal of this article.
Some properties of liquid Pu were nevertheless measured experimentally. These are density, energy, heat capacity, speed of sound, compressibility, viscosity, and surface tension.
The density of liquid Pu was measured in the range up to 1200 K in [2,3]:
d = 17.567 − 1.451·10−3(T − 273) g/cm3
At 950 K, this formula yields a density of 16.58 g/cm3. According to the reference book [4], at 938 K, the figure obtained is close to 16.50 g/cm3.
Bearing in mind the physical structure of EAM and MEAM, one must calculate the energy U of the models with respect to a system of non-interacting atoms at rest. The energy of such a system can be chosen as equal to zero. The energy of a substance is easy to calculate if its heat of evaporation ΔH is known. To calculate the energy U, it should be noted that, during the transition to the ideal gas state, ΔU = ΔH − RT. Subtracting the kinetic energy of an ideal gas (3/2) RT, one finds the change in energy during the transition of a substance to the state of non-interacting atoms at rest ΔU = ΔH − (5/2) RT. Consequently, the energy of a substance with respect to a gas at rest (i.e., to the origin) is equal to U = −ΔH + (5/2) RT. These estimates are not entirely accurate, since the properties of Pu gas deviate from the properties of an ideal gas [5]. According to [5,6], the heat of vaporization of Pu at the melting point is 336.6 ± 1.42 kJ/mol. Hence, the energy of liquid Pu near the melting point Tm is U = −317.7 kJ/mol. The report [5] provides data on the enthalpy of Pu at temperatures up to 2500 K.
An important characteristic of liquid Pu is its heat capacity Cp = 41.2 J/mol/K at the melting point Tm, which is significantly higher than the classical value 3R = 24.94 J/mol/K [5]. Already at 298 K, the heat capacity of solid Pu (35 J/mol/K) exceeds the classical value. This excess is due to the heat capacity of conduction electrons and the internal degrees of freedom of atoms. Monatomic Pu gas in the range of 400–500 K has a heat capacity of 2.76R, which is close to the classical value of (5/2) R. However, already in the range of 900–1000 K, the heat capacity of the gas is 3.56 R and, in the range of 2400–2500 K, Cp = 7.4 R [5]. Here, the internal degrees of freedom of atoms must be considered in calculations.
In the work [7] measurements of electrical resistance, thermal expansion, enthalpy, compressibility, Grüneisen coefficient, sound speed, and heat capacity ratio Cp/Cv were carried out at temperatures up to 4000 K. An increase in sound speed was noted at temperatures up to 2000 K and a decrease in sound speed with further heating. The reason considered is the delocalization of 5f electrons. Accordingly, the bulk modulus and Grüneisen coefficient change with a maximum at 2000–2200 K. With a decrease in density, the Cp/Cv ratio increases (up to 1.40 at 4000 K).
All calculations of the self-diffusion coefficients of liquid Pu were performed using the molecular dynamics (MD) method. In the case of shear viscosity, both a conventional experiment (damping of torsional oscillations of a cylinder with liquid) and the MD method were used. Data on self-diffusion [8,9] and shear viscosity [9,10,11,12,13] have been published. In [9], the self-diffusion coefficients and viscosity of Pu were calculated at temperatures up to 1400 K. The surface tension σ of liquid Pu was measured in [14]. In the range of 913–1200 K, the value of σ = 550 − b (T − 913) mN/m, where b = 0.08–0.15.
In the early work of Wittenberg [15], the hard sphere model was applied. The compressibility of the metal could be correctly described, but viscosity and surface tension values were underestimated. Then, the potential of the modified embedded atom model (MEAM) was proposed for liquid Pu [1]. The parameters of this potential were found (but not given) considering the known properties of the liquid phase and six crystalline phases of Pu. This potential was applied for the molecular dynamics (MD) modeling of Pu. It allows agreement with experiment to be obtained for some important properties of the models: energy (3.80 eV/atom), melting temperature (1000 K), and bulk moduli for α, β, and γ phases of Pu. The decrease in volume upon melting was also confirmed.
Further analysis of the properties of liquid Pu was carried out using the MEAM potential [8]. The models contained 2048 atoms in the main cube. The pair correlation function (PCF) of liquid Pu at 950 K, as well as the self-diffusion coefficient D and shear viscosity η at 900–1300 K were calculated. At the melting temperature (913 K), the values of D = 2.3·10−6 cm2/s and η = 2.52 mPa·s were found to be significantly underestimated in relation to the experimental values (D ~10−5 cm2/s and η = 6.30 mPa·s [12,13]). Apparently, the MEAM potential [1], calculated under conditions of insufficient initial data, required clarification.
In this work, the EAM interparticle potential of Pu is reconstructed based on the known pair correlation function (PCF) and the density of liquid Pu. Using this potential, computer modeling of Pu is performed at temperatures of 500–5000 K.
2. Materials and Methods
A case of successful calculation of the interparticle potential at a significant lack of experimental data can be considered in the search of interparticle potential of liquid uranium [16]. Pair contribution to the EAM potential was chosen as the Morse potential, and the parameters of the embedding potential were selected using the dependence of the density of liquid on temperature. In this paper, an attempt to construct a model of a liquid Pu metal based on the known pair correlation function (PCF) and density was realized. The interparticle EAM potential was calculated and computer modeling of Pu was carried out at temperatures of 500–5000 K.
Several methods for constructing models of liquids and amorphous substances based on known diffraction data (structural factors or pair correlation functions) were previously proposed [17]. The main results were previously obtained for simple liquids with short-range pair potentials. A similar problem has appeared in the case of Pu. To calculate the interparticle potential of liquid Pu, it was decided to use its pair correlation function (PCF) near the melting point, which is calculated in [8]. The Schommers algorithm [18] was used, which allows the construction of a liquid model with simultaneous restoration of the interparticle potential.
There is little data on the structure of liquid Pu. No direct diffraction experiment could be found due to the difficulties of working with fissile materials. However, the pair correlation function g(r) (PCF) of Pu was calculated by the MEAM method at 950 K [8] (r is the interparticle distance). We scanned the PCF graph of liquid Pu [8] at 950 K (see Figure 1). Hereafter let us call this function PCF-1. It has the usual appearance for simple liquids, with the height of the first peak slightly less than 3.0 and with a coordinate of 3.175 Å. Let us denote the particle number density by n = N/V (N is the number of particles in a volume V, n = 0.04091 at/Å3). If one plots the dependence of g(r) on the value of rn1/3 at 950 K, the graph for Pu almost coincides with that in the case of liquid Al at 943 K [8].
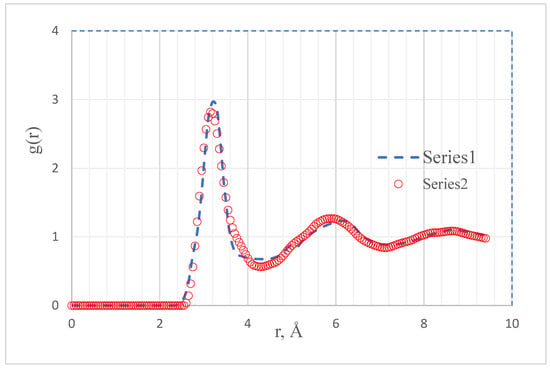
Figure 1.
Pair correlation function of Pu at 950 K. 1—data scan [8]. 2—converted PCF of liquid aluminum at 943 K [19].
Additional information on the structural characteristics is provided by checking Pu for the feasibility of the main topological criteria of the PCF shape. The structural features of a liquid metal can be analyzed using relationships describing the shape of the PCF of simple liquids. As shown in [20], in the case of simple one-component liquids with pair interaction, there is a relationship between the coordinate of the 1st peak of the PCF r1, the height of this peak g(r1), the minimum interparticle distance rmin in this liquid, and the volume per 1 atom v1 = V/N. Let us define the quantities d = (V/N)1/3 (N is the number of atoms in volume V), ρ1 = r1/d, and ρmin = rmin/d. The maximum possible value of ρmin in one-component disordered systems with central interaction is 1.0673 [20]. Let us introduce the notation y = ρmin−1 − 1.0673−1. Analysis of 32 computer models with different potentials and real structures of liquid metals allows the relationship to be obtained [20]:
gc(ρ1) = 1 + 0.600/y0.77 + 0.0001/y3
Deviations from this relationship are minor and, on average, do not exceed ±5%. Thus, the ratio of the peak heights S = g(ρ1)/gc(ρ1) for a real PCF to the “theoretical” value should be S = 1 ± 0.05 in the case of simple liquids and amorphous substances. Deviations to the smaller value should be topologically forbidden and to the larger value can be allowed for systems with non-central interaction. Note that the left (descending) branch of the 1st PCF peak of the system, i.e., the minimum interparticle distance, plays a large role in calculations. This characteristic of the PCF plays an important role in the construction of models of liquid metals, but it is the least known from experiment.
From this position, let us consider the PCF-1 of liquid Pu obtained by the MEAM method in [8]. The parameters of this PCF are given in Table 1. Judging by the values of S from Table 1, the structure of liquid Pu with such parameters as those of the PCF [8] at a temperature of 950 K is topologically realizable, but a centrally symmetrical structure with such PCF cannot really exist, since the value of S (i.e., the height of the 1st peak) is too large. Consequently, it is impossible to construct a model with central interaction and with exactly the same PCF.

Table 1.
Characteristics of the Pu PCF.
Nevertheless, we can try to build a model M1 with the same target PCF-1 as curve 1 in Figure 1 and to see what we will have. Let us call this virtual substance para-Pu. For this purpose, the Schommers algorithm [18] was applied. The potential in this algorithm is calculated iteratively during the calculation process. At each iteration with a trial potential, the difference between the obtained PCF and the specified (target) PCF is calculated, and a correction to the current pair potential is determined in the form of a table.
Let us denote by g0(ri) the diffraction (“target”) PCF and by g(ri) the PCF of the model constructed with some trial potential φ(ri). Then, a new approximation of the potential is calculated according to the Schommers algorithm [18] by the formula:
φ′(ri) = φ(ri) + α ln[g(ri)/g0(ri)]
Here α is an empirical coefficient regulating the rate of convergence of the results to the asymptotic limit. Using potential φ′(ri), a new model of liquid is constructed, new PCFs g(r) are found, etc., until the difference between the diffraction and model PCFs becomes small enough. Since in the MD method the PCFs are calculated as histograms, the discrepancy between them can be found numerically as standard deviations (“residuals”):
Here g0(rj) is the histogram of the target PCF, g(rj) is the histogram of the model PCF, n1 and n2 are the summation boundaries of the tabular data, and j is the number of the histogram element. As n1, the number of the first non-zero element of the PCF was chosen, and n2 was determined by the cutting radius of the interaction. If the value of Rg is several hundredths, then the graphs of the functions g0(r) and g(r) are visually indistinguishable. Therefore, the iterative process can be carried out until the residual values of the order of 0.01 are reached.
3. Results
The initial model of the Schommers algorithm at 950 K contained 2048 particles in the main cube with an edge length of 36.751 Å (density N/V = 0.04126 at/Å3 or 16.58 g/cm3). The copper potential was used as a seed [21]. At distances less than rmin = 2.40 Å, the values of Pu potential are not determined in the Schommers procedure and were chosen empirically in the form of an ascending branch:
φ(r), eV = 2.51097 + 0.025(rmin − r)2 + 10.5486(rmin − r) + 25.03(rmin − r)2.20.
The Pu model (M1) at 950 K was constructed in 140 Schommers’ iterations using the PCF-1. The details of the modeling are described, for example, in [17]. In this algorithm, the interparticle potential φ1(r) was calculated in the form of a table with a step of 0.05 Å and a cutting radius of 9.40 Å. The characteristics of the structure of this model are given in Table 1. The deviation of the parameter S of the target PCF-1 from the topological standard led to the same deviation for the PCF of the M1 model. The discrepancy between the PCF of the M1 model and the PCF-1 Pu was Rg = 0.078, which could not be reduced. It means that the PCF-1 is really not physical.
And that is not all. It turned out that the models constructed by this method practically do not expand when heated to 2000 K. For example, the model had a density of 16.543 g/cm3 at 950 K and 16.514 g/cm3 at 2000 K. In this case, the coefficient of volume expansion is an order of magnitude smaller than that of ordinary metals, which means that the resulting potential is very close to a symmetrical parabola. This solution to the problem and the potential φ1(r) itself had to be rejected.
The second variant was based on the indication of the authors [8] that the PCF of liquid Pu at 950 K and aluminum at 943 K are very similar if the rn1/3 values are plotted on the abscissa axis (n = N/V is the density). In the case of Pu at 950 K, the density n = 0.04126 at/Å3 and, for Al, it is slightly higher: n = 0.06029. The structural parameters of aluminum at 943 K are quite acceptable; the height of the first peak of the PCF is 2.828 and the coefficient S = 0.9899 is very close to unity. Therefore, we constructed a model of Pu using the PCF of aluminum at 943 K [19]. To do this, it was necessary to take the aluminum PCF, stretch its abscissa axis by 0.060291/3 = 0.3921 times, and then reduce it by 0.041261/3 = 0.3455 times, that is, stretch it by 1.13488 times. The resulting PCF (PCF-2) is shown in Figure 2.
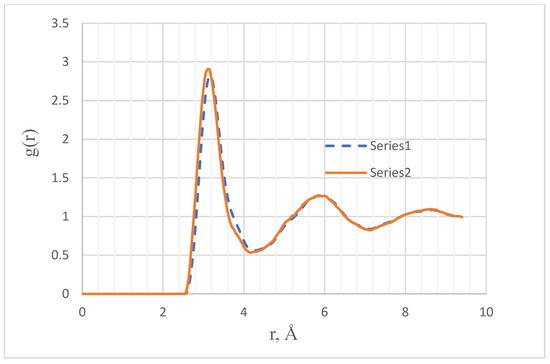
Figure 2.
PCF of Pu at 950 K. Series 1—diffraction PCF-2, calculated using the PCF of aluminum at 943 K. Series 2—PCF of the M2 model of liquid Pu, constructed at 950 K via Schommers algorithm.
Further calculations consisted of reconstructing the interparticle potential φ2(r) of a liquid metal using the Schommers algorithm, which generated the potential φ2(r) and PCF-2 function. Since the PCF-2 is no longer a function of the natural Pu, although close to it, the resulting interparticle potential will be a certain approximation to the exact potential.
Using the Schommers algorithm, the spherically symmetric pair potential φ2(r) was calculated, and a liquid metal model M2 was constructed at 950 K. The discrepancy between the PCF M2 and PCF-2 is 0.1074. The density of the model was 16.58 g/cm3 and is exactly equal to the data (1). The pressure of this model is 0.04 GPa and is quite close to zero. The energy of the model (−317.15 kJ/mol) is almost exactly equal to the energy of real Pu (−317.7) [5]. Table 2 shows the values of the pair potential φ2(r) of the Pu model, which was then used as the pair contribution φ(r) to the EAM potential for modeling Pu. The potential graph is shown in Figure 3.

Table 2.
Pair potential φ2(r), obtained by the Schommers algorithm from the corrected PCF of liquid aluminum at 943 K [19].

Figure 3.
Pair contribution φ2(r) in the potential EAM of liquid Pu.
The data presented in the table can be approximated by piecewise continuous polynomials but with some loss of accuracy.
The characteristics of the PCF-2 structure are given in Table 3. The above-described method of recalculating the PCF of aluminum to the PCF-2 leads to an underestimated S value of the target structure, so that difficulties could arise with constructing a computer model. However, the structure of the M2 model constructed by the Schommers algorithm partially corrects the shortcomings of the calculated PCF-2. The discrepancy between the PCFs of these models is quite large (0.1071), while, in the case of good results of the Schommers algorithm, it can be 0.01–0.04. As can be seen from Figure 2, this discrepancy is due to a very small shift of the sharp first peak of PCF along the abscissa axis.

Table 3.
Characteristics of the PCF-2 structure and M2 model.
The embedded atom model (EAM) potential. In this paper, the EAM potential [22] was applied. It has the form:
Here Upot is the potential energy of the system, Φ(ρi) is the embedding potential of the i-th atom, depending on the effective electron density ψ at the location of the center of the atom, and the second sum over pairs of atoms—the pair contribution—contains the usual pair potential calculated above by the Schommers algorithm. The effective electron density at the location of the atom is created by the surrounding atoms and is determined by the formula:
where ψ(rij) is the contribution to the effective electron density from the neighbor number j. It is convenient to choose the function ψ(r) in the form:
ψ(r) = p1 exp(−p2r)
Embedding potential is taken as piecewise function of the form:
where ρ0 = 1 and, for ρ = ρi, the function Φ(ρ) itself and its first derivative are continuous. The function φ(ρ) and all coefficients a, b, and c are expressed in eV. The coordinates of the division points on the abscissa axis increase in the sequence ρ3 < ρ2 < ρ1 < ρ0 < ρ4. As a result, the EAM potential is determined by the parameters p1, p2, a1, c1–c4, and ρ1–ρ4, which allow, in principle, the properties of the models to be fitted to the selected experimental data. This fitting is carried out based on the dependence of the density and energy of the metal on the temperature along the binodal, as well as on the data of static compression. Expressions for ρ < ρ0 are used when modeling states with normal and reduced density and for ρ > ρ4—for compressed states. The compressed states are not considered here. The parameter p2 in (8) is adjustable. The parameter p1 was determined in such a way as to obtain the average value <ρ> = ρ0 = 1 for the liquid model in the “standard” state (near the melting point). With this value of <ρ>, the embedding potential has almost no effect on the motion of particles, since dΦ(ρ)/dρ is close to zero at ρ ≈ 1. Coefficient a1 is determined through the energy of the model in the “standard” state at ρ = 1, and the coefficient c1 is determined through the bulk modulus in this state. The coefficients c2–c4 are selected based on the dependence of the metal density on temperature along the binodal. The coefficients a2–a4 and b2–b4 are calculated from the continuity condition of the embedding potential and its derivative at the points ρi. Note that, in the state at ρ = ρ0 = 1, the contribution from the embedding potential disappears, and the properties of the liquid are determined only by the pair contribution.
Φ(ρ) = a1 + c1 (ρ − ρ0)2 at ρ1 ≤ ρ ≤ ρ4,
Φ(ρ) = ai + bi (ρ − ρi−1) + ci (ρ − ρi−1)2 at ρi ≤ ρ ≤ ρi−1 (i = 2,3),
Φ(ρ) = [a4 + b4(ρ − ρ3) + c4(ρ − ρ3)2] [2ρ/ρ3 − (ρ/ρ3)2] at ρ ≤ ρ3,
Φ(ρ) = ai + bi (ρ − ρi−1) + ci (ρ − ρi−1)2 at ρi ≤ ρ ≤ ρi−1 (i = 2,3),
Φ(ρ) = [a4 + b4(ρ − ρ3) + c4(ρ − ρ3)2] [2ρ/ρ3 − (ρ/ρ3)2] at ρ ≤ ρ3,
The characteristics of the Pu potential are given in Table 4. The coefficients p1 and p2 were selected using the condition that, in the “standard state”, namely near the melting point, the average value of the effective electron density of atoms <ρ> is equal to unity. The coefficients of ci can be determined by the dependence of the liquid density on temperature. Considering the values of density and energy of real Pu, the coefficients of the expression for the EAM potential can be determined (see Table 4).

Table 4.
Coefficients for embedding potential of Pu.
The Pu models with a size of 2048 particles in the main cube were constructed using the MD method with a time step of 0.0022t0, where t0 is an internal time unit equal to 1.5904·10−13 s. This step was selected from the condition of minimal drift of the total energy of the system in the NVE mode. Particle displacements were calculated using the L. Verlet algorithm. The potential cutoff radius was 9.40 Å. The results of the simulation of liquid Pu are given in Table 5.

Table 5.
Calculated properties of Pu obtained by MD with EAM potential (8).
Figure 4 shows the dependence of the density of Pu models on temperature. This dependence is linear at T > Tm but, in the supercooling region, where T < 913 K, upward deviations are observed.
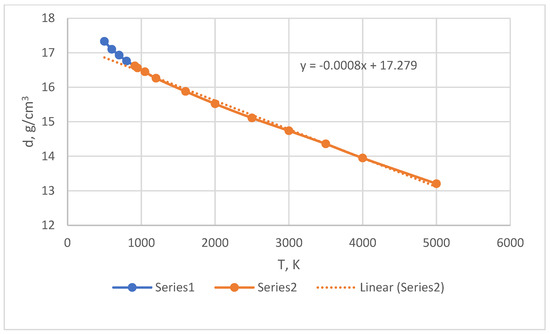
Figure 4.
Density of Pu models with EAM potential. The dotted line is a linear approximation. 1—supercooling, 2—normal liquid.
The calculated heat capacities Cv and Cp are given in Table 6. Our computer calculation slightly overestimates the ratio Cp/Cv (by ~0.02), but the temperature dependencies of the heat capacities of models and real Pu are generally the same.

Table 6.
Heat capacity Cv and Cp of Pu.
According to [7], the sound speed during heating passes through a maximum at 2000 K. At liquid densities above 15 g/cm3 (i.e., at 900–2500 K, see Table 5), the bulk modulus KT of liquid Pu changes little and is close to 24 GPa and, with further heating, it decreases with a slope of 3.6 GPa/(g/cm3). We calculated the isothermal modulus KT using the dependence of the model pressure on the volume at a constant temperature in the NVE ensemble. The values of the modulus at temperatures up to 5000 K are given in Table 5. Our calculations show that the dependence of the modulus on temperature really changes little at T < 2500 K, and then it begins to decrease with heating in accordance with experiment. These features can be explained by assuming that 5f electrons of Pu play the role of valence electrons because of delocalization, and the increase in the sound speed during heating (maximum at 2500 K) is caused by the hybridization of 5f electrons with 6d7s electrons of the conduction band of Pu [7].
The self-diffusion coefficients D of liquid Pu were measured via the time dependence of the mean square atomic displacements. The values of the coefficient D at temperatures of 913–5000 K are given in Table 7 and shown in Figure 5, where the notation D5 = D × 105 is adopted. They are well straightened in logarithmic coordinates and approximated by the equation:
ln D5 = 1.5019lnT − 10.063, or D = 4.263·10−10 T1.5019 cm2/s.

Table 7.
Coefficients of self-diffusion D and dynamic viscosity η of liquid Pu.
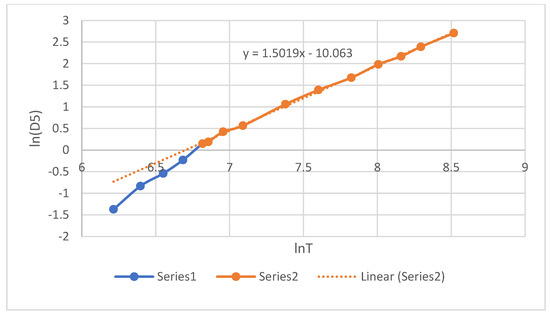
Figure 5.
Self-diffusion coefficients of Pu. EAM potential. 1—supercooling region, 2—normal liquid.
Equations of this type are well satisfied for liquid metals, but the exponent at T is usually close to 2.0 (2.0047 for Rb, 2.2109 for Cu, 1.7411 for Tl, etc.). For example, in the case of liquid uranium, the expression D = 5.17 × 10−12 T2.1029 cm2/s was obtained [16].
The graph in Figure 5 shows that, upon transition into the supercooling region (T < 913 K), the coefficient D begins to deviate downwards from expression (10). The models seem to sense that they have entered the supercooling region. In the theory of simple liquids, sensitivity of this kind is not expected, since the models are actually one-component. Analysis of the structure of the models revealed only a gradual decrease in the coordination number upon heating from 13.33 at 500 K to 10.64 at 5000 K. In this case, the coordinate of the first peak shifts from 3.14 to 3.12 Å.
Analysis of the distributions of Voronoi polyhedra at 500 K shows no signs of crystallization, but the number of most common polyhedra grows almost 3 times with respect to that of 950 K. It seems that the Pu model predicts an amorphous state at T < 500 K.
This data can be compared with the diffusion characteristics of hard-sphere liquids. The effective diameter σ of a hard sphere can be found from the condition that the packing fraction of a hard-sphere system (HSS) γ near the melting point of liquid metals is ~0.45. For Pu at 913 K, the condition γ = (N/V) (πσ3/6) = 0.45 yields σ = 2.75 Å. This value is slightly smaller than the usual atomic diameter of Pu (3.02 Å). In the case of liquid Si and Ge, the interparticle potential is indeed close to the hard-sphere potential with a step down [23]. This allows us to check the applicability of the formula for the self-diffusion coefficient of the hard-sphere model [24]:
where n = (N/V) σ3, N is the number of particles in volume V, σ is the effective diameter of the sphere, m is its mass, and D0 = (3/8) σ(kT/πm)1/2. Multiplying the numerator and denominator of the fraction in the brackets by Avogadro’s number, one obtains the following at T = 913 K: σ = 2.75 Å, N/V = 0.041354 at/Å3, n = 0.8591, D0 = (3/8) 2.279 × 10− × (8.314 × 107 × 913/π/243.06)1/2 = 1.028 × 10−4 cm2/s, and, finally, DHS = 2.13 × 10−5 cm2/s. This value is in poor agreement with the figure of 1.16 × 10−5 obtained by the MD method. The reason is that, unlike Si and Ge, the pair contribution to the interparticle potential of Pu (Figure 3) differs significantly from the hard-sphere one. The value of D found by the MEAM method (2.3 × 10−6 cm2/s at 913 K [8]) is obviously greatly underestimated.
DHS = (D0/n) (1 − n/1.09) (1 + n2(0.4 − 0.83 n2)),
Table 7 presents the literature data on the self-diffusion of liquid Pu obtained theoretically in comparison with our calculations. MEAM data [8] are much lower than ours. Quantum-mechanical-based calculations, in terms of both quantum molecular dynamics (QMD) and orbital-free molecular dynamics (OFMD), were carried out in [9] using the VASP package. These data are overestimated in relation to ours by about 1.5 times but, upon heating, the difference between them decreases and, at 2500 K, consists of only 4%.
It was difficult to calculate the viscosity of liquid Pu using the Green–Kubo equations [25] due to the large scatter of results. However, the steady-state flow method can be used [26]. If an external force of the form:
acting on each atom is included in the molecular dynamics model located in the main cube with periodic boundary conditions, then a steady-state double flow of liquid along the z axis should arise in the model, and the velocity profile should also have the form vz = v0 sin(2πx/L). The solution to the hydrodynamic problem has the form [26]:
Fz = F0sin(2πx/L),
Here η is the dynamic viscosity of the liquid, N/V is the particle number density, L is the edge length of the main cube, and F0 and v0 are defined above. In our case, with a model size of 2048 atoms in the main cube with periodic boundary conditions, a steady-state laminar flow should arise along the z axis at coordinates 0 < x < L/2 and in the opposite direction at L/2 < x < L. For verification, the main cube was conditionally divided into 10 sections with coordinates 0 < x < 0.1L, 0.1L < x < 0.2L, etc., and, in each section, the average value of the projection of the velocity of atoms <vz> in the MD run was determined. If the force F0 had an order of magnitude of 0.01 eV/Å, then the profile of the average velocity <vz> in z direction had the form of a sinusoid. An example of the distribution of velocities vz for the case with F0 = 0.01 eV/Å is given below:
Layer number: 1 2 3 4 5 6 7 8 9 10
1000<vz>, Å/Δt: 2.6 4.3 6.5 5.7 2.8 −2.8 −7.0 −5.9 −4.4 −1.9
Here Δt is the MD time step: Δt = 0.01t0. Indeed, the dependence of vz on x has a sinusoidal shape. When the external force was reduced to F0 = 0.002 eV/Å, the velocity profile became chaotic. The MD program calculated the average value of the particle velocity projection <vz> with coordinates 0 < x < L/2 and found the viscosity η using formula (13), considering that, for a sinusoidal profile, the value v0 = (π/2) <vz>. Typically, the viscosity was calculated on 10–15 MD runs with 5000 steps each. The standard deviation of the viscosity value from the average was ~9%. With the specified modeling parameters, there is no noticeable heating of the model with normal temperature control, and the pressure remains acceptable in value, with fluctuations of about 0.01 GPa.
The steady-flow method was used to calculate the dynamic viscosity of Pu at temperatures up to 5000 K (see Table 7). Our data are in good agreement with measurements [12,13] near melting point but decrease with further heating more slowly than the calculations in [9,10,11]. The values of Pu viscosity at temperatures up to 5000 K are shown in Figure 6. The graph also shows the viscosity values in the supercooled state (T < 913 K).
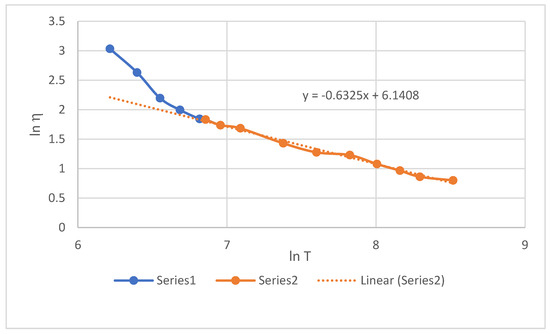
Figure 6.
Dynamic viscosity of Pu in the range 500–5000 K. Markers—viscosity of liquid Pu (see Equation (14)). 1—supercooling interval, 2—normal liquid.
At temperatures of 913–5000 K, the viscosity can be described by an expression like the formula for the self-diffusion coefficient (10):
Ln η, mPa·s = −0.6325lnT + 6.1408, or η, mPa·s = 464.4·T−0.6325
The viscosity of supercooled metal, like self-diffusion, is sensitive to entering the supercooling region.
The MD calculations with the EAM potential can be assessed using the Stokes–Einstein equation, which relates the self-diffusion coefficient D to the viscosity η. It is usually valid for simple liquids [27,28,29,30], including liquid metals:
Here ra denotes the effective hard-sphere radius of the atom. Taking D = 1.16·10−5 cm2/s and ra = σ/2 = 1.375·10−8 cm, we find an estimate of the viscosity of Pu at the melting point: η = 6.30 mPa·s. This value coincides well with the viscosity of Pu of 6.30 mPa·s, measured near the melting point [10,12,13,14].
If the Formula (14) is valid, the relation Dη/T = const should be satisfied. Using the results for the values of D and η obtained in the simulation with the EAM potential, the dependence of the values Dη/T on temperature can be calculated. They are given in Table 7 (the values of Z1 = 1010Dη/T in units of g·cm/(s2K)). The values of Dη/T depend rather weakly on temperature, so that the Stokes–Einstein relation (14) is fulfilled quite well for liquid Pu in the entire range of 913–5000 K.
In the work [30], a correction to the Stokes–Einstein equation is proposed, in which this equation takes the form DηV1/3/T = const, where V is the volume [9]. The values of Z2 = Z1(V/V913)1/3 are also given in Table 7. For Pu, Z2 = 7.31 ± 0.52, i.e., the deviations do not exceed 7%, and the Stokes–Einstein equation with this correction is fulfilled very well. In theoretical calculations, an underestimation of viscosity is observed at elevated temperatures [9,11].
Additional information about liquid Pu is provided by calculating its surface properties. It is possible to calculate the excess surface energy of nanoclusters (not surface tension!) by constructing a series of them with different sizes. Following the standard approach [31], one can write the energy of a spherical nanoparticle of radius R as:
where N is the number of atoms in the cluster. Here bN2/3 is considered generally as the excess surface energy. Dividing it by the surface area, we obtain the specific surface energy σE = bN2/3/4πR2. The number of atoms in a spherical drop is (4/3) πR3/v0, where v0 = Vmol/NA (Vmol is the molar volume and NA is Avogadro’s number). Hence, σE = (4π/3)2/3(1/4π) b/v02/3.
E = aN + bN2/3, or E/N = a + bN−1/3
To calculate the values σE, a series of Mackay icosahedral Pu nanoclusters with a free surface and particle numbers of 13, 55, 147, 309, 561, 923, 1415, and 2869 were constructed and simulated at 950 K. Their energies are shown in Figure 7. The value at N → ∞ (−3.2919 eV/atom) was obtained by conventional modeling of liquid Pu. For all N > 13 the graph is perfectly straightened, and b = 5.8155 eV/at2/3. Considering that, at 950 K, Vmol = 14.60 cm3/mol, we obtain as a result σE = 2.30 J/m2. This value is much greater than the real surface tension of ~0.55 J/m2 [14]. It means that the term bN2/3 is not only the common excess surface energy but also contains contributions from the bulk nanoparticle atoms.
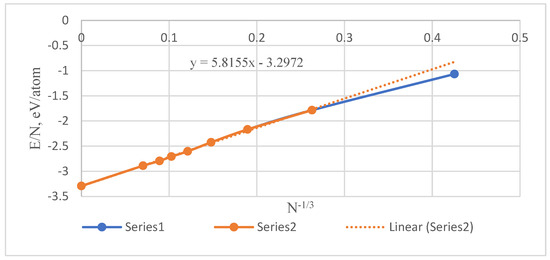
Figure 7.
Energy of Pu nanoclusters at 950 K with 13–2869 particles.
4. Discussion
This paper presents an attempt to construct a model of liquid metal based solely on its pair correlation function (PCF) and density. Analysis of the topological characteristics of liquid metal allowed us to determine the extent to which this PCF can correspond to the structure of a real liquid.
The procedure for calculating the pair potential using the Schommers algorithm is stable and allows us to confidently reconstruct the interparticle potential via the shape of the PCF. In the case of Pu, a testing potential was previously discovered at which the expansion coefficient of liquid metal turned out to be abnormally low, an order of magnitude less than the usual values. This potential was calculated using the Schommers algorithm and the original PCF Pu obtained in [8]. For example, in calculations with this potential in the NpT ensemble, the densities of the liquid at temperatures of 950 and 2000 K were equal to 16.543 and 16.514 g/cm3, respectively, i.e., the coefficient of volume expansion α was very low. For real Pu in this range, the coefficient α = 6.18·10−5 K−1, i.e., 40 times greater.
The Pu potential obtained using the structure of liquid aluminum turned out to be more accurate. Several properties of Pu models—density, heat capacity, and compressibility—showed a rather weak dependence on temperature. With heating to 5000 K, only a small increase in Cp to ~30 J/mol/K is observed. This agrees with the data of [5], where the heat capacity of real liquid Pu does not depend on temperature at all. Consequently, the small excess heat capacity of the Pu models (in relation to the classical value 3R) is due to the shape of the potential, and the high heat capacity of real Pu is due to the internal degrees of freedom of the atoms. The contribution from the conduction electrons is apparently small, since their heat capacity would be visible over a wide temperature range. The calculated heat capacity ratios Cp/Cv (Table 6) are in good agreement with the experimental data [7].
Three important properties of liquid metal—density, diffusion rate, and viscosity—deviate from high-temperature trends in the same low-temperature ranges. Using the EAM potential, it was possible to calculate the values of the self-diffusion coefficients in the entire range from 500 to 5000 K. It should be noted that the order of magnitude of Pu self-diffusion coefficients is typical for metals (D ~10−5 cm2/s near the melting point). Theoretical calculations [8,9] do not agree with our results. The temperature dependence D(T) at T > Tm is well approximated by the expression D = aTb, which follows from the Swalin theory [32]. Arrhenius-type dependences do not reflect the physical picture here, since the act of diffusion in simple liquids does not require activation.
The results of calculations of the dynamic viscosity of Pu by the laminar flow method look promising [26]. Here, good agreement with experiment was obtained for temperatures near Tm [12,13]. In the supercooling region, the viscosity increases to ~20 mPa·s, i.e., an order of magnitude higher than the usual value for liquid metals. Real Pu behaves as a fairly viscous liquid. Liquid Pu models are also rather viscous and, in addition, are prone to strong supercooling, so they easily retain the properties of a liquid even when supercooled by 400 K. At temperatures above Tm, the Stokes–Einstein relation (15) with a correction [30] is quite well satisfied. The behavior of self-diffusion coefficient and viscosity at temperatures below the melting point is noteworthy. These properties seem to indicate the fact of transition to a supercooling state, although the theory of simple liquids does not give special importance to entering a two-phase region in the actual absence of a second phase. It seems quite probable that characteristic structure changes, such as signs of dimerization, could appear in the supercooling region of real Pu and its models. However, the pair correlation functions of the Pu models at 500–913 K do not show any special deviations from the normal form. As an example, one can cite the PCF of supercooled Pu at 500 K (see Figure 8).
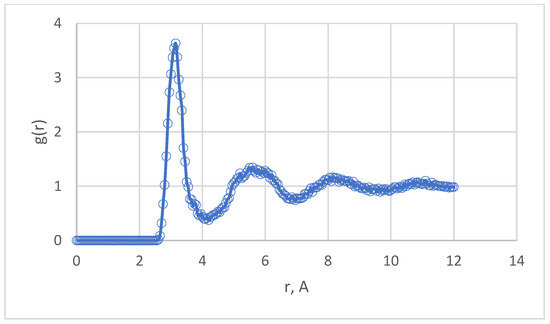
Figure 8.
PCF of supercooled Pu model at 500 K.
This graph has a form typical of liquid metals, and the sign of supercooling is only the increased height of the first peak, equal to 3.63.
5. Conclusions
Analysis of the properties of real Pu and its models shows that the models with the EAM potential constructed in this work adequately describe some important properties of real Pu. A reasonable agreement is obtained (see Table 5 and Table 7) for bulk module [7], self-diffusion [9], and viscosity [12,13], albeit not at all temperatures. This EAM potential may be applied for the investigation of the amorphous metal as well as to highly dispersed states.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
I deeply thank Alexander Landa, Michael Baskes, and Leonid Burakovsky for their very helpful advice.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Baskes, M.I. Atomistic model of plutonium. Phys. Rev. B 2000, 62, 15532–15537. [Google Scholar] [CrossRef]
- Olsen, C.E.; Sandenaw, T.A.; Herrick, C.C. The Density of Liquid Plutonium Metal; LA-2358; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1959. [CrossRef][Green Version]
- Wittenberg, L.J.; Ofte, D.; Rohr, W.G.; Rigney, D.V. Density and viscosity of liquid Pu-U alloys. Met. Trans. 1971, 2, 287–290. [Google Scholar] [CrossRef]
- Filiand, M.A.; Semenova, E.I. The Properties of Rare Elements; Handbook. Ed.; Metallurgy: Moscow, Russia, 1964. (In Russian) [Google Scholar][Green Version]
- Mulford, R.N.R. Thermodynamic Functions for Pure Plutonium; LA-2813; Chemistry Tid-4500; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1963.[Green Version]
- Chirkin, V.C. Thermophysical Properties of Materials in Nuclear Technology; Atomizdat: Moscow, Russia, 1968. (In Russian) [Google Scholar][Green Version]
- Boivineau, M. What’s new on plutonium up to 4000 K? J. Nucl. Mater. 2001, 297, 97–106. [Google Scholar] [CrossRef]
- Cherne, F.J.; Baskes, M.I.; Holian, B.L. Predicted transport properties of liquid plutonium. Phys. Rev. B 2003, 67, 092104. [Google Scholar] [CrossRef]
- Kress, J.D.; Cohen, J.S.; Kilcrease, D.P.; Horner, D.A.; Collins, L.A. Quantum molecular dynamics simulations of transport properties in liquid and dense-plasma plutonium. Phys. Rev. E 2011, 83, 026404. [Google Scholar] [CrossRef]
- Ofte, D.; Wittenberg, L.J. Viscosity-Composition Relationship in Molten Plutonium-Iron Alloys. Trans. Am. Soc. Met. 1964, 57, 916. [Google Scholar]
- Postovalov, V.G.; Romanov, E.P.; Kondrat’ev, V.P.; Kononenko, V.I. Theory of Transport in Liquid Metals: Calculation of Dynamic Viscosity. High Temp. 2003, 41, 762–770. [Google Scholar] [CrossRef]
- Jones, L.V.; Ofte, D.; Rohr, W.G.; Wittenberg, L.J. The Viscosity and Density of molten Plutonium Metal and a Plutonium-Cerium-Cobalt Eutectic Alloy. Trans. Am. Soc. Met. 1962, 55, 819. [Google Scholar]
- Ofte, D.; Rohr, W.G. Viscosity, density, and liquidus temperature of molten Pu-1 wt. % Ga alloy. J. Nucl. Mater. 1965, 15, 231–233. [Google Scholar] [CrossRef]
- Rohr, W.G. Liquid Plutonium—A Review of its Physical Properties. Nucl. Appl. 1967, 3, 550–555. [Google Scholar] [CrossRef]
- Wittenberg, L.J. A Model for Liquid Uranium and Plutonium with Implications on the Adjacent Solid Phases. In Plutonium 1975 and Other Actinides: Proceedings of the 5th International Conference on Plutonium and Other Actinides; Blank, H., Linder, R., Eds.; North Holland Publisher: Baden-Baden, Germany, 1976; p. 71. [Google Scholar][Green Version]
- Belashchenko, D.K.; Smirnova, D.E.; Ostrovski, O.I. Molecular-dynamic simulation of the thermophysical properties of liquid uranium. High Temp. 2010, 48, 363–375. [Google Scholar] [CrossRef]
- Belashchenko, D.K. Liquid Metals: From Atomistic Potentials to Properties, Shock Compression, Earth’ Core and Nanoclusters; NOVA: New York, NY, USA, 2018; ISBN 978-1-53613-140-6. [Google Scholar][Green Version]
- Schommers, W. Pair potentials in disordered many-particle systems: A study for liquid gallium. Phys. Rev. A 1983, 28, 3599–3605. [Google Scholar] [CrossRef]
- Waseda, Y. The Structure of Non-Crystalline Materials: Liquids and Amorphous Solids; McGraw-Hill: New York, NY, USA, 1980; 325p, ISBN 9780070684263/007068426X. [Google Scholar][Green Version]
- Belashchenko, D.K. Metals. Metally 1989, 3, 136. (In Russian) [Google Scholar]
- Doyama, M.; Kogure, Y. Embedded atom potentials in fcc and bcc metals. Comput. Mater. Sci. 1999, 14, 80–83. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Belashchenko, D.K. Applicability of Embedded Atom Model (EAM) Potentials to Liquid Silicon and Germanium. Russ. J. Phys. Chem. A 2024, 98, 3172–3184. [Google Scholar] [CrossRef]
- Speedy, R.J. Diffusion in the hard sphere fluid. Mol. Phys. 1987, 62, 509–515. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids; Elsevier: Cambridge, MA, USA, 2006; ISBN 978-0-12-387032-2. [Google Scholar][Green Version]
- Gosling, E.M.; McDonald, I.; Singer, K. On the calculation by molecular dynamics of the shear viscosity of a simple fluid. Mol. Phys. 2006, 26, 1475–1484. [Google Scholar] [CrossRef]
- Sigurgeirsson, H.; Heyes, D.M. Transport coefficients of hard sphere fluids. Mol. Phys. 2009, 101, 469–482. [Google Scholar] [CrossRef]
- Cappelezzo, M.; Capellari, C.A.; Pezzin, S.H.; Coelho, L.A.F. Stokes-Einstein relation for pure simple fluids. J. Chem. Phys. 2007, 126, 224516. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, W. LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. J. Comput. Educ. 1905, 9, 781–785. [Google Scholar] [CrossRef]
- Zwanzig, R. On the relation between self-diffusion and viscosity of liquids. J. Chem. Phys. 1983, 79, 4507–4508. [Google Scholar] [CrossRef]
- Belashchenko, D.K. On the Geometry and Thermodynamics of Nanoclusters. Russ. J. Phys. Chem. 2015, 89, 516. [Google Scholar] [CrossRef]
- Swalin, R.A. On the theory of self-diffusion in liquid metals. Acta Met. 1959, 7, 736–740. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).