Optimal Operating Patterns for the Energy Management of PEMFC-Based Micro-CHP Systems in European Single-Family Houses
Abstract
1. Introduction
- An optimal EMS is designed.
- The parameters of the optimal EMS are adjusted (determination of the prediction horizon).
- The economic performance of the optimal EMS is evaluated in 46 scenarios belonging to the European framework, and it is compared with those achieved by four typical rule-based EMSs.
- The behavior of the optimal EMS is investigated in order to identify optimal operating patterns.
- Whether or not the results of Hawkes et al. [17] will be the same for a PEMFC-based system.
- If their conclusions remain valid for a wider energy price range, which is what exists in Europe.
- What effect stack degradation has on the optimal EMS behavior.
2. Methods
2.1. Design of the Optimal EMS
- Acquires process state information (demands, TES state of charge (SOC), prices, etc.).
- Acquires a prediction of the energy demand profiles for a given time horizon.
- Calculates the sequence of control action values that minimize the operating cost of the micro-CHP system within the prediction horizon.
- Applies the values of instant k and returns to step 1.
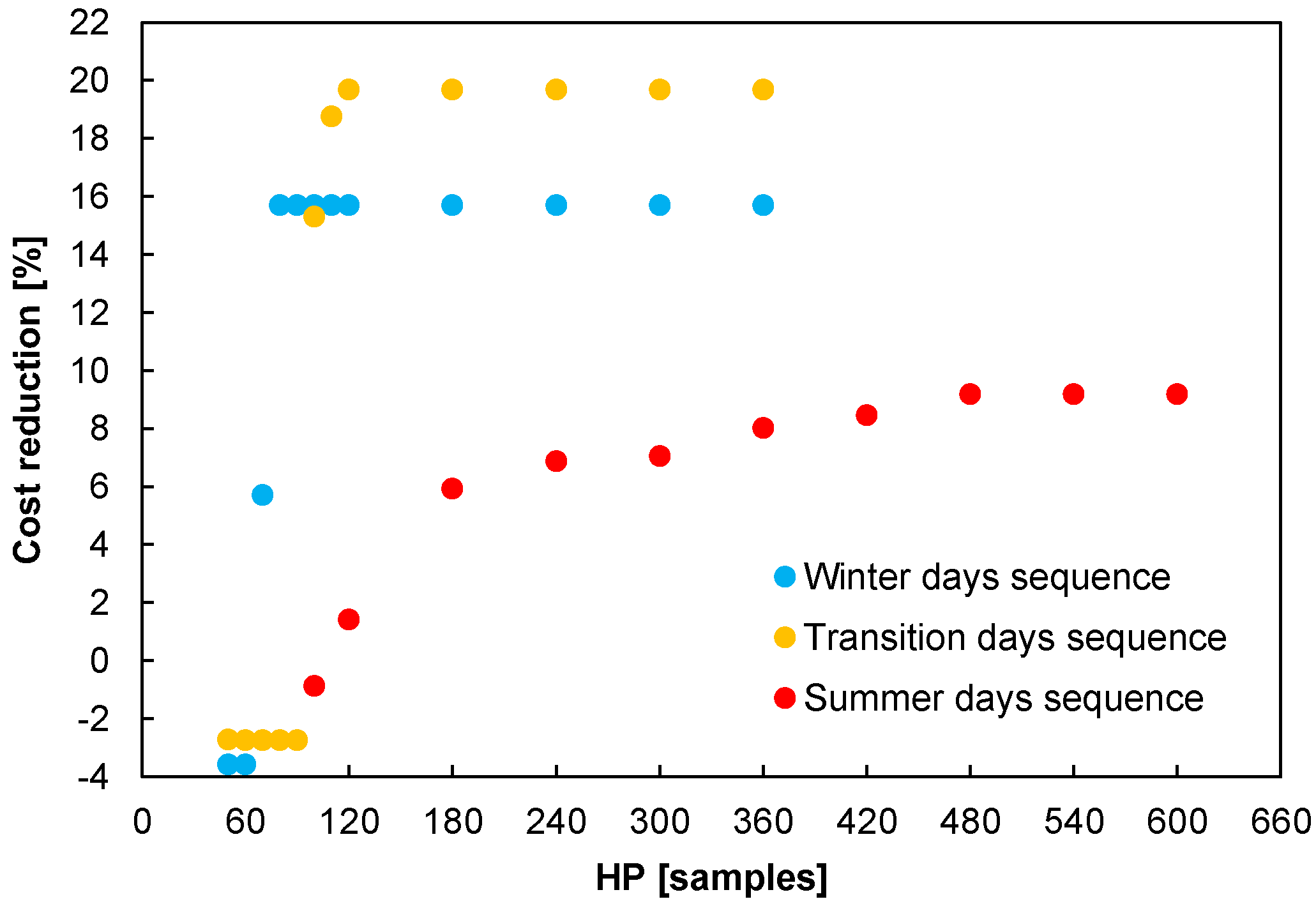
2.2. Determination of the Prediction Horizon
3. Results
3.1. Evaluation of the Economic Performance of the Optimal EMS
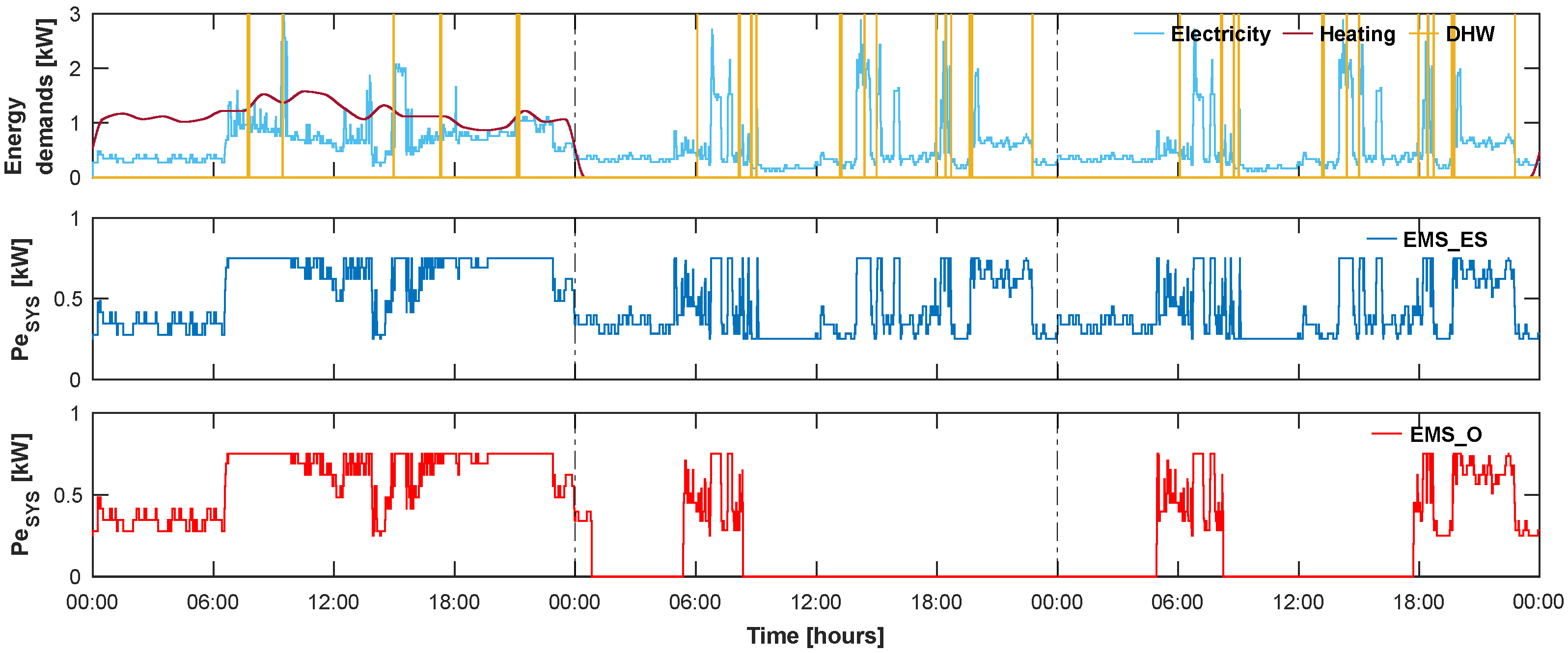
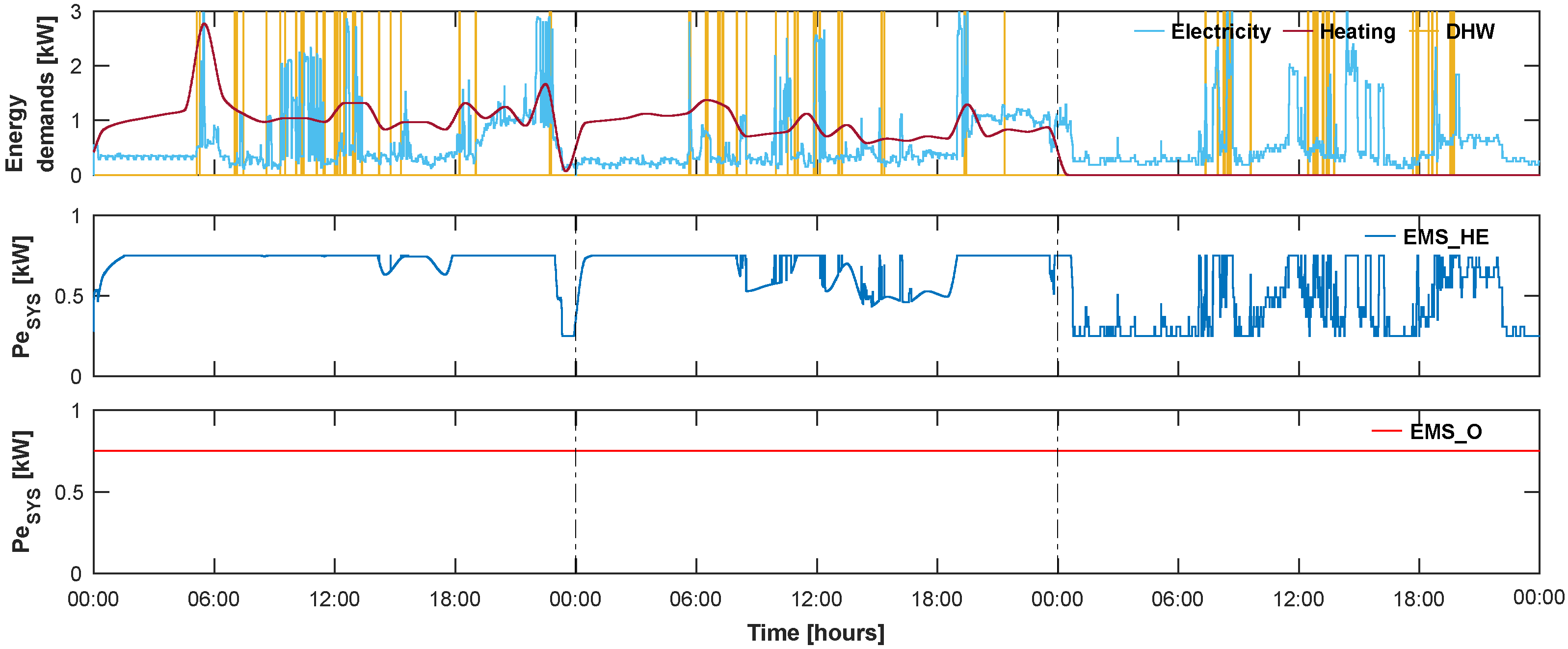
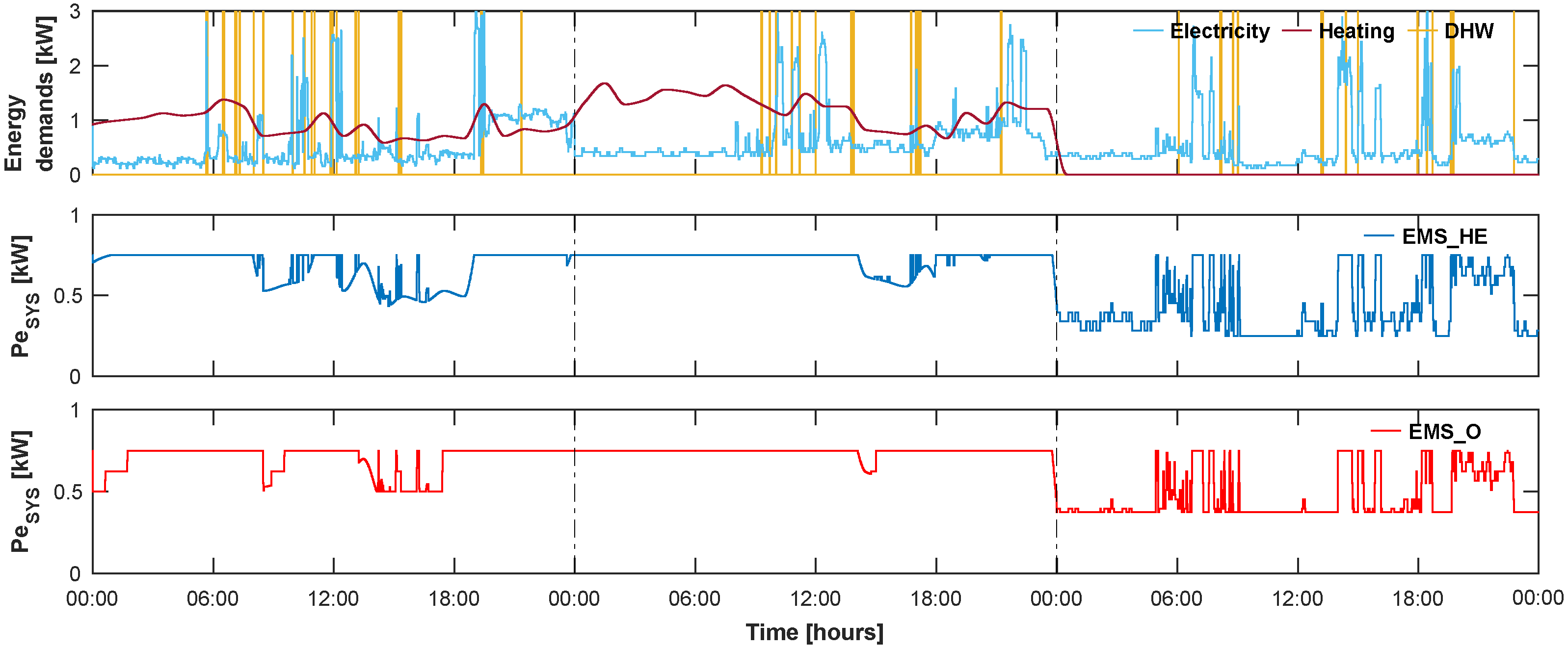
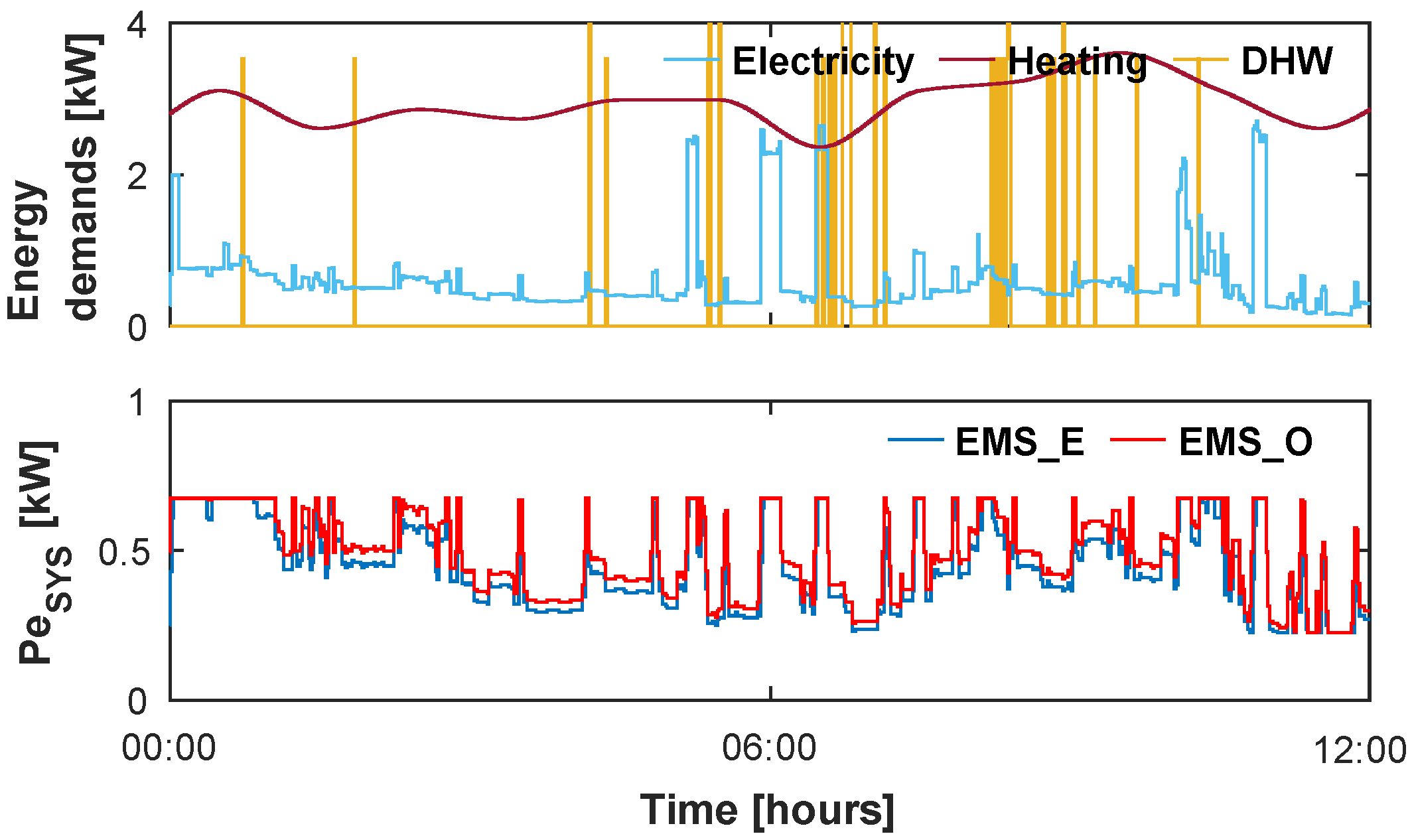
3.2. Investigation of the Behavior of the Optimal EMS
- Following the electricity demand.
- Following the greater of the demands, electricity and heat.
- Turning off the micro-CHP system.
- Setting the micro-CHP system to maximum power.
- Other behaviors that are similar but not identical to 1 or 2.
4. Discussion
4.1. Economic Performance of the Optimal EMS
4.2. Behavior of the Optimal EMS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit | |
| Objective function | |||
| F | Micro-CHP system operating cost. | EUR | |
| Decision variables | |||
| Piecewise electrical output, segment n, . | kW | ||
| Segment n state, , . | - | ||
| Auxiliary boiler set point. | kW | ||
| Heat dumping system set point. | kW | ||
| Electricity bought from the grid. | kW | ||
| Electricity sold to the grid. | kW | ||
| Electricity buy/sell state, . | - | ||
| Micro-CHP system startup cost. | EUR | ||
| Micro-CHP system shutdown cost. | EUR | ||
| Other variables | |||
| Micro-CHP system set point. | kW | ||
| Electricity generated by the micro-CHP system. | kW | ||
| Micro-CHP system on/off. | - | ||
| Hot water tank state of charge. | % | ||
| Electricity demand. | kW | ||
| Thermal energy demand (heating and DHW). | kW | ||
| Heating demand. | kW | ||
| Domestic hot water demand. | kW | ||
| Constants | |||
| Prediction horizon. | samples | ||
| Sample time. | min | ||
| Natural gas price. | EUR/kWh | ||
| Electricity price. | EUR/kWh | ||
| Feed-in tariff price. | EUR/kWh | ||
| Micro-CHP system nominal electrical efficiency. | - | ||
| D | Stack degradation level. | - | |
| Auxiliary boiler thermal efficiency. | - | ||
| Heat dumping system coefficient. | - | ||
| Minimum SOC. | % | ||
| Maximum SOC. | % | ||
| Micro-CHP system startup time. | min | ||
| Maximum electricity bought. | kW | ||
| Maximum electricity sold. | kW | ||
| Micro-CHP system startup cost. | EUR | ||
| Micro-CHP system shutdown cost. | EUR | ||
| Micro-CHP system ramp up limit. | kW/min | ||
| Micro-CHP system ramp down limit. | kW/min | ||
| Auxiliary boiler minimum power. | kW | ||
| Auxiliary boiler maximum power. | kW | ||
| Heat dumping system minimum power. | kW | ||
| Heat dumping system maximum power. | kW | ||
| Other symbols and abbreviations | |||
| Domestic hot water | - | ||
| Percentage points | - | ||
| Best rule-based | - | ||
| a 0: not fully dispatched; 1: fully dispatched. b 0: buy; 1: sell. | |||
Appendix A. Linearization

References
- Dodds, P.E.; Staffell, I.; Hawkes, A.D.; Li, F.; Grünewald, P.; McDowall, W.; Ekins, P. Hydrogen and fuel cell technologies for heating: A review. Int. J. Hydrogen Energy 2015, 40, 2065–2083. [Google Scholar] [CrossRef]
- van der Spek, M.; Banet, C.; Bauer, C.; Gabrielli, P.; Goldthorpe, W.; Mazzotti, M.; Munkejord, S.T.; Røkke, N.A.; Shah, N.; Sunny, N.; et al. Perspective on the hydrogen economy as a pathway to reach net-zero CO2 emissions in Europe. Energy Environ. Sci. 2022, 15, 1034–1077. [Google Scholar] [CrossRef]
- Staffell, I.; Scamman, D.; Abad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef]
- Li, Q.; Hao, Y.; Sun, L. Modeling and evaluation of a steam and power cogeneration system of proton exchange membrane fuel cell coupled high temperature heat pump. Chem. Eng. J. 2025, 505, 159432. [Google Scholar] [CrossRef]
- European Commission Recognises Fuel Cells as a Strategic Net-Zero Technology. News Dated March 17, 2023. PACE. Available online: https://pace-energy.eu/fuel-cells-net-zero-technology/ (accessed on 16 December 2024).
- PACE: Pathway to a Competitive European Fuel Cell Micro-Cogeneration Market. Available online: https://pace-energy.eu/ (accessed on 10 January 2025).
- Korteweg, H. The Bridge to Large Scale Market Uptake. European-Wide Field Trials for Residential Fuel Cell Micro-Cogeneration. PACE: Pathway to a Competitive European Fuel Cell Micro-Cogeneration Market. Presentation Given on 26 April 2023. Available online: https://pace-energy.eu/what-role-for-fuel-cell-micro-chp-in-europes-future-energy-system/ (accessed on 10 January 2025).
- Adam, A.; Fraga, E.S.; Brett, D.J. A modelling study for the integration of a PEMFC micro-CHP in domestic building services design. Appl. Energy 2018, 225, 85–97. [Google Scholar] [CrossRef]
- Ang, S.M.C.; Fraga, E.S.; Brandon, N.P.; Samsatli, N.J.; Brett, D.J. Fuel cell systems optimization—Methods and strategies. Int. J. Hydrogen Energy 2011, 36, 14678–14703. [Google Scholar] [CrossRef]
- Staffell, I. Fuel Cells for Domestic Heat and Power: Are They Worth It? Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2010. [Google Scholar]
- 6154104 GB 4/2020; Viessmann. Product Data sheet. Vitovalor PT2. Micro CHP Unit on Fuel Cell Basis with Integral Gas Condensing Boiler. Viessmann Werke GmbH & Co. KG, D-35107: Allendorf, Germany.
- Staffell, I.; Green, R.; Kendall, K. Cost targets for domestic fuel cell CHP. J. Power Sources 2008, 181, 339–349. [Google Scholar] [CrossRef]
- Ito, H. Economic and environmental assessment of residential micro combined heat and power system application in Japan. Int. J. Hydrogen Energy 2016, 41, 15111–15123. [Google Scholar] [CrossRef]
- Löbberding, L.; Madlener, R. Techno-economic analysis of micro fuel cell cogeneration and storage in Germany. Appl. Energy 2019, 235, 1603–1613. [Google Scholar] [CrossRef]
- Navarro, S.; Herrero, J.M.; Blasco, X.; Pajares, A. Rule-based energy management strategies for PEMFC-based micro-CHP systems: A comparative analysis. Heliyon 2024, 10, e37685. [Google Scholar] [CrossRef] [PubMed]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Model Predictive Control of Microgrids; Springer Nature: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-24569-6. [Google Scholar]
- Hawkes, A.D.; Leach, M.A. Cost-effective operating strategy for residential micro-combined heat and power. Energy 2007, 32, 711–723. [Google Scholar] [CrossRef]
- Houwing, M.; Negenborn, R.R.; De Schutter, B. Demand Response with Micro-CHP Systems; IEEE: Piscataway, NJ, USA, 2011; Volume 99, pp. 200–213. [Google Scholar] [CrossRef]
- Hawkes, A.D.; Brett, D.J.L.; Brandon, N.P. Fuel cell micro-CHP techno-economics: Part 1—model concept and formulation. Int. J. Hydrogen Energy 2009, 34, 9545–9557. [Google Scholar] [CrossRef]
- Shaneb, O.A.; Taylor, P.C.; Coates, G. Optimal online operation of residential μCHP systems using linear programming. Energy Build. 2012, 44, 17–25. [Google Scholar] [CrossRef]
- Ren, H.; Gao, W. Economic and environmental evaluation of micro CHP systems with different operating modes for residential buildings in Japan. Energy Build. 2010, 42, 853–861. [Google Scholar] [CrossRef]
- Alahäivälä, A.; Heß, T.; Cao, S.; Lehtonen, M. Analyzing the optimal coordination of a residential micro-CHP system with a power sink. Appl. Energy 2015, 149, 326–337. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mohammadi, M. Optimization of the micro combined heat and power systems considering objective functions, components and operation strategies by an integrated approach. Energy Convers. Manag. 2020, 208, 112610. [Google Scholar] [CrossRef]
- Oh, S.D.; Kim, K.Y.; Oh, S.B.; Kwak, H.Y. Optimal operation of a 1-kW PEMFC-based CHP system for residential applications. Appl. Energy 2012, 95, 93–101. [Google Scholar] [CrossRef]
- Ozawa, A.; Kudoh, Y. Performance of residential fuel-cell-combined heat and power systems for various household types in Japan. Int. J. Hydrogen Energy 2018, 43, 15412–15422. [Google Scholar] [CrossRef]
- Hawkes, A.D.; Aguiar, P.; Hernandez-Aramburo, C.A.; Leach, M.A.; Brandon, N.P.; Green, T.C.; Adjiman, C.S. Techno-economic modelling of a solid oxide fuel cell stack for micro combined heat and power. J. Power Sources 2006, 156, 321–333. [Google Scholar] [CrossRef]
- Ren, H.; Gao, W.; Ruan, Y. Optimal sizing for residential CHP system. Appl. Therm. Eng. 2008, 28, 514–523. [Google Scholar] [CrossRef]
- VDI. Referenzlastprofile von Ein- und Mehrfamilienhäusern für den Einsatz von KWK-Anlagen: [Eng: Reference load Profiles of Single-Family and Multi-Family Houses for the Use of CHP Systems]; 27.100, 91.140.10(4655); Beuth Verlag: Düsseldorf, Germany, 2008. [Google Scholar]
- Sánchez, E.P.P. Desarrollo de un Sistema de Gestión de Energía Eléctrica y Térmica en Viviendas Unifamiliares (Micro-CHP) con Pilas de Combustible. Master’s Thesis, Universitat Politècnica de València, Valencia, Spain, 2019. Available online: http://hdl.handle.net/10251/129431 (accessed on 11 May 2025).



| Hawkes et al. [17] a | Hawkes et al. [19] | Houwing et al. [18] | Ren et al. [21] b | Shaneb et al. [20] | This study | |
|---|---|---|---|---|---|---|
| Micro-CHP system technology | SOFC | PEMFC | PEMFC | PEMFC | PEMFC | PEMFC |
| Gas engine | Gas engine | |||||
| Stirling engine | ||||||
| Stack degradation | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| Auxiliary energy losses | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ |
| Heat losses in the TES | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ |
| Part-load electrical efficiency | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ |
| TES charge and discharge efficiencies | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| Micro-CHP ramp constraints | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ |
| Startup and shutdown times | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| Startup and shutdown costs | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| Heat dumping cost | ✗ | ✗ | ✗ | ✓ | ||
| Optimization problem formulation | NLP e | MILP | MILP | MILP | MILP | |
| Optimization horizon | 1 day | 1 day | 1 day | 1 day | 1 day | 8 h |
| Demand profiles resolution | 5 min | 5 min | 15 min | 1 h | 1 h | 1 min |
| Time period studied | Annual | Annual/lifetime | Annual | Annual | Annual | Annual |
| Demand profiles representativeness | Indicative of UK average residential demand | One large UK dwelling in north London | Indicative of NL average residential demand | One single-family house in Kitakyushu, Japan | One dwelling in North West of London | Reference load profiles according to VDI Guide- line 4655 |
| Simulation approach | Unk. | Sample day profiles | Complete annual profiles | Unk. | Complete annual profiles | Complete annual profiles |
| Number of parameters studied | 2 | 5 | 1 | 1 | 4 | 5 |
| Parameters whose influence is studied | Energy prices | Start/stop costs | Electricity tariff structures | Micro-CHP technology | FiT | Energy prices |
| FiT | Ramp limits | Government incentives | FiT | |||
| Maximum turndown | Carbon tax | Stack degradation | ||||
| Minimum up-time | PEMFC nominal power | Climate zone | ||||
| Stack degradation | HPR demand side | |||||
| Number of scenarios evaluated | 15 | 6 | 3 | 2 | 60 | 46 |
| Number of EMSs compared | 3 | 1 | 2 | 2 | 3 | 5 |
| EMSs compared | Heat-led | Optimal strategy | Heat-led | Minimum CO2 operation | Heat-led | Heat-led |
| Electricity-led | Optimal strategy | Optimal strategy | Electricity-led | Electricity-led | ||
| Optimal strategy | Optimal strategy | Heat-and-electricity-led | ||||
| Electricity-led switch off in summer | ||||||
| Optimal strategy |
| Characteristic | Value |
|---|---|
| Nominal electrical power (BOL) | 0.75 kW |
| Minimum electrical power | 0.25 kW |
| Nominal thermal power (BOL) | 1.07 kW |
| Electrical efficiency (BOL) | 31.3% (HHV) |
| Thermal efficiency (BOL) | 44.7% (HHV) |
| Maximum ramp | 0.2 kW/min |
| Startup time | 45 min |
| Natural gas consumption at startup | 1.5 kW |
| Power consumption at startup | 75 W |
| Shutdown time | 5 min |
| Power consumption during shutdown | 50 W |
| Auxiliary boiler nominal thermal power | 26.5 kW |
| Auxiliary boiler efficiency | 93% |
| Tank volume | 200 L |
| Tank temperature range | 50–70 °C |
| Tank capacity | 4.572 kWh |
| Characteristic | Value |
|---|---|
| Type of building | Single-family house |
| Location | Oberhausen, Germany |
| N° of occupants | 3 |
| Annual heating demand | 11,000 kWh |
| Annual electricity demand | 5250 kWh |
| Annual DHW demand | 1500 kWh |
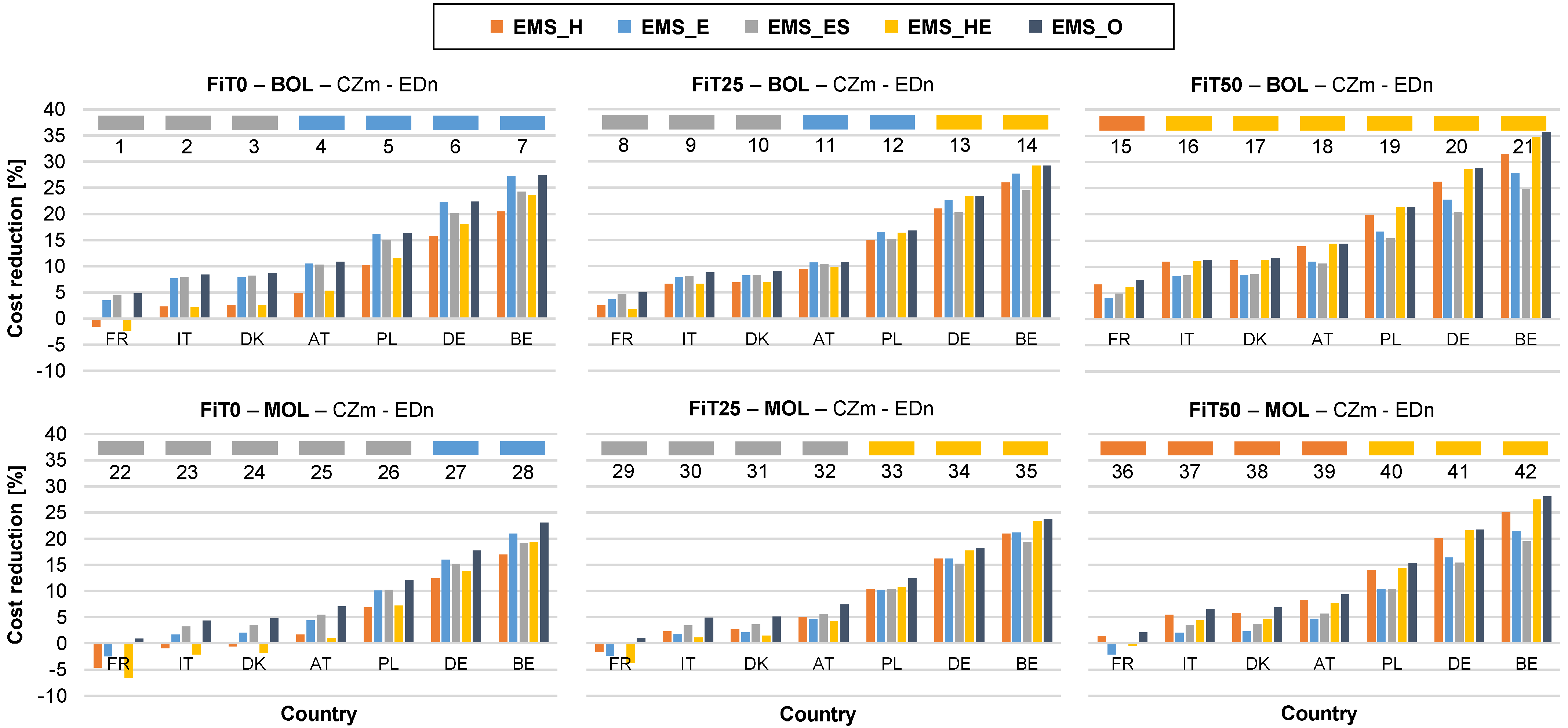
| Sce. | Ctry. | Spark Gap | FiT | D | CZ | HPR | EMS_H | EMS_E | EMS_ES | EMS_HE | EMS_O | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [ct/kWh] | [ct/kWh] | [-] | [%] | [-] | [-] | [-] | [%] | [%] | [%] | [%] | [%] | [pp] | [%] | [%] | ||
| 1 | FR | 19.33 | 6.78 | 2.85 | 0 | BOL | CZm | EDn | −1.5 | 3.5 | 4.5 | −2.3 | 4.9 | 0.4 | 5.1 | 0.3 |
| 2 | IT | 22.59 | 7.03 | 3.21 | 0 | BOL | CZm | EDn | 2.3 | 7.7 | 7.9 | 2.2 | 8.4 | 0.5 | 5.6 | 0.3 |
| 3 | DK | 29.00 | 8.95 | 3.24 | 0 | BOL | CZm | EDn | 2.6 | 7.9 | 8.2 | 2.5 | 8.7 | 0.5 | 5.2 | 0.3 |
| 4 | AT | 22.16 | 6.36 | 3.48 | 0 | BOL | CZm | EDn | 4.9 | 10.5 | 10.3 | 5.3 | 10.9 | 0.4 | 8.3 | 0.3 |
| 5 | PL | 15.48 | 3.76 | 4.12 | 0 | BOL | CZm | EDn | 10.2 | 16.2 | 15.0 | 11.5 | 16.3 | 0.1 | 5.5 | 0.3 |
| 6 | DE | 31.93 | 6.47 | 4.94 | 0 | BOL | CZm | EDn | 15.8 | 22.3 | 20.1 | 18.1 | 22.4 | 0.1 | 0.7 | 0.4 |
| 7 | BE | 27.02 | 4.68 | 5.77 | 0 | BOL | CZm | EDn | 20.5 | 27.3 | 24.3 | 23.6 | 27.5 | 0.2 | 0.7 | 0.3 |
| 8 | FR | 19.33 | 6.78 | 2.85 | 25 | BOL | CZm | EDn | 2.5 | 3.7 | 4.6 | 1.8 | 5.0 | 0.4 | 8.8 | 3.4 |
| 9 | IT | 22.59 | 7.03 | 3.21 | 25 | BOL | CZm | EDn | 6.6 | 7.9 | 8.1 | 6.6 | 8.8 | 0.7 | 8.6 | 3.8 |
| 10 | DK | 29.00 | 8.95 | 3.24 | 25 | BOL | CZm | EDn | 6.9 | 8.2 | 8.3 | 6.9 | 9.1 | 0.8 | 8.6 | 3.8 |
| 11 | AT | 22.16 | 6.36 | 3.48 | 25 | BOL | CZm | EDn | 9.4 | 10.7 | 10.4 | 9.8 | 10.7 | 0.0 | 13.5 | 3.5 |
| 12 | PL | 15.48 | 3.76 | 4.12 | 25 | BOL | CZm | EDn | 15.0 | 16.5 | 15.2 | 16.4 | 16.8 | 0.3 | 8.8 | 3.7 |
| 13 | DE | 31.93 | 6.47 | 4.94 | 25 | BOL | CZm | EDn | 21.0 | 22.6 | 20.3 | 23.4 | 23.4 | 0.0 | 1.9 | 0.5 |
| 14 | BE | 27.02 | 4.68 | 5.77 | 25 | BOL | CZm | EDn | 26.0 | 27.6 | 24.5 | 29.2 | 29.2 | 0.0 | 1.8 | 0.5 |
| 15 | FR | 19.33 | 6.78 | 2.85 | 50 | BOL | CZm | EDn | 6.6 | 3.9 | 4.8 | 6.0 | 7.4 | 0.8 | 6.4 | 0.4 |
| 16 | IT | 22.59 | 7.03 | 3.21 | 50 | BOL | CZm | EDn | 10.9 | 8.1 | 8.3 | 11.0 | 11.3 | 0.3 | 12.6 | 0.6 |
| 17 | DK | 29.00 | 8.95 | 3.24 | 50 | BOL | CZm | EDn | 11.2 | 8.4 | 8.5 | 11.3 | 11.6 | 0.3 | 12.6 | 0.5 |
| 18 | AT | 22.16 | 6.36 | 3.48 | 50 | BOL | CZm | EDn | 13.9 | 10.9 | 10.6 | 14.4 | 14.4 | 0.0 | 11.2 | 0.6 |
| 19 | PL | 15.48 | 3.76 | 4.12 | 50 | BOL | CZm | EDn | 19.9 | 16.7 | 15.4 | 21.3 | 21.4 | 0.1 | 4.4 | 1.2 |
| 20 | DE | 31.93 | 6.47 | 4.94 | 50 | BOL | CZm | EDn | 26.2 | 22.8 | 20.5 | 28.6 | 28.9 | 0.3 | 3.1 | 2.0 |
| 21 | BE | 27.02 | 4.68 | 5.77 | 50 | BOL | CZm | EDn | 31.5 | 27.9 | 24.8 | 34.8 | 35.8 | 1.0 | 11.1 | 0.0 |
| 22 | FR | 19.33 | 6.78 | 2.85 | 0 | MOL | CZm | EDn | −4.6 | −2.4 | −0.1 | −6.6 | 0.9 | 1.0 | 10.4 | 2.3 |
| 23 | IT | 22.59 | 7.03 | 3.21 | 0 | MOL | CZm | EDn | −0.9 | 1.7 | 3.2 | −2.1 | 4.4 | 1.2 | 8.9 | 2.4 |
| 24 | DK | 29.00 | 8.95 | 3.24 | 0 | MOL | CZm | EDn | −0.6 | 2.0 | 3.5 | −1.8 | 4.8 | 1.3 | 7.8 | 2.5 |
| 25 | AT | 22.16 | 6.36 | 3.48 | 0 | MOL | CZm | EDn | 1.7 | 4.4 | 5.5 | 1.0 | 7.1 | 1.6 | 6.7 | 2.5 |
| 26 | PL | 15.48 | 3.76 | 4.12 | 0 | MOL | CZm | EDn | 6.9 | 10.1 | 10.2 | 7.2 | 12.1 | 1.9 | 7.5 | 2.7 |
| 27 | DE | 31.93 | 6.47 | 4.94 | 0 | MOL | CZm | EDn | 12.4 | 16.0 | 15.1 | 13.8 | 17.7 | 1.7 | 5.8 | 3.1 |
| 28 | BE | 27.02 | 4.68 | 5.77 | 0 | MOL | CZm | EDn | 17.0 | 21.0 | 19.2 | 19.3 | 23.0 | 2.0 | 3.8 | 3.2 |
| 29 | FR | 19.33 | 6.78 | 2.85 | 25 | MOL | CZm | EDn | −1.6 | −2.3 | 0.0 | −3.6 | 1.1 | 1.1 | 12.0 | 3.3 |
| 30 | IT | 22.59 | 7.03 | 3.21 | 25 | MOL | CZm | EDn | 2.3 | 1.8 | 3.4 | 1.1 | 4.9 | 1.5 | 9.4 | 4.4 |
| 31 | DK | 29.00 | 8.95 | 3.24 | 25 | MOL | CZm | EDn | 2.6 | 2.1 | 3.6 | 1.5 | 5.1 | 1.5 | 9.4 | 4.4 |
| 32 | AT | 22.16 | 6.36 | 3.48 | 25 | MOL | CZm | EDn | 5.0 | 4.6 | 5.6 | 4.3 | 7.4 | 1.8 | 8.6 | 4.8 |
| 33 | PL | 15.48 | 3.76 | 4.12 | 25 | MOL | CZm | EDn | 10.4 | 10.2 | 10.3 | 10.8 | 12.4 | 1.6 | 25.1 | 4.9 |
| 34 | DE | 31.93 | 6.47 | 4.94 | 25 | MOL | CZm | EDn | 16.2 | 16.2 | 15.2 | 17.7 | 18.2 | 0.5 | 19.7 | 5.2 |
| 35 | BE | 27.02 | 4.68 | 5.77 | 25 | MOL | CZm | EDn | 21.0 | 21.2 | 19.4 | 23.4 | 23.8 | 0.4 | 3.1 | 2.0 |
| 36 | FR | 19.33 | 6.78 | 2.85 | 50 | MOL | CZm | EDn | 1.4 | −2.1 | 0.1 | −0.5 | 2.1 | 0.7 | 10.4 | 1.3 |
| 37 | IT | 22.59 | 7.03 | 3.21 | 50 | MOL | CZm | EDn | 5.5 | 2.0 | 3.5 | 4.4 | 6.6 | 1.1 | 6.9 | 1.9 |
| 38 | DK | 29.00 | 8.95 | 3.24 | 50 | MOL | CZm | EDn | 5.8 | 2.3 | 3.7 | 4.7 | 6.9 | 1.1 | 7.0 | 1.9 |
| 39 | AT | 22.16 | 6.36 | 3.48 | 50 | MOL | CZm | EDn | 8.3 | 4.7 | 5.7 | 7.7 | 9.4 | 1.1 | 7.0 | 1.9 |
| 40 | PL | 15.48 | 3.76 | 4.12 | 50 | MOL | CZm | EDn | 14.0 | 10.4 | 10.4 | 14.4 | 15.3 | 0.9 | 10.5 | 2.0 |
| 41 | DE | 31.93 | 6.47 | 4.94 | 50 | MOL | CZm | EDn | 20.1 | 16.4 | 15.4 | 21.6 | 21.7 | 0.1 | 5.8 | 2.3 |
| 42 | BE | 27.02 | 4.68 | 5.77 | 50 | MOL | CZm | EDn | 25.1 | 21.4 | 19.5 | 27.5 | 28.1 | 0.6 | 4.0 | 3.0 |
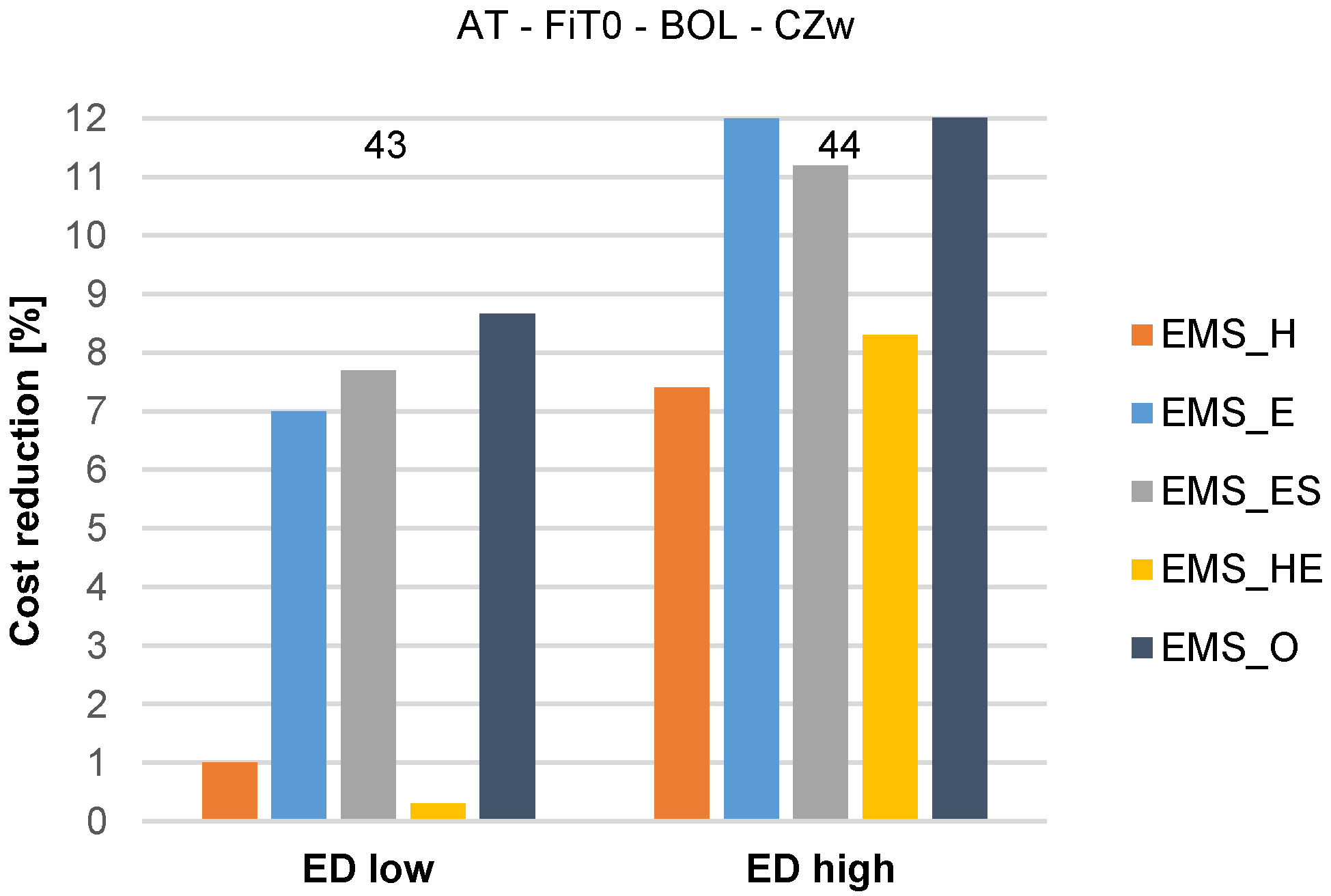
| 43 | AT | 22.16 | 6.36 | 3.48 | 0 | BOL | CZw | EDl | 1.0 | 7.0 | 7.7 | 0.3 | 8.7 | 1.0 | 7.3 | 0.5 |
| 44 | AT | 22.16 | 6.36 | 3.48 | 0 | BOL | CZw | EDh | 7.4 | 12.0 | 11.2 | 8.3 | 12.1 | 0.1 | 15.5 | 0.3 |
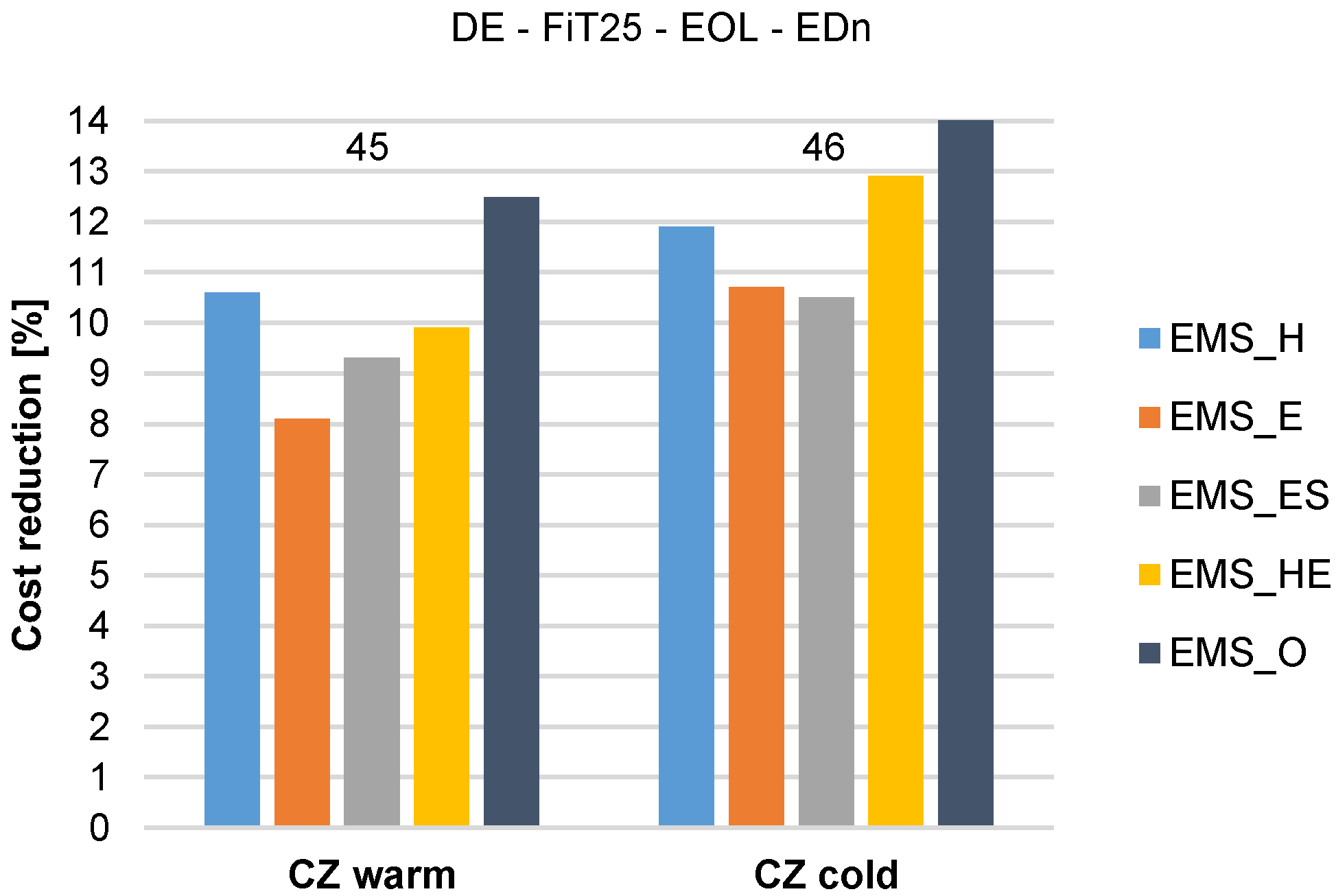
| 45 | DE | 31.93 | 6.47 | 4.94 | 25 | EOL | CZw | EDn | 10.6 | 8.1 | 9.3 | 9.9 | 12.5 | 1.9 | 17.8 | 4.9 |
| 46 | DE | 31.93 | 6.47 | 4.94 | 25 | EOL | CZc | EDn | 11.9 | 10.7 | 10.5 | 12.9 | 14.0 | 1.1 | 16.4 | 6.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, S.; Herrero, J.M.; Blasco, X.; Pajares, A. Optimal Operating Patterns for the Energy Management of PEMFC-Based Micro-CHP Systems in European Single-Family Houses. Appl. Sci. 2025, 15, 7527. https://doi.org/10.3390/app15137527
Navarro S, Herrero JM, Blasco X, Pajares A. Optimal Operating Patterns for the Energy Management of PEMFC-Based Micro-CHP Systems in European Single-Family Houses. Applied Sciences. 2025; 15(13):7527. https://doi.org/10.3390/app15137527
Chicago/Turabian StyleNavarro, Santiago, Juan Manuel Herrero, Xavier Blasco, and Alberto Pajares. 2025. "Optimal Operating Patterns for the Energy Management of PEMFC-Based Micro-CHP Systems in European Single-Family Houses" Applied Sciences 15, no. 13: 7527. https://doi.org/10.3390/app15137527
APA StyleNavarro, S., Herrero, J. M., Blasco, X., & Pajares, A. (2025). Optimal Operating Patterns for the Energy Management of PEMFC-Based Micro-CHP Systems in European Single-Family Houses. Applied Sciences, 15(13), 7527. https://doi.org/10.3390/app15137527







