Abstract
This study established a numerical model for a foundation pit at the Zhongyilu Station of the Wuhan Metro Line 12, using Plaxis3D version 2021 finite element software to examine the horizontal displacement of the diaphragm wall, ground surface settlement, and differential settlement between the diaphragm wall and the lattice columns across various construction stages. A comparison with the cut-and-cover method prompted the adoption of a strategy that integrates segmental pouring of the main structure and the installation of internal supports to optimize the original scheme. The results indicated that as the foundation pit was excavated, both the horizontal displacement of diaphragm wall and the ground surface settlement gradually increased, while the differential settlement between the diaphragm wall and the lattice columns shows exhibited an initial decrease followed by an increase. In comparison to the cut-and-cover method, the cover-and-cut method demonstrated greater efficacy in controlling foundation pit deformation and minimizing disturbances to surrounding environment. As the number of segmental pouring layers and support levels increased, the overall deformation of the foundation pit showed a gradual decreasing trend, and the differential settlement between the diaphragm wall and the lattice columns continued to fluctuate. When each floor slab was poured in three layers with two supports placed in the middle, the maximum horizontal displacement of the diaphragm wall could be reduced by 22.47%, and the maximum ground surface settlement could be decreased by 19.01%. The findings in this research can provide valuable basis and reference for the design and construction of similar projects.
1. Introduction
The construction of urban subway stations frequently occurs in densely populated areas. The excavation of foundation pits can lead to significant risks, including damage to existing subway tunnels, ground subsidence, structural damage to buildings, the uplift of diaphragm walls, and the failure of support systems [1,2,3,4,5,6,7,8]. The iterative update of subway construction methods has greatly promoted the rapid development of infrastructure. Farzi et al. [9] compared conventional and widely used methods; an appropriate and safe support system was proposed for excavation in urban areas depending on construction, structural, and economic conditions. Hsiung et al. [10] established a three-dimensional finite element model by considering a top-down construction method, a supporting system of concrete slabs, and the influence of the soil modulus. Bozkurt et al. [11] studied the influence of lime–cement stability on foundation pit support by using the finite element method. The 2D finite element analyses were performed with advanced constitutive models for both natural clay and stabilized soil, performing a laboratory test made on both field-mixed and laboratory-mixed stabilized clay samples. Russo et al. [12] carried out a 3D numerical simulation study of the Chiaia station of the Naples Metro Line 6 to predict and control the deformation of a deep foundation pit in order to safeguard the safety of the adjacent Basilica Santa Maria degli Angeli. Lin et al. [13] analyzed the similarities and differences in force and deformation between foundation pits excavated by the zonal method and those excavated by the conventional method.
Nevertheless, the considerable excavation depth associated with foundation pits continues to pose challenges, particularly concerning excessive deformation. Previous studies have indicated that the deformation resulting from the cover-and-cut method is generally smaller than that associated with the cut-and-cover method; however, the mechanism of the deformation of the surrounding environment caused by different excavation methods is still not yet fully understood [14,15]. For instance, Jamsawang et al. [16] examined a foundation pit in Bangkok using the top-down method and analyzed deformation and stress patterns when employing a deep mixing cement–soil wall as a retaining structure. Their findings revealed that the construction of the structural slab effectively mitigates the horizontal displacement of the retaining wall. Li et al. [17] proposed the channel excavation method. Yang et al. [18] compared a foundation pit project constructed using the top-down method with relevant international case studies to analyze the mechanical behaviors observed during excavation. Ou et al. [19] explored deformation and stress characteristics throughout the top-down construction process by measuring the stress of the middle columns, the displacement and bending moment of the diaphragm wall, and the ground surface settlement. Their observational results emphasize the necessity of considering creep factors during excavation analysis in soft clay conditions. Whittle et al. [20] proposed a deformation algorithm for retaining structures in a foundation pit constructed via the nonlinear top-down method and evaluated its predictive accuracy through comparison with the measured data. Alkhdour et al. [21] present rational design strategies based on field and numerical analyses to optimize stability while reducing the length of soil nails for a comprehensive understanding of deformation control in deep excavations, particularly in the context of alternative retaining systems such as soil nail walls. They demonstrated that numerical simulations can effectively predict soil deformation.
The intermediate columns represent a unique structural system in the top-down method. During the construction process, these columns endure substantial vertical loads, which prompts extensive research on their displacement characteristics and differential settlement patterns. Based on the analyses of field measurements, researchers such as Cai et al. [22] and Ono et al. [23] have suggested that controlling differential settlement should be prioritized during the construction of the top-down structure. The Technical Specification for Foundation Pit Engineering [24], issued by Shanghai Engineering Construction, states that the differential settlement between the intermediate columns and the diaphragm wall of the foundation pit must not exceed 20 mm and 1/400 of the spacing between the intermediate columns. Sun et al. [25] simulated the most unfavorable conditions for differential settlement and identified that the maximum differential settlement occurs prior to the formation of the bottom slab. Based on measured data from a project in Tianjin and numerical simulations, Su et al. [26] proposed a phased control method and a differential settlement control standard for the top-down construction of a subway station. Guo et al. [27] investigated the differential heaving and settlement between the vertical support structures in a foundation pit constructed using the top-down method in soft soil areas and analyzed the mechanisms and influencing factors. They also provided recommendations for mitigating differential heaving and settlement in design.
In summary, research on the differential settlement in foundation pits constructed using the top-down method remains relatively limited. However, such differential settlement directly impacts the feasibility of employing this construction technique. Subway stations, which are often located in bustling areas with limited construction sites and surrounded by dense structures and complex traffic patterns, benefit from the top-down construction method due to its advantages in minimizing noise, dust, and disruptions to traffic, thus reducing the impact on local residents. Consequently, the top-down construction method is increasingly favored for subway station projects in urban environments. This study established a numerical analysis model using Plaxis3D to examine the horizontal displacement of the diaphragm wall, ground surface settlement, and differential settlement between the diaphragm wall and the lattice columns across various construction stages. Furthermore, a comparison was made with the cut-and-cover method. Finally, optimized analysis of the original construction scheme was conducted by implementing a construction scheme involving the multiply segmented pouring of the main structure and the erection of internal supports. The innovation of this scheme lies in the combination of internal supports and the cover–cut method, which can effectively control the differential settlement of piles and walls and the deformation of the surrounding environment.
2. Project Overview
Zhongyilu Station serves as a transfer hub for Lines 8, 12 and 21. It is strategically located at the intersection of Houhu Avenue and the crossroads of the Zhongyilu–Tazihu East Road in the Jiang’an District. A plan view of the foundation pit is illustrated in Figure 1. This foundation pit is constructed using the cut-and-cover method.
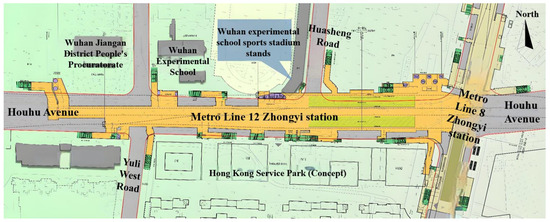
Figure 1.
Overall plan of Zhong Yi Station.
The station features a three-storey underground frame structure, with an overall length of 519.2 m. The structural width and height of the standard section are 49.5 m and 25.29 m, respectively. The roof is covered with approximately 3.2 m of soil. The main structure dimensions of the station are as follows: the clear floor height of the first floor from top to bottom is 7.1 m, that of the second floor is 7.4 m, and that of the third floor is 7.7 m. Among these, the thickness of the top slab of the main structure is 0.9 m, the thickness of the floor slabs of the first and second basement floors is 0.4 m, the thickness of the floor is 1.3 m, and the thickness of the side walls is 0.85 m. The primary construction method employed for the station is the top-down method, which integrates support structures and the main structures effectively. The diaphragm wall has a thickness of 1.5 m, while the upper retaining structure is 0.2 m thick. The lattice columns and bored piles had diameters of 900 mm and 2300 mm, respectively, and both the retaining and main structures were constructed using C35 concrete. The key advantages/disadvantages of excavation methods (top-down, cut-and-cover) are shown in Table 1.

Table 1.
Summarizing the key advantages/disadvantages of excavation methods (top-down, cut-and-cover).
The strata within the excavation depth of the foundation pit are mainly composed of silty clay, silt interbedded with silt sand, and gravel mixed with cobblestones. In contrast, the overall undulation of the top of the bedrock layer is relatively small. The average groundwater level is 2.5 m, and it fluctuates between 1 m and 4 m. The distribution of the soil layers is depicted in Figure 2. The average groundwater level is 2.5 m, and it fluctuates between 1 m and 4 m.
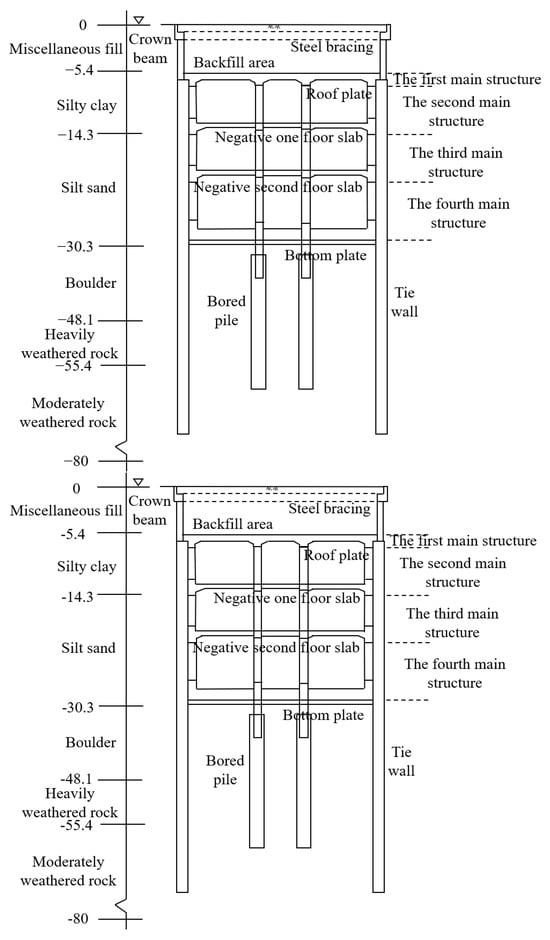
Figure 2.
Standard cross-section of Zhong Yi Station.
3. Numerical Simulation of Deep Foundation Pit
3.1. Model Establishment
Given the complex surrounding environment of the foundation pit, it is essential to conduct a simplified analysis to facilitate subsequent finite element modeling and calculations. This analysis encompassed the following assumptions: (1) the soil conditions within the foundation pit were considered to be horizontally and homogeneously distributed; (2) vehicle loads on the road were converted into uniformly distributed loads acting on the cover plate equal to 20 kPa; (3) a linear elastic plate element model was utilized for the diaphragm wall; (4) a beam element model was employed for the concrete struts; (5) an embedded pile model was utilized for the lattice columns; (6) the numerical simulation process excluded the influence of the diaphragm wall construction and the disturbance of soil caused by construction machinery; (7) time-related effects were not taken into account. Contact between different materials is the default setting, taking into account gravity and earth pressure loads as well as vehicle loads.
In this study, we used the PLAXIS 3D version 2021 program to conduct finite element modeling analysis on a subway foundation pit at the Zhongyilu Station in Wuhan City. According to Saint-Venant’s principle and relevant specifications, the influence range of deep foundation pit excavation was approximately three times that of the excavation depth. The maximum excavation depth for this foundation pit was 28.2 m. Based on actual working conditions, the dimensions of the model were established as 35 m × 160 m × 80 m (x × y × z). The boundary conditions are set as follows: the horizontal displacements at the four sides of the model are constrained to simulate the lateral restraint of the soil in actual engineering; full constraints are applied at the bottom to prevent the model from undergoing unreasonable overall movement; the top is kept free to more realistically reflect the deformation of the soil at the top. In terms of the mesh refinement strategy, we focus on the key areas, with the element size controlled at around 0.1 m to ensure the calculation accuracy of these areas, thereby accurately capturing the detailed changes in stress and deformation. For other non-key areas, larger-sized meshes are used for transition, which not only ensures the simulation accuracy of the key areas but also effectively balances the calculation efficiency of the entire model, avoiding the problems of wasted computing resources and excessive calculation time caused by excessive meshing. In this configuration, the x-axis, y-axis, and z-axis represent the longitudinal, transverse, and vertical directions of the foundation pit, respectively. The numerical model of the foundation pit is illustrated in Figure 3. The support system of the foundation pit comprises a diaphragm wall and an internal support system. The diaphragm wall and steel pipe columns are retained as permanent structures, while the internal supports include reinforced concrete supports, steel supports, and bored piles. The diaphragm wall and the main structure of the foundation pit were modeled using solid elements, whereas the lattice columns and bored piles were simulated using the embedded pile model. The main structural parameters are shown in Table 2.
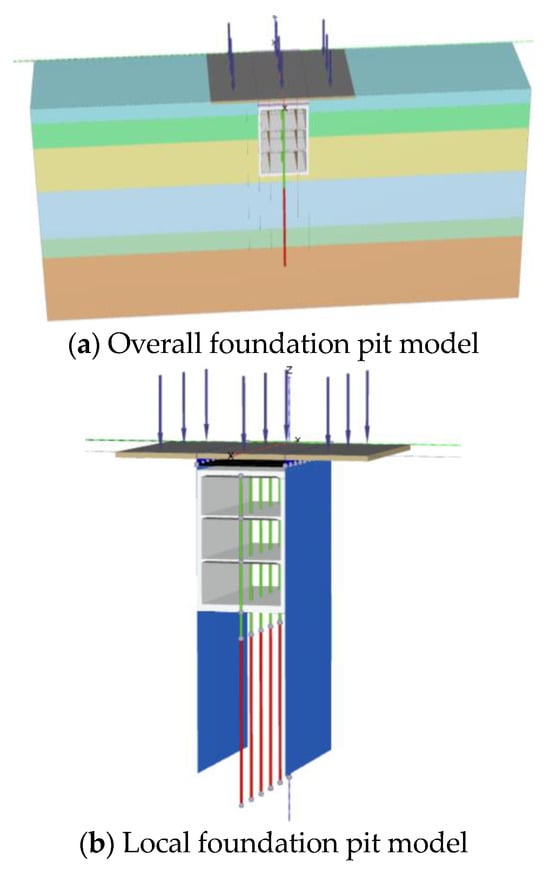
Figure 3.
Numerical model of foundation pit.

Table 2.
Model structure parameters.
3.2. Selection of Model Parameters
Existing practices and studies have indicated that the strain within the soil during the excavation process typically remains in a small strain state. As depicted in Figure 4, the hardening soil small strain (HSS) model exhibits the characteristic whereby the shear modulus of the soil increases with strain. It can effectively capture the hydrostatic pressure and expansibility of soft clay. This model allows for the differentiation of unloading stiffness during loading and reloading, thereby enabling a relatively accurate representation of the behavior induced by soil excavation. Therefore, the HSS model was adopted in this study. The model parameters are all derived from laboratory data, especially the small strain parameter G0. Through a series of dynamic triaxial tests, small-amplitude cyclic shear stresses were applied to the soft soil samples, and the relationship between the shear modulus of the soil samples and the shear strain was measured to determine the value of G0. The main soil parameters obtained are shown in Table 3.
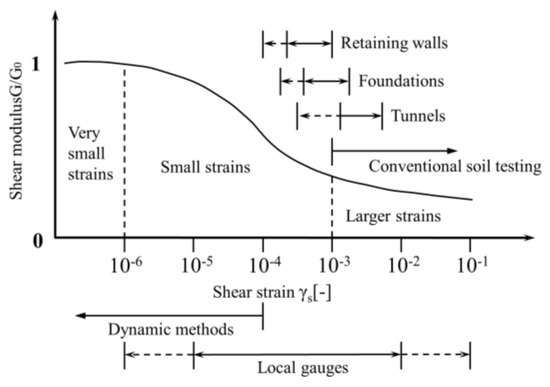
Figure 4.
Characteristic stiffness–strain behavior on logarithmic scale.

Table 3.
Soil constitutive model parameters.
3.3. Validation of the Numerical Model
This study established a three-dimensional finite element model based on a foundation pit project at the Zhongyilu Station of the Wuhan Metro Line 12 to analyze the excavation process. In accordance with the actual project specifications, the model was divided into a total of 11 construction scenarios. The real excavation scenarios were simulated through the activation and passivation of elements within the model. The detailed excavation scenarios are presented in Table 4. Comparative analysis was conducted between the measured and simulated horizontal displacements of the diaphragm wall at the ZQT82 monitoring point of the K foundation pit. The results are illustrated in Figure 5. The simulated and measured horizontal displacements exhibited good agreement, demonstrating the applicability of the numerical model presented in this study.

Table 4.
Finite element analysis conditions.
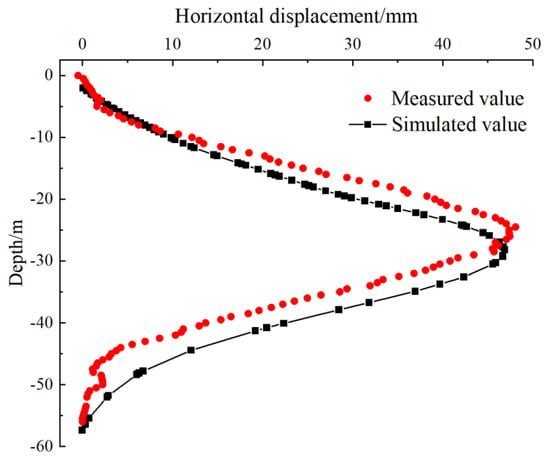
Figure 5.
Measured and simulated horizontal displacement at ZQT82 monitoring points.
3.4. Analysis of Numerical Results
Figure 6 presents the horizontal displacement nephogram of the diaphragm wall in the y-direction and the ground surface settlement nephogram following the excavation of the foundation pit. During the final excavation stage, the horizontal displacement of the diaphragm wall presented a “bow-shaped” pattern, characterized by a significant displacement in the middle and lesser displacements at both sides. This behavior aligns with the deformation characteristics of the diaphragm wall in open-cut foundation pits. Further analysis revealed that the ground surface settlement shows a typical “concave groove” shape. Moreover, the use of the top-down construction method, where the roof of the main structure was poured before backfilling, prevented post-construction settlement of the backfilled soil. Instead, it exhibited a heaving phenomenon. This upward heaving was attributed to the fact that as the excavation progressed and unloading took place at the foundation pit’s bottom, the soil heaved upward in response to the excavation. Consequently, the lattice columns also experienced upward heaving, which was greater than the settlement transmitted downward due to the construction of the upper structure. This disparity primarily accounted for the differential settlement between the diaphragm wall and the lattice columns. Future research should focus on strategies to control such differential settlement during the design and construction stages.

Figure 6.
Deformation nephogram of foundation pit at final excavation stage.
To investigate the stress and deformation characteristics of the foundation pit under different top-down construction conditions, deformation data were extracted at different construction stages, as shown in Figure 7. It was observed that with the excavation of the foundation pit, the horizontal displacement of the diaphragm wall gradually increased, and the depth at which the maximum value occurred gradually moved downward. Further analysis revealed that the majority of the diaphragm wall’s deformation increment, resulting from excavation, primarily occurred below the cast-in-place floor slab, while no significant displacement was observed above this slab. This phenomenon arose because, in the top-down construction method, the floor slab was poured first, and subsequent excavation was conducted only after the slab reached its designed strength. The reinforced concrete utilized for the floor slab possessed high strength and good integrity, which effectively restricted the deformation of the diaphragm wall situated above the floor slab. The maximum horizontal displacements of the diaphragm wall at different excavation stages were 2.01 mm, 11.81 mm, 26.48 mm, and 46.89 mm, respectively.
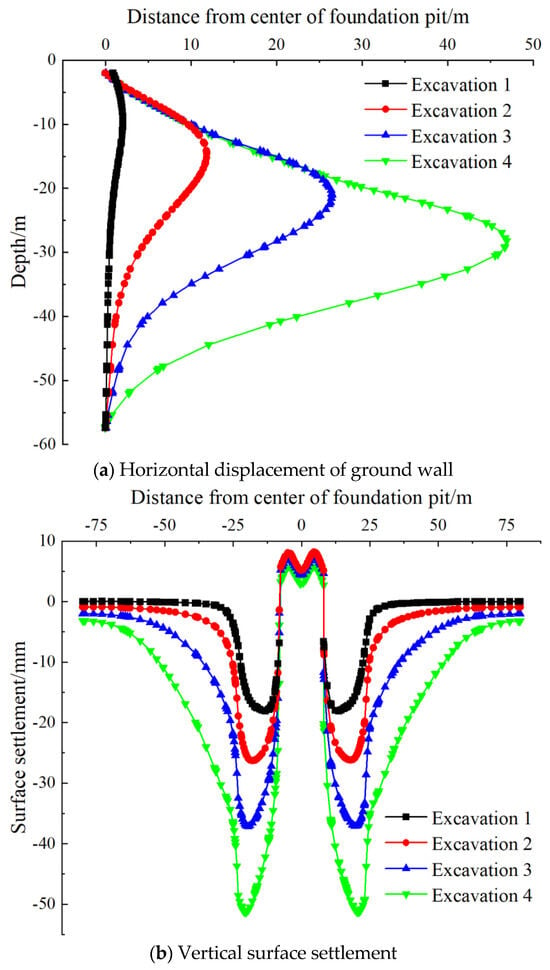
Figure 7.
Deformation nephogram of foundation pit under different excavation scenarios.
Figure 7b revealed that the ground surface settlement gradually increased as the foundation pit was excavated, which was consistent with the change trend of the diaphragm wall displacements. The main influence range of the ground surface settlement caused by excavation extended approximately 0 to 56 m away from the foundation pit boundary, corresponding to about twice the excavation depth. The secondary influence area spans approximately 56 to 75 m away from the boundary, which is about 2.7 times the excavation depth. The maximum ground surface settlements at different excavation stages were −18.11 mm, −26.29 mm, −37.14 mm, and −51.30 mm, respectively.
To investigate the differential settlement between the diaphragm wall and the lattice columns during the top-down construction process, the vertical displacements of both the diaphragm wall and the lattice columns at various excavation stages were extracted to calculate their differential settlement, as presented in Table 5.

Table 5.
Maximum differential settlement between adjacent piles and ground wall (mm).
As previously noted, the primary challenges during the top-down construction process include the differential settlement and the resulting stress redistribution within the main structure. During the construction process, the pouring and solidification of concrete generally require significant time. Therefore, when the first layer of the main structure was poured, the diaphragm wall and the lattice column can be viewed as independent components. The vertical displacements of the diaphragm wall and the lattice column were designated as the baseline for subsequent analysis. This assumption implies that any displacement at this point is considered negligible. Table 5 depicts that during the initial excavation stage, the vertical displacements of the lattice column and the diaphragm wall were −1.23 mm and −0.98 mm, respectively, resulting in a differential settlement of only 0.25 mm. This finding indicated that during the initial excavation stage, the soil unloading rebound induced by the foundation pit excavation was relatively small. This allowed for effective integration between the diaphragm wall and the lattice column, which contributed to the control of differential settlement. As excavation progressed, both the vertical displacements of the diaphragm wall and the lattice column showed a gradual increase, while the differential settlement initially decreased and then increased. This behavior was primarily attributed to the excavation of the foundation pit, which reduced the friction between the diaphragm wall and the surrounding soil. Concurrently, the excavation unloading effects at the pit bottom resulted in an increase in heaving, which is illustrated in Figure 6b. However, the pouring of the main structure led to further compression of the lattice columns, thereby restricting their heaving. This results in a deformation pattern for the lattice column characterized by compression in the upper section and heaving in the lower section, as depicted in Figure 8. Analysis of Figure 8 confirmed that the maximum settlement of the lattice column occurred at its top, resulting in the largest differential settlement between the upper main structure and the diaphragm wall. The differential settlement initially decreased and then increased during the excavation process. This behavior showed that during the initial excavation stage, the diaphragm wall and the lattice column remained relatively independent. Subsequently, both the diaphragm wall and the lattice column reached a phase of relative stability in terms of their settlements. However, as excavation continued, they exhibited signs of separation once again.

Figure 8.
Vertical deformation nephogram of lattice column at final excavation stage.
4. Comparative Analysis of Top-Down Method and Cut-and-Cover Method
The top-down method, the cut-and-cover method (where excavation precedes the construction of the superstructure), the shallow tunneling method, and various combinations of these construction approaches are currently the predominant construction techniques employed worldwide for the construction of subway stations and similar infrastructure.
The cut-and-cover method involves excavating soil from top to bottom. After the excavation is completed, the station building structure is constructed from the bottom to the top. The overall construction period is relatively long. The construction process is relatively simple, there are many working surfaces, the progress and quality are relatively easy to guarantee, and the cost is relatively low. However, during the construction period, a large area of land needs to be occupied for earthwork excavation and structural construction, and the interruption time of traffic is relatively long. The construction sequence of the top-down method is to dig the soil from top to bottom. After one layer is excavated, the station building structure is immediately constructed. Traffic can be restored after the roof is completed. The construction process is complex, and sometimes special equipment is required for soil disposal operations. In the early stage of construction, by quickly completing the roof construction of the main structure and restoring traffic, the interruption time for traffic can be greatly reduced. This section explored the advantages and disadvantages of the top-down and cut-and-cover methods for foundation pit deformation control through numerical simulations.
4.1. Top-Down Method Model Establishment
The numerical model of the cut-and-cover method mirrors that of the top-down method, with the primary distinction being the excavation sequences employed. The specific model parameters are detailed in Section 2. Given the relatively deep excavation depth associated with the cut-and-cover foundation pit, the support structure consists of two concrete struts and six steel struts. The first and fourth struts are constructed from C35 concrete with dimensions of 1000 mm × 1000 mm, with a horizontal spacing of 9 m. The remaining struts utilized ordinary pre-stressed steel with specifications of φ609 mm × 16 mm. The horizontal spacing is 3 m, and the pre-stress is 300 kN [24]. The numerical model of the foundation pit using the cut-and-cover method is depicted in Figure 9, and the excavation sequences are summarized in Table 6, where “…” indicates the cyclic installation of struts and the excavation process, which spans from the installation of the second strut to the completion of the sixth excavation sequence.
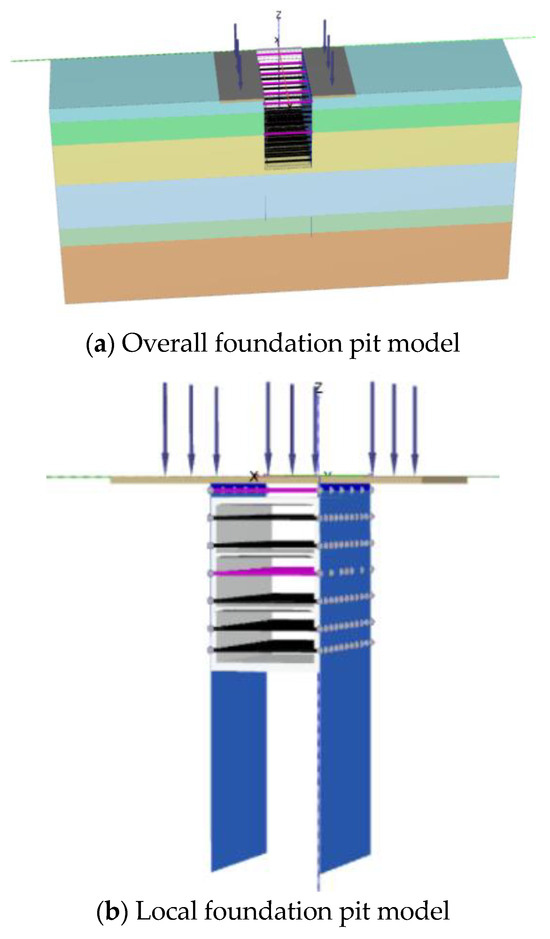
Figure 9.
Numerical model of Top-Down Method foundation pit.

Table 6.
Simulated excavation sequences.
4.2. Comparative Analysis of Simulation Results
4.2.1. Foundation Pit Deformation
Figure 10 illustrates the horizontal displacement of the diaphragm wall and the ground surface settlement outside the pit for both the cut-and-cover method and the top-down method. As depicted in Figure 10a, the deformation patterns of the diaphragm wall resulting from both methods exhibited similarities, characterized by a “bow-shaped” pattern with pronounced deformation in the middle and small deformations at both sides. The maximum deformation of the diaphragm wall associated with the cut-and-cover method reached 49.35 mm, which was generally larger than that observed with the top-down method. This difference can be attributed to the fact that the top-down method uses the floor slab of the main structure as the support framework for the foundation pit. This configuration provided enhanced support stiffness compared to the cut-and-cover foundation pit, which relied on concrete and steel struts. Consequently, this increased stiffness exerted a damping effect on the inward movement of the diaphragm wall towards the pit. Therefore, in the context of this project, the top-down method demonstrated superior performance in controlling the deformation of the retaining structure compared to the cut-and-cover method. Further analysis of Figure 10b shows that the ground surface settlement associated with both construction methods tends to follow a typical “concave groove” shape. The maximum ground surface settlement caused by the cut-and-cover method reaches −48.19 mm, which is slightly smaller than the deformation produced by the top-down method. Analysis of the settlement curve indicated that, on the left side of the “concave groove” shape, the settlement resulting from the top-down method was larger than that of the cut-and-cover method. Conversely, on the right side of the “concave groove” shape, the settlement from the top-down method was smaller than that from the cut-and-cover method. This observation further supports the conclusion that the top-down method is superior to the cut-and-cover method in controlling the deformation of the surrounding environment.
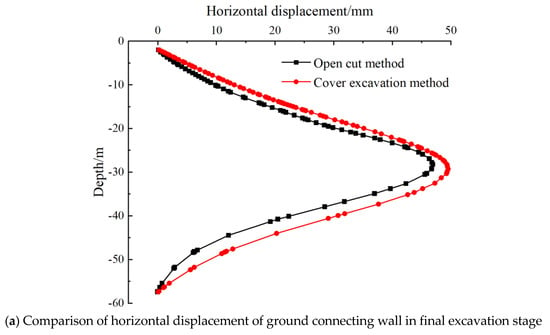
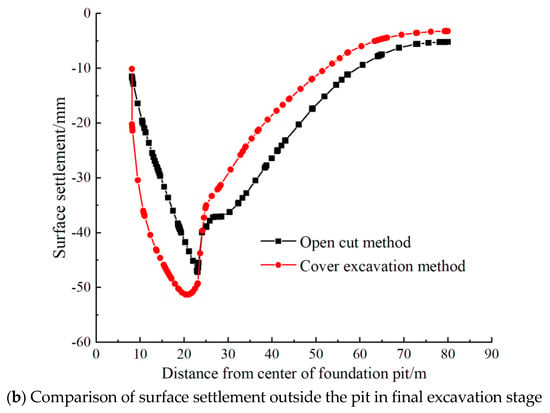
Figure 10.
Deformation of foundation pit for both construction methods.
In conclusion, the comparative analysis indicated that the top-down method is superior in controlling the deformation of the retaining structure and mitigating the effects of construction on the surrounding environment. However, the deformation caused by the top-down method was recorded at 0.23% H (where H is the excavation depth of the foundation pit), which far exceeded the specified limit of 36.0 mm, as outlined in the relevant regulations (where the maximum lateral displacement of the diaphragm wall for a first-class foundation pit is 0.18% H [24]). It can be known that the cover excavation method also cannot meet the safety standards. Therefore, in regions with stringent deformation control requirements, it is recommended to implement servo steel supports or to adopt a construction scheme that integrates multiple construction methods.
4.2.2. Main Structure Internal Force
The maximum longitudinal compressive stress and maximum longitudinal tensile stress of the main structure for the cut-and-cover method and the top-down method during the final construction stage are shown in Table 7. As can be seen from Table 7, the maximum longitudinal compressive stress and maximum longitudinal tensile stress of the cut-and-cover method are both larger than those of the top-down method. Specifically, the maximum longitudinal compressive stress of the cut-and-cover method is 1649 kN/m2 greater than that of the top-down method, an increase of 54.9%; the maximum longitudinal tensile stress of the cut-and-cover method is 120 kN/m2 greater than that of the top-down method, an increase of 6.32%. It can be concluded that the variation range of longitudinal compressive stress is greater than that of longitudinal tensile stress. This is mainly because the top-down method uses steel supports as the support system, making the main structure more uniformly stressed, while the cut-and-cover method uses the stiffness of the main structure itself to resist deformation, resulting in an uneven stress distribution of the main structure, and thus the maximum longitudinal stress of the cut-and-cover method is larger than that of the top-down method.

Table 7.
The longitudinal stress of the main structure of the top-down and cut-and-cover method during the final construction stage.
The bending moments of the main structure’s first floor and fourth floor for the cut-and-cover method and the top-down method during the final construction stage are shown in Figure 11. As can be seen from Figure 11, the maximum positive and negative bending moments of the first floor in the cut-and-cover method are much greater than those of the fourth floor of the cut-and-cover method and the first floor and fourth floor of the top-down method. They reach −1091.7 kN·m/m and 950.0 kN·m/m, respectively. This is mainly because, during the construction of the Cut-and-Cover method, the first floor of the main structure is the first to be constructed. The first floor serves as the first supporting structure of the cover excavation pit and bears most of the soil pressure during the subsequent excavation. As a result, the bending moment at the top plate of the main structure in the cut-and-cover method is the largest. Compared with the difference in bending moments between the first floor and fourth floor in the cut-and-cover method, the bending moments at the first floor and fourth floor in the top-down method are almost the same. This is because, when the main structure is poured in the top-down method, due to the effect of the internal support, the main structure and the internal support jointly bear the soil pressure, making the main structure more evenly stressed.
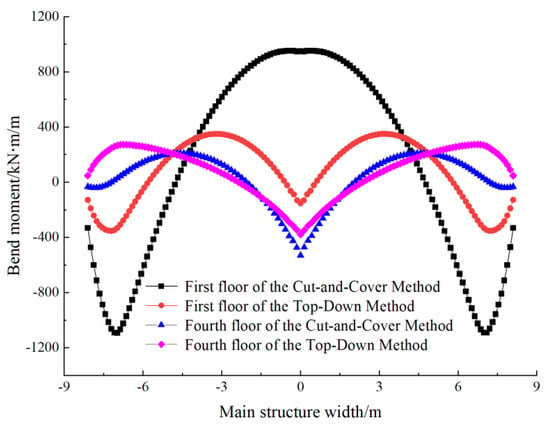
Figure 11.
Final comparison diagram of bending moments of first floor and fourth floor of main structure for cut-and-cover and top-down methods of construction process.
5. Deformation Control Measures
5.1. Determination of Deformation Control Scheme
Due to its unique construction process, the top-down method significantly reduces the duration of road closure associated with construction activities and offers the advantage of rapidly restoring traffic flow. As discussed in Section 3, the top-down method demonstrates superior capabilities compared to the cut-and-cover method in terms of controlling foundation pit deformation and minimizing the impact of construction on the surrounding environment. In practical applications of the top-down method, the roof or floor slab of the main structure functions as a structure element that resists deformation. Analysis in Section 3.4 reveals that the roof or floor slab of the main structure experiences minimal deformation during construction, which effectively restricts the deformation of the diaphragm wall located above the floor slab. Given that this project features a maximum storey height of 9 m, there would inevitably be extended periods without support during the excavation of subsequent foundation pit layers. This condition could lead to the excessive deformation of the retaining structure beneath the foundation pit floor slab, as shown beneath in Figure 7a. Consequently, the deformation associated with the top-down method may not satisfy the requirements imposed in regions that necessitate strict deformation control. In this study, during the top-down construction process, each excavation height was reduced, and a construction method involving segmental pouring of the main structure, along with the addition of internal supports, was implemented, as shown in Figure 12. Plan 2, depicted on the left side of Figure 12, incorporates one steel support between each floor slab. Plan 3, presented on the right side of Figure 12, includes two steel supports between each floor slab. This method meets the functional requirements of structural deformation control while also taking economy into account. All internal supports utilize ordinary pre-stressed steel supports with specifications of φ609 mm × 16 mm. They have a horizontal spacing of 3 m and a pre-stress of 300 kN. Comparing the new schemes with the original construction method facilitates a discussion of their advantages in controlling the deformation of the retaining structure, the vertical displacement of the ground surface, and the differential settlement between the diaphragm wall and the lattice columns.
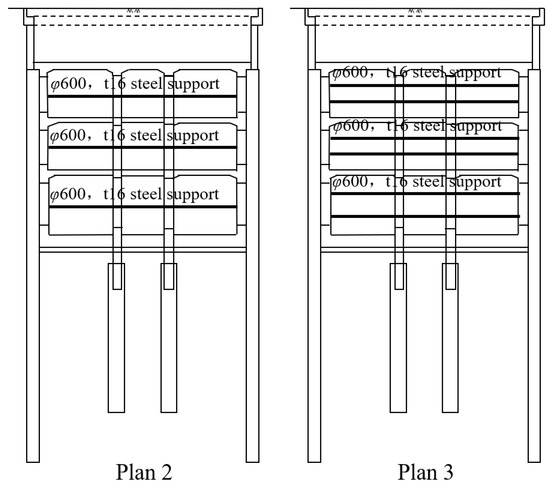
Figure 12.
Schematic diagram of deformation control scheme.
5.2. Comparative Analysis of Deformation Results
5.2.1. Comparative Analysis of Support Structure Deformation
Figure 13 presents a line chart illustrating the maximum deformation points of the diaphragm wall under the three different excavation schemes as a function of excavation depth. As indicated in Figure 13, the maximum horizontal displacements of the diaphragm walls for all three excavation schemes gradually increased with the excavation depth. Plan 3 exhibited the lowest growth rate of the maximum horizontal displacement, with a final maximum displacement of only 31.71 mm, which equated to 0.15% H. Plan 2 provided the second-best deformation control, with a maximum displacement of 36.35 mm at the final excavation sequence, which equated to 0.17% H. The original scheme demonstrated the least effective deformation control. Compared to the excavation method of the original scheme, Plan 3 reduced the maximum horizontal displacement of the diaphragm wall by 15.18 mm, representing a decrease of approximately 32.37%. Meanwhile, Plan 2 achieved a reduction of 10.54 mm, corresponding to a decrease of approximately 22.47%.
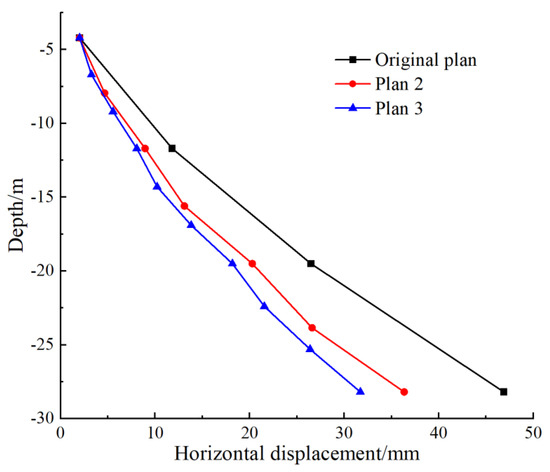
Figure 13.
Maximum horizontal displacement of diaphragm wall at different excavation depths.
5.2.2. Comparative Analysis of Ground Surface Settlement
Figure 14 presents a line chart illustrating the maximum ground surface settlement points of the foundation pit at different excavation depths. A comparison with Figure 13 indicated the existence of consistent variation trends in the horizontal displacement of the diaphragm wall and the ground surface settlement. Plan 3 exhibited the best deformation control, with a maximum ground surface settlement of −37.81 mm after excavation. Plan 2 provided the second-best performance, with a maximum ground surface settlement of −41.55 mm, while the original scheme demonstrated the least effective deformation control. Compared to the excavation method of the original scheme, Plan 3 reduced the maximum ground surface settlement by 13.49 mm (approximately 26.29%), and Plan 2 achieved a reduction of 9.75 mm (about 19.01%). Furthermore, the analysis of diaphragm wall deformation revealed that the range horizontal displacement was consistently greater than the ground surface settlement under the same construction scheme. This observation indicated that the diaphragm wall deformation is more sensitive to the construction scheme than the ground surface settlement. Compared with Plan 2, the maximum horizontal displacement of Plan 3 is reduced by 4.64 mm, or 12.76%. The deformation control effect does not increase significantly.
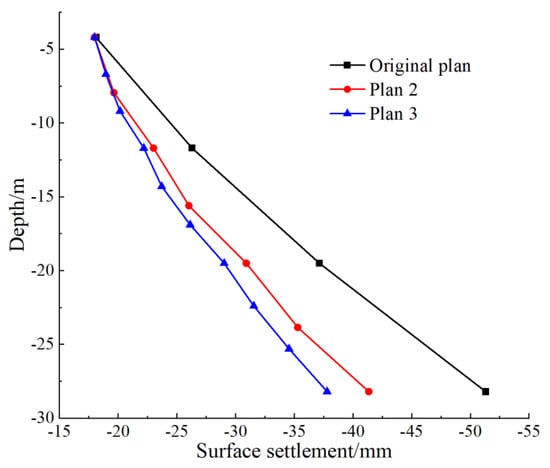
Figure 14.
Maximum ground surface settlement at different excavation depths.
Figure 13 and Figure 14 revealed that increasing the number of segments did not result in the horizontal displacement of the diaphragm wall or the ground surface settlement reaching zero; instead, they converged toward a certain fixed value. During construction, factors such as the operation of construction machinery must be considered, and the segmented storey height should be comprehensively evaluated to determine the optimal construction scheme.
5.2.3. Comparative Analysis of Differential Settlement Between Ground Wall and Lattice Column
The stress release caused by excavation and unloading led to the upward heaving of the soil at the bottom of the foundation pit. Concurrently, the finished main structure caused the lattice columns and the diaphragm wall to bear the load transmitted from the structure. This scenario inevitably resulted in differential settlement between the diaphragm wall and the lattice columns. Controlling this uneven settlement is critical to the success of the top-down construction method and involves implementing various measures during construction. Otherwise, uneven settlement could lead to cracks in the poured floor slabs and beam systems, resulting in leakage and potentially jeopardizing the safety of the permanent structure. Currently, the control standards for differential settlement are largely based on empirical construction experiences. For example, Wang et al. [28] stated that the differential settlement between the diaphragm wall and the lattice columns should not exceed 20 mm or 1/400 of the column spacing length through numerical simulation. They concluded that the floor slab should be poured as promptly as possible to minimize the differential settlement.
Table 8 summarizes the maximum vertical displacements of the diaphragm wall, the maximum vertical displacements of the lattice columns, and the differential settlement between the two under the three different construction schemes. The maximum vertical displacement of the diaphragm wall gradually decreased as the number of segmented excavations increased. Among the three schemes, the original scheme exhibited the largest settlement, while Plan 3 showed the smallest settlement at only −2.97 mm. Conversely, the maximum vertical displacement of the lattice columns showed a gradually increasing trend. The original scheme displayed the smallest settlement, while Plan 3 exhibited the largest settlement at −4.04 mm. This trend can be attributed to the fact that an increase in the number of segments constrained the horizontal displacement of the diaphragm wall, which in turn limited the maximum vertical displacement of the diaphragm wall. However, a smaller horizontal displacement of the diaphragm wall weakened its ability to compress the soil within the foundation pit. Consequently, the heaving of the pit bottom and lattice columns was reduced in comparison to the original excavation scheme. As previously described, the maximum settlement of the lattice column occurred at the top, as illustrated in Figure 8. The pressure transmitted from the main structure and the backfilled soil in the lattice column remained unchanged. Consequently, decreasing the heaving of the lattice column diminished its ability to counteract the vertical displacement of the main structure, resulting in an increase in the settlement at the top of the lattice column. This caused the maximum vertical displacement of the lattice column to increase as the number of segments increased. Further examination of the differential settlement between the diaphragm wall and the lattice column revealed that the differential settlement fluctuated with the increasing number of segments (As shown Table 6). Plan 2 achieved the smallest differential settlement at only 0.55 mm, while Plan 3 recorded the largest differential settlement at 1.07 mm. Wang et al. [28] stated that the differential settlement should not exceed 20 mm. Notably, all three construction schemes met the deformation control requirements. Additionally, as detailed in Section 4.2.1, the horizontal displacements of the diaphragm wall in Plan 3 and Plan 2 were recorded at 0.15% H and 0.17% H, respectively, both of which comply with the regulatory requirement that the maximum horizontal displacement of the diaphragm wall for a first-class foundation pit should not exceed 0.18% H.

Table 8.
Differential deformation under different construction schemes (mm).
5.2.4. Engineering Cost Comparison Analysis
In subway foundation pit projects, the cut-and-cover method is widely adopted due to its ability to reduce the long-term occupation of ground traffic. This paper demonstrates that in engineering practice, by adding steel supports, the deformation of the retaining structure can be effectively controlled. However, the increase in the number of supports will significantly increase the project cost. Therefore, a quantitative correlation between “deformation control requirements” and “economic costs” needs to be established to provide a scientific basis for engineering decision-making.
Based on the actual project overview, the width of the calculation model is 8.2 m, and the longitudinal length is set at 50 m; all the steel supports are made of φ609 × 16 ordinary pre-stressed steel supports, with a horizontal spacing of 3 m. The density of the steel is 7850 kg/m3. Thus, the weight of a single steel support is approximately 1.915 tons. According to the current market price, the comprehensive unit price of the steel supports is 5000 CNY/ton (including material procurement and on-site installation costs), where the material cost accounts for 70% (3500 CNY/ton), and the installation cost accounts for 30% (1500 CNY/ton). The steel supports are reusable materials. After removal, the steel can be recycled, and the recycling price is calculated based on 40% of the material cost (installation costs cannot be recycled). It can be calculated that the net cost (total cycle cost) of a single steel support, the total purchase cost minus the recycling value, is approximately CNY 6894.
The longitudinal length of the foundation pit is 50 m, and the longitudinal support spacing is 3 m per row (that is, one horizontal steel support is set every 3 m). Since the two ends of the foundation pit need to be equipped with sealing supports, the actual number of support rows needs to be calculated by rounding up, which gives approximately 17 steel supports. For Plan 2, 1 steel support is set on each floor, and a total of 3 horizontal supports are needed for the 3-storey main structure; the total number of supports is 51; the total cost is approximately 351,594 yuan (about 352,000 yuan). For Scheme Three, 22 steel supports are set on each floor, and a total of 6 horizontal supports are needed for the 3-storey main structure; the total number of supports is 102; the total cost is approximately CNY 703,188 yuan (about CNY 703,000). Regarding the construction period of the foundation pit, in the original scheme, each floor is poured at once, and the curing time for each floor is approximately 5 days, with a total curing time of 15 days; for Plan 2, each floor is poured in two stages, with a total curing time of 30 days; for Plan 3, each floor is poured in two stages, with a total curing time of 45 days. Regarding the cost of the curing period, since it is relatively small, it is temporarily not included, but Plan 3 has the longest working hours, followed by Plan 2, and Scheme 1 has the shortest.
The economic performance of the scheme is evaluated by the “unit deformation control cost” indicator, that is, “total cost increment/deformation reduction amount”, as shown in Equation (1):
In the formula, Cuc represents the unit cost for deformation control; Ctc represents the total cost increment; and Δδ represents the reduction in deformation.
According to Equation (1), it can be calculated that the unit deformation control cost of Plan 2 is approximately 33,400 CNY/mm; the unit deformation control cost of Plan 3 is approximately 46,300 CNY/mm.
Plan 3 increases the number of steel supports by a factor of 2 (102 vs. 51), but only reduces the deformation by 4.64 mm (15.18 mm vs. 10.54 mm). However, the cost increases by a factor of 2 (703,000 yuan vs. 352,000 yuan), and the unit deformation control cost is 38.6% higher than that of Plan 2 (46,300 CNY/mm vs. 33,400 CNY/mm).
From the perspective of engineering practice, the deformation control of the foundation pit needs to meet the requirements of the specifications (0.17%H), and the deformation reduction amount of Plan 2 (10.54 mm) is sufficient to make the horizontal displacement of the ground wall lower than the control value (assuming the depth of the foundation pit H = 10 m, the control value is 17 mm, the actual displacement of Plan 2 is the original displacement—10.54 mm, if the original displacement is 25 mm, then the displacement of Plan 2 is 14.46 mm, which meets the specifications). Under this premise, the cost advantage of Plan 2 is significant, and the additional working hours are relatively small, which is in line with the “safety–economy” dual-target requirement.
6. Conclusions
This study relied on a foundation pit project at the Zhongyilu Station of the Wuhan Metro Line 12. Numerical simulations were conducted to analyze the influence of different construction stages on the deformation of the foundation pit. The original scheme was optimized through the use of segmental pouring of the main structure and the installation of internal supports. The main conclusions are as follows:
- (1)
- Both the horizontal displacement of the diaphragm wall and the ground surface settlement gradually increased with the excavation of the foundation pit, while the differential settlement between the diaphragm wall and the lattice columns showed a differential settlement that initially decreased then increased.
- (2)
- Comparative analysis with the cut-and-cover method indicated that the top-down method is more effective in terms of controlling the deformation of the foundation pit and reducing the impact of construction activities on the surrounding environment.
- (3)
- A construction scheme was proposed, involving multiple segmented pouring of the main structure and erection of internal supports. This scheme can effectively reduce the deformation of the foundation pit. However, in this project, with the increase in the number of segments, the growth of the deformation control effect is not obvious. Therefore, in this project, considering deformation and economy comprehensively, Plan 2 is selected as the best.
- (4)
- In future research, real-time monitoring data will be incorporated. By installing sensors in actual engineering projects, real-time data on soil deformation, stress, and other key parameters will be collected. This will be used to verify the accuracy of the numerical simulation results and further optimize the model parameters. At the same time, the adaptability and stability of each scheme in diverse geological environments will be evaluated.
Author Contributions
Conceptualization, Y.L. (Yi Liu) and L.H.; methodology, X.T.; software, Y.X.; validation, W.K. and X.T.; formal analysis, Y.L. (Yang Luo); investigation, L.G.; resources; data curation, X.T.; writing—original draft preparation, X.T.; writing—review and editing, L.G.; visualization, L.H.; supervision, Y.L. (Yi Liu); project administration, Y.L. (Yi Liu); funding acquisition, L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 20242BAB204095.
Data Availability Statement
The data presented in this study are available on request from the corresponding author (due to the difficulty in coordinating the data set, this article does not share the corresponding data set).
Conflicts of Interest
Author Yi Liu was employed by the company Hangzhou Nanpai Water Conservancy Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Bin, C.; Benson, H. Observations of the ground and structural behaviours induced by a deep excavation in loose sands. Acta Geotech. 2019, 15, 1577–1593. [Google Scholar]
- Wei, G.; Wang, Q.; Zhou, X.; Feng, F.; Wang, X.; Zhang, L.; Liang, L. Experiments and numerical simulation of the reinforcement effect of channel-steel-reinforced shield tunnel segments under unloading conditions. Eur. J. Environ. Civ. Eng. 2023, 27, 4142–4164. [Google Scholar] [CrossRef]
- Wei, G.; Qi, Y.; Chen, C.; Zhang, S.; Qian, C.; Zhou, J. Analysis of the protective effect of setting isolation piles outside the foundation pit on the underpass tunnel side. Transp. Geotech. 2022, 35, 100791. [Google Scholar] [CrossRef]
- Paulson, B.C.; Msce, M. Underground transit station construction in Japan. J. Constr. Div. 1982, 108, 23–37. [Google Scholar] [CrossRef]
- Tan, Y.; Li, M. Measured performance of a 26 m deep top-down excavation in downtown Shanghai. Can. Geotech. J. 2011, 48, 704–719. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, R.; Kang, Z.; Bin, W. Covered semi-top-down excavation of subway station surrounded by closely spaced buildings in downtown Shanghai: Building response. J. Perform. Constr. Facil. 2016, 30, 04016040. [Google Scholar] [CrossRef]
- Lin, Z.; Xie, S.; Xia, C.; Dou, H. Design and Practice of Deep Foundation Pits for Large Storage Ponds in Complex Environments. Sustainability 2022, 14, 14046. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Zheng, X.; Cao, J.; Chen, Y. Development and Application of Similar Materials for Foundation Pit Excavation Model Test of Metro Station. Appl. Sci. 2022, 12, 12880. [Google Scholar] [CrossRef]
- Farzi, M.; Pakbaz, S.M.; Aminpour, A.H. Selection of support system for urban deep excavations: A case study in Ahvaz geology. Case Stud. Constr. Mater. 2018, 8, 131–138. [Google Scholar] [CrossRef]
- Hsiung, B.C.B.; Yang, K.H.; Aila, W.; Ge, L. Evaluation of the wall deflections of a deep excavation in Central Jakarta using three-dimensional modeling. Tunn. Undergr. Space Technol. 2018, 72, 84–96. [Google Scholar] [CrossRef]
- Bozkurt, S.; Abed, A.; Karstunen, M. Finite element analysis for a deep excavation in soft clay supported by lime-cement columns. Comput. Geotech. 2023, 162, 105687. [Google Scholar] [CrossRef]
- Russo, G.; Nicotera, M.V.; Esposito, I. 3D FEM Back Analysis of the Observed Performance of a Very Deep Excavation in the Historical Center of Naples, Italy. J. Geotech. Geoenviron. Eng. 2024, 150, 04024010. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, Y.; Xu, C.; Chi, M.; Fang, T.; Guan, L.; Feng, G.; Lin, G. Performance of adjacent metro tunnels during deep excavation: A case study in Hangzhou. Transp. Geotech. 2025, 53, 101585. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, W.; Mei, H.; Qin, X.; Wang, J. Analyze the deformation mechanism of foundation pit engineering and its influence on adjacent piers. Acad. J. Eng. Technol. Sci. 2022, 5, 1–4. [Google Scholar]
- Li, Z.; Zhao, G.F.; Deng, X.; Zhu, J.; Zhang, Q. Further development of distinct lattice spring model for stability and collapse analysis of deep foundation pit excavation. Comput. Geotech. 2022, 144, 104619. [Google Scholar] [CrossRef]
- Jamsawang, P.; Jamnam, S.; Jongpradist, P.; Tanseng, P.; Horpibulsuk, S. Numerical analysis of lateral movements and strut forces in deep cement mixing walls with top-down construction in soft clay. Comput. Geotech. 2017, 88, 174–181. [Google Scholar] [CrossRef]
- Li, M.G.; Chen, J.J.; Xu, A.J.; Xia, X.H.; Wang, J.H. Case study of innovative top-down construction method with channel-type excavation. J. Constr. Eng. Manag. 2014, 140, 05014003. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Azzam, R.; Yan, C. Performance of a top-down excavation in shanghai: Case study and numerical exploration. Eur. J. Environ. Civ. Eng. 2022, 26, 7932–7957. [Google Scholar] [CrossRef]
- Ou, C.Y.; Liao, J.T.; Lin, H.D. Performance of diaphragm wall constructed using top-down method. J. Geotech. GeoEnviron. Eng. 1998, 124, 798–808. [Google Scholar] [CrossRef]
- Whittle, A.J.; Hashash, Y.M.A.; Whitman, R.V. Analysis of deep excavation in Boston. J. Geotech. Eng. 1993, 119, 69–90. [Google Scholar] [CrossRef]
- Alkhdour, A.; Yasin, A.A.; Tiutkin, O. Rational design solutions for deep excavations using soil nail wall systems. Min. Miner. Depos. 2023, 17, 110–118. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Martin, C.D. Quantification of rock mass damage in underground excavations from microseismic event monitoring. Int. J. Rock Mech. Min. Sci. 2001, 38, 1135–1145. [Google Scholar] [CrossRef]
- Ono, J.; Murata, K. Construction of a very deep subway station using cut-and-cover method under high groundwater pressure. In Proceedings of the International Congress on Tunnelling and Ground Conditions, Cairo, Egypt, 3–7 April 1994; pp. 57–60. [Google Scholar]
- DG/TJ08-61-2018; Shanghai Engineering Construction Code-Technical Standard for Foundation Pit Engineering. Tongji University Publishing House: Shanghai, China, 2018.
- Sun, Y. Numerical Analysis of Top-Down Construction Technique and Study on Monitoring for Deep Excavation Engineering in Soft-Soil Areas. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Su, J.; Zhang, D.; Gao, Z.; Huang, J.; Xiao, C. Structural Deformation and Control of Subway Station Constructed by Cut and Cover Reverse method. Chins Railw. Sci. 2010, 31, 59–65. [Google Scholar]
- Guo, X.; Xie, X.; Jia, J. Differential displacement control of deep foundation pits in soft clay by use of top-down excavation method. Chin. J. Geotech. Eng. 2012, 34 (Suppl. S1), 72–76. [Google Scholar]
- Wang, Y. Finite element analysis of Differential settlement in the construction of the Cut-and-Cover method. Low-Temp. Build. Technol. 2012, 34, 103–105. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).