Abstract
Balance control in pirouettes has previously been characterized by constraint of the topple angle. However, there is a paucity of research using the margin of stability (MoS) as a dynamic measure of balance related to pirouettes. Therefore, this study aimed primarily to examine the MoS as a metric of balance during a single-turn en dehors pirouette in healthy female amateur ballet dancers. Four participants performed pirouettes until five successful pirouettes were achieved without hopping or loss of balance. Three-dimensional motion capture was used to record the motion trajectories of anatomical markers based on the Plug-in-Gait and Oxford Foot models. Motion synchronized with ground reaction forces was used to calculate the center of pressure (CoP), base of support (BoS), center of the pivot foot, center of mass (CoM), and extrapolated center of mass (XCoM) throughout the turn phase, using laboratory (LCS) and virtual left foot (LFT) coordinate systems. In the LCS and LFT coordinate system, the excursions and patterns of motion of both the CoM and XCoM relative to the CoP were similar, suggesting a neurological relationship. Two different measures of the margin of stability (MoS) in the LFT coordinate system were tabulated: the distance between the (1) XCoM and CoP and (2) XCoM and BoS center. The magnitude of both versions of the MoS was greatest at turn initiation and toe-touch, which was associated with two foot contacts. The MoS values were at a minimum approximately 50% of the stance during the turn phase: close to zero along the anteroposterior (A/P) axis and approximately 50 mm along the mediolateral (M/L) axis. On average, MoS magnitudes were reduced (mean across participants: approximately 20 mm) along the A/P axis, and larger MoS magnitudes (mean across participants: approximately 50 mm) along the M/L axis throughout the turn phase. Although all turns analyzed were completed successfully, the larger MoS values along the M/L axis suggest a fall potential. The variability between trials within a dancer and across participants and trials was documented and showed moderate inter-trial (16% to 51%) and across-participant CV% (range: 10% to 28%), with generally larger variations along the A/P axis. Although our results are preliminary, they suggest that the MoS may be useful for detecting faults in the control of dynamic balance in dehors pirouette performance, as a part of training and rehabilitation following injury.
1. Introduction
The pirouette is a fundamental movement in classical ballet. In this turn, the dancer balances on a single limb while on the toes (pointe) or on the ball of the foot (demi-pointe) and performs one or more whole-body revolutions around a pivot axis through the stance leg [1]. A pirouette is classified by the direction in which the turn is initiated. The direction most often seen in classical ballet choreography and research is the en dehors pirouette. This means that the dancer rotates outward, away from the stance leg. A pirouette can also be performed in en dedans by rotating inwards, toward the stance leg. In either turn, the leg used in push-off is lifted from the ground and held in a retiré position (Figure 1).
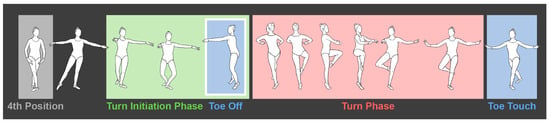
Figure 1.
Two major phases of a pirouette. Prior to turn initiation (green box), the dancer assumes the 4th position (far left). Turn initiation includes the toe-off (blue box) that segues in to the turn phase (red box). The turn is completed with a toe-touch event (2nd blue box).
A pirouette consists of two phases: a turn initiation phase and a turn phase (Figure 1). The turn initiation phase begins with the dancer assuming a static double-leg stance in either the fourth or fifth position [1,2]. In the fourth position, one foot rests about 12 inches in advance of the other, both are turned out, and the weight is divided between them, whereas in the fifth position, the feet are turned out and pressed closely together, with the heel of the one foot against the toe of the other. The turn phase is performed in a single-leg stance while the dancer completes one or more rotations at the pivot point through the stance leg, usually on the metatarsal heads [2]. During this phase, the turn leg works in an open kinematic chain, while the stance leg works in a closed kinematic chain and helps to control posture [3].
The inverted pendulum model (IPM) has been used to analyze the lower extremities’ responses to internal and external perturbations to the body’s center of mass (CoM). The IPM is based on the following assumptions: (1) simplification of the body’s complex mass distribution by distributing it as a single point, i.e., the CoM, located at a fixed distance from the ankle pivot; (2) the legs are considered massless, perfectly rigid, and act as straight lines connecting the CoM to the ankle joint center; (3) the ankle axis is a fixed point, about which the leg rotates; (4) movement occurs in two planes, i.e., sagittal and frontal; and (5) there is no account of the effects of muscles and net joint moments at the knee and hip [4,5]. Related to the IPM, lower extremity muscles are recruited to shift the center of pressure (CoP), which helps to maintain the CoM within the BoS [4]. The CoM is controlled in the sagittal plane by the ankle’s dorsi-/plantar flexor muscles and in the frontal plane by the hip abductor/adductor and ankle invertor/evertor muscles, leading to a change in the CoP as a reaction to these adjustments; that is, changes in the position of the CoP are the central nervous system’s response to perturbations [4]. Winter et al. and Gage et al. demonstrated that the difference between the locations of the CoM and the CoP, when projected on the ground (Figure 2), is positively related to the horizontal acceleration of the body’s CoM [4,5]. Therefore, as the horizontal acceleration of the CoM increases during a task, the distance between the CoP and CoM decreases, and vice versa.
Although the IPM has been validated for examining quiet standing [4,5,6] and gait [7], others have challenged the primary assumptions of the single inverted pendulum for the examination of quiet stance [8,9] and gait [10]. In essence, with regard to postural control, these researchers have suggested that knee [9] and hip [8,9,10] motion during quiet stance cannot be neglected, and that ankle–hip oscillatory patterns are characterized by complex in-phase and anti-phase interactions. These studies suggest that the IPM should be substituted by a double inverted pendulum, which can be characterized as a kind of optimal, biaxial active controller used to minimize the acceleration of the body’s CoM. However, more recently, Morasso et al. [11] demonstrated that while the single IPM may be “literally” an inadequate model to characterize the complexity of postural control because it ignores the ankle–knee–hip interactions, it is functionally correct for experimental studies that focus on the postural oscillations of the CoM.
The IPM model has only recently been applied to the study of ballet. Lott [12] applied the model to investigate how the number of pirouette rotations affected dynamic balance. She found the IPM to be beneficial as a reference model; however, for the intermediate–advanced dancers in her study, she found that their BoS, i.e., CoP, shifted to maintain balance during their turns [12]. These findings differ from the traditional IPM, due to the dynamic nature of a pirouette. It is notable that the IPM does not account for the whole-body axial rotations that occur with a pirouette, and the righting strategies associated with the IPM are based on a fixed BoS, whereas the pirouette is a dynamic movement with dynamic righting strategies, with potential for an unstable BoS.
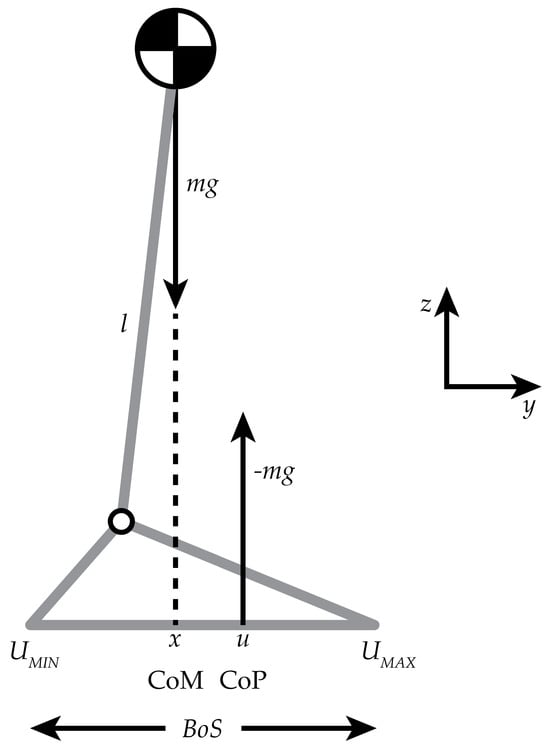
Figure 2.
Inverted pendulum model. The body’s total mass minus the foot mass (m) times gravity (g) is balanced on top of the lower extremity, whose length = l; u = the CoP location; effective ground reaction force = -mg; x = the projected CoM onto the ground; and the BoS is the plantar portion of the foot that is in contact with the ground [13]. The yz plane reflects the orientation of the laboratory coordinate system.
When performing the pirouette, the BoS transitions from a double-leg stance to a single-leg stance, which greatly decreases the area within the BoS. Therefore, an en dehors pirouette requires the body’s CoM to shift toward the stance leg during the turn initiation phase to allow the body’s CoM to remain centered over the stance leg during the turn phase [2]. Velocity is generated during the turn initiation phase to bring the dancer up onto their stance leg and to spin the body around for the desired number of revolutions. Generally, to maintain balance, the CoM must stay within the BoS, but there are other factors involved in maintaining dynamic balance. According to Hof et al. [13], if the velocity of the CoM is directed outward then balance may be lost even if the individual is within the BoS, and if one’s CoM is outside of the BoS but their velocity is directed inward then balance may be maintained. This effect of an individual’s velocity of the CoM during a dynamic movement is expressed as the extrapolated center of mass (XCoM), which is the velocity-adjusted position of the CoM [14]. Applying this concept to investigate turns performed by ballet dancers makes intuitive sense. In generating enough angular velocity to perform the pirouette, a dancer must also be able to control the direction of their velocity to remain balanced during their turn. It has been shown that changes in the relative positions of the CoP and XCoM are useful tools in the examination of balance and its perturbation [14].
The distance between the XCoM and the dancer’s BoS that still allows them to maintain their balance and successfully complete their pirouette has been defined as the margin of stability (MoS) [14]. The MoS is determined as a time series throughout the movement and is the deviation of the XCoM from the BoS; its magnitude provides a metric of the dancer’s dynamic balance. The MoS is thought to be proportional to the impulse needed to unbalance a participant [13]. The MoS could be related to the amount of self-generated impulse or disruption of balance that a dancer experiences during the turn initiation or turn phase of their pirouette. Traditionally, the IPM has been applied to study quiet standing postures, i.e., a static BoS [4,5]. However, using the IPM as a framework, and based on extensive use of the MoS in biomechanics research [15], the CoP, BoS, and XCoM metrics could also provide insight related to the dynamics of dance.
When there is a disruption in balance while walking (i.e., an obstacle, shortened step length, or external push), the person compensates by stepping or moving their arms and trunk to regain balance [14]. The same thing happens with dancers. For example, if there is a disturbance in the turn initiation phase, the dancer will compensate for that disturbance using a hop, allowing their stance foot to travel, or by moving their trunk [16]. Likewise, when attempting to perform multiple revolutions during a pirouette, the body’s center of mass faces more challenges related to the number of turns, which require compensatory actions. The initial direction of the velocity of the CoM and the ability to maintain balance could be a factor in the success of the pirouette. Since the MoS is a function of the excursion of the XCoM from the BoS, this distance will determine whether compensation is needed and to what extent. If the dancer has a minor loss of control associated with a small MoS, they may be able to correct with muscular actions, but if they experience a larger internal or external disturbance they will likely need to hop or will fall out of a turn.
At key points during a pirouette, muscle activation in the trunk, pelvis, and upper and lower extremities during both phases of the pirouette also affects the relationship between the CoM and BoS to maintain balance. The hip and ankle/foot of the stance leg are two joint complexes that play important roles in controlling dynamic balance. The position and kinetics of the hip joint appear to be a vital component in both the generation of momentum and control of the CoM during a pirouette. Zaferiou et al. [17] found that the net angular and linear impulse generation during the turn initiation phase tended to be greater during pirouettes initiated with hip external rotation. The hip also plays an important role on the upper body during a pirouette. During the start of the double-stance phase, the hip joint moments appear to be the main contributor to generating the angular momentum of the upper body [18]. Therefore, as the hip complex and surrounding muscles influence multiple regions of the body, intuition suggests that it is an important factor in whether or not the turn is successful. The use of the IPM to study the pirouette is relevant because the knee of the stance limb is in a relatively close-packed position in extension during the turn phase, so the motion is mainly controlled by key hip and ankle muscles.
In ballet, the topple angle refers to the planar angle between the vertical and a line connecting the dancer’s CoM to the center of the BoS at the floor [6]. Zaferiou et al. [19] found that, for dancers, the average topple angle was five degrees during the turn phase during both double and single pirouettes. One can only remain balanced during a pirouette if the topple angle is small enough that neural control mechanisms can make the needed corrections; however, if the topple angle increases, the dancer will likely have to resort to a hop or end their turn [16]. It has been shown that the topple angle decreases as the number of turns increases, with a significant difference in the topple angle between the single- and triple-turn conditions for elite dancers [1]. Using the IPM as a framework, the topple angle associated with the pirouette might provide additional insight into its relationship with the CoP, CoM, XCoM, and MoS, and with the control mechanisms of successful and unsuccessful single- and multiple-turn pirouettes.
The margin of stability has been used extensively to measure dynamic control in individuals who are prone to falls [20], have Parkinson’s disease [21,22,23], have multiple sclerosis [24,25], have had a stroke [26,27], or have had an amputation [28,29,30]. To the best of our knowledge, the use of measures of dynamic balance within the framework of the IPM to examine the margin of stability during the pirouette is minimal. Tsubaki et al. [31] examined the coordination of laterality, i.e., limb preference in turn initiation, in professional and amateur ballet dancers performing a single pirouette in pointe shoes. For both groups, they found no difference in the CoM–CoP inclination (i.e., toppling) angle between limbs, but they noted that amateurs had a greater anterior tilt during left rotation. Professionals showed a slight difference in hop-up time during right versus left turns. In a related study, Tsubaki et al. [32] measured differences in the rotation axis between professional and elite amateur ballet dancers during an en dehors pirouette with pointe shoes. They reported that professional dancers exhibited a reduced posterior inclination angle and hop-up time during single-leg support in the mid-swing (or mid-turn) phase. Lott [6] examined the ability of healthy, adolescent female dancers to perform as many revolutions in each pirouette as they were capable of doing. Her primary purpose was to evaluate the relationship between specific anthropometric and kinematic variables and the number of successful turns (i.e., n) a dancer could perform. She hypothesized that the prediction of large-n pirouettes would be initiated in a more balanced position (i.e., smaller initial topple angle) or with a larger initial MoS than pirouettes with a reduced n. However, only the normalized BoS distance traveled per revolution was significantly related to n.
Despite Lott’s limited use of the MoS, previous research has shown that this metric can provide insight into activities that require dynamic balance, e.g., gait, stepping over obstacles, etc. [15]. Furthermore, the determination of the MoS metric in healthy elite dancers could provide valuable information that would assist ballet instructors, professional dancers, and collegiate dancers in practice and performance as they work to perfect the control of their pirouettes. Given the gap in the literature on the use of the MoS metric to measure dynamic control of the ballet pirouette, it is clear that additional research is warranted. Therefore, the purpose of this research was to examine the margin of stability and the topple angle as measures of dynamic balance during a single-turn en dehors pirouette in female amateur ballet dancers. We aimed to examine these variables in normal, healthy dancers to begin to create a normative database that could be used to improve performance, evaluate abnormal mechanics in ballet dancers, and assist in the prevention of ballet-related injuries.
2. Materials and Methods
2.1. Participants
Participants were recruited by their response to an email sent out to professional dance companies, pre-professional companies, and dance studios in West Michigan within a 100-mile radius of a local university and other colleges in Michigan with dance programs. Ten dancers responded, and five met the inclusion criteria and participated in data collection, making our sample one of convenience. All of the participants had comparable dance skills and pirouette execution style. They reported at least 10 years’ experience of ballet and other varieties of dance. Additionally, all of the participants were members of amateur or pre-professional companies, except for one who had danced with a professional ballet troupe many years prior to her involvement with this project. Participant #4 was unable to complete turns without hopping, so her data were not analyzed.
Participants were included if they were healthy elite, amateur, or professional ballet dancers between 18 and 40 years old, which was determined based on a medical history and physical examination; no professional dancers were included. Individuals were excluded if they had (1) a significant medical condition or a neurological condition; (2) a significant orthopedic injury to the spine or the upper or lower extremities within the past 12 months; (3) reconstructive joint surgery; (4) pregnancy; or (5) if they were unable to complete a triple pirouette from the 4th position. Before the recruitment of participants and data collection, this study was reviewed and approved by the Office of Research Compliance and Integrity and the Institutional Review Board (19-296-H). Oral and written informed consent was obtained from all of the dancers before all activities related to the project.
2.2. Instrumentation and Experimental Procedures
Marker trajectories were recorded using 16 Vicon MX-T40 cameras at 120 Hz and Nexus motion capture software v2.81 (Vicon Motion System Ltd., Oxford Metrics, UK). Motion data were synchronized with ground reaction forces (GRFs) collected from two force plates (FPs) (1200 Hz) embedded in the laboratory floor (Advanced Mechanical Technology, Inc., Watertown, MA, USA). To prevent slipping, Marley flooring was secured to the surface of FPs three and five. Before data collection, the motion capture volume was calibrated with dimensions of 10 (length) × 2 (width) × 2 (height) m using Vicon Nexus software. This calibration procedure defined the laboratory coordinate system (LCS) at the corner of FP2 (Figure 3).
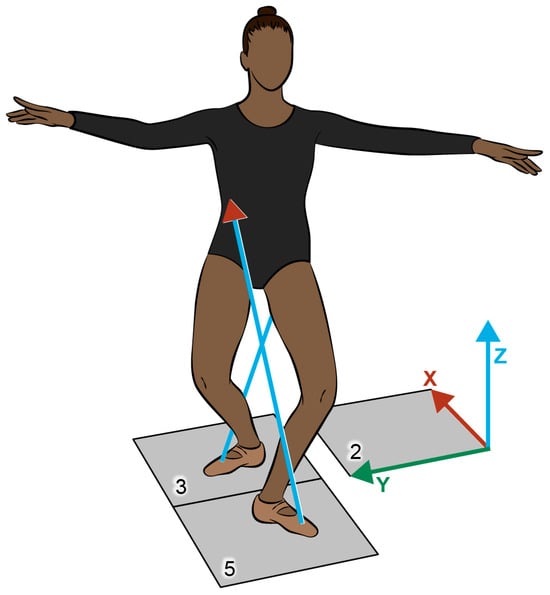
Figure 3.
The laboratory coordinate system established at the corner of FP2, relative to the dancer’s starting position, with positive-x directed posterior, positive-y directed toward the dancer, and positive-z upward relative to the turn initiation position, with the right and left feet placed on FP3 and FP5, respectively. The blue arrows projecting in the z-direction represent vertical ground reaction forces.
Marker placement was consistent with a modification of the full-body Plug-in-Gait (PiG) and Oxford Foot (OFM) models [33,34,35,36]. See Appendix A for a complete description of the marker placements. The PiG model was modified by placing markers on the medial femoral condyles and medial malleoli, a method used in lieu of the knee alignment device. Using the medial markers on the femoral condyles and malleoli improves the location of the knee and ankle joint centers, and the definition of the longitudinal torsional profiles of the thigh and shank. To ensure repeatable rearfoot marker placements, the lateral and medial calcaneal markers were placed the same linear distance from the heel marker (as measured from center to center of the marker spheres by a short centimeter ruler); all three markers were placed at the same height (from the center of the marker spheres) from the floor. The OFM was also modified to not include the bilateral CPG marker (i.e., a peg marker on the posterior end of the calcaneus), due to the increased likelihood of it being displaced or interfering with the placement of the turning foot while in retiré. Accurate and consistent marker placement was ensured by having only one researcher, verified by the laboratory director, place the markers for all test sessions.
Data collection was performed at the University Biomechanics and Motor Performance Laboratory. Before testing, the participants’ health assessment included a medical history and a physical examination that consisted of range of motion, muscular strength tests, and anthropometric measures that were performed by a graduate student, under the supervision of the principal investigator. Anthropometric measurements included body mass, height, leg lengths, inter-ASIS distance, ankle and knee widths, elbow and wrist widths, hand thickness, hip rotation, and tibial torsion. Observational analysis of foot structure in the standing and prone-lying positions, e.g., hindfoot, midfoot, and forefoot, revealed no significant deviations from normal in all participants. An anthropometer was used to determine the inter-ASIS distance, ankle and knee widths, elbow and wrist widths, and hand thickness measures. A tape measure was used for leg length measurements [37,38]. Physical examination and anthropometric measurements were performed by the same researcher for each participant. Markers were placed on the body using two-sided, hypoallergenic tape. Extra tape was applied around the marker bases to minimize marker movement and prevent detachment. Once the markers were placed, the participants had an opportunity to warm up, including dynamic stretching, to prevent injury and to prepare for data collection. To best expose the relevant anatomy for marker placement, the participants wore tight shorts and a sports bra.
2.3. Protocol
2.3.1. Static Standing Calibration and Test Walking Trial
1. A static standing calibration trial was used to establish the participants’ pose, location of anatomical and technical markers, and joint centers.
2. The pose was captured while the participants stood in an anatomical position with their feet shoulder-width apart, knees slightly bent, and arms slightly abducted for four seconds.
3. Following the static trial, a self-selected speed walking trial was conducted and processed to verify the marker placement accuracy and to compare the accuracy of the knees’ frontal and transverse plane kinematics to the laboratory’s control dataset. In the walking trial, the participants traversed the calibrated volume along the positive y-axis (see the LCS in Figure 3).
2.3.2. Pirouette Data Collection
For pirouette data collection, the participants faced in the negative-x direction (relative to the laboratory coordinate system), with both feet on FP5 (Figure 3). The participants were allowed time to practice their turns to become comfortable with the floor surface and attached markers.
1. In preparation for the turn phase, the dancers placed their right leg laterally (positive-y), and then posteriorly (positive-x), onto FP3. The turn phase began when the right leg moved off FP3 (toe-off) and ended when the right leg made ground contact on or near FP3 (toe-touch).
2. A verbal cue was given to the dancer to execute the pirouette. Two pirouette conditions were tested: (1) one turn and (2) three turns, both initiated from the 4th position. The order of the turn trials was randomly assigned at the beginning of each participant’s session to decrease the carry-over effect of fatigue and increase the trials’ consistency.
3. The participants were given 30 s in between each attempted pirouette. The turns were considered successful if the participant executed the desired number of turns without hopping on their stance leg on the force plate surface area within toe-off and toe-touch on or near FP3. Both the one- and three-turn conditions were performed until five successful trials were captured for each condition.
For this study, only data from the single-turn pirouette were analyzed. Of the five successful single-turn trials for each participant, three were analyzed based on the following criteria: (1) the stance leg having maintained contact with the FP5, (2) the greatest amount of time spent in demi-pointe, and (3) the least translation of the BoS across the force plate throughout the turn phase.
2.4. Data Analysis
2.4.1. Data Reduction
Raw marker trajectory and ground reaction force data were reduced using Vicon Nexus v2.8.2. Trajectory data were smoothed using a Woltring filter (MSE 15), and raw ground reaction force data were filtered with a 4th-order, zero-lag Butterworth (high-pass cut-off 10 Hz). Nexus dynamic pipelines were used to determine joint kinematics and kinetics, as well as pirouette cycle events, i.e., initial toe-touch, toe-off (i.e., turn initiation), and second toe-touch. These data were exported to Visual3D biomechanics software v2021.11.3 (C-Motion Inc., Germantown, MD, USA) for recreating the PiG and Oxford Foot models, and for data reduction. The PiG model was modified by using Harrington’s predictive equations to determine the hip joint center [39]. Using a 15-link biomechanical model, the total body CoM was defined as the center of mass in three-dimensional space and was computed as the weighted average of each body segment’s CoM [40,41]. The velocity of the CoM was estimated using a first-order difference formula [40].
The primary variables of interest included the (1) anterior/posterior (A/P) and mediolateral (M/L) excursion of the XCoM from the CoP, and the (2) A/P and M/L excursion of the XCoM from the BoS center. Secondarily, we determined the CoM–CoP angle of inclination, or topple angle, since this has previously been examined as a measure of balance control in dancers. These variables were determined for a one-turn pirouette from the time of right toe-off from FP3 (Figure 3) to the time of right toe-touch on FP3.
The locations of the CoM and CoP, determined in Visual 3D throughout the turn phase, were used to calculate the topple angle [12]. The topple angle was the CoM–CoP inclination angle between the vertical projection of the CoM to the ground and a line connecting the CoM to the most lateral position of the CoP (Figure 4).
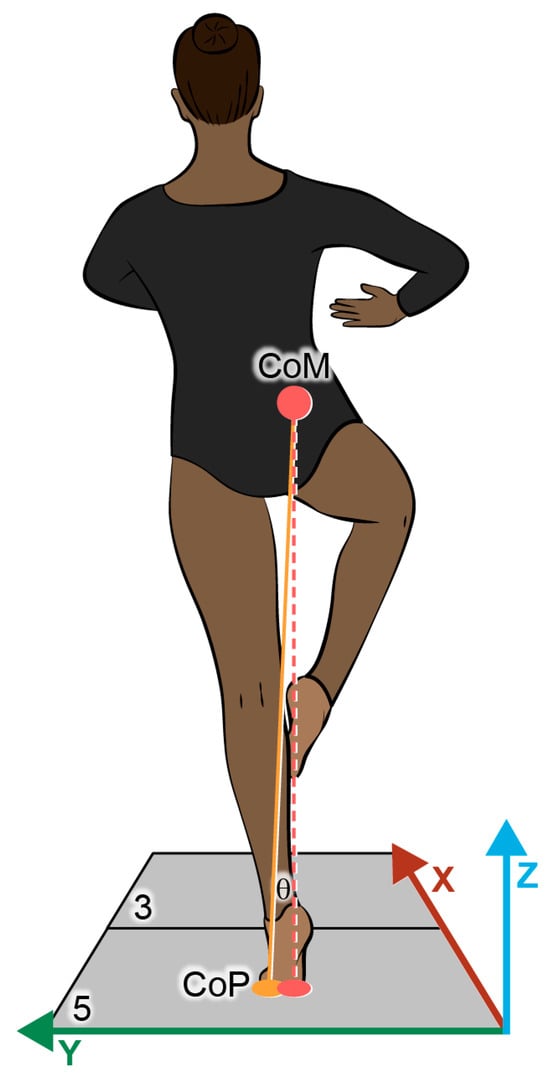
Figure 4.
The topple angle, θ, is the angle between the vertical dotted line and the line connecting the dancer’s CoM to the center of the CoP on the floor. Note the dancer’s position relative to the laboratory coordinate system orientation.
Based on rigid-body and IPM assumptions, the XCoM accounted for the projection of the CoM and its horizontal velocity, and it was computed as follows:
where ; = angular natural frequency of the pendulum, g = 9.81 m/s, and l = leg length (defined as the distance from the CoM and ankle joint center); is the CoM projected to the floor; and is the instantaneous position and velocity of the body’s CoM [13].
The BoS was described as the BoS center, defined by the head and bases of the 1st and 5th metatarsal anatomical markers, and expressed using a virtual foot coordinate system, i.e., virtual LFT left CS, projected to the ground. Based on these four markers, two vectors were created: (1) one from the midpoint of the proximal markers to the midpoint of the distal markers, and (2) one from the midpoint of the lateral proximal and distal markers to the midpoint of the medial proximal and distal markers. These two vectors intersected at a unique point in between all four markers, and that point was projected to the floor. The point created was labeled the BoS center and was used to define the BoS about which the dancer turned (Figure 5).
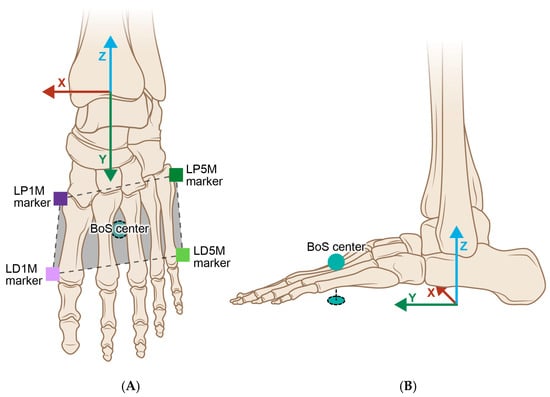
Figure 5.
(A) The BoS center was determined for this study by the boundary created by the left proximal 1st metatarsal (LP1M), left distal 1st metatarsal (LD1M), left proximal 5th metatarsal (LP5M), and left distal 5th metatarsal (LD5M) markers; (B) the virtual LFT foot coordinate system originated at the left ankle joint center and then projected to the floor, with the y-axis representing the A/P direction of the left foot and the x-axis representing the M/L direction of the left foot.
The margin of stability (MoS) during a one-turn pirouette was determined by the XCoM, the CoP, and the BoS center (defined above) in the virtual LFT foot CS, which necessitated transforming the CoP from the LCS to the virtual LFT foot CS. In the first case, the anteroposterior (A/P) and mediolateral (M/L) was determined as follows:
In the second case, the A/P and M/L was determined as follows:
where MoS is the distance in millimeters (mm) between the XCoM and (1) the CoP and (2) the midpoint boundary, i.e., BoS center. The measurements of the distance in mm from XCoM to the CoP and from XCoM to the BoS center were determined along the y- (A/P) and x- (M/L) axes in the virtual LFT foot coordinate system (Figure 6), hereafter referred to as the A/P and M/L axes.
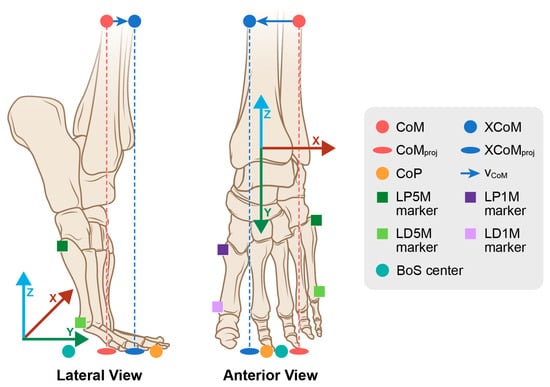
Figure 6.
The MoS was determined in two ways during a successful turn: (1) the distance from the XCoM to the BoS center, and (2) the distance from the XCoM to the CoP. The MoS represents the magnitude of excursion that the XCoM moves relative to the BoS center or the CoP as the dancer balances while turning. Note the orientation of the left foot virtual coordinate system.
2.4.2. Statistical Analysis
Statistical analysis was performed using R: A Language and Environment for Statistical Computing (4.4.3) [R Core Team (2025); R Foundation for Statistical Computing, Vienna, Austria. <https://www.R-project.org/>, accessed on 1 March 2021] and JMP Pro 14 software (SAS Institute Inc., Cary, NC, USA). Demographic data (i.e., gender, age, etc.) were analyzed using descriptive statistics (mean and standard deviation). The sample size was too small to warrant the use of a nested random design for intra- and inter-participant variation. Instead, simple group means without inferential statistics were calculated for the four margin-of-stability metrics (mm) along the A/P and M/L axes of the virtual left coordinate system and the topple angle (degrees).
Each measurement (n = 101) throughout each trial’s turn phase was used to calculate the mean absolute measurement for each trial. The intra-participant standard deviation (SD) and coefficient of variation (CV%) were then calculated between the three trial means for each participant and between the four participant means for inter-participant values. The advantages of using CV% are twofold: (1) it is independent of the units of measurement, and (2) it expresses the standard deviation as a proportion of the mean, accounting for differences in the magnitude of the mean. Thus, the CV is a measure of relative variability. Examining the CV was used to examine the variation across variables as well as participants. Since the CV is a function of the standard deviation, its usefulness may be limited by overly large or small standard deviations when using a small sample size (as in this study).
3. Results
All of the participants were female elite amateur ballet dancers. The demographic characteristics of the participants included mean age (24.25 ± 2.05 years), height (162.1 ± 4.12 cm), body mass (54.08 ± 5.94 kg), and BMI (20.51 ± 1.32 kg/m2).
The positions of the CoM, XCoM, and CoP were determined in two coordinate systems: the laboratory coordinate system (LCS) and the virtual LFT foot coordinate system (LFT CS). A representative participant and trial was used to demonstrate the changes in position for all variables, and to demonstrate the relationship between the CoM, XCoM, and CoP along the A/P and M/L axes of both coordinate systems. A summary of the mean (±1 SD) data across all participants can be found in Appendix B.
3.1. Excursions of the CoM and XCoM Relative to Laboratory and Left Foot Coordinate Systems
3.1.1. CoM and XCoM Relative to the CoP in the LCS
At the beginning of the turn, along the M/L axis, we noted greater excursion of the XCoM away from the LCS origin, i.e., to the right, and beyond the constraint of the CoP. The movement of the CoM was minimal. By approximately 50% of the turn, the CoM and XCoM appeared to converge, and both were within the CoP. At about 75% of the turn, we again noted greater excursion of the XCoM. Prior to toe-touch, i.e., the end of the turn, the movements of the CoM and XCoM again converged but were both somewhat beyond the CoP, which moved farther to the right, i.e., a greater distance from the LCS origin (left graph in Figure 7).
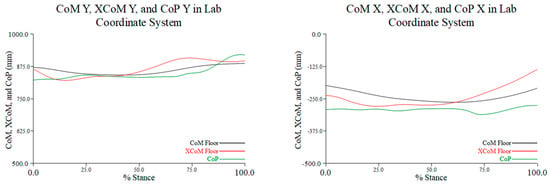
Figure 7.
The location of the projected CoM onto the floor (black), projected XCoM (red), and CoP (green) of the stance leg along the y- (M/L) (graph on the left) and x- (A/P) axes (graph on the right) of the LCS, in percent stance, during the turn phase of a representative trial. For movement along the M/L axis, a larger value indicates movement toward the origin (or to the right); along the A/P axis, a reduced negative value indicates a posterior movement, and a greater negative value indicates a forward movement (see Figure 3).
At the initiation of the turn phase, the CoM was more posterior than the XCoM relative to the CoP, along the A/P (or x) axis in the LCS. At midstance the CoM and XCoM appeared to converge and moved anterior. During the final 25% of the turn, the CoM and XCoM moved posterior, with greater excursion of the XCoM relative to the CoP. The center of pressure maintained a relatively constant position during the entire turn (right graph in Figure 7), more so than its path along the M/L axis.
3.1.2. CoM and XCoM Relative to the CoP in the LFT CS
Along the A/P axis during turn initiation, both the CoM and XCoM moved in an anterior direction relative to a relatively stationary position of the CoP. Just prior to 50% stance during the turn phase, the CoM and XCoM reached a maximum anterior position and moved slightly beyond the CoP. From midstance to toe-touch (100% of stance during the turn phase), both the CoM and XCoM were less anteriorly positioned relative to the CoP; the XCoM exhibited slightly greater excursion than the CoM (left graph in Figure 8).
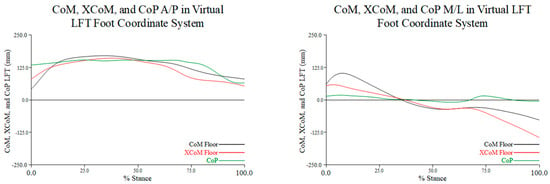
Figure 8.
The location of the projected CoM onto the floor (black), projected XCoM (red), and CoP (green) of the stance leg along the y- (A/P) (graph on the left) and x- (M/L) (graph on the right) axes of the LFT CS, in percent stance, during the turn phase of a representative trial. For movement along the A/P axis, a positive value indicates anterior positioning and posterior movement as the metrics approach the origin, i.e., 0; for movement along the M/L axis, a positive value reflects movement to the right (or medial), and negative values reflect a posterior excursion (see Figure 5).
During turn initiation along the M/L axis, both the CoM and XCoM moved right, i.e., medial, relative to the LFT CS origin, with the CoM a greater distance away. At 50% stance during the turn phase, the positions of the CoM and XCoM converged, having moved to the left, i.e., lateral, of the coordinate system’s origin. At toe-touch, both the CoM and XCoM continued to move further left of the system’s origin, with the XCoM having demonstrated greater excursion (right graph in Figure 8).
Figure 7 and Figure 8 illustrate the position of the CoM and XCoM relative to the CoP in both the LCS and LFT CS. Note that both metrics approached, or briefly passed, the base of the support boundary, which offered a potential for loss of balance. However, since we did not analyze any trial where the dancer hopped or demonstrated other recovery movements, any potential falter was clearly controlled.
3.2. Comparison of the Two Methods for Determining the MoS: XCoM to CoP and XCoM to BoS Center
3.2.1. MoS Excursion Patterns
The magnitudes of the MoSs were greater at turn initiation and toe-touch. During the turn phase along the A/P axis (left graph in Figure 9), the XCoM generally moved from posterior to anterior to posterior relative to both the CoP and BoS center. From approximately 20% to 50% of stance during the turn phase, the MoS was minimized, as the XCoM appeared to be closely aligned with both the CoP and BoS center. At 75% stance during the turn phase, the same pattern of movement of the XCoM relative to each reference point was noted, but with greater distance between the XCoM and the CoP.
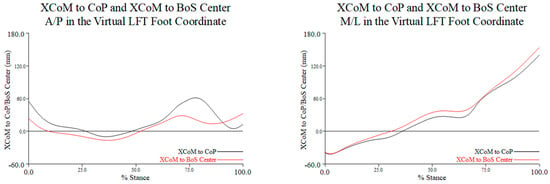
Figure 9.
The distance in millimeters between XCoM and CoP of the stance leg (black) and the distance between the XCoM and BoS center (red) along the A/P (graph on the left) and M/L (graph on the right) axes of the LFT CS throughout the turn phase, in percent stance. Positive values along the A/P axis indicate that the CoP or BoS center is anterior to the XCoM, and negative values indicate that the CoP or BoS center is posterior to the XCoM; positive values along the M/L axis indicate that the CoP or BoS center is medial to the XCoM, and negative values indicate that the CoP or BoS center is lateral to the XCoM. Note: distance is the excursion or movement of the XCoM relative to the CoP and the BoS center.
From turn initiation to toe-touch, the movement of the XCoM along the M/L axis was very similar relative to both the CoP and the BoS center. The minimum magnitude of the MoSs was reached from approximately 20% to 40% of stance during the turn phase. These relationships from 0% to 30% stance during the turn phase indicated that the XCoM was medial to the CoP and the BoS center, which increasingly moved lateral to the reference points by toe-touch (right graph in Figure 9). As noted with MoS along the A/P axis, the MoSs along the M/L axis were largest at the beginning and end of the turn.
3.2.2. Magnitude and Variability of MoS Excursion
At this point, we presented data from a representative trial and participant to demonstrate the general relationships between the CoM, XCoM, CoP, and BoS center and the margin of stability during the one-turn pirouette. We were also interested in the magnitude and variability of the MoS, since it is a marker of control during dynamic activities. Although there are limitations imposed by our sample size, some generalizations can be highlighted by observation from Table 1.
- -
- There was a larger mean MoS in the M/L direction for XCoM to both the CoP and the BoS center.
- -
- Each participant demonstrated the largest coefficients of variation with XCoM to the BoS center in the A/P direction.
- -
- Participants #1 and #5 demonstrated the largest mean MoS in the M/L direction for XCoM to the CoP and the BoS center.
- -
- Participant #2 demonstrated the smallest mean MoS in the A/P direction for XCoM to the CoP and the BoS center.

Table 1.
The mean (mm), SD, and CV for the distance from XCoM to the BoS center and from XCoM to the CoP for each participant in the A/P (y-axis) and M/L (x-axis) directions in the LFT CS.
Table 1.
The mean (mm), SD, and CV for the distance from XCoM to the BoS center and from XCoM to the CoP for each participant in the A/P (y-axis) and M/L (x-axis) directions in the LFT CS.
| Variable | Axis | Participant 1 Mean (SD) mm | CV (%) | Participant 2 Mean (SD) mm | CV (%) | Participant 3 Mean (SD) mm | CV (%) | Participant 5 Mean (SD) mm | CV (%) |
|---|---|---|---|---|---|---|---|---|---|
| XCoM to BoS Center | x | 57.57 (9.82) | 17.06 | 43.87 (10.58) | 24.12 | 41.82 (12.26) | 29.31 | 67.93 (11.03) | 16.24 |
| XCoM to BoS Center | y | 23.13 (11.80) | 51.01 | 12.78 (3.49) | 27.35 | 17.36 (7.65) | 44.04 | 25.24 (8.22) | 32.56 |
| XCoM to CoP | x | 50.34 (9.86) | 19.60 | 40.44 (10.19) | 25.18 | 38.49 (9.21) | 23.94 | 68.22 (10.87) | 15.93 |
| XCoM to CoP | y | 20.29 (0.26) | 1.29 | 18.67 (2.73) | 14.64 | 23.24 (4.95) | 21.29 | 22.21 (5.39) | 24.29 |
We also examined the mean MoS across all participants (Table 2) and made the following observations:
- -
- The MoS in the M/L direction demonstrated greater values.
- -
- There was greater mean variation in the MoS in the M/L direction.
- -
- The largest coefficient of variation was the excursion of the XCoM to the BoS center in the A/P direction.

Table 2.
The mean (mm), SD, and CV for the distance from XCoM to the BoS center and from XCoM to the CoP across the four participants in the A/P (y-axis) and M/L (x-axis) directions in the LFT CS.
Table 2.
The mean (mm), SD, and CV for the distance from XCoM to the BoS center and from XCoM to the CoP across the four participants in the A/P (y-axis) and M/L (x-axis) directions in the LFT CS.
| Variable | Axis | Mean (SD) mm | CV (%) |
|---|---|---|---|
| XCoM to BoS Center | x | 52.80 (12.28) | 14.31 |
| XCoM to BoS Center | y | 19.63 (5.65) | 23.25 |
| XCoM to CoP | x | 49.37 (13.60) | 27.54 |
| XCoM to CoP | y | 21.10 (2.03) | 9.62 |
3.3. Topple Angle
The same participant and representative trial that were used to demonstrate the CoM, XCoM, and COP metrics were used to examine the topple angle. The topple angle was determined in the LFT CS. It reached a maximum of approximately 6.5° at turn initiation and its minimum value around 50% to 60% of stance during the turn phase, and it began to increase as the dancer neared toe-touch (Figure 10).
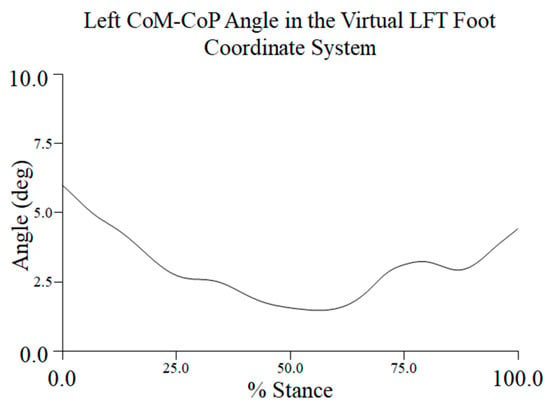
Figure 10.
The topple angle during the turn phase, in percent stance. This angle is created by the vertical projection of the CoM to the ground and a line connecting the CoM to the most lateral position of the CoP.
Group descriptive statistics showed that, across participants, the mean topple angle ranged from approximately 2.8° to 3.9°. The between-trial variability, i.e., coefficient of variation (CV%), for the participants ranged from approximately 11% to 23% and was nearly 20% across the participants (Table 3 and Table 4).

Table 3.
The mean (degrees), SD, and CV for the topple angle within participants in the LFT CS.

Table 4.
The mean (degrees), SD, and CV for the topple angle across all participants in the LFT CS.
4. Discussion
Previous research using the inverted pendulum model to examine the biomechanical properties of pirouettes is limited. The purpose of this research was to measure and examine the MoS and topple angle as measures of dynamic balance during a single-turn pirouette in female amateur ballet dancers.
4.1. Rationale for Using Different Coordinate Systems: Comparison of Dynamic Balance Metrics in the LCS Versus the LFT CS
Dynamic balance was calculated using two different coordinate systems: a laboratory coordinate system (LCS) and left foot coordinate system (LFT CS). The location of the dancer’s starting position on the force plates was never the same during data collection; therefore, the CoP and BoS would have variable initial positions for each trial. Since we decided not to standardize the participants’ fourth-position initial postures, we believed that it was important to analyze our data determined using both the LCS and LFT CS. We believed that using the LFT CS, located on the stance foot that moved with the dancer, would allow for a more consistent representation of the results between trials and across participants, because it was unaffected by the difference in starting locations.
It is important to recall that the orientation of the two coordinate systems was different. In the LCS, the x- and y-axes represented anteroposterior and mediolateral motions, respectively (Figure 3). Because we used FPs #3 and #5 to record the dance turns, the orientation of the left foot on FP3 dictated that its CS would have the x- and y-axes represent mediolateral and anteroposterior motions in the LFT CS, respectively (Figure 5). Therefore, we compared the results that were generated using different coordinate systems: (1) the left graph in Figure 7 to the right graph in Figure 8 for the M/L excursions of the CoM and XCoM, and (2) the right graph in Figure 7 to the left graph in Figure 8 for the A/P excursions of the CoM and XCoM.
Along the mediolateral axes of both coordinate systems, we observed greater excursion of the XCoM than the CoM, relative to the CoP. The greater excursion of the XCoM may be explained by its relationship to its velocity component. However, in the LFT CS, both the CoM and XCoM moved left (lateral) similarly, relative to the CS’s origin during the later part of the turn, with seemingly greater excursions away from the CoP than observed in the LCS. Convergence of the CoM and XCoM movements near midstance (or mid-turn) was shown using either CS. There appeared to be less variation of the CoP during the turn when evaluated using the LFT CS. This may indicate that the dancer’s turn foot may not have translated appreciably during the turn phase in the M/L direction.
The A/P excursion time series in the LCS generally demonstrated a U-shaped pattern. Both the CoM and XCoM moved anterior from turn initiation to about 60% stance during the turn phase and then moved posterior until touch; they remained posterior to the CoP, which remained approximately constant during the turn. Each time series had a unique position, but the XCoM demonstrated a larger excursion throughout the turn. The CoM and XCoM time series in the LFT CS demonstrated an inverted U-shape, and their movement characteristics were similar, with the following exception: from approximately 20% to 60% of stance during the turn phase, they were nearly coincident. Along the A/P axis, excursion of the XCoM was greater only in the LCS. Contrary to what we identified relative to variation in the CoP time series along the M/L axis, there was less variation in the CoP during the turn when evaluated using the LCS, suggesting that translation of the supporting foot in the A/P direction was minimal. In contrast to our data, Lott [12] reported a Pearson’s r = 0.873 between the percent distance movement of the normalized (to dancer’s height) BoS and the number of pirouette revolutions. Based on this finding, Lott concluded that some translation of the body must have occurred in order to maintain balance when performing multiple-turn pirouettes. An apparent inconsistency in the dynamics of the CoP time series analyzed using different coordinate systems in our study suggests that additional research is needed to understand the role of total-body translation during the performance of a pirouette. In summary, we initially intuited that using a virtual coordinate system fixed to the foot would provide more reliable data on the neurological response, i.e., CoP dynamics, to postural challenges during a pirouette. However, that may not be the case, since our results demonstrated that the use of either coordinate system provided meaningful data and insights on dynamic balance metrics during a one-turn pirouette.
4.2. Margin of Stability
The margin of stability, defined as the distance between the XCoM and the border of an individual’s BoS at any given moment, has been proposed as a measure of stability during dynamic situations [13]. In the classic inverted pendulum model, the CoM needs to stay within the boundaries of the BoS to maintain stability [41]. However, Pai and Patton showed that this condition, i.e., CoM within the BoS, was not applicable to dynamic situations, e.g., walking, and that the velocity of the CoM needed to be accounted for when predicting the maintenance of stability [42]. That is, although the CoM lies within the BoS, the CoM velocity is pointing away, so stability may not be achieved if the CoM velocity is sufficiently large. Conversely, if the CoM is outside the BoS, stability may be regained if the CoM velocity is pointing towards the BoS. Based on the work of [42,43], Hof et al. [13], using the linear IPM, derived the extrapolated center of mass as XCoM, as the velocity- and eigenfrequency-adjusted projection of the CoM.
For this study, we defined the MoS using two different equations: (1) BoS center–XCoM and (2) CoP–XCoM. We used the first and fifth metatarsal foot markers (from the OFM) as the boundary of the BoS center to avoid over- or under-estimating the distancing MoS along the A/P and M/L axes. The CoP was used as the preferred reference for determining the MoS, since it represents the neurological response to perturbation. The distance between the XCoM and the BoS center appeared similar to the distance between the XCoM and the CoP along the M/L and A/P axes throughout the turn phase (Figure 9). This suggests that during a single-turn pirouette, the BoS center and the CoP remained near each other, which was expected, since the CoP is the plantar location of the vertical ground reaction force and the BoS center was a discrete point within the forefoot. Our results suggest that either a BoS, as we determined, or the CoP would equally render valid and reliable MoS measures for research related to investigating the mechanics of single- or multi-turn pirouettes.
Using a representative participant and trial, we found that, along the A/P axis, the magnitudes of the MoSs were greater at turn initiation and toe-touch, although they were different (left graph in Figure 9). This greater MoS was likely related to beginning the turn in the fourth position and then making foot contact on FP3 at the end of the turn phase, rather than some compensation for an internal perturbation. During the period from 20% to 50% of stance during the turn phase, the MoS was minimized, as the XCoM appeared to be closely aligned with both the CoP and the BoS center, suggesting a period of good dynamic balance. From turn initiation to toe-touch, the movement of the XCoM along the M/L axis was very similar relative to both the CoP and the BoS center (right graph in Figure 9). The magnitude of the MoSs appeared reduced, from approximately 20% to 40% of stance, during the turn phase, suggesting that this was a period of relatively good postural control. On the other hand, the MoS magnitudes were generally greater along the M/L axis, particularly at the beginning and end of the turn, an indication that balance in the mediolateral direction may have been more challenging. For both methods used to determine the MoS, the greatest mean values, as well as participant and cohort variability, were found along the M/L axis for each individual and for the cohort, which may support our speculation that mediolateral control was more challenging (Table 1 and Table 2).
We determined the coefficient of variation, i.e., CV%, within and across participants because of its potential to provide insight into both biological and inter-individual variability. The inter-trial CVs ranged from 27% to 51% along the A/P and from 16% to 29% along the M/L axes for XCoM to the BoS center, whereas they ranged from 1% to 24% along the A/P and 16% to 25% along the M/L axes for XCoM to CoP. In general, it appears that inter-trial variation was moderately large, yet differences between individuals make it difficult to attribute this primarily to biological variation. The inter-participant CVs for the XCoM to the BoS center along the A/P and M/L axes were 23% and 14%, respectively, while for XCoM to the CoP they were 10% and 28% along the A/P and M/L axes, respectively. Previously, we suggested that control along the M/L axis may have been more challenging. However, the variability both within and between participants generally demonstrated mixed CV% magnitudes of variability for MoS metrics along the A/P and M/L axes, posing a challenge for making any reasonable generalizations. Additional research using different methods is likely needed to further investigate the natural biological variability related to ballet pirouettes.
In a seminal paper, Hof et al. [13] tested their margin of stability theory by collecting force plate data on healthy participants under four standing conditions (5 s)—(1) standing on two feet, (2) standing on one foot, (3) standing tiptoe on two feet, and (4) standing tiptoe on one foot—and a fifth condition: walking on an instrumented treadmill at a self-selected speed. They determined the BoS by recording the extreme boundaries of the CoP collected as the participant stood on one foot (using support to maintain balance) and shifted their weight as much as possible laterally, anteriorly, medially, and posteriorly; in this way, the boundary of the BoS was recorded as a loop of the CoP. Two pieces of information are somewhat germane to our results: First, they reported a mean margin of stability of −9.3 (±14) mm for the standing tiptoe on one foot condition. Although the magnitude of that MoS was much smaller than our results along either the A/P or M/L axes, the “sign” of their value indicated that the MoS was initiated outside the BoS, similar to what we found. Additionally, the smaller MoS magnitude that Hof et al. reported may be related to two factors: (1) our BoS center included a smaller area, and (2) performance of a pirouette is a more dynamic skill. Secondly, the relationships between the CoM, XCoM, and CoP reported by Hof et al. for one-foot tiptoe standing were like the results illustrated in Figure 7 and Figure 8. In the only study similar to ours, Lott [12] examined the MoS associated with the pirouette. She reported a negative MoS value at turn initiation and concluded, based on her cohort who performed multi-turn pirouettes, that dancers initiated pirouettes with the XCoM outside of the BoS, a finding consistent with ours.
4.3. Topple Angle
The stability of a dancer during a pirouette can also be evaluated by examining the topple angle throughout the turn phase. The topple angle from a representative trial and participant was greater at turn initiation and termination, periods when the dancer was in fourth position and toe-touch, respectively. This finding is similar to what we observed with the MoS along both the A/P and M/L axes, suggesting that both of these metrics may be useful in characterizing balance control during the performance of pirouettes. As illustrated in Figure 1, several factors during the early and later phases of the pirouette contribute to a “splaying” of the body’s CoM and, thus, a greater topple angle: (1) the hips are flexed (left)/extended (right) and externally rotated, (2) the arms are away from the body, and (3) both feet are on the ground, with an approximate BoS shoulder-width apart. The topple angle was reduced at 50% of stance during the turn phase, while the dancer balanced on the ball of their turning foot. During this short time period, the location of the CoM must coincide as much as possible with the reactive CoP to maintain the dancer’s balance. As we showed, the approximate midpoint of the turn was also a period when the MoS along both the A/P and M/L axes was minimized. Recall, however, that there was some evidence that the CoP translated as adjustments to control the CoM.
For the participant and trial chosen, the topple angle’s maximum and minimum values were approximately 6.5° and 2.4°, respectively. The mean topple angle from the time series across participants was 3.34° (±0.66)°, with a range of 2.75° to 3.88°. The range of intra-participant (inter-trial) variations (CV%) was 10.9% to 23.3%, values suggestive of biological variability and experience level. The CV% across all participants (19.9%) may also be indicative of differences in skill between dancers.
In our review of the literature, several findings were of interest. Lott and Laws [16] tested nine dancers (eight female, one male) aged 16 ± 2.3 years who had intermediate-to-advanced training. A maximum topple angle of 9.3° ± 1.9° during the attempt at multi-turn pirouettes was reported. In a later study, Lott [12] reported a maximum topple angle of 9.8° ± 6.8° during multi-turn pirouettes in adolescent female dancers (16 ± 1.4 years). Likewise, Lin et al. [3] found that novice dancers, compared to experienced dancers, exhibited greater and more variable topple angles in the anteroposterior and mediolateral directions during the preparatory, double-leg support, and ending phases of a single-turn pirouette. These results likely reflected the reduced expertise in both studies. Zaferiou et al. [19], employing 10 female professional and pre-professional dancers (aged 20.4 ± 3.17 years) in a study of one- and two-turn pirouettes and piqués, reported a mean topple angle of 4° ± 1° for both types of pirouettes. However, for single and double piqués, they reported mean angles of 13° ± 2° and 8° ± 1°, respectively. More recently, Tsubaki et al. [31] measured the topple angle, i.e., posterior inclinations, of single pirouettes, comparing professional and experienced amateur dancers (aged 21.9 ± 2.6 years) donning pointe shoes. They analyzed three phases—turning with double-leg support (TDS), turning with single-leg support (TSSp), and turning with single-leg support in mid-swing (TSSm)—and found no difference between groups in the TDS and TSSp phases. Professional dancers, however, demonstrated a significantly reduced topple angle during TSSm (2.05° ± 0.90° to 3.88° ± 1.67°). As in [12], it appears that the less experienced dancers in [32] exhibited more variability. However, it is difficult to make comparisons between studies, because of methodological differences. For example, our mean topple angles may differ slightly because the CoP was mapped in a foot coordinate system. Moreover, some studies measured the maximum topple angles prior to compensatory hops during multi-turn pirouettes. Our results are most comparable to those reported by Zaferiou et al. [19] and Tsubaki et al. [32]. What our study has added to previous work is an extended look at trial-to-trial and across-participant variability, i.e., CV%. We reported the variability using both standard deviations and coefficients of variation to illustrate the biological variability that is inherent even in elite amateur dancers who completed single-turn pirouettes successfully. This biological variability suggests that the time series of the pirouette balance metrics that we recorded have dynamic (and chaotic) characteristics that cannot be fully understood using the typical linear measures that we used in this study. Thus, future research on the biomechanics of dance and control of dynamic balance should consider tools that are relevant to non-linear time series.
4.4. Methodological Limitations
This study was limited by its small sample size, the inclusion of only female elite and amateur ballet dancers, and the variability in performance experience in the participants. This limits the applicability of this study’s data to male or professional dancers; therefore, further research should be conducted to examine male and professional-level populations. In this study, the dancers were instructed to perform en dehors pirouettes, decreasing the generalizability of the results to other styles of pirouettes. All of the participants chose to perform their turns standing on their left leg, limiting the application of the results to pirouettes performed with a right stance leg. The participants in this study used ballet slippers rather than pointe shoes when performing their turn, to allow for correct marker placement on the foot and ankle, so the results of this study are limited in their applicability to maintaining stability during a single-turn pirouette when wearing ballet shoes. The laboratory setting may also have caused limitations to the dancers’ ability to complete a successful turn by constraining them to land their turn within the area of the force plate. This was done to provide some control of their landing point, for the purpose of recording toe-off and toe-touch of their turn leg to define the start and end of the turn phase. The order of triple or single pirouette turn conditions was randomized by a coin toss to reduce error caused by fatigue across dancers. However, for each dancer, a significant number of turns were performed for each of the turn conditions, which may have added a fatigue component that impacted their performance for both turn conditions. Error due to fatigue from repeated testing was minimized by allowing the dancers breaks between turn trials. Error from soft tissue artifacts related to the use of the PiG model is expected for all studies using motion capture with markers. However, this study did not analyze joint angles or net joint moments, which are affected most by soft tissue artifacts.
4.5. Implications for Further Research
Further research is needed with a larger sample of both male and female professional dancers to analyze the MoS during pirouettes with single and multiple rotations on both the left and right stance legs. This may increase the external validity of the data across ballet dancers, providing insight into faulty mechanics that could lead to injury. Future research involving other styles of pirouettes would also be beneficial to assist with training and improving the performance of amateur and professional dancers. This would provide more information on how to improve their biomechanics with the variety of turn styles seen in ballet choreography. To further increase the applicability to female amateur and professional dancers, further research on MoS and dynamic balance with dancers in pointe shoes would be beneficial, since most of their performances are performed with pointe shoes. Additionally, future research involving dance mechanics should consider alternative methods that improve the validity of the MoS or offer an alternative measure of stability, as suggested by Terry et al. [44] and Kazanski et al. [45], respectively. Terry et al. identified a limitation of the MoS, as originally described by Hof et al. [13], for activities where the CoP is not stationary (e.g., walking, dancing, etc.), and they offered a possible solution. Likewise, Kazanski et al. suggested a MoS-related metric, i.e., probability of instability, which may be a more insightful measure of mediolateral stability. Since the design of this study did not include consideration of inertia forces, future research might also consider methodological approaches that combine the measure of the MoS with the examination of preferred kinematic and muscular synergistic coordination strategies [46]; a combination of musculoskeletal modeling, electromyography, and induced acceleration analysis [47,48,49,50]; the application of whole-body angular momentum [51,52,53] or the mechanics of spinning tops [54] and their relationship to the pirouette motion; or the use of non-linear methods [55,56]. We believe that any combination of the use of biomechanical methods may provide valuable information on the dynamics of balance control in a pirouette. Thus, a better understanding of dynamic balance may be able to assist the dancer in preventing injuries related to incorrect dance mechanics and overuse, or to improve the effectiveness of training and rehabilitation programs.
5. Conclusions
The MoS was used to examine dynamic stability during three successful single-turn pirouettes during the turn phase for each participant. The MoS distance was largest immediately after toe-off and just before toe-touch. The MoS distance was also greater along the M/L axis than the A/P axis. Although the topple angle may also provide some descriptive information on single-turn pirouettes, we believe that the MoS can provide more insightful information on the neurological control of dynamic balance. Margin-of-stability metrics may be useful to analyze amateur and professional dancers, to assist with training and performance, and to help decrease injury related to faulty mechanics.
Author Contributions
Conceptualization, A.D., A.K., N.M. and G.A.; methodology, G.A.; software, D.W.Z.; validation, G.A.; investigation, A.D., A.K., N.M. and G.A.; resources, G.A.; data curation, G.A.; writing—original draft preparation, A.D., A.K. and N.M.; writing—review and editing, A.D., A.K., N.M., D.W.Z. and G.A.; visualization, A.D., A.K., N.M. and G.A.; supervision, G.A.; project administration, G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of Grand Valley State University (protocol code: 19-296-H; approval date: 16 May 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
Lauren Hickox for technical assistance; Samantha Shelton for dance consultation. Lauren Hickox is acknowledged because of her contribution to data reduction but was not a co-author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IPM | Inverted pendulum model |
| CoM | Center of mass |
| XCoM | Extrapolated center of mass |
| BoS | Base of support |
| CoP | Center of pressure |
| MoS | Margin of stability |
| GRF | Ground reaction force |
| FP | Force plate |
| PiG | Plug-in Gait |
| OFM | Oxford Foot model |
| ASIS | Anterior superior iliac process |
| CPG | Peg marker posterior end of the calcaneus |
| CV% | Coefficient of variation percentage |
| A/P | Anteroposterior |
| M/L | Mediolateral |
| LCS | Laboratory coordinate system |
| LFT CS | Virtual left foot coordinate system |
| LP1M | Left proximal first metatarsal |
| LD1M | Left distal first metatarsal |
| LP5M | Left proximal fifth metatarsal |
| LD5M | Left distal fifth metatarsal |
Appendix A
Details of the markers required for the full body Plug-in-Gait (PIG) and Oxford Foot (OFM) biomechanical models.

Figure A1.
Left: anterior; Middle: right lateral; Right: posterior view of marker placement for the modified Plug-in-Gait (PIG) and Oxford Foot (OFM) biomechanical models. The PIG and OFM share several markers at the knee, shank (tibia), and foot. The majority of OFM markers are shown in the foot insets.

Table A1.
Upper and lower body PIG and OFM marker placement.
Table A1.
Upper and lower body PIG and OFM marker placement.
| Marker | Description-Position | Notes | |
|---|---|---|---|
| 1 | RFHD LFHD | Forehead | UBM |
| 2 | RBHD LBHD | Back of head | UBM |
| 3 | RSHO LSHO | Shoulder, Acromioclavicular joint | UBM |
| 4 | RUPA LUPA | Upper arm, 3-marker cluster laterally | UBM |
| 5 | RELB LELB | Elbow, Lateral epicondyle | UBM |
| 6 | RFRM LFRM | Forearm, Lower ⅓ lateral surface | UBM |
| 7 | RWRB LWRB | Wrist marker B, Ulnar styloid process | UBM |
| 8 | RWRA LWRA | Wrist marker A, Radial styloid process | UBM |
| 9 | RFIN LFIN | Finger, Head 3rd metacarpal | UBM |
| 10 | CLAV | Clavicle, Jugular notch | UBM |
| 11 | STRN | Sternum, Xiphoid process | UBM |
| 12 | C7 | Spinus process 7th cervical | UBM |
| 13 | RBAK | Right back (mid scapula) | UBM |
| 14 | T10 | Spinus process 10th thoracic | UBM |
| 15 | RASI LASI | Anterior superior iliac spine | PIG |
| 16 | RPSI LPSI | Posterior iliac spine | PIG |
| 17 | RTHI LTHI | Thigh (mid-lateral) | PIG |
| 18 | RKNE LKNE | Lateral femoral epicondyle | PIG/OFM |
| 19 | RMKNE LMKNE | Medial femoral epicondyle | PIG |
| 20 | RTIB LTIB | Tibia, Mid-lateral | PIG/OFM |
| 21 | RMED LMED | Medial malleoli (apex) | PIG/OFM |
| 22 | RLAT LLAT | Ankle, Lateral malleoli (apex) | PIG/OFM |
| 23 | RTOE LTOE | Midway between 2nd & 3rd metatarsal heads | PIG/OFM |
| 24 | RHEE LHEE | Heel (distal posterior calcaneus) | PIG/OFM |
| 25 | RHFB LHFB | Fibula (head) | OFM |
| 26 | RTUB LTUB | Tibial tubercle | OFM |
| 27 | RSHN LSHN | Mid-tibia (shank) | OFM |
| 28 | RPCA LPCA | Proximal posterior calcaneus | OFM |
| 29 | RSTL LSTL | Sustentaculum tali (apex) | OFM |
| 30 | RLCA LLCA | Lateral calcaneus | OFM |
| 31 | RP1M LP1M | Base 1st metatarsal | OFM |
| 32 | RD1M LD1M | Head 1st metatarsal | OFM |
| 33 | RP5M LP5M | Base 5th metatarsal | OFM |
| 34 | RD5M LD5M | Head 5th metatarsal | OFM |
| 35 | RHLX LHLX | Hallux, 1st proximal phalanx | OFM |
Markers will correspond to numbers and anatomical locations. Additional notes will indicate which model the markers are related to, and which markers are for static trials only; upper body model = UBM; L = left side of the body, R = right side. Note: (1) the RBAK marker has no equivalent marker on the left side (this asymmetry helps the auto labeling routine), (2) OFM shares several PIG marker placements, (3) the medial femoral epicondyle, medial malleoli, proximal calcaneal, and distal 1st metatarsal markers are removed after the static calibration trial, (4) modifications of the PIG and OFM models that were made for this research included use of a 3-cluster marker set for the upper arm and medial femoral epicondyle markers, and elimination of the CPG marker projection off of the mid-posterior calcaneus.
Appendix B
Mean ± 1 SD mm in percent stance across all trials and participants for all dynamic balance metrics examined in this study.
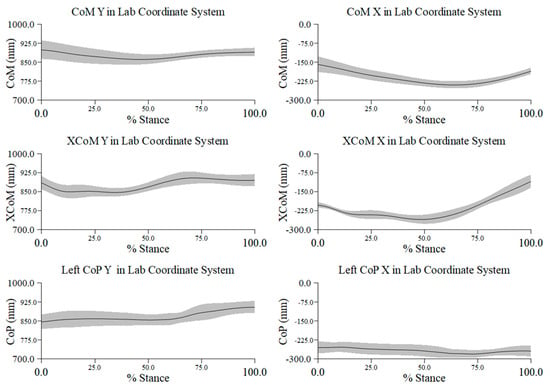
Figure A2.
Mean ± 1 SD mm in percent stance across all trials and participants for the center of mass (CoM), extrapolated center of mass (XCoM), and center of pressure (CoP) along the y- (mediolateral) and x- (anteroposterior) axes in the laboratory coordinate system (LCS). Negative distance along the x-axis is posterior, and along the y-axis it is lateral.
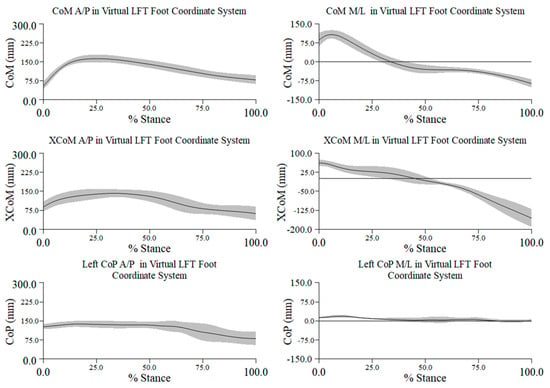
Figure A3.
Mean ± 1 SD mm in percent stance across all trials and participants for the center of mass (CoM), extrapolated center of mass (XCoM), and center of pressure (CoP) along the x- (mediolateral) and y- (anteroposterior) axes in the virtual left foot coordinate system (LFT CS). Negative distance along the x-axis is lateral, and along the y-axis it is posterior.
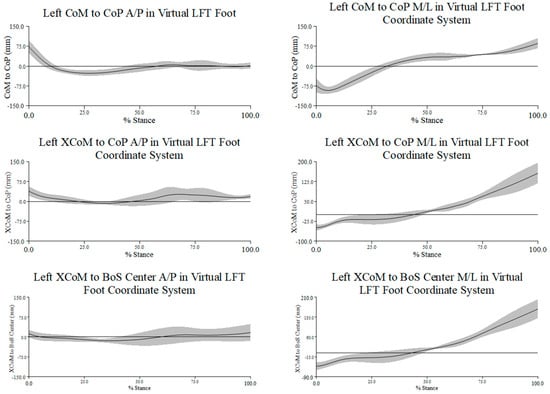
Figure A4.
Mean ± 1 SD mm in percent stance across all trials and participants for the distance from the center of mass (CoM) to the center of pressure (CoP), the extrapolated center of mass (XCoM) to the CoP, and the XCoM to the base-of-support center (BoS center) along the x- (mediolateral) and y- (anteroposterior) axes in the virtual left foot coordinate system (LFT CS). Negative distance along the x-axis represents the distance from the CoP or BoS center lateral to the CoM or XCoM; negative distance along the y-axis represents the distance from CoP or the BoS center posterior to the CoM or XCoM.
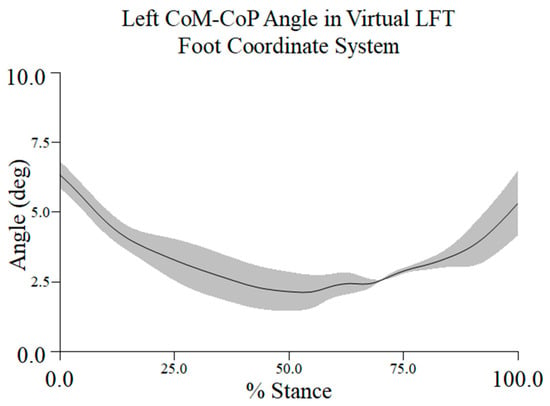
Figure A5.
Mean ± 1 SD mm in percent stance across all trials and participants for the topple angle. The topple angle was created by the vertical projection of the center of mass (CoM) to the ground and a line connecting the CM to the most lateral position of the center of pressure (CoP) in the virtual left foot coordinate system (LFT CS).
References
- Kim, J.; Wilson, M.A.; Singhal, K.; Gamblin, S.; Suh, C.-Y.; Kwon, Y.-H. Generation of vertical angular momentum in single, double, and triple-turn pirouette en dehors in ballet. Sports Biomech. 2014, 13, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Zaferiou, A.M.; Wilcox, R.R.; McNitt-Gray, J.L. Modification of impulse generation during pirouette turns with increased rotational demands. J. Appl. Biomech. 2016, 32, 425–432. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.W.; Su, F.C.; Wu, H.W.; Lin, C.F. Effects of leg dominance on performance of ballet turns (pirouettes) by experienced and novice dancers. J. Sports Sci. 2013, 31, 1781–1788. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A.; Patla, A.E.; Prince, F.; Ishac, M.; Gielo-Perczak, K. Stiffness control of balance in quiet standing. J. Neurophysiol. 1998, 80, 1211–1221. [Google Scholar] [CrossRef]
- Gage, W.H.; Winter, D.A.; Frank, J.S.; Adkin, A.L. Kinematic and kinetic validity of the inverted pendulum model in quiet standing. Gait Posture 2004, 19, 124–132. [Google Scholar] [CrossRef]
- Sung, J.-L.; Hong, C.-Y.; Liu, C.-H.; Lee, P.; Guo, L.-Y.; Lin, N.-H.; Yen, C.-W.; Liaw, L.-J. Characterizing the validity of the inverted pendulum model for quiet standing. J. Health Eng. 2021, 2021, 8884614. [Google Scholar] [CrossRef]
- Jian, Y.; Winter, D.A.; Gilchrist, I.L. Trajectory of the body COG and COP during initiation and termination of gait. Gait Posture 1993, 1, 9–22. [Google Scholar] [CrossRef]
- Günther, M.; Grimmer, S.; Siebert, T.; Blickhan, R. All joints contribute to quiet human stance: A mechanical analysis. J. Biomech. 2009, 42, 2739–2746. [Google Scholar] [CrossRef]
- Suzuki, Y.; Nomura, T.; Casadio, M.; Morasso, P. Intermittent control with ankle, hip, and mixed strategies during quiet standing: A theoretical proposal based on a double inverted pendulum model. J. Theor. Biol. 2012, 310, 55–79. [Google Scholar] [CrossRef]
- McGrath, M.; Howard, D.; Baker, R. The strengths and weaknesses of inverted pendulum models during human walking. Gait Posture 2015, 41, 389–394. [Google Scholar] [CrossRef]
- Morasso, P.; Cherif, A.; Zenzeri, J. Quiet standing: The single inverted pendulum model is not so bad after all. PLoS ONE 2019, 14, e0213870. [Google Scholar] [CrossRef] [PubMed]
- Lott, M.B. Translating the base of support: A mechanism for balance maintenance during rotations in dance. J. Dance Med. Sci. 2019, 23, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Hof, A.L.; Gazendam, M.G.J.; Sinke, W.E. The condition for dynamic stability. J. Biomech. 2005, 38, 1–8. [Google Scholar] [CrossRef]
- Hof, A.L. The ‘extrapolate center of mass’ concept suggests a simple control of balance in walking. Hum. Mov. Sci. 2008, 27, 112–125. [Google Scholar] [CrossRef]
- Curtze, C.; Buurke, T.J.W.; McCrum, C. Notes on the margin of stability. J. Biomech. 2024, 166, 112045. [Google Scholar] [CrossRef]
- Lott, M.B.; Laws, K.L. The physics of toppling and regaining balance during a pirouette. J. Dance Med. Sci. 2012, 16, 167–274. [Google Scholar] [PubMed]
- Zaferiou, A.M.; Flashner, H.; Wilcox, R.R.; McNitt-Gray, J.L. Lower extremity control during turns initiated with and without hip external rotation. J. Biomech. 2017, 52, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Imura, A.; Iino, Y. Regulation of hip joint kinetics for increasing angular momentum during the initiation of a pirouette en dehors in classical ballet. Hum. Mov. Sci. 2018, 60, 18–31. [Google Scholar] [CrossRef]
- Zaferiou, A.M.; Wilcox, R.R.; McNitee-Gray, J.L. Whole-body balance regulation during the turn phase of the piqué and pirouette turns with varied rotational demands. Med. Probl. Perform. Art. 2016, 31, 96–103. [Google Scholar] [CrossRef]
- Bierbaum, S.; Peper, A.; Karamanidis, K.; Arampatzis, A. Adaptive feedback potential in dynamic stability during disturbed walking in the elderly. J. Biomech. 2011, 44, 1921–1926. [Google Scholar] [CrossRef]
- Martelli, D.; Luo, L.; Kang, J.; Kang, U.J.; Fahn, S.; Agrawal, S.K. Adaptation of stability during perturbed walking in Parkinson’s disease. Sci. Rep. 2017, 7, 17875. [Google Scholar] [CrossRef]
- Alderink, G.; Harro, C.; Hickox, L.; Zeitler, D.W.; Bourke, M.; Gosla, A.; Rustmann, S. Dynamic measures of balance during a 90° turn in self-selected gait in individuals with Parkinson’s disease. Appl. Sci. 2023, 13, 5428. [Google Scholar] [CrossRef]
- Harro, C.; Alderink, G.; Hickox, L.; Zeitler, D.W.; Avery, M.; Daman, C.; Laker, D. Dynamic measures of balance during obstacle-crossing in self-selected gait in individuals with mild to moderate Parkinson’s disease. Appl. Sci. 2024, 14, 1271. [Google Scholar] [CrossRef]
- Peebles, A.T.; Reinholdt, A.; Bruetsch, A.P.; Lynch, S.G.; Huisinga, J.M. Dynamic margin of stability during gait is altered in persons with multiple sclerosis. J. Biomech. 2016, 49, 3949–3955. [Google Scholar] [CrossRef]
- Anastasi, D.; Lencioni, T.; Carpinella, I.; Castagna, A.; Crippa, A.; Gervasoni, E.; Corrini, C.; Marzegan, A.; Rabuffetti, M.; Ferrarin, M.; et al. Dynamic balance during walking in people with multiple sclerosis: A cross-sectional study. Proc. Inst. Mech. Eng. H 2023, 237, 199–208. [Google Scholar] [CrossRef]
- Tisserand, R.; Armand, S.; Allali, G.; Schnider, A.; Baillieul, S. Cognitive-motor dual-task interference modulates mediolateral dynamic stability during gait in post-stroke individuals. Hum. Mov. Sci. 2018, 58, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Buurke, T.J.W.; Liu, C.; Park, S.; den Otter, R.; Finley, J.M. Maintaining sagittal plane balance compromises frontal plane balance during reactive stepping in people post-stroke. Clin. Biomech. 2020, 80, 105135. [Google Scholar] [CrossRef] [PubMed]
- Hak, L.; van Dieén, J.H.; van der Wurff, P.; Houdijk, H. Stepping asymmetry among individuals with unilateral transtibial limb loss might be functional in terms of gait stability. Phys. Ther. 2014, 94, 1480–1488. [Google Scholar] [CrossRef]
- Curtze, C.; Hof, A.L.; Otten, B.; Postema, K. Balance recovery after an evoked forward fall in unilateral transtibial amputees. Gait Posture 2020, 32, 336–341. [Google Scholar] [CrossRef]
- Rodrigues, F.B.; de Sá e Souza, G.S.; de Mendonça Mesquita, E.; de Sousa Gomide, R.; Baptista, R.R.; Pereira, A.A.; Andrade, A.O.; Fraga Viera, M. Margins of stability of persons with transtibial or transfemoral amputations walking on sloped surfaces. J. Biomech. 2021, 123, 110453. [Google Scholar] [CrossRef]
- Tsubaki, Y.; Kawano, Y.; Lin, C.-F.; Kuno-Mizumura, K. Laterality in body composition of professional and amateur ballet dancers while performing a single pirouette with pointe shoes. Med. Probl. Perform. Art. 2024, 39, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Tsubaki, Y.; Kawano, Y.; Lin, C.-F.; Kuno-Mizumura, M. Differences in the rotation axis between professional and experienced amateur ballet dancers during pirouette en dehors in classical ballet wearing pointe shoes: A pilot study. J. Dance Med. Sci. 2024, 28, 43–50. [Google Scholar] [CrossRef]
- Baker, R. The conventional gait model. In Measuring Walking: A Handbook of Clinical Gait Analysis; Mac Keith Press: London, UK, 2013; pp. 29–49. [Google Scholar]
- Molina-Rueda, F.; Fernández-González, P.; Cuesta-Gómez, A.; Koutsou, A.; Carratalá, M.; Miangolarra-Page, J.C. Test-retest reliability of a conventional gait model for registering joint angles during initial contact and toe-off in healthy subjects. Int. J. Environ. Res. Public Health 2021, 18, 1343. [Google Scholar] [CrossRef] [PubMed]
- Carson, M.C.; Harrington, M.E.; Thompson, N.; O’Connor, J.J.; Theologis, T.N. Kinematic analysis of a multi-segment foot model for research and clinical applications: A repeatability analysis. J. Biomech. 2001, 34, 1299–1307. [Google Scholar] [CrossRef] [PubMed]
- Reay, J.; Leboeuf, F.; Hanssen, B.; Chiu, J.; Jones, R. Repeatability of the Oxford Foot Model: Comparison of a team of assessors with different backgrounds and no prior experience of the Oxford Foot Model. Gait Posture 2022, 92, 191–198. [Google Scholar] [CrossRef]
- Keuhnapfel, A.; Ahnert, P.; Loeffler, M.; Broda, A.; Scholz, M. Reliability of 3D laser-based anthropometry and comparison with classical anthropometry. Sci. Rep. 2016, 6, 26672. [Google Scholar] [CrossRef]
- Neelly, K.; Wallmann, W.; Backus, C.J. Validity of measuring leg length with a tape measure compared to a computed tomography scan. Physiother Theory Pract. 2013, 29, 487–492. [Google Scholar] [CrossRef]
- Harrington, M.E.; Zavatsky, A.B.; Lawson, S.E.M.; Yuan, Z.; Theologis, T.N. Prediction of the hip joint centre in adults, children, and patients with cerebral palsy based on magnetic resonance imaging. J. Biomech. 2007, 40, 595–602. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 82–106. [Google Scholar]
- Winter, D.A. Human balance and posture control during standing and walking. Gait Posture 1995, 3, 193–214. [Google Scholar] [CrossRef]
- Pai, Y.C.; Patton, J. Center of mass velocity-position predictions for balance control. J. Biomech. 1997, 30, 347–354. [Google Scholar] [CrossRef]
- Townsend, M.A. Biped gait stabilization via foot placement. J. Biomech. 1985, 18, 21–38. [Google Scholar] [CrossRef]
- Terry, K.; Stanley, C.; Damiano, D. A new perspective on the walking margin of stability. J. Appl. Biomech. 2014, 30, 737–741. [Google Scholar] [CrossRef] [PubMed]
- Kazanski, M.E.; Cusumano, J.P.; Dingwell, J.B. Rethinking margin of stability: Incorporating step-to-step regulation to resolve the paradox. J. Biomech. 2022, 144, 111334. [Google Scholar] [CrossRef] [PubMed]
- Lott, M.B.; Xu, G. Joint angle coordination strategies during whole body rotations on a single lower-limb support: An investigation through ballet pirouettes. J. Appl. Biomech. 2020, 36, 103–112. [Google Scholar] [CrossRef]
- Hirashima, M. Induced acceleration of three-dimensional multi-joint movements and its application to sports movements. In Theoretical Biomechanics; Klika, V., Ed.; IntechOpen Limited: London, UK, 2011; pp. 303–318. [Google Scholar] [CrossRef]
- Graham, D.F.; Carty, C.P.; Lloyd, D.G.; Lichtwark, G.A.; Barrett, R.S. Muscle contributions to recovery from forward loss of balance by stepping. J. Biomech. 2014, 47, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Sasagawa, S.; Shinya, M.; Nakazawa, K. Interjoint dynamic interaction during constrained human quiet standing examined by induced acceleration. J. Neurophysiol. 2014, 111, 313–322. [Google Scholar] [CrossRef]
- Ogaya, S.; Okita, Y.; Fuchioka, S. Muscle contributions to center of mass excursion in ankle and hip strategies during forward body tilting. J. Biomech. 2016, 49, 3381–3386. [Google Scholar] [CrossRef]
- Neptune, R.R.; Vistamehr, A. Dynamic balance during human movement: Measurement and control mechanisms. J. Biomech. Eng. 2019, 141, 0708011–07080110. [Google Scholar] [CrossRef]
- Begue, J.; Peyrot, N.; Dalleau, G.; Caderby, T. Age-related changes in the control of whole-body angular momentum during stepping. Exp. Gerontol. 2019, 127, 110714. [Google Scholar] [CrossRef]
- Begue, J.; Peyrot, N.; Lesport, A.; Turpin, N.A.; Watier, B.; Dalleau, G.; Caderby, T. Segmental contribution to whole-body angular momentum during stepping in healthy young and old adults. Sci. Rep. 2021, 11, 19969. [Google Scholar] [CrossRef]
- Provatidis, C.G. Revisiting the spinning top. Int. J. Mater. Mech. Eng. 2012, 1, 71–88. [Google Scholar]
- Błażkiewcz, M. Evaluation of geometric attractor structure and recurrence analysis in professional dancers. Entropy 2022, 24, 1310. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N. (Ed.) Nonlinear Analysis for Human Movement Variability; CRC Press, Taylor & Francis Group, LLC: Boca Raton, FL, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).