Experimental and Numerical Flow Assessment of the Main and Additional Tract of Prototype Differential Brake Valve
Abstract
1. Introduction
2. Materials and Methods
2.1. Object of Analysis
2.2. Experimental Research
- Open the solenoid valve 3 supplying the measuring system from the compressed air preparation station and fill the supply tank 6 to the working pressure;
- Close the supply solenoid valve 3, stabilize the pressure in the supply tank 6 and start pressure recording to a *.csv file with the declared sampling time;
- Open the measuring solenoid valve 7 and flow of compressed air from the supply tank 6 to the measuring tank 9 through the brake valve. The flow is caused by the pressure gradient in both tanks;
- After equalizing the pressure in both tanks, end the recording, close the measuring solenoid valve 7, save the *.csv file, open the release solenoid valves 5 and 10, enabling the pressure in both tanks to equalize to the atmospheric pressure, and close it to ensure the re-sealing of the measuring system;
- Ending a measurement sequence after reaching the specified repetition counter causes the program to terminate or loop if the required number of repetitions has not been reached.
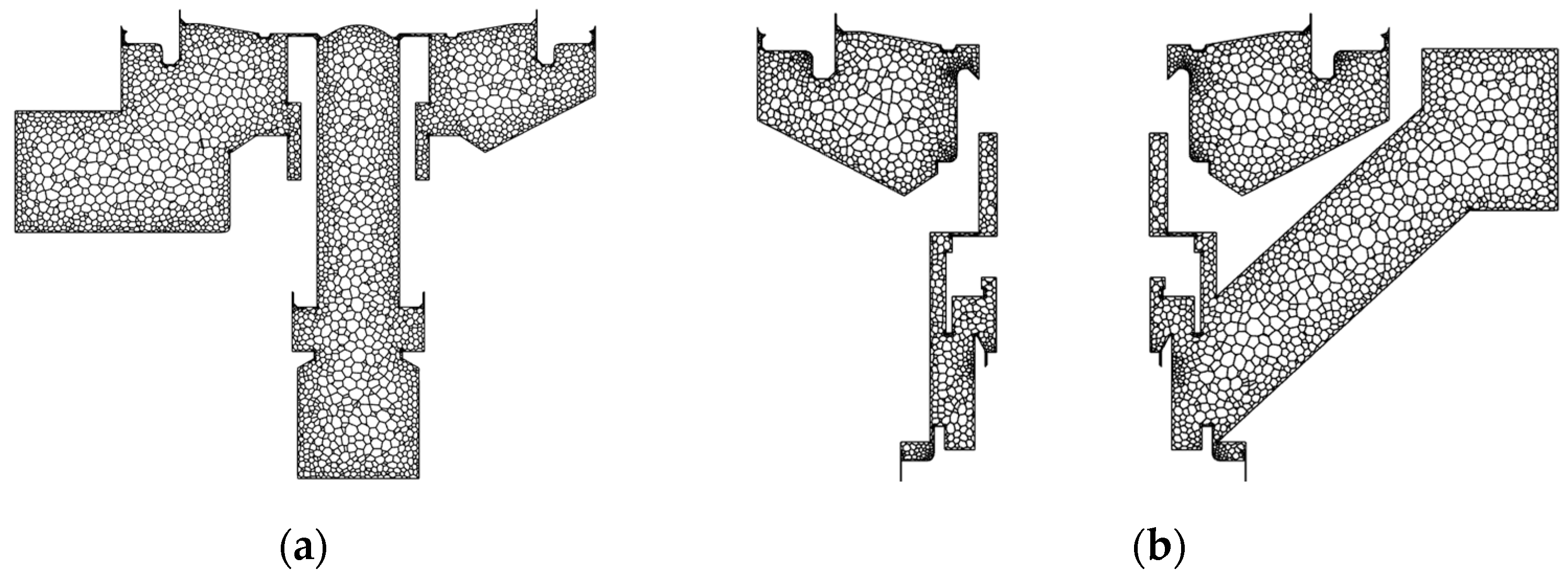
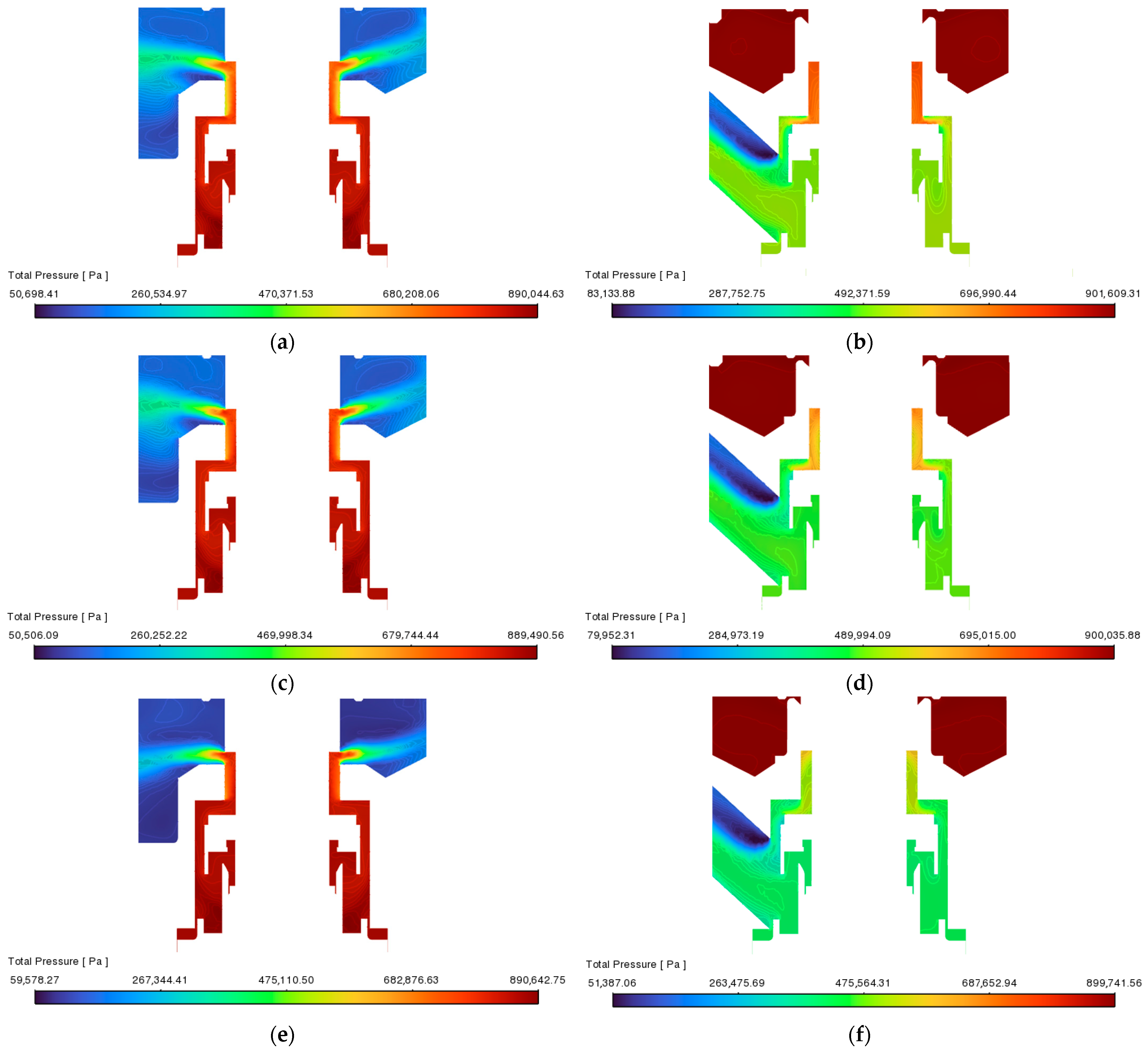
2.3. Numerical Studies in ANSYS Fluent
- assuming a constant initial supply pressure value pin = 901,325 Pa (absolute pressure),
- assuming a constant initial pressure value at the valve outlet pout = 101,325 Pa (absolute pressure),
- assuming a constant initial temperature value in the supply and output connections equal to T = Tin = Tout = 293.15 K.
3. Results
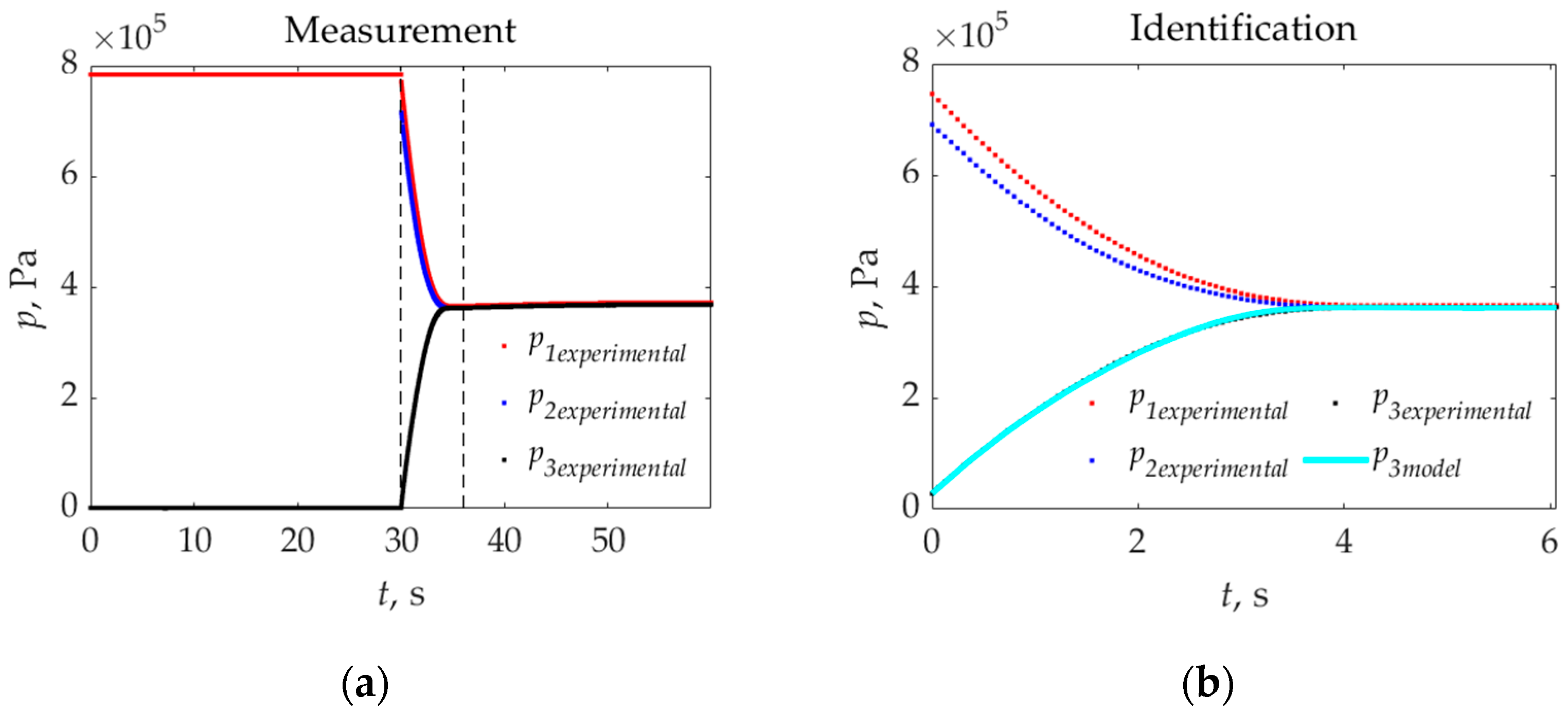
3.1. Experimental Static Flow Characteristics of the Main and Additional Supply Tracts
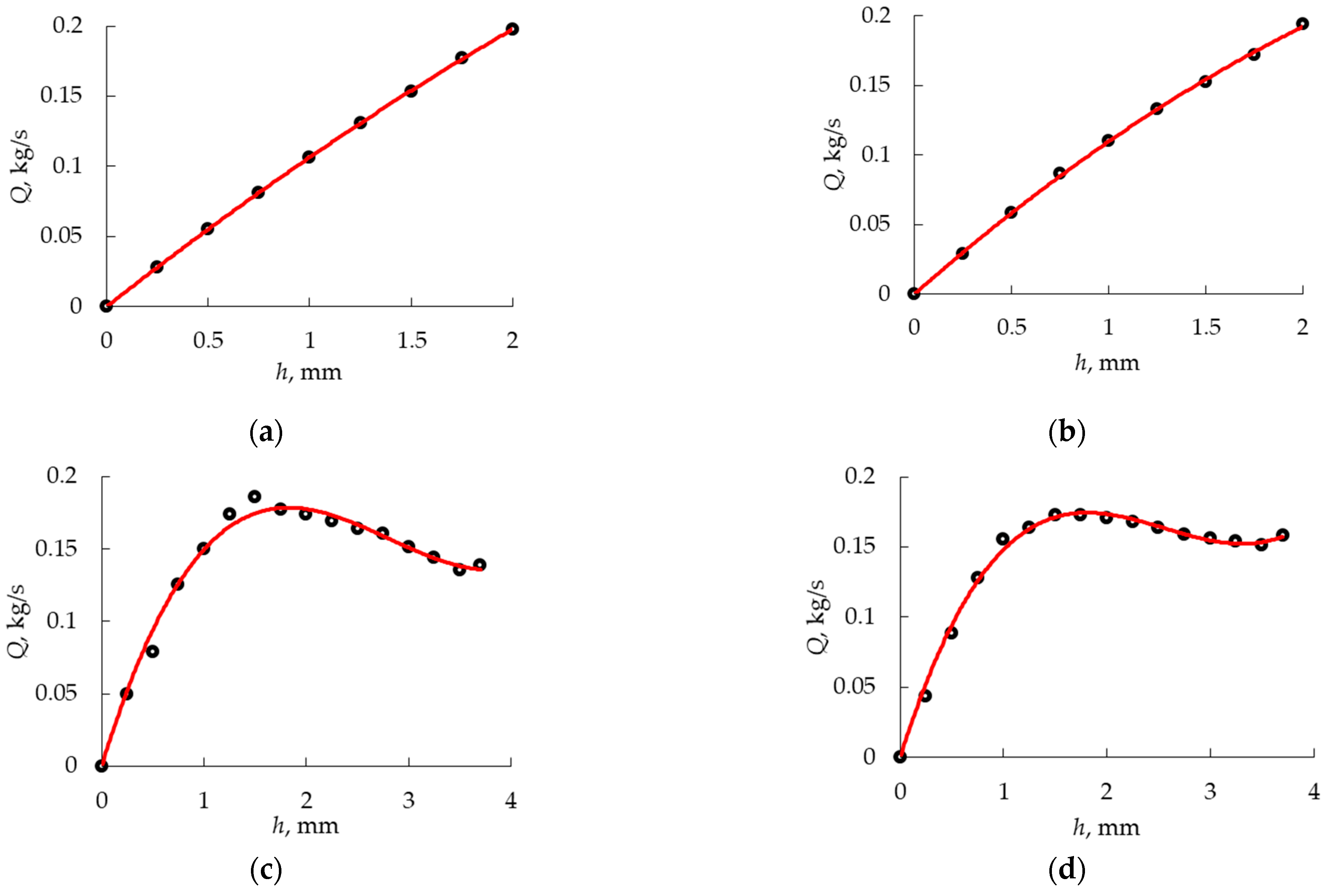
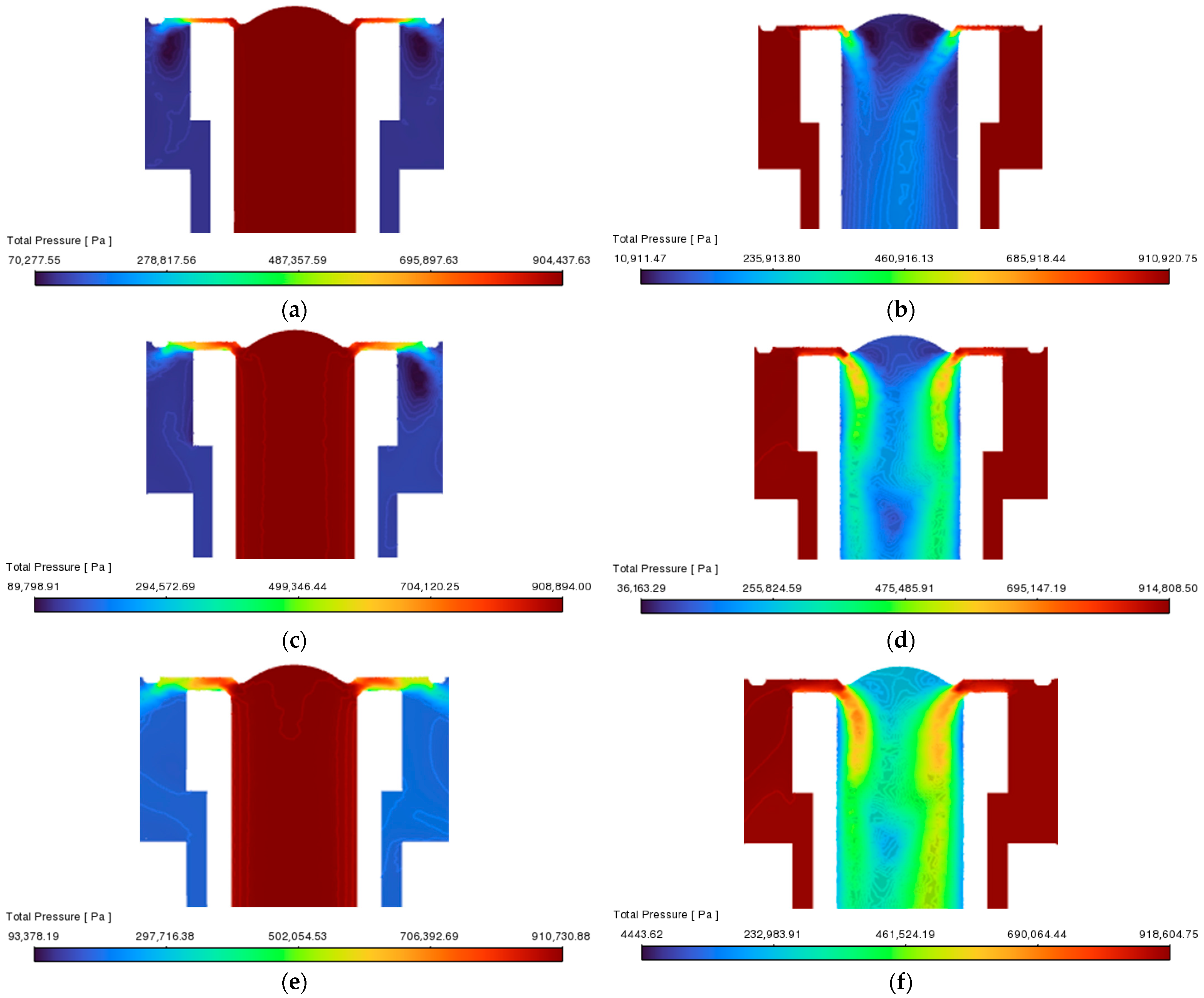
3.2. Numerical Static Flow Characteristics of the Main and Additional Supply Tracts
3.3. Comparison of the Static Flow Characteristics Determined Experimentally and Numerically
4. Discussion
5. Conclusions
- It was confirmed that simplifying the flow characteristics of the tracts to a rectangular shape does not reflect the properties of the valves. The applicability of the numerical approach to assessing the flow of brake valve tracts was verified by comparing the values obtained using computer simulation with those obtained using the analytical approach, which has been repeatedly verified in the literature. In earlier studies by the authors, where the nozzle throughput was subjected to experimental and numerical assessment, the differences between the two methods were smaller, mainly due to the geometry of the system, the presence of seals, and the need to introduce a control system to simulate control operations.
- The movement of the control piston, caused by a sudden increase in pressure at the valve supply port and the piston surface (depending on the flow direction), was observed during the tests. This was the result of the clearance of the threaded connection. Nevertheless, this was the least invasive solution, enabling manual control. It could therefore have had a small impact on the value of the results obtained by the experimental method of this study.
- Preparing the valve’s supply section for experimental tests required the use of additional components to ensure regulation in line with the assumed test conditions. For this purpose, a spring supporting the control piston was used inside the valve body, which ensured the precise adjustment of the piston position and, consequently, the degree of opening of the main or additional supply path.
- Numerical tests using a polyhedral mesh with 500 declared iterations and dimensionless residual indicators at 10−6, representing imbalance in the solver’s differential equations, produced a stable solution, which formed the basis for comparing the results obtained in the numerical and experimental approaches. In numerical modelling, adiabatic flow was assumed, which in real conditions, occurring during experimental tests and the normal operation of the brake valve during service, is a certain simplification. A broader discussion of the impact of temperature on valve operation will form the basis of a dynamic simulation based on multiphysics.
- The discrepancies between both methods assessed using the mean absolute percentage error MAPE were within the range of 0–24%, while the mean value in the entire measurement range was 9.43%, which was mainly influenced by the high MAPE value (17.25%) of the main supply tract during the flow direction resulting from the release of the brake. In the case of a larger sample size, statistical analysis would be necessary, but the aim of the numerical and experimental studies was to assess the possibility of using numerical simulation to determine the pneumatic output of the brake valve, which was achieved by comparing five repetitions of each experimental measurement.
- For the other flow directions of both tracts, the values of the average MAPE index were equal to 5.88%, 9.40% and 5.20%, which proves that, after taking all simplifications into account, the use of simulation methods to evaluate the operation of pneumatic brake valves in a static approach provides satisfactory results.
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| MFR | Mass Flow Rate |
| STEP | Standard for the Exchange of Product Data |
| CSV | Comma-Separated Values |
| FVM | Finite Volume Method |
| A-F | ANSYS Fluent |
References
- Cantone, L.; Ottati, A. A Simplified Pneumatic Model for Air Brake of Passenger Trains. Railw. Eng. Sci. 2023, 31, 145–152. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, L. Research on the Characteristics of a Pneumatic Proportional Valve. J. Phys. Conf. Ser. 2024, 2853, 12043. [Google Scholar] [CrossRef]
- Dindorf, R.; Takosoglu, J.; Wos, P. Review of Compressed Air Receiver Tanks for Improved Energy Efficiency of Various Pneumatic Systems. Energies 2023, 16, 4153. [Google Scholar] [CrossRef]
- Li, G.; Wei, X.; Wang, Z.; Bao, H. Study on the Pressure Regulation Method of New Automatic Pressure Regulating Valve in the Electronically Controlled Pneumatic Brake Systems in Commercial Vehicles. Sensors 2022, 22, 4599. [Google Scholar] [CrossRef]
- Kushaliyev, D.K.; Torebekova, S.O.; Kalshora, E.T.; Korabay, R.B. Analysis of the Main Malfunctions of Hydraulic Cylinders. Bull. L.N. Gumilyov Eurasian Natl. Univ. Tech. Sci. Technol. Ser. 2025, 150, 265–277. [Google Scholar] [CrossRef]
- Romanoski, V.; Oliveira, L.; Figueiredo, G.; Mayer, M.; Maria, K.; Cavalieri Polizeli, K. Dynamic Soil Hydraulic Properties in Regenerative Agriculture: Effects of Crop and Forest Integration in Livestock Systems. Soil. Tillage Res. 2025, 253, 106680. [Google Scholar] [CrossRef]
- European Union. Regulation No 13 of the Economic Commission for Europe of the United Nations (UN/ECE)—Uniform Provisions Concerning the Approval of Vehicles of Categories M, N and O with Regard to Breaking [2016/194]; European Union: Brussels, Belgium, 2015. [Google Scholar]
- Kisiel, M.; Szpica, D.; Czaban, J.; Köten, H. Pneumatic Brake Valves Used in Vehicle Trailers—A Review. Eng. Fail. Anal. 2024, 158, 107942. [Google Scholar] [CrossRef]
- Kamiński, Z.; Kulikowski, K. Measurement and Evaluation of the Quality of Static Characteristics of Brake Valves for Agricultural Trailers. Measurement 2017, 106, 173–178. [Google Scholar] [CrossRef]
- Kisiel, M.; Szpica, D. Suboptimal Analysis of the Differential System of the Conceptual Trailer Air Brake Valve. Appl. Sci. 2024, 14, 6792. [Google Scholar] [CrossRef]
- Kisiel, M.; Szpica, D. Computational Evaluation of the Influence of the Control Piston Bore Throughput on the Differential Action of a Pneumatic Brake Valve. In Proceedings of the 28th International Scientific Conference Transport Means 2024, Kaunas, Lithuania, 2 October 2024. [Google Scholar]
- Dindorf, R. Measurement of Pneumatic Valve Flow Parameters on the Test Bench with Interchangeable Venturi Tubes and Their Practical Use. Sensors 2023, 23, 6042. [Google Scholar] [CrossRef]
- Scheaua, F. Theoretical Characteristics of Fluid Flow within a Pneumatic System. Hidraulica 2019, 1, 64–70. [Google Scholar]
- Kamiński, Z.; Kulikowski, K. Impact of a modified braking valve for static and dynamic characteristics of pneumatic braking systems of agricultural trailers. Int. J. Heavy Veh. Syst. 2021, 28, 291–307. [Google Scholar] [CrossRef]
- Miatluk, M.; Kamiński, Z.; Czaban, J. Characteristic Features of the Airflow of Pneumatic Elements of Agricultural Vehicles. Commision Mot. Power Ind. Agric. 2003, 3, 174–181. [Google Scholar]
- Miatluk, M.; Avtuszko, F. Dinamika Pnievmaticeskich i Gidravliceskich Privodov Avtomobilej; Maszinostrojenije: Moscow, Russia, 1980. [Google Scholar]
- Kaminski, Z. A Simplified Lumped Parameter Model for Pneumatic Tubes. Math. Comput. Model. Dyn. Syst. 2017, 23, 523–535. [Google Scholar] [CrossRef]
- Bautista, M.; Dufresne, L.; Masson, C. Hybrid Turbulence Models for Atmospheric Flow: A Proper Comparison with RANS Models. E3S Web Conf. 2015, 5, 3001. [Google Scholar] [CrossRef]
- Sosnowski, M.; Krzywanski, J.; Grabowska, K.; Gnatowska, R. Polyhedral Meshing in Numerical Analysis of Conjugate Heat Transfer. EPJ Web Conf. 2018, 180, 02096. [Google Scholar] [CrossRef]
- Spiegel, M.; Redel, T.; Zhang, Y.; Struffert, T.; Hornegger, J.; Grossman, R.; Doerfler, A.; Karmonik, C. Tetrahedral vs. Polyhedral Mesh Size Evaluation on Flow Velocity and Wall Shear Stress for Cerebral Hemodynamic Simulation. Comput. Methods Biomech. Biomed. Engin. 2011, 14, 9–22. [Google Scholar] [CrossRef]
- Yamakawa, M.; Konishi, E.; Matsuno, K.; Asao, S. Adaptive Polyhedral Mesh Generation Method for Compressible Flows. J. Comput. Sci. Technol. 2013, 7, 278–285. [Google Scholar] [CrossRef]
- Kisiel, M.; Szpica, D.; Czaban, J. Numerical and Experimental Determination of the Bore Throughput Controlling the Operation of the Differential Section of a Pneumatic Brake Valve. Appl. Sci. 2024, 14, 11690. [Google Scholar] [CrossRef]
- Patil, J.; Palanivelu, S.; Aswar, V.; Sharma, V. Mathematical Model to Evaluate and Optimize the Dynamic Performance of Pneumatic Brake System; SAE Technical Papers 2015; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Ren, X.; Lu, Y.; Wang, F. Research on Pneumatic Test System for the Dynamic Characteristic of Hydraulic Solenoid Valve in Brake-by-Wire System. J. Phys. Conf. Ser. 2023, 2674, 12029. [Google Scholar] [CrossRef]
- Kaminski, Z. Mathematical Modelling of the Trailer Brake Control Valve for Simulation of the Air Brake System of Farm Tractors Equipped with Hydraulically Actuated Brakes. Maint. Reliab. 2014, 16, 637–643. [Google Scholar]
- Kisiel, M.; Szpica, D.; Czaban, J. Concept of a Test Rig for the Determination of Flow Characteristics of Air Brake Valves in Automatic Cycle. In Proceedings of the 27th International Scientific Conference, Palanga, Lithuania, 4 October 2023; pp. 74–79. [Google Scholar]
- Szpica, D.; Kisiel, M.; Czaban, J. Simulation Evaluation of the Influence of Selected Geometric Parameters on the Operation of the Pneumatic Braking System of a Trailer with a Differential Valve. Acta Mech. Autom. 2022, 16, 233–241. [Google Scholar] [CrossRef]
- Miatluk, M.; Czaban, J. Metoda Określania Przewodności Pneumatycznego Regulatora Sił Hamowania Pojazdów. Motrol. Motoryz. Energetyka Rol. 2004, 06, 154–161. [Google Scholar]
- Kulesza, Z.; Miatluk, M. Analiza Procesów Przejciowych w Pneumatycznym Układzie Hamulcowym z Zaworem Przekanikowym. Arch. Mot. 2008, 1, 33–43. [Google Scholar]
- Korbut, M.; Szpica, D.; Panão, M. Modelling of Piston Pneumatic Engine Operation Using the Lumped Method. Energy Convers. Manag. 2024, 306, 118310. [Google Scholar] [CrossRef]
- Chawla, M.; Al-zanaidi, M.A.; Evans, D.J. Linearly Implicit Generalized Trapezoidal Formulas for Nonlinear Differential Equations. Int. J. Comput. Math. 2000, 74, 345–359. [Google Scholar] [CrossRef]
- Selvam, M.; Manickam, R.; Saravanan, V. Nelder—Mead Simplex Search Method—A Study. In Data Analytics and Artificial Intelligence; REST Publisher: Kaveripattinam, India, 2022; Volume 2, p. 2022. ISBN 978-81-948459-4-2. [Google Scholar]
- Wang, P.; Shoup, T. Parameter Sensitivity Study of the Nelder–Mead Simplex Method. Adv. Eng. Softw. 2011, 42, 529–533. [Google Scholar] [CrossRef]
- Marzok, A. Extended Finite Volume Method for Problems with Arbitrary Discontinuities. Comput. Mech. 2025, 1–22. [Google Scholar] [CrossRef]
- Saeed, A.; Alfawaz, T. Finite Volume Method and Its Applications in Computational Fluid Dynamics. Axioms 2025, 14, 359. [Google Scholar] [CrossRef]
- Łebek, M.; Panfil, M. Navier-Stokes Equations for Nearly Integrable Quantum Gases. Phys. Rev. Lett. 2025, 134, 010405. [Google Scholar] [CrossRef]
- Tanaka, K. Air Flow through Suction Valve of Conical Seat: Experimental Research. Part I; Daigaku, T., Kenkyūjo, K., Eds.; Aeronautical Research Institute; Tokyo Imperial University: Bunkyo, Tokyo, 1929. [Google Scholar]
- Yang, W.; Wang, Y.; Yan, L.; Han, Z.; Gerling, D. Online Detection of Inverter Voltage Error Based on the Voltage Oversampling Measurement and Sigmoidal Function Model. IEEE Trans. Power Electron. 2021, 37, 303–312. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, R.; Jiang, Z. Nonlinear Dynamical Model of an Automotive Dual Mass Flywheel. Adv. Mech. Eng. 2015, 7, 1687814015589533. [Google Scholar] [CrossRef]


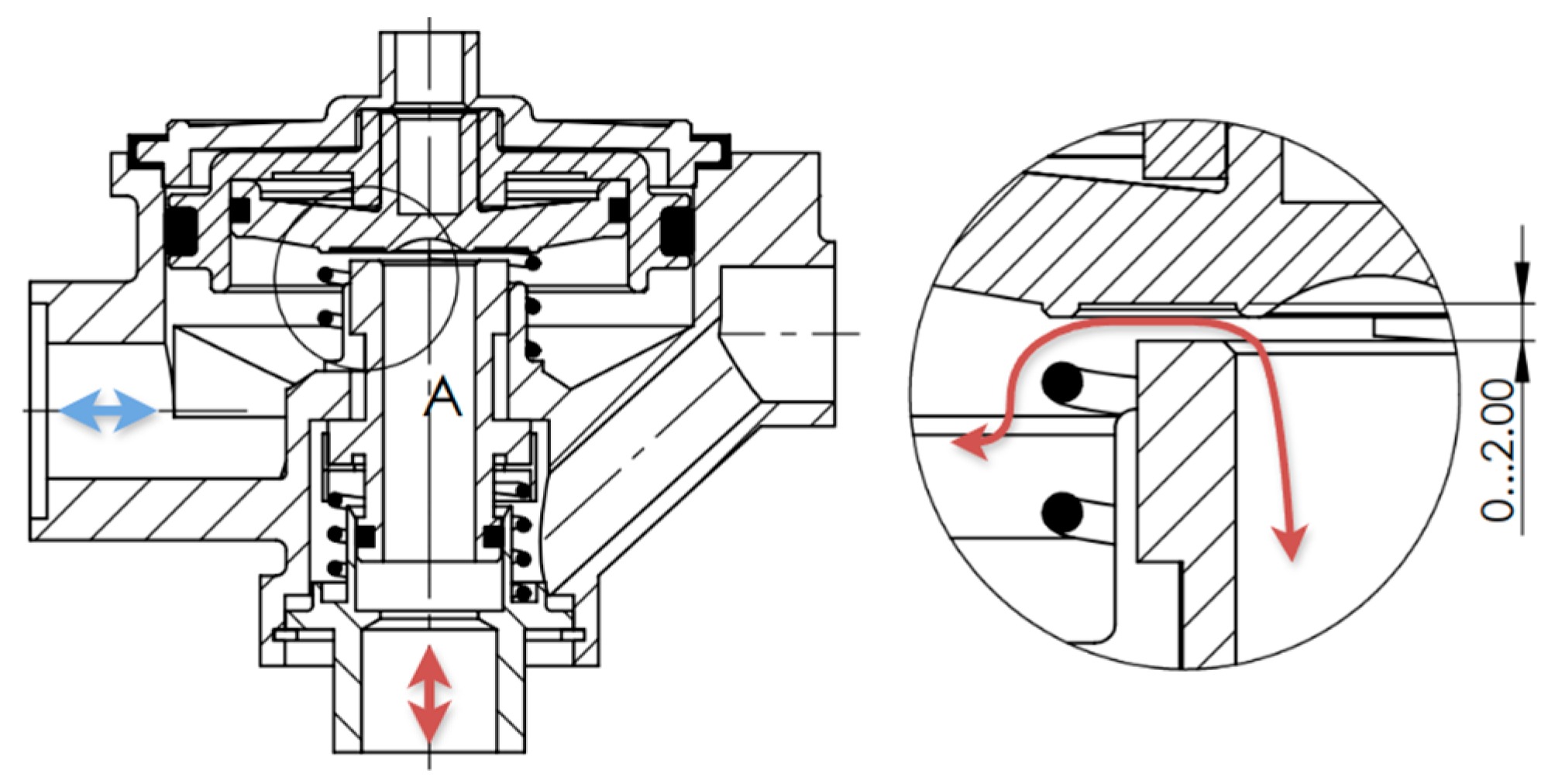
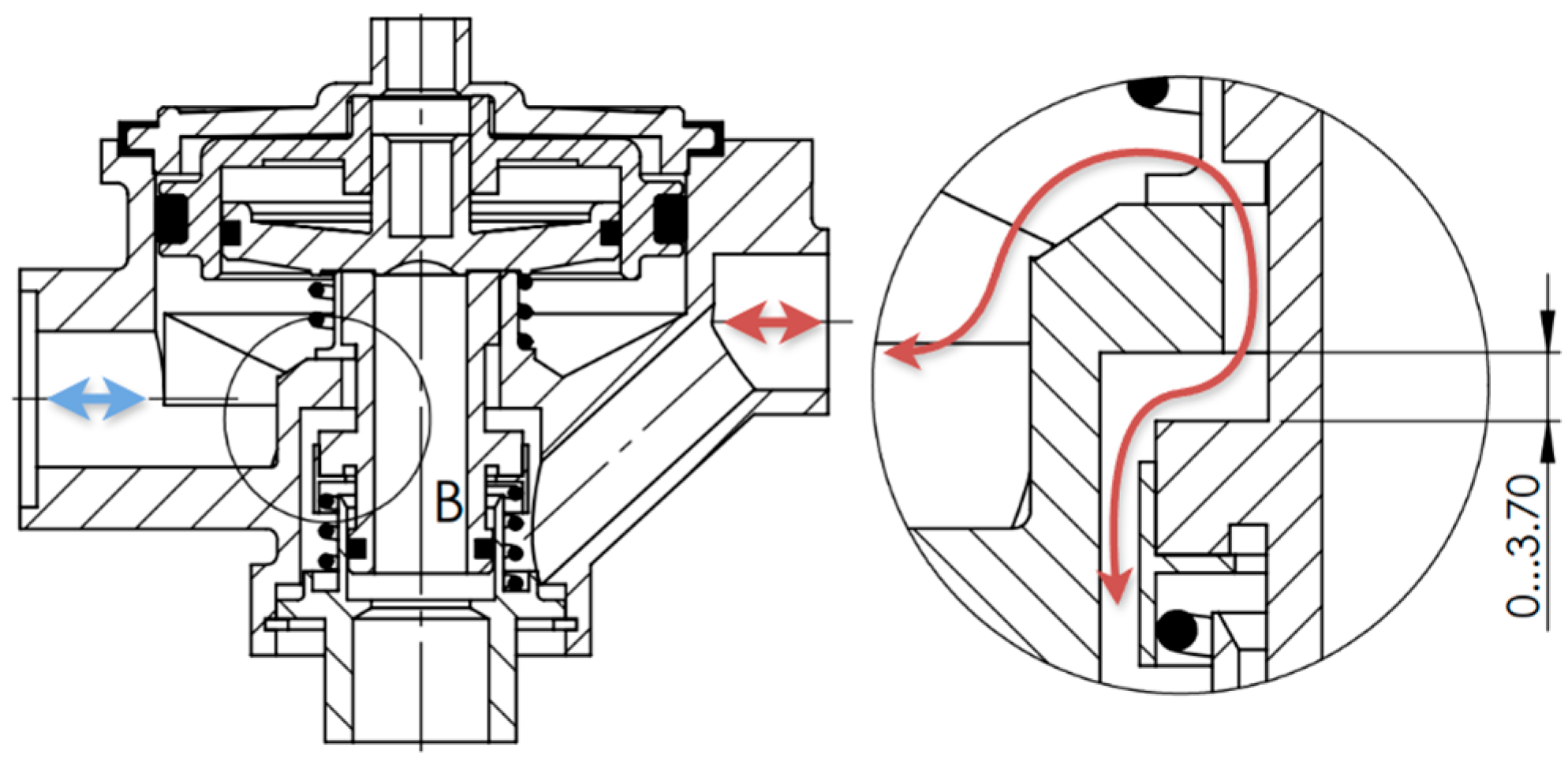


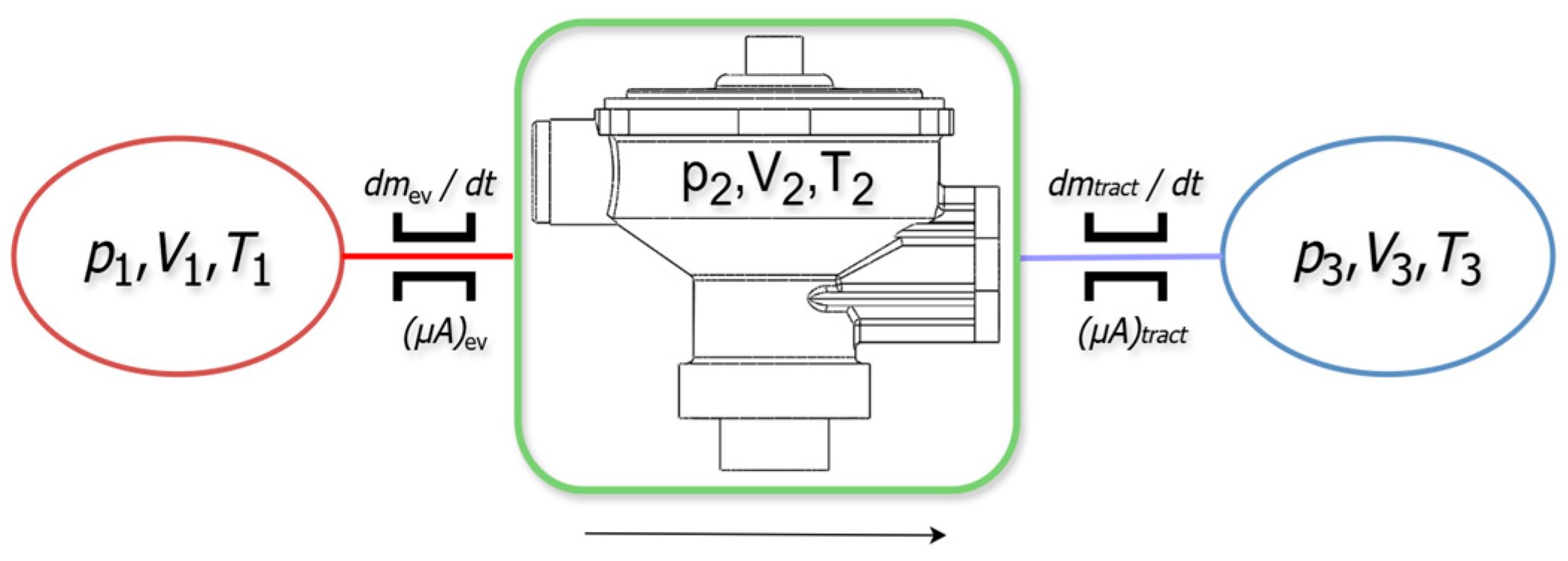

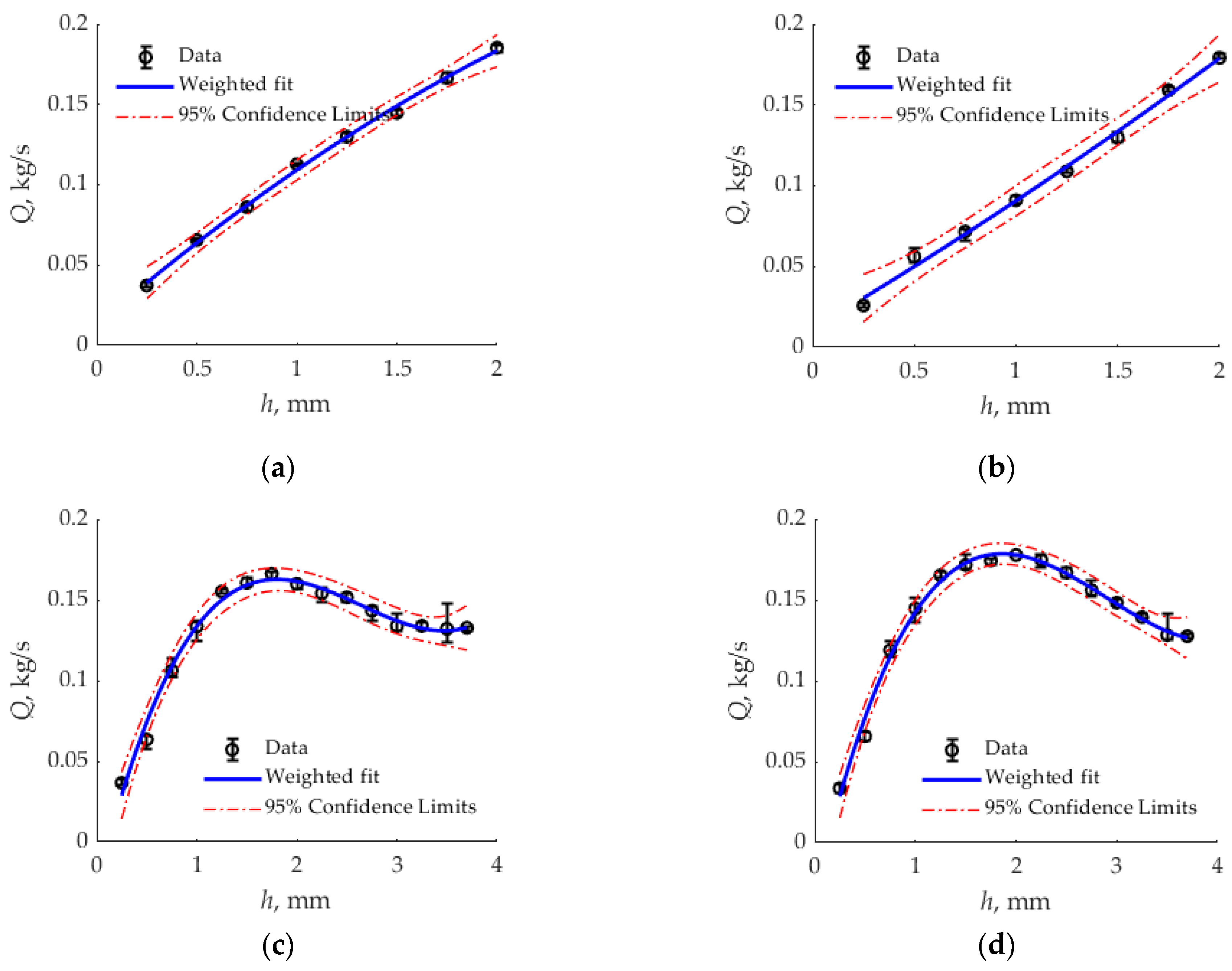
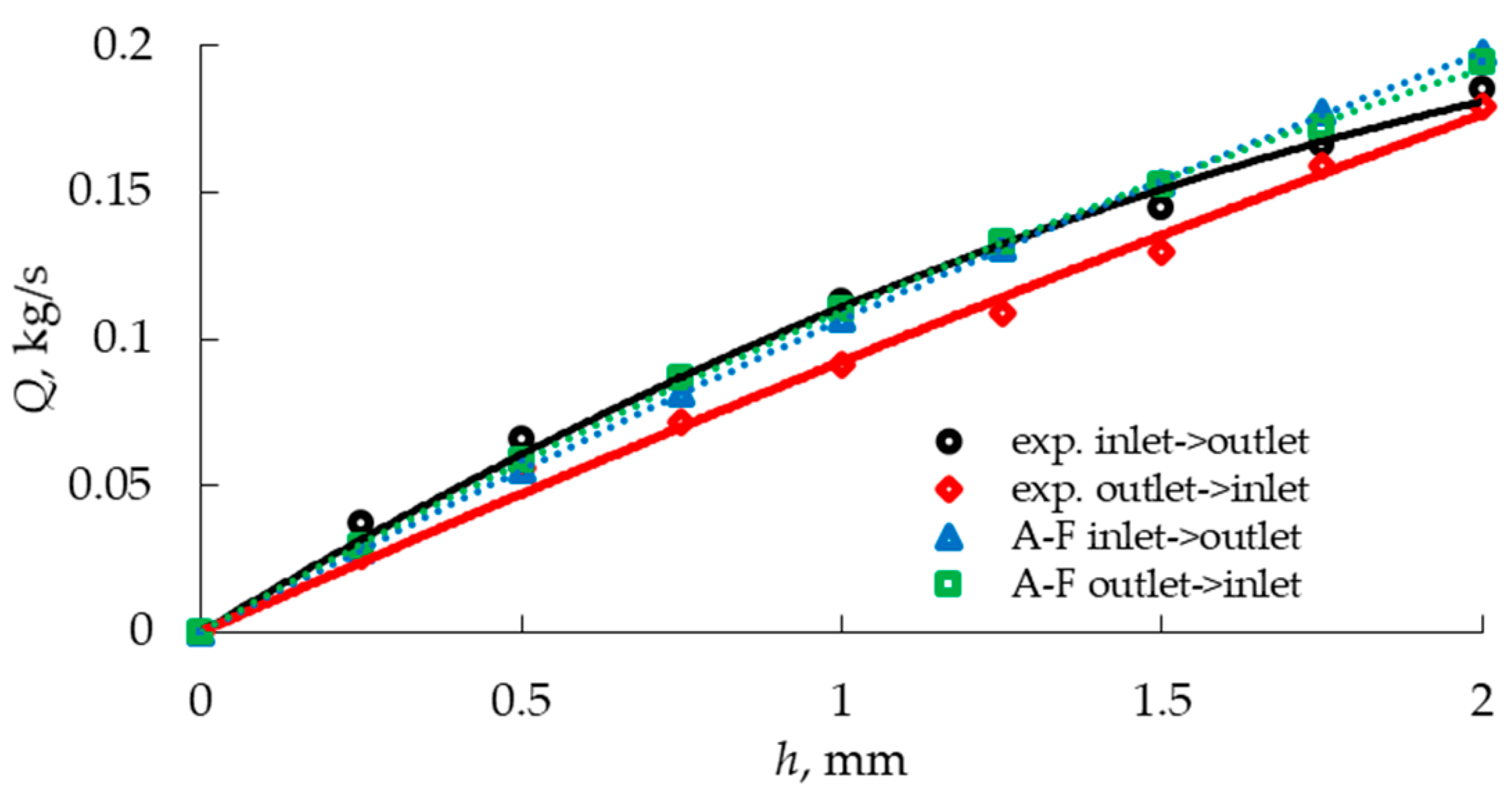
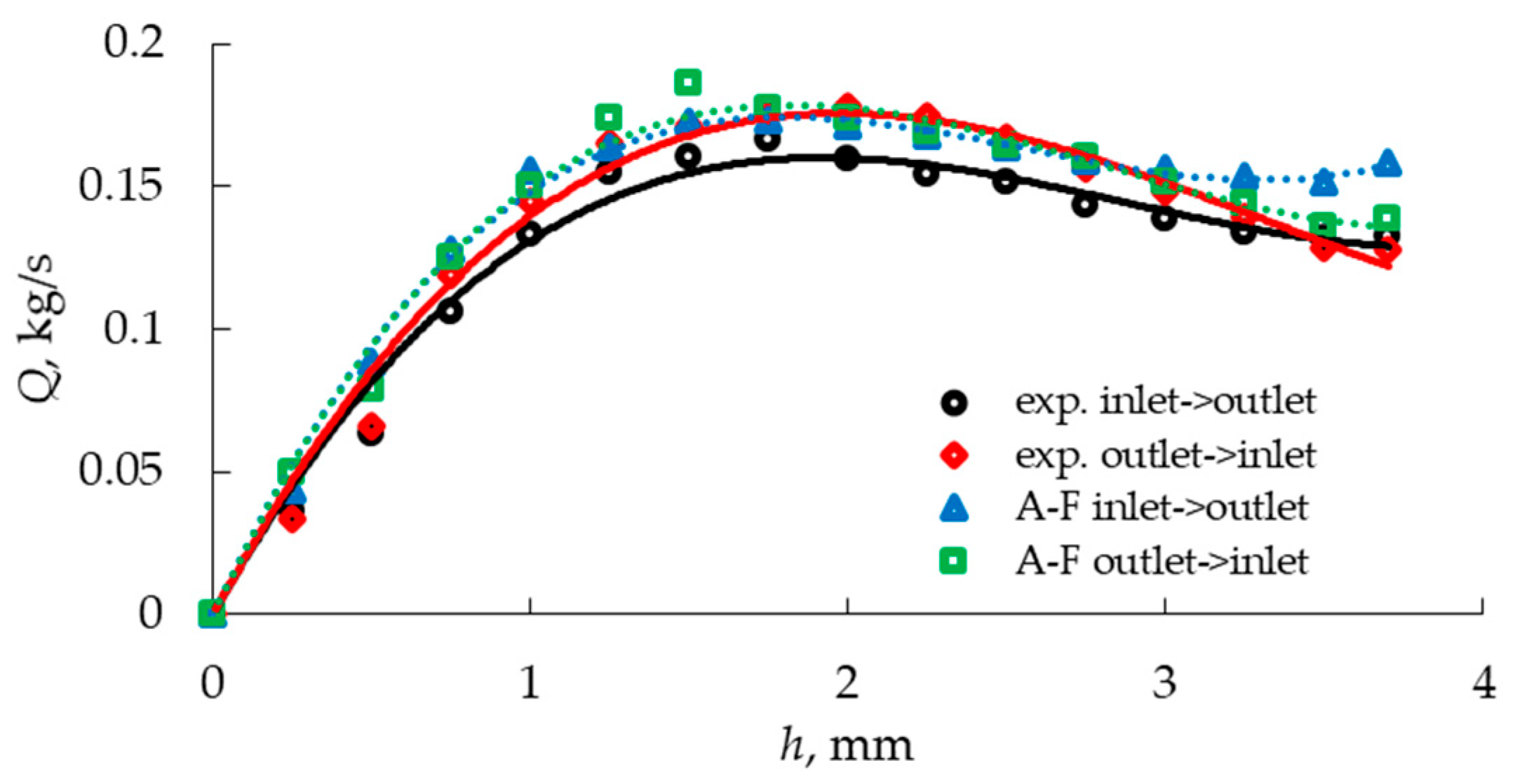
| Tract Opening [mm] | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| Weighted fit | 0 | 0.03158 | 0.06060 | 0.08708 | 0.11100 | 0.13238 | 0.15120 | 0.16748 | 0.18120 |
| MAPE [%] | 0 | 11% | 8% | 7% | 4% | 1% | 1% | 6% | 9% |
| MAE | 0 | 0.00352 | 0.00510 | 0.00596 | 0.00445 | 0.00152 | 0.00190 | 0.00989 | 0.01640 |
| Tract Opening [mm] | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| Weighted fit | 0 | 0.02383 | 0.04715 | 0.06998 | 0.09230 | 0.11413 | 0.13545 | 0.15628 | 0.17660 |
| MAPE [%] | 0 | 22% | 25% | 23% | 19% | 16% | 13% | 10% | 10% |
| MAE | 0 | 0.00524 | 0.01167 | 0.01642 | 0.01776 | 0.01880 | 0.01699 | 0.01568 | 0.01763 |
| Tract Opening [mm] | 0 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 |
|---|---|---|---|---|---|---|---|---|
| Weighted fit | 0 | 0.04526 | 0.08161 | 0.10991 | 0.13100 | 0.14574 | 0.15499 | 0.15959 |
| MAPE [%] | 0 | 10% | 4% | 14% | 15% | 19% | 20% | 11% |
| MAE | 0 | 0.00167 | 0.00674 | 0.01814 | 0.02451 | 0.01811 | 0.01783 | 0.01346 |
| 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 3.70 | |
| 0.16040 | 0.15827 | 0.15406 | 0.14862 | 0.14280 | 0.13745 | 0.13344 | 0.13175 | |
| 8% | 7% | 7% | 8% | 6% | 5% | 2% | 5% | |
| 0.01065 | 0.00989 | 0.00992 | 0.01056 | 0.01363 | 0.01634 | 0.01800 | 0.02645 |
| Tract Opening [mm] | 0 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 |
|---|---|---|---|---|---|---|---|---|
| Weighted fit | 0 | 0.04710 | 0.08564 | 0.11631 | 0.13980 | 0.15679 | 0.16796 | 0.17400 |
| MAPE [%] | 0 | 6% | 8% | 8% | 7% | 11% | 11% | 2% |
| MAE | 0 | 0.00269 | 0.00688 | 0.00911 | 0.01031 | 0.01733 | 0.01791 | 0.00316 |
| 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 3.70 | |
| 0.17560 | 0.17343 | 0.16819 | 0.16055 | 0.15120 | 0.14083 | 0.13011 | 0.12176 | |
| 1% | 2% | 2% | 0% | 0% | 2% | 4% | 14% | |
| 0.00171 | 0.00419 | 0.00382 | 0.00004 | 0.00011 | 0.00327 | 0.00560 | 0.01678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kisiel, M.; Szpica, D. Experimental and Numerical Flow Assessment of the Main and Additional Tract of Prototype Differential Brake Valve. Appl. Sci. 2025, 15, 7483. https://doi.org/10.3390/app15137483
Kisiel M, Szpica D. Experimental and Numerical Flow Assessment of the Main and Additional Tract of Prototype Differential Brake Valve. Applied Sciences. 2025; 15(13):7483. https://doi.org/10.3390/app15137483
Chicago/Turabian StyleKisiel, Marcin, and Dariusz Szpica. 2025. "Experimental and Numerical Flow Assessment of the Main and Additional Tract of Prototype Differential Brake Valve" Applied Sciences 15, no. 13: 7483. https://doi.org/10.3390/app15137483
APA StyleKisiel, M., & Szpica, D. (2025). Experimental and Numerical Flow Assessment of the Main and Additional Tract of Prototype Differential Brake Valve. Applied Sciences, 15(13), 7483. https://doi.org/10.3390/app15137483







