A Study of the Flexural Performance of Fiber-Reinforced Anchored Shotcrete Single-Layer Lining in a Hard Rock Tunnel Based on the Thickness Ratio
Abstract
1. Introduction
2. Materials and Methods
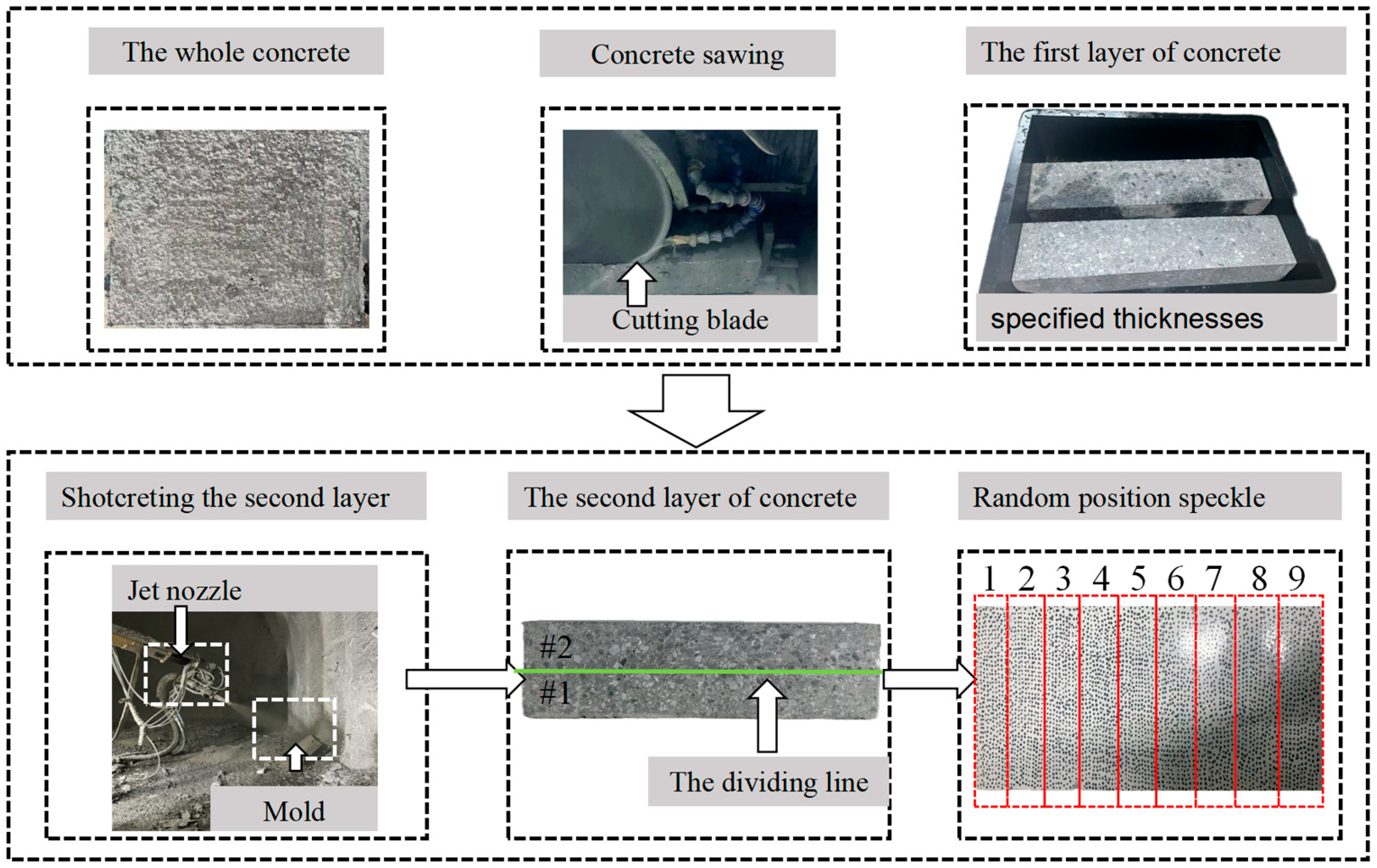
2.1. Test Materials
2.2. Test Methods
3. Test Results and Analysis
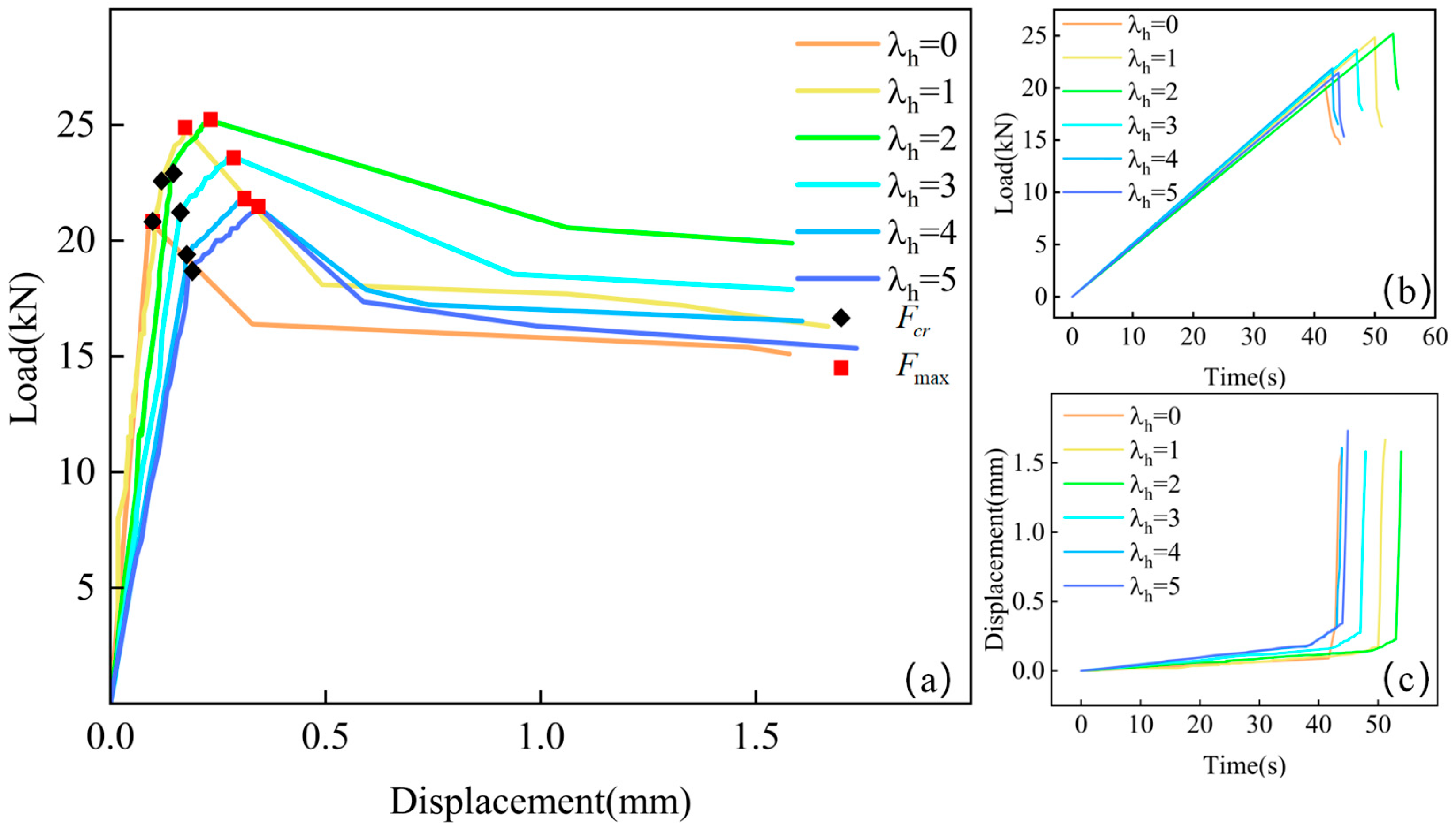
3.1. Axial Load–Displacement Curves Analysis
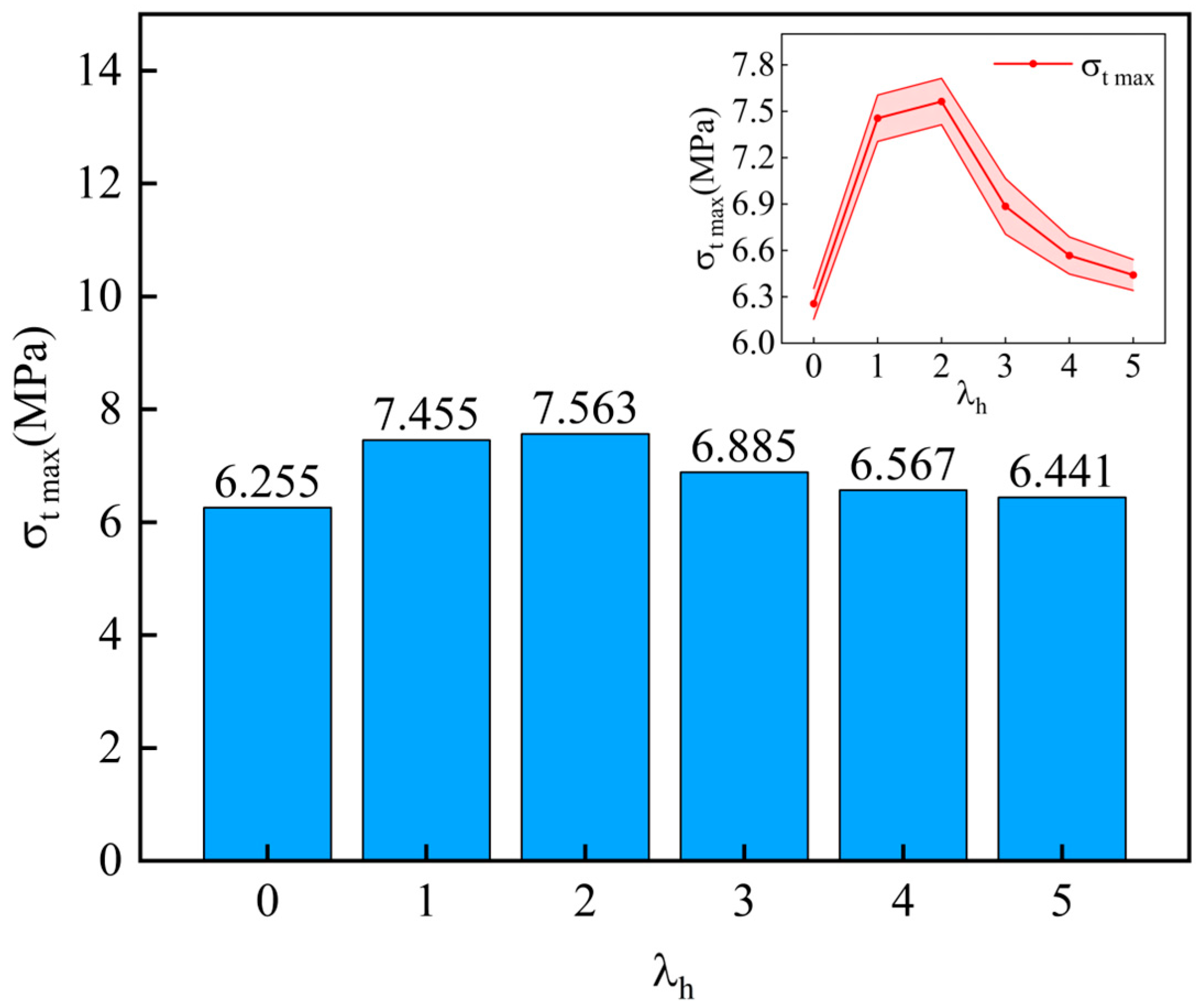
3.2. Flexural Performance Analysis
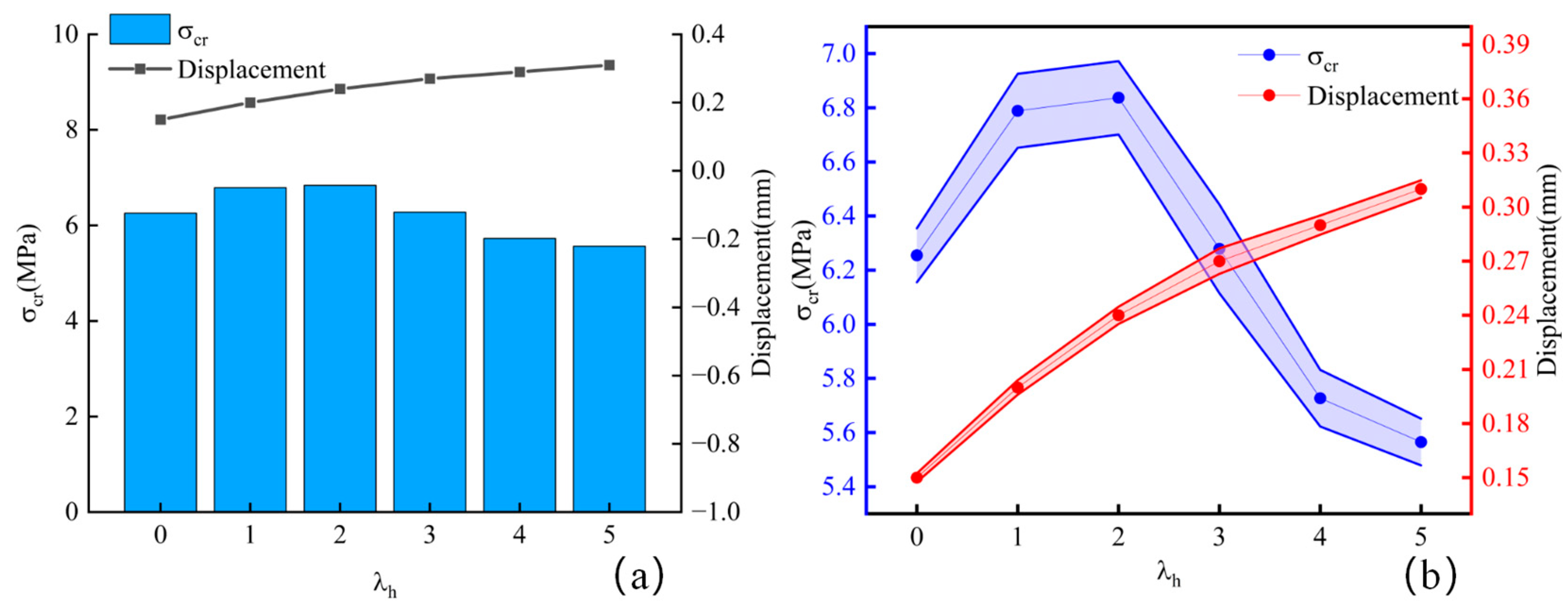
3.3. Cracking Stress Analysis
3.4. Flexural Toughness Analysis
4. Analysis of the Damage Pattern of Fiber Shotcrete Laminated Beams Based on the Thickness Ratio
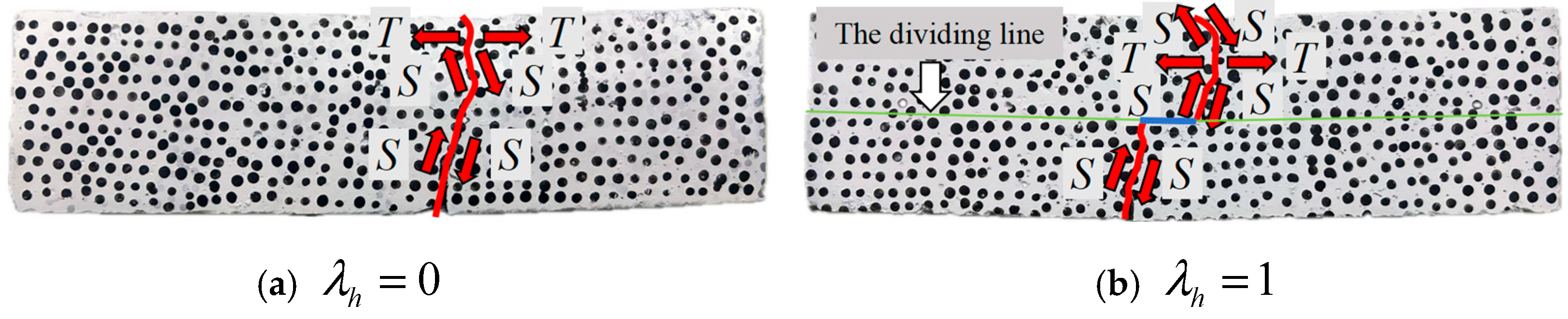
4.1. Macroscopic Damage Pattern of Fiber Shotcrete Laminated Beams Based on the Thickness Ratio
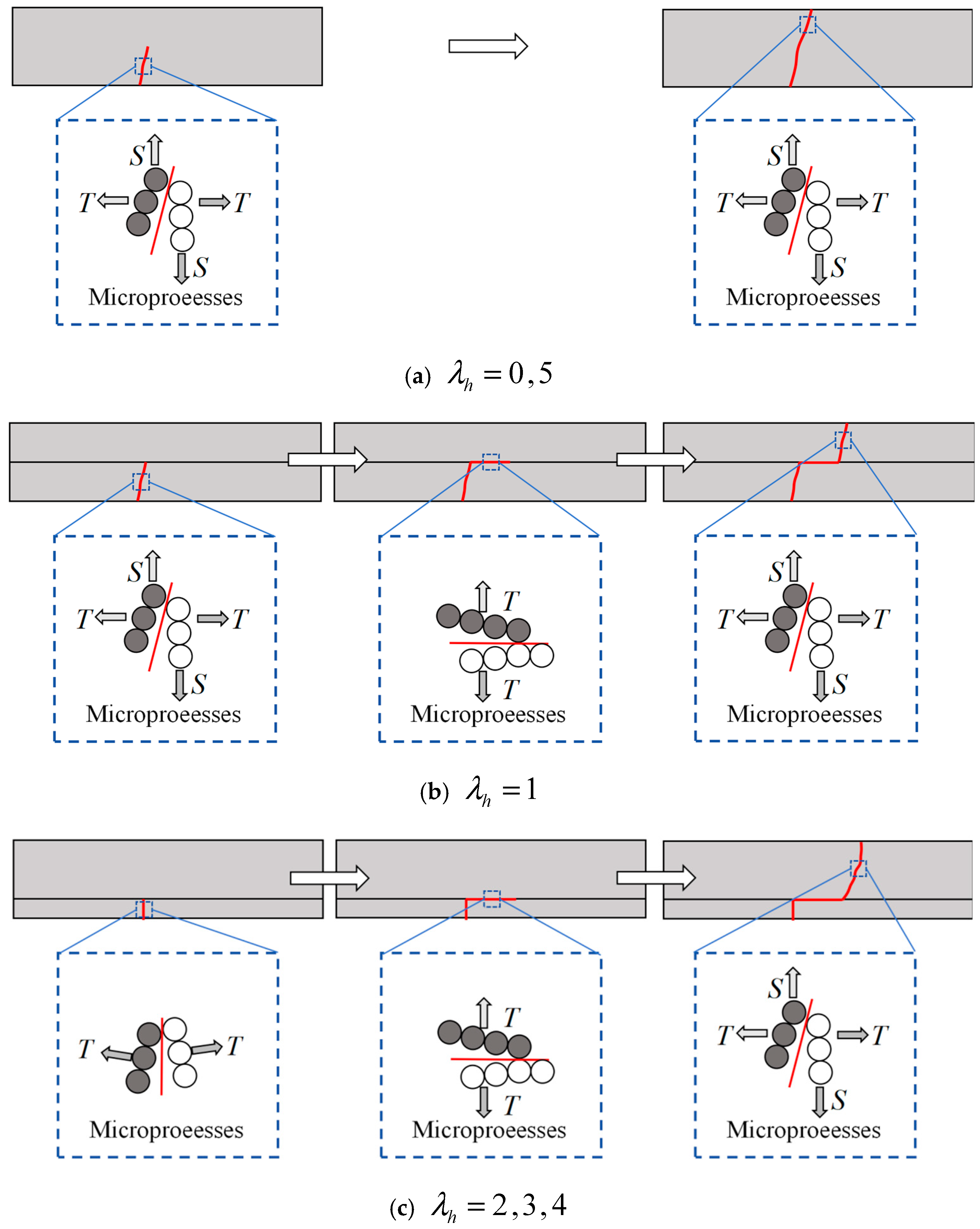
4.2. Microscopic Damage Patterns of Fiber Shotcrete Stacked Beams Based on the Thickness Ratio
4.3. Thickness Ratio-Based Damage Mechanism of Fiber Shotcrete Stacked Beams
5. Calculation of Fiber-Sprayed Concrete Stacked Beams with Flexural Stiffness Correction
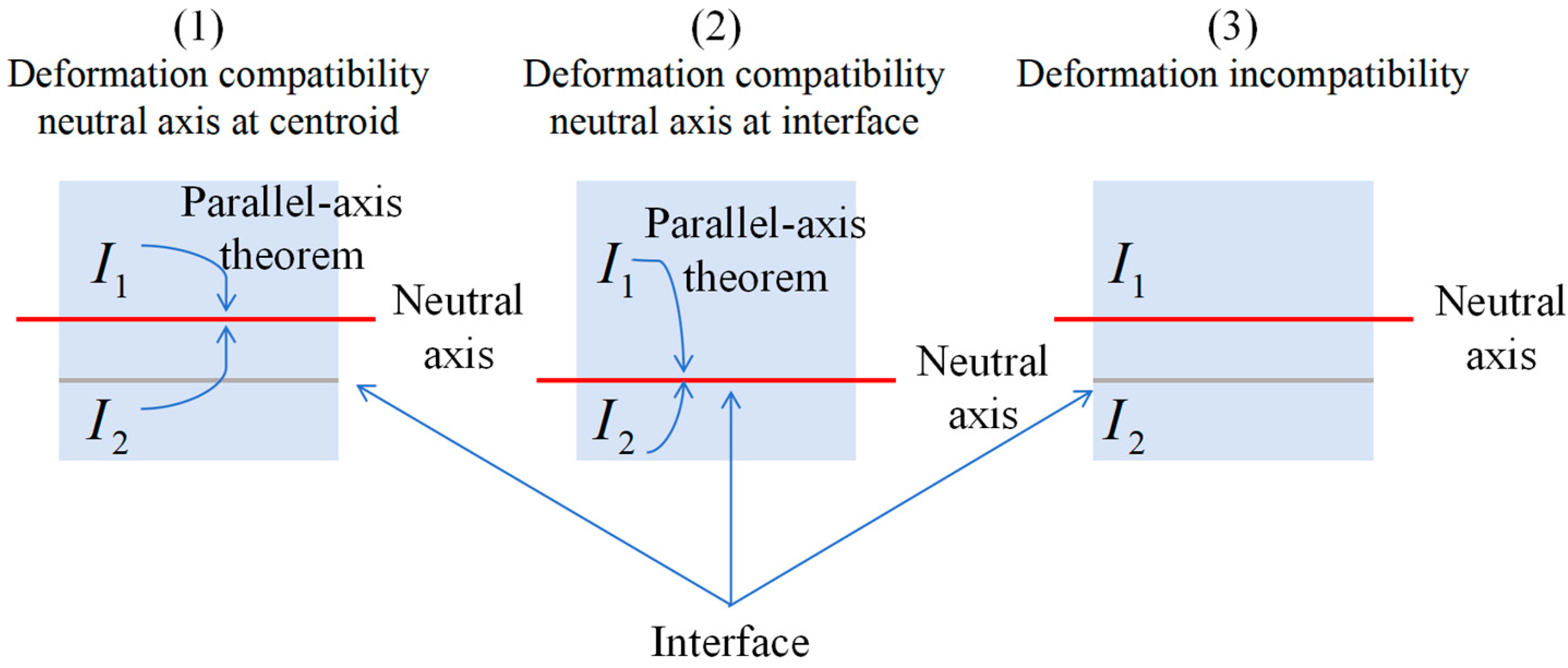
5.1. Theory of Fiber-Sprayed Concrete Stacked Beam Flexural Stiffness Calculation
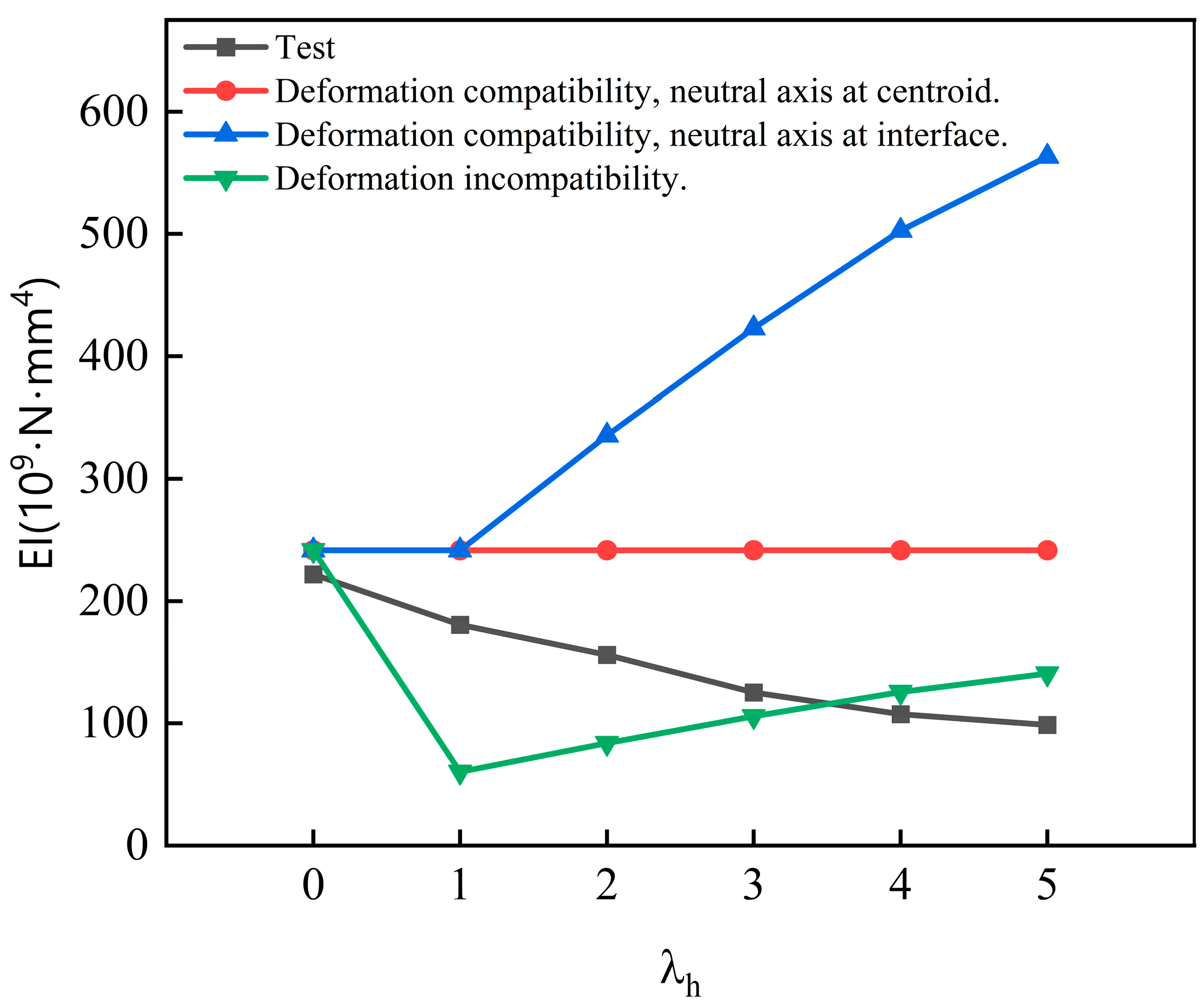
5.2. Comparative Analysis of the Flexural Stiffness Calculation Theory and the Test in This Paper
5.3. Modified Calculation of Fiber-Sprayed Concrete Stacked Beams Considering the Thickness Ratio
5.4. Theoretical Verification of the Modified Theory of Laminated Beams
6. Conclusions
- (1)
- The flexural ultimate load values of the specimens first increase and then decrease as the thickness ratio increases. The maximum flexural ultimate load occurs when the thickness ratio is 2, with a 20.9% increase in flexural ultimate load compared to the thickness ratio of 0.
- (2)
- The flexural toughness of the specimens increases and then decreases with the increase in the thickness ratio. When the thickness ratio is 2, the flexural toughness of the specimen reaches its maximum, which is 25% higher compared to the thickness ratio of 0 (unstratified specimen).
- (3)
- Layered construction affects the failure mode of the shotcrete single-layer lining structure. At thickness ratios ranging from one to five, cracks develop with a transverse abrupt change at the parting interface. All shotcrete beams exhibit mixed-mode failure, with the proportion of flexural failure cracks increasing as the thickness ratio increases.
- (4)
- Layered construction will cause the effective bending stiffness of shotcrete beams to be reduced, and the larger the thickness ratio, the more obvious the reduction in the effective bending stiffness of shotcrete beams. On this basis, the interface influence coefficient is proposed, and the bending stiffness correction is carried out by combining the theory of stacked beams, which supplements the insufficiency of single-layer lining in the calculation of structural bending stiffness and can provide theoretical support for the calculation related to tunnel support.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zucca, M.; Valente, M. On the Limitations of Decoupled Approach for the Seismic Behaviour Evaluation of Shallow Multi-Propped Underground Structures Embedded in Granular Soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Zhang, J. Research on Key Technologies of TGP Advance Geological Prediction Data Collection. Prog. Geophys. 2020, 35, 1618–1625. [Google Scholar]
- Zhao, D.; Yu, Y.; Zhao, W.Q. Research on the Target Reliability Index of Railway Tunnel Lining. J. Railway Eng. Soc. 2015, 32, 51–56. [Google Scholar]
- Li, S.; Chen, W.; Hu, J.; Zhang, D.; Chen, L. Flexural Behavior of Unbonded Prestressed Concrete Composite Beams Manufactured with Glass-Fiber-Reinforced Lightweight Aggregate Concrete and Conventional Concrete. Iran. J. Sci. Technol., Trans. Civ. Eng. 2023, 48, 2031–2047. [Google Scholar] [CrossRef]
- Chunxiang, Q.; Patnaikuni, I. Properties of High-Strength Steel Fiber-Reinforced Concrete Beams in Bending. Cem. Concr. Compos. 1999, 21, 73–81. [Google Scholar] [CrossRef]
- Yan, X.; Gao, Y.; Luo, Y.; Bi, Y.; Xie, Y. Effect of Different Steel Fiber Types on Mechanical Properties of Ultra-High Performance Concrete. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1167, 012001. [Google Scholar] [CrossRef]
- Tang, C.W. An Extended Special Issue on Advances in High-Performance Fiber-Reinforced Concrete. Appl. Sci. 2023, 13, 10688. [Google Scholar] [CrossRef]
- Lifshitz Sherzer, G.; Ribakov, Y. Modeling Complex Material Interactions to Replicate and Uncover Mechanisms Driving the Performance of Steel Fiber-Reinforced Concrete Cylinders. Appl. Sci. 2025, 15, 3445. [Google Scholar] [CrossRef]
- Prieto, T.G.; Prieto, M.I.; Leal, A.; Ferrández, D. Mechanical Behavior of Carbon Fiber-Reinforced Concrete Structures After Structural Failure. Appl. Sci. 2025, 15, 1783. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, X. Experimental Study on Mechanical Properties of Graded EPS–Steel Fiber-Reinforced Concrete. Appl. Sci. 2025, 15, 1980. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Hason, M.M.; Sharba, A.A.K.; Hanoon, A.N.; Amran, M.; Magbool, H.M.; Gamil, Y. Experimental and Environmental Investigations of the Impacts of Wood Sawdust on the Performance of Reinforced Concrete Composite Beams. Case Stud. Constr. Mater. 2023, 19, e02550. [Google Scholar] [CrossRef]
- Gao, D.; Jing, J.; Chen, G.; Yang, L. Experimental Investigation on Flexural Behavior of Hybrid Fibers Reinforced Recycled Brick Aggregates Concrete. Constr. Build. Mater. 2019, 227, 116652. [Google Scholar] [CrossRef]
- Ramadan, R.; Jahami, A.; Khatib, J.; El-Hassan, H.; Elkordi, A. Improving Structural Performance of Reinforced Concrete Beams with Phragmites Australis Fiber and Waste Glass Additives. Appl. Sci. 2023, 13, 4206. [Google Scholar] [CrossRef]
- Mahmood, A.; Noman, M.T.; Pechočiaková, M.; Amor, N.; Petrů, M.; Abdelkader, M.; Militký, J.; Sozcu, S.; Hassan, S.Z.U. Geopolymers and Fiber-Reinforced Concrete Composites in Civil Engineering. Polymers 2021, 13, 2099. [Google Scholar] [CrossRef] [PubMed]
- Blikharskyy, Z.; Markiv, T.; Turba, Y.; Hunyak, O.; Blikharskyy, Y.; Selejdak, J. Mechanical and Fracture Properties of Air-Entrained FRC Containing Zeolitic Tuff. Appl. Sci. 2023, 13, 9164. [Google Scholar] [CrossRef]
- Lalinde, L.F.; Mellado, A.; Borrachero, M.V.; Monzó, J.; Payá, J. Durability of Glass Fiber Reinforced Cement (GRC) Containing a High Proportion of Pozzolans. Appl. Sci. 2022, 12, 3696. [Google Scholar] [CrossRef]
- Ahmad, J.; Zaid, O.; Pérez, C.L.-C.; Martínez-García, R.; López-Gayarre, F. Experimental Research on Mechanical and Permeability Properties of Nylon Fiber Reinforced Recycled Aggregate Concrete with Mineral Admixture. Appl. Sci. 2022, 12, 554. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J.; Geng, S.; Qiu, X.; Jiang, P.; Zhou, J.; Jia, S.; Yao, Z. Exploring the Effects of Cementitious Capillary Crystalline Waterproof Material on the Properties of Cement with/without Mineral Admixture: A Comparison of Rheology, Hydration Process, and Self-Healing Behavior. Constr. Build. Mater. 2025, 470, 140546. [Google Scholar] [CrossRef]
- Li, M.; Meng, F.; Zhang, L.; Wu, Q. Experimental and Numerical Study on Flexural Behavior of Prefabricated Bottom Slabs with Rabbeted Grouting Splicing Joints. Structures 2024, 70, 107755. [Google Scholar] [CrossRef]
- He, Q.; Wu, Y.; Hu, C.; Yang, K.; Yi, W. Experimental Study of the Two-Way Mechanical Behavior of Tightly Spliced Prestressed Reinforced Concrete Laminated Slab. J. Struct. Eng. 2025, 151, 04025063. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, Z.; Lei, F. Experimental study on the stress characteristics of single-layer lining of steel fiber reinforced concrete tunnels considering interlayer effects. China Civ. Eng. J. 2019, 52, 116. [Google Scholar]
- Mitroulis, K.; Mellios, N.; Spyridis, P.; Bergmeister, K. Composite Action in Tunnel Linings by Use of Shear Connectors in Concrete Interfaces. In Life-Cycle of Structures and Infrastructure Systems; CRC Press: Boca Raton, FL, USA, 2023; pp. 2269–2276. [Google Scholar]
- Deng, Y.; Li, G.; Zhang, J.; Weng, S. Study on composite surface of waterproof single-layer lining by tests. J. Railway Sci. Eng. 2022, 19, 776. [Google Scholar]
- Xie, Y.Z.; Zhang, W.D.; Wu, X.; Ueda, T. Nonlinear Analysis of Full-Range Bending Process of Prefabricated and Cast-in-Place Concrete Composite Beams Considering Interface Debonding. Structures 2025, 74, 108588. [Google Scholar] [CrossRef]
- Xie, Y.Z.; Zhang, W.D.; Wu, X.; Ueda, T. Nonlinear Fatigue Analysis Model of Prefabricated Concrete Composite Beams with Wet Connection Considering Interface Debonding under Cyclic Loading. Eng. Struct. 2025, 328, 119741. [Google Scholar] [CrossRef]
- Su, J.; Bloodworth, A. Utilizing Composite Action to Achieve Lining Thickness Efficiency for Sprayed Concrete Lined (SCL) Tunnels. In Proceedings of the ITA-AITES World Tunnel Congress 2016 (WTC 2016), San Francisco, CA, USA, 22–28 April 2016; Society for Mining, Metallurgy and Exploration: Englewood, CO, USA, 2016; Volume 1, pp. 84–93. [Google Scholar]
- Deng, J.; Zhou, X.; Zhuang, Y.; Liu, L.; Bai, Y. Mechanical Characteristics of Lining Structure Considering the Contact Effect between Composite Lining Layers. Sci. Technol. Eng. 2023, 23, 9268–9278. [Google Scholar]
- Feng, X.; Lu, Y.; Lu, B.; Yuan, C.; Li, S. Mechanical Behavior of Composite Shell Lining Structures Based on Cohesion Models. KSCE J. Civ. Eng. 2024, 28, 5373–5383. [Google Scholar] [CrossRef]
- Özütok, A.; Madenci, E. Static Analysis of Laminated Composite Beams Based on Higher-Order Shear Deformation Theory by Using Mixed-Type Finite Element Method. Int. J. Mech. Sci. 2017, 130, 234–243. [Google Scholar] [CrossRef]
- Tan, Z. Solution to Bi-Layer Beams on Elastic Foundation. ACTA Mech. Sin.-Chin. Ed. 1997, 29, 751–754. [Google Scholar]
- Tan, Z.-m.; Guo, J.-j.; Chen, J.-l. Solutions of Double-Layer Plates with Two-Way Spring Interlayers on Elastic Foundations. Appl. Math. Mech. 2016, 37, 382–390. [Google Scholar]
- Shi, B.; Zhu, W.; Yang, H.; Liu, W.; Tao, H.; Ling, Z. Experimental and Theoretical Investigation of Prefabricated Timber-Concrete Composite Beams with and without Prestress. Eng. Struct. 2020, 204, 109901. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Xie, T.; Yang, J. Flexural Behaviour and Cost Effectiveness of Layered UHPC-NC Composite Beams. Eng. Struct. 2022, 273, 115060. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zhu, H.; Yang, L.H. The Optimal Rubber Layer Height of Crumb Rubber Concrete Sandwich Beam. Indust. Construct. 2007, 37, 253–256. [Google Scholar]
- Zhang, J.; Leung, C.K.Y.; Cheung, Y.N. Flexural Performance of Layered ECC-Concrete Composite Beam. Compos. Sci. Technol. 2006, 66, 1501–1512. [Google Scholar] [CrossRef]
- Liu, H.; Xiao, J.; Ding, T. Flexural Performance of 3D-Printed Composite Beams with ECC and Recycled Fine Aggregate Concrete: Experimental and Numerical Analysis. Eng. Struct. 2023, 283, 115865. [Google Scholar] [CrossRef]
- Wang, H.L.; Shi, H.W.; Qian, P.L.; Bai, Y.L.; Liu, S.Z.; Yang, Z.Q. Flexural Behaviors of GFRP-Reinforced Engineered Cementitious Composite (ECC)-Concrete Composite Beams. Eng. Struct. 2025, 332120097, 120097. [Google Scholar] [CrossRef]
- Zaki, Y.; Abouhussien, A.; Hassan, A. Acoustic Emission Analysis of the Cracking Behavior in ECC-LWSCC Composites. Appl. Sci. 2025, 15, 594. [Google Scholar] [CrossRef]
- Yan, Z.; Wei, Y.; Du, H.; Chen, J.; Ding, M.; Li, G. Experimental and Theoretical Study on Flexural Performance of Reinforced Bamboo-Concrete Composite Beams. Eng. Struct. 2025, 325, 119503. [Google Scholar] [CrossRef]
- Xiamen City Construction Science Research Institute Group Co., Ltd.; Xiamen Tefang Construction Engineering Group Co., Ltd. JGJ/T 372-2016 Technical Specification for Application of Sprayed Concrete; China Architecture & Building Press: Beijing, China, 2016. [Google Scholar]
- Research Institute of Highway Ministry of Transport. Test Methods of Cement and Concrete for Highway Engineering; People’s Traffic Publishing House Co., Ltd.: Beijing, China, 2021. [Google Scholar]
- Norwegian Concrete Association. Sprayed Concrete for Rock Support: NB 7E; Norwegian Concrete Association: Oslo, Norway, 2024. [Google Scholar]
- Li, G.F. Application of Composite Lining Technology in Mining Method Tunnels. Shanxi Archit. 2022, 48, 162–164+179. [Google Scholar]
- Li, L.Y.; Yang, J.S.; Xie, Z.; Xue, J.; Zheng, J. Study on the Mechanical Characteristics of Tunnel Single-Layer Lining Structure Based on FLAC3D. J. Highway Transp. Res. Dev. 2019, 36, 74–82. [Google Scholar]
- ASTM C1609/C1609M-07; Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2007.
- Wong, L.N.Y.; Einstein, H.H. Systematic Evaluation of Cracking Behavior in Specimens Containing Single Flaws under Uniaxial Compression. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, J.; Zhang, Y.; Qiang, Q. Finite Element Analysis of Failure Modes of Blast-Loaded R/C Beams. Eng. Mech. 2001, 18, 1–8. [Google Scholar]
- Xu, K.; Wang, W.; Zhang, L. The compressive strength and establishment its prediction model of concrete with recycled coarse aggregates from different sources. Mater. Rep. 2025, 39, 23110068-9. [Google Scholar]








| Fibroid | Cement | Ganister Sand | Coarse Aggregate | Fine Aggregate | Water | |
|---|---|---|---|---|---|---|
| Typology | Dopant | |||||
| PP fiber | 4 | 394 | 36 | 844 | 914 | 172 |
| Performance | Tensile Strength/MPa | Elastic Modulus /GPa | Length/mm | Diameter /mm | Aspect Ratio | Density | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Norm | 550 | 9 | 30 | 0.8 | 37.5 | 0.95 | 0.22 |
| Typology | Intensity | Uniaxial Compressive Strength | Elastic Modulus | Poisson’s Ratio |
|---|---|---|---|---|
| concrete | 2.5 | 41 | 29 | 0.25 |
| Working Condition | Initial Spray Thickness/mm | Re-Spray Thickness/mm | |
|---|---|---|---|
| A1 | 0 | 100 | 0 |
| A2 | 1 | 50 | 50 |
| A3 | 2 | 33.3 | 67.7 |
| A4 | 3 | 25 | 75 |
| A5 | 4 | 20 | 80 |
| A6 | 5 | 16.7 | 83.3 |
| Working Condition | /kN | /mm | /kN | /mm | /MPa | /MPa |
|---|---|---|---|---|---|---|
| A1 | 20.85 | 0.09 | 20.85 | 0.15 | 6.255 | 6.255 |
| A2 | 22.63 | 0.12 | 24.85 | 0.22 | 6.789 | 7.455 |
| A3 | 22.79 | 0.14 | 25.21 | 0.38 | 6.837 | 7.563 |
| A4 | 20.93 | 0.16 | 22.95 | 0.46 | 6.279 | 6.885 |
| A5 | 19.09 | 0.17 | 21.89 | 0.52 | 5.727 | 6.567 |
| A6 | 18.55 | 0.18 | 21.17 | 0.57 | 5.565 | 6.351 |
| Working Condition | ||||
|---|---|---|---|---|
| Assumption (1) | Assumption (2) | Assumption (3) | ||
| A1 | 0 | 241.67 × 109 | 241.67 × 109 | 241.67 × 109 |
| A2 | 1 | 241.67 × 109 | 241.67 × 109 | 60.42 × 109 |
| A3 | 2 | 241.67 × 109 | 335.64 × 109 | 83.91 × 109 |
| A4 | 3 | 241.67 × 109 | 422.92 × 109 | 105.73 × 109 |
| A5 | 4 | 241.67 × 109 | 502.67 × 109 | 125.67 × 109 |
| A6 | 5 | 241.67 × 109 | 563.24 × 109 | 140.81 × 109 |
| Working Condition | ||||
|---|---|---|---|---|
| A1 | 0 | 20.85 | 0.09 | 222.01 × 109 |
| A2 | 1 | 22.63 | 0.12 | 180.73 × 109 |
| A3 | 2 | 22.79 | 0.14 | 156.00 × 109 |
| A4 | 3 | 20.93 | 0.16 | 125.36 × 109 |
| A5 | 4 | 19.09 | 0.17 | 107.62 × 109 |
| A6 | 5 | 18.55 | 0.18 | 98.76 × 109 |
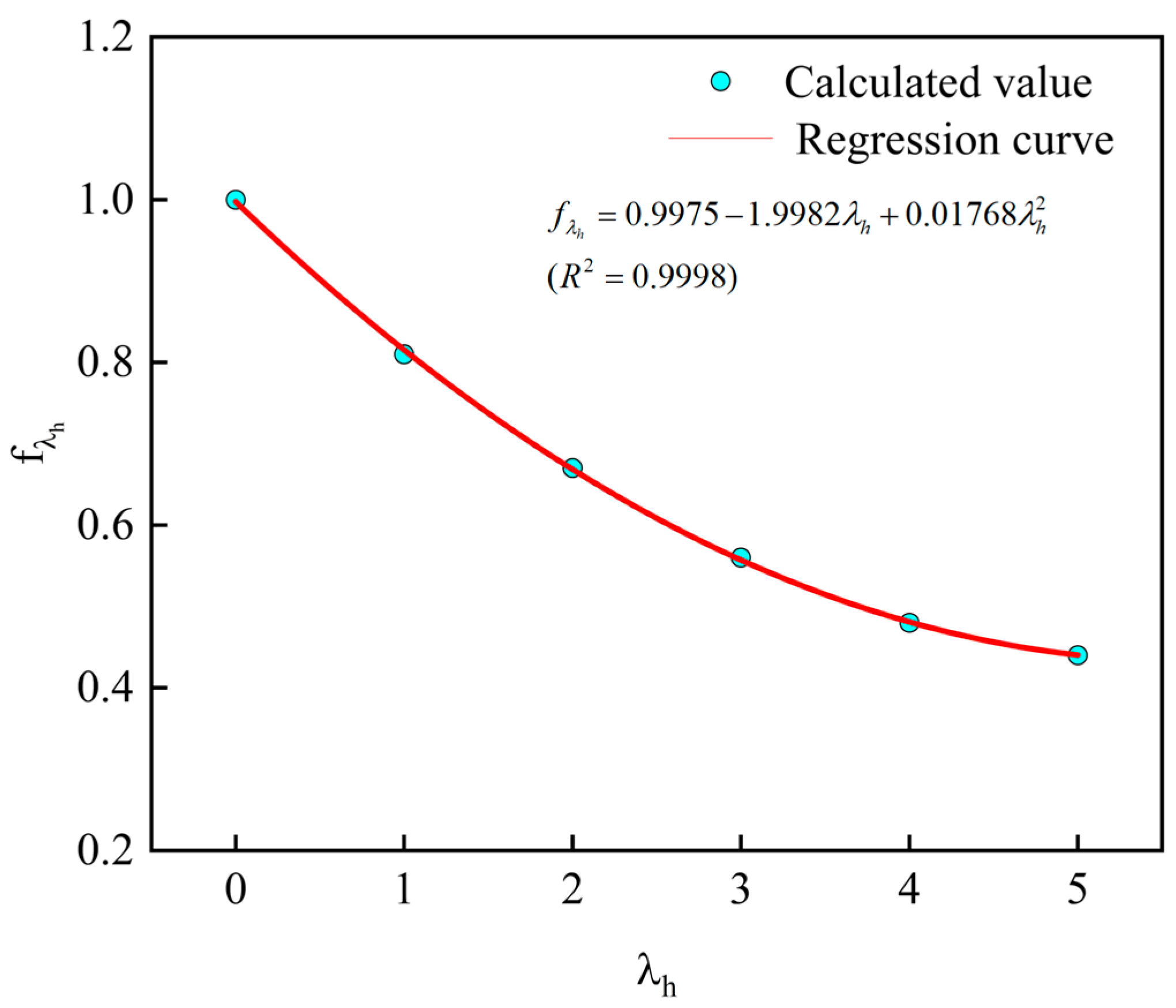
| Working Condition | |||
|---|---|---|---|
| A1 | 0 | 222.01 × 109 | 1 |
| A2 | 1 | 180.73 × 109 | 0.81 |
| A3 | 2 | 156.00 × 109 | 0.70 |
| A4 | 3 | 125.36 × 109 | 0.56 |
| A5 | 4 | 107.62 × 109 | 0.46 |
| A6 | 5 | 98.76 × 109 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Zhong, Z.; Xu, M.; Hu, X.; Zhu, K.; Cao, P. A Study of the Flexural Performance of Fiber-Reinforced Anchored Shotcrete Single-Layer Lining in a Hard Rock Tunnel Based on the Thickness Ratio. Appl. Sci. 2025, 15, 7473. https://doi.org/10.3390/app15137473
Wu M, Zhong Z, Xu M, Hu X, Zhu K, Cao P. A Study of the Flexural Performance of Fiber-Reinforced Anchored Shotcrete Single-Layer Lining in a Hard Rock Tunnel Based on the Thickness Ratio. Applied Sciences. 2025; 15(13):7473. https://doi.org/10.3390/app15137473
Chicago/Turabian StyleWu, Mengjun, Zuliang Zhong, Miao Xu, Xuebing Hu, Kaixin Zhu, and Peng Cao. 2025. "A Study of the Flexural Performance of Fiber-Reinforced Anchored Shotcrete Single-Layer Lining in a Hard Rock Tunnel Based on the Thickness Ratio" Applied Sciences 15, no. 13: 7473. https://doi.org/10.3390/app15137473
APA StyleWu, M., Zhong, Z., Xu, M., Hu, X., Zhu, K., & Cao, P. (2025). A Study of the Flexural Performance of Fiber-Reinforced Anchored Shotcrete Single-Layer Lining in a Hard Rock Tunnel Based on the Thickness Ratio. Applied Sciences, 15(13), 7473. https://doi.org/10.3390/app15137473






