Abstract
Considering a computational service as a set of processes, several issues can impact its performance, such as failures and shutdowns. Many strategies can be used to reduce this impact as the assignment of one service in several machines or the distribution of machines in different locations by respecting some constraints such as process dependency and capacity. The Machine Reassignment Problem is a hard problem that consists of a set of machines with associated resources and processes already assigned to these machines. The goal is to obtain a redistribution of the processes according to some optimization criteria, satisfying a set of constraints. In this work, we propose an efficient collaborative local search algorithm to solve the Machine Reassignment Problem. We pay special attention to designing an easily understandable algorithm that requires less computational resources than other more sophisticated well-known approaches in the literature. We show that our approach is effective using the ROADEF competition instances as a benchmark and that can obtain high-quality solutions.
1. Introduction
The emerging development of technologies that provide cloud services and data storage is generating great interest in improving service quality and minimizing the usage of resources. This paper addresses the Machine Reassignment Problem (MRP) proposed by Google in 2012 in the context of the ROADEF/EURO challenge [1]. This problem consists of a set of machines with available resources such as CPU, memory, and Hard Disk and processes requiring significant computational resources. Initially, each process is assigned to a machine. The MRP consists of optimizing the process reassignments for the best available resource usage. This is measured by objective functions, satisfying several constraints such as machines’ capacities, dependencies, and process distribution. Many approaches have been proposed to solve MRP from the ROADEF competition, which we briefly review in Section 2. A brief introduction to the MRP is presented in Section 3. The problem is a NP-hard problem [2] that involves several types of constraints to satisfy and also considers five objectives functions that, properly weighted, should be able to determine optimal solutions. In this work, we propose a simple local search algorithm based on Hill Climbing (HC) and Simulated Annealing (SA). Our goal is to propose a simple and adaptable approach that can compete with sophisticated algorithms that require much computational resources. Our approach has been specially designed to manage all constraints and all objectives of the problem. This is an important contribution in solving this problem compared to other methods proposed in the literature [2]. Moreover, the structure of the proposed approach could be extended to some other problems that present similar characteristics.
In Section 4, we present the details of our approach. We evaluate it using 30 benchmark instances from the ROADEF competition. Section 5 presents the results and statistical comparison with the best well-known results from the literature. It is important to remark that our approach can reach high-quality solutions in most problem instances using a simple but specialized local search approach. Finally, we present some conclusions and future work in Section 6.
2. Related Work
In this section, we briefly review some of the works presented for MRP related to this paper. A review of the main approaches is presented in [2]. The authors also propose a classification of the approaches. According to [2], the main features of approaches can be related to the use of local search to solve the problem or a collaboration of local search and exhaustive search approaches; the reduction in the size of neighborhoods given the complex nature of the problem; the inclusion of pre-processing steps to focus the search on specific areas of the space to analyze; and the incorporation of modifications to the objective function to assign more relevance to specific costs.
In [3], a variable neighborhood search method is presented. The local search algorithm explores four types of neighborhoods: Shift, Swap, Chain, which attempts to move a series of processes at the same time, and which tries to move big processes to a target machine while shifting processes to make sufficient space. The authors remark that moving big processes (concerning their requirements) in the early stages of the algorithm should be a priority. They also present a lower bound of the total cost function based on the individual lower bounds of load and balance costs. In [4], the authors improve their previous incorporating a restart procedure, a mechanism to deal with random seeds, and removing the exploration neighborhood.
Team S38 have presented two models for MRP for competition [5]: A Mixed Integer Linear Programming (MILP) and a Constraint Programming (CP) model. Their strategy was to apply Large Neighborhood Search (LNS) to both models, using CPLEX software [6] in the MILP model and a custom specifically designed LNS in the CP case. Their LNS algorithm creates and solves sub-problems iteratively. In the MILP model, the subset of processes is reassigned considering a timeout; on the other hand, the CP LNS is divided into three main phases: selecting a sub-problem in which a subset of processes and machines are also selected; creating the sub-problem in the computer’s memory, for which they evaluate the most efficient way to do it; and then optimize the sub-problem. In the last phase, they use a systematic search, with a stopping criterion based on the number of failures and a given threshold. In [7], improvements to the LNS algorithm proposed in [5] are presented. These include a complete analysis of parameter values, and a two-phase model of clustering of parameters and solving is incorporated. In [8], authors present a hybrid MIP-based large neighborhood search heuristic approach. It combines a Hill Climbing and a Large Neighborhood Search (LNS), which uses Mixed Integer Linear Programming (MIP) to solve sub-problems. Starting from the initial solution, it executes HC to improve the solution quickly and then uses LNS to perform additional improvements. In [9], a Simulated Annealing algorithm and lower bounds for the cost function are presented, obtained with the same formula as [3]. A search operator composed of two sub-moves is used. Shift and Swap are applied disjointedly according to a probability parameter. In [10], a Simulated Annealing-based hyper-heuristic approach is proposed. The general schema used is based on three phases. To generate the heuristics, four types of moves are considered: Shift, Swap, Backtracking (which consists of solving a sub-problem in a similar way to [5]), and Double Shift. In [11], authors model the MRP as a bin packing problem and introduce a local search-based heuristic to solve it. Their approach uses a multi-start system based on an Iterated Local Search framework. In [12], the problem is seen as a Vector Bin Packing perspective (VBP). In this case, the authors propose a generalization of VBP that allows distinct capacities of bins for each dimension. They analyze some structural properties of the MRP that allow decomposing it into smaller sub-problems and show that the studied heuristics are flexible enough to be adapted to the MRP. In [13], authors present an algorithm to solve MRP using a parallel evolutionary approach. Several heterogeneous Simulated Annealing algorithms are executed in parallel on a multi-core architecture. The authors report lower values than the best algorithms from the literature. In [14], the authors propose a hyper-heuristic approach that incorporates four main steps: local search algorithm selection and its corresponding search operators. The results show competitive and stable performance compared to the state-of-the-art methods. An in-depth analysis of state-of-the-art approaches can be found in [2].
Nowadays, most related research is focused on machine virtualization and its efficient management [15,16,17,18].
The use of machine learning approaches opens a new perspective of improvement for heuristic-based approaches [19,20].
Moreover, a large number of studies consider the multi-objective nature of the assignment problem optimizing objectives such as placement time, power consumption, and resource wastage [21]; performance, dependability, and cost [22]. Most of these approaches use heuristic search techniques such as particle swarm optimization in [23] or hybrid approaches such as particle swarm optimization and flower pollination optimization in [21], specialized heuristics and genetic algorithms in [24], or branch-and-bound algorithm with Lagrange decomposition combined with heuristic methods in [25]. Unlike most hybrid approaches in the literature, our main aim is to propose a simple and specialized algorithm able to adaptively change the focus of the search process depending on the current state of the search process. The components of our algorithm work sequentially, hence the effect of different phases could be studied separately to understand the relevance of each step in the whole process.
3. Machine Reassignment Problem
The Machine Reassignment Problem (MRP) consists of the re-assignment of a set of processes to a set of machines. An initial assignment is given, where all the processes are distributed over the machines. Starting from that initial assignment, the goal is to obtain a re-assignment of all or part of the processes to optimize the usage of the available resources. This problem was initially presented in the ROADEF/EURO challenge 2012 [1] and has some similarities with well-known problems such as the Generalized Assignment Problem (GAP) [26] and the Vector Bin Packing Problem (VBPP) [27].
The problem considers processes that need to be assigned to machines considering their resource requirements and belong to services, services that correspond to sets of processes that have dependence relationships, machines that are equipment where the processes are assigned and consume resource capacities (each machine belongs to a location and a neighborhood), locations that determine machines distributions (some processes of a given service should be asked to be assigned to machines with a particular distributions), and neighborhoods that are sets of machines, different from locations. Further details of the problem being solved in this work, including the detailed mathematical model, can be found in [2].
4. Our Approach: SMaRT
In this section, we introduce our algorithm to solve the MRP. Before describing the structure of our algorithm, we require the following definitions:
Given a set of n processes and a set of k machines , we define a representation for the MRP as an array A of size n where indicates that the process is assigned to the machine . This representation allows us to quickly identify which machine each process is and to satisfy the constraint that each process must be assigned to one machine. The array must be checked to ensure that all processes have been assigned.
We define the evaluation function as the minimization of the weighted sum of the costs shown in Equation (1). To compute the evaluation function, the algorithm considers only the costs associated with a move.
4.1. General Structure of the Algorithm
Our approach consists of three main phases (Figure 1). It is important to remark that the algorithm works with feasible solutions in all phases.
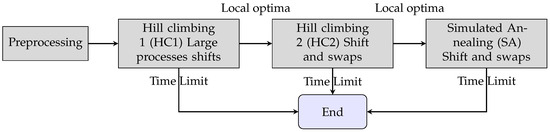
Figure 1.
General structure of the SMaRT algorithm.
The idea here is first to preprocess the instance data to discard infeasible assignments and then search using fast search approaches to obtain high-quality solutions in reduced execution times. If search approaches become stuck on local optima, the next step is executed. HC1 and HC2 use different movements in order to satisfy the most complex constraints first, then the algorithm used, HC or SA, depends only on the local optima HC finds during its search in the different cases being solved. Eventually, when the large processes shifts move does not become trapped in local optima, final solutions can be obtained only using this step of the algorithm. If during HC1 the algorithm becomes stuck and still has available execution time, it can perform HC2 to continue searching on different neighborhoods. If the algorithm becomes stuck using HC2 and still has available time, it can use the SA strategy that allows escaping from local optima.
- Preprocessing of the data: the aim is to pre-compute useful information to reduce the search space.
- Hill Climbing procedures: Hill Climbing has two steps. The first one, HC1, focuses on overloaded machines. The procedure tries to move the biggest processes from the machines that strongly increase the objective function value. The second step is HC2, which uses as initial solution the feasible solution obtained by HC1. It applies Shift and Swap moves and changes the solution using the first-improvement criteria.
- Simulated Annealing (SA): This approach uses Shift and Swap moves. This procedure includes a strategy to perform dynamic control of the temperature.
4.2. Preprocessing of the Data
The following methods are implemented to preprocess the data. The data come from the problem instances available at Roadef competence. In each instance, the information of processes, machines, services, and neighborhoods are read and analyzed by the algorithm to allow the following analyses:
Filtering the domain of the processes: We analyze each process to determine whether it is possible to assign it to each machine, removing those where the process cannot be assigned from its domain. This is achieved by considering the transient resources of the machines, which is occupied even after all processes are moved to another machine. Accordingly, considering the transient usage, the machines whose available space is not enough for a process are removed.
Identifying processes that are fixed to their initial machine: After the domain filter, we look for those processes whose transient resources requirement is so high that they can only stay on their initial machine since there is no other machine with enough available space for them (in terms of the transient resources). These processes are not considered to perform moves to generate new solutions, but they stay fixed on the initial machine during the whole algorithm execution. Moreover, a machine with a fixed process is removed from the domain of the rest of the processes from the same service (spreading the conflict constraint), which are rechecked to see whether this change in domain causes them to become stuck on their machines, and so on. This causes a reduction in the search space by using only a subset of processes and machines to generate new solutions.
Calculating the lower bound of the cost function: This is achieved by calculating the lower bound of the load cost and balance cost, as proposed in [3,4,5,9,28].
Calculating a size measure for the processes: To sort the processes, we use a size measure for each one, which is calculated as the weighted sum of the requirements of each resource. The weights are related to the shortage level of each resource, and there is a relationship between the total requirement for that resource among all processes and the total capacity among all machines. This method to determine the size of a process was proposed in [12], appearing as a better alternative than the size of a process as a sum of its requirements. This measure allows us to prioritize those processes that not only have more requirements but also require more from the scarce resources. Mathematically, the size is calculated as
Preprocessing processes are executed considering their effect on all other preprocesing steps. Fixed processes can determine the impossibility of assigning some other processes to these machines during the filtering domain step. These cascade effects are considered until a stable stage is reached.
All the information computed during the preprocessing phase is stored using proper data structures in order to be efficiently used during the search processes of next steps.
4.3. Hill Climbing
The goal of the first step is to improve the objective function by moving the largest processes from the machines with the highest load cost. Algorithm 1 shows the structure of the first Hill Climbing (HC1).
| Algorithm 1: HC1 algorithm |
 |
This HC phase uses a move called the Size Discriminant Excluding Shift (SDES) that works as follows:
- Select the machines loaded most (ordered by total cost) and from them select the processes with the largest size, ordered by the size according to Equation (2) (line 5). The ordered lists of machines are stored in proper data structures that are initialized during the preprocessing considering fixed processes and are updated according to the structure of current solution.
- With the selected processes, make a shift movement, moving them to other machines (excluding the most loaded machines of that iteration), maintaining the feasibility, and looking for the best improvement from all possible reassignments (Line 11).
- Once the SDES shift is applied in the current iteration, the machines are reordered, and a new iteration starts.
The selection criteria are the following:
- Choose the first machine within the most overloaded in which at least one process can be moved to any of the remaining machines and produce an improvement. When checking the possible moves for each process, choose the move that makes the best improvement among all processes on the same machine.
The algorithm stops when no more improving neighbors can be found or when the time limit is reached (Lines 3 and 19).
Once HC1 stops, the candidate solution obtained is given to the second HC. Algorithm 2 shows the structure of the second Hill Climbing (HC2).
| Algorithm 2: HC2 algorithm |
 |
HC2 continues the search using swap and shift moves:
- Shift of processes: A process is removed from one machine and inserted into another. This movement provides variability because it increases and decreases the number of processes in a machine.
- Swap of processes: Two processes from different machines are removed and assigned to the other machine. This move causes larger changes in the candidate solution in only one step and increases diversification.
The mechanism to generate a new solution is as follows:
- Generate a new neighbor by applying shift to the current solution.
- Generate a new neighbor by applying a swap to the same current solution.
- Selection criteria: The best neighbor generated from both moves is selected when it is better than the current solution. Ties are broken by choosing the swap move, which gives more diversity (Line 3).
The number of processes considered to swap is limited to a maximum number established by a parameter called .
Furthermore, every time the current solution changes, the lists of processes used to apply shift and swap are randomized (Line 8). Randomization is performed using random permutations with the aim of considering different sets each movement application. This changes the order in which the processes are considered to generate neighbors, and especially for the swap, it gives a possibility to participate in those processes that were beyond the limit considered. This randomization is also executed in the worst-case scenario, i.e., every time the entire neighborhood has been generated for any of the moves (up to in the swap case).
The algorithm stops when no more improving neighbors can be found or when the time limit has been reached (Line 2 and 5).
4.4. Simulated Annealing (SA)
Algorithm 3 shows the main structure of the SMaRT procedure. It runs after HC2 (Line 2) and works only with feasible solutions. The general purpose of this step is to allow the algorithm to visit other regions of the search space by using dynamic temperature control to properly manage the diversification and intensification during the search process. To achieve this, efficiently and adaptively, the initial temperature is established using a distance measure between the current evaluation function value and the theoretical lower bound value (Line 19).
| Algorithm 3: SMaRT algorithm |
 |
The algorithm uses two mechanisms as parameter control: cooling and reheating. The cooling mechanism is performed after a given number of iterations to reduce the level of diversification of the search (Line 28). On the other hand, after a given number of iterations without improvement of the solution, the reheating mechanism is used to increase the diversification level and allow the algorithm to scape from local optima (Line 19).
Simulated Annealing uses, as the second HC, Shift and Swap moves. The difference is in the selection mechanism and the temperature control. After generating the best neighbor of Shift and Swap, the difference between the selected neighbor and the current solution is evaluated:
- If the difference is negative or zero, that is, it improves or maintains the value of the objective function, the neighbor is immediately accepted (Line 10).
- If the difference is positive, the acceptance of the neighbor is determined using the temperature criteria (Line 14). That is, the probability of acceptance is , where is the difference in the objective function value, and T is the current temperature.
Parameter Control Mechanisms
The temperature is controlled as follows:
- Initial temperature: Since SA explores almost the same neighborhood as HC2, the starting point of SA may be a local optimum. For this, a high initial temperature is established, based on a parameter called and considering the value of the objective function concerning the total cost’s lower bound as follows:whereAccording to Equation (4), the temperature increases by taking the parameter , and amplifying it or decreasing it depending on how distant the current solution is concerning the cost lower bound and the initial solution. If the value of the objective function is too close to the lower bound, takes a value , where its square value is and decreases due to this factor. With this, the algorithm accepts solutions of worse quality but very close to the current solution, maintaining the exploitation of the nearby zone instead of moving too far from other regions of the search space.On the other hand, as the value of the objective function increases faster than the lower bound, becomes greater than one, so is multiplied several times and the temperature increases significantly, allowing exploration of the search space.It is important to mention that the change in temperature concerning allows the algorithm to adapt dynamically, regardless of the instance. This is because the is a normalized value, and it is not affected by the different magnitudes of the cost values of different instances. For example, consider , and . In this case, . This means the temperature increases and promotes an exploration phase. On the other side, consider the same conditions as before, but . In this case, . For this current solution, the temperature decreases, and the algorithm focuses on an intensification phase.
- Reheat: The algorithm also has a mechanism to reheat when a certain number of iterations without improvement of the solution is reached. The temperature is also set by using Equation (3).
- Rule to cool down: The cooling is also finished when a specific number of iterations is reached. A temperature reduction factor is used as in [9,28].
5. Experiments
The Machine Reassignment Problem was proposed in ROADEF/EURO 2012 [1]. In the problem definition presented on website [1], the problem constraints and details are specified along with the instances format and expected output.
5.1. ROADEF/EURO Challenge 2012
Each presented algorithm was executed only once with a time limit of 300 s. A specific metric to rank each algorithm was defined using , where I is the instance in which the score is obtained, R is the initial solution, S is the solution found by the algorithm, and B is the best solution found in the challenge among all algorithms for that specific instance. This score function has the benefit of not being influenced by the difference in costs between instances because it is a normalized value [7]. The total score of a group of instances was obtained by the addition of the scores of each instance.
We consider only the Best Cost indicator based on the specifications considered for the ROADEF competition as established in [29]. Here, the scores of all teams for each given instance were computed as the gap of their best cost divided by the cost of the reference solution. For all the competition stages, the score of each team was computed as the sum of its scores on all instances of the corresponding dataset. Also, as specified in [29], we fixed the maximum execution time to compare the approaches in the same conditions. Moreover, the Best Cost values allow a direct comparison against all state-of-the-art approaches.
Instances
All instances are available on the website of the challenge [1]; there are 30 in total, divided into three main groups, A, B, and X. These instances are widely used as benchmarks with different algorithms in the literature. The general characteristics of each instance, along with the best cost functions found in the challenge, can be seen in Table 1. In addition, in [7], the authors show remarkable information: considering the best solution costs of the competition, the initial solution is reduced on average by for each instance. This can be used as a measure of performance when comparing algorithms.

Table 1.
Characteristics of the instances in the competition.
We performed several experiments to test the performance and quality of the proposed algorithm SMaRT. To achieve this, we used the instances of groups B and X used for the competition. As an evaluation metric, the sum of the averages of the ROADEF scores associated with each instance was used in a similar way that each team was evaluated in the competition. The advantage of using this value is that it is not influenced by differences in objective function values of instances of different characteristics. All tests were performed on a Ubuntu 14.04.5 operating-based computer with Intel (R) Core (TM) i7-2600 CPU @ 3.40 GHz processor and 15 GB of RAM memory. The algorithm, executed in the instances of Group A, obtained results that would have allowed it to classify. On the other hand, the instances of Groups B and X of the final phase were used in the comparison of the proposed algorithm versus the results of ROADEF and the literature. The algorithm was executed with a time limit of 300 s, as required in the competition.
5.2. Experiment Design
We calibrate SMaRT algorithm using ParamILS [30]. We divide our experiments into two sections:
- Using the parameter values obtained by ParamILS, we compare our scores with the best results obtained for each instance of the final phase and with the results obtained by the first five teams of the competition.
- We execute the improved versions of the algorithms of teams S41 [4] and S38 [7], which showed the best results in the literature in the context of the competition. It is important to remark that we execute these three algorithms in the same machine and using the same 31 seeds and a maximum execution time of 300 s. These algorithms are available online, under open source license. The average of the results obtained with all seeds is used for comparisons.
5.3. Parameter Tuning
The tuning process can be seen as an algorithm design process. Tuning methods have been extensively used to assist the automated design of algorithms [31,32]. Here, we set the main parameter values of our approach to obtain the best resource balance between the different stages by tuning the following parameters:
| (HC1) | 10, 16, 17, 25, 33, 41, 45. |
| (HC1) | 10, 16, 17, 25, 33, 41, 45. |
| (HC2 and SA) | 500; 700; 1000; 1100; 1200; 1300. |
| (SA) | 770,000; 790.000; 810,000; 830,000; 850,000; 880,000. |
| Iterations without improvement before reheat (SA) | 15,000; 17,500; 18,900; 19,500; 20,000; 30,000. |
| Iterations before cooling (SA) | 4000; 4200; 4400; 4600; 4800. |
| (SA) | 0.96; 0.965; 0.97; 0.975; 0.98. |
Given that each instance must run for 5 min, we selected the instances from each group that presented the greatest challenge for the algorithm: Instances B_1, B_2, B_3 and B_7 from Group B and Instances X_1, X_2, X_3 and X_7 from Group X. Finally, the values found by ParamILS were = 16, = 16, = 1000, = 810,000, = 18,900, : 4400, : 0.97.
5.4. Comparison with the Best of ROADEF
Table 2 summarizes the best qualification and final phase scores and their associated competing teams. Table 3 shows the best quality values reported in the ROADEF challenge for each instance. Moreover, it also shows the average, best, and worst results obtained by our algorithm SMaRT and their corresponding score. It is important to note that the best values reported as Best ROADEF in this table are not associated with a unique solving algorithm. These values correspond to the best values found for each instance by any of the algorithms in the competition. The maximum execution times of all these experiments is fixed to 300 s as established by the ROADEF competition.

Table 2.
Best 5 scores for each phase.

Table 3.
Comparison of SMaRT with the best results of ROADEF for Instance Sets B and X. Bold font show the cases when equal or best results were found using SMaRT.
We show in bold the cases when equal or best results were found using in each problem instance using SMaRT algorithm. From these results, we can observe that SMaRT obtains good quality results, reporting consistently better values on Instances B_1 and X_1. These are shown as negative scores in the table. Looking at the worst results of SMaRT, all of them are close to the average values. Moreover, by computing the sum of scores and considering it as the total score, as used in the ROADEF challenge, the worst-case results of SMaRT also obtain a competitive total score, while the average-case and the best-case are better than those in the challenge.
Additionally, Table 4 shows the comparison of SMaRT with the five best algorithms in the final phase of the ROADEF competition. This table shows the results published by the algorithms proposed in the competition and is currently available at https://roadef.org/challenge/2012/en/results.php (accessed on 28 June 2025). It only lists the average results for each instance. No team obtained the best results on all of the problem instances. In this case, we divide the set of instances into the hardest instances and the easiest ones. We consider the hardest instances as those where only one team found the best value in the competition. These instances were B_1, B_3, B_5, B_7, X_1, and X_2. We consider the easiest instances as those where at least two teams found the best values of the competition. These instances were B_4, B_6, B_9, X_4, X_5, X_6, X_8, and X_9. The hardest instances are listed in boldface in Table 4, and the easiest are shown in normal font. For the easiest instances, SMaRT obtained the same performance as the other algorithms, finding the minimum values on each problem instance. For the hardest instances, our algorithm was able to obtain better scores than most of the analyzed teams, especially on Instances B_1 and X_1.

Table 4.
Comparison of SMaRT with the five best teams of ROADEF for Instance Sets B and X. Bold font show the cases when equal or best results were found using SMaRT.
5.5. Comparison with the Current Best Algorithms from the Literature: S41 and S38
The authors of Algorithms S41 and S38 presented a new, improved version of their algorithm after the competition on [4,7], respectively. In these papers, they reported new best results for the instances of Sets B and X, using similar experimental scenarios as those defined by ROADEF. According to [4], the total score obtained by the new version of S41 were for average and best results. These scores were obtained based on 100 runs with a maximum execution time of 300 s. On the other hand, the authors of [7] reported that Team S38 obtained a reduced new total score of using four cores to solve Instances B.
Statistical Analysis
Table 5 summarizes the average and best solutions obtained when executing the available versions of these algorithms in the same conditions as SMaRT. All these executions were performed in the same hadware specified in Section Instances considering a maximum execution time of 300 s per run.

Table 5.
Comparison of SMaRT with the improved versions of S41 and S38 teams for Instance Sets B and X.
The Wilcoxon signed-rank test was used to study the statistical differences among the performance of SMaRT, S41, and S38. The analysis is performed separately for instances of Groups B and X. There are no ties in these analyses because of the precision level of 14 decimal positions obtained for the scores. A p-value = 0.007 for Group B and p-value = 0.018 for Group X allow us to conclude with confidence that SMaRT is statistically significantly better than S41. The comparison of S38 and SMaRT shows p-values = 0.000 for Group B and group X, allowing us to conclude that SMaRT obtains results statistically significantly better than S38.
6. Conclusions
In this work, we proposed an algorithm to solve hard instances of the Machine Reassignment Problem, a challenge presented by Google for the ROADEF-Euro in 2012. SMaRT is a local search procedure composed of two Hill Climbing and Simulated Annealing steps. Each Hill Climbing is focused on a different optimization goal. Thus, their collaboration allows the algorithm to obtain good quality solutions. HC1 aims to quickly improve a given initial solution, focusing on moving the larger processes from the most overloaded machines with the SDES move, while HC2 searches to improve as much as possible the objective function through simple shift and swap moves. It is important to note that for many tested instances, the only combination of both HCs can obtain results of very good quality and highly competitive. This is mainly due to the use of the SDES move in HC1, which allows for balancing the load between the machines, improving the objective function. The Simulated Annealing procedure enables the algorithm to escape from the local optima and to diversify the search to other promising zones of the search space. Using SMaRT, it is possible to solve the instances quickly and efficiently in a fixed amount of time of 300 s.
Our Simulated Annealing procedure uses a dynamic control of the temperature related to the objective function value and the distance from the lower bound of the cost function. This prevents too much time spent using excessively high-temperature values. Thus the algorithm can quickly converge to high-quality solutions within the time limit required.
We proposed a collaborative algorithm composed of simple local search procedures that is easy to understand and has shown a good performance, including for hard instances, compared to more sophisticated approaches.
7. Future Work
Some possible heuristics to implement that add variability to the initial solution are those presented in [12], in which it was established that it is possible to order processes using some well-known functions for the Bin Packing from the literature. A feature that could provide significant improvements in the algorithm’s computation times could be the use of a feasibility allocation matrix to not only discard those processes that must be assigned to their initial machine but also to order the list of processes based on the number of machines to which they can be assigned, thus providing another method to assign the most conflicting processes first and avoid infeasible regions of the search space. One of the most difficult constraints to address in this problem is the neighborhoods of the processes associated with a service. The movement of processes is severely constrained once the algorithm progresses and the neighborhoods become filled. For a new version, we consider the level of available capacity of each neighborhood and prioritize in the initial stages of the algorithm the allocation of processes to machines whose neighborhoods have more available space. Last, we plan to integrate ideas coming from the application of machine learning approaches to improve optimization search, specially the use of data-driven methods to re-model the problem structure changing the objective functions parameters to adapt the search considering changes in the environment related to machines that fail or break down.
Author Contributions
Conceptualization, D.C. and M.-C.R.; investigation, D.C. and M.-C.R.; methodology, D.C., M.-C.R. and E.M.; software, D.C.; supervision, M.-C.R. and E.M.; validation, D.C., M.-C.R. and E.M.; writing—original draft, D.C., M.-C.R. and E.M.; writing—review and editing, M.-C.R. and E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Fondecyt Project 1241112. Elizabeth Montero was supported by Fondecyt Project 1230365.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Problem instances are available in the specified website.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Google ROADEF/EURO CHALLENGE. 2011–2012: Machine Reassignment Problem. Artificial Intelligence. 2012, pp. 9–47. Available online: http://challenge.roadef.org/2012/en/ (accessed on 1 June 2025).
- Canales, D.; Rojas-Morales, N.; Riff, M.C. A Survey and a Classification of Recent Approaches to Solve the Google Machine Reassignment Problem. IEEE Access 2020, 8, 88815–88829. [Google Scholar] [CrossRef]
- Gavranović, H.; Buljubašić, M.; Demirović, E. Variable Neighborhood Search for Google Machine Reassignment problem. Electron. Notes Discret. Math. 2012, 39, 209–216. [Google Scholar] [CrossRef]
- Gavranović, H.; Buljubašić, M. An efficient local search with noising strategy for Google Machine Reassignment problem. Ann. Oper. Res. 2014, 242, 19–31. [Google Scholar] [CrossRef]
- Mehta, D.; O’Sullivan, B.; Simonis, H. Comparing Solution Methods for the Machine Reassignment Problem. In Principles and Practice of Constraint Programming, Proceedings of the 18th International Conference, CP 2012, Québec City, QC, Canada, 8–12 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 782–797. [Google Scholar] [CrossRef]
- CPLEX. IBM ILOG CPLEX Optimization Studio. Available online: http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/ (accessed on 4 September 2020).
- Malitsky, Y.; Mehta, D.; O’Sullivan, B.; Simonis, H. Tuning Parameters of Large Neighborhood Search for the Machine Reassignment Problem. In Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Proceedings of the 10th International Conference, CPAIOR 2013, Yorktown Heights, NY, USA, 18–22 May 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 176–192. [Google Scholar] [CrossRef]
- Jaśkowski, W.; Szubert, M.; Gawron, P. A hybrid MIP-based large neighborhood search heuristic for solving the machine reassignment problem. Ann. Oper. Res. 2015, 242, 33–62. [Google Scholar] [CrossRef][Green Version]
- Portal, G.M. An Algorithmic Study of the Machine Reassignment Problem. Bachelor’s Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2012. [Google Scholar]
- Hoffmann, R.; Riff, M.C.; Montero, E.; Rojas, N. Google challenge: A hyperheuristic for the Machine Reassignment problem. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 846–853. [Google Scholar]
- Masson, R.; Vidal, T.; Michallet, J.; Penna, P.H.V.; Petrucci, V.; Subramanian, A.; Dubedout, H. An iterated local search heuristic for multi-capacity bin packing and machine reassignment problems. Expert Syst. Appl. 2013, 40, 5266–5275. [Google Scholar] [CrossRef]
- Gabay, M.; Zaourar, S. Vector bin packing with heterogeneous bins: Application to the machine reassignment problem. Ann. Oper. Res. 2015, 242, 161–194. [Google Scholar] [CrossRef]
- Turky, A.; Sabar, N.R.; Song, A. Cooperative evolutionary heterogeneous simulated annealing algorithm for google machine reassignment problem. Genet. Program. Evolvable Mach. 2017, 19, 183–210. [Google Scholar] [CrossRef]
- Turky, A.; Sabar, N.R.; Dunstall, S.; Song, A. Hyper-heuristic local search for combinatorial optimisation problems. Knowl.-Based Syst. 2020, 205, 106264. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Fan, G.; Li, Z.; Xu, J.; Li, J. Handling hierarchy in cloud data centers: A Hyper-Heuristic approach for resource contention and energy-aware Virtual Machine management. Expert Syst. Appl. 2024, 249, 123528. [Google Scholar] [CrossRef]
- Luo, J.Y.; Chen, L.; Chen, W.K.; Yuan, J.H.; Dai, Y.H. A cut-and-solve algorithm for virtual machine consolidation problem. Future Gener. Comput. Syst. 2024, 154, 359–372. [Google Scholar] [CrossRef]
- Durairaj, S.; Sridhar, R. Coherent virtual machine provisioning based on balanced optimization using entropy-based conjectured scheduling in cloud environment. Eng. Appl. Artif. Intell. 2024, 132, 108423. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Xu, M.; Shao, L. Massive-Scale Aerial Photo Categorization by Cross-Resolution Visual Perception Enhancement. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 4017–4030. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chang, X.; Chen, L.; Phung, D.; Zhang, X.; Yang, Y.; Hauptmann, A.G. Pair-based Uncertainty and Diversity Promoting Early Active Learning for Person Re-identification. ACM Trans. Intell. Syst. Technol. 2020, 11, 21. [Google Scholar] [CrossRef]
- Li, J.; Lin, J. A probability distribution detection based hybrid ensemble QoS prediction approach. Inf. Sci. 2020, 519, 289–305. [Google Scholar] [CrossRef]
- Mejahed, S.; Elshrkawey, M. A multi-objective algorithm for virtual machine placement in cloud environments using a hybrid of particle swarm optimization and flower pollination optimization. PeerJ Comput. Sci. 2022, 8, e834. [Google Scholar] [CrossRef]
- Guérout, T.; Gaoua, Y.; Artigues, C.; Da Costa, G.; Lopez, P.; Monteil, T. Mixed integer linear programming for quality of service optimization in Clouds. Future Gener. Comput. Syst. 2017, 71, 1–17. [Google Scholar] [CrossRef]
- Li, S.; Pan, X. Adaptive management and multi-objective optimization of virtual machine in cloud computing based on particle swarm optimization. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 102. [Google Scholar] [CrossRef]
- Quan, Z.; Wang, Y.; Liu, X.; Ji, Z. Multi-objective evolutionary scheduling based on collaborative virtual workflow model and adaptive rules for flexible production process with operation reworking. Comput. Ind. Eng. 2024, 187, 109848. [Google Scholar] [CrossRef]
- Wang, G.; Ben-Ameur, W.; Ouorou, A. A Lagrange decomposition based branch and bound algorithm for the optimal mapping of cloud virtual machines. Eur. J. Oper. Res. 2019, 276, 28–39. [Google Scholar] [CrossRef]
- Yagiura, M.; Ibaraki, T.; Glover, F. An ejection chain approach for the generalized assignment problem. INFORMS J. Comput. 2004, 16, 133–151. [Google Scholar] [CrossRef]
- Ray, A. There is no APTAS for 2-dimensional vector bin packing: Revisited. Inf. Process. Lett. 2024, 183, 106430. [Google Scholar] [CrossRef]
- Portal, G.M.; Ritt, M.; Borba, L.M.; Buriol, L.S. Simulated annealing for the machine reassignment problem. Ann. Oper. Res. 2015, 242, 93–114. [Google Scholar] [CrossRef]
- Murat Afsar, H.; Artigues, C.; Bourreau, E.; Kedad-Sidhoum, S. Machine reassignment problem: The ROADEF/EURO challenge 2012. Ann. Oper. Res. 2016, 242, 1–17. [Google Scholar] [CrossRef][Green Version]
- Hutter, F.; Hoos, H.; Leyton-Brown, K.; Stützle, T. ParamILS: An automatic algorithm configuration framework. J. Artif. Intell. Res. 2009, 36, 267–306. [Google Scholar] [CrossRef]
- KhudaBukhsh, A.; Xu, L.; Hoos, H.; Leyton-Brown, K. SATenstein: Automatically building local search SAT solvers from components. In Proceedings of the 21st International Jont Conference on Artifical Intelligence, Pasadena, CA, USA, 11–17 July 2009; pp. 517–524. [Google Scholar]
- Hoos, H.H. Automated Algorithm Configuration and Parameter Tuning. In Autonomous Search; Hamadi, Y., Monfroy, E., Saubion, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–71. [Google Scholar] [CrossRef]
- Brandt, F.; Speck, J.; Völker, M. Constraint-based large neighborhood search for machine reassignment. Ann. Oper. Res. 2016, 242, 63–91. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
