Load Weight Estimation in Electric Forklifts via DC–DC Converter Power Signal Analysis of the Electro-Hydraulic Lifting System
Abstract
1. Introduction
2. Materials and Methods
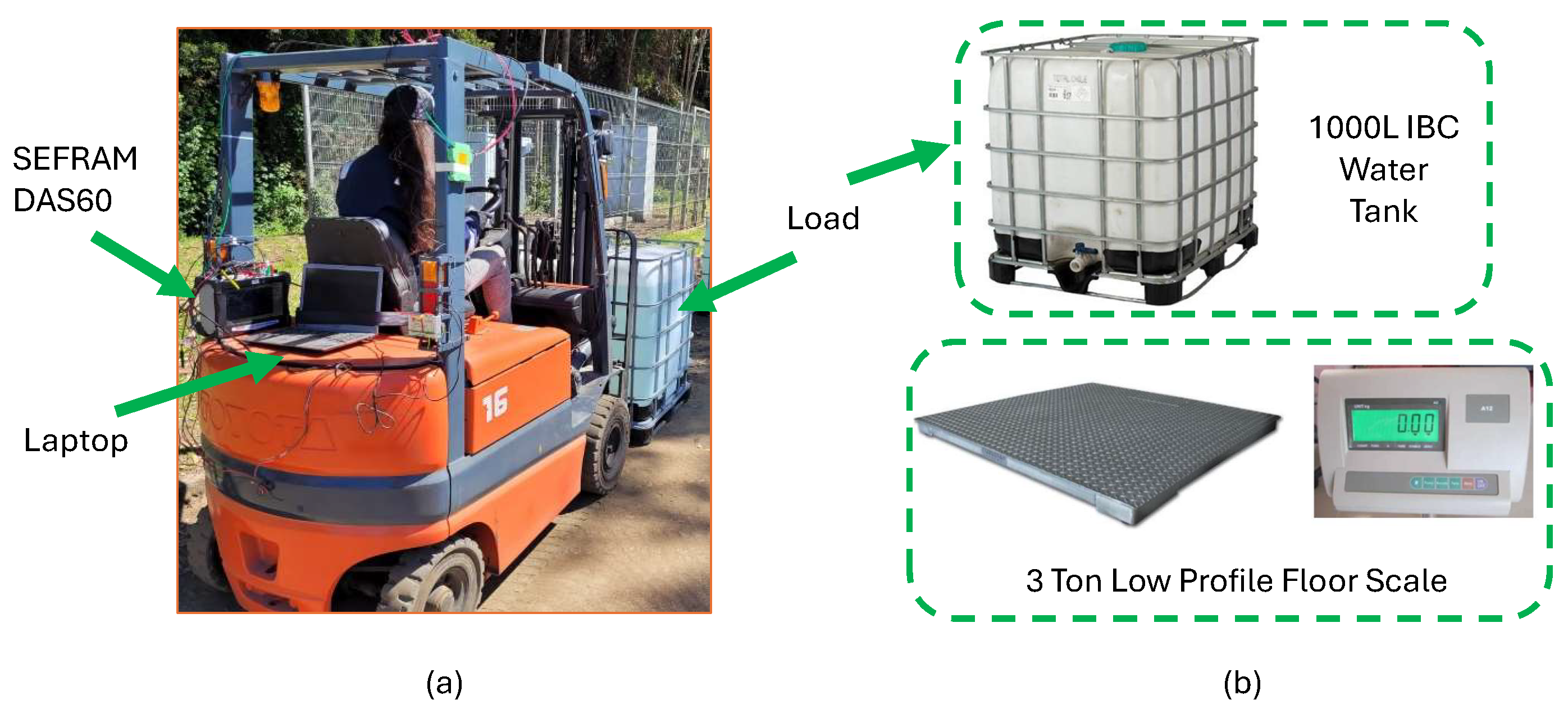
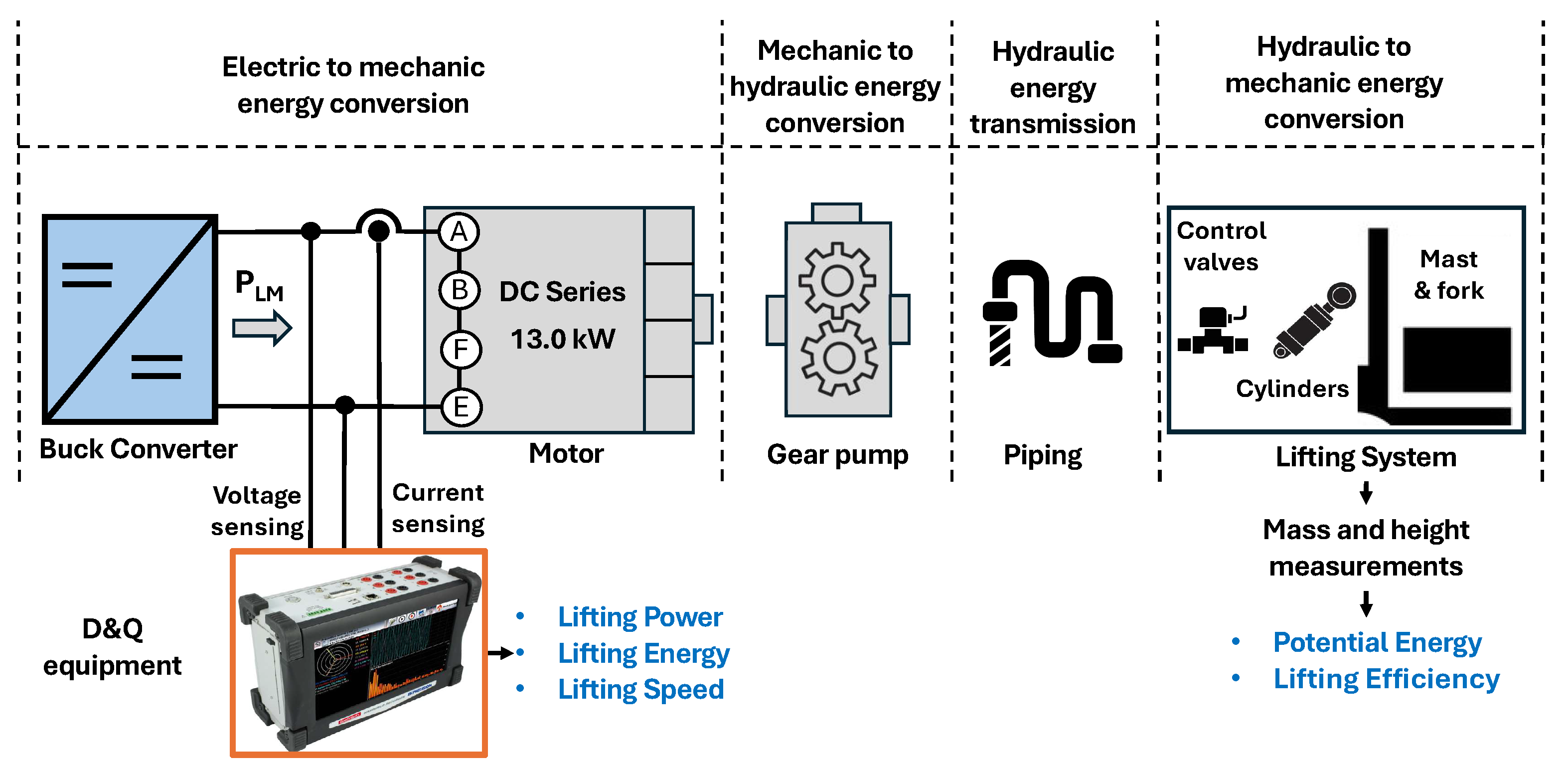
2.1. Experimental Setup
2.2. Experimental Tests
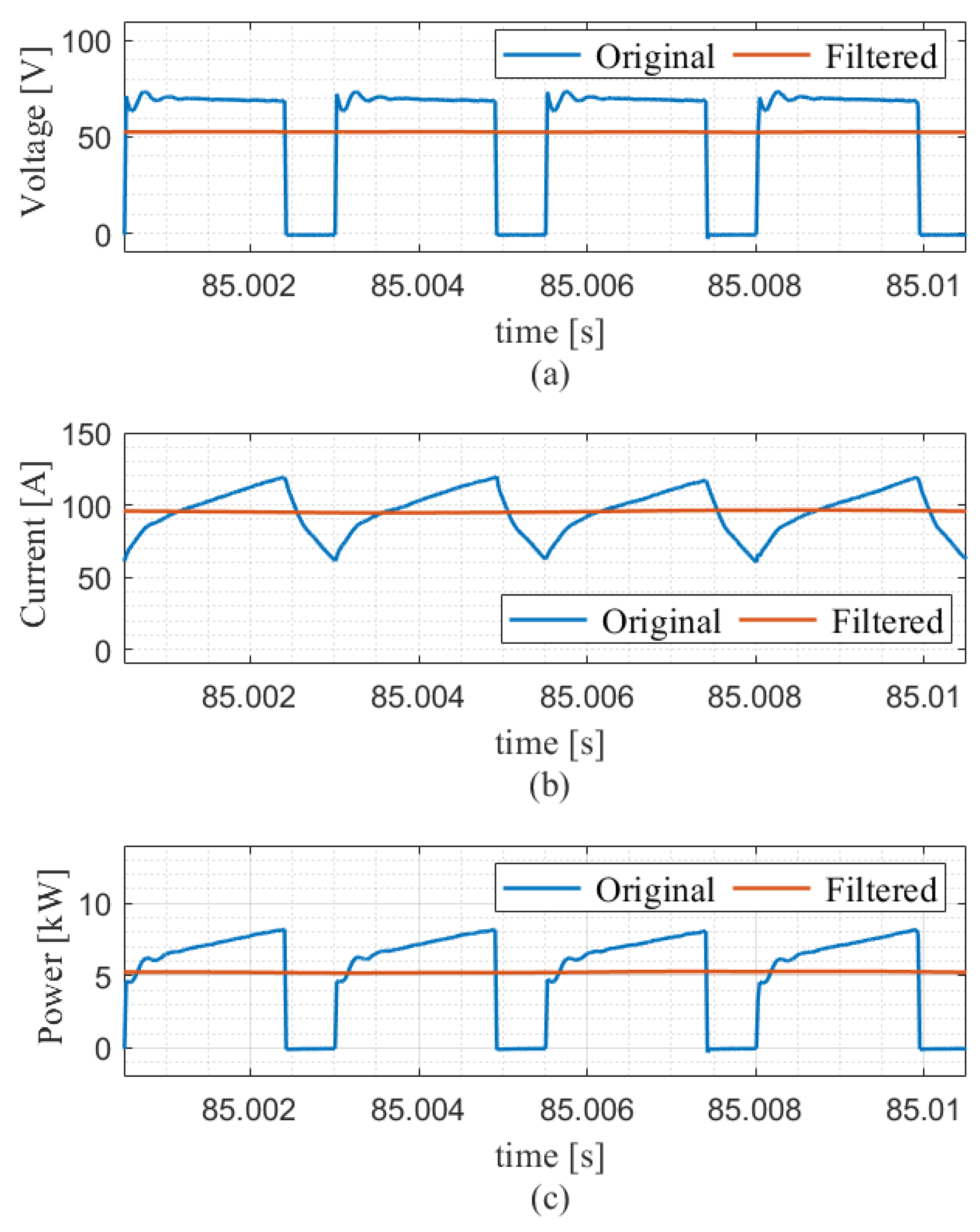
2.3. Data Conditioning
3. Results
3.1. Energy Boxplot
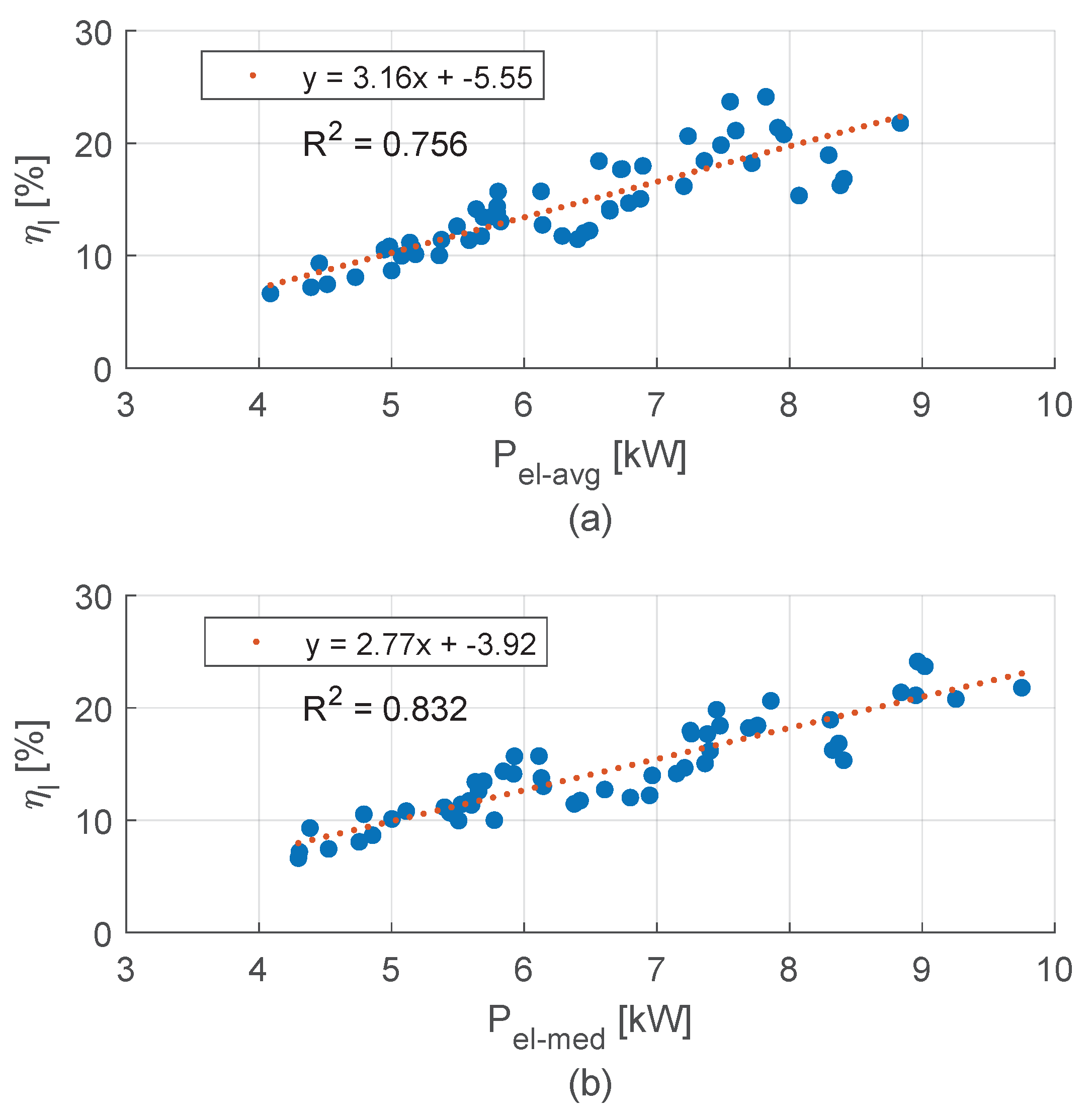
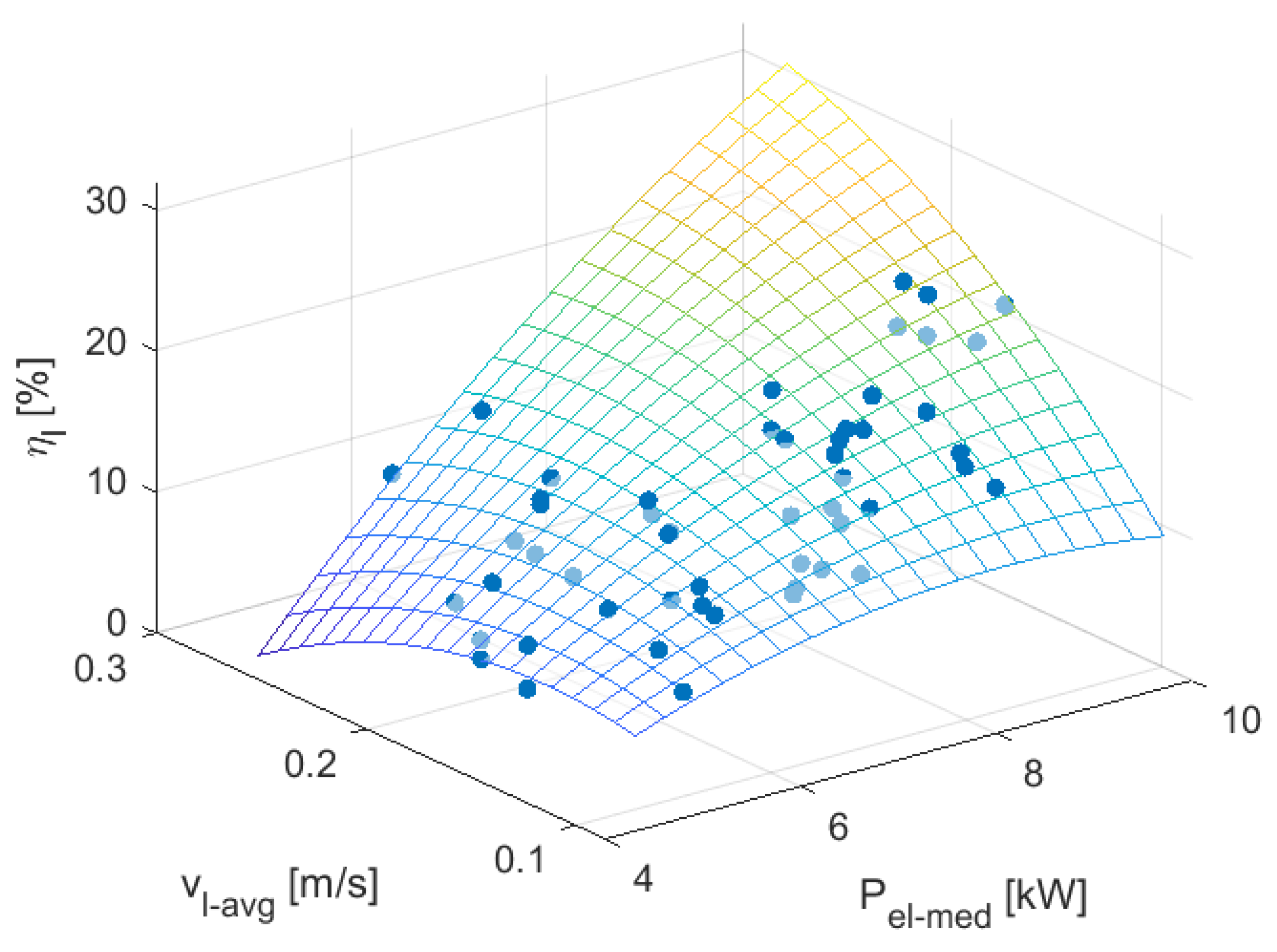
3.2. Lifting Energy and Efficiency
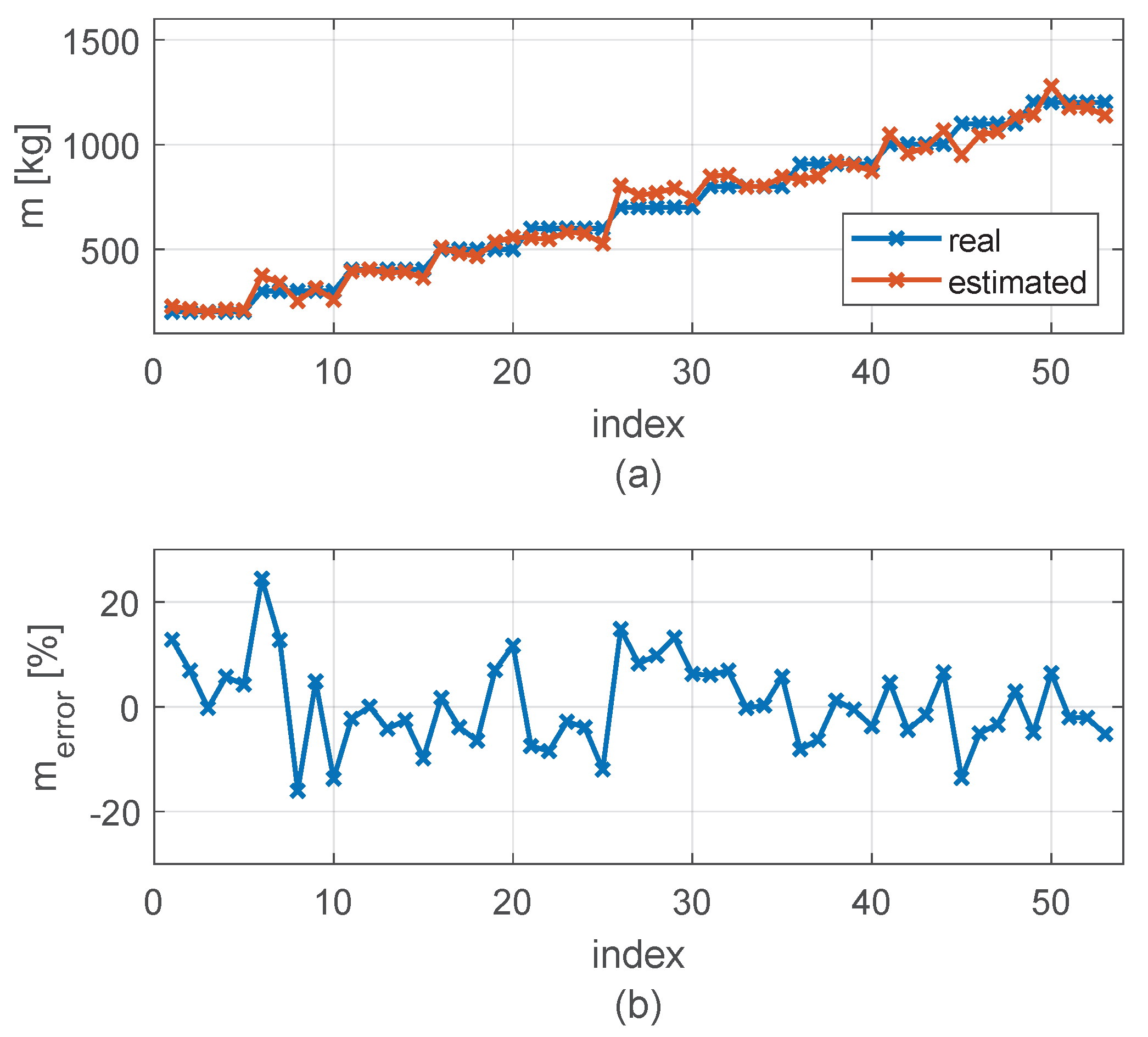
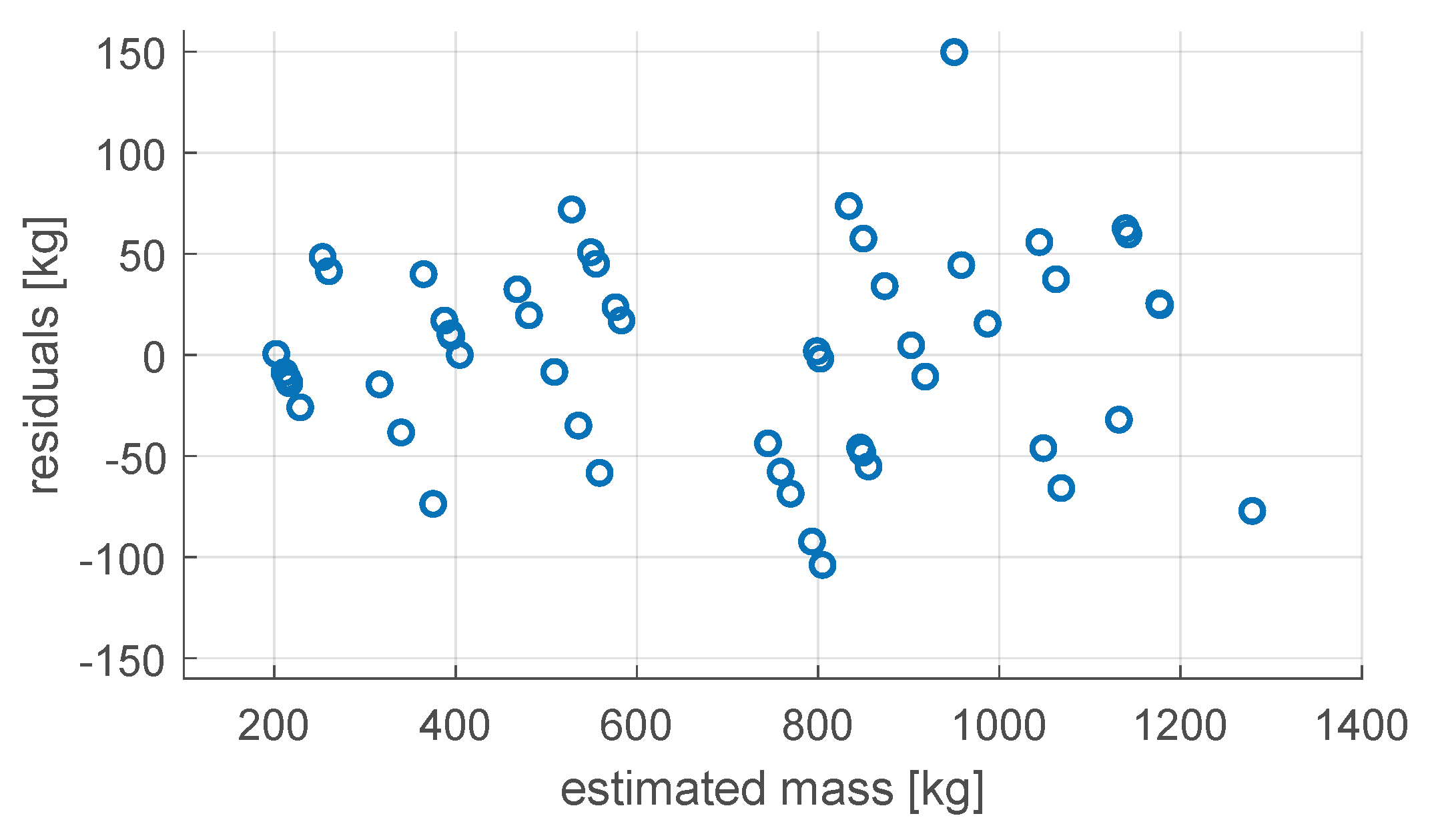
3.3. Estimation of Load Weight
- Measurement of lifting power and energy: The instantaneous power at the lifting motor is recorded during the lifting cycle. From this signal, three important variables are extracted: the electrical lifting energy (), the median electric lifting power (), and the average lifting speed (). These metrics are required inputs for the following stages.
- Estimation of lifting efficiency: The lifting efficiency is estimated using either the linear or the multivariable regression model derived in the previous section. In the linear case, efficiency is expressed as a function of the median lifting power only. In contrast, the multivariable model incorporates both the median lifting power and the average lifting speed to capture the combined effect of electrical and kinematic variables. When the linear approximation is used, the following model is applied:where a and b are regression coefficients obtained from the empirical data. In this case a = 2.77 b = −3.92.In the case of the multivariable approximation, the following model is applied:where Table 3 shows the numerical values of the regression coefficients .
- Estimation of potential energy: The estimated potential energy () is then computed by rearranging the definition of lifting efficiency:where is the electrical energy measured during the lifting cycle (step 1).
- Estimation of transported mass: From the estimated potential energy, the estimated transported mass () is derived using the gravitational energy equation:where h is the fixed lifting height used in step 1 ( in this case).
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Artal-Sevil, J.S.; Bernal-Agustín, J.; Dufo-López, R.; Domínguez-Navarro, J.A. Forklifts, automated guided vehicles, and horizontal order pickers in industrial environments. Energy management of an active hybrid power system based on batteries, PEM fuel cells, and ultracapacitors. Renew. Energy Power Qual. J. 2017, 1, 859–864. [Google Scholar] [CrossRef]
- Paul, T.; Mesbahi, T.; Durand, S.; Flieller, D.; Uhring, W. Sizing of lithium-ion battery/supercapacitor hybrid energy storage system for forklift vehicle. Energies 2020, 13, 4518. [Google Scholar] [CrossRef]
- Pedrazzi, S.; Morini, E.; Nasti, M.; Pizzileo, S.; Allesina, G. Green hydrogen powered forklifts in industrial transport: Case study of an Italian fruit and vegetable market. Int. J. Heat Technol. 2022, 40, 145–150. [Google Scholar] [CrossRef]
- Martini, A.; Bonelli, G.P.; Rivola, A. Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model. Machines 2020, 8, 26. [Google Scholar] [CrossRef]
- Lee, J.G.; Kim, Y.S.; Lee, J.H. Preventing Forklift Front-End Failures: Predicting the Weight Centers of Heavy Objects, Remaining Useful Life Prediction under Abnormal Conditions, and Failure Diagnosis Based on Alarm Rules. Sensors 2023, 23, 7706. [Google Scholar] [CrossRef]
- Zajac, P.; Dragasius, E.; Roik, T. Energy Consumption When Transporting Pallet Loads Using a Forklift with an Anti Slip Pad Preventing Damage. Energies 2021, 14, 8423. [Google Scholar] [CrossRef]
- Gong, W. Simulation study on energy recovery system of heavy electric forklift. In Proceedings of the SPIE—The International Society for Optical Engineering, Chongqing, China, 7–9 July 2023; Volume 12923, p. 129230L. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, D.; Wang, Y.; Wang, L.; Li, Y.; Du, M.; Chen, H. Energy management strategy development of a forklift with electric lifting device. Energy 2017, 128, 435–446. [Google Scholar] [CrossRef]
- Minav, T.; Virtanen, A.; Laurila, L.; Pyrhonen, J. Storage of energy recovered from an industrial forklift. Autom. Constr. 2012, 22, 506–515. [Google Scholar] [CrossRef]
- Shengjie, F.; Chen, H.; Haoling, R.; Tianliang, L.; Cheng, M.; Chen, Q. Potential Energy Recovery System for Electric Heavy Forklift Based on Double Hydraulic Motor-Generators. Appl. Sci. 2020, 10, 3996. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Y.; Zhang, Z.; Zhang, O.; Lun, F. Research Summary on Energy Saving Technology of Forklift Lifting System. In Proceedings of the 5th International Conference on Electromechanical Control Technology and Transportation (ICECTT), Nanchang, China, 15–17 May 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 62–65. [Google Scholar] [CrossRef]
- Conte, M.; Genovese, A.; Ortenzi, F.; Vellucci, F. Hybrid battery-supercapacitor storage for an electric forklift: A life-cycle cost assessment. J. Appl. Electrochem. 2014, 44, 523–532. [Google Scholar] [CrossRef]
- Dezza, F.; Musolino, V.; Piegari, L.; Rizzo, R. Hybrid battery–supercapacitor system for full electric forklifts. IET Electr. Syst. Transp. 2019, 9, 16–23. [Google Scholar] [CrossRef]
- Kierzkowski, A.; Kisiel, T.; Restel, F. Method of Reducing Energy Consumption during Forklift Operator Training in Cargo Terminals Utilizing Virtual Reality. Energies 2024, 17, 1153. [Google Scholar] [CrossRef]
- Kasahara, M.; Mori, Y. Relation between overturn and the center of gravity of a forklift truck. In Proceedings of the 56th Annual Conference Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017. [Google Scholar] [CrossRef]
- Vita, L.; Gattamelata, D. Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment. Appl. Sci. 2023, 13, 1206. [Google Scholar] [CrossRef]
- Berdiev, A.; Bahadirov, G.; Dong, Z.; Xuelin, W. Dynamic analysis of the AGV Forklift. In Proceedings of the 2022 2nd International Conference on Electronic Information Engineering and Computer Technology (EIECT), Yan’an, China, 28–30 October 2022; pp. 269–275. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Real-time estimation of center of gravity position for lightweight vehicles using combined AKF-EKF method. IEEE Trans. Veh. Technol. 2014, 63, 4221–4231. [Google Scholar] [CrossRef]
- Sarker, A.; Amin, S.A.; Tamzid, S.M.T.H.; Chisty, N.A. Design and implementation of a forklift with dynamic stability. In Proceedings of the 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 21–23 December 2017; pp. 658–663. [Google Scholar] [CrossRef]
- Xia, G.; Li, J.; Tang, X.; Zhang, Y.; Zhao, L.; Wang, S. Anti-Rollover Control of a Counterbalance Forklift Based on Roll Energy Classification. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 5796–5814. [Google Scholar] [CrossRef]
- Xia, G.; Xia, Y.; Tang, X.; Zhao, L.; Hu, J. Anti-Rollover Control Based on Stable Zone Partition of Counterbalanced Forklift Trucks. Int. J. Automot. Technol. 2021, 22, 1529–1543. [Google Scholar] [CrossRef]
- Xia, G.; Li, J.; Tang, X.; Zhang, Y.; Hu, J. Anti-Rollover of the Counterbalanced Forklift Truck Based on Model Predictive Control. J. Mech. Sci. Technol. 2021, 35, 1909–1921. [Google Scholar] [CrossRef]
- Choi, M.; Ahn, S.; Seo, J.O. VR-Based Investigation of Forklift Operator Situation Awareness for Preventing Collision Accidents. Accid. Anal. Prev. 2020, 136, 105404. [Google Scholar] [CrossRef]
- Abdellatif, M.; Shoeir, M.; Talaat, O.; Gabalah, M.; Elbably, M.; Saleh, S. Design of an Autonomous Forklift Using Kinect. MATEC Web Conf. 2018, 153, 1–5. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Kelouwani, S.; Gaudreau, M.-A.; Zeghmi, L.; Amamou, A.; Bahmanabadi, H.; Allani, B.; Graba, M. Energy-efficient motion planning of an autonomous forklift using deep neural networks and kinetic model. Expert Syst. Appl. 2023, 237, 121623. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, Z.; Zhang, W.; Li, K.; He, Z. Small Object Detection and Intelligent Loading Based on YOLOv5 for Unmanned Forklifts. Appl. Sci. 2021, 11, 10607. [Google Scholar] [CrossRef]
- Motroni, A.; Michelini, G.; Pazzaglia, P.; Tarasconi, A. A Real-Time Localization and Traceability System for Forklifts Based on Sensor Fusion of UWB and IMU. Sensors 2022, 22, 8437. [Google Scholar] [CrossRef]
- Occupational Safety and Health Administration (OSHA). Powered Industrial Trucks (Forklift) eTool. Available online: https://www.osha.gov/etools/powered-industrial-trucks/operating-forklift/load-handling (accessed on 1 October 2024).
- Hammerl, R. Vehicle Wheel Speed-Based Determination or Estimation of a Load Weight of a Load Carried by a Commercial Vehicle. U.S. Patent US2016041028 AA, 23 May 2017. [Google Scholar]
- Kretschmer, S. Procede Pour Determiner Le Poids D’Une Charge D’Un Chariot Elevateur. French Patent FR2972253A1, 17 May 2019. [Google Scholar]
- Zajac, P.; Rozic, T. Energy consumption of forklift versus standards, effects of their use and expectation. Energy 2021, 239, 122187. [Google Scholar] [CrossRef]






| Number of Tests | Load Weight (kg) |
|---|---|
| 5 | 202.5 |
| 5 | 301.5 |
| 5 | 404.5 |
| 5 | 500.5 |
| 5 | 600.0 |
| 5 | 701.0 |
| 5 | 800.5 |
| 5 | 907.5 |
| 5 | 1002.5 |
| 5 | 1100.0 |
| 5 | 1202.0 |
| Total: 55 |
| Index | Load | ||||||
|---|---|---|---|---|---|---|---|
| [kg] | [kW] | [kW] | [kJ] | [kJ] | [m/s] | [%] | |
| 1 | 4.09 | 4.30 | 59.88 | 0.1365 | 6.63 | ||
| 2 | 4.52 | 4.53 | 53.31 | 0.1694 | 7.45 | ||
| 3 | 202.5 | 4.39 | 4.30 | 55.28 | 3.97 | 0.1589 | 7.19 |
| 4 | 5.36 | 5.77 | 39.68 | 0.2701 | 10.01 | ||
| 5 | 4.73 | 4.76 | 49.15 | 0.1924 | 8.08 | ||
| 6 | 5.08 | 5.51 | 59.32 | 0.1711 | 9.97 | ||
| 7 | 5.16 | 5.44 | 55.45 | 0.1860 | 10.67 | ||
| 8 | 301.5 | 4.46 | 4.38 | 63.52 | 5.91 | 0.1403 | 9.31 |
| 9 | 5.14 | 5.4 | 52.99 | 0.1939 | 11.16 | ||
| 10 | 4.94 | 4.79 | 56.12 | 0.1762 | 10.54 | ||
| 11 | 4.98 | 5.11 | 73.36 | 0.1359 | 10.81 | ||
| 12 | 5.64 | 5.92 | 56.13 | 0.2009 | 14.13 | ||
| 13 | 404.5 | 5.69 | 5.63 | 59.15 | 7.93 | 0.1925 | 13.41 |
| 14 | 5.76 | 5.69 | 58.91 | 0.1954 | 13.47 | ||
| 15 | 6.13 | 6.11 | 50.48 | 0.2427 | 15.71 | ||
| 16 | 5.38 | 5.53 | 86.02 | 0.1250 | 11.41 | ||
| 17 | 5.00 | 4.86 | 113.28 | 0.0883 | 8.67 | ||
| 18 | 500.5 | 5.18 | 5.00 | 97.04 | 9.82 | 0.1068 | 10.12 |
| 19 | 5.80 | 6.13 | 71.31 | 0.1626 | 13.77 | ||
| 20 | 5.82 | 6.14 | 75.33 | 0.1546 | 13.03 | ||
| 21 | 5.49 | 5.66 | 93.30 | 0.1178 | 12.61 | ||
| 22 | 5.80 | 5.84 | 81.93 | 0.1415 | 14.36 | ||
| 23 | 600.0 | 5.58 | 5.60 | 103.54 | 11.77 | 0.1079 | 11.37 |
| 24 | 5.68 | 5.59 | 100.38 | 0.1131 | 11.72 | ||
| 25 | 5.80 | 5.93 | 74.97 | 0.1548 | 15.70 | ||
| 26 | 6.45 | 6.80 | 114.42 | 0.1128 | 12.02 | ||
| 27 | 6.29 | 6.42 | 117.00 | 0.1075 | 11.75 | ||
| 28 | 701.0 | 6.40 | 6.38 | 119.99 | 13.75 | 0.1067 | 11.46 |
| 29 | 6.65 | 6.96 | 98.28 | 0.1352 | 13.99 | ||
| 30 | 6.14 | 6.61 | 107.97 | 0.1137 | 12.73 | ||
| 31 | 6.49 | 6.95 | 128.51 | 0.1010 | 12.22 | ||
| 32 | 6.79 | 7.21 | 107.06 | 0.1268 | 14.66 | ||
| 33 | 800.5 | 6.74 | 7.26 | 88.67 | 15.70 | 0.1520 | 17.71 |
| 34 | 6.89 | 7.25 | 87.34 | 0.1579 | 17.98 | ||
| 35 | 6.64 | 7.15 | 110.88 | 0.1198 | 14.16 | ||
| 36 | 6.56 | 7.48 | 96.67 | 0.1358 | 18.41 | ||
| 37 | 6.73 | 7.38 | 100.70 | 0.1336 | 17.68 | ||
| 38 | 907.5 | 7.20 | 7.40 | 110.05 | 17.80 | 0.1309 | 16.17 |
| 39 | 6.88 | 7.36 | 118.23 | 0.1163 | 15.05 | ||
| 40 | 7.48 | 7.45 | 89.74 | 0.1668 | 19.83 | ||
| 41 | 7.59 | 8.95 | 93.11 | 0.1631 | 21.12 | ||
| 42 | 7.36 | 7.76 | 106.70 | 0.1379 | 18.43 | ||
| 43 | 1002.5 | 7.72 | 7.69 | 107.91 | 19.66 | 0.1430 | 18.22 |
| 44 | 7.91 | 8.84 | 91.97 | 0.1720 | 21.38 | ||
| 45 | 7.23 | 7.86 | 104.59 | 0.1383 | 20.63 | ||
| 46 | 7.55 | 9.02 | 91.04 | 0.1659 | 23.70 | ||
| 47 | 1100.0 | 7.82 | 8.97 | 89.42 | 21.57 | 0.1749 | 24.13 |
| 48 | 7.96 | 9.25 | 103.78 | 0.1533 | 20.79 | ||
| 49 | 8.07 | 8.41 | 153.70 | 0.105 | 15.34 | ||
| 50 | 8.83 | 9.75 | 108.17 | 0.1633 | 21.79 | ||
| 51 | 1202.0 | 8.41 | 8.37 | 140.00 | 23.58 | 0.1201 | 16.84 |
| 52 | 8.38 | 8.32 | 145.07 | 0.1156 | 16.25 | ||
| 53 | 8.29 | 8.31 | 124.41 | 0.1333 | 18.95 |
| Coefficient | Value |
|---|---|
| Aspect | Pressure-Sensor-Based Method | Load-Cell-Based Method | Power-Based Method (This Work) |
|---|---|---|---|
| Measurement Accuracy | High accuracy due to direct measurement of hydraulic pressure | Very high accuracy; direct force measurement | Moderate accuracy; depends on correlation between power and efficiency |
| Installation Complexity | Requires invasive installation into the hydraulic circuit; may require fluid disconnection | Requires mechanical integration into the lifting mechanism or forks | Non-intrusive; could use existing voltage and current signals |
| System Integration | Needs additional hardware, wiring, and calibration procedures | May require structural adaptation and dedicated interface circuits | Easily integrates with existing forklift control/monitoring systems |
| Cost and Maintenance | Higher cost due to sensor exposure to hydraulic environment and periodic recalibration | High cost; sensitive to mechanical wear | Low cost; no extra sensors required |
| Scalability and Replicability | Limited by system-specific hydraulic architecture | Limited by forklift model and structural variations | Highly scalable and replicable across forklift models with electric drive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acevedo, J.P.; Monsalve, C.; Vergara, S.; León, R.; Barraza, R.; Ramírez, G. Load Weight Estimation in Electric Forklifts via DC–DC Converter Power Signal Analysis of the Electro-Hydraulic Lifting System. Appl. Sci. 2025, 15, 7470. https://doi.org/10.3390/app15137470
Acevedo JP, Monsalve C, Vergara S, León R, Barraza R, Ramírez G. Load Weight Estimation in Electric Forklifts via DC–DC Converter Power Signal Analysis of the Electro-Hydraulic Lifting System. Applied Sciences. 2025; 15(13):7470. https://doi.org/10.3390/app15137470
Chicago/Turabian StyleAcevedo, Juan Pablo, Cristian Monsalve, Samuel Vergara, Ricardo León, Rodrigo Barraza, and Guillermo Ramírez. 2025. "Load Weight Estimation in Electric Forklifts via DC–DC Converter Power Signal Analysis of the Electro-Hydraulic Lifting System" Applied Sciences 15, no. 13: 7470. https://doi.org/10.3390/app15137470
APA StyleAcevedo, J. P., Monsalve, C., Vergara, S., León, R., Barraza, R., & Ramírez, G. (2025). Load Weight Estimation in Electric Forklifts via DC–DC Converter Power Signal Analysis of the Electro-Hydraulic Lifting System. Applied Sciences, 15(13), 7470. https://doi.org/10.3390/app15137470






