Mechanical Response and Fatigue Life Analysis of Asphalt Pavements Under Temperature-Load Coupling Conditions
Abstract
1. Introduction
2. Methodology
2.1. Structural and Material Parameters
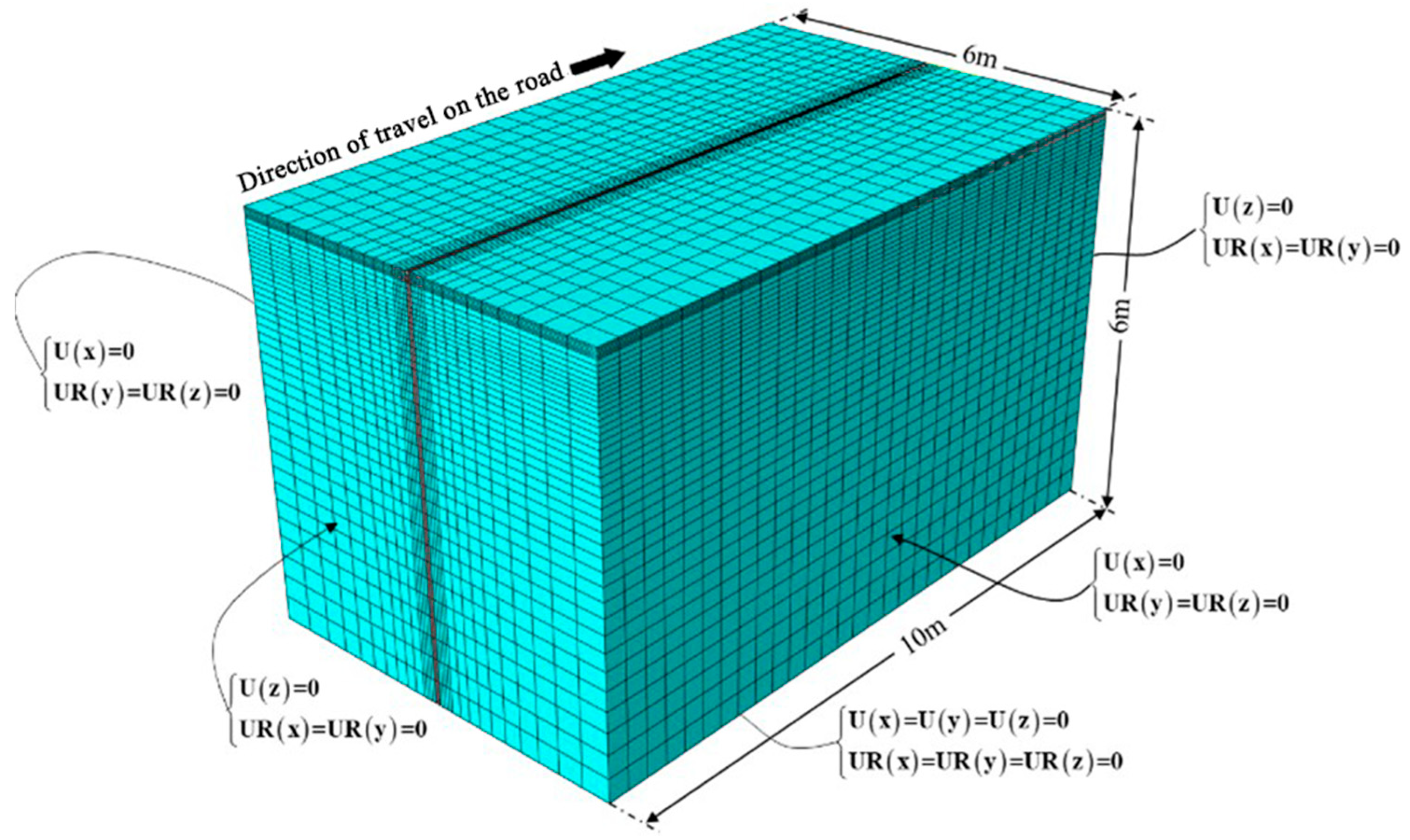
2.2. Model Establishment
2.2.1. Assumptions
- (1)
- The structural surface material of asphalt pavement is homogeneous, continuous, and isotropic viscoelastic. Subgrade, subbase, and soil base are homogeneous, continuous, and isotropic elastic materials.
- (2)
- The soil base extends indefinitely in depth, with the remaining layers of limited thickness.
- (3)
- Temperature and heat transfer continuity in each structural layer.
- (4)
- Pavement structural temperature field variations are only related to the roadway along the depth direction.
- (5)
- No consideration of the effect of moisture on pavement structure.
2.2.2. Introduction to the Model
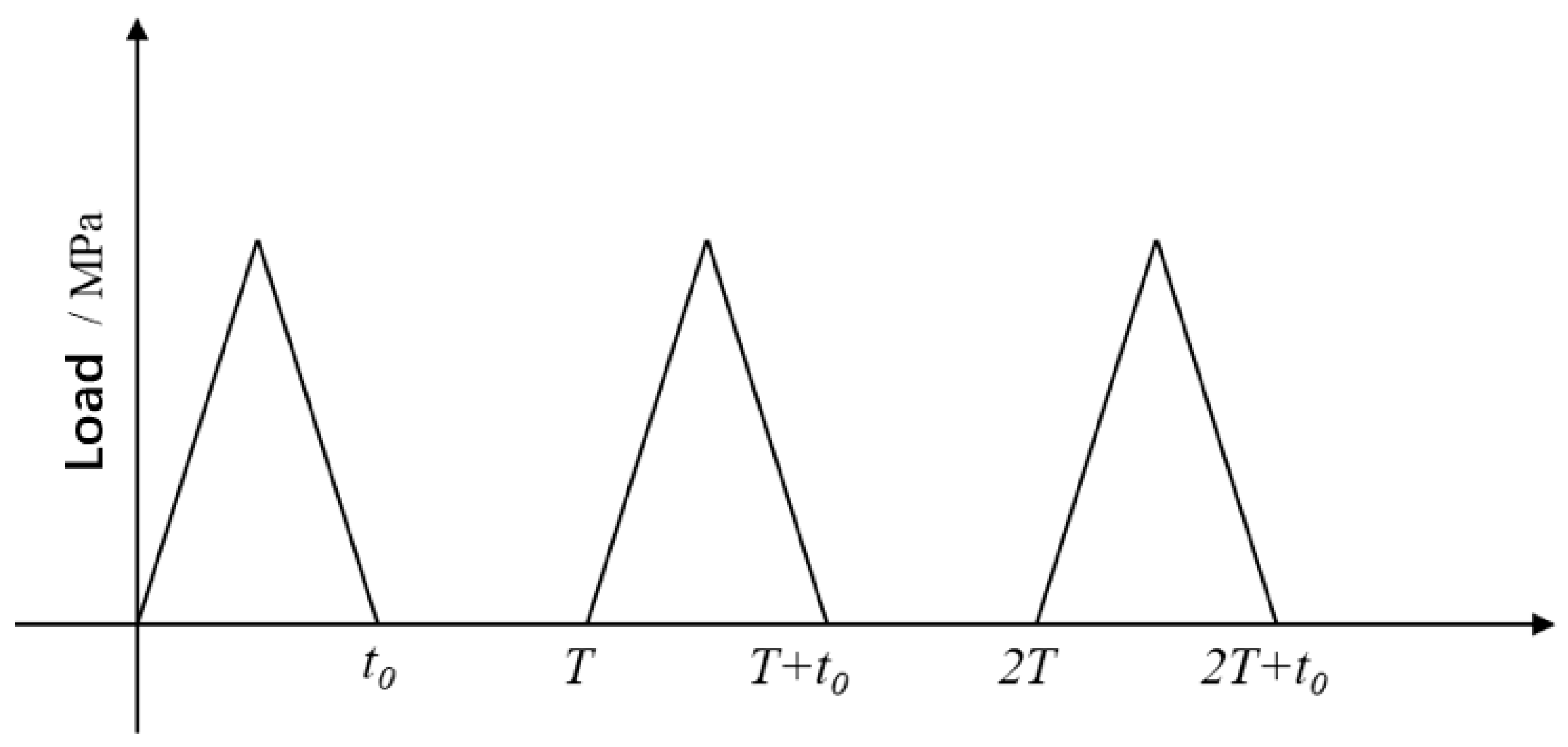
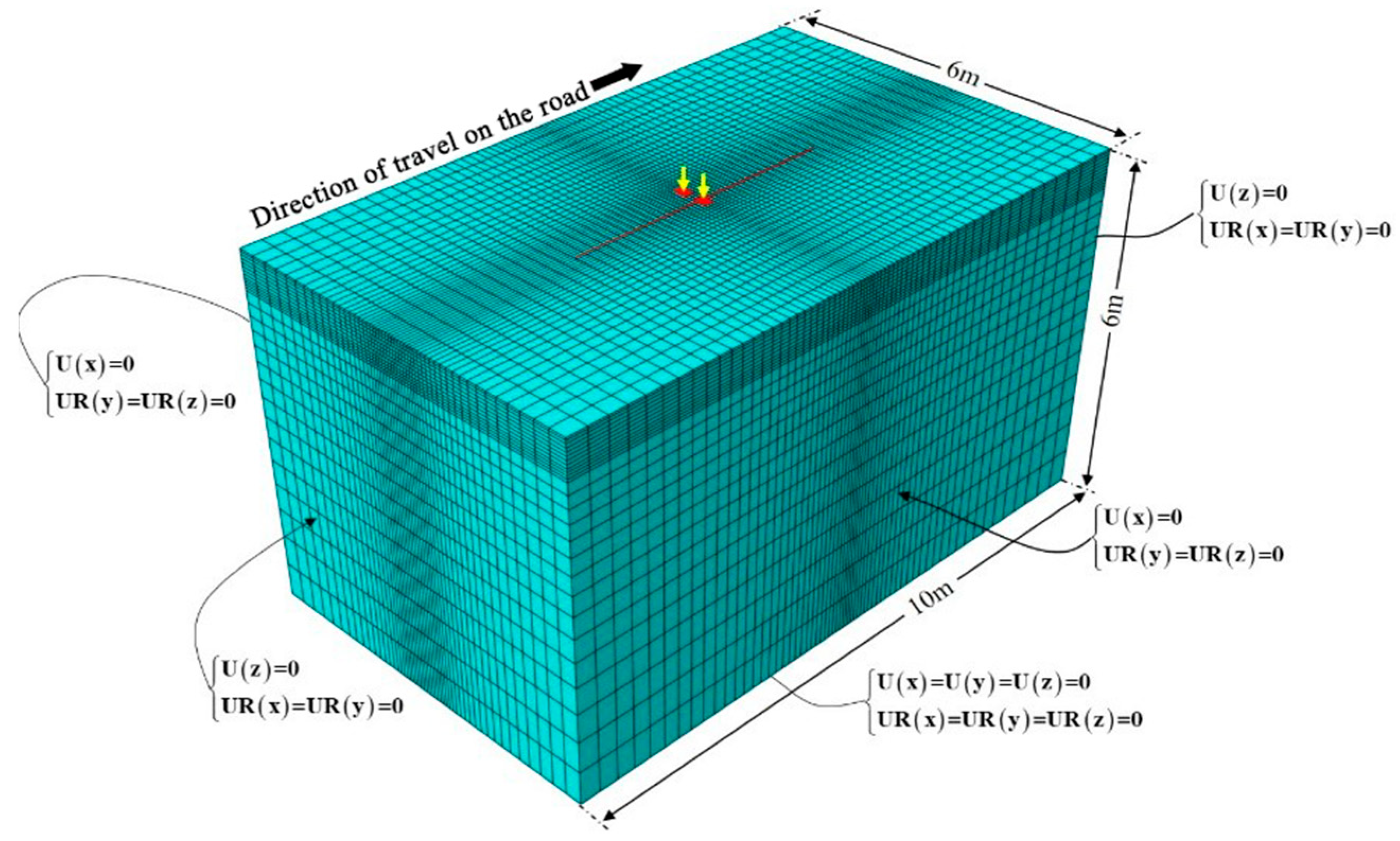
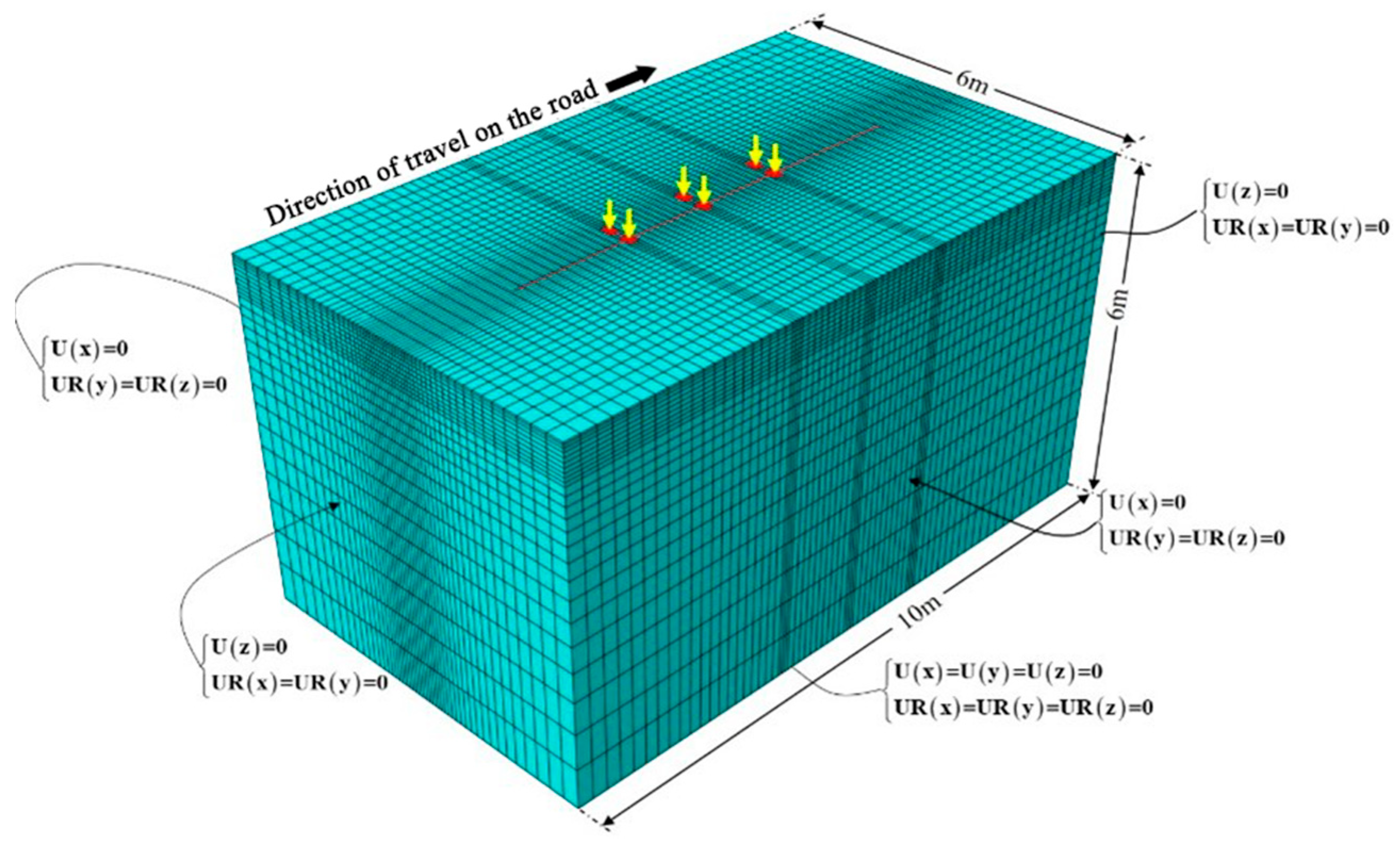
2.2.3. Vehicle Load Modeling
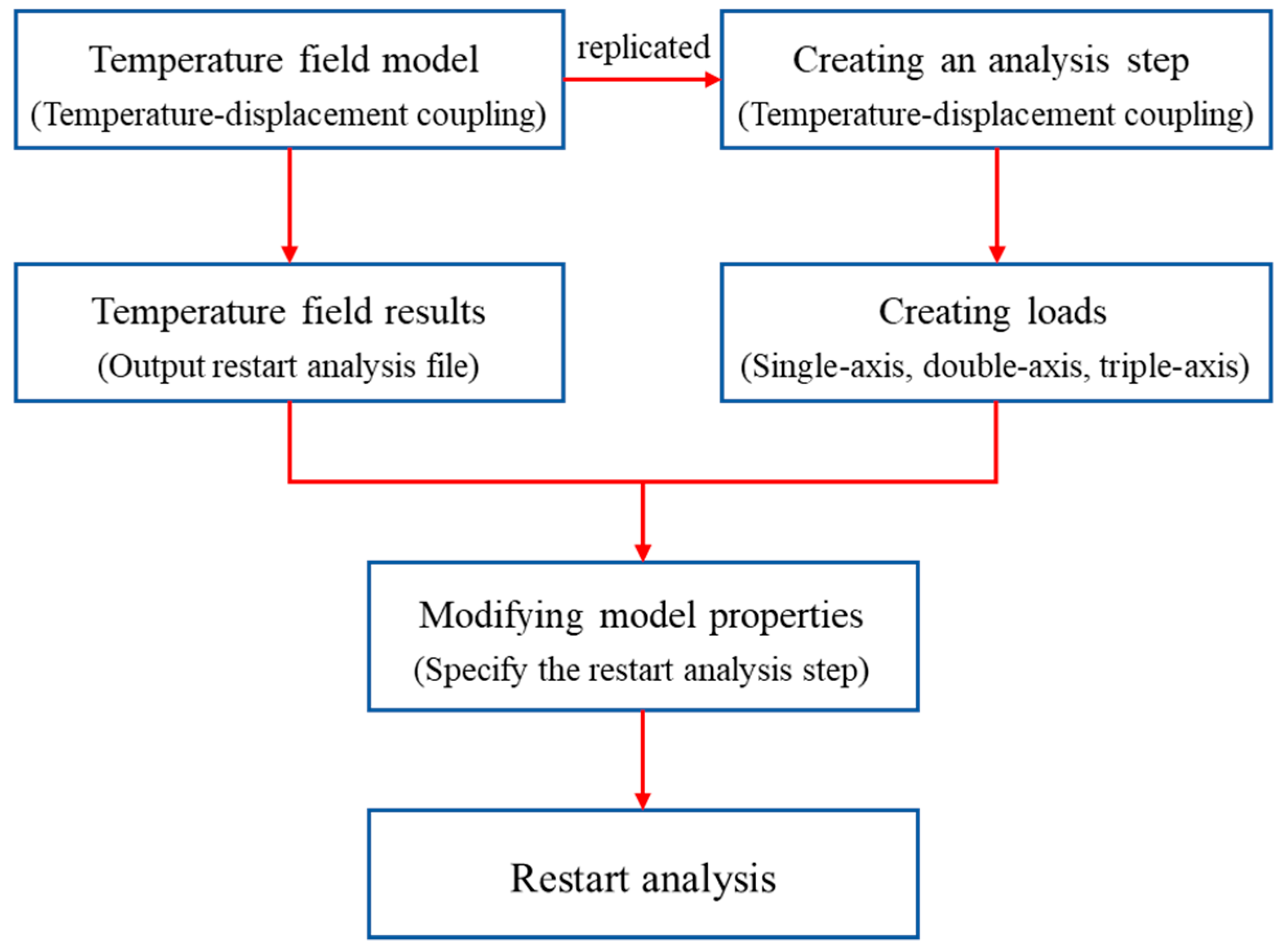
2.3. Temperature-Load Coupling
3. Results and Discussion
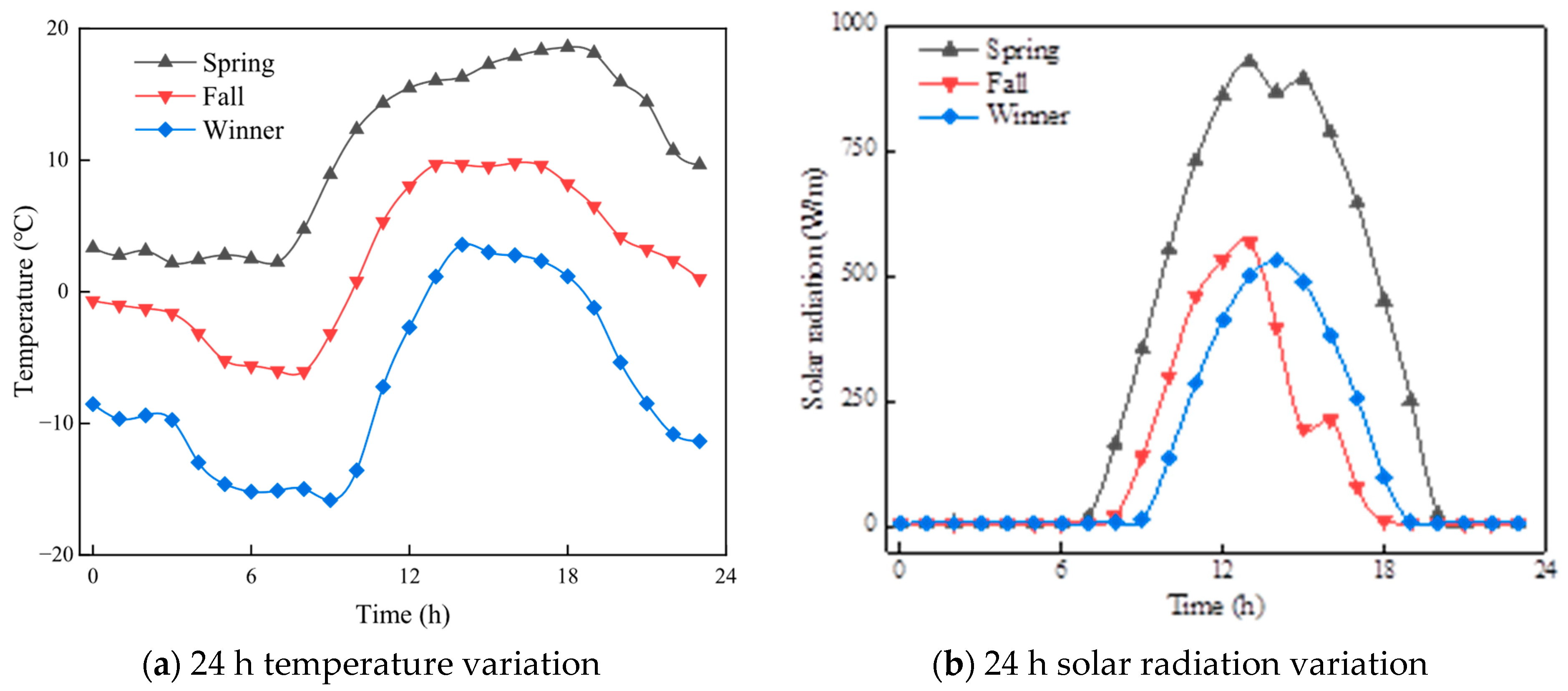
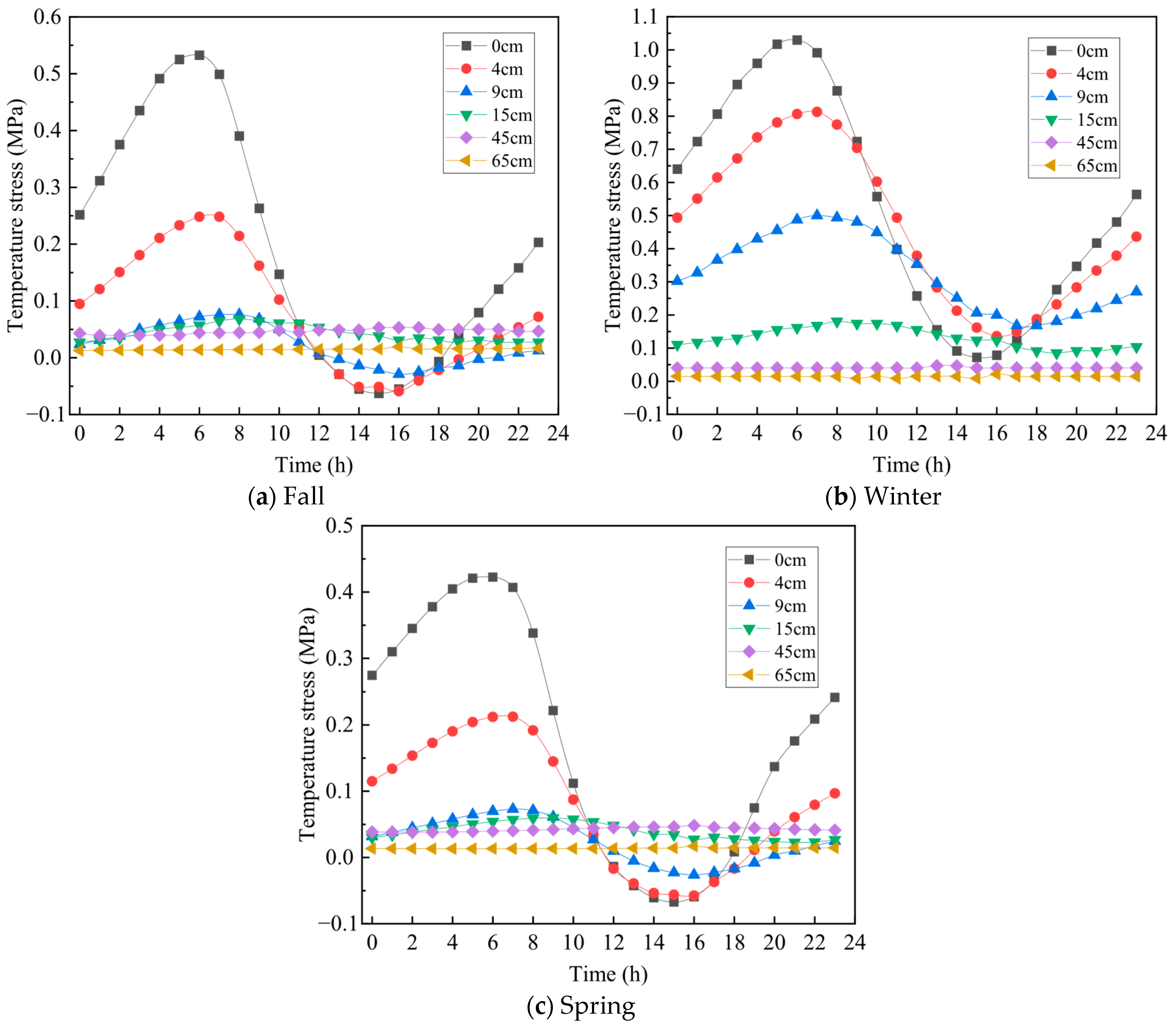
3.1. Temperature Stress of Pavement Under Typical Temperature Conditions
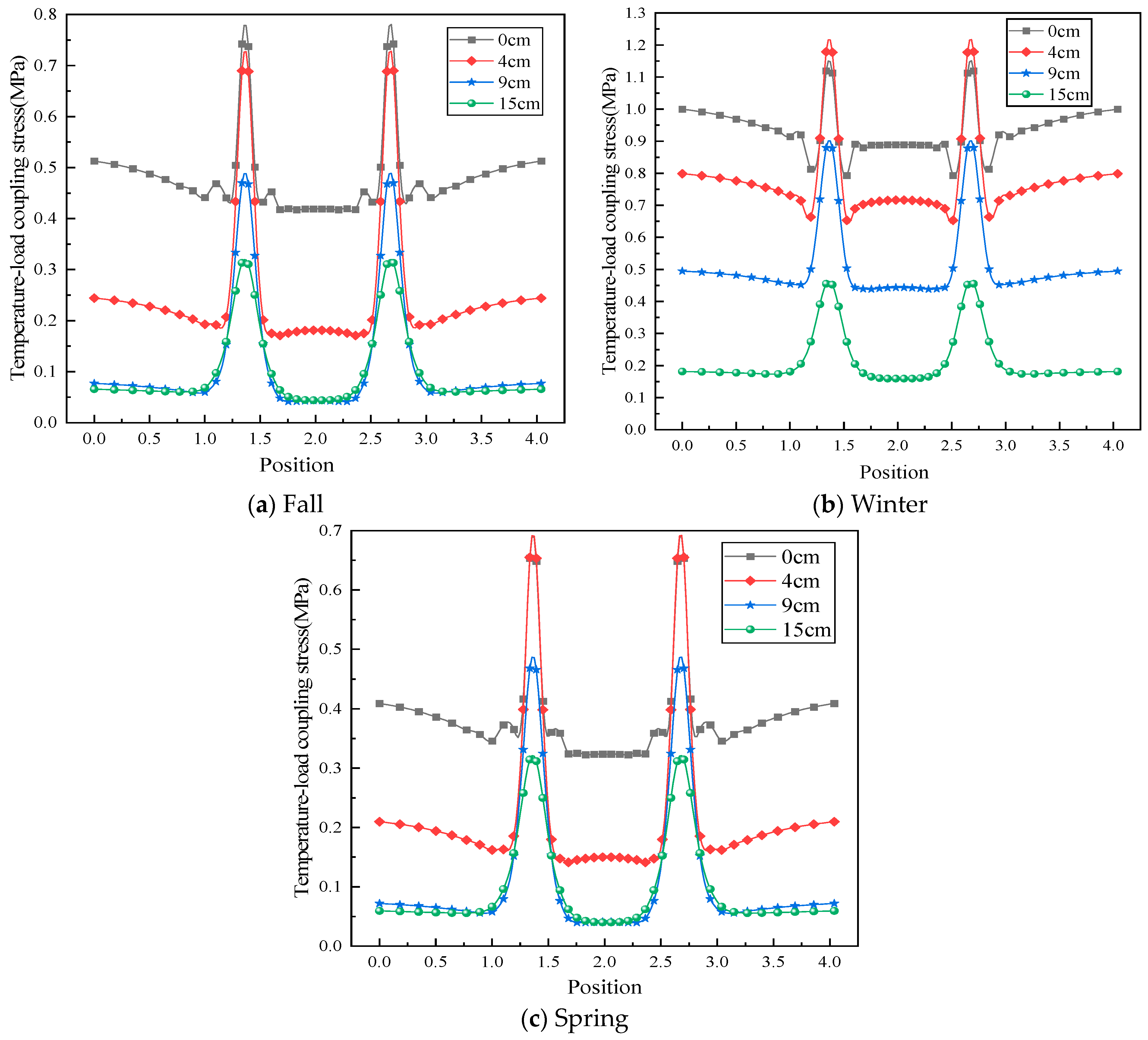
3.2. Load-Temperature Coupled Stress Analysis
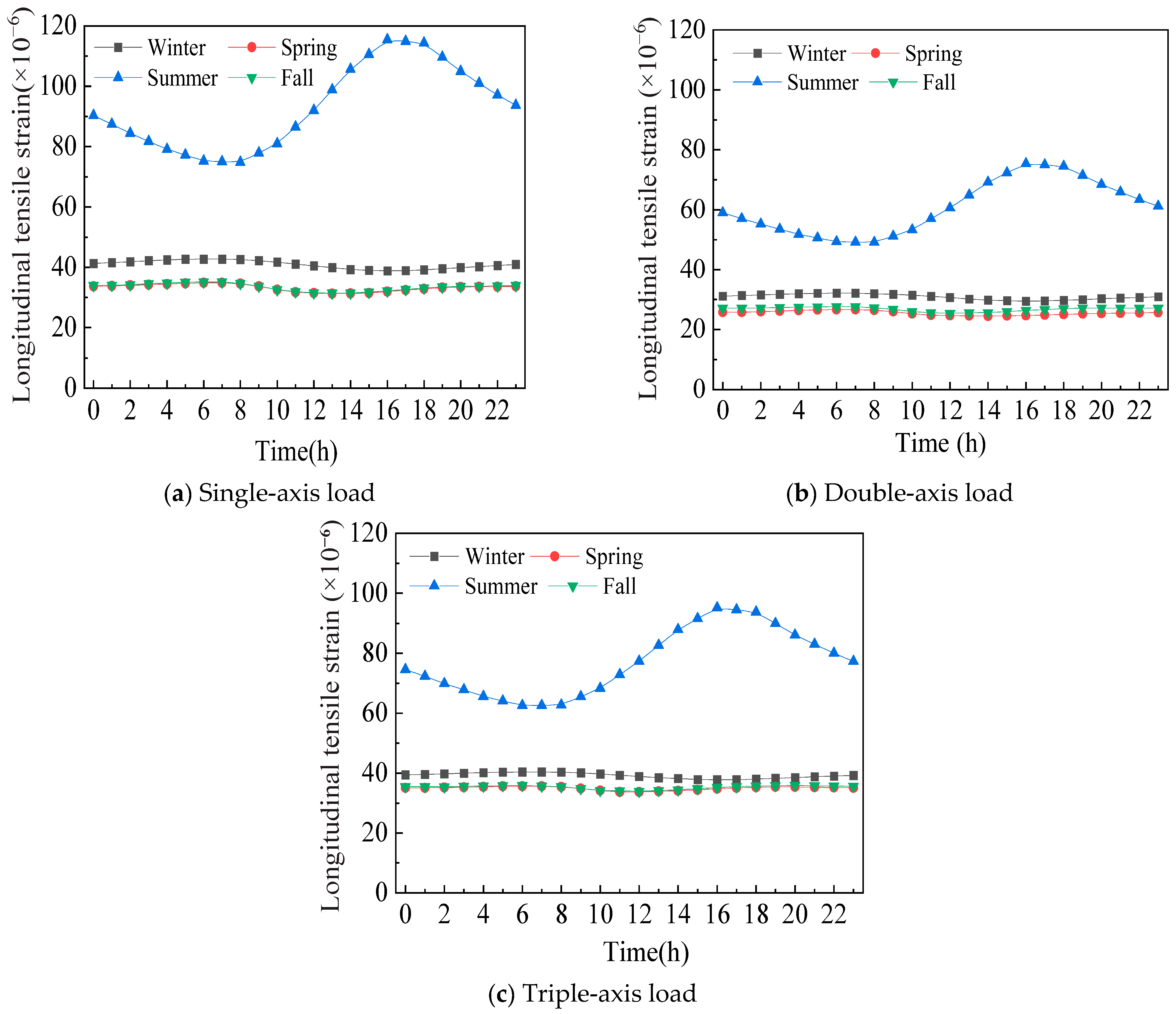
3.2.1. Single-Axis Load-Temperature Coupling Stress
3.2.2. Double-Axis Load-Temperature Coupling Stress
3.2.3. Triple-Axis Load-Temperature Coupled Stress
3.3. Evaluation of Environmental Effects
3.3.1. Environmental Effects of Single-Axis Loading
3.3.2. Environmental Effects of Double-Axis Loading
3.3.3. Environmental Effects of Triple-Axis Loading
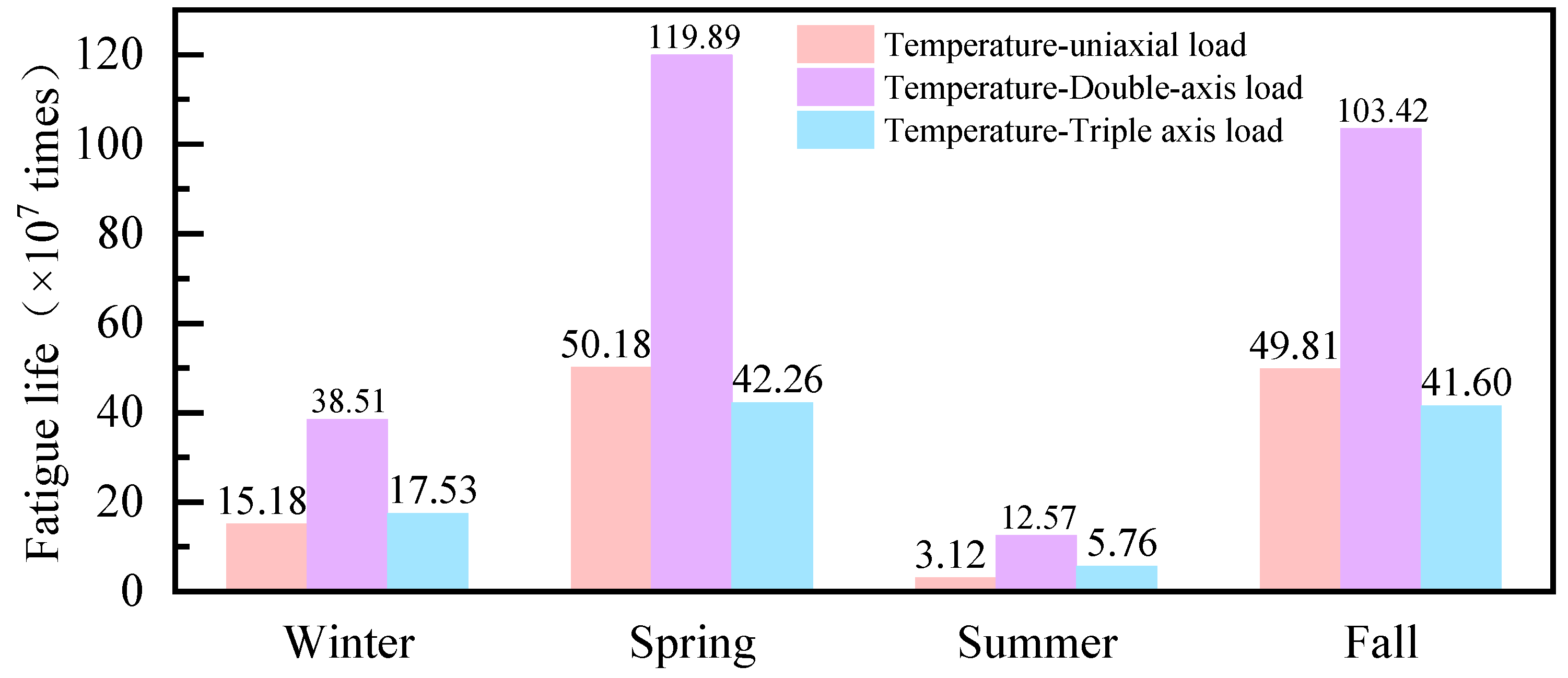
3.4. Fatigue Life Analysis of Pavement Under Coupling
4. Conclusions
- (1)
- The temperature stresses in each structural layer show regular variations, with complete tensile stresses in winter and alternating tensile and compressive stresses in spring and fall.
- (2)
- The winter temperature difference is more serious than the fall and spring temperature differences in terms of damage to the pavement, and since the maximum tensile stress on the road surface in winter reaches 1.0228 MPa, the pavement is very susceptible to cracking due to tension.
- (3)
- The temperature-load coupling stress varies periodically, and the temperature stress has less influence on the coupling stress in spring and fall and more influence in winter.
- (4)
- Under traveling load, the coupling stress and its influence range decrease with the increase in depth, while the farther away from the wheel load position, the smaller the traveling load disturbance. The maximum coupling stresses appear directly below the wheel loads under single-axle and double-axle loads and below the wheel loads on both sides under triple-axle loads.
- (5)
- Under the most unfavorable loading conditions, the degree of influence of environmental effects along the depth direction gradually decreases in winter, and it first decreases and then increases in spring and autumn. Overall, the difference in the degree of environmental effects along the depth direction under different axle loads is not significant, which is 70.53%, 41.90%, 27.13%, and 23.77%, in order.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jing, C.; Zhang, J.; Song, B. An innovative evaluation method for performance of in-service asphalt pavement with semi-rigid base. Constr. Build. Mater. 2020, 235, 117376. [Google Scholar] [CrossRef]
- Shi, Z.; Yue, J.; Xu, L.; Wang, X. Peridynamics for Fracture Analysis of Reflective Cracks in Semi-Rigid Base Asphalt Pavement. Appl. Sci. 2022, 12, 3486. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Y. Reflective crack in semi-rigid base asphalt pavement under temperature-traffic coupled dynamics using XFEM. Constr. Build. Mater. 2019, 214, 280–289. [Google Scholar] [CrossRef]
- Millien, A.; Dragomir, M.L.; Wendling, L.; Petit, C.; Iliescu, M. Geogrid Interlayer Performance in Pavements: Tensile-Bending Test for Crack Propagation. In 7th RILEM International Conference on Cracking in Pavements; Scarpas, A., Kringos, N., Al-Qadi, I., Loizos, A., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 1209–1218. [Google Scholar]
- Assogba, O.C.; Tan, Y.; Sun, Z.; Lushinga, N.; Bin, Z. Effect of vehicle speed and overload on dynamic response of semi-rigid base asphalt pavement. Road Mater. Pavement Des. 2021, 22, 572–602. [Google Scholar] [CrossRef]
- Shan, J.; Shao, H.; Li, Q.; Sun, P. Comparison of Real Response and Theoretical Modeling of Pavement with Thick Asphalt Layers under Heavy Traffic Load. Adv. Civ. Eng. 2019, 2019, 8097890. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Wang, X. Full-scale field testing on a highway composite pavement dynamic responses. Transp. Geotech. 2015, 4, 13–27. [Google Scholar] [CrossRef]
- Barriera, M.; Lebental, B.; Pouget, S. Towards road pavement response under moving loads. Road Mater. Pavement Des. 2019, 20 (Suppl. 1), S480–S499. [Google Scholar] [CrossRef]
- Beskou, N.D.; Hatzigeorgiou, G.D.; Theodorakopoulos, D.D. Dynamic inelastic analysis of 3-D flexible pavements under moving vehicles: A unified FEM treatment. Soil Dyn. Earthq. Eng. 2016, 90, 420–431. [Google Scholar] [CrossRef]
- Bai, T.; Cheng, Z.; Hu, X.; Fuentes, L.; Walubita, L.F. Viscoelastic modelling of an asphalt pavement based on actual tire-pavement contact pressure. Road Mater. Pavement Des. 2021, 22, 2458–2477. [Google Scholar] [CrossRef]
- Zhao, X.; Shen, A.; Ma, B. Temperature response of asphalt pavement to low temperatures and large temperature differences. Int. J. Pavement Eng. 2020, 21, 49–62. [Google Scholar] [CrossRef]
- Wang, X.; Ma, X. Responses of Semi-Rigid Base Asphalt Pavement with Interlayer Contact Bonding Model. Adv. Civ. Eng. 2020, 2020, 8841139. [Google Scholar] [CrossRef]
- Kettil, P.; Engström, G.; Wiberg, N.E. Coupled hydro-mechanical wave propagation in road structures. Comput. Struct. 2005, 83, 1719–1729. [Google Scholar] [CrossRef]
- Xue, Q.; Liu, L.; Zhao, Y.; Chen, Y.-J.; Li, J.-S. Dynamic behavior of asphalt pavement structure under temperature-stress coupled loading. Appl. Therm. Eng. 2013, 53, 1–7. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, X.; Qian, Z.; Li, X. Mechanical behavior of asphalt pavement on steel-concrete composite beam bridge under temperature-load coupling. Constr. Build. Mater. 2023, 403, 133099. [Google Scholar] [CrossRef]
- Yang, J.; Tan, L.; Qi, X.; Zhang, C. Investigation on permanent deformation in steel-concrete composite beam bridge deck pavement under temperature-load coupling effect. Front. Mater. 2023, 10, 1284928. [Google Scholar] [CrossRef]
- Wang, X.; Li, K.; Zhong, Y.; Xu, Q.; Li, C. XFEM simulation of reflective crack in asphalt pavement structure under cyclic temperature. Constr. Build. Mater. 2018, 189, 1035–1044. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.; Yang, J.; Wang, H. Numerical Simulation on Reflective Cracking Behavior of Asphalt Pavement. Appl. Sci. 2021, 11, 7990. [Google Scholar] [CrossRef]
- Erlingsson, S. Impact of Water on the Response and Performance of a Pavement Structure in an Accelerated Test. Road Mater. Pavement Des. 2010, 11, 863–880. [Google Scholar] [CrossRef]
- Dan, H.-C.; He, L.-H.; Zhao, L.-H.; Chen, J.-Q. Coupled hydro-mechanical response of saturated asphalt pavement under moving traffic load. Int. J. Pavement Eng. 2015, 16, 125–143. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, H. Evaluation of Hydroplaning Risk on Permeable Friction Course using Tire–Water–Pavement Interaction Model. Transp. Res. Rec. 2018, 2672, 408–417. [Google Scholar] [CrossRef]
- Biswal, D.R.; Sahoo, U.C.; Dash, S.R. Structural response of an inverted pavement with stabilised base by numerical approach considering isotropic and anisotropic properties of unbound layers. Road Mater. Pavement Des. 2020, 21, 2160–2179. [Google Scholar] [CrossRef]
- Cortes, D.D.; Santamarina, J.C. The LaGrange case history: Inverted pavement system characterisation and preliminary numerical analyses. Int. J. Pavement Eng. 2013, 14, 463–471. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, M.; Xiao, R.; Polaczyk, P.; Bai, Y.; Huang, B. An investigation of structural responses of inverted pavements by numerical approaches considering nonlinear stress-dependent properties of unbound aggregate layer. Constr. Build. Mater. 2021, 303, 124505. [Google Scholar] [CrossRef]
- Sahoo, U.C.; Reddy, K.S. Effect of nonlinearity in granular layer on critical pavement responses of low volume roads. Int. J. Pavement Res. Technol. 2010, 3, 320. [Google Scholar]
- Saad, B.; Mitri, H.; Poorooshasb, H. Three-dimensional dynamic analysis of flexible conventional pavement foundation. J. Transp. Eng. 2005, 131, 460–469. [Google Scholar] [CrossRef]
- Allen, R.G.; Trezza, R.; Tasumi, M. Analytical integrated functions for daily solar radiation on slopes. Agric. For. Meteorol. 2006, 139, 55–73. [Google Scholar] [CrossRef]
- Aziz, A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Zhao, S.; Wang, Y. Structural health monitoring of concrete dams using long-term air temperature for thermal effect simulation. Eng. Struct. 2019, 180, 642–653. [Google Scholar] [CrossRef]
- Lv, S.; Yuan, J.; Peng, X.; Zhang, N.; Liu, H.; Luo, X. A structural design for semi-rigid base asphalt pavement based on modulus optimization. Constr. Build. Mater. 2021, 302, 124216. [Google Scholar] [CrossRef]
- Zhao, Y.; Alae, M.; Fu, G. Investigation of mechanisms of top-down fatigue cracking of asphalt pavement. Road Mater. Pavement Des. 2018, 19, 1436–1447. [Google Scholar] [CrossRef]
- Yu, J.; Tsai, B.-W.; Zhang, X.; Monismith, C. Development of asphalt pavement fatigue cracking prediction model based on loading mode transfer function. Road Mater. Pavement Des. 2012, 13, 501–517. [Google Scholar] [CrossRef]
- Norouzi, A.; Kim, D.; Kim, Y.R. Numerical evaluation of pavement design parameters for the fatigue cracking and rutting performance of asphalt pavements. Mater. Struct. 2016, 49, 3619–3634. [Google Scholar] [CrossRef]






| Parameter | AC-16 | AC-20 | AC-25 | Cement-Treated Base | Subgrade | Soil Base |
|---|---|---|---|---|---|---|
| Thicknesses (m) | 0.04 | 0.05 | 0.06 | 0.30 | 0.20 | - |
| Density (kg/m3) | 2300 | 2100 | 2050 | 2200 | 2100 | 1800 |
| Poisson’s ratio | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.40 |
| Thermal conductivity (J/m·h·°C) | 3240 | 3960 | 4680 | 5616 | 5148 | 5616 |
| Specific heat (J/kg·°C) | 800 | 850 | 900 | 911.7 | 1040 | 1040 |
| Solar radiation absorption | 0.90 | |||||
| Road surface emissivity | 0.81 | |||||
| Temperature (°C) | AC-16 | AC-20 | AC-25 | |||
|---|---|---|---|---|---|---|
| Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | |
| −30 | 12,467.5 | 1.20 × 10−5 | 12,530.8 | 1.30 × 10−5 | 9200.3 | 1.20 × 10−5 |
| −20 | 8580.2 | 1.40 × 10−5 | 8367.6 | 1.60 × 10−5 | 5421.7 | 1.50 × 10−5 |
| −10 | 5741.3 | 1.70 × 10−5 | 4810.5 | 2.10 × 10−5 | 3345.6 | 1.80 × 10−5 |
| 0 | 3828.5 | 2.00 × 10−5 | 3142.4 | 2.60 × 10−5 | 2958.2 | 2.20 × 10−5 |
| 10 | 2693.5 | 2.30 × 10−5 | 1978.4 | 2.40 × 10−5 | 1637.2 | 2.00 × 10−5 |
| 20 | 1756 | 2.50 × 10−5 | 1441 | 2.10 × 10−5 | 1285.3 | 1.80 × 10−5 |
| 30 | 1188.1 | 2.30 × 10−5 | 1185.6 | 1.80 × 10−5 | 1073.2 | 1.60 × 10−5 |
| 40 | 824.6 | 1.70 × 10−5 | 857.6 | 1.50 × 10−5 | 890.3 | 1.40 × 10−5 |
| 50 | 564.3 | 1.40 × 10−5 | 616.5 | 1.20 × 10−5 | 610.2 | 1.40 × 10−5 |
| 60 | 383.8 | 1.20 × 10−5 | 384.7 | 1.00 × 10−5 | 364.2 | 1.00 × 10−5 |
| Temperature (°C) | Cement Stabilized Gravel Base | Cement-Lime Gravel Subgrade | Soil Base | |||
|---|---|---|---|---|---|---|
| Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | Elastic Modulus (MPa) | Temperature Shrinkage Coefficient (°C−1) | |
| 50 | 1500 | 2.50 × 10−5 | 1000 | 5.50 × 10−5 | 60 | 5.0 × 10−5 |
| 35 | 2.35 × 10−5 | 4.80 × 10−5 | ||||
| 25 | 1.72 × 10−5 | 2.53 × 10−5 | ||||
| 15 | 0.72 × 10−5 | 1.38 × 10−5 | ||||
| 5 | 0.05 × 10−5 | 1.25 × 10−5 | ||||
| −5 | 0.83 × 10−5 | 0.63 × 10−5 | ||||
| −15 | 0.50 × 10−5 | 4.00 × 10−5 | ||||
| Structural Level | Maximum Tensile Stress (MPa) | ||
|---|---|---|---|
| Fall | Winter | Spring | |
| Top surface course | 0.250 | 0.816 | 0.212 |
| Intermediate layer | 0.081 | 0.500 | 0.073 |
| Under surface layer | 0.066 | 0.178 | 0.060 |
| Base | 0.053 | 0.047 | 0.046 |
| Subgrade | 0.019 | 0.021 | 0.017 |
| Depth (m) | Winter Stress (MPa) | Spring Stress (MPa) | Fall Stress (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | |
| 0 | 1.028 | 1.233 | 0.83 | 0.422 | 0.787 | 0.54 | 0.532 | 0.873 | 0.61 |
| 0.04 | 0.816 | 1.337 | 0.61 | 0.212 | 0.815 | 0.26 | 0.250 | 0.853 | 0.29 |
| 0.09 | 0.500 | 1.019 | 0.49 | 0.073 | 0.601 | 0.12 | 0.081 | 0.603 | 0.13 |
| 0.15 | 0.178 | 0.551 | 0.32 | 0.060 | 0.391 | 0.15 | 0.066 | 0.396 | 0.17 |
| Depth (m) | Winter Stress (MPa) | Spring Stress (MPa) | Fall Stress (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | |
| 0 | 1.028 | 1.120 | 0.92 | 0.422 | 0.654 | 0.65 | 0.532 | 0.743 | 0.72 |
| 0.04 | 0.816 | 1.186 | 0.69 | 0.212 | 0.655 | 0.32 | 0.250 | 0.690 | 0.36 |
| 0.09 | 0.500 | 0.880 | 0.57 | 0.073 | 0.468 | 0.16 | 0.081 | 0.468 | 0.17 |
| 0.15 | 0.178 | 0.455 | 0.39 | 0.060 | 0.312 | 0.19 | 0.066 | 0.310 | 0.21 |
| Depth (m) | Winter Stress (MPa) | Spring Stress (MPa) | Fall Stress (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | Temperature Stress | Coupling Stress | Percentage | |
| 0 | 1.028 | 1.182 | 0.87 | 0.422 | 0.739 | 0.57 | 0.532 | 0.827 | 0.64 |
| 0.04 | 0.816 | 1.274 | 0.64 | 0.212 | 0.752 | 0.28 | 0.250 | 0.788 | 0.32 |
| 0.09 | 0.500 | 0.959 | 0.52 | 0.073 | 0.543 | 0.13 | 0.081 | 0.545 | 0.15 |
| 0.15 | 0.178 | 0.507 | 0.35 | 0.060 | 0.348 | 0.17 | 0.066 | 0.353 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, L.; Gao, Y.; Dong, Y.; Liu, Y.; Li, B. Mechanical Response and Fatigue Life Analysis of Asphalt Pavements Under Temperature-Load Coupling Conditions. Appl. Sci. 2025, 15, 7441. https://doi.org/10.3390/app15137441
Liu Z, Zhang L, Gao Y, Dong Y, Liu Y, Li B. Mechanical Response and Fatigue Life Analysis of Asphalt Pavements Under Temperature-Load Coupling Conditions. Applied Sciences. 2025; 15(13):7441. https://doi.org/10.3390/app15137441
Chicago/Turabian StyleLiu, Zhenzheng, Le Zhang, Yuan Gao, Yanying Dong, Yuhang Liu, and Bo Li. 2025. "Mechanical Response and Fatigue Life Analysis of Asphalt Pavements Under Temperature-Load Coupling Conditions" Applied Sciences 15, no. 13: 7441. https://doi.org/10.3390/app15137441
APA StyleLiu, Z., Zhang, L., Gao, Y., Dong, Y., Liu, Y., & Li, B. (2025). Mechanical Response and Fatigue Life Analysis of Asphalt Pavements Under Temperature-Load Coupling Conditions. Applied Sciences, 15(13), 7441. https://doi.org/10.3390/app15137441








