A Review of the Methods Used in the Study of Creep Behavior of Fiber-Reinforced Composites and Future Developments

Featured Application

Composite materials have become an extremely important class of materials used in engineering, and any novelty related to these materials is welcome for the industry. The presented analysis of the different ways of determining the mechanical properties of fiber-reinforced composites allows us to choose the optimal method to determine these properties, depending on the purpose of using these materials. In this way, significant savings can be made in the costs involved in the design process and determining the service life.

Abstract

This paper presents the main methods for analyzing the creep of fiber-reinforced composite materials used by researchers. Creep is a characteristic property of composites made of a fiber-reinforced matrix and determines the acceptability of some materials in various engineering applications. The paper attempts to update the works in the field with recent research and analyzes the main methods for modeling these types of materials, the calculation methods, and the results obtained by researchers. It thus provides a framework for researchers to choose the most appropriate calculation method for the specific application studied. The results that have already become classics, along with the results that have appeared recently and special cases, are critically presented in the paper. Future research directions are highlighted for the various methods described and for the field as a whole.

1. Introduction

The study of creep behavior in fiber-reinforced composites must take into account a number of parameters such as material complexity, environmental conditions, challenges in modeling and testing, scale effects, and the need for interdisciplinary approaches for certain applications. All these problems are due to the very varied and often contradictory properties of the fibers and matrix materials, as well as the complexity of simulating real-world conditions (high temperatures, humidity levels, and different loading scenarios). A broad approach to encompass all these challenges requires both advanced experimental methods and sophisticated modeling techniques to improve the accuracy of predictions for the mechanical properties and in-service behavior of these materials. The analysis of creep behavior of fiber composite materials is a field in continuous development, determined by the existing evolution in the field of fiber composite materials. The current moment is characterized by an explosive dynamic of practical applications that also involves the strong advance of technologies used in manufacturing, modeling techniques, and the need to improve the properties of the materials used. The development of the field is in several directions that can be easily identified.

First of all, the manufacture of nanofibers and nanomaterials has obviously led to their use (carbon nanotubes and grapheme) as fillers and offers materials with improved mechanical properties, including creep behavior [1,2,3]. Numerous aspects of the use of nanofibers have been studied by researchers, and theoretical creep models have been developed, taking into account the nanofiber or grapheme weight ratio [4,5,6,7]. The emergence of hybrid composites represents another relatively recent trend. So, combining different fibers with different properties (glass, carbon, aramide, and so on) within the same composite, it is possible to obtain a composite with improved creep properties by leveraging the particular properties offered by each type of fiber. It is possible to improve the load transfer and the stability at different temperatures and, as a consequence, achieve a better creep behavior [8,9,10,11,12,13]. Multiscale modeling that bridges the gap between macroscale (entire composite structure) and microscale (fiber and matrix) behaviors is probably going to be the main focus of future research. These models might more precisely forecast the material’s long-term creep performance by capturing the behavior at the microscopic level [14,15,16,17,18,19]. A paper that presents many aspects of the study of creep behavior for fiber-reinforced composites is [20]. In this paper, useful and frequently used models are described: the micromechanical model, homogenization techniques, the Mori–Tanaka method, and the finite element method (FEM). The advantages and disadvantages of each method are analyzed. The theoretical results obtained in the paper and applied to several real cases are then verified with experimental measurements. The research results (models, calculation methods, and conclusions) can be easily extended to other types of composite materials with similar structures.

Applications in the field of artificial intelligence involve in-depth knowledge of the mechanical properties of composite materials, including creep behavior [21,22]. By identifying intricate patterns and nonlinear correlations in data that conventional models would overlook, machine learning (ML) algorithms can greatly improve the accuracy of creep behavior predictions in composite materials. Numerous parameters, including matrix and fiber characteristics, temperature, stress levels, fiber orientation, duration, and environmental factors, affect creep in composites in real-world applications. Some interactions may not be captured by the simplifications used in a traditional model. More sophisticated models (nonlinear, multi-dimensional) can be obtained through the application of machine learning (ML), such as neural networks and decision trees. This approach has been applied in several papers dedicated to cutting-edge applications in the field of research [23,24,25,26,27].

Predictive models are being pushed to include integrated damage mechanics in order to account for the intricate damage evolution during creep, which includes matrix cracking, fiber–matrix interface degradation, and delamination. These models would provide more accurate lifetime and failure forecasts by taking into consideration material degradation over time [28,29,30,31,32,33].

Laboratory testing of composites, to verify to what extent the proposed or used models approach the real behavior of the materials, is an extremely important step. For this reason, there are numerous works and proposals for procedures according to which the experiments should be performed [34,35,36,37,38,39].

Engineering applications encompass a wide range of environments and conditions in which composite materials are placed. For this reason, it is necessary to know how fiber-reinforced composites respond to very different environmental factors (humidity, UV radiation, temperature, and thermal cycles). Composites are currently used in the aerospace industry, the automotive industry, construction, infrastructure, medical technology, etc. It is also necessary to know the creep–fatigue interaction to cover the wide range of applications of composites [40,41,42,43,44,45,46,47,48].

A combination of several disciplines, such as materials science, mechanical engineering, environmental science, and computational modeling, is required. Collaboration between academia, industry, and government institutions is necessary. This can lead to the development of new standards, test methods, and modeling techniques that provide better predictions [49,50,51,52].

Accelerated testing protocols are increasingly being applied to save time during the design and development of a new product. Robotics and advanced automation are increasingly used to perform tests on a large number of specimens, through more efficient collection and analysis of experimental data [53,54,55,56,57,58].

Understanding creep in composites is crucial for their design and use in a variety of sectors, particularly those where materials are exposed to continuous pressures over time. Creep is the slow, time-dependent deformation of a material under continuous stress. The analysis of the main results obtained so far shows us the main difficulties and problems encountered in the study of the creep behavior of fiber-reinforced composite materials. Some of the difficulties encountered by researchers in the presented literature are listed below:

• Complex constitutive models are necessary because of the profound heterogeneity of the composite materials, where the phases (fiber and matrix) have very different mechanical and physical properties, with complex interactions and parameters varying in time. The distribution of the materials in composites can be non-uniform, and the materials can be nonlinear and can exhibit both elastic and plastic deformation over time. As a consequence, it is necessary to use anisotropic and viscoelastic/viscoplastic models to obtain an accurate creep prediction.
• Interfacial behavior plays an important role in creep behavior. The creep performance is greatly impacted by delamination or microcracking, which can result from a weak or weakly bonded surface. The stress transfer between fibers and matrix can be strongly influenced by the nature and quality of these interactions.
• Damage behavior remains one of the problems that arise in the study of creep evolution, which includes microcracking and delamination (microscopic cracks and delamination in the materials can accelerate the creep process). To the extent that the two phenomena (creep and microcracking/delamination) are mutually reinforcing, this represents a very important aspect. The failure mechanisms, as a consequence, must be studied in order to offer an accurate lifetime prediction.
• Scale effects, how microstructural phenomena influence macroscopic creep, are difficult to understand and model. Creep behavior can be greatly influenced by the size, shape, and lay-up arrangement of the composite material, and these effects are frequently hard to generalize across many composite systems.
• For the creep phenomenon, environmental factors become important. Fiber-reinforced composites’ creep behavior can be altered over time by moisture, UV radiation, or harsh chemicals that weaken the matrix or degrade the fibers. Composite sites may simultaneously experience cyclic loading (fatigue) and continuous loading (creep) in real-world applications. In this sense, the image shown to us is intricate and requires meticulous research and modeling.
• Extensive experimental data and sophisticated computational techniques are required for prediction models, which integrate several elements, including material qualities, loading conditions, and environmental parameters, into a single model.
• To fully understand the creep behavior of these materials, testing under a range of loading scenarios and orientations is necessary. Because creep behavior is intrinsically time-dependent, it necessitates extensive testing, which can take months or even years. Because of this, collecting enough experimental data for different loading circumstances, temperatures, and habitats is difficult and costly.

In conclusion, investigating creep behavior in fiber-reinforced composites entails tackling intricate problems with temperature sensitivity, material heterogeneity, interfacial characteristics, damage evolution, and testing difficulties. Combining theoretical, computational, and experimental methods is necessary to solve these issues. Understanding creep in composites is crucial for their design and use in a variety of sectors, particularly those where materials are exposed to continuous pressures over time. Future investigations into the behavior of creep in fiber-reinforced composites will probably be influenced by developments in material science, testing procedures, computational approaches, and environmental factors. Enhancing modeling skills, integrating real-time monitoring, improving matrix and fiber characteristics, and developing more sustainable composite systems will be the main areas of focus. Fiber-reinforced composites that can tolerate long-term creep deformation in demanding applications will become more robust, effective, and dependable as a result of these developments.

This study completes the reviews performed over the five decades of composite material research by introducing new calculation methods that have benefited from the appropriate calculation technique and new mechanical testing tools. It can thus provide a more comprehensive and up-to-date view of the calculation models of the flow phenomenon in composites.

2. Fiber-Reinforced Plastics

2.1. Linear Viscoelastic Behavior

In the characterization of viscoelastic materials, it is essential to differentiate between linear and nonlinear material behavior. In general, linear viscoelastic theory can be applied for the characterization of polymeric materials only when the stresses (or strains) are sufficiently low. It is therefore important to recognize the conditions that must be satisfied if linearity is to be assumed. In fact, not one but both of the criteria that comprise the definition of linear behavior must be verified for a linear material behavior to prevail. This is essential since there are some important composite materials that satisfy the one criterion normally taken as sufficient for linearity, and yet these materials are highly nonlinear. Perhaps a word of caution should be added at this point when attributing a linear viscoelastic behavior to a matrix. Even at modest composite loading, portions of the matrix may be sufficiently highly loaded so that the composite response may be nonlinear. This can possibly cause errors in theoretical predictions. The two criteria that must be met in order for the material response to be considered linear will now be described [59,60,61,62,63].

(a)

Homogeneity

This property, sometimes referred to as the proportionality property, states that a proportional change in input history causes the same proportional change in response. In other words, if the stress (input) is doubled, the strain response (output) doubles. This property can be written as follows:

$$\epsilon [k\sigma (t)]=k\epsilon [\sigma (t)],$$

(1)

where k is a constant.

(b)

Superpositions

This property, on the other hand, which is not restricted to proportional changes, states that the response due to the sum of two or more inputs is identical to the sum of the responses due to each input applied separately, i.e.,

$$\epsilon [{\sigma }_I(t)+{\sigma }_E(t)+\dots ]=\epsilon [{\sigma }_I(t)]+\epsilon [{\sigma }_E(t)]+\dots ,$$

(2)

It is of significance to point out that if a material satisfies condition (a) of the superposition, it will automatically satisfy the proportionality condition (b), but the opposite is not true. The assumption made by many investigators that, for a material, the homogeneity property alone is sufficient for the linear behavior to prevail is not justified since the material response may be quite nonlinear. Thus, it is essential to apply the superposition test if the material is to be examined for linear viscoelastic behavior. As stated earlier, Boltzmann’s superposition principle is a consequence of the linear behavior of the material, which is only applicable in the linear range.

2.2. The Rheological Model for Creep

The “spring” and “dashpot” are the basic elements of rheological models, which are used as comprehensive methods to describe creep and relaxation phenomena. The “spring” represents the time-independent elastic behavior, whereas the “dashpot” reflects the transient, linear viscous response [64,65,66,67,68]. The response of a single Kelvin element consisting of a spring and a dashpot connected in parallel, when under a constant applied stress $\sigma ={\sigma }_{a}H(t)$, is as follows:

$$\epsilon (t)={\displaystyle \frac{{\sigma }_a}{E}}\left(1-e^{-{\displaystyle \frac{E}{\eta }}t}\right),$$

(3)

or

$$D(t)={\displaystyle \frac{1}{E}}\left(1-e^{-{\displaystyle \frac{t}{\tau }}}\right),$$

(4)

where D is creep compliance, E is the modulus of the spring, $\tau =E/\eta$ is the retardation time, and $\eta$ is the dashpot coefficient. The creep behavior of a viscoelastic material can be described more accurately if “m” Kelvin elements are connected in series, eventually with an additional free spring constant E_o. This results in the generalized Kelvin model, for which the overall creep strain is given by the Prony–Dirichlet series:

$$\epsilon (t)={\sigma }_a\left[{\displaystyle \frac{1}{E_o}}+{\displaystyle \sum _{j=1}^m\frac{1}{E_j}\left(1-e^{-\frac{t}{{\tau }_j}}\right)}\right].$$

(5)

The above model is capable of providing an approximation of any monotonically increasing creep compliance function of the material in the linear loading range. By increasing the number of Kelvin units “m”, the approximation becomes more accurate. For the case when an infinite number of Kelvin elements are connected, the creep strain may be given by the following equation:

$$\epsilon (t)={\sigma }_a\left[D_o+{\displaystyle {\int }_0^{\infty }\phi \left(\tau \right)\left(1-e^{-\frac{t}{\tau }}\right)d\tau }\right],$$

(6)

where $D_o=1/E_o$ is the initial time-independent compliance due to a free spring, and fi represents the continuous retardation spectrum, i.e., a distribution function of the retardation time. This is in contrast to discrete retardation times, when the number of the Kelvin units is finite.

2.3. Nonlinear Viscoelastic Behavior

The well-developed constitutive equations of linear viscoelasticity can be utilized to characterize polymeric materials when the stress–strain relationship is linear. This corresponds to those cases where the applied stresses (or strains) are sufficiently low, for which the constitutive relations can be formulated on the basis of Boltzmann’s superposition principle. It is interesting to note that nonlinear viscoelastic analysis may prevail even for very low stress levels when extremely long-term prediction of the material behavior is to be made. An example of such a loading condition is given by Hiel [69] for a creep test on FM-300 adhesive. This reference highlights that the stress at which material behavior tends to become nonlinear decreases with increasing time point. This observation implies that, for a proper and complete characterization of viscoelastic materials, a nonlinear time-dependent constitutive equation must be developed. This, in turn, suggests that the magnitude of applied load (stress or strain) must be accounted for when establishing a nonlinear formulation of polymeric composite materials. A number of techniques have been applied to represent the nonlinear viscoelastic behavior. Laederman [70] modified the Boltzmann superposition integral slightly so that stress dependence can be accounted for. In this approach, the creep compliance, for instance, consists of time-dependent as well as time-independent portions, where only the stress dependence of the former is taken into consideration. The method is useful but unfortunately not general enough to describe nonlinear behavior [71,72,73,74,75].

2.4. The Method of Multiple Integrals

Green and Rivlin [76,77] formulated a nonlinear viscoelastic constitutive relation involving multiple integral representations. They are very attractive since, due to their complete generality, any degree of nonlinearity can be accounted for, and they can be applied to any type of class of materials. These equations have been used by several investigators in order to experimentally evaluate the kernels, i.e., the stress-, temperature-, and moisture-dependent material properties. Experimental requirements of the above theory become impractical when the viscoelastic material contains a high degree of nonlinearity, thus making experimental evaluation of the kernels extremely difficult. Using this method, the nonlinear viscoelastic behavior (creep behavior, for example) for a one-directional case can be represented by the following equation:

$$\begin{array}{l}\epsilon (t)={\displaystyle {\int }_0^t{D}_1\left(t-{\tau }_1\right)\frac{\partial \sigma }{\partial {\tau }_1}}d{\tau }_1+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^t{D}_2\left(t-{\tau }_1,t-{\tau }_2\right)\frac{\partial \sigma }{\partial {\tau }_1}\frac{\partial \sigma }{\partial {\tau }_2}}d{\tau }_{1}d{\tau }_2}\\ +{\displaystyle {\int }_0^t{\displaystyle {\int }_0^t{\displaystyle {\int }_0^t{D}_3\left(t-{\tau }_1,t-{\tau }_2,t-{\tau }_3\right)\frac{\partial \sigma }{\partial {\tau }_1}\frac{\partial \sigma }{\partial {\tau }_2}}d{\tau }_{1}d{\tau }_{2}d{\tau }_3}}+\dots \dots \end{array}.$$

(7)

The first term of the equation reflects the linear viscoelastic behavior of the material defined by Bolzman’s integral representation of linear theory, while the second and higher-order terms represent deviations from linear behavior. The accuracy of the above approach becomes higher as the number of terms increases. For a simple uniaxial isothermal creep test with a suddenly applied load,

$$\sigma ={\sigma }_{a}H(t),$$

(8)

It becomes

$$\epsilon (t)={\sigma }_a{D}_1(t)+{\sigma }_a^2{D}_2(t,t)+{\sigma }_a^3{D}_3(t,t,t)+\dots .$$

(9)

In order to determine the “kernels” $D_k^{\prime }$, it becomes necessary to conduct creep tests under “k” different stress levels.

2.5. Findley Approach to Nonlinear Viscoelasticity

A nonlinear viscoelastic technique was proposed by Findley [78,79] and has been used by several investigators to accurately characterize the nonlinear creep behavior of materials. It is an empirical approach, and it is based on a power law with nonlinear coefficients:

$$\epsilon (t)={\epsilon }_o+p{t}^n,$$

(10)

where

$${\epsilon }_{\sigma }=\epsilon {\prime }_o\sinh \left({\displaystyle \frac{\sigma }{{\sigma }_{\epsilon }}}\right),$$

(11)

and

$$p=p\prime \sinh \left({\displaystyle \frac{\sigma }{{\sigma }_p}}\right).$$

(12)

2.6. Method of Nonlinearity Factors

This method was developed by Shapery [80] and has been used successfully by several investigators [81,82]. The sample single-integral constitutive equations have been derived from the thermodynamic theory of irreversible processes and can be used as either strains or stresses as the entering state variables. As opposed to the multi-integral forms presented earlier, the kernels contained in these equations are much easier to evaluate experimentally, often requiring only uniaxial creep tests (followed by a recovery period). This formulation can be used to predict the behavior of polymer both with and without fiber reinforcements. The nonlinear viscoelastic constitutive equation for uniaxial creep-type loading is given as follows:

$$\epsilon (t)=g_o{D}_o\sigma +g_1{\displaystyle {\int }_{-\infty }^t∆D(\phi -\phi \prime )\frac{d}{d\tau }}\left(g_2\sigma \right)d\tau .$$

(13)

Here, $D_o=D(0)$ and $∆D(\phi )$ are the instantaneous and transient components of the linear viscoelastic creep compliance, respectively. Moreover, $\phi$ and $\phi \prime$ are reduced time parameters and are defined as follows:

$$\phi \equiv {\displaystyle {\int }_0^t\frac{dt\prime }{a_{\sigma }}} ; \phi \prime \equiv \phi \left(\tau \right)\equiv {\displaystyle {\int }_0^{\tau }\frac{dt\prime }{a_{\sigma }}} .$$

(14)

The nonlinearity factors $g_o,g_1$ and the time-shift factor $a_{\sigma }$ are stress-dependent material properties. It is readily seen that the familiar Boltzmann’s superposition principle for linear viscoelastic behavior is recovered by setting $g_o=g_1=g_2=a_{\sigma }=1$. Furthermore, Leadermann’s modified superposition principle introduced earlier can be obtained by substituting $g_o=g_1=a_{\sigma }=1$ in Equation (13), yielding

$$\epsilon (t)=D_o\sigma +{\displaystyle {\int }_{-\infty }^t∆D(t-\tau \prime )\frac{d}{d\tau }}\left(g_2\sigma \right)d\tau .$$

(15)

The nonlinearity factors in Equation (13) have certain thermodynamic significance. According to Schapery [81], changes in $g_o,g_1$, and $g_2$ arise from the third- and higher-order dependence of Gibbs free energy on the applied stress, while changes in $a_{\sigma }$ reflect similar dependence of both entropy production and free energy. In fact, $a_{\sigma }$ may in general be a function of both stress and strain, and their time rates of change. The time-shift factor $a_{\sigma }$ tends to accelerate or decelerate the influence of time and is a function of stress and may, in some cases, reflect the effect of moisture content. For composites with a fixed test environment, the nonlinear parameters $g_o,g_1$, and $g_2$ depend on the stress level and fiber angle.

2.7. General Conclusions

• The main hypothesis used in most of the calculus of plastic composites is that these materials exhibit linear viscoelastic properties. Two conditions must be satisfied to have this: homogeneity (proportionality) and the superposition principle. Many materials may appear linear but are not; superposition must be tested to confirm linear behavior. Very clearly, Boltzmann’s superposition principle is valid only within the linear range.
• The nonlinear viscoelastic behavior may occur at low stress levels over long timescales. Boltzmann’s principle fails for nonlinear behavior. Nonlinear constitutive models must consider the stress–strain magnitude. A modified superposition (Leaderman) can be used. The method of multiple integrals (Green and Rivlin) represents a highly general framework using multiple integrals to capture any degree of nonlinearity and can model complex dependencies (stress, moisture, and temperature). Higher-order terms represent deviations from linear behavior.
• Findley’s Approach is an empirical model for nonlinear creep based on a power law with nonlinear coefficients and is widely used for its simplicity and practical applicability.
• The method of nonlinearity factors (Shapery) is derived from thermodynamic principles, is easier to implement experimentally than multiple integrals, and uses stress-dependent nonlinearity and time-shift factors to model material behavior.

3. Micromechanical Analysis

3.1. Basic Considerations

Micromechanical analysis of composites represents the basic method used to study and predict the behavior of composite materials using the structure of this at the microscopic level. So, it is possible to consider the mechanical interactions between the fiber and matrix and to obtain the properties of the material as a whole at a macromechanical scale. Micromechanics describes how the properties and geometry of individual phases contribute to the overall behavior. This method involves modeling the microstructure (e.g., fiber shape, material, geometry, size, orientation, and distribution), the stress–strain relationships, failure mechanisms, and stiffness to predict overall physical properties (elastic modulus, strength, and thermal conductivity).

Micromechanical analysis has the possibility to provide other information about the material, such as understanding damage initiation (cracking), optimizing the design of microstructure (fiber volume fraction, geometry, alignment, etc.), and simulating behavior under different loading conditions. This method works together with other methods, techniques, and procedures such as analytical methods, the Mori–Tanaka method, or FEM and enables reducing the needs for a physical prototype [83,84,85,86,87].

3.2. Micromechanical Methods

3.2.1. Model

In this section, the properties of the various components, such as the fiber and matrix, as well as their interactions, are used to derive the overall composite properties in a micromechanical analysis. In fact, the fibers in a unidirectional composite are dispersed at random throughout the matrix. Nonetheless, it makes sense to take into account some periodicity in the fiber distribution. There are many models for different fiber arrangements. For our purposes, we present a standard model, from which it is possible to develop more complicated arrangements. This model is made simpler by periodicity and symmetry. The square array in Figure 1 illustrates this circumstance. For composites reinforced with fibers, the following assumptions are considered valuable:

-

The X₂–X₃ plane has a rectangular array of fibers that are expanded in the X₁ direction. According to our presentation, the polymeric matrix is nonlinearly viscoelastic but isotropic, and the fibers are linearly elastic and anisotropic. Indeed, these presumptions may be changed in the case of the nonlinear material.

-

Under load, no cracks or holes may form since the interaction between the fibers and matrix is only mechanical.

Figure 1. Square fiber packing geometry of a unidirectional composite.

Figure 1. Square fiber packing geometry of a unidirectional composite.

-

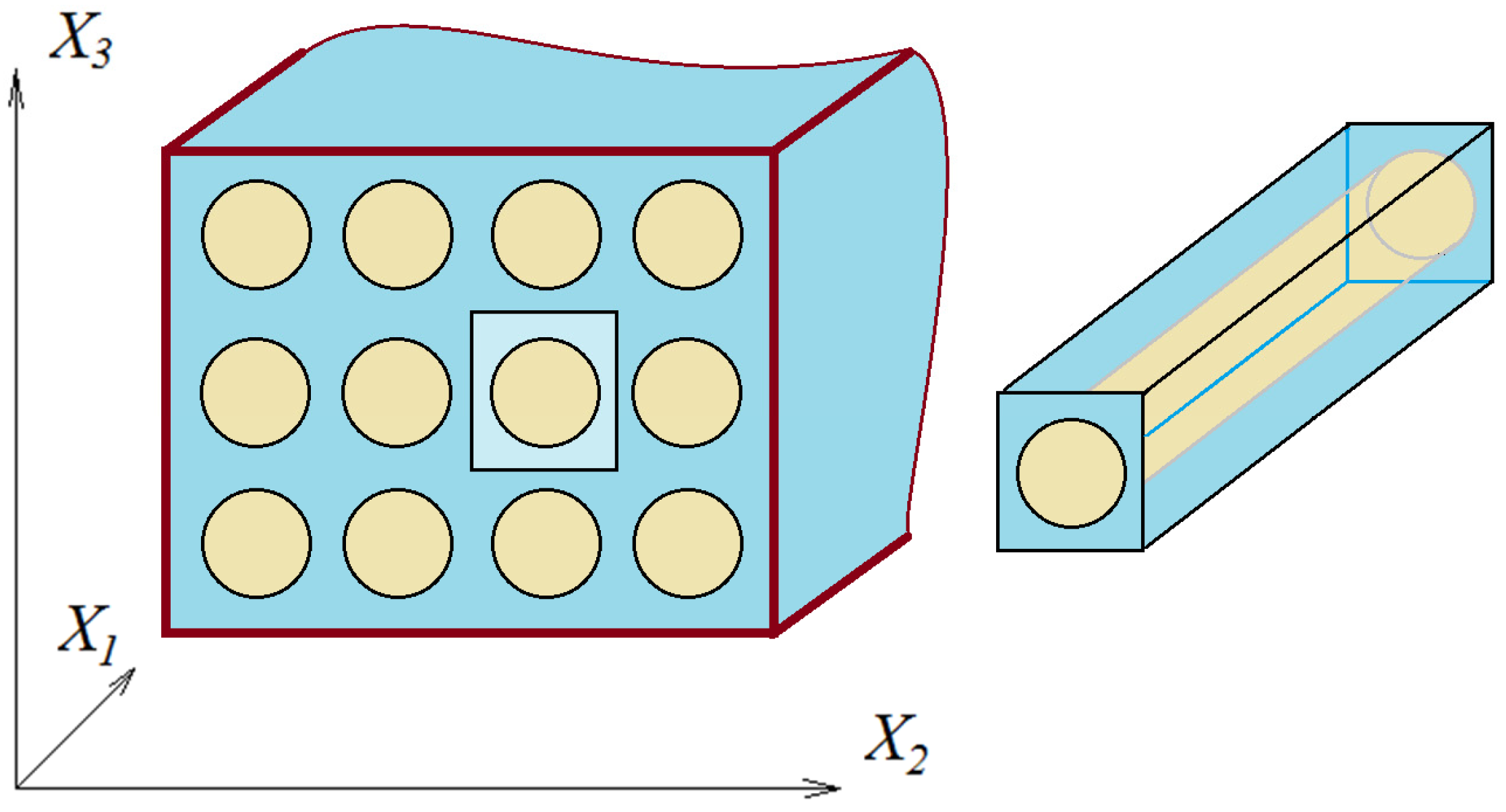
The problem’s size and complexity are decreased by the aforementioned regular and periodic packing, which enables the study of a representative cell. Note that one of the recurring units of the periodical pattern depicted in Figure 1 is displayed in Figure 2a. The fiber is thought to have a transversal section that is circular. As seen in Figure 2b, the representative unit cell (RUC) (or representative volume element—RVE) can therefore be made up of two subcells, each representing a quarter of a fiber and the corresponding matrix material. In addition, the unit cells are thought to be tiny in relation to the composite’s overall dimensions.

For each subcell in the representative cell, a local reference frame (X₁, $x_2^{(\lambda )}$, $x_3^{(\lambda )}$), with its origin located as shown in Figure 2 is introduced. “$\lambda$” is used to symbolically represent both fiber ($\lambda =f$) and matrix ($\lambda =m$) constituents. Furthermore, the displacement in each of the two subcells is expressed in a first-order linear expansion as a function of the distance from the origin to the local coordinate axes [27,28]. This means that the displacement at any point in the subcell is as follows:

$$u_i^{(\lambda )}=u_i^{o(\lambda )}+x_2^{(\lambda )}{\xi }_i^{(\lambda )}+x_3^{(\lambda )}{\zeta }_i^{(\lambda )}\hspace{1em};\hspace{1em}i=1,2,3\hspace{0.33em}\hspace{0.33em}.$$

(16)

With $u_i^o$, the component j of the displacement of the origin of the local reference frame is noted along the xi axis. ${\xi }_i^{(\lambda )}$ and ${\zeta }_i^{(\lambda )}$ are coefficients representing the linear dependence on $x_2^{(\lambda )}$ and $x_3^{(\lambda )}$, respectively. The aim of this presentation is to establish the relationship between the average stresses and average strains in the composite. These relationships will offer us the coefficient of the overall constitutive law. The strain–displacement relationships of anisotropic bodies yield the following:

$${\epsilon }_{ij}^{(\lambda )}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i^{(\lambda )}}{\partial x_j}}+{\displaystyle \frac{\partial u_j^{(\lambda )}}{\partial x_i}}\right)\hspace{1em};\hspace{1em}i,j=1,2,3$$

(17)

when $i\ne j$, it can be used in the notation ${\gamma }_{ij}^{(\lambda )}=2{\epsilon }_{ij}^{(\lambda )};$ $i,j=1,2,3\hspace{0.33em};\hspace{1em}i\ne j;$ for the engineering shear strain. Substituting Equation (16) into Equation (17), we obtain

$$\begin{gathered} {\epsilon }_{11}^{(\lambda )}={\displaystyle \frac{\partial u_i^{o(\lambda )}}{\partial X_1}} ; {\epsilon }_{22}^{(\lambda )}={\xi }_2^{(\lambda )} ; {\epsilon }_{33}^{(\lambda )}={\zeta }_3^{(\lambda )}; \\ {\gamma }_{23}^{(\lambda )}=\lfloor {\xi }_3^{(\lambda )}+{\zeta }_2^{(\lambda )}\rfloor ;{\gamma }_{31}^{(\lambda )}=\left[{\displaystyle \frac{\partial u_3^{o(\lambda )}}{\partial X_1}}+{\zeta }_1^{(\lambda )}\right] ; {\gamma }_{12}^{(\lambda )}=\left[{\displaystyle \frac{\partial u_2^{o(\lambda )}}{\partial X_1}}+{\xi }_1^{(\lambda )}\right] . \end{gathered}$$

(18)

The overall behavior of the fiber-reinforced composite should be considered viscoelastic. The nonlinear viscoelastic material subjected to uniaxial creep loading and in isothermal conditions is according to Schapery’s relation [80]:

$$\epsilon (t)=D_n\hspace{0.17em}{\sigma }_n .$$

(19)

In Equation (19), we have

$$D_n=g_o{D}_o+g{\displaystyle \sum _{j=1}^m{D}_j\left(1-e^{-t/r_j}\right)} .$$

(20)

For the matrix, this can be written as

$${\epsilon }_{ij}^{(m)}=D_n\left[1+\nu (t)\right]{\sigma }_{ij}^{(m)}-D_n\hspace{0.17em}\nu (t)\hspace{0.17em}{\sigma }_{kk}^{(m)}{\delta }_{ij} .$$

(21)

In Equation (21), $D_n$ is obtained using Equation (20), $\nu (t)$ represents the time-dependent Poisson’s ratio, and ${\delta }_{ij}$ is Kronecker’s delta.

To obtain the composite’s general behavior, the following phases are necessary:

The first step is to identify the stresses that an externally applied constant load causes in each subcell. It is necessary to provide continuity of traction along the phase interfaces. The induced strains in each subcell must then be used to calculate the strains in the representative cell. It is important to remember that all strains and stresses are assessed on an average basis. All displacements must be continuous across the unit cell’s subcell boundaries and between neighboring cells in order for the composite to be considered continuous.

Finally, the constitutive law will be determined considering the Hook law, which correlates the average stresses and strains determined above [88,89,90,91,92].

3.2.2. Average Stresses in RUC

Having volume V and a rectangular parallel-piped shape, the composite specimen in question has edges parallel to the coordinate axes (X₁, X₂, X₃). Calculating the average stress ${\overline{\sigma }}_{ij}$ in RUC is the issue that will be covered next [93,94,95,96,97]. This is a sample of the entire composite that is typical of the bulk material from a structural perspective, while also having a suitable amount of the constituent materials. As a result, the characteristics of the complete composite are defined by the characteristics of the RUC.

The average of the stress distribution over the volume is determined using the following equation:

$${\overline{\sigma }}_{ij}={\displaystyle \frac{1}{V}}{\displaystyle \underset{V}{\int }{S}_{ij}dV}.$$

(22)

Considering a RUC as a one-quarter of a fiber in the composite square matrix, we obtain the following for (22):

$${\overline{\sigma }}_{ij}={\displaystyle \frac{1}{A}}\left({\overline{S}}_{ij}^{(f)}{A}_f+{\overline{S}}_{ij}^{(m)}{A}_m\right) .$$

(23)

In Equation (23), ${\overline{S}}_{ij}^{(\lambda )}$ is the average stresses in RUC, A is the total area of the cell A, and $A_{\lambda }$ is the area of the subcells. For the sake of simplicity in computation, a unit depth of the composite is considered, i.e., V = A × 1. For the case presented here, when the fibers are circular, it results in the following:

$$A={(R+h/2)}^2; A_f=\pi R^2/4 ; A_m={(R+h/2)}^2-\pi R^2/4$$

(24)

We obtain

$${\overline{\sigma }}_{ij}={\displaystyle \frac{1}{{\left(R+\frac{h}{2}\right)}^2}}\left\{{\displaystyle \frac{\pi R^2}{4}}{\overline{S}}_{ij}^{(f)}+\left[{\left(R+{\displaystyle \frac{h}{2}}\right)}^2-{\displaystyle \frac{\pi R^2}{4}}\right]{\overline{S}}_{ij}^{(m)}\right\}$$

(25)

The average stress in fiber and matrix is as follows:

$${\overline{S}}_{ij}^{(\lambda )}={\displaystyle \frac{1}{A_{\nu }}}{\displaystyle \underset{A}{\int }{\sigma }_{ij}^{(\lambda )}}dA={\displaystyle \frac{1}{A_{\nu }}}{\displaystyle \iint {\sigma }_{ij}^{(\lambda )}d{x}_{2}d{x}_3}$$

(26)

Changing the Cartesian coordinates to polar coordinates, the Jacobian is as follows:

$$J={\displaystyle \frac{\partial (x_2,x_3)}{\partial (r,\theta )}}=\left|\begin{array}{cc}\cos \theta & \sin \theta \\ -r\sin \theta & r\cos \theta \end{array}\right|=r$$

(27)

For subcell “f”, Equation (26) has the following form in polar coordinates:

$${\overline{S}}_{ij}^{(f)}={\displaystyle \frac{4}{\pi R^2}}{\displaystyle {\int }_0^{\pi /2}{\displaystyle {\int }_0^R{\sigma }_{ij}^{(f)}}}rdrd\theta$$

(28)

In Equation (28), ${\sigma }_{ij}^{(f)}$ represents the classic Hook law of the transversely isotropic material. Using Equation (18) in the Hook law, we have

$${\overline{S}}_{ij}^{(f)}=\left\{\begin{array}{c}{C}_{11}{\epsilon }_{11}^{(f)}+C_{12}\left({\epsilon }_{22}^{(f)}+{\epsilon }_{33}^{(f)}\right)\\ C_{12}{\epsilon }_{11}^{(f)}+C_{22}{\epsilon }_{22}^{(f)}+C_{23}{\epsilon }_{33}^{(f)}\\ C_{12}{\epsilon }_{11}^{(f)}+C_{23}{\epsilon }_{22}^{(f)}+C_{22}{\epsilon }_{33}^{(f)}\\ C_{66}{\gamma }_{23}^{(f)}\\ C_{44}{\gamma }_{31}^{(f)}\\ C_{44}{\gamma }_{12}^{(f)}\end{array}\right\}=\left\{\begin{array}{c}{C}_{11}{\displaystyle \frac{\partial u_1^{o(f)}}{\partial X_1}}+C_{12}\left({\xi }_2^{(f)}+{\zeta }_3^{(f)}\right)\\ C_{12}{\displaystyle \frac{\partial u_1^{o(f)}}{\partial X_1}}+C_{22}{\xi }_2^{(f)}+C_{23}{\zeta }_3^{(f)}\\ C_{12}{\displaystyle \frac{\partial u_1^{o(f)}}{\partial X_1}}+C_{23}{\xi }_2^{(f)}+C_{22}{\zeta }_3^{(f)}\\ C_{66}\left[{\xi }_3^{(f)}+{\zeta }_2^{(f)}\right]\\ C_{44}\left[{\displaystyle \frac{\partial u_3^{o(f)}}{\partial X_1}}+{\zeta }_1^{(f)}\right]\\ C_{44}\left[{\displaystyle \frac{\partial u_2^{o(f)}}{\partial X_1}}+{\xi }_1^{(f)}\right]\end{array}\right\}$$

(29)

Now, we apply the same procedure to determine the average stresses for subcell “m”. Based on the local coordinate of subcell “m”, considering both Cartesian and polar coordinates, it is possible to write the following:

$${\overline{S}}_{ij}^{(m)}={\displaystyle \frac{1}{{\left(R+\frac{h}{2}\right)}^2-\frac{\pi R^2}{4}}}\left({\displaystyle {\int }_0^{R+h/2}{\displaystyle {\int }_0^{R+h/2}{\sigma }_{ij}^{(m)}d{x}_{2}d{x}_3-{\displaystyle {\int }_0^{\pi /2}{\displaystyle {\int }_0^R{\sigma }_{ij}^{(m)}rdrd\theta }}}}\right)$$

(30)

Equation (30), together with Equations (18) and (27), yields

$${\displaystyle \frac{\partial u_1^o}{\partial X_1}}=D_n\left[1+\nu (t)\right]{\overline{S}}_{11}^{(m)}-D_n\left[\nu (t)\right]{\overline{S}}_{kk}^{(m)};$$

(31)

$${\xi }_2^{(m)}=D_n\left[1+\nu (t)\right]{\overline{S}}_{22}^{(m)}-D_n\left[\nu (t)\right]{\overline{S}}_{kk}^{(m)};$$

(32)

$${\zeta }_3^{(m)}=D_n\left[1+\nu (t)\right]{\overline{S}}_{33}^{(m)}-D_n\left[\nu (t)\right]{\overline{S}}_{kk}^{(m)};$$

(33)

$${\xi }_3^{(m)}+{\zeta }_2^{(m)}=2D_n\left[1+\nu (t)\right]{\overline{S}}_{23}^{(m)};$$

(34)

$${\displaystyle \frac{\partial u_3^{o(m)}}{\partial X_1}}+{\zeta }_1^{(m)}=2D_n\left[1+\nu (t)\right]{\overline{S}}_{31}^{(m)};$$

(35)

$${\displaystyle \frac{\partial u_2^{o(m)}}{\partial X_1}}+{\xi }_1^{(m)}=2D_n\left[1+\nu (t)\right]{\overline{S}}_{12}^{(m)}.$$

(36)

Equations (31)–(36) represent a system of equations relating the subcell stresses in the matrix $S_{ij}^{(m)}$ to the microvariables ${\xi }_i^{(m)}$ and ${\zeta }_i^{(m)}$.

3.2.3. Continuity Conditions

As mentioned earlier, throughout the representative cell, the continuity conditions of displacements at the interface between the subcells and the adjacent unit cells must be fulfilled. This turn means that the continuity conditions must be satisfied in both X₂ and X₃ directions within the composite, as described below.

Inspecting Figure 3, the following conditions hold:

$$x_2^{(f)}=X_2^i\mp X_2^{(f)}=\mp R\cos \theta ,$$

(37)

and

$$x_2^{(m)}=X_2^i\mp X_2^{(m)}=\pm \left({\displaystyle \frac{h}{2}}+R-R\cos \theta \right)$$

(38)

Upon substitution of Equations (37) and (38) into Equation (16) for $\lambda =f$ and $\lambda =m$, viz.,

$$u_i^{(f)}=u_i^{o(f)}\mp R\cos \theta {\xi }_i^{(f)}+x_3^{(f)}{\zeta }_i^{(f)},$$

(39)

$$u_i^{(m)}=u_i^{o(m)}\pm \left({\displaystyle \frac{h}{2}}+R-R\cos \theta \right){\xi }_i^{(m)}+x_3^{(m)}{\zeta }_i^{(m)}.$$

(40)

where

$$u_i^{o(f)}=u_i^{o(f)}(X_2^{(f)}),$$

(41)

$$u_i^{o(m)}=u_i^{o(m)}(X_2^{(m)}).$$

(42)

It is necessary to take into account the average of the requirement for continuity of displacements at the interface between the two subcells. So,

$$\begin{gathered} {\displaystyle {\int }_{-\pi /2}^{\pi /2}\left[u_i^{o(f)}\mp R\cos \theta {\xi }_i^{(f)}+x_3^{(f)}{\zeta }_i^{(f)}\right]R\cos \theta d\theta =} \\ {\displaystyle {\int }_{-\pi /2}^{\pi /2}\left[u_i^{o(m)}\pm \left(\frac{h}{2}+R-R\cos \theta \right){\xi }_i^{(m)}+x_3^{(m)}{\zeta }_i^{(m)}\right]R\cos \theta d\theta }. \end{gathered}$$

(43)

After some calculus, we have

$$u_i^{o(f)}\left(X_2^{(f)}\right)\pm {\displaystyle \frac{\pi R}{2}}{\xi }_i^{(f)}=u_i^{o(m)}\left(X_2^{(m)}\right)\mp \left(h+2R-{\displaystyle \frac{\pi R}{2}}\right){\xi }_i^{(m)}.$$

(44)

From Equation (44), the continuity conditions of displacements in the $X_2$ direction are determined as follows:

$$u_i^{o(f)}=u_i^{o(m)}=u_i^o.$$

(45)

Equation (45) expresses the continuity of displacement for the two neighboring cells: $\lambda =f$ and $\lambda =m$.

3.2.4. Average Strains in RUC

The average of the internal strain over volume is expressed as follows:

$${\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{V}}{\displaystyle {\int }_V{\epsilon }_{ij}dV},$$

(46)

and, for a representative cell,

$${\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{A}}{\displaystyle \sum _{\lambda =f,m}{\overline{\epsilon }}_{ij}^{(\lambda )}{A}_{\lambda }}{\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{A}}{\displaystyle \sum _{\lambda =f,m}{\overline{\epsilon }}_{ij}^{(\lambda )}{A}_{\lambda }},$$

(47)

where notations ${\overline{\epsilon }}_{ij}^{(\lambda )}$ and $A_{\lambda }$ are the same as before. Using Equations (16) and (18) for $i=j=1$, the following is obtained:

$${\overline{\epsilon }}_{ij}^{(\lambda )}={\displaystyle \frac{\partial u_1^o}{\partial X_1}}.$$

(48)

Considering (24), we have

$${\overline{\epsilon }}_{11}={\displaystyle \frac{1}{{\left(R+\frac{h}{2}\right)}^2}}\left\{{\displaystyle \frac{\pi R^2}{4}}{\displaystyle \frac{\partial u_1^o}{\partial X_1}}+\left[{\left(R+{\displaystyle \frac{h}{2}}\right)}^2-{\displaystyle \frac{\pi R^2}{4}}\right]{\displaystyle \frac{\partial u_1^o}{\partial X_1}}\right\},$$

(49)

or, after some calculus,

$${\overline{\epsilon }}_{11}={\displaystyle \frac{\partial u_1^o}{\partial X_1}}.$$

(50)

Now that all the equations required to anticipate the composite’s overall behavior have been established, it is reasonable to draw out instances to assess the analysis’s applicability. As was previously indicated, the specimen undergoes a complex three-axial condition of stress even in a uniaxial test. In order to allow the stress-dependent material properties $g_o,g_1,g_2$ and $a_{\sigma }$ to rely on a single invariant instead of the applied stress provided by Equations (25) and (26), it is appropriate to have an octahedral shear stress in the matrix. The octahedral shear stress in the matrix is introduced as this so-called equivalent stress.

Since the analysis is performed at the microlevel, the same analogy may be applied here to let the material properties be a function of $S_{oct}^{(m)}$, an equivalent stress in the subcell “m” defined below.

$$S_{oct}^{(m)}={\left\{{\displaystyle \frac{1}{2}}\left[{\left({\overline{S}}_{11}^{(m)}-{\overline{S}}_{22}^{(m)}\right)}^2+{\left({\overline{S}}_{22}^{(m)}-{\overline{S}}_{33}^{(m)}\right)}^2+{\left({\overline{S}}_{33}^{(m)}-{\overline{S}}_{11}^{(m)}\right)}^2\right]+3\left[{\left({\overline{S}}_{12}^{(m)}\right)}^2+{\left({\overline{S}}_{23}^{(m)}\right)}^2+{\left({\overline{S}}_{31}^{(m)}\right)}^2\right]\right\}}^{{\displaystyle \frac{1}{2}}}$$

(51)

It should be mentioned that the process used to solve the unknowns is gradual in nature. This implies that the process is carried out again until the variables of interest are identified at the desired time, and that the unknown variables are assessed gradually over time. However, a set of thirteen algebraic equations must be solved at each time step. The equations contain unknown variables: the stresses ${\overline{S}}_{11}^{(\lambda )}$, ${\overline{S}}_{22}^{(\lambda )}$, and ${\overline{S}}_{33}^{(\lambda )}$ (six unknowns); the microvariables ${\xi }_2^{(\lambda )}$ and ${\zeta }_3^{(\lambda )}$ (four unknowns); the average strains ${\overline{\epsilon }}_{11}$, ${\overline{\epsilon }}_{22}$, and ${\overline{\epsilon }}_{33}$ (three unknowns).

As previously stated, a relationship between the fiber’s stress in the representative unit cell and the average stress in the matrix is sought. It should be noted that Aboudi’s model [98,99] may oversimplify the actual situation by assuming that the neighbouring subcells of the representative unit cell (RUC) have equal average stresses. In practice, the unit cell’s two phases may experience differing average stresses and strains [100,101,102,103,104]. Generally speaking, the following relations can be used in the X₂ direction if the unidirectional composite is in a biaxial state of stress transverse to the fiber direction, specifically, in the (X₂, X₃) plane

$${\overline{S}}_{22}^{(f)}={\alpha }_f{\overline{\sigma }}_{22}, \mathrm{and}: {\overline{S}}_{22}^{(m)}={\alpha }_m{\overline{\sigma }}_{22},$$

(52)

or in a simplified form, the following relation is obtained:

$${\overline{S}}_{22}^{(f)}={\displaystyle \frac{{\alpha }_f}{{\alpha }_m}}{\overline{S}}_{22}^{(m)}.$$

(53)

Similarly, we obtain the following in the X₃ direction:

$${\overline{S}}_{33}^{(f)}={\displaystyle \frac{{\beta }_f}{{\beta }_m}}{\overline{S}}_{33}^{(m)}.$$

(54)

The concentration factors ${\alpha }_{\lambda }$ and ${\beta }_{\lambda }$ must be according to the following correlation:

$${\alpha }_f{v}_f+{\alpha }_m{v}_m=1,$$

(55)

and

$${\beta }_f{v}_f+{\beta }_m{v}_m=1.$$

(56)

If the composite is loaded in only one of the directions (X₂ or X₃), in the other direction, it can be written as follows:

$${\overline{S}}_{33}^{(f)}=-{\displaystyle \frac{v_m}{v_f}}{\overline{S}}_{33}^{(m)} , \mathrm{and} {\overline{S}}_{22}^{(f)}=-{\displaystyle \frac{v_m}{v_f}}{\overline{S}}_{22}^{(m)}.$$

(57)

3.3. Results and Real World Applications

Regarding the micromechanics analysis of the present study, the analysis is capable of modeling a unidirectional composite subjected to longitudinal and/or transverse normal loading. Usually, a finite element software is used to help determine the field of stress and strain. The constitutive material parameters, which are a function of time and temperature, are introduced into the model. Schapery’s nonlinear constitutive equation for isothermal uniaxial loading conditions is incorporated into the analysis to take into account the nonlinear viscoelastic behavior. From the numerous experimental results, several examples presented in this section demonstrate the potential application of the present method. For the triaxial stress state that is presented in the composite as a result of uniaxial loading, the equivalent stress from the matrix is considered so that all viscoelastic parameters are dependent on a single invariant. Poisson’s ratio turned out to be a very weak function of time or almost independent of time, an observation that greatly simplified the constitutive equation.

For example, there is a rich body of literature regarding creep behavior in ceramic matrix composites. A three-dimensional analysis of a viscoplastic matrix with progressive deterioration is presented for ceramic matrix composites subjected to creep [105]. The theoretical development followed the theory of Hill’s orthotropic plastic potential, and the temperature dependence was of the Arrhenius type. The results obtained were compared with the existing data in the literature, obtained from measurements. Micromechanical analysis was used for a complex application regarding the creep analysis of minicomposites with ceramic matrix [106]. Local stresses were high enough to cause microcracks in the matrix. In order to perform the analysis, the shear retardation of the fiber was considered. The creep response of the fiber was obtained using a linear Burgers model. One application was for a unidirectional SiCf/SiC minicomposite system for which experimental measurements were also made for validation. The global deformation of a composite material composed of a brittle matrix reinforced with long, continuous fibers is studied in [107]. The aim of the work is to determine the in-service behavior of composites with silicon carbide or oxide matrices. The experimental results confirm the efficiency of the model used in the study.

The study of unidirectional fiber-reinforced composites has been an intense field of study for researchers, probably mainly due to the possibility of an easier approach to calculations within the developed models. Thus, different models have been developed for different cases encountered in engineering practice. For example, the creep behavior that occurs in unidirectional fiber-reinforced metal matrix composites due to interface diffusion is studied in [108]. A micromechanical model is proposed for this material that provides results faster and with an accuracy comparable to the results obtained using FEM. A micromechanical model analysis for a composite made of elastic fibers reinforcing resin with viscoelastic but nonlinear behavior is performed in [109]. The viscoelastic behavior is expressed by Schapery’s relation. The fibers are made of graphite and reinforce epoxy resin. Creep tests conducted over a period of 8 h validate the model proposed by the authors. The inelastic response of a glass fiber epoxy composite (Vicotex NVE 913/28%/192/EC9756 300MM produced by HEXCEL Composites Ltd., Amityville, New York USA) is obtained, based on a micromechanical model, which builds on the micromodel proposed by Hashin [110]. Experimental verifications validate the theoretical ones in this case as well. The off-axis creep response of hybrid polymer matrix composites (HPMCs) reinforced with unidirectional carbon fibers and silica nanoparticles is predicted using a multi-step homogenization technique [111]. Assessing the viscoelastic characteristics of the silica nanoparticle–polymer nanocomposite is the first stage. In the second step, a unit cell-based micromechanical model is used to extract the off-axis viscoelastic behavior of HPMCs from the homogenized nanocomposite and carbon fiber properties. A novel micromechanics technique for forecasting the development of total creep strain under continuous applied stress and the transverse creep rate caused by interface diffusion in unidirectional fiber-reinforced composites is provided in [112]. Based on the applied stress, fiber volume percentage, fiber radius, and the modulus ratio between the fiber and the matrix, an analytical solution for the creep rate caused by interfacial diffusion is found. A detailed analysis of micromechanical models is carried out in [113].

The study of biomaterials is a field of interest at the moment due to ecological concerns and the recycling of the materials used. A major capability that models used for the study of biocomposites must possess is to capture material damage. Such a viscoelastic micromechanical creep model is developed in [114] and is applied to the analysis of wood-polymer composites affected by moisture. Composites obtained from recycled packaging are studied in [115], made from natural fibers and polyethylene. The influence of loading time, loading type, temperature, and fiber–matrix micromechanical bonding is studied. The study of creep for different types of new composite materials, used in various engineering applications, has been performed in dedicated studies for longitudinally reinforced titanium composites [116], atrix composites [117], carbon fiber-reinforced microcomposites reinforcing different types of matrix [118], powder metallurgy aluminum alloys [119], or particulate composites [120]. Various aspects of interest arising in the modeling of creep of fiber-reinforced composites can be found in [121,122,123,124,125,126,127,128,129].

3.4. Future Developments

Based on the literature in the field, extensively analyzed in the previous sections, the following development directions can be identified in the micromechanical analysis of the creep of fiber-reinforced composite materials:

• A combined approach of micromechanical models with different physical conditions can be considered. For example, thermal, mechanical, and environmental effects can be integrated. Additionally, behavior in high temperatures or corrosive environments can be considered. Thermal and chemical–mechanical coupling in the development of models can be an area of interest. Also, investigating the effect of residual thermal stresses on creep is a way forward.
• The complexity of engineering systems requires the incorporation of models of time-dependent interface behavior that explicitly account for interfacial creep and debonding mechanisms under long-term loading and consider the effect of interface strength degradation and damage evolution over time.
• It is also necessary to consider, for a better description of creep phenomena, the microstructural heterogeneity, including statistical distributions of different parameters defining the RUC as fiber orientation, volume fraction, and fiber–matrix geometry, and develop stochastic micromechanical models.
• The study of systems using multiscale approaches is a constant in current research in all engineering fields. It can be beneficial to use finite element-based micromechanics with continuum-level models to enable the accurate life predictions of composite components and use hierarchical modeling to bridge scales from a nano (e.g., fiber–matrix interface) to macro (component) level.
• Coupling micromechanical creep models with damage mechanics offers a better prediction in the initiation and growth of microcracks, fiber breaks, or matrix cavitation. At the same time, the simulation of creep rupture processes helps researchers to predict the time to failure under various stress levels.
• Using the specific properties and conditions of a material can provide information that helps develop more accurate models or provide results in a shorter time. This can be used to analyze applications such as turbine blades (ceramic matrix composites), automotive heat shields (metal matrix composites), and aerospace panels (polymer matrix composites).
• As in all fields, the use of machine learning is starting to become important in the field as well. It is possible to combine machine learning algorithms with micromechanical simulations to accelerate creep property predictions, use surrogate models trained on high-fidelity micromechanical simulations to explore large design spaces, or apply physics-informed neural networks (PINNs) to incorporate constitutive creep laws into ML models with physical constraints.

4. Analytical Methods

4.1. Estimation of Bound

Variational approaches that provide upper and lower bounds on the modulus of elasticity or other elastic constants (such as bulk modulus, shear modulus, Poisson’s ratio, etc.) are among the most often used techniques. The difference between the two limits indicates how accurate the estimates are in this method. Additionally, it can be detrimental for specific concentrations of the composite material’s phases. They are typically fairly imprecise and are derived for certain types of boundary conditions. The elastic constants for a polymeric material reinforced with parallel, cylindrical fibers arranged in a rectangular pattern are found in this presentation. The process is straightforward, and the desired values can be achieved for applications with high precision.

Numerous methods for predicting the constraints on the elastic/viscoelastic parameter of a multi-phase (or two-phase) composite are provided in the literature. The majority of the studies that have been conducted to evaluate the limits of the fiber-reinforced composite’s effective elastic/viscoelastic properties make the assumption that both phases exhibit isotropic material behavior. Scarce effort has been made in the literature to address situations where the reinforcing phase, for example, has anisotropic or transversally isotropic characteristics. An illustration of this would be a graphite/epoxy composite, in which the fiber exhibits anisotropic behavior, while the matrix material is thought to be isotropic.

Let us take a quick look at some of the approaches found in the literature to gain a better understanding of these issues. The problem of parallel fibers that are sufficiently long to allow for the disregard of end effects is taken into consideration while calculating the bounds on elastic/viscoelastic moduli. A cylindrical specimen with a much larger cross-section than the fiber cross-section might be used to illustrate the material. Since the fiber direction and the specimen’s longitudinal axis coincide, it may be assumed that the fiber runs continuously along the specimen’s length because end effects are disregarded.

Additionally, it is expected that the specimen is transversally isotropic and statistically homogeneous. Predicting the bound on an elastic/viscoelastic property of such a specimen based on its geometrical characteristics and the elastic/viscoelastic moduli of its constituents is the problem to be examined. Let us first assume that the two parts are linear and isotropic in order to illustrate the challenges of obtaining the constraints on the characteristic values of a composite using an analytical approach. Assume that the lower bounds of the bulk and shear moduli are represented by $K_{23}^{+}$ and $G_{23}^{+}$, respectively, and the upper bounds by $K_{23}^{-}$ and $G_{23}^{+}$.

It should be noted that the upper and lower bounds on the characteristic parameters are denoted by “+” and “−” upper indices in this section and the ones that follow, as in $E_{11}^{+}$, $E_{11}^{-}$, ${\nu }_{12}^{+}$, ${\nu }_{12}^{-}$. The aforementioned bounds can be predicted using a variety of methods found in the literature. The constraints on the bulk modules $K_{23}$, the longitudinal Young’s modulus $E_{11}$, and Poisson’s ratio ${\nu }_1={\nu }_{12}={\nu }_{13}$ can be obtained by applying Hill’s theory [130,131,132]. The volume ratios of fiber ${\nu }_f$ and matrix ${\nu }_m$ are used to calculate these bounds:

$$K_{23}^{+}={\displaystyle \frac{v_f{K}_f\left(K_m+G_m\right)+v_m{K}_m\left(K_f+G_f\right)}{v_f\left(K_m+G_f\right)+v_m\left(K_f+G_f\right)}}\hspace{1em};$$

(58)

$$K_{23}^{-}={\displaystyle \frac{v_f{K}_f\left(K_m+G_m\right)+v_m{K}_m\left(K_f+G_m\right)}{v_f\left(K_m+G_m\right)+v_m\left(K_f+G_m\right)}}\hspace{1em}.$$

(59)

In this relationship, the fiber and matrix phases are represented by the plane-strain bulk modulus $K_{\lambda }$ and the shear modulus $G_{\lambda }$, respectively, where $\lambda =f,m$ (fiber–matrix). These bounds are thought to be more striking than the traditional relationships proposed by Voigt (V) and Reuss (R), which are stated as follows:

$$K_{23}^{+}=K_V=v_f{K}_f+v_m{K}_m\hspace{1em},$$

(60)

and

$$K_{23}^{-}=K_R={\displaystyle \frac{1}{\frac{v_f}{K_f}+\frac{v_m}{K_m}}}\hspace{1em}.$$

(61)

The bulk modulus is

$$G_{23}^{+}=G_V=v_f{G}_f+v_m{G}_m\hspace{1em}$$

(62)

and

$$G_{23}^{-}=G_R={\displaystyle \frac{1}{\frac{v_f}{G_f}+\frac{v_m}{G_m}}}\hspace{1em},$$

(63)

is the shear modulus.

The Hill result for the longitudinal Young’s modulus E₁₁ is as follows:

$$E_{11}^{+}=E_{1mix}+{\displaystyle \frac{4{\left({\nu }_f-{\nu }_m\right)}^2{v}_m{v}_f}{\frac{v_f}{K_m}+\frac{v_m}{K_f}+\frac{1}{G_f}}},$$

(64)

$$E_{11}^{-}=E_{1mix}+{\displaystyle \frac{4{\left({\nu }_f-{\nu }_m\right)}^2{v}_m{v}_f}{\frac{v_f}{K_m}+\frac{v_m}{K_f}+\frac{1}{G_m}}}.$$

(65)

In these relations, $E_{1mix}$ represents the modulus calculated with the law of mixture, viz.,

$$E_{1mix}=v_f{E}_f+v_m{E}_m.$$

(66)

Finally, the bounds on Poisson’s ratio can be obtained via the following equations:

$${\nu }_1^{+}={\displaystyle \frac{{\nu }_{1mix}+\left({\nu }_f-{\nu }_m\right)\left(\frac{1}{K_m}-\frac{1}{K_f}\right)v_m{v}_f}{\frac{v_f}{K_m}+\frac{v_m}{K_f}+\frac{1}{G_f}}};$$

(67)

$${\nu }_1^{-}={\displaystyle \frac{{\nu }_{1mix}+\left({\nu }_f-{\nu }_m\right)\left(\frac{1}{K_m}-\frac{1}{K_f}\right)v_m{v}_f}{\frac{v_f}{K_m}+\frac{v_m}{K_f}+\frac{1}{G_m}}}.$$

(68)

In Equation (68), we have

$${\nu }_{1mix}=v_f{\nu }_f+v_m{\nu }_m.$$

(69)

An example showing some of these bounds is presented in Figure 4 and Figure 5.

In [99], Hashin used the followings relations for the bulk modulus $K_{23}$:

$$K_{23}^{+}=K_f+{\displaystyle \frac{{\nu }_m}{\frac{1}{K_m-K_f}+\frac{{\nu }_f}{K_f+G_f}}}\hspace{1em};$$

(70)

$$K_{23}^{-}=K_m+{\displaystyle \frac{{\nu }_f}{\frac{1}{K_f-K_m}+\frac{{\nu }_m}{K_m+G_m}}}\hspace{1em}.$$

(71)

For the share modulus, $G_{23}$ is obtained as follows:

$$G_{23}^{+}=G_f+{\displaystyle \frac{{\nu }_m}{\frac{1}{G_m-G_f}+\frac{{\nu }_f\left(K_f+2G_m)\right)}{2G_f\left(K_f+G_f\right)}}}\hspace{1em};$$

(72)

$$G_{23}^{-}=G_m+{\displaystyle \frac{{\nu }_f}{\frac{1}{G_f-G_m}+\frac{{\nu }_m(K_m+2G_m)}{2G_m(K_m+G_m)}}}\hspace{1em},$$

(73)

and, for the axial shear modulus, $G_1=G_{12}=G_{13}$.

$$G_1^{+}=G_f+{\displaystyle \frac{{\nu }_m}{\frac{1}{G_m-G_f}+\frac{{\nu }_f}{2G_f}}}\hspace{1em};$$

(74)

$$G_1^{-}=G_m+{\displaystyle \frac{{\nu }_f}{\frac{1}{G_g-G_m}+\frac{{\nu }_m}{2G_m}}}\hspace{1em}.$$

(75)

According to the results, there is a significant discrepancy between the bounds, which means that this formulation of the bounds cannot be very interesting from an engineering perspective.

It should be noted that not all five of the effective models needed for the characterization of the transversally isotropic composite can be produced using Hill’s [133,134,135,136] and Hashin’s [137,138,139,140,141] theories. Establishing all the relationships needed to derive the compliance matrix and, consequently, the time-dependent strain in a creep experiment is essential. The two phases of the composite are regarded as isotropic, which is another drawback of the aforementioned theories [142,143,144,145,146]. Keep in mind that the concentration of the two phases—rather than the shape of the reinforcing phase—is taken into account when calculating the aforementioned boundaries. As a result, it is reasonable to assume that these boundaries might occasionally differ significantly.

4.2. Mori–Tanaka Approach

The Mori–Tanaka theory is applied to determine the elastic/viscoelastic coefficients of the biphasic composite reinforced with long, anisotropic fibers [147]. The RUC(RVE) is used for this. It consists of a viscoelastic epoxy matrix reinforced with uniformly distributed, monotonically aligned, parallel fibers. In light of the aforementioned theory, the resulting composite is considered orthotropic. However, the composite body in question is considered transversely isotropic if the fibers of the elliptical cylinders are randomly oriented. The elliptical fibers are defined by the ratio (see Figure 6), which is 1 if the fibers are circular.

Zhao and Weng [148] combine Mori–Tanaka’s [147] mean-field theory with Eshelby’s [149] method for a cylindrical fiber with an elliptical section.

The two phases are regarded as isotropic materials in [150,151]. The fibers are thought to exhibit anisotropic behavior in our investigation. The current investigation’s contribution to the research of these materials for determining the elastic/viscoelastic constants for this kind of composite is represented by this method. In practical applications, it is especially crucial to obtain engineering constants that are as close to reality as possible. All of the elastic constants required to characterize an orthotropic material, especially those that are transversely isotropic, may be computed using the Mori–Tanaka method. By obtaining the creep curves, the compliance matrix may be constructed, enabling an experimental verification of the results.

Now, let us look at a two-phase composite reinforced with fibers evenly distributed throughout the matrix. We use (CM) to indicate a comparative material. Examine both the CM and the RVE, the actual composite, under the same boundary traction $\overline{\sigma }$. Boundary traction is a type of traction that is applied at the RVE’s end, or boundary surface. There is a traction $\overline{\sigma }$ observed since the loading condition for the RVE and the actual composite is the same. The matrix of elastic coefficients $C_m$ and the fiber’s elastic coefficients $C_f$ is used. It is clear that the average strain field in the matrix and the average strain in (CM), where the mean stress is $\overline{\sigma }$, are different under traction.

Consider $\tilde{\epsilon }$ the difference between the average values of the strain. Between the two kinds of material, there is a different mean stress $\tilde{\sigma }$. In CM, the relationship between the mean strain field ${\epsilon }^0$ and the mean stress field $\overline{\sigma }$ is as follows:

$$\overline{\sigma }=C_m{\epsilon }^0 .$$

(76)

The mean strain field in the composite is ${\epsilon }^m={\epsilon }^0+\overline{\epsilon }$ and the mean stress field is ${\sigma }^m=\overline{\sigma }+\tilde{\sigma }$. This results in

$${\sigma }^m=\overline{\sigma }+\tilde{\sigma }=C_m({\epsilon }^0+\overline{\epsilon }) .$$

(77)

The mean strain field in the fiber differs from that in the matrix through an additional term ${\epsilon }^{pt}$, so ${\epsilon }^f={\epsilon }^m+{\epsilon }^{pt}={\epsilon }^0+\tilde{\epsilon }+{\epsilon }^{pt}$. A similar mean stress field differs by the term ${\sigma }^{pt}$: ${\sigma }^f=\overline{\sigma }+\tilde{\sigma }+{\sigma }^{pt}$. The stress–strain is as follows:

$${\sigma }^f=\overline{\sigma }+\tilde{\sigma }+{\sigma }^{pt}=C_f({\epsilon }^0+\tilde{\epsilon }+{\epsilon }^{pt}) ,$$

(78)

or

$${\sigma }^f=\overline{\sigma }+\tilde{\sigma }+{\sigma }^{pt}=C_f({\epsilon }^0+\tilde{\epsilon }+{\epsilon }^{pt})=C_m({\epsilon }^0+\tilde{\epsilon }+{\epsilon }^{pt}-{\epsilon }^{\ast }) ,$$

(79)

with

$${\epsilon }^{pt}=P{\epsilon }^{\ast } .$$

(80)

P is the Eshelby’s transformation tensor, where the symmetry property P_ikjl = P_jikl = P_ijtk is valid [139].

The average stress in the whole RVE is as follows:

$$\begin{array}{l}\overline{\sigma }=v_f{\sigma }_f+v_m{\sigma }_m=v_f(\overline{\sigma }+\tilde{\sigma }+{\sigma }^{pt})+v_m(\overline{\sigma }+\tilde{\sigma })\\ =(v_f+v_m)\overline{\sigma }+(v_f+v_m)\tilde{\sigma }+v_f{\sigma }^{pt}=\overline{\sigma }+\tilde{\sigma }+v_f{\sigma }^{pt}\end{array} .$$

(81)

reduced to

$$\tilde{\sigma }=-v_f{\sigma }^{pt} .$$

(82)

For the strain, a similar procedure offers the follows:

$$\overline{\epsilon }=-v_f({\epsilon }^{pt}-{\epsilon }^{\ast })=-v_f(P{\epsilon }^{\ast }-{\epsilon }^{\ast })=-v_f(P-I){\epsilon }^{\ast } .$$

(83)

Here, I is denoted as the unit tensor.

Substituting Equation (83) into Equation (79), we have

$$C_f\left[{\epsilon }^0-v_f\left(P-I\right){\epsilon }^{\ast }+P{\epsilon }^{\ast }\right]=C_m\left[{\epsilon }^0-v_f\left(P-I\right){\epsilon }^{\ast }+P{\epsilon }^{\ast }-{\epsilon }^{\ast }\right] .$$

(84)

After some calculus, this is reduced to

$$\left[C_f\left(-v_f\left(P-I\right)+P\right)+C_m\left(v_f\left(P-I\right)-P+I\right)\right]{\epsilon }^{\ast }+\left(C_f-C_m\right){\epsilon }^0=0 .$$

(85)

and finally, it is reduced to

$$\left[\left(C_f-C_m\right)\left(v_{m}P+v_{f}I\right)+C_m\right]{\epsilon }^{\ast }+\left(C_f-C_m\right){\epsilon }^0=0 .$$

(86)

Using Equation (80), we have

$$\begin{array}{l}{\epsilon }_{11}^{\ast }={\displaystyle \frac{1}{A}}\left(A_{11}{\epsilon }_{11}^0+A_{12}{\epsilon }_{22}^0+A_{13}{\epsilon }_{33}^0\right)\hspace{1em};\hspace{1em}\\ {\epsilon }_{22}^{\ast }={\displaystyle \frac{1}{A}}\left(A_{21}{\epsilon }_{11}^0+A_{22}{\epsilon }_{22}^0+A_{23}{\epsilon }_{33}^0\right)\hspace{1em};\\ {\epsilon }_{33}^{\ast }={\displaystyle \frac{1}{A}}\left(A_{31}{\epsilon }_{11}^0+A_{32}{\epsilon }_{22}^0+A_{33}{\epsilon }_{33}^0\right)\hspace{1em}.\end{array}$$

(87)

where $A_{ij}$ can be found in literature (i.e., [139]). Considering the definitions for the shear strain, the following is obtained [139]:

$$\begin{gathered} {\epsilon }_{12}^{\ast }={\displaystyle \frac{\left(G_{12,f}-G_m\right)}{\left(G_{12,f}-G_m\right)\left(2v_m{P}_{1212}+v_f\right)+G_m}}{\epsilon }_{12}^0; \\ {\epsilon }_{23}^{\ast }={\displaystyle \frac{\left(G_{23,f}-G_m\right)}{\left(G_{23,f}-G_m\right)\left(2v_m{P}_{2323}+v_f\right)+G_m}}{\epsilon }_{23}^0; \\ {\epsilon }_{31}^{\ast }={\displaystyle \frac{\left(G_{31,f}-G_m\right)}{\left(G_{31,f}-G_m\right)\left(2v_m{P}_{3131}+v_f\right)+G_m}}{\epsilon }_{31}^0. \end{gathered}$$

(88)

We subject the examined composite and the comparison material to a pure traction ${\overline{\sigma }}_{11}$ in order to calculate the longitudinal Young’s modulus $E_m$ of an orthotropic body. Then, it follows that ${\overline{\sigma }}_{11}=E_{11}{\overline{\epsilon }}_{11}$ for the composite and ${\overline{\sigma }}_{11}=E_m{\overline{\epsilon }}_{11}^0$; ${\overline{\epsilon }}_{22}^0={\overline{\epsilon }}_{33}^0=-{\nu }_m{\overline{\epsilon }}_{11}^0$ if the comparison material is considered.

Equation (87) offers th following:

$$\begin{array}{l}{\overline{\epsilon }}_{11}={\overline{\epsilon }}_{11}^0+v_f{\overline{\epsilon }}_{11}^{\ast }={\overline{\epsilon }}_{11}^0+v_f\left({\displaystyle \frac{A_{11}}{A}}{\overline{\epsilon }}_{11}^0+{\displaystyle \frac{A_{12}}{A}}{\overline{\epsilon }}_{22}^0+{\displaystyle \frac{A_{13}}{A}}{\overline{\epsilon }}_{33}^0\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\overline{\epsilon }}_{11}^0\left(1+v_f{a}_{11}\right)-v_f{a}_{12}{v}_m{\overline{\epsilon }}_{11}^0-v_f{a}_{13}{v}_m{\overline{\epsilon }}_{11}^0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\overline{\epsilon }}_{11}^0\left[1+v_f\left[a_{11}-v_m\left(a_{12}+a_{13}\right)\right]\right]\end{array}.$$

(89)

Here, $a_{ij}=A_{ij}/A$, with $A_{ij}$ and $A$ defined in [139].

This results in

$$E_{11}={\displaystyle \frac{{\overline{\epsilon }}_{11}^0}{{\overline{\epsilon }}_{11}}}{E}_m={\displaystyle \frac{E_m}{1+v_f\left[a_{11}-v_m\left(a_{12}+a_{13}\right)\right]}} .$$

(90)

For the other directions, similarly, we obtain the following results for Young’s moduli:

$$E_{22}={\displaystyle \frac{{\overline{\epsilon }}_{22}^0}{{\overline{\epsilon }}_{22}}}{E}_m={\displaystyle \frac{E_m}{1+v_f\left[a_{22}-v_m\left(a_{21}+a_{23}\right)\right]}} .$$

(91)

and

$$E_{33}={\displaystyle \frac{{\overline{\epsilon }}_{33}^0}{{\overline{\epsilon }}_{33}}}{E}_m={\displaystyle \frac{E_m}{1+v_f\left[a_{33}-v_m\left(a_{31}+a_{32}\right)\right]}} .$$

(92)

The shear moduli can be obtained using the following relations:

$${\overline{\sigma }}_{12}=2G_{12}{\overline{\epsilon }}_{12\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{\sigma }}_{12}=2G_m{\overline{\epsilon }}_{12}^0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} .$$

(93)

Recall that

$${\overline{\epsilon }}_{12}={\overline{\epsilon }}_{12}^0+v_f{\overline{\epsilon }}_{12}^{\ast }={\epsilon }_{12}^{\ast }-v_f{\displaystyle \frac{G_{12,f}-G_m}{\left(G_{12,f}-G_m\right)\left(2v_m{P}_{1212}+v_f\right)+G_m}}{\epsilon }_{12}^0 .$$

(94)

From Equation (93), $G_{12}$ is obtained as follows:

$$G_{12}=G_m\left(1+{\displaystyle \frac{v_f}{\frac{G_m}{G_{12,f}-G_m}+2v_m{P}_{1212}}}\right) .$$

(95)

In the same way, we have

$$G_{23}=G_m\left(1+{\displaystyle \frac{v_f}{\frac{G_m}{G_{23,f}-G_m}+2v_m{P}_{2323}}}\right).$$

(96)

and

$$G_{31}=G_m\left(1+{\displaystyle \frac{v_f}{\frac{G_m}{G_{31,f}-G_m}+2v_m{P}_{3131}}}\right).$$

(97)

For Poisson’s ratio, classic relations are used:

$${\overline{\epsilon }}_{22}=-v_m{\overline{\epsilon }}_{11}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{\epsilon }}_{22}^0=\hspace{0.17em}{\overline{\epsilon }}_{33}^0=-v_m{\overline{\epsilon }}_{11}^0\hspace{0.17em} .$$

(98)

where

$$\begin{array}{l}{\overline{\epsilon }}_{11}={\overline{\epsilon }}_{11}^0+v_f{\overline{\epsilon }}_{11}^{\ast }={\overline{\epsilon }}_{11}^0+v_f{a}_{11}{\overline{\epsilon }}_{11}^0+v_f{a}_{12}{\overline{\epsilon }}_{22}^0+v_f{a}_{13}{\overline{\epsilon }}_{33}^0\\ ={\overline{\epsilon }}_{11}^0\left(1+v_f{a}_{11}\right)+v_f{a}_{12}{\overline{\epsilon }}_{22}^0+v_f{a}_{13}{\overline{\epsilon }}_{33}^0\end{array} .$$

(99)

We obtain

$${\overline{\epsilon }}_{22}={\overline{\epsilon }}_{22}^0+v_f{\overline{\epsilon }}_{22}^{\ast }=v_f{a}_{21}{\overline{\epsilon }}_{11}^0+{\overline{\epsilon }}_{22}^0\left(1+v_f{a}_{22}\right)+v_f{a}_{23}{\overline{\epsilon }}_{33}^0 .$$

(100)

and this results in

$$\begin{array}{l}{\overline{\epsilon }}_{11}=\left[\left(1+v_f{a}_{11}\right)-v_f{a}_{12}{v}_m-v_f{a}_{13}{v}_m\right]{\overline{\epsilon }}_{11}^0\\ =\left[v_f{a}_{21}-v_m\left(1+v_f{a}_{22}\right)-v_m{v}_f{a}_{23}\right]{\overline{\epsilon }}_{11}^0\end{array} .$$

(101)

Now, using Equation (87), we have

$$v_{12}=-{\displaystyle \frac{{\overline{\epsilon }}_{22}}{{\overline{\epsilon }}_{11}}}=-{\displaystyle \frac{v_f{a}_{21}-v_m\left(1+v_f{a}_{22}\right)-v_m{v}_f{a}_{23}}{1+v_f{a}_{11}-v_f{a}_{12}{v}_m-v_f{a}_{13}{v}_m}} .$$

(102)

or

$$v_{12}={\displaystyle \frac{v_m-v_f\left[a_{22}-v_m\left(a_{21}+a_{23}\right)\right]}{1+v_f\left[a_{11}-v_m\left(a_{12}+a_{13}\right)\right]}} .$$

(103)

In a similar way, the following is obtained:

$$v_{23}={\displaystyle \frac{v_m-v_f\left[a_{22}-v_m\left(a_{21}+a_{23}\right)\right]}{1+v_f\left[a_{33}-v_m\left(a_7+a_8\right)\right]}} .$$

(104)

and

$$v_{31}={\displaystyle \frac{v_m-v_f\left[a_{33}-v_m\left(a_{31}+a_{32}\right)\right]}{1+v_f\left[a_{11}-v_m\left(a_{12}+a_{13}\right)\right]}} .$$

(105)

This study presents a method that uses uniquely determined values to provide the elastic/viscoelastic constants of the composite. The bounded methods that are often employed to determine these values provide the lower and upper bounds. The method’s uniqueness depends on the fibres’ anisotropy or transverse isotropy behavior. Schapery’s constitutive equation [80] is used to assess the material’s temporal response.

4.3. Results and Applications (Mori-Tanaka Theory)

Numerous works have addressed the problem of determining elastic constants using analytical boundary methods. Particular loading situations of RVE were sought in which stress and strain could be determined, and stress energy or strain energy was calculated. By comparing with the exact values of these quantities, upper or lower limits of the elastic constants were determined. Additionally, numerous studies have used these results for the study of certain new materials.

An example of using the method to determine the physical properties of a composite is presented in [152]. The fibers are considered to be uniform. A comparison with other methods used shows that the inner and upper edges are the best estimate provided, even if not spectacular, so the method proves to be useful. A phenomenological–mechanistic model is used to study the strength of fiber-reinforced composite beams [153]. A composite panel is composed of thin transversely isotropic layers (laminas). Each of the laminae is composed of unidirectional layers. The predictions obtained follow the experimental load–strain curves in four-point bending until the failure process begins to dominate.

A study of the influence of microstructural parameters in the case of composites is described in [154]. The stiffness moduli of composites are determined as a function of fiber orientation and under arbitrary loading conditions. Compared to micromechanical theories, the method proves to be more practical for predicting the stiffness modulus of fiber composites in terms of accuracy and simplicity. Some studies [155,156,157,158,159] apply analytical methods to determine upper and lower bounds of elastic constants for various engineering applications. Two different approaches to the study of unidirectional composites are presented in [160]. The stress concentration factors around broken fibers in a three-dimensional model with a hexagonal matrix are determined by the two methods. Parametric studies are first performed, and the results are compared with experiments and other existing theories. A 3D finite element model for predicting damage initiation, propagation, and fracture toughness of TC33/epoxy unidirectional carbon fiber-reinforced polymer (CFRP) laminates under biaxial loading is developed in [161]. The carbon fibers are assumed to be linearly elastic, and the matrix is considered to have an elastoplastic behavior defined by the extended Drucker–Prager plastic yielding model. An analytical determination of the out-of-plane modulus of thin QI-CFRP specimens is made using a modified form of three-dimensional laminate theory [162]. The modulus calculated in this way is the lower bound of the apparent bending moduli, and that calculated with three-dimensional laminate theory is the upper bound.

The Mori–Tanaka method has proven to be a very efficient method for estimating elastic constants. A confirmation is the rich literature that uses this method and the engineering applications that apply it in design calculations. Some significant contributions that used the method are presented below. For glass-reinforced polyvinyl chloride (PVC) plastics, the Mori–Tanaka method is used, and the results are compared with 3D numerical calculations for creep deformation and creep failure [163]. The comparison validates the Mori–Tanaka model as a practical tool to predict the effect of fiber length and fiber volume fraction on creep deformation and creep failure. A composite reinforced with short fibers, differently oriented in the matrix, is studied to determine the creep behavior [164]. The fibers are assumed to have the same length. According to the Mori–Tanaka mean field theory, and considering that the effect of an imperfect interface can be expressed by a modified Eshelby tensor, the effect of the weakened interface on the creep behavior for a nearly unidirectional composite is determined.

The Mori–Tanaka method has been analyzed and used in numerous applications [165,166,167,168,169]. The linear elastic behavior of fiber-reinforced concrete (FRC) is studied by the Mori–Tanaka homogenization method [170]. The estimates obtained for the overall stiffness are very close to the solutions obtained by applying FEM. The validity of the model is achieved by comparison with the experimentally obtained values in the literature. A model for determining the elastic constants of particulate polymer composites, especially for high volume concentrations, is described in [171]. The model also includes the interaction between two elementary particles. The effective creep compliance and the constitutive law at a constant loading rate are estimated. The results are compared with those obtained with the Mori–Tanaka method. A new homogenization model, which uses the viscoelastic constitutive law with an Eshelby micromechanical model and incremental Mori–Tanaka schemes for large volume fractions, is proposed in [172]. The model is intuitive and simple and is verified by direct numerical simulation and experimental DMA (dynamic mechanical analysis) results. It can thus be used for multiscale analysis of viscoelastic composite materials. An estimation of the properties of a short fiber-reinforced composite with complex fiber orientation and stochastically weakened interfaces using the mean field theory developed by Mori–Tanaka is presented in [173]. For certain loading cases, an inadequate distribution of fiber orientation can lead to a quantitative deterioration of the creep behavior. Other interesting results regarding the application of the Mori–Tanaka method are given in [174,175,176,177,178,179,180,181,182].

4.4. Future Development

Further developments in the field of fibrous composite materials studied using the Mori–Tanaka method and bounding methods (e.g., Hashin–Shtrikman bounds, Voigt–Reuss bounds) could span several key areas, particularly given the ongoing advances in multiscale modeling, materials design, and computational tools. The most promising directions are enumerated in the following:

• Using machine learning (ML) models to integrate the Mori–Tanaka formalism to predict effective properties from microstructural data more efficiently is one of the directions. In this way, ML can help to approximate the results of computationally expensive simulations for real-time design.
• Multiscale and multi-physics modeling represents an important future direction of development. This means a coupling between FEA and micromechanics to develop extended models for composites subjected to coupled physical fields (e.g., piezoelectric fibrous composites, magnetoactive polymers).
• Time-dependent and nonlinear behavior represent important aspects that must be incorporated into the models. Extended models must be developed to account for time-dependent responses in polymer matrix composites. Another aspect is the damage and failure modelling: combining Mori–Tanaka with continuum damage mechanics or phase-field models for progressive failure predictions.
• The bounded model remains important in design due to its simplicity. Enhanced bounding methods can be used for complex microstructures tailored to composites with more irregular, graded, or hierarchical structures.
• Bioinspired and smart composites with bioinspired fiber architectures or self-healing composites using modified homogenization schemes have a large field of application. More nuanced field interaction will be used in modeling smart composites.
• Another direction is represented by experimental validation and digital twins, combining homogenization methods with digital materials testing (e.g., X-ray CT + FEM) for real-time feedback and validation.

5. Homogenized Viscoelastic Coefficients

5.1. General Considerations in Homogenization

The basic idea of the homogenization theory is to model the behavior of the complex microstructure (usually a repetitive structure) of the composite so as to obtain a homogeneous material having equivalent macroscopic properties. Because composite materials frequently feature intricate microstructures (such as fibers embedded in a matrix), and because it is computationally costly or impractical to directly simulate every detail at large scales, it is crucial for modeling composites. A material that is essentially inhomogeneous but is constituted at the microstructure level by identical, repetitive, or certain symmetries is considered homogeneous and respects the theory of elasticity as a whole, exactly as a homogeneous material. Practically, the homogenization theory is a mathematical method to average the mechanical and physical properties of an inhomogeneous material. Currently, homogenization theory is used in numerous engineering applications to determine the properties of a body considered as a solid composed of a homogeneous material. This mathematical theory’s foundations are laid out in [183,184,185,186,187,188]. By considering the characteristics of both the fibers (which may be strong and stiff) and the matrix (which may be more flexible), homogenization theory would assist in determining the overall stiffness and strength of a fiber-reinforced composite material, such as glass fibers embedded in a polymer matrix. Homogenization enables an averaged material description that streamlines the analysis while preserving the fundamental behavior of the composite, as opposed to modeling each individual fiber and its interaction with the matrix. Predicting the mechanical, thermal, or electrical behavior of composite materials is frequently performed using homogenization. In structural, automotive, and aerospace engineering, for example, it aids in forecasting the stiffness, strength, deformation, and creep behavior of fiber-reinforced composites. This approach aims to generate macroscopic constitutive equations that combine the influence of microstructural characteristics on the creep response of the material and characterize the overall behavior of the composite.

5.2. The Homogenized Method

One benefit of the homogenization theory is that it makes it possible to investigate differential equations with coefficients that vary quickly or periodically. After averaging procedures, engineering constants (which are helpful in engineering practice) are produced. As a result, a material with a periodic structure can be considered homogeneous. Thus, an equation with constant coefficients is used in the modeling instead of a differential equation with periodic coefficients that vary greatly. This is how microstructured materials (composite materials are also included in this class) are included in the continuum notion. In this section, the creep response of a unidirectional composite reinforced with fibers is examined using a computational approach. The classic presentation of the homogenization method developed by Sanchez Palencia [183] (Figure 7).

Considering the valuable hypothesis from the theory of elasticity, the stress tensor ${\sigma }^{\delta }$ for a repeating unit cell (RVE) that forms the composite of size $\delta$ must satisfy the classic equations:

$$\begin{gathered} {\displaystyle \frac{\partial {\sigma }_{11}^{\delta }}{\partial x_1}}+{\displaystyle \frac{\partial {\tau }_{12}^{\delta }}{\partial x_2}}+{\displaystyle \frac{\partial {\tau }_{13}^{\delta }}{\partial x_3}}=f_1(x); \\ {\displaystyle \frac{\partial {\tau }_{21}^{\delta }}{\partial x_1}}+{\displaystyle \frac{\partial {\sigma }_{22}^{\delta }}{\partial x_2}}+{\displaystyle \frac{\partial {\tau }_{23}^{\delta }}{\partial x_3}}=f_2(x); \\ {\displaystyle \frac{\partial {\tau }_{31}^{\delta }}{\partial x_1}}+{\displaystyle \frac{\partial {\tau }_{32}^{\delta }}{\partial x_2}}+{\displaystyle \frac{\partial {\sigma }_{33}^{\delta }}{\partial x_3}}=f_3(x), \end{gathered}$$

(106)

The tensor is symmetric, so ${\sigma }_{ij}^{\delta }={\sigma }_{ji}^{\delta }$, for $i,j=1,2,3$.

The contour conditions that the displacements must satisfy are as follows:

$${\left.u^{\delta }\right|}_{{\partial }_1\Omega }=\tilde{u} .$$

(107)

The boundary conditions on contour ${\partial }_2\Omega$, (${\partial }_1\Omega \cup {\partial }_2\Omega =\partial \Omega$) of the RVE are as follows:

$$\begin{gathered} {\sigma }_{11}^{\delta }{n}_1+{\tau }_{12}^{\delta }{n}_2+{\tau }_{13}^{\delta }{n}_3=T_1(x); \\ {\tau }_{21}^{\delta }{n}_1+{\sigma }_{22}^{\delta }{n}_2+{\tau }_{23}^{\delta }{n}_3=T_2(x); \\ {\tau }_{31}^{\delta }{n}_1+{\tau }_{32}^{\delta }{n}_2+{\sigma }_{33}^{\delta }{n}_3=T_3(x). \end{gathered}$$

(108)

The Hook’s Law has the following form:

$${\left\{\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\tau }_{23}\\ {\tau }_{31}\\ {\tau }_{12}\end{array}\right\}}^{\delta }=\left[\begin{array}{cccccc}{C}_{1111}& C_{1122}& C_{1133}& & & \\ C_{2211}& C_{2222}& C_{2233}& & 0& \\ C_{3311}& C_{3322}& C_{3333}& & & \\ & & & C_{2323}& & \\ & 0& & & C_{3131}& \\ & & & & & C_{1212}\end{array}\right]{\left\{\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ {\gamma }_{23}\\ {\gamma }_{31}\\ {\gamma }_{13}\end{array}\right\}}^{\delta }.$$

(109)

or,

$${\sigma }^{\delta }=C{\epsilon }^{\delta } .$$

(110)

Using the averaging methods, these coefficients are obtained. The method to obtain is presented in [139,189]. It results in two ways to obtain these coefficients:

• Using the local equations, the strain and stress field, and the averages are determined, obtaining the homogenized coefficients after averaging;
• Using the variational formulation and determining a special function w^kh that can also help us determine the homogenized coefficients.

In the first way, the field of stress and strain should be obtained. Rarely can the exact stress and strain field be determined, and therefore, a numerical method must be applied to obtain these data. The most commonly used method in application is the finite element method (FEM).

5.3. Results and Applications

The homogenization method has been used extensively since the beginning to determine the creep behavior of unidirectional composites reinforced with continuous fibers. We will show that there are two main methods of using the method, one involving the determination of the real stress and strain field for an RVE and then averaging the property values, and the second using a variational method. The first method is applied in [189], where FEM is used to determine the stresses and strains. It is considered that the constituent fiber is an isotropic linear elastic material and that the matrix is isotropic linear elastic and nonlinear viscoelastic. The results obtained with these calculations for determining the creep behavior are validated with experimental results. Other results using the classical homogenization theory for the analysis of a composite reinforced with carbon fibers, together with experimental tests to validate the results, are presented in [190]. Creep analysis of polymer matrix composites using homogenization theory for time-dependent nonlinear composites is presented in [191]. Studies on carbon fiber-reinforced plastic (CFRP) laminates and glass fiber-reinforced plastic (GFRP) laminates have also been conducted. Experimental validation is obtained on uniaxially loaded specimens. The use of a homogenization method using Eshelby tensors is presented in [192] and enables the calculation of the creep of fiber composites. The micromechanical model is validated through comparison with experimentally obtained data on the flow of the studied material. The conclusion obtained in the study is that the creep of fiber-reinforced composites can be adapted by an appropriate design.

Fiber-reinforced concrete is modeled as an aged linear viscoelastic composite material reinforced with ellipsoidal inclusions embedded in a viscoelastic cement matrix in [193]. The time-dependent deformations of the concrete are validated with experimental measurements.

In [194], a multi-stage homogenization is performed for a hybrid composite with a polymer matrix reinforced with unidirectional carbon fibers together with silica nanoparticles. After determining the viscoelastic behavior of the silica nanoparticles, a classical micromechanical model is used to analyze the composite, using the homogenization method. The results are in agreement with the experimental determinations made in the paper. Homogenization methods are designed to improve the viscoelastic properties of a randomly oriented chopped glass fiber-reinforced plastic in [195]. Notably, 3D numerical calculations for creep deformations are used. The conclusion obtained is that for a given creep load, the material life increases with increasing fiber volume fraction. The thermomechanical tensile and creep behavior of PEEK 7002/carbon fiber composites in tensile and creep tests, presented in [196], uses a multiscale approach. The study shows a similarity of behavior between the polymer and the composites. An algorithm is proposed to perform such an analysis. A multiscale optimization method for a composite material is presented in [197]. The paper aims to establish the composition of short fiber-reinforced polymer (SFRP) materials that will exhibit a desired behavior in service (mechanical properties to meet the requirements of the manufacturer). The paper illustrates the procedures followed in such an enterprise, which is also described in the paper.

Different applications have been addressed for different types of resin and reinforcement materials, with the homogenization theory proving its power in obtaining correct and useful results. Thus, the influence of boundary conditions on carbon-fiber-reinforced polymer [198], the creep behavior of long and short fiber-reinforced viscoelastic composites [199], homogenization models for multiscale problems for linearly viscoelastic 3D interlock woven composites [200], the anisotropic mechanical behavior of short fiber-reinforced composite [201] or long fiber-reinforced composite [202] or current engineering applications, such as the use of Ti-based matrix composites reinforced by SiC fibres [203], were studied. The different types of composite materials used in real-world applications have also led to numerous models obtained by applying mathematical methods of homogenization [204,205,206,207,208,209,210,211].

Within fiber-reinforced composites, there can be different constructive solutions. For those reinforced with short fibers, the local fiber orientation has a strong influence on the physical/mechanical properties. In [212], a two-step methodology is used to develop a suitable model: first, for a series of sample orientations, a numerical model known in the literature is used. Then, to describe a general orientation state, these effective models are interpolated. Symmetry considerations reduce the fiber orientation cases by half. The method is applied to analyze the viscoelastic creep behavior of a PA66 material reinforced with short glass fibers [213]. Multiscale models have proven their effectiveness in the analysis of composite materials. The behavior of the material at the macroscale is determined by the behavior of the components at the microscale and the environmental factors and loading conditions [214,215,216,217,218].

There are many other situations where composite materials are used, with different geometric structures and different materials, in different environmental conditions, with different loads, subjected to long-term stresses that require creep studies. Some of them are presented in [219,220,221,222,223,224].

5.4. Future Developments in Homogeniuzation

Advances in materials science, computer tools, and multiscale modeling methodologies are driving a rapid evolution in the future of homogenization methods used to investigate creep behavior in composites. The following are the most prominent directions of development in future studies:

• A multiscale or multi-physics modeling approach, a widely used type of analysis, can be considered due to its existing computational possibilities. Currently, directions necessary in current engineering applications are being pursued, such as developing homogenization frameworks (for coupled phenomena, such as thermomechanical, viscoelastic/viscoplastic interactions or damage); coupling creep with oxidation, thermal gradients, and phase transformation; embedding microstructural evolution during creep (grain growth, void formation); or capturing interface behavior and its evolution (e.g., fiber–matrix debonding).
• Further development of numerical calculation methods includes FE2 (finite element squared), applying reduced order modeling (ROM) to reduce high computational costs, incorporating time-dependent behavior (creep laws) into microscale FE models and using adaptive methods to reduce the number of representative volume elements and therefore the dimension of the system [189,190,191,192,193,194].
• ML and AI can be used to accelerate the homogenization process using ML-based constitutive models that can evolve with damage and time. This results in a real-time prediction of creep properties from microstructure descriptors. ML can replace or accelerate homogenization processes. Instead of solving the RVE repeatedly, an ML model is trained on pre-computed data to instantly predict effective creep properties.
• Existing homogenization methods should be developed to adapt to creep strain evolution and introduce new internal variables such as creep strain, damage, and history-dependent responses.
• Recognizing the fact that the microstructure of composites is often non-deterministic, stochastic homogenization can be introduced in analysis to quantify uncertainty in creep life prediction. Spectral or Monte Carlo methods can be used to simulate the variability in the distribution of phases in a composite.
• High-resolution experimental data (micro-CT, SEM) can be directly integrated into homogenization. So, using digital volume correlation (DVC), it is possible to validate the creep strain field at different scales, and through direct 3D scans, it is possible to build RVEs directly and introduce them in numerical analysis.
• One important direction of study is the micro-damage evolution (cracking and fiber breakage) within homogenization schemes.

All these research method developments have wide applicability in CFRPs and GFRPs (aerospace and automotive under high-temperature applications); C/composites, where creep is important in thermal protection systems; metal matrix composites (MMCs) (for high-temp structural uses); and ceramic matrix composites (CMCs). Here, creep and damage are tightly coupled. Validation of the homogenized methods is performed by comparing the values obtained by applying this method with the values obtained by experimental procedures. This is carried out in the paper reviewed in the next section.

By reducing the system to an equivalent homogeneous material, homogenization theory in composite materials enables scientists and engineers to understand and forecast the behavior of complicated multi-phase materials. This method is crucial for improving composites’ performance and design in a range of technical applications.

6. Finite Element Method

6.1. FEM Used to Determine the Field of Strain and Stress in a RUC

The FEM is a powerful tool to study the response of a composite materials [225,226,227,228,229,230,231]. We do not insist on presenting the basics of the method. FEM is instead presented in conjunction with the study of composites (Figure 8).

Consider an FE model where the boundary conditions are taken as $u_i={\alpha }_{ij}{x}_j$ (where ${\alpha }_{ij}={\alpha }_{ji}$). The average strains computed for such behavior of the material are ${\overline{\epsilon }}_{ij}={\alpha }_{ij}$. This results in the following:

$${\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{V}}{\displaystyle {\int }_{\mathrm{\Gamma }}{\epsilon }_{ij}dV=}{\displaystyle \frac{1}{2V}}{\displaystyle {\int }_{\mathrm{\Gamma }}\left(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j}\right)dV}.$$

(111)

Using Green’s theorem, we have

$$\begin{gathered} {\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{2V}}{\displaystyle {\int }_{\partial \hspace{0.17em}\mathrm{\Gamma }}\left(n_i{u}_j+n_j{u}_i\right)ds}= \\ ={\displaystyle \frac{1}{2V}}\left({\displaystyle {\int }_{\partial \hspace{0.17em}\mathrm{\Gamma }}{n}_i{\alpha }_{jk}{x}_{k}ds}+{\displaystyle {\int }_{\partial \hspace{0.17em}\mathrm{\Gamma }}{n}_j{\alpha }_{il}{x}_{l}ds}\right)= \\ ={\displaystyle \frac{1}{2V}}\left({\alpha }_{jk}{\displaystyle {\int }_{\partial \hspace{0.17em}\mathrm{\Gamma }}{n}_i{x}_{k}ds}+{\alpha }_{il}{\displaystyle {\int }_{\partial \hspace{0.17em}\mathrm{\Gamma }}{n}_j{x}_{l}ds}\right). \end{gathered}$$

(112)

In our case, it can be written as follows:

$$\begin{gathered} {\overline{\epsilon }}_{ij}={\displaystyle \frac{1}{2V}}\left({\alpha }_{jk}{\displaystyle {\int }_{\hspace{0.17em}\mathrm{\Gamma }}\frac{\partial x_k}{\partial x_i}dV}+{\alpha }_{il}{\displaystyle {\int }_{\hspace{0.17em}\mathrm{\Gamma }}\frac{\partial x_l}{\partial x_j}dV}\right)= \\ ={\displaystyle \frac{1}{2V}}\left({\alpha }_{jk}{\displaystyle {\int }_{\hspace{0.17em}\mathrm{\Gamma }}{\delta }_{ki}dV}+{\alpha }_{il}{\displaystyle {\int }_{\hspace{0.17em}\mathrm{\Gamma }}{\delta }_{lj}dV}\right)={\displaystyle \frac{1}{2V}}\left({\alpha }_{ji}+{\alpha }_{ij}\right)={\alpha }_{ij} \end{gathered}$$

(113)

The FEM can be used to obtain average values of strains and stresses, viz. ${\overline{\sigma }}_{22},{\overline{\sigma }}_{33},{\overline{\sigma }}_{11},{\overline{\sigma }}_{23}={\overline{\tau }}_{23},{\overline{\epsilon }}_{22},{\overline{\epsilon }}_{33},{\overline{\epsilon }}_{11},{\overline{\epsilon }}_{23}=1/2\hspace{0.17em}{\gamma }_{23}$, considering the case of plane strain. Using these averages, the constants of the unidirectional composite can be evaluated. The rule of mixture is applied. To obtain the longitudinal elastic modulus $E_{11}$, the rule of the mixture is used:

$$E_{11}=E_f{\nu }_f+E_m{\nu }_m$$

(114)

where

$${\nu }_f={\displaystyle \frac{A_f}{A}}\hspace{1em};\hspace{1em}{\nu }_f={\displaystyle \frac{A_m}{A}}\hspace{1em},$$

(115)

and $A=A_f+A_m$. $A_f$ is denoted as the cross-section of the fiber, and $A_m$ is the cross-section of the matrix.

In the plane strain case, the constitutive law is considered:

$$\begin{gathered} {\overline{\sigma }}_{22}=C_{22}{\overline{\epsilon }}_{22}+C_{23}{\overline{\epsilon }}_{33}; \\ {\overline{\sigma }}_{33}=C_{23}{\overline{\epsilon }}_{22}+C_{22}{\overline{\epsilon }}_{33}; \\ {\overline{\sigma }}_{11}=C_{12}\left({\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}\right); \\ {\overline{\tau }}_{23}=C_{66}\hspace{0.17em}{\overline{\gamma }}_{23}, \end{gathered}$$

(116)

or

$$\left[\begin{array}{cc}{\overline{\epsilon }}_{22}& {\overline{\epsilon }}_{33}\\ {\overline{\epsilon }}_{33}& {\overline{\epsilon }}_{22}\end{array}\right]\left\{\begin{array}{c}{C}_{22}\\ C_{23}\end{array}\right\}=\left\{\begin{array}{c}{\overline{\sigma }}_{22}\\ {\overline{\sigma }}_{33}\end{array}\right\}$$

(117)

from which we obtain

$$\left\{\begin{array}{c}{C}_{22}\\ C_{23}\end{array}\right\}={\displaystyle \frac{1}{{\overline{\epsilon }}_{22}^2-{\overline{\epsilon }}_{33}^2}}\left[\begin{array}{cc}{\overline{\epsilon }}_{22}& -{\overline{\epsilon }}_{33}\\ -{\overline{\epsilon }}_{33}& {\overline{\epsilon }}_{22}\end{array}\right]\left\{\begin{array}{c}{\overline{\sigma }}_{22}\\ {\overline{\sigma }}_{33}\end{array}\right\}.$$

(118)

or explicitly

$$C_{22}={\displaystyle \frac{{\overline{\sigma }}_{22}{\overline{\epsilon }}_{22}-{\overline{\sigma }}_{33}{\overline{\epsilon }}_{33}}{{\overline{\epsilon }}_{22}^2-{\overline{\epsilon }}_{33}^2}}\hspace{1em};\hspace{1em}{C}_{23}={\displaystyle \frac{{\overline{\sigma }}_{33}{\overline{\epsilon }}_{22}-{\overline{\sigma }}_{22}{\overline{\epsilon }}_{33}}{{\overline{\epsilon }}_{22}^2-{\overline{\epsilon }}_{33}^2}}\hspace{1em}$$

(119)

For $C_{12}$ and $C_{66}$, this results in the following:

$$C_{12}={\displaystyle \frac{{\overline{\sigma }}_{11}}{{\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}}}\hspace{1em};\hspace{1em}{C}_{66}={\displaystyle \frac{{\overline{\tau }}_{23}}{{\overline{\gamma }}_{23}}}\hspace{1em}$$

(120)

The fibers are oriented along the “X₁” direction and distributed in the “X_2–3” plane, which is referred to as the plane of isotropy. For a transversely isotropic body, one can utilize the relation for the bulk modulus $K_{23}$ in the plane “2–3”:

$$K_{23}={\displaystyle \frac{C_{22}+C_{33}}{2}}={\displaystyle \frac{{\overline{\sigma }}_{22}+{\overline{\sigma }}_{33}}{2\left({\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}\right)}}\hspace{1em}.$$

(121)

The longitudinal Poisson’s ratio can be computed now:

$${\nu }_1={\nu }_{21}={\nu }_{31}={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{C_{11}-E_{11}}{K_{23}}}\right)}^{1/2}={\displaystyle \frac{C_{12}}{C_{22}+C_{33}}}={\displaystyle \frac{{\overline{\sigma }}_{11}}{\left({\overline{\sigma }}_{22}+{\overline{\sigma }}_{33}\right)}}\hspace{1em}.$$

(122)

and the shear modulus is as follows:

$$G_{23}={\displaystyle \frac{C_{22}-C_{33}}{2}}={\displaystyle \frac{{\overline{\sigma }}_{22}-{\overline{\sigma }}_{33}}{2\left({\overline{\epsilon }}_{22}-{\overline{\epsilon }}_{33}\right)}}\hspace{1em}.$$

(123)

or

$$G_{23}=C_{66}={\displaystyle \frac{{\overline{\sigma }}_{23}}{2{\overline{\epsilon }}_{23}}}\hspace{1em}.$$

(124)

The following parameter is introduced:

$$\Psi =1+{\displaystyle \frac{4{\nu }_1^2{K}_{23}}{E_{11}}}\hspace{1em}\hspace{1em},$$

(125)

Using this notation, the transverse moduli and the corresponding Poisson’s ratio can then be expressed as follows:

$$E_{22}=E_{33}={\displaystyle \frac{4G_{23}{K}_{23}}{K_{23}+\Psi G_{23}}}\hspace{1em},$$

(126)

and

$${\nu }_{23}={\displaystyle \frac{K_{23}-\Psi G_{23}}{K_{23}+\Psi G_{23}}}\hspace{1em},$$

(127)

respectively.

Until now, the expressions for $E_{11},\hspace{0.33em}{E}_{22}=E_{33},\hspace{0.33em}{\nu }_{12}={\nu }_{13},\hspace{0.33em}{\nu }_{23},\hspace{0.33em}{G}_{23},K_{23}$ have been obtained. Considering the relations

$$C_{22}+C_{33}=2K_{23}\hspace{1em};\hspace{1em}{C}_{22}-C_{33}=2G_{23}\hspace{1em},$$

(128)

one may obtain

$$C_{22}=K_{23}+G_{23}\hspace{1em};\hspace{1em}{C}_{23}=K_{23}-G_{23}\hspace{1em}.$$

(129)

Recall that

$$C_{44}=G_1=G_{12}=G_{13}\hspace{1em};\hspace{1em}{C}_{12}={\nu }_1\left(C_{22}+C_{23}\right)=2{\nu }_1{K}_{23}\hspace{1em}$$

(130)

and

$$C_{11}=E_{11}+{\displaystyle \frac{2C_{12}^2}{C_{22}+C_{23}}}=E_{11}+4{\nu }_1^2{K}_{23}=\Psi E_{11}\hspace{1em}.$$

(131)

It is concluded that, knowing the values for the material constants, one can obtain the above coefficients with the equations determined before.

Now, the FEM is used to compute the average stresses and strains in a general three-dimensional case. These are ${\overline{\sigma }}_{11},{\overline{\sigma }}_{22},{\overline{\sigma }}_{33},{\overline{\sigma }}_{12}={\overline{\tau }}_{12},{\overline{\sigma }}_{23}={\overline{\tau }}_{23},{\overline{\sigma }}_{31}={\overline{\tau }}_{31},$ ${\overline{\epsilon }}_{11},{\overline{\epsilon }}_{22},{\overline{\epsilon }}_{33},{\overline{\epsilon }}_{12}=1/2\hspace{0.17em}{\gamma }_{12},{\overline{\epsilon }}_{23}=1/2\hspace{0.17em}{\gamma }_{23},{\overline{\epsilon }}_{31}=1/2\hspace{0.17em}{\gamma }_{31}$. The elastic constants that characterize a transversely isotropic composite can be found using the stress and strain components mentioned above. The classic Hooke’s law can be used to write the following relations:

$$\begin{gathered} {\overline{\sigma }}_{11}=C_{11}{\overline{\epsilon }}_{11}+C_{12}{\overline{\epsilon }}_{22}+C_{12}{\overline{\epsilon }}_{33} \\ {\overline{\sigma }}_{22}=C_{12}{\overline{\epsilon }}_{11}+C_{22}{\overline{\epsilon }}_{22}+C_{23}{\overline{\epsilon }}_{33} \\ {\overline{\sigma }}_{33}=C_{12}{\overline{\epsilon }}_{11}+C_{23}{\overline{\epsilon }}_{22}+C_{22}{\overline{\epsilon }}_{33} \\ {\overline{\sigma }}_{23}={\overline{\tau }}_{23}=\left(C_{11}-C_{23}\right){\overline{\epsilon }}_{23}={\displaystyle \frac{1}{2}}\left(C_{11}-C_{23}\right){\overline{\gamma }}_{23} \\ {\overline{\sigma }}_{31}={\overline{\tau }}_{31}=2C_{44}{\overline{\epsilon }}_{31}=C_{66}{\overline{\gamma }}_{31} \\ {\overline{\sigma }}_{12}={\overline{\tau }}_{12}=2C_{44}{\overline{\epsilon }}_{12}=C_{66}{\overline{\gamma }}_{12} \end{gathered}$$

(132)

The last equation of Equation (132) offers the following:

$$C_{44}={\displaystyle \frac{{\overline{\sigma }}_{12}}{2\hspace{0.17em}{\overline{\epsilon }}_{12}}}={\displaystyle \frac{{\overline{\tau }}_{12}}{{\overline{\gamma }}_{12}}}=G_{12}=G_{13}=G_1$$

(133)

which represents the shear modulus in a plane normal to the x₂x₃ plane. Subtracting the third equation from the second in Equation (132), we have

$${\overline{\sigma }}_{22}-{\overline{\sigma }}_{33}=\left(C_{22}-C_{33}\right)\left({\overline{\epsilon }}_{22}-{\overline{\epsilon }}_{33}\right)$$

(134)

which can replace the fourth relation in Equation (132). So, there exists a system of six linear equations, from which four are independent, but they contain five unknowns, and only four of the elastic constants can be determined. The fifth relation can be considered the rule of mixture to compute the longitudinal Young’s modulus $E_{11}$:

$$E_{11}=E_f{v}_f+E_m{v}_m.$$

(135)

With $E_{11}$ thus obtained, one can replace the redundant fourth relation with the following:

$$E_{11}=C_{11}-{\displaystyle \frac{2C_{12}^2}{C_{22}+C_{23}}}.$$

(136)

Adding the second and third relations in Equation (132), we have

$${\overline{\sigma }}_{22}+{\overline{\sigma }}_{33}-{\displaystyle \frac{2C_{12}{\overline{\epsilon }}_{11}}{{\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}}}=C_{22}+C_{23}.$$

(137)

From the first relation in Equation (132), we have

$$C_{11}={\displaystyle \frac{{\overline{\sigma }}_{11}-C_{12}\left({\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}\right)}{{\overline{\epsilon }}_{11}}}.$$

(138)

Substituting into that of $E_{11}$, the following is obtained:

$$E_{11}={\displaystyle \frac{{\overline{\sigma }}_{11}}{{\overline{\epsilon }}_{11}}}+C_{12}{\displaystyle \frac{{\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}}{{\overline{\epsilon }}_{11}}}-{\displaystyle \frac{2C_{12}^2\left({\overline{\epsilon }}_{22}+{\overline{\epsilon }}_{33}\right)}{\left({\overline{\sigma }}_{22}+{\overline{\sigma }}_{33}-2C_{12}{\overline{\epsilon }}_{11}\right)}}.$$

(139)

and it is possible to obtain the coefficient $C_{12}$. Other methods to compute these coefficients can be found in [232,233].

6.2. Results and Applications

There is extensive research in this field. Some more interesting and useful results are presented in this section.

A FEM model using the Galerkin method for stress in a platelet-reinforced composite subjected to axial loading is presented in [234]. The results obtained were validated with 3D analytical and EM models (ANSYS). The shear stress at the interface was investigated. Different porous microstructures, with different boundary conditions, finite dimensions, and homogeneous and isotropic models, have different behaviors regarding permeability at the macroscopic level of the fibrous medium [235]. A microstructural model is developed for this study. Numerical experiments using FEM suggest a unique relationship, based on the power law, for determining the permeability. FEM is applied to the analysis of a unidirectional fiber composite considering two different materials, T800 carbon fibers reinforcing a Fibredux 6376C epoxy matrix and IM6 carbon fibers reinforcing an APC2 thermoplastic material, as presented in [236]. Experimental results validate the proposed model and show an excellent agreement between the results obtained by calculation and the experimental ones. The stress analysis and prediction of the steady-state creep deformation of short-fiber composites subjected to axial loading are described in [237]. The fiber–matrix interface is assumed to be perfect, and the steady-state creep behavior is classically defined by an exponential law. Analytical results are validated using FEM. Very good agreement is found between the analytical and FEM results for all stress components.

FEM has been the main method used in the calculation of stress and strain in most creep behavior study applications in which their determination is necessary, as it is a well-verified method (for example, [238,239,240,241,242,243]). A metal matrix composite is studied in [244]. For these materials, numerical models for estimating strain and stress are well-developed and have been studied for a long time. For the investigated material with a load perpendicular to the fiber axis, FEM determinations are performed. The results are compared with experimental verifications for a model composite with AA6061 matrix reinforced with single-crystal sapphire (reinforcement volume fraction 10%). The average values obtained experimentally validate the results of the numerical model. The development and use of a finite element model (FEM) to simulate the creep of a prestressed glued laminated timber system under external loading is reported in [245]. A variety of applications are presented in the literature certifying the usefulness of applying these theoretical methods [246,247,248,249,250,251,252,253,254,255,256,257,258].

6.3. Future Developments of FEM

Although the FEM is frequently used to investigate creep behavior in fiber-reinforced composites, there are still considerable untapped research potential in this area. Some encouraging directions for further research on using FEM to examine creep in fiber composites are described below.

Creep occurs at multiple scales (fiber, matrix, and interface). As a consequence, the multiscale modeling of creep becomes a perfect method to study these phenomena. So, it is possible to develop hierarchical or concurrent multiscale FEM models and to connect microscale material behavior with macroscale performance. A direction of research is to incorporate micromechanical models for fiber–matrix interactions during long-term creep.

Creep is a behavior that extends over a period of time, resulting in changes in the interface; it often degrades over time under creep conditions. It is necessary to develop a time-dependent interface model and to implement cohesive zone models or other interfacial degradation models within FEM frameworks that evolve over time due to creep.

The development of nonlinear and viscoelastic/viscoplastic constitutive models is necessary to integrate advanced time-dependent constitutive models (e.g., Schapery, Findley, or Anand-type models) into FEM codes for better prediction accuracy under various loading histories.

Another direction is by introducing thermocreep coupling in FEM. Creep is highly sensitive to temperature, especially in high-performance composites. Developing thermomechanical FEM models that couple heat transfer and creep deformation, including anisotropic thermal conductivity and expansion, is a goal to pursue.

Long-term creep can cause damage such as matrix cracking, fiber breakage, and delamination. So, it is useful to incorporate continuum damage mechanics (CDM) or progressive failure models in FEM to simulate damage accumulation due to creep.

Because creep simulations can be computationally intensive, it can be beneficial to use machine learning or surrogate models trained on FEM results to speed up predictions, particularly for design optimization or real-time structural health monitoring.

The results of long-term models established to develop benchmark datasets should be validated, and FEM–experiment hybrid studies should be promoted, especially with digital image correlation (DIC) and in situ microscopy techniques.

Additive manufacturing (3D Printing) can introduce complex fiber orientations and voids. The use of FEM to study how non-traditional fiber architectures affect creep and optimize them for long-term reliability using simulation can be beneficial.

Natural fiber composites have different creep behavior and are gaining popularity. It is necessary to adapt FEM tools to model creep in biocomposites, accounting for environmental effects like moisture and biodegradation.

Finite element squared (FE²) is a computational homogenization technique that integrates two levels of finite element analyses. The first level is at the macroscopic scale, which represents the overall structural behavior of the composite material. The second level, at the microscopic scale, captures the detailed behavior of the material’s microstructure, such as fiber–matrix interactions. FE² provides a detailed, physics-based approach to modeling creep behavior by capturing both macroscopic and microscopic responses. The method is used to numerically homogenize materials whose behavior depends on complex microstructures. It does this by solving finite element models at both the macro- and microscales simultaneously. To do this, the following procedure is applied: First, the macromodel is discretized using standard finite elements. Then, it is assigned an RVE at each Gauss point considered in the discretization. This is a microscale model showing the material’s internal layout (fibers, voids, etc.). The boundary conditions are applied to the RVE. The stress response at the microscale is computed (which may include creep, damage, plasticity, etc.). Now, the average stress from the RVE is inputted back into the macromodel, and this stress is used to continue solving the macrolevel problem. This two-way communication (macro/micro) happens at every time step (especially important in time-dependent problems like creep). When analyzing creep—a time-dependent deformation under constant stress—FE² allows for the simulation of both immediate and long-term material responses by considering both scales simultaneously.

The necessity of this method is due to the following: creep is highly sensitive to local microstructure, including fiber orientation, distribution, and interface behavior, and FE² allows these microstructural effects to influence the global behavior; it handles nonlinear, time-dependent behaviors like viscoelasticity or viscoplasticity naturally, and it can simulate micro-damage evolution and feed that into the overall structural response.

However, the method has some disadvantages: it is very computationally expensive, since an RVE problem is solved for every Gauss point and every time step; it requires parallel computing or reduced-order models to be practical for large structures or long-term creep simulations; moreover, implementing FE² is non-trivial and is often performed in advanced research codes (like in-house solvers or frameworks like MultiscaleFE, MFront, or FEAP).

7. Testing Methods

Both conventional and specialized methods are frequently used in tests on fiber-reinforced composites to assess their creep behavior and other mechanical characteristics. Understanding how fiber-reinforced composites react over time to different stressors, strains, and environmental circumstances is facilitated by these tests. The primary tests carried out in the study of creep behavior are presented below. Testing methods are related to the results that need to be obtained from testing. For this reason, there are several types of tests that are performed in the laboratory. A standard test machine is presented in Figure 9.

The most common tests used to study these materials are creep tests, which assess the time-dependent deformation of fiber-reinforced composites under constant load (creep) over an extended period. A constant load (or constant stress) creep test is performed when the specimen is subjected to a constant load at a constant temperature. It is possible to measure the primary, secondary, and tertiary creep phases. Both thermoset and thermoplastic composites can be studied. Thus, the creep strain vs. time curves and the creep rate are obtained. The standard procedure normally used in experiments is the following:

• Test specimens are loaded with a constant tensile or compressive load.
• Deformation (strain) is measured at different time intervals to monitor how it changes over time.
• Testing is carried out at various temperatures and environmental conditions. So, it is possible to study the composite’s behavior under different operating conditions.

With the help of these types of tests, linear or nonlinear creep can be studied, the creep rate can be determined (generally decreases over time), temperature sensitivity can be evaluated (typically exhibiting higher creep rates at elevated temperatures), and the increase in lifetime with an increase in fiber volume fraction can be studied.

In addition to the standard creep study procedure, there are different variations in which these tests are performed or additional tests, which are related to the context for which the tests are performed:

• Constant strain (or stress relaxation) tests are performed when the material is strained to a fixed level, and the decay in stress is measured over time. So, it is possible to study the viscoelastic behavior of polymer matrix composites (PMCs). The results obtained are stress vs. time and relaxation modulus.
• A creep rupture test is very similar to that performed under constant load, but the focus is on time to failure under a constant stress and temperature. So, it is possible to obtain the durability/lifetime of a composite under long-term loads. It yields time to rupture vs. applied stress.
• Accelerated creep testing represents a class of tests conducted at higher-than-service temperatures or stresses to accelerate failure. To interpret the results, the time–temperature superposition and time–stress superposition principles are used.
• Dynamic mechanical analysis (DMA) is performed using oscillating stress to measure viscoelastic properties. This method is used mainly when short-term creep compliance and modulus measurements should be obtained.
• A bending creep test (flexural creep) in a three-point or four-point setup is used to study the real-world loading in structures composed of beams or panels.
• Thermal cycling tests are used for the study of composites under varying thermal conditions (expansion and contraction) to simulate real-world conditions experienced in aerospace, automotive, and other industries. In these tests, the specimens are exposed to high and low temperatures for a certain number of cycles, and thermal expansion, dimensional stability, and residual stresses are determined. Thermal expansion can lead to residual stresses, which may cause microcracking or delamination over time and matrix degradation, fiber–matrix debonding, or interlaminar shear failure.
• Impact resistance tests determine the ability of fiber-reinforced composites to withstand sudden and high-intensity forces. The energy absorbed during fracture is measured. Impact can cause delamination or fiber fracture, especially if the bonding between the matrix and fibers is weak.
• Moisture absorption tests measure how the fiber-reinforced composite absorbs moisture, which can affect its mechanical properties. Usually, the specimens are immersed in water at room temperature or elevated temperatures, and their mass change is measured over time. Moisture likely causes a reduction in tensile strength and modulus.
• X-ray or Micro-CT scanning is performed following the internal damage assessment (microcracks, delamination, or voids within the composite). These methods can reveal defects that may not be detectable through traditional methods.

8. Conclusions

Future research on composite creep behavior is heading in the direction of a more precise, effective, and multiscale understanding, which is made possible in large part by sophisticated modeling tools, cleverer data integration, and innovative material systems. Key research trends and future directions are broken down as follows:

Development of multiscale and multi-physics modeling: Researchers have simulated creep from the fiber–matrix level up to the whole structure by merging microstructural, mesoscale, and macroscale models. This aids in capturing the effects of voids, fiber–matrix interactions, and other microstructural elements on long-term deformation. A new field of research is the integration of molecular dynamics (MD), micromechanics, and finite element (FE) methods for holistic creep simulations.

Creep behavior was already predicted from simulation or experimental data using machine learning and artificial intelligence. In order to maintain the physical plausibility of predictions, hybrid models can integrate ML with physics-based modeling (also known as “physics-informed ML”). To support the design and life prediction of composite structures in service, real-time predictive systems using AI can be built.

Digital twins and accelerated testing can help optimize creep testing procedures while cutting expenses and time. Using real-time data input, virtual models of composite parts may continuously replicate creep behavior. Digital twins can be used in the automotive and aerospace industries to track and forecast damage caused by creep in real time.

Growing interest in bioinspired materials and 3D woven, braided, or architected composites raises the need for new creep theories or AI-assisted models because these materials typically have distinct creep reactions that are difficult for conventional models to anticipate.

Probabilistic models are driven by variations in manufacturing flaws, service conditions, and material qualities. To increase the reliability of predictions and account for uncertainties, they must make use of probabilistic machine learning models and Bayesian techniques.

Microcracking, delamination, and fiber breaking necessitate damage-coupled creep models (real-world creep is not just a gradual deformation—it is associated with other factors). Current applications typically overlook progressive degradation.

Developing long-lasting composites requires an understanding of how environmental influences affect creep behavior. In order to forecast material performance under real-world circumstances, recent research has concentrated on modeling the combined effects of temperature, moisture, and mechanical loading on creep.

The industry demands recyclable composites and sustainability. It is necessary to understand and model the long-term creep behavior of green materials, such as biobased matrices and natural fibers, as they become more prevalent.