Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions
Abstract
1. Introduction
2. Methodology
2.1. Data Compilation
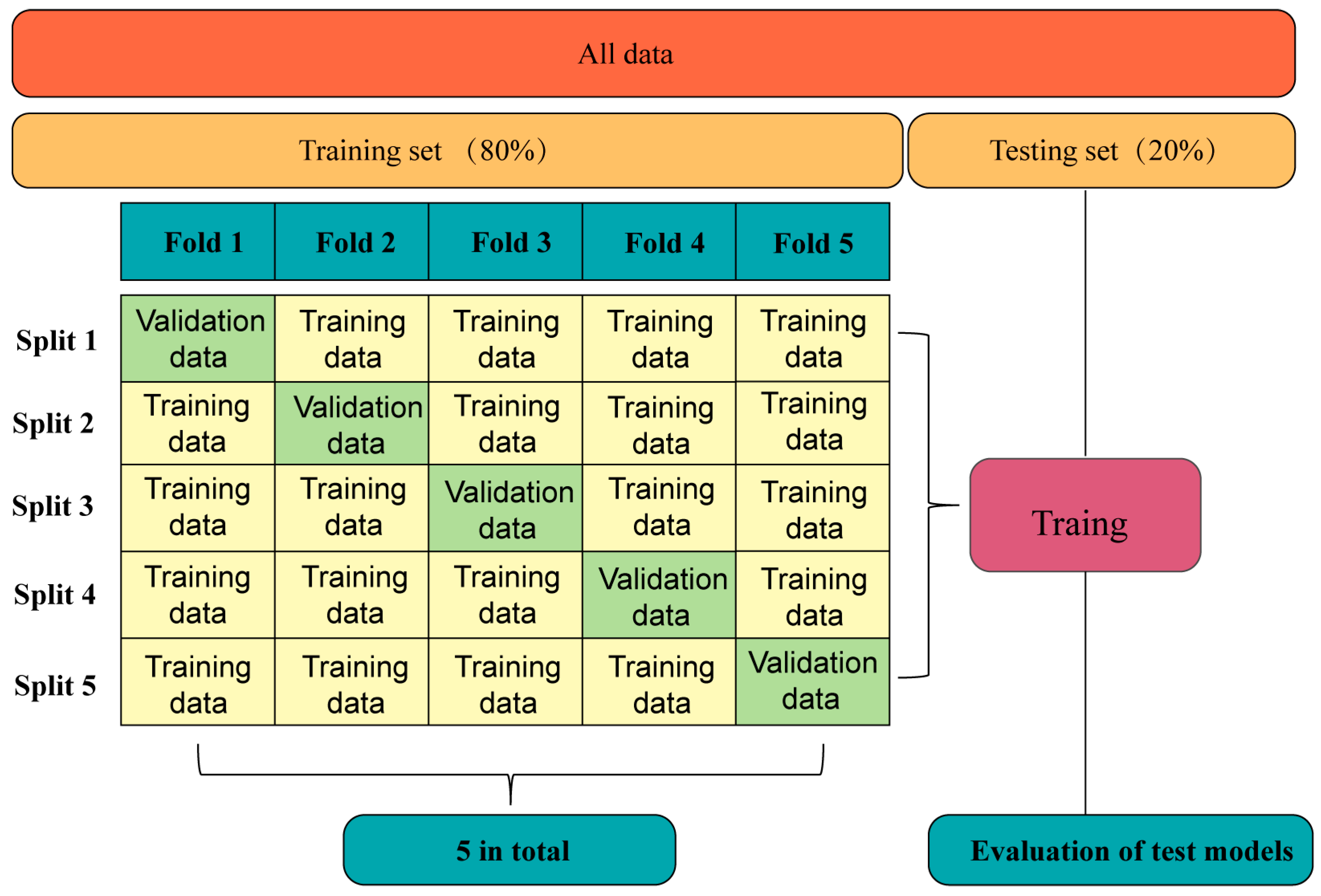
2.2. Data Cleaning and Preprocessing
2.3. Machine Learning Model
2.3.1. Support Vector Regression
2.3.2. Linear Multidimensional Regression
2.3.3. Random Forest
2.3.4. Decision Tree Regression
2.3.5. K-Nearest Neighbors Regression
2.3.6. Ridge Regression
2.3.7. Gaussian Process Regression
2.3.8. Neural Network Regression
2.4. Metrics for Assessing Predictive Accuracy
3. Results and Discussion
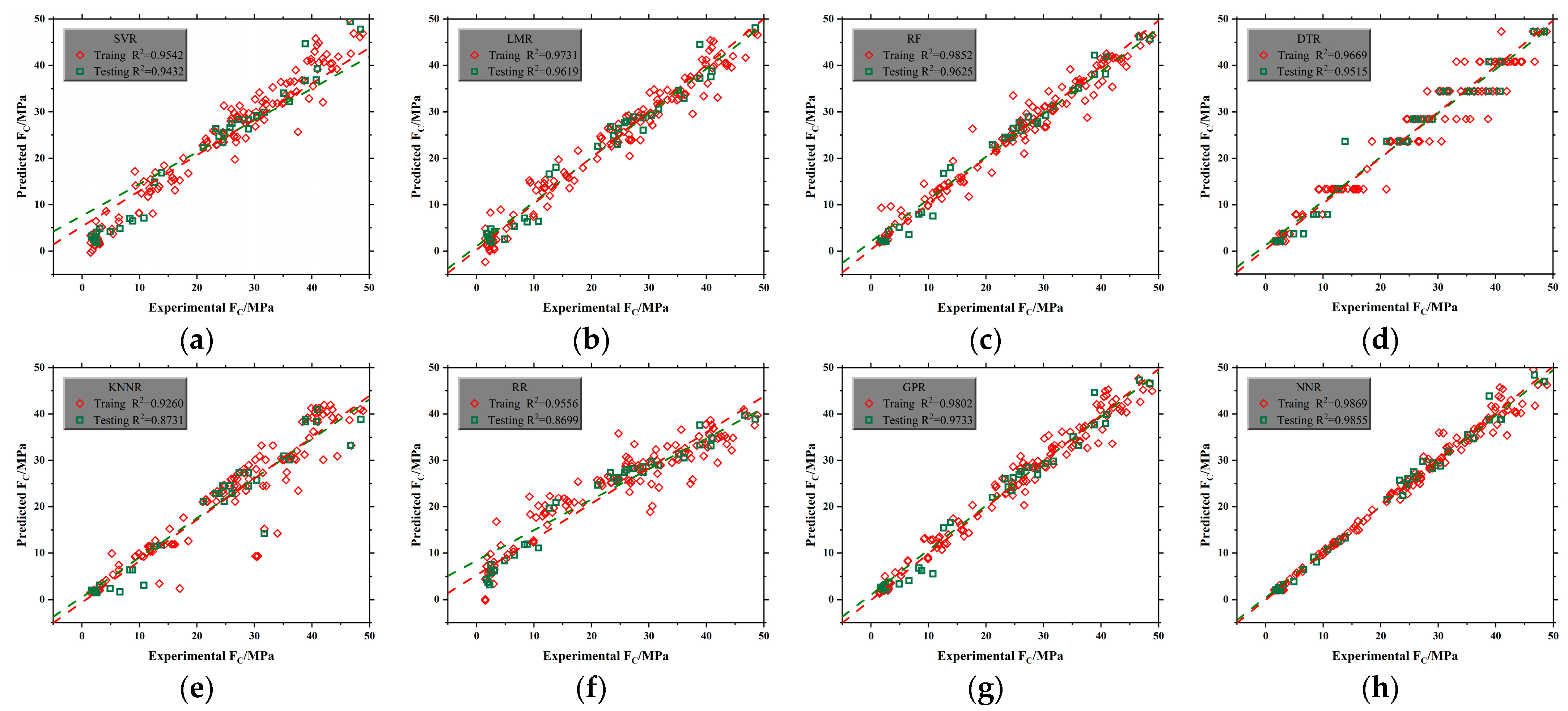
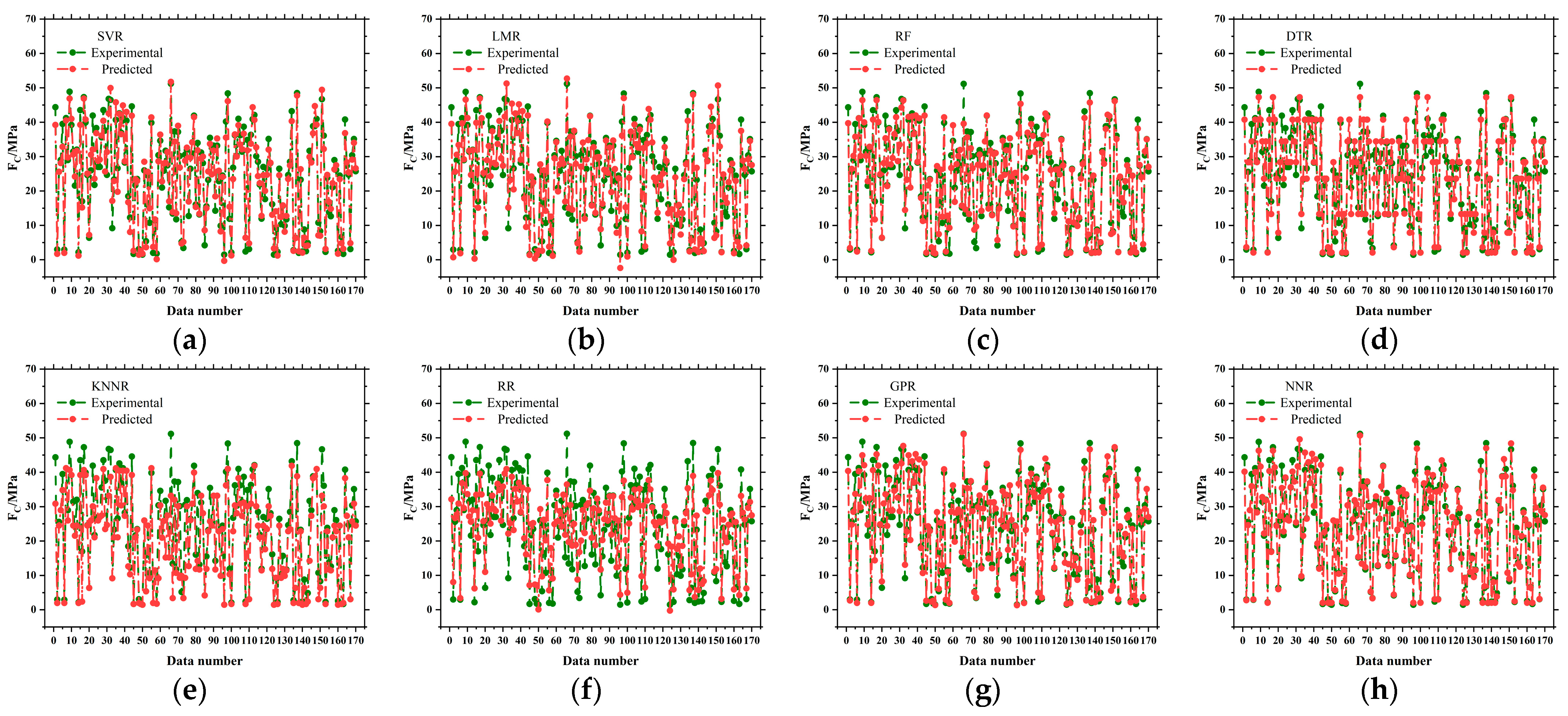
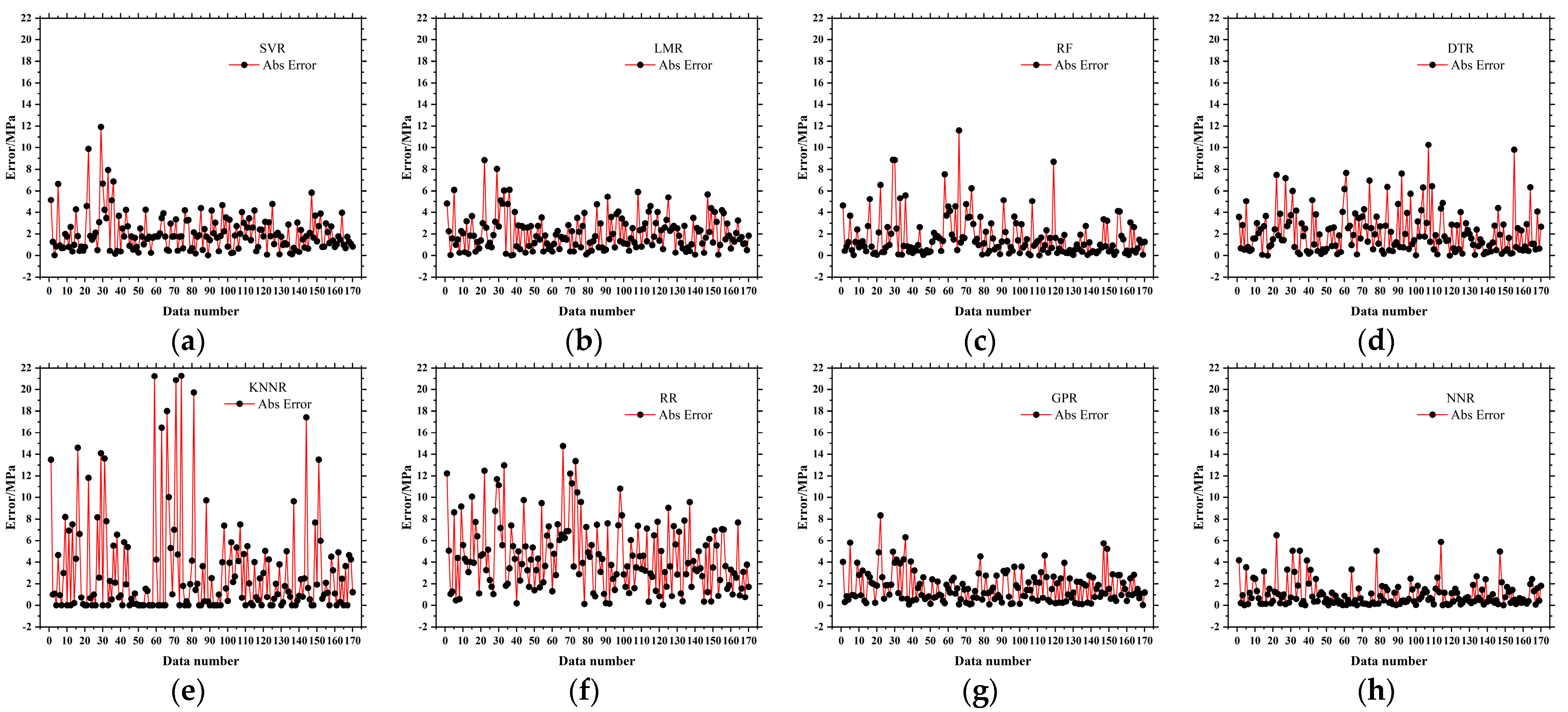
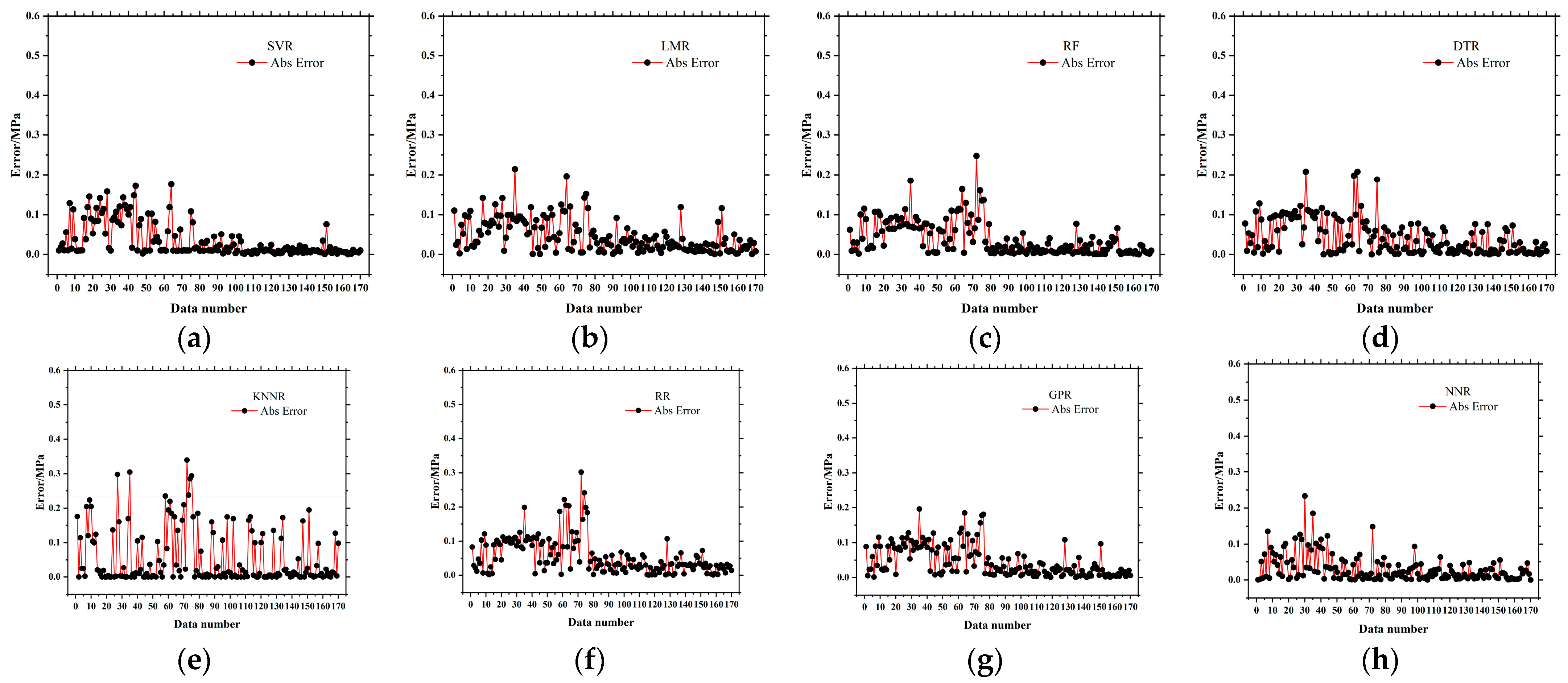
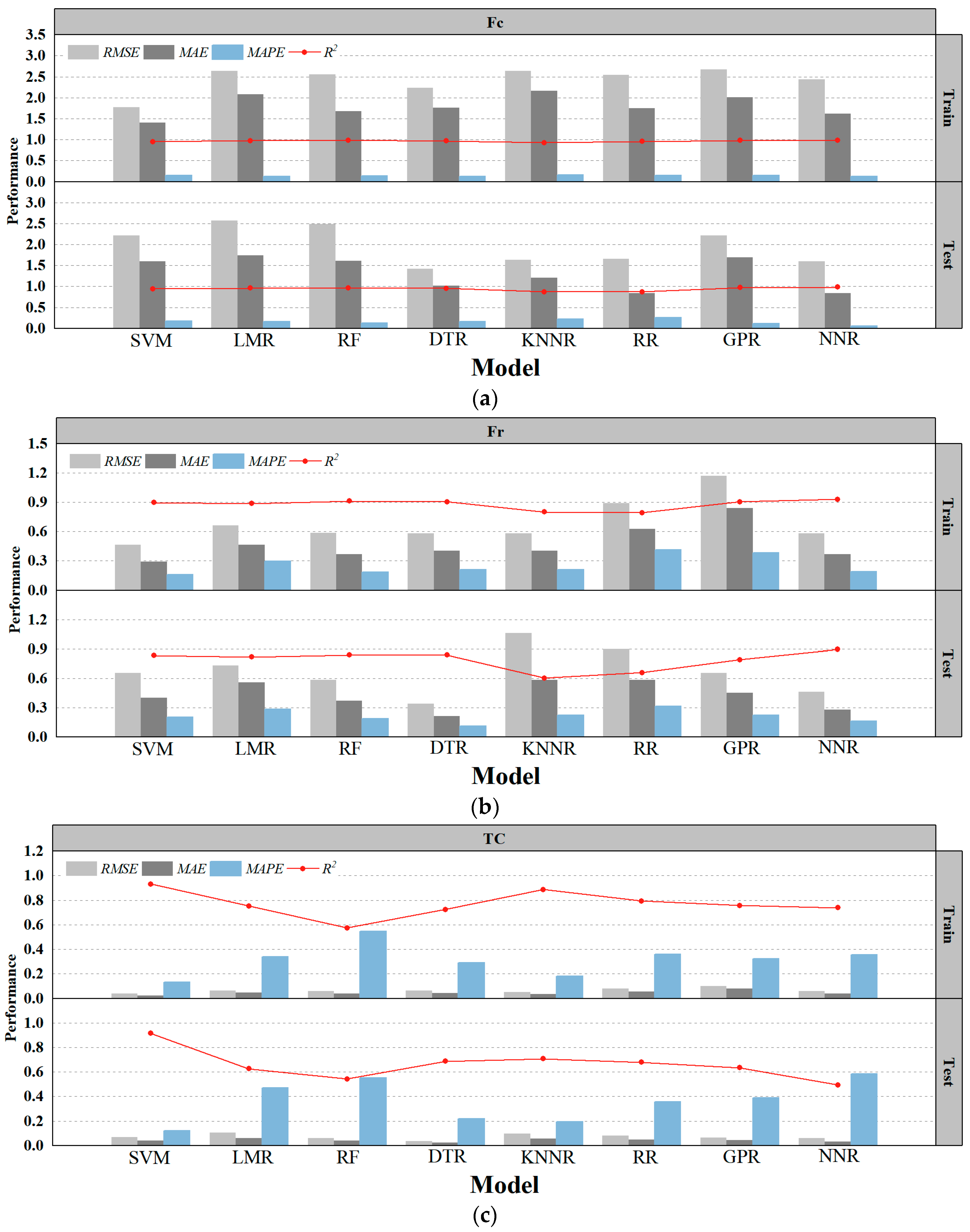
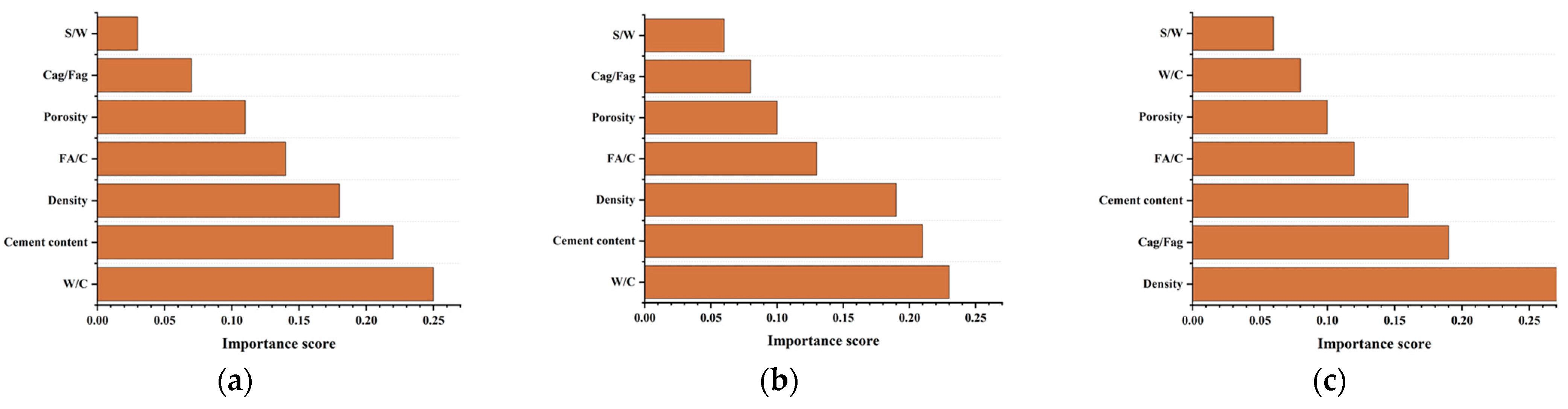
3.1. Machine Learning-Based Prediction of Compressive Strength
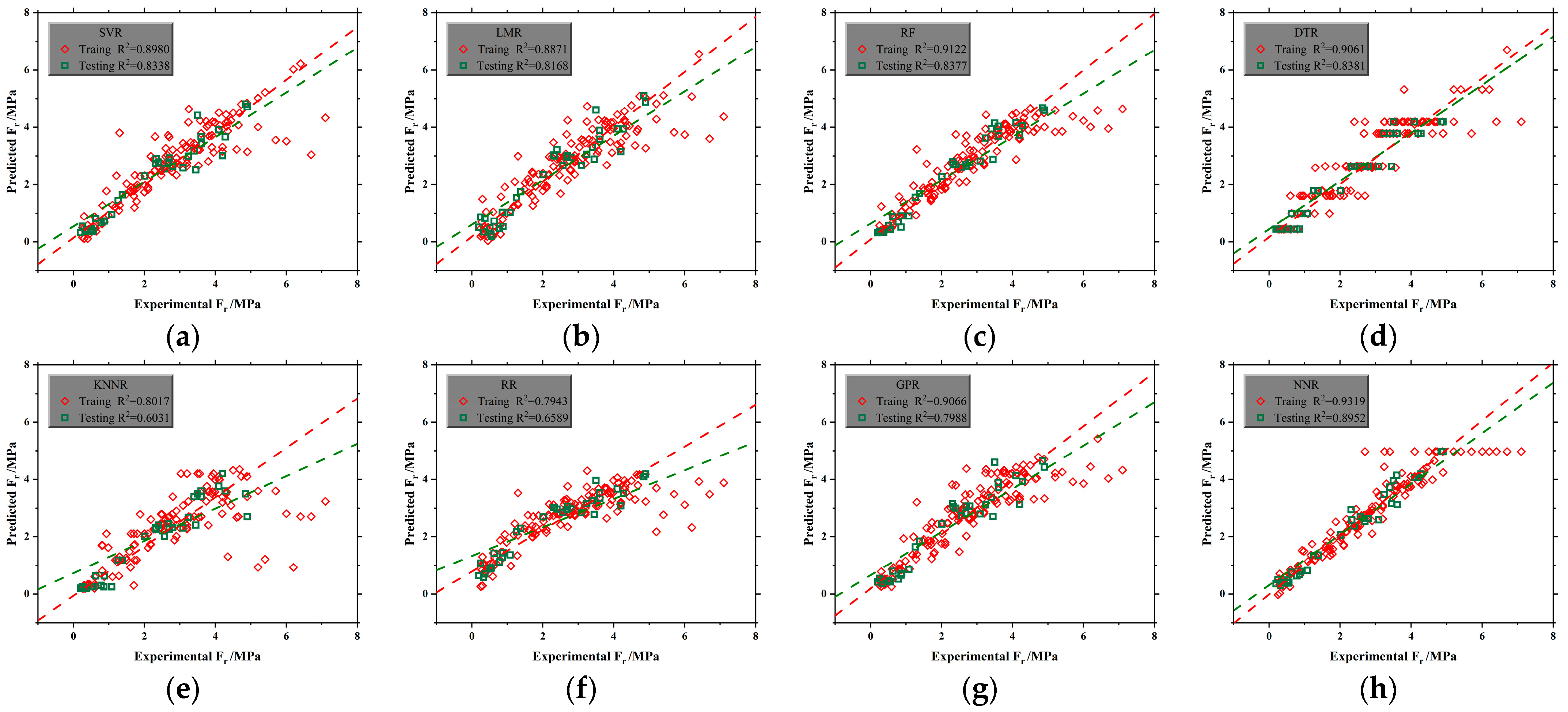
3.2. Machine Learning-Based Prediction of Flexural Strength
3.3. Machine Learning-Based Prediction of Thermal Conductivity
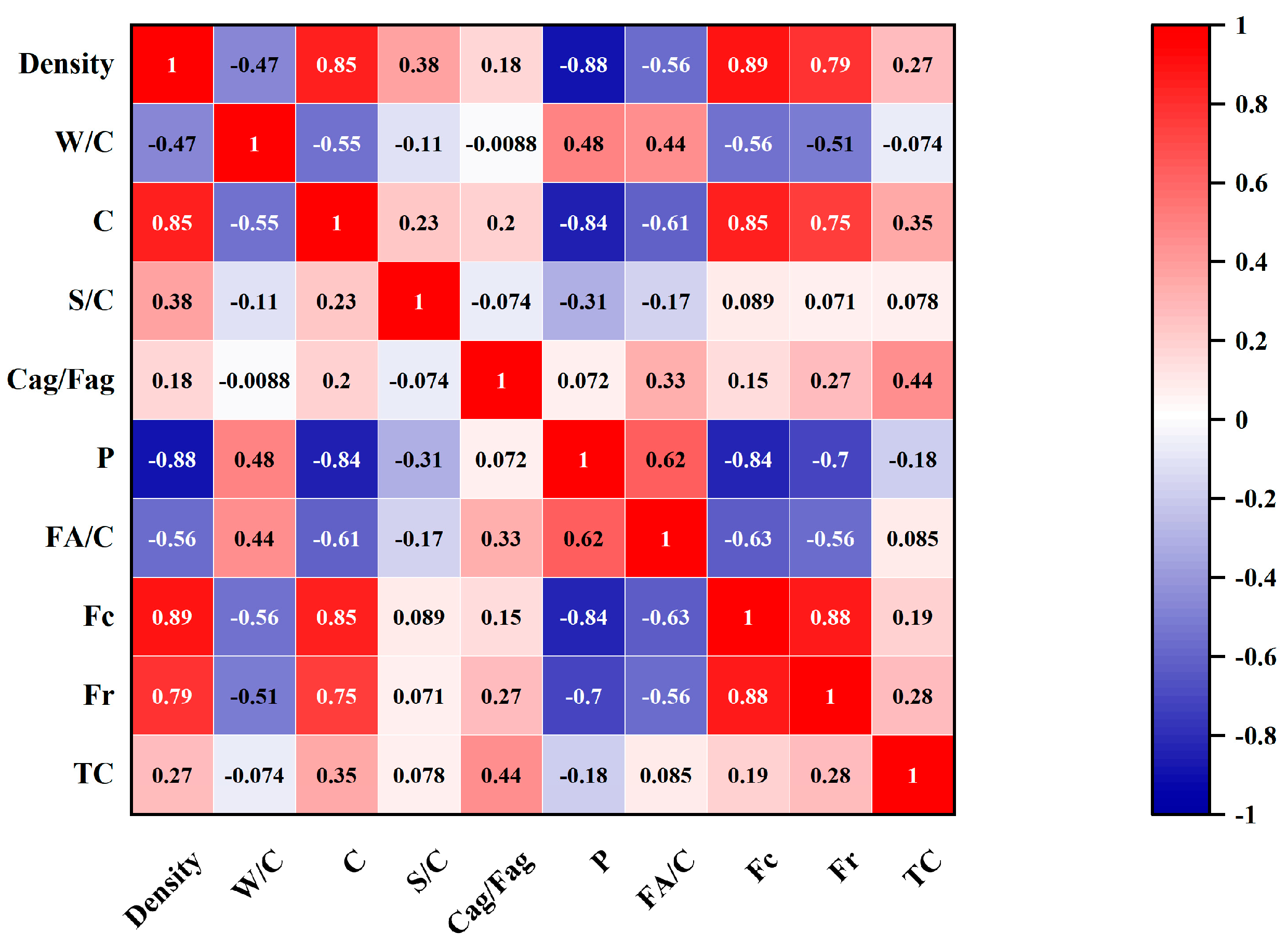
3.4. Validations and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohamed, A.M.; Tayeh, B.A.; Majeed, S.S.; Aisheh, Y.I.A.; Salih, M.N.A. Ultra-Light Foamed Concrete Mechanical Properties and Thermal Insulation Perspective: A Comprehensive Review. J. CO2 Util. 2024, 83, 102827. [Google Scholar] [CrossRef]
- Pan, Z.; Li, H.; Liu, W. Preparation and Characterization of Super Low Density Foamed Concrete from Portland Cement and Admixtures. Constr. Build. Mater. 2014, 72, 256–261. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, Z.; Niu, Y.; Li, J.; Zhang, Y. Study on the Preparation and Properties of High-Porosity Foamed Concretes Based on Ordinary Portland Cement. Mater. Des. 2016, 92, 949–959. [Google Scholar] [CrossRef]
- Tayeh, B.A. Effects of Marble, Timber, and Glass Powder as Partial Replacements for Cement. J. Civ. Eng. Constr. 2018, 7, 63–71. [Google Scholar] [CrossRef]
- Datta, S.D.; Rana, M.J.; Assafi, M.N.; Mim, N.J.; Ahmed, S. Investigation on the Generation of Construction Wastes in Bangladesh. Int. J. Constr. Manag. 2023, 23, 2260–2269. [Google Scholar] [CrossRef]
- Yang, S.; Wang, X.; Hu, Z.; Li, J.; Yao, X.; Zhang, C.; Wu, C.; Zhang, J.; Wang, W. Recent advances in sustainable lightweight foamed concrete incorporating recycled waste and byproducts: A review. Constr. Build. Mater. 2023, 403, 133083. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Z.; Amin, M.N.; Ahmed, B.; Khan, K.; Arifeen, S.U.; Althoey, F. Foam Concrete for Lightweight Construction Applications: A Comprehensive Review of the Research Development and Material Characteristics. Rev. Adv. Mater. Sci. 2024, 63, 20240022. [Google Scholar] [CrossRef]
- Cao, W.; Lv, X.; Li, J.; Lu, J.X.; Moon, J.; Poon, C.S. Enhancing the Mechanical and Thermal Properties of Foam Concrete by Incorporating Glass Lightweight Microspheres. Constr. Build. Mater. 2024, 447, 138103. [Google Scholar] [CrossRef]
- Wu, G.; Chen, W.; Tan, X.; Zhao, W.; Jia, S.; Tian, H.; Yang, J. Performance of New Type of Foamed Concrete in Supporting Tunnel in Squeezing Rock. Int. J. Geomech. 2020, 20, 04019173. [Google Scholar] [CrossRef]
- Lee, S.C. Prediction of Concrete Strength Using Artificial Neural Networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Nguyen, H.; Vu, T.; Vo, T.P.; Thai, H.T. Efficient Machine Learning Models for Prediction of Concrete Strengths. Constr. Build. Mater. 2021, 266, 120950. [Google Scholar] [CrossRef]
- Van, L.T.; Kim, D.V.; Xuan, H.N.; Tho, V.D.; Bulgakov, B.I.; Alexandrova, O.V. Modelling of the Effect of the Water-Cement Ratios on Properties Foam Concrete. J. Phys. Conf. Ser. 2019, 1425, 012189. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Ahmed, H.U.; Rafiq, S.K.; Ahmad, D.A. Machine Learning Approach for Predicting Compressive Strength in Foam Concrete Under Varying Mix Designs and Curing Periods. Smart Constr. Sustain. Cities 2023, 1, 16. [Google Scholar]
- Liu, J.; Ge, T.; Wu, Y.; Chen, R. Effect of Sand-to-Cement Ratio on Mechanical Properties of Foam Concrete. Buildings 2022, 12, 1969. [Google Scholar] [CrossRef]
- Amran, Y.M.; Farzadnia, N.; Ali, A.A. Properties and Applications of Foamed Concrete: A Review. Constr. Build. Mater. 2015, 101, 990–1005. [Google Scholar] [CrossRef]
- Kearsley, E.P.; Wainwright, P.J. The Effect of High Fly Ash Content on the Compressive Strength of Foamed Concrete. Cem. Concr. Res. 2001, 31, 105–112. [Google Scholar] [CrossRef]
- De Nicolo, B.; Pani, L.; Pozzo, E. Strain of Concrete at Peak Compressive Stress for a Wide Range of Compressive Strengths. Mater. Struct. 1994, 27, 206–210. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Yang, D.; Liu, H.; Chan, A.H.C. Experimental and Theoretical Studies on Effect of Height-to-Diameter Ratios on Failure Forms and Mechanical Characteristics of Foamed Concrete. J. Mater. Civ. Eng. 2019, 31, 04018341. [Google Scholar] [CrossRef]
- Sargam, Y.; Wang, K.; Cho, I.H. Machine Learning Based Prediction Model for Thermal Conductivity of Concrete. J. Build. Eng. 2021, 34, 101956. [Google Scholar] [CrossRef]
- Sargam, Y.; Faytarouni, M.; Riding, K.; Wang, K.; Jahren, C.; Shen, J. Predicting Thermal Performance of a Mass Concrete Foundation—A Field Monitoring Case Study. Case Stud. Constr. Mater. 2019, 11, e00289. [Google Scholar] [CrossRef]
- Sargam, Y.; Wang, K.; Alleman, J.E. Effects of Modern Concrete Materials on Thermal Conductivity. J. Mater. Civ. Eng. 2020, 32, 04020058. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Song, Z.W.; Zhang, F. An Experimental Study on Thermal Conductivity of Concrete. J. Build. Mater. 2010, 13, 17–21. [Google Scholar]
- Demirboğa, R. Thermal Conductivity and Compressive Strength of Concrete Incorporation with Mineral Admixtures. Build. Environ. 2007, 42, 2467–2471. [Google Scholar] [CrossRef]
- Jierula, A.; Li, H.; Chen, Y.; Wu, C.; Wu, X.; Yin, H. Study on the Influence of Density and Water–Cement Ratio on the Cement Utilization, Fluidity, Mechanical Properties, and Water Absorption of Foam Concrete. Buildings 2024, 14, 3550. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Ullah, H.S.; Khushnood, R.A.; Farooq, F.; Ahmad, J.; Vatin, N.I.; Ewais, D.Y.Z. Prediction of Compressive Strength of Sustainable Foam Concrete Using Individual and Ensemble Machine Learning Approaches. Materials 2022, 15, 3166. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X.; Wang, L.; Li, Y. Foam Concrete: A State-of-the-Art and State-of-the-Practice Review. Adv. Mater. Sci. Eng. 2020, 2020, 6153602. [Google Scholar] [CrossRef]
- Salami, B.A.; Iqbal, M.; Abdulraheem, A.; Jalal, F.E.; Alimi, W.; Jamal, A.; Bardhan, A. Estimating Compressive Strength of Lightweight Foamed Concrete Using Neural, Genetic and Ensemble Machine Learning Approaches. Cem. Concr. Compos. 2022, 133, 104721. [Google Scholar] [CrossRef]
- Elhishi, S.; Elashry, A.M.; El-Metwally, S. Unboxing Machine Learning Models for Concrete Strength Prediction Using XAI. Sci. Rep. 2023, 13, 19892. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Batool, F.; Islam, K.; Nehdi, M.L. Explainable Ensemble Learning Predictive Model for Thermal Conductivity of Cement-Based Foam. Constr. Build. Mater. 2024, 421, 135663. [Google Scholar] [CrossRef]
- Rosa, A.C.; Elomari, Y.; Calderón, A.; Mateu, C.; Haddad, A.; Boer, D. Methodology for the Prediction of the Thermal Conductivity of Concrete by Using Neural Networks. Appl. Sci. 2024, 14, 7598. [Google Scholar] [CrossRef]
- Lie, T.T.; Kodur, V.K.R. Thermal and Mechanical Properties of Steel-Fibre-Reinforced Concrete at Elevated Temperatures. Can. J. Civ. Eng. 1996, 23, 511–517. [Google Scholar] [CrossRef]
- Zhou, Z.; Hu, J.; Li, F.; Zhang, J.; Lei, M. Elastic Modulus Prediction Model of Foamed Concrete Based on the Walsh Formula. Appl. Sci. 2022, 12, 5142. [Google Scholar] [CrossRef]
- Song, I.; Tong, T.; Im, J.; Ceylan, H.; Cho, I.H. Impacts of Fractional Hot-Deck Imputation on Learning and Prediction of Engineering Data. In A Computational Framework for Data-Driven Infrastructure Engineering Using Advanced Statistical Learning, Prediction, and Curing; Iowa State University: Ames, IA, USA, 2018. [Google Scholar]
- Taiwo, R.; Yussif, A.M.; Adegoke, A.H.; Zayed, T. Prediction and Deployment of Compressive Strength of High-Performance Concrete Using Ensemble Learning Techniques. Constr. Build. Mater. 2024, 451, 138808. [Google Scholar] [CrossRef]
- Batool, F.; Prasad, N.N.; Bindiganavile, V. Statistical Modeling of Thermal Conductivity for Cement-Based Foam. J. Build. Eng. 2018, 19, 449–458. [Google Scholar] [CrossRef]
- Zhang, Z.; Provis, J.L.; Reid, A.; Wang, H. Mechanical, Thermal Insulation, Thermal Resistance and Acoustic Absorption Properties of Geopolymer Foam Concrete. Cem. Concr. Compos. 2015, 62, 97–105. [Google Scholar] [CrossRef]
- Xian, G.; Liu, Z.; Wang, Z.; Zhou, X. Study on the Performance and Mechanisms of High-Performance Foamed Concrete. Materials 2022, 15, 7894. [Google Scholar] [CrossRef]
- Dong, K.; Chen, S.; Liu, J.; Shi, X.; Zhang, J.; Meng, J. Effect of Nano- and Micron-Materials on the Thermal Properties Behavior in Wet Environments and Heat Transfer Mechanism of Foam Concrete. J. Build. Eng. 2025, 107, 112725. [Google Scholar] [CrossRef]
- Othman, R.; Jaya, R.P.; Muthusamy, K.; Sulaiman, M.; Duraisamy, Y.; Abdullah, M.M.A.B.; Sandu, A.V. Relation between Density and Compressive Strength of Foamed Concrete. Materials 2021, 14, 2967. [Google Scholar] [CrossRef]
- Dhasindrakrishna, K.; Pasupathy, K.; Ramakrishnan, S.; Sanjayan, J. Progress, Current Thinking and Challenges in Geopolymer Foam Concrete Technology. Cem. Concr. Compos. 2021, 116, 103886. [Google Scholar] [CrossRef]
- Zhu, Y.; Feng, M.; Zhu, H.; Zhang, M.; Wang, Z.; Guo, Z. Thermal Conductivity of Fiber-Reinforced Foam Concrete Filled with Crumb Rubber Powders. Innov. Infrastruct. Solut. 2024, 9, 421. [Google Scholar] [CrossRef]
- Hanif, A.; Diao, S.; Lu, Z.; Fan, T.; Li, Z. Green Lightweight Cementitious Composite Incorporating Aerogels and Fly Ash Cenospheres–Mechanical and Thermal Insulating Properties. Constr. Build. Mater. 2016, 116, 422–430. [Google Scholar] [CrossRef]
- Strzałkowski, J.; Garbalińska, H. Thermal and Strength Properties of Lightweight Concretes with the Addition of Aerogel Particles. Adv. Cem. Res. 2016, 28, 567–575. [Google Scholar] [CrossRef]
- Hu, N.; Liu, Y.; Ke, L.; Ye, Y.; Jia, J.; Sun, Z.; Chen, D. Preparation and Frothing Mechanism of Froth Concrete Based on Solid Waste: A Review. Constr. Build. Mater. 2023, 401, 132831. [Google Scholar] [CrossRef]
- Hajimohammadi, A.; Ngo, T.; Mendis, P.; Kashani, A.; van Deventer, J.S.J. Alkali Activated Slag Foams: The Effect of the Alkali Reaction on Foam Characteristics. J. Clean. Prod. 2017, 147, 330–339. [Google Scholar] [CrossRef]
- Bagheri, A.; Ghahremani, G. Macroporosity-Based Prediction Models for Mechanical Properties of Foamed Concrete. Mag. Concr. Res. 2022, 74, 945–955. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, D.; Wang, S.; Chen, X.; Wu, X.; Han, Z.; Liu, Y. Quantitative Analysis of Pore Structure’s Impact on Early Mechanical Properties and Durability of Foam Concrete: Macroscopic and Mesoscopic Insights. Constr. Build. Mater. 2025, 459, 139775. [Google Scholar] [CrossRef]
- Gao, Z.H.; Chen, B.; Chen, J.L.; Yuan, Z.Y. Pore Structure and Mechanical Properties of Foam Concrete under Freeze-Thaw Environment. Acta Mater. Compos. Sin. 2024, 41, 827–838. [Google Scholar]
- Xu, F.; Gu, G.; Zhang, W.; Wang, H.; Huang, X.; Zhu, J. Pore Structure Analysis and Properties Evaluations of Fly Ash-Based Geopolymer Foams by Chemical Foaming Method. Ceram. Int. 2018, 44, 19989–19997. [Google Scholar] [CrossRef]
- Liu, M.Y.J.; Alengaram, U.J.; Jumaat, M.Z.; Mo, K.H. Evaluation of Thermal Conductivity, Mechanical and Transport Properties of Lightweight Aggregate Foamed Geopolymer Concrete. Energy Build. 2014, 72, 238–245. [Google Scholar] [CrossRef]
- Mydin, M.A.O.; Abdullah, M.M.A.B.; Sor, N.H.; Omar, R.; Dulaimi, A.; Awoyera, P.O.; Deifalla, A.F. Thermal Conductivity, Microstructure and Hardened Characteristics of Foamed Concrete Composite Reinforced with Raffia Fiber. J. Mater. Res. Technol. 2023, 26, 850–864. [Google Scholar] [CrossRef]
- Gołaszewski, J.; Klemczak, B.; Smolana, A.; Gołaszewska, M.; Cygan, G.; Mankel, C.; Koenders, E.A. Effect of Foaming Agent, Binder and Density on the Compressive Strength and Thermal Conductivity of Ultra-Light Foam Concrete. Buildings 2022, 12, 1176. [Google Scholar] [CrossRef]
- Batool, F.; Rafi, M.M.; Bindiganavile, V. Microstructure and Thermal Conductivity of Cement-Based Foam: A Review. J. Build. Eng. 2018, 20, 696–704. [Google Scholar] [CrossRef]
- Kumar, N.V.; Arunkumar, C.; Senthil, S.S. Experimental Study on Mechanical and Thermal Behavior of Foamed Concrete. Mater. Today Proc. 2018, 5, 8753–8760. [Google Scholar] [CrossRef]
- Mydin, M.A.O.; Sor, N.H.; Althoey, F.; Özkılıç, Y.O.; Abdullah, M.M.A.B.; Isleem, H.F.; Tawfik, T.A. Performance of Lightweight Foamed Concrete Partially Replacing Cement with Industrial and Agricultural Wastes. Ain Shams Eng. J. 2023, 14, 102546. [Google Scholar] [CrossRef]
- Li, L.; Wang, W.; Wang, Y.; Li, D.; Zhuang, M.L. Experimental Study on Pore Structure Characteristics and Thermal Conductivity of Fibers Reinforced Foamed Concrete. PLoS ONE 2023, 18, e0287690. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Q.; Shi, Y.; Zheng, G.; Li, Q.; Chen, H.; Cheng, X. Effects of Different Control Methods on the Mechanical and Thermal Properties of Ultra-Light Foamed Concrete. Constr. Build. Mater. 2020, 262, 120082. [Google Scholar] [CrossRef]
- Zhang, J.; Su, Y.; Xiong, Y.; He, J.; Xu, Q.; Gao, H. Influence of Foam Content on Mechanical Properties and Thermal Conductivity of Ceramsite Foam Concrete. Sci. Rep. 2025, 15, 16860. [Google Scholar] [CrossRef]
- Feng, S.; Gao, Y.; Xiao, H.; Xue, C. Influence of Fibers and Bubble Structure on Thermal Conductivity and Mechanical Performances of Foam Concrete. Constr. Build. Mater. 2024, 445, 137956. [Google Scholar] [CrossRef]
- Xiao, J.; Hao, L.; Cao, W.; Ye, T. Influence of Recycled Powder Derived from Waste Concrete on Mechanical and Thermal Properties of Foam Concrete. J. Build. Eng. 2022, 61, 105203. [Google Scholar] [CrossRef]
- Othuman Mydin, M.A.; Wang, Y.C. Thermal and Mechanical Properties of Lightweight Foamed Concrete at Elevated Temperatures. Mag. Concr. Res. 2012, 64, 213–224. [Google Scholar] [CrossRef]
- Wei, J.; Wang, T.; Zhong, Y.; Zhang, Y.; Leung, C.K. Performance Evaluation of Foamed Concrete with Lightweight Aggregate: Strength, Shrinkage, and Thermal Conductivity. Materials 2024, 17, 3869. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Garrecht, H. Effects of Mixing Techniques and Material Compositions on the Compressive Strength and Thermal Conductivity of Ultra-Lightweight Foam Concrete. Materials 2024, 17, 2640. [Google Scholar] [CrossRef]
- Bayraktar, O.Y.; Kaplan, G.; Gencel, O.; Benli, A.; Sutcu, M. Physico-Mechanical, Durability and Thermal Properties of Basalt Fiber Reinforced Foamed Concrete Containing Waste Marble Powder and Slag. Constr. Build. Mater. 2021, 288, 123128. [Google Scholar] [CrossRef]
- Kilincarslan, Ş.; Davraz, M.; Akça, M. The Effect of Pumice as Aggregate on the Mechanical and Thermal Properties of Foam Concrete. Arab. J. Geosci. 2018, 11, 289. [Google Scholar] [CrossRef]
- Gökçe, H.S.; Hatungimana, D.; Ramyar, K. Effect of Fly Ash and Silica Fume on Hardened Properties of Foam Concrete. Constr. Build. Mater. 2019, 194, 1–11. [Google Scholar] [CrossRef]
- Chen, B.; Liu, N. A Novel Lightweight Concrete-Fabrication and Its Thermal and Mechanical Properties. Constr. Build. Mater. 2013, 44, 691–698. [Google Scholar] [CrossRef]
- Rong, X.; Zhang, X.; Zhang, J.; Xu, W.; Zhang, Z. Study on Mechanical and Thermal Properties of Alkali-Excited Fly Ash Aerogel Foam Concrete. Constr. Build. Mater. 2023, 408, 133770. [Google Scholar] [CrossRef]
- Wang, L.; Liu, P.; Jing, Q.; Liu, Y.; Wang, W.; Zhang, Y.; Li, Z. Strength Properties and Thermal Conductivity of Concrete with the Addition of Expanded Perlite Filled with Aerogel. Constr. Build. Mater. 2018, 188, 747–757. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Qin, S.; Deng, R. Effect of Foaming Gas on the Physical and Mechanical Properties of Foamed Concrete. Constr. Build. Mater. 2025, 478, 141465. [Google Scholar] [CrossRef]
- Wongkvanklom, A.; Posi, P.; Kasemsiri, P.; Sata, V.; Cao, T.; Chindaprasirt, P. Strength, Thermal Conductivity and Sound Absorption of Cellular Lightweight High Calcium Fly Ash Geopolymer Concrete. Eng. Appl. Sci. Res. 2021, 48, 487–496. [Google Scholar]
- Chen, G.; Wang, K. Mechanical and Thermal Properties of Glass Fibre-Reinforced Ceramsite-Foamed Concrete. Indoor Built Environ. 2018, 27, 890–897. [Google Scholar] [CrossRef]
- Maglad, A.M.; Mydin, M.A.O.; Majeed, S.S.; Tayeh, B.A.; Mostafa, S.A. Development of Eco-Friendly Foamed Concrete with Waste Glass Sheet Powder for Mechanical, Thermal, and Durability Properties Enhancement. J. Build. Eng. 2023, 80, 107974. [Google Scholar] [CrossRef]
- Batool, F.; Bindiganavile, V. Quantification of Factors Influencing the Thermal Conductivity of Cement-Based Foam. Cem. Concr. Compos. 2018, 91, 76–86. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Wu, J.; Deng, Y.; Zheng, X.; Cui, Y.; Zhao, Z.; Chen, Y.; Zha, F. Hydraulic Conductivity and Strength of Foamed Cement-Stabilized Marine Clay. Constr. Build. Mater. 2019, 222, 688–698. [Google Scholar] [CrossRef]
- Zhu, C.; Dong, B.; Lazorenko, G.; Fang, G.; Wang, Y.; Zuo, J. Sandy Soil Based Foam Concrete with Ultra-Small Pore Structure Through In-Situ Mechanical Frothing. J. Build. Eng. 2024, 91, 109675. [Google Scholar] [CrossRef]
- He, J.; Gao, Q.; Song, X.; Bu, X.; He, J. Effect of Foaming Agent on Physical and Mechanical Properties of Alkali-Activated Slag Foamed Concrete. Constr. Build. Mater. 2019, 226, 280–287. [Google Scholar] [CrossRef]
- Mydin, M.A.O. Effective thermal conductivity of foamcrete of different densities. Concr. Res. Lett. 2011, 2, 181–189. [Google Scholar]
- Zhang, S.; Qi, X.; Guo, S.; Zhang, L.; Ren, J. A Systematic Research on Foamed Concrete: The Effects of Foam Content, Fly Ash, Slag, Silica Fume and Water-to-Binder Ratio. Constr. Build. Mater. 2022, 339, 127683. [Google Scholar] [CrossRef]
- Li, T.; Huang, F.; Zhu, J.; Tang, J.; Liu, J. Effect of Foaming Gas and Cement Type on the Thermal Conductivity of Foamed Concrete. Constr. Build. Mater. 2020, 231, 117197. [Google Scholar] [CrossRef]
- Shang, X.; Qu, N.; Li, J. Development and Functional Characteristics of Novel Foam Concrete. Constr. Build. Mater. 2022, 324, 126666. [Google Scholar] [CrossRef]
- Martínez-Merino, L.I.; Puerto, J.; Rodríguez-Chía, A.M. Ordered Weighted Average Support Vector Regression. Expert Syst. Appl. 2025, 274, 126882. [Google Scholar]
- Anand, P.; Rastogi, R.; Chandra, S. A Class of New Support Vector Regression Models. Appl. Soft Comput. 2020, 94, 106446. [Google Scholar] [CrossRef]
- Guo, L.; Xia, L.; Moore, J.B. Robust Recursive Identification of Multidimensional Linear Regression Models. Int. J. Control 1988, 48, 961–979. [Google Scholar] [CrossRef]
- Altork, Y. Comparative Analysis of Machine Learning Models for Wind Speed Forecasting: Support Vector Machines, Fine Tree, and Linear Regression Approaches. Int. J. Thermofluids 2025, 10, 1217. [Google Scholar] [CrossRef]
- Wen, H.; Li, J.; Liao, M.; Di, M.; Hu, J.; Liu, B. A Hybrid-Optimized Random Forest Interpretable Model for Debris Flow Susceptibility by Prior Model-Based Negative Sampling. Adv. Space Res. 2025, 76, 202–220. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J.; Zhao, G.; Wang, X.; Cong, W.; Yuan, M.; Tao, J. NIDS-CNNRF Integrating CNN and Random Forest for Efficient Network Intrusion Detection Model. Internet Things 2025, 32, 101607. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and Regression Trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and Tuning Strategies for Random Forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Chou, J.S.; Tsai, C.F.; Pham, A.D.; Lu, Y.H. Machine Learning in Concrete Strength Simulations: Multi-Nation Data Analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Cao, J. Prediction and Evaluation of Thermal Conductivity in Nanomaterial-Reinforced Cementitious Composites. Cem. Concr. Res. 2023, 172, 107240. [Google Scholar] [CrossRef]
- Naved, M.; Asim, M.; Ahmad, T. Prediction of Concrete Compressive Strength Using Deep Neural Networks Based on Hyperparameter Optimization. Cogent Eng. 2024, 11, 2297491. [Google Scholar] [CrossRef]
- Amiri, M.; Hatami, F. Prediction of Mechanical and Durability Characteristics of Concrete Including Slag and Recycled Aggregate Concrete with Artificial Neural Networks (ANNs). Constr. Build. Mater. 2022, 325, 126839. [Google Scholar] [CrossRef]
- Ghunimat, D.; Alzoubi, A.E.; Alzboon, A.; Hanandeh, S. Prediction of Concrete Compressive Strength with GGBFS and Fly Ash Using Multilayer Perceptron Algorithm, Random Forest Regression and K-Nearest Neighbor Regression. Asian J. Civ. Eng. 2023, 24, 169–177. [Google Scholar] [CrossRef]
- Aiyer, B.G.; Kim, D.; Karingattikkal, N.; Samui, P.; Rao, P.R. Prediction of Compressive Strength of Self-Compacting Concrete Using Least Square Support Vector Machine and Relevance Vector Machine. KSCE J. Civ. Eng. 2014, 18, 1753–1758. [Google Scholar] [CrossRef]
- Zou, Z.; Peng, B.; Xie, L.; Song, S. Enhanced Gaussian Process Model for Predicting Compressive Strength of Ultra-High-Performance Concrete (UHPC). Materials 2024, 17, 6140. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Mohammed, A.S.; Ulrikh, D.V. Data-Driven Compressive Strength Prediction of Fly Ash Concrete Using Ensemble Learner Algorithms. Buildings 2022, 12, 132. [Google Scholar] [CrossRef]
- Sah, A.K.; Hong, Y.M. Performance Comparison of Machine Learning Models for Concrete Compressive Strength Prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef]
- Shevade, S.K.; Keerthi, S.S.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to the SMO Algorithm for SVM Regression. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, L.; Wang, W.; Zhang, G.; Xu, L.; Fan, D.; Yu, R. Development of Compressive Strength Prediction Platform for Concrete Materials Based on Machine Learning Techniques. J. Build. Eng. 2023, 80, 107977. [Google Scholar] [CrossRef]
- Wen, Z.; Zhou, R.; Su, H. MR and Stacked GRUs Neural Network Combined Model and Its Application for Deformation Prediction of Concrete Dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
- Sun, H.; Burton, H.V.; Huang, H. Machine Learning Applications for Building Structural Design and Performance Assessment: State-of-the-Art Review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- Nehdi, M.; Djebbar, Y.; Khan, A. Neural Network Model for Preformed-Foam Cellular Concrete. ACI Mater. J. 2001, 98, 402–409. [Google Scholar]
- Abd, A.M.; Abd, S.M. Modelling the Strength of Lightweight Foamed Concrete Using Support Vector Machine (SVM). Case Stud. Constr. Mater. 2017, 6, 8–15. [Google Scholar]
- Asadzadeh, S.; Khoshbayan, S. Multi-Objective Optimization of Influential Factors on Production Process of Foamed Concrete Using Box-Behnken Approach. Constr. Build. Mater. 2018, 170, 101–110. [Google Scholar] [CrossRef]
- Su, M.; Zhong, Q.; Peng, H.; Li, S. Selected machine learning approaches for predicting the interfacial bond strength between FRPs and concrete. Constr. Build. Mater. 2021, 270, 121456. [Google Scholar] [CrossRef]
- Zhao, W.; Feng, S.; Liu, J.; Sun, B. An Explainable Intelligent Algorithm for the Multiple Performance Prediction of Cement-Based Grouting Materials. Constr. Build. Mater. 2023, 366, 130146. [Google Scholar] [CrossRef]
- Vargas, J.F.; Oviedo, A.I.; Ortega, N.A.; Orozco, E.; Gómez, A.; Londoño, J.M. Machine-Learning-Based Predictive Models for Compressive Strength, Flexural Strength, and Slump of Concrete. Appl. Sci. 2024, 14, 4426. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, M.; Yuan, H.; Sabri, M.M.S.; Li, X. Prediction of the Compressive Strength for Cement-Based Materials with Metakaolin Based on the Hybrid Machine Learning Method. Materials 2022, 15, 3500. [Google Scholar] [CrossRef]
- Wang, S.; Abdulridha, A.; Bravo, J.; Naito, C.; Quiel, S.; Suleiman, M.; Oztekin, A. Thermal Energy Storage in Concrete: Review, Testing, and Simulation of Thermal Properties at Relevant Ranges of Elevated Temperature. Cem. Concr. Res. 2023, 166, 107096. [Google Scholar] [CrossRef]
- Wu, M.; Li, M.; Xu, C.; He, Y.; Tao, W. The Impact of Concrete Structure on the Thermal Performance of the Dual-Media Thermocline Thermal Storage Tank Using Concrete as the Solid Medium. Appl. Energy 2014, 113, 1363–1371. [Google Scholar] [CrossRef]
- Kursuncu, B.; Gencel, O.; Bayraktar, O.Y.; Shi, J.; Nematzadeh, M.; Kaplan, G. Optimization of Foam Concrete Characteristics Using Response Surface Methodology and Artificial Neural Networks. Constr. Build. Mater. 2022, 337, 127575. [Google Scholar] [CrossRef]
- Cavalline, T.L.; Castrodale, R.W.; Freeman, C.; Wall, J. Impact of Lightweight Aggregate on Concrete Thermal Properties. ACI Mater. J. 2017, 114, 945. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the Use of Cross-Validation for Time Series Predictor Evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Joshi, D.A.; Menon, R.; Jain, R.K.; Kulkarni, A.V. Deep Learning Based Concrete Compressive Strength Prediction Model with Hybrid Meta-Heuristic Approach. Expert Syst. Appl. 2023, 233, 120925. [Google Scholar] [CrossRef]
- Chiew, F.H. Prediction of Blast Furnace Slag Concrete Compressive Strength Using Artificial Neural Networks and Multiple Regression Analysis. In Proceedings of the 2019 International Conference on Computer and Drone Applications (IConDA), Kuala Lumpur, Malaysia, 18–20 December 2019; pp. 54–58. [Google Scholar]
- Huang, Q.; Hong, D.; Niu, B.; Long, D.; Zhang, Y. An Interpretable Deep Learning Strategy for Effective Thermal Conductivity Prediction of Porous Materials. Int. J. Heat Mass Transf. 2024, 221, 125064. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Chen, Y.; Chang, J.Q.; Wei, D.F.; Jiang, Z.M. Machine Learning-Based Compressive Strength Prediction for Concrete: An Adaptive Boosting Approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Batool, F.; Bindiganavile, V. Air-void size distribution of cement based foam and its effect on thermal conductivity. Constr. Build. Mater. 2017, 149, 17–28. [Google Scholar] [CrossRef]
- Chou, J.S.; Chiu, C.K.; Farfoura, M.; Al-Taharwa, I. Optimizing the Prediction Accuracy of Concrete Compressive Strength Based on a Comparison of Data-Mining Techniques. J. Comput. Civ. Eng. 2011, 25, 242–253. [Google Scholar] [CrossRef]
- Khan, A.Q.; Awan, H.A.; Rasul, M.; Siddiqi, Z.A.; Pimanmas, A. Optimized Artificial Neural Network Model for Accurate Prediction of Compressive Strength of Normal and High Strength Concrete. Clean. Mater. 2023, 10, 100211. [Google Scholar] [CrossRef]
- Chaabene, W.B.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Bhanja, S.; Sengupta, B. Investigations on the Compressive Strength of Silica Fume Concrete Using Statistical Methods. Cem. Concr. Res. 2002, 32, 1391–1394. [Google Scholar] [CrossRef]
- Zain, M.F.M.; Abd, S.M. Multiple Regression Model for Compressive Strength Prediction of High Performance Concrete. J. Appl. Sci. 2009, 9, 155–160. [Google Scholar] [CrossRef]

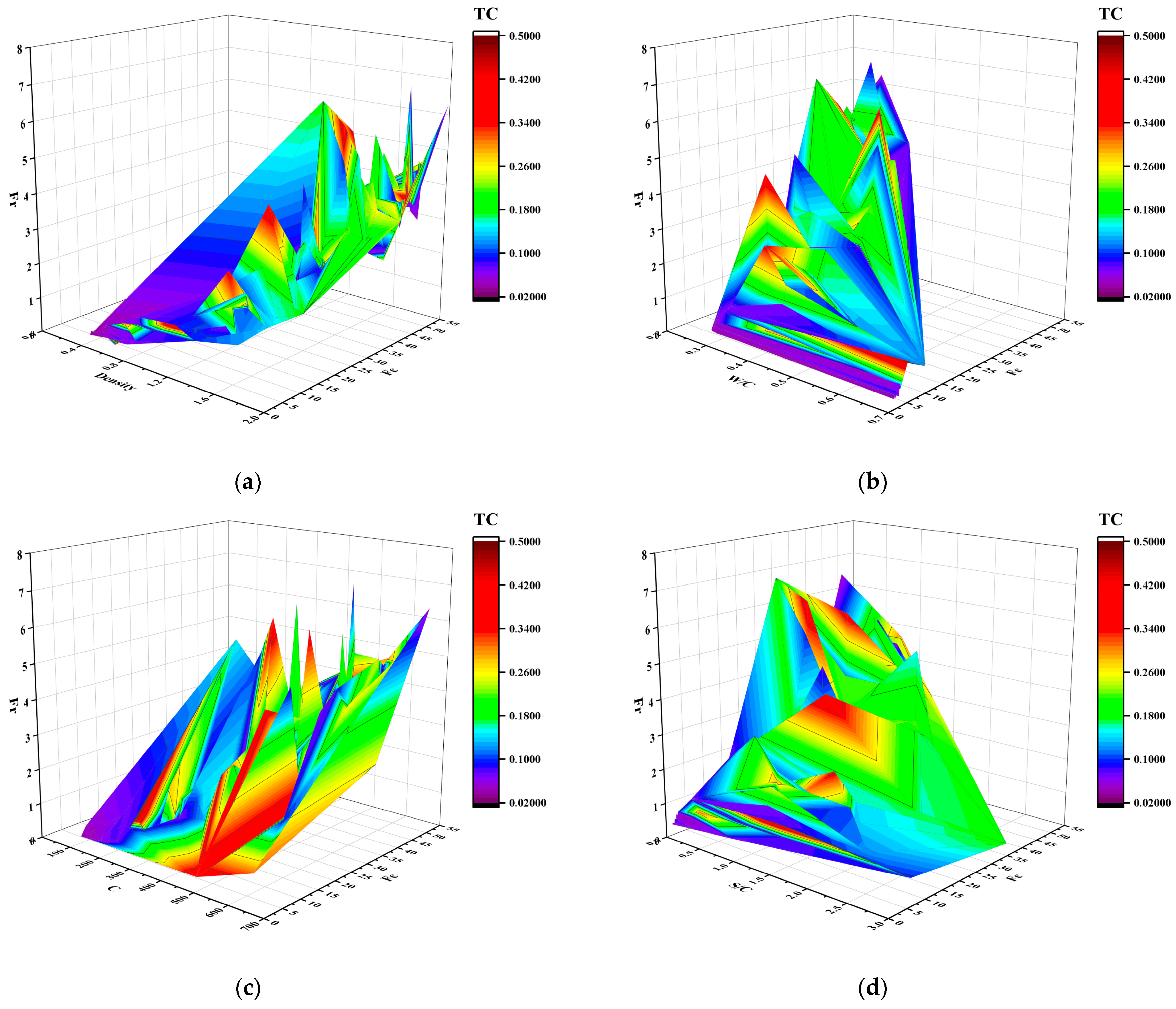
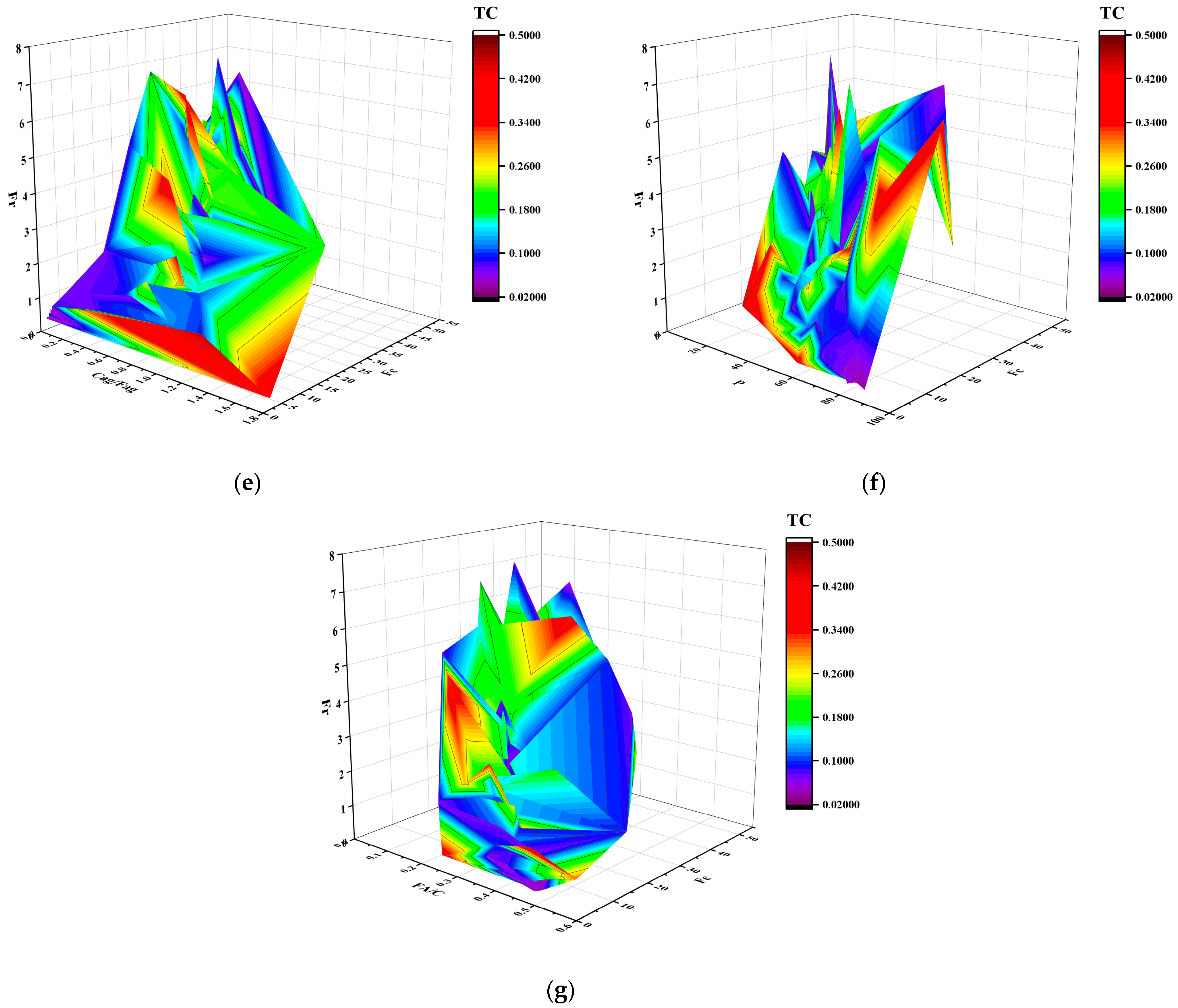
| Statistics | Density (g/cm3) | W/C Ratio | Cement Content (kg/m3) | S/C Ratio | Cag/Fag Ratio | P (%) | FA/C Ratio | Compressive Strength (MPa) | Flexural Strength (MPa) | Thermal Conductivity Coefficient (W/m·K) |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.53 | 0.41 | 414.94 | 0.99 | 0.43 | 37.61 | 0.22 | 24.15 | 2.63 | 0.15 |
| Max | 2.07 | 0.70 | 673 | 3.61 | 1.8 | 88 | 0.6 | 51.2 | 7.1 | 0.46 |
| Min | 0.43 | 0.26 | 120 | 0 | 0 | 8 | 0 | 15 | 0.2 | 0.04 |
| Range | 1.64 | 0.44 | 553 | 3.61 | 1.8 | 80 | 0.6 | 49.7 | 6.9 | 0.42 |
| Median | 1.65 | 0.35 | 445.5 | 1 | 0.4 | 32 | 0.18 | 26.06 | 2.66 | 0.16 |
| SE | 0.03 | 0.01 | 9.82 | 0.05 | 0.02 | 1.67 | 0.01 | 1.08 | 0.12 | 0.01 |
| Mode | 1.64 | 0.30 | 480 | 1 | 0 | 28 | 0.2 | 1.5 | 2.9 | 0.18 |
| Skewness | −1.21 | 1.35 | −0.72 | 0.61 | 0.78 | 0.79 | 0.57 | −0.16 | 0.29 | 0.85 |
| Kurtosis | 3.35 | 3.94 | 2.75 | 3.76 | 4.98 | 2.54 | 2.38 | 1.89 | 2.57 | 3.53 |
| SD | 0.43 | 0.12 | 0.12 | 0.68 | 0.31 | 21.91 | 0.14 | 14.01 | 1.55 | 0.01 |
| Evaluation Parameters | RMSE (Root Mean Squared Error) | MAE (Mean Absolute Error) | MAPE (Mean Absolute Percentage Error) | R2 (Coefficient of Determination) |
|---|---|---|---|---|
| Equation | ||||
| Range | [0, +∞) | [0, +∞) | [0%, +∞) | (−∞, 1] |
| Optimal value | 0 | 0 | 0% | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sun, W.; Ayti, A.; Chen, W.; Liu, Z.; Gómez-Zamorano, L.Y. Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions. Appl. Sci. 2025, 15, 7125. https://doi.org/10.3390/app15137125
Li L, Sun W, Ayti A, Chen W, Liu Z, Gómez-Zamorano LY. Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions. Applied Sciences. 2025; 15(13):7125. https://doi.org/10.3390/app15137125
Chicago/Turabian StyleLi, Leifa, Wangwen Sun, Askar Ayti, Wangping Chen, Zhuangzhuang Liu, and Lauren Y. Gómez-Zamorano. 2025. "Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions" Applied Sciences 15, no. 13: 7125. https://doi.org/10.3390/app15137125
APA StyleLi, L., Sun, W., Ayti, A., Chen, W., Liu, Z., & Gómez-Zamorano, L. Y. (2025). Machine Learning Modeling of Foam Concrete Performance: Predicting Mechanical Strength and Thermal Conductivity from Material Compositions. Applied Sciences, 15(13), 7125. https://doi.org/10.3390/app15137125








