Study on the Propulsion Characteristics of a Flapping Flat-Plate Pumping Device
Abstract
Featured Application
Abstract
1. Introduction
2. Physical Model
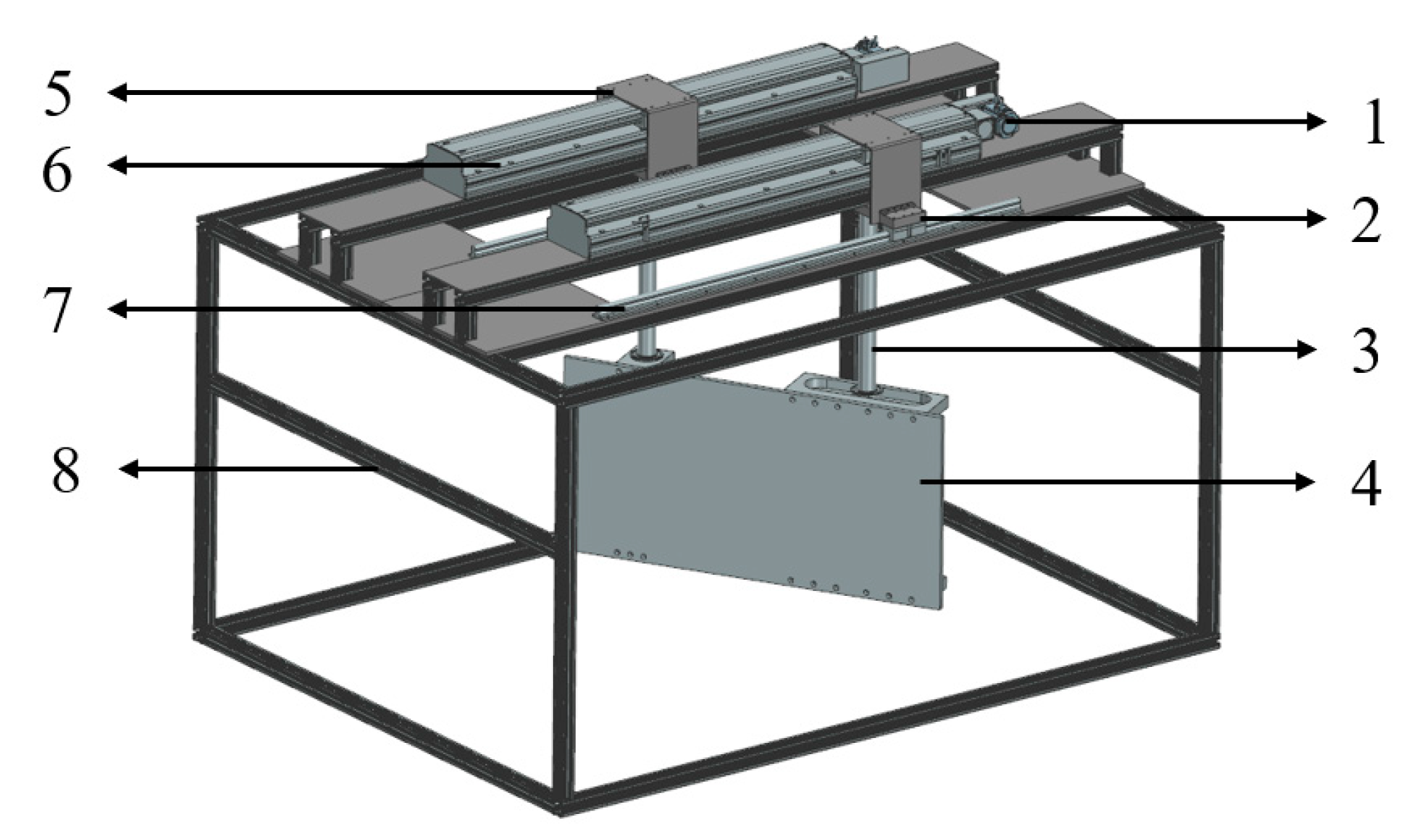
2.1. Structure and Working Principle of the Flapping Flat-Plate Device
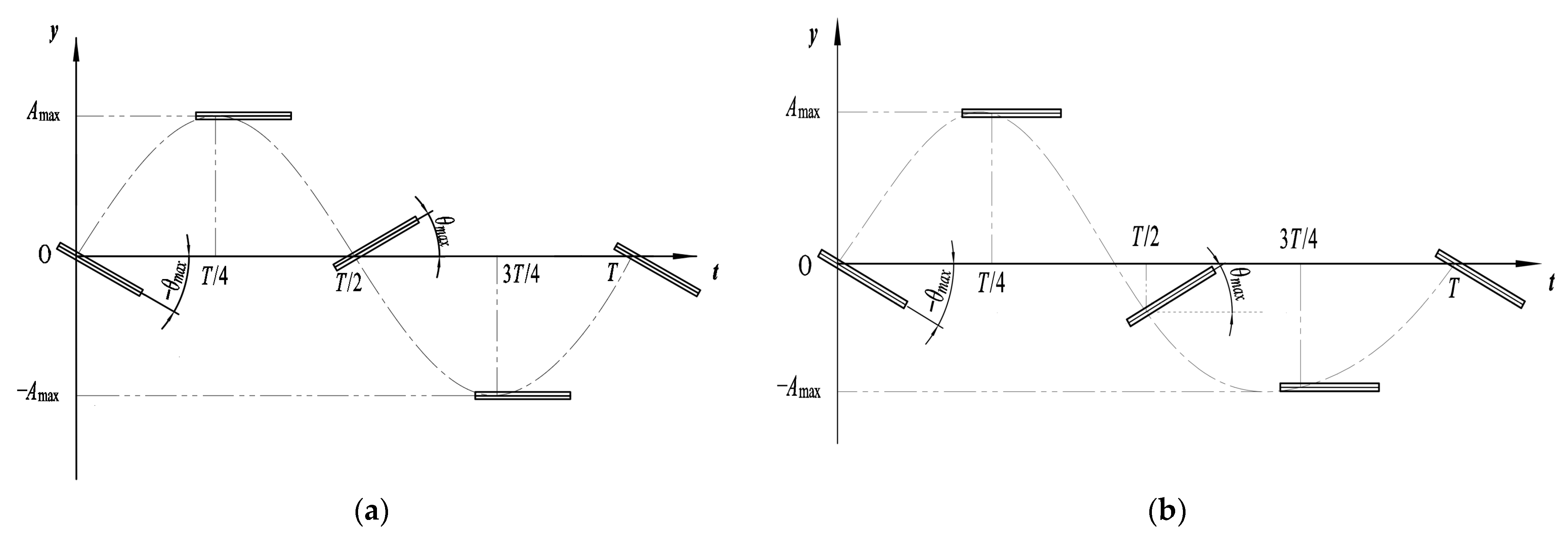
2.2. Motion Model
2.3. Hydrodynamic Performance Parameters
3. Numerical Simulation Method
3.1. Governing Equations and Turbulence Model
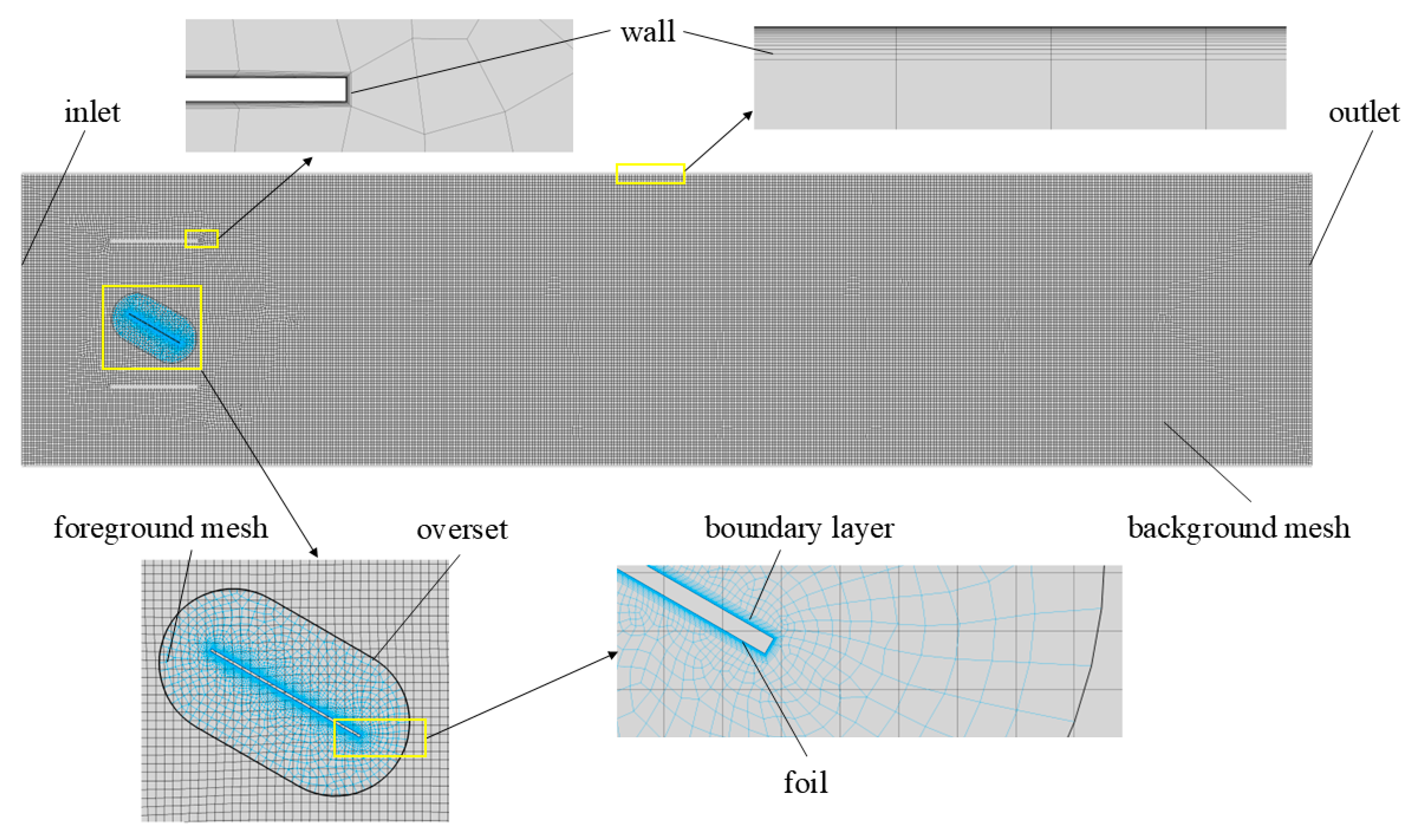
3.2. Mesh Generation and Computational Setup
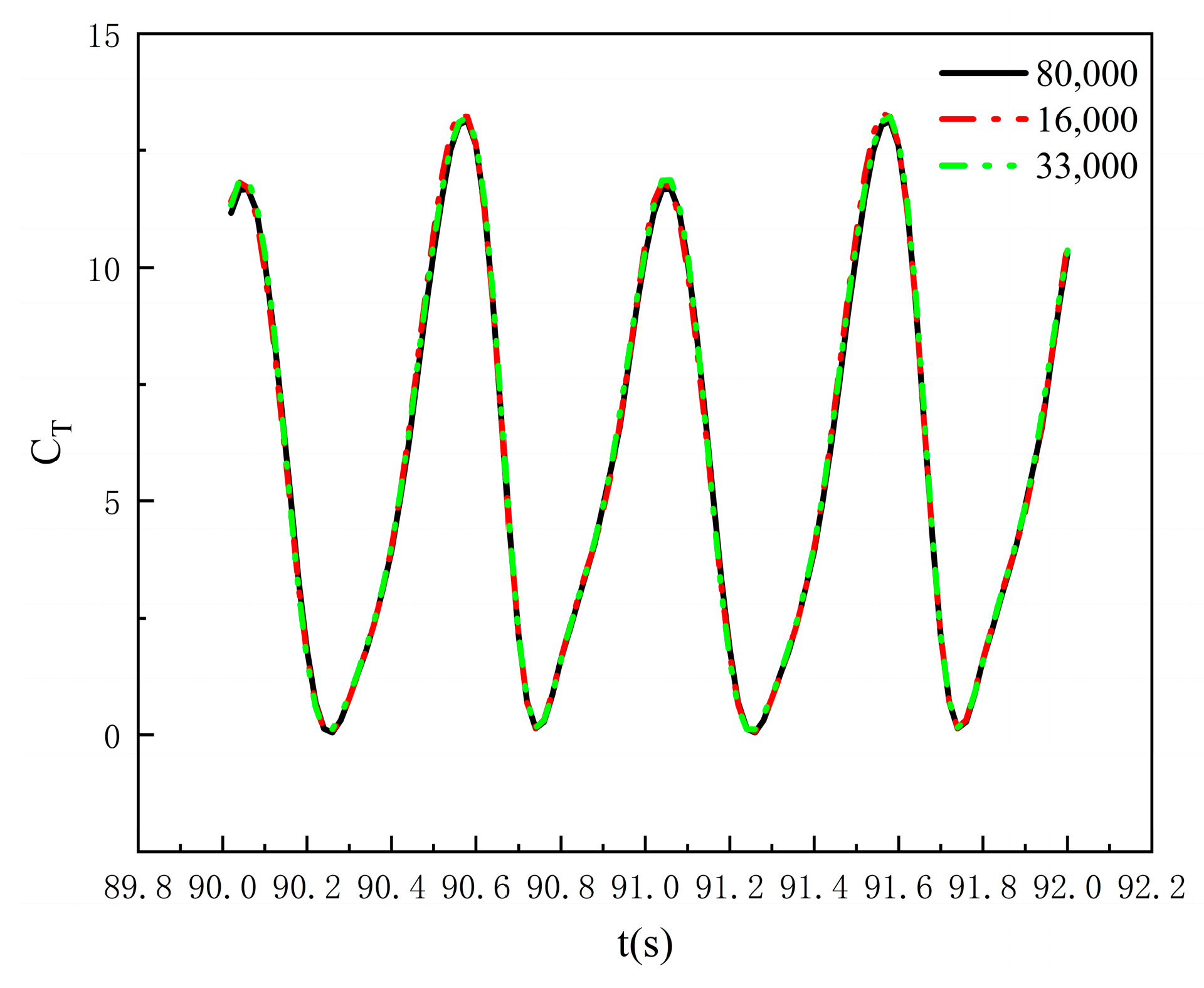
3.3. Grid Independence Verification
3.4. Method Validation
4. Results
4.1. Impact of Flapping Mode on Water Body
4.1.1. Effect of Flapping Mode on Thrust and Lift
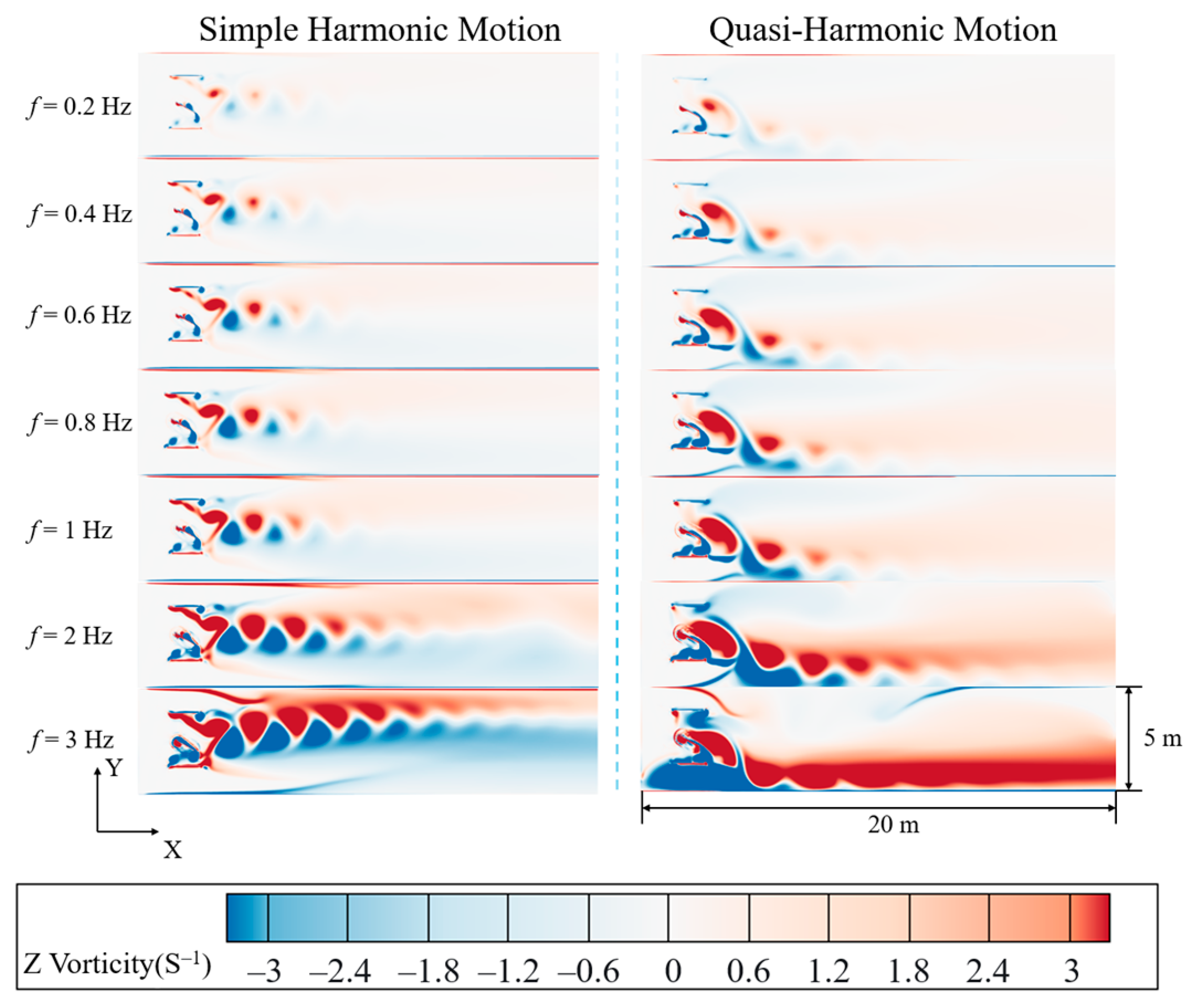
4.1.2. Effect of Motion Mode on the Flow Field
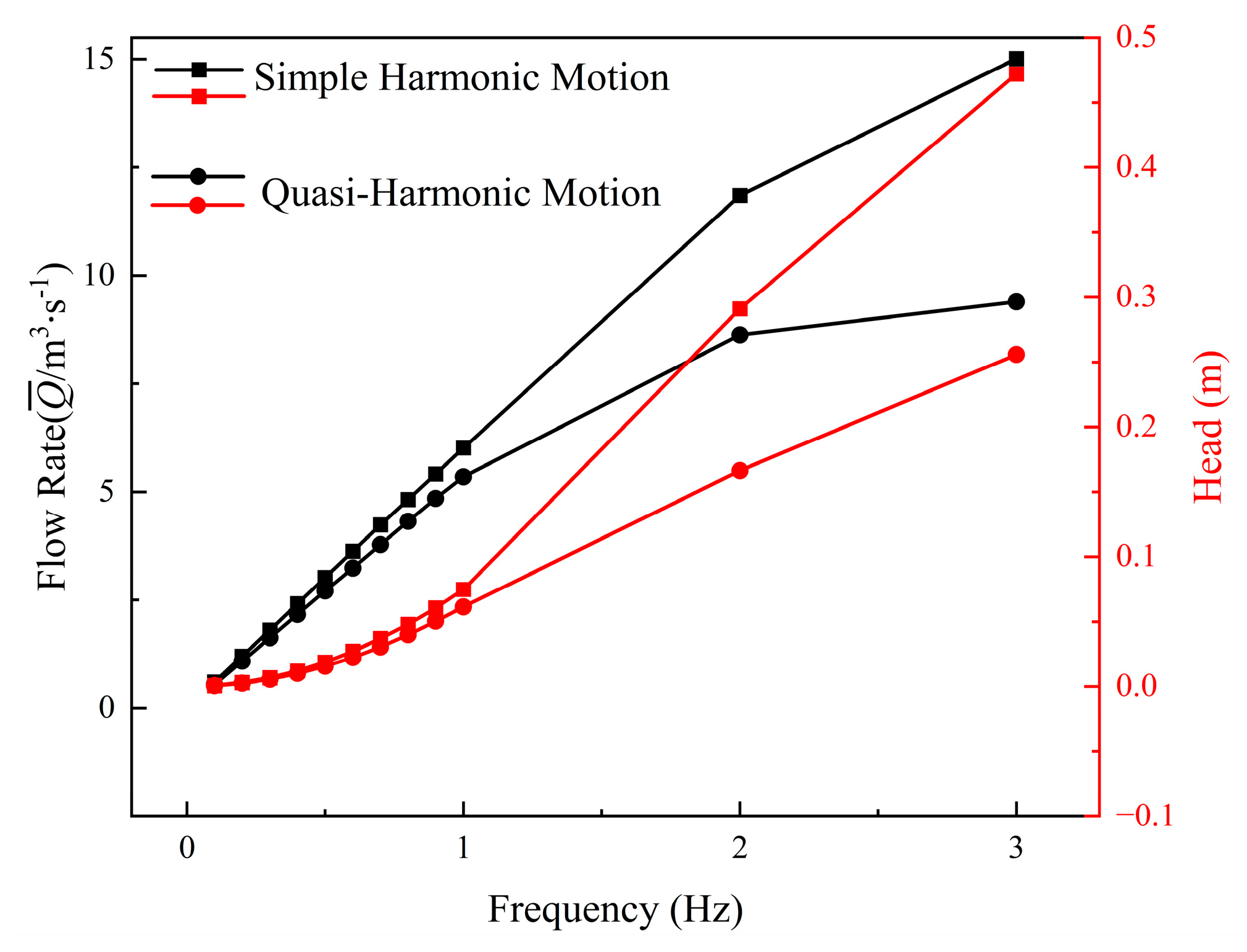
4.1.3. Effect of Motion Mode on Water-Pushing Performance
4.2. Effect of Flow Channel Structure on the Water Body
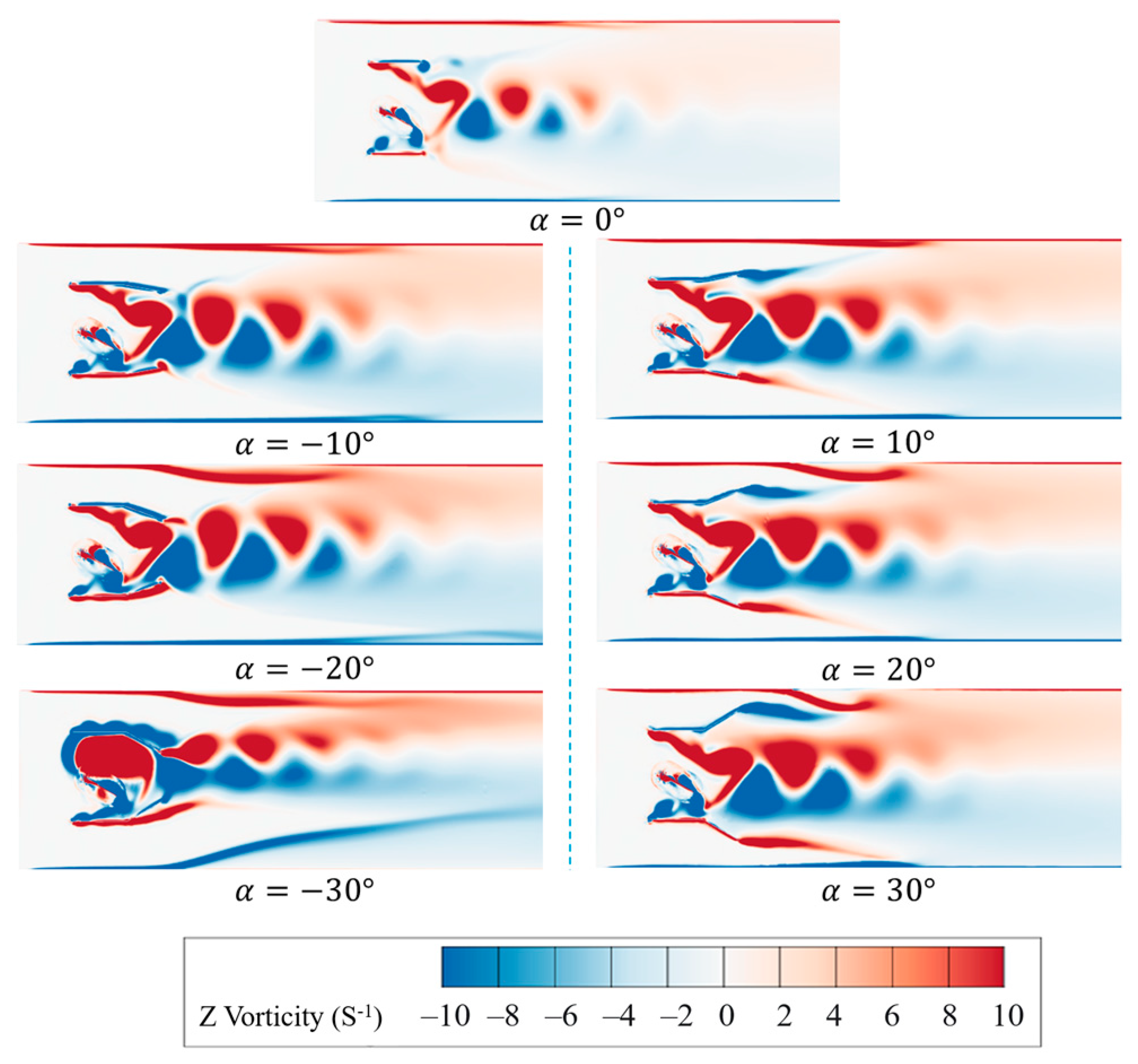
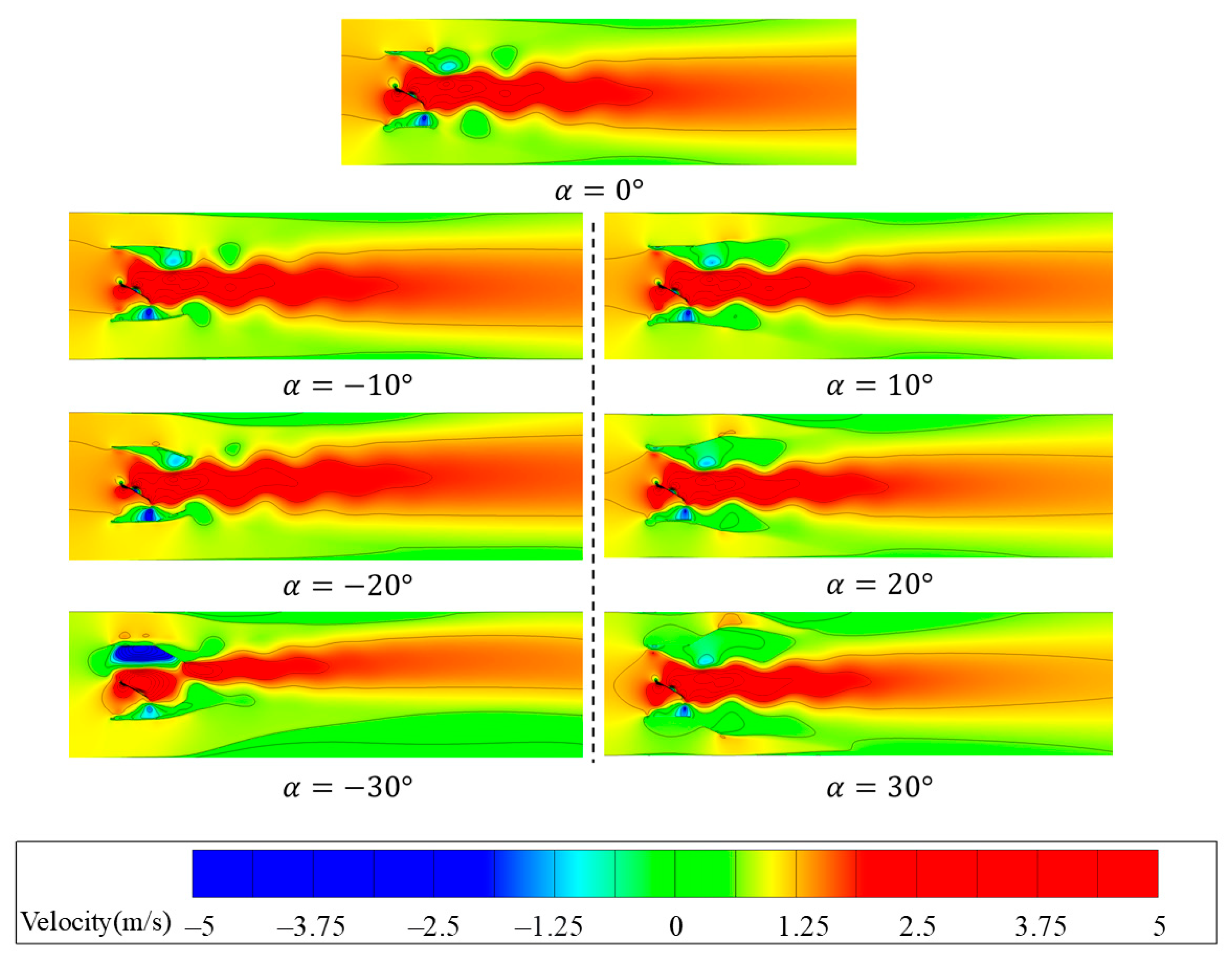
4.2.1. Effect of Flow Channel Structure on the Flow Field
4.2.2. Effect of Flow Channel Structure on Water-Pushing Performance
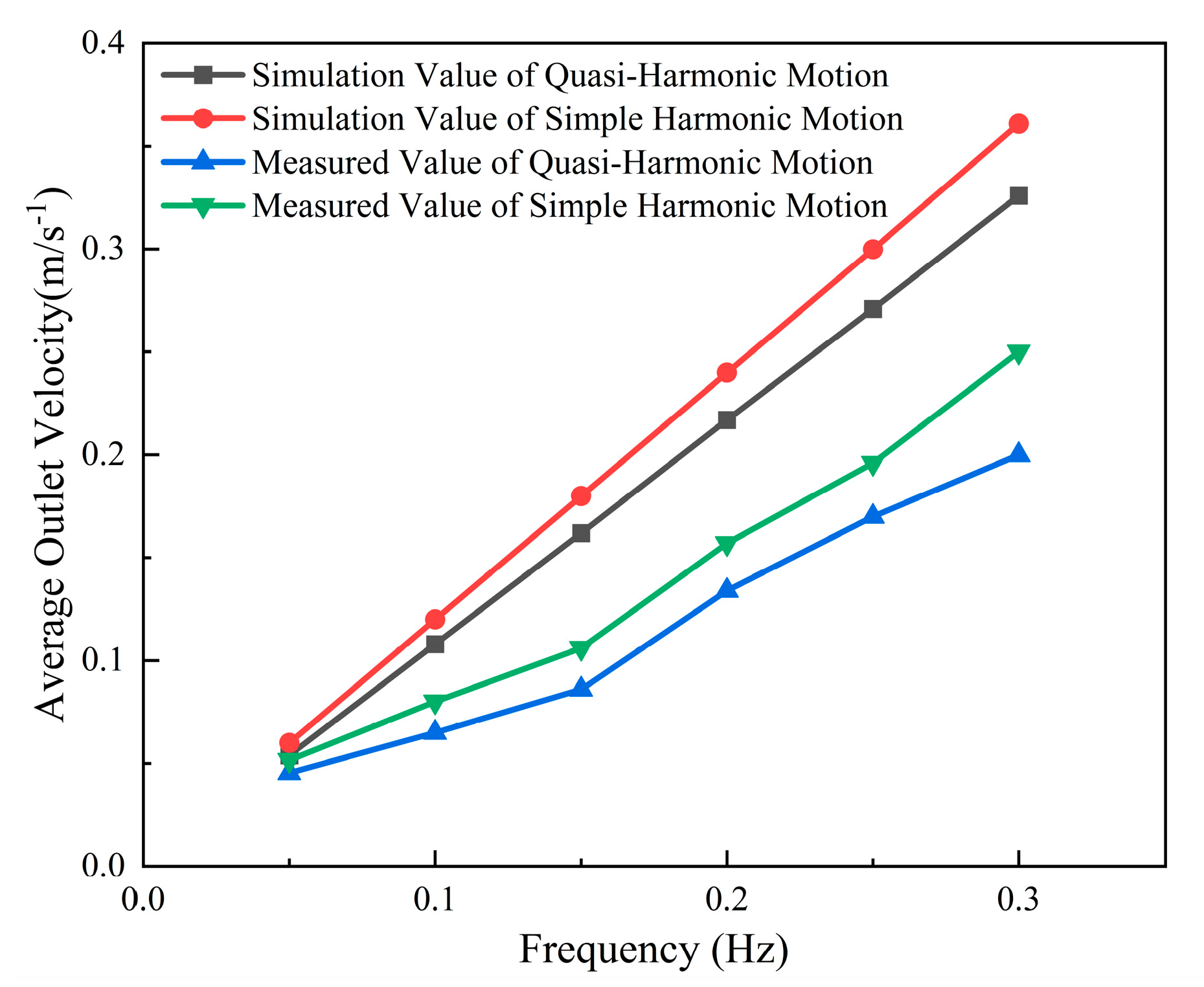
4.3. Experimental Validation
5. Conclusions
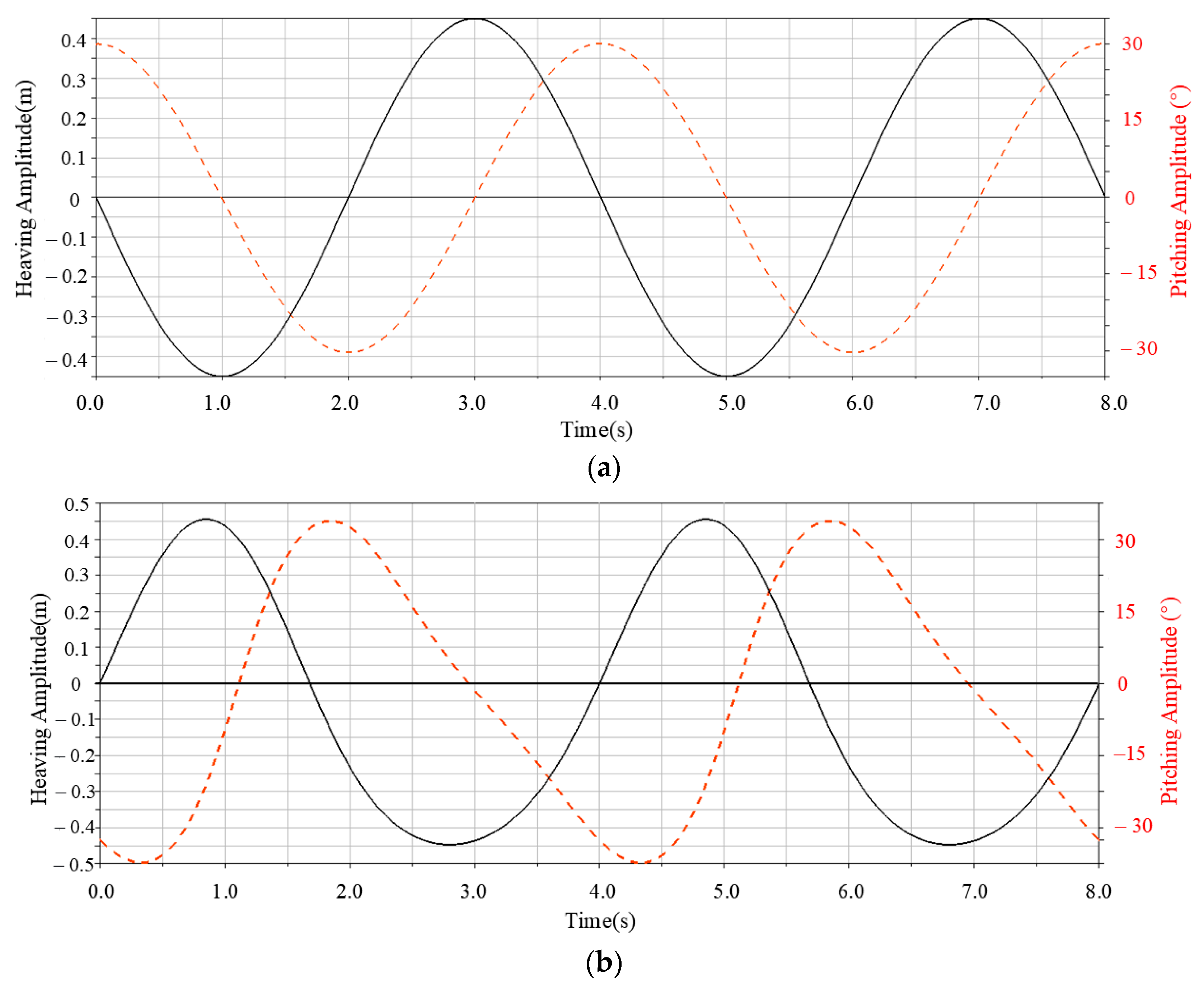
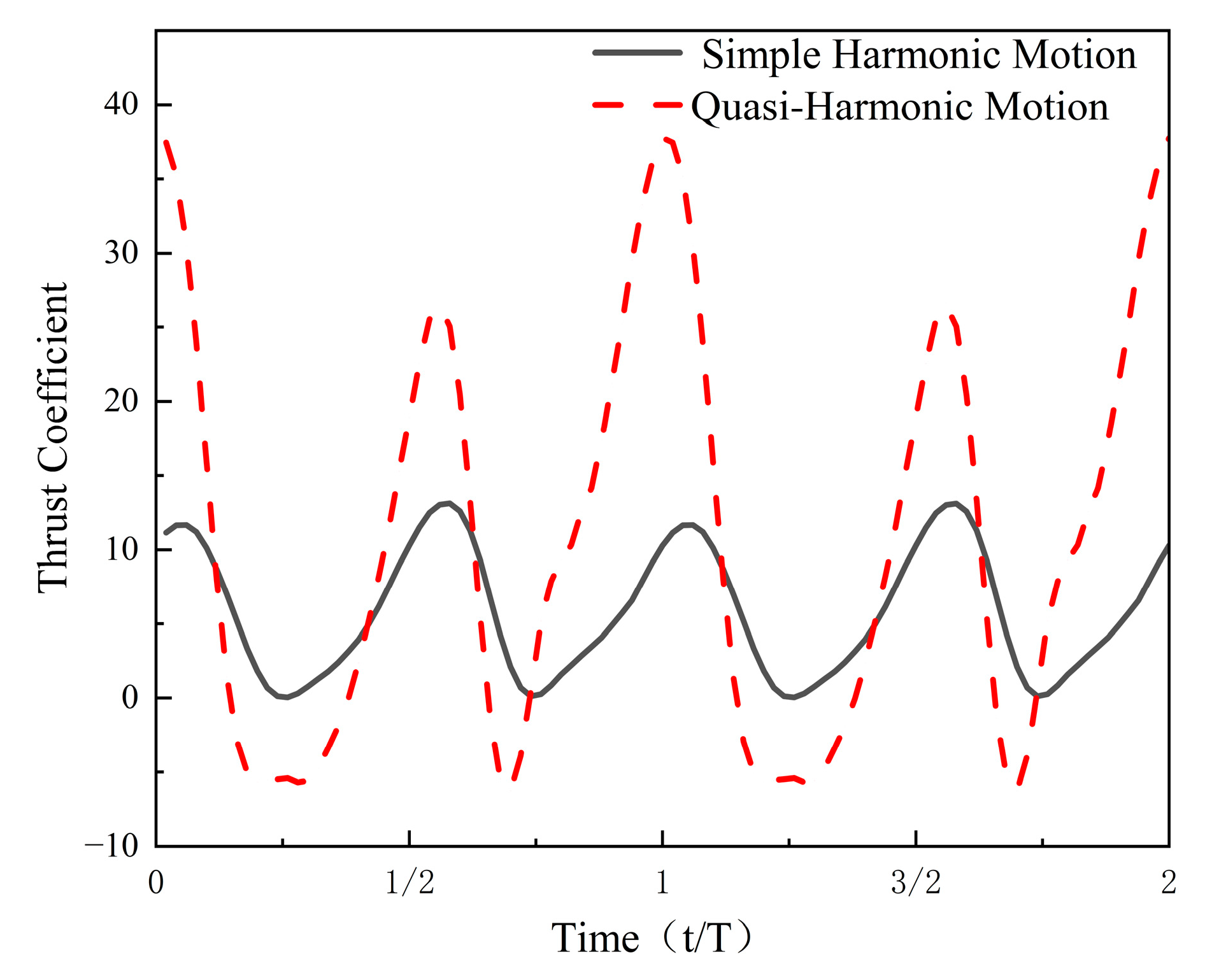
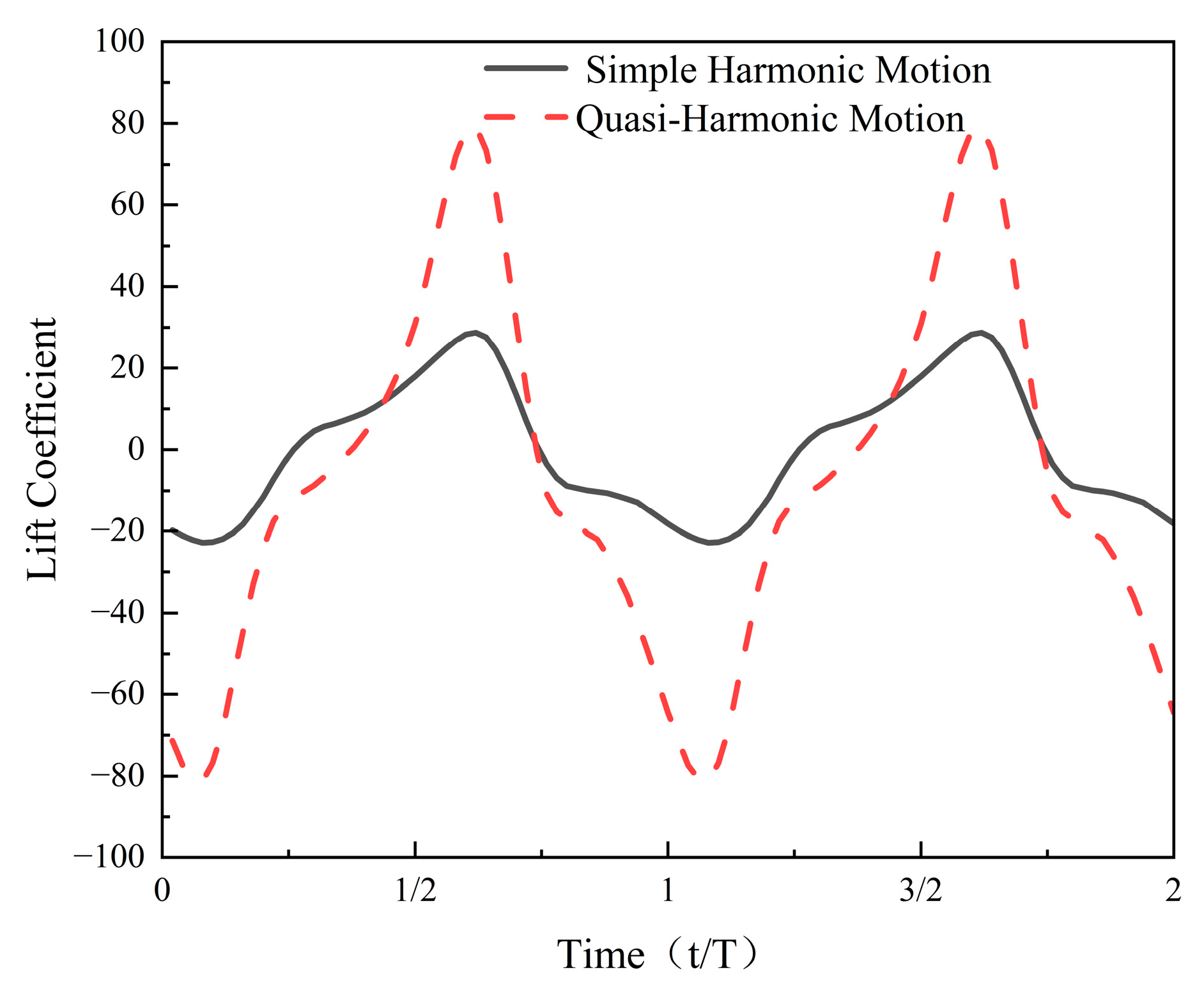
- Both simple harmonic and quasi-harmonic motions generate reverse Kármán vortex streets, but differences exist in wake structure and thrust characteristics. The wake generated by simple harmonic motion exhibits good symmetry, while the wake in quasi-harmonic motion deflects downward, with the degree of deflection increasing as the flapping frequency rises.
- Simple harmonic motion maintains a relatively high pumping efficiency overall, reaching a maximum of 21.5% at a flapping frequency of 0.7 Hz. In contrast, the pumping efficiency of quasi-harmonic motion fluctuates more significantly across frequencies, with a peak of 17.8% at 0.6 Hz. At this frequency, the pumping efficiency of simple harmonic motion is still 20.2% higher than the peak value of quasi-harmonic motion.
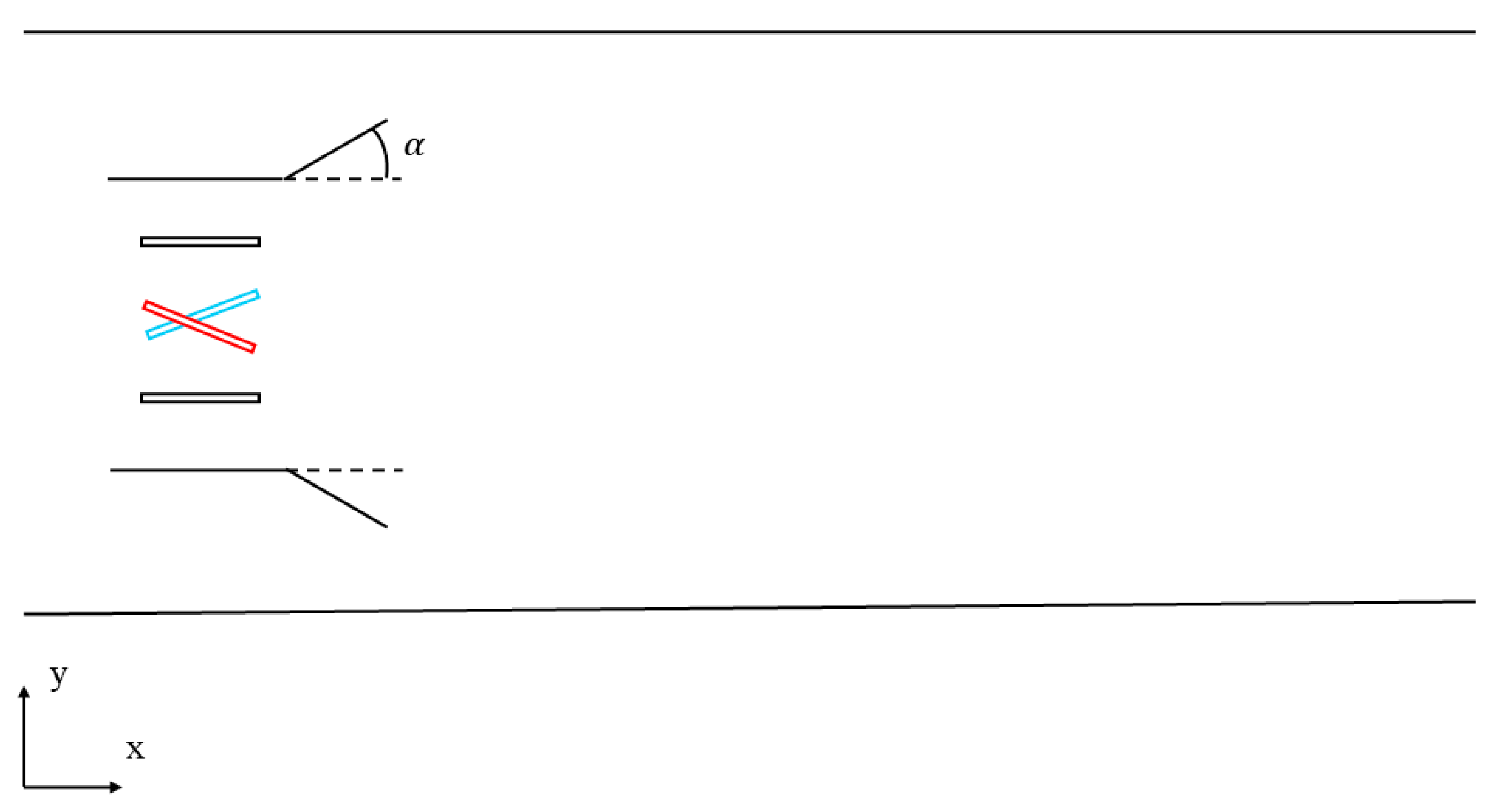
- Variation in the channel outlet angle does not significantly change the number of vortices but does affect their spatial distribution. Negative outlet angles enhance flow separation at the channel exit, resulting in more concentrated vortices near the outlet. However, at α = −30°, a distinct recirculation region appears above the outlet, causing the wake to deflect upward and compromising the directionality of water propulsion. In contrast, positive outlet angles cause the fluid to stretch along the outlet direction under wall shear effects, forming elongated vortex structures. As the angle increases, the boundary layer entrainment effect becomes more pronounced, altering the wake expansion pattern and leading to reduced water-pushing performance.
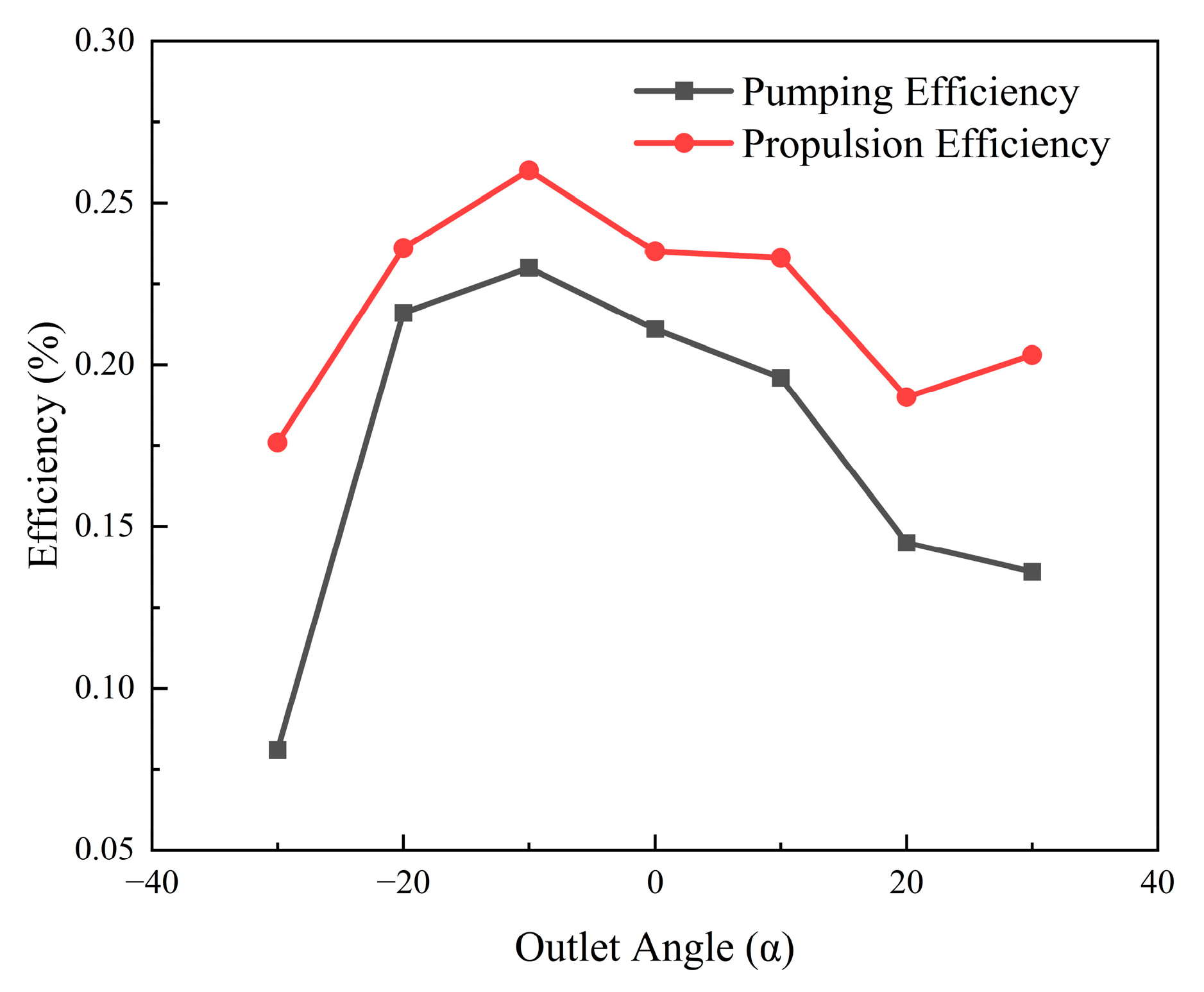
- With variation in the channel outlet angle, pumping efficiency and propulsion efficiency exhibit a strong positive correlation. Both reach their peak values at α = −10°, with pumping efficiency at 22.9% and propulsion efficiency at 25.9%. Compared to α = 0°, pumping efficiency increases by 8.5% and propulsion efficiency by 10.2%. A moderate negative angle helps enhance fluid propulsion performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, D.; Lu, P.; Yu, G. Study On The Activity of the Contaminative Water and the Impact on the Water Pollution of Change in Urban River-Net in the East Plain Region of China. Environ. Eng. 2011, 29, 59–62. [Google Scholar]
- Ma, C.; Tang, Z.; Xu, K.; He, W.; Zhao, M. Study on Water Replenishment Scheduling Strategies for Water Quality Improvement of Urban River Network in Plain Area: A Case Study of Urban Central River Network in Tianjin. South-to-North Water Transf. Water Sci. Technol. 2017, 15, 81–87. [Google Scholar]
- Wang, C.; Wei, Z.; Zhang, L.; Zuo, J. Experimental Study on Improvement of Water Environment by Water Diversion in Plain River Networks. J. Hohai Univ. (Nat. Sci.) 2005, 2, 136–138. [Google Scholar]
- Hu, Y. Analysis of Water Analysis of the Effects of Water Diversion Works for Water Environment Improvement in the Hangjiahu District. Master’s Thesis, Zhejiang University, Hangzhou, China, 2010. [Google Scholar]
- Chen, L.; Xu, L.; Zhang, X.; Yan, S.; Wang, D. Characteristics of Pressure Fluctuation in Pump System with Low Head. J. Drain. Irrig. Mach. Eng. 2020, 38, 121–126+144. [Google Scholar]
- Yu, S.; Li, Y.; Cheng, Y.; Shi, Y.; Cheng, Y.; Huang, Y.; Zhu, Y.; Pan, H.; Yue, Z.; Zheng, K. The Impacts of Water Diversion on Hydrodynamic Regulation of Plain River Network. J. Lake Sci. 2021, 33, 462–473. [Google Scholar]
- Jin, Q.; Chen, K.; Yuan, L. Motion Simulation Analysis of Three-Joint Caudal Fin Robotic Fish. Mach. Tool Hydraul. 2023, 51, 45–49. [Google Scholar]
- Katzschmann, R.K.; DelPreto, J.; MacCurdy, R.; Rus, D. Exploration of Underwater Life with an Acoustically Controlled Soft Robotic Fish. Sci. Robot. 2018, 3, eaar3449. [Google Scholar] [CrossRef]
- Hua, E.; Tang, S.; Chen, W.; Xie, R.; Guo, X. Analysis on Influence of Swinging Modes of Swing Hydrofoil on Water Propulsion. J. Hydroelectr. Eng. 2022, 41, 93–103. [Google Scholar]
- Yu, J.; Zhou, Z.; Liu, J. Research Progress and Analysis on Multiple Autonomous Underwater Vehicle Systems. Inf. Control. 2021, 50, 129–140. [Google Scholar]
- Xu, J.; Sun, H. Experimental Studies of Passive Oscillating Hydrofoil for Tidal Current Energy Extracting. J. Harbin Eng. Univ. 2016, 37, 248–253. [Google Scholar]
- Totpal, D.A.; Siala, F.F.; Liburdy, A.J. Energy Harvesting of an Oscillating Foil at Low Reduced Frequencies with Rigid and Passively Deforming Leading Edge. J. Fluids Struct. 2018, 82, 329–342. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, H.; Wang, Q.; Zhang, B. Optimization of Multi-Organism Cooperative Propulsion Efficiency of Bionic Thunniform Fish Robot. J. South China Univ. Technol. (Nat. Sci. Ed.) 2018, 46, 109–115+122. [Google Scholar]
- Lin, T.; Xia, W.; Pecora, R.; Wang, K.; Hu, S. Performance Improvement of Flapping Propulsions from Spanwise Bending on a Low-Aspect-Ratio Foil. Ocean. Eng. 2023, 284, 115305. [Google Scholar] [CrossRef]
- Hua, E.; Xiang, M.; Sun, Q.; Wang, T.; Song, Y.; Lu, C. Bidirectional Fluid–Structure Interaction Study on Hydrofoil Hardness and Oscillation Mode Optimization. Appl. Sci. 2025, 15, 825. [Google Scholar] [CrossRef]
- Ding, H.; Song, B.; Tian, L. Exploring Propulsion Performance Analysis of Bionic Flapping Hydrofoil. J. Northwest. Polytech. Univ. 2013, 31, 150–156. [Google Scholar]
- Du, X.; Zhang, Z. Numerical Analysis of Influence of Four Flapping Modes on Propulsion Performance of Underwater Flapping Foils. Eng. Mech. 2018, 35, 249–256. [Google Scholar]
- Liu, H.; Su, Y.; Pang, Y. Influence of Non-Sinusoidal Oscillation on the Hydrodynamic Performance of Hydrofoils. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 44, 15–20. [Google Scholar]
- Peng, L.; Yu, Z.; Zhang, W.; Wang, N.; Luo, J. Effects of Different Paddling Motion Patterns and Flexibility on Hydrofoil Propulsion Performance. Ocean. Eng. 2023, 288 Pt 1, 116086. [Google Scholar] [CrossRef]
- Wu, F.; Dong, X.; Wu, Y.; Ma, D.; Feng, X. Hydraulic Properties of the Flow in a Gradual Shrinking and Sudden Enlarging Channel. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2017, 38, 61–67. [Google Scholar]
- Li, Y.; Wang, J.; Chen, J. Numerical Investigation of Pitching Foil’s Propulsive Performance with Wall Effect. Nav. Archit. Ocean. Eng. 2020, 36, 26–31. [Google Scholar]
- Wang, J.; Meng, Z.; Feng, W.; Han, A.; Xie, Y.H.; Xie, D.M. Effect of Shroud on the Energy Extraction Performance of Oscillating Foil. Energy 2022, 239, 122387. [Google Scholar]
- Bin, X.; Qiyu, M.; Diangui, H. Research on Energy Harvesting Properties of a Diffuser-Augmented Flapping Wing. Renew. Energy 2021, 180, 271–280. [Google Scholar]
- Dahmani, F.; Sohn, C. Effect of Convergent Duct Geometry on the Energy Extraction Performance of Tandem Oscillating Hydrofoils System. J. Fluids Struct. 2020, 95, 102949. [Google Scholar] [CrossRef]
- Hadi, S.; Madjid, A.; Masoud, D. Numerical Study to Evaluate the Important Parameters Affecting the Hydrodynamic Performance of Manta Ray’s in Flapping Motion. Appl. Ocean. Res. 2021, 109, 102559. [Google Scholar]
- Hua, E.; Luo, H.; Xie, R.; Chen, W.; Tang, S.; Su, Z. Design and Test of Flapping Hydrofoil Bionic Water Pumping Device. Trans. Chin. Soc. Agric. Mach. 2023, 54, 155–162. [Google Scholar]
- Brinker, A.; Rösch, R. Factors Determining the Size of Suspended Solids in a Flow-Through Fish Farm. Aquac. Eng. 2005, 33, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Zhang, Z. Hydrodynamic study of bionic propulsion for 2-D flapping foil. Chin. J. Hydrodyn. 2006, 632–639. [Google Scholar]
- Zi, D.; Wang, F.; Tao, R.; Hou, Y. Research for Impacts of Boundary Layer Grid Scale on Flow Field Simulation Results in Pumping Station. J. Hydraul. Eng. 2016, 47, 139–149. [Google Scholar]
- Hu, F.; Zhao, W.; Huang, Y.; Yu, J. Study on Propulsion Performance of Three-dimensional Passive Swinging Hydrofoil on Wave Glider. J. Mech. Eng. 2020, 56, 243–249. [Google Scholar]
- Mountris, K.A.; Pueyo, E. Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method. Appl. Sci. 2023, 13, 11460. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Naji, A.; Lee, T.-L.; Cavoretto, R.; Young, D.L. Bending analysis of quasicrystal plates using adaptive radial basis function method. J. Comput. Appl. Math. 2024, 450, 115990. [Google Scholar] [CrossRef]
- Read, D.; Hover, F.; Triantafyllou, M. Forces on Oscillating Foils for Propulsion and Maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar] [CrossRef]
- Chen, Y.; Zhan, J.; Wu, J.; Wu, J. A Fully-Activated Flapping Foil in Wind Gust: Energy Harvesting Performance Investigation. Ocean. Eng. 2017, 138, 112–122. [Google Scholar] [CrossRef]
- Duy, Q.N.; Chengwang, L. Hydrodynamic Characteristics of a Confined Circular Cylinder in Cross-Flows. Ocean. Eng. 2021, 221, 108567. [Google Scholar]
- Zhang, G. Hydrodynamic Hydrodynamic Analysis and Experimental Study on Swinging Propulsion of Two-Dimensional Rigid Wing. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, E.; Lin, Y.; Li, S.; Wu, X.; Xiang, M. Study on the Propulsion Characteristics of a Flapping Flat-Plate Pumping Device. Appl. Sci. 2025, 15, 7034. https://doi.org/10.3390/app15137034
Hua E, Lin Y, Li S, Wu X, Xiang M. Study on the Propulsion Characteristics of a Flapping Flat-Plate Pumping Device. Applied Sciences. 2025; 15(13):7034. https://doi.org/10.3390/app15137034
Chicago/Turabian StyleHua, Ertian, Yang Lin, Sihan Li, Xiaopeng Wu, and Mingwang Xiang. 2025. "Study on the Propulsion Characteristics of a Flapping Flat-Plate Pumping Device" Applied Sciences 15, no. 13: 7034. https://doi.org/10.3390/app15137034
APA StyleHua, E., Lin, Y., Li, S., Wu, X., & Xiang, M. (2025). Study on the Propulsion Characteristics of a Flapping Flat-Plate Pumping Device. Applied Sciences, 15(13), 7034. https://doi.org/10.3390/app15137034




