Research on Control Technology of Large-Section Water-Bearing Broken Surrounding Rock Roadway
Abstract
1. Introduction
2. Engineering Summary and Analysis of Surrounding Rock Failure Characteristics
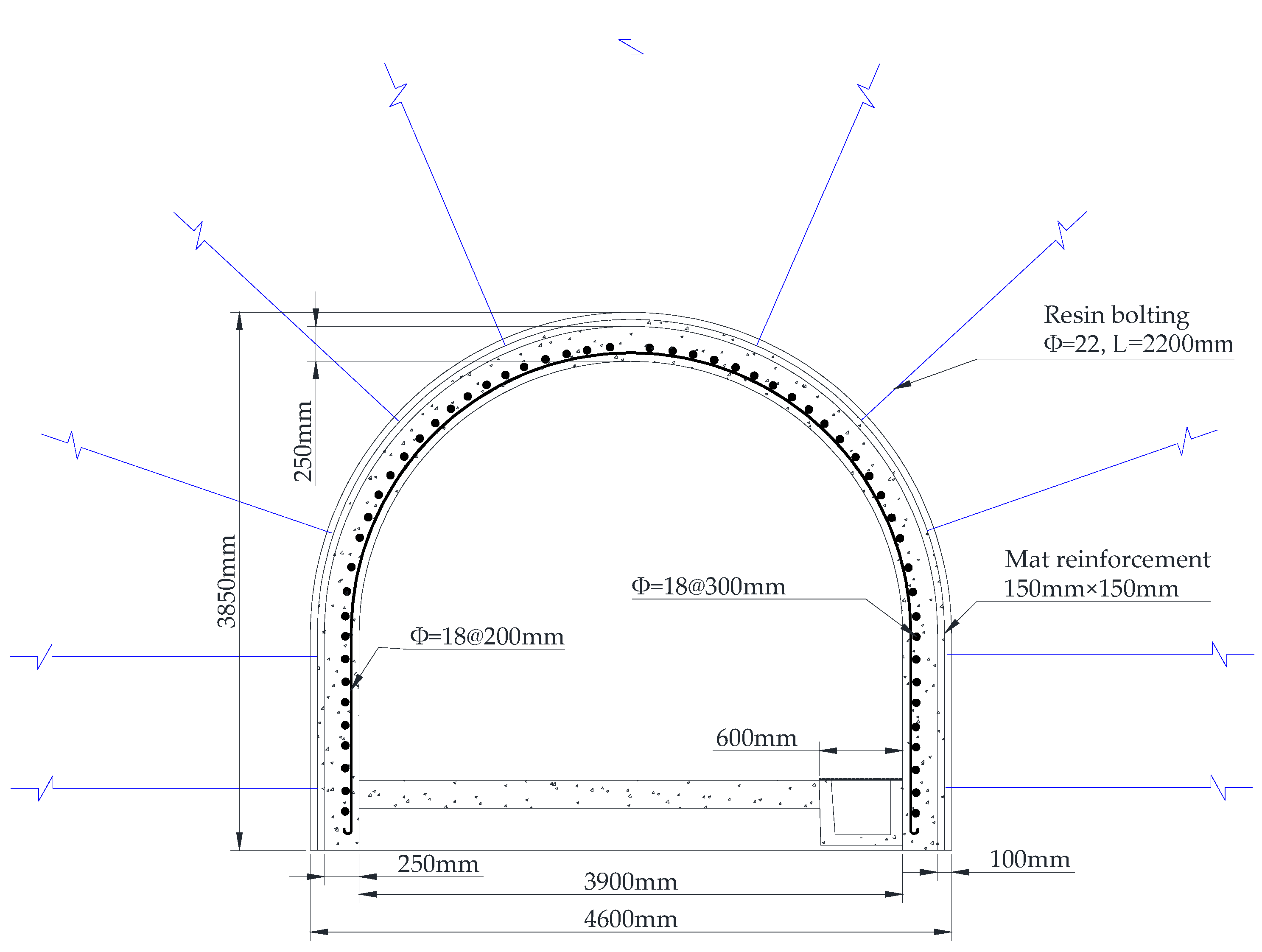
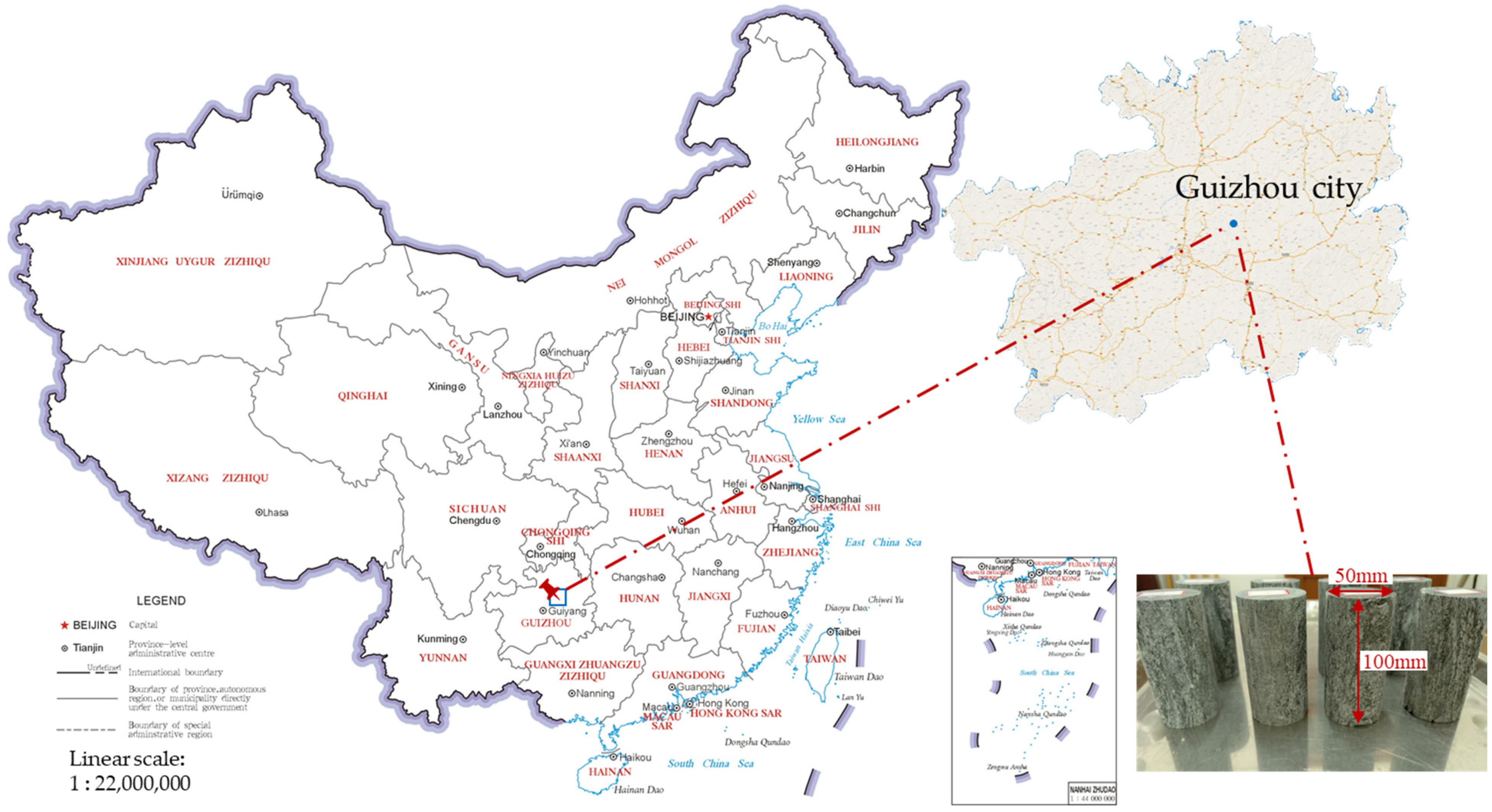
2.1. Engineering Summary
2.2. Analysis of Failure Characteristics of Surrounding Rock of Roadway
3. Analysis of Influence Range and Displacement of Roadway Surrounding Rock Fracture Zone Under Pore Water Pressure
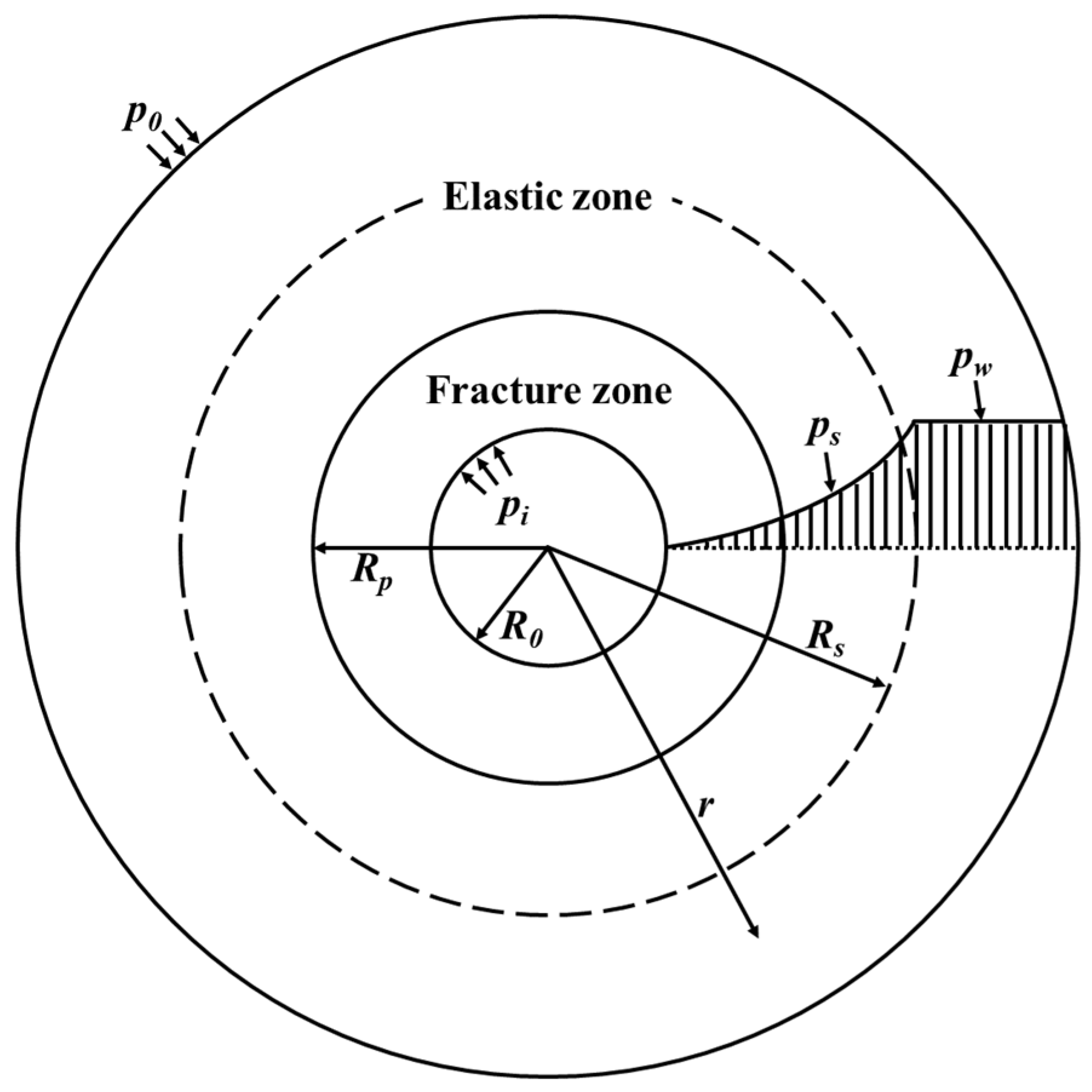
3.1. Theoretical Model Establishment and Analysis of Roadway
- C—Cohesion;
- E—Elastic modulus;
- φ—Angle of internal friction;
- μ—Poisson’s ratio.
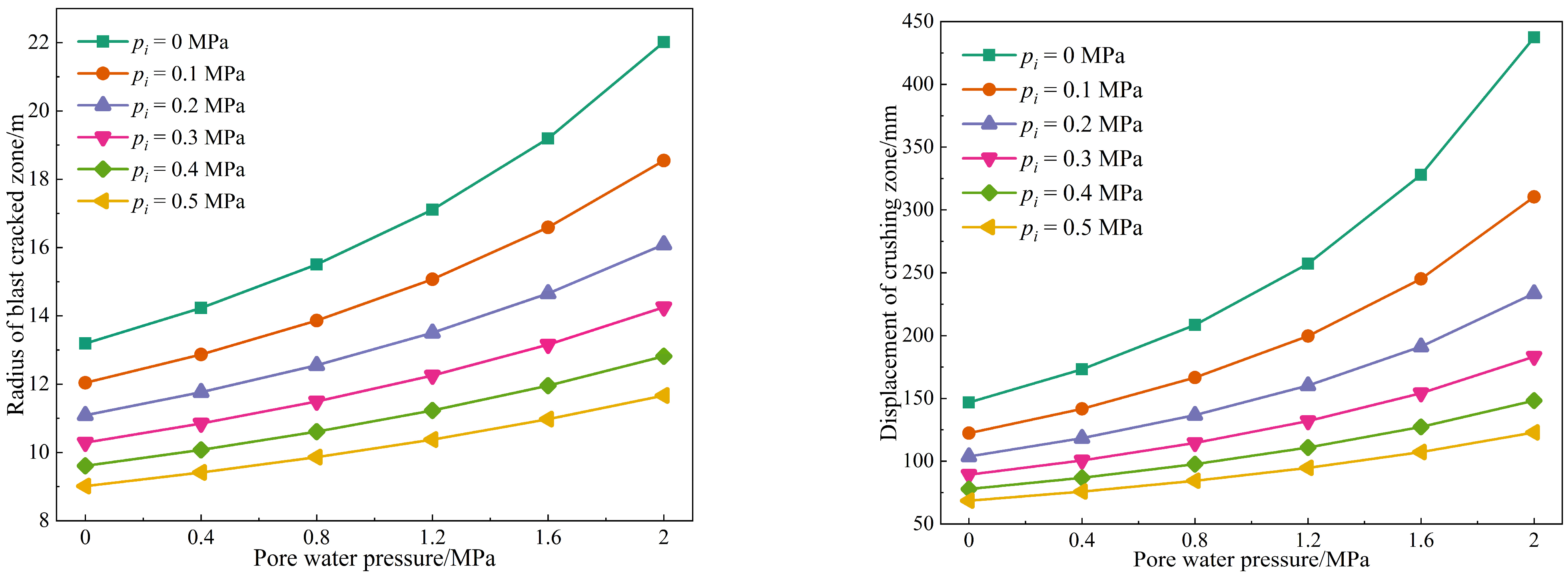
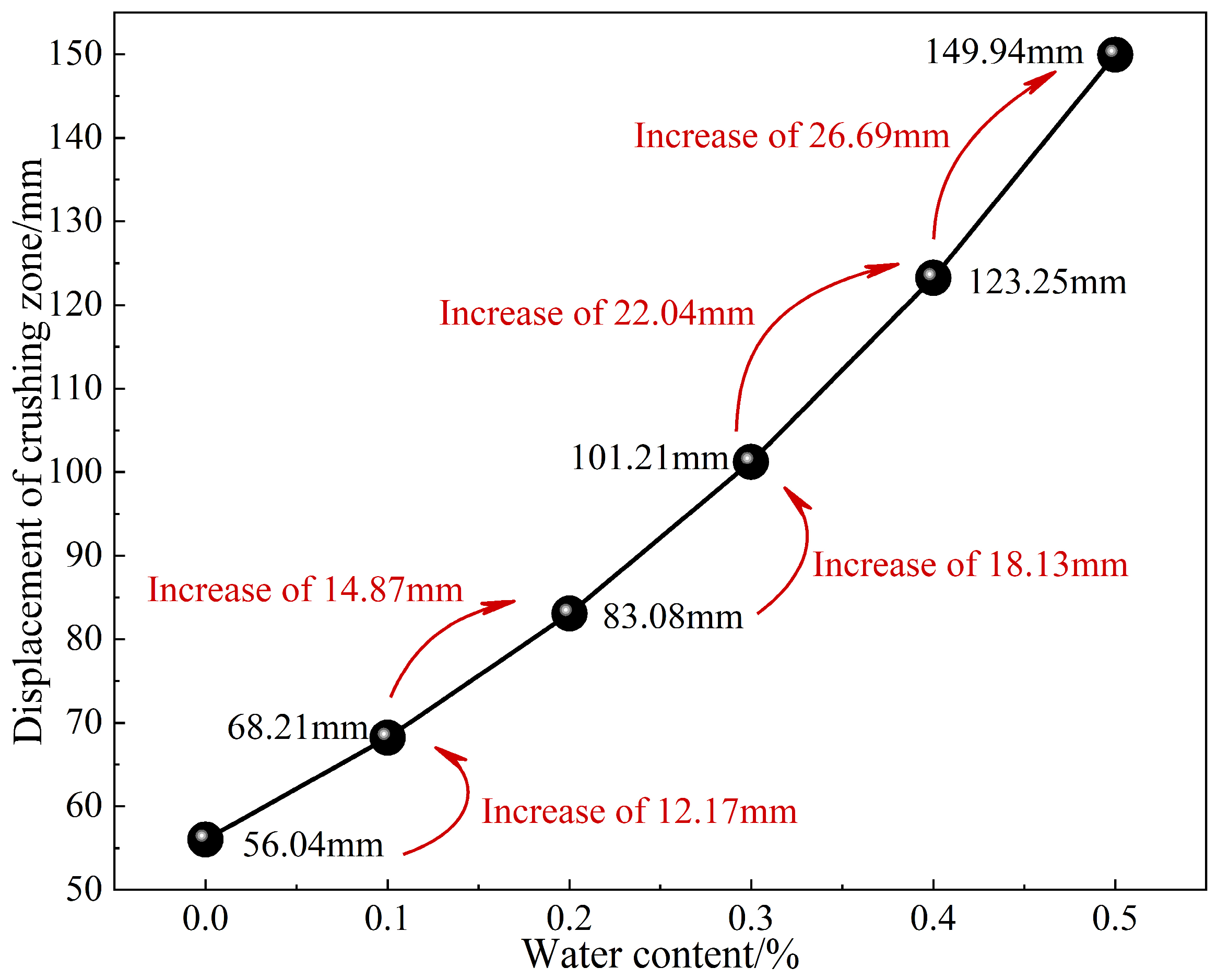
3.2. Analysis of the Influence of Pore Water Pressure on the Radius and Displacement of the Fracture Zone
Analysis of the Influence of Pore Water Pressure on the Range and Displacement of the Fracture Zone
4. Physical and Mechanical Research and Analysis of Water-Bearing Broken Surrounding Rock
5. Numerical Simulation Analysis
5.1. Numerical Modeling
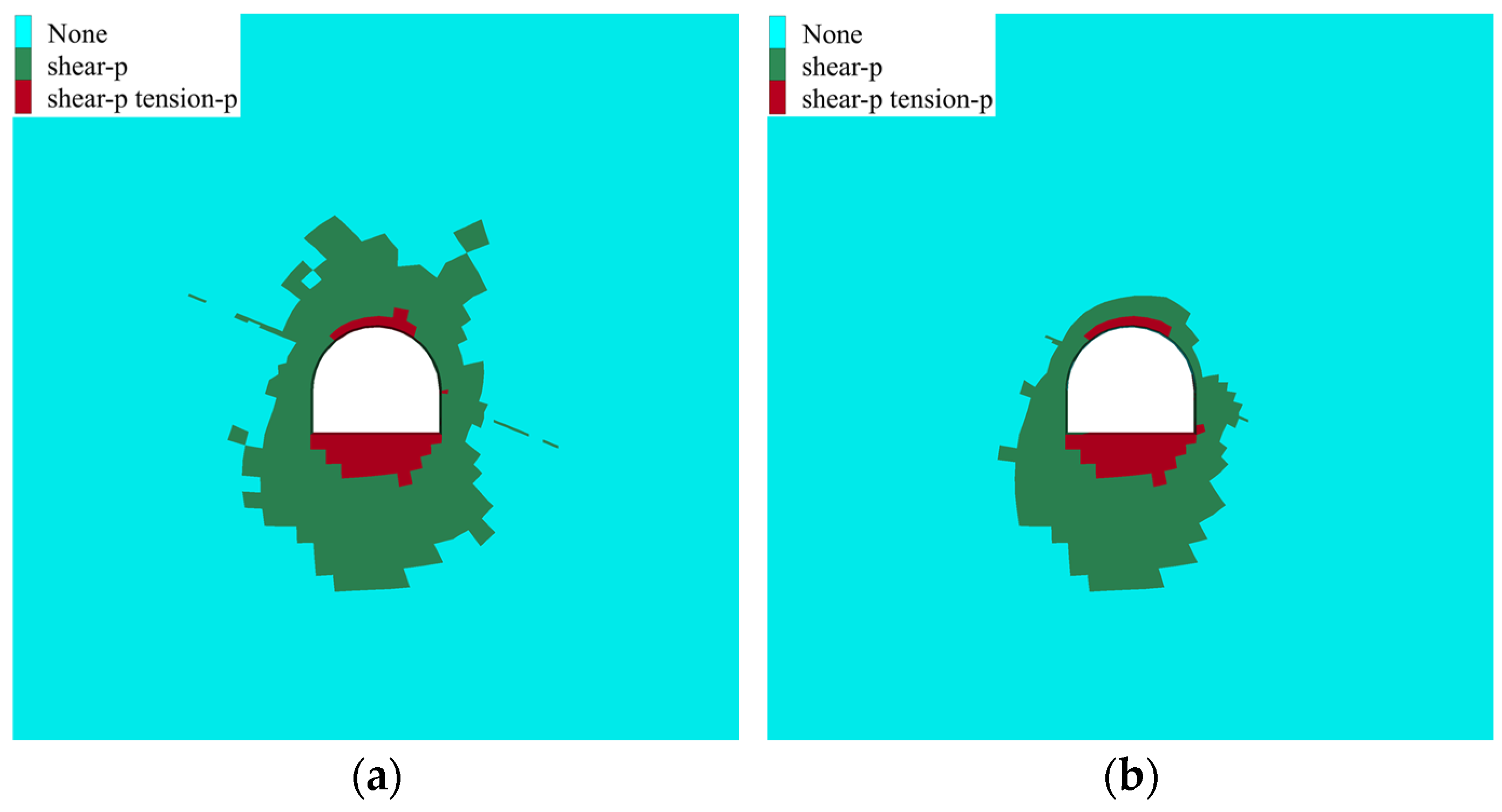
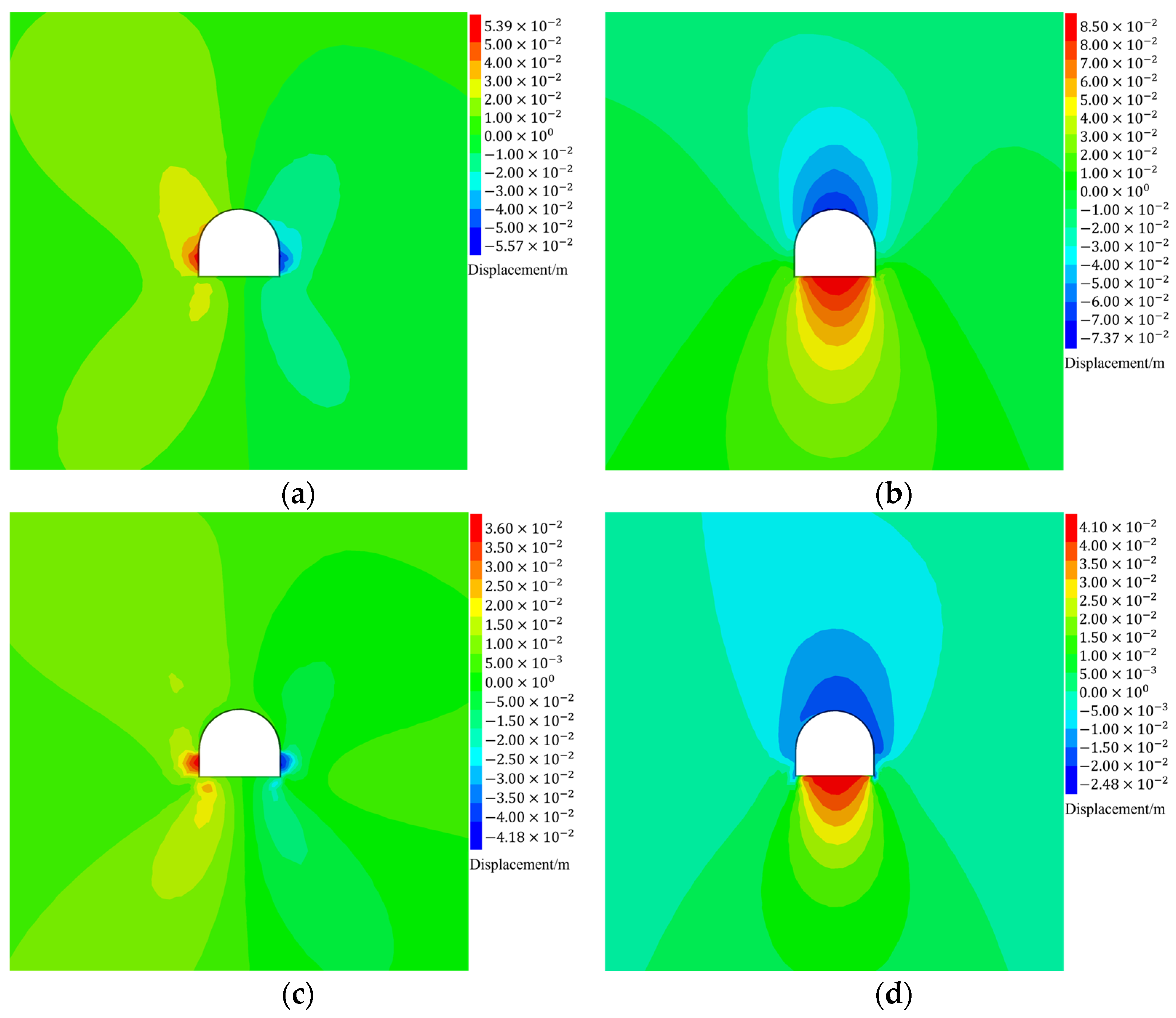
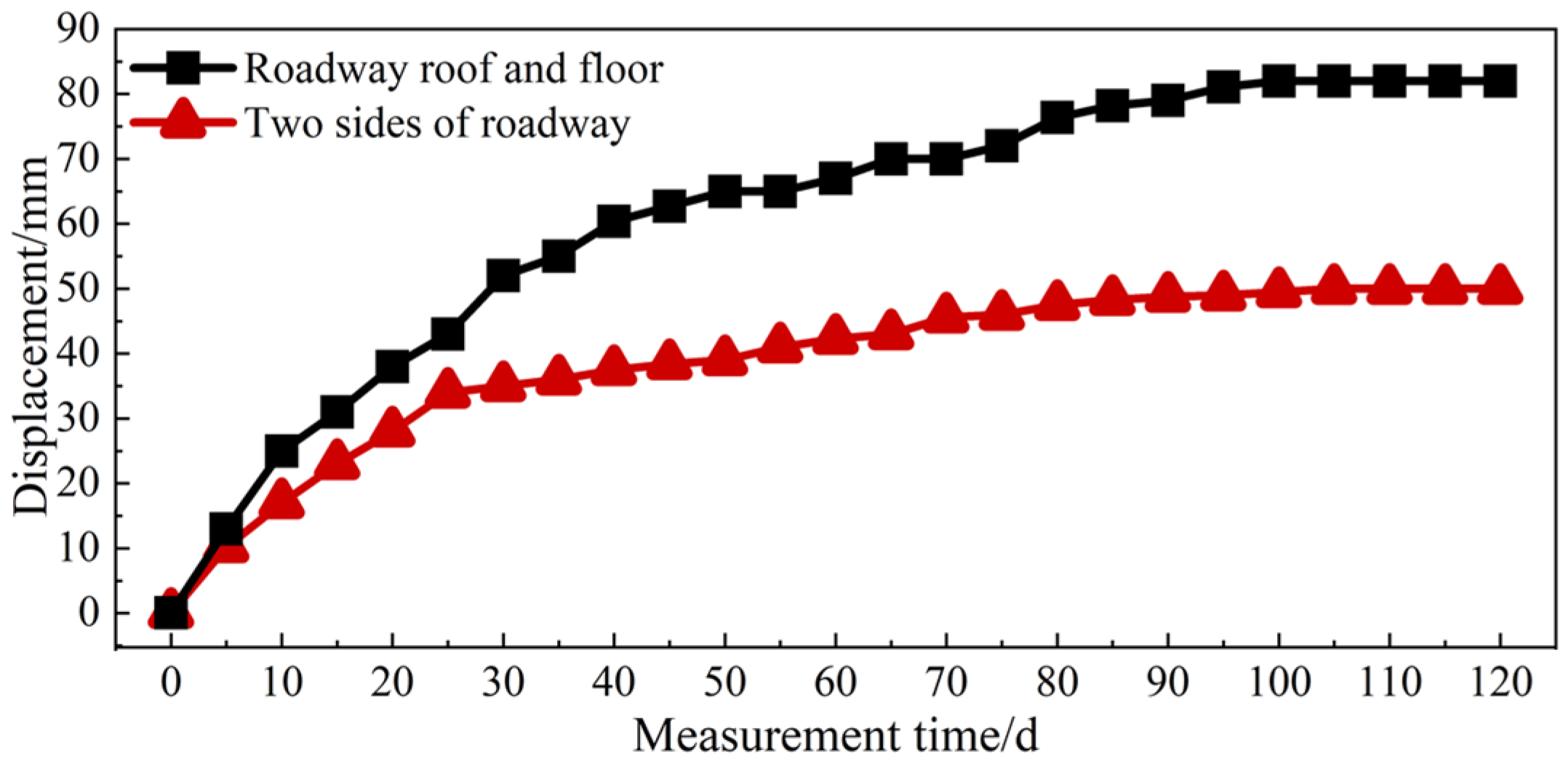
5.2. Comparative Analysis of Numerical Simulation Results
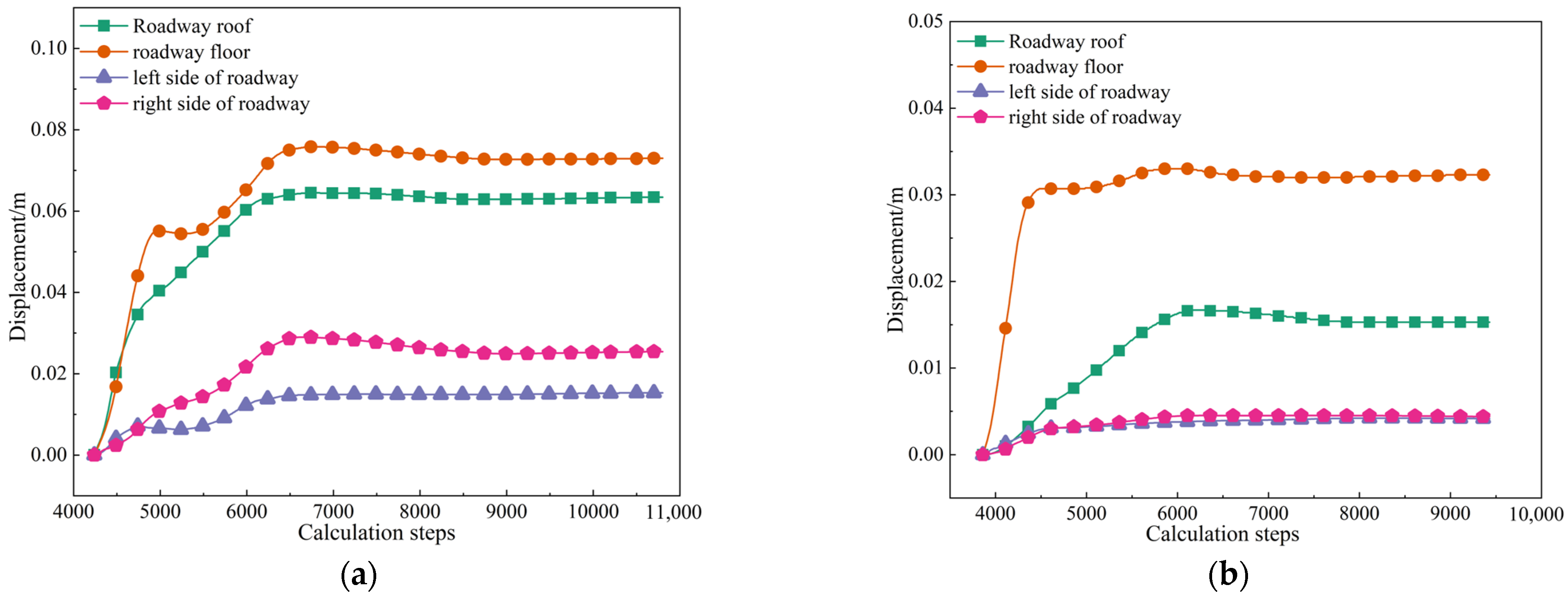
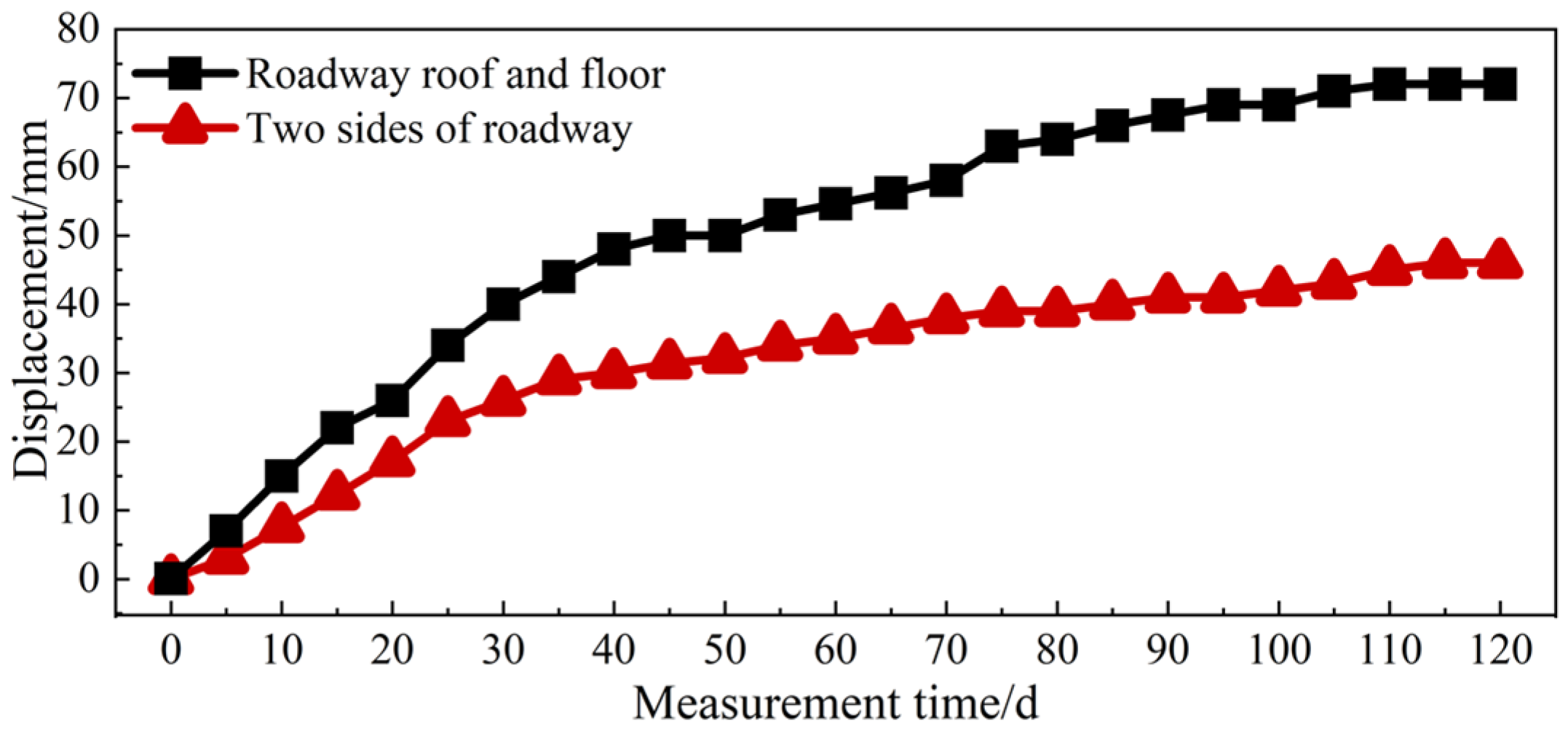
5.3. Analysis of On-Site Monitoring Effect
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hua, Z.; Fan, G.; Shi, J.; Chen, X.; Xu, J.; Zheng, Y.; Ren, S. Failure mechanism and control of underground wall rock under the effect of water pressure stress. Coal Eng. 2024, 56, 126–134. [Google Scholar]
- Yang, K.; Zhang, Z.; Chi, X.; Lü, X.; Wei, Z.; Liu, W. Experimental study on crack evolution and damage characteristics of water bearing sandstone under cyclic loading. Rock Soil Mech. 2022, 43, 1791–1802. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, J.; Li, T.; Chen, S.; Zhang, G.; Lü, P.; Teng, P. Timeliness of damage and deterioration of mechanical properties of coal-rock combined body under water-rock interaction. J. China Coal Socirty 2021, 46 (Suppl. S2), 701–712. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, J.; Kong, D.; Gu, Y.; Du, G.; Wang, J. A quantitative method for water inrush risk from fractured rocks based on nonlinear seepage theory. J. China Coal Soc. 2024, 49, 4520–4541. [Google Scholar] [CrossRef]
- Liu, Y.; Rong, C.; Wang, B.; Wang, S.; Niu, B.; Yang, M.; Li, M. Theoretical Solution of Roadway Stability Considering Intermediate Principal Stress and Seepage. Sci. Technol. Eng. 2023, 23, 14525–14531. [Google Scholar]
- Cao, Y.; Chen, Y.; Huang, Z.; Liu, C.; Qiu, D. STUDY on EVALUATION INDEX of BRITTLENESS CHARACTERISTICS of GRANITE UNDER DIFFERENT WATER CONTENT CONDITIONS. J. Eng. Geol. 2020, 28, 29–38. [Google Scholar] [CrossRef]
- Zhang, E.; Yang, G.; Tang, L.; Yang, Q.; Xie, Z. Study on influence of water content to damage and degradation laws of argillaceous siltstone. Coal Sci. Technol. 2019, 47, 14–20. [Google Scholar] [CrossRef]
- Hashiba, K.; Fukui, K. Effect of Water on the Deformation and Failure of Rock in Uniaxial Tension. Rock Mech. Rock Eng. 2015, 48, 1751–1761. [Google Scholar] [CrossRef]
- Karakul, H.; Ulusay, R. Empirical correlations for predicting strength properties of rocks from P-wave velocity under different degrees of saturation. Rock Mech. Rock Eng. 2013, 46, 98–99. [Google Scholar] [CrossRef]
- Song, H.; Li, S.; Zhang, Q.; Guo, Y.; Xu, G. The Acoustic Emission Stage Characteristics and Damage Evolution of Argillaceous Siltstone. Chin. J. Undergr. Space Eng. 2024, 20, 72–81. [Google Scholar]
- Zhang, Z.; Chi, X.L.; Yang, K.; Lyu, X.; Wang, Y. Studies on the Deformation and Macro-Micro-Damage Characteristics of Water-Bearing Sandstone under Cyclic Loading and Unloading Tests. ACS Omega 2023, 8, 19843–19852. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.; Shi, T.; Wang, J.; Zhang, C. Damage characteristics and model of rock triaxial cyclic stress and relaxation under stress-seepage coupling. Heliyon 2024, 11, e41568. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Zan, Y.; Wang, D.; Wang, S.; Yang, Z.; Zeng, Y.; Wei, G.; Shi, X. Numerical Simulation of Fracture Failure Propagation in Water-Saturated Sandstone with Pore Defects Under Non-Uniform Loading Effects. Water 2025, 17, 1725. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, Y.; Zhang, L.; Zhang, S. Experimental and Numerical Simulations of Pore Structures and Seepage Characteristics of Deep Sandstones. Processes 2023, 11, 3411. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, J.G.; Wang, W.J.; Lyu, Y.C.; Guo, J.W.; Cao, Q.J.; Li, W.C. Controlling principles of surrounding rock in soft and broken roadway based on the distribution pattern of plastic zone. J. Min. Saf. Eng. 2020, 37, 451–460. [Google Scholar] [CrossRef]
- Zareifard, M.R.; Fahimifar, A. Analytical solutions for the stresses and deformations of deep tunnels in an elastic-brittle-plastic rock mass considering the damaged zone. Tunn. Undergr. Space Technol. 2016, 58, 186–196. [Google Scholar] [CrossRef]
- Peng, W.; Zhu, H.; Wang, Q. Stress distribution law of surrounding rock bearing structure of broken surrounding rock roadway. J. Cent. South Univ. (Sci. Technol.) 2023, 54, 2447–2458. [Google Scholar]
- Xie, P.; Fang, J.; Hu, B.; Zhang, B.; Zhang, X.; Duan, S. Deformation and failure characteristics of soft rock tunnel surrounding rock under mining and water immersion conditions. J. Mine Autom. 2024, 50, 27–35+92. [Google Scholar] [CrossRef]
- Yu, K.; Ren, F.; Puscasu, R.; Lin, P.; Meng, Q. Optimization of combined support in soft-rock roadway. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2020, 103, 103502. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, C.; Yu, W.; Wu, H.; Peng, W.; Peng, G.; Liu, X.; Dong, E. Stability control method of surrounding rock in deep roadway with large deformation. J. China Coal Soc. 2016, 41, 2921–2931. [Google Scholar] [CrossRef]
- Song, G. Roadway surrounding rock control technology of weakly cemented soft rock with rich alkaline water. Coal Eng. 2023, 55, 58–62. [Google Scholar]
- Qu, J.; Liu, Q.; Ma, H. Support Deformation Induced Clearance Invasion and Treatment for a Pelitic Soft-Rock Tunnel Passing through a Water-Rich Fault Zone. Mod. Tunn. Technol. 2017, 54, 181–189. [Google Scholar] [CrossRef]




| p0/MPa | p0/MPa | η | φ/° | E/GPa | μ |
|---|---|---|---|---|---|
| 10.36 | 0.8 | 0.3 | 22 | 12 | 0.5 |
| Specimen Number | Immersion Time | Initial Mass | Quality After Soaking | Water Content | Mean Value of Moisture Content |
|---|---|---|---|---|---|
| (h) | (g) | (g) | (%) | (%) | |
| W0 | 0 | 530 | 530 | 0 | 0 |
| W1-1 | 5 | 537.1 | 537.68 | 0.11 | 0.11 |
| W1-2 | 536.98 | 537.51 | 0.1 | ||
| W1-3 | 537.21 | 537.85 | 0.12 | ||
| W2-1 | 13 | 536.7 | 537.82 | 0.21 | 0.22 |
| W2-2 | 534.96 | 536.12 | 0.22 | ||
| W2-3 | 539.49 | 540.67 | 0.22 | ||
| W3-1 | 24 | 521.91 | 523.46 | 0.3 | 0.29 |
| W3-2 | 519.08 | 520.52 | 0.28 | ||
| W3-3 | 533.54 | 535.08 | 0.29 | ||
| W4-1 | 192 | 532.2 | 534.42 | 0.42 | 0.41 |
| W4-2 | 529.29 | 531.41 | 0.4 | ||
| W4-3 | 525.6 | 527.75 | 0.41 |
| Lithologic Characters | Bulk Modulus | Shear Modulus | Cohesion | Angle of Internal Friction | Volumetric Weight | Porosity |
|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (MPa) | (°) | (kg/m3) | (%) | |
| Dolomite | 10 | 8.6 | 5 | 38 | 2750 | 0.2 |
| Slate | 5.12 | 2.31 | 2.32 | 28 | 2690 | 0.5 |
| Soft rock strata | 1.5 | 0.4 | 0.52 | 20 | 2750 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Feng, S. Research on Control Technology of Large-Section Water-Bearing Broken Surrounding Rock Roadway. Appl. Sci. 2025, 15, 7011. https://doi.org/10.3390/app15137011
Peng W, Feng S. Research on Control Technology of Large-Section Water-Bearing Broken Surrounding Rock Roadway. Applied Sciences. 2025; 15(13):7011. https://doi.org/10.3390/app15137011
Chicago/Turabian StylePeng, Wenqing, and Shenghua Feng. 2025. "Research on Control Technology of Large-Section Water-Bearing Broken Surrounding Rock Roadway" Applied Sciences 15, no. 13: 7011. https://doi.org/10.3390/app15137011
APA StylePeng, W., & Feng, S. (2025). Research on Control Technology of Large-Section Water-Bearing Broken Surrounding Rock Roadway. Applied Sciences, 15(13), 7011. https://doi.org/10.3390/app15137011







