A High-Conversion Ratio Multiphase Converter Realized with Generic Modular Cells
Abstract
1. Introduction
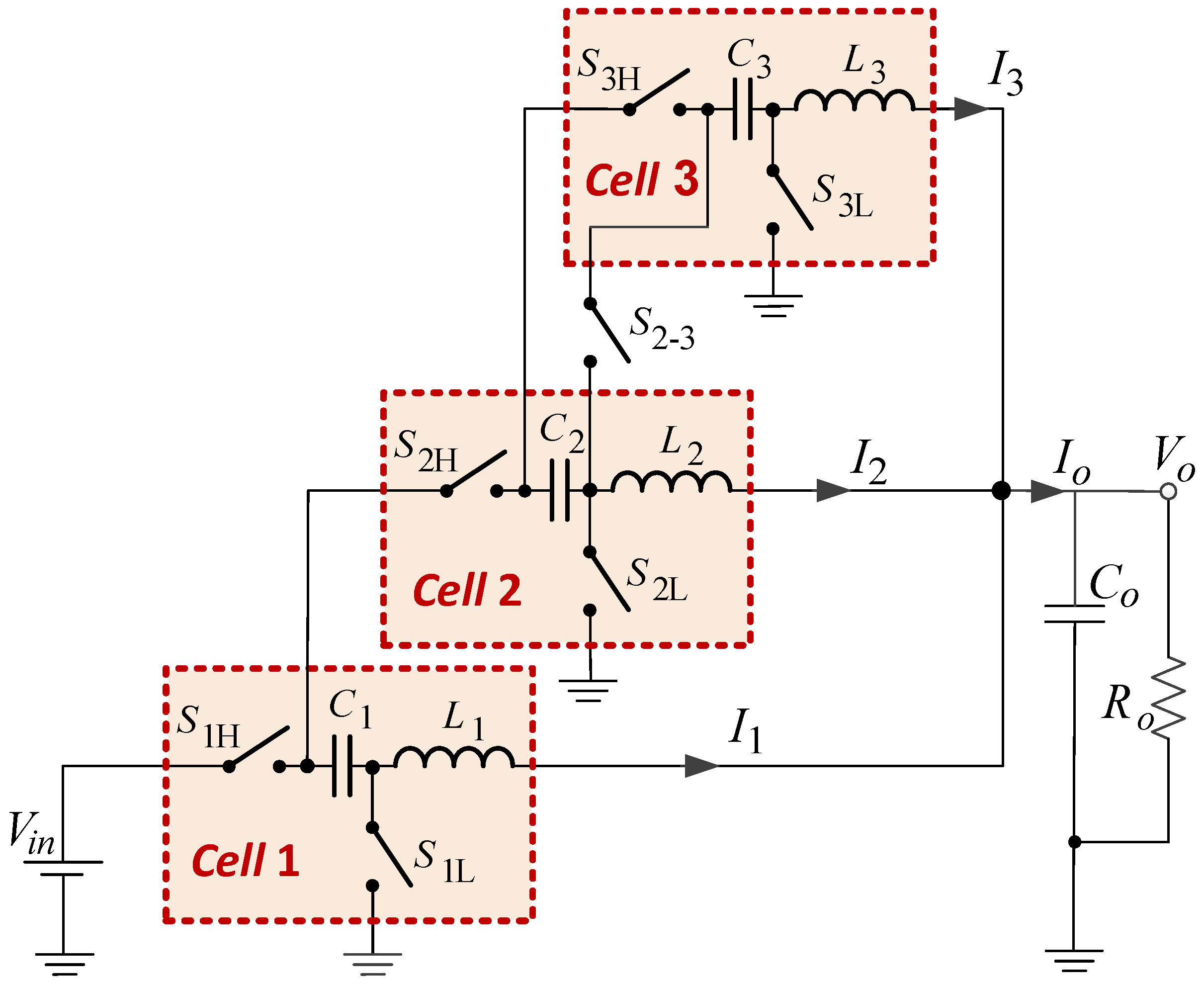
2. Modular Multiphase Step-Down Converter
3. Steady State Analysis
3.1. Conversion Ratio
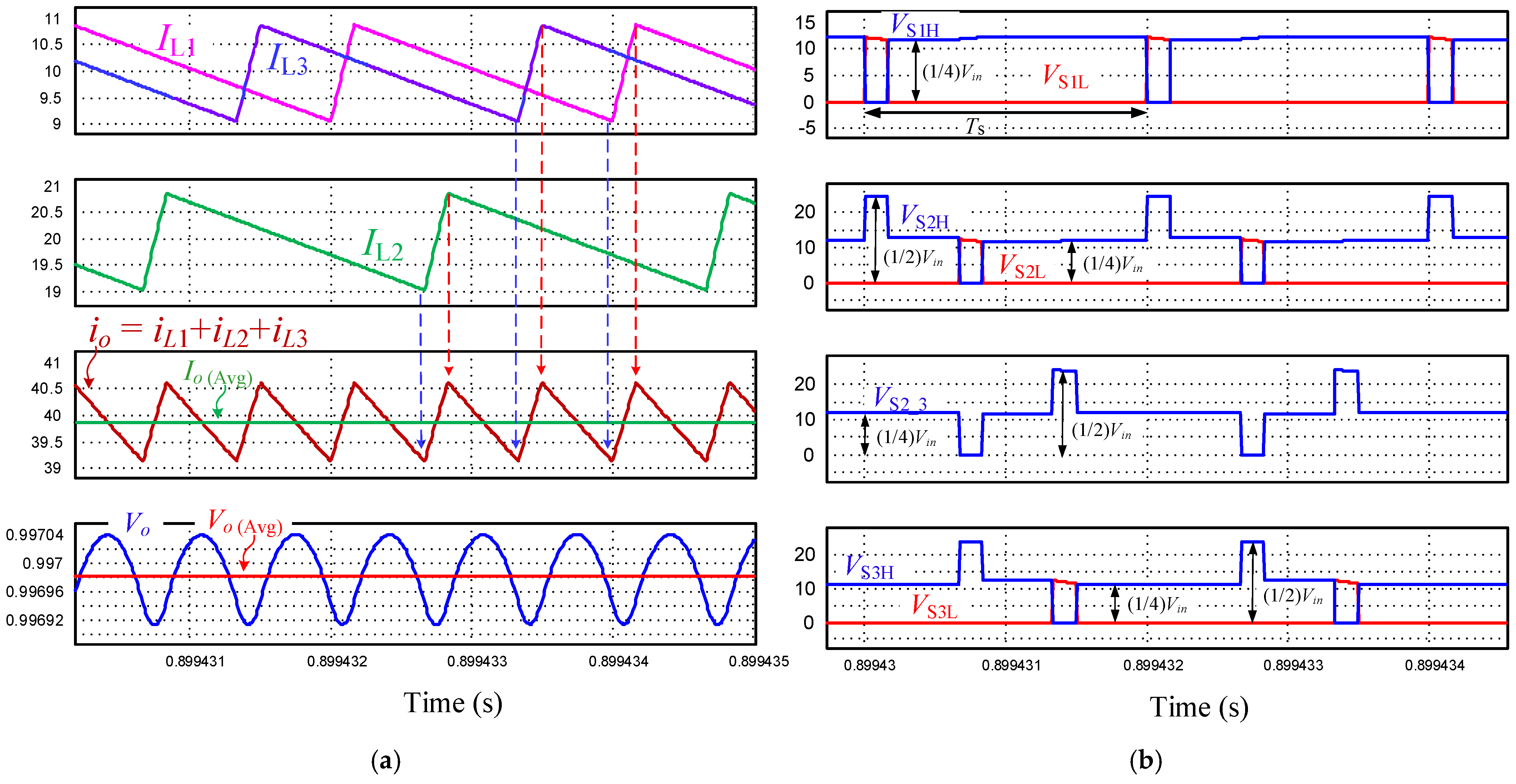
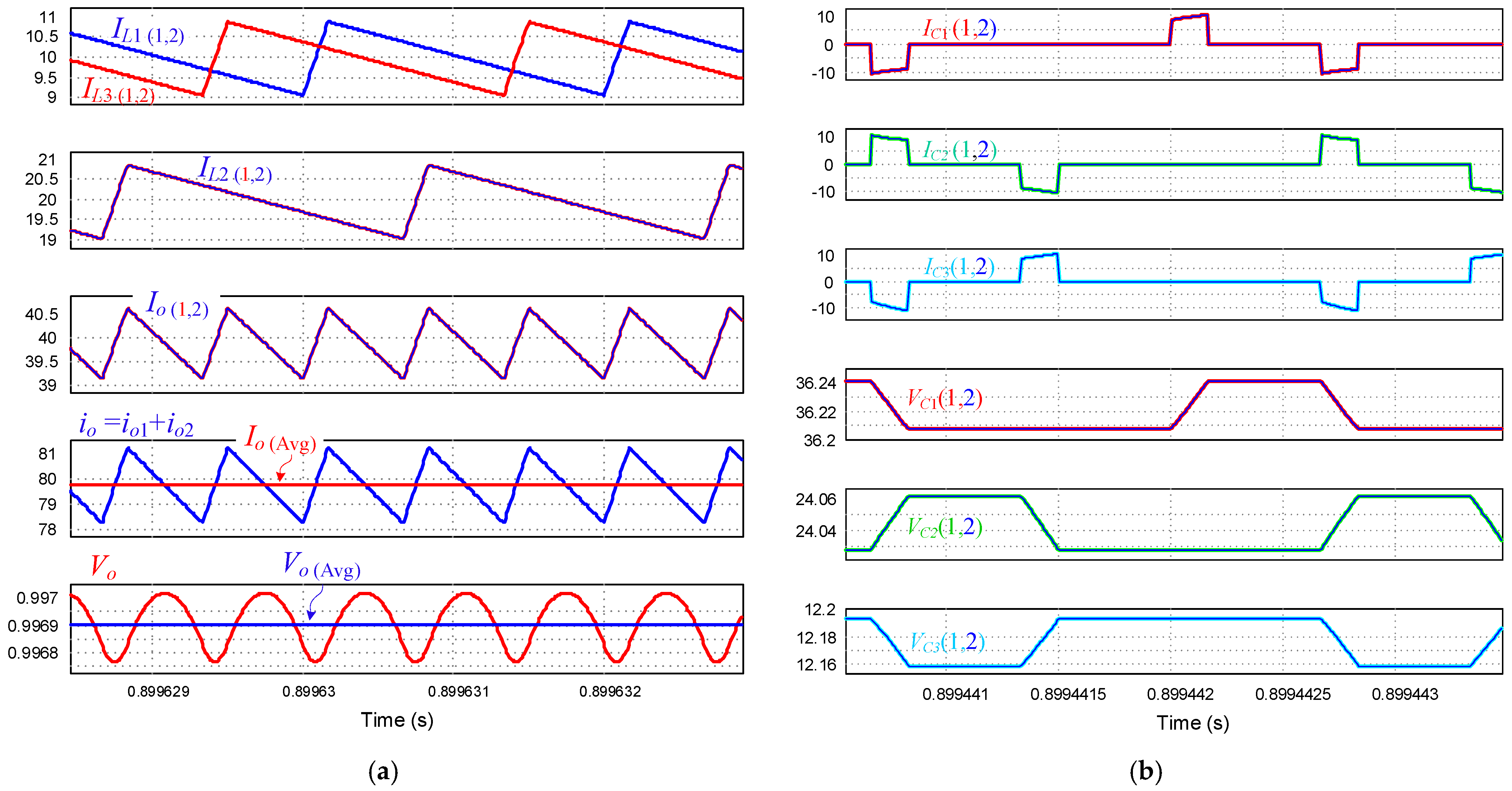
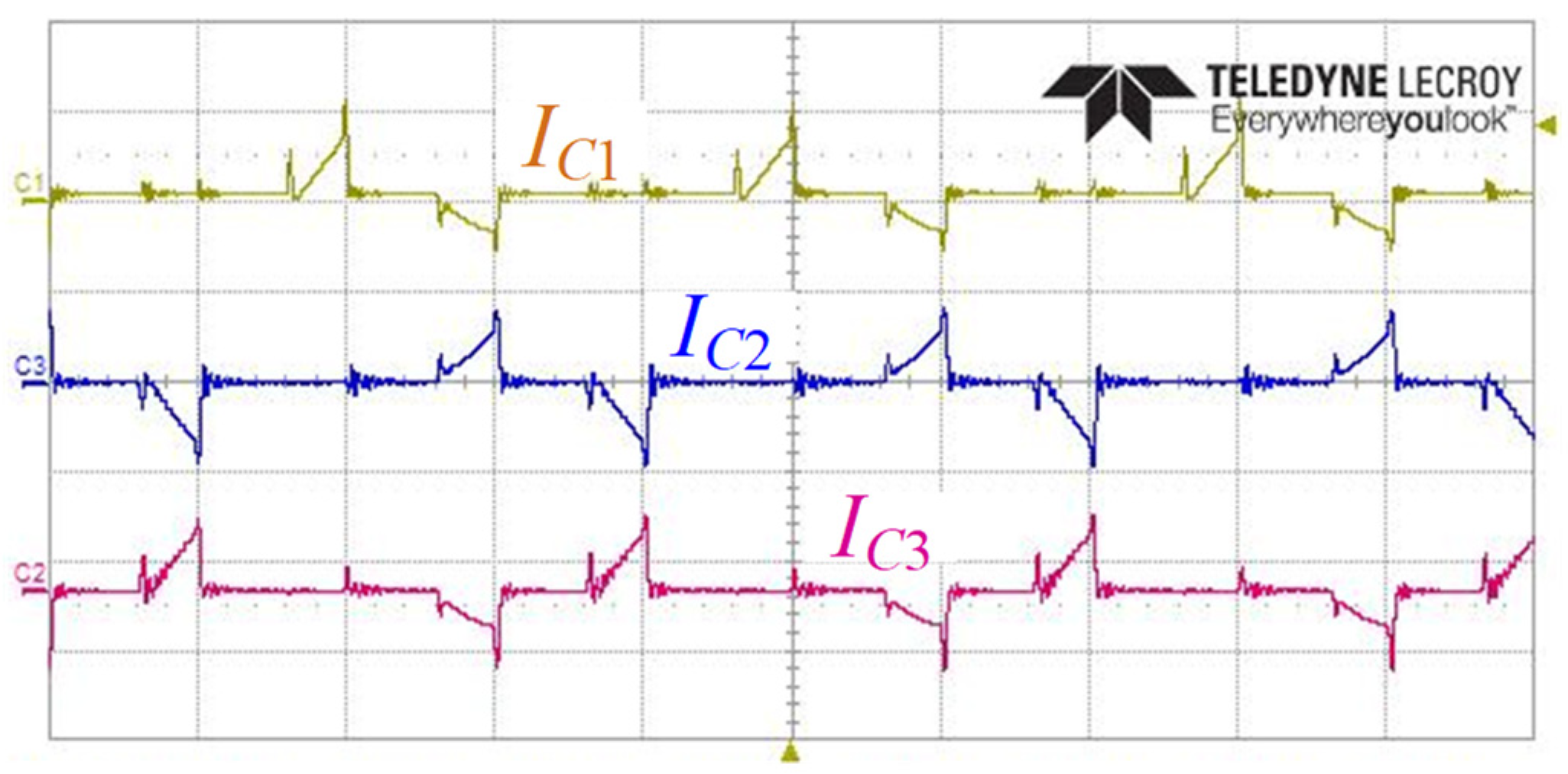
3.2. Inductors’ Currents and Balancing
3.3. Soft Charge/Discharge
3.4. Switches Voltage Stress
3.5. CCM–DCM Boundary
4. Extension for Higher Order Converters
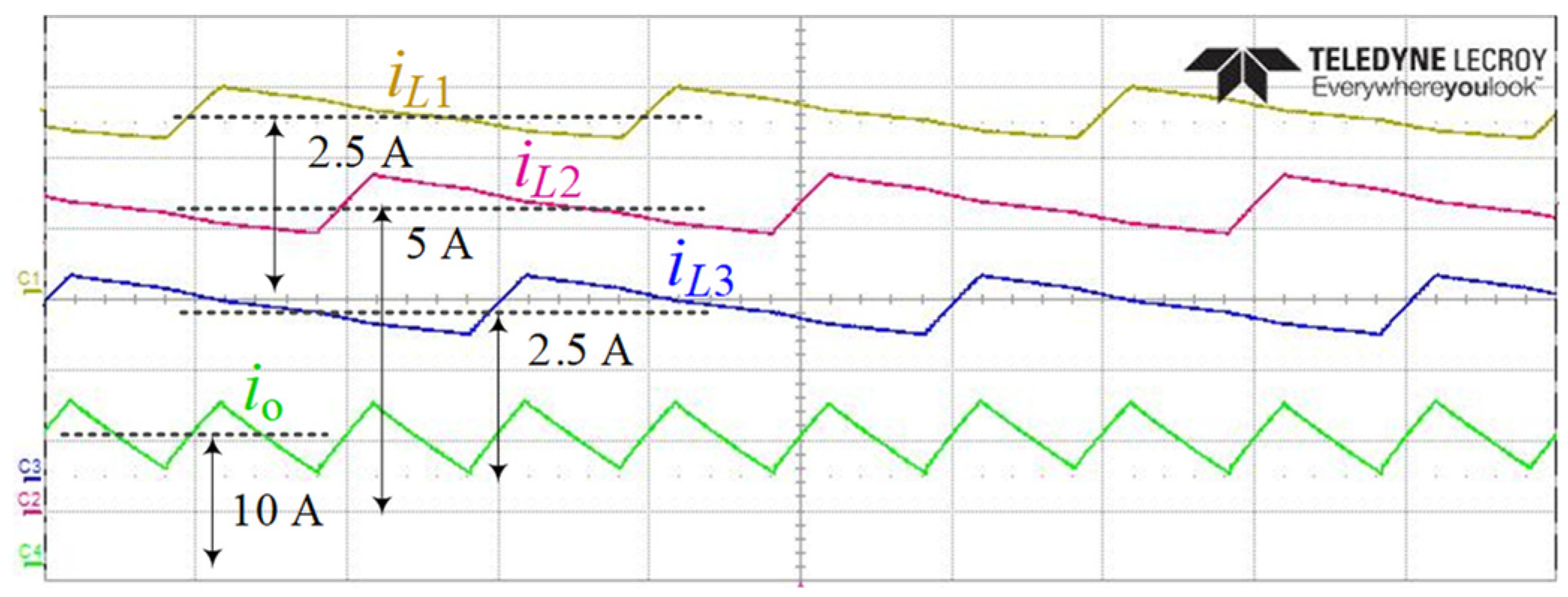
5. Simulation and Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ericsson Mobility Report. Available online: https://www.ericsson.com/en/mobility-report/reports (accessed on 20 June 2021).
- NRDC. Data Center Efficiency Assessment. Available online: https://www.nrdc.org/sites/default/files/data-center-efficiency-assessment-IP.pdf (accessed on 5 August 2014).
- Dayarathna, M.; Wen, Y.; Fan, R. Data center energy consumption modeling: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 732–794. [Google Scholar] [CrossRef]
- Dumitrescu, C.; Pleşca, A. Overview on energy efficiency parameters in data centers. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 153–156. [Google Scholar]
- Frachtenberg, E. Holistic datacenter design in the open compute project. Computer 2012, 45, 83–85. [Google Scholar] [CrossRef]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. 48-V voltage regulator module with PCB winding matrix transformer for future data centers. IEEE Trans. Ind. Electron. 2017, 64, 9302–9310. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Pilawa-Podgurski, R.C.N. The cascaded resonant converter: A hybrid switched-capacitor topology with high power density and efficiency. IEEE Trans. Power Electron. 2020, 35, 4946–4958. [Google Scholar] [CrossRef]
- Liu, W.C.; Ye, Z.; Pilawa-Podgurski, R.C.N. A 97% peak efficiency and 308 A/in3 current density 48-to-4 V two-stage resonant switched capacitor converter for data center applications. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 468–474. [Google Scholar]
- Liu, W.C.; Pilawa-Podgurski, R.C. Bi-lateral energy resonant converter (berc) with merged two-stage inductor for 48-to-12V applications. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 30 November 2020; pp. 1–6. [Google Scholar]
- Baek, J.; Wang, P.; Elasser, Y.; Chen, Y.; Jiang, S.; Chen, M. Legopol: A 48V-1.5V 300A merged-two-stage hybrid converter for ultrahigh-current microprocessors. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 490–497. [Google Scholar]
- Ursino, M.; Saggini, S.; Jiang, S.; Nan, C. High density 48V-to-PoL VRM with hybrid pre-regulator and fixed-ratio buck. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 498–505. [Google Scholar]
- Ye, Z.; Abramson, R.A.; Syu, Y.L.; Pilawa-Podgurski, R.C.N. MLB-PoL: A high-performance hybrid converter for direct 48 V to point-of-load applications. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 30 November 2020. [Google Scholar]
- Batarseh, M.; Wang, X.; Batarseh, I. Nonisolated half bridge buck-based converter for VRM application. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2393–2398. [Google Scholar]
- Oraw, B.S.; Ayyanar, R. Voltage regulator optimization using multi winding coupled inductors and extended duty ratio mechanisms. IEEE Trans. Power Electron. 2009, 24, 1494–1505. [Google Scholar] [CrossRef]
- Xu, M.; Sun, J.; Lee, F.C. Voltage divider and its application in the two-stage power architecture. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, APEC’06, Dallas, TX, USA, 19–23 March 2006; pp. 499–505. [Google Scholar]
- Ye, Z.; Abramson, R.A.; Pilawa-Podgurski, R.C.N. A 48-to-6V multi-resonant-doubler switched-capacitor converter for data center applications. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 475–481. [Google Scholar]
- Abramson, R.A.; Ye, Z.; Pilawa-Podgurski, R.C.N. A high performance 48-to-8 v multi-resonant switched-capacitor converter for data center applications. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–10. [Google Scholar]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. Single-stage high-efficiency 48/1 V sigma converter with integrated magnetics. IEEE Trans. Ind. Electron. 2020, 67, 192–202. [Google Scholar] [CrossRef]
- Halamicek, M.; McRae, T.; Prodić, A. Cross-coupled series-capacitor quadruple step-down buck converter. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020. [Google Scholar]
- Kirshenboim, O.; Peretz, M.M. High-efficiency nonisolated converter with very high step-down conversion ratio. IEEE Trans. Power Electron. 2017, 32, 3683–3690. [Google Scholar] [CrossRef]
- Das, R.; Seo, G.; Maksimovic, D.; Le, H.P. An 80-w 94.6%-efficient multi-phase multi-inductor hybrid converter. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1–6. [Google Scholar]
- Das, R.; Le, H.P. A Regulated 48V-to-1V/100A 90.9%-Efficient Hybrid Converter for POL Applications in Data Centers and Telecommunication Systems. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1997–2001. [Google Scholar]
- Jang, Y.; Jovanovic, M.M.; Panov, Y. Multi-phase buck converters with extended duty cycle. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, APEC’06, Dallas, TX, USA, 19–23 March 2006; pp. 38–44. [Google Scholar]
- Youssef, M.; Jain, P.K. Analysis and design of a novel LLC 48V resonant self-oscillating voltage regulator module. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 252–258. [Google Scholar]
- Youssef, M.; Jain, P.K. A 48V resonant voltage regulator module with a new current mode controller. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Jang, Y.; Jovanovic, M.M.; Panov, Y. Nonisolated Power Conversion System Having Multiple Switching Power Converters. U.S. Patent 7 230 405, 12 June 2007. [Google Scholar]
- Abe, K.; Nishijima, K.; Harada, K.; Nakano, T.; Nabeshima, T.; Sato, T. A novel three-phase buck converter with bootstrap driver circuit. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1864–1871. [Google Scholar]
- Nishijima, K.; Harada, K.; Nakano, T.; Nabeshima, T.; Sato, T. Analysis of double step-down two-phase buck converter for VRM. In Proceedings of the INTELEC 05-Twenty-Seventh International Telecommunications Conference, Berlin, Germany, 18–22 September 2005; pp. 497–502. [Google Scholar]
- Matsumoto, K.; Nishijima, K.; Sato, T.; Nabeshima, T. A two-phase high step down coupled-inductor converter for next generation low voltage CPU. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011; pp. 2813–2818. [Google Scholar]
- Chuang, C.F.; Pan, C.T.; Cheng, H.C. A novel transformer-less interleaved four-phase step-down DC converter with low switch voltage stress and automatic uniform current-sharing characteristics. IEEE Trans. Power Electron. 2016, 31, 406–417. [Google Scholar] [CrossRef]
- Shanoy, P.S.; Amaro, M.; Morroni, J.; Freeman, D. Comparison of a buck converter and a series capacitor buck converter for high frequency, high conversion ratio voltage regulators. IEEE Trans. Power Electron. 2016, 31, 7006–7015. [Google Scholar] [CrossRef]
- Lee, I.O.; Cho, S.Y.; Moon, G.W. Interleaved buck converter having low switching losses and improved step-down conversion ratio. IEEE Trans. Power Electron. 2012, 27, 3664–3675. [Google Scholar] [CrossRef]
- Jain, P.; Prodic, A.; Gerfer, A. Wide-input high power density flexible converter topology for DC-DC applications. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2553–2560. [Google Scholar]
- Hamo, E.; Evzelman, M.; Peretz, M.M. High-Conversion Ratio Multi-Phase VRM Realized with Stacking of Generic Series-Capacitor-Buck Converter Cells. In Proceedings of the 2022 IEEE 23rd Workshop on Control and Modeling for Power Electronics (COMPEL), Tel Aviv, Israel, 20–23 June 2022; pp. 1–6. [Google Scholar]
- Ahsanuzzaman, S.M.; Ma, Y.; Pathan, A.A.; Prodic, A. A low-volume hybrid step-down DC-DC converter based on the dual use of flying capacitor. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2497–2503. [Google Scholar]
- Meynard, T.A.; Foch, H. Multilevel converters and derived topologies for high power conversion. In Proceedings of the IECON’95—21st Annual Conference on IEEE Industrial Electronics, Orlando, FL, USA, 6–10 November 1995; pp. 21–26. [Google Scholar]
- Du, X.; Zhou, L.; Tai, H.M. Double-frequency buck converter. IEEE Trans. Ind. Electron. 2009, 56, 1690–1698. [Google Scholar]
- Middlebrook, R.D. Transformerless DC-to-DC converters with large conversion ratios. IEEE Trans. Power Electron. 1988, 3, 484–488. [Google Scholar] [CrossRef]
- Oraw, B.; Ayyanar, R. Small signal modeling and control design for new extended duty ratio, interleaved multiphase synchronous buck converter. In Proceedings of the INTELEC 06-Twenty-Eighth International Telecommunications Energy Conference, Providence, RI, USA, 10–14 September 2006; pp. 1–8. [Google Scholar]
- Radić, A.; Prodić, A. Buck converter with merged active charge-controlled capacitive attenuation. IEEE Trans. Power Electron. 2012, 27, 1049–1054. [Google Scholar] [CrossRef]
- Roberts, G.; Prodić, A. Modulation improvements for high-phase-count series-capacitor buck converters. IEEE Open J. Power Electron. 2024, 5, 1071–1092. [Google Scholar] [CrossRef]
- Naradhipa, A.M.; Li, Q. Partial phase overlap control for multiphase series capacitor buck converter. In Proceedings of the 2023 IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; pp. 1–7. [Google Scholar]
- Li, C.Y.; Nien, C.F.; Lin, L.; Chen, H.C. A generalized current balancing control for series-capacitor buck converter with interleaved phase angle. In Proceedings of the 2023 IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; pp. 1–5. [Google Scholar]
- Majumder, P.; Kapat, S.; Kastha, D. Fast transient state feedback digital current mode control design in series capacitor buck converters. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 2080–2085. [Google Scholar]
- Wang, Z.; Fang, P. Modular series capacitor buck topology for point of load applications with duty cycle freer. In Proceedings of the 2023 IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; pp. 1–8. [Google Scholar]
- Ibarra, E.; Arias, A.; de Alegría, I.M.; Otero, A.; de Mallac, L. Digital control of multiphase series capacitor buck converter prototype for the powering of HL-LHC inner triplet magnets. IEEE Trans. Ind. Electron. 2022, 69, 10014–10024. [Google Scholar] [CrossRef]
- Yousefzadeh, V.; Alarcon, E.; Maksimovic, D. Three-level buck converter for envelope tracking applications. IEEE Trans. Power Electron. 2006, 21, 549–552. [Google Scholar] [CrossRef]
- Muhammad, H.R. Power Electronics: Circuits, Devices and Applications; Prentice-Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Hart, D.W. Power Electronics; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Shenoy, P.S.; Lazaro, O.; Amaro, M.; Ramani, R.; Wiktor, W.; Lynch, B.; Khayat, J. Automatic current sharing mechanism in the series capacitor buck converter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2003–2009. [Google Scholar]
- Lei, Y.; Pilawa-Podgurski, R.C.N. A general method for analyzing resonant and soft-charging operation of switched-capacitor converters. IEEE Trans. Power Electron. 2015, 30, 5650–5664. [Google Scholar] [CrossRef]
- Evzelman, M.; Ben-Yaakov, S. Average-current-based conduction losses model of switched capacitor converters. IEEE Trans. Power Electron. 2013, 28, 3341–3352. [Google Scholar] [CrossRef]
- Hamo, E.; Evzelman, M.; Peretz, M.M. Modeling and analysis of resonant switched-capacitor converters with free-wheeling ZCS. IEEE Trans. Power Electron. 2015, 30, 4952–4959. [Google Scholar] [CrossRef]
- Texas Instruments. Multiphase Buck Design from Start to Finish. Application Report 2021. Available online: https://www.ti.com/lit/an/slva882b/slva882b.pdf?ts=1748214604321&ref_url=https%253A%252F%252Fwww.google.com%252F (accessed on 10 May 2025).










| State | Stress (Vin = 48 V, M = 1/48) | ||||||
|---|---|---|---|---|---|---|---|
| Switch | I | II | III | IV | V | VI | Vmax [V] |
| S1L | Vin-VC1 | 0 | 0 | 0 | 0 | 0 | 12 |
| S1H | 0 | Vin-VC1 | Vin-VC1 | Vin-VC1 | Vin-VC1 | Vin-VC1 | 12 |
| S2L | 0 | 0 | VC3 | 0 | 0 | 0 | 12 |
| S2H | Vin-VC2 | VC1-VC2 | 0 | VC1-VC2 | VC1-VC2 | VC1-VC2 | 24 |
| S2-3 | VC3 | VC3 | 0 | VC3 | VC2 | VC3 | 24 |
| S3L | 0 | 0 | 0 | 0 | VC2-VC3 | 0 | 12 |
| S3H | VC2-VC3 | VC2-VC3 | VC2 | VC2-VC3 | 0 | VC2-VC3 | 24 |
| # of Cells | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| Switch | ||||||||
| SxL (x ≥ 1) 1 | (1/3)Vin | (1/4)Vin | (1/5)Vin | (1/6)Vin | (1/7)Vin | (1/8)Vin | (1/9)Vin | |
| SxH (x > 1) 2 | (2/3)Vin | (2/4)Vin | (2/5)Vin | (2/6)Vin | (2/7)Vin | (2/8)Vin | (2/9)Vin | |
| Power Stage | ||
|---|---|---|
| Component | P/N | Value/Type |
| Input voltage-Vin | 48 V | |
| Output voltage-Vout | 1–1.5 V | |
| Switching freq.-fsw | 333 kHz per Ph. | |
| Input capacitor-Cin | EEE-FK2A221AV | 220 µF, 100 V |
| Output capacitor-Cout | EEF-GX0D561R | 560 µF, 2 V |
| Inductors-L1, L2, L3 | XAL1580_401MEB | 0.4 µH, 60 A |
| Capacitors-C1, C2, C3 | C5750X7S2A106M | 10 µF, 100 V |
| MOSFETs (RDS on) | NVMFD5C446NL | 2.2 mΩ, 145 A |
| Load resistance-Rload | 10–100 mΩ | |
| Floating Driver | ||
| Driver | 2EDF7275F | |
| Isolated DC/DC | TDR 3-1212SM | |
| Digital Section | ||
| Microcontroller | dsPIC33FJ16GS502 | 16 bit, 40 MIPS |
| Buffers and Drivers | MC74VHC244DWR2G | |
| Topology /Reference | Voltage Ratio (Vo/Vin) | Regulated | Tested Range (Vin to Vo) | # L 1 | # C 1 | Capacitors Stress 2 | Active Components | Switches Stress 2 (Vblocking) | Peak Efficiency [%] (Power Stage) |
|---|---|---|---|---|---|---|---|---|---|
| This Work -x3 LC Cells | D/4 | Yes | 48 to 1–1.8 V | 3 | 3 | (3Vin/4), (Vin/2), (Vin/4) | 7 SW | 5 × (Vin/4), 2 × (Vin/2) | 97.8 (40 A/1.8 V) 95.6 (38 A/1 V) |
| Multiphase Buck-5ph. [55] | D | Yes | 12 to 1.8 V | 5 | 0 | -- | 10 SW | 10 × (Vin) | 94.8 (55 A/1.8 V) |
| Series Cap Buck-3ph. [27] | D/3 | Yes | 19 to 1.2 V; 16.8 to 0.9 V | 3 | 2 | (2Vin/3), (Vin/3) | 6 SW | 2 × (2Vin/3), 4 × (Vin/3) | 93 (5 A/1.2 V) |
| Multi-Resonant- Doubler [16] | Fixed- ratio | No | 48 to 6 V | 1 | 3 | (4Vo), (2Vo), (Vo) | 10 SW | 4 × (4Vo), 3 × (2Vo), 3 × (Vo) | 98.6 (5 A/6 V) |
| Multi-Resonant Cascaded Series-Parallel Converter [17] | Fixed- ratio | No | 48 to 8 V | 1 | 3 | 1 × (3Vo), 2 × (Vo) | 10 SW | 4 × (3Vo), 2 × (2Vo), 4 × (Vo) | 99 (5 A/8 V) |
| Cross-Coupled Series-Capacitor Quadruple Buck Converter [19] | D/4 | Yes | 48 to 1 V | 2 | 3 | 1 × (Vin/2), 2 × (Vin/3) | 8 SW, 2x Diodes | 6 × (Vin/4), 2 × (Vin/2) | 94.5 (15 A/1 V) 95.1 (17 A/1.8 V) |
| Seven-Level Multiphase Multi-Inductor Hybrid Converter [21] | D/6 | Yes | 48 to 1–2 V | 3 | 5 | (5Vin/6), (4Vin/6), (3Vin/6), (2Vin/6), (Vin/6) | 9 SW | NA | 94.6 (8 A/2 V) 92 (7 A/1 V) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamo, E.; Evzelman, M.; Peretz, M.M. A High-Conversion Ratio Multiphase Converter Realized with Generic Modular Cells. Appl. Sci. 2025, 15, 6818. https://doi.org/10.3390/app15126818
Hamo E, Evzelman M, Peretz MM. A High-Conversion Ratio Multiphase Converter Realized with Generic Modular Cells. Applied Sciences. 2025; 15(12):6818. https://doi.org/10.3390/app15126818
Chicago/Turabian StyleHamo, Eli, Michael Evzelman, and Mor Mordechai Peretz. 2025. "A High-Conversion Ratio Multiphase Converter Realized with Generic Modular Cells" Applied Sciences 15, no. 12: 6818. https://doi.org/10.3390/app15126818
APA StyleHamo, E., Evzelman, M., & Peretz, M. M. (2025). A High-Conversion Ratio Multiphase Converter Realized with Generic Modular Cells. Applied Sciences, 15(12), 6818. https://doi.org/10.3390/app15126818








