Optimizing Energy Forecasting Using ANN and RF Models for HVAC and Heating Predictions
Abstract
1. Introduction
1.1. Literature Review
1.2. Contributions
- It addresses the impact of Industry 5.0 on energy demand, specifically within the context of sustainability and meeting current market needs while minimizing environmental impact.
- It fills a gap in energy consumption forecasting by integrating artificial intelligence approaches, specifically Artificial Neural Networks (ANNs) and Random Forests (RFs), into the Industry 5.0 framework.
- It implements and compares ANN and RF models using real-world energy consumption data from two specific locations in Spain (LUCIA, FUHEM) using a house-developed code based on MATLAB.
- It evaluates and compares the performance of ANN and RF models in predicting energy demand using a comprehensive set of metrics, including Root Mean Square Percentage Error (RMSPE), Root Mean Square Relative Percentage Error (RMSRPE), Mean Absolute Percentage Error (MAPE), Mean Absolute Relative Percentage Error (MARPE), Kling–Gupta Efficiency (KGE), and the coefficient of determination (R2).
2. Methodology
2.1. Data Collection
2.2. Data Preprocessing
Data Normalizing
2.3. Model Development (ANN)
Mathematical Model (ANN)
2.4. Model Development (RF)
Mathematical Model (RF)
- Tree Construction:
- For each tree :
- Draw a bootstrap sample by randomly selecting instances from the training dataset .
- At each node within the tree, randomly select a subset of mmm features from the total set of features.
- Determine the optimal split at the node using a specific criterion, such as Gini impurity for classification tasks or Mean Squared Error for regression problems.
2.5. Evaluation Metrics
2.6. Optimization Procedures
- Split the dataset into three parts: 70% for training, 15% for validation, and 15% for testing.
- Choose the network architecture and set the training parameters.
- Train the model with the training dataset.
- Validate the model’s performance using the validation dataset.
- Iterate steps 2 to 4, experimenting with various architectures and training settings.
- Identify the optimal network architecture based on validation results.
- Evaluate the selected final model using the test dataset to assess its performance.
3. Results and Discussions
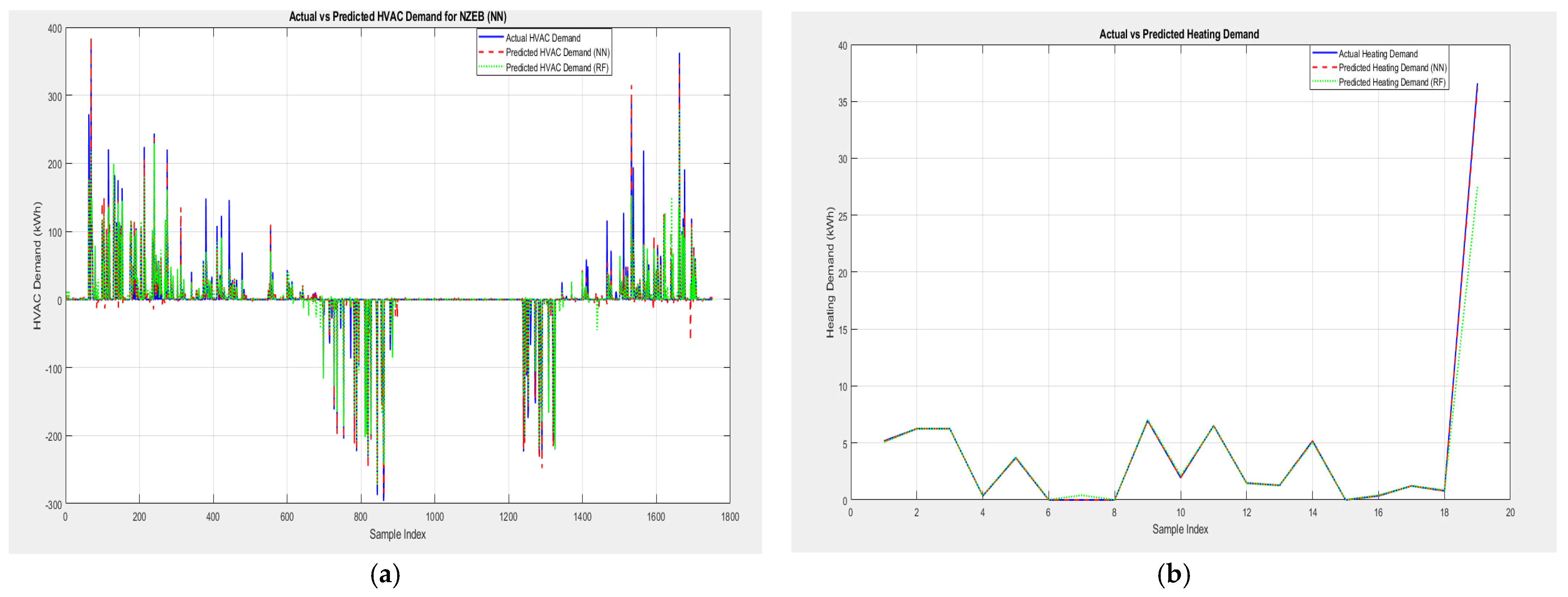
3.1. Actual and Predicted Energy Demand
3.2. Evaluation of Performance Metrics
3.2.1. Correlations of Heatmap
3.2.2. Evaluation Metrics (MAPE, RMSPE, KGE, NSE, R2)
3.2.3. Regression for (ANN)
3.2.4. Training State for (ANN)
3.2.5. Performance (ANN)
3.3. Sensitivity Analysis, Feature Importance, and Computational Complexity
3.4. Summary of Results
3.5. Practical Applications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| List of symbols | |
| Variable | Description |
| Input vector: Represents the input features to the neural network, where is the number of input parameters. | |
| The sum of inputs to the -th neuron in the first hidden layer, calculated as a weighted sum of inputs. | |
| The weight associated with the connection from the -th input to the -th neuron. | |
| The output of the -th neuron in the first hidden layer after applying the activation function. | |
| Index for neurons in the second hidden layer, indicating the connection from the first hidden layer. | |
| The sum of inputs to the -th neuron in the second hidden layer, calculated similarly to the first layer. | |
| The output of the -th neuron in the second hidden layer, processed through an activation function. | |
| y | The predicted output for energy demand from the output layer of the neural network. |
| The bias term for the -th neuron in the first hidden layer. | |
| The bias term for the -th neuron in the second hidden layer. | |
| The learning rate used in the backpropagation algorithm to update weights and biases. | |
| The total number of neurons in the first hidden layer. | |
| The total number of input features. | |
| Total number of trees in the Random Forest. | |
| Number of instances from the training set used to create a bootstrap sample . | |
| The feature to split on based on a chosen criterion (e.g., Gini impurity for classification, Mean Squared Error for regression). | |
| The proportion of class in the node | |
| The total number of instances at the node. | |
| The predicted output for regression tasks, calculated as the average of predictions from individual trees. | |
| The actual output value for regression tasks. | |
| The predicted class in classification tasks, determined by majority vote among the trees. | |
| Out-of-bag observations, which are instances not included in a tree’s bootstrap sample, used for performance estimation. | |
| An indicator function that equals 1 if the predicted class does not match the actual class . | |
| List of abbreviations | |
| ANN | Artificial Neural Network |
| RF | Random Forest |
| RMSPE | Root Mean Square Percentage Error |
| MAPE | Mean Absolute Percentage Error |
| MARE | Mean Absolute Relative Error |
| RMSRE | Root Mean Squared Relative Error |
| KGE | Kling–Gupta Efficiency |
| NSE | Nash–Sutcliffe Efficiency |
| nZEB | Near-Zero-Energy Building |
| AI | Artificial Intelligence |
| IoT | Internet of Things |
| HVAC | Heating, Ventilation, and Air Conditioning |
| NAR | Nonlinear Autoregressive |
| MSHD | Method of Spatial Homogenization Decomposition |
| SVR | Support Vector Machine |
| ReLU | Rectified Linear Unit |
| OOB | Out-of-Bag |
| CDF | Cumulative Distribution Function |
| LM | Levenberg–Marquardt |
References
- Rane, N. ChatGPT and Similar Generative Artificial Intelligence (AI) for Building and Construction Industry: Contribution, Opportunities and Challenges of Large Language Models for Industry 4.0, Industry 5.0, and Society 5.0. Oppor. Chall. Large Lang. Models Ind. 2023, 4. [Google Scholar] [CrossRef]
- Musarat, M.A.; Irfan, M.; Alaloul, W.S.; Maqsoom, A.; Ghufran, M. A Review on the Way Forward in Construction through Industrial Revolution 5.0. Sustainability 2023, 15, 13862. [Google Scholar] [CrossRef]
- Ghobakhloo, M.; Iranmanesh, M.; Tseng, M.-L.; Grybauskas, A.; Stefanini, A.; Amran, A. Behind the Definition of Industry 5.0: A Systematic Review of Technologies, Principles, Components, and Values. J. Ind. Prod. Eng. 2023, 40, 432–447. [Google Scholar] [CrossRef]
- Rožanec, J.M.; Novalija, I.; Zajec, P.; Kenda, K.; Tavakoli Ghinani, H.; Suh, S.; Veliou, E.; Papamartzivanos, D.; Giannetsos, T.; Menesidou, S.A. Human-Centric Artificial Intelligence Architecture for Industry 5.0 Applications. Int. J. Prod. Res. 2023, 61, 6847–6872. [Google Scholar] [CrossRef]
- Korodi, A.; Nițulescu, I.-V.; Fülöp, A.-A.; Vesa, V.-C.; Demian, P.; Braneci, R.-A.; Popescu, D. Integration of Legacy Industrial Equipment in a Building-Management System Industry 5.0 Scenario. Electronics 2024, 13, 3229. [Google Scholar] [CrossRef]
- Ghobakhloo, M.; Iranmanesh, M.; Mubarak, M.F.; Mubarik, M.; Rejeb, A.; Nilashi, M. Identifying Industry 5.0 Contributions to Sustainable Development: A Strategy Roadmap for Delivering Sustainability Values. Sustain. Prod. Consum. 2022, 33, 716–737. [Google Scholar] [CrossRef]
- Ikudayisi, A.E.; Chan, A.P.C.; Darko, A.; Adedeji, Y.M.D. Integrated Practices in the Architecture, Engineering, and Construction Industry: Current Scope and Pathway towards Industry 5.0. J. Build. Eng. 2023, 73, 106788. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy Models for Demand Forecasting—A Review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Radwan, M.; Alhussan, A.A.; Ibrahim, A.; Tawfeek, S.M. Potato Leaf Disease Classification Using Optimized Machine Learning Models and Feature Selection Techniques. Potato Res. 2024, 513, 1–25. [Google Scholar] [CrossRef]
- Eed, M.; Alhussan, A.A.; Qenawy, A.-S.T.; Osman, A.M.; Elshewey, A.M.; Arnous, R. Potato Consumption Forecasting Based on a Hybrid Stacked Deep Learning Model. Potato Res. 2024, 68, 809–833. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A Review of Artificial Intelligence Based Building Energy Use Prediction: Contrasting the Capabilities of Single and Ensemble Prediction Models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Ciulla, G.; D’amico, A.; Brano, V.L.; Traverso, M. Application of Optimized Artificial Intelligence Algorithm to Evaluate the Heating Energy Demand of Non-Residential Buildings at European Level. Energy 2019, 176, 380–391. [Google Scholar] [CrossRef]
- Vieri, A.; Gambarotta, A.; Morini, M.; Saletti, C. An Integrated Artificial Intelligence Approach for Building Energy Demand Forecasting. Energies 2024, 17, 4920. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial Intelligence and Machine Learning Approaches to Energy Demand-Side Response: A Systematic Review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A Review on Artificial Intelligence Based Load Demand Forecasting Techniques for Smart Grid and Buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Salem, K.M.; Rady, M.; Aly, H.; Elshimy, H. Design and Implementation of a Six-Degrees-of-Freedom Underwater Remotely Operated Vehicle. Appl. Sci. 2023, 13, 6870. [Google Scholar] [CrossRef]
- El-kenawy, E.-S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag Goose Optimization: Nature-Inspired Optimization Algorithm. Expert Syst. Appl. 2024, 238, 122147. [Google Scholar] [CrossRef]
- Yassen, M.A.; Abdel-Fattah, M.G.A.; Ismail, I.; El Kenawy, E.-S.M.; Moustafa, H.E.-D. An AI-Based System for Predicting Renewable Energy Power Output Using Advanced Optimization Algorithms. J. Artif. Intell. Metaheuristics 2024, 8, 1–8. [Google Scholar] [CrossRef]
- El-Sayed, E.; Eid, M.M.; Abualigah, L. Machine Learning in Public Health Forecasting and Monitoring the Zika Virus. Metaheuristic Optim. Rev. 2024, 1, 1–11. [Google Scholar] [CrossRef]
- Ferlito, S.; Atrigna, M.; Graditi, G.; De Vito, S.; Salvato, M.; Buonanno, A.; Di Francia, G. Predictive Models for Building’s Energy Consumption: An Artificial Neural Network (ANN) Approach. In Proceedings of the 2015 XVIII Aisem Annual Conference, Trento, Italy, 3–5 February 2015; pp. 1–4. [Google Scholar]
- Li, Z.; Dai, J.; Chen, H.; Lin, B. An ANN-Based Fast Building Energy Consumption Prediction Method for Complex Architectural Form at the Early Design Stage. Build. Simul. 2019, 12, 665–681. [Google Scholar] [CrossRef]
- Ekici, B.B.; Aksoy, U.T. Prediction of Building Energy Consumption by Using Artificial Neural Networks. Adv. Eng. Softw. 2009, 40, 356–362. [Google Scholar] [CrossRef]
- Verma, A.; Prakash, S.; Kumar, A. ANN-based Energy Consumption Prediction Model up to 2050 for a Residential Building: Towards Sustainable Decision Making. Environ. Prog. Sustain. Energy 2021, 40, e13544. [Google Scholar] [CrossRef]
- Orosa, J.A.; Vergara, D.; Costa, Á.M.; Bouzón, R. A Novel Method for NZEB Internal Coverings Design Based on Neural Networks. Coatings 2019, 9, 288. [Google Scholar] [CrossRef]
- Arida, M.; Nassif, N.; Talib, R.; Abu-Lebdeh, T. Building Energy Modeling Using Artificial Neural Networks. Energy Res. J. 2017, 7, 24–34. [Google Scholar] [CrossRef][Green Version]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The Daily and Hourly Energy Consumption and Load Forecasting Using Artificial Neural Network Method: A Case Study Using a Set of 93 Households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial Neural Network Model for Forecasting Sub-Hourly Electricity Usage in Commercial Buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Cáceres, L.; Merino, J.I.; Díaz-Díaz, N. A Computational Intelligence Approach to Predict Energy Demand Using Random Forest in a Cloudera Cluster. Appl. Sci. 2021, 11, 8635. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest Based Hourly Building Energy Prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H. Nonlinear Autoregressive and Random Forest Approaches to Forecasting Electricity Load for Utility Energy Management Systems. Sustain. Cities Soc. 2019, 45, 460–473. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Piedad, E., Jr.; Kuo, C.-C. Energy Consumption Load Forecasting Using a Level-Based Random Forest Classifier. Symmetry 2019, 11, 956. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Zhang, L.; Feng, Z. Enhancing Building Energy Efficiency Using a Random Forest Model: A Hybrid Prediction Approach. Energy Rep. 2021, 7, 5003–5012. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic Hourly Solar Forecasting Using Machine Learning Models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, Y.; Huang, L.; Zheng, M.; Yuan, H.; Zeng, R. A comprehensive review and future research directions of ensemble learning models for predicting building energy consumption. Energy Build. 2025, 115589. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Li, Y.-Z.; Jiang, H.; Huang, Z. Research on Household Energy Demand Patterns, Data Acquisition and Influencing Factors: A Review. Sustain. Cities Soc. 2023, 99, 104916. [Google Scholar] [CrossRef]
- Salem, K.M.; Rey-Hernández, J.M.; Rey-Martínez, F.J.; Elgharib, A.O. Assessing the Accuracy of AI Approaches for CO2 Emission Predictions in Buildings. J. Clean. Prod. 2025, 513, 145692. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, M.K.; Fu, N.; Liu, J.; Wang, J.; Srebric, J. Investigating the Impact of Data Normalization Methods on Predicting Electricity Consumption in a Building Using Different Artificial Neural Network Models. Sustain. Cities Soc. 2024, 118, 105570. [Google Scholar] [CrossRef]
- Fast, M.; Assadi, M.; De, S. Development and Multi-Utility of an ANN Model for an Industrial Gas Turbine. Appl. Energy 2009, 86, 9–17. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic Concepts of Artificial Neural Network (ANN) Modeling and Its Application in Pharmaceutical Research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for Developing ANN Models and Its Application to the Assessment of the Quality of the ANN Model Development Process in Drinking Water Quality Modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Elkatatny, S.; Tariq, Z.; Mahmoud, M. Real Time Prediction of Drilling Fluid Rheological Properties Using Artificial Neural Networks Visible Mathematical Model (White Box). J. Pet. Sci. Eng. 2016, 146, 1202–1210. [Google Scholar] [CrossRef]
- Betiku, E.; Omilakin, O.R.; Ajala, S.O.; Okeleye, A.A.; Taiwo, A.E.; Solomon, B.O. Mathematical Modeling and Process Parameters Optimization Studies by Artificial Neural Network and Response Surface Methodology: A Case of Non-Edible Neem (Azadirachta Indica) Seed Oil Biodiesel Synthesis. Energy 2014, 72, 266–273. [Google Scholar] [CrossRef]
- Pavlenko, I.; Trojanowska, J.; Ivanov, V.; Liaposhchenko, O. Scientific and Methodological Approach for the Identification of Mathematical Models of Mechanical Systems by Using Artificial Neural Networks. In Innovation, Engineering and Entrepreneurship; Springer: Berlin/Heidelberg, Germany, 2019; pp. 299–306. [Google Scholar]
- Farnaaz, N.; Jabbar, M.A. Random Forest Modeling for Network Intrusion Detection System. Procedia Comput. Sci. 2016, 89, 213–217. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of Support Vector Machine, Random Forest, and Genetic Algorithm Optimized Random Forest Models in Groundwater Potential Mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geoinf. 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random Forests: From Early Developments to Recent Advancements. Syst. Sci. Control Eng. Open Access J. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Mocanu, E.; Gibescu, M.; Stappers, B.; van Alst, W. Deep Learning versus Traditional Machine Learning Methods for Aggregated Energy Demand Prediction. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for Forecasting Building Energy Consumption—A Systematic Review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar] [CrossRef]
- Forootan, M.M.; Larki, I.; Zahedi, R.; Ahmadi, A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability 2022, 14, 4832. [Google Scholar] [CrossRef]
- Elreafay, A.M.; Salem, K.M.; Abumandour, R.M.; Dawood, A.S.; Al Nuaimi, S. Effect of Particle Diameter and Void Fraction on Gas–Solid Two-Phase Flow: A Numerical Investigation Using the Eulerian–Eulerian Approach. Comput. Part. Mech. 2024, 12, 289–311. [Google Scholar] [CrossRef]
- Robinson, C.; Dilkina, B.; Hubbs, J.; Zhang, W.; Guhathakurta, S.; Brown, M.A.; Pendyala, R.M. Machine Learning Approaches for Estimating Commercial Building Energy Consumption. Appl. Energy 2017, 208, 889–904. [Google Scholar] [CrossRef]
- Yokoyama, R.; Wakui, T.; Satake, R. Prediction of Energy Demands Using Neural Network with Model Identification by Global Optimization. Energy Convers. Manag. 2009, 50, 319–327. [Google Scholar] [CrossRef]
- Ikeda, S.; Ooka, R. A New Optimization Strategy for the Operating Schedule of Energy Systems under Uncertainty of Renewable Energy Sources and Demand Changes. Energy Build. 2016, 125, 75–85. [Google Scholar] [CrossRef]
- Salem, K.M.; Elreafay, A.M.; Abumandour, R.M.; Dawood, A.S. Modeling Two-Phase Gas-Solid Flow in Axisymmetric Diffusers Using Cut Cell Technique: An Eulerian-Eulerian Approach. Bound. Value Probl. 2024, 2024, 150. [Google Scholar] [CrossRef]
- Abumandour, R.M.; El-Reafay, A.M.; Salem, K.M.; Dawood, A.S. Numerical Investigation by Cut-Cell Approach for Turbulent Flow through an Expanded Wall Channel. Axioms 2023, 12, 442. [Google Scholar] [CrossRef]
- Nagai, T. Optimization Method for Minimizing Annual Energy, Peak Energy Demand, and Annual Energy Cost through Use of Building Thermal Storage/Discussion. ASHRAE Trans. 2002, 108, 43. [Google Scholar]
- Bahlawan, H.; Morini, M.; Pinelli, M.; Poganietz, W.-R.; Spina, P.R.; Venturini, M. Optimization of a Hybrid Energy Plant by Integrating the Cumulative Energy Demand. Appl. Energy 2019, 253, 113484. [Google Scholar] [CrossRef]
- Ferrara, M.; Rolfo, A.; Prunotto, F.; Fabrizio, E. EDeSSOpt–Energy Demand and Supply Simultaneous Optimization for Cost-Optimized Design: Application to a Multi-Family Building. Appl. Energy 2019, 236, 1231–1248. [Google Scholar] [CrossRef]














| Reference Number | Mathematical Model | Variables | Proposed | Time Period | Accuracy |
|---|---|---|---|---|---|
| Ferlito et al. [20] | ANN | -Weather conditions -Building structure and characteristics -Energy consumption of components (like lighting and HVAC systems) -Level of occupancy | Forecasting building energy demand | 2011–2013 | RMSPE 15.7% to 17.97% |
| Li et al. [21] | ANN | -Building energy consumption | Fast energy consumption prediction for complex architecture | 2015–2016 | Cooling/Heating: ±10% (MCD); Total: ±10% (MSHD) |
| Ekici et al. [22] | ANN | -Orientation of the building -Insulation thickness (ranging from 0 to 15 cm) -Transparency ratio (15%, 20%, and 25%) | Predicting building energy needs using orientation, insulation, and transparency ratio | 2006–2007 | Deviation: 3.43%; Prediction rate: 94.8–98.5% |
| Verma et al. [23] | ANN | -Predicted temperature and relative humidity -Building characteristics -Energy consumption components | Energy consumption prediction for a 2BHK multizone building (two bedrooms, one living room, one kitchen, and two toilets) | 2001–2017 | 95% coefficient bounds |
| Orosa et al. [24] | ANN | -Weather conditions -Real vapor permeability of internal coverings --Behavioral groups of indoor ambiences | Modeling permeable coverings for nZEB indoor conditions | 2019–2020 | The Mean Absolute Error (MAE) or Mean Squared Error (MSE) values. |
| Arida et al. [25] | ANN | -Geometrical characteristics -Shape factor -Areas of building | Forecasting total building energy consumption | 2014–2016 | CV or RMSE: 1.7–7.7% |
| Cáceres et al. [28] | RF | -Apartment area -Number of occupants -Electrical appliance consumption | Household energy demand forecasting using Big Data | 2011–2014 | RMSPE, MAPE, R2 |
| Wang et al. [29] | RF | -Parameter settings of the Random Forest (RF) -Influential features- | Hourly building energy prediction for educational buildings | 2014–2015 | RF outperformed RT by 14–25% and SVR by 5–5.5% |
| Ahmad and Chen [30] | NARM, LMSR, RF | -Weather changes -Medium-term (MT) and long-term (LT) predictions | Medium-term and long-term energy prediction for utilities and industrial customers | 2009 | CV of LSBoost: 5.019% (summer), 3.159% (autumn), 3.292% (winter), 3.184% (spring) |
| Chen et al. [31] | RF | -Historical data of energy consumption -Classification levels -Prediction methods | Predicts actual numerical energy values, then classifies into levels (low, average, high) | 2016 | Execution time across 3, 5, and 7 energy level cases |
| Liu et al. [32] | RF-ANN | -Heat transfer coefficients -Solar radiation absorption coefficients -Window–wall ratio | Predicting building energy consumption based on building envelope design parameters | 2015 | Predicted RMSE is 0.0115, and R2 is 0.933, which reflect the high accuracy of the RF prediction model |
| Zone | Rated Capacity (kW) | Rated Flow (m3/s) | Total Refrigeration Load (kW) | Sensible Load (kW) | Latent Load (kW) | Air Temperature (°C) | Humidity (%) | Max. Refrigeration Hour | Max. Operating Temperature (°C) |
|---|---|---|---|---|---|---|---|---|---|
| Zone 1 | 5.95 | 0.407 | 5.17 | 4.8 | 0.37 | 24 | 51.2 | Jul 11:00 | 29.81 |
| Zone 3 | 11.13 | 0.896 | 9.68 | 9.68 | 0 | 23 | 49.7 | Aug 14:00 | 31.2 |
| Zone 10 | 8.2 | 0.57 | 7.13 | 6.72 | 0.42 | 24 | 54.3 | Jul 15:00 | 31.12 |
| Zone 9 | 7.25 | 0.509 | 6.31 | 6.01 | 0.3 | 24 | 55.2 | Jul 15:00 | 29.03 |
| Zone 8 | 7.2 | 0.506 | 6.26 | 5.97 | 0.29 | 24 | 55.3 | Jul 15:00 | 28.85 |
| Zone 7 | 7.19 | 0.506 | 6.25 | 5.96 | 0.29 | 24 | 55.3 | Jul 15:00 | 28.83 |
| Zone 6 | 7.18 | 0.505 | 6.25 | 5.96 | 0.29 | 24 | 55.3 | Jul 15:00 | 28.82 |
| Zone 5 | 7.19 | 0.505 | 6.25 | 5.96 | 0.29 | 24 | 55.3 | Jul 15:00 | 28.83 |
| Zone 2 | 3.54 | 0.241 | 3.08 | 3.08 | 0 | 25 | 44.4 | Aug 14:00 | 29.87 |
| Zone 4 | 0.5 | 0.04 | 0.43 | 0.43 | 0 | 23.01 | 43.8 | Aug 07:00 | 28.55 |
| Zone 24 | 5.1 | 0.41 | 4.44 | 4.44 | 0 | 23 | 49.7 | Aug 14:00 | 29.13 |
| Zone 22 | 0.4 | 0.027 | 0.35 | 0.35 | 0 | 25 | 44.4 | Aug 14:00 | 28.56 |
| Zone 23 | 0.35 | 0.024 | 0.31 | 0.31 | 0 | 25 | 44.4 | Aug 14:00 | 29.6 |
| Zone 26 | 4.16 | 0.287 | 3.62 | 3.39 | 0.23 | 24 | 53.7 | Jul 15:00 | 30.6 |
| Component | Equation | NO. Equation |
|---|---|---|
| Input Layer: The network takes input features | (1) | |
| First Hidden Layer: Each neuron j in the first hidden layer computes a weighted sum of its inputs | (2) | |
| This sum is then passed through an activation function f | (3) | |
| Second Hidden Layer: Each neuron k in the second hidden layer takes the outputs from the first hidden layer as inputs | (4) | |
| This sum is then passed through an activation function f | (5) | |
| Output Layer: The output layer produces the final prediction for energy demand | (6) | |
| Backpropagation Algorithm | (7) |
| Component | Equation | NO. Equation |
|---|---|---|
| The split criterion for a node n can be expressed as follows | (8) | |
| Prediction | (9) | |
| The predicted class is given by the majority vote among all trees | (10) | |
| Out-of-bag error | (11) |
| Component | Equation | NO. Equation |
|---|---|---|
| Root Mean Square Percentage Error (RMSPE) | (12) | |
| Root Mean Square Relative Percentage Error (RMSRPE): | (13) | |
| Mean Absolute Percentage Error (MAPE) | (14) | |
| Mean Absolute Relative Percentage Error (MARPE) | (15) | |
| Kling–Gupta Efficiency (KGE) | (16) | |
| Nash–Sutcliffe Efficiency (NSE) | (17) | |
| Coefficient of Determination (R2) | (18) |
| Metric | Lucia ANN | Lucia RF | FUHEM ANN | FUHEM RF |
|---|---|---|---|---|
| Mean Absolute Percentage Error (MAPE) | 0.0207% | 0.5426% | ||
| Root Mean Squared Error Percentage (RMSPE) | 0.1004% | 2.0903% | ||
| Mean Absolute Relative Percentage Error (MARPE) | 3.562% | 6.1% | 0.0033% | 0.0468% |
| Root Mean Squared Relative Error (RMSRE) | 20.12% | 24.56% | 0.0055% | 0.00796% |
| Correlation with Actual Demand | 0.9627 | 0.9445 | 1 | 0.9948 |
| KGE | 0.9373 | 0.7501 | 0.9872 | 0.7401 |
| NSE | 0.9267 | 0.8870 | 0.9998 | 0.9316 |
| R-Squared (R2) | 0.9267 | 0.8870 | 0.9998 | 0.9316 |
| Training Set R-Value | 0.9774 | - | 1 | - |
| Validation Set R-Value | 0.97171 | - | 1 | - |
| Test Set R-Value | 0.96979 | - | 1 | - |
| Training Time | 40 s | 2.8 s | 1.1 s | 0.3 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, K.M.; Rey-Hernández, J.M.; Elgharib, A.O.; Rey-Martínez, F.J. Optimizing Energy Forecasting Using ANN and RF Models for HVAC and Heating Predictions. Appl. Sci. 2025, 15, 6806. https://doi.org/10.3390/app15126806
Salem KM, Rey-Hernández JM, Elgharib AO, Rey-Martínez FJ. Optimizing Energy Forecasting Using ANN and RF Models for HVAC and Heating Predictions. Applied Sciences. 2025; 15(12):6806. https://doi.org/10.3390/app15126806
Chicago/Turabian StyleSalem, Khaled M., Javier M. Rey-Hernández, A. O. Elgharib, and Francisco J. Rey-Martínez. 2025. "Optimizing Energy Forecasting Using ANN and RF Models for HVAC and Heating Predictions" Applied Sciences 15, no. 12: 6806. https://doi.org/10.3390/app15126806
APA StyleSalem, K. M., Rey-Hernández, J. M., Elgharib, A. O., & Rey-Martínez, F. J. (2025). Optimizing Energy Forecasting Using ANN and RF Models for HVAC and Heating Predictions. Applied Sciences, 15(12), 6806. https://doi.org/10.3390/app15126806









