Neural Network Method for Distance Prediction and Impedance Matching of a Wireless Power Transfer System
Abstract
1. Introduction
2. Materials and Methods
2.1. Neural Network
2.1.1. Neural Network Model on Impedance Dataset
2.1.2. Neural Network Model on Phase Dataset
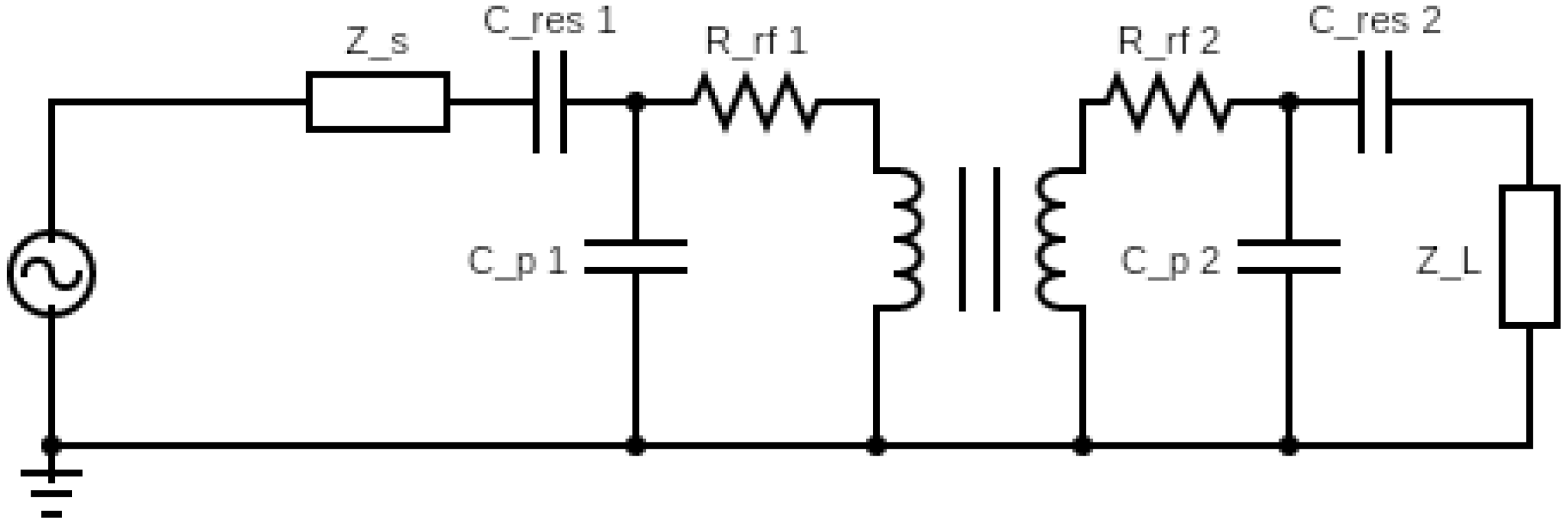
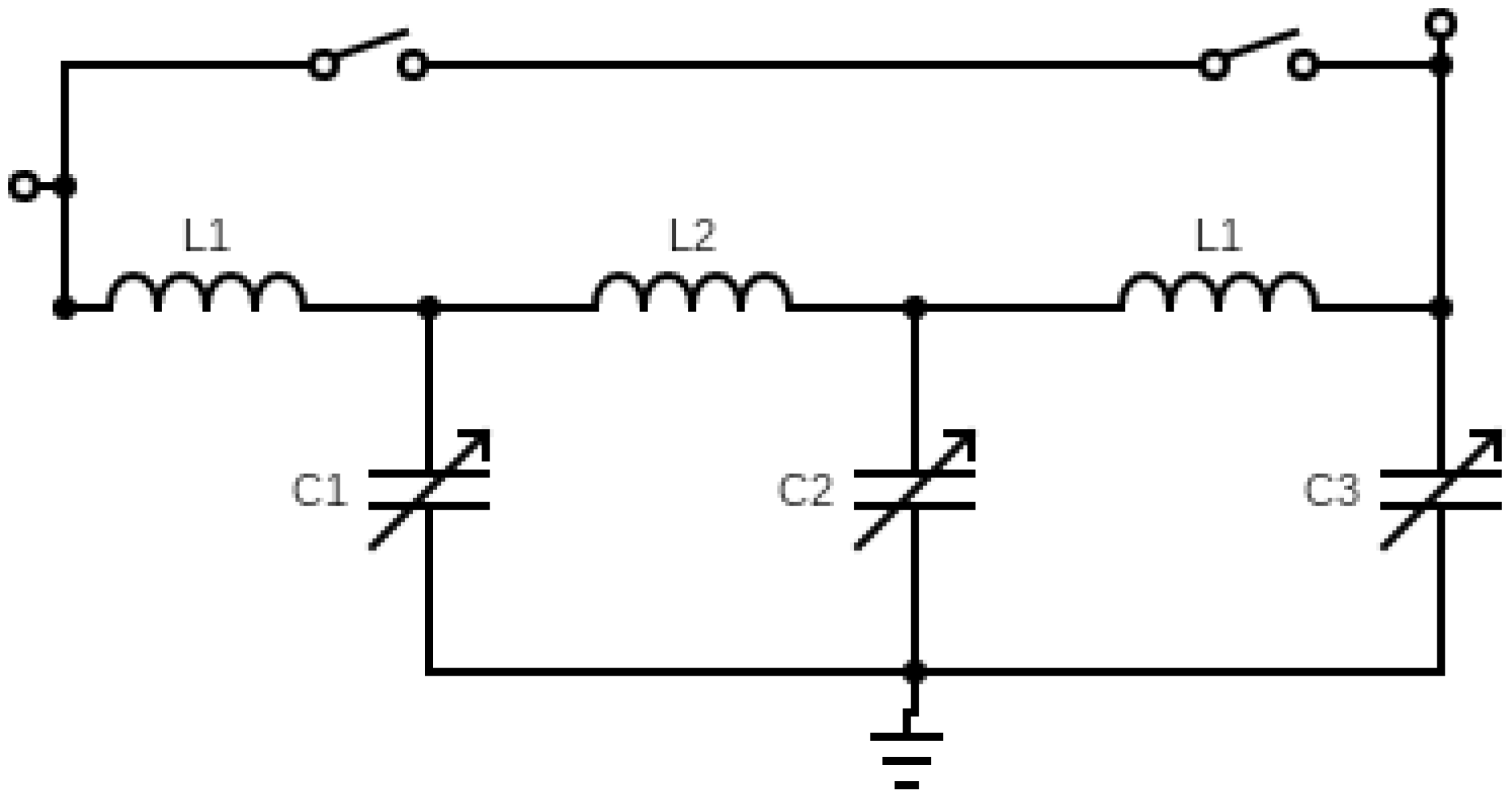
3. WPT System: Experimental and Simulated Data
3.1. WPT System Impedance
3.2. WPT System Phase
4. Results
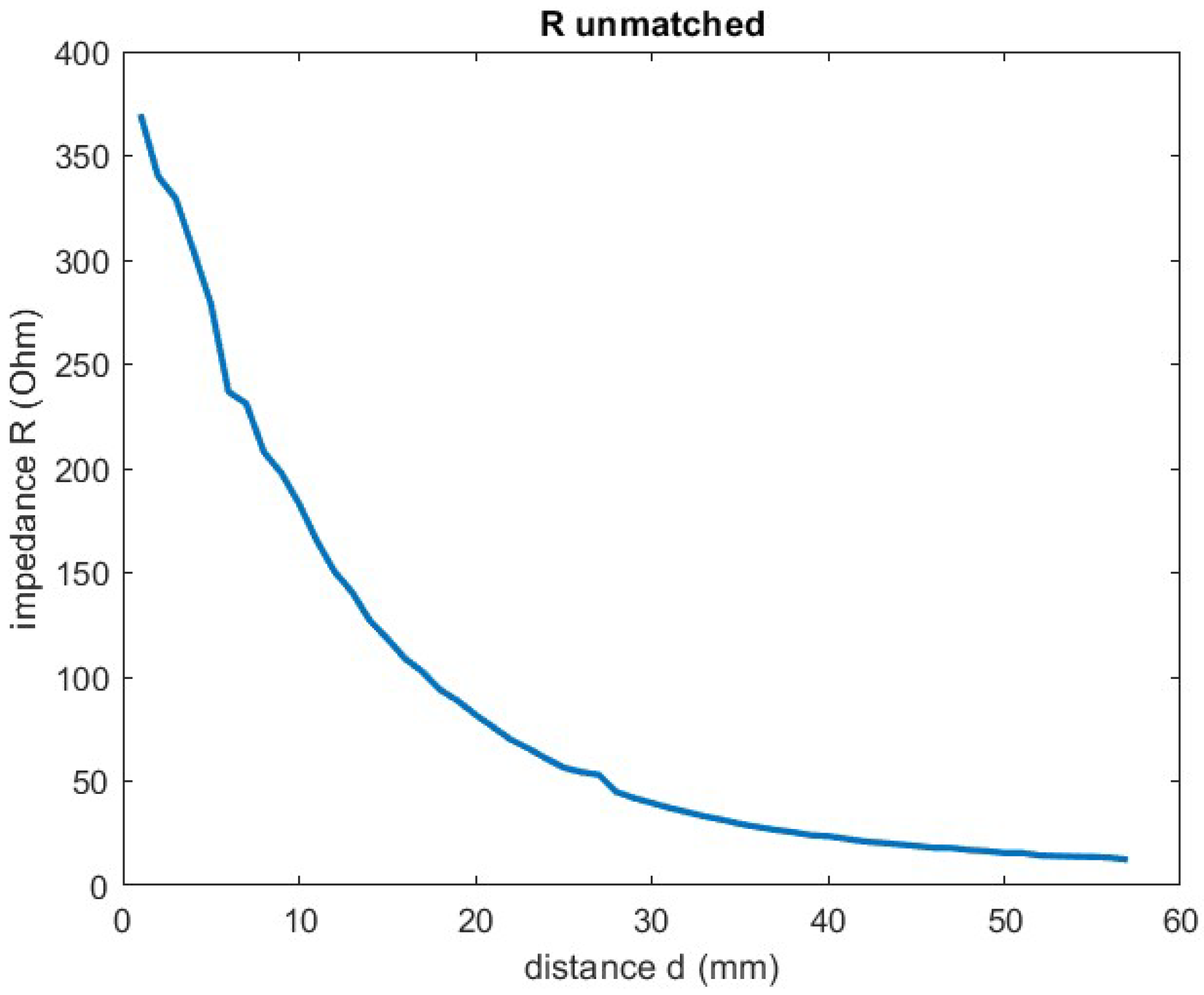
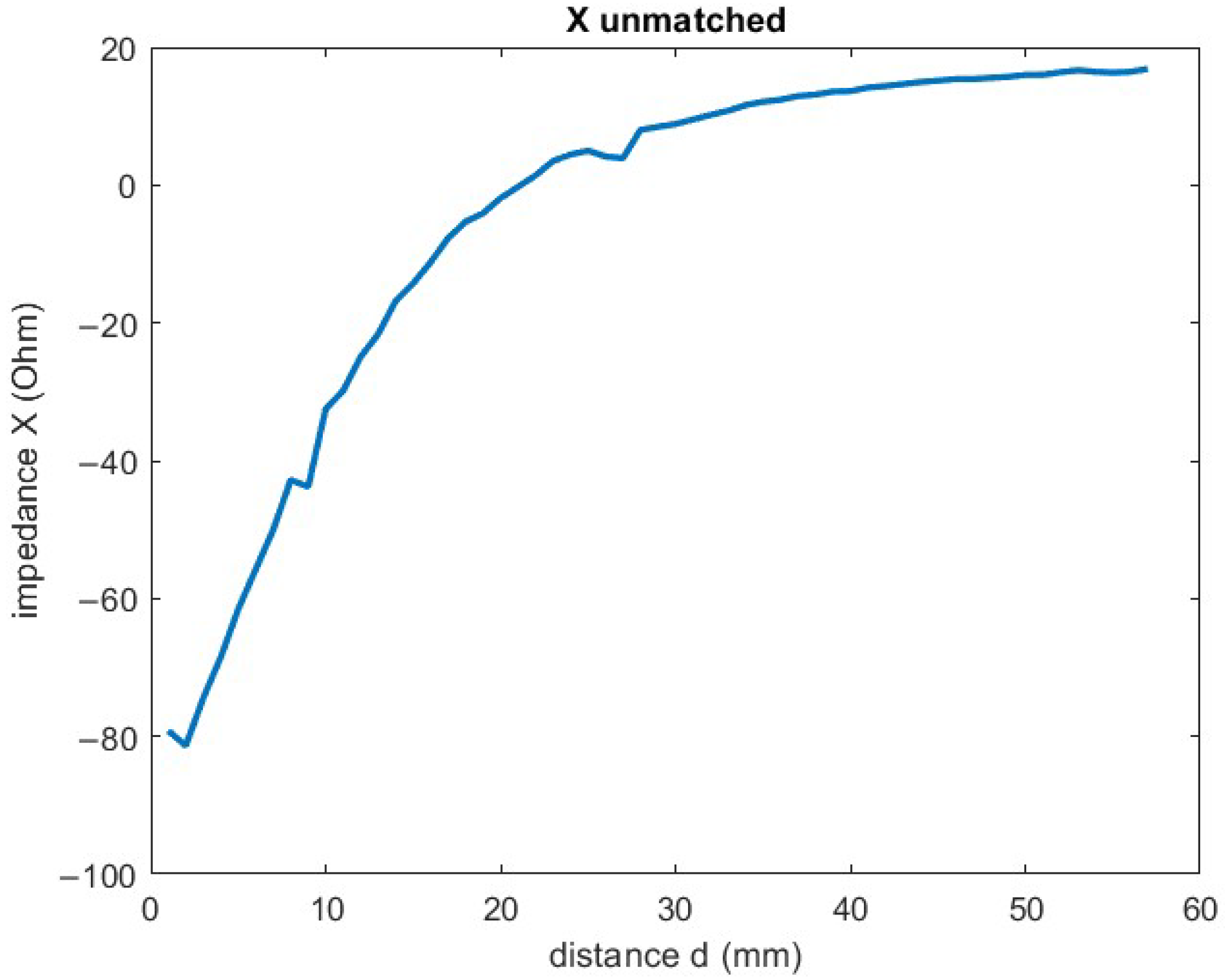
4.1. Simulation Results
4.2. Experimental Results
4.3. Results on the Phase Dataset
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Zhao, D.; Jiang, Y.; Li, Y.; Yu, X.; Wang, S.; Wu, M.; Wang, X.; Tang, Y. Precise Coil Inductance Prediction with Transfer Learning Improved Deep Neural Networks in WPT Systems. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 2092–2098. [Google Scholar]
- Allotta, B.; Pugi, L.; Reatti, A.; Corti, F. Wireless power recharge for underwater robotics. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Romano, D.; Angelo, L.D.; Kovacevic-Badstubner, I.; Grossner, U.; Parise, M.; Antonini, G. Efficient Partial Elements Computation for the Non-Orthogonal PEEC Method Including Conductive, Dielectrics, and Magnetic Materials. IEEE Trans. Magn. 2022, 58, 7000611. [Google Scholar] [CrossRef]
- Santoro, L.; Quercio, M.; Canova, A.; Sesana, R. Measuring thermal and electrical performances of additively manufactured magnetic shielding material: An active thermography approach. Nondestruct. Test. Eval. 2024, 39, 2692–2715. [Google Scholar] [CrossRef]
- Corti, F.; Bertolini, V.; Faba, A.; Cardelli, E.; Reatti, A. Design procedures for series-series wpt systems: A comparative analysis. Comput. Electr. Eng. 2024, 119, 109511. [Google Scholar] [CrossRef]
- Pugi, L.; Reatti, A.; Corti, F. Application of modal analysis methods to the design of wireless power transfer systems. Meccanica 2019, 54, 321–331. [Google Scholar] [CrossRef]
- Parise, M.; Quercio, M.; Laudani, A. Efficient Analytical Evaluation of Inductive Coupling Strength in Wireless Power Transfer Systems. IEEE Access 2024, 12, 143263–143271. [Google Scholar] [CrossRef]
- Lazzeroni, P.; Mariuzzo, I.; Quercio, M.; Repetto, M. Economic, Energy, and Environmental Analysis of PV with Battery Storage for Italian Households. Electronics 2021, 10, 146. [Google Scholar] [CrossRef]
- Canova, A.; Gruosso, G.; Quercio, M. Characterization of Electromagnetic Device by Means of Spice Models. Int. J. Emerg. Technol. Adv. Eng. 2021, 11, 12–22. [Google Scholar] [CrossRef]
- Parise, M.; Loreto, F. Quasi-Static Explicit Expression for the Flux Linkage Between Noncoplanar Coils in Wireless Power Transfer Systems Above a Lossy Ground. IEEE Trans. Electromagn. Compat. 2023, 65, 1857–1867. [Google Scholar] [CrossRef]
- Parise, M.; Loreto, F.; Romano, D.; Antonini, G.; Ekman, J. Accurate computation of mutual inductance of non coaxial pancake coils. Energies 2021, 14, 4907. [Google Scholar] [CrossRef]
- Parise, M.; Antonini, G.; Romano, D. On the Flux Linkage between Pancake Coils in Resonance-Type Wireless Power Transfer Systems. Int. J. Antennas Propag. 2020, 2020. [Google Scholar] [CrossRef]
- Canova, A.; Corti, F.; Laudani, A.; Lozito, G.M.; Quercio, M. Innovative shielding technique for wireless power transfer systems. IET Power Electron. 2023, 17, 962–969. [Google Scholar] [CrossRef]
- Canova, A.; Quercio, M. A Shielding System Proposal for the Cabling of Electric Glass Melters. IEEE Open J. Ind. Appl. 2023, 4, 1–10. [Google Scholar] [CrossRef]
- Alzahrani, A. Neural Networks Frequency Control for Static Wireless Power Transfer Systems. In Proceedings of the 2024 10th International Conference on Applied System Innovation (ICASI), Kyoto, Japan, 17–21 April 2024; pp. 122–124. [Google Scholar]
- Lozito, G.M.; Quercio, M.; Sabino, L.; Laudani, A. A Comparative Analysis on Different Deep Neural Network Models for Magnetic Hysteresis with Distorted Excitation Waveforms. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–6. [Google Scholar]
- Parise, M. On the Voltage Response of Homogeneous Earth Models in Central Loop Electromagnetic Sounding. Int. J. Antennas Propag. 2022, 2022. [Google Scholar] [CrossRef]
- Bertolini, V.; Corti, F.; Cardelli, E. Effects of Misalignment on Output Voltage Stability in SS Controlled Wireless Power Transfer Systems with Different Control Strategies. In Proceedings of the 2024 International Wireless Communications and Mobile Computing (IWCMC), Ayia Napa, Cyprus, 27–31 May 2024; pp. 1074–1079. [Google Scholar]
- Intravaia, M.; Becchi, L.; Bindi, M.; Corti, F.; Lozito, G.M.; Alfonso, C.G.; Luchetta, A.; Reatti, A. LCC-S Compensated Wireless Power Transfer: System Optimization Using Genetic Algorithms. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar]
- Parise, M. Evaluation of the Inductive Coupling between Coplanar Concentric Coils in the Presence of the Ground. Int. J. Antennas Propag. 2024, 2024. [Google Scholar] [CrossRef]
- Quercio, M.; Lozito, G.M.; Corti, F.; Fulginei, F.R.; Laudani, A. Recent Results in Shielding Technologies for Wireless Electric Vehicle Charging Systems. IEEE Access 2024, 12, 16728–16740. [Google Scholar] [CrossRef]
- Intravaia, M.; Lozito, G.M.; Becchi, L.; Corti, F.; Luchetta, A.; Reatti, A. Failure Prevention Based on Principal Component Analysis and Machine Learning for Wireless Power Transfer Systems. In Proceedings of the 2024 IEEE 22nd Mediterranean Electrotechnical Conference (MELECON), Porto, Portugal, 25–27 June 2024; pp. 213–218. [Google Scholar]
- Quercio, M.; Galbusera, F.; Canova, A.; Demir, A.G.; Gruosso, G.; Previtali, B. Electromagnetic shielding properties of LPBF produced Fe2.9wt.%Si alloy. J. Phys. Energy 2023, 5, 045003. [Google Scholar] [CrossRef]
- Franco, F.L.; Ricco, M.; Cirimele, V.; Apicella, V.; Carambia, B.; Grandi, G. Electric Vehicle Charging Hub Power Forecasting: A Statistical and Machine Learning Based Approach. Energies 2023, 16, 2076. [Google Scholar] [CrossRef]
- Quercio, M.; Galbusera, F.; Posković, E.; Franchini, F.; Ferraris, L.; Canova, A.; Gruosso, G.; Demir, A.G.; Previtali, B. Characterization of LPBF Produced Fe2.9wt.%Si for Electromagnetic Actuator. IEEE Access 2023, 11, 134822–134833. [Google Scholar] [CrossRef]
- Palermo, M.; Forconi, F.; Belloni, E.; Quercio, M.; Lozito, G.M.; Fulginei, F.R. Optimization of a feedforward neural network’s architecture for an HVAC system problem. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; pp. 1–6. [Google Scholar]
- Parise, M.; Tamburrelli, V.; Antonini, G. Mutual impedance of thin-wire circular loops in near-surface applications. IEEE Trans. Electromagn. Compat. 2019, 61, 558–563. [Google Scholar] [CrossRef]
- Parise, M.; Antonini, G.; Di Paola, L. A Rigorous Explicit Expression for the Mutual Inductance of Two Co-Axial Thin-Wire Coil Antennas Placed above a Layered Ground. Energies 2023, 16, 7586. [Google Scholar] [CrossRef]
- Canova, A.; Giaccone, L.; Quercio, M. A proposal for performance evaluation of low frequency shielding efficiency. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; Volume 2021, pp. 935–939. [Google Scholar]
- Quercio, M.; Campanelli, F.; Canova, A. Passive loop optimisation for HV Joint zone. In Proceedings of the IEEE EUROCON 2023—20th International Conference on Smart Technologies, Torino, Italy, 6–8 July 2023; pp. 343–348. [Google Scholar]
- Stella, M.; Faba, A.; Fulginei, F.R.; Quercio, M.; Scorretti, R.; Bertolini, V.; Sabino, L.; Tiismus, H.; Kallaste, A.; Cardelli, E. Experimental measurements and numerical modelling of additively manufactured Fe-Si cores. J. Magn. Magn. Mater. 2024, 591, 171752. [Google Scholar] [CrossRef]
- Santoro, L.; Sesana, R.; Diller, J.; Radlbeck, C.; Mensinger, M. Dissipative and thermal aspects in cyclic loading of additive manufactured AISI 316L. Eng. Fail. Anal. 2024, 163, 108446. [Google Scholar] [CrossRef]
- Santoro, L.; Razza, V.; Maddis, M.D. Nugget and corona bond size measurement through active thermography and transfer learning model. Int. J. Adv. Manuf. Technol. 2024, 133, 5883–5896. [Google Scholar] [CrossRef]
- Quercio, M.; del Pino Lopez, J.C.; Grasso, S.; Canova, A. Numerical and experimental analysis of thermal behaviour of high voltage power cable in unfilled ducts. Sci. Rep. 2024, 14, 20599. [Google Scholar] [CrossRef]
- Quercio, M.; Barlassina, L.; Canova, A. Characterization of the shielding properties of a power transformer enclosure. In Proceedings of the IEEE EUROCON 2023—20th International Conference on Smart Technologies, Torino, Italy, 6–8 July 2023; pp. 349–353. [Google Scholar]
- Laudani, A.; Fulginei, F.R.; Palermo, M.; Quercio, M.; Corti, F.; Lozito, G.M. On the Identification of One diode PV model by reduced forms and different metrics. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; pp. 1–7. [Google Scholar]
- Asghar, R.; Fulginei, F.R.; Quercio, M.; Mahrouch, A. Artificial Neural Networks for Photovoltaic Power Forecasting: A Review of Five Promising Models. IEEE Access 2024, 12, 90461–90485. [Google Scholar] [CrossRef]
- Risi, B.G.; Riganti-Fulginei, F.; Laudani, A.; Quercio, M. Compensation Admittance Load Flow: A Computational Tool for the Sustainability of the Electrical Grid. Sustainability 2023, 15, 14427. [Google Scholar] [CrossRef]
- Yue, K.; Liu, Y.; Zhang, X.; He, R.; Fu, M. Identifying Complete Set of Parameters Using Transmitter Side Information for Multi-transmitter Wireless Power Transfer Systems. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 1128–1132. [Google Scholar]
- Lopera, J.R.; Fischbacher, R.; Pestros, R.; Pommerenke, D.; Auinger, B.; Grosinger, J. Adaptive NFC WPT System Implementing Neural Network-Based Impedance Matching with Bypass Functionality. In Proceedings of the 2023 IEEE/MTT-S International Microwave Symposium—IMS 2023, San Diego, CA, USA, 11–16 June 2023; pp. 879–882. [Google Scholar] [CrossRef]
- Romero Lopera, J.; Grosinger, J. S-Parameter Measurements of an AI-Enhanced Adaptive Wireless Power Transfer System. IEEE Dataport 2023. [Google Scholar] [CrossRef]
- Martínez, A.; González, C.; Jaramillo, A.; Cárdenas, D.; Chong, A.V. Low-cost, microcontroller-based phase shift measurement system for a wireless power transfer prototype. HardwareX 2022, 11, e00311. [Google Scholar] [CrossRef]
- Martínez, A.; González, C.; Jaramillo, A.; Cárdenas, D.; Chong, A.V. Experimental data validating the optimization of a wireless power transfer prototype employing a novel phase shift measurement system and frequency control. Data Brief 2022, 45, 108675. [Google Scholar] [CrossRef]
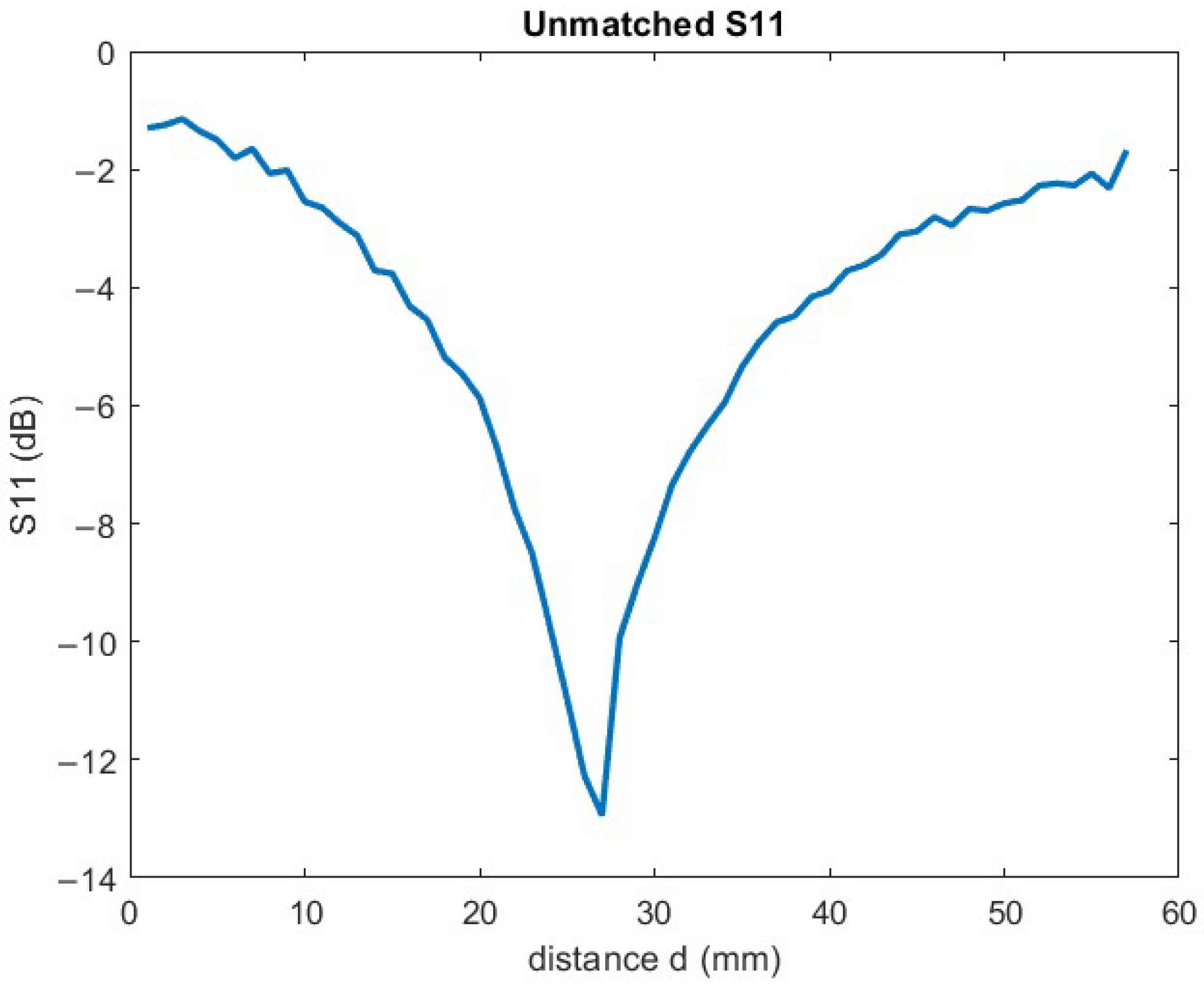
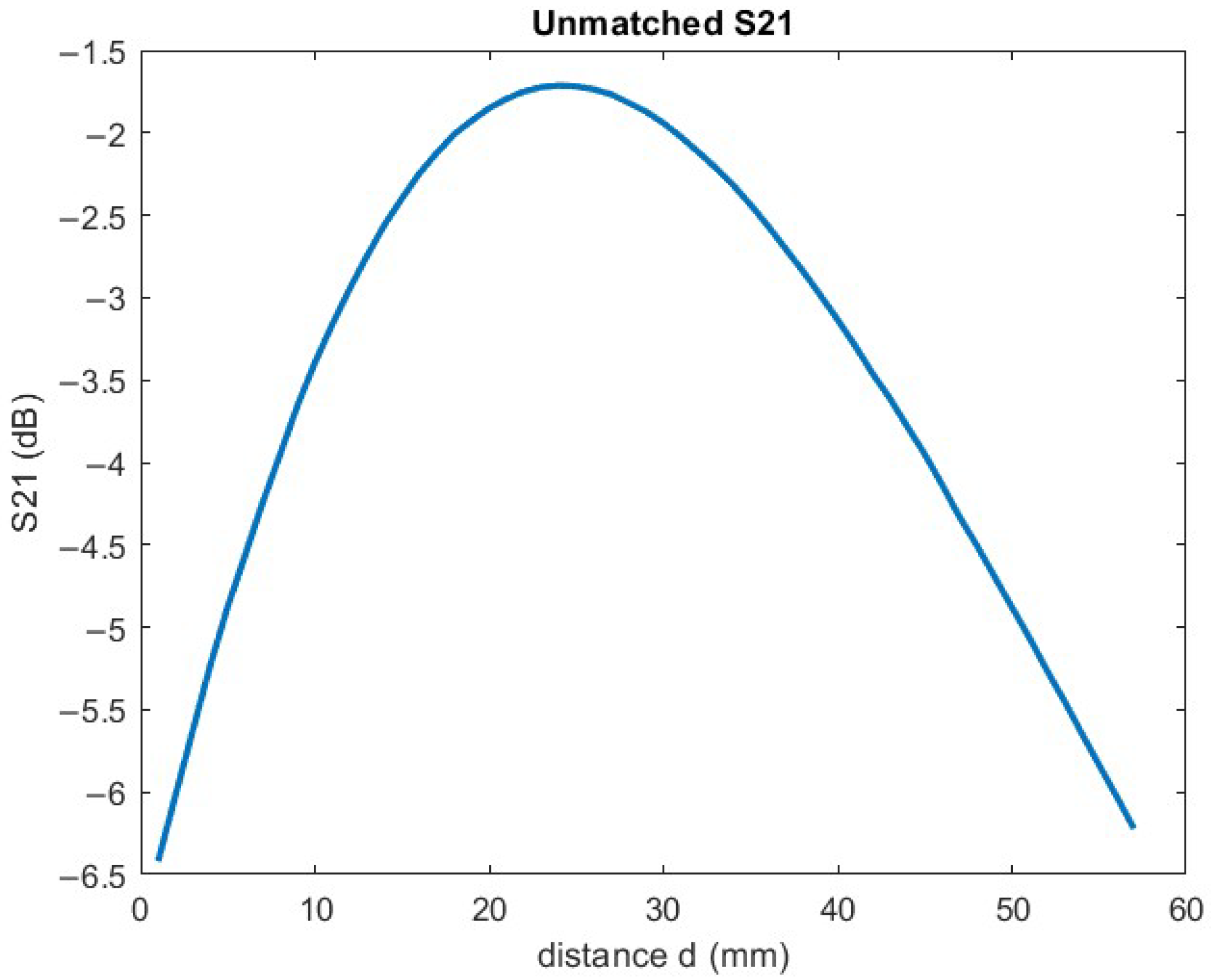
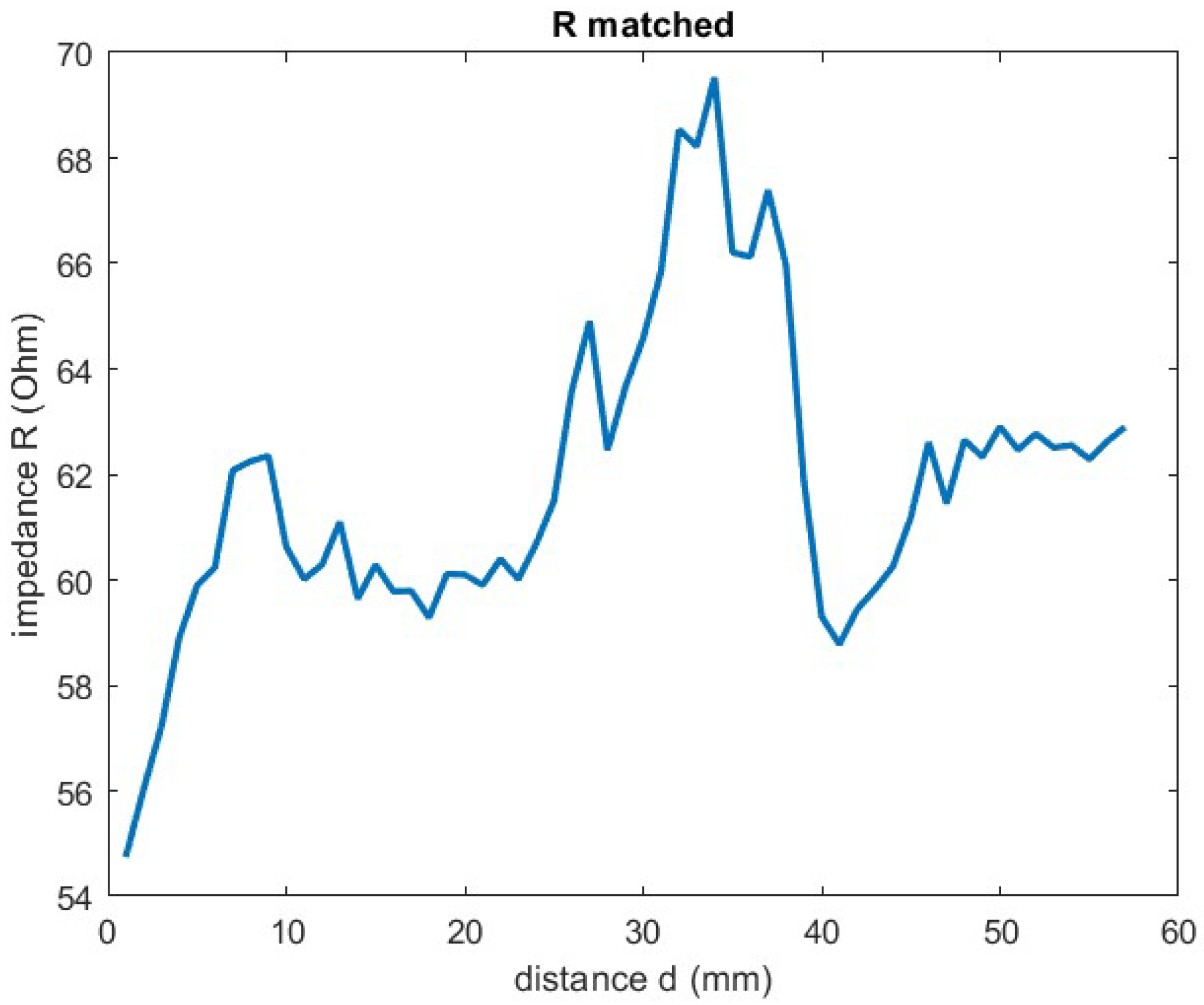


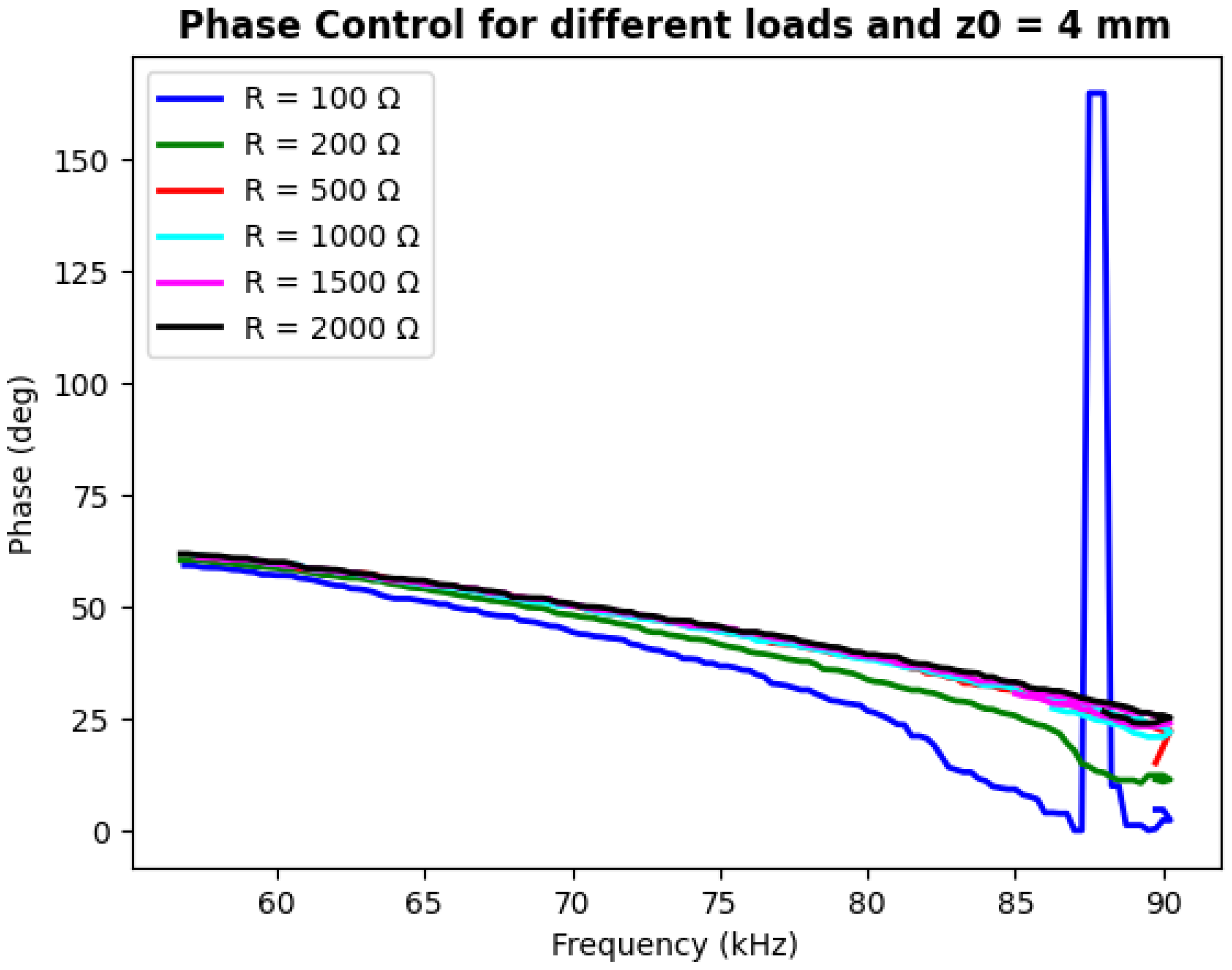
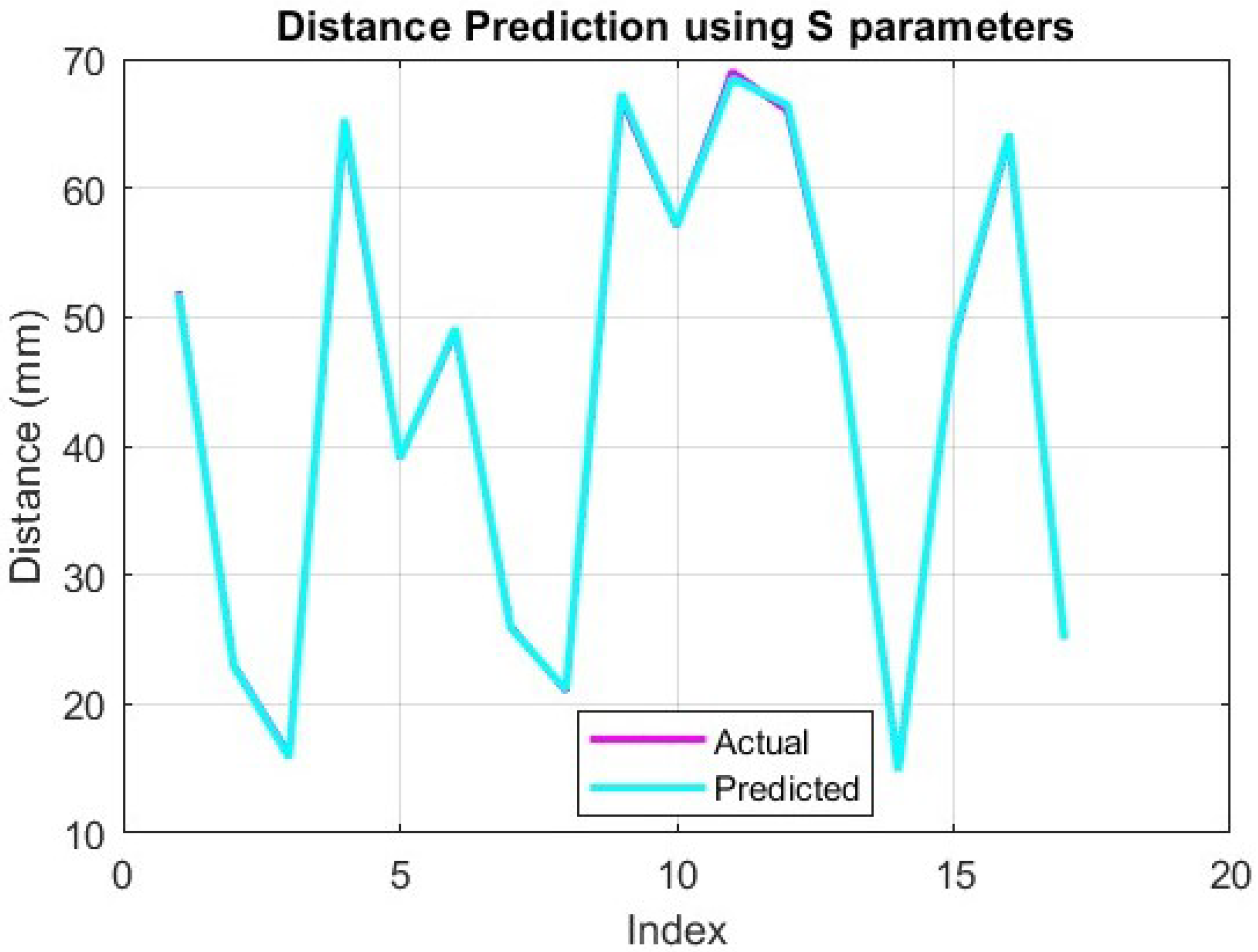

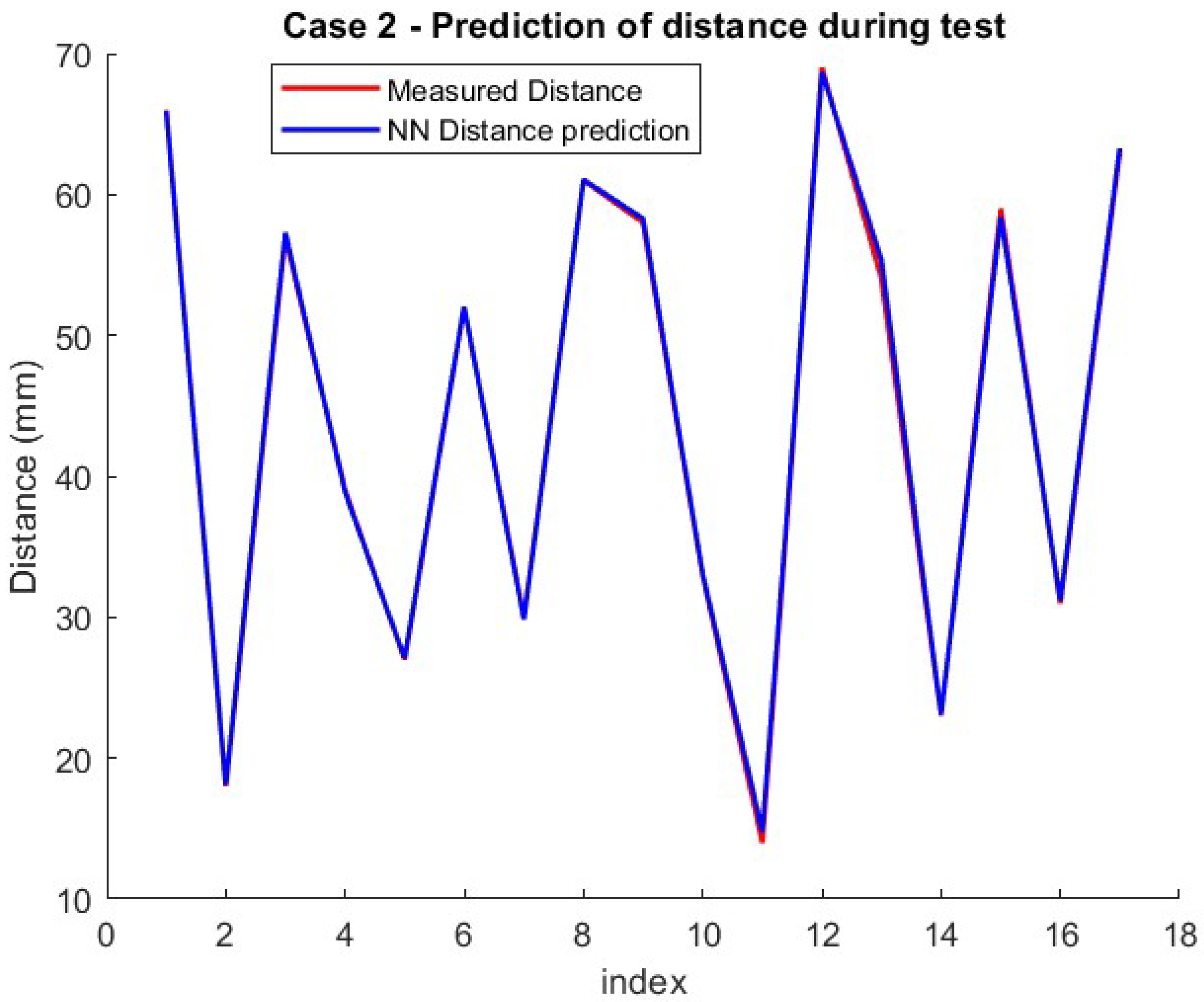
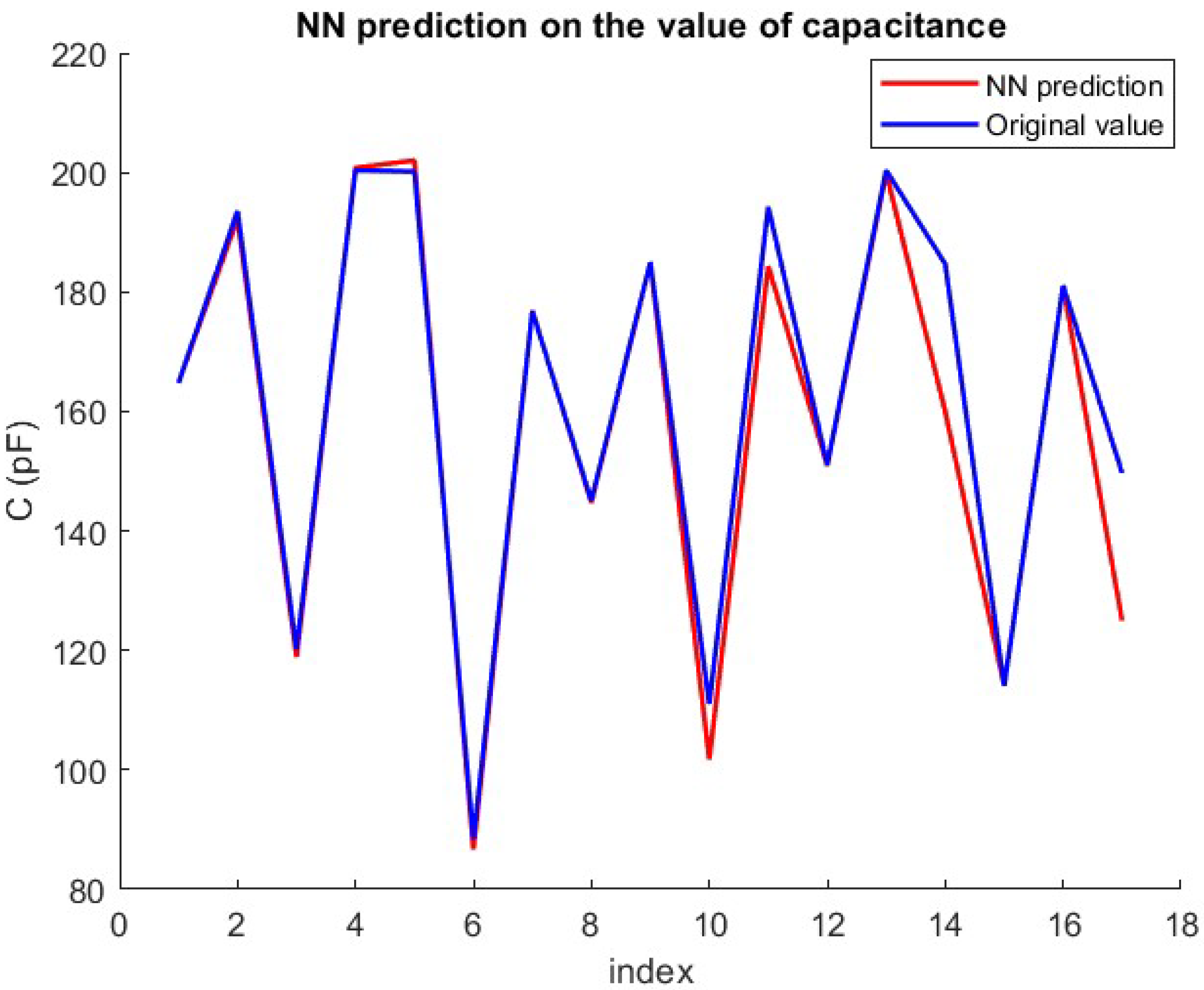
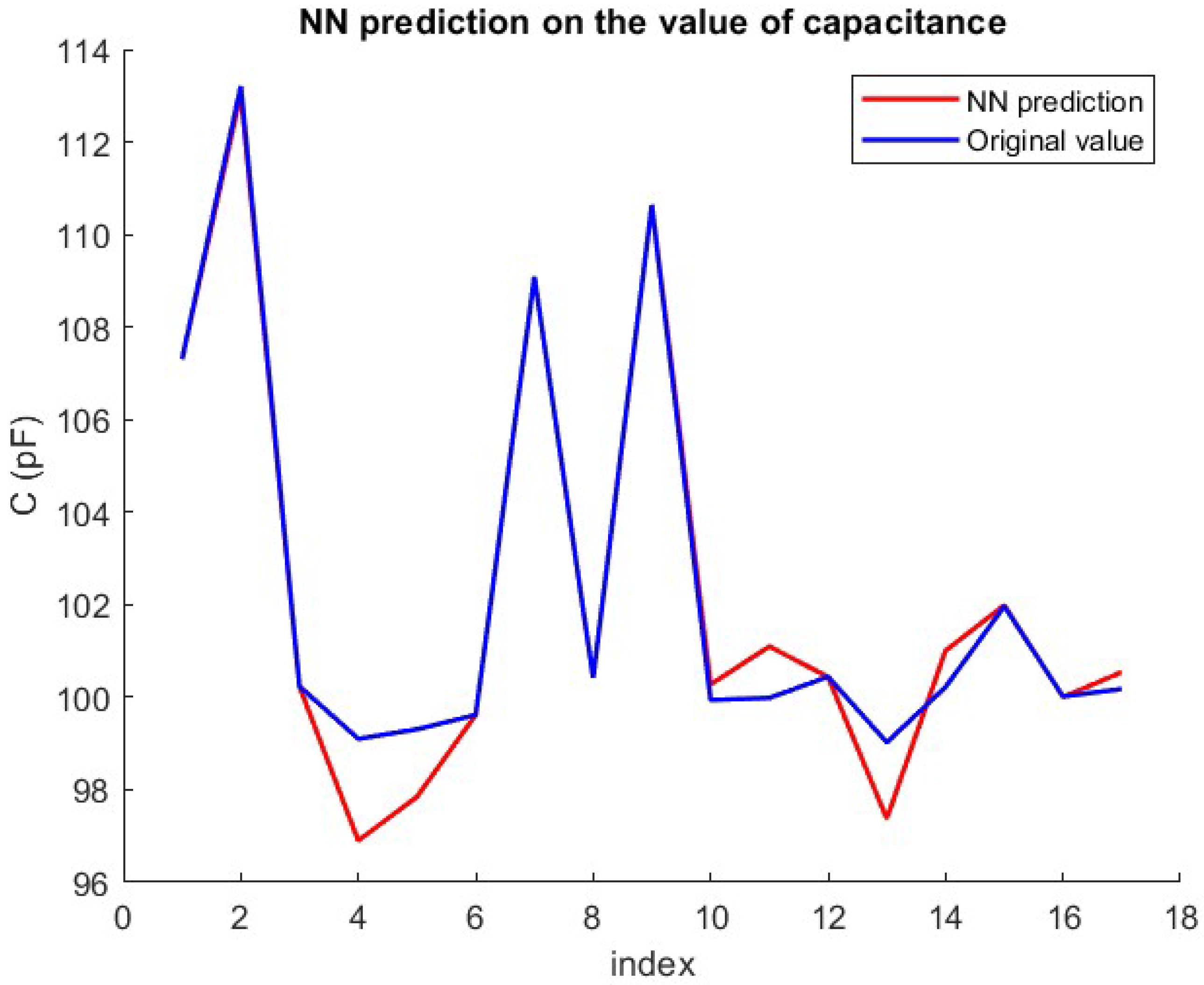
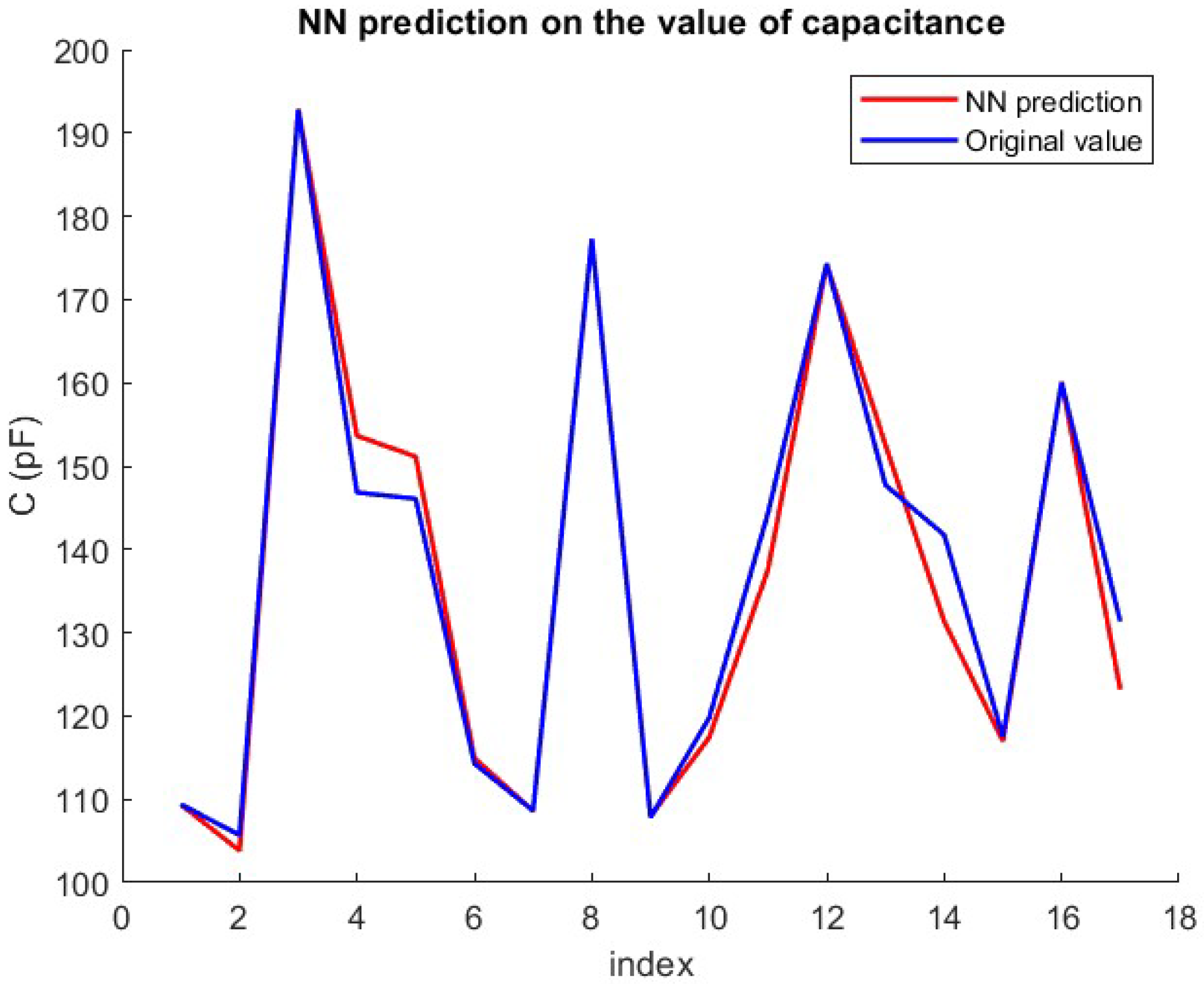

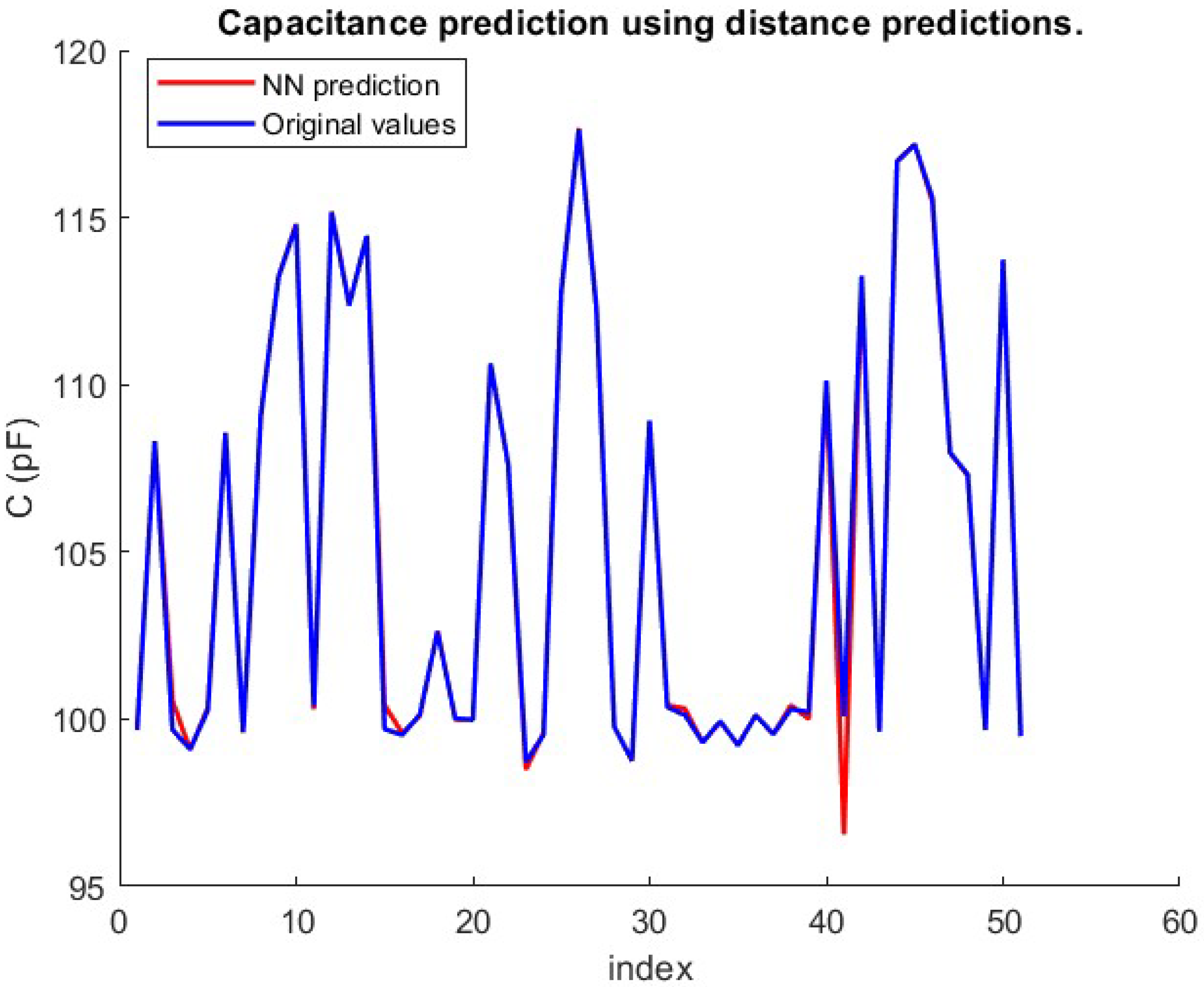


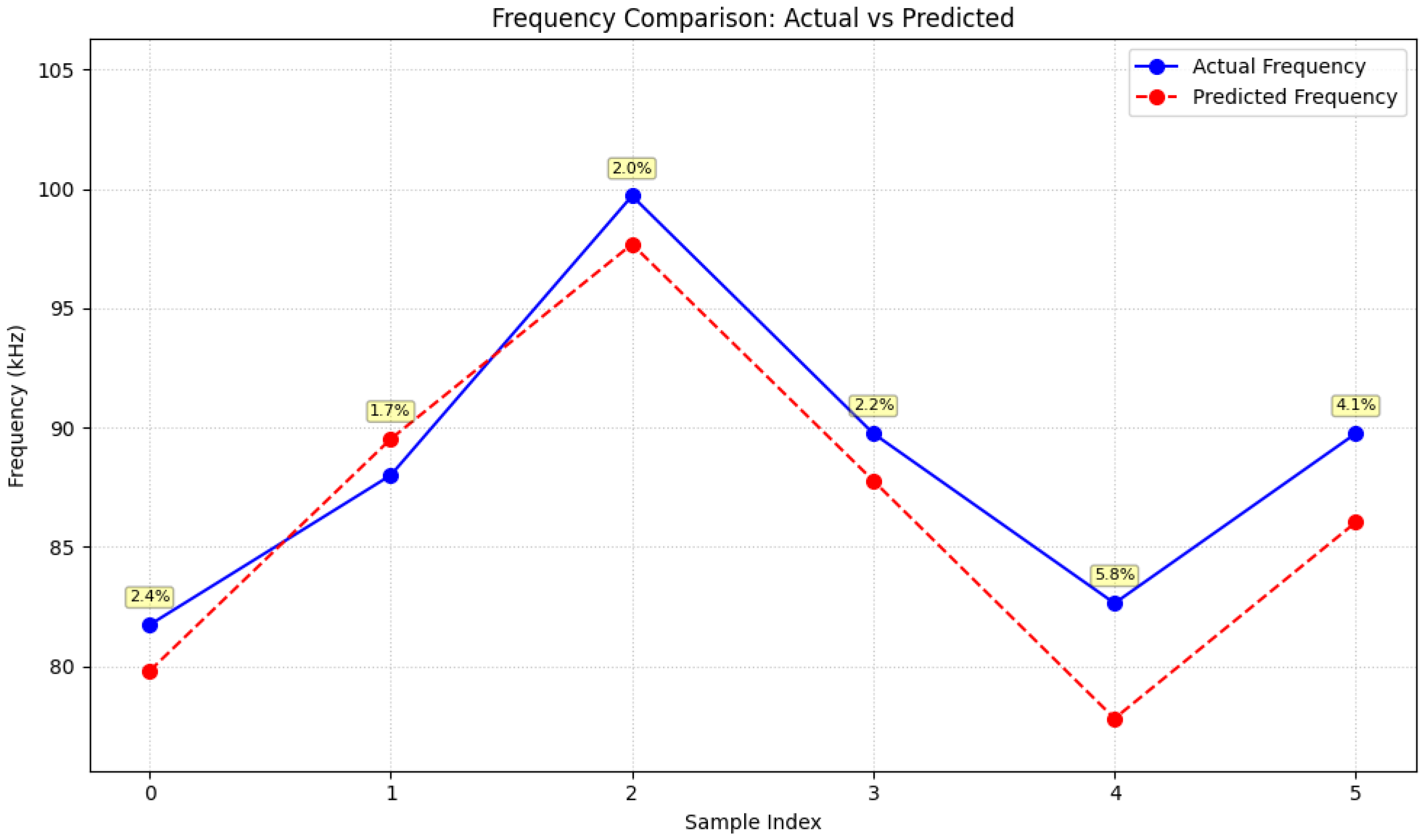
| NN Parameters | d | C | C from d | Frequency–Phase |
|---|---|---|---|---|
| INPUT data | S or Z | S or Z | S or Z and d | phase(0), f(0), R, |
| OUTPUT data | Distance | Capacitance | Capacitance | |
| Dataset size | 57 | 57 | 57 | 18 |
| Layers | 1 | 2 | 2 | 2 |
| Neurons | 10 | 10, 10 | 10, 10 | 20, 10 |
| Epochs | 100 | 1000 | 1000 | 500 |
| Optimizer | trainlm | trainlm | trainlm | ADAM |
| Activation function | sigmoid | sigmoid | sigmoid | ReLU |
| Metrics and loss | MSE | MSE | MSE | MSE and MAE |
| Learning rate | 0.1 | 0.05 | 0.1 | 0.001 |
| Goal | 3 × 10−5 | 2 × 10−7 | 2 × 10−7 | 0 |
| Min grad | 1 × 10−7 | 1 × 10−7 | 1 × 10−7 | Not specified |
| Batch size | Not used | Not used | Not used | 4 |
| Validation | Not used | Not used | Not used | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabino, L.; Milillo, D.; Crescimbini, F.; Riganti Fulginei, F. Neural Network Method for Distance Prediction and Impedance Matching of a Wireless Power Transfer System. Appl. Sci. 2025, 15, 6351. https://doi.org/10.3390/app15116351
Sabino L, Milillo D, Crescimbini F, Riganti Fulginei F. Neural Network Method for Distance Prediction and Impedance Matching of a Wireless Power Transfer System. Applied Sciences. 2025; 15(11):6351. https://doi.org/10.3390/app15116351
Chicago/Turabian StyleSabino, Lorenzo, Davide Milillo, Fabio Crescimbini, and Francesco Riganti Fulginei. 2025. "Neural Network Method for Distance Prediction and Impedance Matching of a Wireless Power Transfer System" Applied Sciences 15, no. 11: 6351. https://doi.org/10.3390/app15116351
APA StyleSabino, L., Milillo, D., Crescimbini, F., & Riganti Fulginei, F. (2025). Neural Network Method for Distance Prediction and Impedance Matching of a Wireless Power Transfer System. Applied Sciences, 15(11), 6351. https://doi.org/10.3390/app15116351







