Thermal and Exergetic Performance Assessment of an ORC Coupled with Thermal Energy Storage Using Thermal Oils for Low-Grade Heat Recovery

Abstract

The transition towards sustainable energy systems demands efficient utilization of low- and medium-temperature thermal sources, which offer a promising alternative to pollutant energy carriers like fossil fuels. Among these, solar thermal, geothermal, and residual heat emerge as leading candidates for clean energy generation. Organic Rankine Cycles (ORCs) stand out as robust technologies capable of converting these thermal sources into electricity with high efficiency. A critical factor in ORC performance lies in the effective transfer of heat from the thermal source to the working fluid. This study systematically evaluates various thermal oils as intermediate heat transfer media, aiming to optimize their selection based on key performance indicators. The analysis focuses on thermal and exergetic efficiencies, alongside mass and volumetric flow rates of both the working fluid and the thermal oil. The findings reveal that the integration of thermal oils notably boosts the exergetic efficiency of the ORC system, underscoring their pivotal role in maximizing energy conversion from sustainable heat sources.

1. Introduction

Efficient energy use is crucial for mitigating climate change driven by anthropogenic carbon dioxide (CO₂) emissions, primarily from fossil fuel consumption [1,2] and other greenhouse gases (GHGs), such as hydrofluorocarbons (HFCs) [3]. Enhancing energy efficiency has been identified as one of the most cost-effective measures to curb GHG emissions [4].

In this context, Organic Rankine Cycles (ORCs) have emerged as a prominent technology due to their operational flexibility, compact design, and capacity to harness low-grade thermal energy for electricity generation or mechanical work [2,5]. Traditional methods for improving ORC performance have focused on optimizing working conditions [6,7] and selecting appropriate working fluids to maximize thermal and exergetic efficiencies [8,9]. ORC optimization strategies prioritize increasing the heat source temperature to elevate the vapor pressure of the working fluid, thereby enhancing the mechanical work output [10,11].

Several studies have investigated the use of fluids such as R134a, R245fa, and R236fa for improved thermal conversion. However, these compounds are being phased out, mandated by the Kigali Amendment due to their high global warming potential (GWP) [12,13,14]. Furthermore, beyond fluid optimization, innovative designs have integrated thermal energy storage (TES) subsystems into ORCs to enhance heat transfer efficiency, system stability, and continuous power generation even during fluctuations in thermal input [15,16].

For instance, an ORC pilot plant with a TES chamber has been experimentally analyzed, and it demonstrated enhanced system stability and efficiency under varying thermal loads [17]. These configurations not only improve energy efficiency but also enhance operational flexibility, particularly in applications involving intermittent or low-temperature heat sources. TES units commonly employ intermediate fluids, such as commercial thermal oils, to decouple the ORC from the primary heat source, thereby mitigating exergy destruction and improving control over the heat exchange process [18,19,20]. This thermal decoupling enables more resilient system performance under variable heat input conditions, promoting sustainable energy conversion. Integrating indirect heating improves energy efficiency and supports sustainable energy utilization by enhancing renewable energy integration and reducing greenhouse gas emissions [21,22,23,24,25].

Daniarta et al. [15] modeled the TES and the heater for an ORC system utilizing hydrocarbons as the working fluid and phase change materials as the TES fluid. The results indicate that altering the evaporator temperature significantly affects the TES sizing parameter in ORC systems.

Paramita et al. [22] analyzed a Carnot battery as an energy recovery system. The Carnot battery comprises three primary subsystems: an ORC, TES, and a heat pump. Ethylene glycol is used as the HTF to charge the TES system. The results suggest that the dual-source charging approach of the Carnot battery enhances efficiency in energy recovery and generation.

Rahim et al. [23] simulated a solar-driven ORC, analyzing the impact of the cycle’s parameters on performance in terms of exergy, energy, and exergo-economic factors. The cited study employed water as the HTF and a parabolic trough collector (PTC) as the heat exchanger. An increase in pinch temperature was found to result in a slight decrease in energy and exergy efficiencies while increasing total irreversibility.

Kannaiyan et al. [24] examined the performance of a PTC using different HTFs and design parameters under varying geographical and weather conditions. Thermal energy was collected using thermal oil, molten salt, and water, and the system’s performance was evaluated as a function of solar radiation inputs.

In a study by Assareh et al. [25], a polygeneration system was modeled and optimized based on solar and geothermal renewable energies. This system produced electricity, cooling, freshwater, and hydrogen. The study utilized thermal oils as HTFs, which were evaluated and assessed for selection in PTC applications. The system generated 1140 kW of electrical energy with a thermal efficiency of 32%. Furthermore, the authors highlighted that selecting the HTF is crucial in optimizing these systems.

Additionally, modifications of HTFs using nanoparticles have been investigated to enhance the fluids’ properties. For instance, Vikraman et al. [26] utilized ZnO nanoparticles to improve thermal conductivity and reduce the viscosity of the HTF. Similarly, Ravikumar et al. [27] employed strontium oxide, barium oxide, and strontium oxide–barium oxide nanoparticles for the same purpose in Therminol-brand commercial thermal oils. Other studies have explored the use of aluminium oxide and copper oxide nanoparticles [28], demonstrating enhanced thermal conductivity, albeit with increased viscosity. These results highlight the potential of hybrid nanofluids in solar thermal systems, heat exchangers, and industrial cooling applications.

This study presents a comprehensive thermodynamic analysis of an ORC system enhanced by a TES unit operating with three industrial thermal oils. Two TES configurations were evaluated to analyze the impact of temperature profiles and pinch-point temperatures on energy delivery quality and overall system performance. An integrated simulation model is developed to assess thermal (${\eta }_I$) and exergetic (${\eta }_{II}$) efficiencies, net power output, mass and volumetric flow rates, and key design parameters of the heat exchangers.

The primary objective of this work is to identify optimal conditions and configurations that maximize system efficiency while minimizing irreversibilities, providing clear guidelines for the sustainable design of ORC-TES systems in industrial applications, leveraging low-temperature waste heat sources.

2. Thermodynamic Theory and Modeling

2.1. Thermodynamic Model

Figure 1a shows a basic ORC fed by a thermal source, while Figure 1b displays the same layout connected to a TES system that operates with a thermal oil. In the standard ORC, depicted in Figure 1a, a saturated liquid (1) is compressed in a pump, obtaining a subcooled liquid (2). The liquid is heated until a saturated liquid at high pressure (3l) and then vaporized (3). These isobaric processes (2 to 3) obtain energy from exhaust gases. Finally, the saturated vapor (3) is expanded until the condenser pressure is reached (4). In contrast, in Figure 1b, the thermal source energizes the boiler while the remaining energy is used to heat a thermal oil. The oil preheats the fluid from the subcooled liquid to saturation. The rest of the cycle is identical to the previously described.

The configuration of Figure 1 are represented in the temperature vs. entropy projection in Figure 2. Figure 2 represents the thermal source (exhaust gases) in crimson lines, while the TES unit is depicted in blue. In both cases, the points of the cycle are illustrated in green. The latter profile shows three fundamental points for analyzing the source. The thermal source enters the boiler or heat exchanger with a temperature $T_{\mathrm{i},\mathrm{s}}$. After the phase change of the working fluid, the temperature of the thermal source is $T_{\mathrm{m},\mathrm{s}}$, constituting an intermediated temperature of the source. The remaining energy from the thermal source is then delivered to the working fluid to preheat the saturated liquid after the compression in the pump, yielding a final temperature of $T_{\mathrm{o},\mathrm{s}}$.

Figure 2b displays two different TES configurations representing the limiting conditions of the system. The C1 is set to have a thermal oil with a temperature near to the thermal source with a pinch point, $T_{\mathrm{pp},\mathrm{C}1}$, as a fixed parameter. The second configuration, C2, is defined as having a pinch point $T_{\mathrm{pp},\mathrm{C}2}$ as a function of the outlet temperature of the condenser, as shown in the blue lines. In both cases, configurations can be set using the design of the heat exchanger, the temperature of the thermal source, and the mass flow of oil or the heated fluid. The entropy scales in Figure 2 are merely illustrative. It is important to remark that the pinch-point temperature is defined differently depending on the configuration, as shown in Figure 2b.

Although adding an extra heat exchanger and integrating thermal oil as an intermediate medium enhances the thermal and exergetic efficiencies of the ORC system, it is important to acknowledge the economic implications associated with this configuration. ORCs typically operate within a low power range, where the cost-effectiveness of additional components must be carefully evaluated. The increase in efficiency provided by the thermal oil loop does not necessarily translate into proportional net power gains, which may affect the financial viability of the system, particularly in small- to medium-scale applications. Consequently, this configuration is better suited for larger-scale installations where the efficiency improvements are more likely to offset the additional capital and operational costs.

The thermal efficiency of a power cycle is determined by the ratio between the net power output, ${\dot{W}}_{\mathrm{n}}$, to the energy used in the process, ${\dot{Q}}_h$. In a single-stage ORC, where each piece of equipment has the same mass flow, the thermal efficiency, ${\eta }_{\mathrm{I}}$, is given by

$${\eta }_{\mathrm{I}}={\displaystyle \frac{{\dot{W}}_{\mathrm{n}}}{\dot{Q}}}$$

(1)

The added heat is the sum of the amount of energy of the heater and the boiler, $\dot{Q}={\dot{Q}}_{\mathrm{h}}+{\dot{Q}}_{\mathrm{b}}$. Additionally, the net work may be written as ${\dot{W}}_{\mathrm{n}}=\dot{Q}-{\dot{Q}}_{\mathrm{c}}$, ${\dot{Q}}_{\mathrm{c}}$ being the amount of extracted heat in the condenser.

The amount of heat can be calculated by the enthalpy differences between two points of the cycle. For instance, for the heater stage, the energy change is given by

$${\dot{Q}}_{\mathrm{h}}=\dot{m}\left({\tilde{H}}_{3l}-{\tilde{H}}_2\right)=-{\dot{m}}_{\mathrm{s}}\left({\tilde{H}}_{o,\mathrm{s}}-{\tilde{H}}_{c,\mathrm{s}}\right)$$

(2)

where the subscripts represent the same nomenclature shown in Figure 2. The ORC uses R134a, one of the most common, widespread, and cost-effective working fluids [29,30]. Furthermore, R134 has low flammability, an acceptable GWP, and high availability. The thermophysical properties were obtained using the multiparametric equation of state (EOS) proposed by Tillner and Roth [31]. The Tillner–Roth EOS is regarded as equivalent to experimental data, demonstrating remarkable accuracy: deviations for vapor pressure are within ±0.05% at temperatures above 220 K and within ±20 Pa at lower temperatures. Liquid density predictions are highly precise, with deviations below ±0.01%, while isochoric heat capacity estimates maintain errors around ±1.00%. Consequently, thermal properties such as enthalpy and entropy also exhibit deviations of less than ±1.00%. All calculations were performed using Wolfram Mathematica (12.0.0.0) [32].

The flow-specific exergy can be defined as [33]

$${\psi }_k={\tilde{H}}_k-{\tilde{H}}_0-T_0\left({\tilde{S}}_k-{\tilde{S}}_0\right)$$

(3)

where the subscript k concerns the cycle’s flows, while the subscript 0 represents the dead-point condition, chosen at a temperature of 293.15 K.

In a simple and adiabatic tube-and-shell heat exchanger, the supplied exergy is obtained through the decrease in the hot-flow exergy. Additionally, the recovered exergy is the increase in the cold-flow exergy, as long as it is not at a lower temperature than the surroundings [20,33]. Therefore, the exergetic efficiency between the heater-boiler and the source yields

$${\eta }_{\mathrm{II}}={\eta }_{\mathrm{II},\mathrm{s}}=-{\displaystyle \frac{\dot{m}\left({\psi }_3-{\psi }_2\right)}{{\dot{m}}_s\left({\psi }_{o,s}-{\psi }_{i,s}\right)}}$$

(4)

In the same way, which is evaluated as heater-boiler exergetic efficiency, the heater and the boiler can be separately assessed. This study is centred on the evaluation of heater exergetic efficiency. The latter can be written as

$${\eta }_{\mathrm{II},\mathrm{h}}=-{\displaystyle \frac{\dot{m}\left({\psi }_{3l}-{\psi }_2\right)}{{\dot{m}}_s\left({\psi }_{m,s}-{\psi }_{o,s}\right)}}$$

(5)

Adding the TES between the thermal source and the working fluid changes Equation (4). Considering C1 and C2, the exergetic efficiency for both configurations can be expressed as

$${\eta }_{\mathrm{II},\mathrm{C}1}={\eta }_{\mathrm{II},\mathrm{C}2}=-{\displaystyle \frac{\dot{m}\left({\psi }_{3l}-{\psi }_2\right)}{{\dot{m}}_o\left({\psi }_{o,o}-{\psi }_{o,i}\right)}}$$

(6)

where the differences in the TES exergies for both configurations are given by

$${\psi }_{o,o}-{\psi }_{o,i}={\int }_{T_1}^{T_2}\left(1-{\displaystyle \frac{T_0}{T}}\right)C_{P,o}dT$$

(7)

where $T_0$ is the dead-point temperature, while $T_1$ and $T_2$ are the operational temperatures. Additionally, the isobaric heat capacity of the thermal oil, $C_{P,o}$, may be function of the temperature.

The selection process was conducted among 28 thermal oils, based on an initial analysis of their density, viscosity, heat capacity, thermal conductivity, and operational temperature range. The density was required to be lower than 1000 kg m⁻³ (A), while the viscosity needed to remain under 20 cSt (B) to ensure low energy consumption during pumping. The heat capacity and thermal conductivity were prioritized to be as high as possible to enhance heat absorption efficiency. A minimum heat capacity threshold of 2 J g⁻¹K⁻¹ was established (C), whereas thermal conductivity was considered acceptable for all thermal oils due to its low variability. Furthermore, the operational temperature range needed to be between 0 and 300 °C (D).

Table 1. Analyzed commercial thermal oils including their critical thermophysical data and selection criteria.

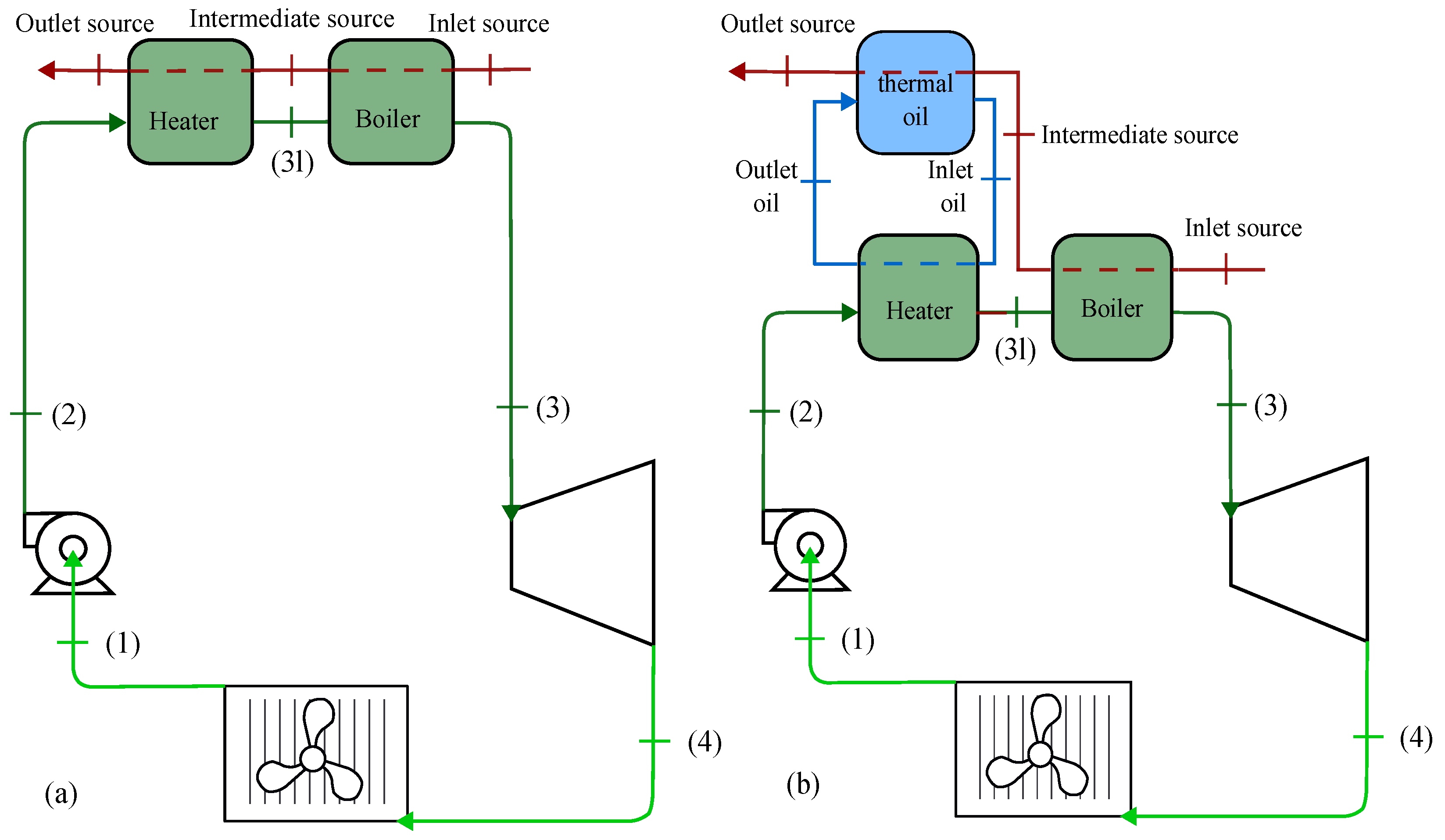
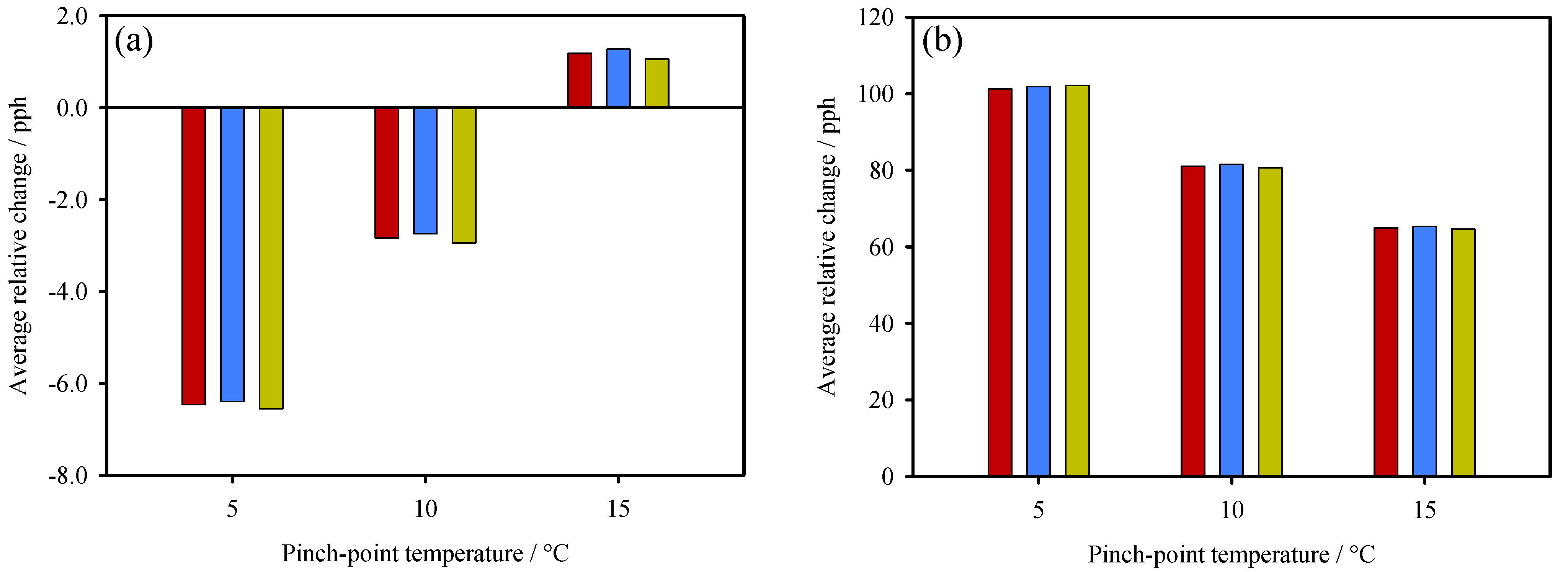
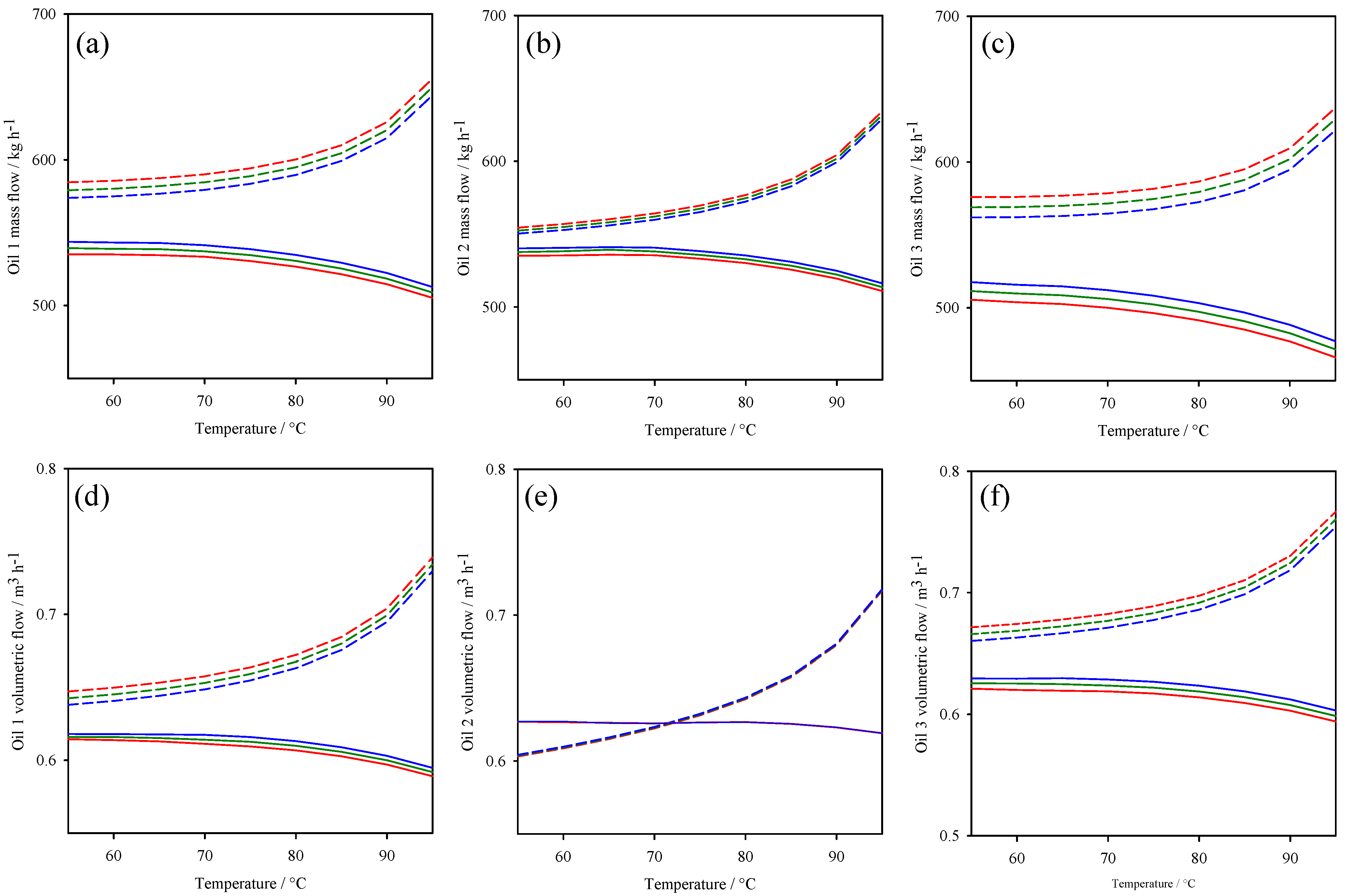
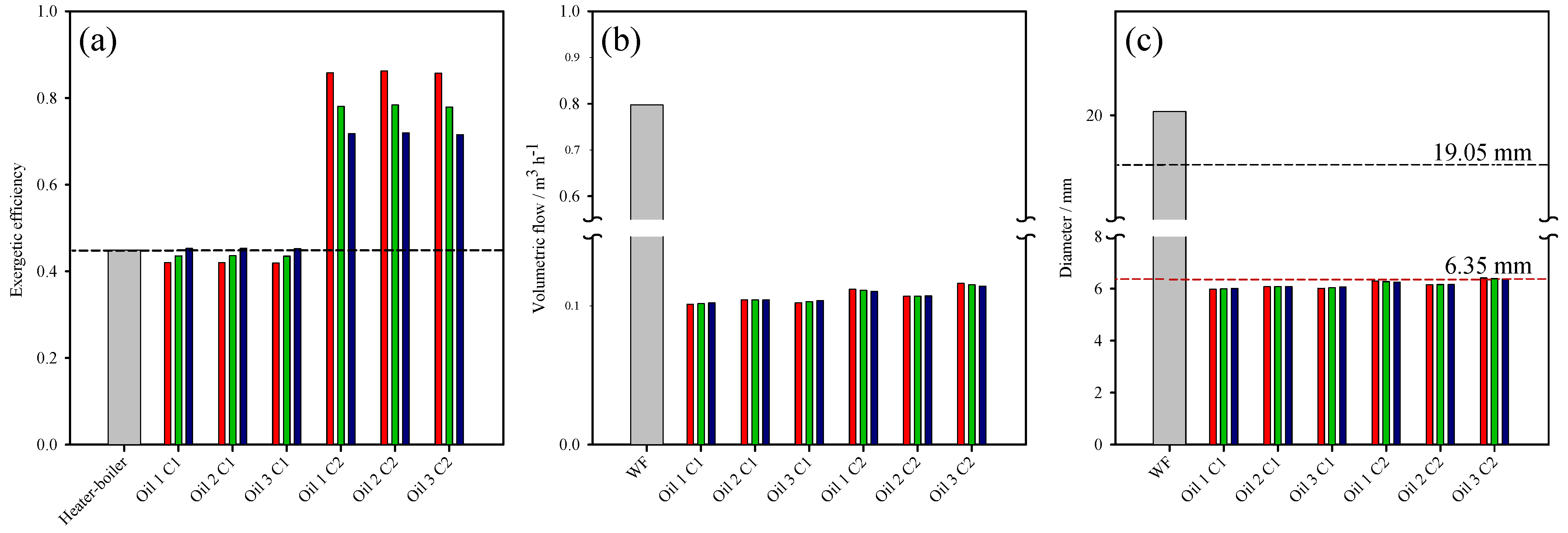
	Commercial Name	Heat	Low.	High	Density	Viscosity	Criteria	Ref.
		Capacity	Tem.	Tem.	Point	40 °C
		J g−1 °C−1	°C	°C	kg m−3	cSt
1	HTF-FDA HT1 NSF	2.10	−10	325	873	37.1	B	[34]
2	HTF-HIGH FP	2.10	−6	275	903	490.0	B, D	[35]
3	HTF-PLUS	2.00	−40	280	864	20.5	B, D	[36]
4	Therminol 66	1.84	−3	345	995	29.6	B, C	[37]
5	Therminol VP-1	1.78	12	400	1064	2.5	A, C, D	[38]
6	Therminol 75	1.77	80	385	1041	4.1	A, C, D	[39]
7	Therminol VP-3	1.96	2	330	935	2.0	C, D	[40]
8	Therminol 72	1.77	−14	380	1079	5.7	A, C	[41]
9	Therminol 59	1.94	−49	315	977	4.0	C	[42]
10	Therminol 54	2.19	−28	280	858	19.0	D	[43]
11	Therminol XP	2.18	−20	315	879	23.7	B	[44]
12	Therminol LT	2.09	−75	315	867	0.8	-	[45]
13	Therminol VLT	2.29	−115	175	749	0.7	D	[46]
14	Therminol D-12	2.41	−94	230	763	1.2	D	[47]
15	Shell HT Oil S2	2.40	−12	320	857	25.0	B	[48]
16	Shell HT Oil S4X	2.23	−30	300	823	34.3	B	[49]
17	Chevron HT OIL 22	2.32	−13	343	853	23.1	B	[50]
18	Chevron HT OIL 46	2.32	−15	316	859	41.1	B	[50]
19	Paratherm HR	2.10	−13	357	961	11.0	-	[51]
20	Paratherm NF	2.20	−4	332	884	20.0	-	[52]
21	Paratherm GLT	2.20	−11	302	877	41.0	B	[53]
22	Paratherm HE	2.20	3	332	863	41.5	B, D	[54]
23	Paratherm OR	2.31	4	260	881	40.1	B, D	[55]
24	CALFLO Synthetic	2.40	−48	226	799	5.2	D	[56]
25	CALFLO AF	2.20	−42	316	870	55.0	B	[57]
26	CALFLO HTF	2.20	−18	343	877	35.9	B	[58]
27	CALFLO LT	2.30	−57	225	906	7.5	D	[59]
28	CALFLO XR	2.22	−27	288	840	15.0	D	[60]

summarizes the elimination criteria.

The three commercial thermal oils that pass all criteria are Therminol LT ($\overline{M}=134$ g/mol) [45], Paratherm HR ($\overline{M}=240$ g/mol) [51], and Paratherm NF ($\overline{M}=340$ g/mol) [52]. The isobaric heat capacity of the selected thermal oils had been fitted to experimental data [45,51,52] by a second-order polynomial as

$${\displaystyle \frac{C_{P,o}}{\overline{M}R}}={\alpha }_1+{\alpha }_{2}T+{\alpha }_3{T}^2$$

(8)

Table 2. Isobaric heat capacity parameters for the selected thermal oils, valid in the temperature range of 313.15 to 493.15 K. All fittings exhibit an R² greater than 0.998.

	Commercial Name	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2·{10}^2$	${\mathit{\alpha }}_3·{10}^6$	Ref.
			K−1	K−2
Oil 1	Therminol LT	12.8067	5.5078	2.4950	[45]
Oil 2	Paratherm HR	43.8256	2.8091	46.8136	[51]
Oil 3	Paratherm NF	7.7397	23.0976	−15.0726	[52]
		${\mathbf{\gamma }}_{\mathbf{1}}$	${\mathbf{\gamma }}_{\mathbf{2}}$	${\mathbf{\gamma }}_{\mathbf{3}}·{\mathbf{10}}^{\mathbf{4}}$
		kg m−3	kg m−3K−1	kg m−3K−2
Oil 1	Therminol LT	1027.42	−0.3530	−6.8775	[45]
Oil 2	Paratherm HR	1188.77	−0.7852	0.1843	[51]
Oil 3	Paratherm NF	1081.53	−0.6787	0.1990	[52]

shows the constants, ${\alpha }_i$ for the thermal oils heat capacity in the temperature range between 313.15 to 493.15 K.

Table 3. Input parameters and boundary conditions for ORC thermally powered by thermal energy recovery.

	Value	Range
	ORC
Turbine displaced volume	120.00 cm3	-
Turbine revolutions per minute	2900.00 rpm	-
Boiler saturation temperature	-	330.15 to 368.15 K
Condenser temperature	303.15 K	-
Expander isentropic efficiency	1.0	-
Pump isentropic efficiency	1.0	-
	Energy source and TES
Exhaust gases temperature	-	493.15 K to 373.15 K
Pinch point temperature	-	5, 10, and 15 K

presents the assumptions that delimit this study’s scope, including using an ORC turbine with a displaced volume of 120 cm³ per revolution. A steam turbine is probably the most flexible driver available to the industry. With the advent of modern precision gears, turbine speeds are seldom below 1200 rpm and may be as high as 25,000 rpm [61]. This study is considered 2900 rpm for the operation of the ORC turbine. The condenser has a fixed temperature of 303.15 K. Moreover, the driving equipment is perfectly isentropic, i.e., their efficiency is 100%. In any event, the efficiency of the turbomachinery does not influence the exergetic evaluation of the isobaric stages.

Combustion exhaust gas is used as the thermal source. The gas is modeled using the standard air assumptions and data [62]. The air temperature entering the ORC is fixed at 493.15 K. In contrast, the outlet temperature is fixed at 373.15 K. Consequently, the mass flow ratio of the thermal source varies depending on the energy the working fluid needs to reach the saturated vapor state. As shown in Table 3, three values for the pitch point temperature are considered in typical operation ranges. The enthalpy and entropy of the air are calculated using a second-order polynomial [63]. Furthermore, to simplify the analysis, the system is considered to have steady-state conditions in all components, and the heat and friction losses in the system are neglected.

2.2. Heat Exchanger Sizing Model

In order to size the shell-and-tube heat exchanger used for the heat transfer between the thermal oil and the refrigerant, the mass flow oil that passes through the heat exchanger is the key parameter. The mass flow refrigerant is obtained using compressor load [63,64], which is given by

$$\dot{m}=V_d{R}_v{\rho }_4$$

(9)

where $V_d$ is the displaced volume in m³ h⁻¹, $R_v$ the volumetric performance, and ${\rho }_4$ the working fluid density in the turbine outlet. This density is related to the maximum value that may take the vapor density in an ORC. Therefore, it is also related to the maximum value of mass flow working fluid that may be leveraged in the turbine. Further, $R_v=1-0.03r_c$ is a function of the compression relation, $r_c=P_3/P_1$.

The oil mass flow in the heat exchanger varies depending on the energy the working fluid needs to reach the saturated vapor state. Therefore, their values also depend on the mass flow of working fluid. To compute the volumetric flow, $\dot{V}=\dot{m}/\rho$, the density as a function of the temperature is obtained by a fitted second-order polynomial. Table 2 shows the constants, ${\gamma }_i$, for

$$\rho ={\gamma }_1+{\gamma }_{2}T+{\gamma }_3{T}^2$$

(10)

The velocity in the heat exchanger is a critical variable. Shell-side velocity lies between 0.6 to 1.5 m/s for water and similar liquids, and the number of tubes is chosen so that the tube-side velocity for water and similar liquids lies between 0.9 to 2.4 m/s [65,66]. In this work, the velocity is used as a function of the volumetric flow and piping diameter concerning the selection and sizing of the piping, fitting, valves, and pumps in hydraulic systems [67]. The velocity can calculated as

$$v=353.678{\displaystyle \frac{\dot{V}}{D^2}}$$

(11)

where v is the velocity in m/s, $\dot{V}$ is the volumetric flow in m³ h⁻¹, and D is the interior tube diameter in mm, limited to the commercial diameter (DN or NPS). The heat exchanger’s base case comprises six tubes, as in Pasupuleti’s work [65].

3. Thermodynamic Behavior of the ORC-TER System

To elucidate the performance enhancement introduced by the integration of an intermediate energy accumulator based on thermal oil, a direct-heated ORC configuration is employed as a benchmark. Figure 3 presents the thermal and exergetic efficiencies for the three evaluated scenarios: the two TES configurations (C1 and C2) and the direct thermal source case, each assessed as a function of the boiler saturation temperature. The thermal efficiency, ${\eta }_{\mathrm{I}}$, as depicted in Figure 3a, demonstrates no sensitivity to the inclusion of a TES system. This outcome is consistent with the thermodynamic expectation that the mode of heat delivery to the boiler does not influence the first-law performance of the cycle. Furthermore, a positive correlation between boiler saturation temperature and thermal efficiency was observed, reflecting the classical behavior of Rankine-based systems. Notwithstanding these trends, the selection of operational parameters must account for critical system constraints, including the need to avoid proximity to the working fluid critical point [68], to operate below the maximum allowable pressure of construction materials, and to ensure a sufficiently high vapor quality at the turbine outlet [14] to mitigate the risk of mechanical degradation.

Furthermore, Figure 3b illustrates the exergetic efficiency of both TES configurations at a fixed pinch temperature of 10 °C concerning the working fluid, compared to the direct-heated benchmark, depicted in black. C2 exhibits a markedly higher exergetic efficiency than C1. This result highlights the importance of aligning the thermal oil temperature with the working fluid profile, maintaining proximity to the system’s saturation temperature while preserving the specified pinch temperature difference. From a design perspective, this alignment enables more effective utilization of the available thermal potential, reduces irreversibilities in the heat transfer process, and maximizes the quality of the delivered energy.

As illustrated in Figure 3b, the improvement in heat delivery quality is substantial when thermal oil is employed to indirectly preheat the working fluid. Consequently, it is essential to evaluate the influence of thermal oil properties and pinch-point temperature on this effect. Figure 4 presents the average relative percentage difference in exergetic efficiency for the three thermal oils analyzed.

In C1, shown in Figure 4a, exergetic efficiency decreases at low pinch-point temperatures and exhibits only a slight improvement as the pinch-point increases, with minimal variation across the different oils. Conversely, C2, shown in Figure 4b, demonstrates a pronounced increase in exergetic efficiency at low pinch-point temperatures, reaching up to a twofold improvement. These findings indicate that C2, combined with a low pinch-point temperature, yields superior performance. Nevertheless, the pinch-point must be sufficiently high to ensure adequate heat transfer, depending on the heat exchanger design.

The characteristics of the system impose constraints on the working fluid flow rate, while turbine specifications define the flow demands and the mechanical output. Equipment design and dimensions are also established based on these parameters. Figure 5a illustrates the mass flow rate, whereas Figure 5b presents the volumetric flow rate. Although volumetric flow is the primary variable for equipment sizing and scaling, the mass flow exhibits a distinct minimum near 80 °C. This trend provides a practical guideline for system optimization, as selecting a boiler temperature in proximity to this minimum allows for a balanced design that reduces equipment size while maintaining efficient operation.

Once the working fluid flow rates are characterized, it becomes essential to compare them with the thermal oil flows, which constitutes a critical design parameter for the boiler. Figure 6a–c illustrates the mass flow rates of the thermal oils, while Figure 6d–f presents the corresponding volumetric flow rates as functions of the working fluid saturation temperature, under three different pinch-point temperature conditions. In all mass flow cases, C2 exhibits higher flow rates compared to the configuration that follows the working fluid temperature profile. A similar behavior is observed in the volumetric flows, where the thermophysical properties of each oil influence the slope and magnitude of the curves. For instance, Oil 2 displays limited thermal expansion across the evaluated pinch-point temperature range. Additionally, a notable variation in flow behavior is observed at higher working fluid temperatures (above approximately 80 °C), where flow rates either significantly increase or decrease depending on the configuration. This effect must be considered in the design of heat exchangers. Although C2 achieves superior efficiency, it also demands higher flow rates, which in turn increases the required heat transfer surface and equipment size. Therefore, while elevated working fluid temperatures enhance system efficiency, their impact on the physical dimensions and overall feasibility of the thermal equipment must be carefully balanced during the design phase.

Figure 7 provides a general overview of the thermodynamic behavior of the cycle in the absence of the thermal oil heating system. Although the behaviors are independent of the thermal oil configuration, the analysis offers valuable insights into the internal heat distribution and phase change characteristics. In Figure 7a, the black bold line represents the total heat input to the boiler, while the crimson line denotes the heat distribution between the boiler and the heater. An inverse trend is observed: as the boiler temperature approaches the critical point of the working fluid, the heat in the boiler decreases, whereas the heat absorbed in the heater increases. Despite the differing heat transfer mechanisms, the total energy input remains almost constant, maintaining thermal balance and aiding in equipment sizing. Additionally, Figure 7b presents the vapor fraction at the boiler outlet. As shown, increasing the boiler temperature results in a higher proportion of liquid phase at the outlet. However, the vapor fraction remains below 0.90 in all cases, ensuring stable operation within the design specifications.

The previous analysis indicates that the design and operational parameters converge to favorable values around 80 °C for R134a, the working fluid under study. Therefore, a detailed discussion of system performance at the aforementioned temperature is warranted to elucidate its behavior near optimal operating conditions. This evaluation should account not only for thermal and exergetic efficiencies but also for design and sizing considerations of the involved components.

Figure 8 presents the performance of the overall system at an operating temperature of 80 °C. In Figure 8a, the exergetic efficiencies of all configurations are displayed. The grey line denotes the reference case of a direct-heated ORC, while the grouped bars represent the results obtained using different thermal oils. A general decrease in exergetic efficiency is observed when C1 is employed, except for a pinch-point temperature of 15 °C, which slightly exceeds the benchmark. Conversely, C2 consistently enhances the quality of heat delivery from a second-law perspective.

Figure 8b shows the corresponding volumetric flow rates. These remain consistent across the thermal oils and are significantly lower than the flow rate of the working fluid. Figure 8c illustrates the resulting pipe diameters, determined based on average flow velocities. The calculated diameters fall within standard commercial ranges: approximately 6.35 mm (3/8 in) for thermal oil circuits and 19.05 mm (3/4 in) for the working fluid lines. Even though the flow rate can determine the pipe diameters, the sizing of the TES unit is fundamentally a heat transfer problem, where the critical variables are the heat source availability and economic aspects [69].

These results indicate that the most influential factors in system performance are the configuration and operating conditions rather than the specific choice of thermal oil, as key design parameters remain comparable across all tested fluids.

4. Concluding Remarks

This study evaluated the energy transfer quality from a residual heat source to a working fluid in an ORC, using a shell-and-tube TES unit as the benchmark configuration, with the aim of identifying the key factors that influence thermal and exergetic efficiencies. The results indicate that both efficiencies increase as boiler temperatures approach the critical point of the working fluid.

In particular, for the direct-heated ORC, thermal efficiency was primarily influenced by the temperature difference between the boiler and the heat source, achieving a maximum value of approximately 50%.

The integration of a TES system with an optimized temperature profile significantly improved the exergetic efficiency. Two extreme configurations were evaluated: one replicating the thermal source profile and the other mimicking the isobaric heating profile of the working fluid. The latter demonstrated superior performance, reaching exergetic efficiencies of nearly 90%. Interestingly, the pinch-point temperature showed a negligible impact on the system’s thermal efficiency.

Additionally, all tested thermal oils presented similar mass and volumetric flow rates, internal velocities, and required pipe diameters, aligning well with commercially available tubing (6.35 mm). Among them, Thermal Oil 2 exhibited the most favorable behavior due to its thermal stability and minimal variation in thermophysical properties under operating conditions. These findings suggest that system configuration and operating conditions are more decisive for performance than the specific choice of thermal oil, as key design parameters remained consistent across all fluids tested.