Kinematic Analysis of an Omnidirectional Tracked Vehicle

Abstract

This article addresses the problem of controlling an omni-tracked vehicle equipped with parallel, fully overlapping omnidirectional tracks. A kinematic model is presented that enables the determination of the vehicle body’s displacement relative to the ground, regardless of the orientation of the free rollers. The objective of this study is to demonstrate the potential of using the proposed model for controlling an omni-tracked vehicle. The novelty of this work lies in the modular approach—isolating a unit composed of two omni-tracks from the overall vehicle structure. A numerical model of the omni-tracked vehicle is also developed, allowing for the dynamic simulation of its motion. The results of the simulation are compared with those obtained from the kinematic model to assess their consistency. In the final part of this article, the results are reanalyzed, and conclusions are drawn regarding the applicability of the kinematic model in the control of omni-tracked vehicles.

1. Introduction

Omnidirectional robots and vehicles represent a class of machines specifically designed to enable movement in any direction without changing the angular orientation of their body [1]. This capability is achieved through the use of specialized wheels or tracks [2], or alternatively, by employing conventional wheels in conjunction with additional systems. The majority of research in the field of omnidirectional robots predominantly concentrates on different types of wheeled vehicles [3,4].

The earliest known wheel specifically designed to enable omnidirectional motion is the omni wheel, patented in 1919 [5]. This design incorporates a series of free rollers mounted around the wheel’s circumference. These non-driven free rollers are barrel shaped to reduce vibration during operation and oriented perpendicularly to the wheel axis [6]. Another well-known solution enabling omnidirectional movement is the Mecanum wheel, also referred to as the “Swedish wheel” or “Ilon wheel”. Like the omni wheel, it includes rollers on its perimeter; however, in this case, the rollers are commonly mounted at a 45° angle to both the wheel axis and the lateral plane. When integrated with appropriate control algorithms and mechanical configurations, Mecanum wheels allow a vehicle to move in any direction, at any angle [7]. Another type of omnidirectional wheel is the Liddiard wheel patented in 2016 by William Liddiard [8]. This design consists of torus tires mounted on rims, on which they rest against rows of transversely mounted rollers—both free and driven. Movement along the wheel axis is achieved through the rotation of the entire wheel, while lateral movement results from moving the torus tire freely over the rollers [7,9]. Omnidirectional motion can also be realized using spherical elements. In such solutions, the intermediary element between the robot’s corpus and the ground is a sphere [10]. Depending on the particular solution, robots equipped with this type of omnidirectional drive have from one to several driven spheres. The sphere, due to its shape, can roll in a free direction without resistance, which is used to achieve omnidirectional motion. In addition to the developments characterized above, typical cylindrical wheels can also be adapted for omnidirectional movement. Each wheel then has two drives—a rolling drive and a rotational drive on an axis perpendicular to the ground plane [11]. However, due to the large number of drives required to control a chassis equipped with such wheels, in many cases, the choice of this solution proves uneconomical [12]. For this reason, this solution is typically reserved for applications where certain aspects unique to these wheels are required [13], such as providing the ability to move in any direction without changing the orientation of the body under heavy load.

Omnidirectional mobility is not limited to wheeled solutions. It can also be achieved using other elements mediating between the body of the mobile robot and the ground. One such approach involves the use of specially engineered omnidirectional crawler systems, which can be implemented in tracked vehicles.

Tracked vehicles with omnidirectional capabilities offer potential advantages in specialized operational scenarios, where they may outperform both conventional tracked systems and wheeled omnidirectional platforms. These scenarios include rescue and inspection robots operating in urban environments where accidents or disasters have occurred. Tight spaces, typically in technical corridors or ventilation shafts, can present challenges for tracked vehicles. Areas directly affected by disasters, such as passageways partially covered by debris or technical platforms twisted by falling elements, can present an obstacle that is impossible to overcome for wheeled omnidirectional vehicles. Vehicles on omnidirectional chassis are able to maneuver and operate in such conditions.

Omnidirectional crawler systems can generally be classified into two categories: active and passive. The first category encompasses vehicles utilizing crawler-based chassis in which, in addition to the primary driven tracks, supplementary active components are integrated into the individual links of the track. Transverse motion is facilitated by actuating these auxiliary elements, which typically take the form of rollers or mini-tracks mounted perpendicularly to the robot’s longitudinal axis. Omnidirectional mobility is thus achieved through a coordinated combination of movement along the main axis—resulting from the rolling motion of the track—and lateral displacement—enabled by the activation of these transverse drive elements. A conceptual design of such a drive system is presented in [14], where the authors address the challenge of navigating a tracked vehicle across loose terrain featuring numerous obstacles. The concept of a crawler drive with active elements can also be found in article [15], which discusses issues related to the experimental testing of a mobile robot equipped with two parallel plate crawlers with active transverse drive.

The second category of omnidirectional tracked vehicles includes platforms equipped with a minimum of three independently driven tracks (Figure 1), with additional elements on the links, usually in the form of free rollers. An example of a single crawler segment with a non-driven roller is shown in Figure 2.

There are solutions that include chassis equipped with both three and four independently driven tracks, located at either 120° or 90° angles to each other [16,17,18], as seen in Figure 3. These vehicles operate in a similar manner to platforms based on Kiwi Drive chassis [19].

Among omni-track vehicles with passive rollers, the most frequently studied configurations are platforms featuring four equally spaced, independently driven tracks. The classification of such systems is typically based on the relative arrangement of the track pairs and the orientation of the passive rollers mounted on individual links. A distinction is made here between groups of vehicles with free rollers arranged symmetrically or asymmetrically. In terms of track configuration, the systems are further classified as non-overlapping, partially overlapping, or fully overlapping (Figure 4).

One of the earliest studies on such chassis was published in 2014 [20], analyzing the kinematics of a robot equipped with symmetrically arranged, fully overlapping tracks. The paper also presented results from a simplified simulation of a robot motion using symmetrical, partially overlapping tracks, which revealed a curvature in the actual motion trajectory compared to the planned motion during both longitudinal and lateral movements.

A publication from 2015 [21] covered the issues raised in [20]. It discusses a chassis consisting of three tracks located at an angle of 120°, four tracks located at an angle of 90°, and a symmetrical, completely non-overlapping chassis in two variants in the location of the free rollers. The study examined the influence of roller angles on the achieved speed and presented field test results of a prototype robot with a chassis in a symmetrical, completely non-overlapping arrangement. The research included the measurement of current consumption during the execution of specific types of movement, as well as the effect of the robot’s angular orientation on the efficiency of the movement of climbing hills.

In 2018, another study [22] described the construction of two vehicle demonstrators with a symmetrical, completely non-westerly track system. The first vehicle, measuring 0.8 × 1.2 m (width and length), was equipped with additional drives to lift the tracks. The second demonstrator was a full-sized vehicle with dimensions of 2.5 × 3.5 m and the same track arrangement. The publication details a number of tests to which the vehicle in question was subjected and presents possible concepts for the industrial use of the proposed chassis.

The most comprehensive study to date was published in 2020 [23], focusing on the numerical and experimental studies of a full-sized omni-tracked vehicle—a 5t forklift equipped with a symmetrical, non-overlapping track system. The paper provides a mathematical model of the kinematics for the selected chassis type and an analysis of how roller orientation affects movement speed. The numerical model of the vehicle in question is then presented, and the results of the simulations of the different variants of motion are presented. In the section on bench tests, an analysis of current consumption during different types of movement is presented, as well as the results of the measurement of the drive speed.

Another study from the last five years [24] described centre-point steering models for omni-track vehicles in typical track systems. The authors introduced the phenomenon of slippage between the track roller and the ground in the steering models. In addition, they proposed a mechanism for correcting the angular velocity of the vehicle body during movement. They conducted a series of numerical simulations, as well as experimental tests, demonstrating significant improvements in handling properties for specific chassis.

More of the latest research [25] describes the experimental testing of a lightweight prototype omni-tracked robot in a parallel, fully overlapping track system. It describes the robot’s construction process and proposes an algorithm for static directional correction, the effectiveness of which was confirmed by experimental studies.

Last year’s study [26] deals with experimental research on the prototype of an omni-track robot in a parallel, fully overlapping tracks system. It contains a description of the construction of the prototype, as well as the results of the experimental testing of the dynamic direction correction module. This module, on the basis of the current driving parameters, allows for the determination of corrective values, enabling the robot to more accurately follow a predetermined trajectory.

In omni-track vehicles, the direction of movement is achieved by controlling the individual tracks’ drives. In the direction parallel to the direction of the axis of the free roller in contact with the ground, there is much greater resistance to movement than in the perpendicular direction. Thanks to this, combined with the relative motion of individual tracks, it is possible to achieve omnidirectional mobility. In order to properly control an omni-track vehicle, it is necessary to be able to induce body motion in the selected direction. For this purpose, a kinematic analysis of the omni-track vehicle is necessary.

A kinematic analysis of the other types of omnidirectional vehicles can be found in articles [27,28]. The first article deals with the kinematic analysis of a vehicle equipped with four omnidirectional wheels. The wheels in the analyzed platform are oriented to each other at an angle of 90°. The second article focuses on both the kinematic and dynamic modelling of a vehicle equipped with four Mecanum wheels. In both cases, the methodology presented is based on the analysis of each wheel (reduced to a free roll having contact with the ground at a given moment) separately. The analysis of a typical tracked vehicle is considered in [29], using the example of an autonomous tracked vehicle. This work presents a comprehensive control scheme for tracked vehicles, including both kinetic and dynamic models during movement in difficult terrain. The work considers the control of the vehicle using various models that take into account, among other things, the slippage of the crawler during turns. The kinematic analysis addresses the issues of the mutual motion of bodies. It assumes that the bodies have a fixed length, are rigid, and are not subject to deformation. The kinematic analysis completely neglects the external forces, masses, and inertia of the bodies. The motion of the bodies is due solely to kinematic forcing, i.e., specific characteristics of the change in the position of the individual bodies over time [30,31]. To control an omni-tracked vehicle, it is necessary to derive kinematic equations describing the relationships between the linear velocity of individual crawlers and the speed and resulting direction of the motion of the platform body. These equations will make it possible to calculate the control values for individual drives.

In the work on the comprehensive manipulator control strategy [32], the first steps were to develop the kinematics and dynamics. On their basis, it was possible to develop a strategy for the precise tracking of the manipulator’s trajectory. This work concerns the kinematic analysis of an omni-tracked vehicle with tracks in a parallel, fully overlapping configuration. This article will present the equations of kinematics for controlling an omni-tracked vehicle, with the help of which control values will be determined for the selected examples of preset motion trajectories. Next, the numerical simulations of the dynamic model of the omni-track vehicle will be carried out. The proposed dynamic model will be intentionally idealized. No additional variables such as vibrations, accidental external forces, or substrate inhomogeneity will be considered. Then, the results obtained by both methods will be compared. The aim of this work is to demonstrate that under ideal conditions, the proposed kinematic model can replace the dynamic model. Such a finding could support the development of a robust control system for a real omni-tracked robot, regardless of its track layout, as well as immeasurable external factors, such as a non-homogeneous ground or accidental external forces. The last part of the article presents a comparison of the results and discusses the implications of the findings.

2. Materials and Methods

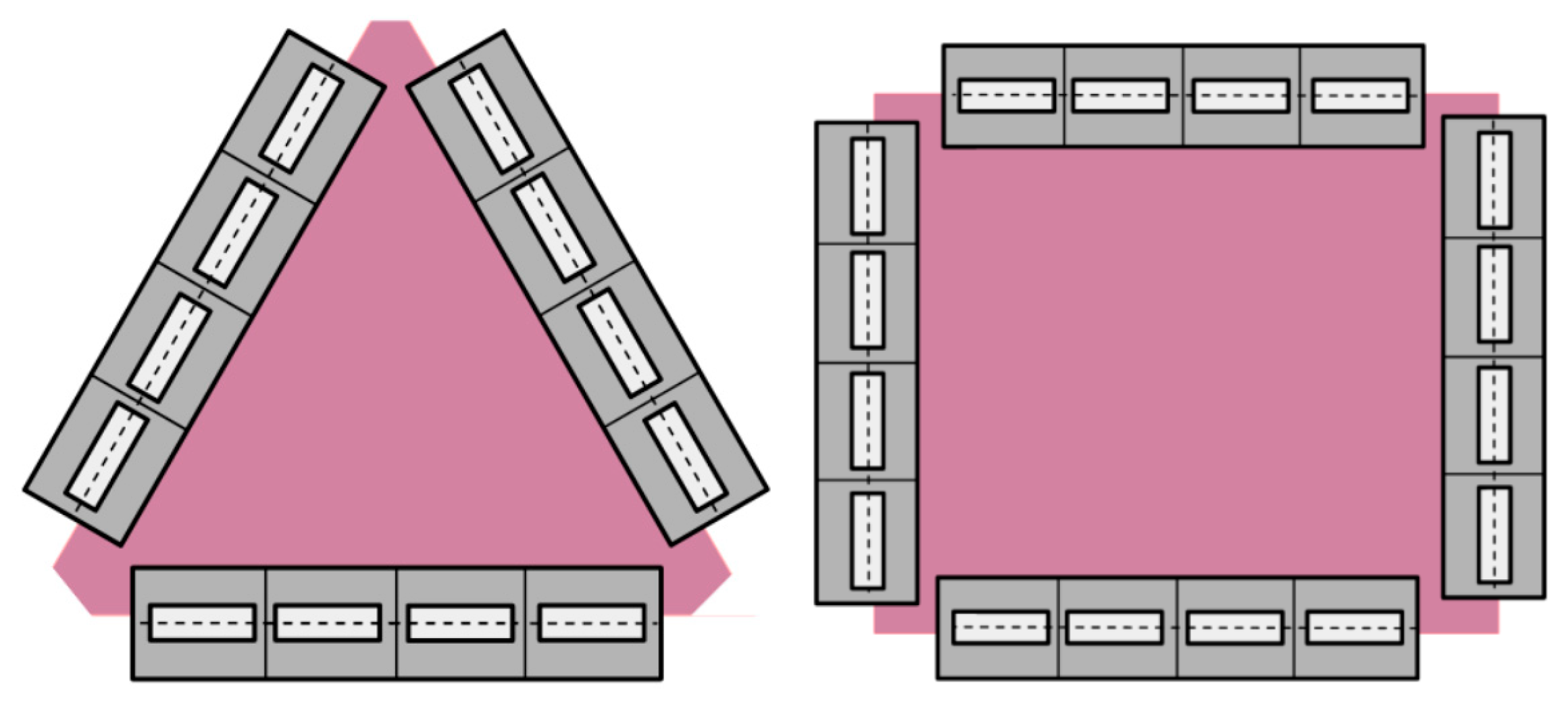
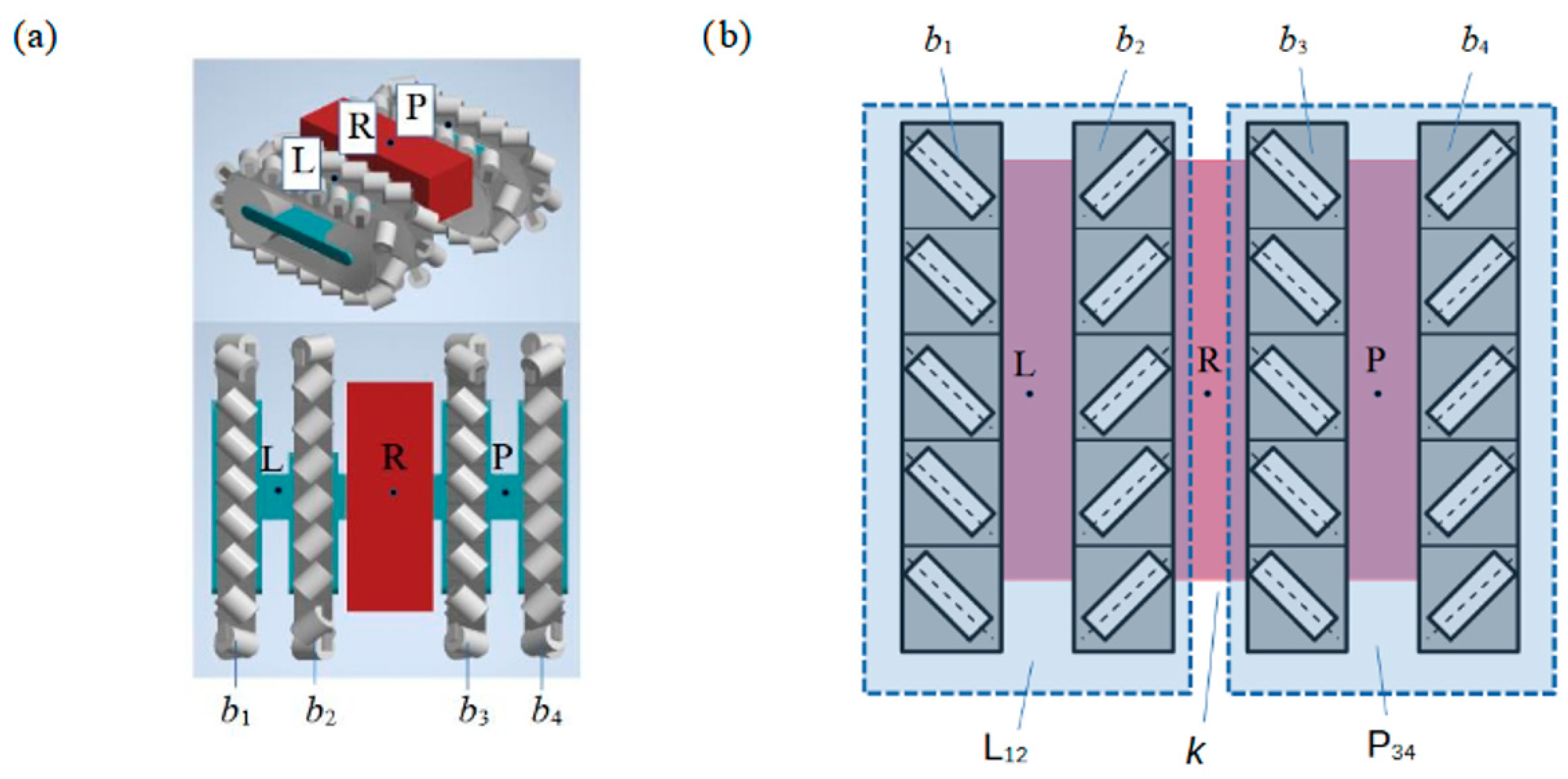
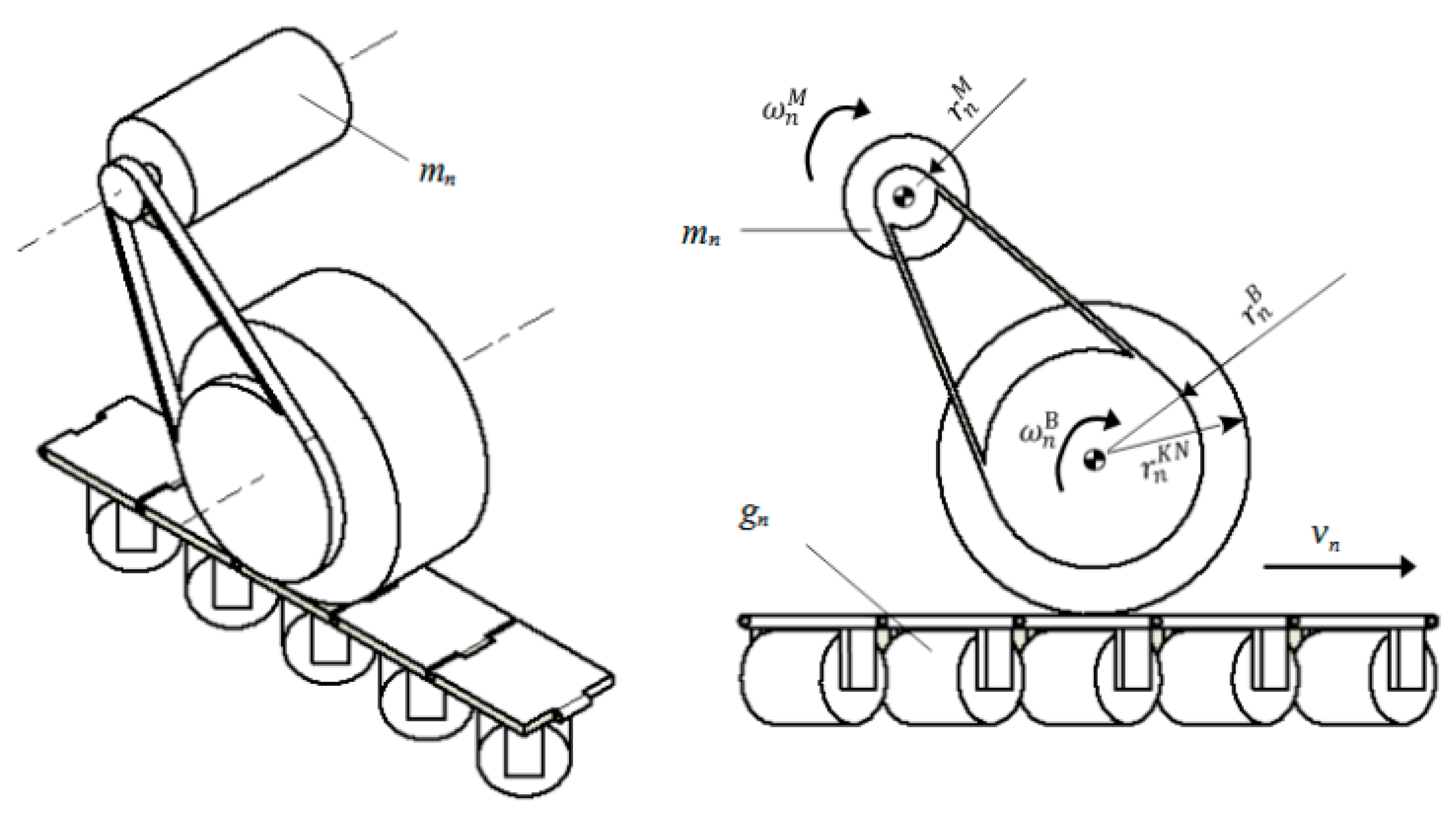
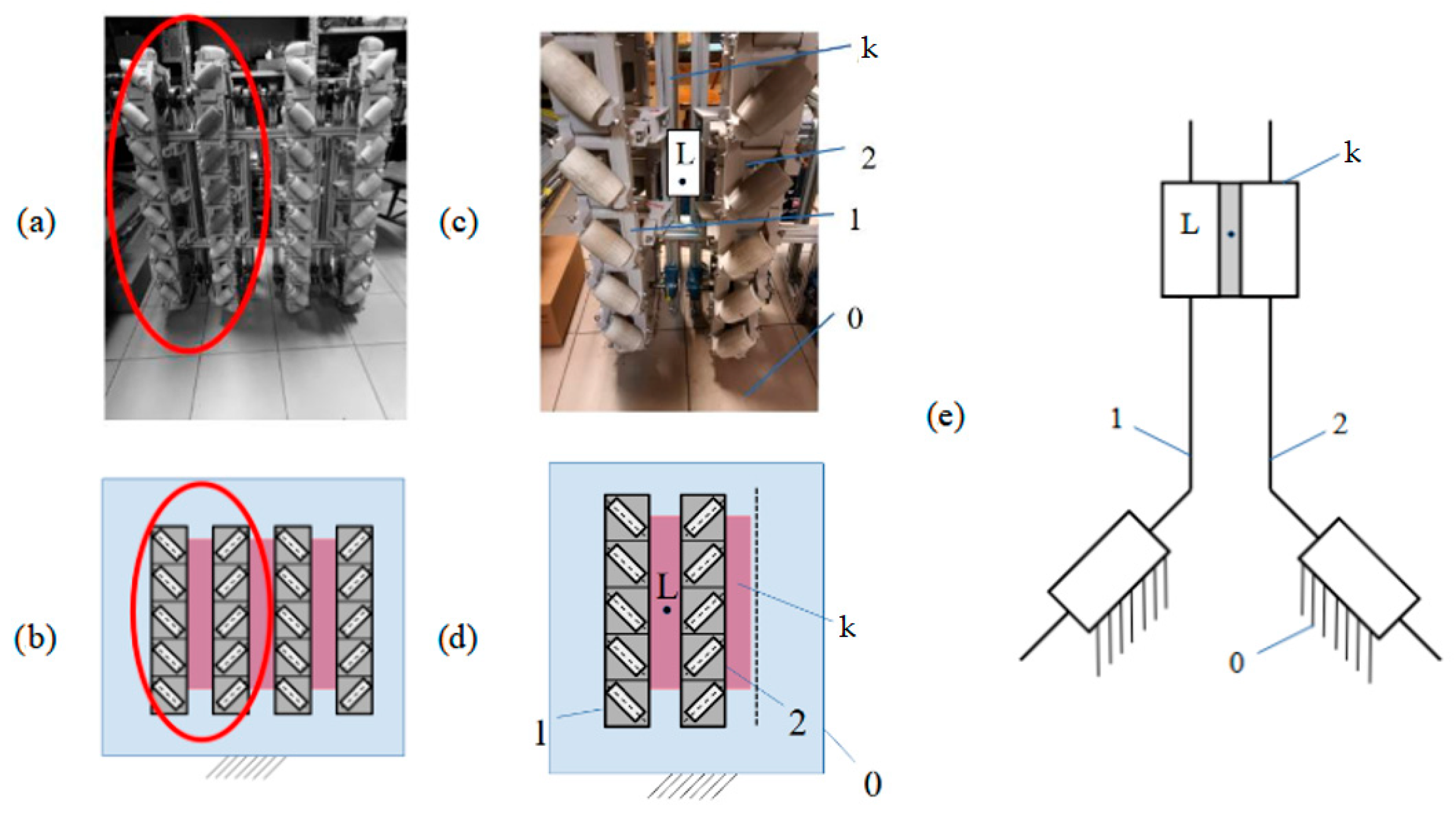
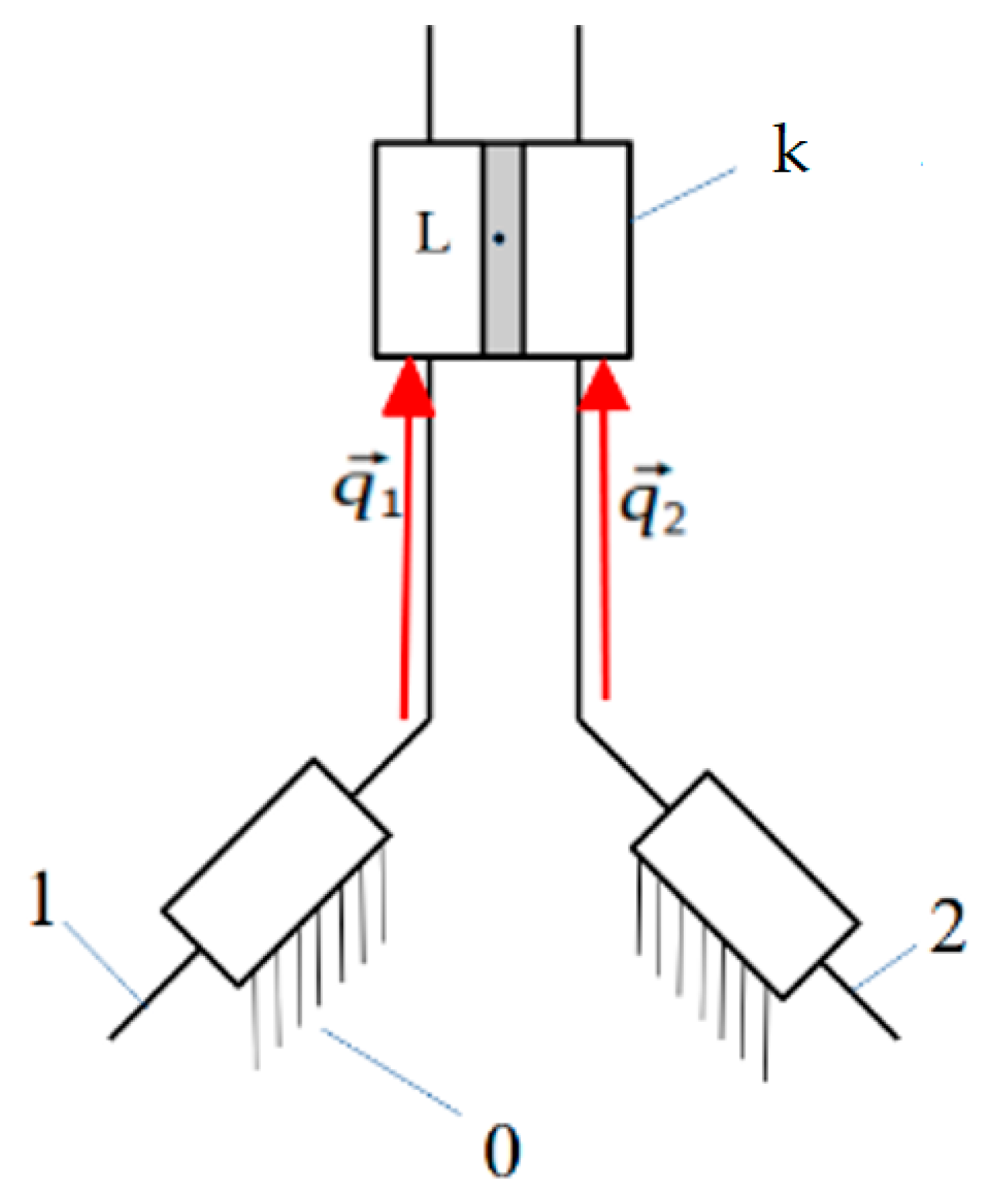
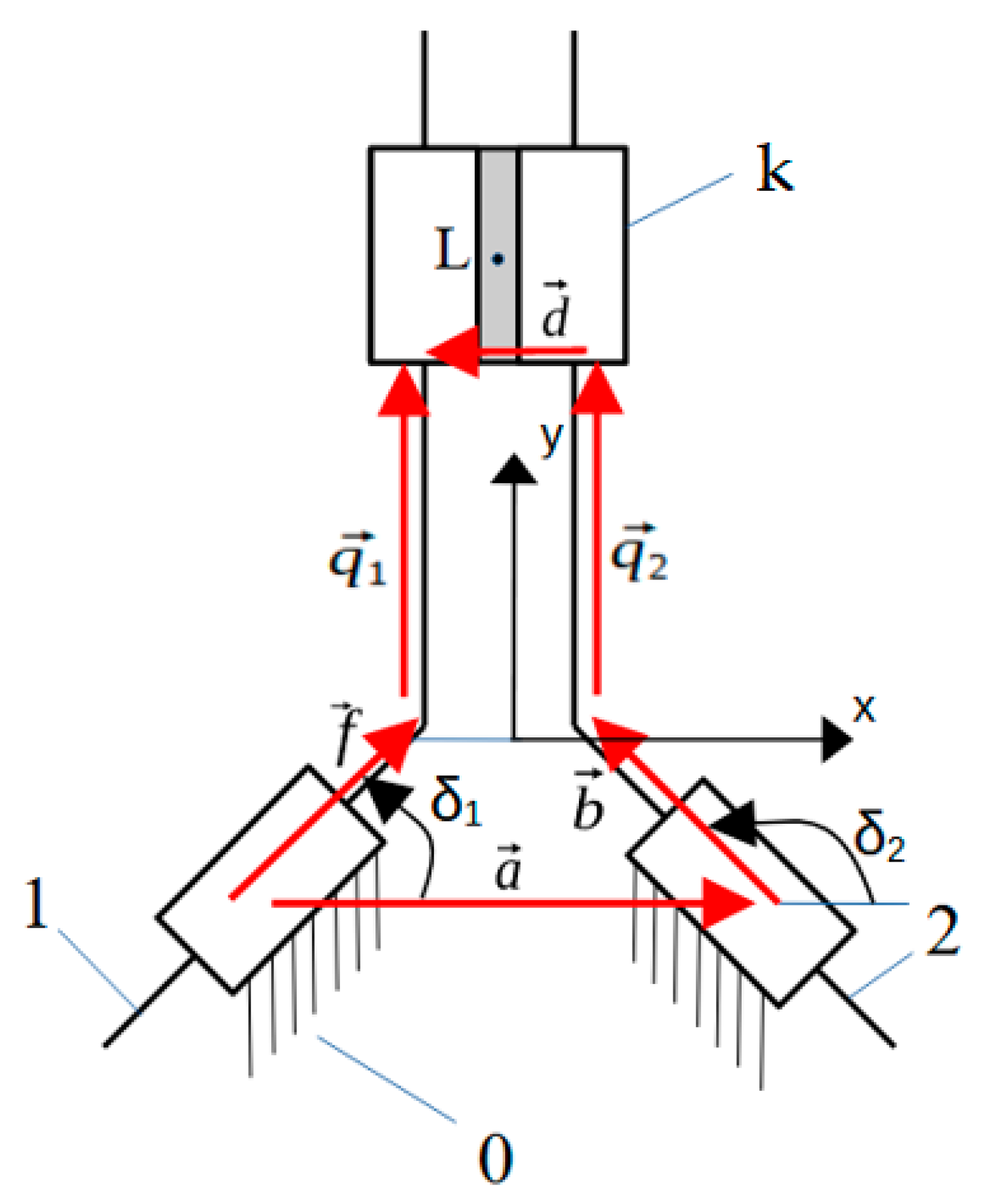
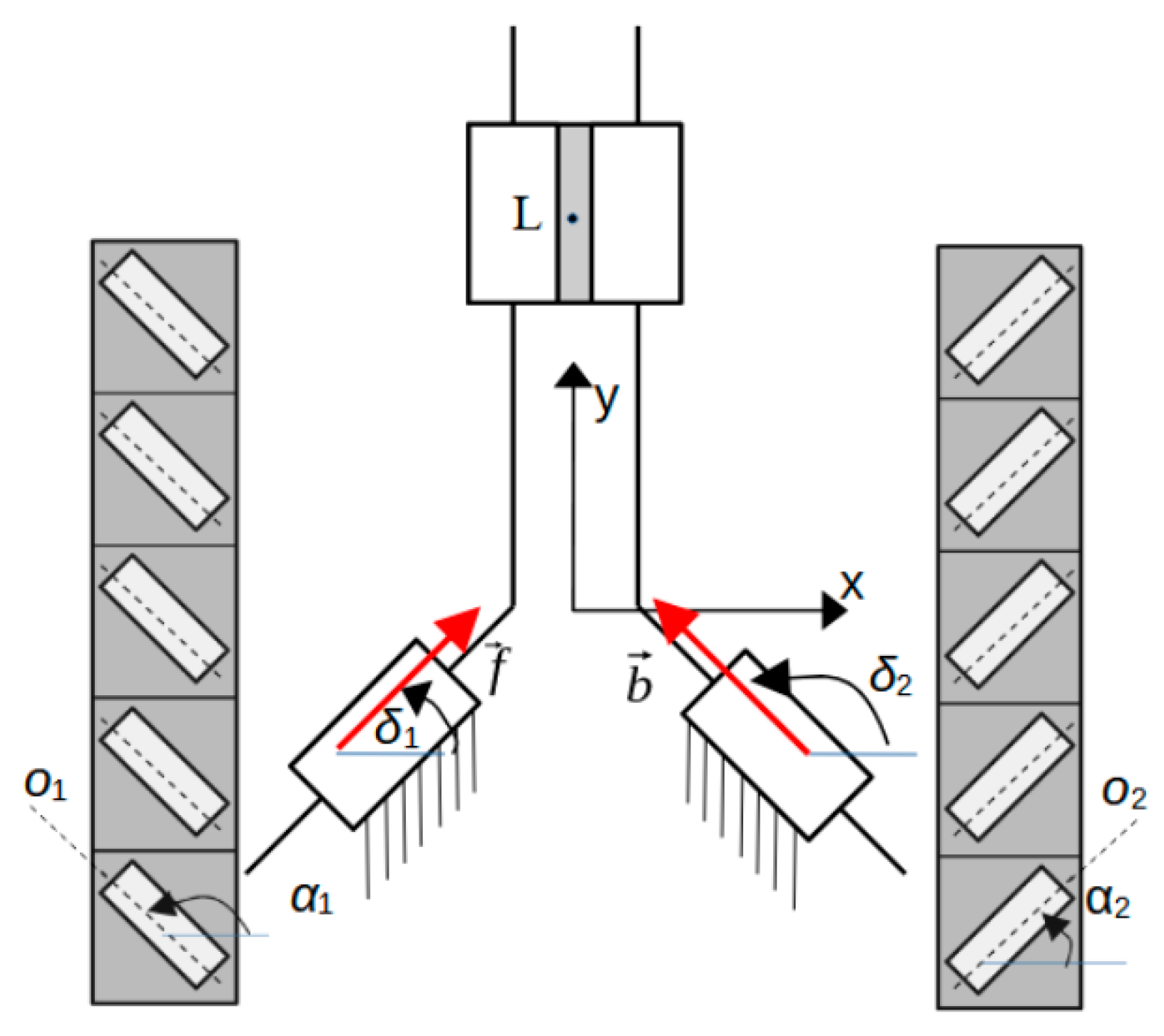
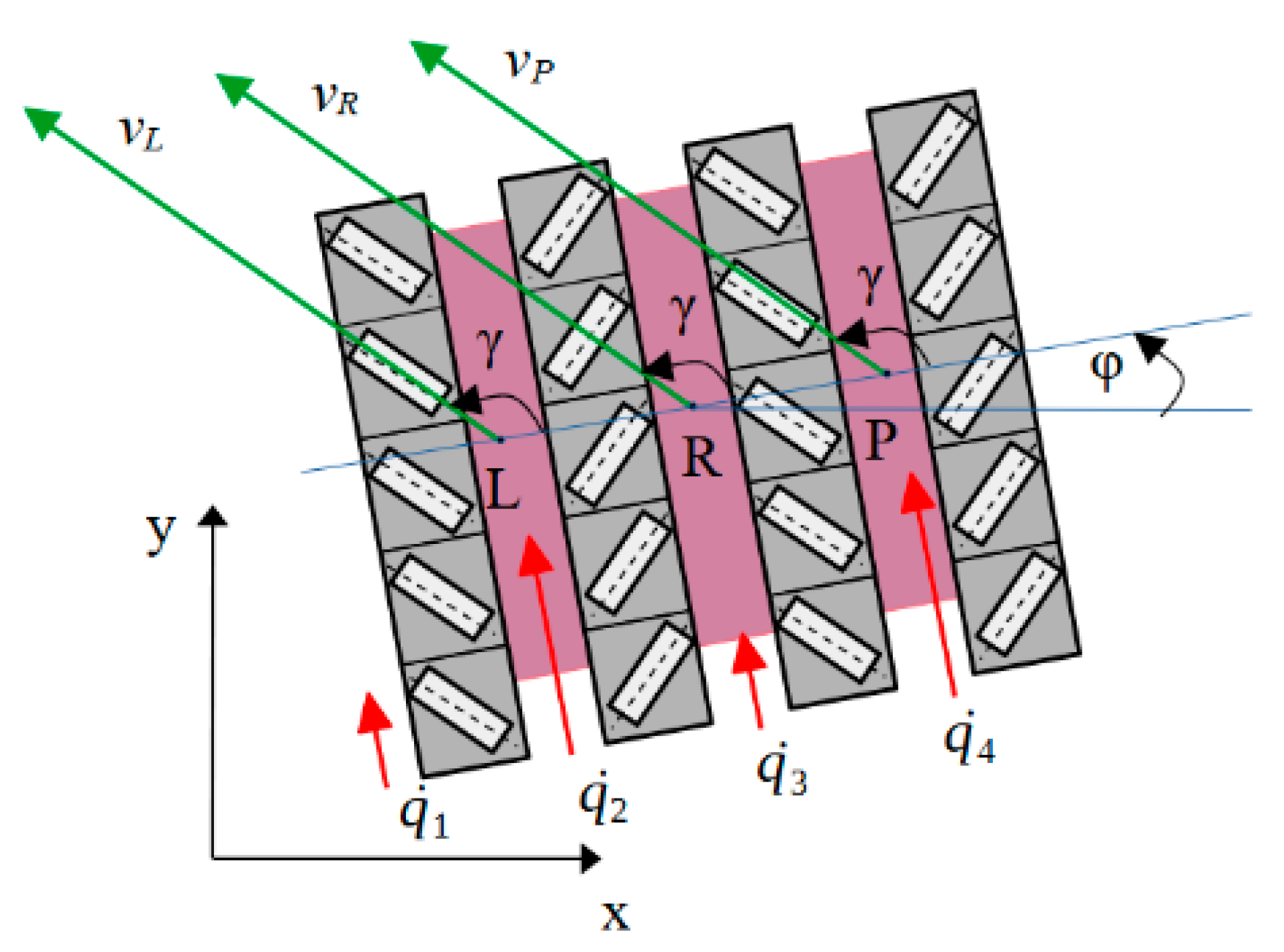
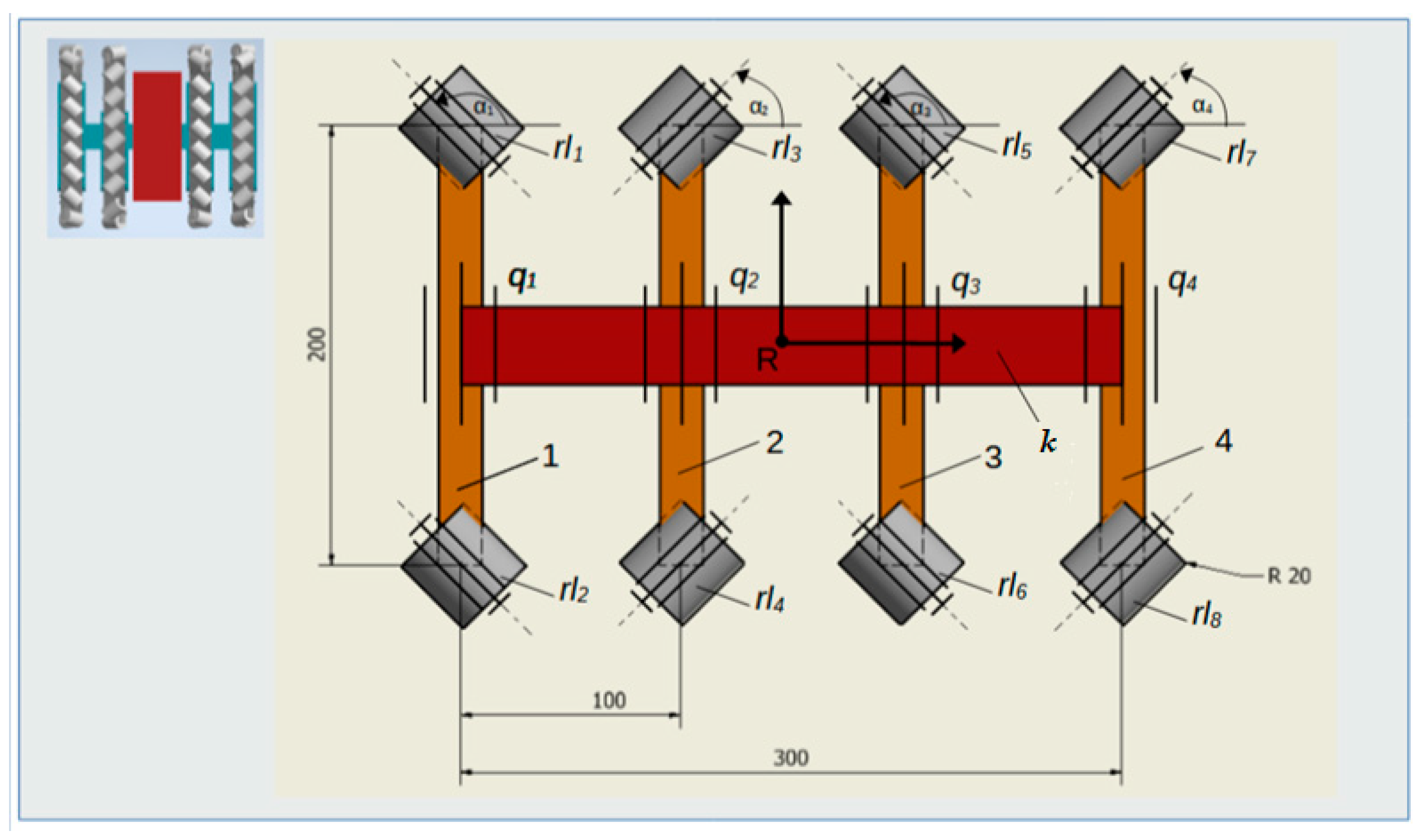
2.1. Kinematic Model

The model proposed in this article enables the representation of a wide range of omni-track vehicles. It can be used to describe a mechanism (a pair of tracks, referred to as a module) with any configuration of free rollers, including asymmetric ones. Both tracks must be the same length, i.e., the same number of rollers in contact with the ground. Unbalanced forces may appear in the case of disproportion in length, which may affect the vehicle’s trajectory. The model can also be used to describe a tracked vehicle composed of any number of modules and their mutual configuration.

An omni-track vehicle with fully overlapping tracks has four tread systems bn designated as n = 1, …, 4 and a body k. Adjacent tread systems can be divided into pairs, hereinafter referred to as modules. The first module, referred to hereafter as L₁₂, consists of b₁ and b₂. The second module, referred to as P₃₄, consists of b₃ and b₄. A typical omni-track vehicle consists of two identical, parallel modules. At the geometric centre of the body, k, which is also the centre of the robot, a point R is determined, which is the same as the centre of the robot. In the geometric centre of module L₁₂, point L is determined, while in the geometric centre of module P₃₄, point P is determined. A schematic of the vehicle, along with a solid model, is shown in Figure 5.

A single running system b_n consists of a track g_n, a rotary drive mn, a gearbox, and a drive wheel. The wheel connected to the drive, whose speed is denoted as ${\omega }_n^M$, is the active wheel of the gearbox. The gearbox sets the passive wheel in motion, whose speed is denoted as ${\omega }_n^B$. The passive wheel is connected to the drive wheel of the track. The drive wheel forces the track g_n to move with a speed of v_n, as shown in Figure 6.

The gear ratio between the drive and the passive gear $i_{MBn}$ can be described by the formula:

$$i_{MBn}={\displaystyle \frac{ {\omega }_n^M}{{\omega }_n^B}}={\displaystyle \frac{ r_n^B}{r_n^M}}$$

(1)

• n—tracked running gear number n = 1, …, 4;
• $r_n^B$—radius of the passive wheel of running gear n;
• $r_n^M$—radius of the active wheel of running gear n;
• ${\omega }_n^B$—angular velocity of the passive wheel of running gear n;
• ${\omega }_n^M$—angular velocity of the active wheel of running gear n.

The linear velocity $v_n$ of the gn track can be described by the formula:

$$v_n={\omega }_n^M i_{MBn} r_n^{KN}$$

(2)

$r_n^{KN}$—radius of the driving wheel of the running gear n.

Equation (2) describes the velocity $v_n$ of the movement of the track section gn in contact with the ground relative to the vehicle body k. This velocity will be referred to in the latter part of this article as the track velocity. Based on the calculated velocities of the individual tracks, it is possible to determine the direction and velocity of the movement of point R, located on the robot body k. The body moves in a translational motion, so the velocity vectors of all points belonging to a given body will be equal. It can, therefore, be assumed that in order to determine the direction and value of the velocity vector of point R, it is sufficient to determine the orientation and value of the velocity vector of a single module, i.e., point L in the case of module L₁₂ or point P in the case of module P₃₄. A kinematic model of a single module consisting of two running systems was proposed. All resistance to the motion was omitted. It was assumed that there would be no slippage during the interaction of the free roller with the flat ground. This means that the connection between the ground and the free roller can be treated as a class I translational pair. The orientation of the roller relative to the track does not change during movement. Therefore, both of these elements can be replaced by one body consisting of two bodies fixed relative to each other at an angle corresponding to the orientation angle of the roller. The movement of the track relative to the vehicle body is always rectilinear. Therefore, the connection of the track with the body can be presented as a class I progressive pair. In order to enable the movement of the tracks relative to the body, this track must be equipped with one drive. The proposed model of a single omnidirectional vehicle module consists of a base 0, two guides 1 and 2, each of which consists of two bodies oriented and fixed relative to each other, and a body k, with two parallel mounted sliders. The diagram of the proposed simplification of the omni-track vehicle mechanism is shown in Figure 7, while the kinematic diagram is shown in Figure 8. For the purposes of the presented example, it was assumed that this is a model of the L₁₂ module, with the geometric centre at point L, which consists of running systems 1 and 2, modelled by links 1 and 2.

The mobility of the mechanism in question was calculated using the formula for the mobility of the wedge mechanism:

$$W=2(k-1)-p_1$$

(3)

• $W$—mobility;
• $k$—number of bodies;
• $p_1$—number of pairs of class I.
• For k = 4 and $p_1$ = 4, mobility W is W = 2.

The discussed mechanism (Figure 8) has two degrees of freedom. This means that two kinematic excitations (drives) are necessary for control. The first one, called q₁, describes the displacement of link 1 relative to body k. The second drive, called q₂, forces the displacement between link 2 and body k. In this model, link k represents the body of the omni-tracked vehicle. Links 1 and 2 are the left and right tracks (g₁ and g₂), respectively. This means that the velocities of the drives $\dot{q}$₁ and $\dot{q}$₂ are equal to the linear movement velocities of the tracks relative to body k of the vehicle. The analysis of the discussed mechanism was performed using vector equations. In the proposed mechanism, the position of the links can be described by a one vector constraint equation (Figure 9).

The equations of this mechanism can be written as

$$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{q_1 }+\overrightarrow{d}+\overrightarrow{q_2}-\overrightarrow{f}=0$$

The lengths of vectors $\overrightarrow{a}, \overrightarrow{ q_1 }, \overrightarrow{d} \mathrm{a}\mathrm{n}\mathrm{d}\overrightarrow{q_2}$ and angles ${\delta }_1$ and ${\delta }_1$ are known (Figure 9). Vectors $\overrightarrow{q_1 }$ and $\overrightarrow{q_2}$ describe the given kinematic excitations, i.e., the displacement of the tracks relative to the body k. Vectors $\overrightarrow{a}$ and $\overrightarrow{d}$ define the geometry of the system. The lengths of vectors $\overrightarrow{b}$ and $\overrightarrow{f}$ are sought, based on which the displacement of the vehicle body k relative to the base 0 can be determined. Vector $\overrightarrow{a}$ is parallel to the x-axis of the global coordinate system and is located on the base. Its length is equal to the distance between the conventional places of attachment of the sliders. In kinematic analysis, the rectilinear guide can perform only a sliding motion in the slider in the direction parallel to the slider. This means that for this analysis, it does not matter at what distance from each other they are; the points at which the sliders will be located will be assumed. The angular orientation ${\delta }_1$, ${\delta }_2$ of these sliders is identical to the angle α of the orientation of the free rollers. Vector $\overrightarrow{b}$ is the length of the extension of guide 2 in relation to the previously assumed point at which the slider was located on the base. It should be emphasized that this slider is only a theoretical construct—its presence is necessary to introduce interaction between the track and the ground into the model. The orientation of vector $\overrightarrow{b}$ described as ${\delta }_2$ is forced by the direction of guide 2, while its length is variable. Angle ${\delta }_2$ depends on the design parameters of the omni-tracks. Its value is 90° greater than angle ${\mathsf{\alpha }}_2$, defining the angular orientation of the free axis of the roller $o_2$ in relation to the transverse axis of the track (Figure 10). As a result, the vector $\overrightarrow{b}$ and the free roller axis $o_2$ are perpendicular to each other.

The vector $\overrightarrow{q_2}$ is parallel to the y-axis of the global coordinate system. Its length is the same as the linear displacement of the track g₂ relative to the body. This means that it is a known value resulting from the set control. The vector $\overrightarrow{d}$ is parallel to the x-axis of the global coordinate system. It is the distance between the model elements representing the tracks. This vector represents the track spacing in a single drive module of an omni-track vehicle. The vector $\overrightarrow{q_1}$ is the same as the linear displacement of the tracks g₂ relative to the body. It is parallel to the y-axis, and its length results from the adopted control. The vector $\overrightarrow{f}$, like the vector $\overrightarrow{b}$, represents the length of slide extension 1 relative to the theoretically adopted slider located on the base. It is oriented at an angle ${\delta }_1$, which depends on the angle of orientation of the free roller on the track under consideration. The value ${\delta }_1$ is 90° smaller than the angle ${\mathsf{\alpha }}_2$. In addition, the vector $\overrightarrow{f}$ closes the chain.

By projecting the vectors onto the individual axes, the following system of equations can be obtained, describing the position of the various components of the mechanism:

$$\left\{\begin{array}{c}0=\mathrm{a}+b cos {\delta }_2-d-f cos {\delta }_1\\ 0=b sin {\delta }_2-q_1+q_2-f sin {\delta }_1\end{array}\right.$$

(4)

The values of q₁ and q₂ are given. The values sought are b and f. Solving the above system of equations will determine the values of b and f. Thus, given the known values of q₁ and q₂, the displacement ${\Delta r}_L$ of point L with respect to the ground can be determined from the following relationship:

$${\Delta r}_L=f+q_1=b+q_2$$

(5)

After differentiating the equations describing the position with respect to time t once, a system of equations describing the relationship between velocities in the mechanism in question will be formed:

$$\left\{\begin{array}{c}0=\dot{b} cos {\delta }_2-\dot{f} cos {\delta }_1\\ 0=\dot{b} sin {\delta }_2-{\dot{q}}_1+{\dot{q}}_2-\dot{f} sin {\delta }_1\end{array}\right.$$

(6)

Based on the determined values of the velocity vectors $\overrightarrow{\dot{b}}$ and $\overrightarrow{\dot{f}}$, it is possible to determine the velocity $\overrightarrow{v_{\mathrm{L}}}$ of the point L of the module in question based on the following equation:

$$\overrightarrow{v_{\mathrm{L}}}=\overrightarrow{\dot{b}}+\overrightarrow{{\dot{q}}_2}=\overrightarrow{\dot{f}}+ \overrightarrow{{\dot{q}}_1}$$

(7)

$$\overrightarrow{v_{\mathrm{L}}}=\left[\begin{array}{c}{v}_{\mathrm{L}}^x\\ v_{\mathrm{L}}^y\end{array}\right]=\left[\begin{array}{c}\dot{b}\mathrm{c}\mathrm{o}\mathrm{s} {\delta }_2\\ \dot{b}\mathrm{s}\mathrm{i}\mathrm{n} {\delta }_2+{\dot{q}}_2\end{array}\right]=\left[\begin{array}{c}\dot{f} \mathrm{c}\mathrm{o}\mathrm{s} {\delta }_1\\ \dot{f} \mathrm{s}\mathrm{i}\mathrm{n} {\delta }_1+{\dot{q}}_1\end{array}\right]$$

(8)

The orientation of the vector $\overrightarrow{v_{\mathrm{L}}}$ is denoted as γ. The angle can be calculated using the atan2 function based on the following formula:

$$\gamma =atan2\left(v_{\mathrm{L}}^y,v_{\mathrm{L}}^x\right)$$

(9)

The atan2 function returns the angle of the straight line drawn through the centre of the coordinate system and the given point and the x-axis. The proposed kinematic model of a single omni-track module is controlled by two drives. It allows the body to move in any direction without having to change the angular orientation of the body. It therefore differs from the existing models of typical tracked vehicles, in which the angular orientation of the body must be changed to achieve movement in a direction other than the main axis. In further steps, it is possible to develop the proposed model by analyzing any number of modules (pairs of track running systems) to obtain more complex vehicles.

The article considers an omni-track vehicle consisting of two track modules connected by a body k. The geometric centre of the body k contains point R, which will be the subject of further considerations. The modules are arranged in the same direction, in a completely overlapping manner. During the simulation, only the translational motion of the vehicle will be studied, which means that both modules must be controlled in the same way. This means that if the kinematic excitations $q_1=q_3$ and $q_2=q_4$ and the velocities ${\dot{q}}_{1 }$= ${\dot{q}}_3$ and ${\dot{q}}_2={\dot{q}}_4$ are maintained, the equality (10) will hold.

The vector $\overrightarrow{S_{\mathrm{L}}}$ and $\overrightarrow{v_{\mathrm{L}}}$ displacement determines the velocity of point L, which is equal to the displacement and velocity of points R and P on the body k:

$$\begin{gathered} \overrightarrow{S_{\mathrm{L}}}=\overrightarrow{S_{\mathrm{R}}}=\overrightarrow{S_P} \\ \overrightarrow{v_{\mathrm{L}}}=\overrightarrow{v_{\mathrm{R}}}=\overrightarrow{v_{\mathrm{P}}} \end{gathered}$$

(10)

Based on Equation (4), assuming the spacing between the theoretical sliders is equal to the distance between the tracks d, we can determine the formula for the new position $\overrightarrow{S_R}$ of point R at the given excitations $q_1=q_3$ and $q_2=q_4$:

$$\overrightarrow{S_R}=\left[\begin{array}{c}{S}_R^x\\ S_R^y\end{array}\right]=\left[\begin{array}{c}b\cos {\delta }_2\\ b\sin {\delta }_2+q_2\end{array}\right]=\left[\begin{array}{c}f \mathrm{c}\mathrm{o}\mathrm{s} {\delta }_1\\ f \mathrm{s}\mathrm{i}\mathrm{n} {\delta }_1+q_1\end{array}\right]$$

(11)

whereas the velocity $\overrightarrow{v_R}$ and its orientation γ are analogous to the case based on Equations (8) and (9):

$$\overrightarrow{v_R}=\left[\begin{array}{c}{v}_R^x\\ v_R^y\end{array}\right]=\left[\begin{array}{c}\dot{b}\cos {\delta }_2\\ \dot{b}\sin {\delta }_2+{\dot{q}}_2\end{array}\right]=\left[\begin{array}{c}\dot{f} \mathrm{c}\mathrm{o}\mathrm{s} {\delta }_1\\ \dot{f} \mathrm{s}\mathrm{i}\mathrm{n} {\delta }_1+{\dot{q}}_1\end{array}\right]$$

(12)

$$\gamma =atan2\left(v_R^y,v_R^x\right)$$

(13)

As can be seen from Equations (12) and (13), the value of the velocity vector $\overrightarrow{v_{\mathrm{R}}}$ and its direction γ depend only on the speed of the tracks ${\dot{q}}_1$ and ${\dot{q}}_2$. This means that it is possible to control the speed of the R-point located on the k body in such a way as to achieve movement of the R-point in any direction without changing the angular orientation φ of the k body, as shown in Figure 11.

2.2. Simulation Model

The considerations in Section 2.1 apply to the kinematic model. Any aspects due to slippage between rollers and the ground or uneven drives are ignored here. However, these effects will affect the actual platform. For this reason, the simulation studies of driving dynamics have been carried out, which will demonstrate the validity of using the developed kinematic model to control the platform under development. The numerical simulation will verify that the proposed kinematic model captures the behaviour of the dynamic model with sufficient accuracy.

Numerical studies were carried out in the HEXAGON ADAMS 2022 system for the dynamic analysis of multibody systems. It developed a solid model of an omni-track vehicle consisting of four rigid bodies numbered 1, … 4, with base 0 and body k. Links 1, … 4 and modelling tracks g₁, … g₄ are connected to body k by translational joint pairs. Translational motion kinematic forcing q₁, … q₄ is placed between the individual beams and the body. The change in the value of kinematic excitations over time was described by a linear function. The free rollers are designated as rl₁, … rl₈. Each beam is connected to two rollers by revolute joint pairs. The rollers rl₁, … rl₈ are fixed with respect to the main axis of the vehicle at an angle of α. Rollers connected to beams 1 and 3 were oriented at angles ${\mathsf{\alpha }}_1$ and ${\mathsf{\alpha }}_3$, while rollers connected to beams 2 and 4 were oriented at angles ${\mathsf{\alpha }}_2$ and ${\mathsf{\alpha }}_4$. Contact forces were defined between the substrate and the rollers using contact forces. The Coulomb friction model was used. The parameters of these forces, selected on the basis of the literature [33,34,35], are shown in

Table 1. Dynamic simulation parameters.

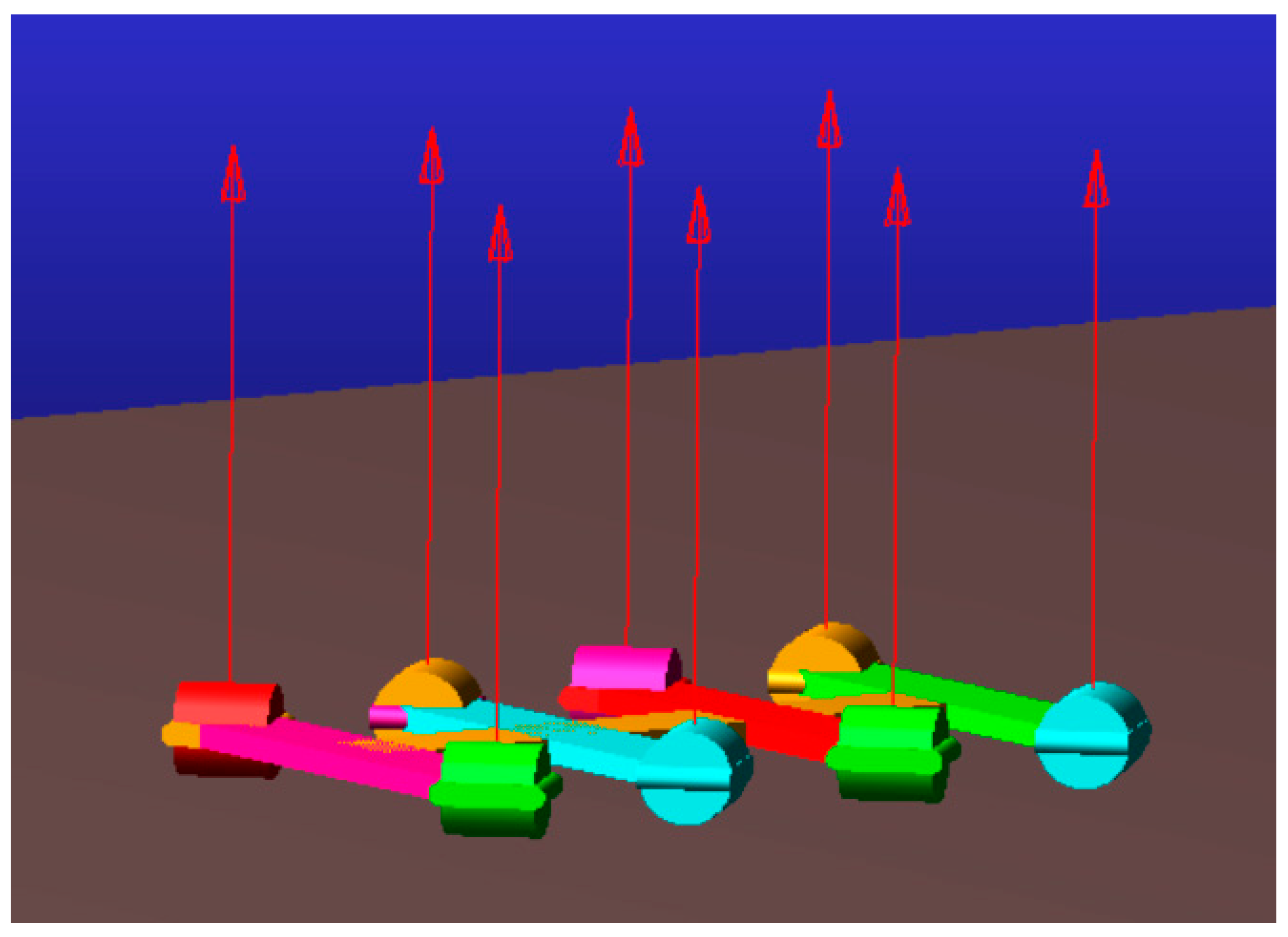
Stiffness	20 N/mm	Static Coefficient	1
Force Exponent	2.2	Dynamic Coefficient	0.85
Damping	1 Ns/mm	Stiction Transition Velocity	10 mm/s
Penetration Depth	1 mm	Friction Transition Velocity	2000 mm/s

. The friction coefficient between the rollers and the substrate corresponds to the friction between rubber and concrete. The model has a mobility of 18, of which 4 displacements q₁, … q₄ are controlled. The view of the model with markings is shown in Figure 12. Figure 13 shows the geometric dimensions of the model. The total weight of the model was 100 kg. The vehicle mass was concentrated primarily in the section representing the body k. Its mass was set at 86 kg.

A dynamic simulation was performed. The simulation step was 5 ms. During the first second of the simulation, the translation pairs did not move. Only the gravitational force acted on the model, balanced by the force of the substrate on the rollers. This gave the model time to stabilize. Then, one second of motion was simulated. The GSTIFF solver was used for the simulation. The error parameter was set to 0.001, formulation I3.

A visualization of an example simulation is shown in Figure 14, while Figure 15 shows the trajectory obtained during this simulation.

2.3. Research Plan

The research was divided into two stages. The first involved the determination of the VR velocity vector for different free roll orientation angles α and different set speeds of individual tracks $\dot{\mathrm{q}}$ based on the presented kinematic equations. Then, numerical simulations were carried out for the same angles α and set speeds $\dot{q}$. The results obtained were compared. The tests were carried out for three sets of free roll orientation angles: ${\mathsf{\alpha }}_1$ = 135°, ${\mathsf{\alpha }}_2$ = 45°; ${\mathsf{\alpha }}_1$ = 150°, ${\mathsf{\alpha }}_2$ = 30°; ${\mathsf{\alpha }}_1$ = 135°, ${\mathsf{\alpha }}_2$ = 30°. Three sets of set velocities were assumed: $\dot{q}$₁ = 0.1 m/s, $\dot{q}$₂ = −0.1 m/s; $\dot{q}$₁ = 0.1 m/s, $\dot{q}$₂ = 0 m/s; $\dot{q}$₁ = 0.1 m/s, $\dot{q}$₂ = 0.05 m/s. Simulations lasted t = 1s. Then, additional verification was performed to check the effect of mass on the obtained accuracy. For ${\mathsf{\alpha }}_1$ = 135°, ${\mathsf{\alpha }}_2$ = 45°, $\dot{q}$₁ = 0.1 m/s, and $\dot{q}$₂ = −0.1 m/s additional simulations were performed, assuming the mass of the models m₁ = 60 kg; m₂ = 80 kg; m₃ = 100 kg; m₄ = 120 kg.

3. Results

Table 2. Values of $\dot{b}$, $\dot{f}$, and $V_{\mathrm{R}}^K$ determined from the kinematic equations for ${\delta }_1$ = 45° and ${\delta }_2$ = 135°.

ID	${\dot{\mathit{q}}}_1$ [m/s]	${\dot{\mathit{q}}}_2$ [m/s]	$\dot{\mathit{b}}$ [m/s]	$\dot{\mathit{f}}$ [m/s]	${\mathit{V}}_{\mathbf{R}}^{\mathit{K}}$ [m/s]
1	100	−100	$100 \sqrt{2}$	$-100 \sqrt{2}$	−100
2	100	0	$50 \sqrt{2}$	$-50 \sqrt{2}$	$50 \sqrt{2}$
3	100	50	${\displaystyle \frac{50 \sqrt{2}}{2}}$	$-{\displaystyle \frac{50 \sqrt{2}}{2}}$	${\displaystyle \frac{50 \sqrt{10}}{2}}$

,

Table 3. Values of $\dot{b}$, $\dot{f}$, and $V_{\mathrm{R}}^K$ determined from the kinematic equations for ${\delta }_1$ = 30° and ${\delta }_2$ = 150°.

ID	${\dot{\mathit{q}}}_1$ [m/s]	${\dot{\mathit{q}}}_2$ [m/s]	$\dot{\mathit{b}}$ [m/s]	$\dot{\mathit{f}}$ [m/s]	${\mathit{V}}_{\mathbf{R}}^{\mathit{K}}$ [m/s]
4	100	−100	200	−200	$100 \sqrt{3}$
5	100	0	100	−100	100
6	100	50	50	−50	$50 \sqrt{3}$

and

Table 4. Values of $\dot{b}$, $\dot{f}$, and $V_{\mathrm{R}}^K$ determined from kinematic equations for ${\delta }_1$ = 30° and ${\delta }_2$ = 135°.

ID	${\dot{\mathit{q}}}_1$ [m/s]	${\dot{\mathit{q}}}_2$ [m/s]	$\dot{\mathit{b}}$ [m/s]	$\dot{\mathit{f}}$ [m/s]	${\mathit{V}}_{\mathbf{R}}^{\mathit{K}}$ [m/s]
7	100	−100	${\displaystyle \frac{400\sqrt{3}}{\sqrt{6}+\sqrt{2}}}$	${\displaystyle \frac{-400}{\sqrt{3}+1}}$	~129.8
8	100	0	${\displaystyle \frac{200\sqrt{3}}{\sqrt{6}+\sqrt{2}}}$	${\displaystyle \frac{-200}{\sqrt{3}+1}}$	~89.8
9	100	50	${\displaystyle \frac{100\sqrt{3}}{\sqrt{6}+\sqrt{2}}}$	${\displaystyle \frac{-100}{\sqrt{3}+1}}$	~87.6

summarize the velocity values $V_{\mathrm{R}}^K$ obtained by analytical methods based on the equations of kinematics. The free roller orientation angles and set velocities from which $V_{\mathrm{R}}^K$ was determined are described in Section 2.3.

The results obtained using the kinematic equations were compared with the results of numerical simulation. It was assumed that the robot model starts movement at point (0, 0).

Table 5. End positions R^S of point R obtained by simulation and end positions R^K of point R obtained by equations, along with end position deviation Δe_x, Δe_y, and e, and simulation time t = 1 s.

ID	${\mathit{R}}_{\mathit{x}}^{\mathit{S}}$ [mm]	${\mathit{R}}_{\mathit{y}}^{\mathit{S}}$ [mm]	${\mathit{R}}_{\mathit{x}}^{\mathit{K}}$ [mm]	${\mathit{R}}_{\mathit{y}}^{\mathit{K}}$ [mm]	Δex [mm]	Δey [mm]	Δe [mm]	e [%]
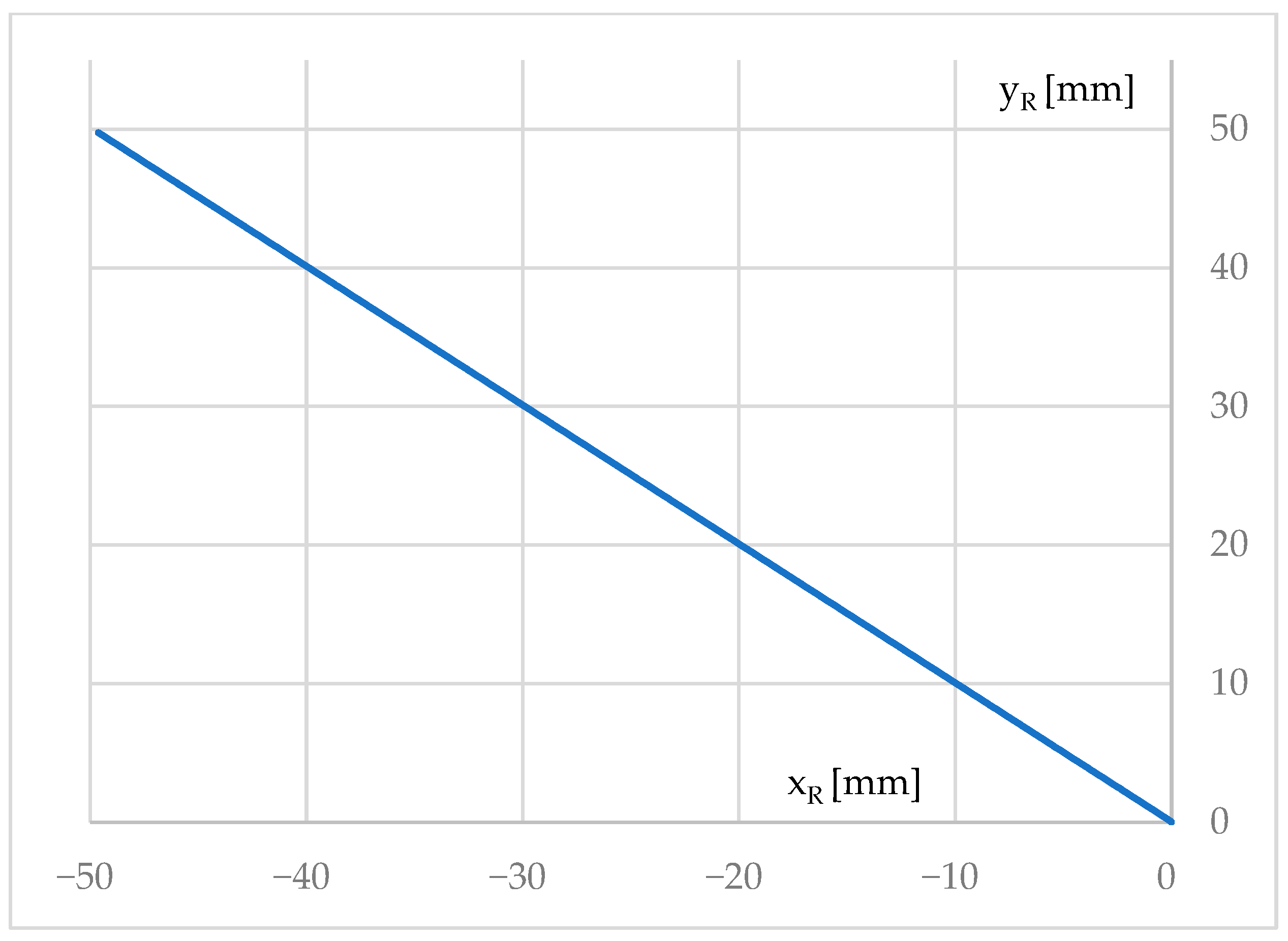
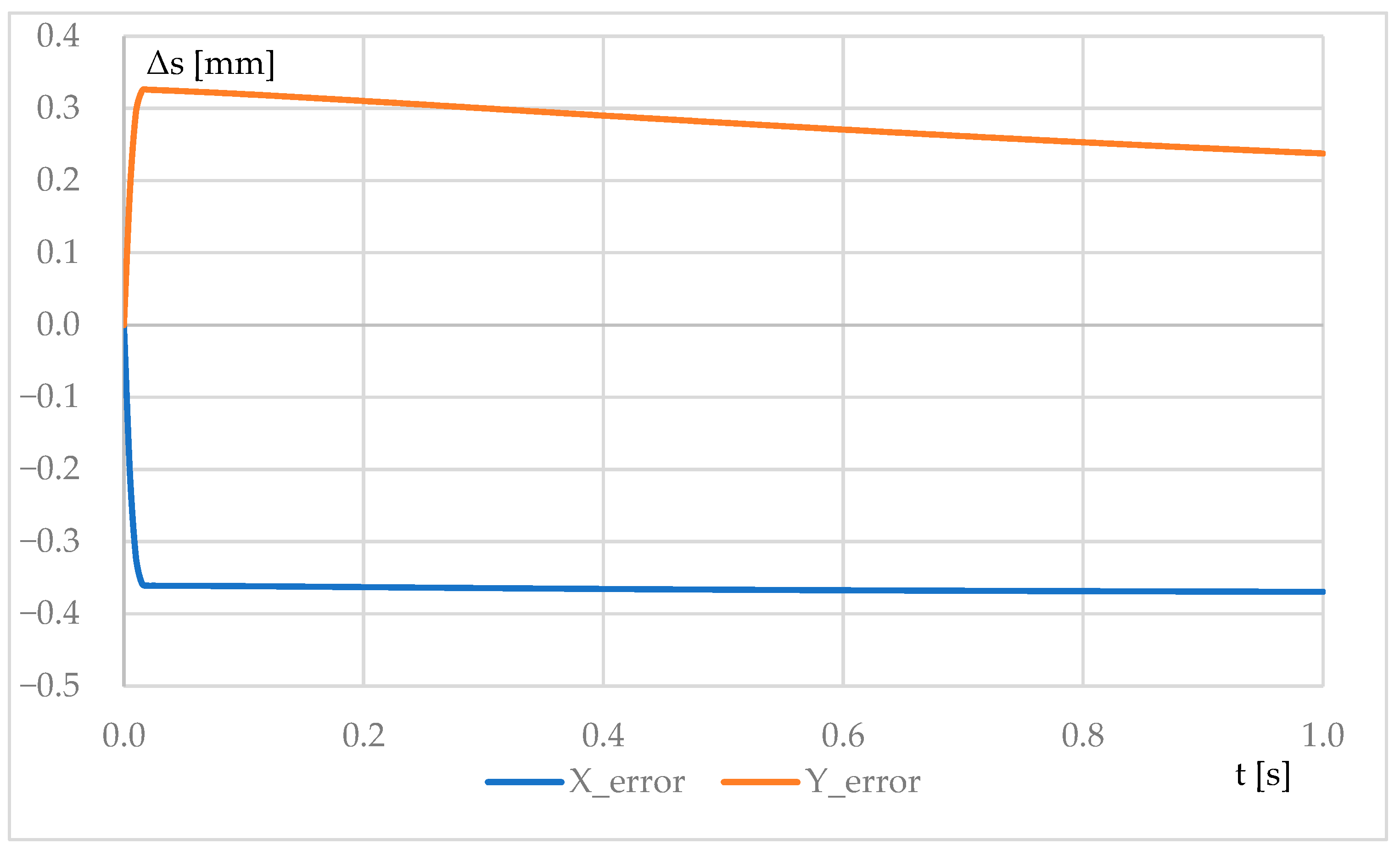
1	−99.07	0.34	−100	0	−0.93	−0.34	0.99	0.99
2	−49.63	49.76	−50	50	−0.37	0.24	0.44	0.62
3	−24.72	74.75	−25	75	−0.28	0.25	0.38	0.47
4	−169.15	1.83	−173.2	0	−4.05	−1.83	4.44	2.57
5	−85.38	49.78	−86.6	50	−1.22	0.22	1.24	1.24
6	−42.71	74.81	−43.3	75	0.59	0.19	0.62	0.72
7	−126.64	27.22	−126.79	26.79	−0.15	−0.57	0.59	0.46
8	−62.72	62.99	−63.4	63.4	0.68	0.41	0.79	0.88
9	−31.25	81.38	−31.7	81.7	−0.45	0.32	0.55	0.63

shows the robot’s final position (x, y) after 1 s of movement determined by numerical simulation, the reference positions determined by the kinematic equations, and the differences in the x and y axes for the final position. The values in Table 5 were determined based on Formula (11). The ${\Delta e}_x$ and ${ \Delta e}_y$ values were determined based on the difference in the position of point R obtained from the dynamic simulation of $R_x^S$ and $R_y^S$ and the kinematic equations $R_x^K$ $R_y^K$. Value $\Delta e$ is the sum of these errors, while $e$ is the ratio, expressed as a percentage, of the error to the assumed trajectory length obtained from the kinematic equations. Figure 16 shows a plot of the R-point position error versus time for an example run. The sequence numbers in Table 5 correspond to the sequence numbers in Table 2, Table 3 and Table 4.

$$\begin{gathered} { \Delta e}_x=R_x^K-R_x^S \\ { \Delta e}_y=R_y^K-R_y^S \end{gathered}$$

(14)

$$\Delta e=\sqrt{{{(R}_x^S)}^2+{{(R}_y^S)}^2}$$

(15)

$$e={\displaystyle \frac{\Delta e}{\sqrt{{{(R}_x^K)}^2+{{(R}_y^K)}^2}}}$$

(16)

The results of an additional simulation verifying the effect of mass on the obtained results are summarized in

Table 6. End positions R^S of point R obtained by simulation and end positions R^K of point R obtained by equations, along with end position deviation Δe_x, Δe_y, and e, simulation time t = 1 s for ${\mathsf{\alpha }}_1$ = 135°, ${\mathsf{\alpha }}_2$ = 45°, $\dot{q}$₁ = 0.1 m/s, and $\dot{q}$₂ = −0.1 m/s, and different m_n.

mn [kg]	${\mathit{R}}_{\mathit{x}}^{\mathit{S}}$ [mm]	${\mathit{R}}_{\mathit{y}}^{\mathit{S}}$ [mm]	${\mathit{R}}_{\mathit{x}}^{\mathit{K}}$ [mm]	${\mathit{R}}_{\mathit{y}}^{\mathit{K}}$ [mm]	Δex [mm]	Δey [mm]	Δe [mm]	e [%]
60	−99.04	0.35	−100	0	−0.96	−0.35	1.02	1.02
80	−99.06	0.34	−100	0	−0.94	−0.34	1.00	1.00
100	−99.07	0.34	−100	0	−0.93	−0.34	0.99	0.99
120	−99.08	0.33	−100	0	−0.92	−0.33	0.98	0.98

.

4. Discussion

The results, summarized in Table 5, indicate that the described kinematic model reproduces the numerically simulated behaviour of omni-track vehicle movement with high accuracy. The largest deviation between the target position (−173.2, 0) and the obtained final position (−169.15, 1.83) was 4.45 mm, which corresponds to 2.6% of the assumed distance. This deviation occurred during simulation number 4, for ${\delta }_1=$ 30° and ${\delta }_2=$ 150°, for speeds q₁ = 0.1 m/s and q₂ = −0.1 m. In most other cases, the error between the theoretical and simulation-obtained final position did not exceed 1% of the assumed movement distance, typically ranging between 0.4 and 1 mm. The greatest inconsistencies were observed for simulations with rollers oriented at angles ${\delta }_1=$ 30° and ${\delta }_2=$ 150°. This suggest that as the angle of the orientation of the free roll increases (the direction of movement of the roll becomes closer and closer to the straight line perpendicular to the direction of movement of the omni-track), the differences between the simulation result and the equations of kinematics increase from 0.47–0.99% to 0.72–2.57% of the assumed distance. This phenomenon is consistent with expectations. If, in the presented model, the angles ${\delta }_1$ and ${\delta }_2$ are 0° and 180°, respectively, the basic dimensions of the model will change in such a way that the mechanism will assume a peculiar configuration. As a result, the mechanism will no longer be controllable with the proposed actuators. The same effect could be obtained if the values of the angles ${\delta }_1$ and ${\delta }_2$ were 90°. Thus, it can be concluded that the closer to the singular configuration, the greater the discrepancy between the kinematic model and the numerical simulation result. This, in turn, would likely translate into similar behaviour of the actual omni-track vehicle. Studies of the effect of mass on the accuracy of trajectory mapping (summarized in Table 6) show that increasing the vehicle mass has a marginal effect. Doubling the vehicle mass, from 60 kg to 120 kg, resulted in a reduction in the final error from 1.02% to 0.98%.

5. Conclusions

The article presents a kinematic model of a pair of tracks of an omnidirectional vehicle. This model represents a separate component of an omni-track vehicle. If needed, it can be extended to analyze the motion of any type of omni-track vehicles, consisting of a larger number of pairs of tracks, which is a novelty in relation to most existing works. The model enables the determination of the vehicle body’s displacements relative to the ground for any orientation of the free rollers, based on the predefined displacements of the tracks relative to the body. This article presents the body of the vehicle, obtained on the basis of this model, for the selected orientation angles of the free rolls and the preset speeds of individual tracks. A numerical model of the omni-track vehicle was also developed, allowing the dynamic simulation of motion. This model includes mass properties and ground contact forces acting on the rollers, enabling a realistic simulation of the vehicle’s movement. A comparative study between numerical simulation results and those obtained from the kinematic model showed that the kinematic approach accurately reflects the real dynamic behaviour of the vehicle. Therefore, it provides a solid foundation for controlling a real omni-track system. Thanks to the compact and simple structure of the proposed kinematic model, it is possible to implement it on units with relatively low computational power, especially for typical roller angles of 45° and 135°. Using the proposed model to control a vehicle with a different roller orientation is still possible, but the errors between the theoretical and actual vehicle trajectory will be higher.

In parallel with the work described in this article, experimental research was conducted on a real prototype of an omni-track vehicle. Experimental studies, not included in this article, have shown that changing the ground on which the robot moves can worsen the driving properties of an uncorrected driving system by an order of magnitude. The concept of implementing the presented kinematic model is based on the use of on-board sensors, such as the IMU orientation sensor, which will enable the real-time reading of the vehicle’s angular orientation relative to its initial position. Thanks to this, using the proposed kinematic model, it will be possible to determine corrective values for the control system, which will enable restoring the set direction of movement; for example, using the PID controller and feedback of the current orientation angle. Going a step further, sensor fusion can be used. Based on data from the encoders of individual running systems, accelerometer and gyroscope readings, as well as the orientation sensor, one can try to recreate the actual trajectory of the omni-tracked vehicle. This operation should be possible regardless of the external forces acting on it or the surface irregularities, without the need to use external positioning systems such as GPS or cameras and markers. A detailed description of this experimental research and its results will be published in a separate publication. The further research will include the verification of the control system’s effectiveness during real-world vehicle operation—both in translational motion and in motion involving changes in angular orientation.