Abstract
In this paper, a winding inter-turn fault (ITF) diagnosis algorithm for electrical machines in integrated motor and drive (IMD) systems is proposed based on impedance analysis using space voltage vectors. An ITF alters the stator resistance, causing an imbalance in the motor’s impedance depending on the phase connection. This impedance asymmetry can be effectively utilized for fault diagnosis. However, in IMD systems, direct impedance measurement through mechanical terminal access is difficult due to the integrated structure. To address this, the impedance of the induction motor is analyzed electrically, without the need for physical disconnection, allowing practical implementation within integrated systems. The specific phase angle of the space voltage vector in the three-phase inverter is analyzed to replicate the electrical conditions of mechanical terminal configurations. Based on this approach, a fault diagnosis algorithm was developed by analyzing the variation in stator current and impedance with respect to space voltage vector angles. The effectiveness of the proposed method was verified through experimental validation using a 12kW three-phase induction motor and terminal box.
1. Introduction
With the recent rapid growth of the electric vehicle (EV) industry, integrated motor and drive (IMD) systems, which simultaneously provide high power density and efficiency, have attracted significant attention across various industrial sectors [1,2]. IMD systems offer several advantages, including reduced installation space, lower wiring losses, suppression of electromagnetic interference, and improved overall system efficiency [3,4]. Furthermore, an IMD system enables the elimination of components such as transformers and filters and offers the benefits of an optimized cooling structure and modular design, making it particularly well suited for EV applications that demand high power density [5,6]. In line with this trend, extensive research has been conducted on compact, high-frequency IMD systems that employ PCB-based stators and GaN-based switching devices. Integrated designs incorporating GaN devices capable of operating at frequencies above 1 MHz have emerged as promising solutions for both reducing system size and suppressing current ripple [7,8].
Electrical faults such as inter-turn faults (ITFs), bearing failures, and insulation breakdowns in motors—critical components in EV systems—can lead to system shutdowns, fires, and serious safety incidents during operation. As a result, diagnostic technologies, including fault-tolerant design approaches, have become increasingly important [9]. In particular, autonomous driving systems require immediate fault response and sustained control system stability due to the limited possibility of driver intervention [10,11]. Recent studies have applied hybrid optimization algorithms for fault diagnosis and parameter estimation in power systems and electrical drives. These approaches offer improved robustness and accuracy in noisy or nonlinear environments [11,12].
Motor faults that can occur during operation are diverse, and diagnostic approaches and countermeasures vary depending on the fault type. In general, motor faults are categorized into electrical, magnetic, and mechanical faults [13]. Electrical faults include inter-turn short circuits (ITSCs), phase-to-phase short circuits, and phase-to-ground faults [14,15,16,17]. Magnetic faults consist of demagnetization and magnetic asymmetry [18,19], while mechanical faults include bearing failures, rotor eccentricity, broken rotor bars, and air-gap asymmetry. Other possible faults include sensor failures and inverter faults [20,21,22]. Among these, ITSC faults are considered the most severe, as they can lead to total winding failure within a short period and generate significant torque ripple [23,24]. This occurs because a localized short between turns produces extremely high circulating currents, resulting in severe overheating, insulation breakdown, and ultimately catastrophic motor failure or even fire [25,26]. In particular, ITFs can rapidly destroy the entire winding and, in the case of permanent magnet (PM) motors, may even cause magnet demagnetization, posing a serious threat to overall system reliability [27,28].
Various methods have been developed to diagnose ITFs due to their severity. These methods are considered to be among the most critical aspects of motor fault diagnosis [28,29,30,31,32,33]. In [28,29,30], the widely adopted approach of motor current signature analysis (MCSA) is introduced. MCSA techniques are generally categorized into FFT-based spectrum analysis, time–frequency analysis (e.g., wavelet transform and Hilbert–Huang transform), and other methods. However, spectrum-analysis-based methods are highly sensitive to high-frequency noise and load variations, which can degrade diagnostic reliability. In [27], artificial intelligence (AI)-based diagnostic techniques, including neural networks and support vector machines (SVMs), have also been actively explored. However, AI-based approaches require large amounts of labeled fault data for effective training, and acquiring sufficient and diverse fault data under various operating conditions remains a major challenge in real-world industrial environments. Furthermore, conventional model-based methods require complex mathematical modeling and are susceptible to uncertainties in motor parameters [31,32].
ITF diagnosis based on impedance analysis in induction motors (IMs) was introduced in a previous study [33]. The impedance characteristics of six winding connections were analyzed, and the phase of impedance was calculated to diagnose the ITF. The six winding connections are required to calculate the phase of impedance for ITF diagnosis. Although the introduced ITF diagnosis method is simplified compared to other methods, it presents practical limitations when applied to real industrial systems such as electric vehicles (EVs), which commonly utilize IMD systems. In these systems, the physical disconnection of the inverter from the motor is required to perform offline measurements, which significantly limits the applicability of the approach in IMD systems.
This paper proposes an offline ITF diagnosis algorithm for IMD systems based on impedance analysis and the space voltage vector control of a three-phase inverter. The proposed method enables fault detection without mechanical separation between the motor and the inverter, making it highly suitable for IMD-based applications. Assuming an ITF occurs in phase A, the terminal impedances are analyzed and compared to identify the maximum and minimum impedance values. Although ITFs can be diagnosed through terminal resistance measurements, the terminal configuration in IMD systems differs due to the integrated structure of the motor and inverter. Therefore, the space voltage vector of the three-phase inverter is analyzed for each switching state. A fault diagnosis algorithm is proposed based on both the impedance characteristics and the space voltage vector analysis. To validate the proposed algorithm, an experimental setup was constructed using a 12 kW three-phase induction motor (IM), an inverter, fault resistance, and a terminal box for winding connections. The algorithm was verified for both Y and Δ connections without requiring access to mechanical terminal connections.
Here, we provide a summary of the main contributions of our work:
- (1)
- To diagnose the ITF, the impedance of electrical machine is analyzed for the terminal connection. The terminal connection is implemented electrically through the space vector control of the three-phase inverter, eliminating the need for inverter disconnection or access to terminal connections when the ITF of the electrical machine is diagnosed.
- (2)
- The proposed method does not require the tracking of time-varying operational parameters, thereby simplifying implementation compared to online diagnostic approaches. Furthermore, a low-complexity algorithm based on phase impedance comparison across six space voltage vectors is employed, enhancing compatibility with embedded systems and real-time control platforms.
- (3)
- A 12 kW three-phase IM was manufactured, and an experimental environment was implemented to verify the proposed algorithm for ITF diagnosis. The proposed ITF diagnosis algorithm was verified through the measurement of impedance for the space voltage vector for Y and Δ connections.
This paper is organized as follows: Section 2 describes the analysis of the impedance characteristics under ITF conditions in phase A for both Y and Δ connections. Section 3 presents the space voltage vector analysis corresponding to inverter switching states and proposes the ITF diagnosis algorithm based on impedance variation. Section 4 describes the experimental validation using the fabricated IM and terminal box. Section 5 concludes the paper.
2. Impedance Analysis of Inter-Turn Fault of Induction Motor
2.1. Mathematical Model of Induction Motor with Inter-Turn Fault
Figure 1 shows the configuration of an induction motor under ITF conditions with Y and delta connections. In the event of an ITF in phase A, fault resistance appears in parallel with the winding of the faulty phase. This additional parallel path results in reduced impedance in the fault phase, leading to an imbalance in the per-phase impedance of the stator. The resulting asymmetry in impedance can be effectively utilized as a diagnostic feature for identifying ITF in induction motors. The impedance of healthy and fault phases can be expressed as follows:
where
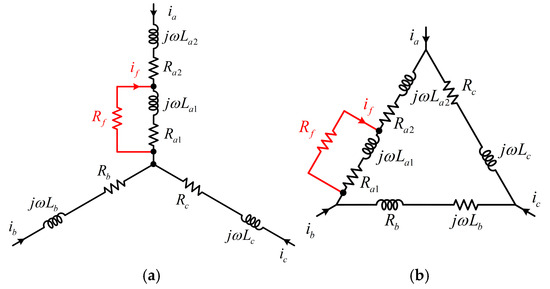
Figure 1.
Configuration of inter-turn fault in IM: (a) Y connection; (b) Δ connection.
Zh and Zf denote the impedances of healthy and fault phases, respectively. Ra and La represent the phase resistance and inductance of the healthy phase, respectively. Ra1 and La1 are the resistance and inductance of the fault phase with the fault resistance connected in parallel. Ra2 and La2 denote the resistance and inductance of the fault phase without the fault resistance. Rf is the fault resistance, and ω is the electrical angular speed. By subtracting Equation (3) from Equation (2), the impedance of the fault phase is expressed as follows:
Since the fault resistance is connected in parallel with the phase impedance, the fault phase impedance becomes lower than that of the healthy phase, as shown in Equation (4). This indicates that impedance imbalance occurs under ITF conditions, and the impedance of the fault phase is lower than that of the healthy phase. In the next subsection, the impedance analysis of the motor connection is provided to propose the fault diagnosis.
2.2. Impedance Analysis with Y Connection
When an ITF occurs in phase A, the terminal connection is considered to analyze the impedance for the Y connection, as shown in Figure 2. The impedance analysis is conducted for the terminal connection configuration. When the two phases are connected as shown in Figure 2a–c, the terminal impedance can be expressed as follows:
where Za-b, Zc-a, and Zb-c denote the terminal impedances corresponding to the connections between phases A and B, C and A, and B and C, respectively. Since the fault impedance is lower than the healthy impedance, as shown in Equation (4), the terminal impedance comparison is as follows.
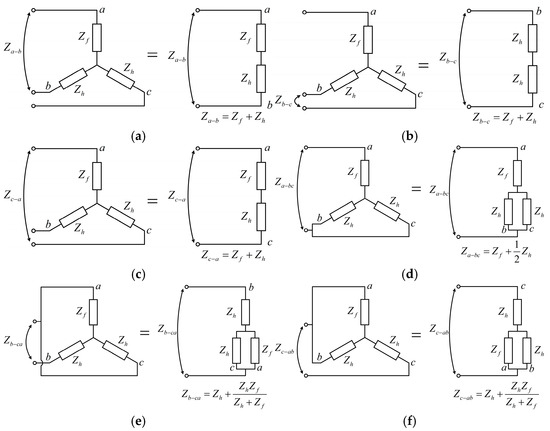
Figure 2.
Impedance analysis for a Y connection with a phase A fault: (a) a-b; (b) b-c; (c) c-a; (d) a-bc; (e) b-ca; (f) c-ab.
From Equation (6), the specific terminal impedance is greater than the other terminal impedances. If an ITF occurs in a different phase, the specific terminal impedance increases when the two corresponding phases are connected.
The impedance for the terminal connection between phase A and the midpoint of phases B and C, denoted as Za-bc and shown in Figure 2f, is calculated as in Equation (7).
Similarly, the impedances for connections b-ca and c-ab, represented in Figure 2d,e, are given by Equation (8).
A comparison between (7) and (8) reveals that the impedance of the a-bc configuration is greater than those of the b-ca and c-ab, as summarized in Equation (9).
From Equation (9), the specific impedance of a given terminal connection configuration is lower than that of the other configurations. If a fault occurs in phase B or C, the impedance becomes either maximum or minimum, depending on the specific terminal connection. Table 1 presents the maximum and minimum impedance values for each fault phase and terminal connection when an ITF occurs in phase A with the Y connection.

Table 1.
Impedance analysis results for a Y connection with a phase A fault.
2.3. Impedance Analysis with Δ Connection
Figure 3 illustrates the terminal configuration of an IM with a Δ connection when an ITF occurs in phase A. As shown in Figure 3, three terminals are available, enabling various inter-terminal connection configurations. Depending on the selected terminal pair, the measured impedance varies due to the presence of fault resistance in the affected phase. The impedance measured between phases A and B, as shown in Figure 3a, is expressed in Equation (10).
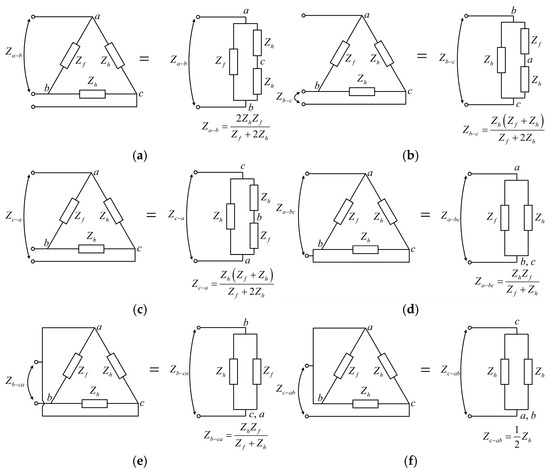
Figure 3.
Impedance analysis for a Δ connection with a phase A fault: (a) a-b; (b) b-c; (c) c-a; (d) a-bc; (e) b-ca; (f) c-ab.
In the same way, the impedance values for terminal pairs b-c and c-a, corresponding to Figure 3b,c, are described in Equation (11).
Under ITF conditions, the impedance of the fault phase decreases due to the fault resistance being placed in parallel with the stator winding. As a result, the impedance of the a-b connection becomes lower than those of the b-c and c-a connections, as demonstrated in Equation (12).
The impedance for the terminal connection between c and the midpoint of a-b, denoted as c-ab and shown in Figure 3f, is calculated as in Equation (13).
Likewise, the impedances for connections a-bc and b-ca, represented in Figure 3d,e, are given by Equation (14).
A comparison of Equations (13) and (14) reveals that the impedance of the c-ab configuration is greater than those of the a-bc and b-ca connections, as summarized in Equation (15).
When a fault occurs in phase B or C, the impedance becomes either a maximum or a minimum, depending on the specific terminal connection. Table 2 presents the maximum and minimum impedance values for each fault phase and terminal configuration. This information enables effective ITF diagnosis based on impedance characteristics.

Table 2.
Impedance analysis results for Δ connection with phase A fault.
However, in IMD systems, such as those used in electric vehicles, mechanical access to motor terminals is often limited or impractical. A diagnostic approach based on space voltage vector control is proposed to address this limitation by emulating terminal connection conditions electrically, without physical rewiring.
3. Inter-Turn Fault Diagnosis of Integrated Motor and Drive Systems
As shown in Section 2, impedance is analyzed for the terminal configuration when an ITF occurs in phase A with both Y and Δ connections. Physical terminal access is required to measure impedances. However, such access is often limited or impractical in IMD systems. In this section, the space voltage vector method is employed to analyze the impedance.
3.1. Space Voltage Vector in Three-Phase Inverter
There are six switching components in a three-phase inverter, as shown in Figure 4a. Each phase has two switching states (ON and OFF), resulting in three possible configurations: (1) upper switch ON, lower switch OFF: ‘1’; (2) upper switch OFF, lower switch ON: ‘0’; (3) both switches OFF: ‘-’. In a three-phase inverter, the possible voltage states are expressed as shown in Figure 4b. The space voltage vector is defined as follows:
where V is the space voltage vector, Vm is the magnitude of the space voltage vector, and θm is the phase angle of the space voltage vector. The space voltage vector is determined by the switch states for each phase. Table 3 shows the phase angles of the space voltage vector corresponding to each switching state.
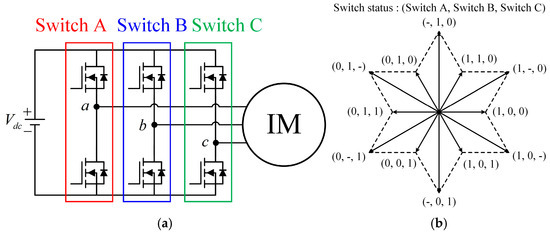
Figure 4.
Three-phase inverter configuration and space voltage vectors for switching conditions: (a) integrated motor and drive system; (b) space voltage vectors based on switching conditions for each phase.

Table 3.
Phase of space voltage vector for switching conditions.
3.2. Terminal Connection for Space Voltage Vector
Since the space voltage vector is determined by the switching states for each phase, as shown in Figure 4 and Table 3, the terminal connection is implemented for the space voltage vector as shown in Figure 5. In the phase with a space voltage vector of 0° the resulting terminal connection corresponds to a-bc, as illustrated in Figure 5a. At 30°, the configuration results in a terminal connection equivalent to c-a, as shown in Figure 5b. In the same way, each space voltage vector position shown in Figure 5 yields an electrical connection that corresponds directly to a specific mechanical terminal connection described in Figure 2 and Figure 3. Table 4 summarizes the relationship between the phase of the space voltage vector and the equivalent terminal connections. This correspondence demonstrates that terminal connections can be realized based on the space voltage vector in the three-phase inverter. The alternating voltage is applied to the motor for the space voltage vector, and the calculated impedance from the measured phase current can be used in the fault diagnosis, as shown in Section 2. As a result, ITF diagnosis can be achieved electrically without the need for the physical reconnection of motor terminals in IMD systems.
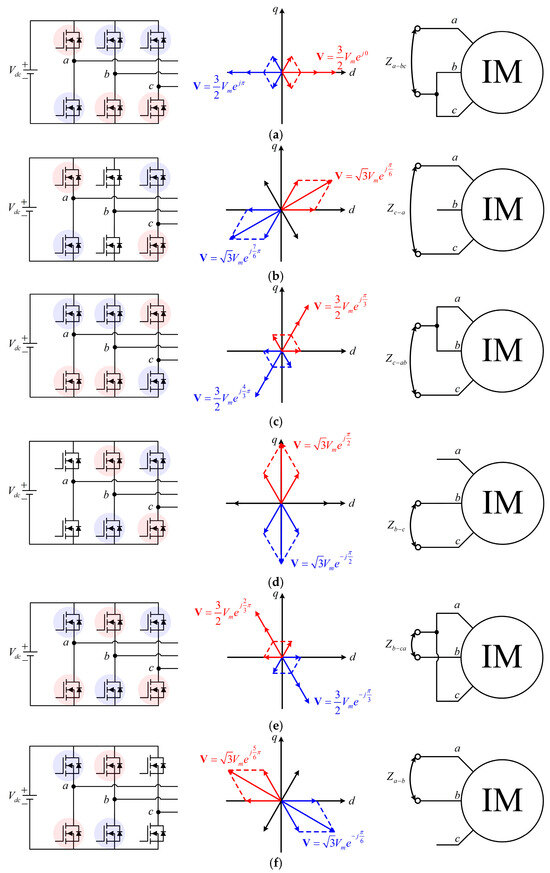
Figure 5.
Switching status, space voltage vector, and terminal connection in IMD with three-phase inverter: (a) 0°; (b) 30°; (c) 60°; (d) 90°; (e) 120°; (f) 150°.

Table 4.
Terminal connections for phases of space voltage vector.
3.3. Fault Diagnosis Algorithm
The terminal connections are implemented based on the space voltage vector by the three-phase inverter. Based on the impedance and space voltage vector, the ITF algorithm is proposed as shown in Figure 6. The alternating voltage is applied to the motor according to the phase of the space voltage vector through the three-phase inverter. The impedances corresponding to each phase of the space voltage vector are calculated from the input voltage and measured phase currents. The fault diagnosis is performed by identifying the maximum and minimum impedances associated with each phase of the space voltage vector. For example, when an ITF occurs in phase A with the Δ connection, the phases of the space voltage vector corresponding to the maximum and minimum impedance values are 60° and 150°, respectively, as shown in Figure 6b. In the same way, when the ITF occurs in phase B or C, the fault diagnosis can be performed as shown in Figure 6.
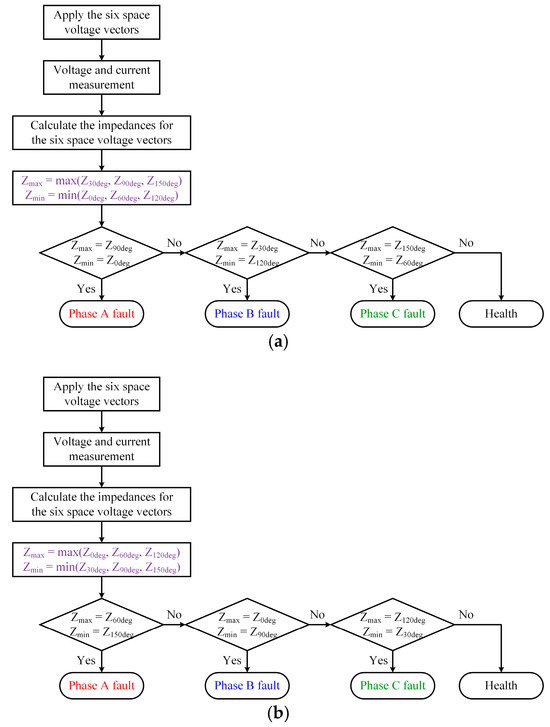
Figure 6.
Inter-turn fault diagnosis algorithm: (a) Y connection; (b) Δ connection.
4. Experimental Verification
This section presents the experimental verification of the proposed fault diagnosis algorithm. A 12 kW three-phase IM from RENAULT TWIZY, used for EV applications, is described in Table 5. The motor parameters and fault resistance were measured using the impedance analyzer. The phase resistance of the IM was 11.5 mΩ, and a fault resistance of 3.6 mΩ was considered. Figure 7 shows the manufactured IM and terminal box used to implement the winding connections and simulate fault conditions. The windings of the IM were separated, as shown in Figure 8, and connected through the terminal box. The experimental setup for ITF diagnosis is shown in Figure 9. The test motor was coupled to a dynamometer system, and both Y and Δ connections were implemented through the terminal box. A three-phase inverter was used to apply the space voltage vector to the IM. Fault diagnosis was conducted with both Y and Δ connections, as illustrated in Figure 10. The fault resistance was connected in parallel with the faulty phase. The voltage and current were measured using voltage and current sensors, such as the HAH1DR series from LEM, and the impedance was calculated for each space voltage vector. The measured voltage and current were converted to digital values using an analog-to-digital converter in a digital signal processor (DSP), specifically the TMS320F28069, to enable impedance calculation. Moreover, the calculated impedance, the phase of the space voltage vector, and the diagnostic status were converted back to analog signals via the DSP’s digital-to-analog converter and displayed on an oscilloscope. The experimental results for the Y and Δ connections are shown in Figure 11 and Figure 12, respectively. As shown in Figure 11, when an ITF occurs in phase A, the impedance reaches its maximum at a phase angle of 90° and its minimum at 0°, corresponding to the specific phase angles of the space voltage vector in the three-phase inverter. When the fault occurs in phase B, the maximum impedance is observed at 30° and the minimum at 120°. Similarly, for a fault in phase C, the impedance is maximized at 150° and minimized at 60°. As demonstrated in Figure 12, the measured impedance values for each fault condition were analyzed based on measured currents. By comparing the impedance at each space voltage vector phase, the presence and location of the fault are determined based on the fault diagnosis algorithm shown in Figure 6. As shown in Figure 11 and Figure 12, the fault diagnosis algorithm was verified and conducted within 3.5 s.

Table 5.
Specification of test motor.

Figure 7.
Manufacture and experimental environment: (a) stator; (b) rotor; (c) terminal box.
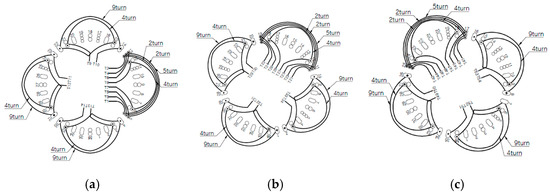
Figure 8.
Winding configuration for validation of inter-turn fault algorithm: (a) phase A; (b) phase B; (c) phase C.

Figure 9.
Experimental environment for inter-turn fault diagnosis: (a) motor and terminal box; (b) fault situation; (c) inverter for fault diagnosis.

Figure 10.
Connections for experiment: (a) Y connection; (b) Δ connection.
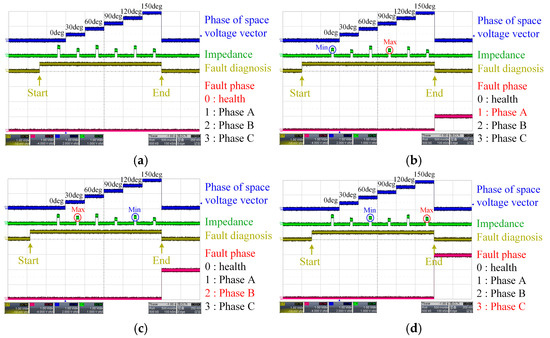
Figure 11.
Experiment results for Y connection: (a) healthy; (b) fault phase A; (c) fault phase B; (d) fault phase C.
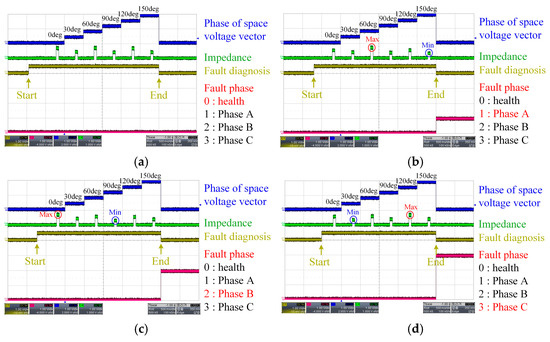
Figure 12.
Experiment results for Δ connection: (a) healthy; (b) fault phase A; (c) fault phase B; (d) fault phase C.
5. Conclusions
In this paper, an inter-turn fault diagnosis algorithm is proposed based on impedance analysis and space voltage vector control for IMD systems. The terminal impedances when an inter-turn fault occurs in phase A are analyzed, revealing specific maximum and minimum impedance patterns with both Y and Δ connections. The space voltage vectors of a three-phase inverter are also analyzed according to the switching states of each phase. A fault diagnosis algorithm is proposed by associating the terminal connections with the phases of the space voltage vector. An experimental setup, including a 12 kW three-phase induction motor from RENAULT TWIZY and a terminal box for winding connections, was implemented to validate the proposed algorithm. The impedances for each space voltage vector were calculated using a DSP (TMS320F28069) based on measured current and voltage and they were displayed on the oscilloscope using the processor’s DAC. Inter-turn faults and various winding connections were implemented through the terminal box to emulate different fault conditions. The proposed diagnosis algorithm was verified through the experimental results for faults in each phase for both Y and Δ connections, and the fault diagnosis was conducted within 3.5 s. This approach provides a practical and reliable solution for fault detection in highly integrated EV drive systems where mechanical access to motor terminals is restricted. Furthermore, the proposed ITF diagnosis does not require prior information about the electrical machine, such as healthy impedance, as it relies on the maximum and minimum impedance values associated with six space voltage vectors. Future research will focus on analyzing the frequency dependence of measured impedance to determine the optimal frequency range for reliable fault detection. To enhance diagnostic robustness, meta-heuristic techniques, such as genetic algorithms for optimization and support vector machines for classification, will also be investigated.
Author Contributions
Conceptualization, J.A. and H.K.; methodology, H.K.; software, J.A.; validation, J.A. and H.K.; formal analysis, H.K.; investigation, J.A.; resources, J.L.; data curation, J.A.; writing—original draft preparation, J.A. and H.K.; writing—review and editing, J.L. and H.K.; visualization, J.A.; supervision, J.L. and H.K.; project administration, H.K.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (RS-2023-00237024, Development and demonstration of medium-sized variable speed high-power motor).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Azab, M. A Review of Recent Trends in High-Efficiency Induction Motor Drives. Vehicles 2025, 7, 15. [Google Scholar] [CrossRef]
- Zhang, B.; Song, Z.; Liu, S.; Huang, R.; Liu, C. Overview of Integrated Electric Motor Drives: Opportunities and Challenges. Energies 2022, 15, 8299. [Google Scholar] [CrossRef]
- Wu, X.; Geng, Y.; Li, M.; Wang, W.; Tu, M. Inter-Turn Short Circuit Diagnosis of Permanent Magnet Synchronous Motor Based on Siamese Convolutional Neural Network Under Small Fault Samples. IEEE Sensors J. 2024, 24, 26982–26993. [Google Scholar] [CrossRef]
- Bahrami-Fard, M.; Chen, T.; Winchell, E.; Fahimi, B. Integrated Induction Motor Drive for Variable Speed Industrial Applications. IEEE Trans. Power Electron. 2025, 40, 7176–7188. [Google Scholar] [CrossRef]
- Gulsuna, O.; Tokgoz, F.; Karakaya, F.; Keysan, O. Design and Analysis of a GaN-Based Megahertz Integrated Motor Drive for a PCB Motor. IEEE Trans. Ind. Electron. 2024, 71, 15435–15444. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Gu, C.; Li, J.; Zhang, H.; Zhao, H. Characterizations of PM Synchronous Motor with an Integrated Common-Mode Voltage Filter. IEEE Trans. Ind. Appl. 2024, 60, 353–366. [Google Scholar]
- Nam, D.W.; Hong, M.K.; Jo, N.R.; Jung, D.H.; Kim, W.H. Design of Coil Patterns for an Axial Flux Permanent Magnet Synchronous Motor with PCB Stator. IEEE Access 2025, 13, 12936–12944. [Google Scholar] [CrossRef]
- Naradhipa, A.M.; Kim, S.; Yang, D.; Choi, S.; Yeo, I.; Lee, Y. Power Density Optimization of 700 kHz GaN-Based Auxiliary Power Module for Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 5610–5621. [Google Scholar] [CrossRef]
- Hwang, K.Y.; Kim, S.I.; Song, B.K. Single Winding Type Determination of Dual Winding Three-Phase Motor Considering Overheat Problem in Integrated Electric Braking System of Autonomous Vehicles. IEEE Trans. Transp. Electrific. 2023, 9, 656–666. [Google Scholar] [CrossRef]
- Sun, X.; Song, C.; Zhang, Y.; Sha, X.; Diao, N. An Open-Circuit Fault Diagnosis Algorithm Based on Signal Normalization Preprocessing for Motor Drive Inverter. IEEE Trans. Instrum. Meas. 2023, 72, 3513712. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives–State of the Art and Future Challenges. IEEE Access 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Gupta, V.; Sultana, M.; Khanna, A. Hybrid optimization-based approach for transmission line parameter identification in the presence of noise. Data Anal. J. 2023, 9, 100182. [Google Scholar]
- Jin, L.; Wang, X.; Mao, Y.; Lu, L.; Wang, Z. Online Attribute Matching Based Few-Sample Data-Driven Diagnosis of Electrical Faults in PMSM Drive. IEEE Trans. Power Electron. 2024, 39, 2620–2631. [Google Scholar] [CrossRef]
- Tokgoz, F.; Gülsuna, Ö.; Karakaya, F.; Cakal, G.; Keysan, O. Mechanical and Thermal Design of an Optimized PCB Motor for an Integrated Motor Drive System with GaNFETs. IEEE Trans. Energy Convers. 2023, 38, 653–661. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.; Huang, Z.; Mu, S. Analysis of Stator Internal Phase-to-Phase Short Circuit in the 12-Phase Synchronous Generator with Rectifier-Load System. IEEE Trans. Energy Convers. 2018, 33, 299–311. [Google Scholar] [CrossRef]
- Yuan, W.; Li, Y.; Xu, L.; Li, T.; Chen, X. A Fast Faulty Phase Selection Method Considering Fault Tolerance for Single Phase to Ground Fault in Distribution Networks. IEEE Trans. Instrum. Meas. 2023, 72, 3533212. [Google Scholar] [CrossRef]
- Yuan, J.; Feng, C.; Ji, Y.; Liu, X.; Dong, X.; Liu, J. Faulty Feeder Detection for Successive Single Phase-to-Ground Faults Based on Line Model Recognition and Correlation Comparison. IEEE Trans. Power Del. 2025, 40, 750–763. [Google Scholar] [CrossRef]
- Gao, C.; Gao, B.; Xu, X.; Si, J.; Hu, Y. Automatic Demagnetization Fault Location of Direct-Drive Permanent Magnet Synchronous Motor Using Knowledge Graph. IEEE Trans. Instrum. Meas. 2024, 73, 3502312. [Google Scholar] [CrossRef]
- Bonet-Jara, J.; Pons-Llinares, J.; Gyftakis, K.N. Comprehensive Analysis of Principal Slot Harmonics as Reliable Indicators for Early Detection of Interturn Faults in Induction Motors of Deep-Well Submersible Pumps. IEEE Trans. Ind. Electron. 2023, 70, 11692–11702. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.H.; Lee, W.K.; Lee, J.S. Rapid Control Prototyping and Analysis of a Fault Diagnosis and Amplifying Algorithm for Broken Rotor Bar Induction Motor Drives. IEEE Access 2025, 13, 19064–19074. [Google Scholar] [CrossRef]
- Kang, Y.; Yao, L. Fault Diagnosis for Permanent Magnet Synchronous Motor with Demagnetization Fault and Sensor Fault. IEEE Trans. Instrum. Meas. 2024, 73, 3533311. [Google Scholar] [CrossRef]
- Ma, J.; Bai, X.; Ma, F.; Zhuo, S.; Sun, B.; Li, C. Convolutional Neural Network Design Based on Weak Magnetic Signals and Its Application in Aircraft Bearing Fault Diagnosis. IEEE Sens. J. 2024, 24, 36031–36043. [Google Scholar] [CrossRef]
- Niu, G.; Dong, X.; Chen, Y. Motor Fault Diagnostics Based on Current Signatures: A Review. IEEE Trans. Instrum. Meas. 2023, 72, 3520919. [Google Scholar] [CrossRef]
- Lang, W.; Hu, Y.; Gong, C.; Zhang, X.; Xu, H.; Deng, J. Artificial Intelligence-Based Technique for Fault Detection and Diagnosis of EV Motors: A Review. IEEE Trans. Transp. Electrific. 2022, 8, 384–406. [Google Scholar] [CrossRef]
- Chen, C.S.; Lin, C.J.; Yang, F.J.; Lin, F.C. Model Design of Inter-Turn Short Circuits in Internal Permanent Magnet Synchronous Motors and Application of Wavelet Transform for Fault Diagnosis. Appl. Sci. 2024, 14, 9570. [Google Scholar] [CrossRef]
- Qin, Y.; Li, G.J.; Jia, C.; McKeever, P. Investigation of Inter-Turn Short-Circuit Fault of PM Machines Using PWM Voltage-Based Modeling. IEEE Trans. Transp. Electrific. 2024, 10, 1324–1334. [Google Scholar] [CrossRef]
- Cui, R.; Fan, Y.; Li, C. On-Line Inter-Turn Short-Circuit Fault Diagnosis and Torque Ripple Minimization Control Strategy Based on OW Five-Phase BFTHE-IPM. IEEE Trans. Energy Convers. 2018, 33, 2200–2209. [Google Scholar] [CrossRef]
- Chen, Q.; Han, X.; Liu, G.; Zhao, W.; Shi, H. Inter-Turn Fault Diagnosis and Control for Five-Phase PMSMs by Disturbance Observer. IEEE Trans. Ind. Electron. 2024, 71, 13901–13909. [Google Scholar] [CrossRef]
- Dongare, U.V.; Umre, B.S.; Ballal, M.S.; Dongare, V.P. Online Inter-Turn Fault Detection in Wound Rotor Induction Motors Based on VI Loci Pattern. IEEE Trans. Ind. Appl. 2024, 60, 411–425. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Ghafarokhi, P.S.; Kudelina, K. Transient Modeling and Recovery of Non-Stationary Fault Signature for Condition Monitoring of Induction Motors. Appl. Sci. 2021, 11, 2806. [Google Scholar] [CrossRef]
- Zhang, J.; Zhan, W.; Ehsani, M. Fault-Tolerant Control of PMSM with Inter-Turn Short-Circuit Fault. IEEE Trans. Energy Convers. 2019, 34, 2267–2275. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. The Cluster Computation-Based Hybrid FEM-Analytical Model of Induction Motor for Fault Diagnostics. Appl. Sci. 2020, 10, 7572. [Google Scholar] [CrossRef]
- Gu, B.-G. Offline Interturn Fault Diagnosis Method for Induction Motors by Impedance Analysis. IEEE Trans. Ind. Electron. 2018, 65, 5913–5920. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).