A Study on the Consistency and Efficiency of Student Performance Evaluation Methods: A Mathematical Framework and Comparative Simulation Results
Abstract
1. Introduction
2. Materials and Method
2.1. Summative Evaluation
2.1.1. Formalization of the Summative Assessment Protocol
2.1.2. Simulation Procedure for the Summative Scheme
2.2. The Rubric
2.2.1. Mathematical Setup for the Rubric
2.2.2. Simulation Procedure for the Rubric Protocol
2.3. The Systematic Task-Based Assessment Method (STBAM)
2.3.1. Formalization of ST, the Direct Modulus of the Systematic Task-Based Assessment Method
Simulation Procedures for the ST Device
2.3.2. The ST-FIS, a Fuzzy Inference System-Based Modulus for the STBAM Scheme
Key Elements of the Mathematical Representation of an ST-Fuzzy Inference System (ST-FIS)
- 1.
- Fuzzy sets
- 2.
- Input variables
- 3.
- Output variables
- 4.
- Rule base
2.3.3. Fundamental Processes of an ST-Fuzzy Inference System (ST-FIS)
Fuzzification
Rule Evaluation Procedure
Aggregation Process
Defuzzification Process
2.3.4. Simulation Procedure for the ST-FIS Arrangement
2.4. A Note on the Concept of an Objective Grades
2.5. Formalization of the Consistency and Efficiency Indicators
3. Results
3.1. Variation Ranges for the , , and Indicators
and -Based Method Performance Comparison Criteria
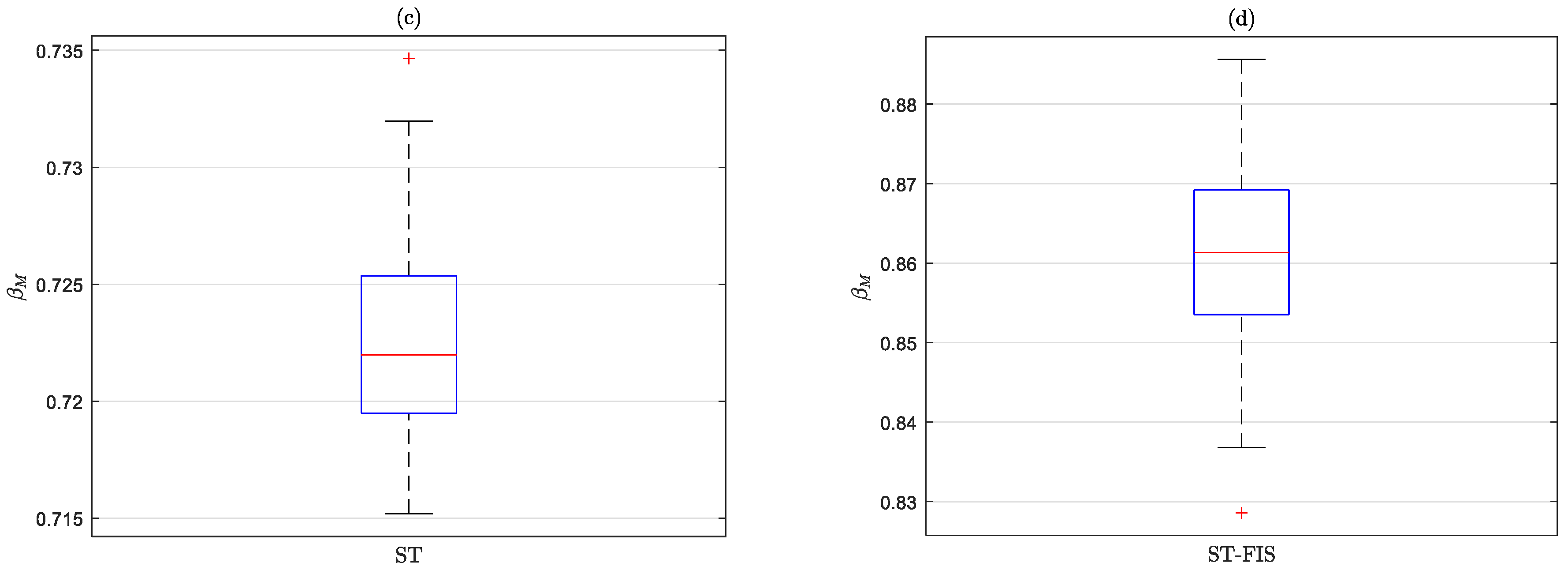
3.2. Calculations Related to , and Indicators Based on Simulated Grade Data and Pondered–Normalized Complexity Pointer Values
3.3. Ordering Relationships for the , and Indicators
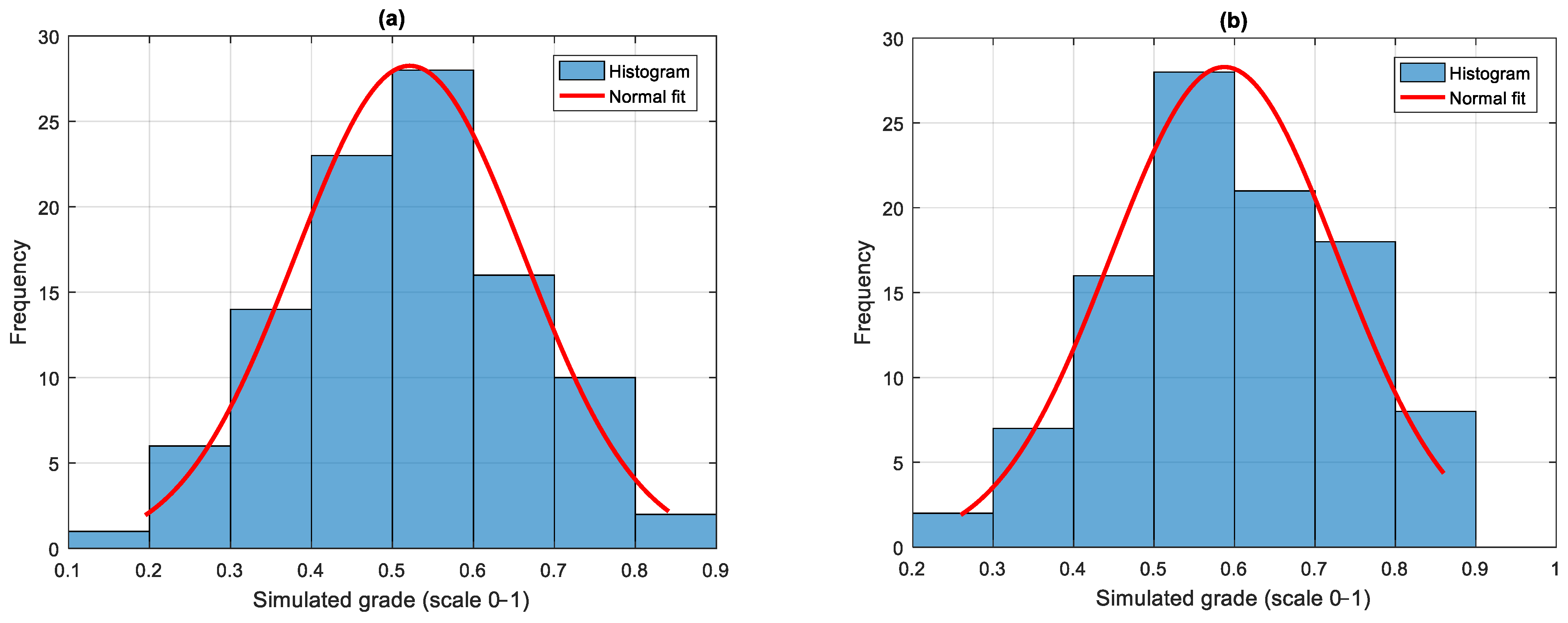
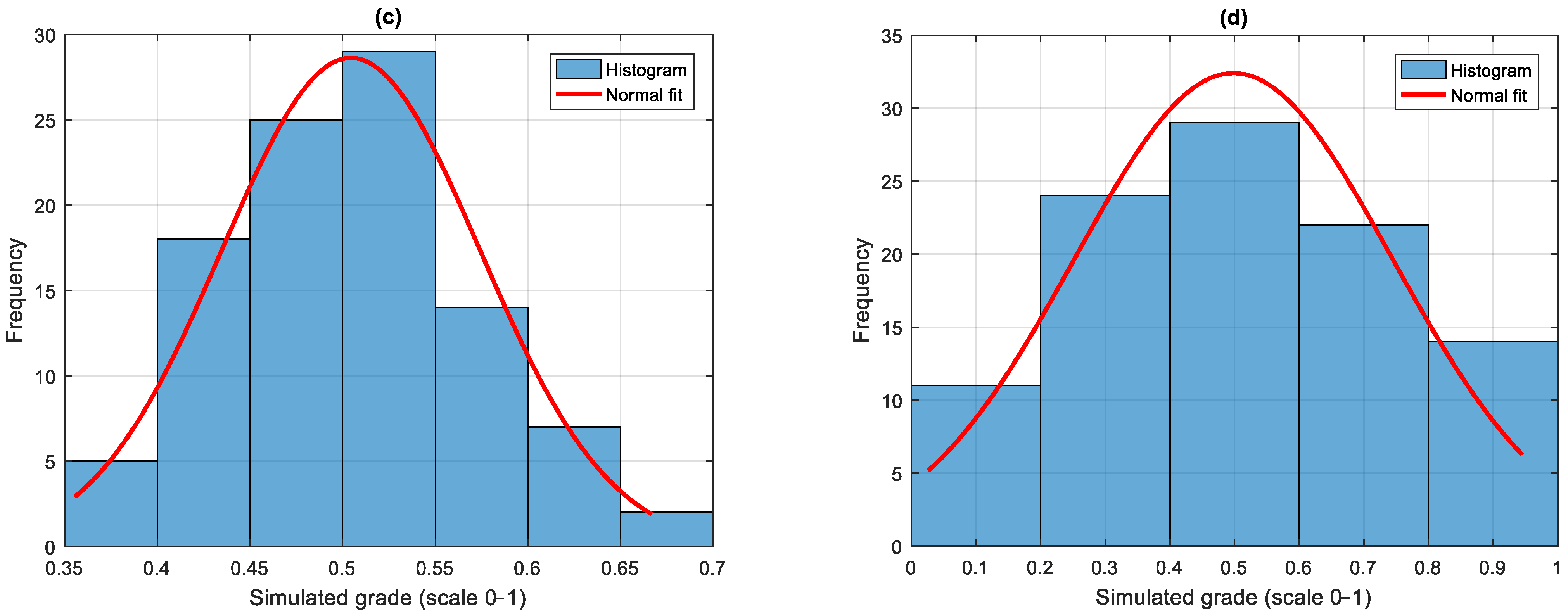
3.4. Assessing the Distribution and Spread of Simulated Grades
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Summative Assessment Method
Appendix A.1. Defining the Sections That Make Up the Activity A to Be Evaluated
Appendix A.2. Defining the Weights of Each of the Learning Section
Appendix A.3. Specifying the Scores Assigned to the -th Student in the Different Sections
Appendix A.4. Assigning the Matrix of Objective Scores for the -th Student in Different Sections
Appendix A.5. Calculation Example of the Rating Estimation Error Relative to
Appendix A.6. Obtaining as Determined by the Cumulative Estimation Error
Appendix A.7. Obtaining the Complexity Consistency and Eficience Indexes Values
| Equation | Component | Elements | Operations |
|---|---|---|---|
| (A2) | 5 | 5 | |
| (A3) | 5 | 5 | |
| (A7) | 5 | 9 |
Appendix B. The Rubric Method
Appendix B.1. Establishing , and the and Matrices
| Confusing information and lacking coherence. | Information barely improved, still lacking coherence. | Information understandable, but several inconsistencies. | Information is clear and coherent with some exceptions. | Information is clear and coherent at all times. | |
| The analysis is very superficial or non-existent. | The analysis has scarcely any depth and is still superficial. | The analysis is superficial and shows a basic understanding of the topic. | The analysis is adequate. It shows a good understanding of the topic. | The analysis is thorough. It demonstrates a complete understanding. | |
| Does not use reliable sources or present evidence. | Mentions sources but lacks evidence. | Uses some sources, not all of them reliable or well integrated. | Uses reliable sources, not always integrated effectively. | Uses trusted sources and integrates them effectively. | |
| Lacks originality and creativity. | Requires more originality; shows poor creativeness. | Shows originality and creativity. | Displays a good level of originality and creativity. | Demonstrates a high level of originality and creativity. | |
| Poor presentation and inconsistent inappropriate formatting. | Presentation acceptable but still inappropriate formatting. | Acceptable presentation but with several errors in the format. | Good presentation, with minor errors in formatting. | Presentation is professional and formatting is consistent and adequate. |
Appendix B.2. Defining the Matrix
Appendix B.3. Defining the Matrix and the Performance Vector
Appendix B.4. Calculate the Grade
Appendix B.5. The Rating Estimation Error in the Rubric’s Evaluation of Student
Appendix B.6. Estimation of the Mean Absolute Deviation
Appendix B.7. Obtaining the Complexity Consistency and Eficience Indexes Values
| Equation | Component | Elements | Operations |
|---|---|---|---|
| (A13) | 5 | ||
| (A15) | 5 | ||
| (A17) | 5 | 25 | |
| (25) and (A19) | 25 | 25 | |
| (A20) | 5 | 9 | |
| (A21) | 2 | 1 |
Appendix C. The ST Method
Appendix C.1. Agreeing to Equation (45), We Arrange the Matrix Hosting a Number of Directions
- (Cognitive Attributes)—Knowledge required for the task
- (Practical Application Attributes)—How knowledge is applied
- : (Performance and Behavioral Attributes)—Cognitive engagementDirection : Problem-Solving Application (task: apply identified concepts to solve a given problem)
- (Cognitive Attributes)
- (Practical Application Attributes)
- (Performance and Behavioral Attributes)Direction Research and Evidence Integration (task: find and integrate external sources into analysis)
- (Cognitive Attributes)
- (Practical Application Attributes)
- (Performance and Behavioral Attributes)Direction : Practical Implementation or Experimentation (task: conduct an experiment or case study, record observations, and analyze results)
- (Cognitive Attributes)
- (Practical Application Attributes)
- (Performance and Behavioral Attributes)Direction : Reflection and Synthesis (task: reflect on learning experience and articulate personal insights)
- (Cognitive Attributes)
- (Practical Application Attributes)
- (Performance and Behavioral Attributes)
Appendix C.2. Performance Marks or
Appendix C.3. Total Number of Indicators for
Appendix C.4. Numbers of Indicators Showing a Binary Pointer
| ) | ) | ) | ) |
|---|---|---|---|
| 🗴 | ✓ | ✓ | |
| 🗴 | ✓ | 🗴 | |
| ✓ | ✓ | ||
| ✓ | |||
| ✓ | |||
| 🗴 | 🗴 | ✓ | |
| ✓ | ✓ | ||
| ✓ | |||
| 🗴 | |||
| ✓ | |||
| 🗴 | ✓ | ✓ | |
| 🗴 | ✓ | ||
| 🗴 | 🗴 | ||
| 🗴 | |||
| 🗴 | ✓ | ✓ | |
| ✓ | 🗴 | ✓ | |
| 🗴 | 🗴 | ||
| ✓ | |||
| ✓ | ✓ | 🗴 | |
| ✓ | ✓ | 🗴 | |
| ✓ | 🗴 | ||
| ✓ | |||
| 🗴 | |||
| Totals |
Appendix C.5. Numbers of Indicators in , , and
Appendix C.6. Total Number of Indicators Composing the ST Scheme
Appendix C.7. Vector of Inputs
Appendix C.8. Assigning the Grade
Appendix C.9. Estimating the Absolute Deviation
Appendix C.10. Estimating the Mean Absolute Deviation
Appendix C.11. Obtaining the Complexity Consistency and Eficience Indexes Values
| Equation | Operations (M) | ||
|---|---|---|---|
| (A38) | 5 | ||
| (A41) | 10 | ||
| 8 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| (A42) | | 26 | 23 |
| (A43) | 15 | 12 | |
| (A44) | 15 | 12 | |
| (A45) | 1 | ||
| (A46) | 3 | ||
| (A47) | 2 | 1 |
Appendix D. The ST-FIS Method
Appendix D.1. Acquiring Input Variables
| MF | Equation | |||||||
|---|---|---|---|---|---|---|---|---|
| L | 0.8 | ----- | ----- | ----- | ----- | (A89) | ||
| ----- | ----- | ----- | ----- | (A90) | ||||
| 8.8 | ----- | ----- | ----- | (A91) | ||||
| P | ----- | ----- | ----- | ----- | (A92) | |||
| ----- | ----- | ----- | ----- | 5.5 | (A93) | |||
| 7.04 | ----- | ----- | ----- | (A94) | ||||
| A | 0 | ----- | (A95) | |||||
| 18 | ----- | ----- | (A96) | |||||
| D | ----- | (A99) | ||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
| ----- | (A99) | |||||||
Appendix D.2. Output Variable
Appendix D.3. Rule Base
Appendix D.4. Fuzzification
Appendix D.5. Rule Evaluation
Appendix D.6. Aggregation Process
Appendix D.7. Defuzzification Process
Appendix D.8. Assigning an Objetive Grade
Appendix D.9. Rating Error Relative to
Appendix D.10. Mean Absolute Deviation
Appendix D.11. Obtaining the Complexity Consistency and Eficience Indexes Values
| Equation | Component | Elements | Operations |
|---|---|---|---|
| (A38) | 5 | ||
| (A41) | 10 | ||
| 8 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| (A42) | | 26 | 23 |
| (A43) | 15 | 12 | |
| (A44) | 15 | 12 | |
| (A45) | 1 | ||
| (A46) | 3 | ||
| Fuzzification | |||
| (A107) | . | 1 | |
| (A108) | . | 1 | |
| (A109) | . | 1 | |
| Rule evaluation | |||
| (A103)–(A120) | 1 | ||
| Aggregation process | |||
| (A122) | 1 | ||
| Defuzzification process | |||
| (A123) | 2 |
Appendix E. Glossary
| Term and Symbol | Definition |
|---|---|
| Number of components, elements, and operations in the assessment method’s structure. | |
| Normalization | Rescaling of values to the range [0.1, 1] to ensure comparability across methods. |
| Complexity Indicator. | |
| Mean Absolute Deviation: average deviation between simulated and objective scores. | |
| Consistency indicator: measures reliability by combining and . | |
| Efficiency indicator: evaluates the trade-off between consistency and complexity. | |
| Indicator Function that returns 1 if a condition is true and 0 otherwise. | |
| FIS | Fuzzy Inference System: a analyzing method that handles gradual or imprecise information. |
| Summative | Traditional assessment method based on assigning weights to learning sections and calculating weighted averages of scores. It does not model uncertainty or competence dimensions. |
| Rubric | Evaluation tool with structured criteria and performance levels for qualitative scoring. |
| STBAM or ST | Systematic Task-Based Assessment Method that evaluates students based on specific tasks and indicators grouped into Learning, Procedure, and Attitude categories and emphasizes observable competencies and instructional alignment. |
| ST-FIS | Systematic Task-Based Assessment Method with an integrated Fuzzy Inference System aimed to model complex performance and reduce subjectivity. |
References
- CSAI. Valid and Reliable Assessments. Update, CSAI, The Center on Standards and Assessment Implementation. 2018. Available online: https://files.eric.ed.gov/fulltext/ED588476.pdf (accessed on 24 March 2025).
- Palmer, N. Tools to Improve Efficiency and Consistency in Assessment Practices Whilst Delivering Meaningful Feedback. In Proceedings of the ICERI2022 Proceedings, Seville, Spain, 7–9 November 2022; pp. 1069–1078. [Google Scholar]
- Scott, S.; Webber, C.F.; Lupart, J.L.; Aitken, N.; Scott, D.E. Fair and equitable assessment practices for all students. Assess. Educ. Princ. Policy Pract. 2013, 21, 52–70. [Google Scholar] [CrossRef]
- Hull, K.; Lawford, H.; Hood, S.; Oliveira, V.; Murray, M.; Trempe, M.; Jensen, M. Student anxiety and evaluation. Coll. Essays Learn. Teach. 2019, 12, 23–35. [Google Scholar] [CrossRef]
- Guevara Hidalgo, E. Impact of evaluation method shifts on student performance: An analysis of irregular improvement in passing percentages during COVID-19 at an Ecuadorian institution. Int. J. Educ. Integr. 2025, 21, 4. [Google Scholar] [CrossRef]
- Glaser, R.; Chudowsky, N.; Pellegrino, J.W. (Eds.) Knowing What Students Know: The Science and Design of Educational Assessment; National Academies Press: Washington, DC, USA, 2001. [Google Scholar]
- Tutunaru, T. Improving Assessment and Feedback in the Learning Process: Directions and Best Practices. Res. Educ. 2023, 8, 38–60. [Google Scholar] [CrossRef]
- Bhat, B.A.; Bhat, G.J. Formative and summative evaluation techniques for improvement of learning process. Eur. J. Bus. Soc. Sci. 2019, 7, 776–785. [Google Scholar]
- Guskey, T.R. Addressing inconsistencies in grading practices. Phi Delta Kappan 2024, 105, 52–57. [Google Scholar] [CrossRef]
- Cambridge International Examinations. Developing Your School with Cambridge: A Guide for School Leaders; Director Education: Hong Kong, China, 2016. [Google Scholar]
- Ahea, M.M.A.B.; Ahea, M.R.K.; Rahman, I. The Value and Effectiveness of Feedback in Improving Students’ Learning and Professionalizing Teaching in Higher Education. J. Educ. Pract. 2016, 7, 38–41. [Google Scholar]
- Tinkelman, D.; Venuti, E.; Schain, L. Disparate methods of combining test and assignment scores into course grades. Glob. Perspect. Account. Educ. 2013, 10, 61. [Google Scholar]
- Malouff, J.M.; Thorsteinsson, E.B. Bias in grading: A meta-analysis of experimental research findings. Aust. J. Educ. 2016, 60, 245–256. [Google Scholar] [CrossRef]
- Newman, D.; Lazarev, V. How Teacher Evaluation is affected by Class Characteristics: Are Observations Biased. Empower. Educ. Evid.-Based Decis. 2015, 1–11. [Google Scholar]
- Anderson, L.W. A Critique of Grading: Policies, Practices, and Technical Matters. Educ. Policy Anal. Arch. 2018, 26, 49. [Google Scholar] [CrossRef]
- Von Hippel, P.T.; Hamrock, C. Do test score gaps grow before, during, or between the school years? Measurement artifacts and what we can know in spite of them. Sociol. Sci. 2019, 6, 43–80. [Google Scholar] [CrossRef] [PubMed]
- Lauck, L.V. Grade Distribution and Perceptions of School Culture and Climate In a New Secondary School. Ph.D. Thesis, Rockhurst University, Kansas City, MO, USA, 2019. [Google Scholar]
- Royal, K.D.; Guskey, T.R. The Perils of Prescribed Grade Distributions: What Every Medical Educator Should Know. Online Submiss. 2014, 2, 240–241. [Google Scholar]
- Harris, D. Let’s Talk About Grading, Maybe: Using Transparency About the Grading Process To Aid in Student Learning. Seattle UL Rev. 2021, 45, 805. [Google Scholar]
- Dubois, P.; Lhotte, R. Consistency and Reproducibility of Grades in Higher Education: A Case Study in Deep Learning. arXiv 2023, arXiv:2305.07492. Available online: https://arxiv.org/abs/2305.07492 (accessed on 24 March 2025).
- Tyler, J.H.; Taylor, E.S.; Kane, T.J.; Wooten, A.L. Using student performance data to identify effective classroom practices. Am. Econ. Rev. 2010, 100, 256–260. [Google Scholar] [CrossRef][Green Version]
- Muñoz, M.A.; Guskey, T.R. Standards-based grading and reporting will improve education. Phi Delta Kappan 2015, 96, 64–68. [Google Scholar] [CrossRef]
- Lamarino, D.L. The benefits of standards-based grading: A critical evaluation of modern grading practices. Curr. Issues Educ. 2014, 17, 2. [Google Scholar]
- Leal-Ramírez, C.; Echavarría-Heras, H.A. An Integrated Instruction and a Dynamic Fuzzy Inference System for Evaluating the Acquirement of Skills through Learning Activities by Higher Middle Education Students in Mexico. Mathematics 2024, 12, 1015. [Google Scholar] [CrossRef]
- Gronlund, N.E. Assessment of Student Achievement, 8th ed.; Allyn & Bacon Publishing, Longwood Division: Boston, MA, USA, 1998; pp. 1–300. [Google Scholar]
- Yambi, T.D.A.C.; Yambi, C. Assessment and Evaluation in Education; University Federal do Rio de Janeiro: Rio de Janeiro, Brazil, 2018. [Google Scholar]
- Ghaicha, A. Theoretical Framework for Educational Assessment: A Synoptic Review. J. Educ. Pract. 2016, 7, 212–231. [Google Scholar]
- Struyven, K.; Dochy, F.; Janssens, S. Students’ perceptions about evaluation and assessment in higher education: A review. Assess. Eval. High. Educ. 2005, 30, 325–341. [Google Scholar] [CrossRef]
- Royal, K.D.; Guskey, T.R. Does mathematical precision ensure valid grades? What every veterinary medical educator should know. J. Vet. Med. Educ. 2015, 42, 242–244. [Google Scholar] [CrossRef] [PubMed]
- Sikora, A.S. Mathematical Theory of Student Assessment Through Grading. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=085fd7628dc0d7e7c0e22dc458c81d4e50c44dee (accessed on 24 March 2025).
- Benton, T.; Elliott, G. The reliability of setting grade boundaries using comparative judgement. Res. Pap. Educ. 2016, 31, 352–376. [Google Scholar] [CrossRef]
- Hanania, M.I. Mathematical Methods Applicable to the Standardization of Examinations. Master’s Thesis, American University of Beirut, Beirut, Lebanon, 1947. [Google Scholar]
- Fitzpatrick, J.L.; Sanders, J.R.; Worthen, B.R.; Wingate, L.A. Program Evaluation: Alternative Approaches and Practical Guidelines; Pearson: Boston, MA, USA, 2012. [Google Scholar]
- Shepard, L.A. The role of assessment in a learning culture. Educ. Res. 2000, 29, 4–14. [Google Scholar] [CrossRef]
- Stufflebeam, D.L.; Coryn, C.L. Evaluation Theory, Models, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Taras, M. Assessing Assessment Theories. Online Educ. Res. J. 2012, 3, 1–13. [Google Scholar]
- Astin, A.W. Assessment for Excellence: The Philosophy and Practice of Assessment and Evaluation in Higher Education; Rowman & Littlefield Publishers: Lanham, MD, USA, 2012. [Google Scholar]
- Chen, H.T. Theory-Driven Evaluation: Conceptual Framework, Application and Advancement; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2012; pp. 17–40. [Google Scholar]
- Gipps, C. Beyond Testing (Classic Edition): Towards a Theory of Educational Assessment; Routledge: London, UK, 2011. [Google Scholar]
- Wiliam, D. Integrating formative and summative functions of assessment. In Working Group; King’s College London: London, UK, 2000; Volume 10. [Google Scholar]
- Hurskaya, V.; Mykhaylenko, S.; Kartashova, Z.; Kushevska, N.; Zaverukha, Y. Assessment and evaluation methods for 21st century education: Measuring what matters. Futur. Educ. 2024, 4, 4–17. [Google Scholar] [CrossRef]
- Galamison, T.J. Benchmarking: A Study of the Perceptions Surrounding Accountability, Instructional Leadership, School Culture, Formative Assessments and Student Success. Ph.D. Thesis, University of Houston, Houston, TX, USA, 2014. [Google Scholar]
- Goldberger, S.; Keough, R.; Almeida, C. Benchmarks for Success in High School Education. Putting Data to Work in School to Career Education Reform; LAB at Brown University: Boston, MA, USA, 2000. [Google Scholar]
- Dunn, D.S.; McCarthy, M.A.; Baker, S.C.; Halonen, J.S. Using Quality Benchmarks for Assessing and Developing Undergraduate Programs; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Knight, P.T. Summative Assessment in Higher Education: Practices in Disarray. Stud. High. Educ. 2002, 27, 275–286. [Google Scholar] [CrossRef]
- Yorke, M. Summative Assessment: Dealing with the ‘Measurement Fallacy’. Stud. High. Educ. 2011, 36, 251–273. [Google Scholar] [CrossRef]
- Harlen, W.; Crick, R.D.; Broadfoot, P.; Daugherty, R.; Gardner, J.; James, M.; Stobart, G. A Systematic Review of the Impact of Summative Assessment and Tests on Students’ Motivation for Learning; University of Bristol, Evidence-Based Practice Unit: Bristol, UK, 2002. [Google Scholar]
- Ishaq, K.; Rana, A.M.K.; Zin, N.A.M. Exploring Summative Assessment and Effects: Primary to Higher Education. Bull. Educ. Res. 2020, 42, 23–50. [Google Scholar]
- Bijsterbosch, H. Professional Development of Geography Teachers with Regard to Summative Assessment Practices. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2018. [Google Scholar]
- Ekwue, U.N. A Hybrid Exploration of the Impact of Summative Assessment on A-level Students’ Motivation and Depth of Learning and the Extent to Which This Is a Reflection of the Self. Ph.D. Thesis, King’s College London, London, UK, 2015. [Google Scholar]
- Stevens, D.D. Introduction to Rubrics: An Assessment Tool to Save Grading Time, Convey Effective Feedback, and Promote Student Learning; Routledge: New York, NY, USA, 2023. [Google Scholar]
- Steinberg, M.P.; Kraft, M.A. The sensitivity of teacher performance ratings to the design of teacher evaluation systems. Educ. Res. 2017, 46, 378–396. [Google Scholar] [CrossRef]
- Thompson, M.K.; Clemmensen, L.K.H.; Ahn, B.U. The effect of rubric rating scale on the evaluation of engineering design projects. Int. J. Eng. Educ. 2013, 29, 1490–1502. [Google Scholar]
- Humphry, S.M.; Heldsinger, S.A. Common structural design features of rubrics may represent a threat to validity. Educ. Res. 2014, 43, 253–263. [Google Scholar] [CrossRef]
- Sadler, D.R. Indeterminacy in the use of preset criteria for assessment and grading. Assess. Eval. High. Educ. 2009, 34, 159–179. [Google Scholar] [CrossRef]
- Brookhart, S.M.; Chen, F. The quality and effectiveness of descriptive rubrics. Educ. Rev. 2015, 67, 343–368. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mousse, M.A.; Almufti, S.M.; García, D.S.; Jebbor, I.; Aljarbouh, A.; Tsarev, R. Application of fuzzy logic for evaluating student learning outcomes in E-learning. In Proceedings of the Computational Methods in Systems and Software; Springer: Cham, Switzerland, 2023; pp. 175–183. [Google Scholar]
- Ballester, L.; Colom, A.J. Lógica difusa: Una nueva epistemología para las Ciencias de la Educación. Rev. Educ. 2006, 340, 995–1008. [Google Scholar]
- Sripan, R.; Suksawat, B. Propose of fuzzy logic-based students’ learning assessment. In Proceedings of the ICCAS 2010, Gyeonggi-do, Republic of Korea, 27–30 October 2010; pp. 414–417. [Google Scholar]
- Hegazi, M.O.; Almaslukh, B.; Siddig, K. A fuzzy model for reasoning and predicting student’s academic performance. Appl. Sci. 2023, 13, 5140. [Google Scholar] [CrossRef]
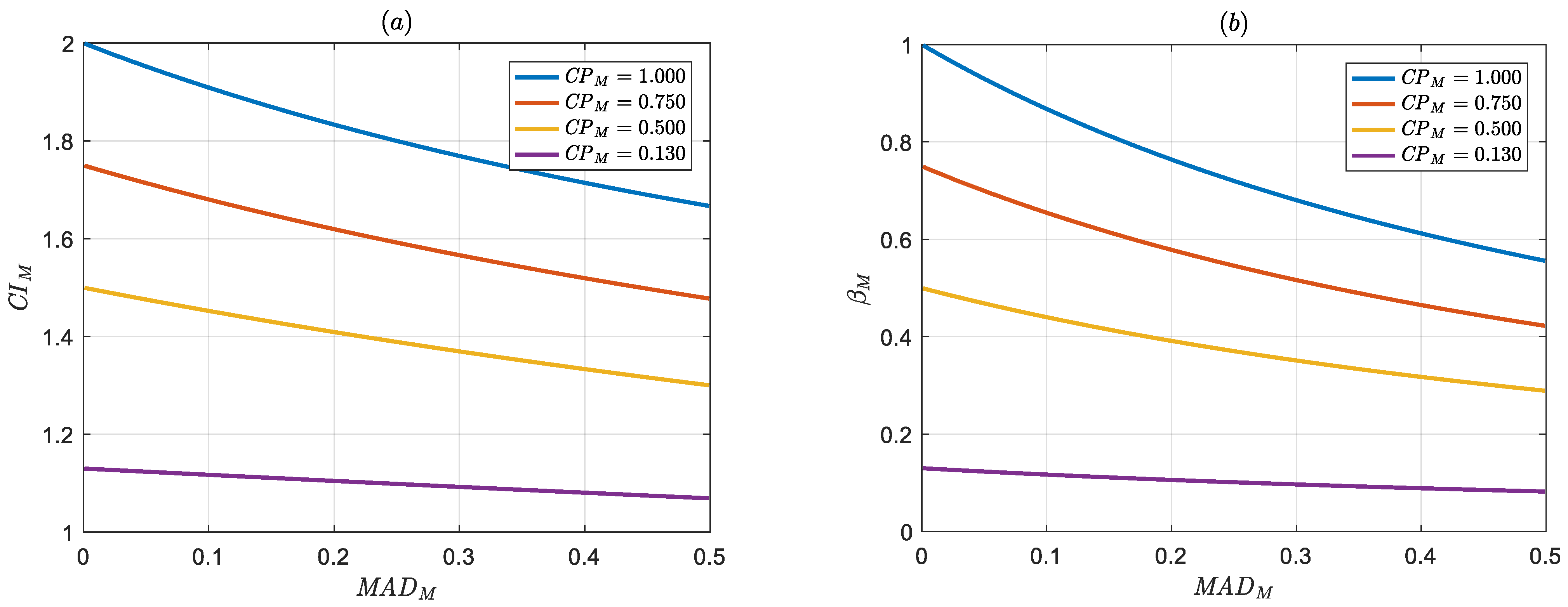


| Method | |||
|---|---|---|---|
| Summative | 3 | 15 | 19 |
| Rubric | 6 | 47 | 60 |
| ST | 8 | 112 | 48 |
| ST-FIS | 13 | 110 | 53 |
| (min) | (min) | (min) |
| 3.00 | 15.00 | 19.00 |
| (Max) | (Max) | (max) |
| 13 | 112 | 60 |
| Method | |||
|---|---|---|---|
| Summative | 0.23 | 0.13 | 0.31 |
| Rubric | 0.46 | 0.41 | 1.00 |
| ST | 0.61 | 1.00 | 0.80 |
| ST-FIS | 1.00 | 0.98 | 0.88 |
| 0.4 | 0.3 | 0.3 | 0.13 | 1.0 |
| 0.13 | |||
| 1.00 | 2.0 |
| Summative | 0.11 | 0.23 | 1.20 | 0.20 |
| Rubric | 0.13 | 0.61 | 1.54 | 0.52 |
| ST | 0.07 | 0.79 | 1.73 | 0.71 |
| ST-FIS | 0.06 | 0.96 | 1.91 | 0.88 |
| Summative | 0.00086 | 0.00018 | 0.00018 |
| Rubric | 0.00096 | 0.00050 | 0.00060 |
| ST | 0.00051 | 0.00036 | 0.00050 |
| ST-FIS | 0.0010 | 0.00089 | 0.0012 |
| Method | Mean | Standard Deviation | Chi-Squared Statistic | Degrees of Freedom | p-Value |
|---|---|---|---|---|---|
| Summative | 0.5214 | 0.1412 | 1.0663 | 2 | 0.5868 |
| Rubric | 0.5874 | 0.1410 | 3.1181 | 3 | 0.3738 |
| ST | 0.5044 | 0.0697 | 1.3905 | 3 | 0.7078 |
| ST-FIS | 0.4982 | 0.2463 | 3.5090 | 2 | 0.1730 |
| Feature | Summative | Rubric | STBAM |
|---|---|---|---|
| Underlying logic | Weighted arithmetic | Weighted criteria + qualitative levels | Competency assestment structure with binary indicators |
| Evaluation units | Learning sections (content areas) | Evaluation criteria | Instructions or “directions” within a task |
| Evaluation of attributes | Implicit | Explicit, but mainly qualitative | Explicit: Learning (L), Procedure (P), Attitude (A) |
| Scoring scale | Continuous, percentage | Discrete, ordinal scale (e.g., 1–5 or 1–4) | Ratio of ✓ marks over total indicators |
| Weighting mechanism | Predefined weights | Predefined weights per criterion | Implicit via the number of indicators per attribute |
| Subjectivity | High | Moderate (due to descriptive guidance) | Reduced: teacher marks presence/absence of observable attributes (✓ or ✗ per observable indicator) |
| Final grade computation | Scalar product of scores and weights | Weighted sum of performance levels | Sum of success indicators divided by total number of indicators |
| Alignment to competencies | Limited | Partial (depends on design) | High (mapped directly to competency-building indicators) |
| Empirical validation feasibility | Low | Moderate | High (traceable indicator-level evaluation) |
| Holistic assessment | No | Partially | Yes (includes knowledge, skills, and attitude dimensions) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leal-Ramírez, C.; Echavarría-Heras, H.A.; Villa-Diharce, E.; Haro-Avalos, H. A Study on the Consistency and Efficiency of Student Performance Evaluation Methods: A Mathematical Framework and Comparative Simulation Results. Appl. Sci. 2025, 15, 6014. https://doi.org/10.3390/app15116014
Leal-Ramírez C, Echavarría-Heras HA, Villa-Diharce E, Haro-Avalos H. A Study on the Consistency and Efficiency of Student Performance Evaluation Methods: A Mathematical Framework and Comparative Simulation Results. Applied Sciences. 2025; 15(11):6014. https://doi.org/10.3390/app15116014
Chicago/Turabian StyleLeal-Ramírez, Cecilia, Héctor Alonso Echavarría-Heras, Enrique Villa-Diharce, and Horacio Haro-Avalos. 2025. "A Study on the Consistency and Efficiency of Student Performance Evaluation Methods: A Mathematical Framework and Comparative Simulation Results" Applied Sciences 15, no. 11: 6014. https://doi.org/10.3390/app15116014
APA StyleLeal-Ramírez, C., Echavarría-Heras, H. A., Villa-Diharce, E., & Haro-Avalos, H. (2025). A Study on the Consistency and Efficiency of Student Performance Evaluation Methods: A Mathematical Framework and Comparative Simulation Results. Applied Sciences, 15(11), 6014. https://doi.org/10.3390/app15116014







