Predicting Dilution in Underground Mines with Stacking Artificial Intelligence Models and Genetic Algorithms
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Regression Models and Genetic Algorithm
2.1.1. Neural Networks: Artificial Neural Network and Extreme Learning Machine
2.1.2. Support Vector Machine
2.1.3. Tree Models: Decision Tree, Random Forest, and Extreme Gradient Boosting
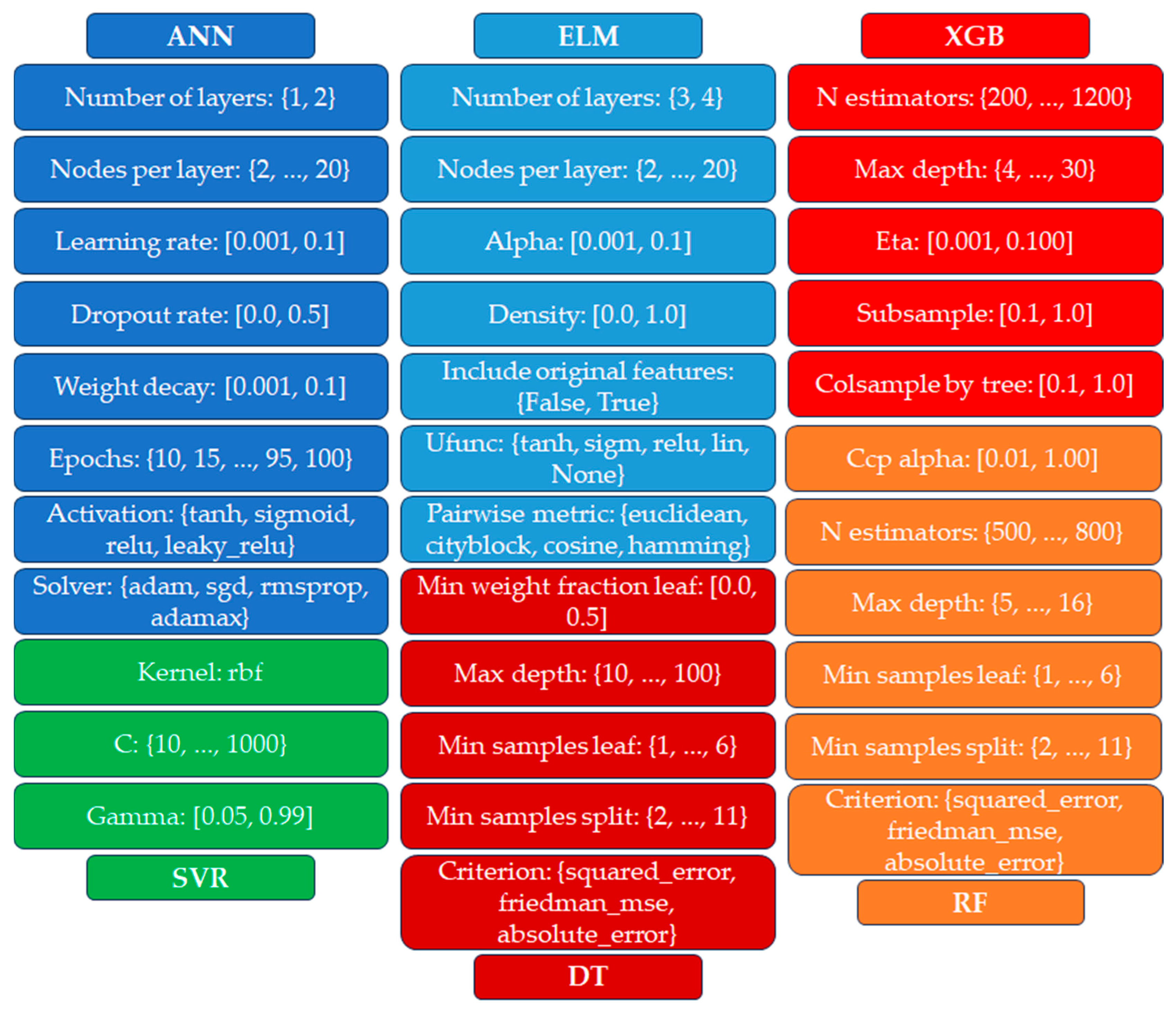
2.1.4. Model Hyperparameters
2.1.5. Stacking
2.1.6. Metrics
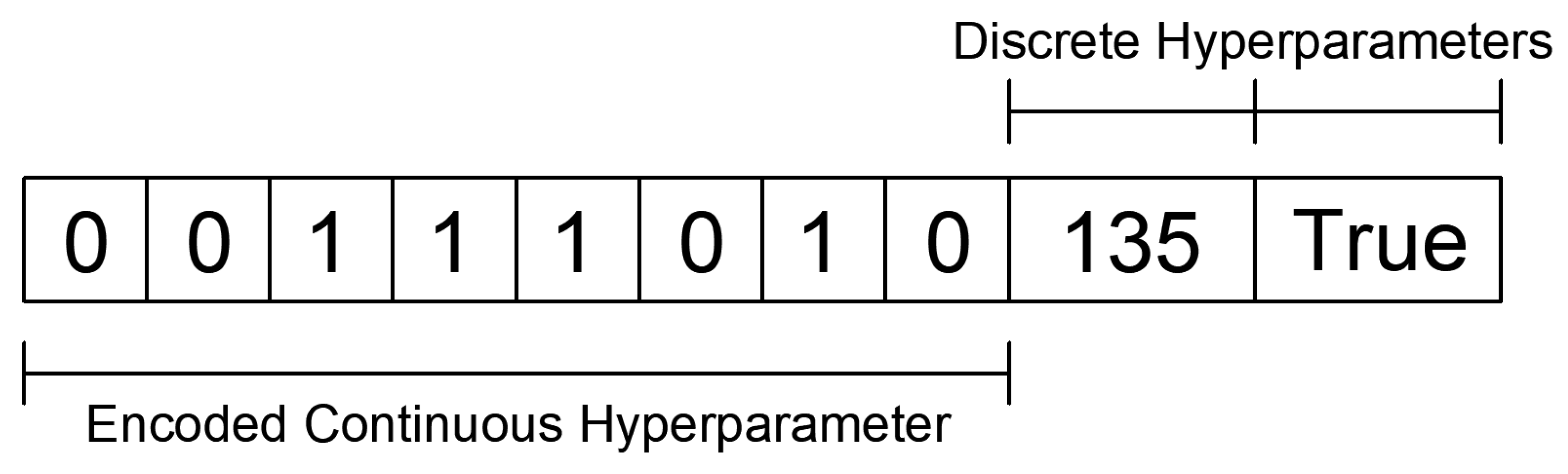
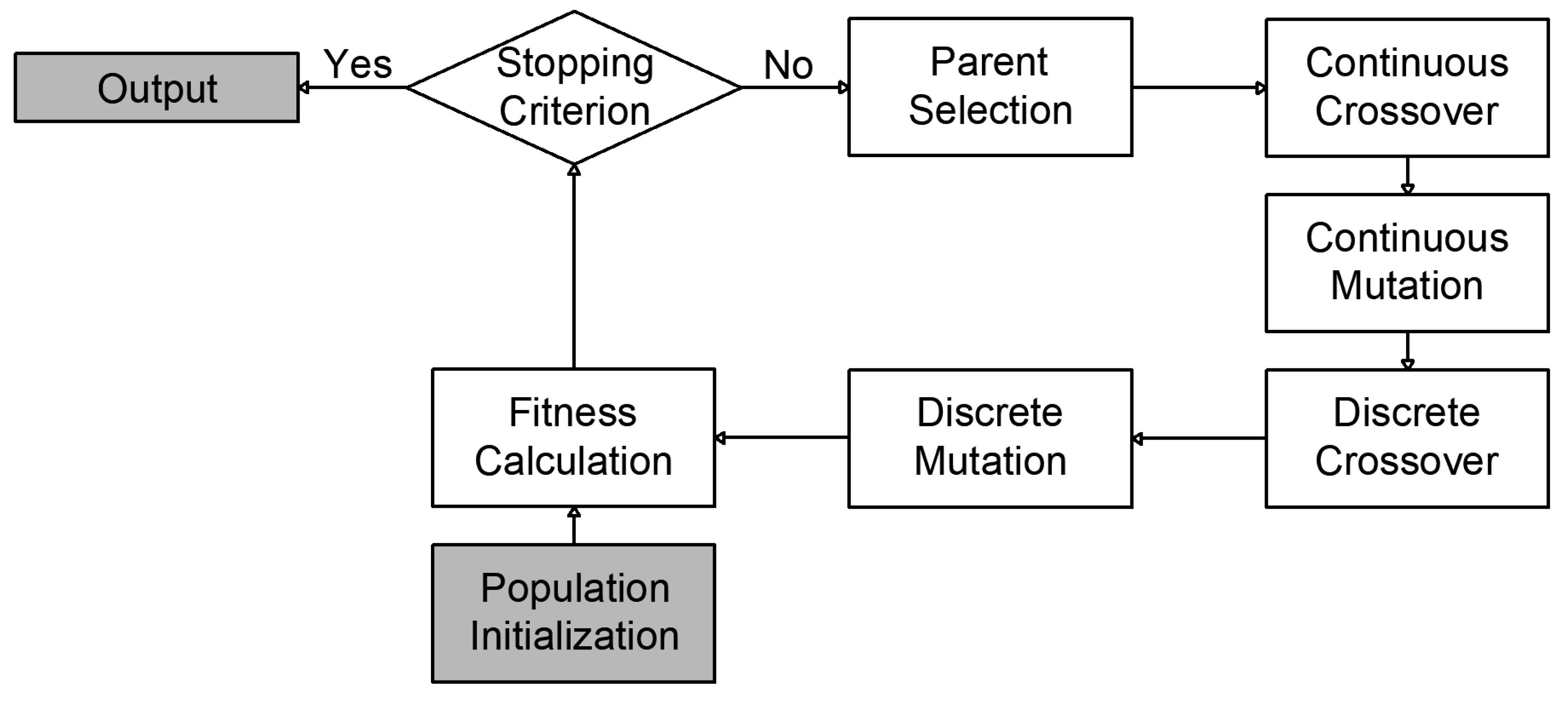
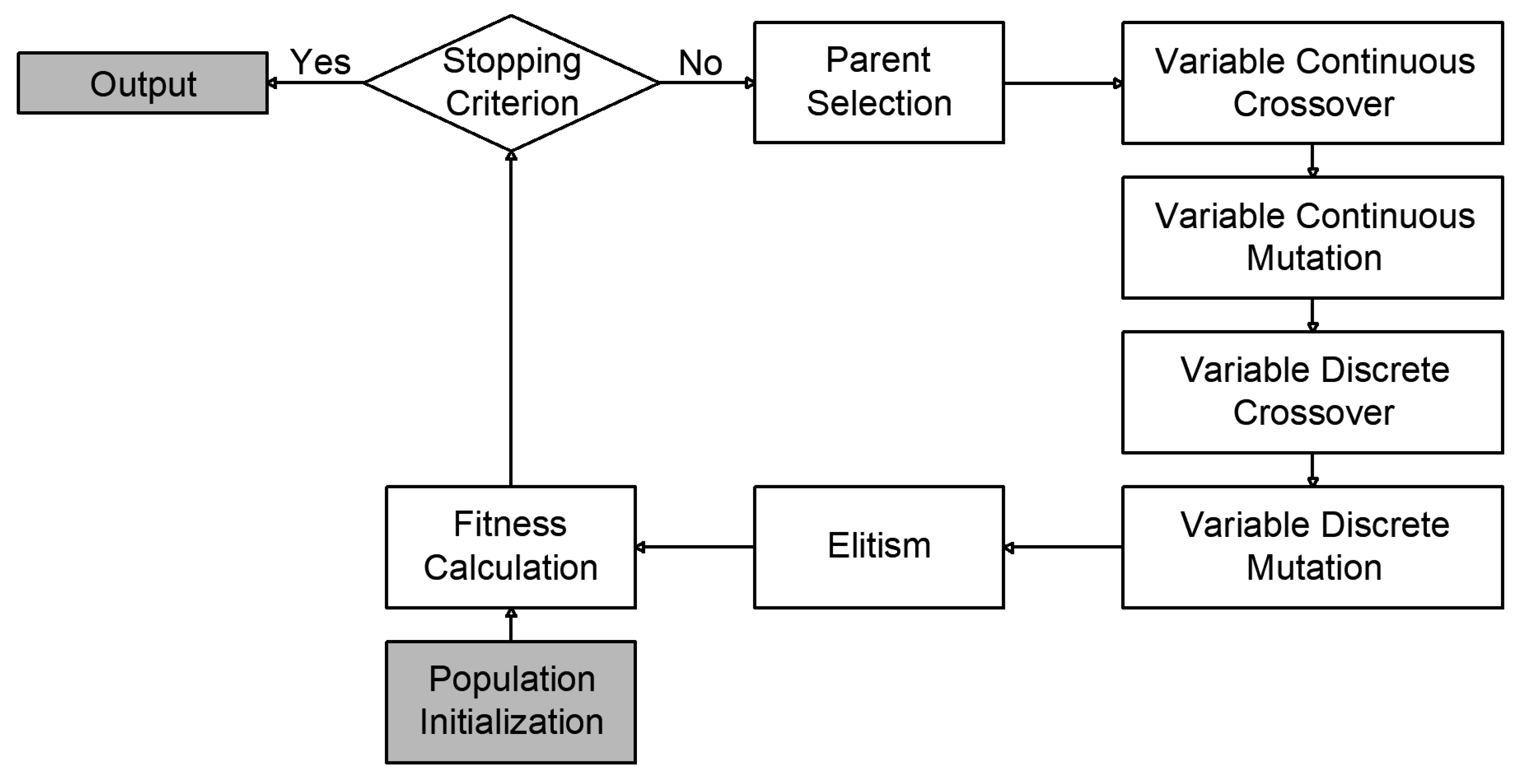
2.1.7. Genetic Algorithms
2.2. Exploratory Data Analysis
2.3. Tuning Model Hyperparameters
| Pseudocode 1. Hyperparameter tuning procedure. |
| Input: A dataset with independent () and dependent () variables; a genetic algorithm ; AI-based models; hyperparameters; . Exploratory data analysis: Checking for the presence of noise data and outliers, identifying the important variables, and performing feature engineering, if necessary. Training and tuning the models: Random generation and storage. Stratification of (5/6 samples); (1/6 samples). Fitting and Transformation of (and , if necessary). Transformation of (and , if necessary). Regardless of whether there is a transformation or not, they will be called and here. Let be the AI-based models, be the hyperparameters of , be the population size, and be the repetitions, where . For : For : For : . end . end . end Output: . |
2.4. Training, Testing, and Validation Metrics
| Pseudocode 2. Training, testing, and validation of the machine learning models. |
| Input: ; (or ); ; (or ); all ; ; . Regardless of whether there is a transformation or not, they will be called and here. Training and Testing Metrics: For : Back Transformation of the data. . . end Validation Metrics: Let be the repetitions, where . For : For : . end . end Output: ; ; . |
- Lowest value (primary criterion).
- Highest value (secondary criterion, used in case of a tie).
- Lowest value (tertiary criterion, used if the first two metrics are identical).
- Smallest population size (if all three performance metrics remain tied).
2.5. Stacking Models Using Ridge Regressor
- Stacking 1: uses the two best base models.
- Stacking 2: uses the three best base models.
- Stacking 3: uses the four best base models.
- Stacking 4: uses the five best base models.
| Pseudocode 3. Building, training, testing, and validation of the stacking models. |
| Input: ; (or ); ; (or ); all ; ; . Regardless of whether there is a transformation or not, they will be called and here. Stacking: Let be the metamodels to be built. For : A certain number of the best models in . . end Training and Testing Metrics: For : Back Transformation of the data. . . end Validation Metrics: Let be the repetitions, where . For : For : . end . end Output: ; ; ; . |
2.6. Nonparametric Statistical Tests
| Pseudocode 4. Nonparametric statistical test procedure. |
| Input: all , ; all , ; . . . Pairwise Testing Comparison: Let be the , , and metrics, and be the probability value for the metric . For : . If : For : . end . end end Output: . |
2.7. General Comments
- scikit-learn: implemented the SVR, DT, RF, XGB, and stacking models.
- skelm: employed for the ELM model.
- PyTorch 2.6.0: used to construct the ANN model.
- Processor: 11th Gen Intel(R) Core i7-1165G7 @ 2.80 GHz.
- Storage: 500 GB SSD.
- Memory: 16 GB RAM.
3. Results and Discussion
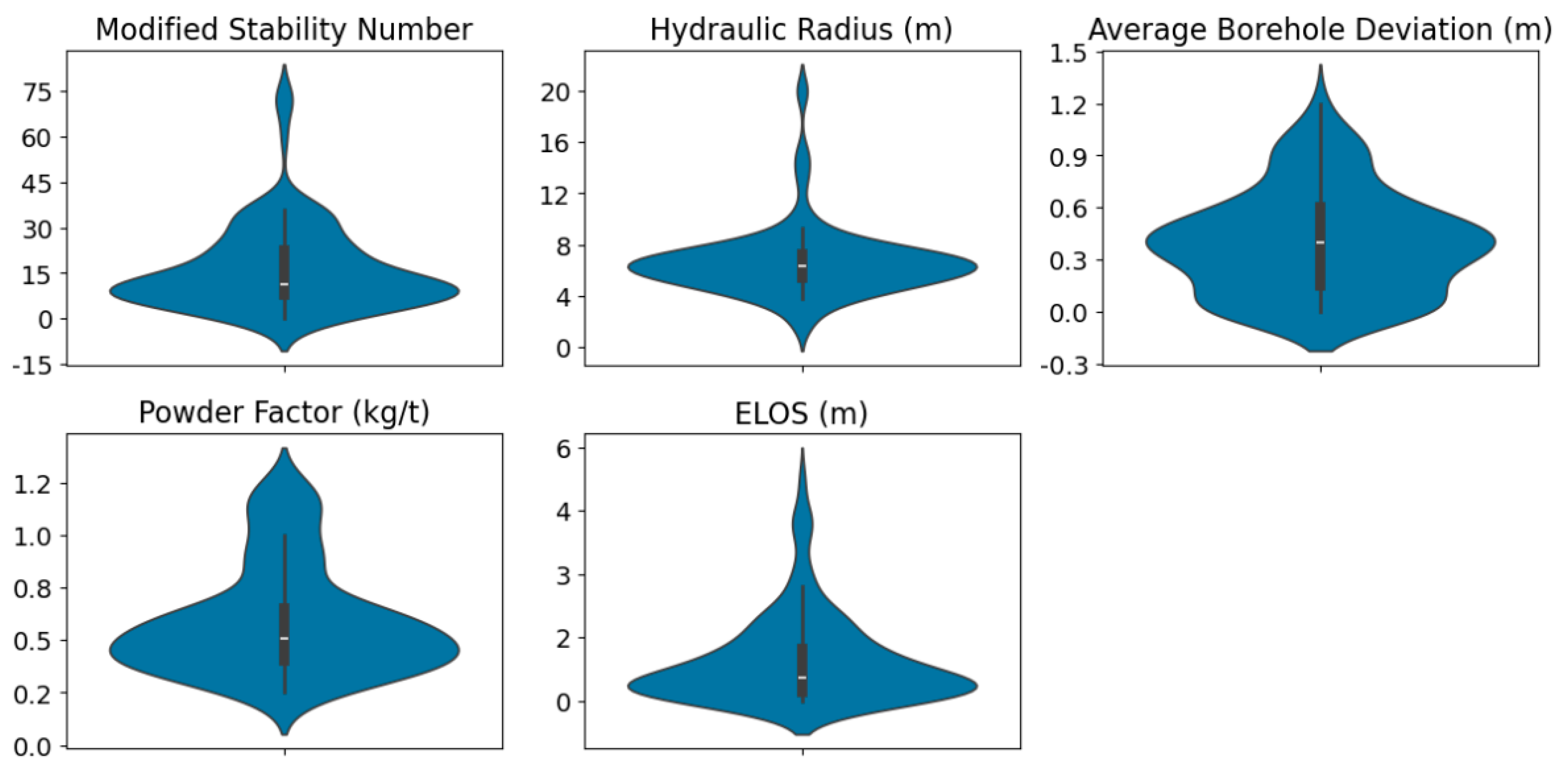
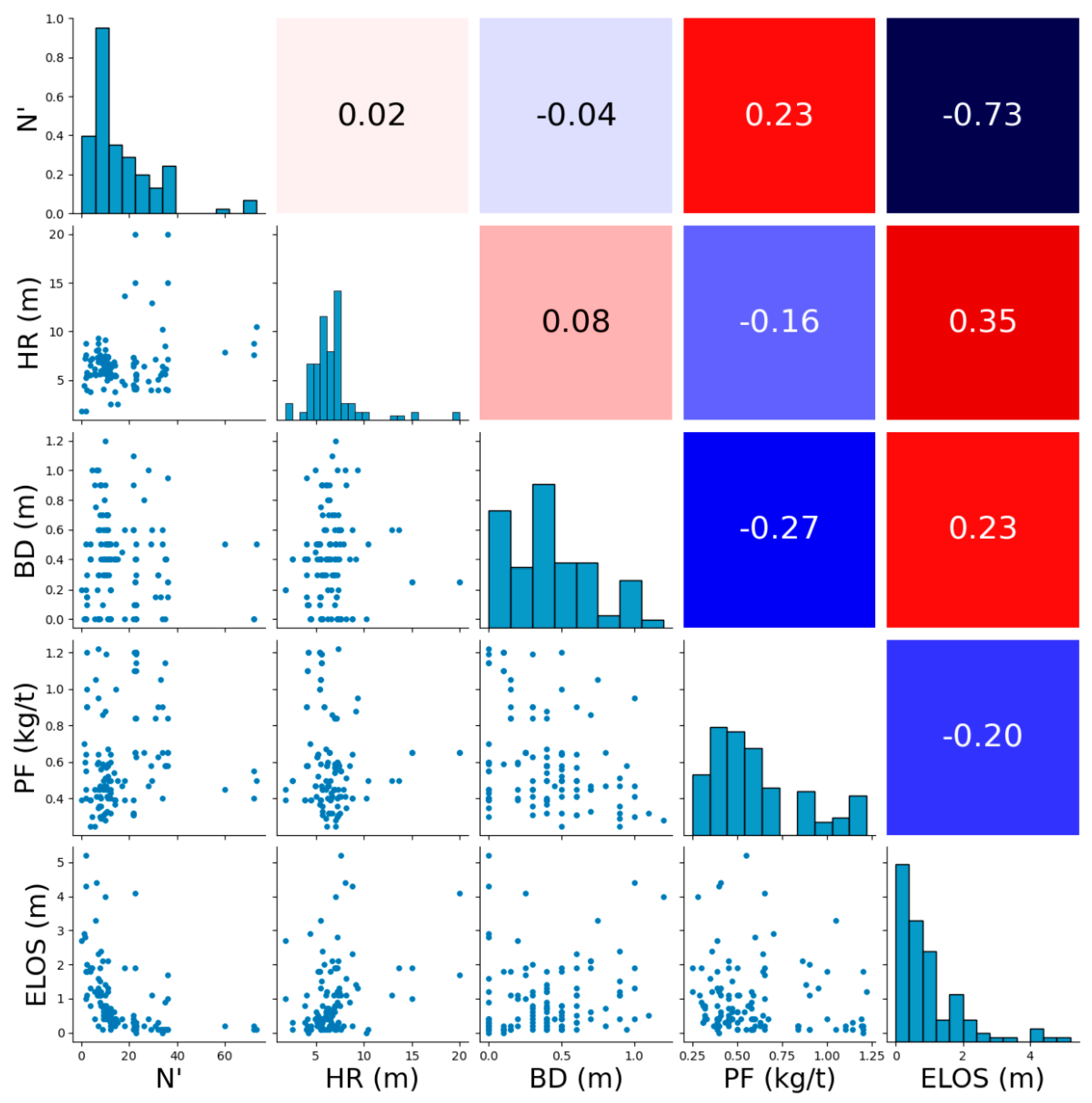
3.1. Exploratory Data Analysis Results
- N′: −73% (strong negative correlation).
- HR: 35% (moderate positive correlation).
- BD: 23% (weak positive correlation).
- PF: −20% (weak negative correlation).
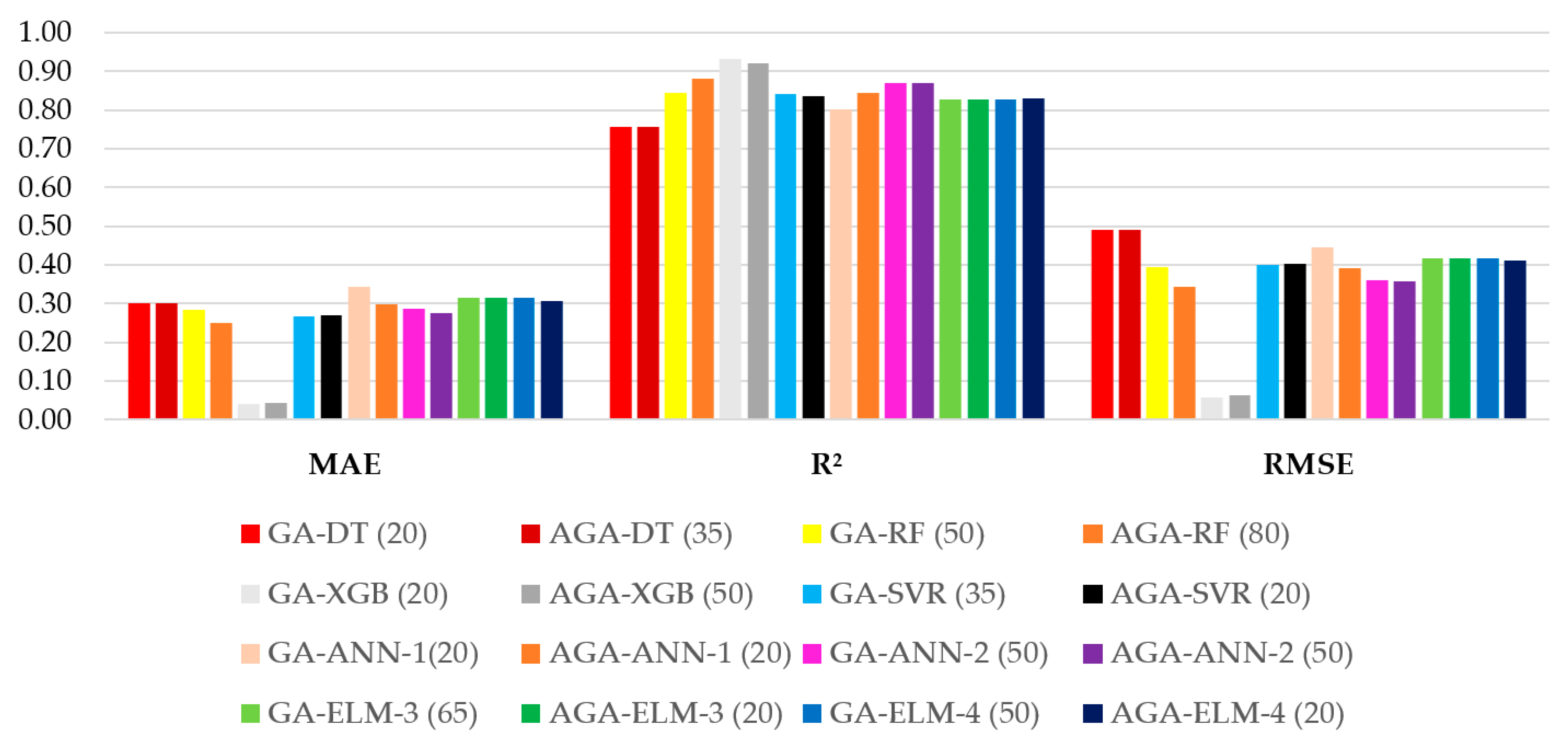
3.2. Hyperparameter Tuning and Metrics for Training, Testing, and Validation
3.3. Building the Stacking Models
- Stacking 1: AGA-ANN-1 (20) and AGA-ELM-3 (20).
- Stacking 2: AGA-ANN-1 (20), AGA-ELM-3 (20), and GA-ANN-2 (50).
- Stacking 3: AGA-ANN-1 (20), AGA-ELM-3 (20), GA-ANN-2 (50), and AGA-SVR (20).
- Stacking 4: AGA-ANN-1 (20), AGA-ELM-3 (20), GA-ANN-2 (50), AGA-SVR (20), and GA-DT (20).
3.4. Statistical Tests Results
3.5. Main Findings of This Study
- Despite the relatively small dataset used for predicting dilution () in underground mines and the low correlation of some independent variables with , the proposed methodology enabled the development of multiple machine learning models capable of accurately predicting from the given dataset.
- The application of genetic algorithms (GA and AGA) with varying population sizes strengthened the hyperparameter tuning process, leading to models with improved generalization capabilities for unseen data.
- Incorporating machine learning models based on different paradigms and strategies provided a robust analytical framework, facilitating the assessment of the strengths and weaknesses of each model within the proposed scope.
- The performance limitations observed in certain models within this study should not be generalized, as machine learning models are highly sensitive to data characteristics and may perform differently when applied to other datasets or problem domains.
- Implementing a cross-validation procedure with 10 folds and 30 repetitions allowed for a more comprehensive analysis, ensuring that even a small dataset could be evaluated rigorously. The statistical tests confirmed the superiority of certain models, while refuting the existence of significant performance differences between others.
- The methodology emphasized the importance of a well-structured validation phase. A simple division into training and testing datasets may bias the results in favor of a specific model configuration, which, when exposed to different data partitions, may fail to maintain its performance.
- The study demonstrated that stacking metamodels built from distinct base models can be equally or even more effective than the use of individual models, as confirmed by the Nemenyi test results.
- Although AGA-ANN-1 (20) was identified as the best-performing model during the testing phase, it was not among the top models in two out of three Nemenyi test evaluations. This finding underscores the risk of relying solely on a single test dataset, particularly when dealing with small datasets, as it may lead to anomalies and models that do not consistently deliver optimal results.
3.6. Limitations of This Study
- The representativeness of the dataset is intrinsically linked to the geological and operational characteristics of the mines from which the data were collected. Therefore, the models developed herein may not generalize effectively to mines with substantially different conditions.
- Potential sampling biases or errors in data collection could have introduced distortions in the training process, leading to models that do not adequately capture the underlying relationships within the studied context.
- The relatively small dataset size (120 samples) imposes limitations on the models’ ability to generalize. In particular, the identification of more subtle patterns may be hindered, and statistical fluctuations across different data partitions may be exacerbated.
- Decisions regarding data transformation strategies, train–test segmentation, choice of machine learning algorithms, and hyperparameter optimization configurations—although carefully considered—may not represent the optimal combination. These choices can impact model performance and generalization capacity.
- The genetic algorithms employed for hyperparameter tuning, while effective in navigating complex search spaces, do not guarantee convergence to global optima. As a result, superior configurations may remain unexplored.
- The performance of the stacking models is inherently constrained by the predictive capabilities of the constituent base models. Consequently, under different scenarios or datasets, the ensemble approach may not yield improved robustness or accuracy.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| List of Abbreviations | |
|---|---|
| ABC: artificial bee colony | LDA: linear discriminant analysis |
| ACO: ant colony optimization | LightGBM: light gradient boosting machine |
| AGA: adaptive genetic algorithm | MABAC: multi-attributive approximation area comparison |
| AI: artificial intelligence | : mean absolute error |
| ALO: ant lion optimizer | ML: machine learning |
| ANFIS: adaptive neuro-fuzzy inference system | MLRA: multi linear regression analysis |
| ANN: artificial neural network | MNRA: multi nonlinear regression analysis |
| AUC: area under the curve | MR: memory replay |
| BD: mean borehole deviation | MSE: mean-square error |
| BO: Bayesian optimization | N′: modified stability number |
| CART: classification and regression tree | ORF: overbreak resistance factor |
| CatBoost: categorical boosting | PCA: principal component analysis |
| CGA: conjugate gradient algorithm | PF: powder factor |
| CNFS: concurrent neuro-fuzzy system | PSO: particle swarm optimization |
| CSO: cuckoo search optimization | Q′: modified rock mass quality index |
| DF21: Deep Forest 21 | R: correlation coefficient |
| DT: decision tree | : coefficient of determination |
| ELM: extreme learning machine | RBN: radial basis network |
| : equivalent linear overbreak slough | RF: random forest |
| EM: expectation maximization | RMR: rock mass rating |
| EWC: elastic weight consolidation | : root-mean-square error |
| FA: firefly algorithm | RNN: recurrent neural network |
| FIS: fuzzy inference system | RQD: rock quality designation |
| FMF: fuzzy membership function | SRF: stress reduction factor |
| GA: genetic algorithm | SSA: sparrow search algorithm |
| GAN: generative adversarial network | SSE: stepwise selection and elimination |
| GBDT: gradient boosting decision tree | SUDI: stope unplanned dilution index |
| GBM: gradient boosting machine | SVM: support vector machine |
| gcForest: grained cascade forest | SVR: support vector regression |
| GPC: Gaussian process classification | TOPSIS: technique for order of preference by similarity to ideal solution |
| GRNN: generalized regression neural network | TSA: tunicate swarm algorithm |
| GSI: geological strength index | UF: undercutting factor |
| GWO: grey wolf optimizer | VAE: variational autoencoder |
| HR: hydraulic radius | WOA: whale optimization algorithm |
| K: average horizontal to vertical stress ratio | WNN: wavelet neural network |
| KNN: k-nearest neighbors | XGB: extreme gradient boosting |
Appendix B
| DT Hyperparameters | Optimized Values |
|---|---|
| Min weight fraction leaf | 0.0412 |
| Max depth | 61 |
| Min samples leaf | 3 |
| Min samples split | 4 |
| Criterion | absolute_error |
| RF Hyperparameters | Optimized Values |
|---|---|
| Ccp alpha | 0.0100 |
| N estimators | 537 |
| Max depth | 5 |
| Min samples leaf | 1 |
| Min samples split | 2 |
| Criterion | absolute_error |
| XGB Hyperparameters | Optimized Values |
|---|---|
| N estimators | 833 |
| Max depth | 27 |
| Eta | 0.0165 |
| Subsample | 0.1529 |
| Colsample by tree | 1.0000 |
| SVR Hyperparameters | Optimized Values |
|---|---|
| Kernel | rbf |
| C | 10.0000 |
| Gamma | 0.0500 |
| ANN-1 Hyperparameters | Optimized Values |
|---|---|
| Number of layers | 1 |
| Layer sizes (nodes per layer) | 15 |
| Learning rate | 0.0484 |
| Dropout rate | 0.0902 |
| Weight decay | 0.0010 |
| Epochs | 30 |
| Activation | relu |
| Solver | adam |
| ANN-2 Hyperparameters | Optimized Values |
|---|---|
| Number of layers | 2 |
| Layer sizes (nodes per layer) | 16, 18 |
| Learning rate | 0.0227 |
| Dropout rate | 0.0157 |
| Weight decay | 0.0041 |
| Epochs | 45 |
| Activation | leaky_relu |
| Solver | adam |
| ELM-3 Hyperparameters | Optimized Values |
|---|---|
| Number of layers | 3 |
| Layer sizes (nodes per layer) | 4, 2, 2 |
| Alpha | 0.1000 |
| Density | 0.1529 |
| Include original features | False, True, True |
| Ufunc | tanh, lin, tanh |
| Pairwise metric | hamming, hamming, Euclidean |
| ELM-4 Hyperparameters | Optimized Values |
|---|---|
| Number of layers | 4 |
| Layer sizes (nodes per layer) | 17, 6, 2, 11 |
| Alpha | 0.0961 |
| Density | 0.9177 |
| Include original features | True, True, True, True |
| Ufunc | tanh, lin, tanh, None |
| Pairwise metric | hamming, hamming, Euclidean, hamming |
References
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining, 3rd ed.; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Pontow, S.J. Evaluation of Methods for Stope Design in Mining and Potential of Improvement by Pre-Investigations. Master’s Thesis, Aalto University, Espoo, Finland, 2019. [Google Scholar]
- Cadenillas, C.T. Prediction of Unplanned Dilution in Underground Mines Through Machine Learning Techniques. Master’s Thesis, McGill University, Montreal, QC, Canada, 2023. [Google Scholar]
- Wang, J. Influence of Stress, Undercutting, Blasting and Time on Open Stope Stability and Dilution. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2004. [Google Scholar]
- Potvin, Y. Empirical Open Stope Design in Canada. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1988. [Google Scholar]
- Clark, L.M. Minimizing Dilution in Open Stope Mining with a Focus on Stope Design and Narrow Vein Longhole Blasting. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1998. [Google Scholar]
- Lima, M.P.; Guimarães, L.J.N.; Gomes, I.F. Numerical modeling of the underground mining stope stability considering time-dependent deformations via finite element method. REM Int. Eng. J. 2024, 77, e230080. [Google Scholar] [CrossRef]
- Panji, M.; Koohsari, H.; Adampira, M.; Alielahi, H.; Marnani, J.A. Stability analysis of shallow tunnels subjected to eccentric loads by a boundary element method. J. Rock Mech. Geotech. Eng. 2016, 8, 480–488. [Google Scholar] [CrossRef]
- Deere, D.U. Technical description of rock cores for engineering purposes. Rock Mech. Rock Eng. 1964, 1, 17–22. [Google Scholar]
- ISRM Commission. Suggested methods for the quantitative description of discontinuities in rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [Google Scholar]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock; Institution of Mining and Metallurgy: London, UK, 1980. [Google Scholar]
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Trans. S. Afr. Inst. Civ. Eng. 1973, 15, 335–344. [Google Scholar]
- Bieniawski, Z.T. Rock mass classifications in rock engineering. In Proceedings of the Exploration for Rock Engineering, Johannesburg, South Africa, 1–5 November 1976. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–239. [Google Scholar] [CrossRef]
- Hoek, E. Strength of rock and rock masses. ISRM News J. 1994, 2, 4–16. [Google Scholar]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; A. A. Balkema: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Hoek, E.; Carranza, C.; Corkum, B. Hoek-Brown failure criterion—2002 Edition. In Proceedings of the NARMS-TAC 2002, Toronto, ON, Canada, 7–10 July 2002. [Google Scholar]
- Grimstad, E.; Barton, N.R. Updating of the Q-system for NMT. In Proceedings of the International Symposium on Sprayed Concrete, Fagernes, Norway, 17–21 October 1993. [Google Scholar]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion: A 1988 update. In Proceedings of the 15th Canadian Rock Mechanics Symposium, Toronto, Canada, 3–4 October 1988. [Google Scholar]
- Diederichs, M.S.; Kaiser, P.K. Tensile strength and abutment relaxation as failure control mechanisms in underground excavations. Int. J. Rock Mech. Min. Sci. 1999, 36, 69–96. [Google Scholar] [CrossRef]
- Adoko, A.C.; Saadaari, F.; Mireku-Gyimah, D.; Imashev, A. A Feasibility Study on The Implementation of Neural Network Classifiers for Open Stope Design. Geotech. Geol. Eng. 2022, 40, 677–696. [Google Scholar] [CrossRef]
- Henning, J.G.; Mitri, H.S. Numerical modelling of ore dilution in blasthole stoping. Int. J. Rock Mech. Min. Sci. 2007, 44, 692–703. [Google Scholar] [CrossRef]
- Heidarzadeh, S.; Saeidi, A.; Rouleau, A. Evaluation of the effect of geometrical parameters on stope probability of failure in the open stoping method using numerical modeling. Int. J. Min. Sci. Technol. 2019, 29, 399–408. [Google Scholar] [CrossRef]
- Cepuritis, P.M.; Villaescusa, E.; Beck, D.A.; Varden, R. Back Analysis of Over-Break in a Longhole Open Stope Operation Using Non-Linear Elasto-Plastic Numerical Modelling. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Cordova, D.P.; Zingano, A.C.; Gonçalves, I.G. Unplanned dilution back analysis in an underground mine using numerical models. REM Int. Eng. J. 2022, 75, 379–388. [Google Scholar] [CrossRef]
- Mathews, K.; Hoek, E.; Wyllie, D.; Stewart, S. Prediction of Stable Excavation Spans at Depths Below 1000 m in Hard Rock Mines; CANMET Report, DSS Serial No OSQ80–00081; Canada Centre for Mineral and Energy Technology: Ottawa, ON, Canada, 1981. [Google Scholar]
- Clark, L.M.; Pakalnis, R.C. An empirical design approach for estimating unplanned dilution from open stope hangingwalls and footwalls. In Proceedings of the CIM’97: 99th Annual General Meeting, Vancouver, BC, Canada, 26 April–1 May 1997; Canadian Institute of Mining, Metallurgy and Petroleum: Vancouver, BC, Canada, 1997. [Google Scholar]
- Suorineni, F.T.; Kaiser, P.K.; Tannant, D.D. Likelihood statistic for interpretation of the stability graph for open stope design. Int. J. Rock Mech. Min. Sci. 2001, 38, 735–744. [Google Scholar] [CrossRef]
- Yuan, J.; Zhou, C.; Zhang, D. Physical model test and numerical simulation study of deformation mechanism of wall rock on open pit to underground mining. Int. J. Eng. 2014, 27, 1795–1802. [Google Scholar]
- Bazaluk, O.; Petlovanyi, M.; Zubko, S.; Lozynskyi, V.; Sai, K. Instability assessment of hanging wall rocks during underground mining of iron ores. Minerals 2021, 11, 858. [Google Scholar] [CrossRef]
- Germain, P.; Hadjigeorgiou, J. Influence of stope geometry and blasting pattern on recorded overbreak. Int. J. Rock Mech. Min. Sci. 1997, 34, 115.e1–115.e12. [Google Scholar] [CrossRef]
- Jang, H.; Topal, E. Optimizing overbreak prediction based on geological parameters comparing multiple regression analysis and artificial neural network. Tunn. Undergr. Space Technol. 2013, 38, 161–169. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Wei, J. Predictions of overbreak blocks in tunnels based on the wavelet neural network method and the geological statistics theory. Math. Probl. Eng. 2013, 2013, 706491. [Google Scholar]
- Jang, H. Unplanned Dilution and Ore-Loss Optimisation in Underground Mines via Cooperative Neuro-Fuzzy Network. Ph.D. Thesis, Curtin University, Perth, WA, Australia, 2014. [Google Scholar]
- Jang, H.; Topal, E.; Kawamura, Y. Unplanned dilution and ore loss prediction in longhole stoping mines via multiple regression and artificial neural network analyses. J. South. Afr. Inst. Min. Metall. 2015, 115, 449–456. [Google Scholar] [CrossRef]
- Jang, H.; Topal, E.; Kawamura, Y. Decision support system of unplanned dilution and ore-loss in underground stoping operations using a neuro-fuzzy system. Appl. Soft Comput. 2015, 32, 1–12. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hossaini, M.F.; Mirzapour, B.; Hajiantilaki, N. Use of fuzzy set theory for minimizing overbreak in underground blasting operations—A case study of Alborz Tunnel, Iran. Int. J. Min. Sci. Technol. 2015, 25, 439–445. [Google Scholar] [CrossRef]
- Mohseni, M.; Ataei, M.; Khaloo Kakaie, R. A new classification system for evaluation and prediction of unplanned dilution in cut-and-fill stoping method. J. Min. Environ. 2018, 9, 873–892. [Google Scholar]
- Mottahedi, A.; Sereshki, F.; Ataei, M. Development of overbreak prediction models in drill and blast tunneling using soft computing methods. Eng. Comput. 2018, 34, 45–58. [Google Scholar] [CrossRef]
- Mottahedi, A.; Sereshki, F.; Ataei, M. Overbreak prediction in underground excavations using hybrid ANFIS-PSO model. Tunn. Undergr. Space Technol. 2018, 80, 1–9. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of open stope hangingwall stability using random forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Capes, G.W. Open Stope Hangingwall Design Based on General and Detailed Data Collection in Unfavourable Hangingwall Conditions. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2009. [Google Scholar]
- Qi, C.; Fourie, A.; Ma, G.; Tang, X.; Du, X. Comparative study of hybrid artificial intelligence approaches for predicting hangingwall stability. J. Comput. Civ. Eng. 2018, 32, 04017086. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Ma, G.; Tang, X. A hybrid method for improved stability prediction in construction projects: A case study of stope hangingwall stability. Appl. Soft Comput. 2018, 71, 649–658. [Google Scholar] [CrossRef]
- Jang, H.; Taheri, S.; Topal, E.; Kawamura, Y. Illumination of contributing parameters of uneven break in narrow vein mine. In Proceedings of the 28th International Symposium on Mine Planning and Equipment Selection—MPES 2019, Perth, WA, Australia, 2–4 December 2019. [Google Scholar]
- Jang, H.; Kawamura, Y.; Shinji, U. An empirical approach of overbreak resistance factor for tunnel blasting. Tunn. Undergr. Space Technol. 2019, 92, 103060. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Armaghani, D.J.; Haghighi, M.; Ghaleini, E.N. A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels. Bull. Eng. Geol. Environ. 2019, 78, 981–990. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Ghaleini, E.N.; Tootoonchi, H.; Armaghani, D.J.; Haghighi, M.; Hedayat, A. Developing a new intelligent technique to predict overbreak in tunnels using an artificial bee colony-based ANN. Environ. Earth Sci. 2019, 78, 8163. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Ghaleini, E.N.; Haghighi, M.; Kanagarajan, S.; Maarefvand, P.; Mohamad, E.T. Overbreak prediction and optimization in tunnel using neural network and bee colony techniques. Eng. Comput. 2019, 35, 1191–1202. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, J. Method of predicting ore dilution based on a neural network and its application. Sustainability 2020, 12, 1550. [Google Scholar] [CrossRef]
- Bazarbay, B.; Adoko, A.C. A Comparison of Prediction and Classification Models of Unplanned Stope Dilution in Open Stope Design. In Proceedings of the 55th U.S. Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 18–25 June 2021. [Google Scholar]
- Bazarbay, B.; Adoko, A.C. Development of a knowledge-based system for assessing unplanned dilution in open stopes. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 062086. [Google Scholar] [CrossRef]
- Mohseni, M.; Ataei, M.; Kakaie, R. Dilution risk ranking in underground metal mines using Multi Attributive Approximation Area Comparison. J. Min. Environ. 2020, 11, 977–989. [Google Scholar]
- Korigov, S.; Adoko, A.C.; Sengani, F. Unplanned dilution prediction in open stope mining: Developing new design charts using Artificial Neural Network classifier. J. Sustain. Min. 2022, 21, 157–168. [Google Scholar] [CrossRef]
- Jorquera, M.; Korzeniowski, W.; Skrzypkowski, K. Prediction of dilution in sublevel stoping through machine learning algorithms. IOP Conf. Ser. Earth Environ. Sci. 2023, 1189, 012008. [Google Scholar] [CrossRef]
- He, B.; Armaghani, D.J.; Lai, S.H. Assessment of tunnel blasting-induced overbreak: A novel metaheuristic-based random forest approach. Tunn. Undergr. Space Technol. 2023, 133, 104979. [Google Scholar] [CrossRef]
- Hong, Z.; Tao, M.; Liu, L.; Zhao, M.; Wu, C. An intelligent approach for predicting overbreak in underground blasting operation based on an optimized XGB model. Eng. Appl. Artif. Intell. 2023, 126, 107097. [Google Scholar] [CrossRef]
- Liu, Y.; Li, A.; Zhang, H.; Wang, J.; Li, F.; Chen, R.; Wang, S.; Yao, J. Minimization of overbreak in different tunnel sections through predictive modeling and optimization of blasting parameters. Front. Ecol. Evol. 2023, 11, 1255384. [Google Scholar] [CrossRef]
- Zhang, W. Research on Blasthole Image Recognition Algorithms and Optimization of Smooth Blasting Parameters of Rock Tunnel. Ph.D. Thesis, Shandong University, Jinan, China, 2020. [Google Scholar]
- Liu, Y.; Li, A.; Wang, S.; Yuan, J.; Zhang, X. A feature importance-based intelligent method for controlling overbreak in drill-and-blast tunnels via integration with rock mass quality. Alex. Eng. J. 2024, 108, 1011–1031. [Google Scholar] [CrossRef]
- Chimunhu, P.; Faradonbeh, R.S.; Topal, E.; Asad, M.W.A.; Ajak, A.D. Development of novel hybrid intelligent predictive models for dilution prediction in underground sub-level mining. Min. Metall. Explor. 2024, 41, 2079–2098. [Google Scholar] [CrossRef]
- Li, C.; Dias, D.; Zhou, J.; Tao, M. Applying a novel hybrid ALO-BPNN model to predict overbreak and underbreak area in underground space. In Applications of Artificial Intelligence in Mining and Geotechnical Engineering; Nguyen, H., Bui, X.-N., Topal, E., Zhou, J., Choi, Y., Zhang, W., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 325–342. [Google Scholar]
- He, B.; Li, J.; Armaghani, D.J.; Hashim, H.; He, X.; Pradhan, B.; Sheng, D. The deep continual learning framework for prediction of blast-induced overbreak in tunnel construction. Expert Syst. Appl. 2025, 264, 125909. [Google Scholar] [CrossRef]
- Cieślik, K.; Milczarek, W. Application of machine learning in forecasting the impact of mining deformation: A case study of underground copper mines in Poland. Remote Sens. 2022, 14, 4755. [Google Scholar] [CrossRef]
- Raschka, S.; Liu, Y.; Mirjalili, V. Machine Learning with PyTorch and Scikit-Learn: Develop Machine Learning and Deep Learning Models with Python; Packt Publishing Ltd.: Birmingham, UK, 2022. [Google Scholar]
- Bataineh, M.; Marler, T. Neural network for regression problems with reduced training sets. Neural Netw. 2017, 95, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Mcculloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Chervonenkis, A.Y. On a class of pattern-recognition learning algorithms. Automation and Remote Control 1964, 25, 838–845. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1996. [Google Scholar]
- Morgan, J.N.; Sonquist, J.A. Problems in the analysis of survey data, and a proposal. J. Am. Stat. Assoc. 1963, 58, 415–434. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGB: A scalable tree boosting system. In Proceedings of the KDD’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Yasser, A.A.; Awwad, E.M.; Al-Razgan, M.; Maarouf, A. Hyperparameter search for machine learning algorithms for optimizing the computational complexity. Processes 2023, 11, 349. [Google Scholar] [CrossRef]
- Ilemobayo, J.A.; Durodola, O.; Alade, O.; Awotunde, O.J.; Olanrewaju, A.T.; Falana, O.; Ogungbire, A.; Osinuga, A.; Ogunbiyi, D.; Ifeanyi, A.; et al. Hyperparameter tuning in machine learning: A comprehensive review. J. Eng. Res. Rep. 2024, 26, 388–395. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Harbor, MI, USA, 1975. [Google Scholar]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Nemenyi, P.B. Distribution-Free Multiple Comparisons. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1963. [Google Scholar]
- Yeo, I.K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnicodi Milano, Milan, Italy, 1992. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Kim, D.-K.; Ryu, D.H.; Lee, Y.; Choi, D.-H. Generative models for tabular data: A review. J. Mech. Sci. Technol. 2024, 38, 4989–5005. [Google Scholar] [CrossRef]


| Range | Design Zones |
|---|---|
| Blast damage only; surface remains self-supporting. | |
| Minor sloughing; some failure of the unsupported stope wall must be anticipated before achieving stability. | |
| Moderate sloughing; significant wall failure expected before achieving stability. | |
| Severe sloughing; large wall failures expected, with potential for collapse. |
| Models | Pop 20 (min) | Pop 35 (min) | Pop 50 (min) | Pop 65 (min) | Pop 80 (min) |
|---|---|---|---|---|---|
| GA-DT | 2 | 2 | 3 | 4 | 8 |
| AGA-DT | 1 | 4 | 6 | 6 | 8 |
| GA-RF | 833 | 1277 | 1889 | 2696 | 4074 |
| AGA-RF | 837 | 1417 | 1935 | 3224 | 4870 |
| GA-XGB | 417 | 633 | 1017 | 1304 | 1551 |
| AGA-XGB | 252 | 525 | 568 | 863 | 969 |
| GA-SVR | 5 | 8 | 10 | 13 | 16 |
| AGA-SVR | 4 | 7 | 11 | 14 | 15 |
| GA-ANN-1 | 165 | 226 | 306 | 328 | 479 |
| AGA-ANN-1 | 132 | 154 | 243 | 447 | 459 |
| GA-ANN-2 | 154 | 183 | 315 | 444 | 565 |
| AGA-ANN-2 | 132 | 259 | 340 | 462 | 501 |
| GA-ELM-3 | 3 | 4 | 6 | 8 | 10 |
| AGA-ELM-3 | 4 | 6 | 8 | 11 | 14 |
| GA-ELM-4 | 5 | 8 | 11 | 11 | 15 |
| AGA-ELM-4 | 5 | 9 | 14 | 18 | 18 |
| Model | ||||||
|---|---|---|---|---|---|---|
| GA-DT (20) | 0.3015 | 0.3499 | 0.7579 | 0.6369 | 0.4920 | 0.6202 |
| AGA-DT (35) | 0.3015 | 0.3499 | 0.7579 | 0.6369 | 0.4920 | 0.6202 |
| GA-RF (50) | 0.2832 | 0.3598 | 0.8449 | 0.5492 | 0.3938 | 0.6911 |
| AGA-RF (80) | 0.2515 | 0.3408 | 0.8810 | 0.6334 | 0.3448 | 0.6232 |
| GA-XGB (20) | 0.0396 | 0.4082 | 0.9321 | 0.5730 | 0.0576 | 0.6726 |
| AGA-XGB (50) | 0.0441 | 0.4354 | 0.9198 | 0.5170 | 0.0626 | 0.7153 |
| GA-SVR (35) | 0.2667 | 0.3346 | 0.8405 | 0.6244 | 0.3994 | 0.6308 |
| AGA-SVR (20) | 0.2685 | 0.3307 | 0.8371 | 0.6375 | 0.4036 | 0.6197 |
| GA-ANN-1(20) | 0.3426 | 0.2510 | 0.8017 | 0.8529 | 0.4454 | 0.3948 |
| AGA-ANN-1 (20) | 0.2986 | 0.1882 | 0.8457 | 0.9508 | 0.3928 | 0.2283 |
| GA-ANN-2 (50) | 0.2868 | 0.2282 | 0.8698 | 0.9059 | 0.3609 | 0.3158 |
| AGA-ANN-2 (50) | 0.2760 | 0.2437 | 0.8711 | 0.8327 | 0.3590 | 0.4210 |
| GA-ELM-3 (65) | 0.3143 | 0.1941 | 0.8262 | 0.9544 | 0.4168 | 0.2198 |
| AGA-ELM-3 (20) | 0.3145 | 0.1940 | 0.8262 | 0.9544 | 0.4169 | 0.2197 |
| GA-ELM-4 (50) | 0.3145 | 0.1940 | 0.8262 | 0.9544 | 0.4169 | 0.2197 |
| AGA-ELM-4 (20) | 0.3055 | 0.2765 | 0.8308 | 0.8504 | 0.4113 | 0.3981 |
| Model | |||
|---|---|---|---|
| GA-DT (20) | 0.4570 ± 0.1479 | 0.4853 ± 0.4181 | 0.6227 ± 0.1966 |
| AGA-DT (35) | 0.4578 ± 0.1484 | 0.4850 ± 0.4184 | 0.6233 ± 0.1968 |
| GA-RF (50) | 0.4196 ± 0.1246 | 0.6167 ± 0.2257 | 0.5574 ± 0.1609 |
| AGA-RF (80) | 0.4194 ± 0.1227 | 0.6183 ± 0.2213 | 0.5563 ± 0.1577 |
| GA-XGB (20) | 0.4315 ± 0.1202 | 0.6098 ± 0.2263 | 0.5619 ± 0.1582 |
| AGA-XGB (50) | 0.4623 ± 0.1249 | 0.5638 ± 0.2400 | 0.5954 ± 0.1606 |
| GA-SVR (35) | 0.3566 ± 0.1010 | 0.7125 ± 0.1705 | 0.3954 ± 0.0150 |
| AGA-SVR (20) | 0.3537 ± 0.1006 | 0.7158 ± 0.1689 | 0.4738 ± 0.1385 |
| GA-ANN-1(20) | 0.3779 ± 0.1004 | 0.7182 ± 0.1357 | 0.4825 ± 0.1213 |
| AGA-ANN-1 (20) | 0.3579 ± 0.1036 | 0.7215 ± 0.1749 | 0.4688 ± 0.1348 |
| GA-ANN-2 (50) | 0.3648 ± 0.0913 | 0.7270 ± 0.1543 | 0.4659 ± 0.1203 |
| AGA-ANN-2 (50) | 0.3544 ± 0.0932 | 0.7436 ± 0.1459 | 0.4531 ± 0.1190 |
| GA-ELM-3 (65) | 0.3544 ± 0.0902 | 0.7440 ± 0.1536 | 0.4484 ± 0.1165 |
| AGA-ELM-3 (20) | 0.3535 ± 0.0908 | 0.7450 ± 0.1496 | 0.4494 ± 0.1160 |
| GA-ELM-4 (50) | 0.3534 ± 0.0914 | 0.7466 ± 0.1468 | 0.4479 ± 0.1177 |
| AGA-ELM-4 (20) | 0.3568 ± 0.0946 | 0.7411 ± 0.1559 | 0.4532 ± 0.1245 |
| Model | ||||||
|---|---|---|---|---|---|---|
| GA-DT (20) | 0.3015 | 0.3499 | 0.7579 | 0.6369 | 0.4920 | 0.6202 |
| AGA-RF (80) | 0.2515 | 0.3408 | 0.8810 | 0.6334 | 0.3448 | 0.6232 |
| GA-XGB (20) | 0.0396 | 0.4082 | 0.9321 | 0.5730 | 0.0576 | 0.6726 |
| AGA-SVR (20) | 0.2685 | 0.3307 | 0.8371 | 0.6375 | 0.4036 | 0.6197 |
| AGA-ANN-1 (20) | 0.2986 | 0.1882 | 0.8457 | 0.9508 | 0.3928 | 0.2283 |
| GA-ANN-2 (50) | 0.2868 | 0.2282 | 0.8698 | 0.9059 | 0.3609 | 0.3158 |
| AGA-ELM-3 (20) | 0.3145 | 0.1940 | 0.8262 | 0.9544 | 0.4169 | 0.2197 |
| GA-ELM-4 (50) | 0.3145 | 0.1940 | 0.8262 | 0.9544 | 0.4169 | 0.2197 |
| Stacking 1 | 0.3023 | 0.2219 | 0.8435 | 0.9356 | 0.3956 | 0.2613 |
| Stacking 2 | 0.2886 | 0.2437 | 0.8514 | 0.8924 | 0.3855 | 0.3376 |
| Stacking 3 | 0.2889 | 0.2177 | 0.8582 | 0.9246 | 0.3766 | 0.2826 |
| Stacking 4 | 0.2881 | 0.2227 | 0.8574 | 0.9241 | 0.3777 | 0.2835 |
| Model | |||
|---|---|---|---|
| GA-DT (20) | 0.4570 ± 0.1479 | 0.4853 ± 0.4181 | 0.6227 ± 0.1966 |
| AGA-RF (80) | 0.4194 ± 0.1227 | 0.6183 ± 0.2213 | 0.5563 ± 0.1577 |
| GA-XGB (20) | 0.4315 ± 0.1202 | 0.6098 ± 0.2263 | 0.5619 ± 0.1582 |
| AGA-SVR (20) | 0.3537 ± 0.1006 | 0.7158 ± 0.1689 | 0.4738 ± 0.1385 |
| AGA-ANN-1 (20) | 0.3579 ± 0.1036 | 0.7215 ± 0.1749 | 0.4688 ± 0.1348 |
| GA-ANN-2 (50) | 0.3648 ± 0.0913 | 0.7270 ± 0.1543 | 0.4659 ± 0.1203 |
| AGA-ELM-3 (20) | 0.3535 ± 0.0908 | 0.7450 ± 0.1496 | 0.4494 ± 0.1160 |
| GA-ELM-4 (50) | 0.3534 ± 0.0914 | 0.7466 ± 0.1468 | 0.4479 ± 0.1177 |
| Stacking 1 | 0.3476 ± 0.0952 | 0.7454 ± 0.1570 | 0.4483 ± 0.1230 |
| Stacking 2 | 0.3500 ± 0.0923 | 0.7445 ± 0.1497 | 0.4501 ± 0.1206 |
| Stacking 3 | 0.3554 ± 0.0936 | 0.7379 ± 0.1487 | 0.4572 ± 0.1195 |
| Stacking 4 | 0.3583 ± 0.0965 | 0.7340 ± 0.1575 | 0.4593 ± 0.1244 |
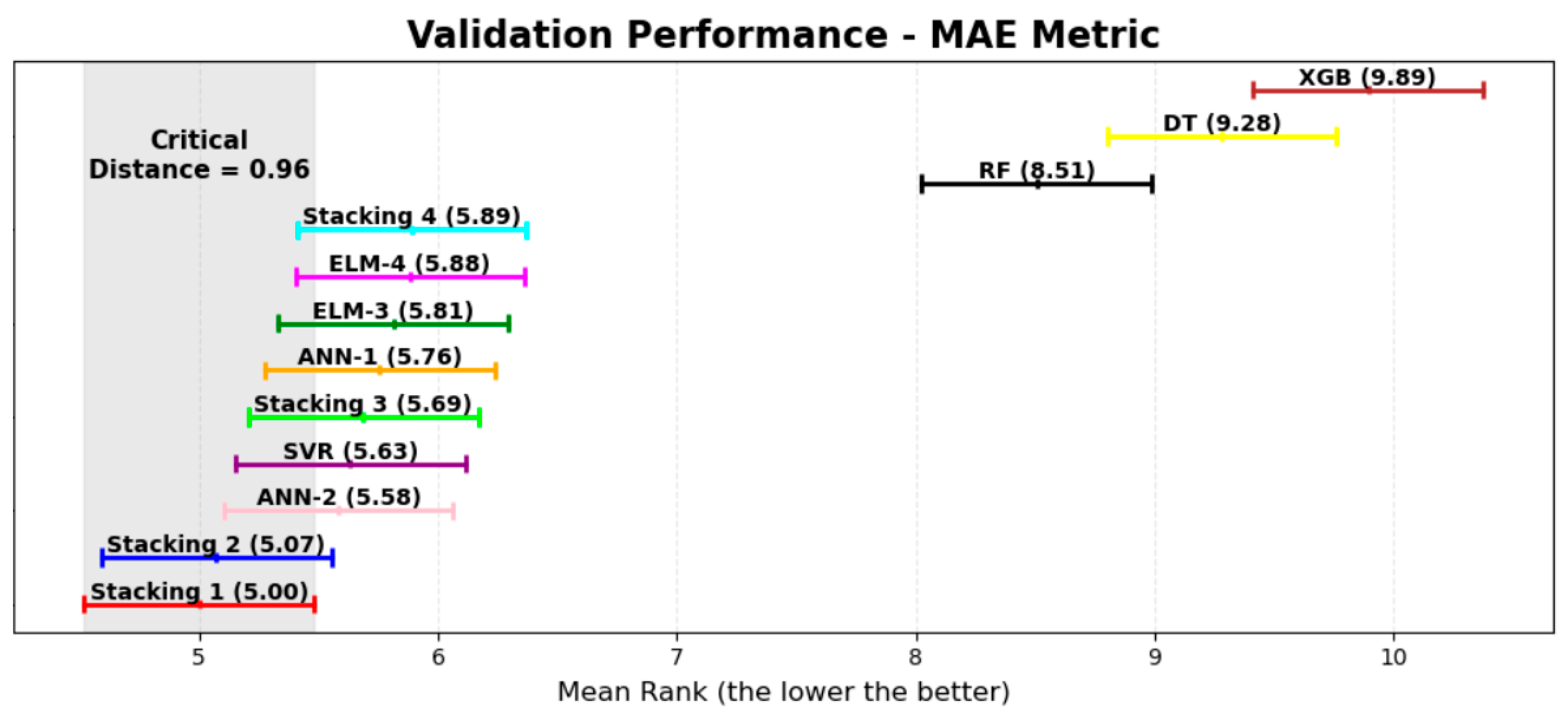
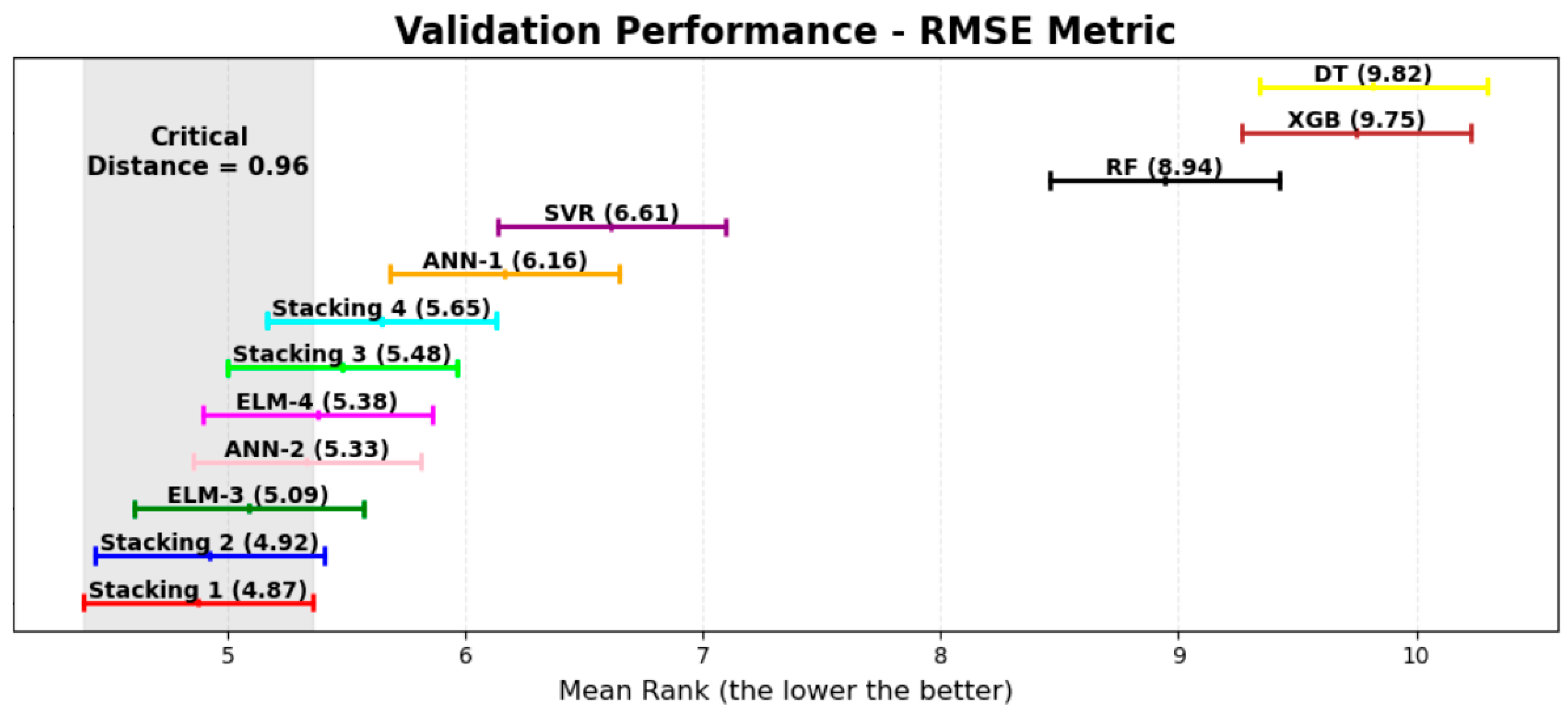
| Models | Rank | Rank | Rank |
|---|---|---|---|
| GA-DT (20) | 9.28 | 3.18 | 9.82 |
| AGA-RF (80) | 8.51 | 4.06 | 8.94 |
| GA-XGB (20) | 9.89 | 3.25 | 9.75 |
| AGA-SVR (20) | 5.63 | 6.39 | 6.61 |
| AGA-ANN-1 (20) | 5.76 | 6.84 | 6.16 |
| GA-ANN-2 (50) | 5.58 | 7.67 | 5.33 |
| AGA-ELM-3 (20) | 5.81 | 7.91 | 5.09 |
| GA-ELM-4 (50) | 5.88 | 7.62 | 5.38 |
| Stacking 1 | 5.00 | 8.13 | 4.87 |
| Stacking 2 | 5.07 | 8.08 | 4.92 |
| Stacking 3 | 5.69 | 7.52 | 5.48 |
| Stacking 4 | 5.89 | 7.35 | 5.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mariz, J.L.V.; Ferraz, T.S.G.; Lima, M.P.; Silva, R.M.A.; Jang, H. Predicting Dilution in Underground Mines with Stacking Artificial Intelligence Models and Genetic Algorithms. Appl. Sci. 2025, 15, 5996. https://doi.org/10.3390/app15115996
Mariz JLV, Ferraz TSG, Lima MP, Silva RMA, Jang H. Predicting Dilution in Underground Mines with Stacking Artificial Intelligence Models and Genetic Algorithms. Applied Sciences. 2025; 15(11):5996. https://doi.org/10.3390/app15115996
Chicago/Turabian StyleMariz, Jorge L. V., Tertius S. G. Ferraz, Marinésio P. Lima, Ricardo M. A. Silva, and Hyongdoo Jang. 2025. "Predicting Dilution in Underground Mines with Stacking Artificial Intelligence Models and Genetic Algorithms" Applied Sciences 15, no. 11: 5996. https://doi.org/10.3390/app15115996
APA StyleMariz, J. L. V., Ferraz, T. S. G., Lima, M. P., Silva, R. M. A., & Jang, H. (2025). Predicting Dilution in Underground Mines with Stacking Artificial Intelligence Models and Genetic Algorithms. Applied Sciences, 15(11), 5996. https://doi.org/10.3390/app15115996







