Boosting Model Interpretability for Transparent ML in TBM Tunneling
Abstract
1. Introduction
2. Interpretability with SHapley Additive exPlanations (SHAP)
- φi (f,x) is the Shapley value for feature i, f is the black box model, and x is the input datapoint.
- z′ is the subset.
- x′ is the simplified input.
- M is the total number of features and |z′|!(M − |z′| − 1)!/M! is the weighting.
- fx is the black box model output and [fx (z′) − fx (z′∖i)] is the contribution.
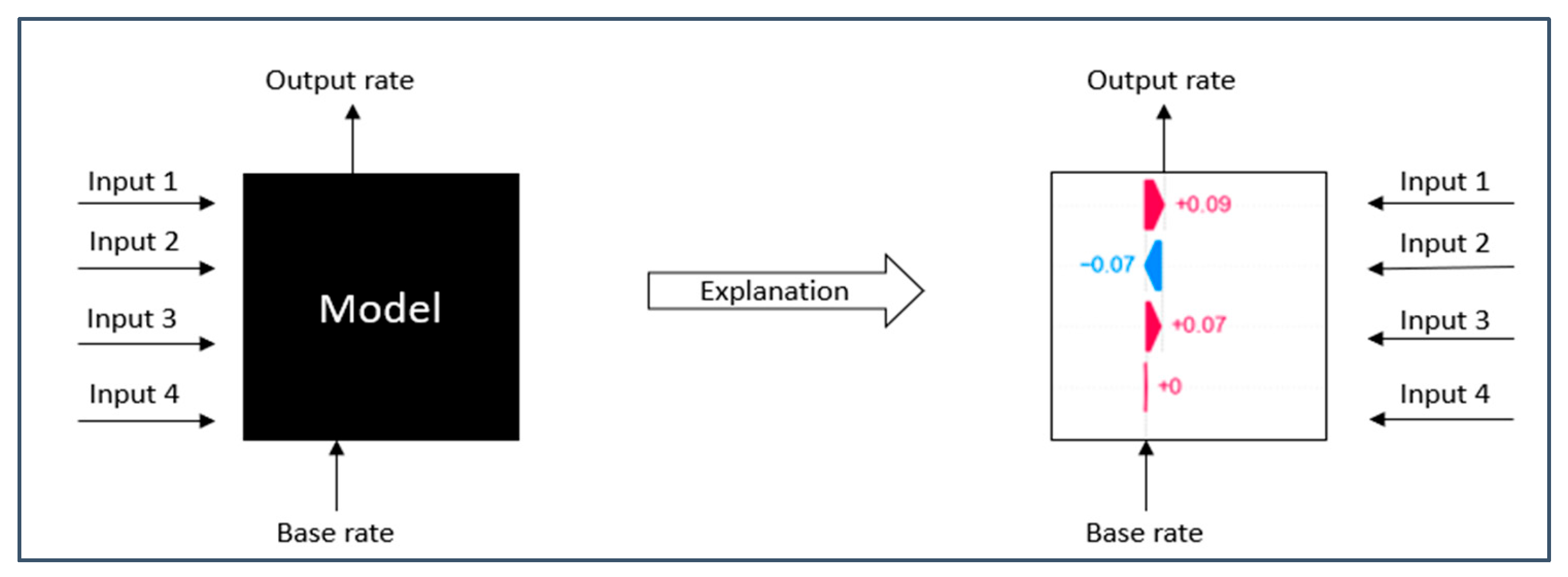
- If x is approximately equal to x′, then g(x′) (Additive Feature Attribution) should be roughly equal to f(x);
- g must conform to the structure where φ0 represents the null output of the model (average output of the model) and φ1 denotes the explained effect of feature 1 (indicating how much feature 1 alters the model’s output). This is referred to as attribution.
- Local accuracy: when the input and simplified input are nearly identical, the explanatory model should match the actual model’s output.
- Missingness: a feature excluded from the model should have zero attribution, indicating no impact on the output.
- Consistency: if a feature’s contribution increases in a new model, its attribution in the explanatory model should not decrease.
- Model understanding: Tree Explainer interprets XGBoost by attributing decisions to individual trees, while Deep Explainer reveals how features influence neural network predictions.
- Complexity comparison: tree models are more interpretable, whereas neural networks are complex; Deep Explainer demystifies the processing in network layers.
- Feature importance: Tree Explainer ranks feature importance for XGBoost, while Deep Explainer highlights impactful features for the ANN.
- Result validation: comparing results across explainers cross-validates findings, boosting confidence in model robustness.
- Task-specific insights: each model excels in different tasks; comparisons highlight their context-specific strengths and weaknesses.
- Decision support: understanding model decision-making is vital for applications like safety and risk assessment, where interpretability is critical.
3. Machine Learning Model Development
3.1. Metro Area of Interest
3.2. EPB Characteristics
3.3. Geology of the Area
4. Results
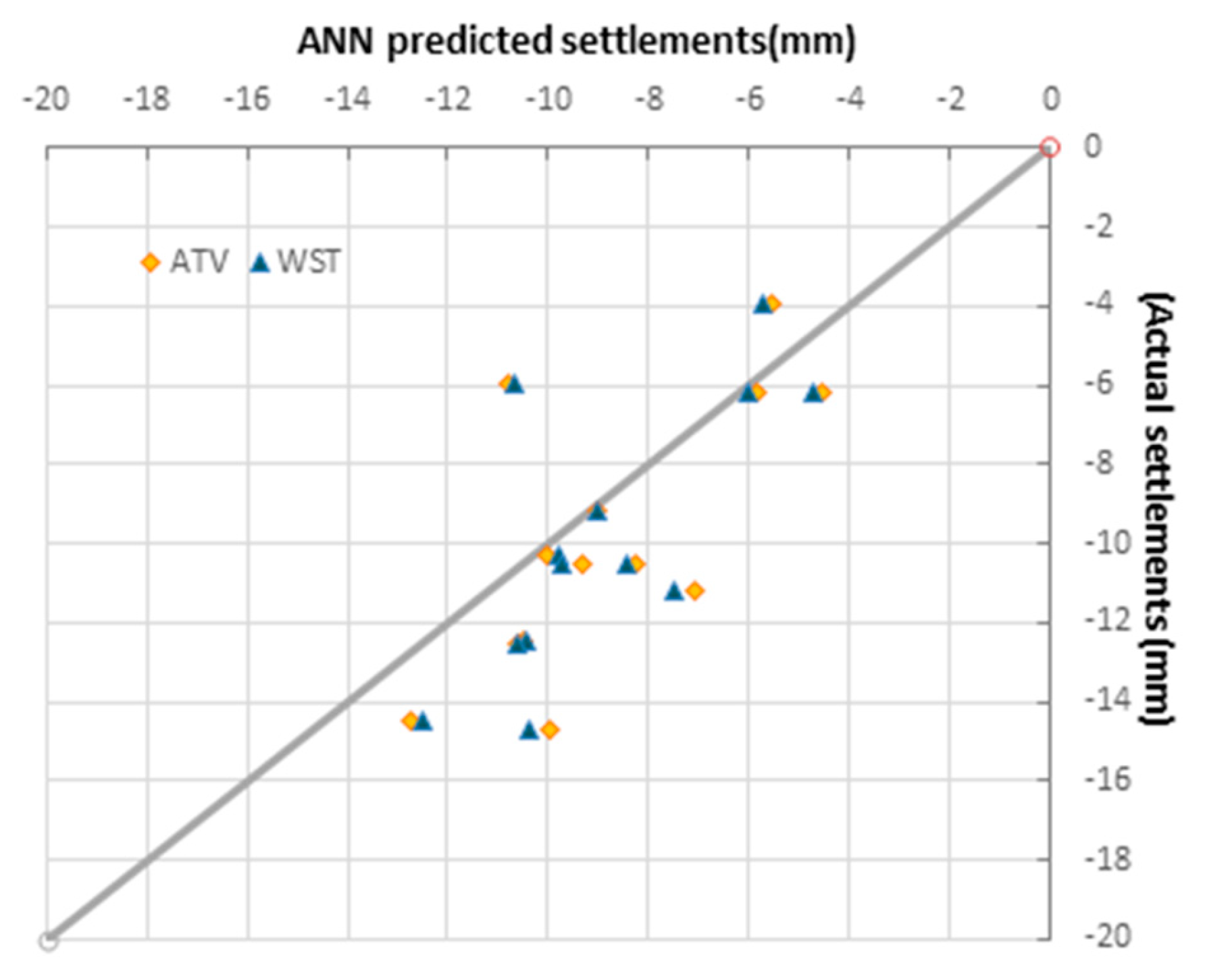
4.1. Surface Settlement Prediction Using ANN
| Volume Loss | Empirical Analysis | FEM Method | Range of Actual Settlements | Avg. of Actual Settlements | Actual Volume Loss |
|---|---|---|---|---|---|
| 0.1% | −3 mm | −3 mm | from −1.80 mm to −22 mm | −8.52 mm | 0.3–0.4% |
| 0.2% | −6 mm | ||||
| 0.3% | −9 mm | −7 mm | |||
| 0.4% | −12 mm | ||||
| 0.5% | −15 mm | ||||
| 0.6% | −18 mm | ||||
| 0.7% | −21 mm | ||||
| 0.8% | −24 mm |
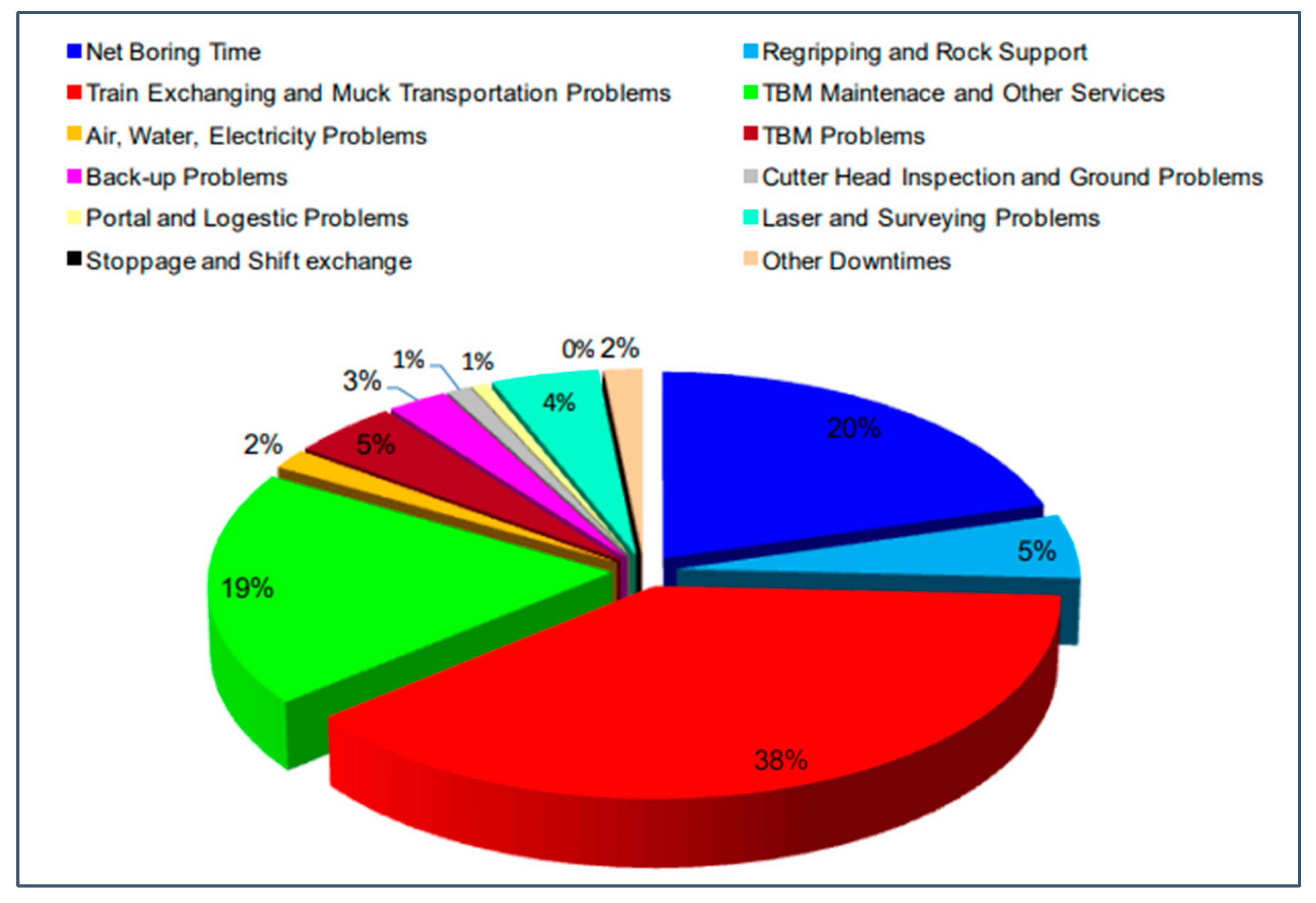
- Head torque (MNm): rotational force on the cutting head, indicating excavation resistance and safe operating limits.
- Head thrust (kN): axial force at the tunnel face, reflecting the machine’s ability to advance through various geological conditions.
- Face pressure (bar): maintains tunnel stability and prevents collapses by applying pressure to the tunnel face.
- Penetration speed (mm/rev): tracks advancement per rotation, reflecting excavation efficiency.
- Grout pressure (bar): stabilizes surrounding soil and prevents settlement through controlled grout injection.
- Screw conveyor speed (rpm): determines material removal efficiency and overall progress.
- Grout volume (L): ensures ground stability and prevents water ingress through precise grout injection.
- Excavated soil (tn/h): indicates soil removal rate, reflecting machine productivity.
- Stop time (min): reducing stoppages enhances productivity, accelerates completion, and minimizes ground settlement risks.
| TBM Operational Parameters | Min | Max | Mean | Std. |
|---|---|---|---|---|
| Head torque (MNm) | 7.10 | 13.50 | 9.98 | 1.32 |
| Head thrust (kN) | 14,514 | 23,842 | 19,166 | 2119 |
| Face pressure (bar) | 0.60 | 1.81 | 1.41 | 0.20 |
| Penetration speed (mm/rev) | 13 | 23 | 18.66 | 2.18 |
| Grout pressure (bar) | 1.5 | 4.0 | 2.5 | 0.5 |
| Screw conveyor (rpm) | 2 | 4.3 | 2.66 | 0.30 |
| Grout volume (L) | 22,138 | 4122 | 6976 | 1611 |
| Excavated soil (tn/h) | 107 | 245 | 199 | 25 |
| Stop time (min) | 3570 | 36 | 131.5 | 428.6 |
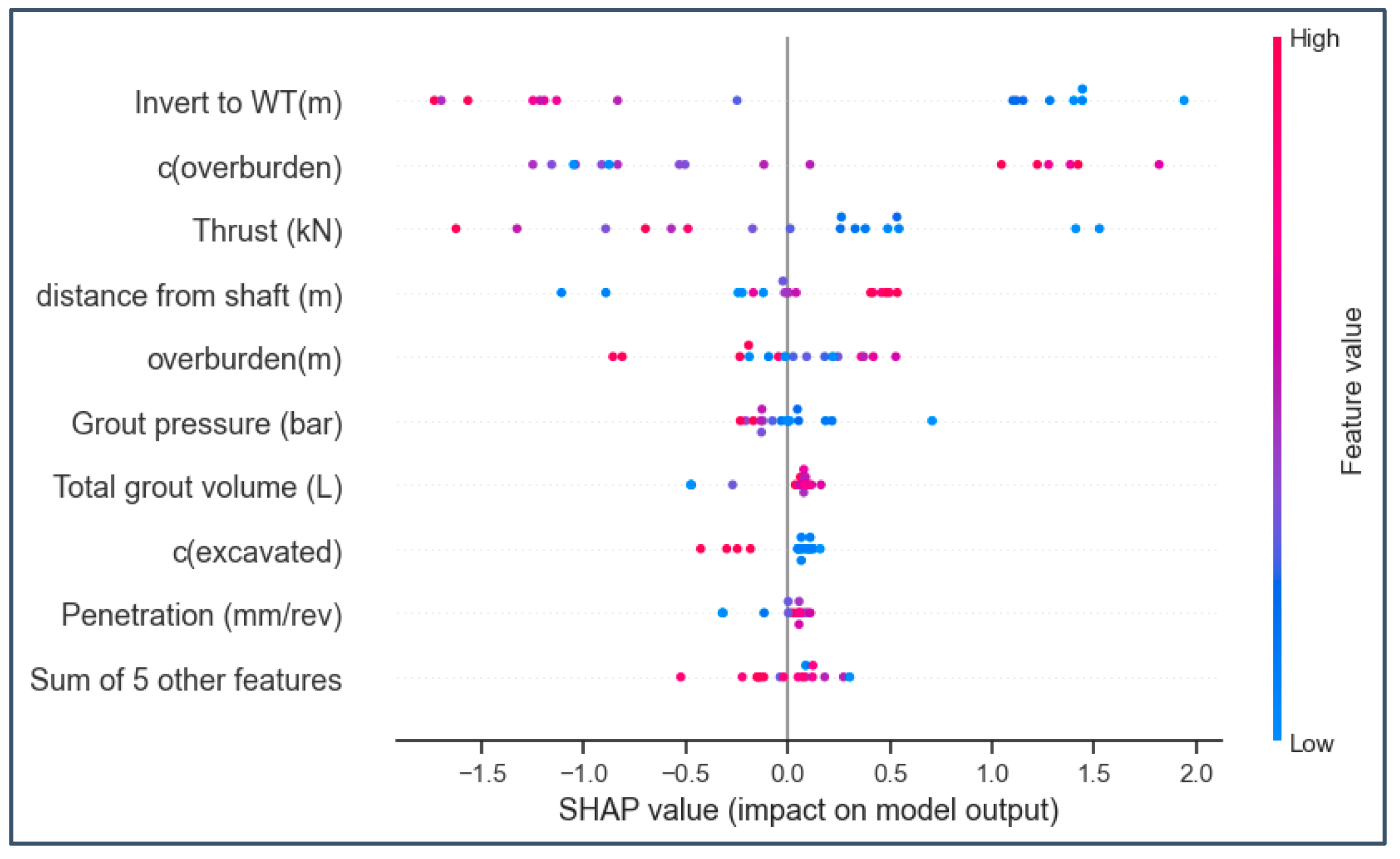
- Cohesion (c) in face area (kN): Measures soil strength at the tunnel face. Higher cohesion enhances stability, reducing collapse risk and aiding safe excavation.
- Cohesion (c) in overburden (kN): Refers to soil strength above the tunnel. Increased cohesion minimizes deformation and settlement risks.
- Angle of friction (φ) in face area: Represents soil resistance to movement at the tunnel face. A higher angle improves stability and reduces collapse risk.
- Angle of friction (φ) in overburden: Indicates soil resistance above the tunnel. A higher angle enhances overall stability and reduces settlement likelihood.
| Geotechnical Parameters | Min | Max | Mean | Std. |
|---|---|---|---|---|
| Cohesion c in face area (c_e) (kN) | 52.4 | 74.8 | 62.1 | 5.6 |
| Cohesion c in overburden (c_o) (kN) | 76.1 | 94.8 | 85.3 | 4.8 |
| Angle of friction φ in face area (f_e) | 35.2 | 41.6 | 36.1 | 0.8 |
| Angle of friction φ in overburden (f_o) | 36.1 | 40.3 | 37.8 | 1.4 |
- Overburden (m): Depth of soil or rock above the tunnel. It determines the load and pressure on the tunnel, influencing stability and design.
- Distance to water table (m): Vertical distance from the tunnel invert to the water table. A shallow water table increases seepage risks, while a deeper one may require enhanced waterproofing.
- Distance from shaft (m): Distance from the tunnel to the access point. A shorter distance can affect TBM launching and cause ground disturbance, while greater distances may lead to ground stress and surface settlements.
| Geometrical Parameters | Min | Max | Mean | Std. |
|---|---|---|---|---|
| Overburden (m) | 12.87 | 15.48 | 14.31 | 0.77 |
| Distance to water table (tunnel invert to WT) (m) | −20.6 | −17.2 | −19.1 | 1.0 |
| Distance from shaft (m) | 0.0 | 283.5 | 131.7 | 83.1 |
4.2. Model Development and Results
- ATV (all the variables): model with all features.
- WST (without stop time): model excluding the stop time parameter.
- WGV (without grout volume): model excluding the grout volume parameter.
- WES (without excavated soil): model excluding the excavated soil parameter.
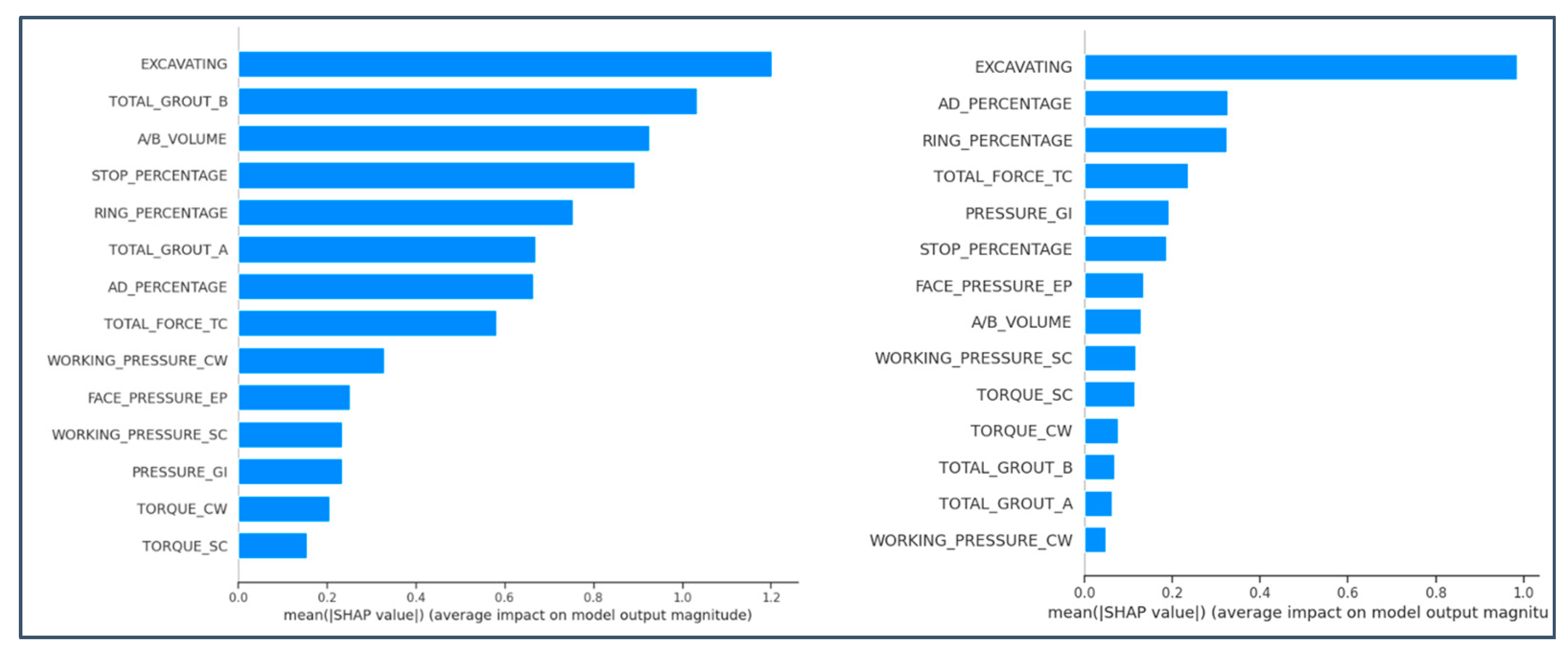
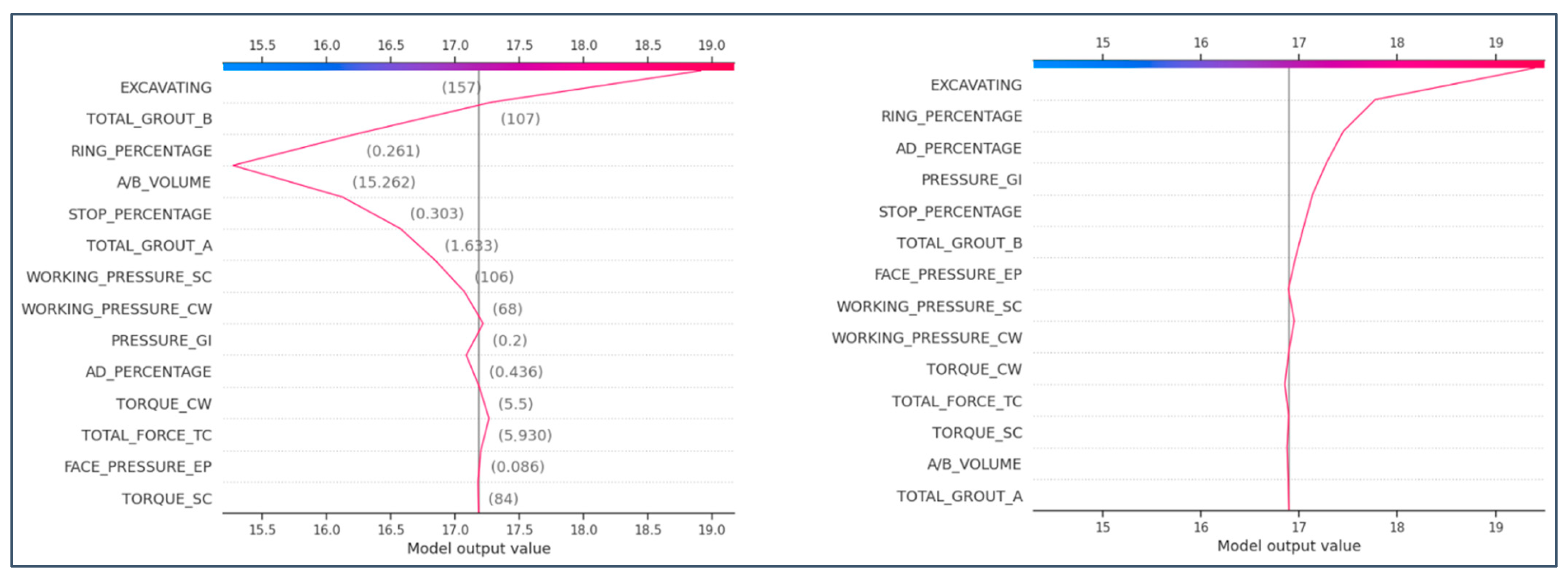
4.3. SHapley Additive exPlanations (SHAP)
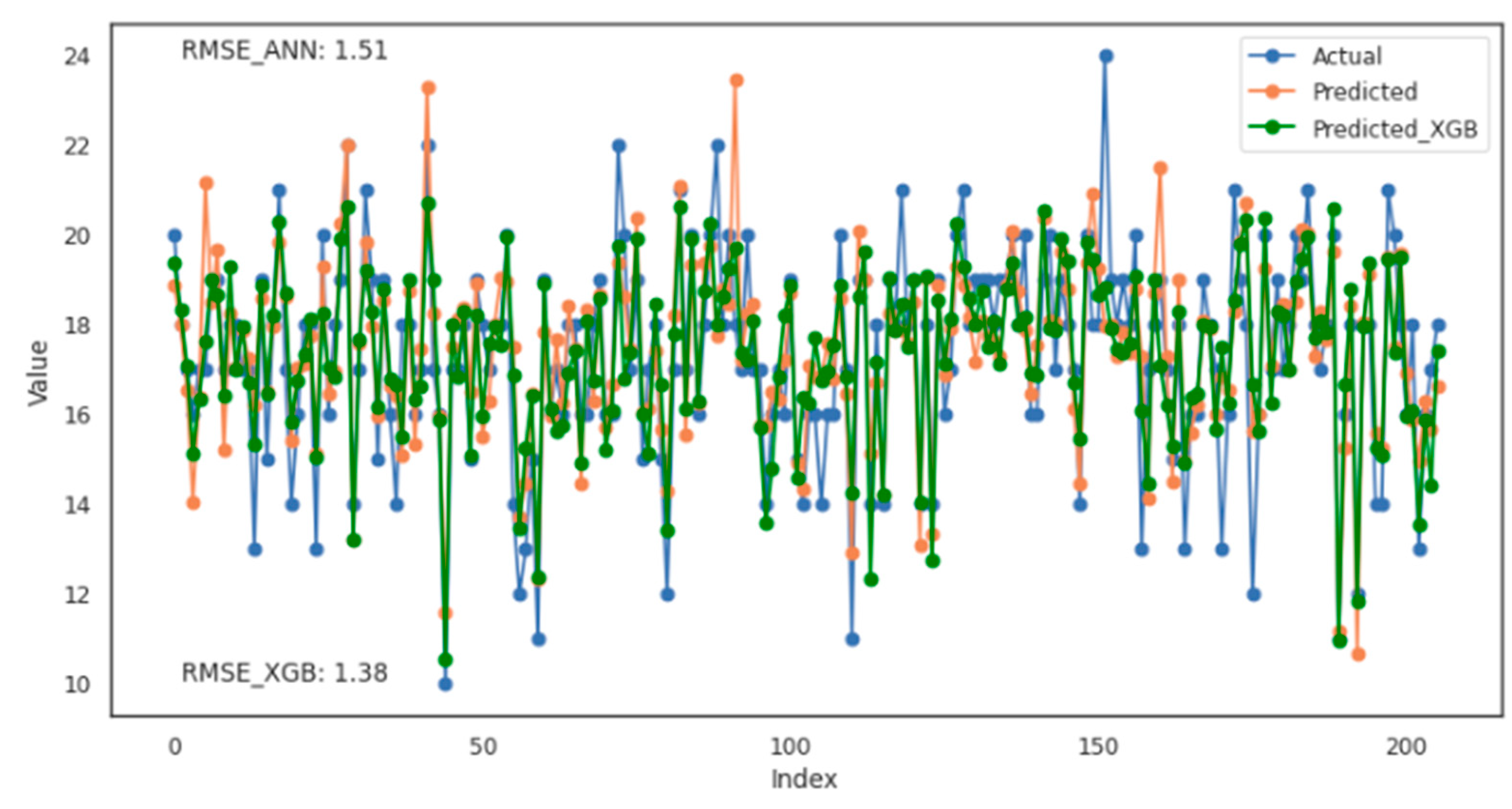
4.4. Penetration Rate Prediction Using ANN and XGBR
4.5. Model Development and Results in Penetration Rate Prediction
4.6. SHapley Additive exPlanations (SHAP) in Penetration Rate Prediction
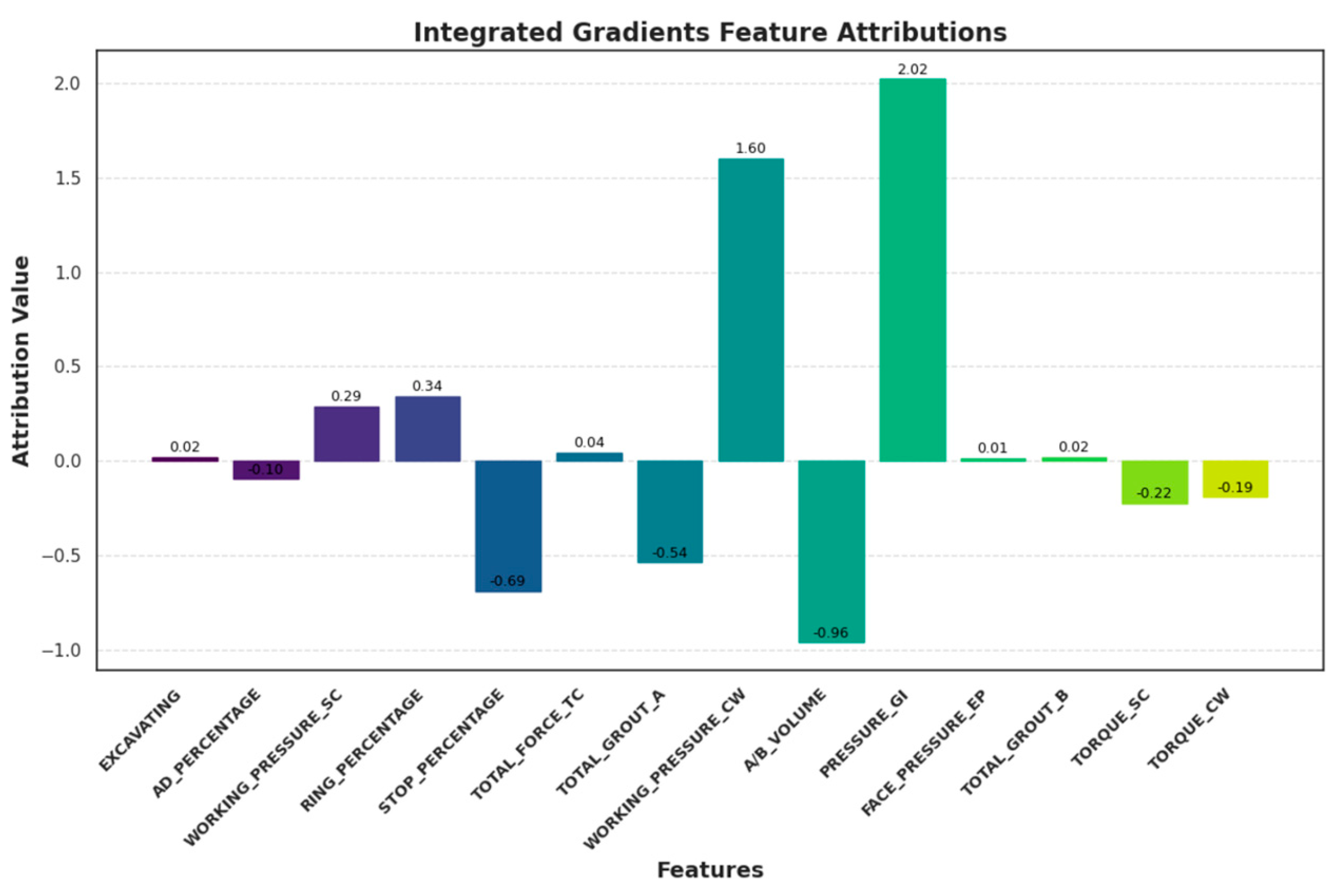
4.7. Other Interpretable Models
- Sensitivity: features with no effect on the prediction receive zero attribution.
- Completeness: the sum of all feature attributions equals the difference between the model’s output at the actual input and the baseline.
- Weight: the number of times a feature is used to split data across all trees.
- Gain: the average information gain from splits involving the feature.
- Cover: the average number of samples covered by splits using the feature.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jamshidi, A. Prediction of TBM penetration rate from brittleness indexes using multiple regression analysis. Model. Earth Syst. Environ. 2018, 4, 383–394. [Google Scholar] [CrossRef]
- Benardos, A.G.; Kaliampakos, D.C. Modelling TBM performance with artificial neural networks. Tunn. Undergr. Space Technol. 2004, 19, 597–605. [Google Scholar] [CrossRef]
- Ghasemi, E.; Yagiz, S.; Ataei, M. Predicting penetration rate of hard rock tunnel boring machine using fuzzy logic. Bull. Eng. Geol. Environ. 2014, 73, 23–35. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Z.; Luo, H.; Wang, S.; Zhao, Y.; Liu, L.; Ling, D.; Jing, L. Tunnel boring machines (TBM) performance prediction: A case study using big data and deep learning. Tunn. Undergr. Space Technol. 2021, 110, 103636. [Google Scholar] [CrossRef]
- Benardos, A. Artificial intelligence in underground development: A study of TBM performance. In Proceedings of the WIT Transactions on the Built Environment, The New Forest, UK, 8–10 September 2008; Volume 102, pp. 21–32. [Google Scholar] [CrossRef]
- Alvarez Grima, M.; Bruines, P.A.; Verhoef, P.N.W. Modeling tunnel boring machine performance by neuro-fuzzy methods. Tunn. Undergr. Space Technol. 2000, 15, 259–269. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Prediction of hard rock TBM penetration rate using particle swarm optimization. Int. J. Rock Mech. Min. Sci. 2011, 48, 427–433. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Mohamad, E.; Narayanasamy, M.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Ninic, J.; Bui, H.-G.; Koch, C.; Meschke, G. Computationally Efficient Simulation in Urban Mechanized Tunneling Based on Multilevel BIM Models. J. Comput. Civ. Eng. 2019, 33. [Google Scholar] [CrossRef]
- Zhao, Z.; Gong, Q.; Zhang, Y.; Zhao, J. Prediction model of tunnel boring machine performance by ensemble neural networks. Geomech. Geoengin. 2007, 2, 123–128. [Google Scholar] [CrossRef]
- Kannangara, K.K.P.M.; Zhou, W.; Ding, Z.; Hong, Z. Investigation of feature contribution to shield tunneling-induced settlement using Shapley additive explanations method. J. Rock Mech. Geotech. Eng. 2022, 14, 1052–1063. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, H.; Wu, B.; Li, G.; Zhou, L. Interpretable predictive model for shield attitude control performance based on XGboost and SHAP. Sci. Rep. 2022, 12, 18226. [Google Scholar] [CrossRef] [PubMed]
- Sirisena, G.; Jayasinghe, T.; Gunawardena, T.; Zhang, L.; Mendis, P.; Mangalathu, S. Machine learning-based framework for predicting the fire-induced spalling in concrete tunnel linings. Tunn. Undergr. Space Technol. 2024, 153, 106000. [Google Scholar] [CrossRef]
- Flor, A.; Sassi, F.; La Morgia, M.; Cernera, F.; Amadini, F.; Mei, A.; Danzi, A. Artificial intelligence for tunnel boring machine penetration rate prediction. Tunn. Undergr. Space Technol. 2023, 140, 105249. [Google Scholar] [CrossRef]
- Ralph Peck, B. Deep Excavations and Tunneling in Soft Ground. In 7th International Conference on Soil Mechanics and Foundation Engineering (Mexico), Mexico: International Society for Soil Mechanics and Geotechnical Engineering. 1969. Available online: https://www.issmge.org/publications/publication/deep-excavations-and-tunneling-in-soft-ground (accessed on 2 December 2024).
- Guglielmetti, V.; Grasso, P.; Mahtab, A.; Xu, S. (Eds.) Mechanized Tunnelling in Urban Areas: Design Methodology and Construction Control, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-0-203-93851-5. [Google Scholar]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar] [CrossRef]
- Lipovetsky, S.; Conklin, M. Analysis of Regression in Game Theory Approach. Appl. Stoch. Models Bus. Ind. 2001, 17, 319–330. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Koukoutas, S.; Sofianos, A. Settlements Due to Single and Twin Tube Urban EPB Shield Tunnelling. Ge-Otechnical Geol. Eng. 2015, 33, 487–510. [Google Scholar] [CrossRef]
- Attiko Metro, S.A. AGHIOS DIMITRIOS—ELLINIKO Extension. Available online: https://www.emetro.gr/?page_id=4179&lang=en (accessed on 2 December 2024).
- Settlements Above Tunnels in the United Kingdom—Their Magnitude and Prediction—Tunnels & Tunnelling International. Available online: https://www.tunnelsonline.info/news/settlements-above-tunnels-in-the-united-kingdom-their-magnitude-and-prediction-6733559 (accessed on 9 January 2024).
- Kantorovich, L.V.; Rubinshtein, S.G. On a Space of Totally Additive Functions. Vestn. St. P. Univ. Math. 1958, 13, 52–59. [Google Scholar]









| Models | MSE (mm) | RMSE (mm) | Average Accuracy | ||
|---|---|---|---|---|---|
| Train | Test | Train | Test | Test | |
| “ATV” | 0.004 | 0.037 | 0.020 | 0.193 | 80.10% |
| “WST” | 0.010 | 0.018 | 0.100 | 0.135 | 80.70% |
| “WGV” | 0.005 | 0.038 | 0.070 | 0.196 | 80.02% |
| “WES” | 0.012 | 0.023 | 0.109 | 0.152 | 79.30% |
| TBM Operational Parameters | Min | Max | Mean | Std. |
|---|---|---|---|---|
| TORQUE CW [MNm] | 4.30 | 13.50 | 9.77 | 1.47 |
| WORKING PRESSURE CW [bar] | 53.00 | 169.00 | 122.35 | 18.27 |
| TOTAL FORCE TC [kN] | 5930.00 | 26,118.00 | 17,903.09 | 2869.86 |
| SPEED TC [mm/min] | 8.00 | 24.00 | 17.17 | 2.19 |
| TORQUE SC [kNm] | 0.00 | 122.00 | 78.47 | 14.74 |
| WORKING_PRESSURE SC [bar] | 0.00 | 154.00 | 98.96 | 18.65 |
| PRESSURE GI [bar] | 0.02 | 3.55 | 1.97 | 0.53 |
| TOTAL GROUT A [L] | 1011.00 | 8817.00 | 6333.44 | 500.90 |
| TOTAL GROUT B [L] | 107.00 | 621.00 | 476.27 | 43.75 |
| A/B VOLUME | 2.14 | 17.67 | 13.36 | 1.16 |
| EXCAVATING [t/h] | 29.00 | 252.00 | 182.44 | 32.06 |
| FACE PRESSURE EP [bar] | 0.00 | 1.97 | 1.29 | 0.28 |
| AD PERCENTAGE | 0.10 | 0.80 | 0.61 | 0.09 |
| RING PERCENTAGE | 0.12 | 0.58 | 0.30 | 0.06 |
| STOP PERCENTAGE | 0.00 | 0.55 | 0.09 | 0.10 |
| Models | MSE (mm/min) | RMSE (mm/min) | Wasserstein Distance | |||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| XGB | 0.38 | 1.90 | 0.62 | 1.38 | 0.33 | 0.42 |
| ANN | 1.06 | 2.26 | 1.03 | 1.50 | 0.30 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sioutas, K.N.; Benardos, A. Boosting Model Interpretability for Transparent ML in TBM Tunneling. Appl. Sci. 2024, 14, 11394. https://doi.org/10.3390/app142311394
Sioutas KN, Benardos A. Boosting Model Interpretability for Transparent ML in TBM Tunneling. Applied Sciences. 2024; 14(23):11394. https://doi.org/10.3390/app142311394
Chicago/Turabian StyleSioutas, Konstantinos N., and Andreas Benardos. 2024. "Boosting Model Interpretability for Transparent ML in TBM Tunneling" Applied Sciences 14, no. 23: 11394. https://doi.org/10.3390/app142311394
APA StyleSioutas, K. N., & Benardos, A. (2024). Boosting Model Interpretability for Transparent ML in TBM Tunneling. Applied Sciences, 14(23), 11394. https://doi.org/10.3390/app142311394







