Damage Indicators for Structural Monitoring of Fiber-Reinforced Polymer-Strengthened Concrete Structures Based on Manifold Invariance Defined on Latent Space of Deep Autoencoders
Abstract
1. Introduction
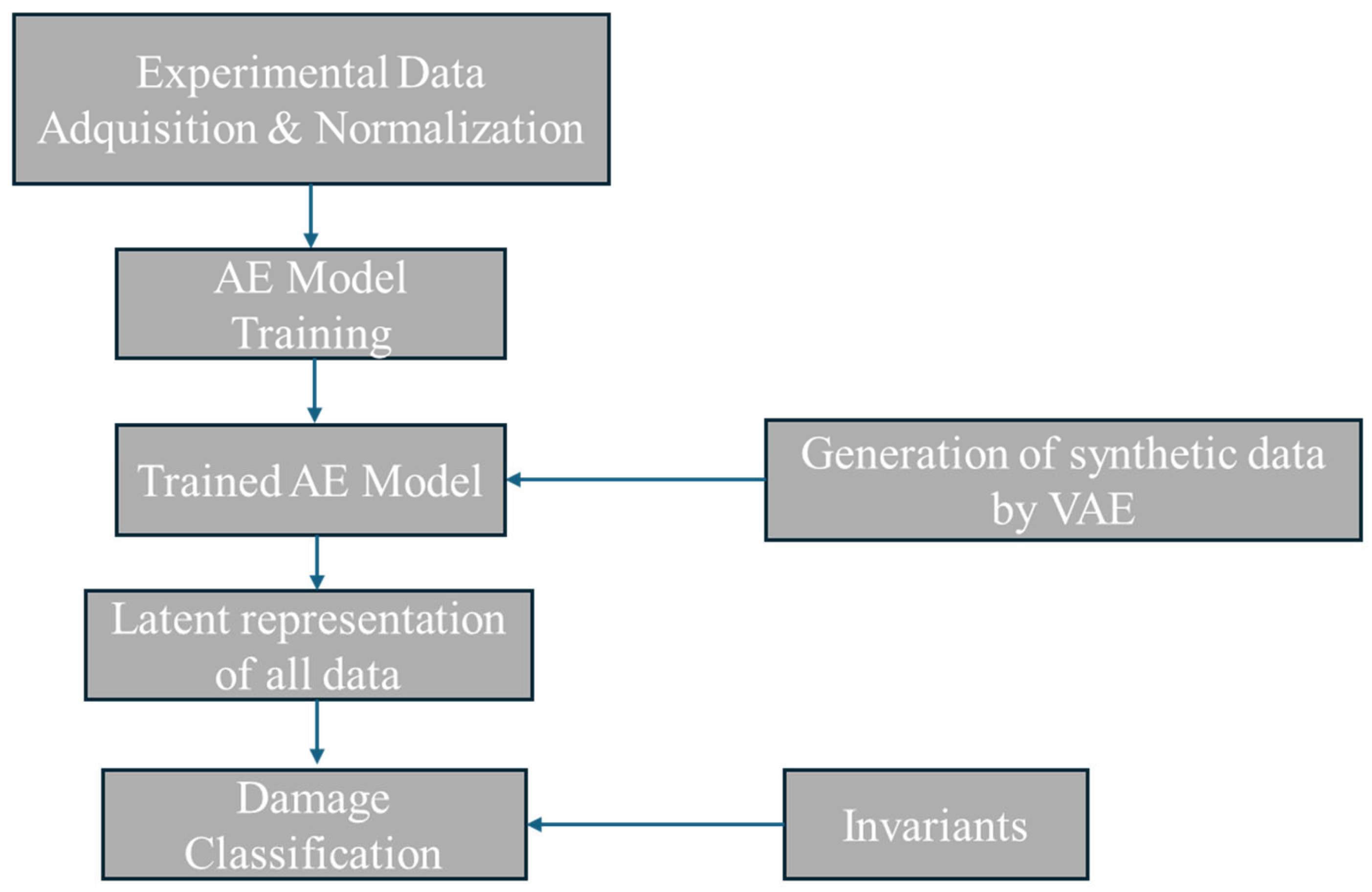
2. Methodology
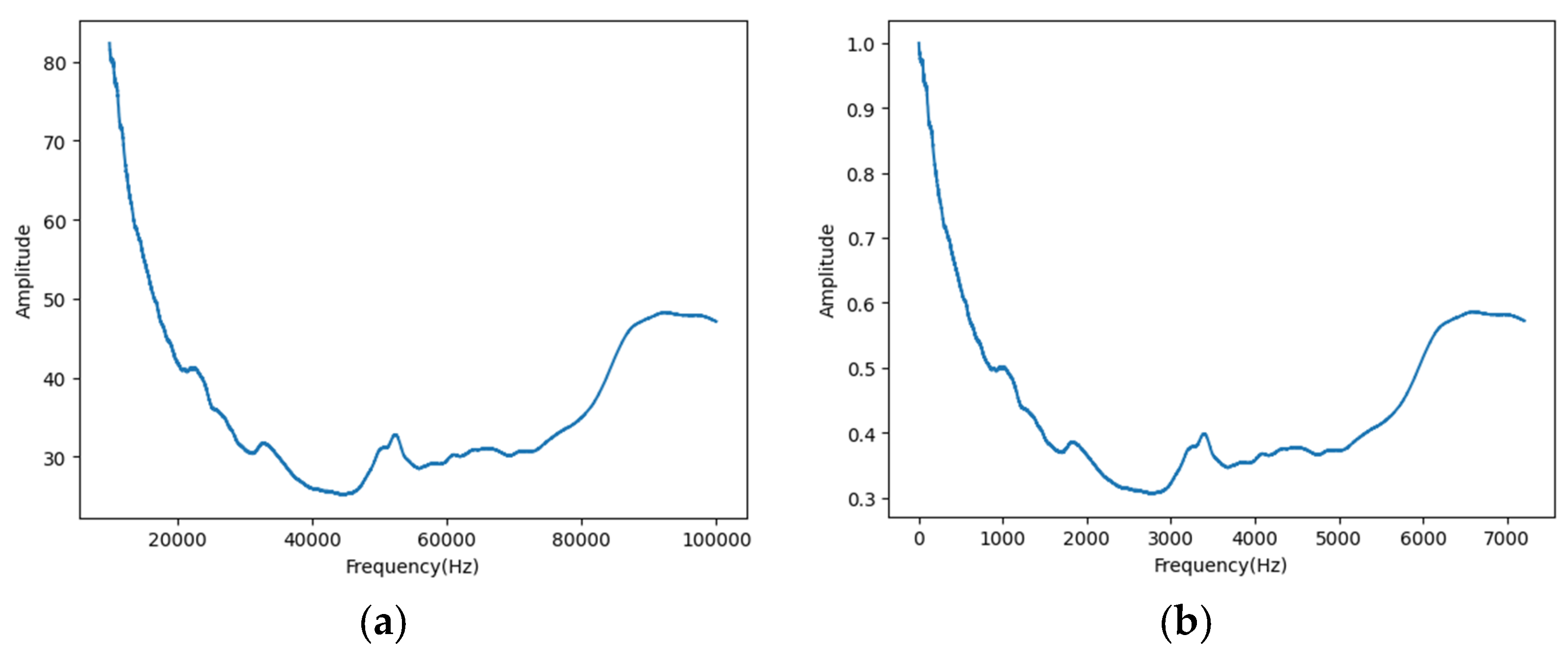
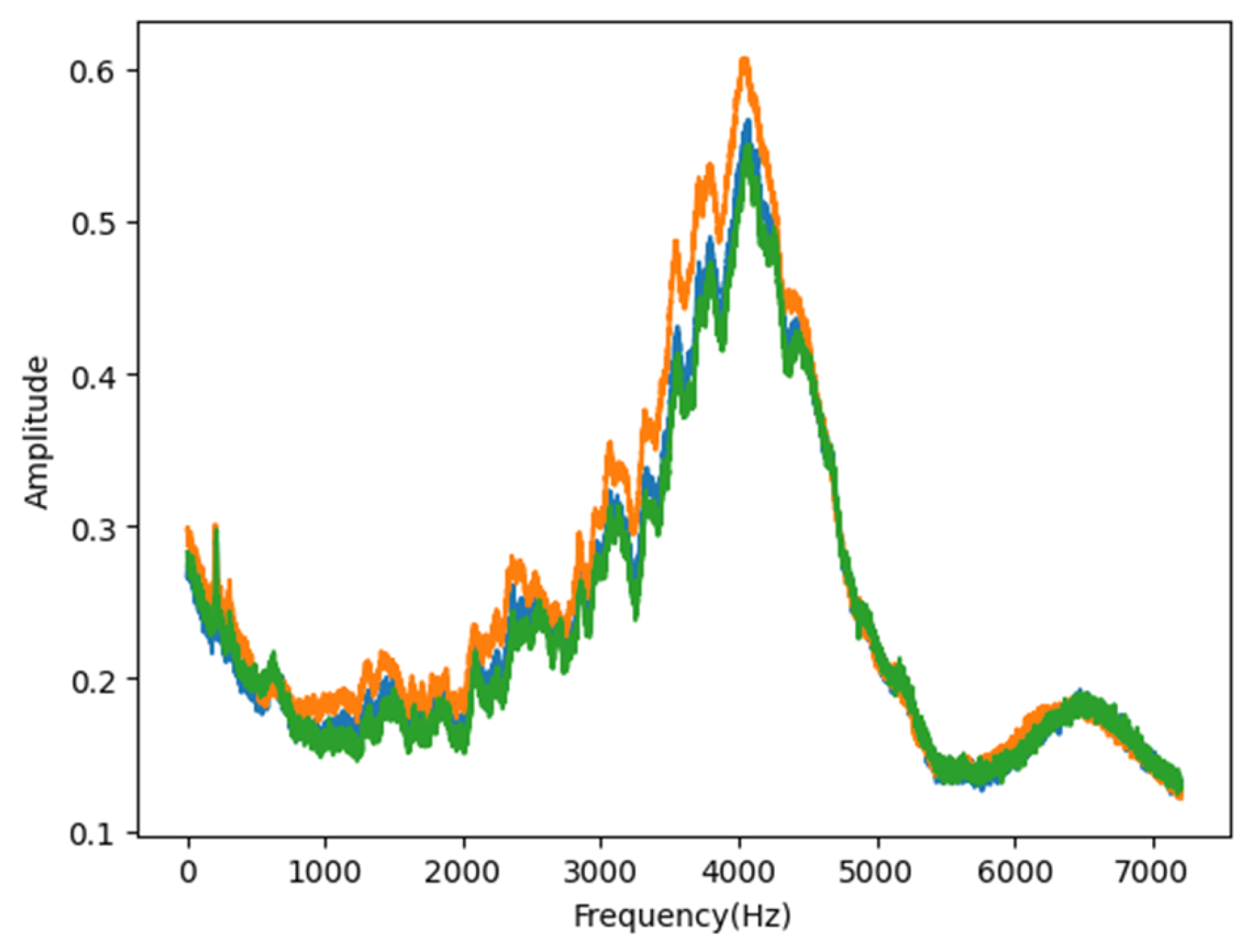
2.1. Collection of Dataset and Data Normalization: EMI Method
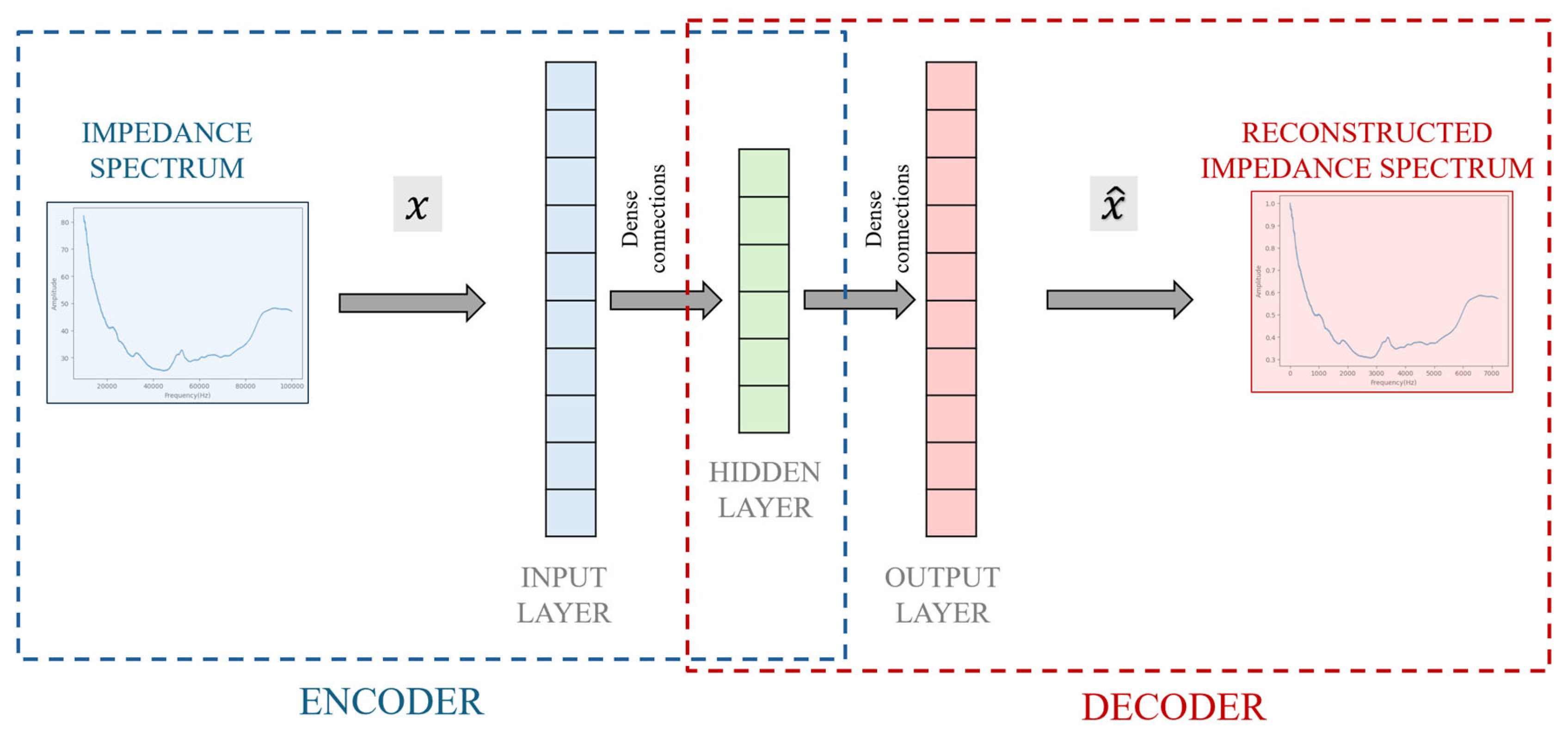
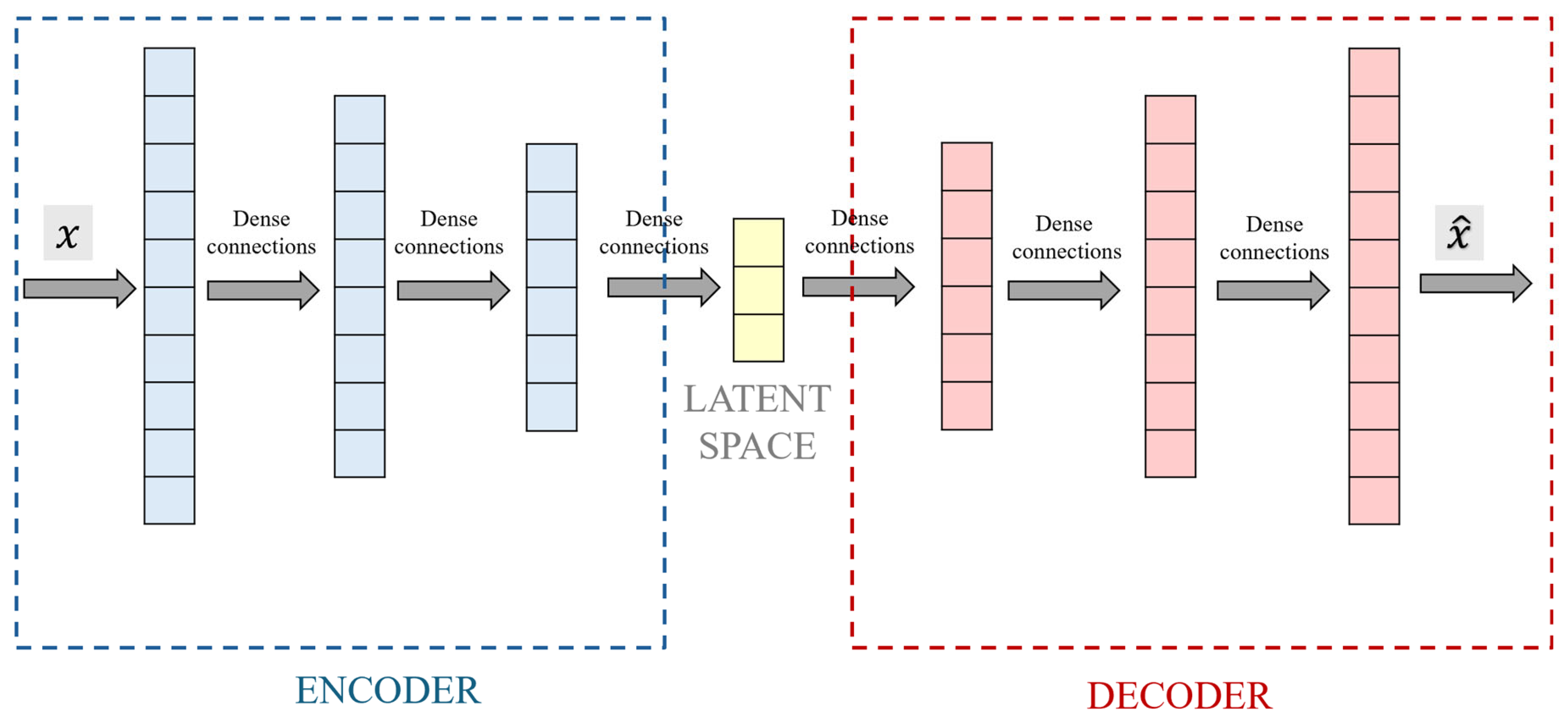
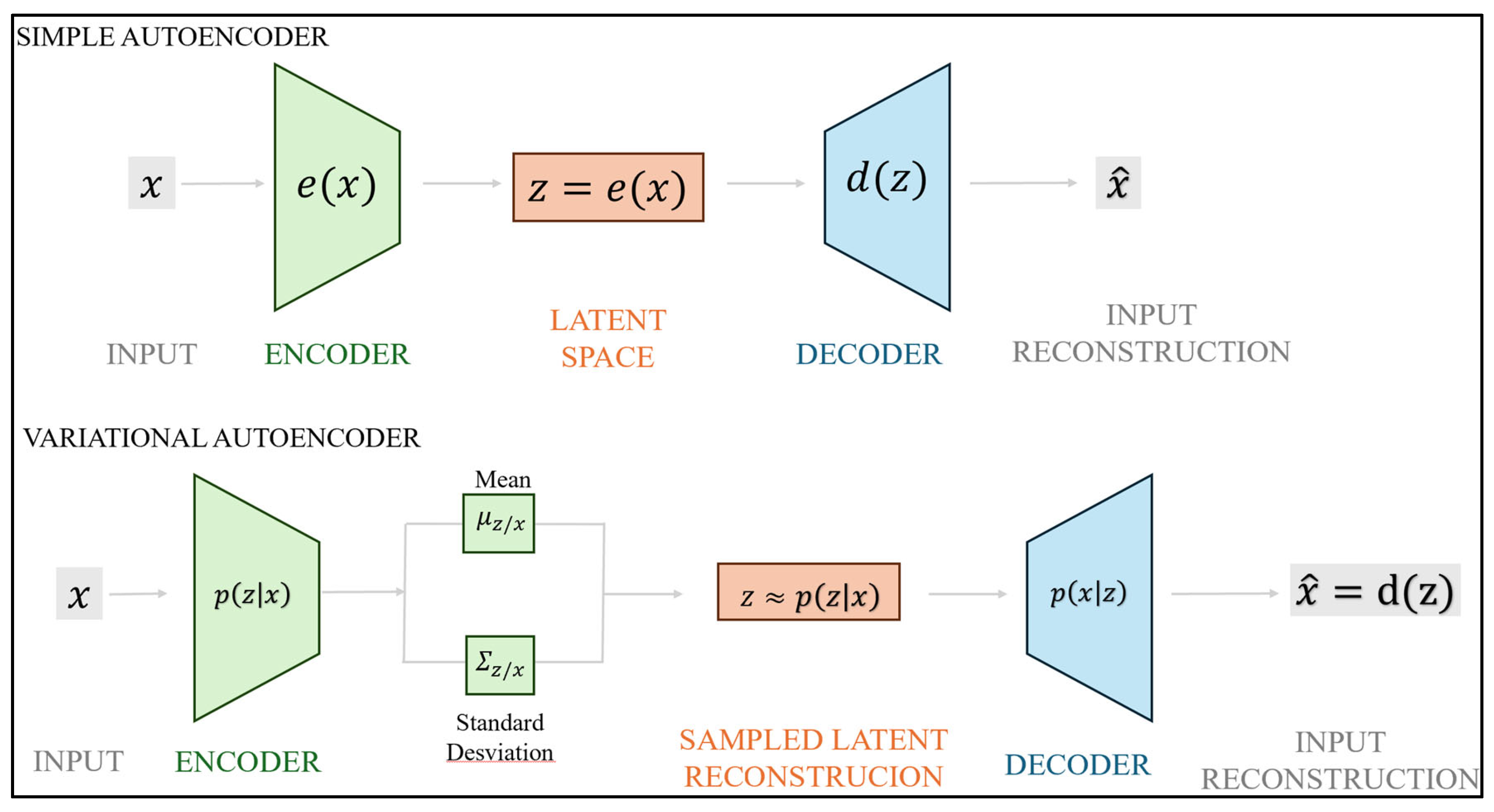
2.2. Deep Autoencoders: Latent Space Classification
2.3. Synthetic Data Generation with Variational Autoencoders
2.4. Damage Identification
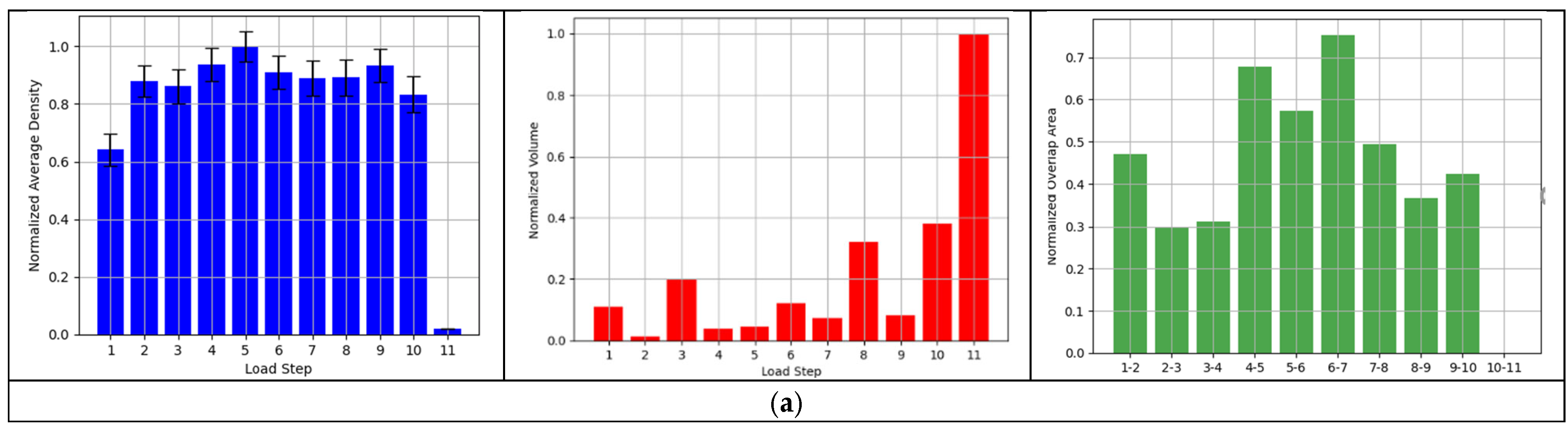
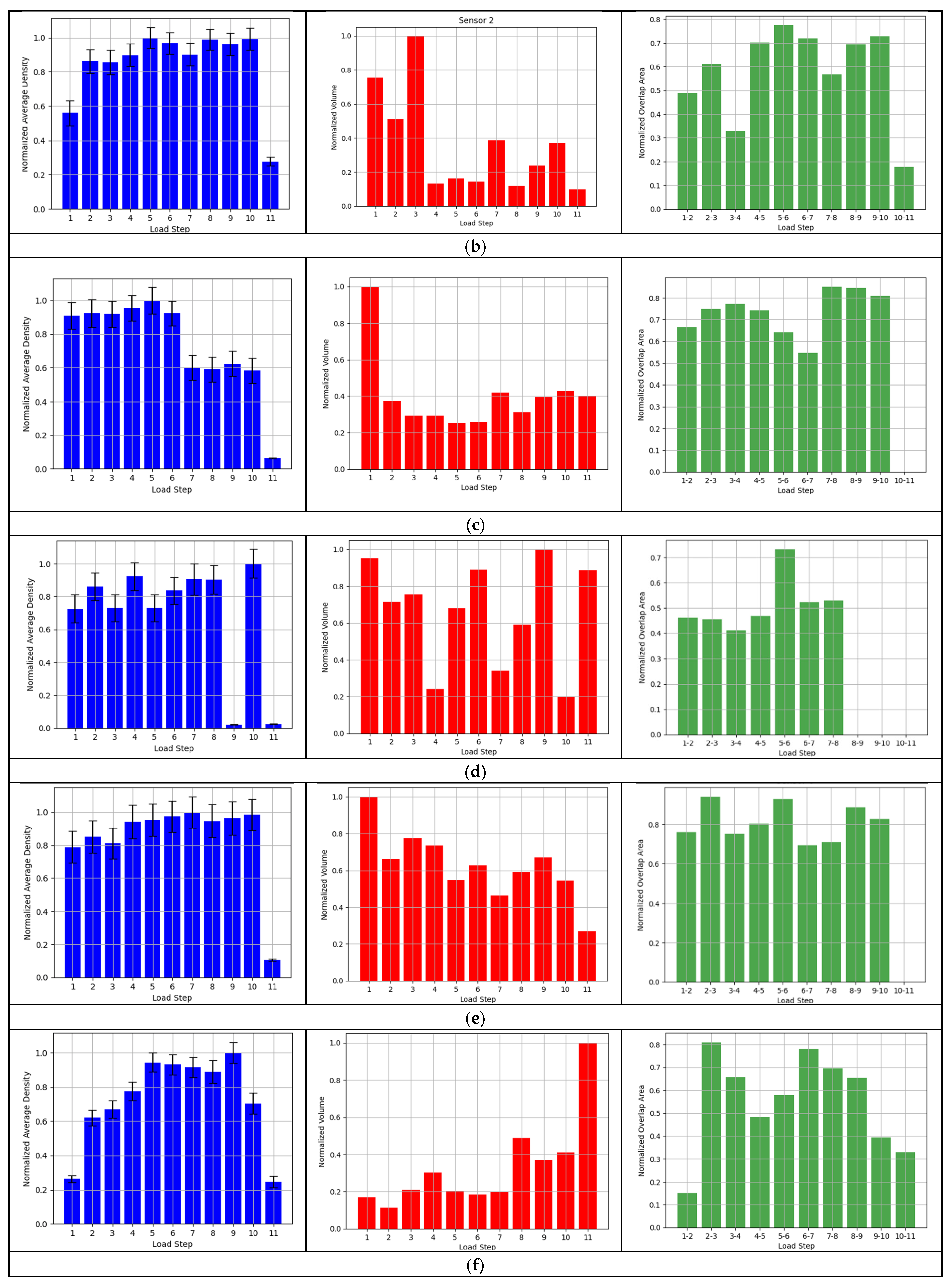
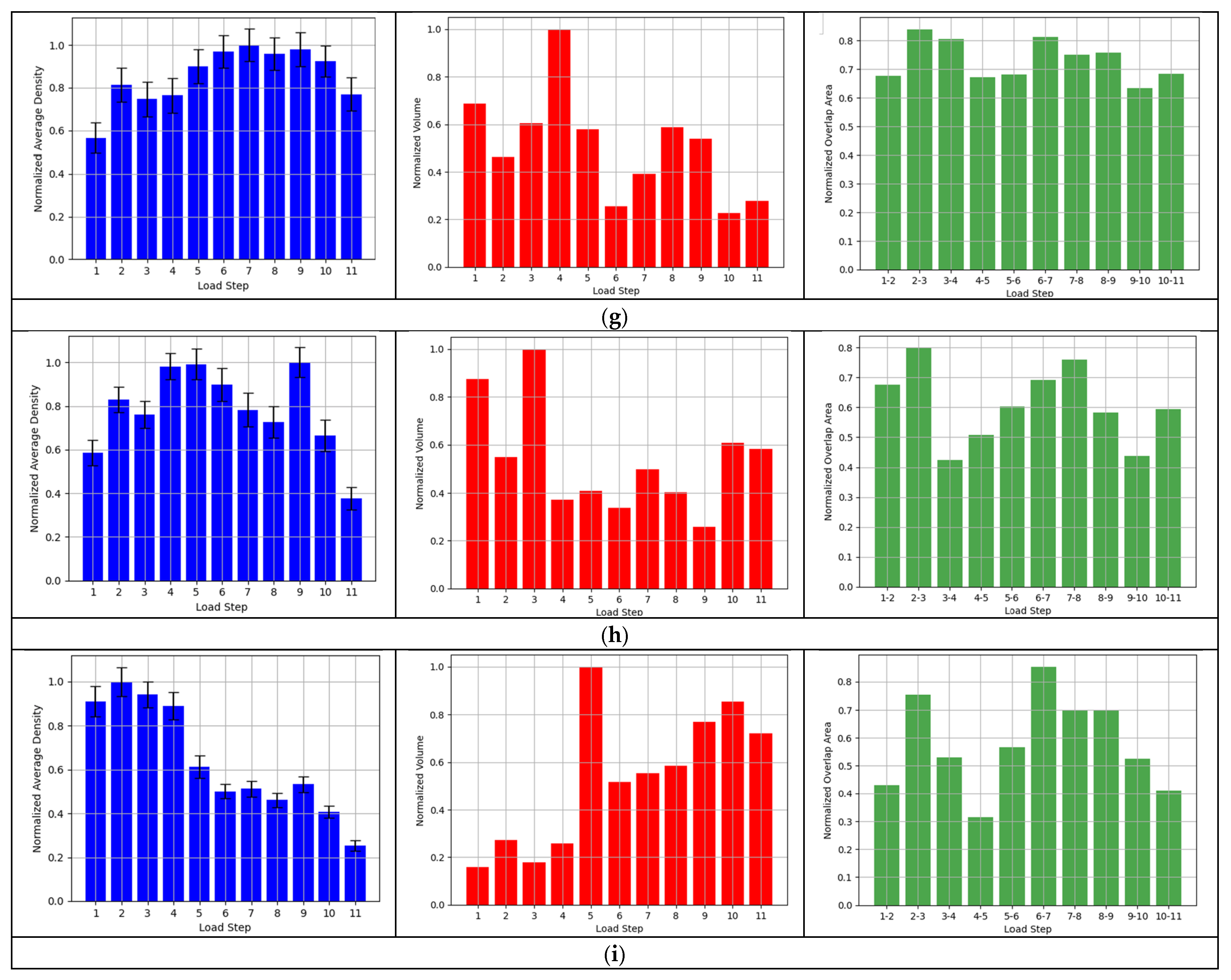
2.4.1. Density
2.4.2. The Volume of the Convex Hull
2.4.3. Ellipse Overlap
2.4.4. An Ensemble Application of the Indicators
- Density provides insights into the concentration and cohesion of data points.
- The volume of the convex hull captures the overall spatial dispersion and geometric configuration.
- Ellipse overlap assesses the dynamic similarity in data distribution between consecutive load steps.
3. Experimental Validation
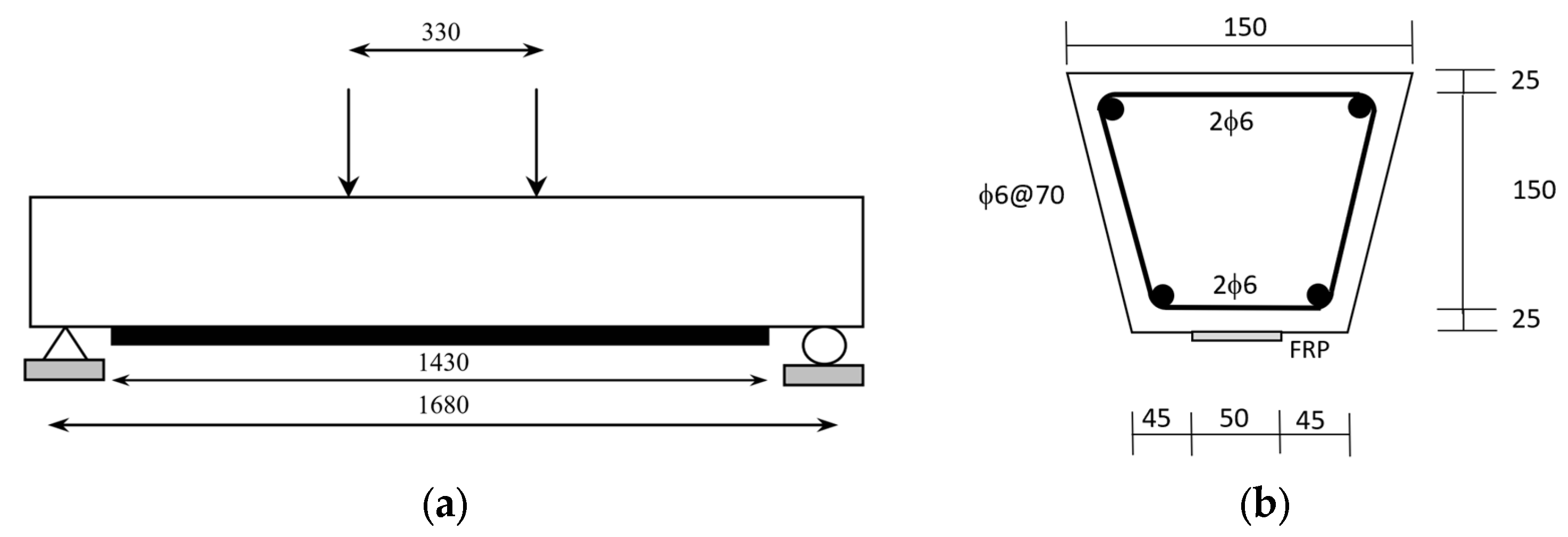
3.1. Experimental Set-Up
3.2. Dataset
3.3. VAE Configuration: Data Augmentation
3.4. Deep Autoencoder Configuration
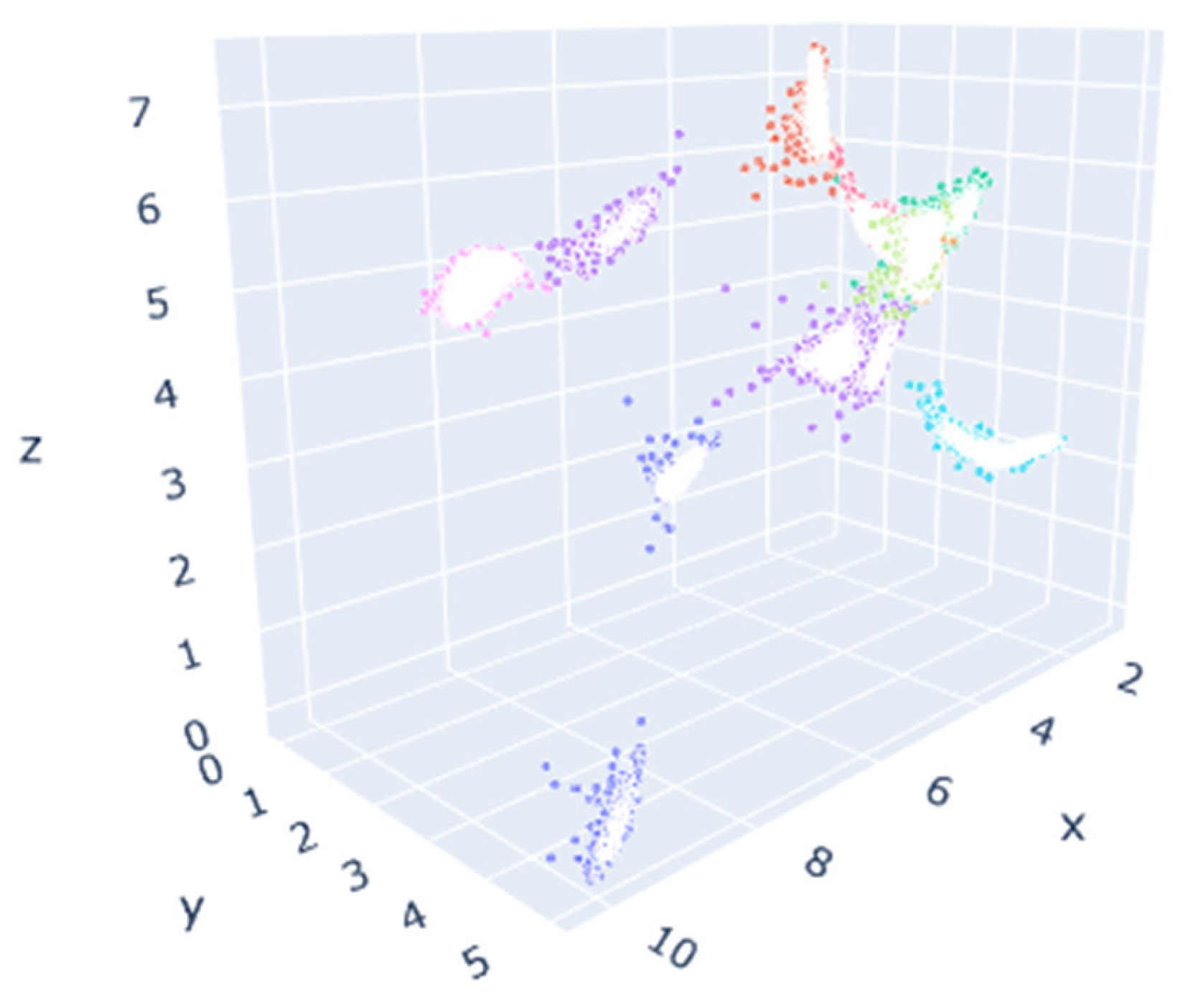
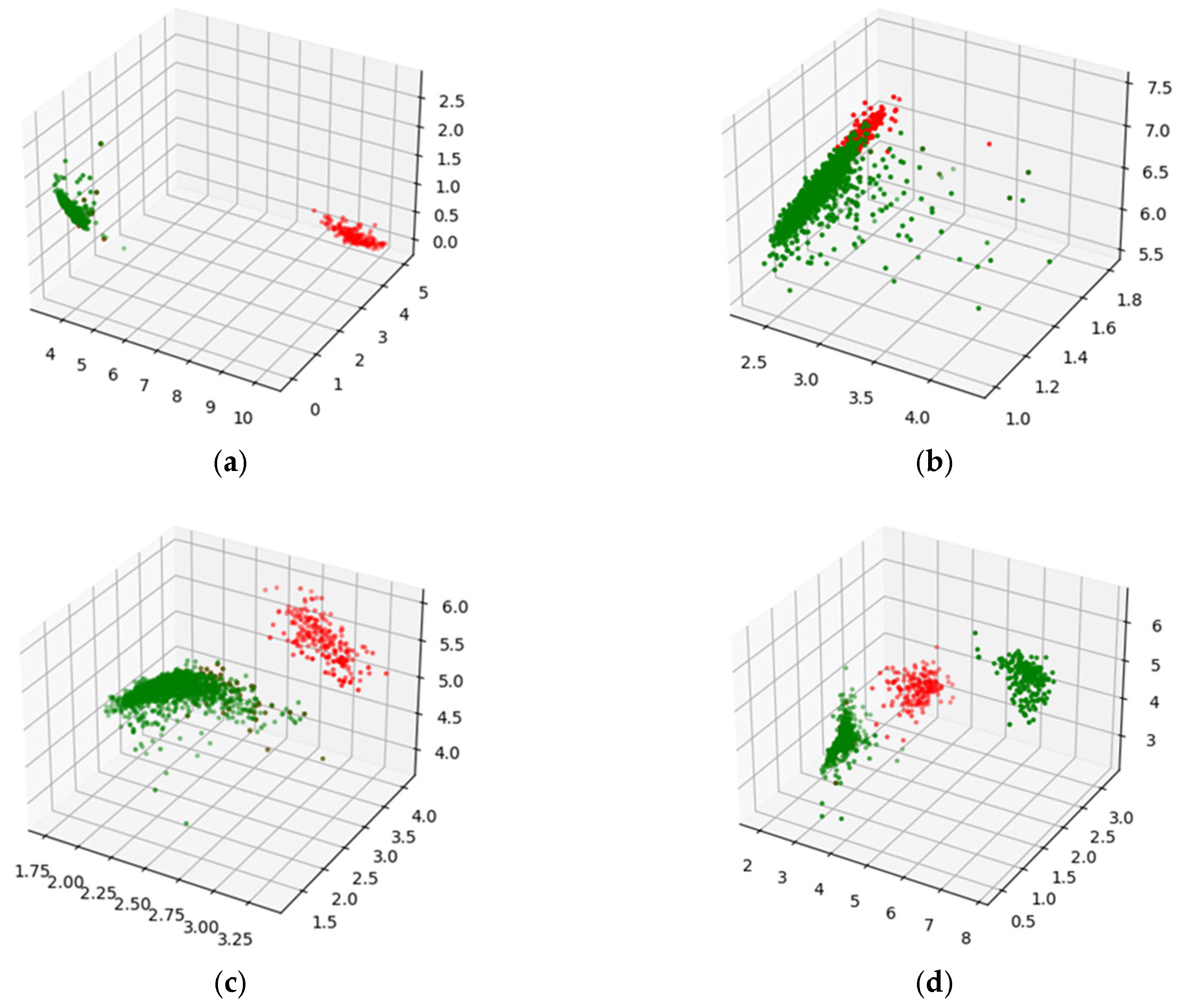
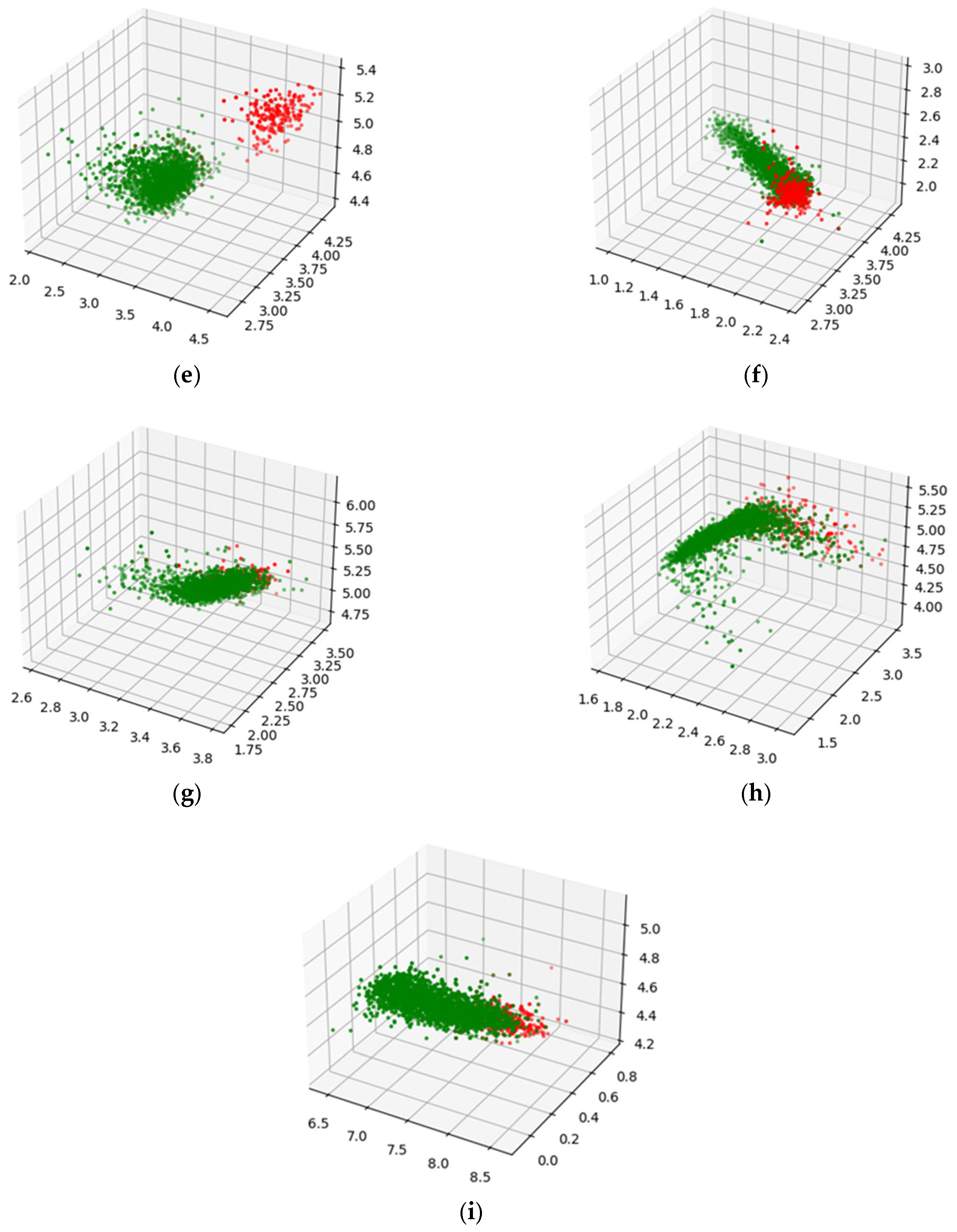
3.5. Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FRPs | Fiber-reinforced polymers |
| PZT | Lead zirconate titanate |
| RC | Reinforced concrete |
| SHM | Structural health monitoring |
| EMI | Electromechanical impedance |
| ML | Machine learning |
| AE | Autoencoder |
| VAE | Variational autoencoder |
| RMSE | Root mean squared error |
| KDE | Kernel Density Estimation |
| MSE | Mean squared error |
| KLD | Kullback–Leibler Divergence |
References
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Ghiasi, A.; Moghaddam, M.K.; Ng, C.T.; Sheikh, A.H.; Shi, J.Q. Damage classification of in-service steel railway bridges using a novel vibration-based convolutional neural network. Eng. Struct. 2022, 264, 114474. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Huang, B.G.; Wang, X.Y.; Xia, Y. Deep learning-based rapid damage assessment of RC columns under blast loading. Eng. Struct. 2022, 271, 114949. [Google Scholar] [CrossRef]
- Ai, D.; Cheng, J. A deep learning approach for electromechanical impedance based concrete structural damage quantification using two-dimensional convolutional neural network. Mech. Syst. Signal Process. 2023, 183, 109634. [Google Scholar] [CrossRef]
- Jiang, T.; Frøseth, G.T.; Rønnquist, A. A robust bridge rivet identification method using deep learning and computer visión. Eng. Struct. 2023, 283, 115809. [Google Scholar] [CrossRef]
- Ahmadian, V.; Beheshti Aval, S.B.; Noori, M.; Wang, T.; Altabey, W.A. Comparative study of a newly proposed machine learning classification to detect damage occurrence in structures. Eng. Appl. Artif. Intel. 2024, 127, 107226. [Google Scholar] [CrossRef]
- Lomazzi, L.; Giglio, M.; Cadini, F. Towards a deep learning-based unified approach for structural damage detection, localisation and quantification. Eng. Appl. Artif. Intel. 2023, 121, 106003. [Google Scholar] [CrossRef]
- Di Mucci, V.M.; Cardellicchio, A.; Ruggieri, S.; Nettis, A.; Renò, V.; Uva, G. Artificial intelligence in structural health management of existing bridges. Autom. Constr. 2025, 167, 105719. [Google Scholar] [CrossRef]
- Sony, S.; Dunphy, K.; Sadhu, A.; Capretz, M. A systematic review of convolutional neural network-based structural condition assessment techniques. Eng. Struct. 2021, 226, 111347. [Google Scholar] [CrossRef]
- Viotti, I.D.; Ribeiro, R.F., Jr.; Gomes, G.F. Damage identification in sandwich structures using Convolutional Neural Networks. Mech. Syst. Signal Process. 2024, 220, 111649. [Google Scholar] [CrossRef]
- Sattarifar, A.; Nestorović, T. Damage localization and characterization using one-dimensional convolutional neural network and a sparse network of transducers. Eng. Appl. Artif. Intel. 2022, 115, 105273. [Google Scholar]
- Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
- Barzegar, V.; Laflamme, S.; Hu, C.; Dodson, J. Ensemble of recurrent neural networks with long short-term memory cells for high-rate structural health monitoring. Mech. Syst. Signal Process. 2022, 164, 108201. [Google Scholar] [CrossRef]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Ni, P. Structural damage identification based on autoencoder neural networks and deep learning. Eng. Struct. 2018, 172, 13–28. [Google Scholar] [CrossRef]
- Ma, X.; Lin, Y.; Ma, H. Structural damage identification based on unsupervised feature-extraction via variational Auto-encoder. Measurement 2020, 160, 107811. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Li, H.; Zhou, B. An unsupervised tunnel damage identification method based on convolutional variational auto-encoder and wavelet packet analysis. Sensors 2022, 22, 2412. [Google Scholar] [CrossRef]
- Römgens, N.; Abbassi, A.; Jonscher, C.; Grießmann, T.; Rolfes, R. On using autoencoders with non-standardized time series data for damage localization. Eng. Struct. 2024, 303, 117570. [Google Scholar] [CrossRef]
- Yang, K.; Kim, S.; Harley, J.B. Unsupervised long-term damage detection in an uncontrolled environment through optimal autoencoder. Mech. Syst. Signal Process. 2023, 199, 110473. [Google Scholar] [CrossRef]
- Perera, R.; Montes, J.; Gomez, A.; Barris, C.; Baena, M. Unsupervised autoencoders with features in the electromechanical impedance domain for early damage assessment in FRP-strengthened concrete elements. Eng. Struct. 2024, 315, 118458. [Google Scholar] [CrossRef]
- González-Muñiz, A.; Díaz, I.; Cuadrado, A.; García-Pérez, D. Health indicator for machine condition monitoring built in the latent space of a deep autoencoder. Reliab. Eng. Syst. Saf. 2022, 224, 108482. [Google Scholar] [CrossRef]
- Kim, K.H.; Shim, S.; Lim, Y.; Jeon, J.; Choi, J.; Kim, B. RaPP: Novelty Detection with Reconstruction along Projection Pathway. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Bi, J.; Zhang, C. An empirical comparison on state-of-the-art multi-class imbalance learning algorithms and a new diversified ensemble learning scheme. Knowl. Based Syst. 2018, 158, 81–93. [Google Scholar] [CrossRef]
- Rezvani, S.; Wang, X. A broad review on class imbalance learning techniques. Appl. Soft Comput. 2023, 143, 110415. [Google Scholar] [CrossRef]
- Davila Delgado, J.M.; Oyedele, L. Deep learning with small datasets: Using autoencoders to address limited datasets in construction management. Appl. Soft Comput. 2021, 112, 107836. [Google Scholar] [CrossRef]
- Barrera-Animas, A.Y.; Davila Delgado, J.M. Generating real-world-like labelled synthetic datasets for construction site applications. Autom. Constr. 2023, 151, 104850. [Google Scholar] [CrossRef]
- De Oliveira, W.D.G.; Berton, L. A systematic review for class-imbalance in semi-supervised learning. Artif. Intell. Rev. 2023, 56, 2349–2382. [Google Scholar] [CrossRef]
- Akkem, Y.; Biswas, S.K.; Varanasi, A. A comprehensive review of synthetic data generation in smart farming by using variational autoencoder and generative adversarial network. Eng. Appl. Artif. Intel. 2024, 131, 107881. [Google Scholar] [CrossRef]
- Mostofi, F.; Tokdemir, O.B.; Togan, V. Generating synthetic data with variational autoencoder to address class imbalance of graph attention network prediction model for construction management. Adv. Eng. Inform. 2024, 62, 102606. [Google Scholar] [CrossRef]
- Mitchell-Heggs, R.; Prado, S.; Gava, G.P.; Go, M.A.; Schultz, S.R. Neural manifold analysis of brain circuit dynamics in health and disease. J. Comput. Neurosci. 2023, 51, 1–21. [Google Scholar] [CrossRef]
- Sun, R.; Sevillano, E.; Perera, R. Identification of intermediate debonding damage in FRP-strengthened RC beams based on a multi-objective updating approach and PZT sensors. Compos. Part B Eng. 2017, 109, 248–258. [Google Scholar] [CrossRef]
- Perera, R.; Sevillano, E.; De Diego, A.; Arteaga, A. Identification of intermediate debonding damage in FRP-plated RC beams based on multi-objective particle swarm optimization without updated baseline model. Compos. Part B Eng. 2014, 62, 205–217. [Google Scholar] [CrossRef]
- Al-Saawani, M.A.; Al-Negheimish, A.I.; El-Sayed, A.K.; Alhozaimy, A.M.A. Finite Element Modeling of Debonding Failures in FRP-Strengthened Concrete Beams Using Cohesive Zone Model. Polymers 2022, 14, 1889. [Google Scholar] [CrossRef] [PubMed]
- Ortiz, J.; Dolati, S.S.K.; Malla, P.; Nanni, A.; Mehrabi, A. FRP-Reinforced/Strengthened Concrete: State-of-the-Art Review on Durability and Mechanical Effects. Materials 2023, 16, 1990. [Google Scholar] [CrossRef] [PubMed]
- Kurata, M.; Li, X.; Fujita, K.; Yamaguchi, M. Piezoelectric dynamic strain monitoring for detecting local seismic damage in steel buildings. Smart Mater. Struct. 2013, 22, 115002. [Google Scholar] [CrossRef]
- Suzuki, A.; Liao, W.; Shibata, D.; Yoshino, Y.; Kimura, Y.; Shimoi, N. Structural Damage Detection Technique of Secondary Building Components Using Piezoelectric Sensors. Buildings 2023, 13, 2368. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Electro-mechanical impedance modeling of active material systems. J. Intell. Mater. Syst. Struct. 1994, 21, 232–252. [Google Scholar] [CrossRef]
- Perera, R.; Huerta, M.C.; Baena, M.; Barris, C. Analysis of FRP-Strengthened Reinforced Concrete Beams Using Electromechanical Impedance Technique and Digital Image Correlation System. Sensors 2023, 23, 8933. [Google Scholar] [CrossRef]
- Cohen, T.S.; Welling, M. Steerable CNNs. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Chen, Y. A tutorial on kernel density estimation and recent advances. Biost. Epidemiol. 2017, 1, 161–187. [Google Scholar] [CrossRef]
- Kim, J.; Scott, C.D. Robust kernel density estimation. J. Mach. Learn. Res. 2012, 13, 2529–2565. [Google Scholar]
- DuraAct Patch Transducers. Available online: https://www.piceramic.com/en/products/piezoceramic-actuators/patch-transducers (accessed on 31 July 2024).




| Test Number | Load Level | Test Code |
|---|---|---|
| 1 | 0 kN | 1 (Baseline) |
| 2 | 6 kN | 2 |
| 3 | 14 kN | 3 |
| 4 | 16 kN | |
| 5 | 25.6 kN | |
| 6 | 26.3 kN | 4 |
| 7 | 31.3 kN | 5 |
| 8 | 32 kN | 6 |
| 9 | 38 kN | 7 |
| 10 | 44 kN | 8 |
| 11 | 47.9 kN | |
| 12 | 53.4 kN | 9 |
| 13 | 63.8 kN | |
| 14 | 70 kN | |
| 15 | 85.5 kN | |
| 16 | 92 kN | 10 |
| 17 | 94 kN | 11 |
| Section | Layer Type | Input | Output | Activation |
|---|---|---|---|---|
| Encoder | Fully connected | 7201 | 2000 | PReLU |
| Fully connected | 2000 | 1000 | PReLU | |
| Fully connected | 1000 | 100 | PReLU | |
| Fully connected | 100 | 50 | PReLU | |
| Mean and log-variance of the latent space distribution | Fully connected | 50 | 25 (Mean) 25 (Log-variance) | |
| Decoder | Fully connected | 25 | 100 | PReLU |
| Fully connected | 100 | 1000 | PReLU | |
| Fully connected | 1000 | 2000 | PReLU | |
| Fully connected | 2000 | 7201 | PReLU |
| Section | Layer Type | Input | Output | Activation |
|---|---|---|---|---|
| Encoder | Fully connected | 7201 | 4000 | PReLU |
| Fully connected | 4000 | 100 | PReLU | |
| Fully connected | 100 | 3 | PReLU | |
| Decoder | Fully connected | 3 | 100 | PReLU |
| Fully connected | 100 | 4000 | PReLU | |
| Fully connected | 4000 | 7209 | PReLU |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montes, J.; Pérez, J.; Perera, R. Damage Indicators for Structural Monitoring of Fiber-Reinforced Polymer-Strengthened Concrete Structures Based on Manifold Invariance Defined on Latent Space of Deep Autoencoders. Appl. Sci. 2025, 15, 5897. https://doi.org/10.3390/app15115897
Montes J, Pérez J, Perera R. Damage Indicators for Structural Monitoring of Fiber-Reinforced Polymer-Strengthened Concrete Structures Based on Manifold Invariance Defined on Latent Space of Deep Autoencoders. Applied Sciences. 2025; 15(11):5897. https://doi.org/10.3390/app15115897
Chicago/Turabian StyleMontes, Javier, Juan Pérez, and Ricardo Perera. 2025. "Damage Indicators for Structural Monitoring of Fiber-Reinforced Polymer-Strengthened Concrete Structures Based on Manifold Invariance Defined on Latent Space of Deep Autoencoders" Applied Sciences 15, no. 11: 5897. https://doi.org/10.3390/app15115897
APA StyleMontes, J., Pérez, J., & Perera, R. (2025). Damage Indicators for Structural Monitoring of Fiber-Reinforced Polymer-Strengthened Concrete Structures Based on Manifold Invariance Defined on Latent Space of Deep Autoencoders. Applied Sciences, 15(11), 5897. https://doi.org/10.3390/app15115897







