Abstract
Traditional structural damage detection relies on multi-sensor arrays (e.g., total stations, accelerometers, and GNSS). However, these sensors have some inherent limitations such as high cost, limited accuracy, and environmental sensitivity. Advances in computer vision technology have driven the research on vision-based structural vibration analysis and damage identification. In this study, an optimized Lucas–Kanade optical flow algorithm is proposed, and it integrates feature point trajectory analysis with an adaptive thresholding mechanism, and improves the accuracy of the measurements through an innovative error vector filtering strategy. Comprehensive experimental validation demonstrates the performance of the algorithm in a variety of test scenarios. The method tracked MTS vibrations with 97% accuracy in a laboratory environment, and the robustness of the environment was confirmed by successful noise reduction using a dedicated noise-suppression algorithm under camera-induced interference conditions. UAV field tests show that it effectively compensates for UAV-induced motion artifacts and maintains over 90% measurement accuracy in both indoor and outdoor environments. Comparative analyses show that the proposed UAV-based method has significantly improved accuracy compared to the traditional optical flow method, providing a highly robust visual monitoring solution for structural durability assessment in complex environments.
1. Introduction
Traditional damage detection primarily involves installing sensors on the structure, such as laser ranging sensors, resistive strain sensors, and acceleration sensors. Employing these sensors incurs substantial labor costs and installation time [1,2]. Additionally, different sensor types have their own limitations. For example, they may have a limited measurement response range, and their accuracy can be affected by temperature and humidity changes. Moreover, the pre-installation wiring layout of sensors, as well as subsequent maintenance and replacement, are also expensive undertakings.
Therefore, many scholars have explored indirect non-contact measurement methods from several angles. For example, Luo et al. [3] utilized a total station to measure the vertical settlement and horizontal displacement before tunnel construction, but the application of total station was limited by the deployment points, such as a large number of equipments, e.g., cables and lighting equipment. Luo et al. [4] proposed an improved Variable Mode Decomposition (VMD) method to obtain accurate displacement trends from the initial GNSS signals. Dai et al. [5] combined the GNSS and Inertial Measurement Unit (IMU) methods and conducted simulation experiments on a shaking table using a three-antenna GNSS/IMU integrated device. However, the GNSS-based method is affected by factors such as signal strength and transmission frequency during satellite transmission, thus affecting the positioning accuracy. Some scholars have investigated the use of Laser Doppler Vibrometer (LDV) for detection. Klun et al. [6] utilized LDV to monitor hydroelectric power plant structures under dynamic conditions and determined the degree of damage of each structural component through the change of eigenfrequency. Schewe et al. [7] validated a drone-mounted LDV inspection system and successfully detected surface defects in cylindrical concrete specimens. Cosoli et al. [8] utilized LDV to scan concrete beams in order to obtain multiple test point data and detect the location of structural damage. Khun et al. [9] placed metal blocks at structural offsets and used LDV to measure the free vibration response of a building model under different offset loads to obtain the material parameters of the building model. However, the limitation of this LDV equipment is the reflection of light through the test points, which is not suitable for comprehensive measurements of large-scale structures. Yaghoubzadehfard et al. [10] scanned and obtained the modal vibration patterns of a footbridge using a device with a radar participation system (IBIS-FS). Morris et al. [11] used Ground Penetrating Radar (GPR) to survey a footbridge and successfully detected defects within the concrete. Although radar systems are suitable for non-contact, high-frequency measurements, the vibration signals are weak and prone to distortion, making accurate measurements challenging.
In recent years, computer vision-related programs and algorithms have been developing rapidly, and more and more scholars have begun to explore the intelligent recognition method that combines image processing technology with deep learning models, and the mainstream methods currently applied to vibration displacement testing include Digital Image Correlation (DIC) method, template matching method, and optical flow method. The DIC method is to process the image data and use the related processing software to calculate the displacement and deformation of the selected area of the object under test, etc. Xiao et al. [12] combined the template matching method with the sub-pixel method to realize the high-precision identification of multi-point damage of the components, and Durand-Texte et al. [13] verified a method that relies on a high-speed camera to measure the unidirectional displacement of the curved flat plate. Durand-Texte et al. [13] validated a method to measure the unidirectional displacement of a curved flat plate by a high-speed camera. Mastrodicasa et al. [14] used a low-speed camera in combination with the DIC method to perform a modal analysis of a wind turbine blade. Wang et al. [15] used DIC to analyze the crack cracking and development mechanism of a concrete beam. The template matching method works as follows: a region of the object under test is selected as a template, and each pixel point in the image is compared and calculated in turn; the higher the similarity, the higher the probability that the object is located at that position. Kimiya et al. [16] developed a camera calibration method combined with the oucc algorithm for high-frequency, large-scale structural vibration testing. Bai et al. [17] successfully eliminated the effects of camera translation and rotation by using the Zernike moments sub-pixel edge detection, the normalized cross-correlation based template matching method, and the pixel fitting method. Zhao et al. [18] designed a strain sensor based on a template-matching algorithm and proved its high accuracy in static and dynamic load tests of structures. Wu et al. [19] successfully extracted displacements and tilts of a large structure using a phase-based algorithm and a template-matching method. Hacıefendioğlu et al. [20] combined the LK optical flow method with an Autore Gressive Moving Averaging (ARMA) model. Enhanced Frequency Domain Decomposition (EFDD) validation experiments were conducted to demonstrate the reliability of the method for vibration measurements. Luan et al. [21] proposed a phase-based enhancement method to successfully track the large displacement motion of an object. Dong et al. [22] effectively eliminated the measurement errors caused by camera motion by phase subtraction based on immobile points. Zheng et al. [23] used the eigen-optical flow method to record the dynamic displacement response of transformer feature points in simulated earthquake experiments. The displacement data obtained were consistent with the sensor data. Al-Qudah and Yang [24] improved the LK optical flow method by using the second-order derivative of the Sobel operator via an algorithm.
Existing optical flow algorithms are prone to displacement calculation bias in complex scenes due to feature point mismatch and platform motion artifacts. In this study, an improved LK optical flow algorithm is proposed, which filters abnormal optical flow vectors through the angle constraint mechanism and combines with the threshold filtering strategy to improve the accuracy of displacement calculation in noisy environments. The system was validated using the MTS system, which provides stable inputs of amplitude and frequency, and helps to quantify the effect of angular constraint thresholds on the measurement error to determine the optimal parameters. The improved algorithm is further applied to vibration camera and UAV live video scenes, and the results show that the accuracy of the method is better than the traditional algorithm, which can effectively eliminate the platform vibration interference and extract more accurate displacement curves.
2. Methods Used in This Study
2.1. LK Optical Flow Method
When an observer views a moving object, the human eye’s retina captures the light from the brightness changes caused by the object’s motion. This allows the eye to track the object’s position at any given moment. In computer vision, the optical flow method leverages this principle. It tracks the position of an object moving relative to a stationary background by calculating the pixel changes in a continuous grayscale image due to the object’s movement [25,26]. The optical flow method primarily computes the velocity vectors along the x-and y-axes of the image to obtain the displacement information of the moving object. Before applying the optical flow method, certain constraints need to be established. Specifically, in a continuous grayscale image, the brightness of the moving object should remain essentially constant between two adjacent frames, and the object’s speed cannot be too high. Equation (1) can be derived from the constant brightness I of the object [27].
In the Equation (1), represent the image in which the coordinate point (x,y) has elapsed time to move the distance along the x-axis and y-axis, respectively. A Taylor series expansion of the right-hand side of the equation to first-order terms yields Equation (2), which is then brought to a simplification to yield Equation (3).
In the Equation (3), both sides of the equation are divided by , then Equation (4) can be obtained, where ==.
A window is set up with the coordinate point (x,y) as the center, and the n pixel points within the window have the same motion, combining these pixel points in Equation (4) can be expressed in a matrix as Equation (5).
In Equation (5), the two-dimensional optical flow vectors u and v can be found by applying the least squares method.
2.2. Improved Methods for the LK Optical Flow Method
When an object vibrates, it may move at a high speed, resulting in large displacements. Additionally, irregular surface reflections or changes in the distance from the light source can cause sharp brightness variations. These factors introduce computational errors in the optical flow method, leading to incorrect tracking of the object’s motion direction. As shown in Figure 1, to obtain more accurate calculation results, when the object undergoes rigid-body motion, the motion direction of each feature point is consistent and can represent the overall motion direction of the object. The motion direction of all feature points can be calculated using Formula (7), and the calculated angle is denoted as A.
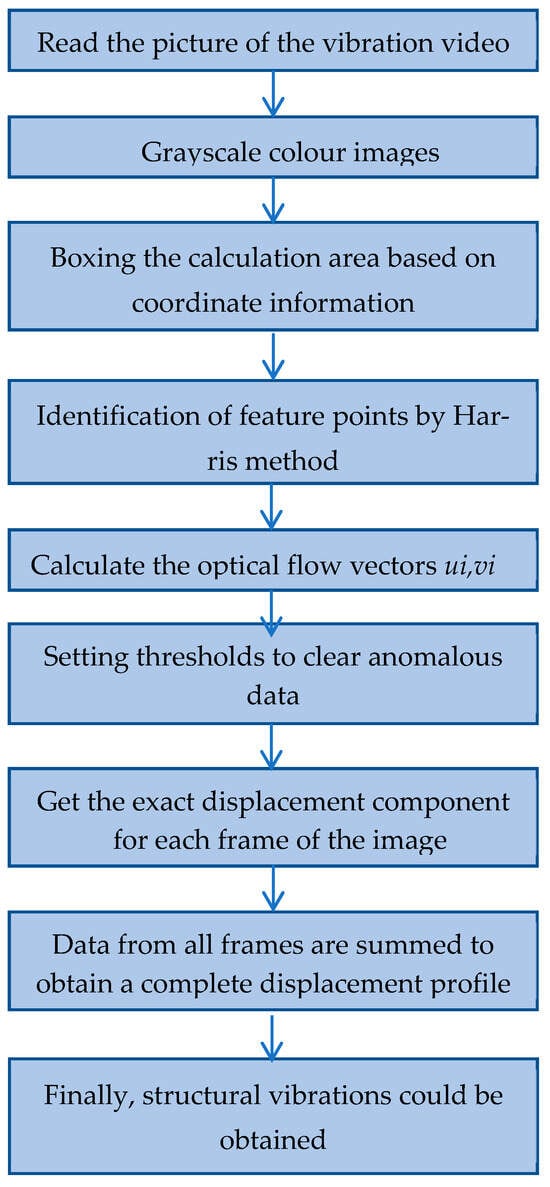
Figure 1.
Flowchart of the Enhanced Optical Flow Method for Precise Vibration Data Acquisition.
After computing the mean M and standard deviation S of the angles for all feature points, the angular deviation of each feature point from the object’s overall motion direction can be derived. The magnitude of the angular deviation |D| is then compared with the standard deviation to filter out feature points with incorrect motion directions. The threshold is mainly set as a multiple of the standard deviation. A smaller threshold can eliminate feature points with obvious errors, but an excessively large threshold might exclude accurate displacement data. Hence, the threshold setting can be adjusted by comparing the number of retained and excluded points and observing the motion trajectories and displacement lengths of each feature point plotted via the optical flow method. Averaging the data from the retained feature points generates the average motion component for the current frame. When combined with the calculation results from the previous frame, the overall displacement data of the object can be obtained. Before using in Equations (7) and (8), the program will calculate the displacement component of each pixel point through Equation (6), and substitute it into the right side of the above equation to get the value of the left side of the equation, and then substitute the calculated angle A and the average value M into Equations (9) and (10) to get the angular deviation D and standard deviation S.
2.3. Camera Shake Elimination
When a camera is recording an object vibrating outdoors, the surrounding environment can induce camera shake. As a result, the motion of the object captured in the video is a combination of the camera’s panning and flipping movements, rather than the object’s actual motion.
2.3.1. Calibrating the Camera’s Flip Motion
When the camera shakes, it may rotate along different axes. During camera rotations, the object being measured is projected onto the screen, causing the object’s shape to be distorted. Thus, to calculate the real-world displacement information of the object, the image must be corrected first. This distorted projection can be rectified using the Planar Homography Transformation Method.
Planar Homography Transformation means that when the projection of an object is mapped in two different planes, the projected images in these different planes can be transformed into one another. In the process of planar homography transformation, four stationary reference points and their pixel coordinates Xi (xi, yi) need to be found first. The image projected from the stationary reference points onto the first frame is regarded as the original image. When the lens rotates, the image projected from the stationary reference points onto the second frame is considered the image to be corrected, with its coordinates Xi’ (xi’, yi’), as depicted in Figure 2.
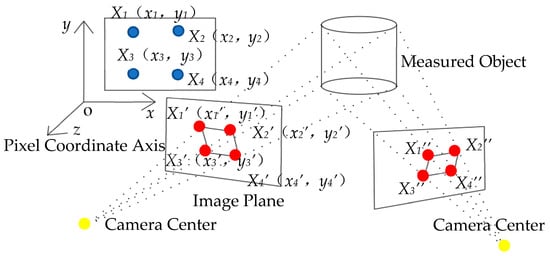
Figure 2.
Image Projections in Diverse Planes upon Camera Inversion, the blue dots are for four stationary reference points on the original image plane, the red dots are for four stationary reference points on other frames.
The second or nth frame image can be corrected to the original image by the operation of the transformation matrix, which is calculated as shown in Equation (11).
where the original image and the uncorrected stationary reference point coordinates can be obtained by the program, the transformation matrix H between the two frames is a 3 × 3 matrix, and one of the unknowns in the H matrix is converted to 1, which in fact only needs to be solved for eight unknowns, which can be solved by the least squares method.
2.3.2. Scale Factor Calculation
After correcting the image, the pixel coordinates of the current frame are converted to real world coordinates by a scale factor , which means the ratio of the actual size of the object L, to the recognized size of the object in the image [28], as in Equation (12) is shown.
2.3.3. Eliminate Camera Panning Motion
When the camera moves translationally in a plane, the true displacement of the object can be derived by subtracting the displacement of the stationary reference. As illustrated in Figure 3, the displacement of the stationary reference can be determined by tracking the movement of the stationary reference point in the video. Let the motion displacement of the object without eliminating camera shake be x0, the motion displacement of camera shake be xd, and the motion displacement of the object after eliminating camera shake be xr [29]. The elimination methods are presented in Equation (13).

Figure 3.
Selection of a Stationary Reference Point to Mitigate and Eliminate Camera Shake Effects.
Figure 4 shows the computational process of obtaining the real displacement from the drone video, the bridge vibration video captured by the drone is grayed out, the pixel coordinates of the reference point and the test point are tracked simultaneously by the improved optical flow method described above. Then images are established to correspond to the mono clinic relationship, and the computed transformation matrix is used for calibration, and after the image plane is calibrated, the drone’s own movement is filtered through the static reference points of the trajectory. The final result is the true displacement of the test point.
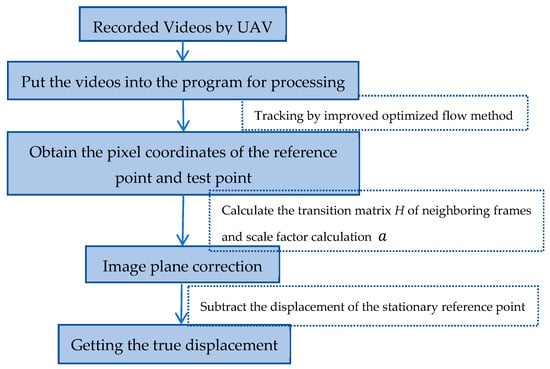
Figure 4.
The computational process of obtaining the real displacement from the drone video.
3. Experiments and Results
3.1. Experimental Setup
To test the effectiveness of the improved method based on the traditional optical flow method and the accuracy of the data obtained in practical applications, an experiment is carried out. The experiment involves measuring the simulated vibration of an MTS hydraulic piston and comparing the vibration displacement data calculated by the traditional optical flow method and its improved program with the actual data output from the experiment, aiming to test the optimization effect of the improved method.
The experimental equipment setup is shown in Figure 5. The camera was placed directly in front of the MTS hydraulic press by using a tripod with the aim of capturing the vibration video at the correct camera angle and position. The MTS hydraulic press was connected to a computer terminal and first, the relevant parameters were set. A simple sinusoidal form of motion is set up by the computer to adjust the different frequencies and amplitudes of vibration required. After start-up, the machine can run stably for a long time. The video recorded by the camera has a resolution of 1920 × 1080 and a frame rate of 30 fps. The captured vibration video is then fed into the computer for processing, and the MATLAB (2024) program detects the characteristic points of the vibration video captured by the camera using the Harris angle detection function. Finally, the displacement increments in the x-axis and y-axis directions for two adjacent frames are output by a program that calculates the equations using the optical flow method, and the results for all frames are summed.

Figure 5.
Layout of the experimental equipment.
Method Validation
In order to verify the improved method developed based on the conventional optical flow method, a MATLAB program is written in accordance with the principle of this improved method. When calculating the optical flow between each pair of adjacent frames, for each feature corner point, the increment dx along the x-axis and the increment dy along the y-axis are computed. Then, the above Formula (7) is applied to determine the corresponding included angle. Feature points with an included angle smaller than the set threshold are removed. The thresholds are set with the standard deviation σ, which is calculated from the arrow angles of all detected feature corner points, as a common factor. Specifically, the thresholds are set as 1×σ, 0.5×σ, and 0.3×σ respectively. The feature corner points eliminated by setting these different thresholds are illustrated in Figure 6.

Figure 6.
The motion trajectories of the detected feature points are represented by arrows. Red arrows signify that the coordinate points at the starting ends of these arrows are the retained feature points, while blue arrows indicate that the coordinate points at the starting ends of their arrows are the eliminated feature points. (a) Shows all the detected feature points along with their corresponding arrows. (b) Displays all the detected feature points whose angles are smaller than the threshold of 1×σ, together with their arrows. (c) Presents all the detected feature point arrows for which the angles are less than the threshold value of 0.5×σ. (d) Illustrates all the detected feature point arrows with angles smaller than the threshold value of 0.3×σ.
In Figure 6, a total of 223 feature angular points are detected. Table 1 presents all the retained feature points and the number of deleted ones when different thresholds are set. The data in the table indicate that when the threshold is set relatively large, fewer feature points with insufficient accuracy are removed. Conversely, as the threshold is set smaller, more angular feature points are eliminated, and the removal effect is more significant. This results in retaining more feature points for which the computed data are more accurate [30].

Table 1.
Quantities of Retained and Removed Feature Corners Under Different Threshold Values.
3.2. Results
3.2.1. No Noise Condition
The experimental setup for the vibration testing of the MTS hydraulic system adopted a sine wave form. The amplitude was set at 10 mm, and the frequencies were set to 0.5 Hz and 1.5 Hz, respectively. The displacement curves of the objects were derived using MATLAB programs implementing both the traditional optical flow method and the improved method. These curves were then compared with the displacement curves output by the MTS. The test results for the vibration at a frequency of 0.5 Hz are depicted in Figure 7. The calculated data show a high degree of synchronization with the real position at each instant. Among them, the displacement curve with a threshold of 0.3×σ is the closest to the displacement curve output by the MTS, yielding the most accurate results, especially in the vicinity of the peak where the comparison is more pronounced.
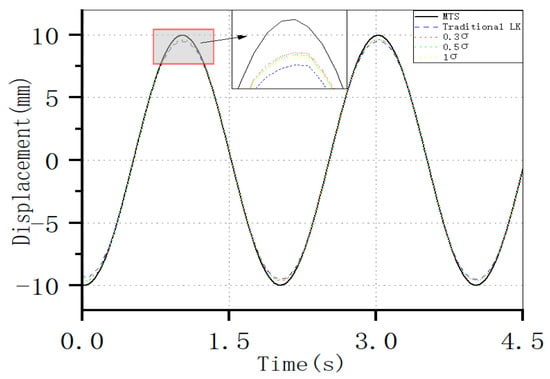
Figure 7.
Comparison between the Data Calculated by the Optical Flow Method Before and After Improvement and the Curve of the MTS Output (at 0.5 Hz).
As illustrated in Figure 7, the main computational error is concentrated in the peak region. The region of interest was defined as centered around the peak point, with a range spanning five frames of the picture before and after the peak as the area for calculating the average accuracy.
The Normalized cross-correlation (NCC) method was used to calculate accuracy between two vibrations. And the how to calculate the NCC is shown in Equation (14). The accuracy for the vibration curve at different regions with a frequency of 0.5 Hz are presented in Table 2. The accuracy of the region of interest stabilizes at approximately 97.0% by using the proposed Improved LK Method, comparing with accuracy at 96% by using the traditional LK Method.
where f is displacement value of the first vibration; is the mean of the first vibration; t is displacement value of the second vibration; is the mean of the second vibration.

Table 2.
Accuracy Comparison of Region of Interest Computation: Traditional LK Method vs. Improved LK Method with a Threshold of 0.3×σ (at 0.5 Hz).
In the vibration test with a frequency of 0.5 Hz, the average error of the calculation results for all frames is 2.0%. The distribution of the calculation errors for all consecutive frames is shown in Figure 8. Here, the errors are mainly concentrated at the peak positions. The distribution pattern of the calculation errors of the improved method is roughly the same as that of the traditional LK method.
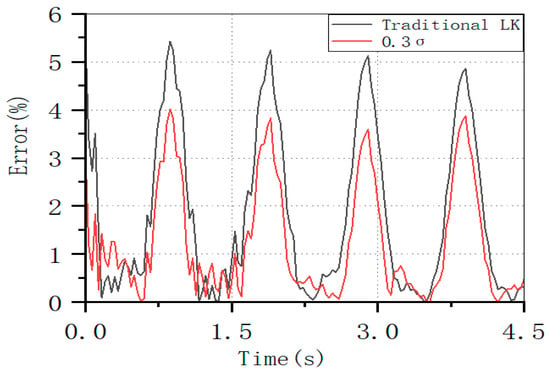
Figure 8.
Comparison of Data Errors Calculated by the Optical Flow Method at Each Temporal Moment: Before and After the Improvement (at 0.5 Hz).
The test results for the vibration at a frequency of 1.5 Hz are presented in Figure 9. The overall waveform of the displacement curve obtained by the improved method generally aligns well with the actual displacement curve output by the MTS machine. Based on the assumptions of the optical flow method, it can be inferred that the object moves faster at 1.5 Hz compared to 0.5 Hz. Moreover, the motion displacement of the object in each frame is greater at 1.5 Hz. As a result, the optical flow method calculation produces larger errors, and these errors are mainly concentrated in the vicinity of the peak values.
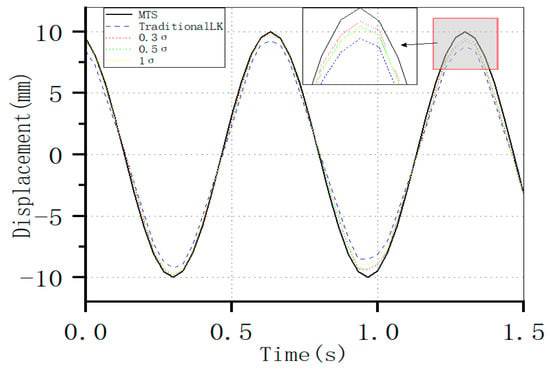
Figure 9.
Comparison between the Data Calculated by the Optical Flow Method Before and After Improvement and the Curves Output by MTS (at 1.5 Hz).
The calculation results of the accuracy of the region of interest for the vibration curve with a frequency of 1.5 Hz are shown in Table 3. The accuracy remains stable at 97.0%, which is much higher than that using the traditional LK method. The average error of the calculation results across all frames is 2.0%.

Table 3.
Accuracy Comparison of Region of Interest Computation: Traditional LK Method versus Improved LK Method with a Threshold of 0.3×σ (at 1.5 Hz).
3.2.2. Noise Condition
To verify the applicability of the improved optical flow method under non-laboratory noisy conditions, vibration was artificially introduced to the fixed camera during the recording of the vibration video [31,32]. Then, in combination with the camera vibration elimination method proposed in this study, comparative experiments were conducted before and after noise removal. The relevant experimental set-ups were the same as those described above. The vibrations of the camera were triggered by hand. In the presence of noise, the improved program with a threshold value of 0.3×σ was used in conjunction with the noise removal method. The test results for the vibration at a frequency of 1.5 Hz are shown in Figure 10. The displacement curves obtained after noise removal using the improved method show a significant improvement in accuracy compared to those before removal. The displacement curves obtained by the improved program are much closer to the displacement curves output by the MTS. The optimization effect is particularly evident near the peak values.
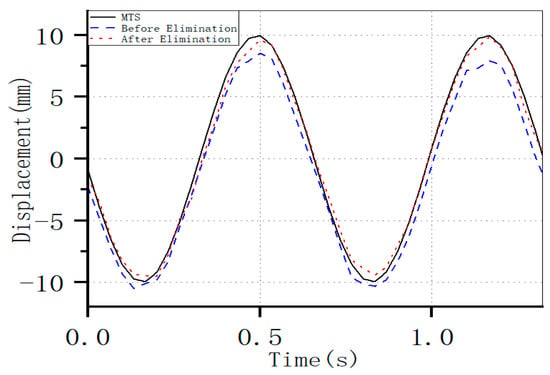
Figure 10.
Comparison of Displacement Curves Before and After Elimination with MTS Output Curves (at 1.5 Hz).
The calculation results of the accuracy of the region of interest for the vibration curve with a frequency of 1.5 Hz are shown in Table 4. Its accuracy is stabilized at 95.6%. Significantly, the data after noise elimination exhibit a substantial improvement in accuracy compared to the original calculated data, with the maximum improvement being approximately 16%.

Table 4.
Comparison of accuracy of region of interest computation (1.5 Hz) after eliminating camera vibration with the improved LK method with a threshold of 0.3×σ.
When using the improved procedure with a threshold value of 0.3×σ and the noise-elimination method for calculations, the test results for the vibration at a frequency of 3 Hz are presented in Figure 11. By applying the improved method to process the noise, it is evident that the results derived from the improved procedure exhibit the same optimization effect.
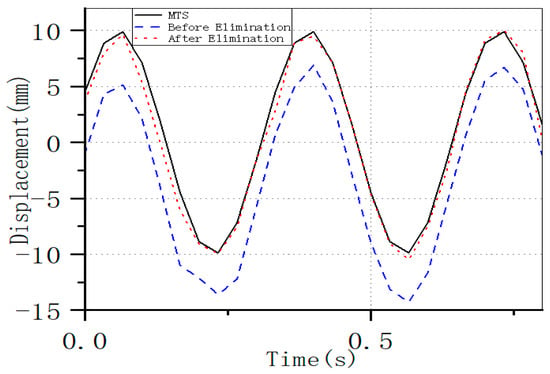
Figure 11.
Comparison of Displacement Curves Before and After Elimination with MTS Output Curves (at 3 Hz).
The calculation results of the accuracy of the region of interest for the 3 Hz frequency vibration curve are presented in Table 5. The accuracy stabilizes at 97.0%. Moreover, the accuracy of the data after noise elimination is also significantly improved, with a maximum increase of approximately 25%.

Table 5.
Comparison of accuracy of region of interest computation (3 Hz) after eliminating camera vibration with the improved LK method with a threshold of 0.3×σ.
4. UAV Experiments
4.1. UAV Experiment in Lab
When a UAV’s on-board camera is used to record video, during flight in the air, the UAV is likely to be influenced by air currents and wind, causing the fuselage to drift and shake. To verify the reliability of the improved method in removing the noise generated by the UAV, comparative experiments were carried out both before and after noise elimination. The experimental setup is illustrated in Figure 12.

Figure 12.
Set up of the UAV experiment.
The experimental configuration was as follows: The MTS hydraulic system was made to vibrate at frequencies of 0.5 Hz and 1 Hz, respectively, with the amplitude set at 10 mm. The UAV was operated, and the camera mounted on the UAV captured the vibration video at a frame rate of 30 frames per second. The experimental equipment is depicted in Figure 13.
Figure 13.
Equipment for the experiment.
The test results at a frequency of 0.5 Hz are presented in Figure 14. Owing to the instability of the UAV’s hovering flight, when the UAV moves away from the MTS, the horizontal distance between the UAV and the vibrating object increases, which leads to a relatively small amplitude of the curves from 0 to 2 s. As illustrated in Figure 15, there is an increase in the horizontal distance from the vibrating object during the movement away from the MTS. Conversely, when the UAV approaches the MTS, the horizontal distance from the vibrating object decreases, causing the amplitude of the curve to be larger in the time interval of 2 to 4 s. Through a comparison with the curves of the MTS, it can be seen that the data obtained after noise removal using the improved method are accurate.
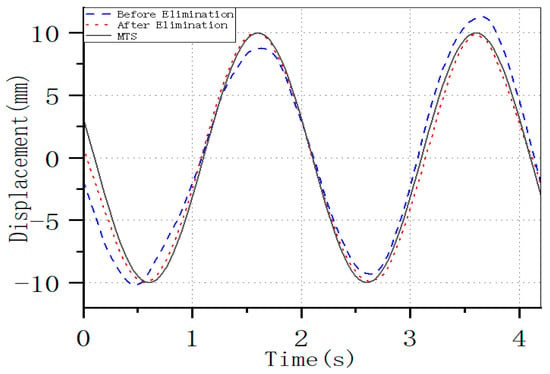
Figure 14.
Comparison of Displacement Curves Before and After Drone Noise Cancellation with MTS Output Curves (at 0.5 Hz).
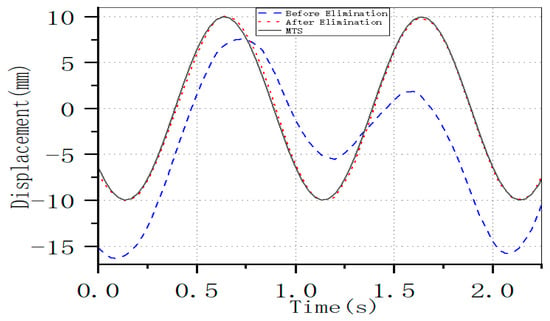
Figure 15.
Comparison of Displacement Curves Before and After Drone Noise Cancellation with MTS Output Curves (at 1 Hz).
As presented in Table 6, the accuracy prior to the elimination of the UAV’s wobble was approximately 89.9%, and after the elimination, it reached around 98.2%, marking an improvement of 8.3%.

Table 6.
Accuracy Comparison of Region of Interest Calculation for Improved LK Method After UAV Wobble Elimination (0.5 Hz).
The test results at 1 Hz are shown in Figure 12. When the horizontal distance between the UAV and the object changes significantly, the improved method is still capable of effectively eliminating the noise and yielding accurate results.
As shown in Table 7, the accuracy before eliminating drone drift was only about 44.3% and after eliminating it was about 98.3%, an improvement of 54.0%, due to the drone’s violent shaking.

Table 7.
Comparison of the accuracy of the region of interest calculation (1 Hz) for the improved LK method after eliminating UAV wobble.
4.2. UAV Experiment Outside Lab
An outdoor setup was arranged with a vibration table. On this table, a test object was firmly secured. This setup allowed for the adjustment of frequency and amplitude parameters to subject the test object to periodic reciprocating motion. As depicted in Figure 16, there were several stationary background reference points behind the vibration table. Two complementary imaging systems were employed for data collection. One was an unmanned aerial vehicle (UAV) fitted with a high-speed camera, and the other was a stationary ground-based camera placed in front of the vibration table. The vibration table produced sinusoidal vibrations at a frequency of 3 Hz and an amplitude of 10 mm. The UAV-mounted camera and the fixed camera recorded videos at frame rates of 60 fps and 30 fps, respectively.
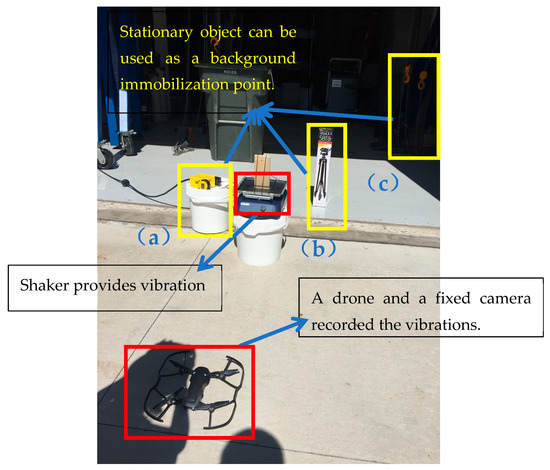
Figure 16.
Equipment layout of UAV experiment outside lab (a) Tool Bucket; (b) Cardboard Box; (c) Iron Mesh.
At the experimental site, multiple stationary objects were selected as reference targets for calculating the UAV’s trajectory. Variations in distances between these stationary objects and the measured object can lead to inaccurate results [33]. To identify the optimal stationary target, comparative analyses were conducted using different stationary objects positioned near the experimental setup.
Three stationary objects—the tool bucket (a), cardboard box (b), and iron mesh (c)—were selected for comparative analysis based on their distance relationships to the experimental setup, as illustrated in Figure 17.
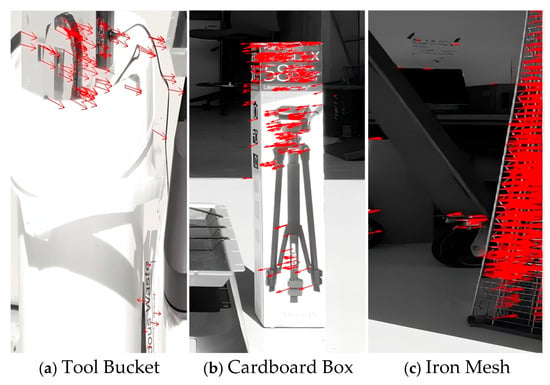
Figure 17.
Separate identification of characteristic corner points of selected stationary objects by the program.
The calculation results using the tool bucket (a) as the stationary target are presented in Figure 18. The UAV motion trajectory derived from this calculation exhibits higher accuracy, with the final displacement curve demonstrating closer alignment to the MTS output.
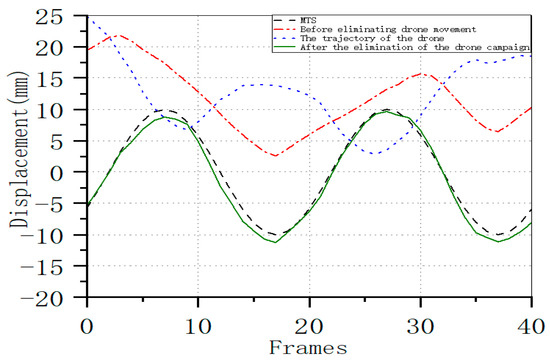
Figure 18.
Comparison of the Displacement Curve After UAV Trajectory Elimination with the MTS Output Curve, Taking the Tool Bucket (a) as the Reference (at 3 Hz).
The calculation results using the cardboard box (b) as the stationary target are presented in Figure 19. The derived UAV trajectory exhibits significant errors, because the cardboard box vibrated due to the wind. The final displacement curve shows substantial deviation from the MTS output.
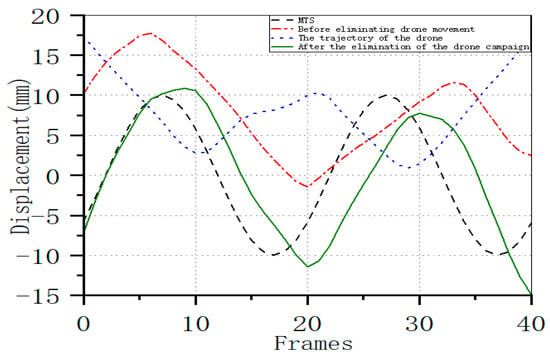
Figure 19.
Displacement Curve After Eliminating UAV Trajectory Compared with the MTS Output Curve, Using the Cardboard Box (b) as the Reference (at 3 Hz).
The calculation results using the iron mesh (c) as the stationary target are presented in Figure 20. The derived UAV trajectory exhibits the largest error, with the final displacement curve demonstrating significant deviation from the MTS output. The possible reason is that iron mesh is too dark to be detected precisely.
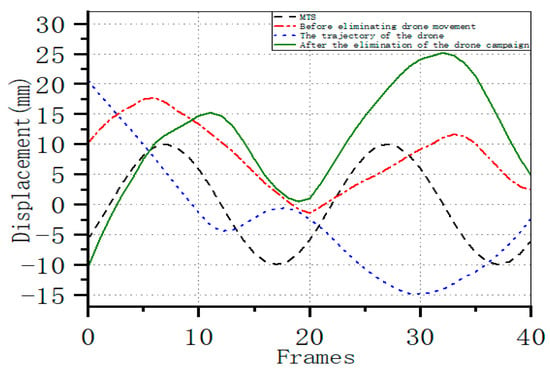
Figure 20.
Displacement Curve After Eliminating UAV Trajectory Compared with the MTS Output Curve, Taking the Iron Mesh (c) as the Reference (at 3 Hz).
As presented in Table 8, the precision of calculation results output from the improved LK method (3 Hz) after elimination of UAV trajectories with different reference points are shown.

Table 8.
Precision of calculation results output from the improved LK method (3 Hz) after elimination of UAV trajectories when different reference points are set up.
As indicated in Figure 21, the displacement curve obtained from the UAV camera, which was calculated using the tool bucket (a) as a stationary target, shows a general similarity to the curve trajectory of the stationary camera. However, there are distinct disparities at the peak points. It is also evident that the curve of the stationary camera is more in line with the curve output by the MTS.
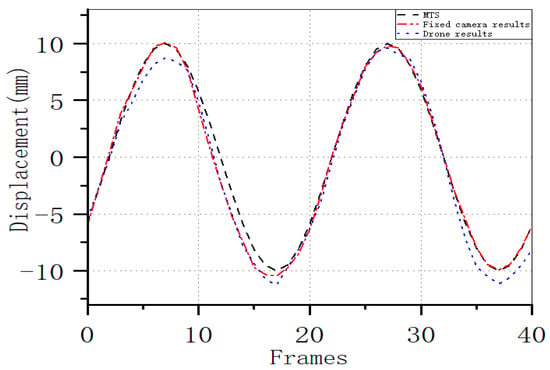
Figure 21.
Comparison of the Displacement Curves Computed by the Improved LK Method with the MTS Output Curves, Where the Displacement Curves are Derived from Data Collected by Fixed Cameras and UAV Cameras.
As shown in Table 9, in the vicinity of the peak, the calculation results of the stationary camera are more accurate, with an average accuracy of about 97.3%, and the calculation error of the UAV camera is slightly larger, with an average accuracy of about 92.9%. As presented in Table 9, within the peak regions, the computed results from the stationary camera demonstrated higher accuracy, achieving an average accuracy of approximately 97.3%. Conversely, the UAV camera’s calculation error was marginally higher, resulting in an average accuracy of approximately 92.9%.

Table 9.
Accuracy Comparison of Region of Interest Calculation for Displacement Curves Derived from the Improved LK Method Based on Fixed and UAV Camera Data.
5. Conclusions
The proposed optimized optical flow-based displacement sensor accurately detected MTS vibrations in laboratory experiments, achieving better accuracy of approximately 97% comparing with the existed optical flow-based displacement sensors. The proposed method maintained structural vibration detection accuracy exceeding 90% when utilizing UAV-recorded vibration videos. Effective compensation for six distinct UAV motions resulted in significant accuracy improvements.
- The optimized optical flow displacement sensor proposed in this work obtains more accurate vibration detection results compared to the original optical flow method.
- The proposed method effectively eliminated the motions of the UAV. In laboratory settings, when the UAV was employed along with the proposed method to measure vibrations, the resulting accuracy was satisfactory.
- The proposed method has successfully eliminated the motions of the UAV. In the field experiment, when using the UAV in conjunction with the proposed method to obtain vibration data, the achieved accuracy is satisfactory.
- In the field experiment, the accuracy of the measurement utilizing the UAV was approximately 93%, whereas the accuracy achieved with the fixed camera was 97%.Potential sources of error may be the lighting condition changes and the blurred image.
- When the proposed method is applied to eliminate the motions of the UAV, different fixed points selected in the background will give rise to varying degrees of errors. There are some ways to avoid these errors, such as fixing the reference point well, selecting reference targets with high contrast, and keeping the reference targets close to the structure.
In summary, the angle-constrained optical flow algorithm proposed in this study realizes the measurement of the motion and structural response of the UAV platform, effectively eliminates the interference of UAV vibration artifacts, and significantly improves the vibration detection accuracy. It provides a new technical path for the application of visual displacement measurement in noisy environments. The limitations of traditional vision sensors are solved, and lightweight, non-contact structural vibration monitoring is realized.
Author Contributions
Conceptualization, X.B.; Funding acquisition, N.L. and Z.Z.; Methodology, X.B., R.X. and Z.Z.; Software, X.B. and R.X.; Supervision, X.B.; Validation, X.B.; Writing—original draft, R.X.; Writing—review and editing, X.B., N.L. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key Laboratory of Architectural Cold Climate Energy Management, Ministry of Education, Jilin Jianzhu University (Grant No. JLJZHDKF022024006); Department of Housing and Urban Rural Development of Jilin Province, China (Grant No. 2023-K-29); The Eighth Batch of Jilin Province’s Youth Science and Technology Talent Support Program (Grant No. QT202412); International Science and Technology Cooperation Project of the Jilin Provincial Department of Science and Technology. (Grant No.20240402065GH).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Han, Q.; Liu, X.; Xu, J. Detection and Location of Steel Structure Surface Cracks Based on Unmanned Aerial Vehicle Images. J. Build. Eng. 2022, 50, 104098. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, Z.; Li, B. Image-based assessment of seismic damage in RC exterior beam-column joints. J. Build. Eng. 2024, 97, 110971. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, J.; Xi, W.; Zhao, P.; Li, J.; Qiao, X.; Liu, Q. Application of a Total Station with RDM to Monitor Tunnel Displacement. J. Perform. Constr. Facil. 2017, 04017030. [Google Scholar] [CrossRef]
- Luo, L.; Shan, D.; Zhang, E. Component extraction method for GNSS displacement signals of long-span bridges. J. Civ. Struct. Health Monit. 2022, 13, 591–603. [Google Scholar] [CrossRef]
- Dai, W.; Li, X.; Yu, W.; Qu, X.; Ding, X. Multi-Antenna Global Navigation Satellite System/Inertial Measurement Unit Tight Integration for Measuring Displacement and Vibration in Structural Health Monitoring. Remote Sens. 2024, 16, 1072. [Google Scholar] [CrossRef]
- Klun, M.; Zupan, D.; Lopatič, J.; Kryžanowski, A. On the Application of Laser Vibrometry to Perform Structural Health Monitoring in Non-Stationary Conditions of a Hydropower Dam. Sensors 2019, 19, 3811. [Google Scholar] [CrossRef]
- Schewe, M.; Ismail, M.A.A.; Rembe, C. Towards airborne laser Doppler vibrometry for structural health monitoring of large and curved structures. Insight 2021, 63, 280–282. [Google Scholar] [CrossRef]
- Cosoli, G.; Martarelli, M.; Mobili, A.; Tittarelli, F.; Revel, G.M. Identification of damages in a concrete beam: A modal analysis based method. J. Phys. Conf. Ser. 2024, 2698, 012014. [Google Scholar] [CrossRef]
- Khun, N.N.; Robinson, T.; Yu, T. Investigating the effect of mass redistribution on damping of building models using a shake table and a laser Doppler vibrometer. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, Civil Infrastructure, and Transportation XVI; SPIE: Bellingham, WA, USA, 2022. [Google Scholar] [CrossRef]
- Yaghoubzadehfard, A.; Lumantarna, E.; Herath, N.; Sofi, M.; Rad, M. Ensemble learning-based structural health monitoring of a bridge using an interferometric radar system. J. Civ. Struct. Health Monit. 2024, 14, 1629–1650. [Google Scholar] [CrossRef]
- Morris, I.; Abdel-Jaber, H.; Glisic, B. Quantitative Attribute Analyses with Ground Penetrating Radar for Infrastructure Assessments and Structural Health Monitoring. Sensors 2019, 19, 1637. [Google Scholar] [CrossRef]
- Xiao, P.; Wu, Z.Y.; Christenson, R.; Lobo-Aguilar, S. Development of video analytics with template matching methods for using camera as sensor and application to highway bridge structural health monitoring. J. Civ. Struct. Health Monit. 2020, 10, 405–424. [Google Scholar] [CrossRef]
- Durand-Texte, T.; Melon, M.; Simonetto, E.; Durand, S.; Moulet, M.-H. Single-camera single-axis vision method applied to measure vibrations. J. Sound Vib. 2020, 465, 115012. [Google Scholar] [CrossRef]
- Mastrodicasa, D.; Ferreira, C.; Lorenzo, E.D.; Peeters, B.; Vaz, M.A.P.; Guillaume, P. DIC using low speed cameras on a scaled wind turbine blade. In Proceedings of the 40th Conference And Exposition On Structural Dynamics (IMAC), Orlando, Fl, USA, 7–10 February 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Surahman, R.; Nagai, K. Shear cracking behavior of pre-damaged PVA-aggregate mixed ECC beams: Direct observation using DIC. Eng. Fract. Mech. 2023, 109757. [Google Scholar] [CrossRef]
- Azimbeik, K.; Mahdavi, S.H.; Rofooei, F.R. Improved image-based, full-field structural displacement measurement using template matching and camera calibration methods. Measurement 2023, 211, 112650. [Google Scholar] [CrossRef]
- Bai, X.; Yang, M.; Zhao, B. Image-Based Displacement Monitoring When Considering Translational and Rotational Camera Motions. Int. J. Civ. Eng. 2021, 20, 1–13. [Google Scholar] [CrossRef]
- Zhao, C.; Bai, B.; Liang, L.; Cheng, Z.; Chen, X.; Li, W.; Zhao, X. Design and Verification of a Novel Structural Strain Measuring Method Based on Template Matching and Microscopic Vision. Buildings 2023, 13, 2395. [Google Scholar] [CrossRef]
- Wu, Z.; Wshenton, H.; Mo, D.; Hmosze, M. Integrated video analysis framework for vision-based comparison study on structural displacement and tilt measurements. J. Struct. Eng. 2021, 147, 05021005. [Google Scholar] [CrossRef]
- Hacıefendioğlu, K.; Kahya, V.; Limongelli, M.G.; Okur, F.Y.; Altunışık, A.C.; Aslan, T.; Pembeoğlu, S.; Duman, C.; Bostan, A.; Aleit, H. Applications of optical flow methods and computer vision in structural health monitoring for enhanced modal identification. Structures 2024, 69, 107414. [Google Scholar] [CrossRef]
- Luan, L.; Zheng, J.; Wang, M.L.; Yang, Y.; Rizzo, P.; Sun, H. Extracting high-precision full-field displacement from videos via pixel matching and optical flow. J. Sound Vib. 2021, 505, 116142. [Google Scholar] [CrossRef]
- Dong, C.-Z.; Celik, O.; Catbas, F.N.; O’brien, E.J.; Taylor, S. Structural displacement monitoring using deep learning-based full field optical flow methods. Struct. Infrastruct. Eng. 2019, 16, 51–71. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.; Pan, F.; Zhou, Z.; Li, Q.; Xu, C. Research on Dynamic Structure Displacement Monitoring Based on Feature Optical Flow Method. In Proceedings of the 2021 6th International Conference on Minerals Source, Geotechnology and Civil Engineering MSGCE, Guangzhou, China, 9–11 April 2021; Available online: https://iopscience.iop.org/article/10.1088/1755-1315/768/1/012127/pdf (accessed on 11 May 2021).
- Al-Qudah, S.; Yang, M. Large Displacement Detection Using Improved Lucas–Kanade Optical Flow. Sensors 2023, 23, 3152. [Google Scholar] [CrossRef]
- Bai, Y.; Demir, A.; Yilmaz, A.; Sezen, H. Assessment and monitoring of bridges using various camera placements and structural analysis. J. Civ. Struct. Health Monit. 2023, 14, 321–337. [Google Scholar] [CrossRef]
- Ghyabi, M.; Lattanzi, D. Computer vision-based video signal fusion using deep learning architectures. J. Civ. Struct. Health Monit. 2025, 1–16. [Google Scholar] [CrossRef]
- Xin, J.; Cao, X.; Xiao, H.; Liu, T.; Liu, R.; Xin, Y. Infrared Small Target Detection Based on Multiscale Kurtosis Map Fusion and Optical Flow Method. Sensors 2023, 23, 1660. [Google Scholar] [CrossRef]
- Chen, S.-H.; Luo, Y.-P.; Liao, F.-Y. Computer vision-based displacement measurement using spatio-temporal context and optical flow considering illumination variation. J. Civ. Struct. Health Monit. 2024, 14, 1765–1783. [Google Scholar] [CrossRef]
- Nie, G.-Y.; Bodda, S.S.; Sandhu, H.K.; Han, K.; Gupta, A. Computer-Vision-Based Vibration Tracking Using a Digital Camera: A Sparse-Optical-Flow-Based Target Tracking Method. Sensors 2022, 22, 6869. [Google Scholar] [CrossRef]
- Choi, H.; Kang, B.; Kim, D. Moving Object Tracking Based on Sparse Optical Flow with Moving Window and Target Estimator. Sensors 2022, 22, 2878. [Google Scholar] [CrossRef]
- Zhao, W.; Li, W.; Fan, B.; Du, Y. Dynamic Characteristic Monitoring of Wind Turbine Structure Using Smartphone and Optical Flow Method. Buildings 2022, 12, 2021. [Google Scholar] [CrossRef]
- Chen, T.; Zhou, Z. An Improved Vision Method for Robust Monitoring of Multi-Point Dynamic Displacements with Smartphones in an Interference Environment. Sensors 2020, 20, 5929. [Google Scholar] [CrossRef]
- Bai, X.; Yang, M. UAV based accurate displacement monitoring through automatic filtering out its camera’s translations and rotations. J. Build. Eng. 2021, 44, 102992. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).